| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 6. Момент количества движения
Для
интереса рассмотрим еще одну операцию – операцию орбитального момента
количества движения. В гл. 15 мы определили оператор ![]() через
через ![]() – оператор поворота на
угол
– оператор поворота на
угол ![]() вокруг
оси
вокруг
оси ![]() .
Рассмотрим сейчас систему, описываемую всего лишь одной-единственной волновой
функцией
.
Рассмотрим сейчас систему, описываемую всего лишь одной-единственной волновой
функцией ![]() ,
которая является функцией одних только координат и не учитывает того факта, что
спин у электрона должен быть направлен либо вверх, либо вниз. Это значит, что
мы собираемся пока пренебречь внутренним моментом количества движения и
намерены думать только об орбитальной части. Чтобы подчеркнуть различие,
обозначим орбитальный оператор
,
которая является функцией одних только координат и не учитывает того факта, что
спин у электрона должен быть направлен либо вверх, либо вниз. Это значит, что
мы собираемся пока пренебречь внутренним моментом количества движения и
намерены думать только об орбитальной части. Чтобы подчеркнуть различие,
обозначим орбитальный оператор ![]() и определим его через оператор поворота
на бесконечно малый угол
и определим его через оператор поворота
на бесконечно малый угол ![]() формулой
формулой
![]()
(напоминаем:
это определение применимо только к состоянию ![]() , у которого нет внутренних спиновых
переменных, а есть только зависимость от координат
, у которого нет внутренних спиновых
переменных, а есть только зависимость от координат ![]() ). Если мы взглянем на
состояние
). Если мы взглянем на
состояние ![]() из
новой системы координат, повернутой вокруг оси
из
новой системы координат, повернутой вокруг оси ![]() на небольшой угол
на небольшой угол ![]() , то увидим новое
состояние:
, то увидим новое
состояние:
![]() .
.
Если
мы решили описывать состояние ![]() в координатном представлении, т. е.
с помощью его волновой функции
в координатном представлении, т. е.
с помощью его волновой функции ![]() , то следует ожидать такого
равенства:
, то следует ожидать такого
равенства:
![]() . (18.68)
. (18.68)
Что
же такое ![]() ?
А вот что. Точка
?
А вот что. Точка ![]() в новой системе координат (на самом
деле
в новой системе координат (на самом
деле ![]() ,
, ![]() , но мы убрали
штрихи) раньше имела координаты
, но мы убрали
штрихи) раньше имела координаты ![]() и
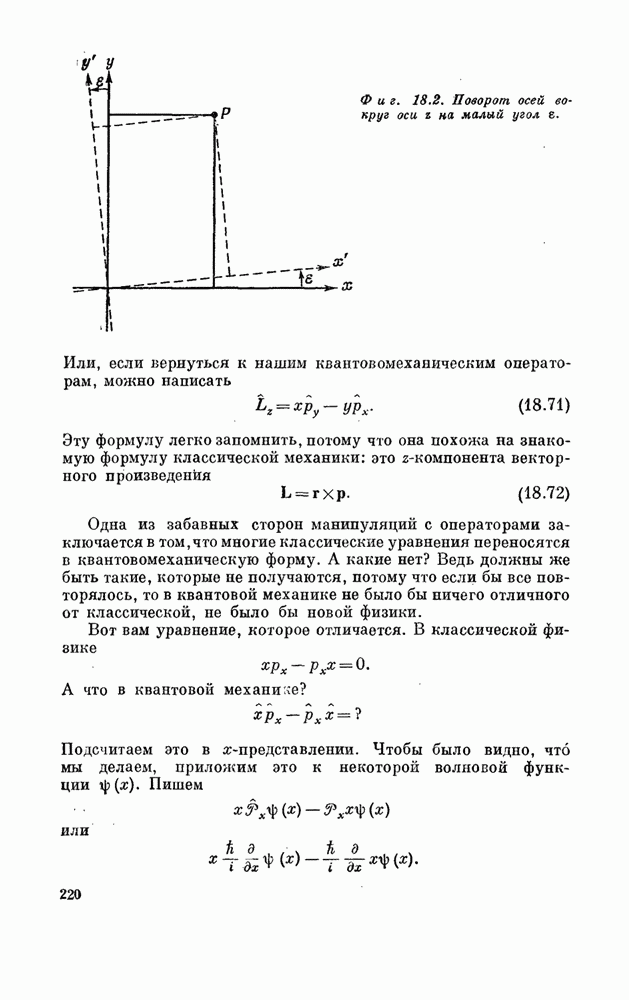
и ![]() (фиг. 18.2).Поскольку амплитуда
того, что электрон окажется в точке
(фиг. 18.2).Поскольку амплитуда
того, что электрон окажется в точке ![]() , не меняется от поворота системы
координат, то можно писать
, не меняется от поворота системы
координат, то можно писать
![]()
(напоминаем,
что ![]() –
малый угол). Это означает, что
–
малый угол). Это означает, что
![]() . (18.69)
. (18.69)
Это и есть наш ответ. Обратите, однако, внимание, что это определение эквивалентно такому:
![]() . (18.70)
. (18.70)
Или, если вернуться к нашим квантовомеханическим операторам, можно написать
![]() . (18.71)
. (18.71)
Эту
формулу легко запомнить, потому что она похожа на знакомую формулу классической
механики: это ![]() -компонента
векторного произведения
-компонента
векторного произведения
![]() . (18.72)
. (18.72)

Фиг. 18.2. Поворот осей вокруг
оси ![]() на
малый угол
на
малый угол ![]() .
.
Одна из забавных сторон манипуляций с операторами заключается в том, что многие классические уравнения переносятся в квантовомеханическую форму. А какие нет? Ведь должны же быть такие, которые не получаются, потому что если бы все повторялось, то в квантовой механике не было бы ничего отличного от классической, не было бы новой физики.
Вот вам уравнение, которое отличается. В классической физике
![]() .
.
А что в квантовой механике?
![]()
Подсчитаем
это в ![]() -представлении.
Чтобы было видно, что мы делаем, приложим это к некоторой волновой функции
-представлении.
Чтобы было видно, что мы делаем, приложим это к некоторой волновой функции ![]() . Пишем
. Пишем
![]()
или
![]() .
.
Вспомним теперь, что производные действуют на всё, что справа. Получаем
![]() . (18.73)
. (18.73)
Ответ
не нуль. Вся операция попросту равнозначна умножению на ![]() :
:
![]() . (18.74)
. (18.74)
Если бы постоянная Планка была равна нулю, то квантовые и классические результаты стали бы одинаковыми и не пришлось бы нам учить никакой квантовой механики!
Отметим,
что если два каких-то оператора ![]() и
и ![]() , взятые в сочетании
, взятые в сочетании
![]() ,
,
не
дают нуля, то мы говорим, что «операторы не перестановочны», или «операторы не
коммутируют». А уравнение наподобие (18.74) называется «перестановочным
соотношением». Вы можете сами убедиться, что перестановочное соотношение для ![]() и
и ![]() (или коммутатор
(или коммутатор ![]() и
и ![]() ) имеет вид
) имеет вид
![]() .
.
Существует еще одно очень важное перестановочное соотношение. Оно относится к моментам количества движения. Вид его таков:
![]() . (18.75)
. (18.75)
Если
вы хотите приобрести некоторый опыт работы с операторами ![]() и
и ![]() , попробуйте доказать эту
формулу сами.
, попробуйте доказать эту
формулу сами.
Интересно
заметить, что операторы, которые не коммутируют, можно встретить и в
классической физике. Мы с этим уже сталкивались, когда говорили о поворотах в
пространстве. Если вы повернете что-нибудь, например книжку, сперва на 90°
вокруг оси ![]() ,
а затем на 90° вокруг оси
,
а затем на 90° вокруг оси ![]() , то получится совсем не то, что было
бы, если бы сначала вы повернули ее на 90° вокруг оси
, то получится совсем не то, что было
бы, если бы сначала вы повернули ее на 90° вокруг оси ![]() , а после на 90° вокруг оси
, а после на 90° вокруг оси
![]() . Именно
это свойство пространства и ответственно за уравнение (18.75).
. Именно
это свойство пространства и ответственно за уравнение (18.75).
| << Предыдущий параграф | Следующий параграф >> |
- Глава 11. РАСПРОСТРАНЕНИЕ В КРИСТАЛЛИЧЕСКОЙ РЕШЕТКЕ
- § 1. Состояния электрона в одномерной решетке
- § 2. Состояния определенной энергии
- § 3. Состояния, зависящие от времени
- § 4. Электрон в трехмерной решетке
- § 5. Другие состояния в решетке
- § 6. Рассеяние на нерегулярностях решетки
- § 7. Захват нерегулярностями решетки
- § 8. Амплитуды рассеяния и связанные состояния
- Глава 12. ПОЛУПРОВОДНИКИ
- § 1. Электроны и дырки в полупроводниках
- § 2. Примесные полупроводники
- § 3. Эффект Холла
- § 4. Переходы между полупроводниками
- § 5. Выпрямление на полупроводниковом переходе
- § 6. Транзистор
- Глава 13. ПРИБЛИЖЕНИЕ НЕЗАВИСИМЫХ ЧАСТИЦ
- § 1. Спиновые волны
- § 2. Две спиновые волны
- § 3. Независимые частицы
- § 4. Молекула бензола
- § 5. Еще немного органической химии
- § 6. Другие применения приближения
- Глава 14. ЗАВИСИМОСТЬ АМПЛИТУД ОТ МЕСТА
- § 1. Как меняются амплитуды вдоль прямой
- § 2. Волновая функция
- § 3. Состояния с определенным импульсом
- § 4. Нормировка состояний с определенной координатой x
- § 5. Уравнение Шредингера
- § 6. Квантованные уровни энергии
- Глава 15. СИММЕТРИЯ И ЗАКОНЫ СОХРАНЕНИЯ
- § 1. Симметрия
- § 2. Симметрия и ее сохранение
- § 3. Законы сохранения
- § 4. Поляризованный свет
- § 5. Распад
- § 6. Сводка матриц поворота
- Глава 16. МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 1. Электрическое дипольное излучение
- § 2. Рассеяние света
- § 3. Аннигиляция позитрония
- § 4. Матрица поворота для произвольного спина
- § 5. Измерение ядерного спина
- § 6. Сложение моментов количества движения
- Глава 17. АТОМ ВОДОРОДА И ПЕРИОДИЧЕСКАЯ ТАБЛИЦА
- § 1. Уравнение Шредингера для атома водорода
- § 2. Сферически симметричные решения
- § 3. Состояния с угловой зависимостью
- § 4. Общее решение для водорода
- § 5. Волновые функции водорода
- § 6. Периодическая таблица
- Глава 18. ОПЕРАТОРЫ
- § 1. Операции и операторы
- § 2. Средние энергии
- § 3. Средняя энергия атома
- § 4. Оператор места
- § 5. Оператор импульса
- § 6. Момент количества движения
- § 7. Изменение средних со временем
- Глава 19. УРАВНЕНИЕ ШРЕДИНГЕРА В КЛАССИЧЕСКОМ КОНТЕКСТЕ. СЕМИНАР ПО СВЕРХПРОВОДИМОСТИ
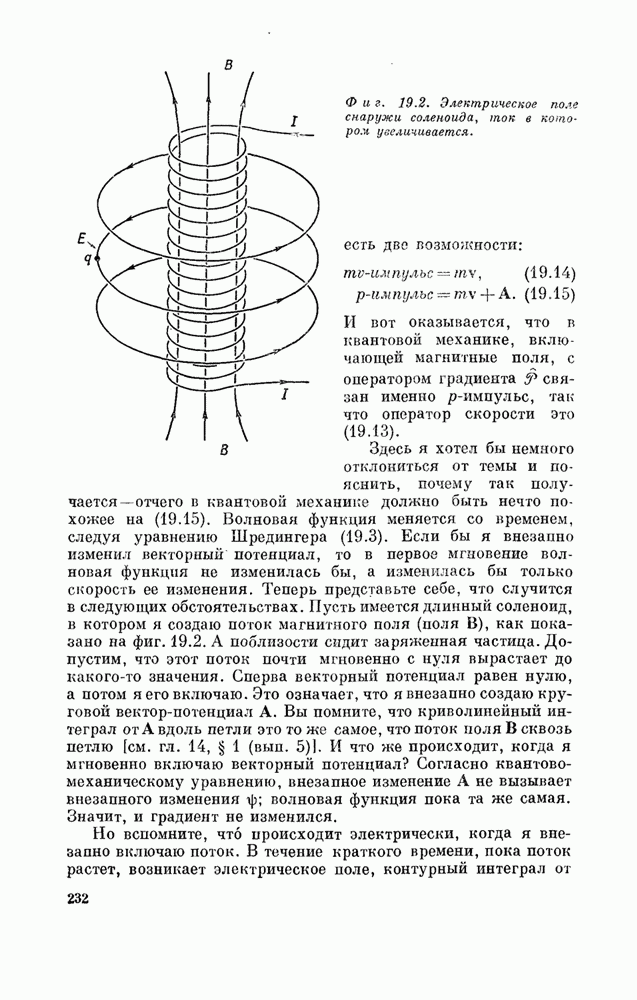
- § 1. Уравнение Шредингера в магнитном поле
- § 2. Уравнение непрерывности для вероятностей
- § 3. Два рода импульсов
- § 4. Смысл волновой функции
- § 5. Сверхпроводимость
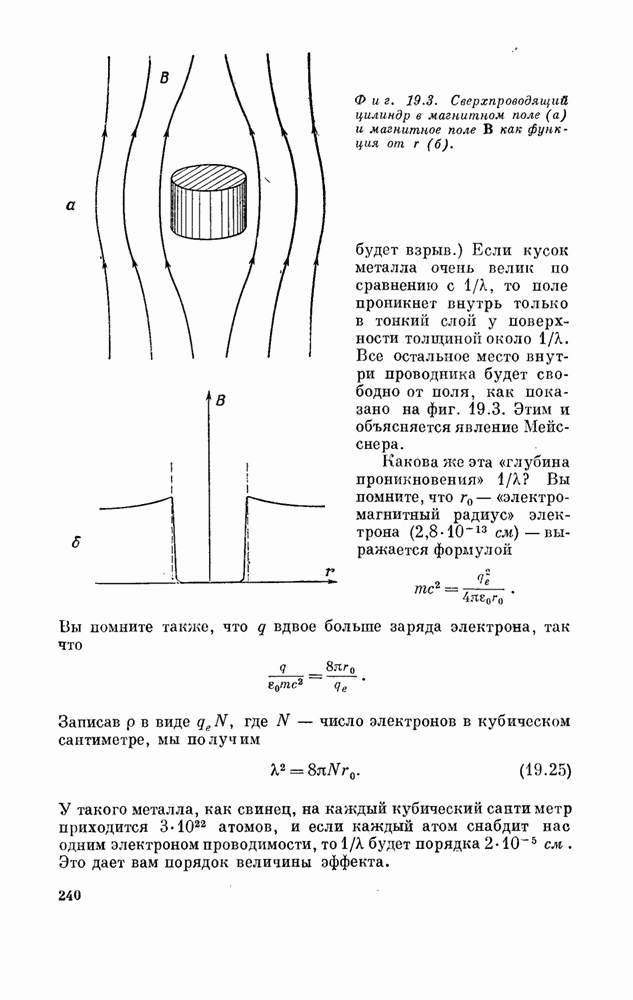
- § 6. Явление Мейсснера
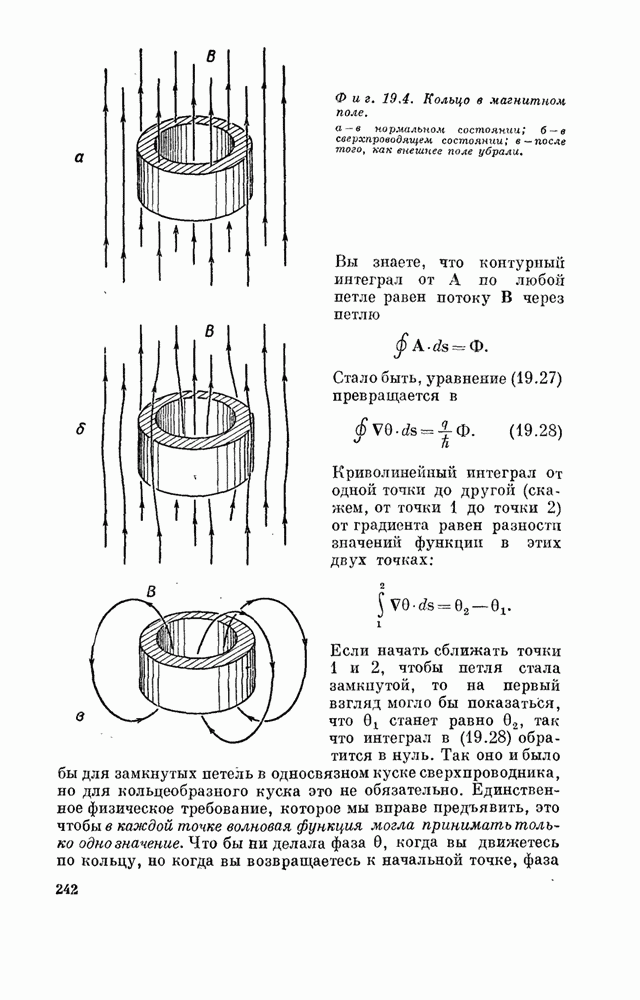
- § 7. Квантование потока
- § 8. Динамика сверхпроводимости
- § 9. Переходы Джозефсона
- Эпилог
- От редактора перевода