§ 5. Измерение ядерного спина

Продемонстрируем теперь пример, где понадобятся только что описанные коэффициенты. Он связан с проделанными не так давно интересными опытами, которые вы теперь в состоянии будете понять. Некоторым физикам захотелось узнать спин одного из возбужденных состояний ядра . Для этого они принялись бомбить углеродную мишень пучком ускоренных ионов углерода и породили нужное им возбужденное состояние  (обозначаемое ) в реакции

,

где  - это -частица, или . Кое-какие из создаваемых таким образом возбужденных состояний  неустойчивы и распадаются таким путем:

.

Значит, на опыте видны возникающие в реакции две -частицы. Обозначим их  и ; поскольку они вылетают с разными энергиями, их можно отличить друг от друга. Кроме того, выбирая , имеющие нужную энергию, мы можем отобрать любые возбужденные состояния .

Опыт ставился так, как показано на фиг. 16.9. Пучок ионов углерода с энергией 16 Мэв был направлен на углеродную пленку. Первая -частица регистрировалась кремниевым детектором, настроенным на прием -частиц с нужной энергией, движущихся вперед (по отношению к падающему пучку ионов ). Вторая -частица регистрировалась счетчиком , поставленным под углом  к . Скорость счета сигналов совпадений от  и  измерялась как функция угла .

Фиг. 16.9. Размещение приборов в опыте по определению спина возбужденных состояний .

Идея опыта в следующем. Прежде всего нужно знать, что спины ,  и -частицы все равны нулю. Назовем направление движения начальных частиц  направлением ; тогда известно, что  должен обладать нулевым моментом количества движения относительно оси . Ведь ни у одной из остальных частиц нет спина; кроме того,  прилетает вдоль оси  и  улетает вдоль оси , так что у них не может быть момента относительно этой оси. И каким бы ни был спин  ядра , мы знаем, что это ядро находится в состоянии . Что же случится, когда распадется на  и другую -частицу? Что ж, -частицу поймает счетчик , а , чтобы сохранить начальный импульс, вынужден будет уйти в противоположную сторону. Относительно новой оси (оси ) не может быть тоже никакой компоненты момента количества движения. А раз конечное состояние имеет относительно новой оси нулевой момент количества движения, то у распада  должна быть некоторая амплитуда того, что , где  - квантовое число компоненты момента количества движения относительно новой оси. Вероятность наблюдать  под углом  будет на самом деле равна квадрату амплитуды (или матричного элемента)

.                  (16.41)

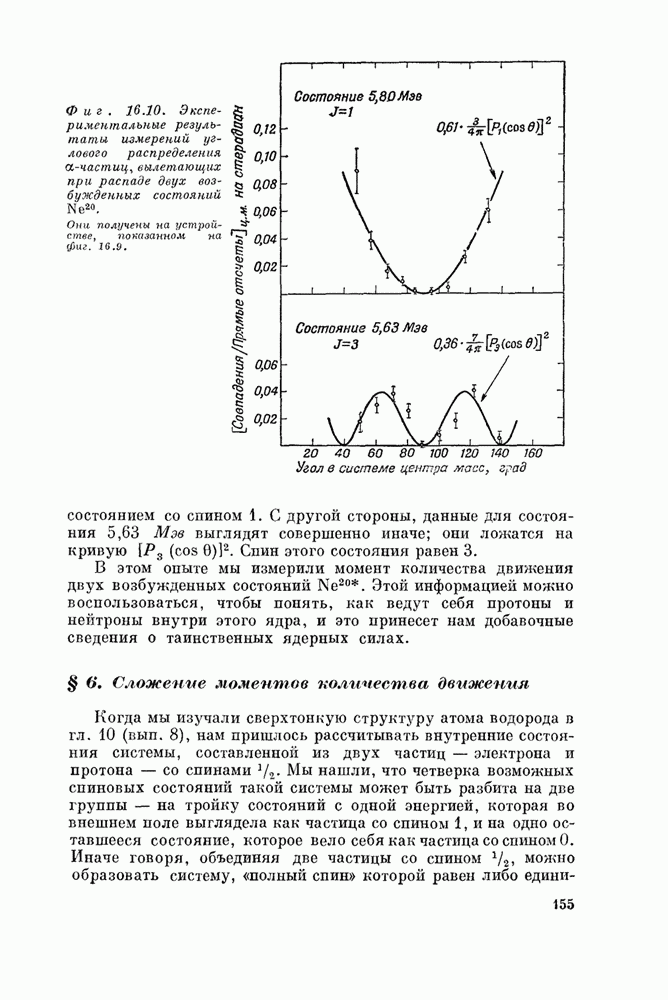
Чтобы получить спин интересующего нас состояния , вычертим интенсивность наблюдений второй -частицы как функцию угла и сравним с теоретическими кривыми для различных значений . Как мы отмечали в конце предыдущего параграфа, амплитуды  - это просто функции . Значит, угловые распределения будут следовать кривым . Экспериментальные результаты для двух возбужденных состояний показаны на фиг. 16.10. Вы видите, что угловое распределение для состояния 5,80 Мэв очень хорошо укладывается на кривую , т. е. оно должно быть состоянием со спином 1. С другой стороны, данные для состояния 5,63 Мэв выглядят совершенно иначе; они ложатся на кривую . Спин этого состояния равен 3.

Фиг. 16.10. Экспериментальные результаты измерений углового распределения -частиц, вылетающих при распаде двух возбужденных состояний .

Они получены на устройстве, показанном на фиг. 16.9.

В этом опыте мы измерили момент количества движения двух возбужденных состояний . Этой информацией можно воспользоваться, чтобы понять, как ведут себя протоны и нейтроны внутри этого ядра, и это принесет нам добавочные сведения о таинственных ядерных силах.