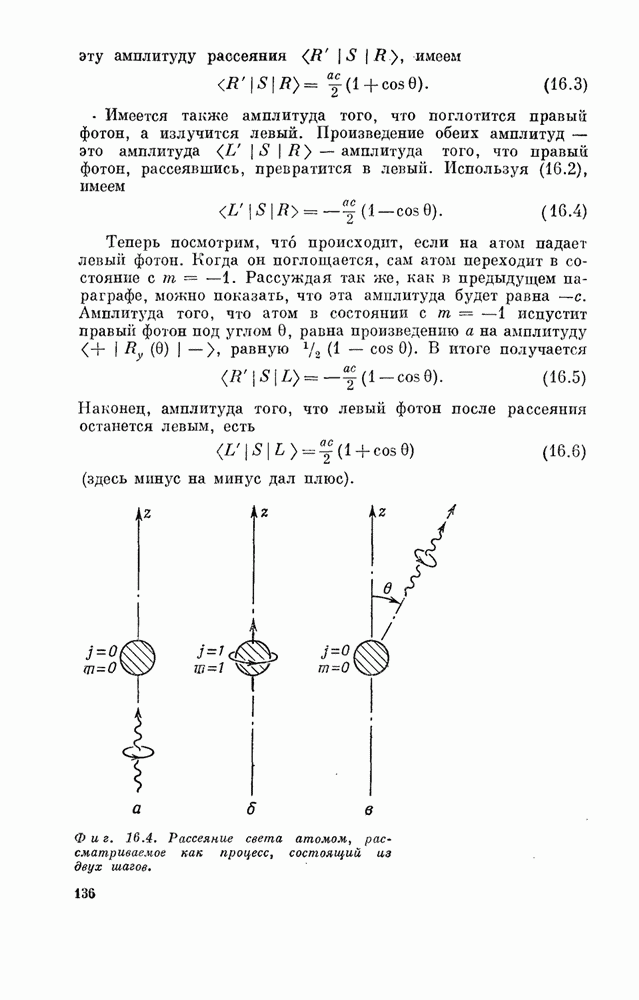
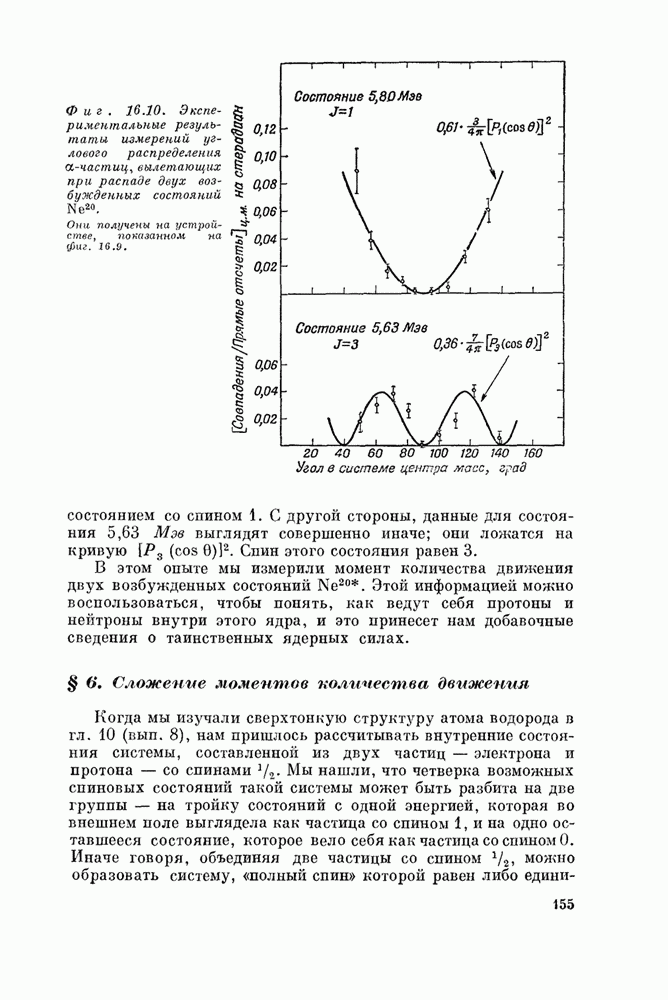
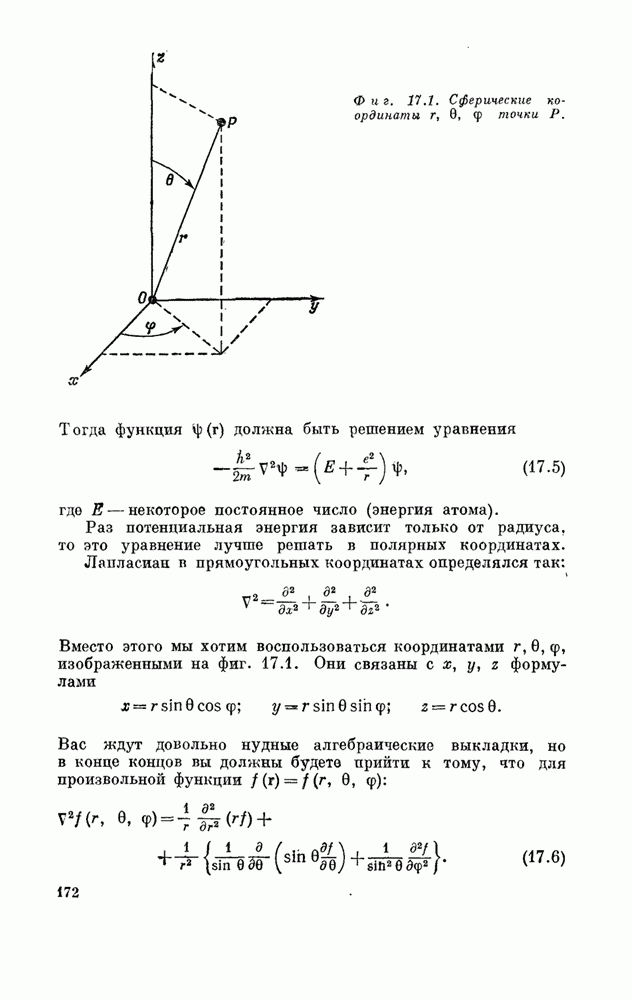
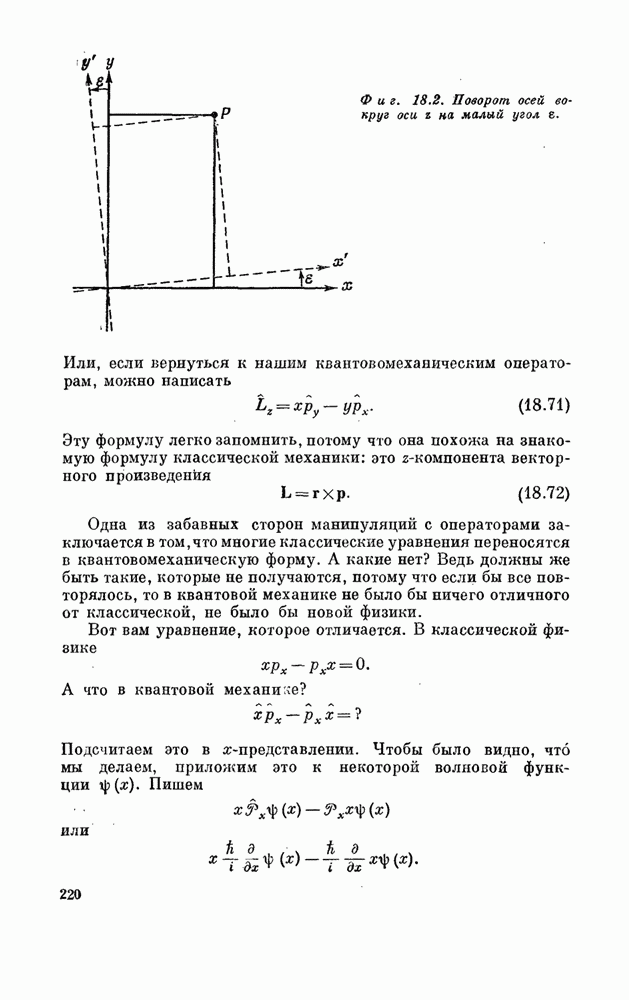
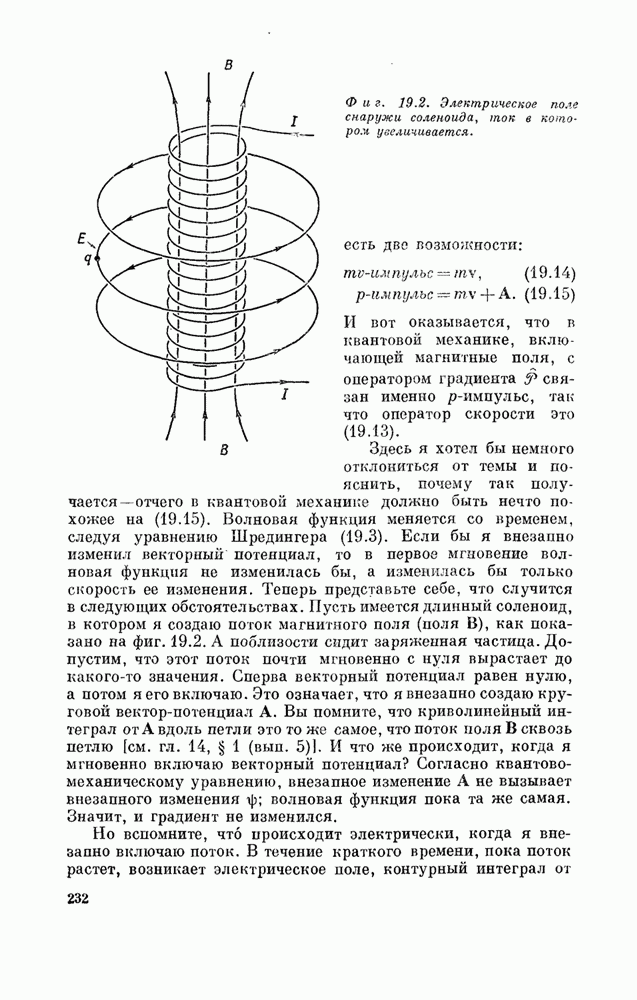
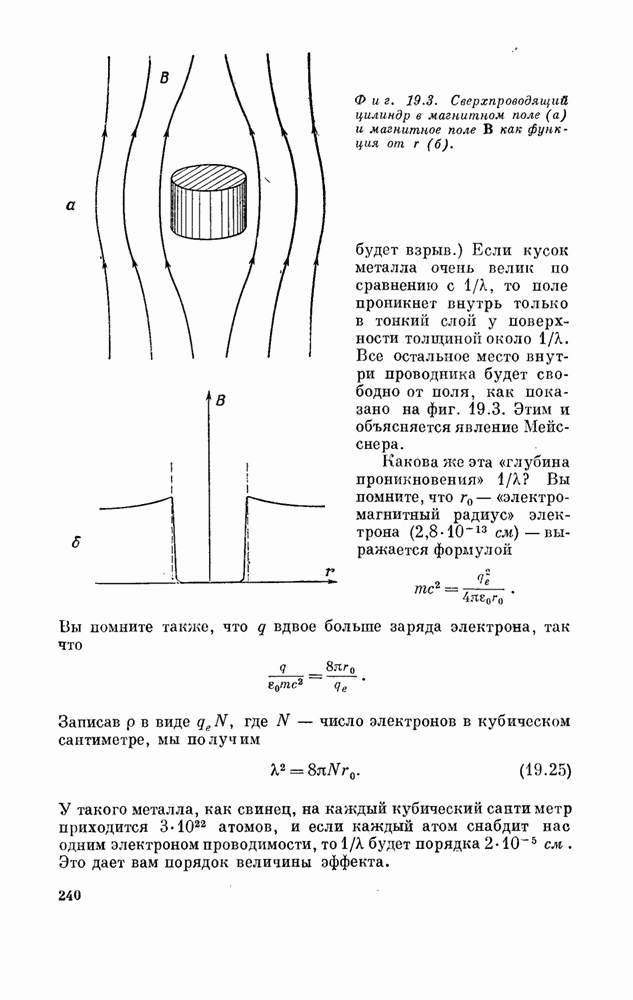
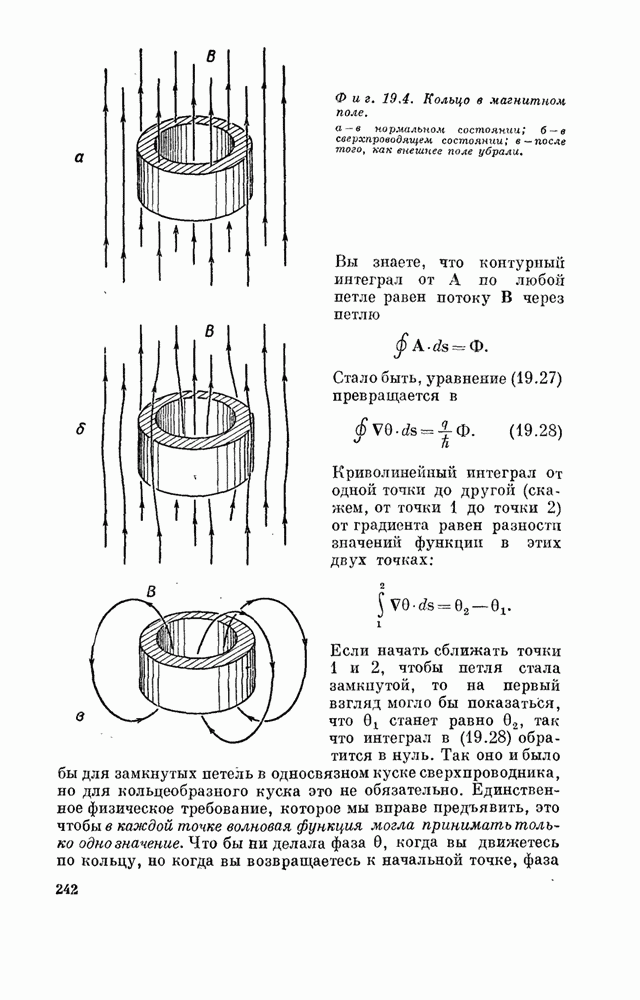
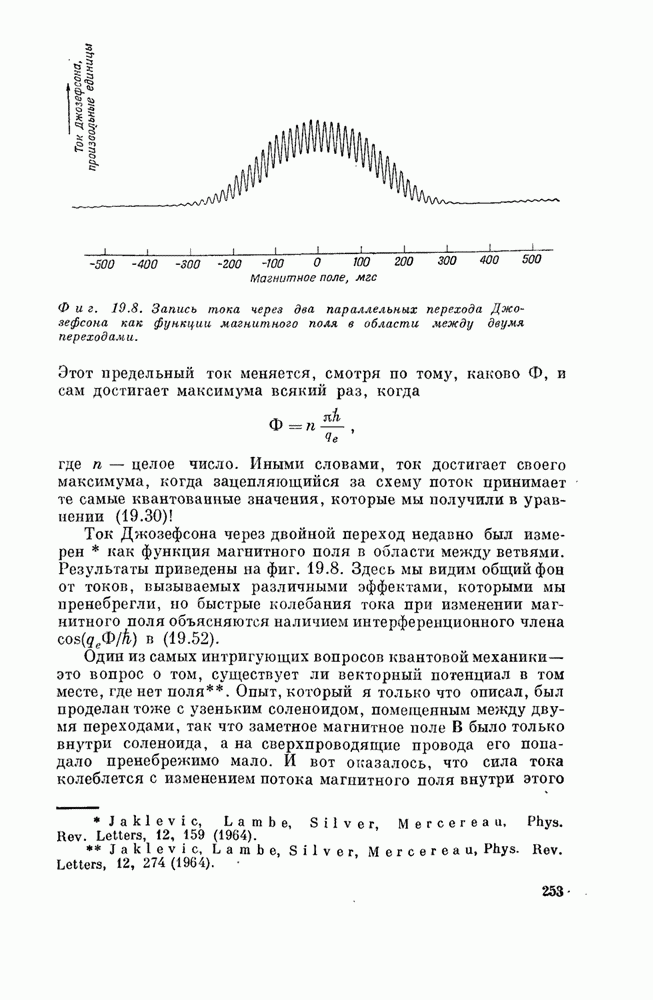
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
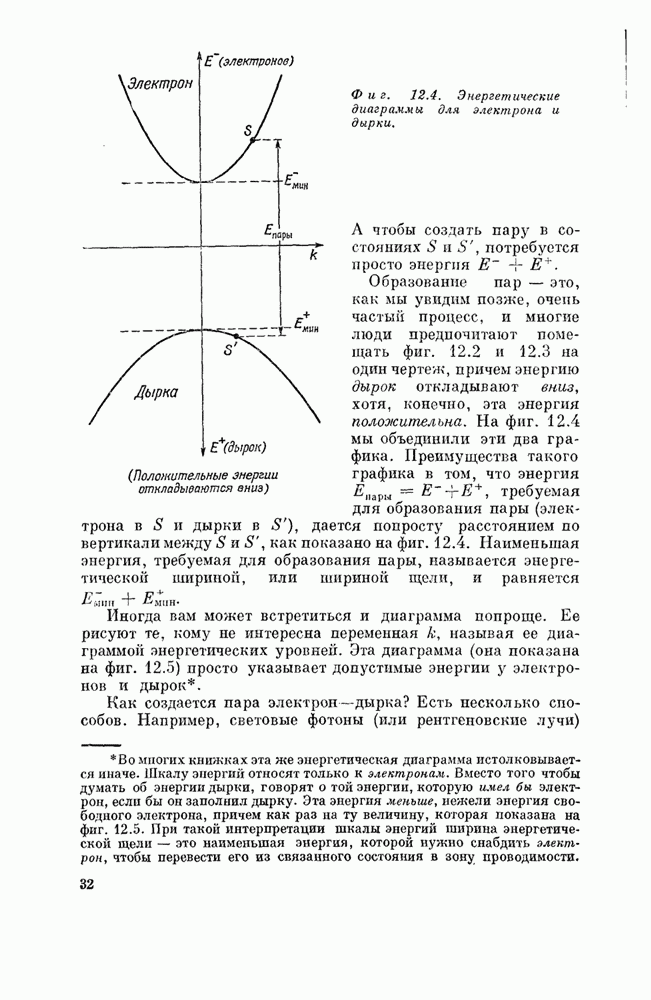
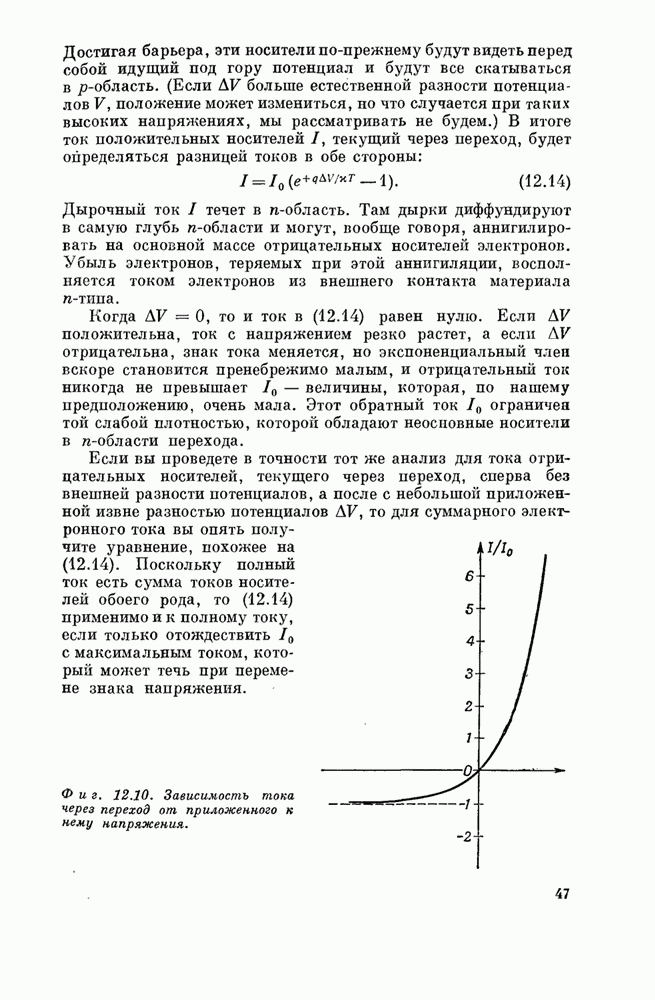
§ 4. Оператор места
Каково
среднее местоположение электрона в атоме? В данном состоянии ![]() каково среднее
значение координаты
каково среднее
значение координаты ![]() ? Разберем одномерный случай, а
обобщение на трехмерный или на системы с большим числом частиц останется на
вашу долю. Мы имеем состояние, описываемое функцией
? Разберем одномерный случай, а
обобщение на трехмерный или на системы с большим числом частиц останется на
вашу долю. Мы имеем состояние, описываемое функцией ![]() , и продолжаем раз за разом
измерять
, и продолжаем раз за разом
измерять ![]() .
Что получится в среднем? Очевидно,
.
Что получится в среднем? Очевидно, ![]() , где
, где ![]() – вероятность обнаружить электрон в
небольшом элементе длины
– вероятность обнаружить электрон в
небольшом элементе длины ![]() возле
возле ![]() . Пусть плотность вероятности
. Пусть плотность вероятности ![]() меняется с
меняется с ![]() так, как показано
на фиг. 18.1. Вероятнее всего вы обнаружите электрон где-то возле вершины
кривой. Среднее значение
так, как показано
на фиг. 18.1. Вероятнее всего вы обнаружите электрон где-то возле вершины
кривой. Среднее значение ![]() тоже придется куда-то на область
невдалеке от вершины, а точнее, как раз на центр тяжести площади, ограниченной
кривой.
тоже придется куда-то на область
невдалеке от вершины, а точнее, как раз на центр тяжести площади, ограниченной
кривой.

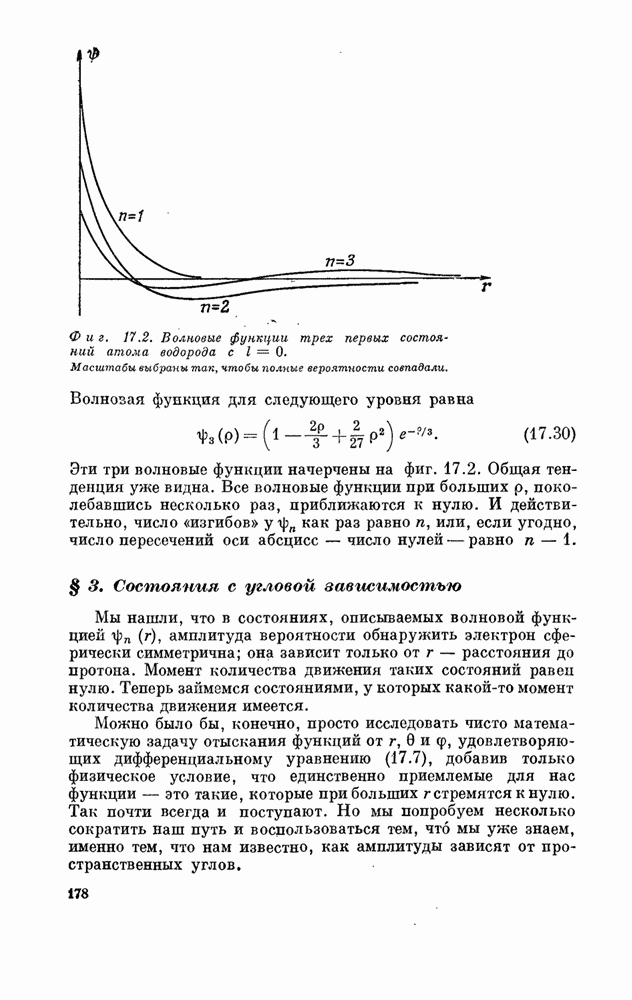
Фиг. 18.1. Кривая плотности вероятности, представляющей локализованную частицу.
Мы
видели раньше, что ![]() , значит, среднее
, значит, среднее ![]() можно записать в виде
можно записать в виде
![]() . (18.33)
. (18.33)
Наше
уравнение для ![]() имеет
тот же вид, что (18.18). Когда мы считали среднюю энергию, мы ставили между
двумя
имеет
тот же вид, что (18.18). Когда мы считали среднюю энергию, мы ставили между
двумя ![]() оператор
оператор
![]() , а
когда считаем среднее положение, ставим просто
, а
когда считаем среднее положение, ставим просто ![]() . (Если угодно, можете рассматривать
. (Если угодно, можете рассматривать ![]() как
алгебраический оператор «умножь на
как
алгебраический оператор «умножь на ![]() ».) Эту параллель можно провести еще
дальше, выразив среднее местоположение в форме, которая соответствует уравнению
(18.18). Предположим, что мы просто написали
».) Эту параллель можно провести еще
дальше, выразив среднее местоположение в форме, которая соответствует уравнению
(18.18). Предположим, что мы просто написали
![]() , (18.34)
, (18.34)
где
![]() , (18.35)
, (18.35)
и
смотрим, не удастся ли найти такой оператор ![]() , чтобы он создавал состояние
, чтобы он создавал состояние ![]() , при котором
уравнение (18.34) не противоречит уравнению (18.33). Иначе говоря, мы должны
найти такое
, при котором
уравнение (18.34) не противоречит уравнению (18.33). Иначе говоря, мы должны
найти такое ![]() ,
чтобы было
,
чтобы было
![]() . (18.36)
. (18.36)
Разложим
сперва ![]() по
по
![]() -представлению:
-представлению:
![]() . (18.37)
. (18.37)
Сравним
затем интегралы в (18.36) и (18.37). Вы видите, что в ![]() -представлении (и только в
этом представлении)
-представлении (и только в
этом представлении)
![]() . (18.38)
. (18.38)
Воздействие
на ![]() оператора
оператора
![]() для
получения
для
получения ![]() равнозначно
умножению
равнозначно
умножению ![]() на
на
![]() для
получения
для
получения ![]() .
Перед нами определение оператора
.
Перед нами определение оператора ![]() в координатном представлении.
в координатном представлении.
(Мы
не задавались целью получить ![]() -представление матрицы оператора
-представление матрицы оператора ![]() . Если вы
честолюбивы, попытайтесь показать, что
. Если вы
честолюбивы, попытайтесь показать, что
![]() . (18.39)
. (18.39)
Тогда вы сможете доказать поразительную формулу
![]() , (18.40)
, (18.40)
т.
е. что оператор ![]() обладает
интересным свойством: когда он действует на базисное состояние
обладает
интересным свойством: когда он действует на базисное состояние ![]() , то это
равнозначно умножению на
, то это
равнозначно умножению на ![]() .)
.)
А
может, вы хотите знать среднее значение ![]() ? Оно равно
? Оно равно
![]() . (18.41)
. (18.41)
Или, если желаете, можно написать и так:
![]() ,
,
где
![]() . (18.42)
. (18.42)
Под
![]() подразумевается
подразумевается
![]() – два
оператора применяются друг за другом. С помощью (18.42) можно подсчитать
– два
оператора применяются друг за другом. С помощью (18.42) можно подсчитать ![]() , пользуясь каким
угодно представлением (базисными состояниями). Если вам нужно знать среднее
значение
, пользуясь каким
угодно представлением (базисными состояниями). Если вам нужно знать среднее
значение ![]() или
любого многочлена по
или
любого многочлена по ![]() , то вы легко это теперь проделаете.
, то вы легко это теперь проделаете.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 11. РАСПРОСТРАНЕНИЕ В КРИСТАЛЛИЧЕСКОЙ РЕШЕТКЕ
- § 1. Состояния электрона в одномерной решетке
- § 2. Состояния определенной энергии
- § 3. Состояния, зависящие от времени
- § 4. Электрон в трехмерной решетке
- § 5. Другие состояния в решетке
- § 6. Рассеяние на нерегулярностях решетки
- § 7. Захват нерегулярностями решетки
- § 8. Амплитуды рассеяния и связанные состояния
- Глава 12. ПОЛУПРОВОДНИКИ
- § 1. Электроны и дырки в полупроводниках
- § 2. Примесные полупроводники
- § 3. Эффект Холла
- § 4. Переходы между полупроводниками
- § 5. Выпрямление на полупроводниковом переходе
- § 6. Транзистор
- Глава 13. ПРИБЛИЖЕНИЕ НЕЗАВИСИМЫХ ЧАСТИЦ
- § 1. Спиновые волны
- § 2. Две спиновые волны
- § 3. Независимые частицы
- § 4. Молекула бензола
- § 5. Еще немного органической химии
- § 6. Другие применения приближения
- Глава 14. ЗАВИСИМОСТЬ АМПЛИТУД ОТ МЕСТА
- § 1. Как меняются амплитуды вдоль прямой
- § 2. Волновая функция
- § 3. Состояния с определенным импульсом
- § 4. Нормировка состояний с определенной координатой x
- § 5. Уравнение Шредингера
- § 6. Квантованные уровни энергии
- Глава 15. СИММЕТРИЯ И ЗАКОНЫ СОХРАНЕНИЯ
- § 1. Симметрия
- § 2. Симметрия и ее сохранение
- § 3. Законы сохранения
- § 4. Поляризованный свет
- § 5. Распад
- § 6. Сводка матриц поворота
- Глава 16. МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 1. Электрическое дипольное излучение
- § 2. Рассеяние света
- § 3. Аннигиляция позитрония
- § 4. Матрица поворота для произвольного спина
- § 5. Измерение ядерного спина
- § 6. Сложение моментов количества движения
- Глава 17. АТОМ ВОДОРОДА И ПЕРИОДИЧЕСКАЯ ТАБЛИЦА
- § 1. Уравнение Шредингера для атома водорода
- § 2. Сферически симметричные решения
- § 3. Состояния с угловой зависимостью
- § 4. Общее решение для водорода
- § 5. Волновые функции водорода
- § 6. Периодическая таблица
- Глава 18. ОПЕРАТОРЫ
- § 1. Операции и операторы
- § 2. Средние энергии
- § 3. Средняя энергия атома
- § 4. Оператор места
- § 5. Оператор импульса
- § 6. Момент количества движения
- § 7. Изменение средних со временем
- Глава 19. УРАВНЕНИЕ ШРЕДИНГЕРА В КЛАССИЧЕСКОМ КОНТЕКСТЕ. СЕМИНАР ПО СВЕРХПРОВОДИМОСТИ
- § 1. Уравнение Шредингера в магнитном поле
- § 2. Уравнение непрерывности для вероятностей
- § 3. Два рода импульсов
- § 4. Смысл волновой функции
- § 5. Сверхпроводимость
- § 6. Явление Мейсснера
- § 7. Квантование потока
- § 8. Динамика сверхпроводимости
- § 9. Переходы Джозефсона
- Эпилог
- От редактора перевода