| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.12. ОПЕРАЦИОННЫЕ СХЕМЫ
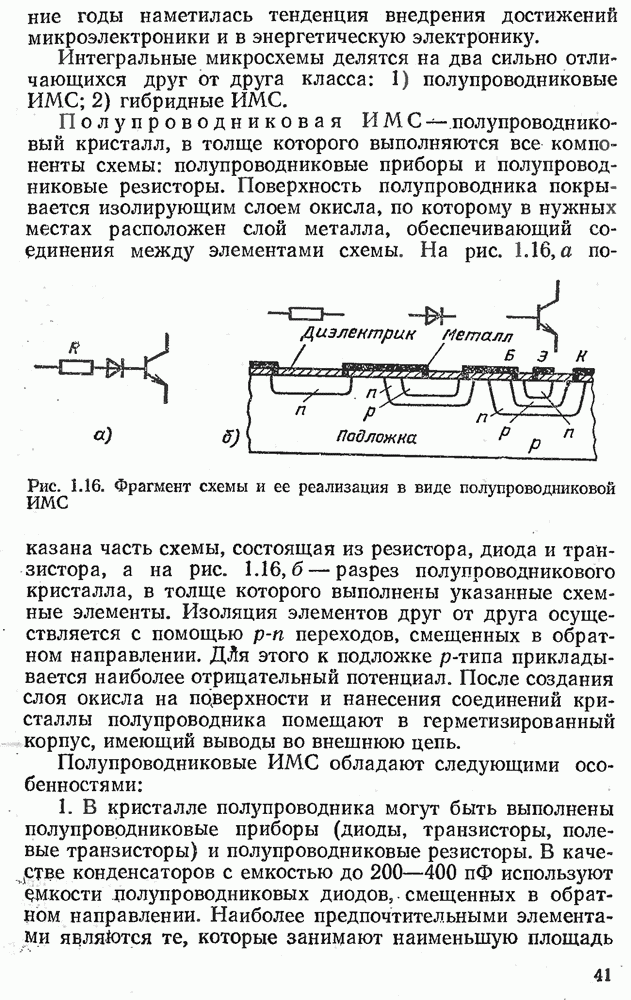
На ОУ создаются схемы, предназначенные для выполнения математических операций над входными сигналами (сложение, вычитание, интегрирование, выделение модуля функции и т.п.). Такие схемы находят широкое применение в устройствах автоматического управления, они составляют основу аналоговых ЭВМ. Наиболее распространенными являются суммирующие и интегрирующие схемы на ОУ, а также ряд схем, в которых ОУ используется в нелинейном режиме (эти схемы рассмотрены в гл. 3).
На рис. 2.21, а приведена схема инвертирующего сумматора. Она собрана на базе ОУ с инвертирующим входом и цепью параллельной ООС (см. § 2.11). Поскольку  ОУ велико,
ОУ велико,

Как и в схеме рис.  Входные токи определяются с учетом того, что между входами ИМС ОУ напряжение равно нулю:
Входные токи определяются с учетом того, что между входами ИМС ОУ напряжение равно нулю:  .
.

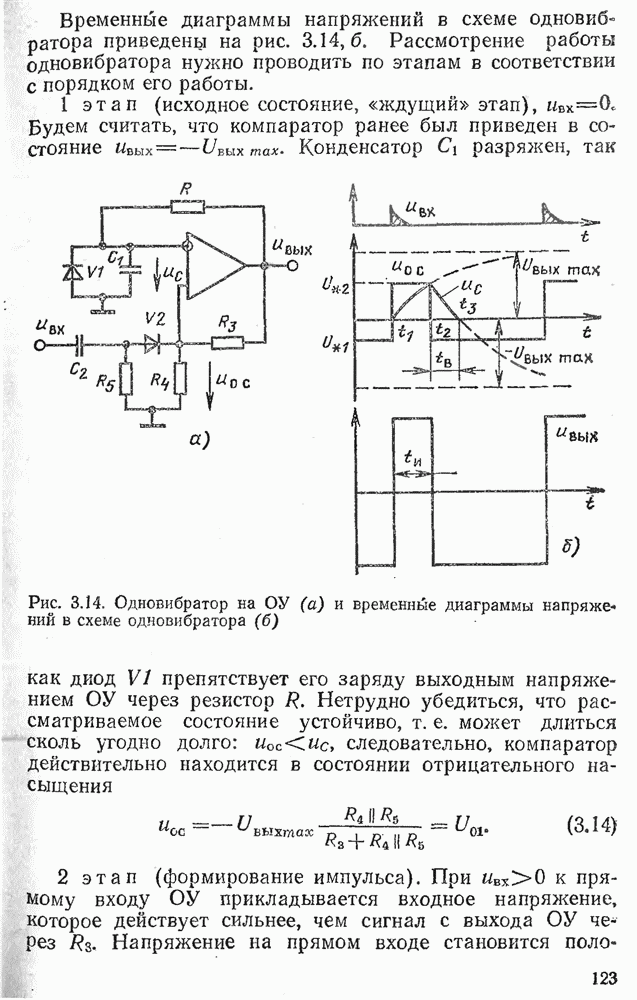
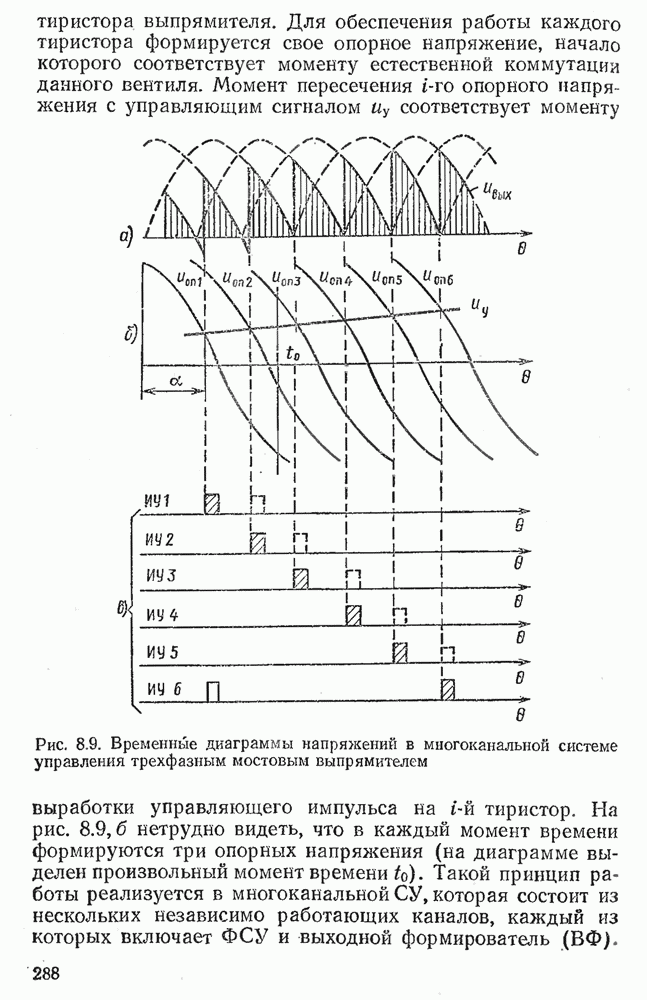
Рис. 2.21. Инвертирующий сумматор на ОУ (а) и временные диаграммы сигналов на его входах и выходе (б)
Тогда из (2.28) следует

отсюда

Знак минус показывает, что наряду с суммированием происходит инвертирование полярности сигналов. На рис.  приведены временные диаграммы, иллюстрирующие работу инвертирующего сумматора.
приведены временные диаграммы, иллюстрирующие работу инвертирующего сумматора.
На рис. 2.22, а приведена схема неинвертирующего сумматора. В основе этой схемы лежит неинвертирующий ОУ с ОС (см. рис. 2.18, а). Выделим названную схему и заменим ее схемой замещения, содержащей  и источник напряжения
и источник напряжения  (выходное сопротивление равно нулю) (рис.
(выходное сопротивление равно нулю) (рис.  ). Так как
). Так как  , то
, то  или по закону Ома
или по закону Ома

Отсюда

где  - число входов сумматора (в рассматриваемой схеме
- число входов сумматора (в рассматриваемой схеме  ).
).

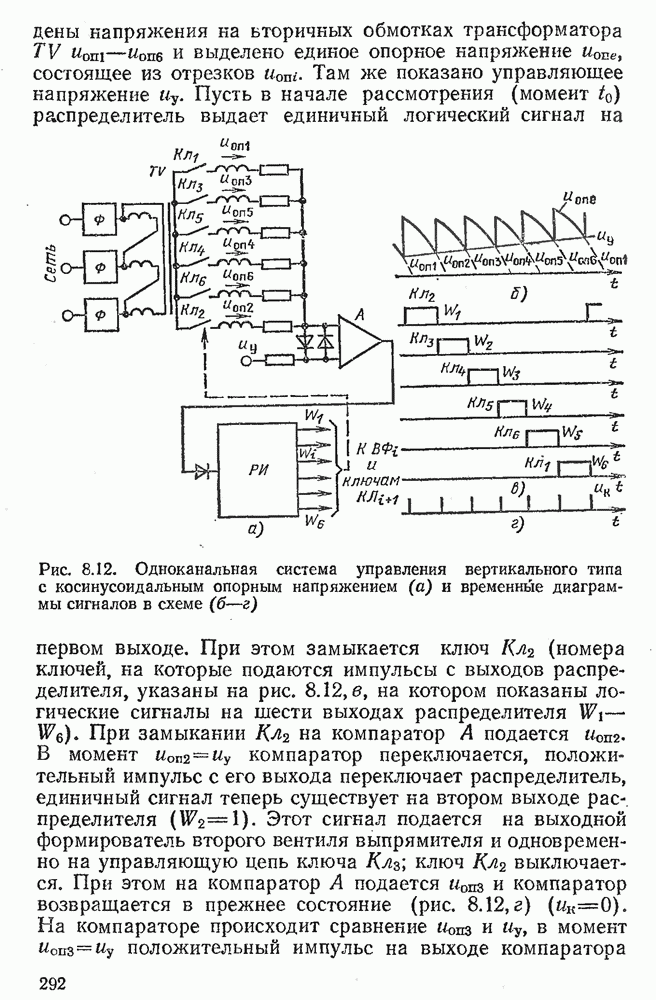
Рис. 2.22. Неинвертирующий сумматор на ОУ (а), его схема замещения (б) и схема вычитателя (в)
Напряжение на выходе ОУ найдем с учетом (2.24):

Таким образом, выходное напряжение пропорционально сумме входных сигналов. Но коэффициент передачи по напряжению схемы рис. 2.22, а зависит от числа входов п. Нетрудно видеть, что ивых однозначно определяется средним входным сигналом: 
На рис. 2.22, в представлена схема вычитателя на ОУ. Рассмотрим его работу методом суперпозиции. Вначале положим  , т. е. закоротим источник
, т. е. закоротим источник  . Тогда схема сводится к неннвертирующему ОУ (рис. 2.18, а), на входе которого включен делитель напряжения с коэффициентом передачи
. Тогда схема сводится к неннвертирующему ОУ (рис. 2.18, а), на входе которого включен делитель напряжения с коэффициентом передачи  . С учетом
. С учетом  . Теперь положим
. Теперь положим  (закоротим источник
(закоротим источник  ). Схема сводится к инвертирующему ОУ (рис. 2.20,а), поскольку подключение к прямому входу резисторов
). Схема сводится к инвертирующему ОУ (рис. 2.20,а), поскольку подключение к прямому входу резисторов  не изменяет потенциал на прямом входе идеального ОУ, у которого входной ток мал. Тогда в соответствии с
не изменяет потенциал на прямом входе идеального ОУ, у которого входной ток мал. Тогда в соответствии с 
В результате воздействия двух сигналов выходное напряжение ОУ  . При
. При  получим
получим

Источник напряжения, управляемый током, получим из схемы рис. 2.20, а при  . При этом
. При этом  и источник сигнала
и источник сигнала  работает в режиме источника тока
работает в режиме источника тока  . Выходное напряжение при учете
. Выходное напряжение при учете  определяется
определяется

Источник тока, управляемый напряжением, получим также из схемы рис. 2.20, а, если включим нагрузку в качестве резистора Тогда

Интегратор на ОУ также создается на базе инвертирующего ОУ (рис. 2.23,а). В цепь ОС включен конденсатор С. Как известно из курса ТОЭ,


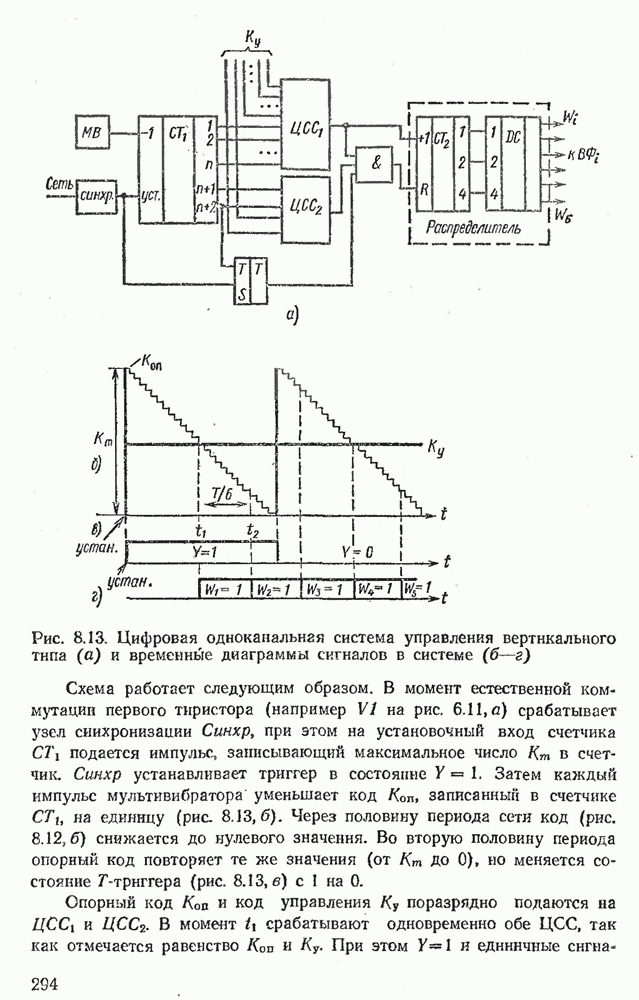
Рис. 2.23. Интегратор на ОУ (а) и временные диаграммы сигналов на его входе и выходе (б)
Поскольку  , то
, то

Напряжение между входами ИМС ОУ равно нулю, поэтому  . Учитывая (2.30) и (2.31), получаем
. Учитывая (2.30) и (2.31), получаем

Схема выполняет математическую операцию интегрирования. Перейдем от неопределенных интегралов к определенным, тогда (2.32) запишется в виде

Выходное напряжение  зависит от начальных условий, т. е. от начального напряжения на конденсаторе момент
зависит от начальных условий, т. е. от начального напряжения на конденсаторе момент  .
.
На рис.  представлены временные диаграммы, иллюстрирующие работу интегратора. При подаче на вход постоянных напряжений на выходе получаем линейно изменяющиеся напряжения.
представлены временные диаграммы, иллюстрирующие работу интегратора. При подаче на вход постоянных напряжений на выходе получаем линейно изменяющиеся напряжения.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава первая. ПОЛУПРОВОДНИКОВЫЕ И МИКРОЭЛЕКТРОННЫЕ ПРИБОРЫ
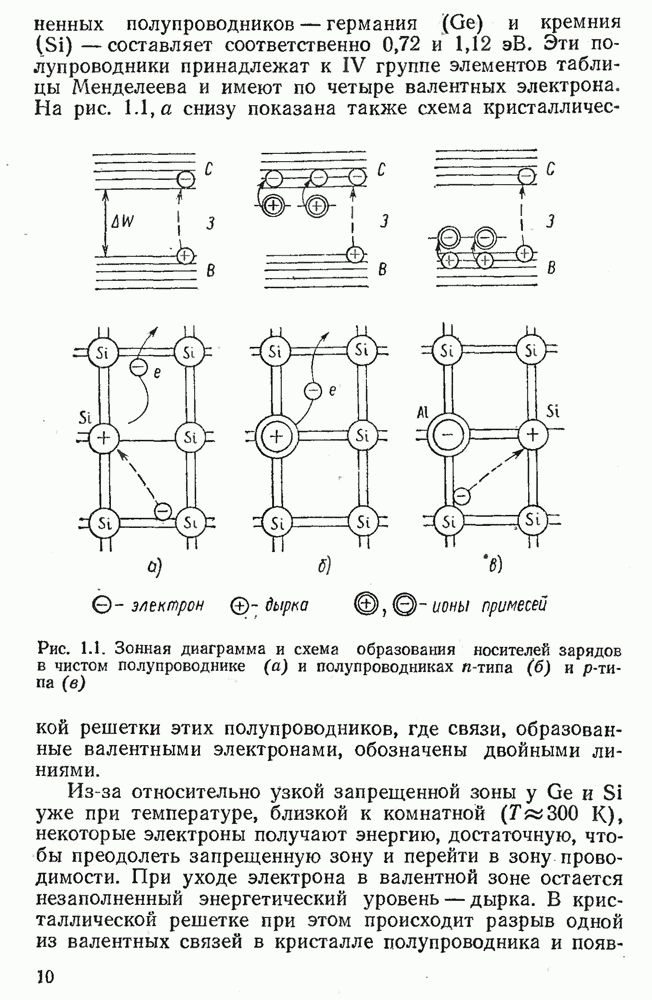
- 1.1. ЭЛЕКТРОПРОВОДНОСТЬ ПОЛУПРОВОДНИКОВ
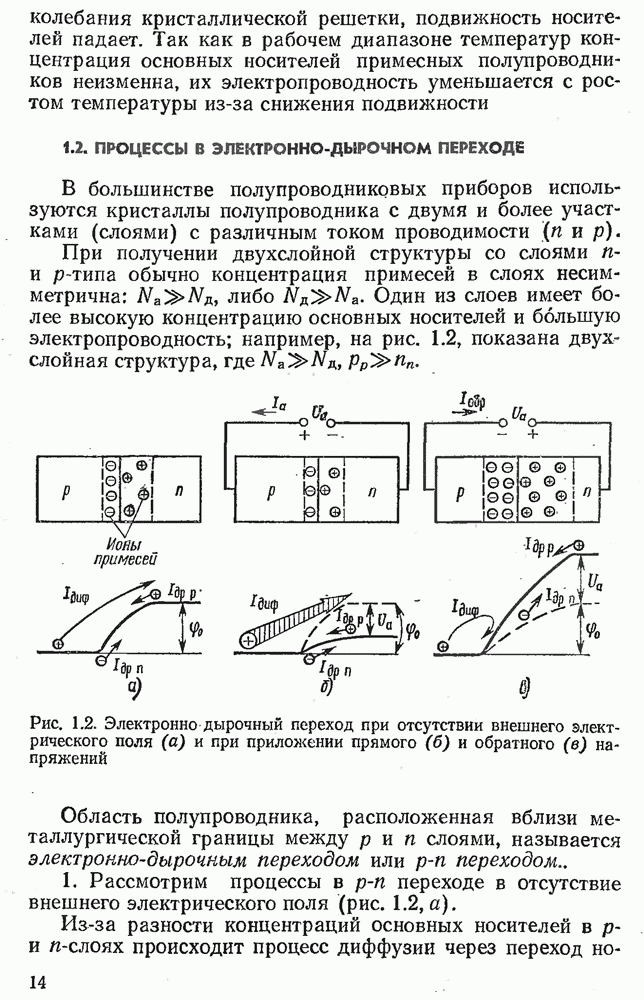
- 1.2. ПРОЦЕССЫ В ЭЛЕКТРОННО-ДЫРОЧНОМ ПЕРЕХОДЕ
- 1.3. ПОЛУПРОВОДНИКОВЫЕ ДИОДЫ
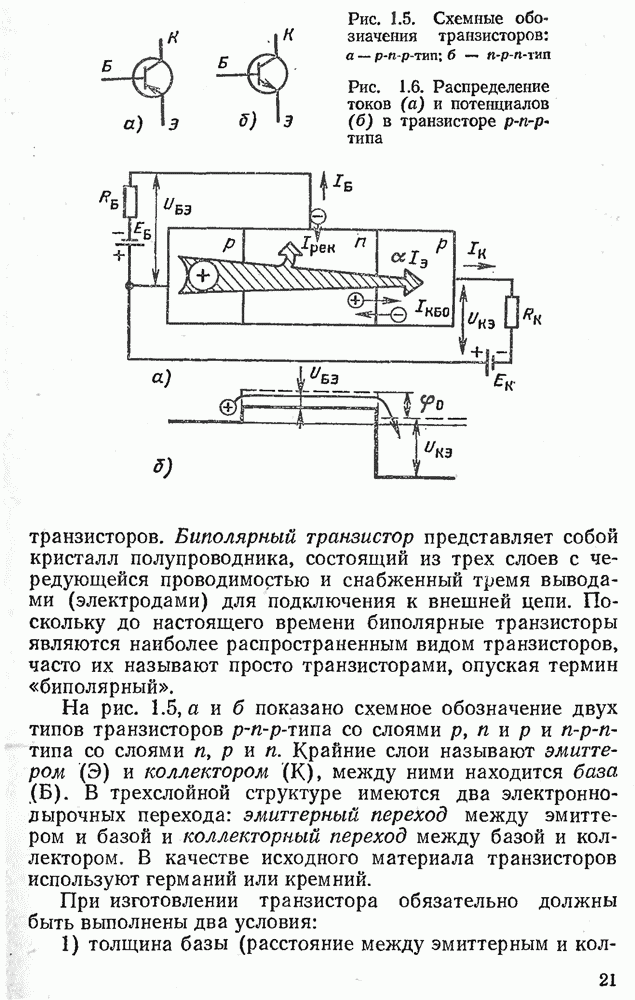
- 1.4. БИПОЛЯРНЫЕ ТРАНЗИСТОРЫ
- 1.5. ХАРАКТЕРИСТИКИ И ПАРАМЕТРЫ БИПОЛЯРНЫХ ТРАНЗИСТОРОВ
- 1.6. ПОЛЕВЫЕ ТРАНЗИСТОРЫ
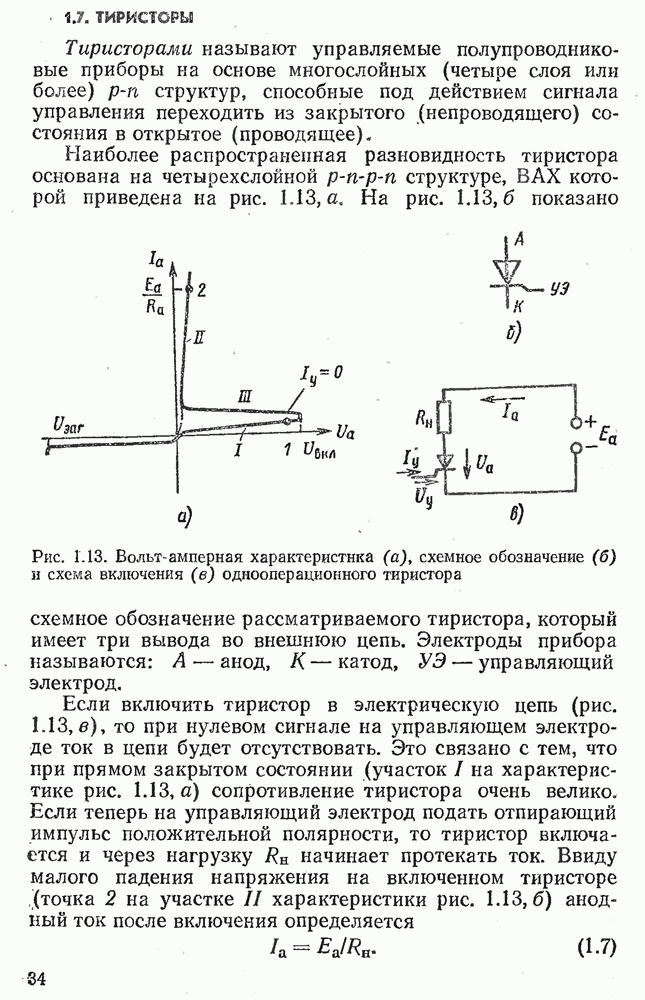
- 1.7. ТИРИСТОРЫ
- 1.8. ПАРАМЕТРЫ И РАЗНОВИДНОСТИ ТИРИСТОРОВ
- 1.9. ИНТЕГРАЛЬНЫЕ МИКРОСХЕМЫ
- 1.10. ПОЛУПРОВОДНИКОВЫЕ ОПТОЭЛЕКТРОННЫЕ ПРИБОРЫ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава вторая. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ
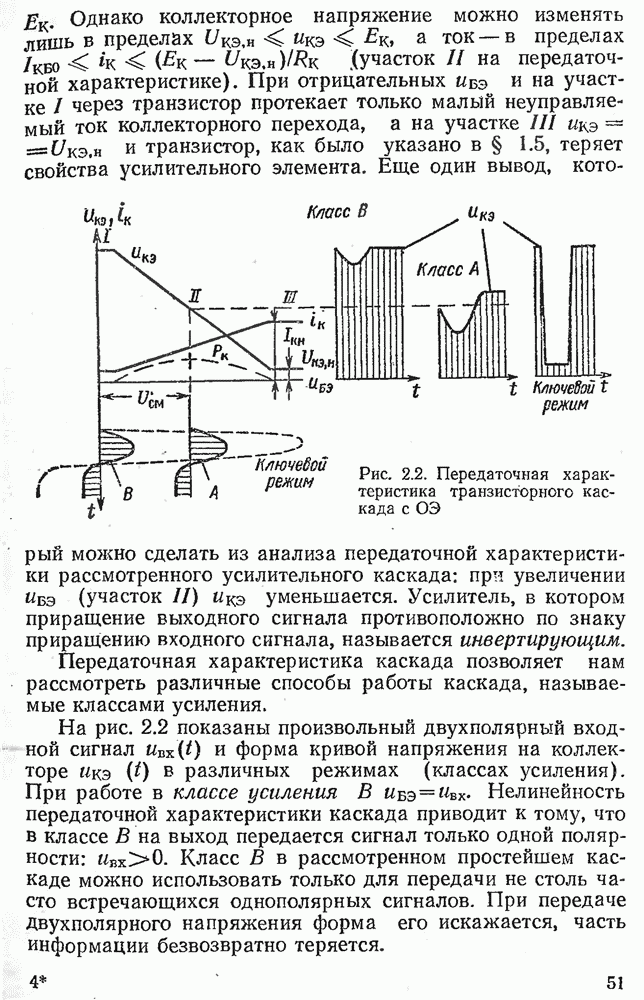
- 2.1. ПЕРЕДАТОЧНАЯ ХАРАКТЕРИСТИКА УСИЛИТЕЛЬНОГО КАСКАДА
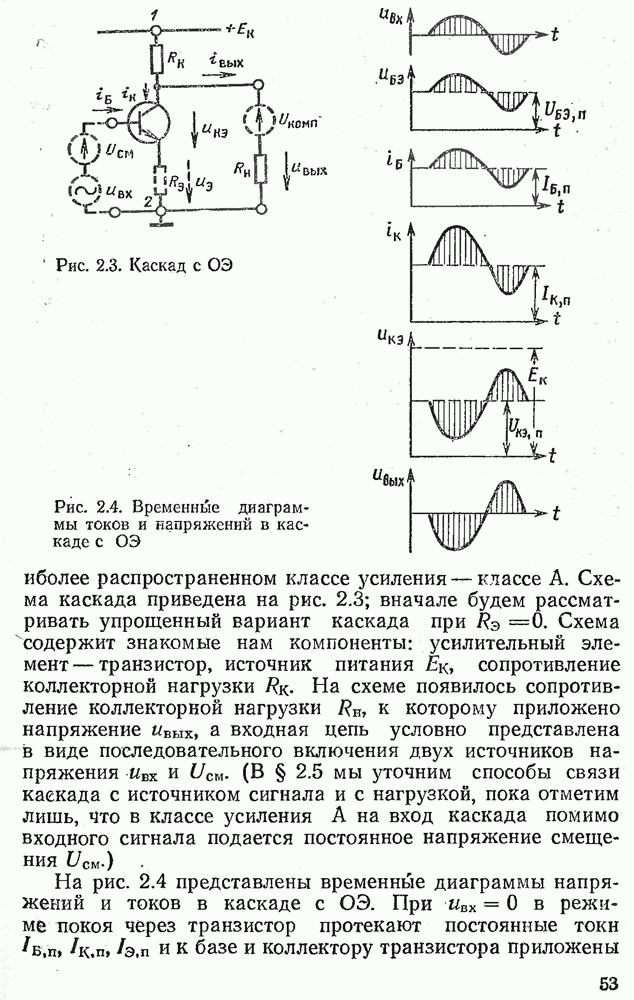
- 2.2. РЕЖИМ ПОКОЯ В КАСКАДЕ С ОБЩИМ ЭМИТТЕРОМ
- 2.3. ОБРАТНЫЕ СВЯЗИ. СТАБИЛИЗАЦИЯ РЕЖИМА ПОКОЯ
- 2.4. СХЕМА ЗАМЕЩЕНИЯ И ОСНОВНЫЕ ПОКАЗАТЕЛИ КАСКАДА С ОЭ
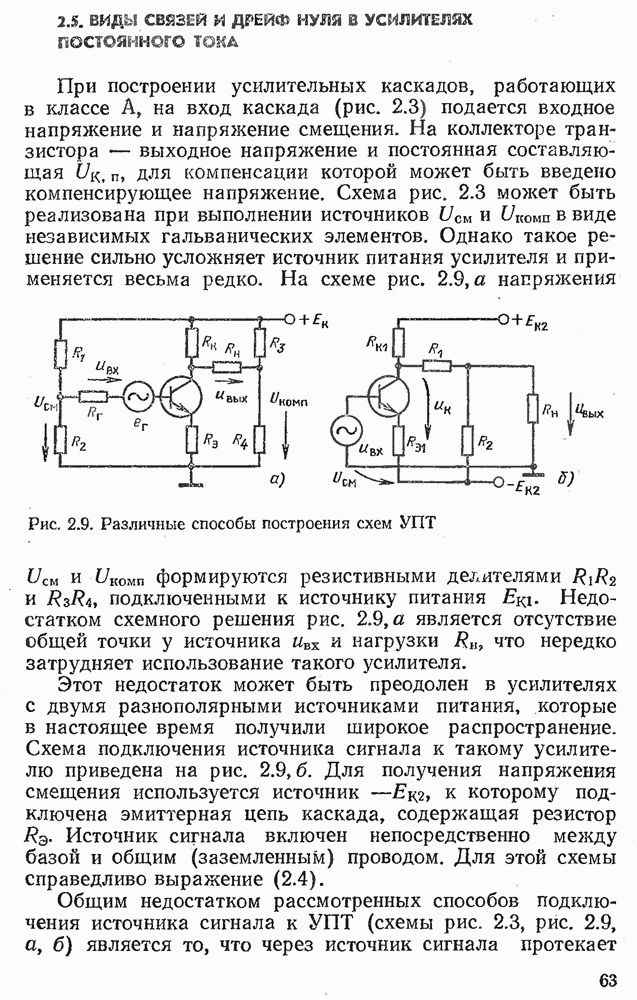
- 2.5. ВИДЫ СВЯЗЕЙ И ДРЕЙФ НУЛЯ В УСИЛИТЕЛЯХ ПОСТОЯННОГО ТОКА
- 2.6. ДИФФЕРЕНЦИАЛЬНЫЙ КАСКАД
- 2.7. КАСКАД С ОБЩИМ КОЛЛЕКТОРОМ
- 2.8. КАСКАД С ОБЩИМ ИСТОКОМ
- 2.9. ОПЕРАЦИОННЫЙ УСИЛИТЕЛЬ
- 2.10. НЕИНВЕРТИРУЮЩИЙ ОПЕРАЦИОННЫЙ УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ
- 2.11. ИНВЕРТИРУЮЩИЙ ОПЕРАЦИОННЫЙ УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ
- 2.12. ОПЕРАЦИОННЫЕ СХЕМЫ
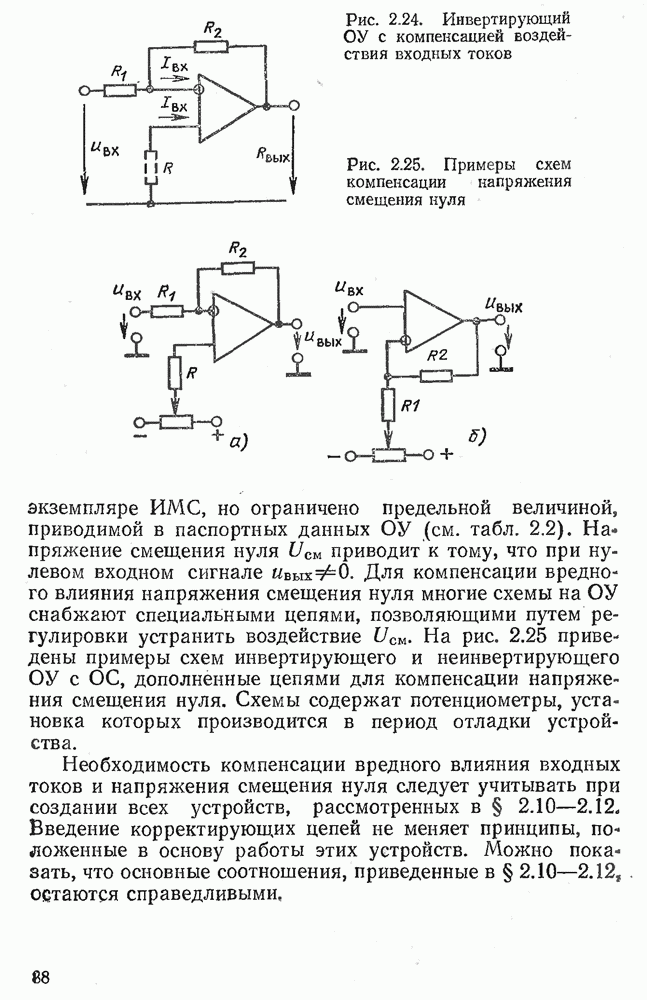
- 2.13. КОМПЕНСАЦИЯ ВХОДНЫХ ТОКОВ И НАПРЯЖЕНИЯ СМЕЩЕНИЯ НУЛЯ
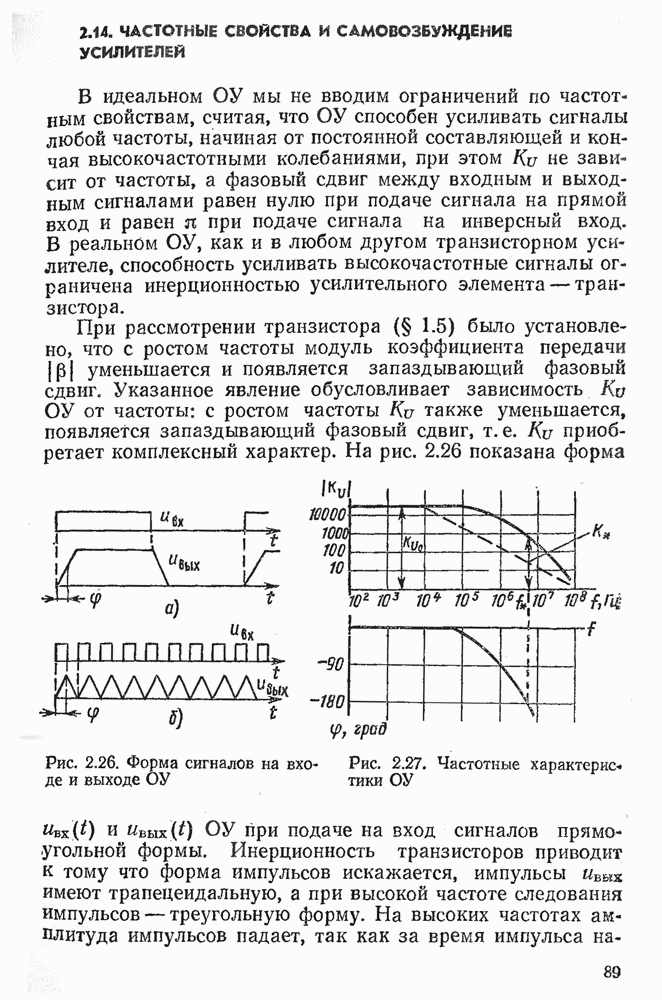
- 2.14. ЧАСТОТНЫЕ СВОЙСТВА И САМОВОЗБУЖДЕНИЕ УСИЛИТЕЛЕЙ
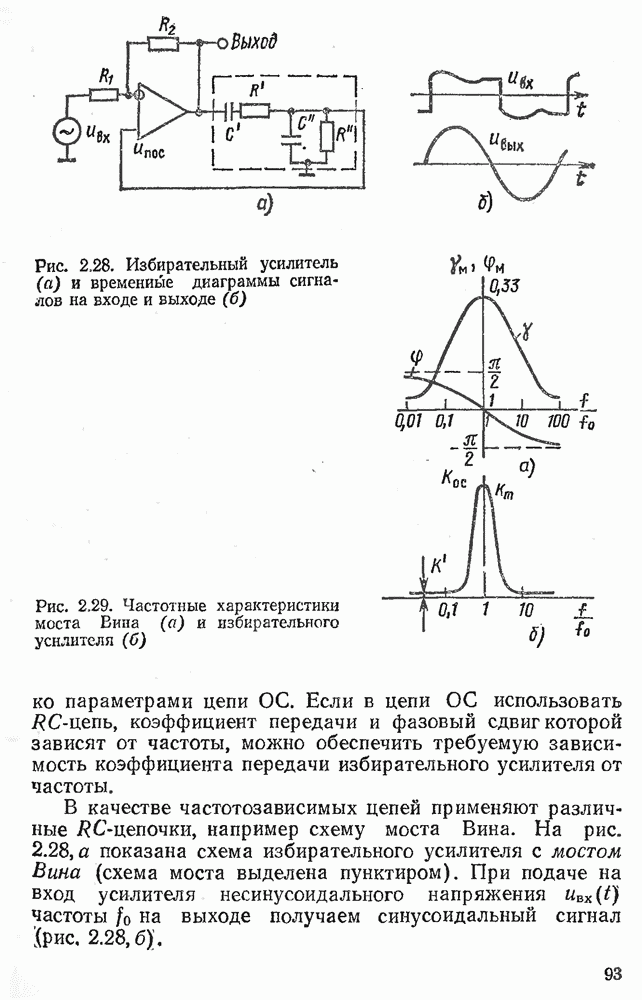
- 2.15. ИЗБИРАТЕЛЬНЫЕ УСИЛИТЕЛИ И ГЕНЕРАТОРЫ СИНУСОИДАЛЬНЫХ КОЛЕБАНИЙ
- 2.16. УСИЛИТЕЛИ С ЕМКОСТНОЙ СВЯЗЬЮ
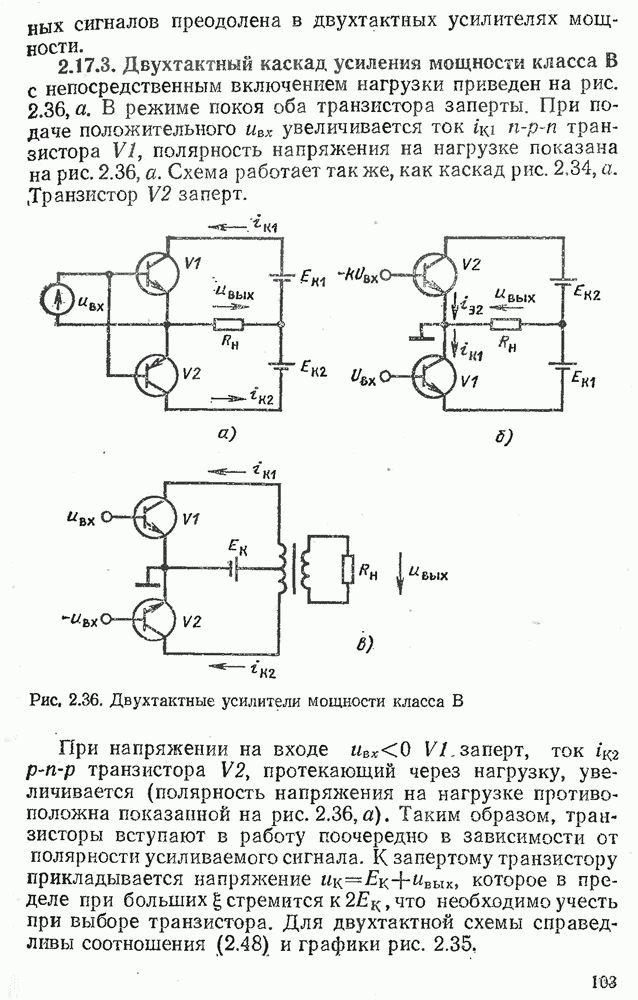
- 2.17. КАСКАДЫ УСИЛЕНИЯ МОЩНОСТИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава третья. ИМПУЛЬСНЫЕ УСТРОЙСТВА
- 3.1. ПРЕИМУЩЕСТВА ПЕРЕДАЧИ ИНФОРМАЦИИ В ВИДЕ ИМПУЛЬСОВ
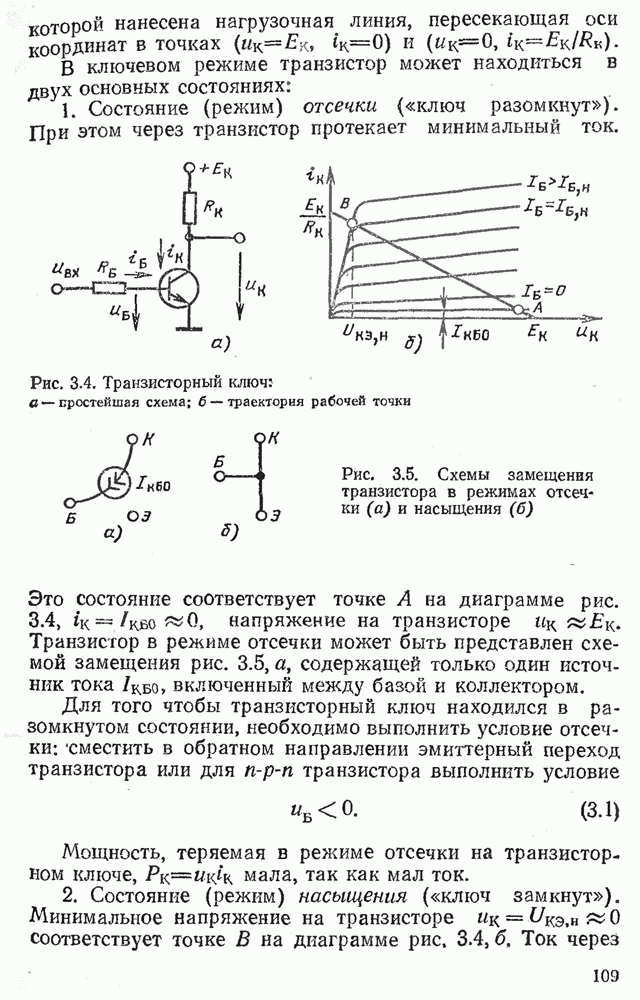
- 3.2. КЛЮЧЕВОЙ РЕЖИМ ТРАНЗИСТОРА
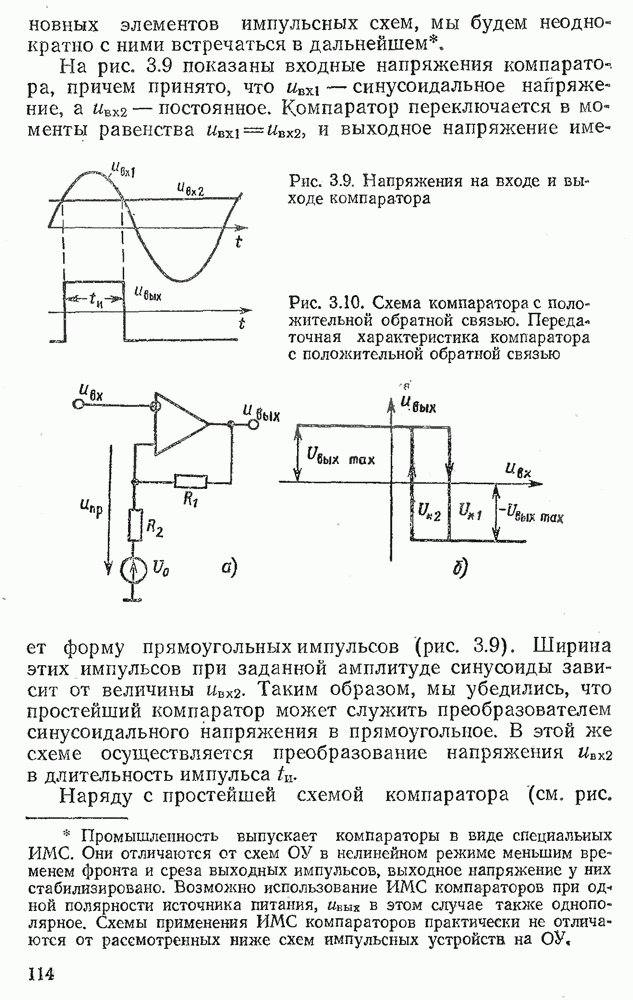
- 3.3. НЕЛИНЕЙНЫЙ РЕЖИМ РАБОТЫ ОПЕРАЦИОННОГО УСИЛИТЕЛЯ. КОМПАРАТОРЫ
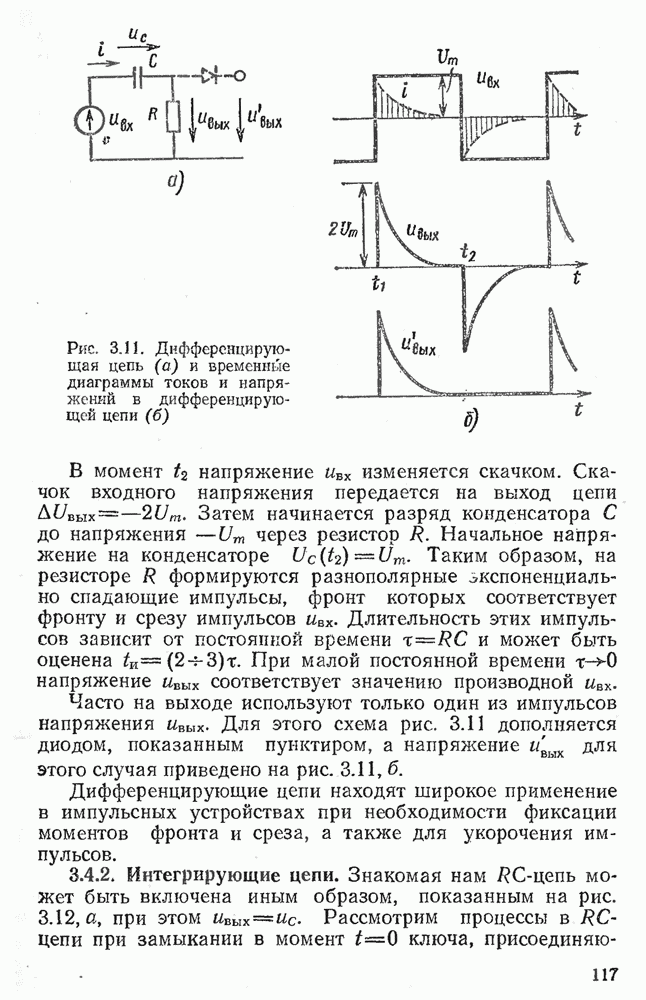
- 3.4. ПРЕОБРАЗОВАНИЕ ИМПУЛЬСНЫХ СИГНАЛОВ С ПОМОЩЬЮ RС-ЦЕПЕЙ
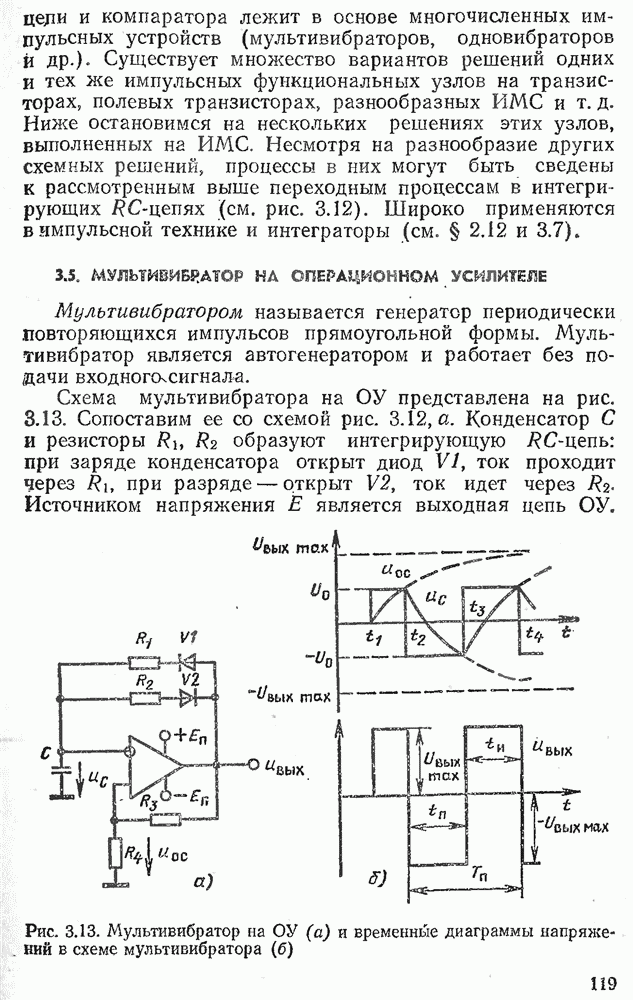
- 3.3. МУЛЬТИВИБРАТОР НА ОПЕРАЦИОННОМ УСИЛИТЕЛЕ
- 3.6. ОДНОВИБРАТОР НА ОПЕРАЦИОННОМ УСИЛИТЕЛЕ
- 3.7. ГЕНЕРАТОРЫ ЛИНЕЙНО ИЗМЕНЯЮЩИХСЯ НАПРЯЖЕНИЙ
- 3.8. МАГНИТНО-ТРАНЗИСТОРНЫЕ ГЕНЕРАТОРЫ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава четвертая. ЛОГИЧЕСКИЕ И ЦИФРОВЫЕ УСТРОЙСТВА
- 4.1. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ И ИХ РЕАЛИЗАЦИЯ
- 4.2. ТИПЫ ЛОГИЧЕСКИХ МИКРОСХЕМ
- 4.3. АЛГЕБРА ЛОГИКИ
- 4.4. КОМБИНАЦИОННЫЕ ЛОГИЧЕСКИЕ УСТРОЙСТВА
- 4.5. МИНИМИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 4.6. КОМБИНАЦИОННЫЕ ИНТЕГРАЛЬНЫЕ МИКРОСХЕМЫ
- 4.7. АСИНХРОННЫЙ RS-ТРИГГЕР
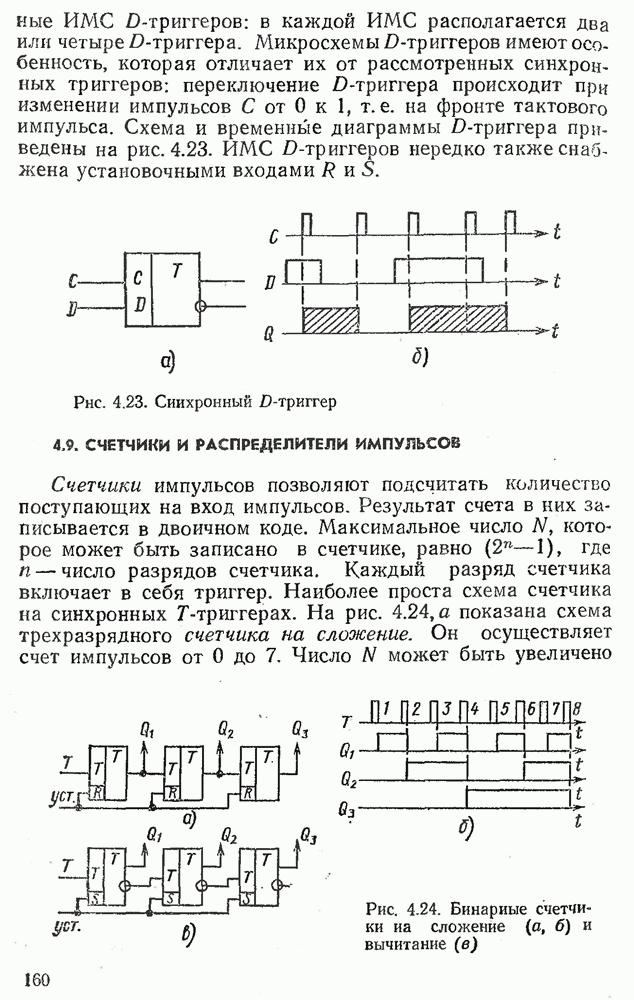
- 4.8. СИНХРОННЫЕ ТРИГГЕРЫ
- 4.9. СЧЕТЧИКИ И РАСПРЕДЕЛИТЕЛИ ИМПУЛЬСОВ
- 4.10. РЕГИСТРЫ
- 4.11. ЦИФРО-АНАЛОГОВЫЕ И АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 4.12. МИКРОПРОЦЕССОРЫ
- 4.13. СИСТЕМА КОМАНД МИКРОПРОЦЕССОРА
- 4.14. ИНДИКАТОРНЫЕ ПРИБОРЫ И УЗЛЫ ЦИФРОВЫХ УСТРОЙСТВ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава пятая. МАЛОМОЩНЫЕ ВЫПРЯМИТЕЛИ ОДНОФАЗНОГО ТОКА
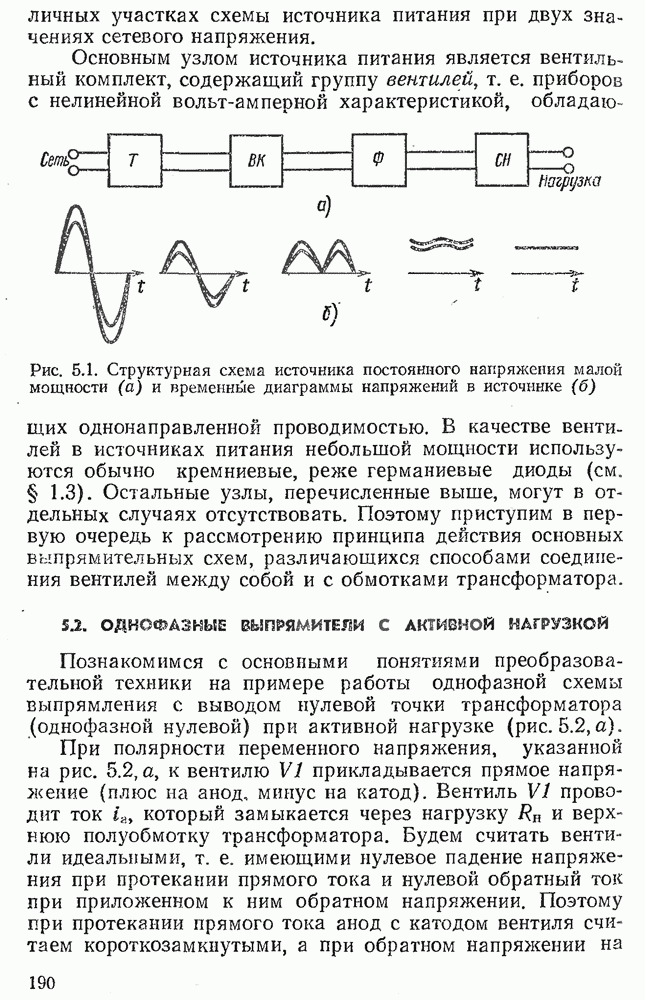
- 5.1. СТРУКТУРА ИСТОЧНИКА ПИТАНИЯ
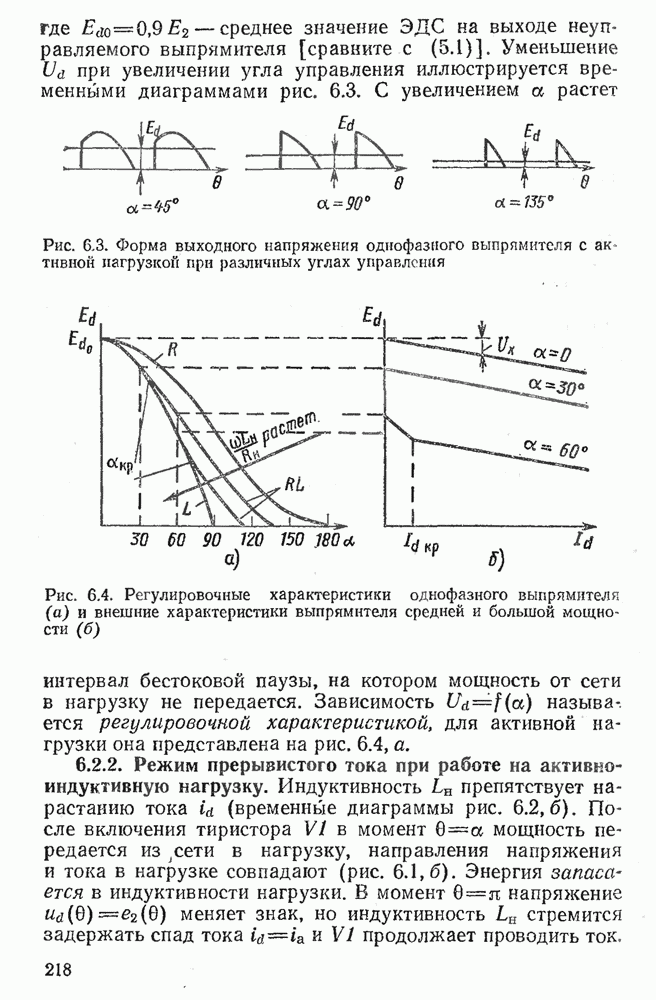
- 5.2. ОДНОФАЗНЫЕ ВЫПРЯМИТЕЛИ С АКТИВНОЙ НАГРУЗКОЙ
- 5.3. ОДНОФАЗНЫЕ ВЫПРЯМИТЕЛИ С АКТИВНО-ИНДУКТИВНОЙ НАГРУЗКОЙ
- 5.4. ФИЛЬТРЫ МАЛОМОЩНЫХ ВЫПРЯМИТЕЛЕЙ
- 5.5. ОСОБЕННОСТИ РАБОТЫ И РАСЧЕТА ВЫПРЯМИТЕЛЯ С ЕМКОСТНЫМ ФИЛЬТРОМ
- 5.6. ВНЕШНИЕ ХАРАКТЕРИСТИКИ МАЛОМОЩНЫХ ВЫПРЯМИТЕЛЕЙ
- 5.7. СТАБИЛИЗАТОРЫ НАПРЯЖЕНИЯ
- 5.8. ИСТОЧНИКИ ПИТАНИЯ С МНОГОКРАТНЫМ ПРЕОБРАЗОВАНИЕМ ЭНЕРГИИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава шестая. ВЕДОМЫЕ СЕТЬЮ ПРЕОБРАЗОВАТЕЛИ СРЕДНЕЙ И БОЛЬШОЙ МОЩНОСТИ
- 6.1. ПРИМЕНЕНИЕ ВЕНТИЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ В ЭНЕРГЕТИКЕ И ЭЛЕКТРОТЕХНИКЕ
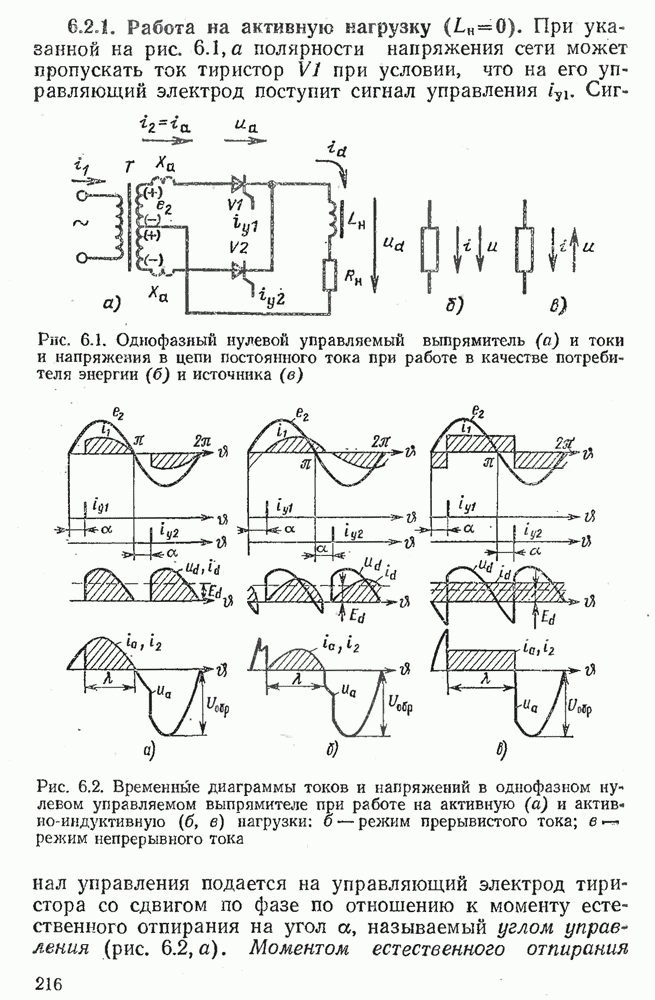
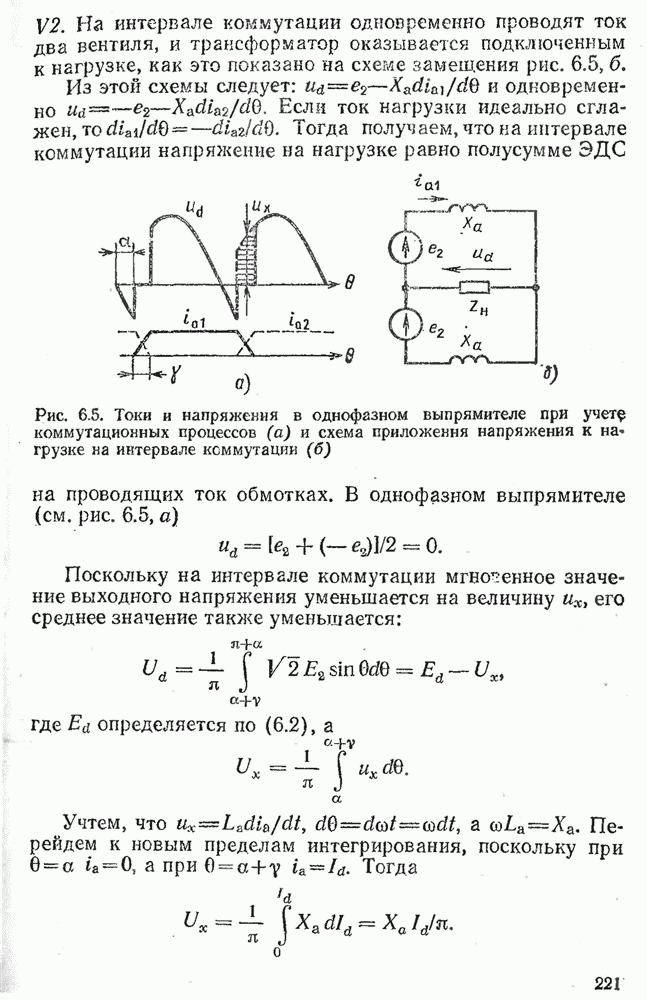
- 6.2. ОДНОФАЗНЫЙ УПРАВЛЯЕМЫЙ ВЫПРЯМИТЕЛЬ
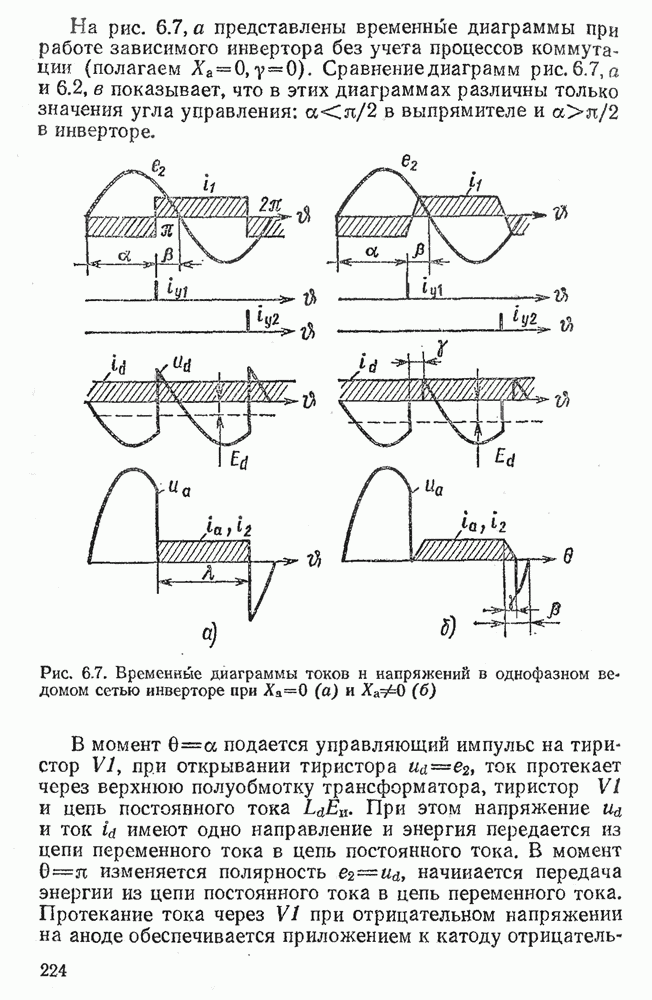
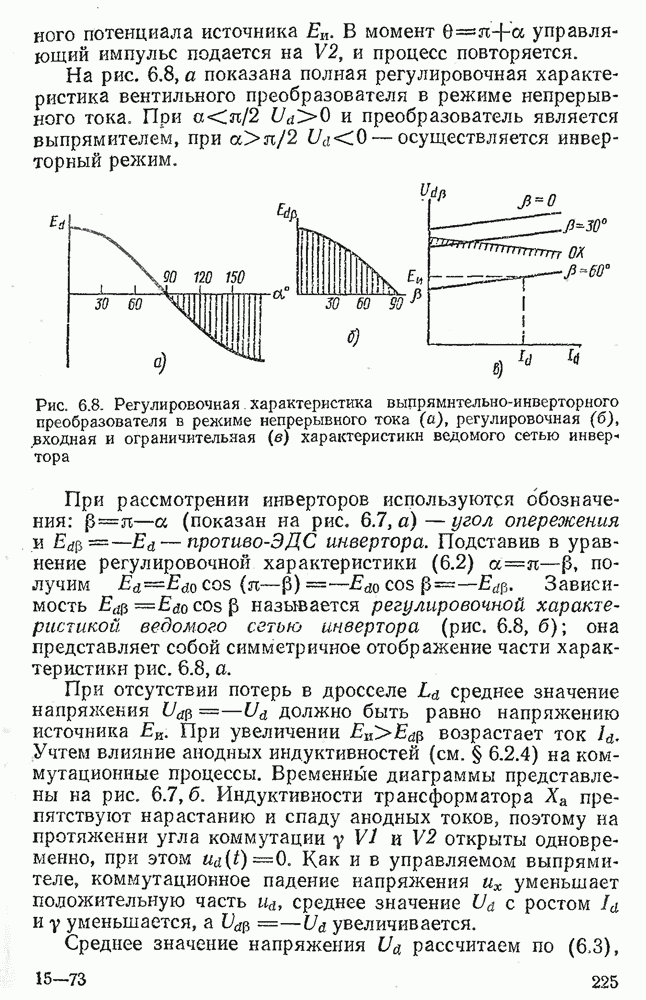
- 6.3. ОДНОФАЗНЫЙ ВЕДОМЫЙ СЕТЬЮ ИНВЕРТОР
- 6.4. ТРЕХФАЗНЫЙ НУЛЕВОЙ ВЫПРЯМИТЕЛЬ
- 6.5. ТРЁХФАЗНЫЙ МОСТОВОЙ ВЫПРЯМИТЕЛЬ
- 6.6. СОСТАВНЫЕ МНОГОФАЗНЫЕ СХЕМЫ ВЫПРЯМЛЕНИЯ
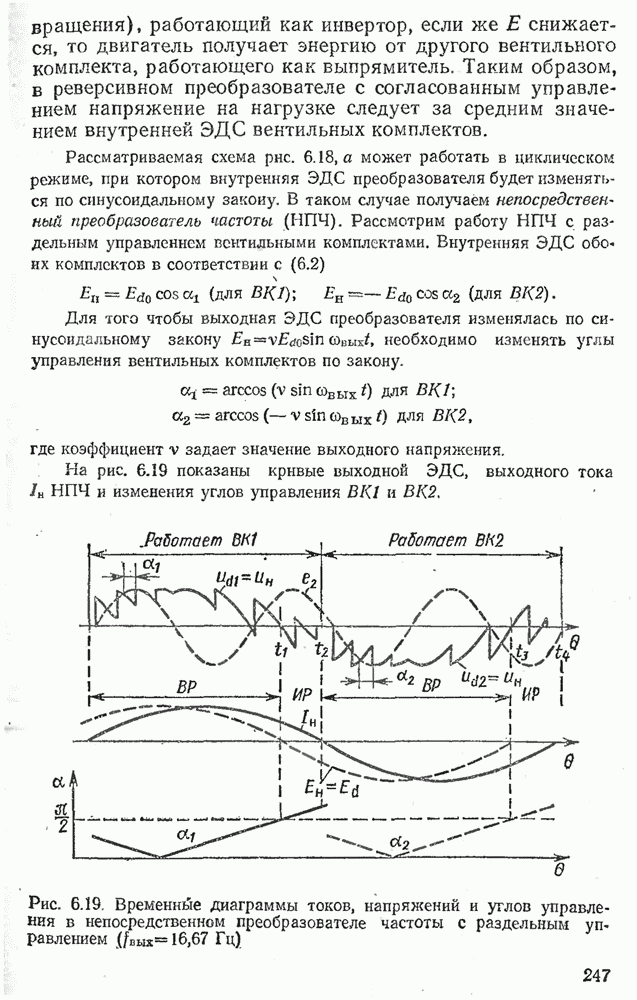
- 6.7. РЕВЕРСИВНЫЕ ВЫПРЯМИТЕЛИ И НЕПОСРЕДСТВЕННЫЕ ПРЕОБРАЗОВАТЕЛИ ЧАСТОТЫ
- 6.8. РЕГУЛИРУЕМЫЕ ПРЕОБРАЗОВАТЕЛИ ПЕРЕМЕННОГО НАПРЯЖЕНИЯ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава седьмая. ВЛИЯНИЕ ВЕНТИЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ НА ПИТАЮЩУЮ СЕТЬ
- 7.1. КОЭФФИЦИЕНТ МОЩНОСТИ ВЕНТИЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ
- 7.2. ВЕНТИЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ С ПОВЫШЕННЫМ КОЭФФИЦИЕНТОМ МОЩНОСТИ
- 7.3. ИСТОЧНИКИ РЕАКТИВНОЙ МОЩНОСТИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава восьмая. СИСТЕМЫ УПРАВЛЕНИЯ ВЕНТИЛЬНЫМИ ПРЕОБРАЗОВАТЕЛЯМИ
- 8.1. ФУНКЦИИ И СТРУКТУРА СИСТЕМ УПРАВЛЕНИЙ
- 8.2. ФАЗОСМЕЩАЮЩИЕ УСТРОЙСТВА (ФСУ)
- 8.3. МНОГОКАНАЛЬНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
- 8.4. ОДНОКАНАЛЬНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава девятая. АВТОНОМНЫЕ ВЕНТИЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.1. СПОСОБЫ РЕГУЛИРОВАНИЯ ПОСТОЯННОГО НАПРЯЖЕНИЯ
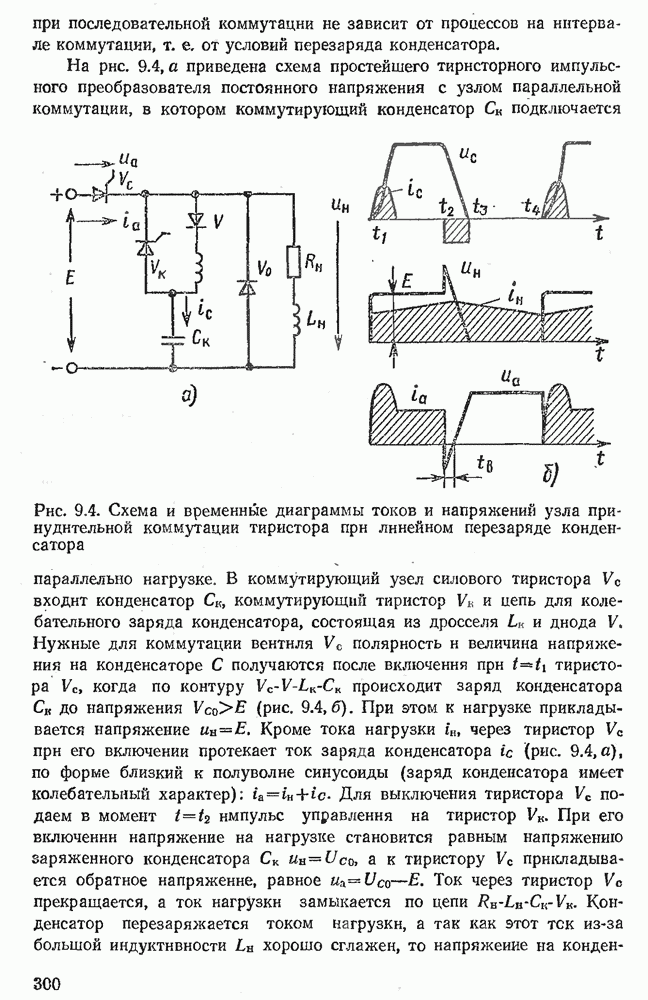
- 9.2. УЗЛЫ КОММУТАЦИИ ОДНООПЕРАЦИОННЫХ ТИРИСТОРОВ
- 9.3. ИНВЕРТОРЫ НАПРЯЖЕНИЯ
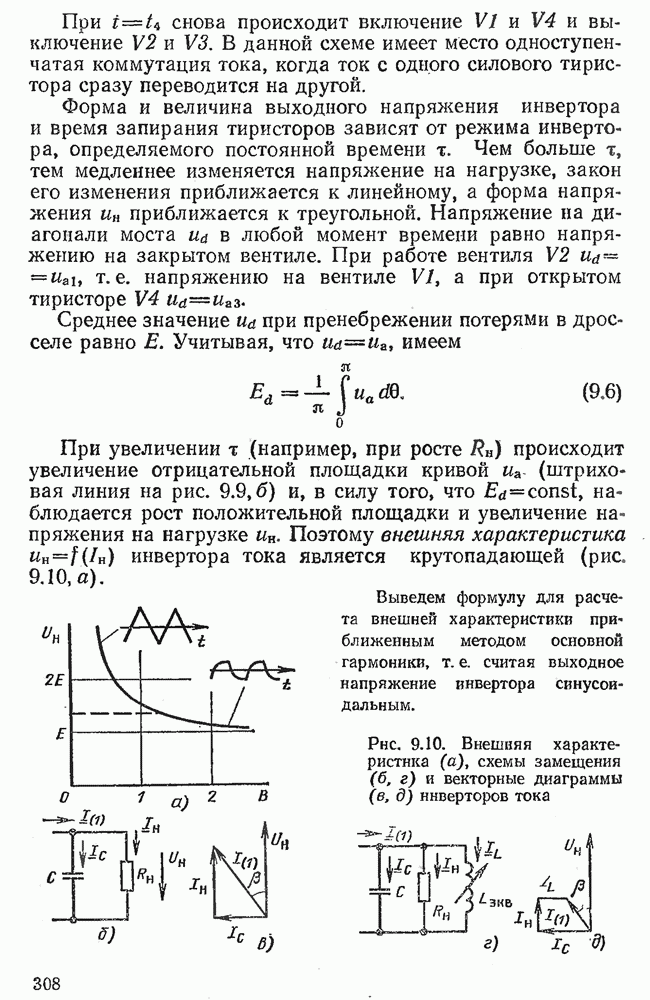
- 9.4. ИНВЕРТОРЫ ТОКА
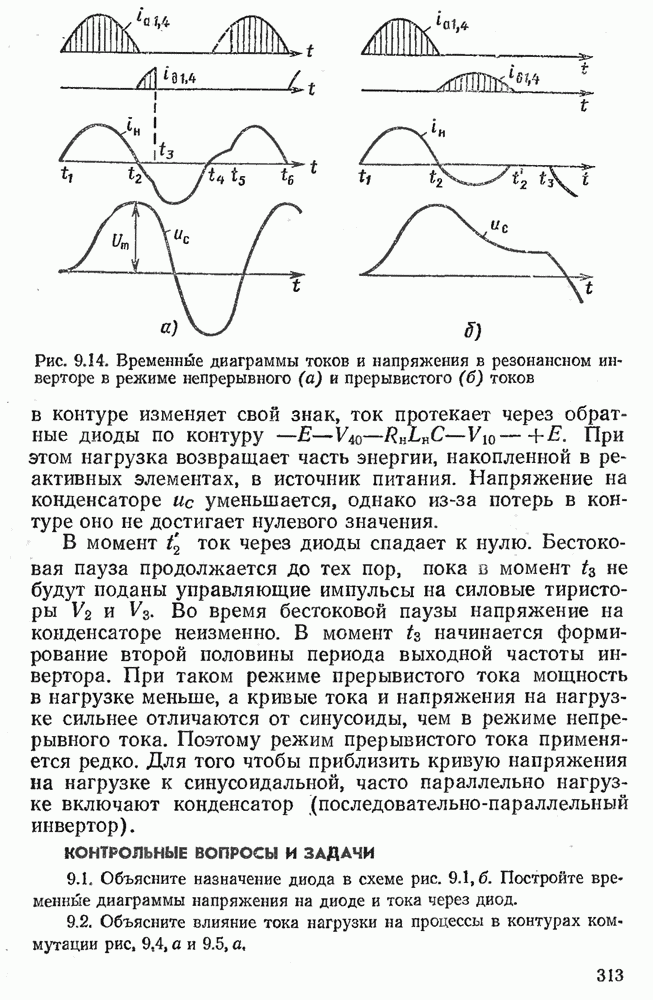
- 9.5. РЕЗОНАНСНЫЕ ИНВЕРТОРЫ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- СПИСОК ЛИТЕРАТУРЫ