| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.5. МИНИМИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
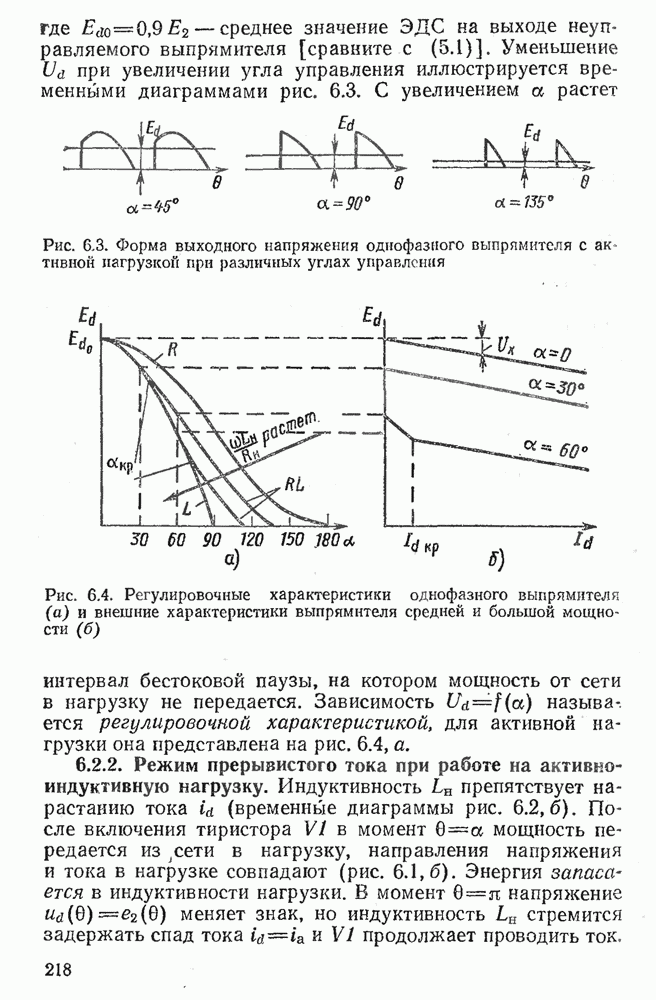
Упрощение логических выражений с помощью тождеств основывается на интуитивных решениях и представляет большие трудности, особенно при большом числе переменных. При этом бывает трудно оценить, является ли полученное выражение простейшим или возможны дальнейшие упрощения.
Минимизацию логических функций можно провести, используя диаграммы Вейча (или аналогичный метод карт Карно). Диаграмма Вейча для функции F четырех переменных А, В, С, D представлена на рис. 4.13. Каждая из переменных принимает два значения, т. е. возможны  комбинаций входных функций. Диаграмма Вейча содержит 16 клеток, каждая из которых соответствует одной из 16 возможных комбинаций входных переменных. На полях диаграммы обозначены значения каждой переменной. Диаграмма состоит
комбинаций входных функций. Диаграмма Вейча содержит 16 клеток, каждая из которых соответствует одной из 16 возможных комбинаций входных переменных. На полях диаграммы обозначены значения каждой переменной. Диаграмма состоит  четырех строк и четырех столбцов.
четырех строк и четырех столбцов.
Рассмотрим минимизацию логической функции на примере.
Дано: Упростить функцию  .
.
Решение разбиваем на четыре операции.
1. Преобразование исходного выражения. При преобразовании необходимо раскрыть скобки и исключить знаки инверсии над комбинацией переменных. Последнее осуществляется с помощью формул де Моргана. Получим

2. Заполнение диаграммы Вейча проводим при наличии в полученном выражении соответствующих комбинаций входных переменных, эти клетки обозначаются знаком 1 (рис. 4.14,а). Если слагаемое не содержит одного или нескольких переменных, то должны заполняться клетки, соответствующие и прямому, и инверсному значениям отсутствующей переменной.

Рис. 4.13. Диаграмма Вейча для функции четырех переменных

Рис. 4.14. К минимизации схемы логического комбинационного устройства: а — диаграмма Вейча; б — схема на элементах 
Например:  . Заполняются клетки ABCD и ABCD.
. Заполняются клетки ABCD и ABCD.
3. Производится «склейка» клеток. Можно склеить (т. е. объединить, лак показано на рис. 4.14, я) целую заполненную строку, целый столбец, полстроки или полстолбца. Можно склеить соседние строки, столбцы, полустроки и полустолбцы. Склейки можно располагать через границы диаграммы Вейча, т. е. объединяя нижиий и верхний, правый и левый края. Одиа склейка может накладываться на другую. Склейки содержат 2, 4, 8 клеток.
Для успешной минимизации нужно расположить на таблице минимальное количество склеек, каждая из которых содержит наибольшее количество клеток.
Склейки для логической функции F показаны на рис. 4.14, а.
4. Расшифровка склеек. Каждая склейка представлена в виде конъюнкции переменных. Второй столбец на диаграмме рис. 4.14, я расшифровывается как АС, так как он охватывает и прямые, и инверсные значения переменных В и D, т. е. от В до D не зависит. Склейка в правой верхней части таблицы расшифровывается как АВ, а склейка из двух клеток в четвертом столбце соответствует ACD. Результат минимизации:

На рис.  приведена схема на элементах
приведена схема на элементах  , реализующая функцию F. При построении схемы использованы стандартные решения, приведенные на рис. 4.11.
, реализующая функцию F. При построении схемы использованы стандартные решения, приведенные на рис. 4.11.
Процедура минимизации функций с помощью диаграмм Вейча очень проста, и ее использование заменяет путь сложных преобразований с помощью тождеств. С помощью диаграмм Вейча можно минимизировать и функции трех переменных, при этом  , т. е. из диаграммы исключают первую и четвертую строки, диаграмма содержит только восемь клеток.
, т. е. из диаграммы исключают первую и четвертую строки, диаграмма содержит только восемь клеток.
Правила склеек не изменяются.
Диаграмма Вейча функции двух переменных содержит четыре клетки.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава первая. ПОЛУПРОВОДНИКОВЫЕ И МИКРОЭЛЕКТРОННЫЕ ПРИБОРЫ
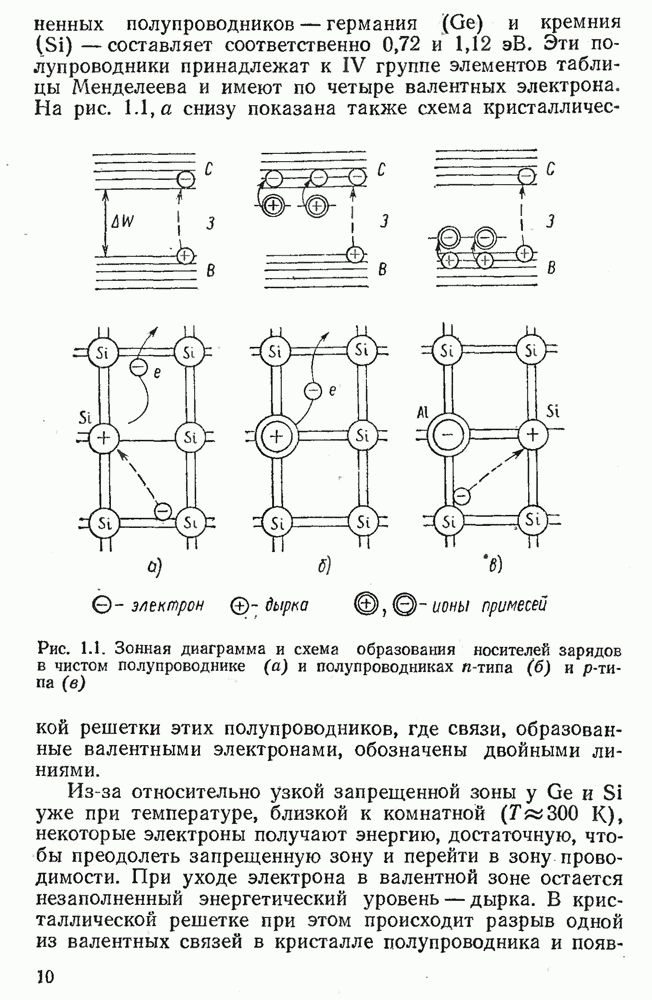
- 1.1. ЭЛЕКТРОПРОВОДНОСТЬ ПОЛУПРОВОДНИКОВ
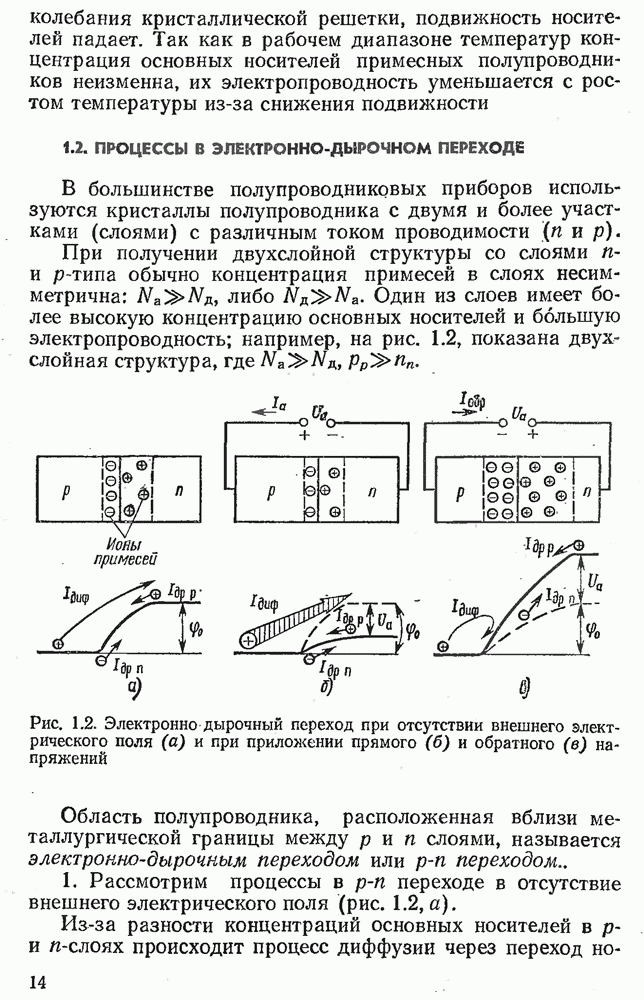
- 1.2. ПРОЦЕССЫ В ЭЛЕКТРОННО-ДЫРОЧНОМ ПЕРЕХОДЕ
- 1.3. ПОЛУПРОВОДНИКОВЫЕ ДИОДЫ
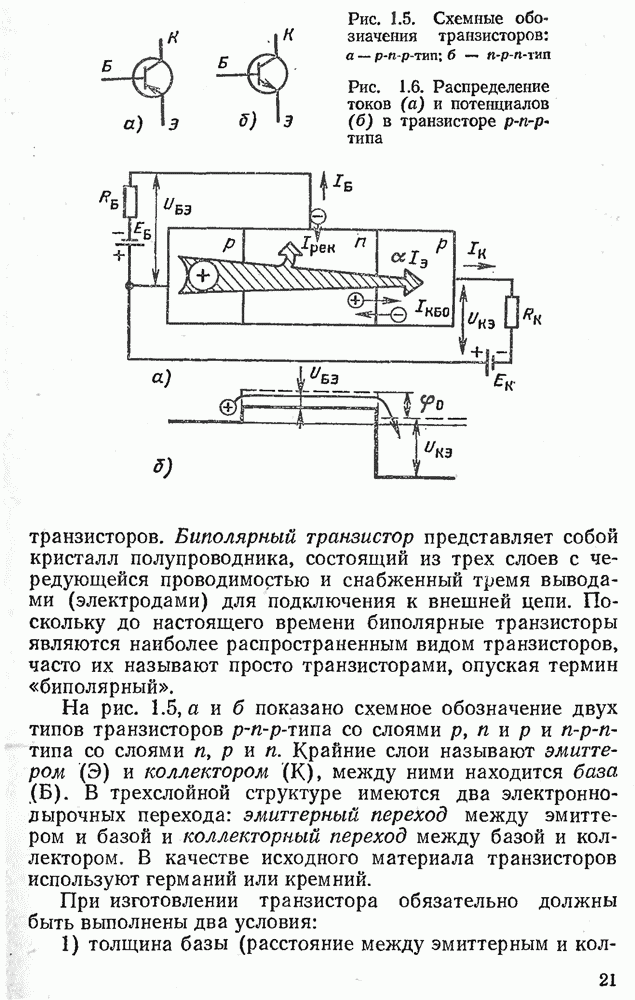
- 1.4. БИПОЛЯРНЫЕ ТРАНЗИСТОРЫ
- 1.5. ХАРАКТЕРИСТИКИ И ПАРАМЕТРЫ БИПОЛЯРНЫХ ТРАНЗИСТОРОВ
- 1.6. ПОЛЕВЫЕ ТРАНЗИСТОРЫ
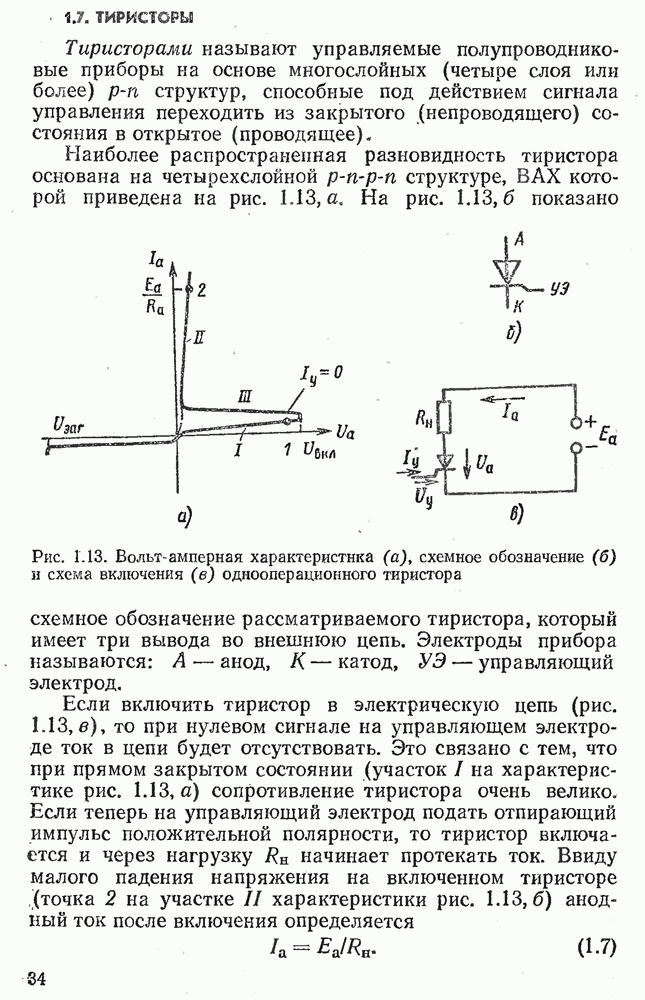
- 1.7. ТИРИСТОРЫ
- 1.8. ПАРАМЕТРЫ И РАЗНОВИДНОСТИ ТИРИСТОРОВ
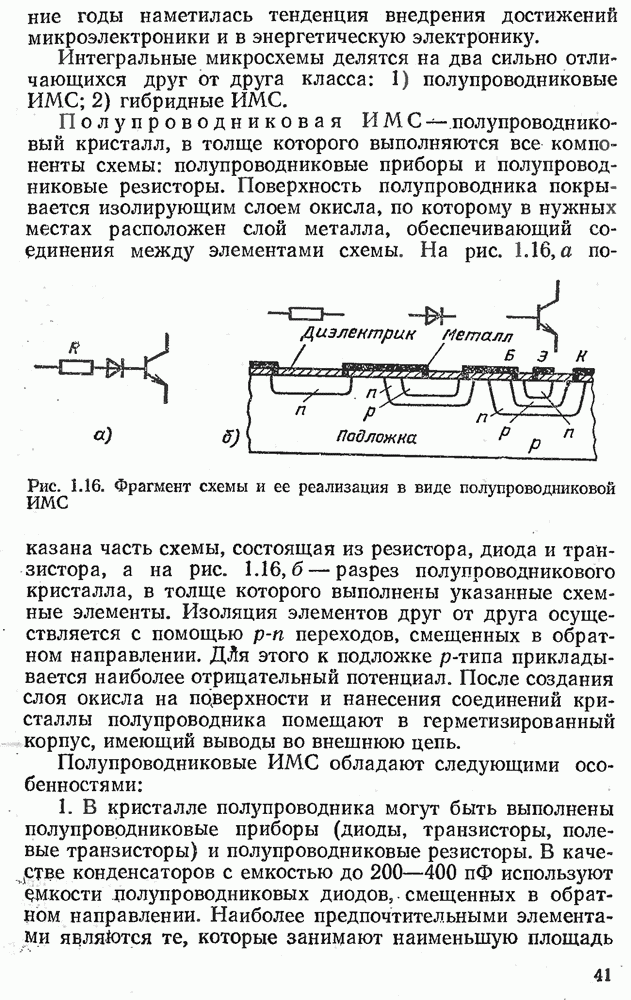
- 1.9. ИНТЕГРАЛЬНЫЕ МИКРОСХЕМЫ
- 1.10. ПОЛУПРОВОДНИКОВЫЕ ОПТОЭЛЕКТРОННЫЕ ПРИБОРЫ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава вторая. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ
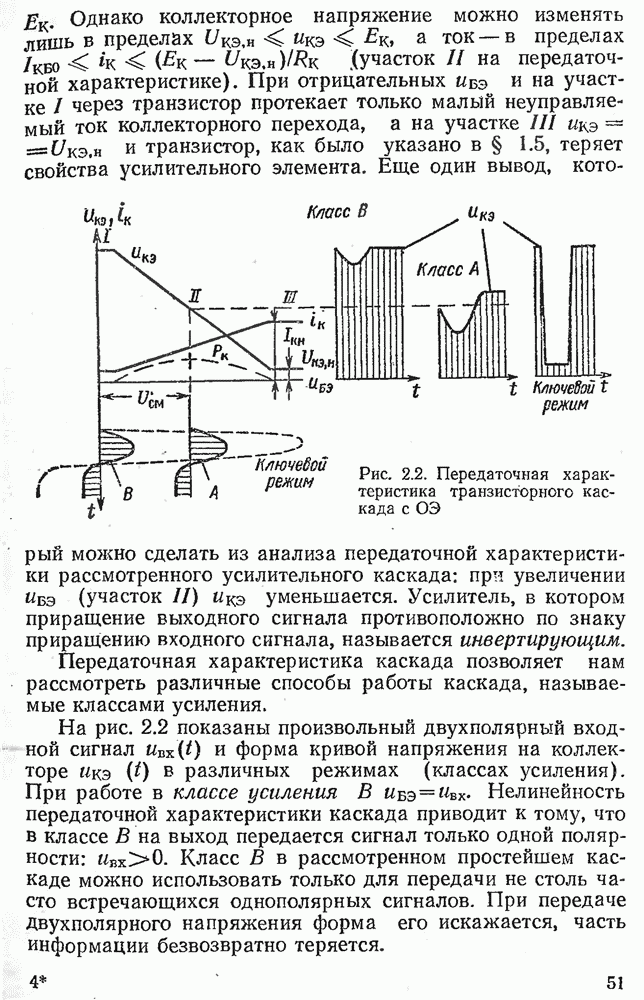
- 2.1. ПЕРЕДАТОЧНАЯ ХАРАКТЕРИСТИКА УСИЛИТЕЛЬНОГО КАСКАДА
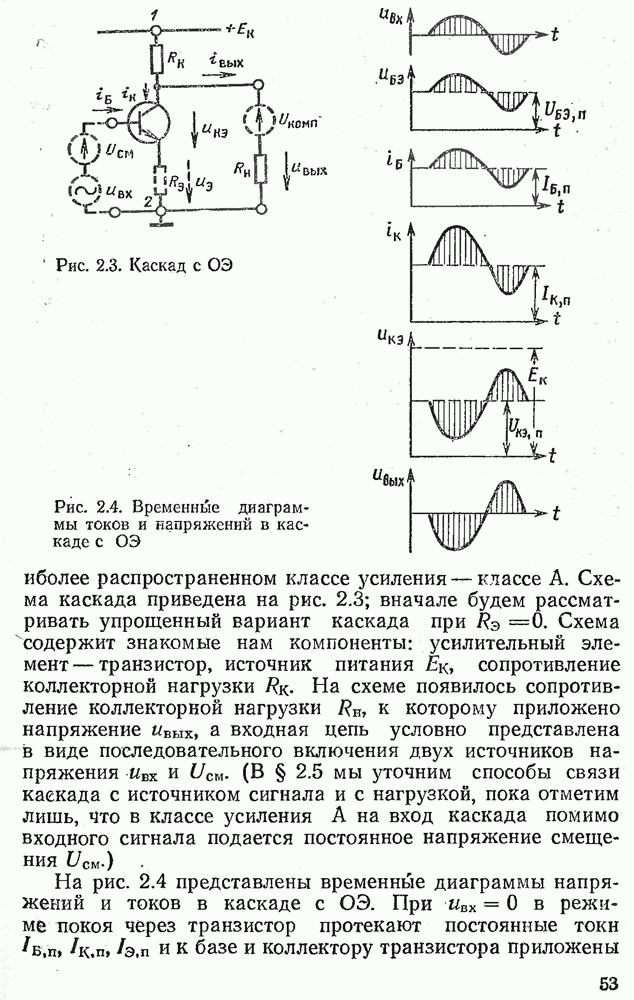
- 2.2. РЕЖИМ ПОКОЯ В КАСКАДЕ С ОБЩИМ ЭМИТТЕРОМ
- 2.3. ОБРАТНЫЕ СВЯЗИ. СТАБИЛИЗАЦИЯ РЕЖИМА ПОКОЯ
- 2.4. СХЕМА ЗАМЕЩЕНИЯ И ОСНОВНЫЕ ПОКАЗАТЕЛИ КАСКАДА С ОЭ
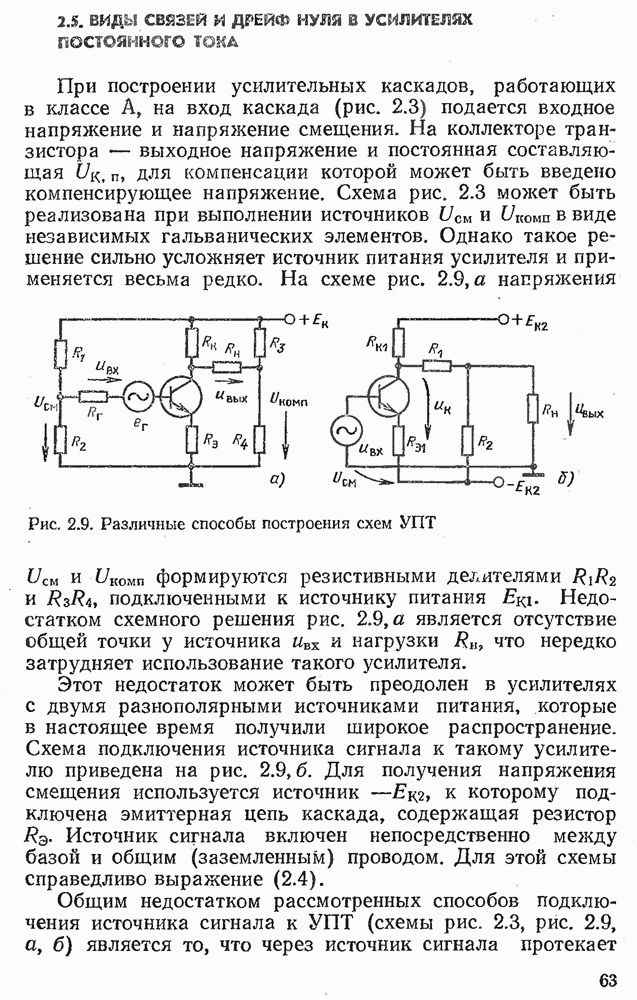
- 2.5. ВИДЫ СВЯЗЕЙ И ДРЕЙФ НУЛЯ В УСИЛИТЕЛЯХ ПОСТОЯННОГО ТОКА
- 2.6. ДИФФЕРЕНЦИАЛЬНЫЙ КАСКАД
- 2.7. КАСКАД С ОБЩИМ КОЛЛЕКТОРОМ
- 2.8. КАСКАД С ОБЩИМ ИСТОКОМ
- 2.9. ОПЕРАЦИОННЫЙ УСИЛИТЕЛЬ
- 2.10. НЕИНВЕРТИРУЮЩИЙ ОПЕРАЦИОННЫЙ УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ
- 2.11. ИНВЕРТИРУЮЩИЙ ОПЕРАЦИОННЫЙ УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ
- 2.12. ОПЕРАЦИОННЫЕ СХЕМЫ
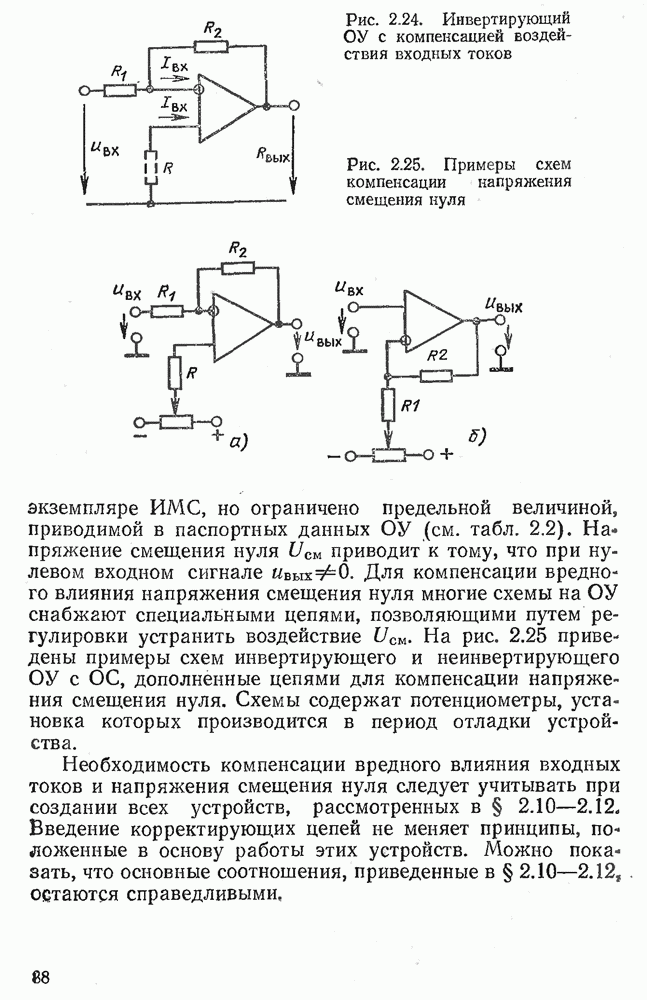
- 2.13. КОМПЕНСАЦИЯ ВХОДНЫХ ТОКОВ И НАПРЯЖЕНИЯ СМЕЩЕНИЯ НУЛЯ
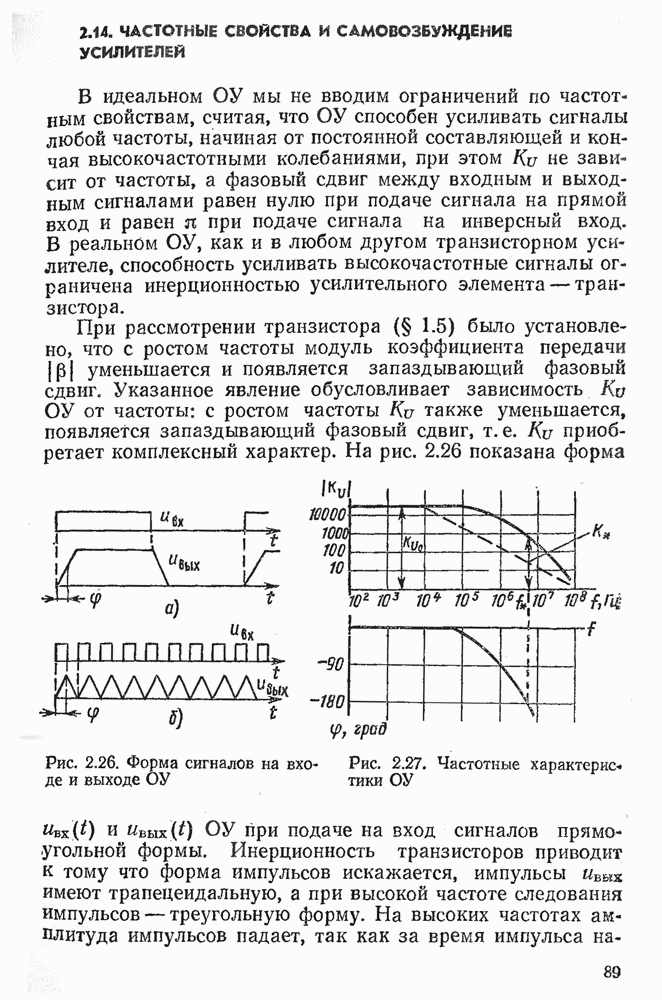
- 2.14. ЧАСТОТНЫЕ СВОЙСТВА И САМОВОЗБУЖДЕНИЕ УСИЛИТЕЛЕЙ
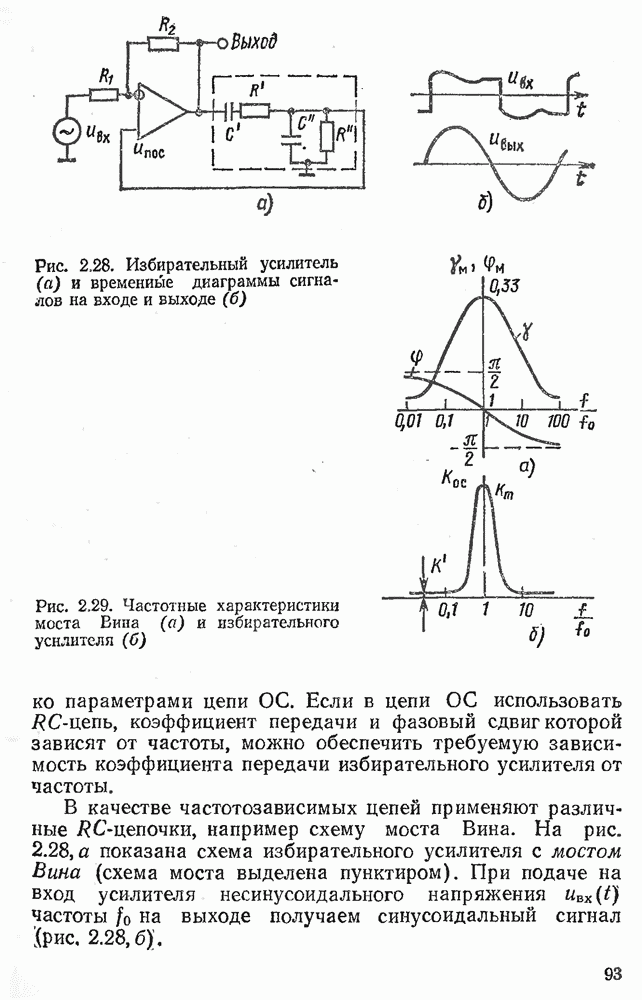
- 2.15. ИЗБИРАТЕЛЬНЫЕ УСИЛИТЕЛИ И ГЕНЕРАТОРЫ СИНУСОИДАЛЬНЫХ КОЛЕБАНИЙ
- 2.16. УСИЛИТЕЛИ С ЕМКОСТНОЙ СВЯЗЬЮ
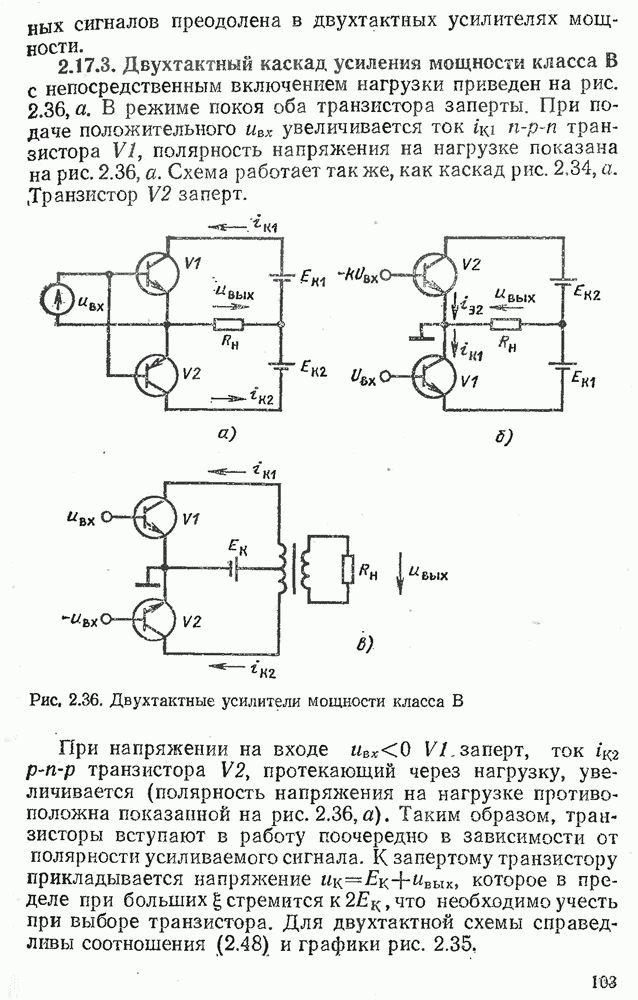
- 2.17. КАСКАДЫ УСИЛЕНИЯ МОЩНОСТИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава третья. ИМПУЛЬСНЫЕ УСТРОЙСТВА
- 3.1. ПРЕИМУЩЕСТВА ПЕРЕДАЧИ ИНФОРМАЦИИ В ВИДЕ ИМПУЛЬСОВ
- 3.2. КЛЮЧЕВОЙ РЕЖИМ ТРАНЗИСТОРА
- 3.3. НЕЛИНЕЙНЫЙ РЕЖИМ РАБОТЫ ОПЕРАЦИОННОГО УСИЛИТЕЛЯ. КОМПАРАТОРЫ
- 3.4. ПРЕОБРАЗОВАНИЕ ИМПУЛЬСНЫХ СИГНАЛОВ С ПОМОЩЬЮ RС-ЦЕПЕЙ
- 3.3. МУЛЬТИВИБРАТОР НА ОПЕРАЦИОННОМ УСИЛИТЕЛЕ
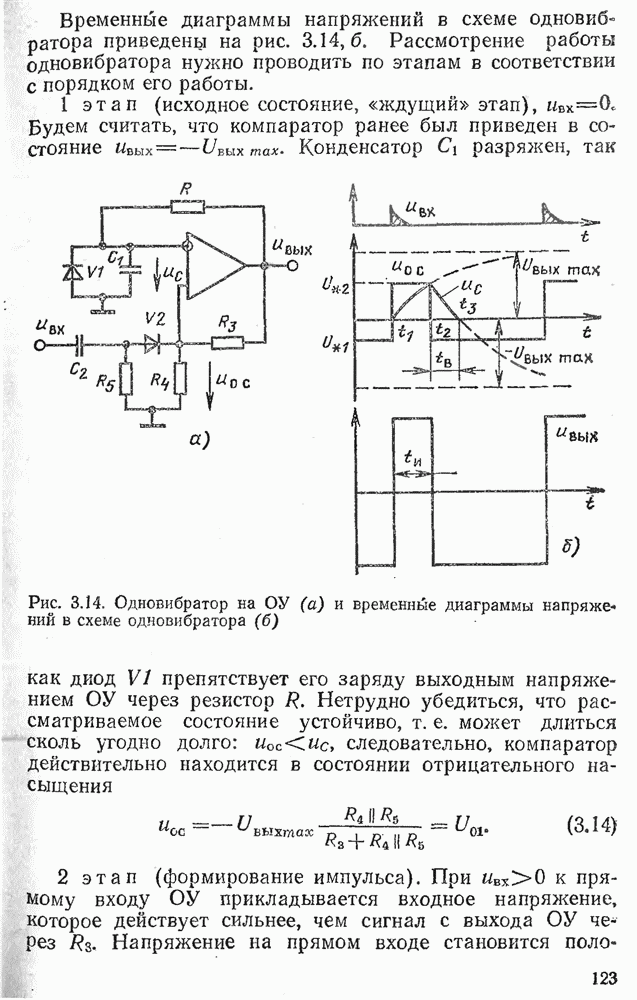
- 3.6. ОДНОВИБРАТОР НА ОПЕРАЦИОННОМ УСИЛИТЕЛЕ
- 3.7. ГЕНЕРАТОРЫ ЛИНЕЙНО ИЗМЕНЯЮЩИХСЯ НАПРЯЖЕНИЙ
- 3.8. МАГНИТНО-ТРАНЗИСТОРНЫЕ ГЕНЕРАТОРЫ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава четвертая. ЛОГИЧЕСКИЕ И ЦИФРОВЫЕ УСТРОЙСТВА
- 4.1. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ И ИХ РЕАЛИЗАЦИЯ
- 4.2. ТИПЫ ЛОГИЧЕСКИХ МИКРОСХЕМ
- 4.3. АЛГЕБРА ЛОГИКИ
- 4.4. КОМБИНАЦИОННЫЕ ЛОГИЧЕСКИЕ УСТРОЙСТВА
- 4.5. МИНИМИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 4.6. КОМБИНАЦИОННЫЕ ИНТЕГРАЛЬНЫЕ МИКРОСХЕМЫ
- 4.7. АСИНХРОННЫЙ RS-ТРИГГЕР
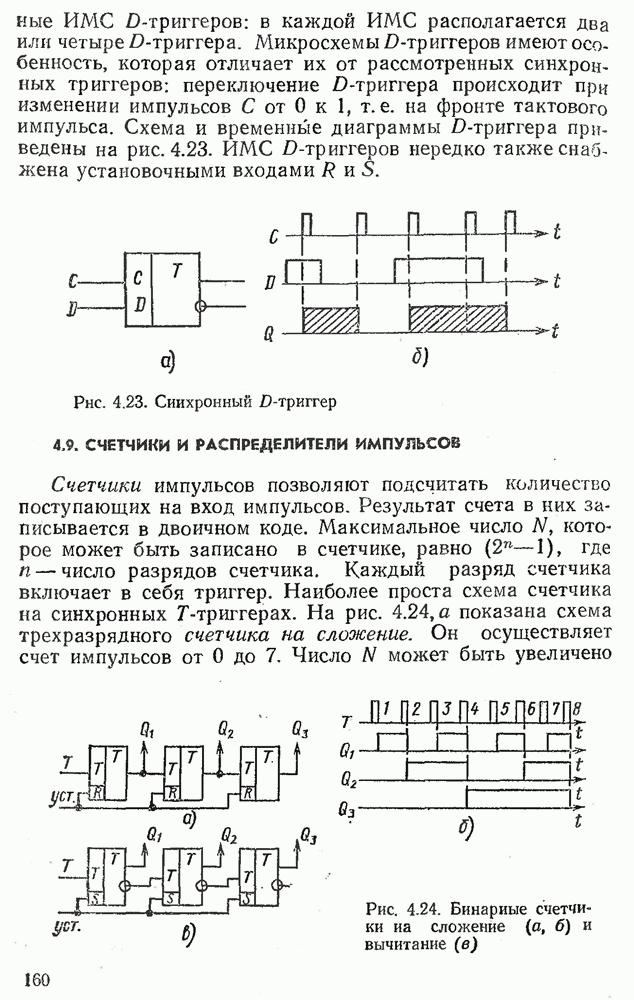
- 4.8. СИНХРОННЫЕ ТРИГГЕРЫ
- 4.9. СЧЕТЧИКИ И РАСПРЕДЕЛИТЕЛИ ИМПУЛЬСОВ
- 4.10. РЕГИСТРЫ
- 4.11. ЦИФРО-АНАЛОГОВЫЕ И АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 4.12. МИКРОПРОЦЕССОРЫ
- 4.13. СИСТЕМА КОМАНД МИКРОПРОЦЕССОРА
- 4.14. ИНДИКАТОРНЫЕ ПРИБОРЫ И УЗЛЫ ЦИФРОВЫХ УСТРОЙСТВ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава пятая. МАЛОМОЩНЫЕ ВЫПРЯМИТЕЛИ ОДНОФАЗНОГО ТОКА
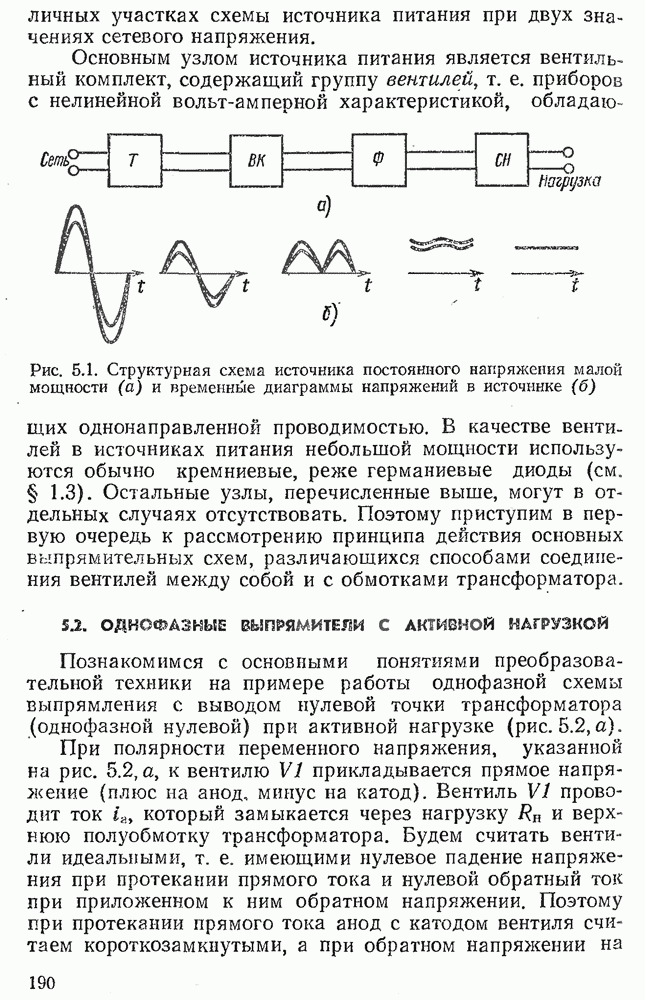
- 5.1. СТРУКТУРА ИСТОЧНИКА ПИТАНИЯ
- 5.2. ОДНОФАЗНЫЕ ВЫПРЯМИТЕЛИ С АКТИВНОЙ НАГРУЗКОЙ
- 5.3. ОДНОФАЗНЫЕ ВЫПРЯМИТЕЛИ С АКТИВНО-ИНДУКТИВНОЙ НАГРУЗКОЙ
- 5.4. ФИЛЬТРЫ МАЛОМОЩНЫХ ВЫПРЯМИТЕЛЕЙ
- 5.5. ОСОБЕННОСТИ РАБОТЫ И РАСЧЕТА ВЫПРЯМИТЕЛЯ С ЕМКОСТНЫМ ФИЛЬТРОМ
- 5.6. ВНЕШНИЕ ХАРАКТЕРИСТИКИ МАЛОМОЩНЫХ ВЫПРЯМИТЕЛЕЙ
- 5.7. СТАБИЛИЗАТОРЫ НАПРЯЖЕНИЯ
- 5.8. ИСТОЧНИКИ ПИТАНИЯ С МНОГОКРАТНЫМ ПРЕОБРАЗОВАНИЕМ ЭНЕРГИИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
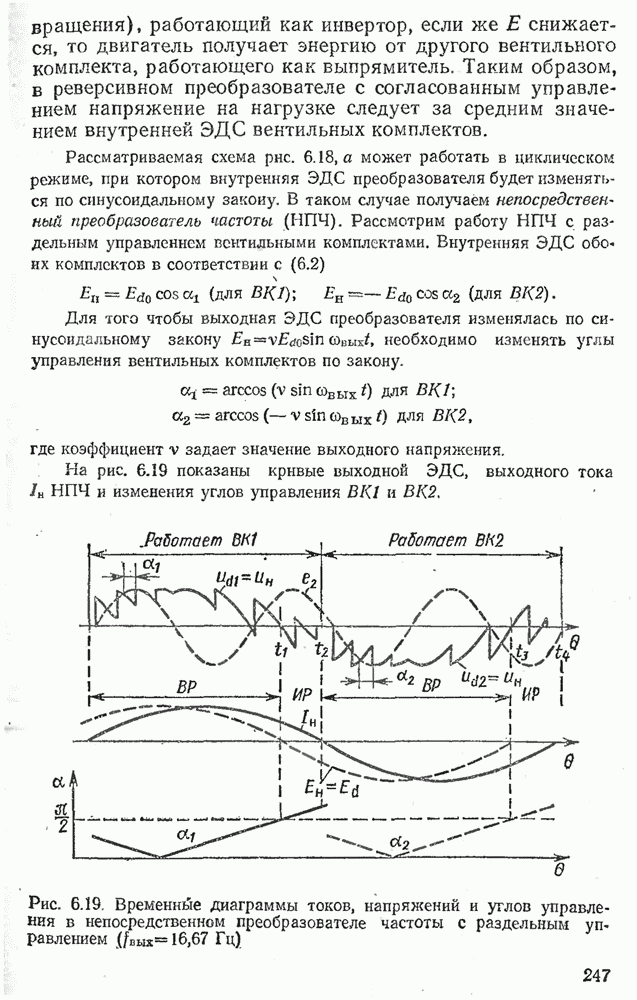
- Глава шестая. ВЕДОМЫЕ СЕТЬЮ ПРЕОБРАЗОВАТЕЛИ СРЕДНЕЙ И БОЛЬШОЙ МОЩНОСТИ
- 6.1. ПРИМЕНЕНИЕ ВЕНТИЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ В ЭНЕРГЕТИКЕ И ЭЛЕКТРОТЕХНИКЕ
- 6.2. ОДНОФАЗНЫЙ УПРАВЛЯЕМЫЙ ВЫПРЯМИТЕЛЬ
- 6.3. ОДНОФАЗНЫЙ ВЕДОМЫЙ СЕТЬЮ ИНВЕРТОР
- 6.4. ТРЕХФАЗНЫЙ НУЛЕВОЙ ВЫПРЯМИТЕЛЬ
- 6.5. ТРЁХФАЗНЫЙ МОСТОВОЙ ВЫПРЯМИТЕЛЬ
- 6.6. СОСТАВНЫЕ МНОГОФАЗНЫЕ СХЕМЫ ВЫПРЯМЛЕНИЯ
- 6.7. РЕВЕРСИВНЫЕ ВЫПРЯМИТЕЛИ И НЕПОСРЕДСТВЕННЫЕ ПРЕОБРАЗОВАТЕЛИ ЧАСТОТЫ
- 6.8. РЕГУЛИРУЕМЫЕ ПРЕОБРАЗОВАТЕЛИ ПЕРЕМЕННОГО НАПРЯЖЕНИЯ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава седьмая. ВЛИЯНИЕ ВЕНТИЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ НА ПИТАЮЩУЮ СЕТЬ
- 7.1. КОЭФФИЦИЕНТ МОЩНОСТИ ВЕНТИЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ
- 7.2. ВЕНТИЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ С ПОВЫШЕННЫМ КОЭФФИЦИЕНТОМ МОЩНОСТИ
- 7.3. ИСТОЧНИКИ РЕАКТИВНОЙ МОЩНОСТИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава восьмая. СИСТЕМЫ УПРАВЛЕНИЯ ВЕНТИЛЬНЫМИ ПРЕОБРАЗОВАТЕЛЯМИ
- 8.1. ФУНКЦИИ И СТРУКТУРА СИСТЕМ УПРАВЛЕНИЙ
- 8.2. ФАЗОСМЕЩАЮЩИЕ УСТРОЙСТВА (ФСУ)
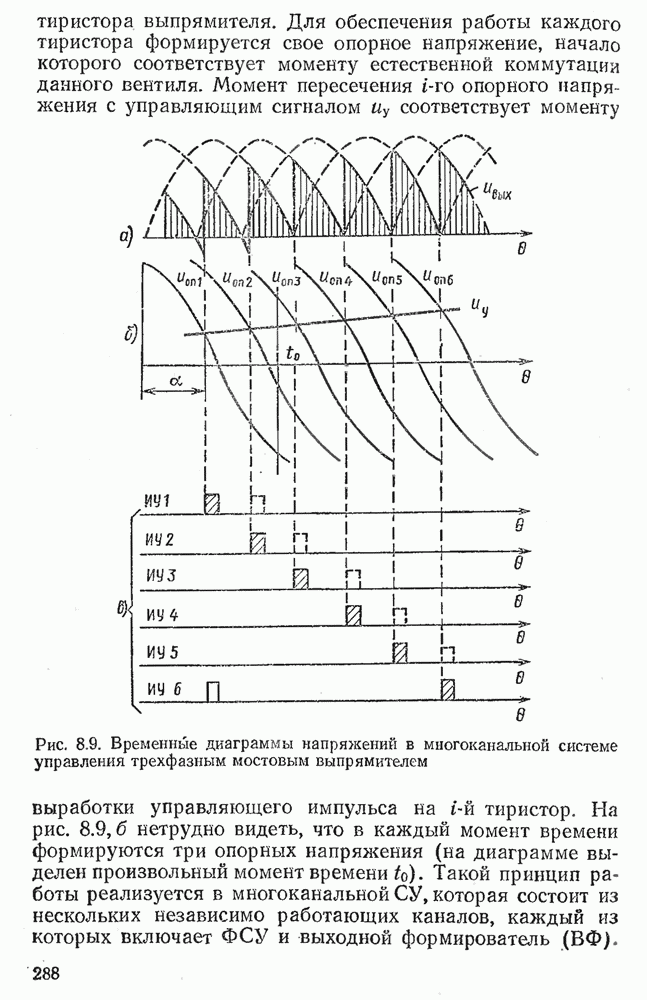
- 8.3. МНОГОКАНАЛЬНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
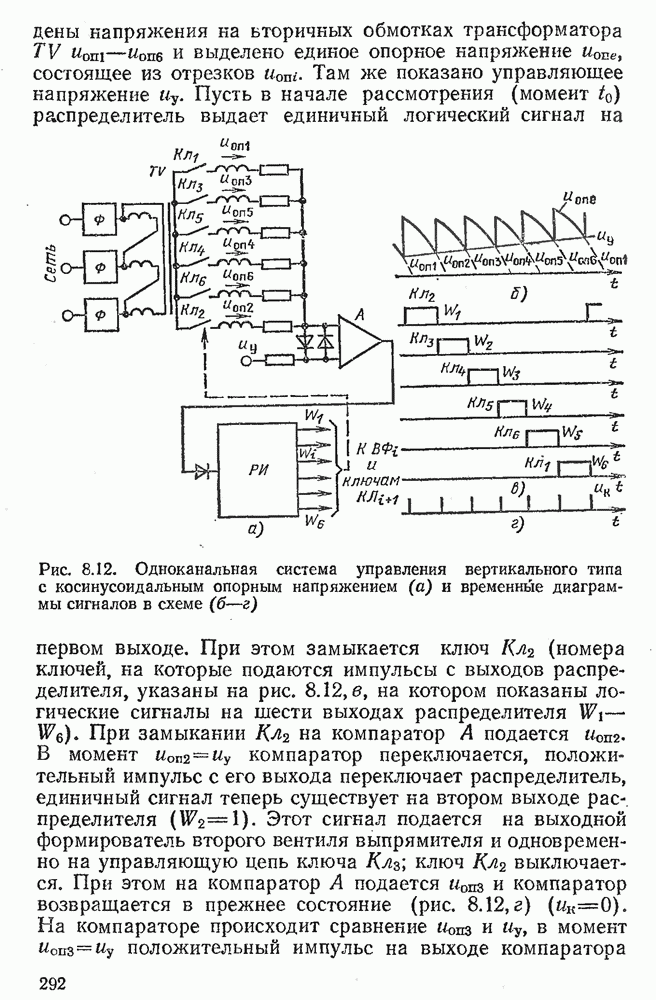
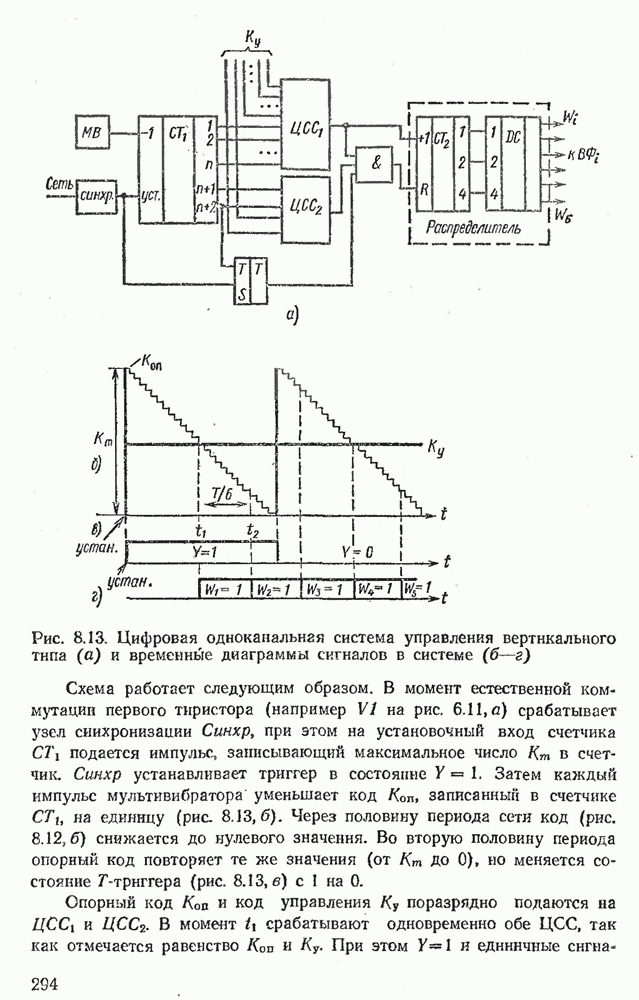
- 8.4. ОДНОКАНАЛЬНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава девятая. АВТОНОМНЫЕ ВЕНТИЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
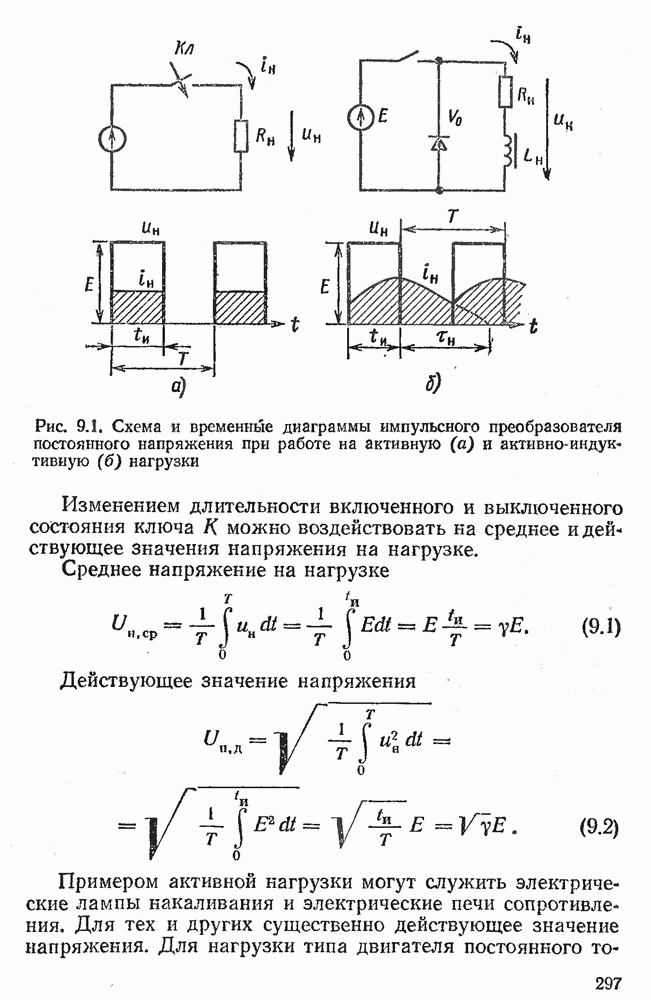
- 9.1. СПОСОБЫ РЕГУЛИРОВАНИЯ ПОСТОЯННОГО НАПРЯЖЕНИЯ
- 9.2. УЗЛЫ КОММУТАЦИИ ОДНООПЕРАЦИОННЫХ ТИРИСТОРОВ
- 9.3. ИНВЕРТОРЫ НАПРЯЖЕНИЯ
- 9.4. ИНВЕРТОРЫ ТОКА
- 9.5. РЕЗОНАНСНЫЕ ИНВЕРТОРЫ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- СПИСОК ЛИТЕРАТУРЫ