| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
4.3. АЛГЕБРА ЛОГИКИ
Алгебра логики является аналогом обычной алгебры. Ее особенность заключается в том, что аргументы и функции принимают только два значения: 0 и 1. Алгебра логики выполняет следующие функции:
1) позволяет математически записывать логические сообщения и связи между ними, что необходимо для определения порядка и принципа работы устройства;
2) позволяет реализовать логические уравнения в виде логических схем, т. е. переходить от аналитического описания процесса к его схемной реализации в виде логического автомата;
3) позволяет проводить реализацию логических автоматов в оптимальном виде (минимальное число элементов, их однородность, надежность функционирования и т. д.).
Логические операции могут быть интерпретированы графически с помощью диаграмм Венна (рис. 4.9). Все поле диаграммы Венна соответствует логической единице ("всегда"), нулевая площадь — логическому нулю («никогда»). Логические функции изображаются в виде кругов (рис. 4.9, а).
Диаграммы Венна позволяют наглядно изобразить логические операции. На рис. 4.9, а заштрихована суммарная площадь переменных А, В. Их суммарная площадь соответствует А+В, т. е. является интерпретацией операции ИЛИ.

Рис. 4.9. Диаграммы Венна
На диаграмме рис. 4.9, б заштрихована площадь А, т. е. графически изображена операция НЕ. Общая площадь фигур А и В заштрихована на рис. 4.9, в и соответствует логическому произведению АВ (операция И).
Порядок действий в алгебре логики следующий: сначала выполняется операция НЕ, затем И и наконец ИЛИ. Как и в обычной алгебре, для изменения порядка действий используются скобки. Не следует забывать, что операций вычитания и деления в алгебре логики нет. Справедливы переместительный и сочетательный законы:

Для осуществления операций над логическими выражениями пользуются рядом тождеств:

Следующие тождества называются формулами де Моргана:

Все тождества могут быть легко доказаны с помощью диаграмм Венна.
Например, на диаграмме рис. 4.9, а заштрихована площадь, соответствующая левой и правой частям тождества (11), на рис. 4.9, г заштрихована площадь, соответствующая левой и правой частям формулы де Моргана (12), а рис. 4.9, д интерпретирует формулу де Моргана (13).
Тождества алгебры логики полезно запомнить. Используя тождества, можно упростить логические уравнения, при этом сводится к минимуму число логических элементов, необходимых для реализации логической функции.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава первая. ПОЛУПРОВОДНИКОВЫЕ И МИКРОЭЛЕКТРОННЫЕ ПРИБОРЫ
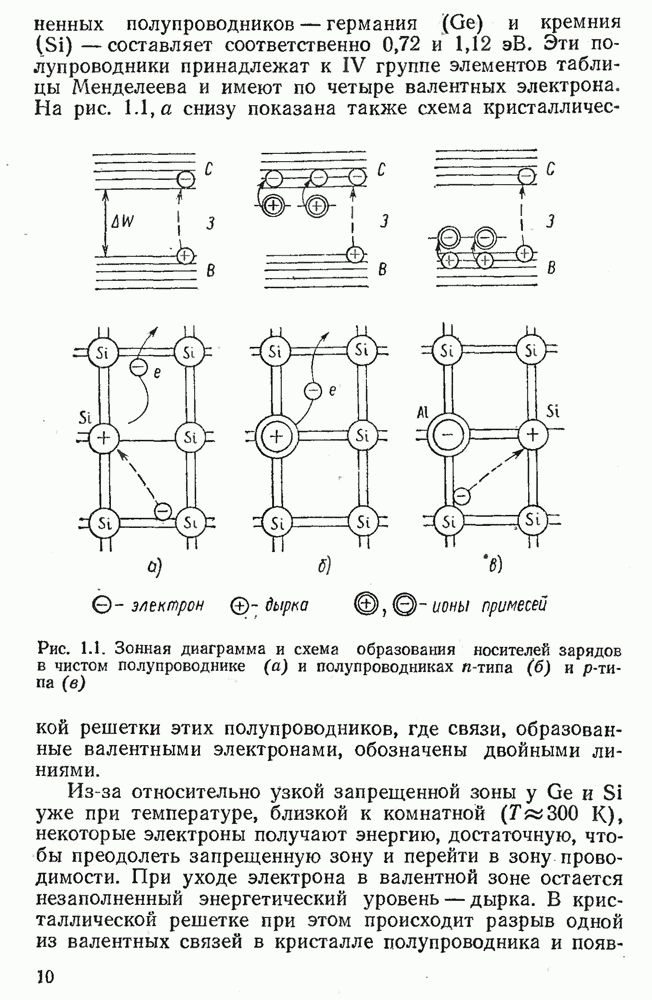
- 1.1. ЭЛЕКТРОПРОВОДНОСТЬ ПОЛУПРОВОДНИКОВ
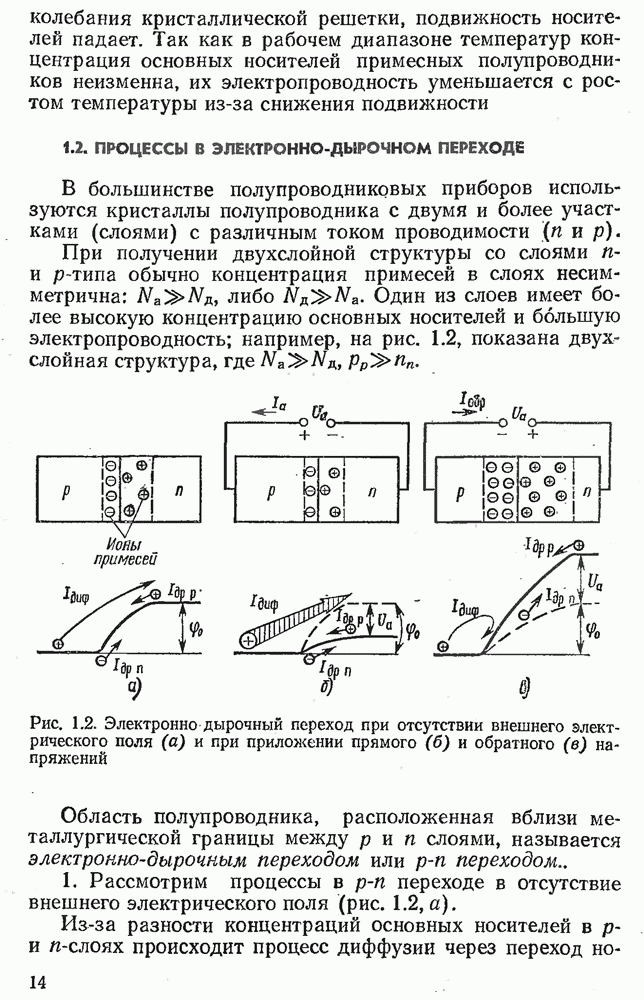
- 1.2. ПРОЦЕССЫ В ЭЛЕКТРОННО-ДЫРОЧНОМ ПЕРЕХОДЕ
- 1.3. ПОЛУПРОВОДНИКОВЫЕ ДИОДЫ
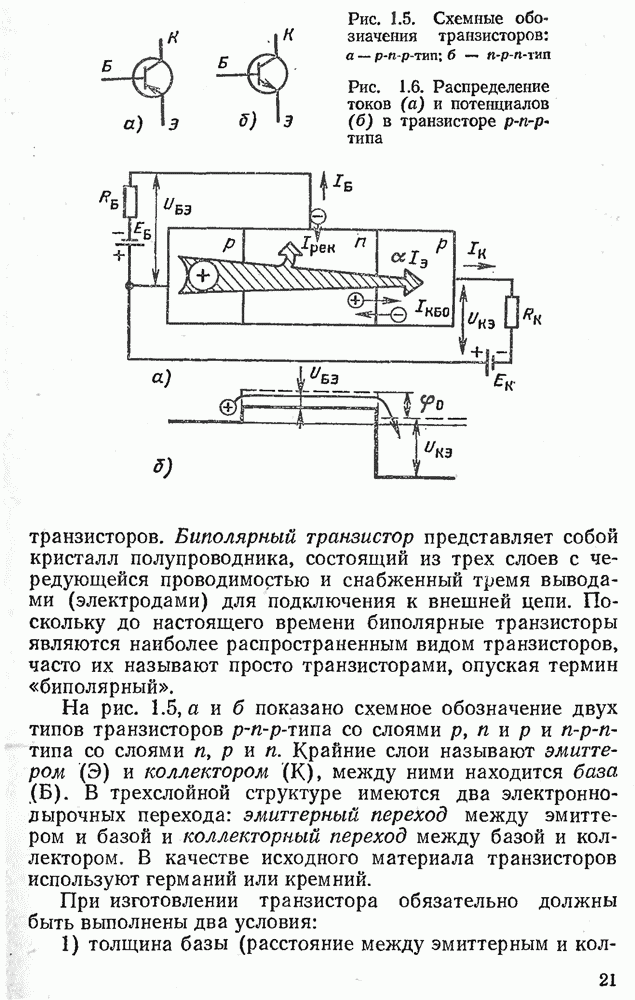
- 1.4. БИПОЛЯРНЫЕ ТРАНЗИСТОРЫ
- 1.5. ХАРАКТЕРИСТИКИ И ПАРАМЕТРЫ БИПОЛЯРНЫХ ТРАНЗИСТОРОВ
- 1.6. ПОЛЕВЫЕ ТРАНЗИСТОРЫ
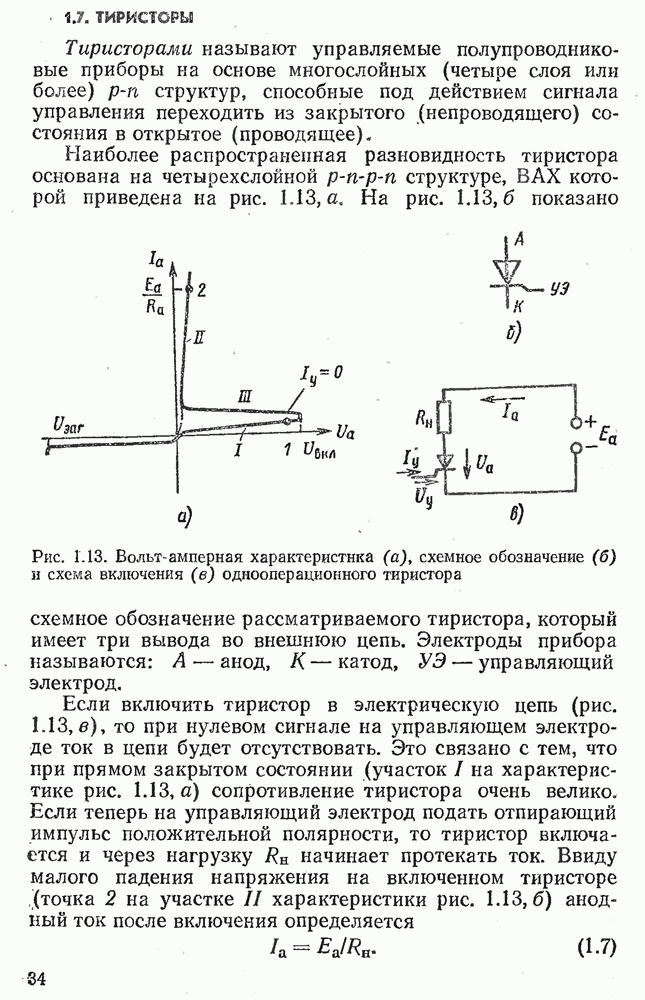
- 1.7. ТИРИСТОРЫ
- 1.8. ПАРАМЕТРЫ И РАЗНОВИДНОСТИ ТИРИСТОРОВ
- 1.9. ИНТЕГРАЛЬНЫЕ МИКРОСХЕМЫ
- 1.10. ПОЛУПРОВОДНИКОВЫЕ ОПТОЭЛЕКТРОННЫЕ ПРИБОРЫ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава вторая. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ
- 2.1. ПЕРЕДАТОЧНАЯ ХАРАКТЕРИСТИКА УСИЛИТЕЛЬНОГО КАСКАДА
- 2.2. РЕЖИМ ПОКОЯ В КАСКАДЕ С ОБЩИМ ЭМИТТЕРОМ
- 2.3. ОБРАТНЫЕ СВЯЗИ. СТАБИЛИЗАЦИЯ РЕЖИМА ПОКОЯ
- 2.4. СХЕМА ЗАМЕЩЕНИЯ И ОСНОВНЫЕ ПОКАЗАТЕЛИ КАСКАДА С ОЭ
- 2.5. ВИДЫ СВЯЗЕЙ И ДРЕЙФ НУЛЯ В УСИЛИТЕЛЯХ ПОСТОЯННОГО ТОКА
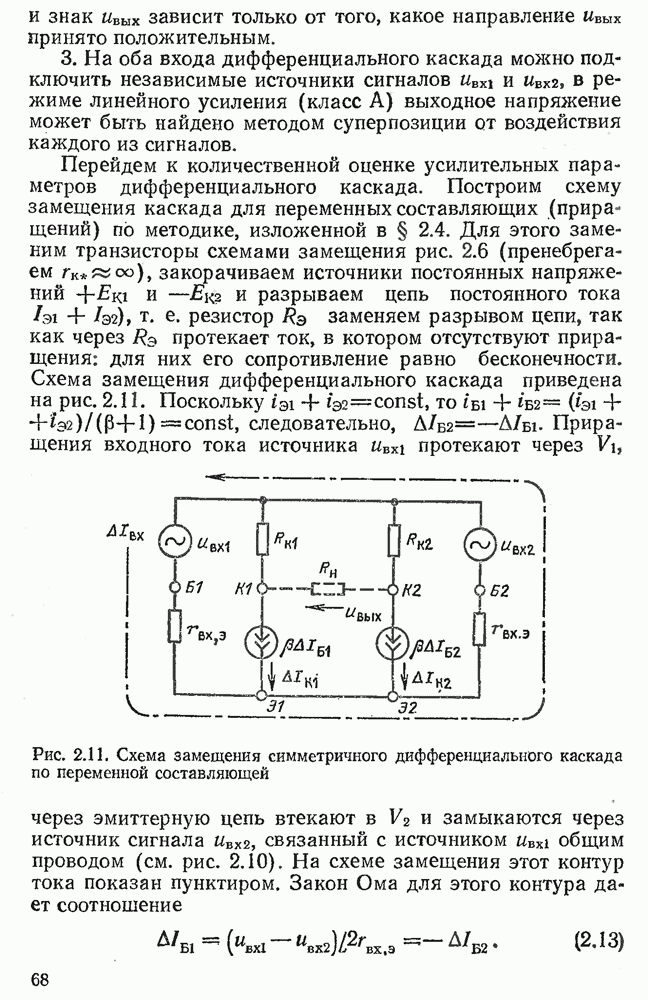
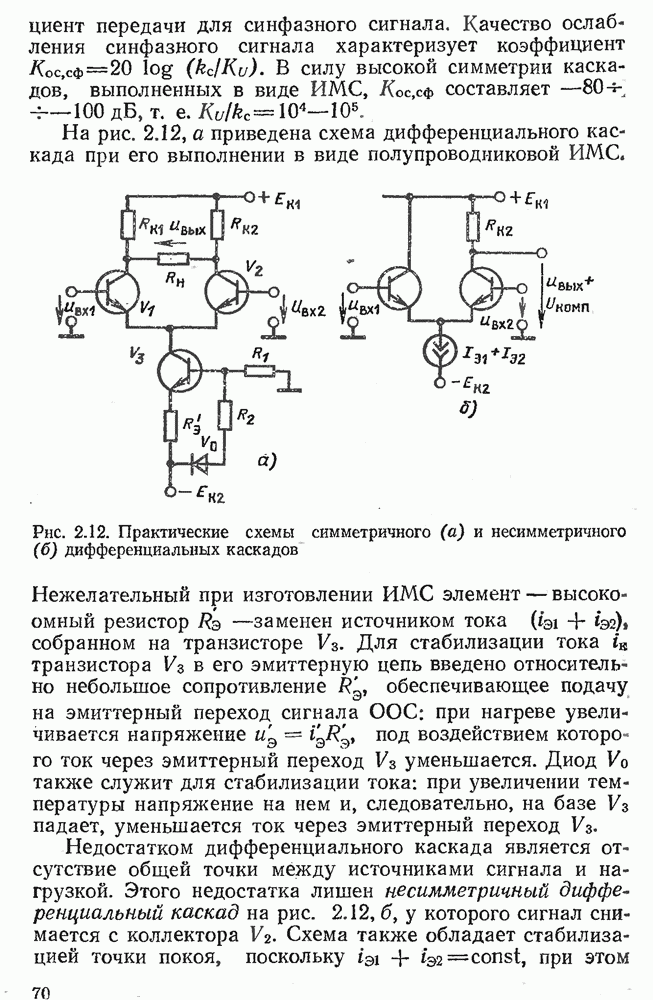
- 2.6. ДИФФЕРЕНЦИАЛЬНЫЙ КАСКАД
- 2.7. КАСКАД С ОБЩИМ КОЛЛЕКТОРОМ
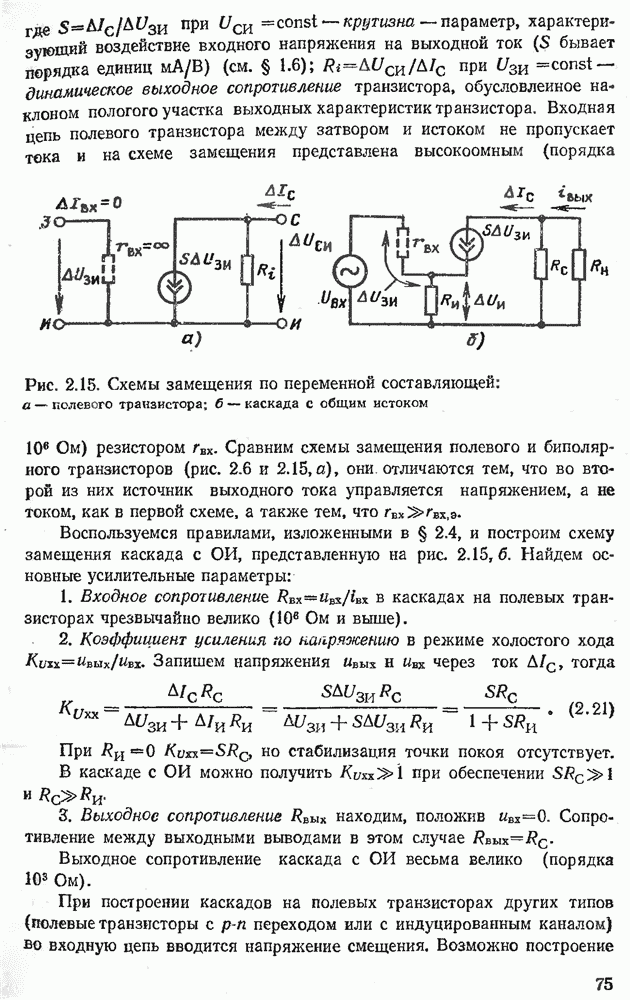
- 2.8. КАСКАД С ОБЩИМ ИСТОКОМ
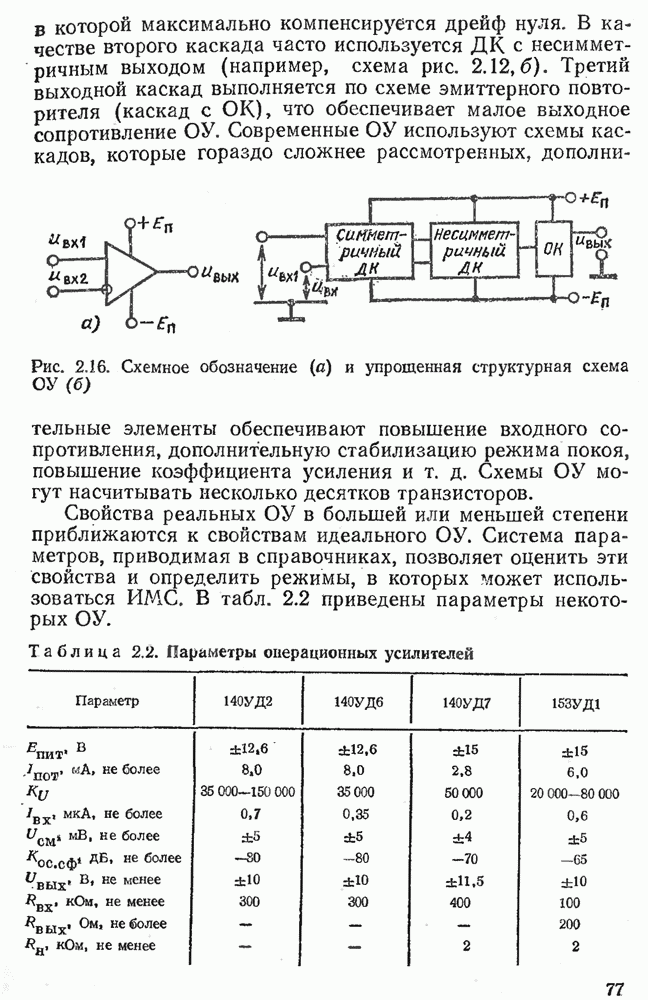
- 2.9. ОПЕРАЦИОННЫЙ УСИЛИТЕЛЬ
- 2.10. НЕИНВЕРТИРУЮЩИЙ ОПЕРАЦИОННЫЙ УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ
- 2.11. ИНВЕРТИРУЮЩИЙ ОПЕРАЦИОННЫЙ УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ
- 2.12. ОПЕРАЦИОННЫЕ СХЕМЫ
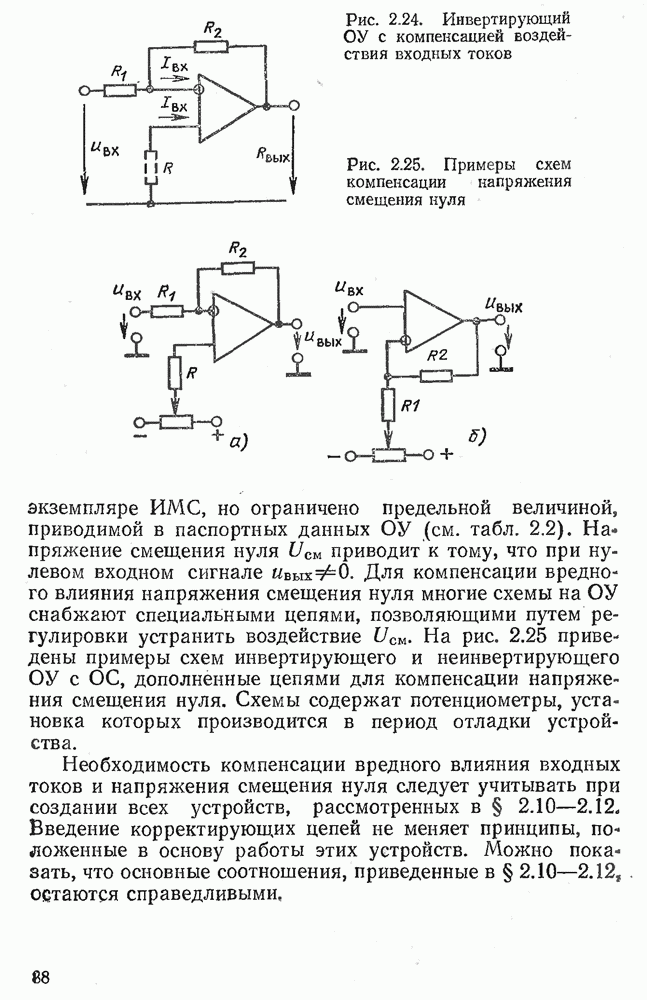
- 2.13. КОМПЕНСАЦИЯ ВХОДНЫХ ТОКОВ И НАПРЯЖЕНИЯ СМЕЩЕНИЯ НУЛЯ
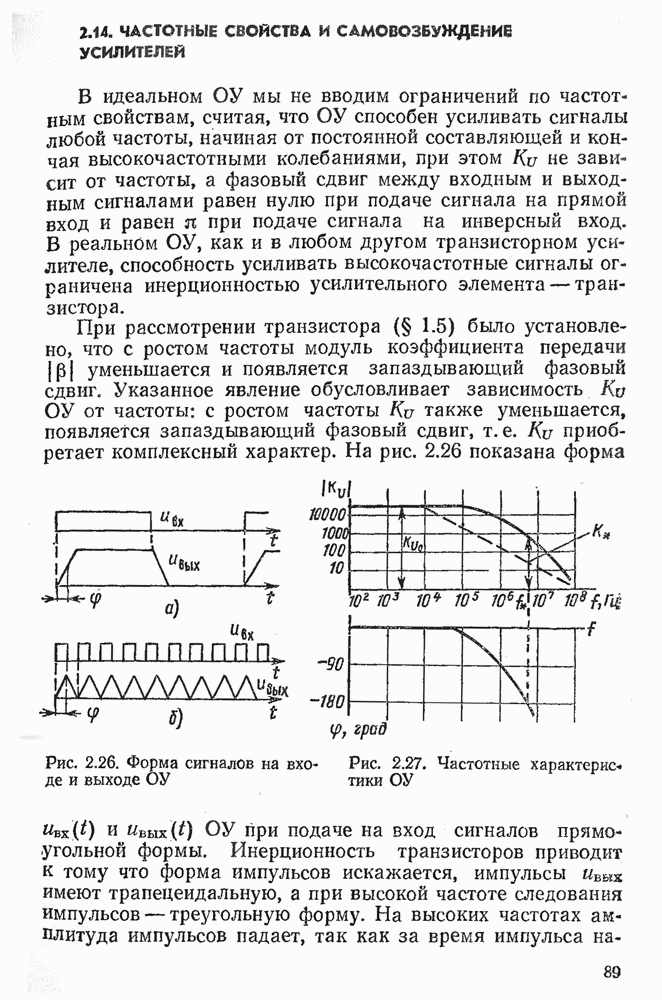
- 2.14. ЧАСТОТНЫЕ СВОЙСТВА И САМОВОЗБУЖДЕНИЕ УСИЛИТЕЛЕЙ
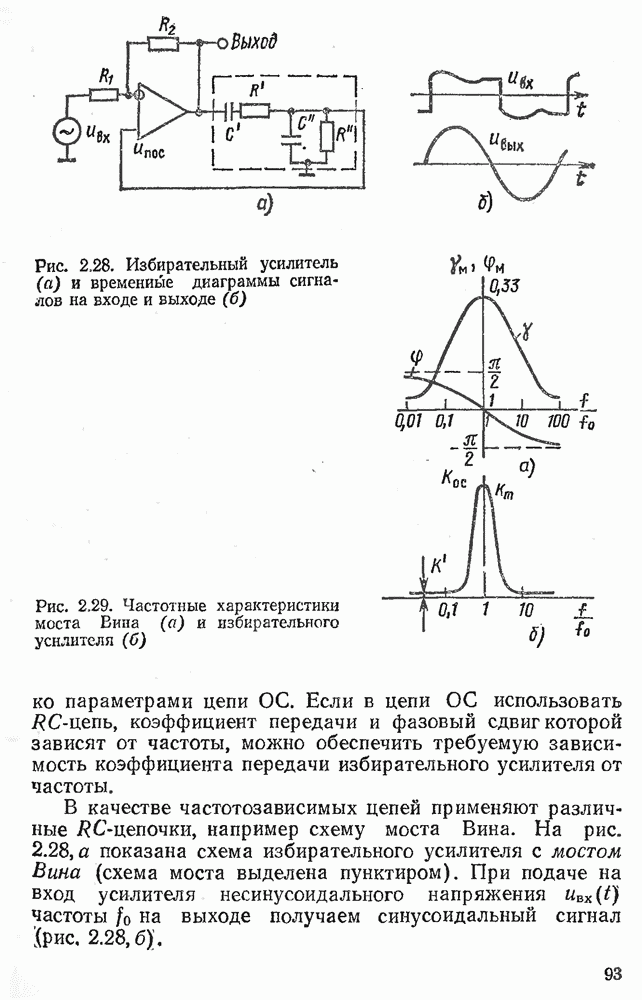
- 2.15. ИЗБИРАТЕЛЬНЫЕ УСИЛИТЕЛИ И ГЕНЕРАТОРЫ СИНУСОИДАЛЬНЫХ КОЛЕБАНИЙ
- 2.16. УСИЛИТЕЛИ С ЕМКОСТНОЙ СВЯЗЬЮ
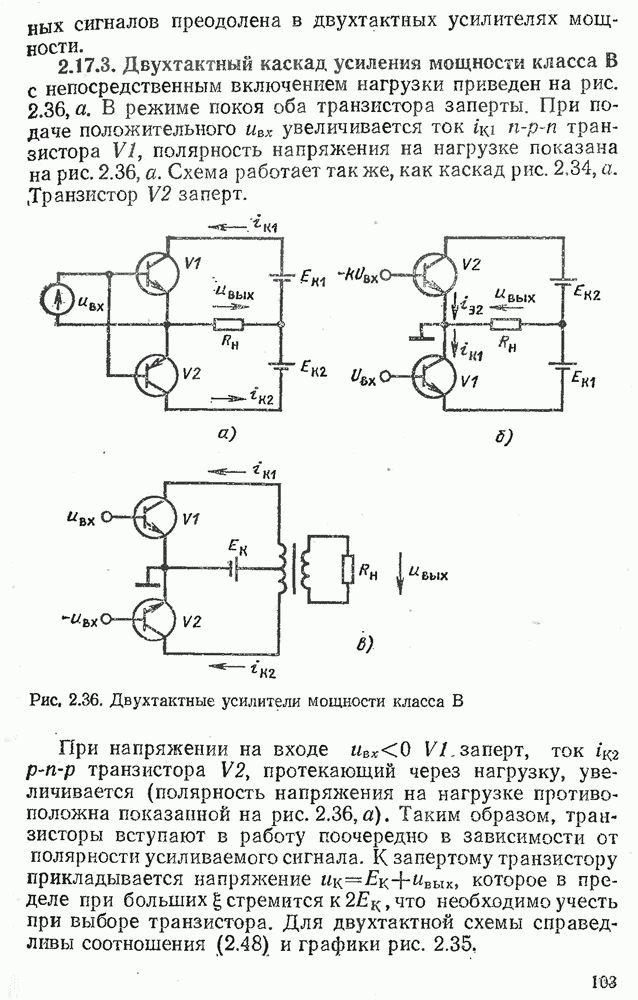
- 2.17. КАСКАДЫ УСИЛЕНИЯ МОЩНОСТИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава третья. ИМПУЛЬСНЫЕ УСТРОЙСТВА
- 3.1. ПРЕИМУЩЕСТВА ПЕРЕДАЧИ ИНФОРМАЦИИ В ВИДЕ ИМПУЛЬСОВ
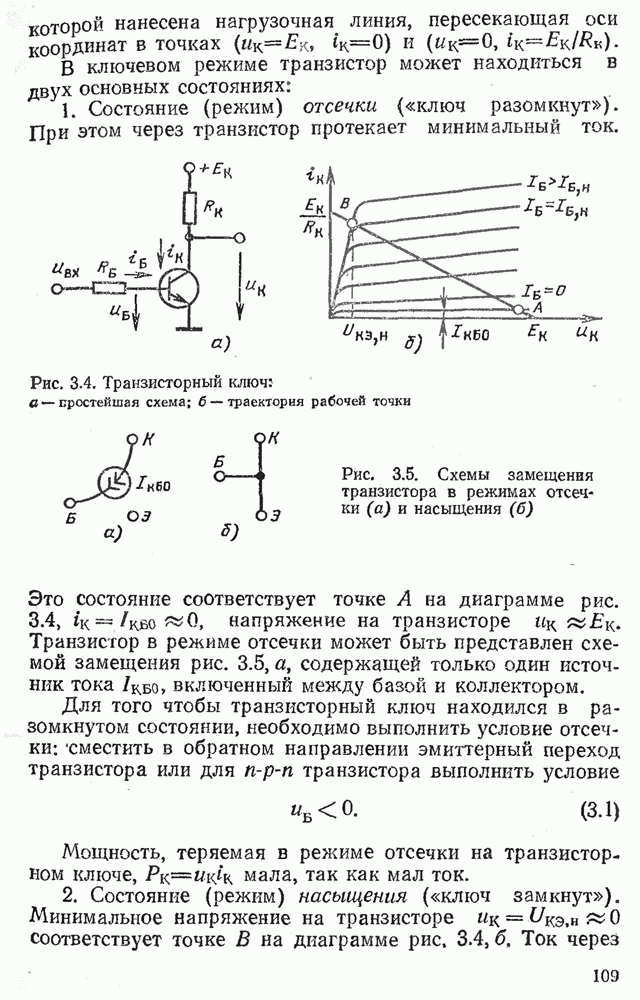
- 3.2. КЛЮЧЕВОЙ РЕЖИМ ТРАНЗИСТОРА
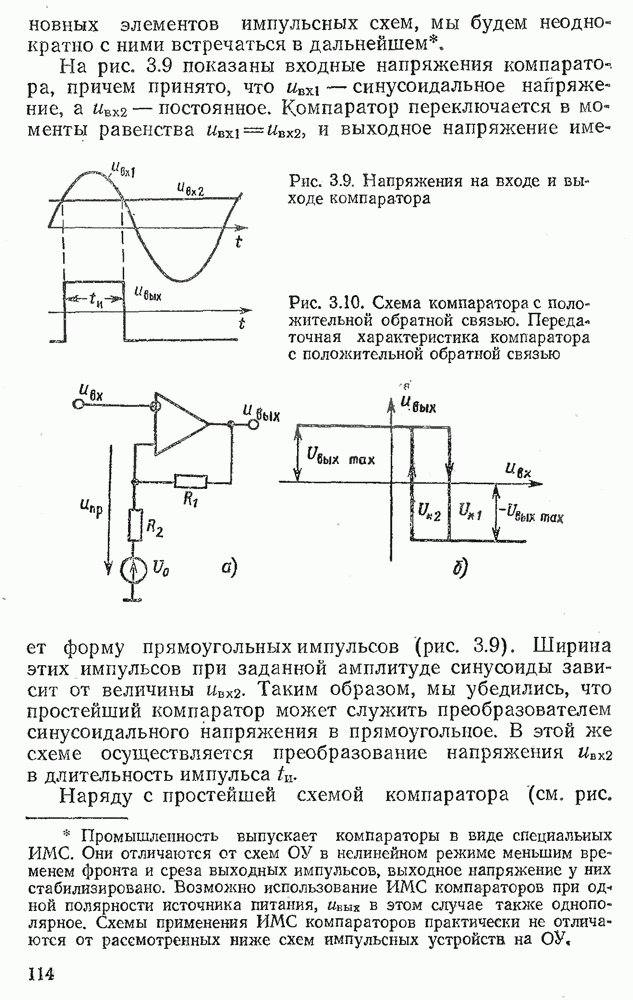
- 3.3. НЕЛИНЕЙНЫЙ РЕЖИМ РАБОТЫ ОПЕРАЦИОННОГО УСИЛИТЕЛЯ. КОМПАРАТОРЫ
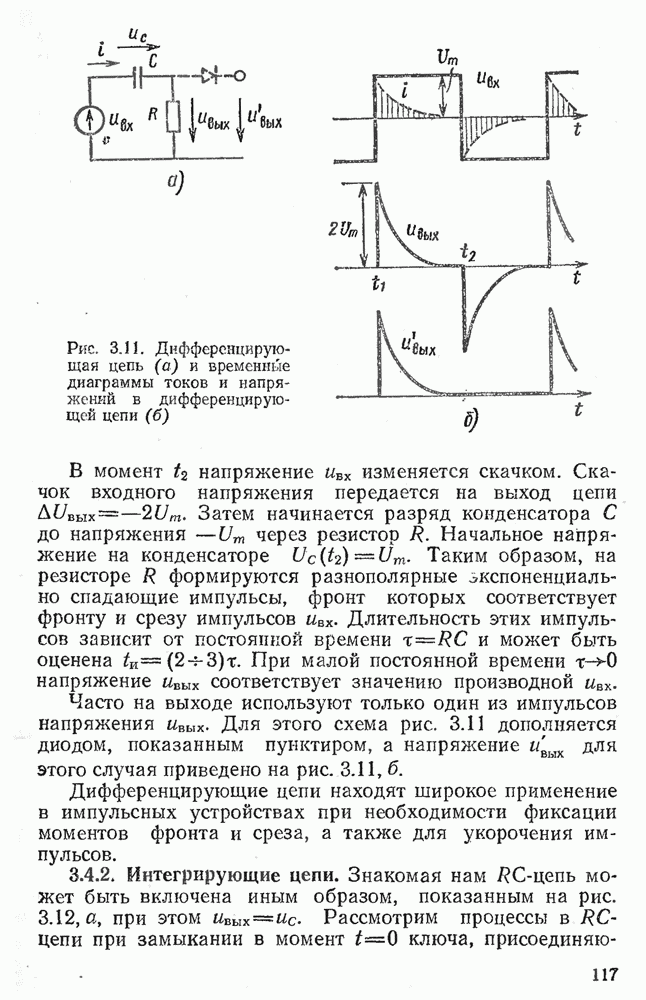
- 3.4. ПРЕОБРАЗОВАНИЕ ИМПУЛЬСНЫХ СИГНАЛОВ С ПОМОЩЬЮ RС-ЦЕПЕЙ
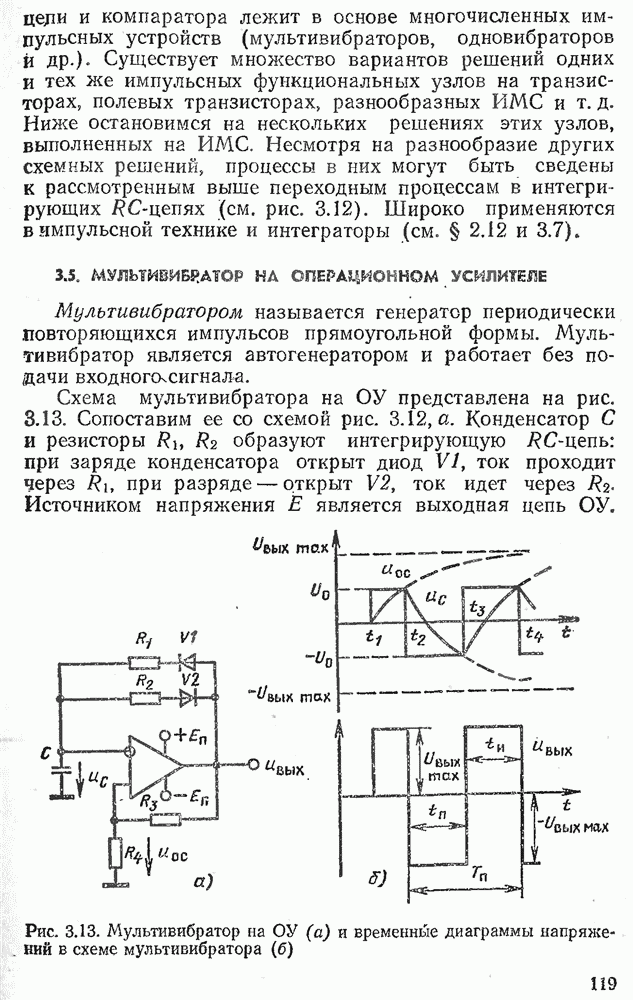
- 3.3. МУЛЬТИВИБРАТОР НА ОПЕРАЦИОННОМ УСИЛИТЕЛЕ
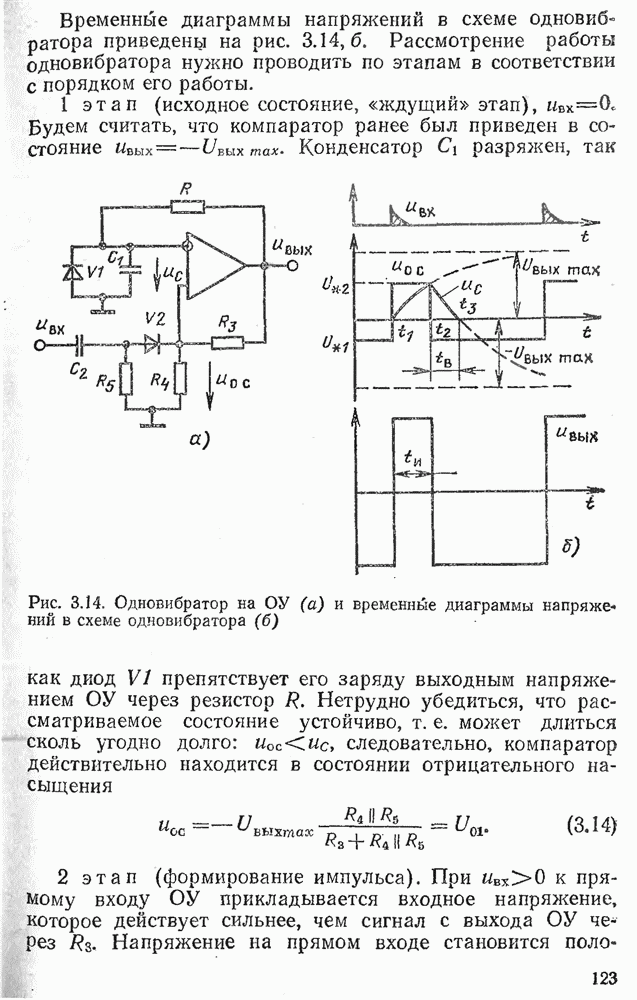
- 3.6. ОДНОВИБРАТОР НА ОПЕРАЦИОННОМ УСИЛИТЕЛЕ
- 3.7. ГЕНЕРАТОРЫ ЛИНЕЙНО ИЗМЕНЯЮЩИХСЯ НАПРЯЖЕНИЙ
- 3.8. МАГНИТНО-ТРАНЗИСТОРНЫЕ ГЕНЕРАТОРЫ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава четвертая. ЛОГИЧЕСКИЕ И ЦИФРОВЫЕ УСТРОЙСТВА
- 4.1. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ И ИХ РЕАЛИЗАЦИЯ
- 4.2. ТИПЫ ЛОГИЧЕСКИХ МИКРОСХЕМ
- 4.3. АЛГЕБРА ЛОГИКИ
- 4.4. КОМБИНАЦИОННЫЕ ЛОГИЧЕСКИЕ УСТРОЙСТВА
- 4.5. МИНИМИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 4.6. КОМБИНАЦИОННЫЕ ИНТЕГРАЛЬНЫЕ МИКРОСХЕМЫ
- 4.7. АСИНХРОННЫЙ RS-ТРИГГЕР
- 4.8. СИНХРОННЫЕ ТРИГГЕРЫ
- 4.9. СЧЕТЧИКИ И РАСПРЕДЕЛИТЕЛИ ИМПУЛЬСОВ
- 4.10. РЕГИСТРЫ
- 4.11. ЦИФРО-АНАЛОГОВЫЕ И АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 4.12. МИКРОПРОЦЕССОРЫ
- 4.13. СИСТЕМА КОМАНД МИКРОПРОЦЕССОРА
- 4.14. ИНДИКАТОРНЫЕ ПРИБОРЫ И УЗЛЫ ЦИФРОВЫХ УСТРОЙСТВ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава пятая. МАЛОМОЩНЫЕ ВЫПРЯМИТЕЛИ ОДНОФАЗНОГО ТОКА
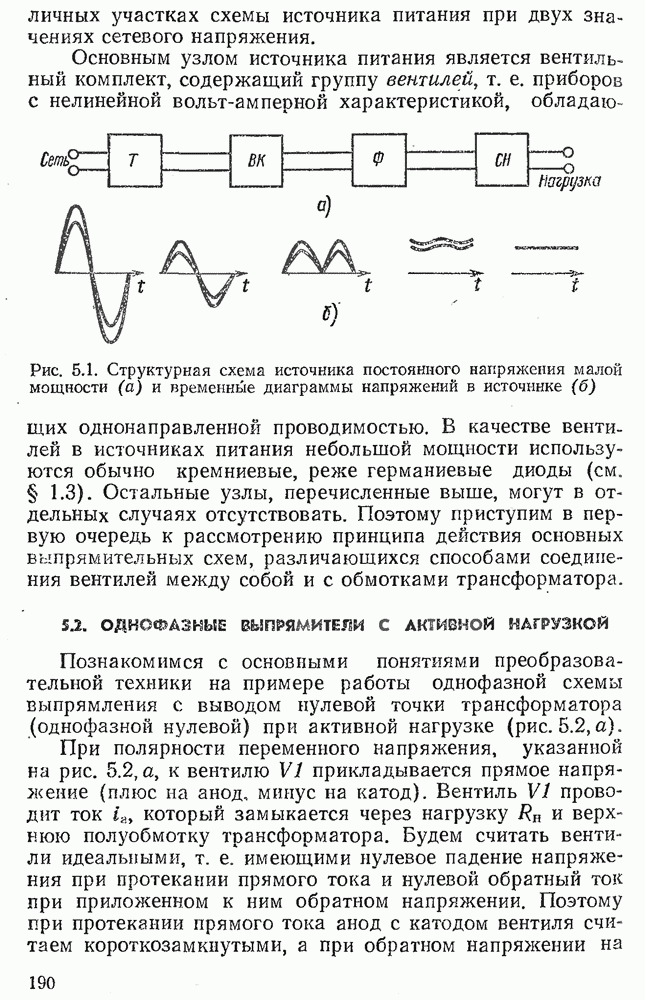
- 5.1. СТРУКТУРА ИСТОЧНИКА ПИТАНИЯ
- 5.2. ОДНОФАЗНЫЕ ВЫПРЯМИТЕЛИ С АКТИВНОЙ НАГРУЗКОЙ
- 5.3. ОДНОФАЗНЫЕ ВЫПРЯМИТЕЛИ С АКТИВНО-ИНДУКТИВНОЙ НАГРУЗКОЙ
- 5.4. ФИЛЬТРЫ МАЛОМОЩНЫХ ВЫПРЯМИТЕЛЕЙ
- 5.5. ОСОБЕННОСТИ РАБОТЫ И РАСЧЕТА ВЫПРЯМИТЕЛЯ С ЕМКОСТНЫМ ФИЛЬТРОМ
- 5.6. ВНЕШНИЕ ХАРАКТЕРИСТИКИ МАЛОМОЩНЫХ ВЫПРЯМИТЕЛЕЙ
- 5.7. СТАБИЛИЗАТОРЫ НАПРЯЖЕНИЯ
- 5.8. ИСТОЧНИКИ ПИТАНИЯ С МНОГОКРАТНЫМ ПРЕОБРАЗОВАНИЕМ ЭНЕРГИИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава шестая. ВЕДОМЫЕ СЕТЬЮ ПРЕОБРАЗОВАТЕЛИ СРЕДНЕЙ И БОЛЬШОЙ МОЩНОСТИ
- 6.1. ПРИМЕНЕНИЕ ВЕНТИЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ В ЭНЕРГЕТИКЕ И ЭЛЕКТРОТЕХНИКЕ
- 6.2. ОДНОФАЗНЫЙ УПРАВЛЯЕМЫЙ ВЫПРЯМИТЕЛЬ
- 6.3. ОДНОФАЗНЫЙ ВЕДОМЫЙ СЕТЬЮ ИНВЕРТОР
- 6.4. ТРЕХФАЗНЫЙ НУЛЕВОЙ ВЫПРЯМИТЕЛЬ
- 6.5. ТРЁХФАЗНЫЙ МОСТОВОЙ ВЫПРЯМИТЕЛЬ
- 6.6. СОСТАВНЫЕ МНОГОФАЗНЫЕ СХЕМЫ ВЫПРЯМЛЕНИЯ
- 6.7. РЕВЕРСИВНЫЕ ВЫПРЯМИТЕЛИ И НЕПОСРЕДСТВЕННЫЕ ПРЕОБРАЗОВАТЕЛИ ЧАСТОТЫ
- 6.8. РЕГУЛИРУЕМЫЕ ПРЕОБРАЗОВАТЕЛИ ПЕРЕМЕННОГО НАПРЯЖЕНИЯ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава седьмая. ВЛИЯНИЕ ВЕНТИЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ НА ПИТАЮЩУЮ СЕТЬ
- 7.1. КОЭФФИЦИЕНТ МОЩНОСТИ ВЕНТИЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ
- 7.2. ВЕНТИЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ С ПОВЫШЕННЫМ КОЭФФИЦИЕНТОМ МОЩНОСТИ
- 7.3. ИСТОЧНИКИ РЕАКТИВНОЙ МОЩНОСТИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава восьмая. СИСТЕМЫ УПРАВЛЕНИЯ ВЕНТИЛЬНЫМИ ПРЕОБРАЗОВАТЕЛЯМИ
- 8.1. ФУНКЦИИ И СТРУКТУРА СИСТЕМ УПРАВЛЕНИЙ
- 8.2. ФАЗОСМЕЩАЮЩИЕ УСТРОЙСТВА (ФСУ)
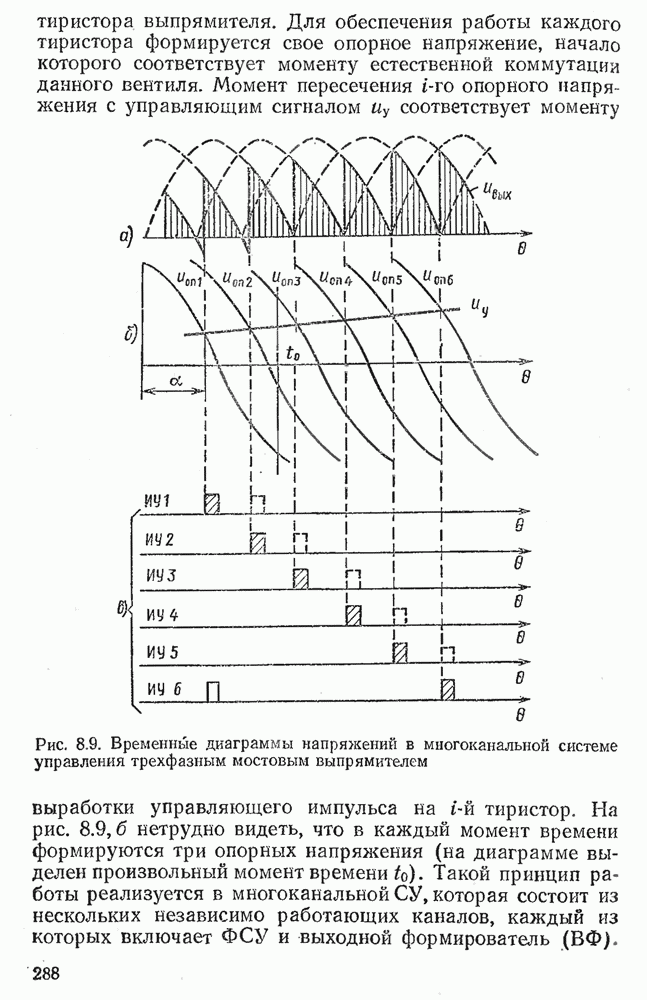
- 8.3. МНОГОКАНАЛЬНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
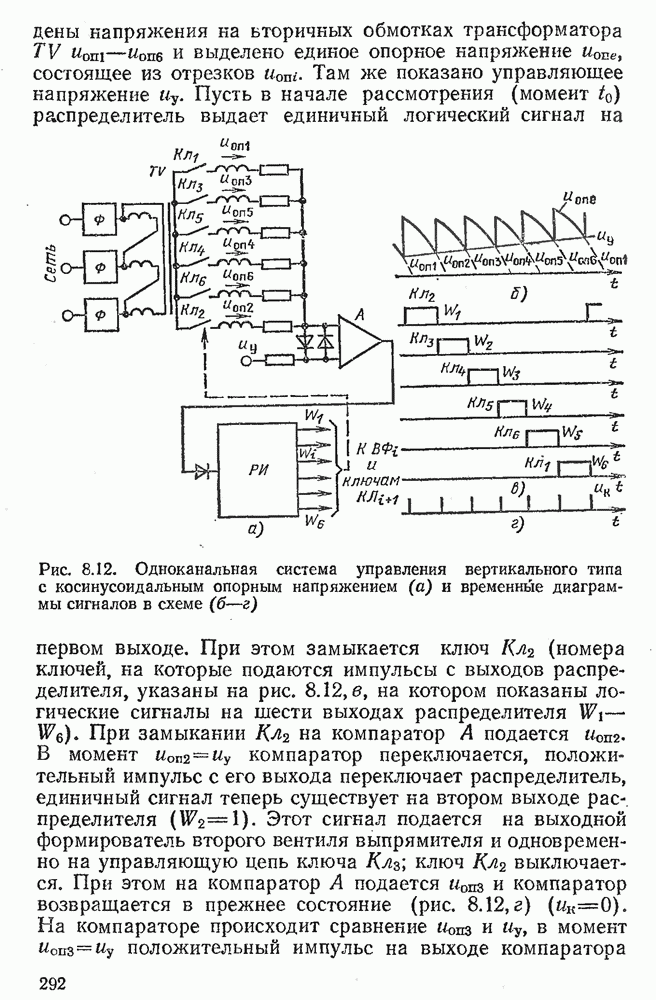
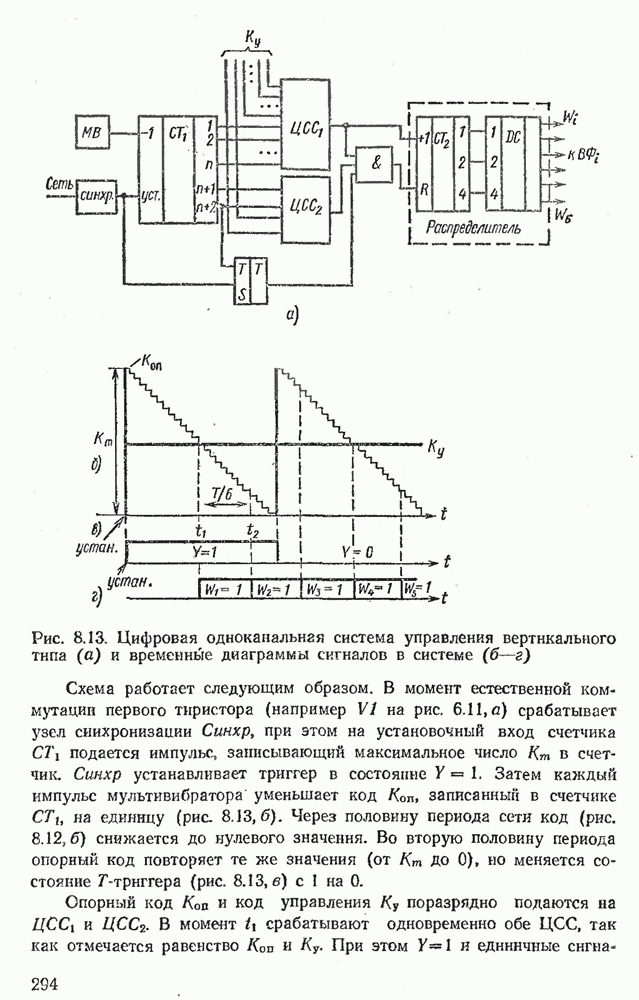
- 8.4. ОДНОКАНАЛЬНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава девятая. АВТОНОМНЫЕ ВЕНТИЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
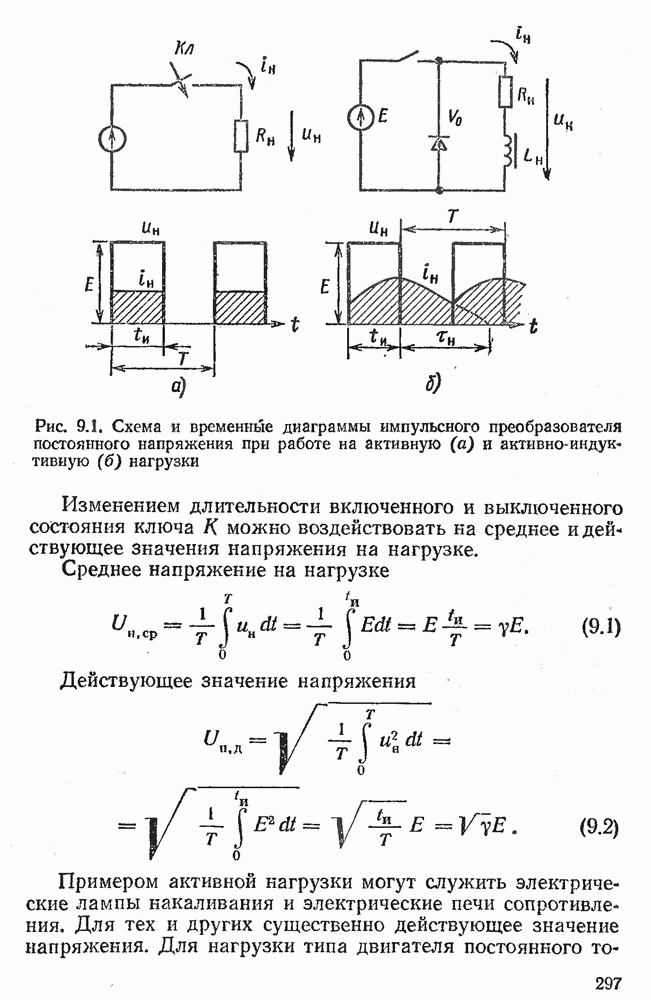
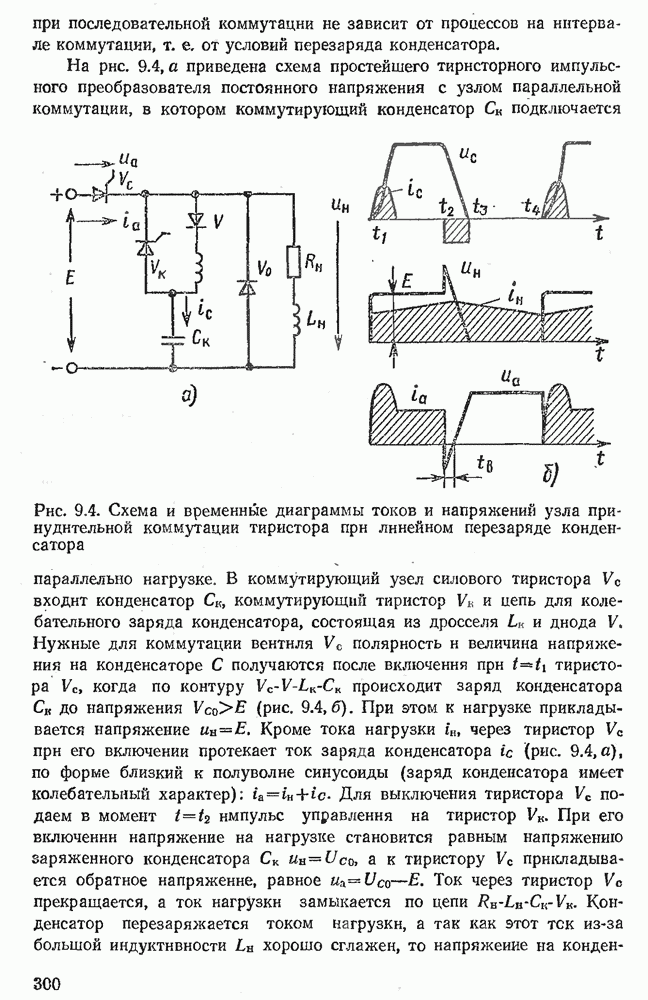
- 9.1. СПОСОБЫ РЕГУЛИРОВАНИЯ ПОСТОЯННОГО НАПРЯЖЕНИЯ
- 9.2. УЗЛЫ КОММУТАЦИИ ОДНООПЕРАЦИОННЫХ ТИРИСТОРОВ
- 9.3. ИНВЕРТОРЫ НАПРЯЖЕНИЯ
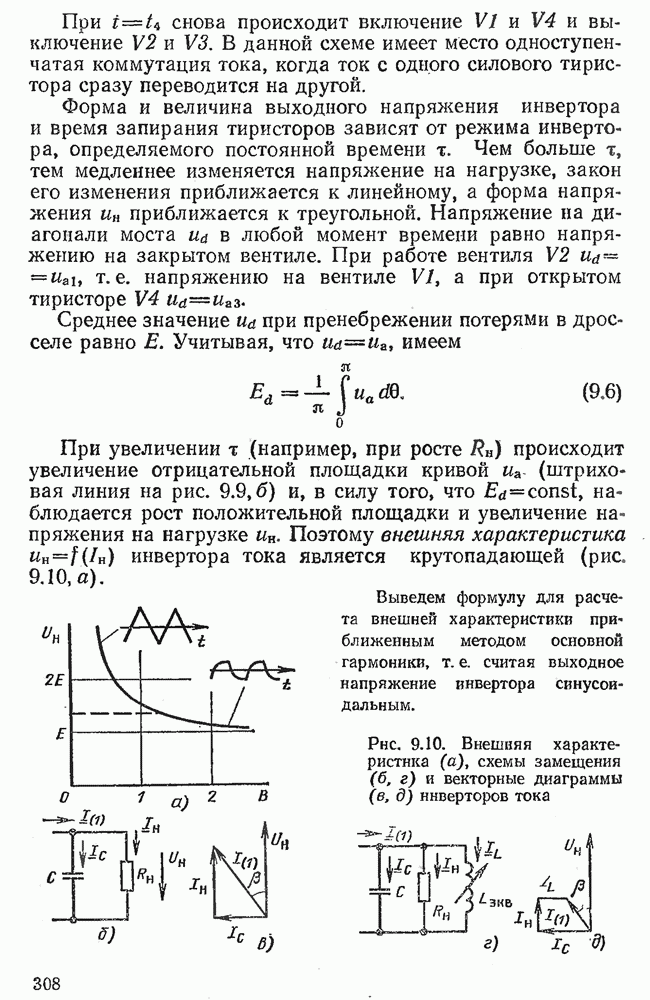
- 9.4. ИНВЕРТОРЫ ТОКА
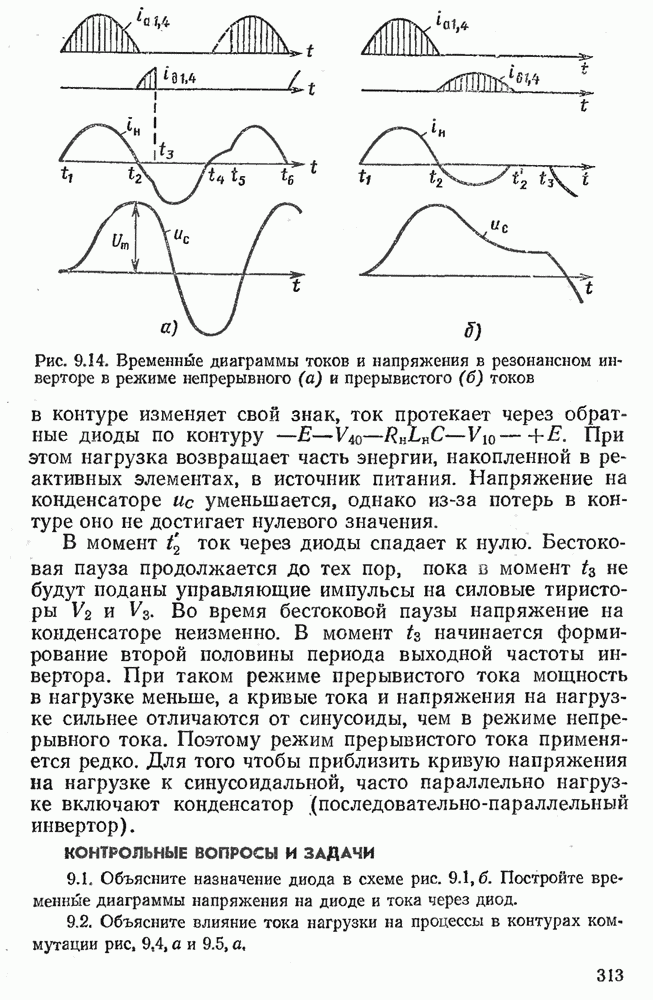
- 9.5. РЕЗОНАНСНЫЕ ИНВЕРТОРЫ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- СПИСОК ЛИТЕРАТУРЫ