| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
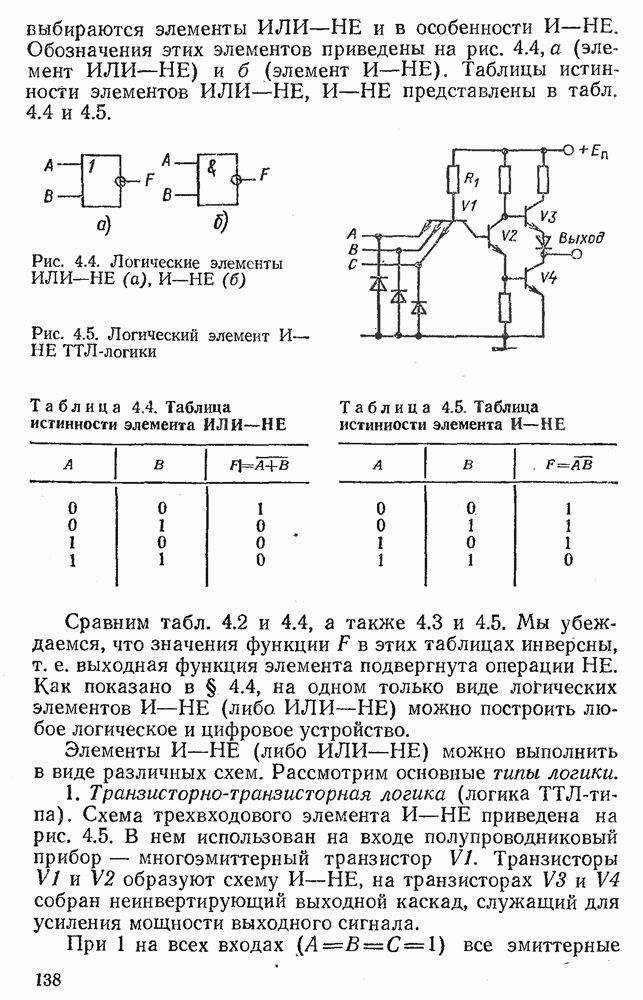
4.4. КОМБИНАЦИОННЫЕ ЛОГИЧЕСКИЕ УСТРОЙСТВА
Логические устройства, выходные функции которых однозначно определяются входными логическими функциями в тот же момент времени, называются комбинационными. Рассмотрим порядок построения комбинационного логического устройства на примере.
Требуется создать логическое устройство для подключения напряжения к агрегату. Агрегат может быть включен непосредственно (А=1) или по команде с диспетчерского пункта (В=1). Агрегат работает только тогда, когда напряжение питания  (логическая функция С=1).
(логическая функция С=1).
Разобьем решение задачи на несколько этапов.
1 этап — составление таблицы истинности. В соответствии с условиями задачи заполняем таблицу истинности, в которой записываем значение выходной функции F в зависимости от входных функций А, В, С для всех возможных вариантов их сочетаний. При трех входных функциях число сочетаний  . Таблица истинности приведена в табл. 4.6.
. Таблица истинности приведена в табл. 4.6.
Таблица 4.6. Таблица истинности логического устройства

2 этап. Составление логического уравнения. Сведения, представленные в таблице истинности, необходимо записать в виде уравнения. Прежде всего выделим строки табл. 4.6, в которых  . Это строки
. Это строки  . Функция F истинна, если входные переменные имеют значения, соответствующие любой из этих строк. Сформулируем это словестно: «Функция F истинна (равна 1), когда истинны не А и В и С (4-я строка) или А и не В и С (6-я строка) или А и В и С (8-я строка). А теперь заменим слово не на знак операции НЕ, слово или на знак операции ИЛИ, а слово и на знак операции И. Получим
. Функция F истинна, если входные переменные имеют значения, соответствующие любой из этих строк. Сформулируем это словестно: «Функция F истинна (равна 1), когда истинны не А и В и С (4-я строка) или А и не В и С (6-я строка) или А и В и С (8-я строка). А теперь заменим слово не на знак операции НЕ, слово или на знак операции ИЛИ, а слово и на знак операции И. Получим

3 этап. Минимизация функции (4.1). Можно создать логическое устройство, которое непосредственно реализует (4.1). Тогда для выполнения двух инверсий будет необходимо два элемента НЕ; трижды выполняется операция И, берем три трехвходовых элемента И; затем выполняем операцию ИЛИ на одном трехвходовом элементе ИЛИ. Всего используем шесть элементов.
Но выражение (4.1) можно упростить. Для этого воспользуемся тождеством (1) и вынесем за скобки общие члены.

Для выражений в скобках применим тождество (2), получим

4 этап. Составление логической схемы. Функция (4.2) содержит две операции: ИЛИ и И. В соответствии с этим схема логического устройства, приведенная на рис. 4.10, а, выполнена на двух элементах. Мы имели возможность убедиться, какие возможности дает алгебра логики для упрощения схемных решений логических устройств.

Рис. 4.10. Варианты схемы комбинационного устройства
Порядок решения задачи, разбиваемой на четыре этапа, сохраняется, если разрабатываются и более сложные комбинационные устройства.
При проектировании логических элементов стремятся использовать ограниченную номенклатуру логических  ментов. В частности, любое устройство может быть реализовано исключительно на элементах
ментов. В частности, любое устройство может быть реализовано исключительно на элементах  . Так, операция НЕ может быть осуществлена на схеме
. Так, операция НЕ может быть осуществлена на схеме  , в котором на каждом из входов переменная А. Тогда
, в котором на каждом из входов переменная А. Тогда  . Схема представлена на рис. 4.11, а. Операция И выполняется
. Схема представлена на рис. 4.11, а. Операция И выполняется

Рис. 4.11. Реализация логических операций НЕ, И, ИЛИ на элементах  схемой рис.
схемой рис.  . Действительно, согласно тождеству
. Действительно, согласно тождеству  . Операция ИЛИ выполняется схемой рис. 4.11,в. Воспользуемся тождеством (9) и формулой де Моргана (12):
. Операция ИЛИ выполняется схемой рис. 4.11,в. Воспользуемся тождеством (9) и формулой де Моргана (12):

Реализуем логическое устройство по уравнению (4.2) на элементах  . Схема представлена на рис.
. Схема представлена на рис.  .
.
Любое устройство может быть воплощено и на элементах ИЛИ—НЕ. Операция НЕ выполняется по схеме рис. 4.12,а:  . Операция ИЛИ реализуется схемой рис. 4.12, б:
. Операция ИЛИ реализуется схемой рис. 4.12, б:  . Операция И выполняется схемой рис. 4.12,в.
. Операция И выполняется схемой рис. 4.12,в.

Рис. 4.12. Реализация логических операций НЕ, ИЛИ, И на элементах ИЛИ—НЕ
Воспользуемся тождеством (9) и формулой де Моргана (13):

Логическое устройство по уравнению (4.2) на элементах ИЛИ — НЕ представлено на рис. 4.10, в.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава первая. ПОЛУПРОВОДНИКОВЫЕ И МИКРОЭЛЕКТРОННЫЕ ПРИБОРЫ
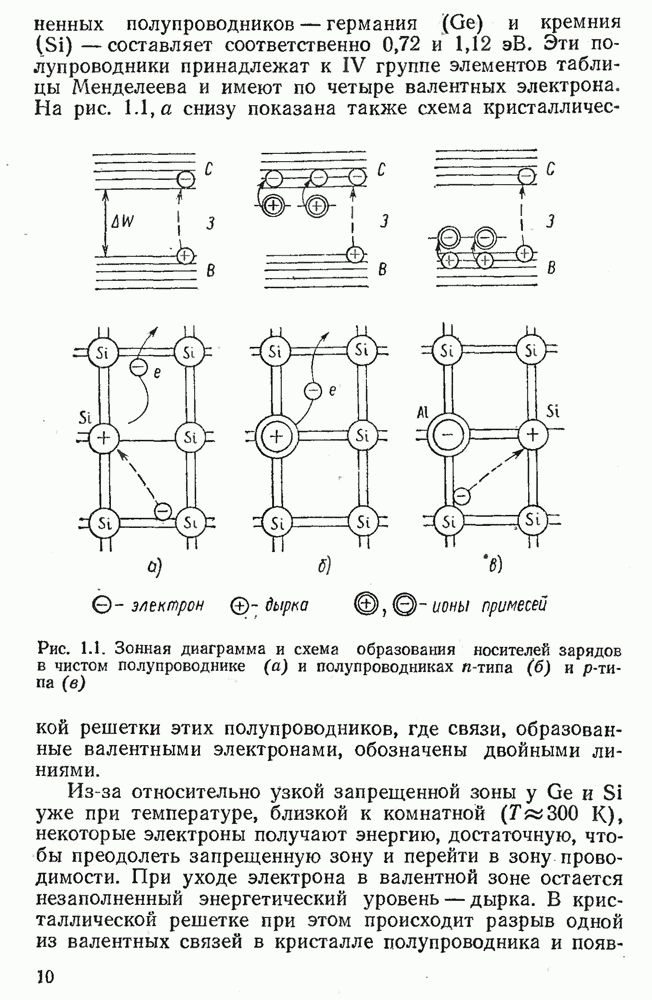
- 1.1. ЭЛЕКТРОПРОВОДНОСТЬ ПОЛУПРОВОДНИКОВ
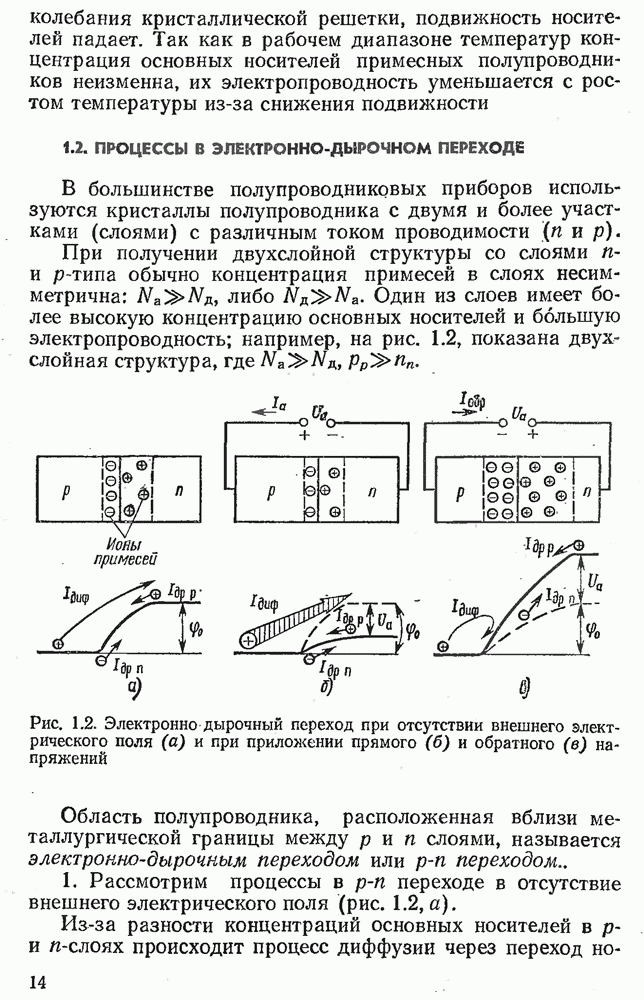
- 1.2. ПРОЦЕССЫ В ЭЛЕКТРОННО-ДЫРОЧНОМ ПЕРЕХОДЕ
- 1.3. ПОЛУПРОВОДНИКОВЫЕ ДИОДЫ
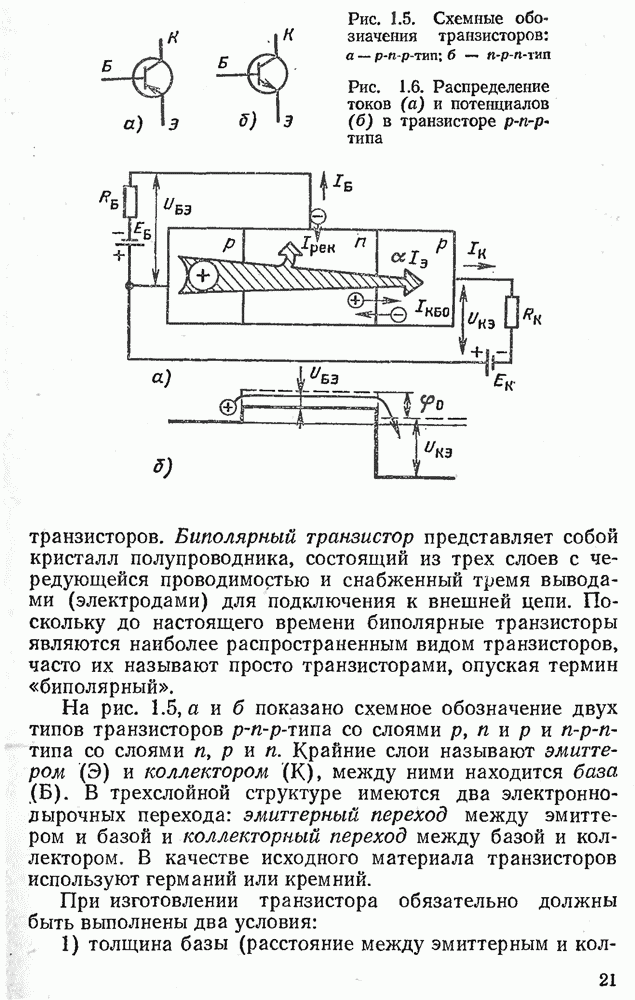
- 1.4. БИПОЛЯРНЫЕ ТРАНЗИСТОРЫ
- 1.5. ХАРАКТЕРИСТИКИ И ПАРАМЕТРЫ БИПОЛЯРНЫХ ТРАНЗИСТОРОВ
- 1.6. ПОЛЕВЫЕ ТРАНЗИСТОРЫ
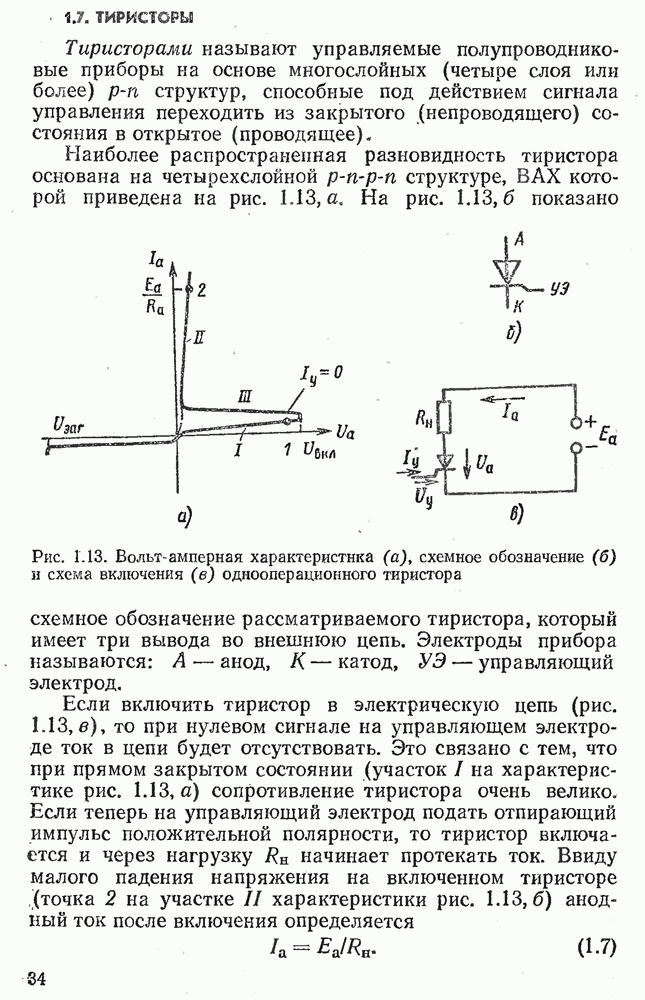
- 1.7. ТИРИСТОРЫ
- 1.8. ПАРАМЕТРЫ И РАЗНОВИДНОСТИ ТИРИСТОРОВ
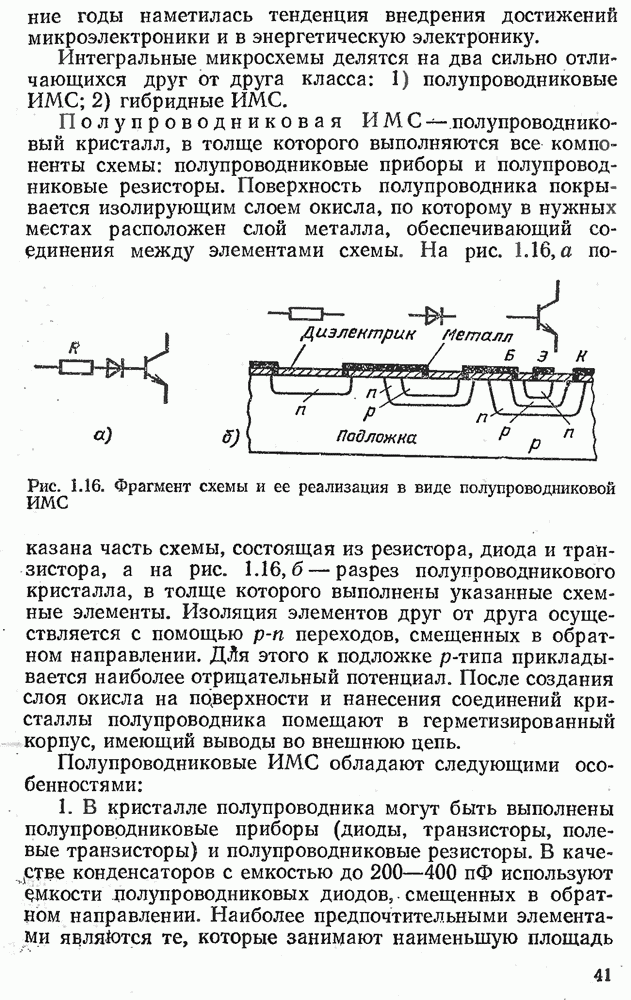
- 1.9. ИНТЕГРАЛЬНЫЕ МИКРОСХЕМЫ
- 1.10. ПОЛУПРОВОДНИКОВЫЕ ОПТОЭЛЕКТРОННЫЕ ПРИБОРЫ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава вторая. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ
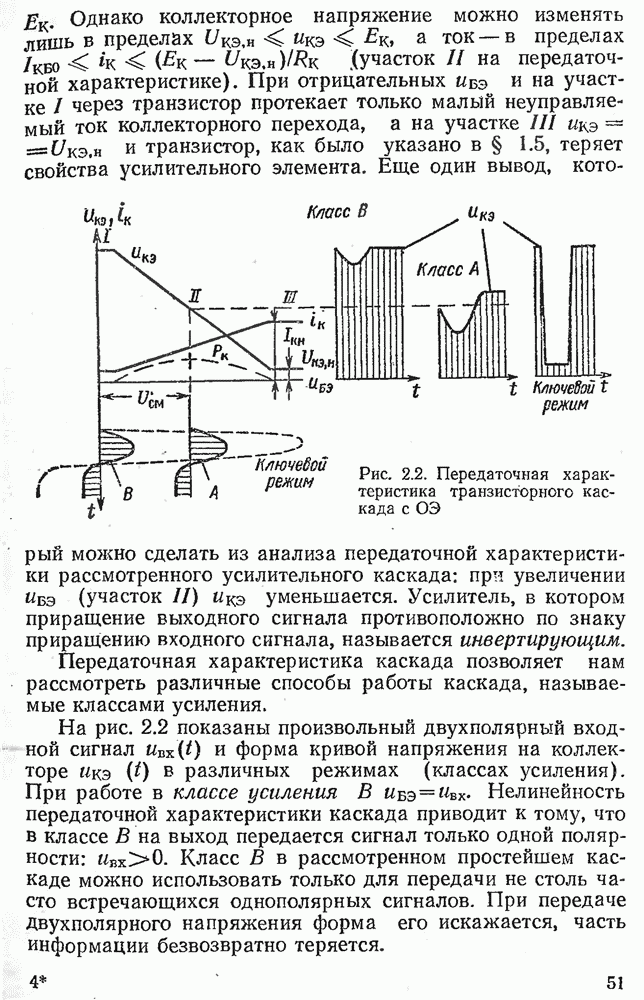
- 2.1. ПЕРЕДАТОЧНАЯ ХАРАКТЕРИСТИКА УСИЛИТЕЛЬНОГО КАСКАДА
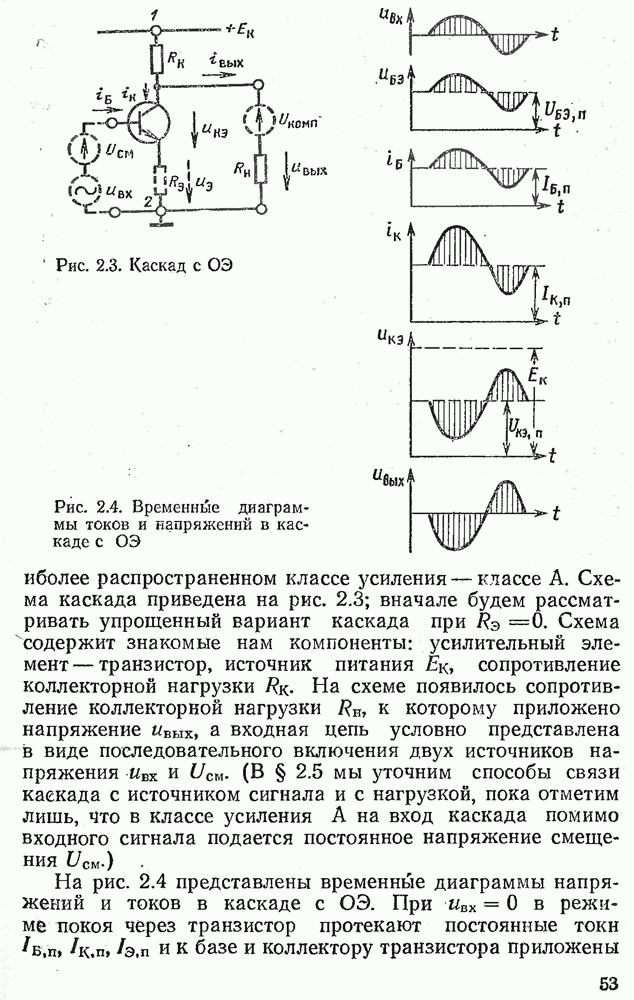
- 2.2. РЕЖИМ ПОКОЯ В КАСКАДЕ С ОБЩИМ ЭМИТТЕРОМ
- 2.3. ОБРАТНЫЕ СВЯЗИ. СТАБИЛИЗАЦИЯ РЕЖИМА ПОКОЯ
- 2.4. СХЕМА ЗАМЕЩЕНИЯ И ОСНОВНЫЕ ПОКАЗАТЕЛИ КАСКАДА С ОЭ
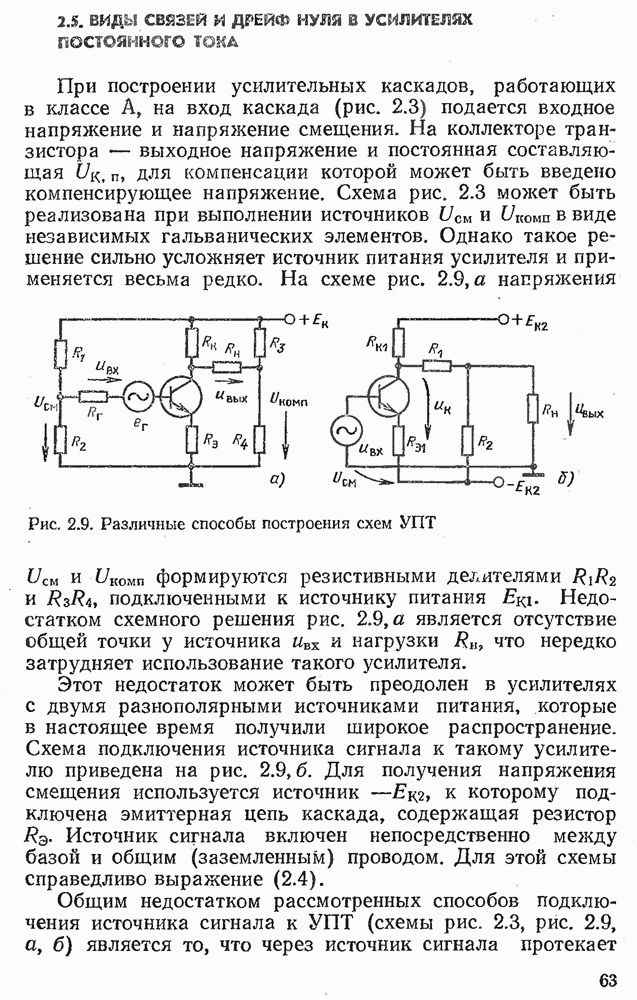
- 2.5. ВИДЫ СВЯЗЕЙ И ДРЕЙФ НУЛЯ В УСИЛИТЕЛЯХ ПОСТОЯННОГО ТОКА
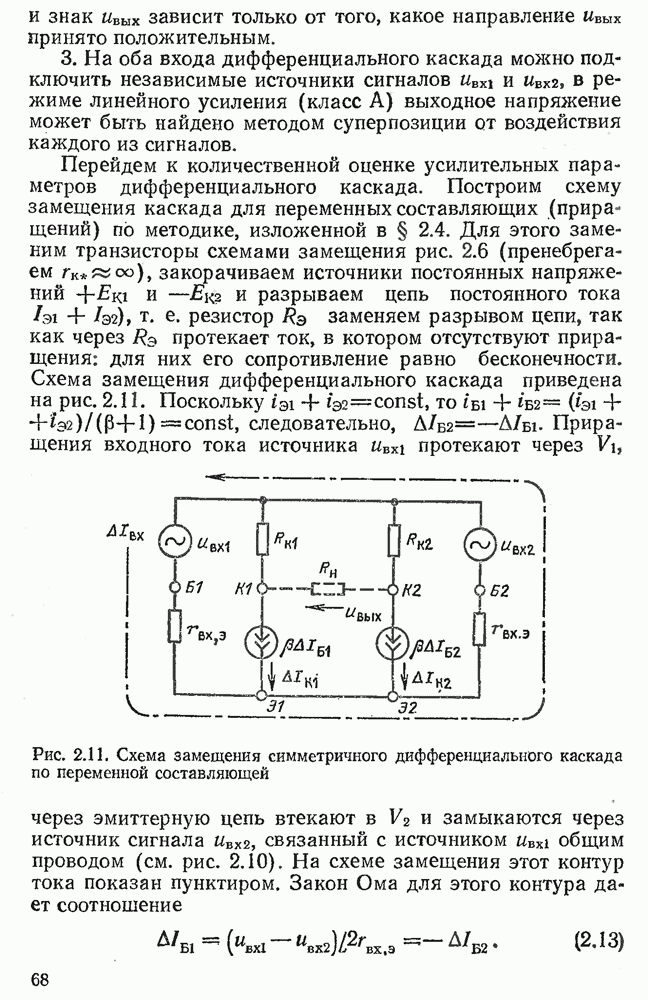
- 2.6. ДИФФЕРЕНЦИАЛЬНЫЙ КАСКАД
- 2.7. КАСКАД С ОБЩИМ КОЛЛЕКТОРОМ
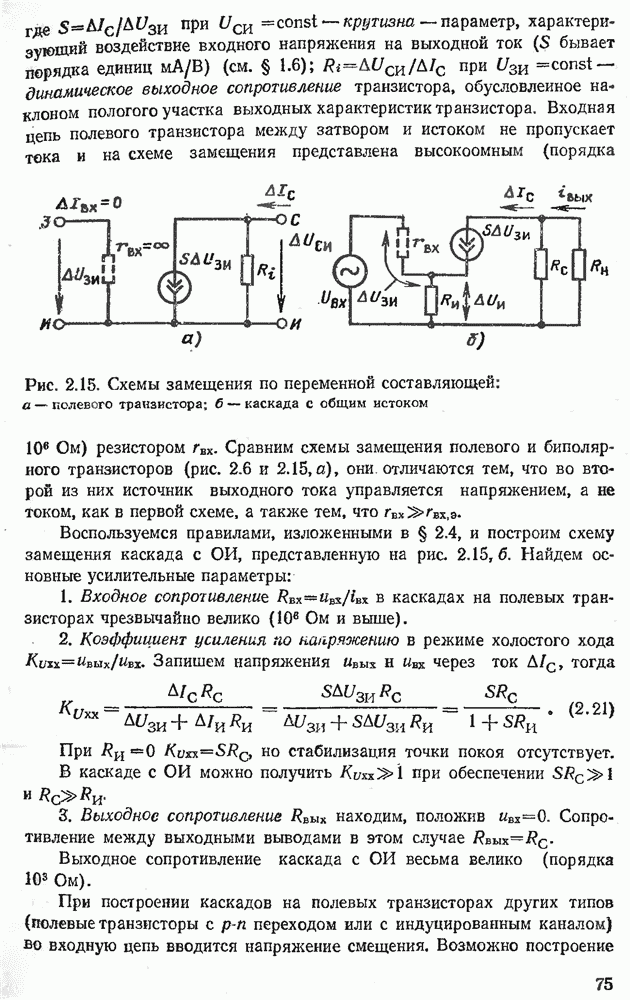
- 2.8. КАСКАД С ОБЩИМ ИСТОКОМ
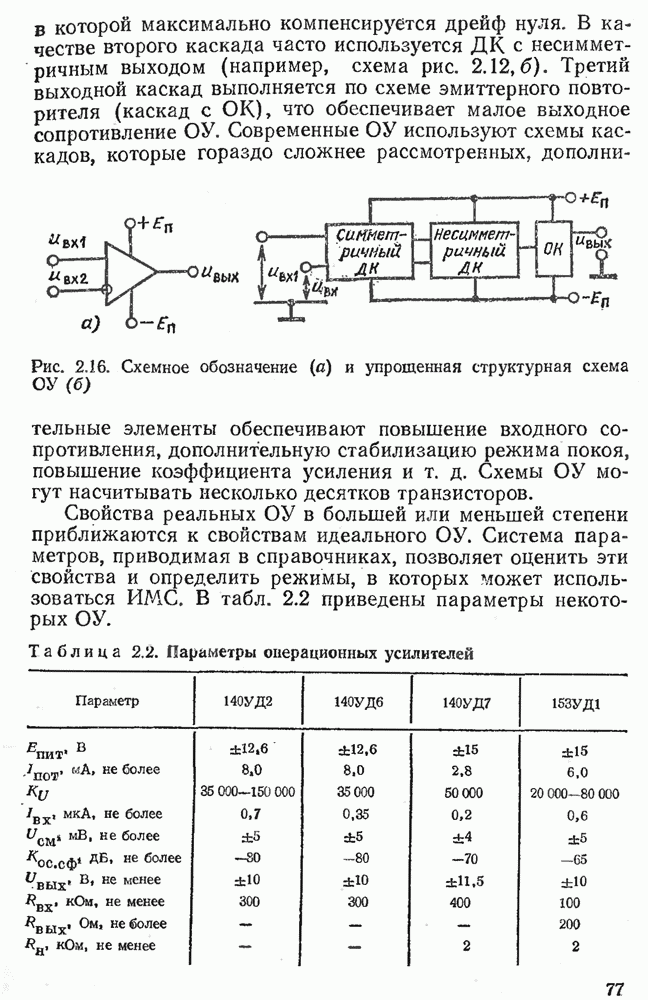
- 2.9. ОПЕРАЦИОННЫЙ УСИЛИТЕЛЬ
- 2.10. НЕИНВЕРТИРУЮЩИЙ ОПЕРАЦИОННЫЙ УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ
- 2.11. ИНВЕРТИРУЮЩИЙ ОПЕРАЦИОННЫЙ УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ
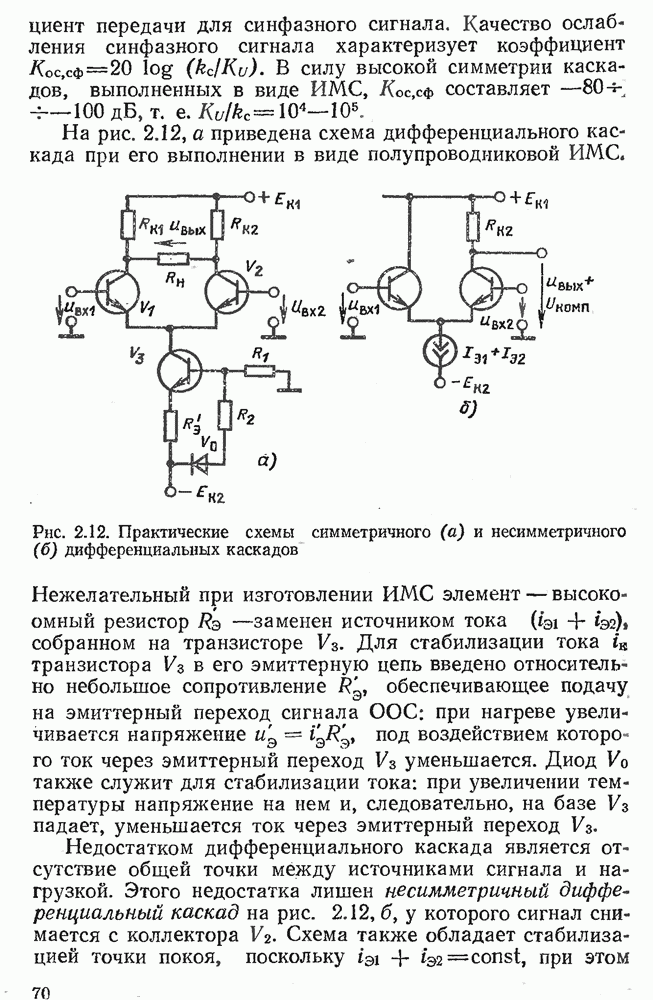
- 2.12. ОПЕРАЦИОННЫЕ СХЕМЫ
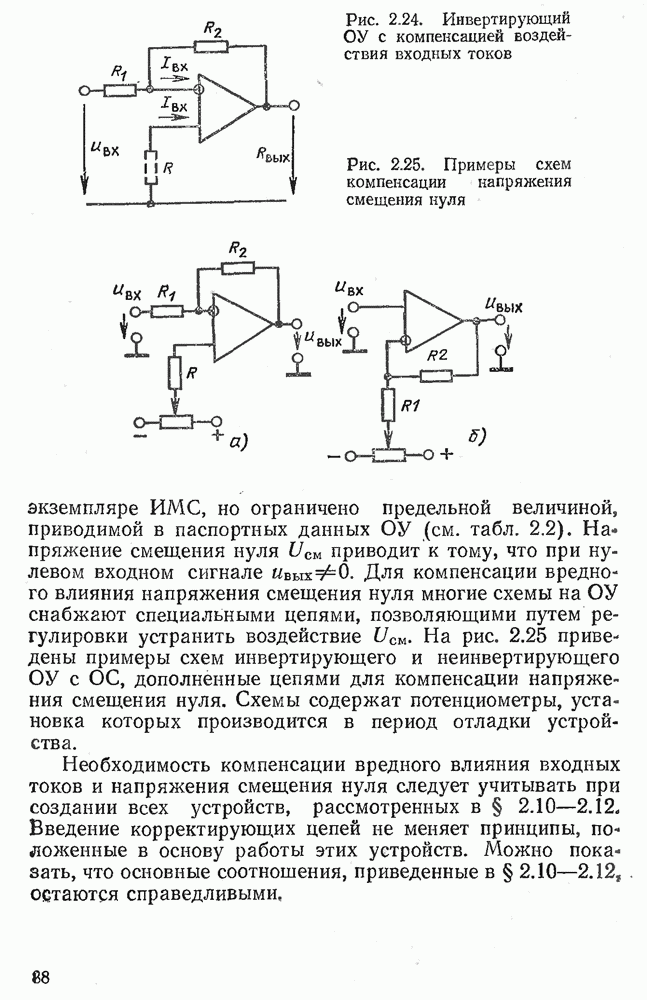
- 2.13. КОМПЕНСАЦИЯ ВХОДНЫХ ТОКОВ И НАПРЯЖЕНИЯ СМЕЩЕНИЯ НУЛЯ
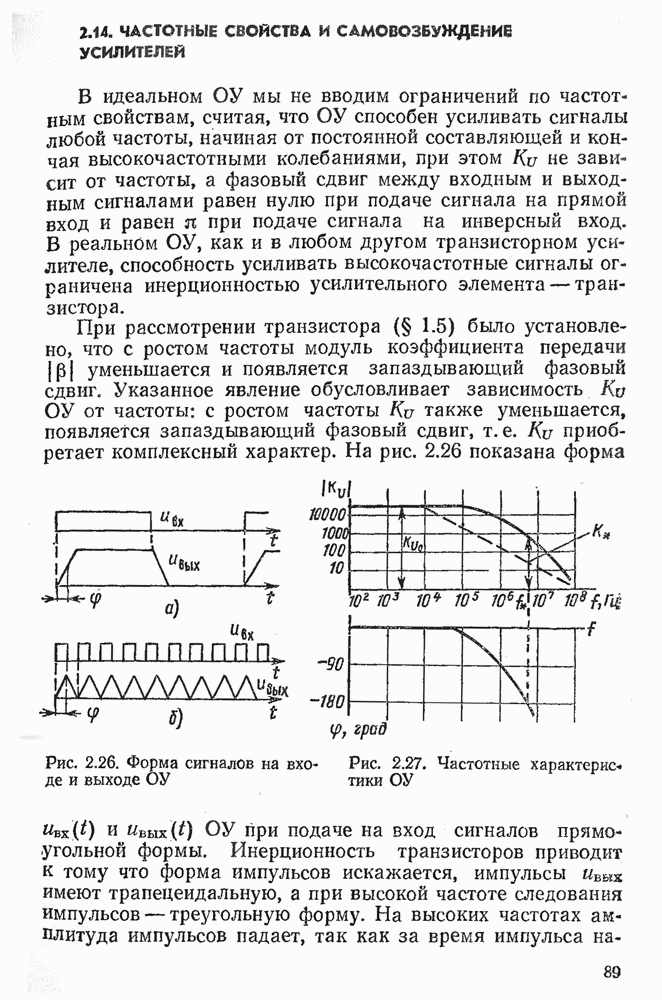
- 2.14. ЧАСТОТНЫЕ СВОЙСТВА И САМОВОЗБУЖДЕНИЕ УСИЛИТЕЛЕЙ
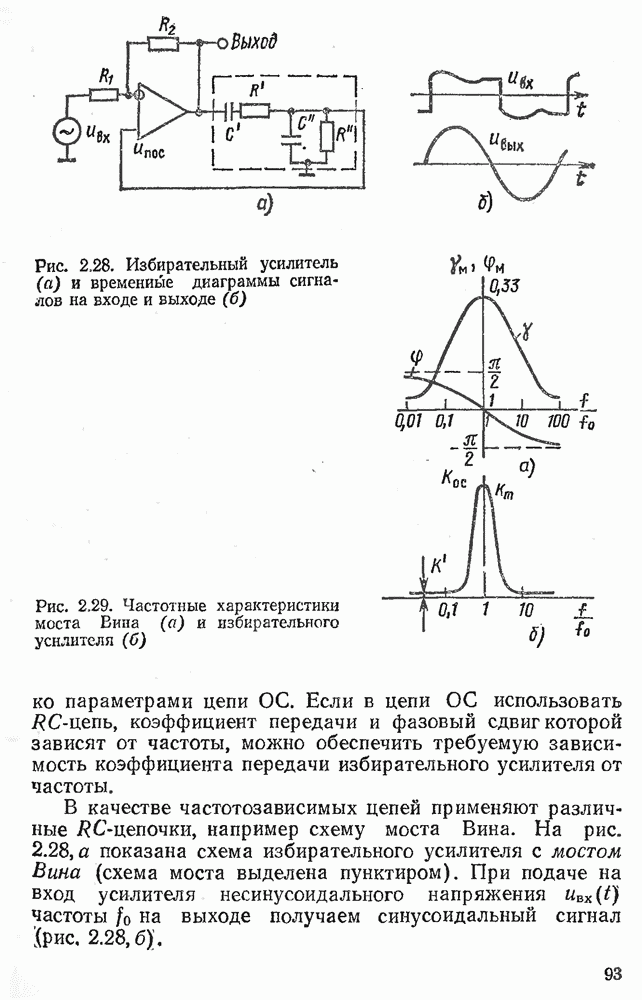
- 2.15. ИЗБИРАТЕЛЬНЫЕ УСИЛИТЕЛИ И ГЕНЕРАТОРЫ СИНУСОИДАЛЬНЫХ КОЛЕБАНИЙ
- 2.16. УСИЛИТЕЛИ С ЕМКОСТНОЙ СВЯЗЬЮ
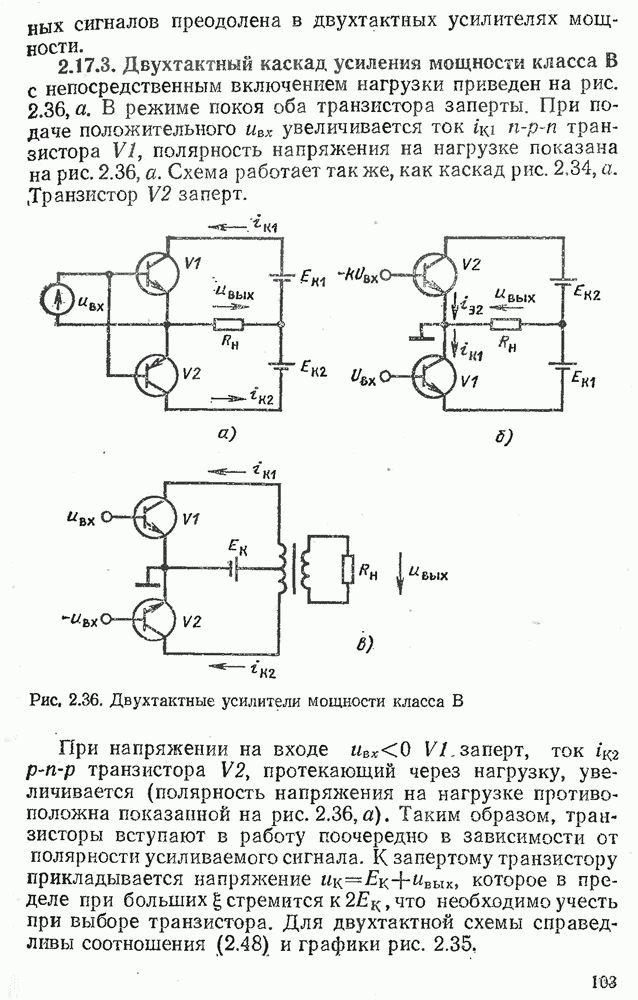
- 2.17. КАСКАДЫ УСИЛЕНИЯ МОЩНОСТИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава третья. ИМПУЛЬСНЫЕ УСТРОЙСТВА
- 3.1. ПРЕИМУЩЕСТВА ПЕРЕДАЧИ ИНФОРМАЦИИ В ВИДЕ ИМПУЛЬСОВ
- 3.2. КЛЮЧЕВОЙ РЕЖИМ ТРАНЗИСТОРА
- 3.3. НЕЛИНЕЙНЫЙ РЕЖИМ РАБОТЫ ОПЕРАЦИОННОГО УСИЛИТЕЛЯ. КОМПАРАТОРЫ
- 3.4. ПРЕОБРАЗОВАНИЕ ИМПУЛЬСНЫХ СИГНАЛОВ С ПОМОЩЬЮ RС-ЦЕПЕЙ
- 3.3. МУЛЬТИВИБРАТОР НА ОПЕРАЦИОННОМ УСИЛИТЕЛЕ
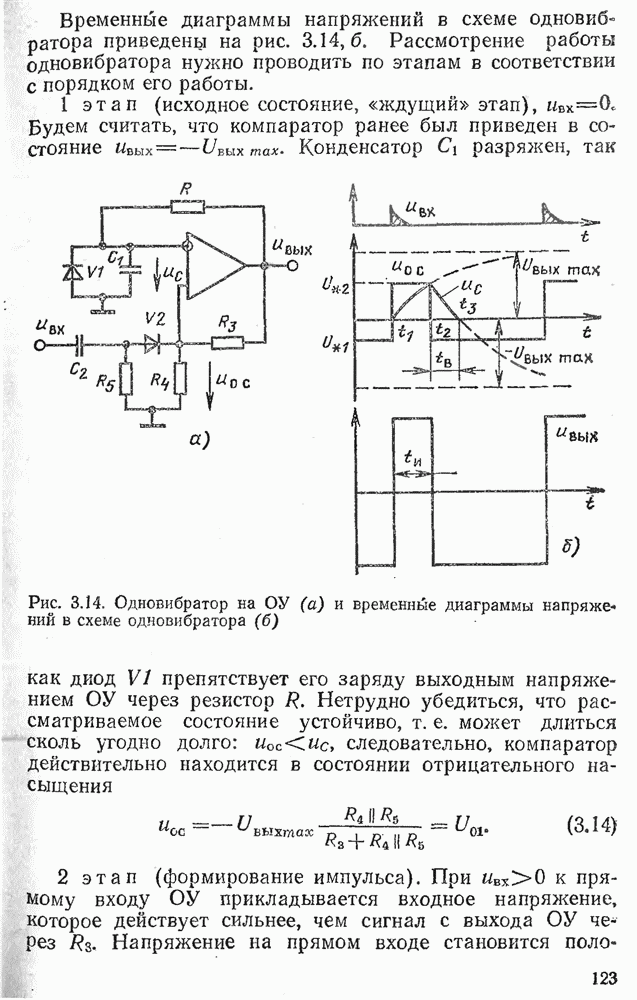
- 3.6. ОДНОВИБРАТОР НА ОПЕРАЦИОННОМ УСИЛИТЕЛЕ
- 3.7. ГЕНЕРАТОРЫ ЛИНЕЙНО ИЗМЕНЯЮЩИХСЯ НАПРЯЖЕНИЙ
- 3.8. МАГНИТНО-ТРАНЗИСТОРНЫЕ ГЕНЕРАТОРЫ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава четвертая. ЛОГИЧЕСКИЕ И ЦИФРОВЫЕ УСТРОЙСТВА
- 4.1. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ И ИХ РЕАЛИЗАЦИЯ
- 4.2. ТИПЫ ЛОГИЧЕСКИХ МИКРОСХЕМ
- 4.3. АЛГЕБРА ЛОГИКИ
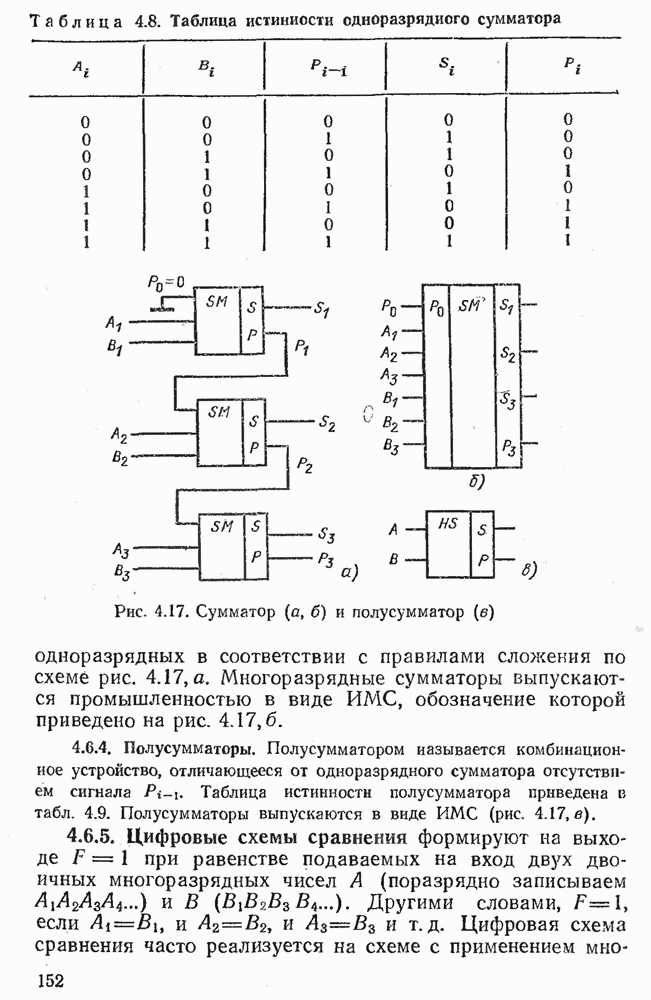
- 4.4. КОМБИНАЦИОННЫЕ ЛОГИЧЕСКИЕ УСТРОЙСТВА
- 4.5. МИНИМИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
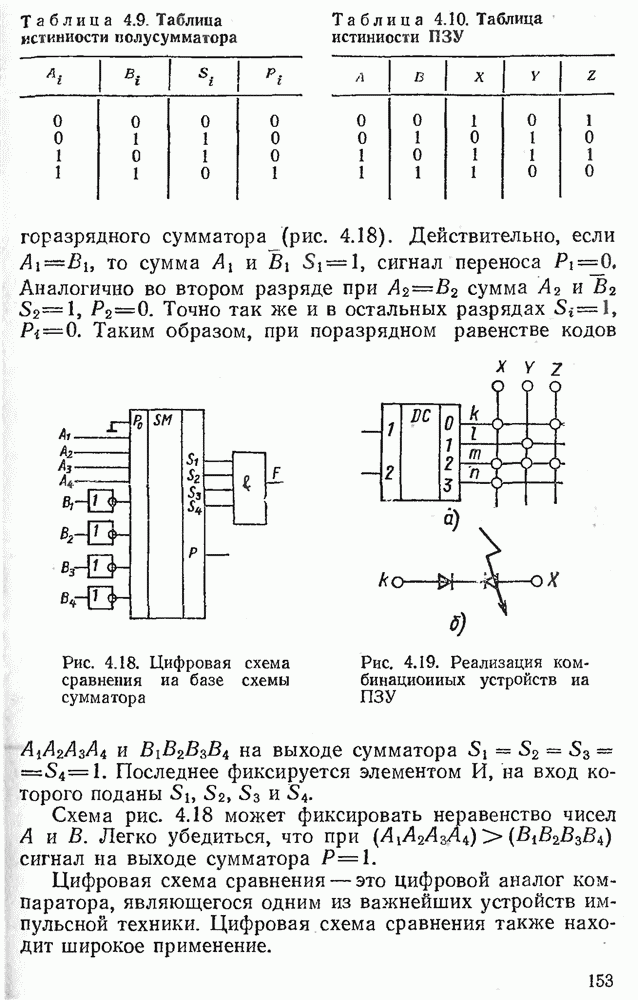
- 4.6. КОМБИНАЦИОННЫЕ ИНТЕГРАЛЬНЫЕ МИКРОСХЕМЫ
- 4.7. АСИНХРОННЫЙ RS-ТРИГГЕР
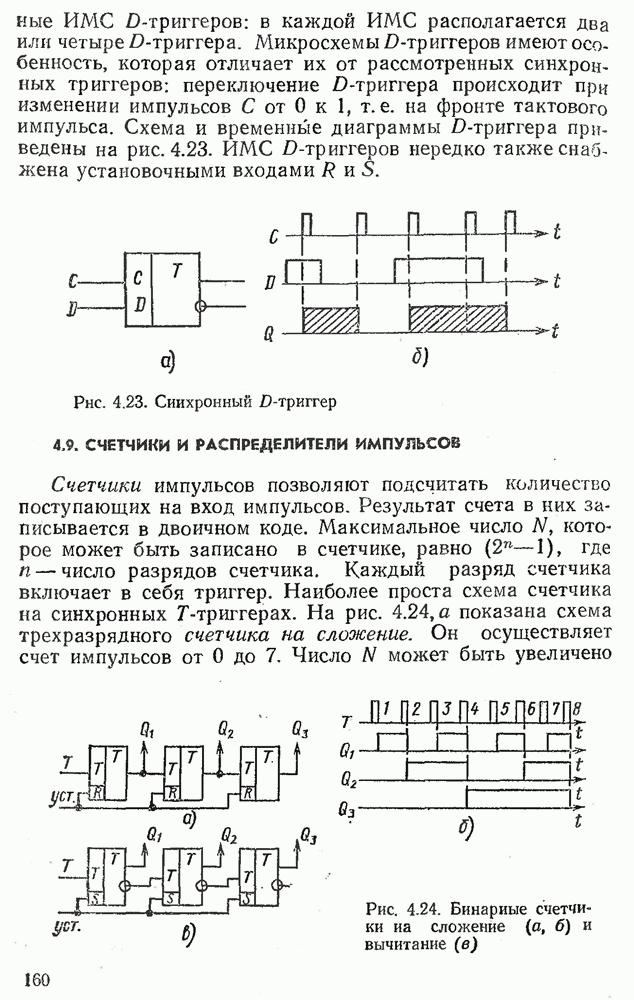
- 4.8. СИНХРОННЫЕ ТРИГГЕРЫ
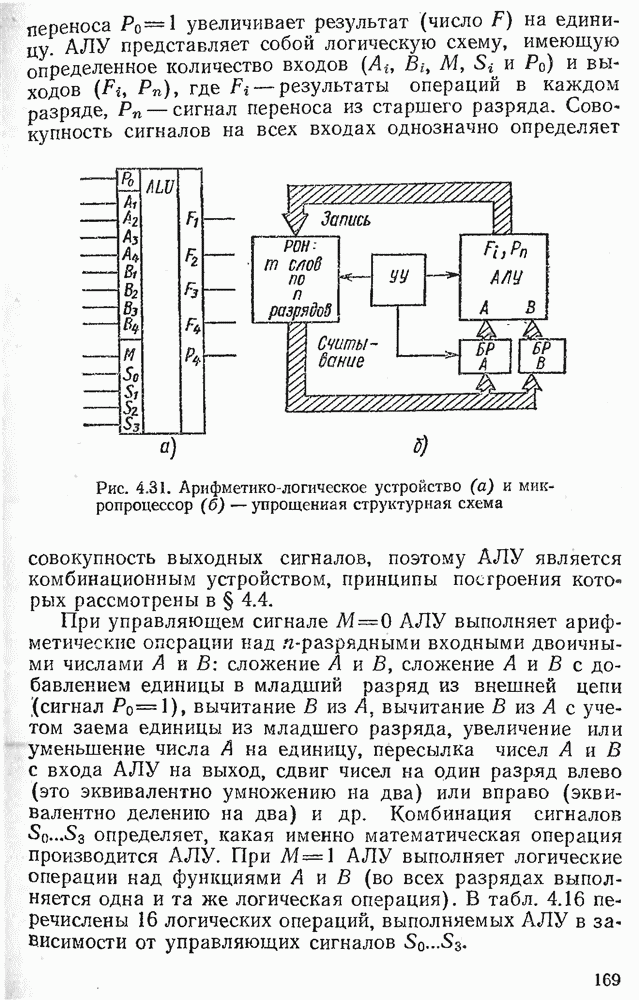
- 4.9. СЧЕТЧИКИ И РАСПРЕДЕЛИТЕЛИ ИМПУЛЬСОВ
- 4.10. РЕГИСТРЫ
- 4.11. ЦИФРО-АНАЛОГОВЫЕ И АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
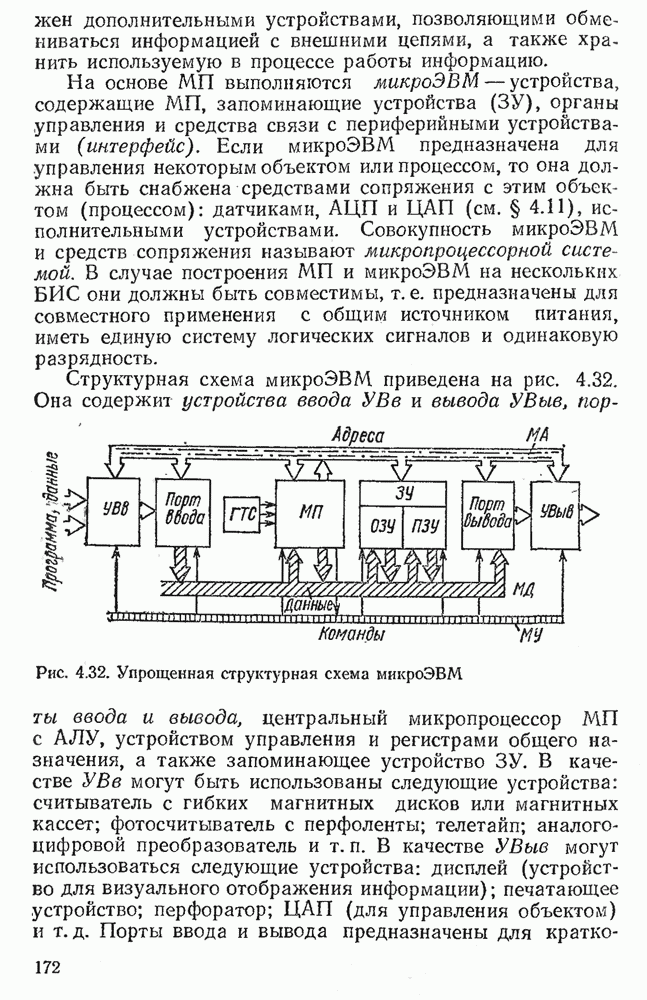
- 4.12. МИКРОПРОЦЕССОРЫ
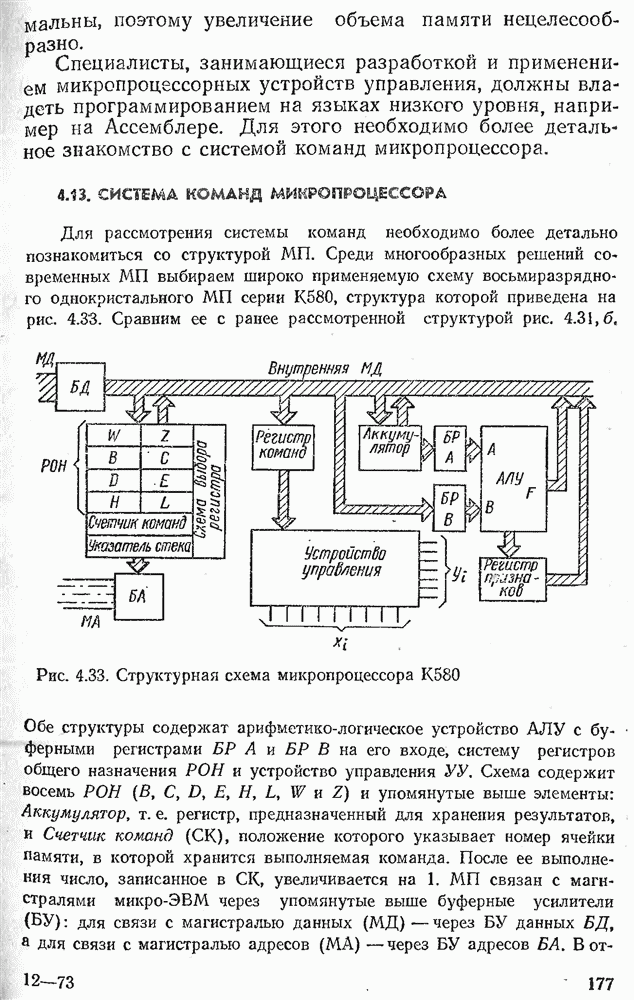
- 4.13. СИСТЕМА КОМАНД МИКРОПРОЦЕССОРА
- 4.14. ИНДИКАТОРНЫЕ ПРИБОРЫ И УЗЛЫ ЦИФРОВЫХ УСТРОЙСТВ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава пятая. МАЛОМОЩНЫЕ ВЫПРЯМИТЕЛИ ОДНОФАЗНОГО ТОКА
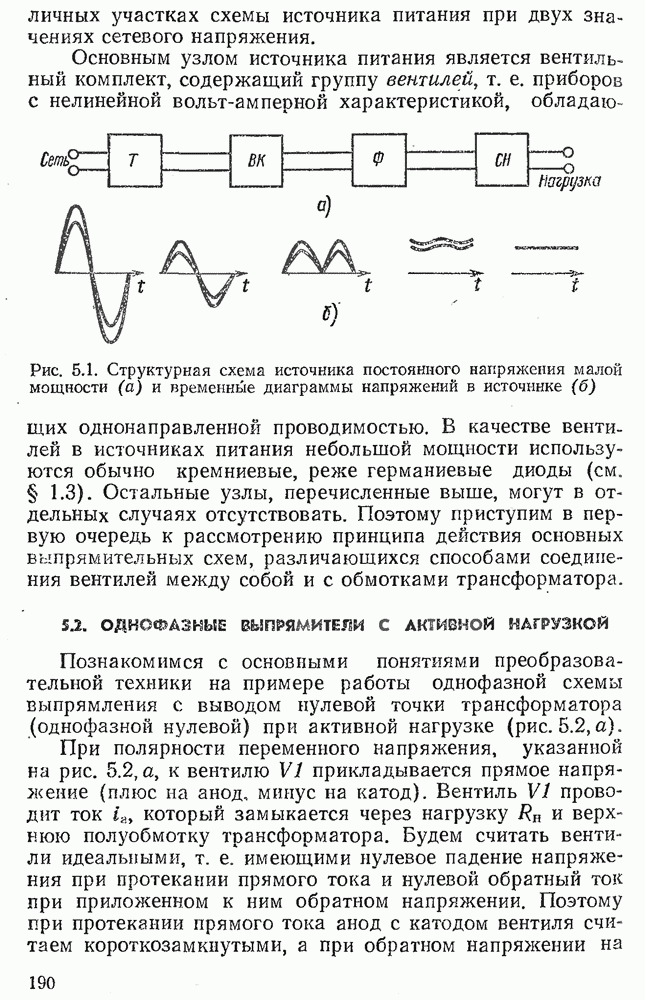
- 5.1. СТРУКТУРА ИСТОЧНИКА ПИТАНИЯ
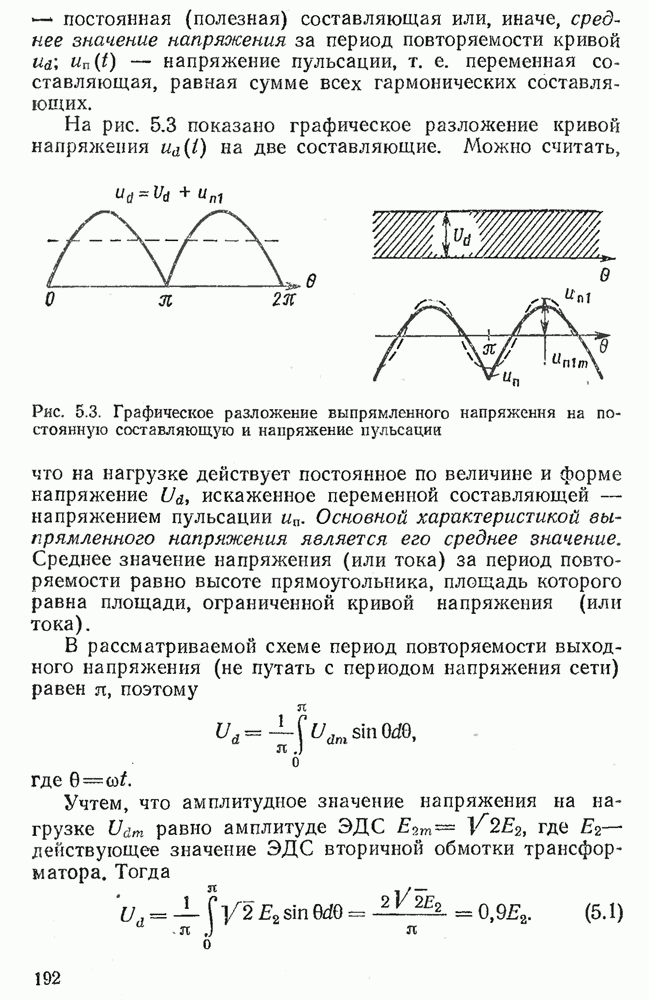
- 5.2. ОДНОФАЗНЫЕ ВЫПРЯМИТЕЛИ С АКТИВНОЙ НАГРУЗКОЙ
- 5.3. ОДНОФАЗНЫЕ ВЫПРЯМИТЕЛИ С АКТИВНО-ИНДУКТИВНОЙ НАГРУЗКОЙ
- 5.4. ФИЛЬТРЫ МАЛОМОЩНЫХ ВЫПРЯМИТЕЛЕЙ
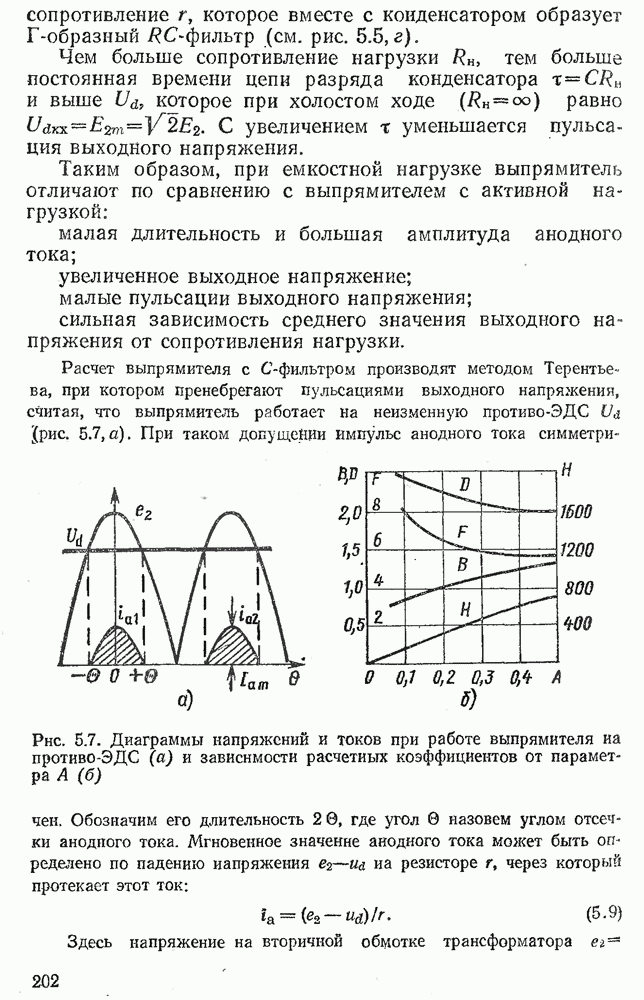
- 5.5. ОСОБЕННОСТИ РАБОТЫ И РАСЧЕТА ВЫПРЯМИТЕЛЯ С ЕМКОСТНЫМ ФИЛЬТРОМ
- 5.6. ВНЕШНИЕ ХАРАКТЕРИСТИКИ МАЛОМОЩНЫХ ВЫПРЯМИТЕЛЕЙ
- 5.7. СТАБИЛИЗАТОРЫ НАПРЯЖЕНИЯ
- 5.8. ИСТОЧНИКИ ПИТАНИЯ С МНОГОКРАТНЫМ ПРЕОБРАЗОВАНИЕМ ЭНЕРГИИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава шестая. ВЕДОМЫЕ СЕТЬЮ ПРЕОБРАЗОВАТЕЛИ СРЕДНЕЙ И БОЛЬШОЙ МОЩНОСТИ
- 6.1. ПРИМЕНЕНИЕ ВЕНТИЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ В ЭНЕРГЕТИКЕ И ЭЛЕКТРОТЕХНИКЕ
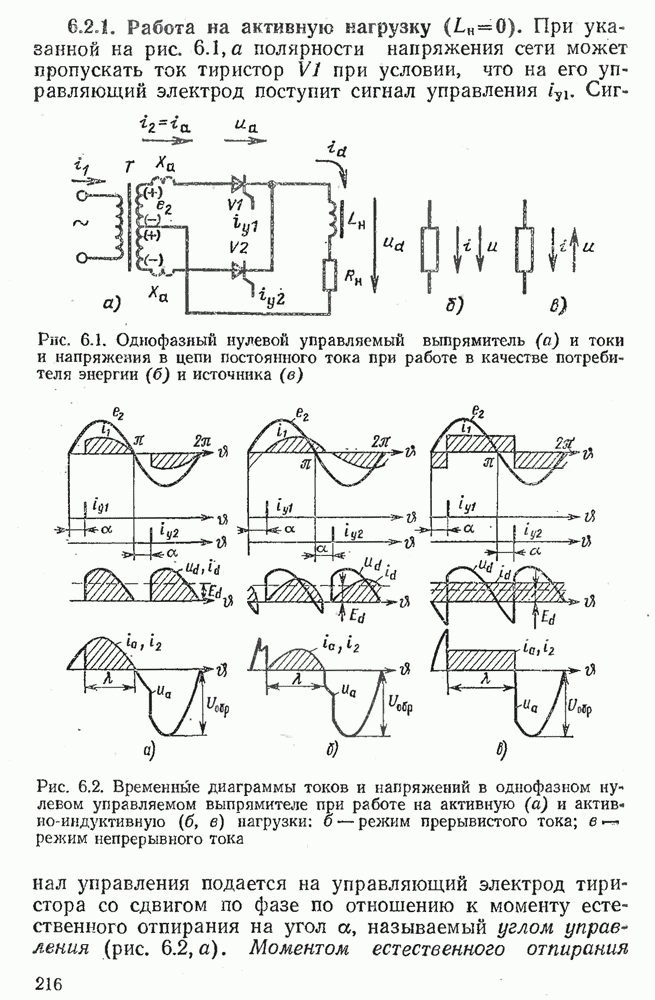
- 6.2. ОДНОФАЗНЫЙ УПРАВЛЯЕМЫЙ ВЫПРЯМИТЕЛЬ
- 6.3. ОДНОФАЗНЫЙ ВЕДОМЫЙ СЕТЬЮ ИНВЕРТОР
- 6.4. ТРЕХФАЗНЫЙ НУЛЕВОЙ ВЫПРЯМИТЕЛЬ
- 6.5. ТРЁХФАЗНЫЙ МОСТОВОЙ ВЫПРЯМИТЕЛЬ
- 6.6. СОСТАВНЫЕ МНОГОФАЗНЫЕ СХЕМЫ ВЫПРЯМЛЕНИЯ
- 6.7. РЕВЕРСИВНЫЕ ВЫПРЯМИТЕЛИ И НЕПОСРЕДСТВЕННЫЕ ПРЕОБРАЗОВАТЕЛИ ЧАСТОТЫ
- 6.8. РЕГУЛИРУЕМЫЕ ПРЕОБРАЗОВАТЕЛИ ПЕРЕМЕННОГО НАПРЯЖЕНИЯ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
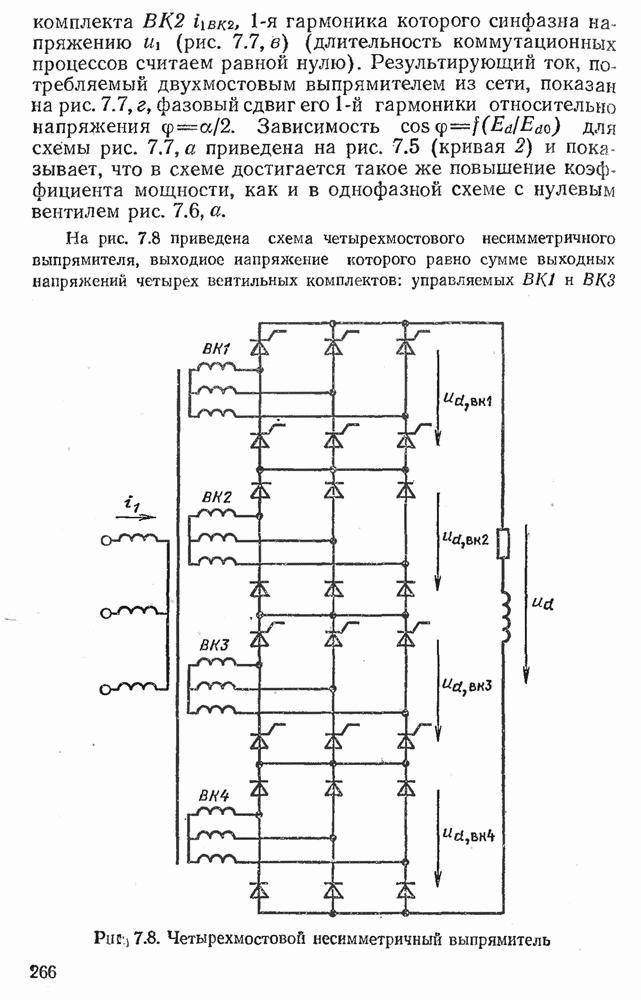
- Глава седьмая. ВЛИЯНИЕ ВЕНТИЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ НА ПИТАЮЩУЮ СЕТЬ
- 7.1. КОЭФФИЦИЕНТ МОЩНОСТИ ВЕНТИЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ
- 7.2. ВЕНТИЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ С ПОВЫШЕННЫМ КОЭФФИЦИЕНТОМ МОЩНОСТИ
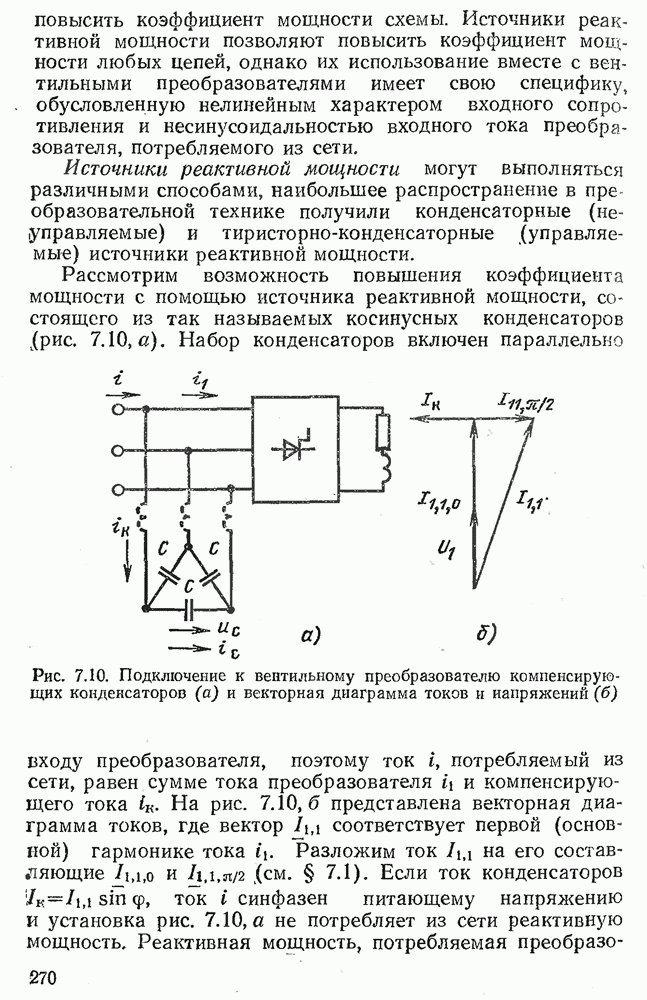
- 7.3. ИСТОЧНИКИ РЕАКТИВНОЙ МОЩНОСТИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
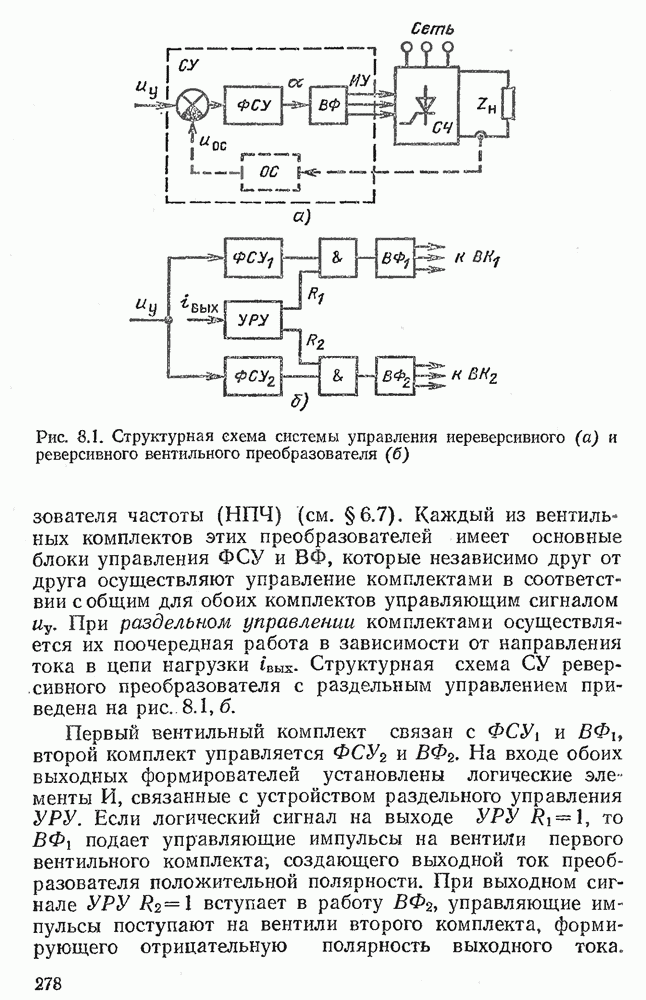
- Глава восьмая. СИСТЕМЫ УПРАВЛЕНИЯ ВЕНТИЛЬНЫМИ ПРЕОБРАЗОВАТЕЛЯМИ
- 8.1. ФУНКЦИИ И СТРУКТУРА СИСТЕМ УПРАВЛЕНИЙ
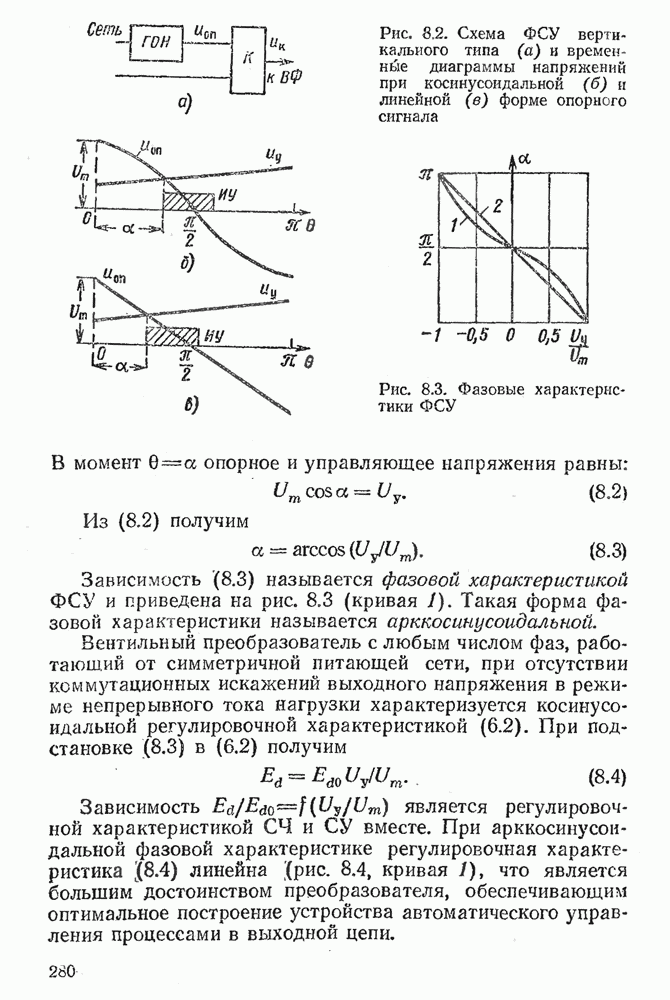
- 8.2. ФАЗОСМЕЩАЮЩИЕ УСТРОЙСТВА (ФСУ)
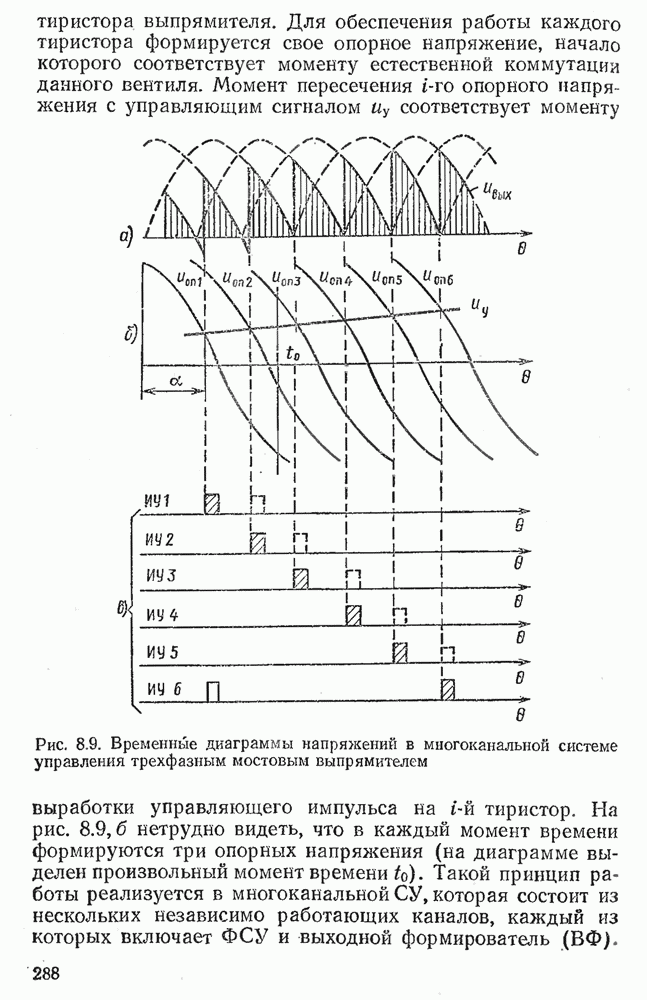
- 8.3. МНОГОКАНАЛЬНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
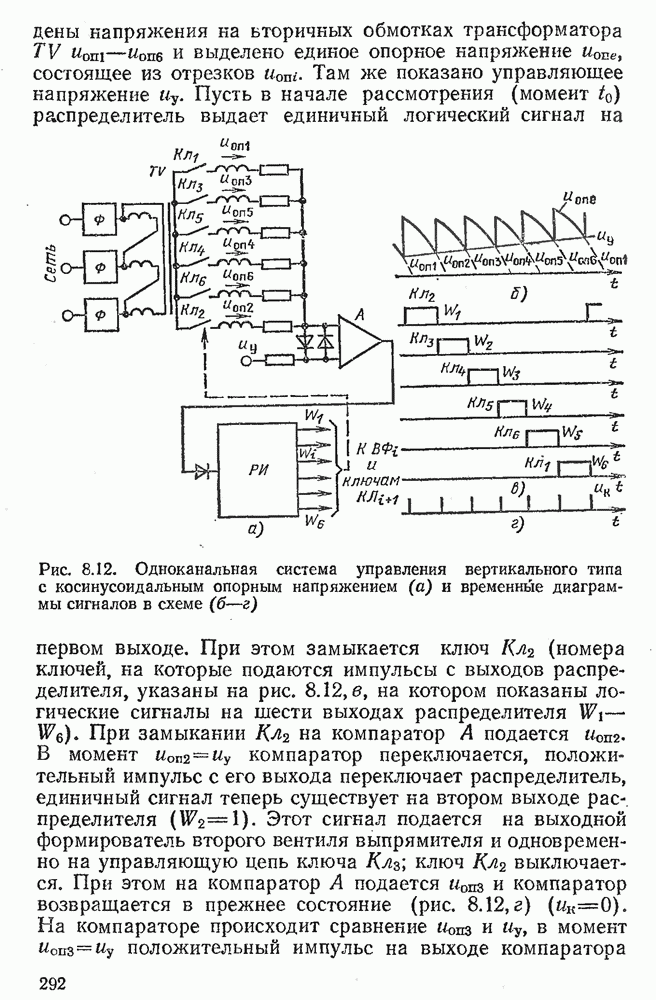
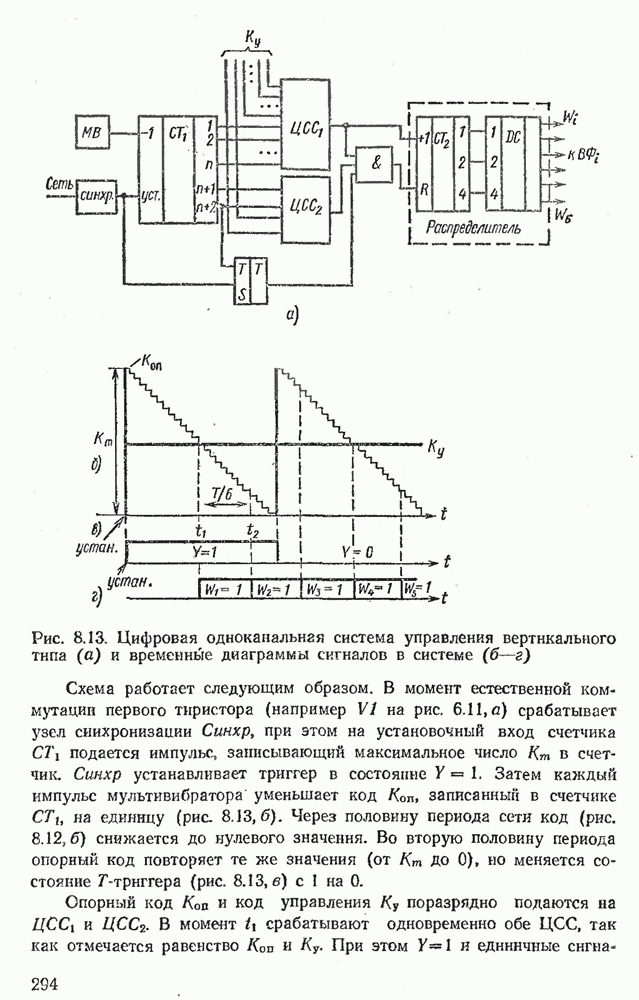
- 8.4. ОДНОКАНАЛЬНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- Глава девятая. АВТОНОМНЫЕ ВЕНТИЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
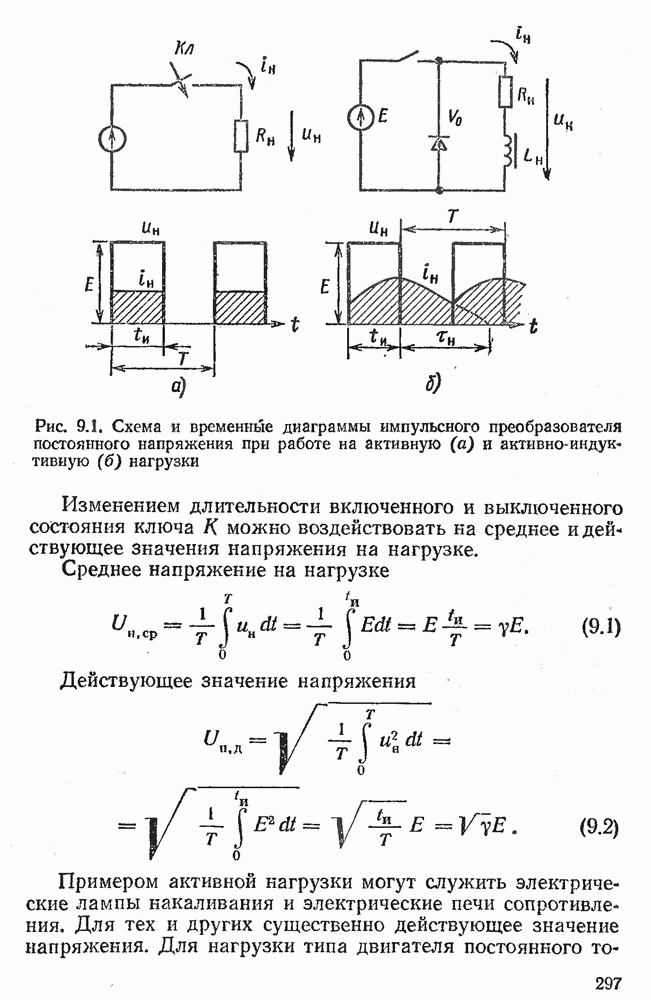
- 9.1. СПОСОБЫ РЕГУЛИРОВАНИЯ ПОСТОЯННОГО НАПРЯЖЕНИЯ
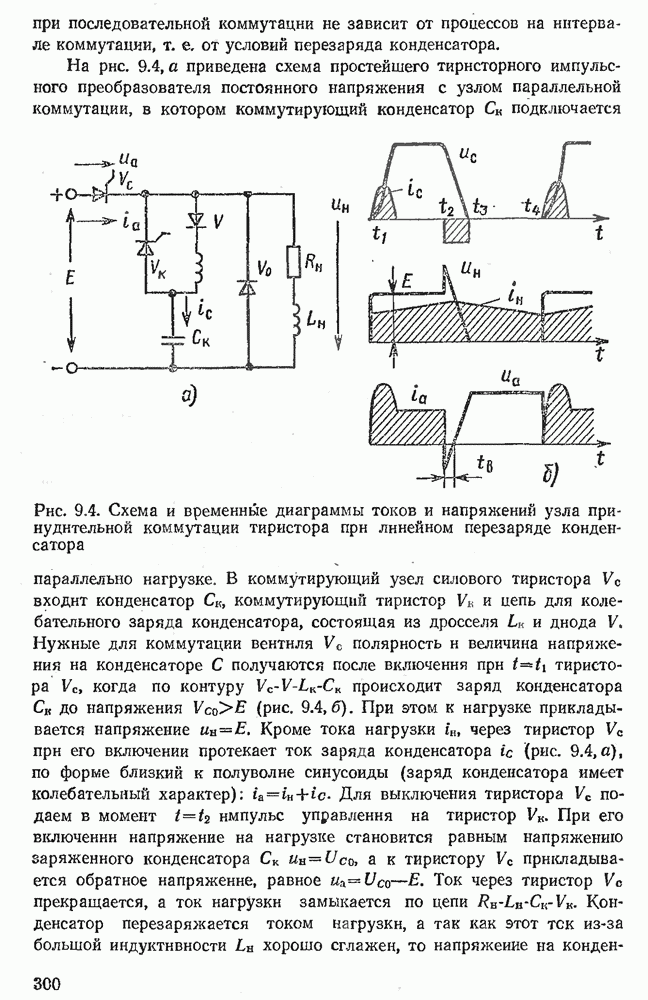
- 9.2. УЗЛЫ КОММУТАЦИИ ОДНООПЕРАЦИОННЫХ ТИРИСТОРОВ
- 9.3. ИНВЕРТОРЫ НАПРЯЖЕНИЯ
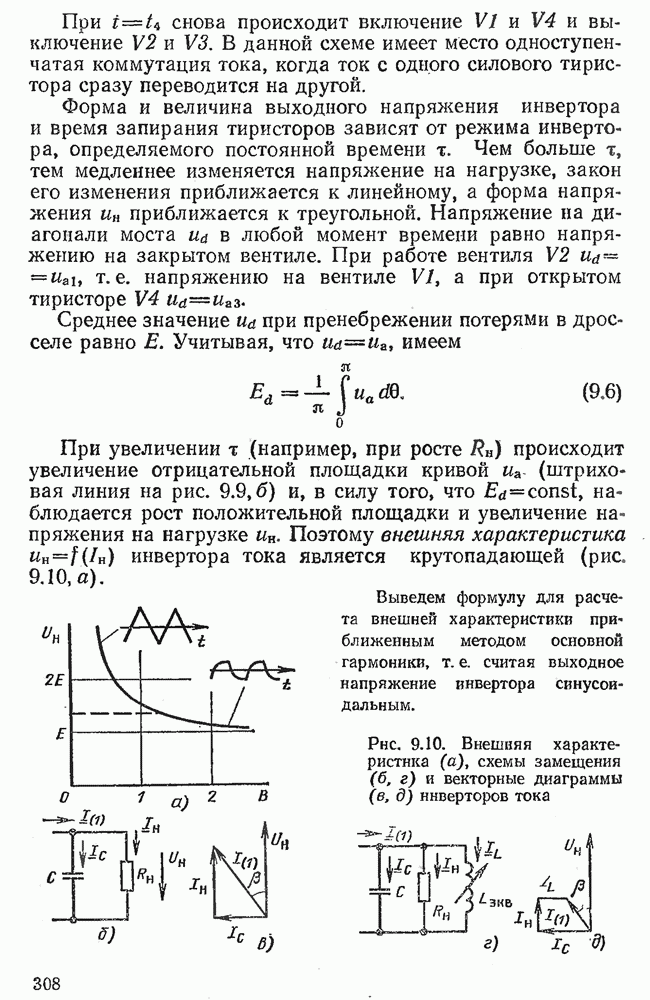
- 9.4. ИНВЕРТОРЫ ТОКА
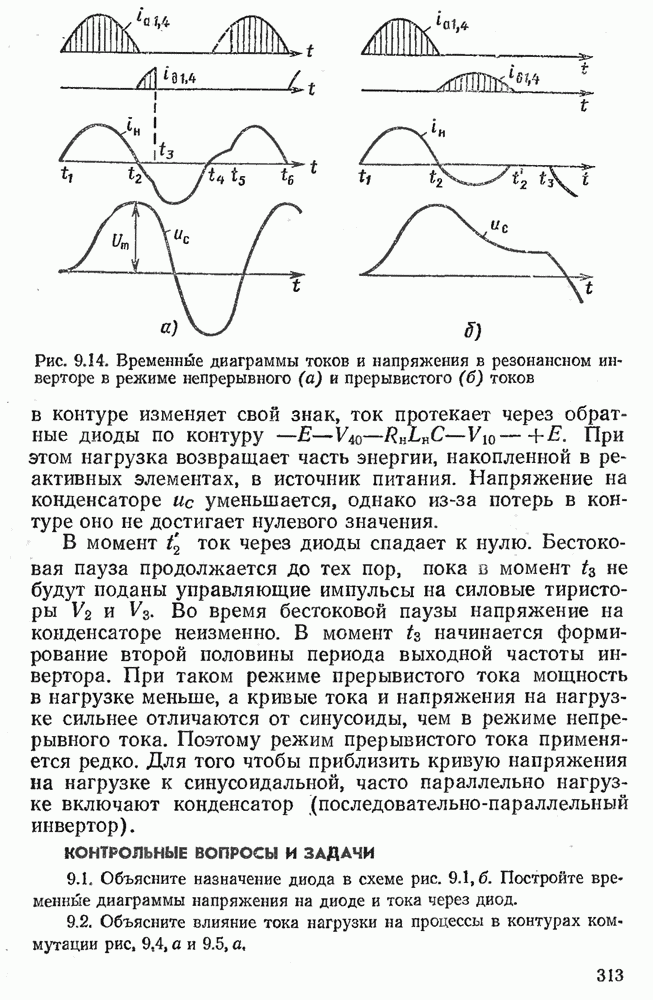
- 9.5. РЕЗОНАНСНЫЕ ИНВЕРТОРЫ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
- СПИСОК ЛИТЕРАТУРЫ