| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.3.1. Коды Грея
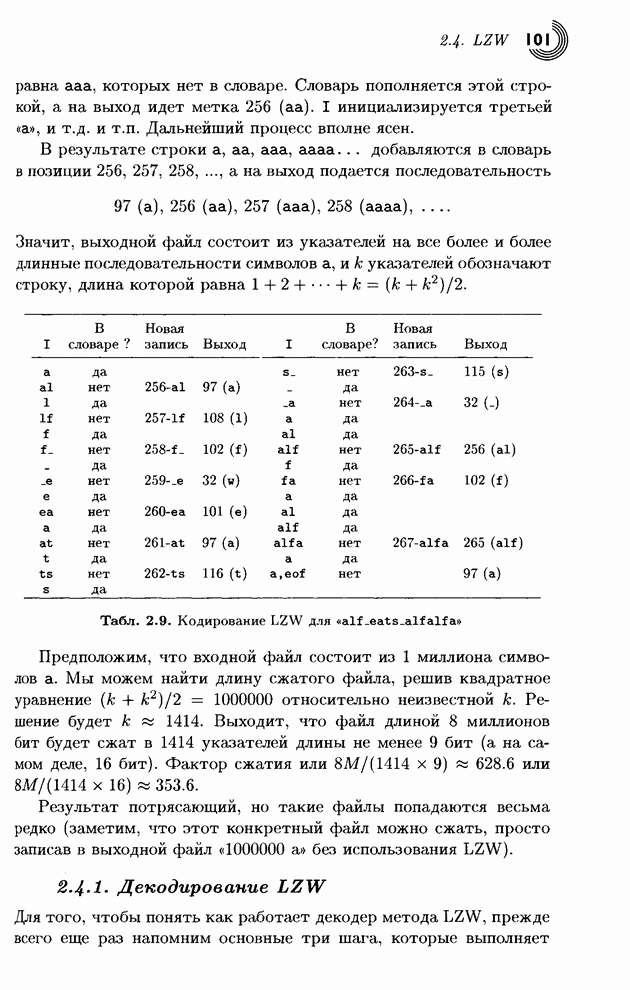
Методы сжатия изображений,
разработанные для конкретных типов графических образов, иногда могут успешно
применяться для компрессии других типов. Например, любой метод сжатия
двухуровневых изображений годится для полутоновых образов, если предварительно
расслоить полутоновой образ на несколько двухуровневых и каждый слой сжимать
независимо. Представим себе изображение с 16 градациями серого цвета. Каждый
пиксел определяется 4 битами, поэтому изображения разделяется на 4
двухуровневых. Однако при таком подходе может нарушиться основной принцип
сжатия изображений. Вообразим себе два прилегающих 4-битных пиксела со
значениями ![]() и
и
![]() . Эти
пикселы имеют близкие значения, но при их разделении на 4 слоя, они будут
различаться во всех 4 слоях! Происходит это из-за того, что в двоичном
представлении числа 7 и 8 различаются во всех четырех разрядах. Для того, чтобы
успешно применить здесь метод сжатия двухуровневых изображений необходимо,
чтобы в двоичном представлении два последовательных числа имели двоичные коды,
различающиеся только на один бит. Такое представление чисел существует и оно
называется рефлексными кодами Грея (RGC, reflected Gray code). Их легко построить, следуя
предлагаемому рекурсивному правилу.
. Эти
пикселы имеют близкие значения, но при их разделении на 4 слоя, они будут
различаться во всех 4 слоях! Происходит это из-за того, что в двоичном
представлении числа 7 и 8 различаются во всех четырех разрядах. Для того, чтобы
успешно применить здесь метод сжатия двухуровневых изображений необходимо,
чтобы в двоичном представлении два последовательных числа имели двоичные коды,
различающиеся только на один бит. Такое представление чисел существует и оно
называется рефлексными кодами Грея (RGC, reflected Gray code). Их легко построить, следуя
предлагаемому рекурсивному правилу.
Начнем с двух однобитных кодов (0, 1). Построим два семейства двухбитных кодов, повторив (0, 1), а потом добавив слева (или справа), сначала 0, а потом 1 к исходным семействам. В результате получим (00, 01) и (10, 11). Теперь следует переставить (отразить) коды второго семейства в обратном порядке и приписать к первому семейству. Тогда получатся 4 двухбитных кода RGC (00, 01, 11, 10), с помощью которых можно кодировать целые числа от 0 до 3, причем последовательные числа будут различаться ровно в одном двоичном разряде. Применяем эту процедуру еще раз и получаем два семейства кодов длины 3: (000, 001, 011, 010) и (110, 111, 101, 100). Объединяем их и получаем 3-битные коды RGC. Проделаем первые три шага для образования 4-битных кодов Грея:
добавить 0: (0000, 0001, 0011, 0010, 0110, 0111, 0101, 0100),
добавить 1: (1000, 1001, 1011, 1010, 1110, 1111, 1101, 1100),
отразить: (1100, 1101, 1111, 1110, 1010, 1011, 1001, 1000).
В табл. 3.6 показано, как
меняются отдельные биты двоичных кодов, представляющих числа от 0 до 32. В этой
таблице в нечетных столбцах приведены обычные двоичные коды целых чисел. Жирным
шрифтом выделены биты числа ![]() , которые отличаются от соответствующих
битов числа
, которые отличаются от соответствующих
битов числа ![]() .
Видно, что бит самого младшего (нулевого) разряда (бит
.
Видно, что бит самого младшего (нулевого) разряда (бит ![]() ) меняется каждый раз, бит
) меняется каждый раз, бит ![]() меняется каждый
второй раз, а в общем случае, бит
меняется каждый
второй раз, а в общем случае, бит ![]() меняется у каждого
меняется у каждого ![]() -го целого числа. В четных
столбцах таблицы помещены все последовательные коды Грея. Под таблицей
приведена рекурсивная функция Matlab, вычисляющая коды Грея.
-го целого числа. В четных
столбцах таблицы помещены все последовательные коды Грея. Под таблицей
приведена рекурсивная функция Matlab, вычисляющая коды Грея.
|
43210 |
Gray |
43210 |
Gray |
43210 |
Gray |
43210 |
Gray |
|
00000 |
00000 |
01000 |
10010 |
10000 |
00011 |
11000 |
10001 |
|
00001 |
00100 |
01001 |
10110 |
10001 |
00111 |
11001 |
10101 |
|
00010 |
01100 |
01010 |
11110 |
10010 |
01111 |
11010 |
11101 |
|
00011 |
01000 |
01011 |
11010 |
10011 |
01011 |
11011 |
11001 |
|
00100 |
11000 |
01100 |
01010 |
10100 |
11011 |
11100 |
01001 |
|
00101 |
11100 |
01101 |
01110 |
10101 |
11111 |
11101 |
01101 |
|
00110 |
10100 |
01110 |
00110 |
10110 |
10111 |
11110 |
00101 |
|
00111 |
10000 |
01111 |
00010 |
10111 |
10011 |
11111 |
00001 |
function b=rgc(a,i)
[r,c]=size(a);
b=[zeros(r,1),a; ones(r,1), flipud(a)];
if i>1, b=rgc(b,i-1); end;
Табл. 3.6. Первые 32 двоичных и RGC кода.
Коды RGC можно построить для целого ![]() , и не прибегая к рекурсивной
процедуре. Достаточно применить функцию «ИСКЛЮЧАЮЩЕЕ ИЛИ» к числу
, и не прибегая к рекурсивной
процедуре. Достаточно применить функцию «ИСКЛЮЧАЮЩЕЕ ИЛИ» к числу ![]() и к его логическому
сдвигу на один разряд вправо. Па языке С это запишется следующими операторами:
и к его логическому
сдвигу на один разряд вправо. Па языке С это запишется следующими операторами: ![]() . Табл. 3.7 (подобная
табл. 3.6) была порождена именно этим выражением.
. Табл. 3.7 (подобная
табл. 3.6) была порождена именно этим выражением.
Можно сделать следующий вывод.
Слой, соответствующий самому старшему двоичному разряду (в обычном
представлении) изображения, подчиняется принципу сжатия в большей, чем слой
самого младшего разряда. Когда соседние пикселы имеют значения, которые
различаются на единицу (равны ![]() и
и ![]() ), шансы на то, что их менее значимые или
более значимые разряды отличаются, одинаковы. Значит, любой метод компрессии,
который будет по отдельности сжимать слои должен или учитывать эту особенность
разрядности слоев, или использовать коды Грея для представления величин
пикселов.
), шансы на то, что их менее значимые или
более значимые разряды отличаются, одинаковы. Значит, любой метод компрессии,
который будет по отдельности сжимать слои должен или учитывать эту особенность
разрядности слоев, или использовать коды Грея для представления величин
пикселов.
|
43210 |
Gray |
43210 |
Gray |
43210 |
Gray |
43210 |
Gray |
|
00000 |
00000 |
01000 |
01100 |
10000 |
11000 |
11000 |
10100 |
|
00001 |
00001 |
01001 |
01101 |
10001 |
11001 |
11001 |
10101 |
|
00010 |
00011 |
01010 |
01111 |
10010 |
11011 |
11010 |
10111 |
|
00011 |
00010 |
01011 |
01110 |
10011 |
11010 |
11011 |
10110 |
|
00100 |
00110 |
01100 |
01010 |
10100 |
11110 |
11100 |
10010 |
|
00101 |
00111 |
01101 |
01011 |
10101 |
11111 |
11101 |
10011 |
|
00110 |
00101 |
01110 |
01001 |
10110 |
11101 |
11110 |
10001 |
|
00111 |
00100 |
01111 |
01000 |
10111 |
11100 |
11111 |
10000 |
a=linspace(0,31,32); b=bitshift(a,-1);
b=bitxor(a,b); dec2bin(b)
Табл. 3.7. Первые 32 двоичных и RGC кода.
На рис. 3.10, 3.11 и 3.12 показаны восемь побитных слоев картинки «попугаи» в обычном двоичном представлении (слева) и в виде кодов Грея (справа). Слои, построенные с помощью программы Matlab, приведены на рис. 3.8. Они занумерованы числами от 8 (самый старший, самый значимый бит) до 1 (самый младший бит). Очевидно, что слой самого младшего бита не показывает никакую корреляцию между пикселами; они случайны или близки к случайным для обоих представлений, двоичного и RGC. Однако, слои от 2 до 5 демонстрируют большую корреляцию пикселов для кодов Грея. Слои с 6 по 8 выглядят по-разному для двоичных кодов и для кодов Грея, но кажутся сильно коррелированными в обоих случаях.
На рис. 3.13 изображены две версии первых 32 кодов Грея в их графическом представлении. На рисунке (b) показаны коды из табл. 3.6, а на рисунке (с) приведены коды из табл. 3.9. Несмотря на то, что оба семейства образуют коды Грея, в них по разному чередуются биты 0 и 1 в разных побитных слоях. На рисунке (b) самый значимый бит меняется 4 раза. Второй значимый бит меняется 8 раз, а биты трех младших разрядов меняются, соответственно, 16, 2 и 1 раз. Если использовать это множество кодов Грея для расслоения изображения, то средние слои, очевидно, обнаружат наименьшую корреляцию между соседними пикселами.

Рис. 3.8. Разделение изображения на слои (Matlab).
|
43210 |
Gray |
43210 |
Gray |
43210 |
Gray |
43210 |
Gray |
|
00000 |
00000 |
01000 |
01100 |
10000 |
11000 |
11000 |
10100 |
|
00001 |
00001 |
01001 |
01101 |
10001 |
11001 |
11001 |
10101 |
|
00010 |
00011 |
01010 |
01111 |
10010 |
11011 |
11010 |
10111 |
|
00011 |
00010 |
01011 |
01110 |
10011 |
11010 |
11011 |
10110 |
|
00100 |
00110 |
01100 |
01010 |
10100 |
11110 |
11100 |
10010 |
|
00101 |
00111 |
01101 |
01011 |
10101 |
11111 |
11101 |
10011 |
|
00110 |
00101 |
01110 |
01001 |
10110 |
11101 |
11110 |
10001 |
|
00111 |
00100 |
01111 |
01000 |
10111 |
11100 |
11111 |
10000 |
a=linspace(0,31,32); b=bitshift(a,-1);
b=bitxor(a,b); dec2bin(b)
Табл. 3.9. Первые 32 двоичных и RGC кода.
В противоположность этому, коды рисунка (с) будут демонстрировать большую корреляцию в слоях старших разрядов, поскольку там смена между 0 и 1 происходит, соответственно, 1, 2 и 4 раза (по старшинству разрядов). А младшие разряды покажут слабую корреляцию пикселов, которая стремится к нулю, как при случайном распределении пикселов. Для сравнения на рис. 3.13 (а) показаны обычные двоичные коды. Видно, что в этих кодах разряды меняются существенно чаще.
Даже поверхностный взгляд на коды Грея рис. 3.13 (с) обнаруживает в них некоторую регулярность. Более тщательное исследование выявляет две важные особенности этих кодов, которые можно использовать при их построении. Первая особенность заключается в периодической смене значений всех пяти разрядов. Легко написать программу, которая сначала установит все пять разрядов в 0, потом будет менять самый правый разряд у каждого второго кода, а остальные четыре разряда будет менять в середине периода своего правого соседнего разряда.

Рис. 3.10. (а) Слои 1 и 2 изображения «попугаи».

Рис. 3.11. (а) Слои 3,4 и 5 изображения «попугаи».

Рис. 3.12. (а) Слои 6,7 и 8 изображения «попугаи».

Рис. 3.13. Первые 32 двоичных и RGC кода.
Другая особенность кодов Грея состоит в том, что вторая половина таблицы является зеркальным отображением первой половины, если самый значимый бит установить в 1. Если первая половина таблицы уже вычислена, то вторая легко получается с помощью этого свойства.
На рис. 3.14 показаны круговые диаграммы, представляющие 4-х и 6-ти битные коды RGC (а), и обычные двоичные коды (b). Слои разрядов показаны в виде колец, причем слой самого значимого бита находится внутри. Видно, что максимальная угловая частота кода RGC в два раза меньше, чему у двоичного кода. Такое циклическое представление кодов Грея не нарушает их структуру, так как первый и последний код также отличаются ровно в одном бите.

Рис. 3.14. Круговая диаграмма двоичных и RGC кодов.
К цветным изображениям также можно применять методы компрессии, разработанные для других типов изображений. Любой метод сжатия полутоновых образов позволяет сжимать цветные изображения. В цветном изображении каждый пиксел состоит из трех цветных компонент (например, RGB). Представим себе цветное изображение, в котором все компоненты состоят из одного байта. Пиксел описывается тремя байтами или 24 битами, но эти биты нельзя рассматривать как одно число. Три пиксела 118|206|12 и 117|206|12 различаются только на единицу в первом компоненте, поэтому они имеют близкие цвета. Если же их рассматривать в виде 24-битных чисел, то они будут сильно различаться, поскольку они разнятся в старшем бите. Любой метод компрессии, который будет основываться на таком различении пикселов, будет сильно неоптимальным. В этом смысле более подходящим является метод разделения изображения на цветные компоненты с их последующим независимым сжатием методом полутоновой компрессии.
Метод взвешенных контекстных деревьев изображений (см. [Salomon 2000 и Ekstrand 96]) является примером использования кодов RGC для сжатия образов.
|
История кодов Грея Эти коды названы в честь Франка Грея (Frank Gray), который запатентовал их использование в кодерах в 1953 году [Gray 53]. Однако эта работа была выполнена существенно раньше; он ее подал для патентования уже в 1947 году. Грей работал исследователем в лаборатории Белла. В течение 1930-х и 1940-х годов он получил несколько патентов в области телевидения. Если верить [Heath 72], то эти коды уже применялись Баудотом (J.M.E.Baudot) в телеграфии в 1870-х годах, но только после изобретения компьютеров эти коды стали широко известны. Коды Баудота состояли из пяти бит на
символ. С их помощью можно представить В августе 1972 в журнале Scientific American были опубликованы две интересные статьи на тему кодов Грея: одна про происхождение двоичных кодов [Heath 72], а другая – [Gardner 72] про некоторые развлекательные аспекты использования этих кодов. |
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие переводчика
- Предисловие автора
- Введение
- Глава 1. Статистические методы
- 1.1. Энтропия
- 1.2. Коды переменной длины
- 1.3. Декодирование
- 1.4. Кодирование Хаффмана
- 1.4.1. Декодирование Хаффмана
- 1.4.2. Средняя длина кода
- 1.5. Адаптивные коды Хаффмана
- 1.5.1. Несжатые коды
- 1.5.2. Модификация дерева
- 1.5.3. Переполнение счетчика
- 1.5.4. Кодовое переполнение
- 1.5.5. Вариант алгоритма
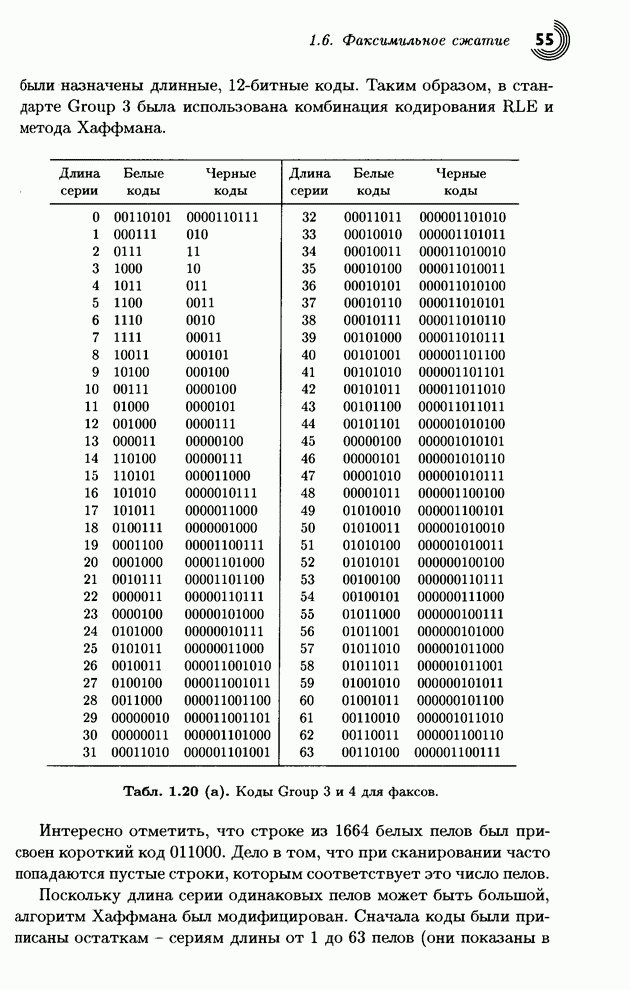
- 1.6. Факсимильное сжатие
- 1.6.1. Одномерное кодирование
- 1.6.2. Двумерное кодирование
- 1.7. Арифметическое кодирование
- 1.7.1. Детали реализации метода
- 1.7.2. Потеря значащих цифр
- 1.7.3. Заключительные замечания
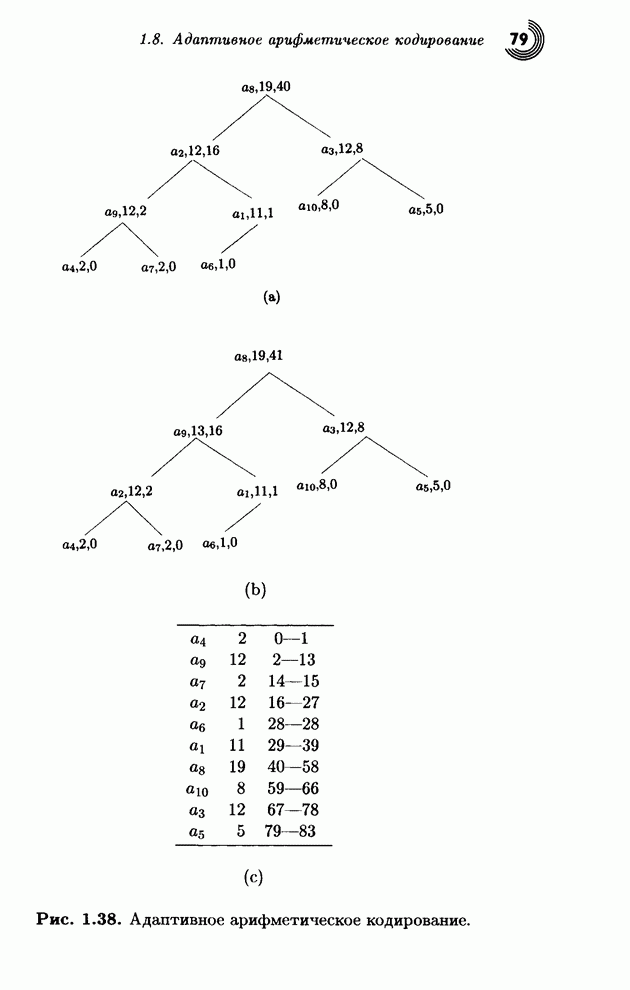
- 1.8. Адаптивное арифметическое кодирование
- ГЛАВА 2 СЛОВАРНЫЕ МЕТОДЫ
- 2.1. LZ77 (скользящее окно)
- 2.1.1. Циклическая очередь
- 2.2. LZSS
- 2.2.1. Недостатки
- 2.3. LZ78
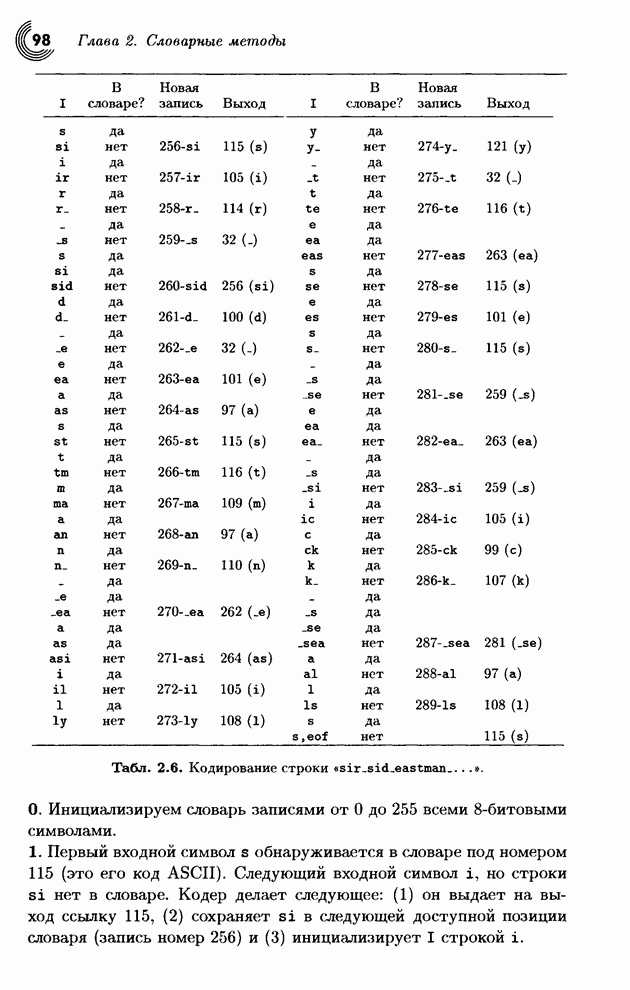
- 2.4. LZW
- 2.4.1. Декодирование LZW
- 2.4.2. Структура словаря LZW
- 2.4.3. LZW в практических приложениях
- 2.5. Заключение
- ГЛАВА 3 СЖАТИЕ ИЗОБРАЖЕНИЙ
- 3.1. Введение
- 3.2. Типы изображений
- 3.3. Подходы к сжатию изображений
- 3.3.1. Коды Грея
- 3.3.2. Метрики ошибок
- 3.4. Интуитивные методы
- 3.4.1. Подвыборка
- 3.4.2. Квантование
- 3.5. Преобразование изображений
- 3.5.1. Ортогональные преобразования
- 3.5.2. Матричные преобразования
- 3.5.3. Дискретное косинус-преобразование
- 3.5.4. Пример
- 3.5.5. Дискретное синус-преобразование
- 3.5.6. Преобразование Уолша-Адамара
- 3.5.7. Преобразование Хаара
- 3.5.8. Преобразование Кархунена-Лоэвэ
- 3.6. Прогрессирующее сжатие изображений
- 3.7. JPEG
- 3.7.1. Светимость
- 3.7.2. DCT
- 3.7.3. Практическое DCT
- 3.7.4. Квантование
- 3.7.5. Кодирование
- 3.7.6. Мода без потери данных
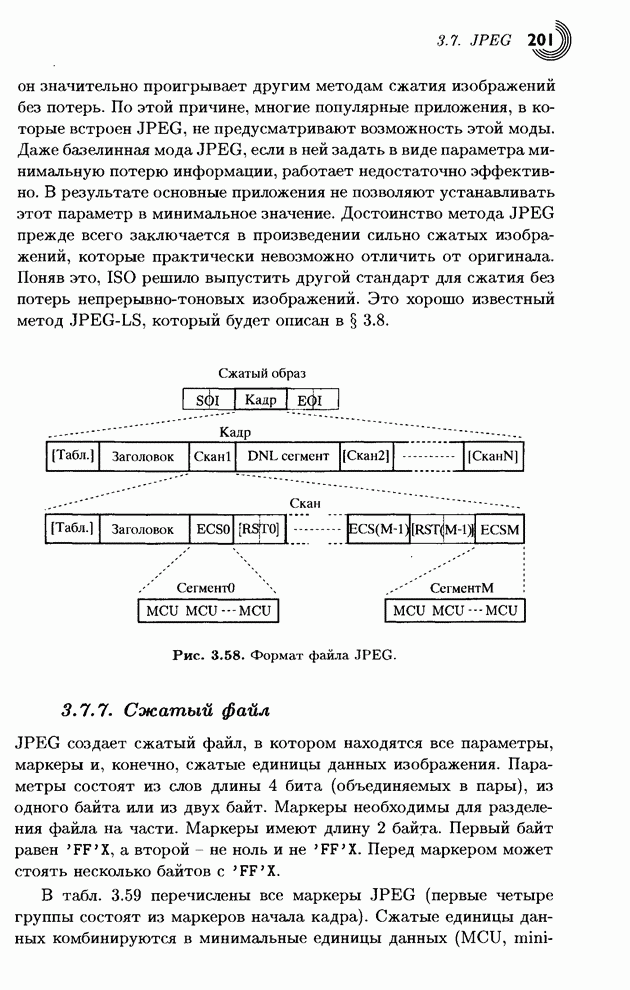
- 3.7.7. Сжатый файл
- 3.7.8. JFIF
- 3.8. JPEG-LS
- 3.8.1. Коды Голомба
- 3.8.2. Основы метода JPEG-LS
- 3.8.3. Кодер
- ГЛАВА 4 ВЕЙВЛЕТНЫЕ МЕТОДЫ
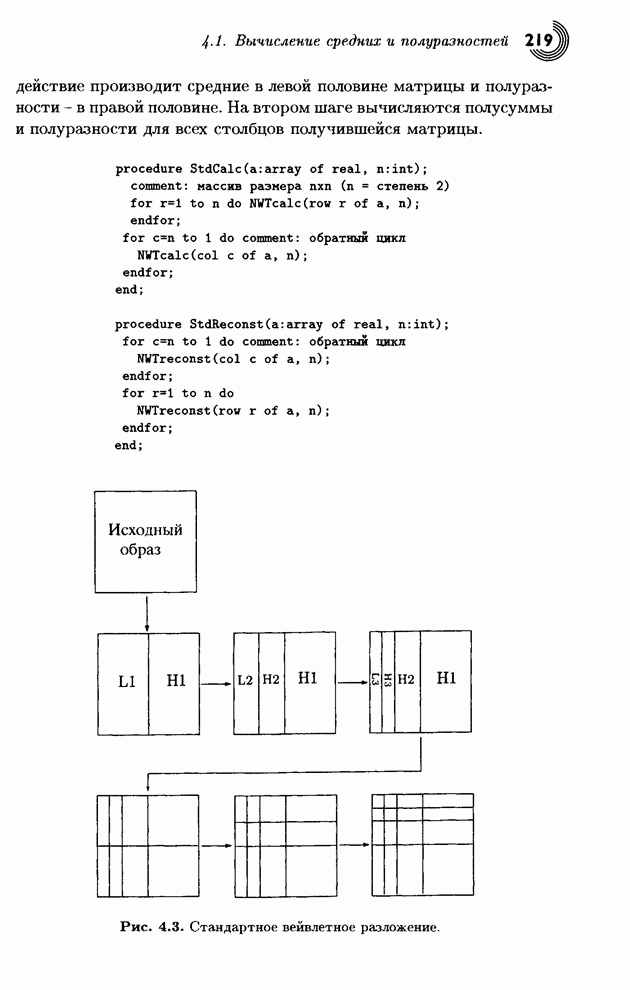
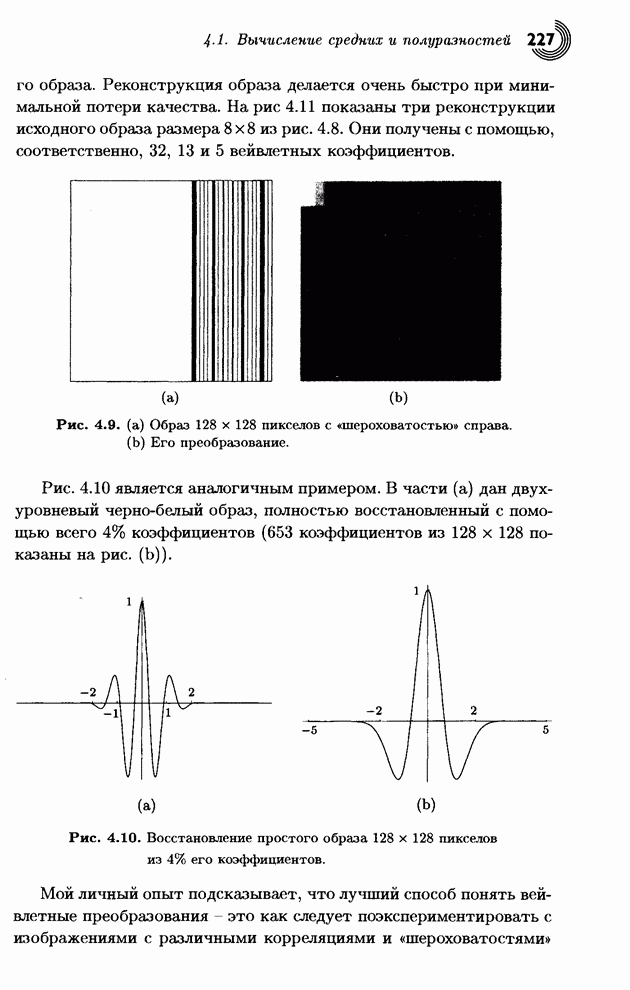
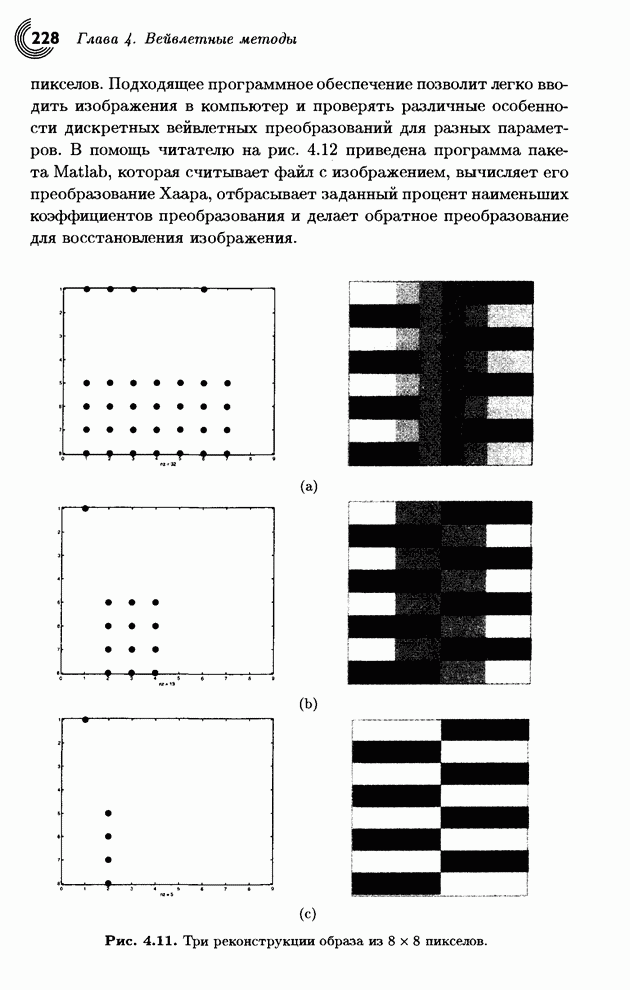
- 4.1. Вычисление средних и полу разностей
- 4.1.1. Обобщение на двумерный случай
- 4.1.2. Свойства преобразования Хаара
- 4.2. Преобразование Хаара
- 4.2.1. Матричная форма
- 4.3. Поддиапазонные преобразования
- 4.4. Банк фильтров
- 4.5. Нахождение коэффициентов фильтра
- 4.6. Преобразование DWT
- 4.7. Примеры
- 4.8. Вейвлеты Добеши
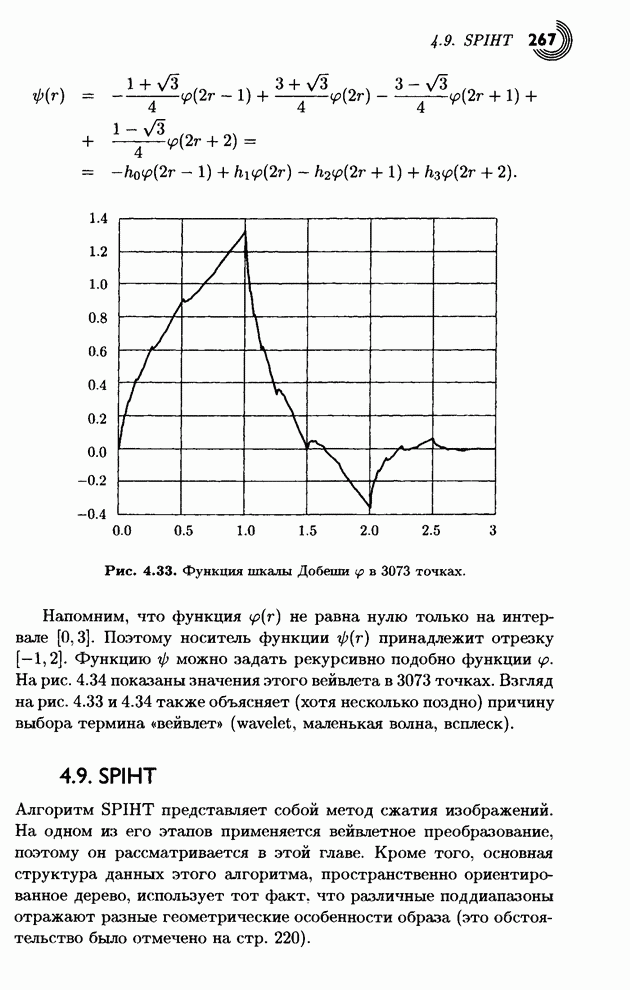
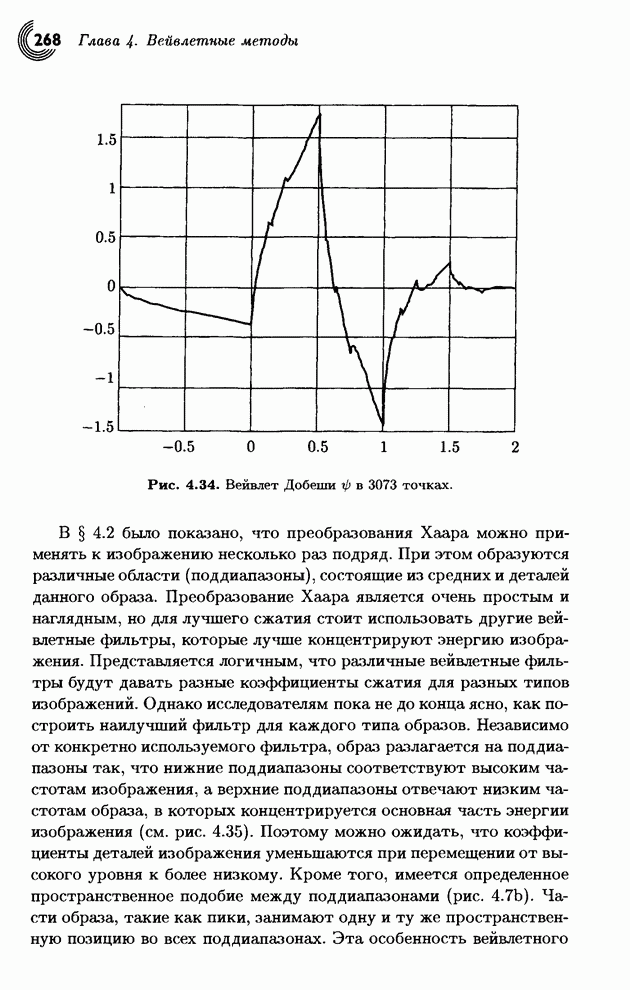
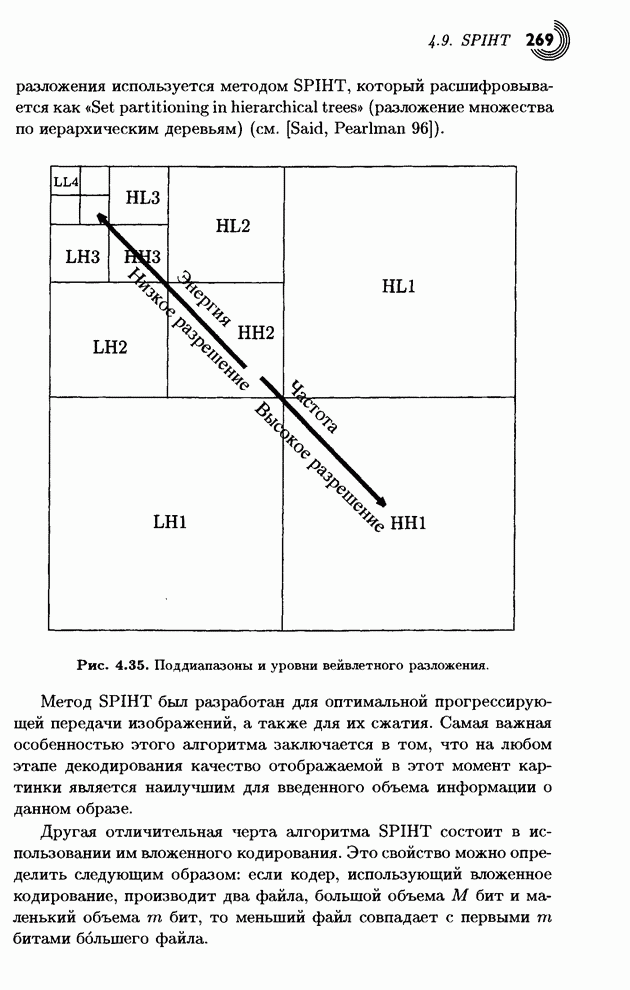
- 4.9. SPIHT
- 4.9.1. Алгоритм сортировки разделением множеств
- 4.9.2. Пространственно ориентированное дерево
- 4.9.3. Кодирование в алгоритме SPIHT
- 4.9.4. Пример
- 4.9.5. QTCQ
- ГЛАВА 5 СЖАТИЕ ВИДЕО
- 5.1. Основные принципы
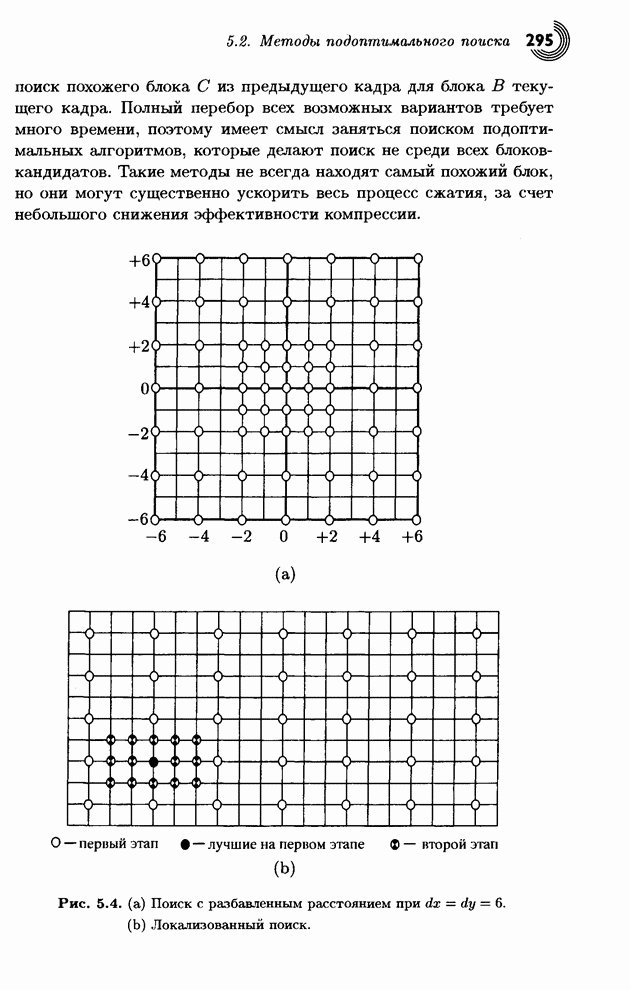
- 5.2. Методы подоптимального поиска
- ГЛАВА 6 СЖАТИЕ ЗВУКА
- 6.1. Звук
- 6.2. Оцифрованный звук
- 6.3. Органы слуха человека
- 6.4. Общепризнанные методы
- 6.5. Сжатие звука в стандарте MPEG-1
- 6.5.1. Кодирование частотной области
- 6.5.2. Формат сжатых данных
- 6.5.3. Психоакустические модели
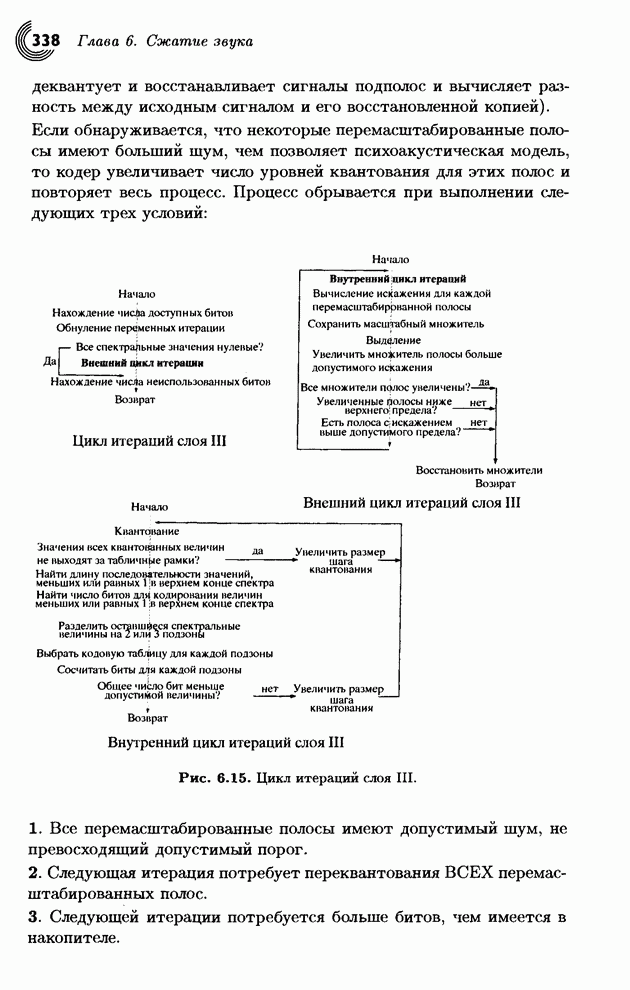
- 6.5.4. Кодирование: слой III
- Литература
- Глоссарий