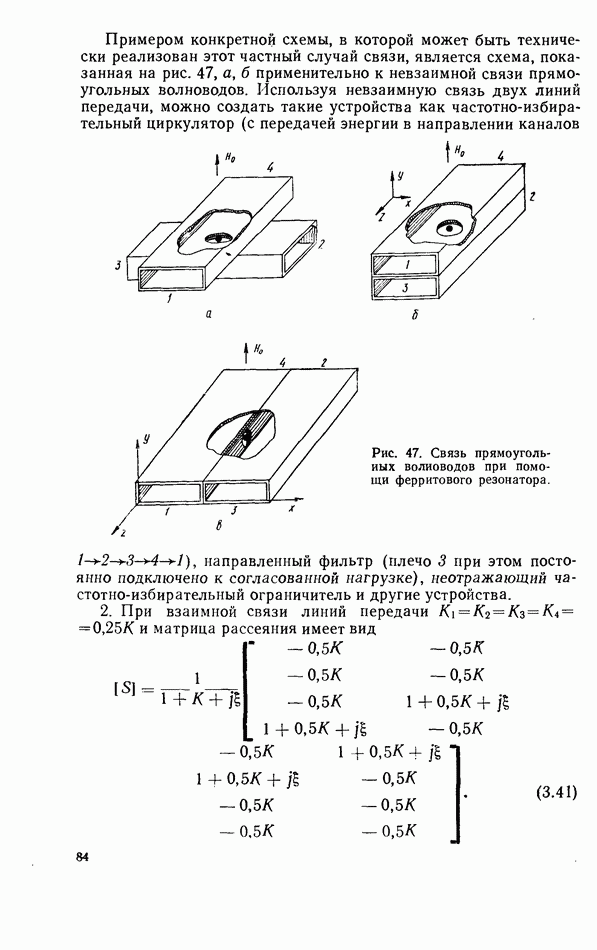
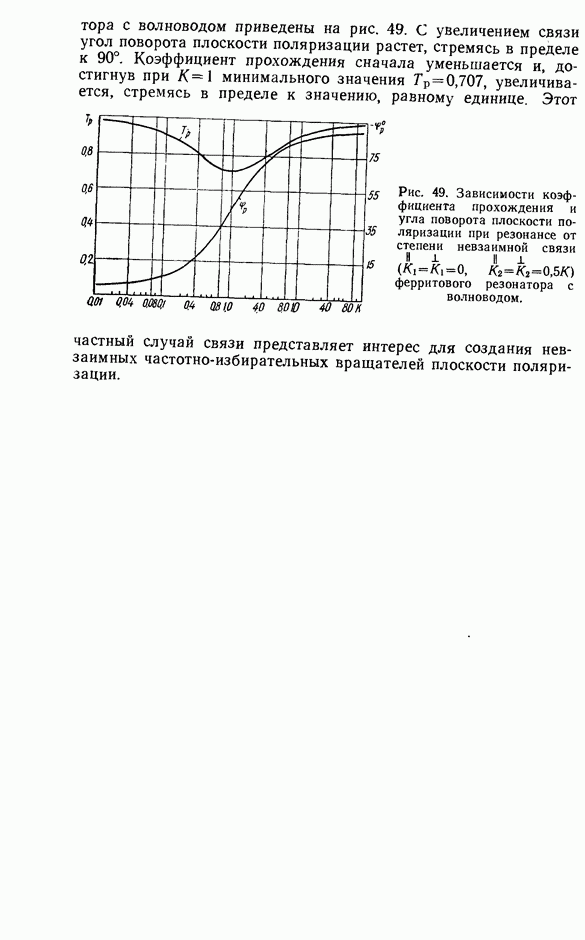
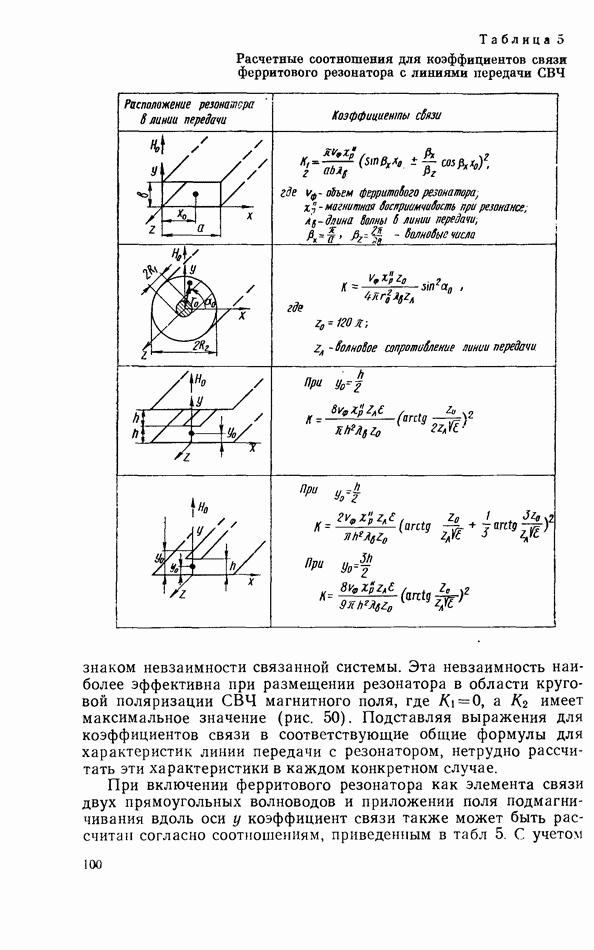
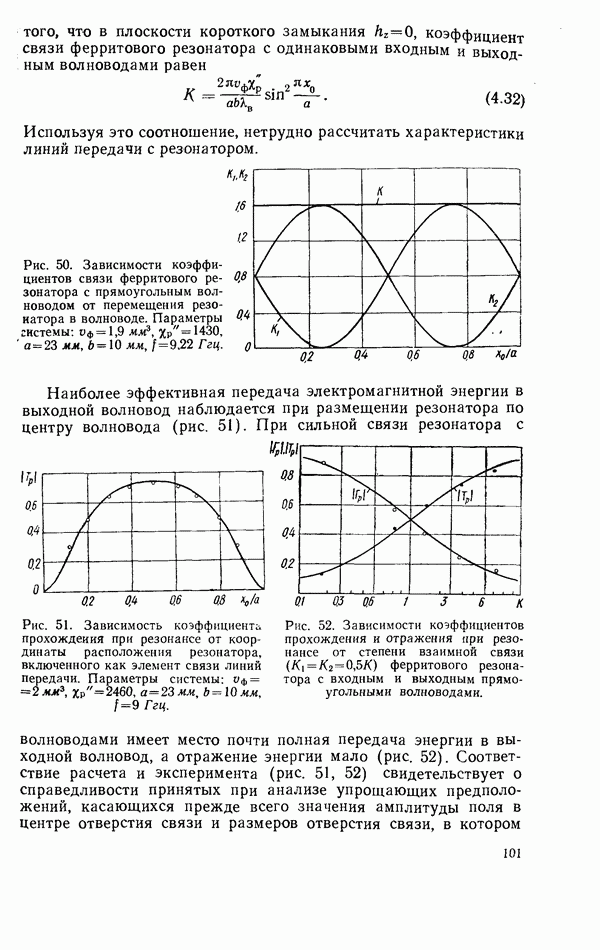
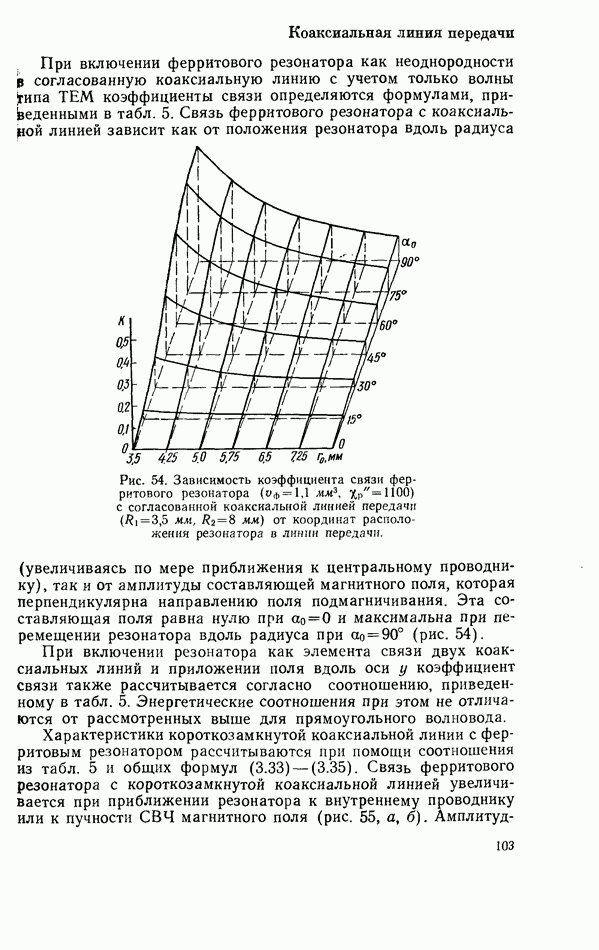
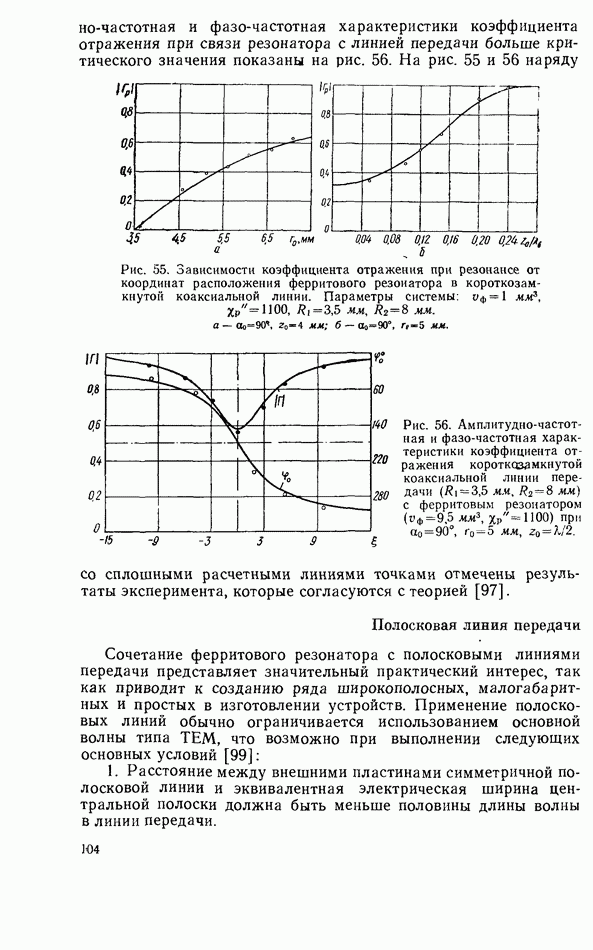
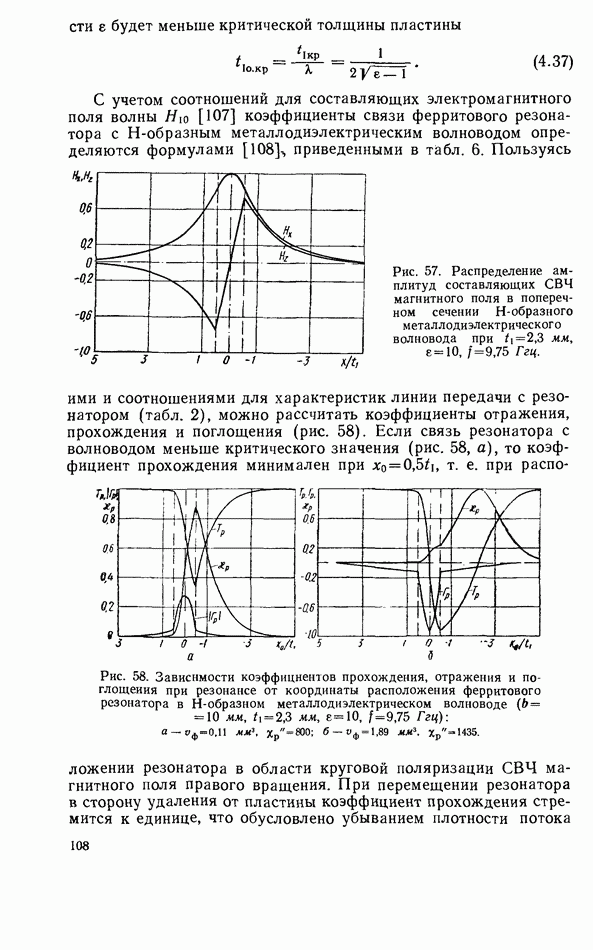
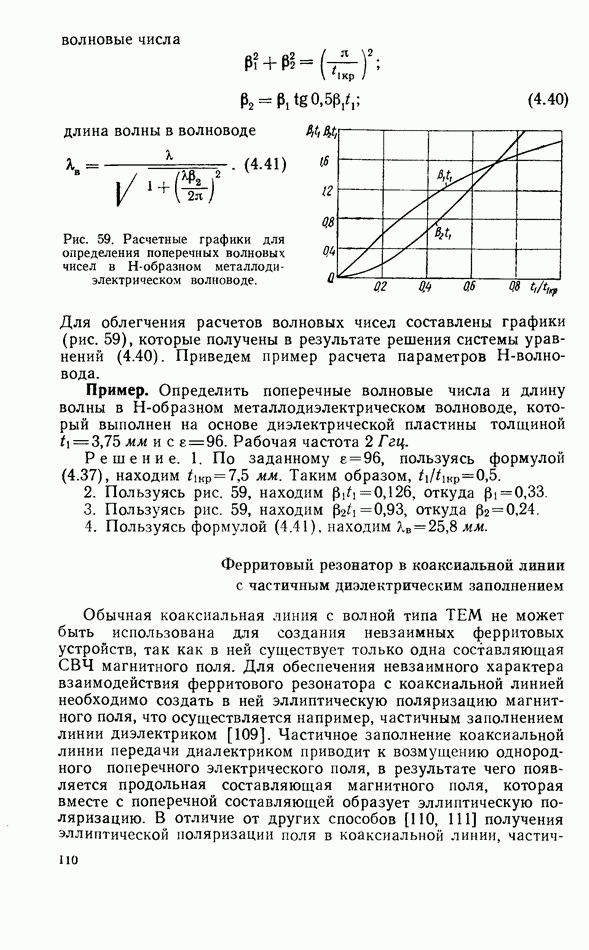
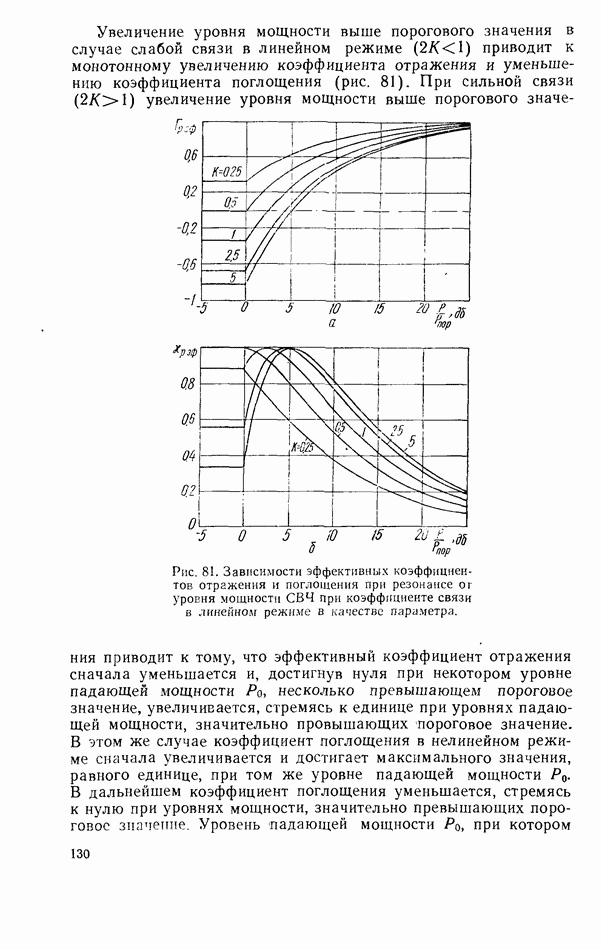
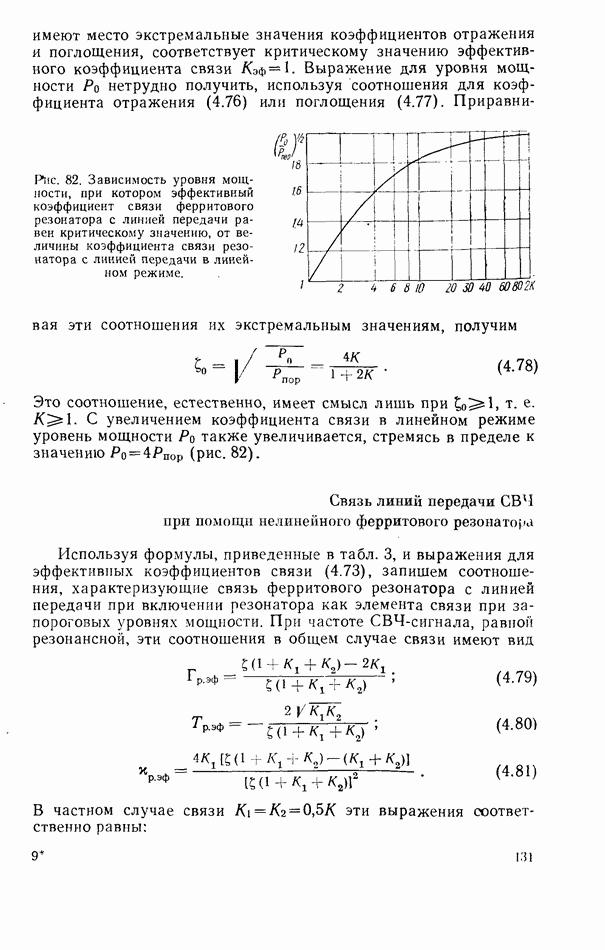
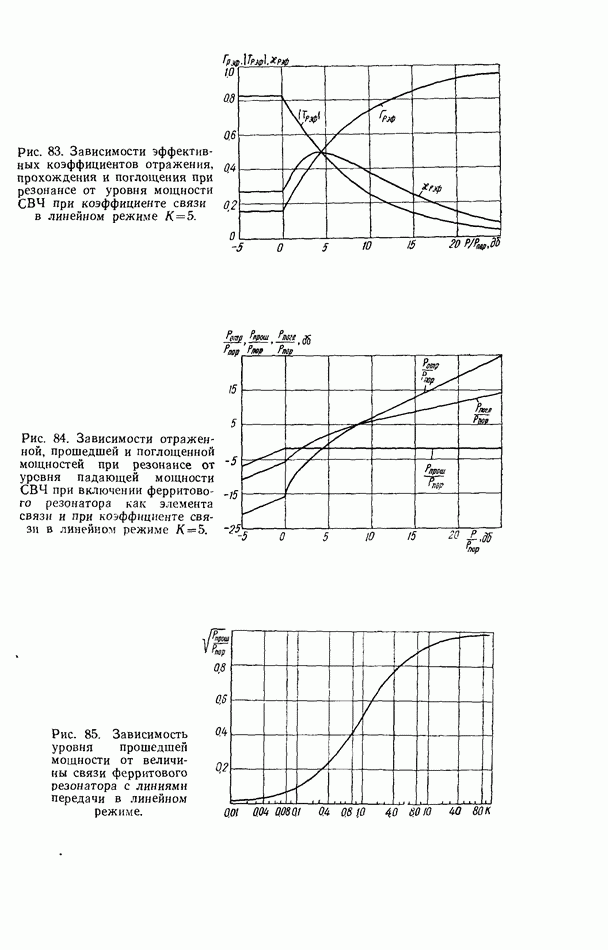
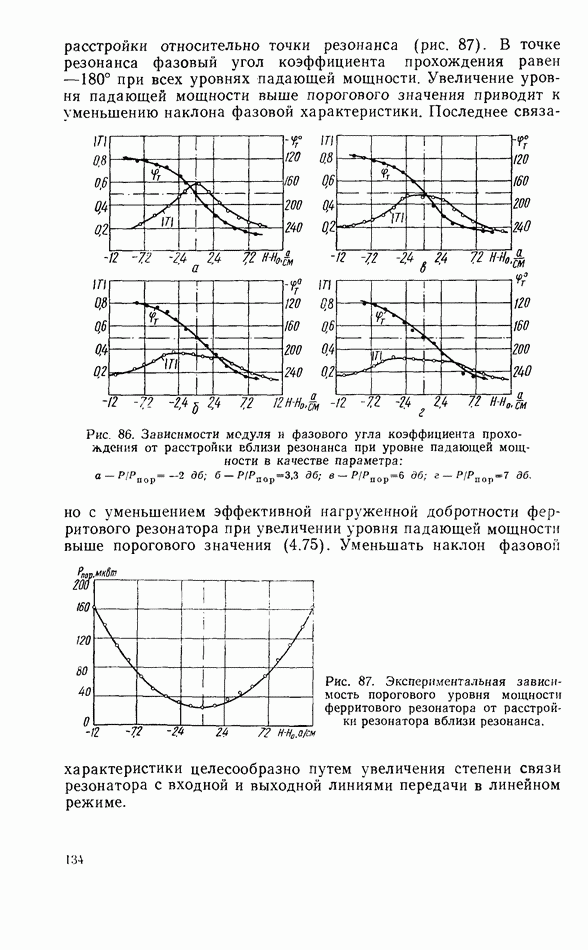
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В АНИЗОТРОПНОМ ДИЭЛЕКТРИЧЕСКОМ СТЕРЖНЕ С «МАГНИТНЫМИ» БОКОВЫМИ СТЕНКАМИ
При анализе воспользуемся обобщенной цилиндрической системой координат  (рис. 10). Ее криволинейные координаты
(рис. 10). Ее криволинейные координаты  лежат в плоскости, перпендикулярной продольной оси z.
лежат в плоскости, перпендикулярной продольной оси z.
Дмплитуды векторов поля в образце в общем случае зависят от поперечных координат  а фазы — от продольной координаты
а фазы — от продольной координаты  Пренебрегая потерями, векторы поля можно представить в виде
Пренебрегая потерями, векторы поля можно представить в виде

где  — продольное волновое число.
— продольное волновое число.

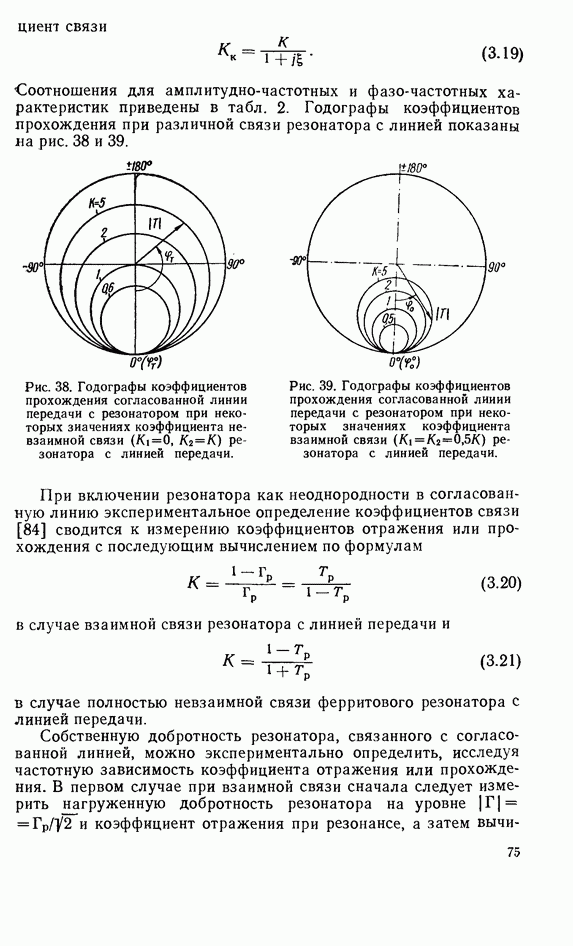
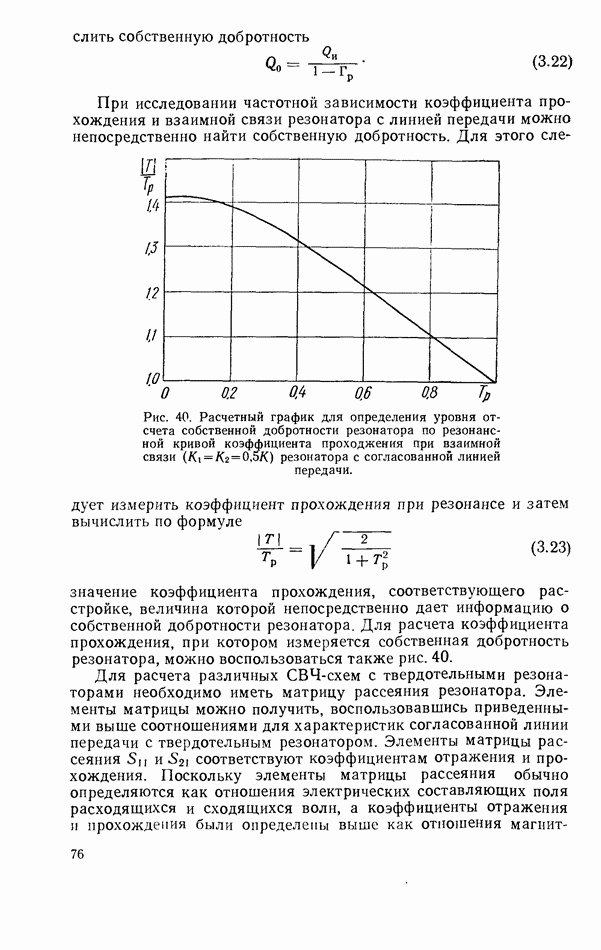
Рис. 10. Анизотропный диэлектрический стержень  в обобщенной цилиндрической системе координат.
в обобщенной цилиндрической системе координат.
Подставив (2.5) в уравнения Макс. велла и разложив векторы по ортам обобщенно-цилиндрической системы координат, получим
(см. скан)
где  коэффициенты Лямэ;
коэффициенты Лямэ;  составляющие диагонального тензора
составляющие диагонального тензора

V Пользуясь уравнениями (2.6) — (2.11), выразим поперечные Компоненты поля через продольны

(см. скан)
где
(см. скан)
Подставляя (2.13)-(2.16) в уравнения (2.8) и (2.11), получим
(см. скан)
Как видно, поперечные компоненты поля могут существовать при  или при
или при  первом случае волны называются электрическими, во втором — магтными. Полагая
первом случае волны называются электрическими, во втором — магтными. Полагая  в (2.17) и (2.18), имеем
в (2.17) и (2.18), имеем
(см. скан)
Аналогично, положив  и (2.18), получим
и (2.18), получим

Таким образом, чистые  и
и  -типы волн могут существовать в случаях, когда
-типы волн могут существовать в случаях, когда  т. е.
т. е.  [34]. Ограничимся в дальнейшем этим случаем анизотропии, когда в поперечном сечении образец можно рассматривать как изотропный с диэлектрической проницаемости
[34]. Ограничимся в дальнейшем этим случаем анизотропии, когда в поперечном сечении образец можно рассматривать как изотропный с диэлектрической проницаемости  а вдоль оси
а вдоль оси  он имеет диэлектрическую проницаемость
он имеет диэлектрическую проницаемость 
Уравнения (2.19) и (2.20) характеризуют волновой характер распространения электромагнитной энергии в диэлектрическом образце. При этом определение структуры поля сводится к интегрированию этих уравнений. Постоянные интегрирования определяются граничными условиями на боковых стенках диэлектрического образца.
Рассмотрим вопрос о Я- и  -типах волн в диэлектрическом образце с «магнитными» боковыми стенками отдельно для прямоугольного и цилиндрического стержней.
-типах волн в диэлектрическом образце с «магнитными» боковыми стенками отдельно для прямоугольного и цилиндрического стержней.
При исследовании прямоугольного диэлектрического образца исйользуем декартову систему координат. Обозначим боковые стенки образца буквами  и расположим оси координат, как показано на рис. 11. Волновое уравнение (2.19) для продольной составляющей поля магнитных волн после перехода к новой системе, в которой
и расположим оси координат, как показано на рис. 11. Волновое уравнение (2.19) для продольной составляющей поля магнитных волн после перехода к новой системе, в которой

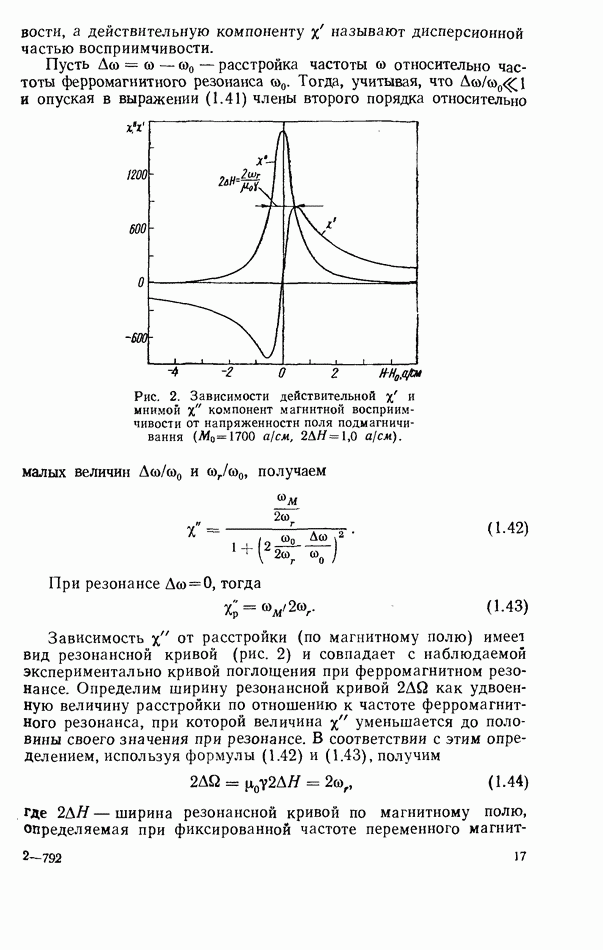
имеет вид

где  поперечное волновое число, которое связано с продольным волновым числом
поперечное волновое число, которое связано с продольным волновым числом  соотношением
соотношением  Решая уравнение (2.24) методом разделения переменных аналогично [43] при граничных условиях (2.3), можно получить выражения Для составляющих электромагнитного поля нечетных
Решая уравнение (2.24) методом разделения переменных аналогично [43] при граничных условиях (2.3), можно получить выражения Для составляющих электромагнитного поля нечетных  -волн диэлектрического стержня
-волн диэлектрического стержня


где  поперечные Еолновые числа;
поперечные Еолновые числа;  целые числа;
целые числа;  постоянная, определяющая амлитуду поля.
постоянная, определяющая амлитуду поля.

Рис. 11. Прямоугольный диэлектрический стержень.

Рис. 12. Цилиндрический диэлектрический стержень.
В этих и последующих уравнениях для составляющих поля в стержне опущен множитель характеризующий волну, распространяющуюся в направлении  с фазовой постоянной, равной
с фазовой постоянной, равной 
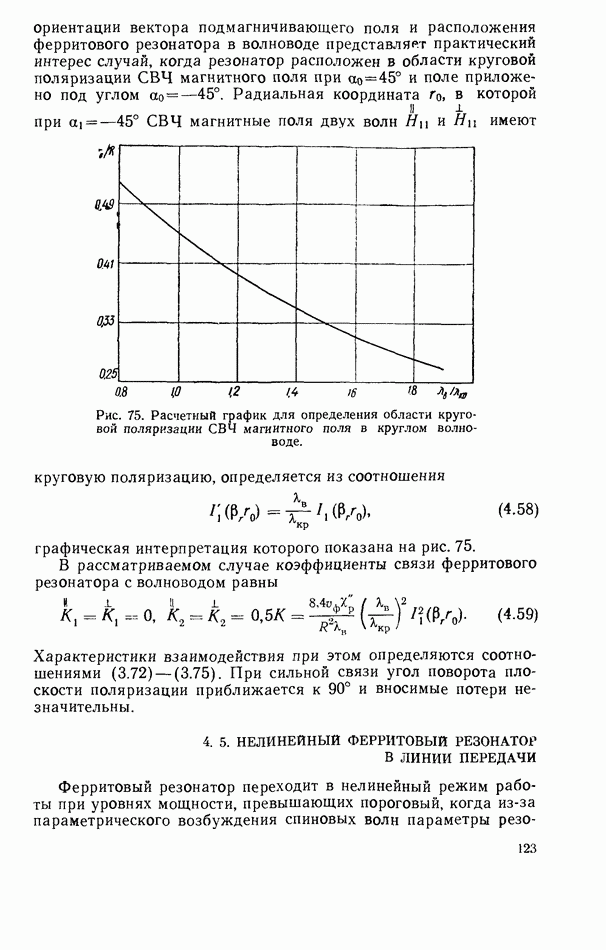
Уравнение (2.21) для продольной составляющей поля электрических волн с учетом (2.23) имеет вид

где  поперечное волновое число, которое отличается от поперечного волнового числа
поперечное волновое число, которое отличается от поперечного волнового числа  -волн из-за анизотропии диэлектрического стержня
-волн из-за анизотропии диэлектрического стержня  Решение этого уравнения при граничных условиях (2.3) приводит к выражениям для составляющих электромагнитного поля четных
Решение этого уравнения при граничных условиях (2.3) приводит к выражениям для составляющих электромагнитного поля четных  -волн анизотропного диэлектрического стержня
-волн анизотропного диэлектрического стержня


здесь  амплитуда поля.
амплитуда поля.
При исследовании цилиндрического диэлектрического образца удобно использовать цилиндрическую систему координат. Обозначим диаметр стержня через  и расположим оси координат, как показано на рис. 12.
и расположим оси координат, как показано на рис. 12.
Уравнение для продольной составляющей поля (2.19) магнитных волн в цилиндрической системе координат с учетом того, что

приводится к виду

где поперечное волновое число, как и раньше, связано с продольным волновым числом соотношением 
Решение уравнения (2.29) аналогично [44] при граничных условиях (2.3) с последующим использованием (2.13) — (2.16) приводит к выражениям для составляющих электромагнитного поля  -волн цилиндрического стержня
-волн цилиндрического стержня

где  функция Бесселя
функция Бесселя  порядка, а поперечное волновое число определяется соотношением
порядка, а поперечное волновое число определяется соотношением  корни уравнения
корни уравнения  сочетание
сочетание  определяет тип
определяет тип  -поля в цилиндрическом стержне.
-поля в цилиндрическом стержне.
Уравнение (2.21) для продольной составляющей поля электрических волн в цилиндрической системе координат имеет вид

где

Из решения этого уравнения аналогично находятся составляющие электромагнитного поля цилиндрического стержня

где поперечное волновое число  корни уравнения
корни уравнения  сочетание
сочетание  определяет тип
определяет тип  -волн в стержне.
-волн в стержне.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава первая. СВОЙСТВА ФЕРРИТОВЫХ РЕЗОНАТОРОВ
- Ферромагнитный резонанс в неограниченной среде без потерь
- 1.2. РЕЗОНАНСНАЯ ЧАСТОТА
- Зависимость резонансной частоты от формы резонатора
- Влияние кристаллографической анизотропии на резонансную частоту
- 1.3. МАГНИТОСТАТИЧЕСКИЕ ВИДЫ КОЛЕБАНИЙ
- 1.4. УЧЕТ ПОТЕРЬ
- 1.5. ДИПОЛЬНЫЙ МОМЕНТ
- 1.6. НЕЛИНЕЙНЫЕ ЯВЛЕНИЯ
- Спиновые волны
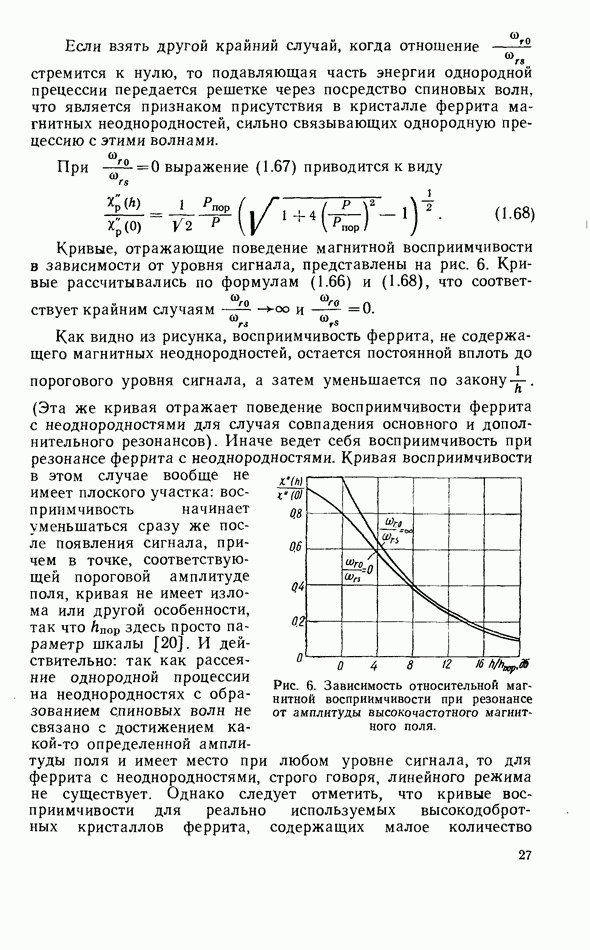
- Пороговая амплитуда высокочастотного магнитного поля
- Восприимчивость при амплитудах поля, превышающих пороговое значение
- 1.7. ПРИМЕНЯЕМЫЕ ДЛЯ ИЗГОТОВЛЕНИЯ МАТЕРИАЛЫ
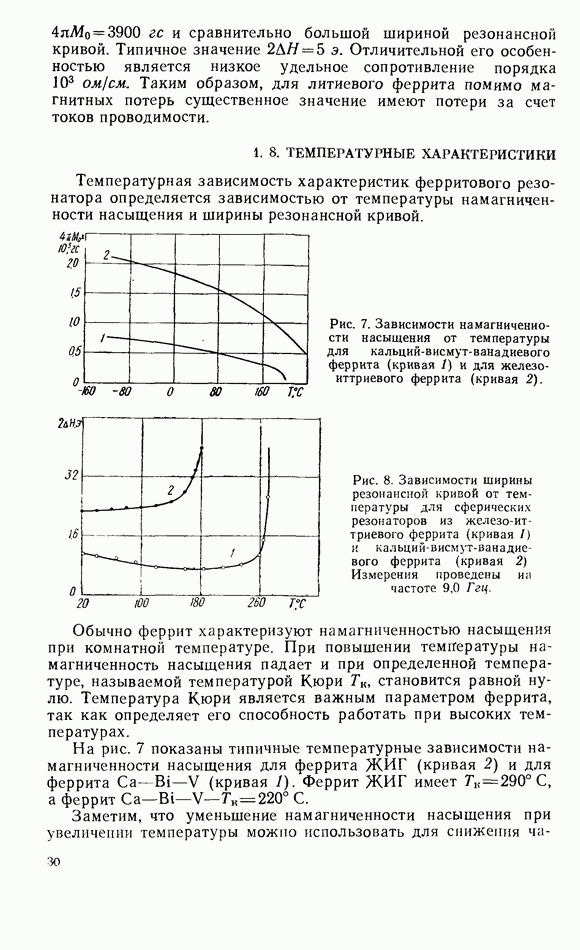
- 1.8. ТЕМПЕРАТУРНЫЕ ХАРАКТЕРИСТИКИ
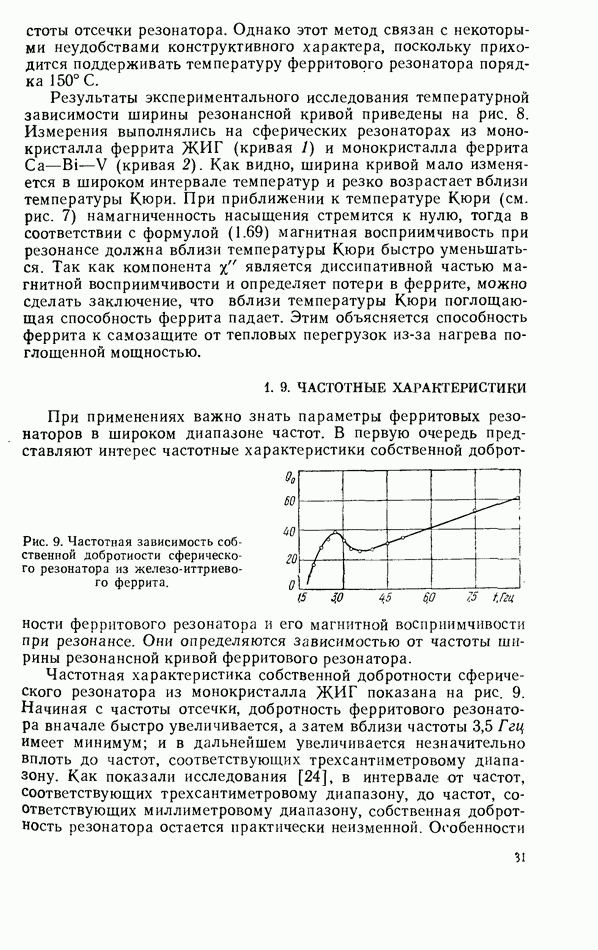
- 1.9. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- Глава вторая. СВОЙСТВА ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 2.2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В АНИЗОТРОПНОМ ДИЭЛЕКТРИЧЕСКОМ СТЕРЖНЕ С «МАГНИТНЫМИ» БОКОВЫМИ СТЕНКАМИ
- 2.3. ПРИБЛИЖЕННЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
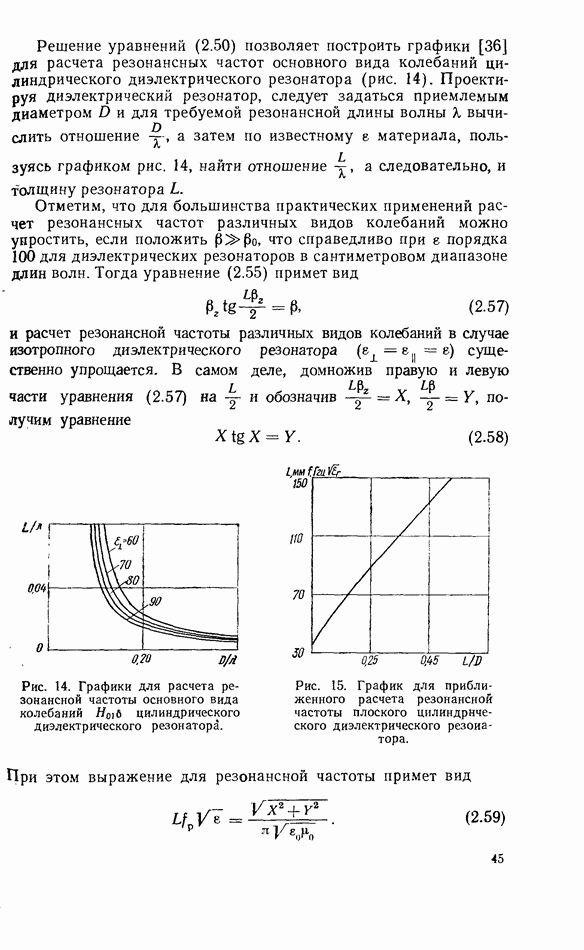
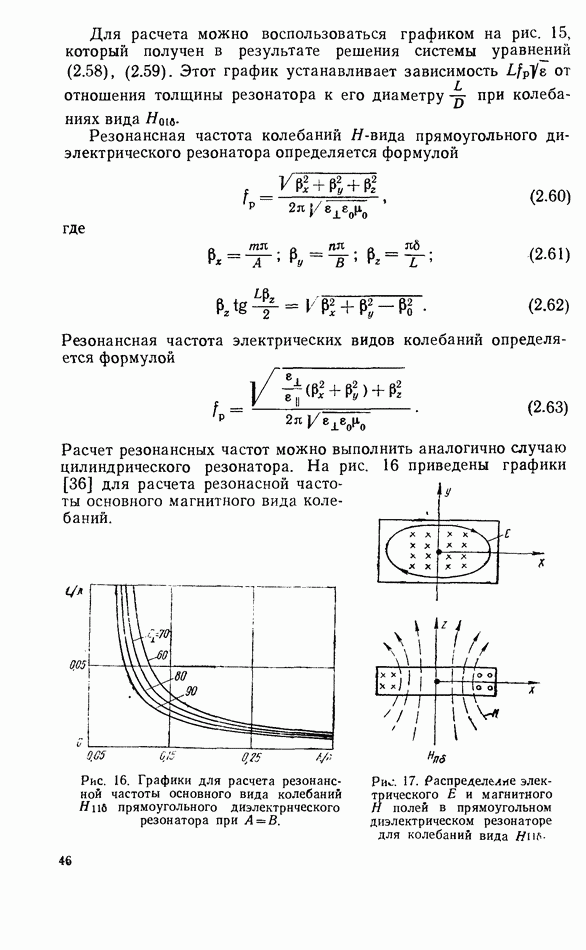
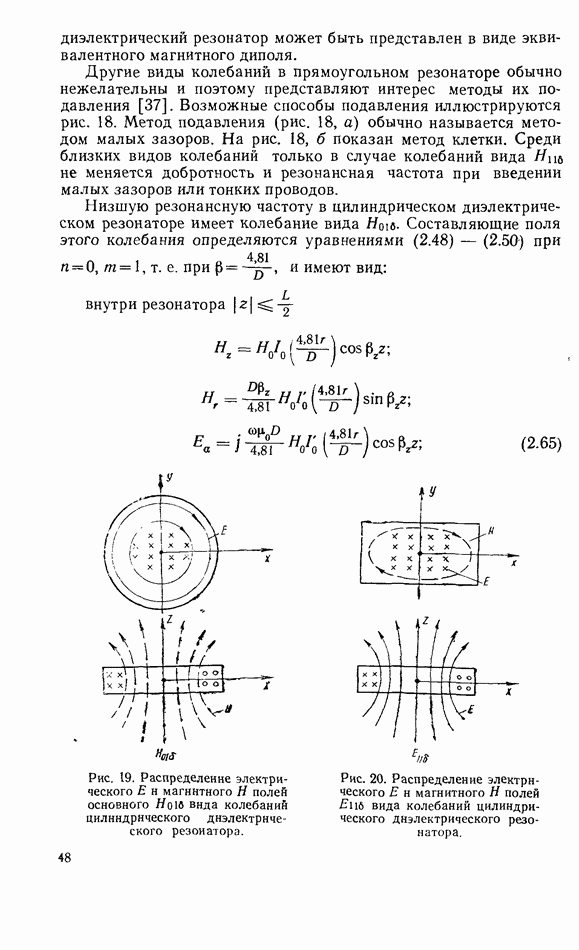
- 2.5. ОСНОВНЫЕ ВИДЫ КОЛЕБАНИЙ
- 2.6. СФЕРИЧЕСКИЕ ДИЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
- 2.7. ВЛИЯНИЕ МЕТАЛЛИЧЕСКИХ СТЕНОК НА ХАРАКТЕРИСТИКИ ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 2.8. ДИПОЛЬНЫЙ МОМЕНТ
- 2.9. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ
- 2.10. СООТНОШЕНИЕ МЕЖДУ АМПЛИТУДАМИ СВЧ МАГНИТНОГО ПОЛЯ
- 2.11. ДВОЙНЫЕ ДИЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
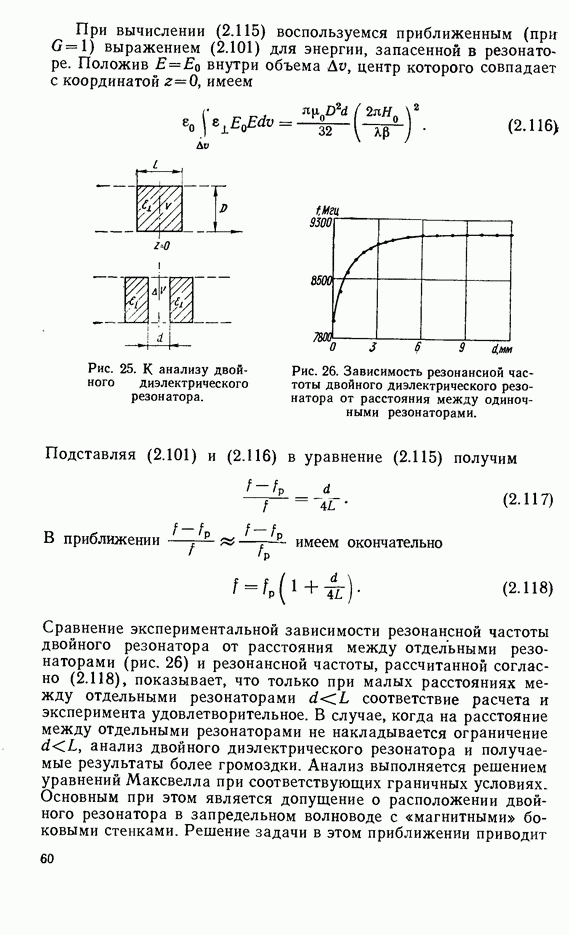
- 2.12. ТЕМПЕРАТУРНЫЕ ХАРАКТЕРИСТИКИ
- Глава третья. ХАРАКТЕРИСТИКИ ЛИНИЙ ПЕРЕДАЧИ СВЧ С ФЕРРИТОВЫМИ И ДИЭЛЕКТРИЧЕСКИМИ РЕЗОНАТОРАМИ
- 3.2. МЕТОДЫ РАСЧЕТА СВЧ-СХЕМ С ТВЕРДОТЕЛЬНЫМИ РЕЗОНАТОРАМИ
- 3.3. СВЯЗЬ ТВЕРДОТЕЛЬНОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ СВЧ
- 3.4. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В НЕСОГЛАСОВАННОЙ ЛИНИИ ПЕРЕДАЧИ
- 3.5. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР, ВКЛЮЧЕННЫЙ КАК ЭЛЕМЕНТ СВЯЗИ ЛИНИЙ ПЕРЕДАЧИ
- 3.6. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В КОРОТКОЗАМКНУТОЙ ЛИНИИ ПЕРЕДАЧИ
- 3.7. КОМБИНИРОВАННЫЕ СХЕМЫ ВКЛЮЧЕНИЯ ТВЕРДОТЕЛЬНОГО РЕЗОНАТОРА
- 3.8. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ С НЕСКОЛЬКИМИ РАСПРОСТРАНЯЮЩИМИСЯ ВОЛНАМИ
- Глава четвертая. СВЯЗЬ ТВЕРДОТЕЛЬНЫХ РЕЗОНАТОРОВ С ЛИНИЯМИ ПЕРЕДАЧИ СВЧ
- 4.2. СВЯЗЬ ФЕРРИТОВОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ
- 4.3. ФЕРРИТОВЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ ЗАМЕДЛЕННЫХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
- 4.4. РЕЗОНАНСНЫЙ ПОВОРОТ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ В ВОЛНОВОДЕ С ФЕРРИТОВЫМ РЕЗОНАТОРОМ
- 4.5. НЕЛИНЕЙНЫЙ ФЕРРИТОВЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ
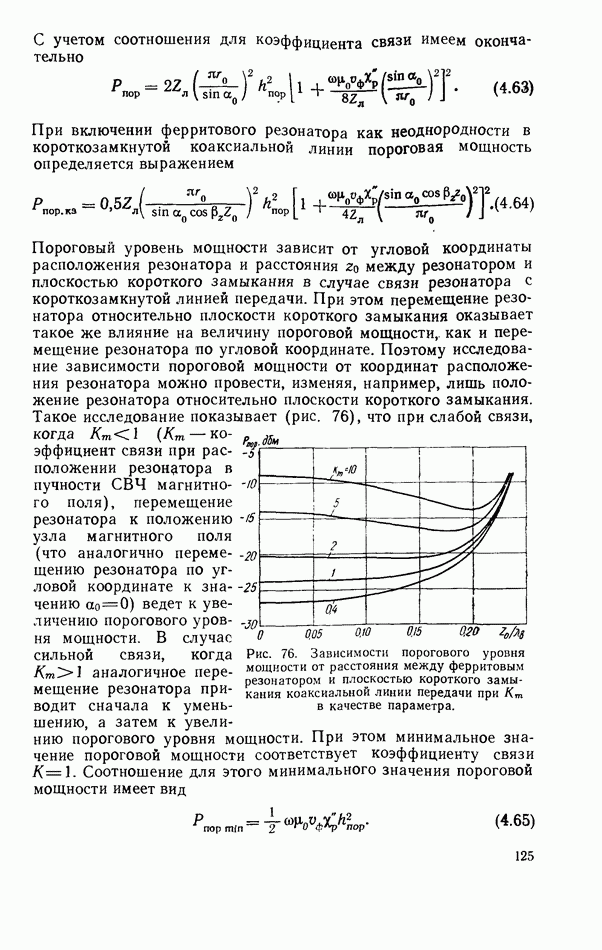
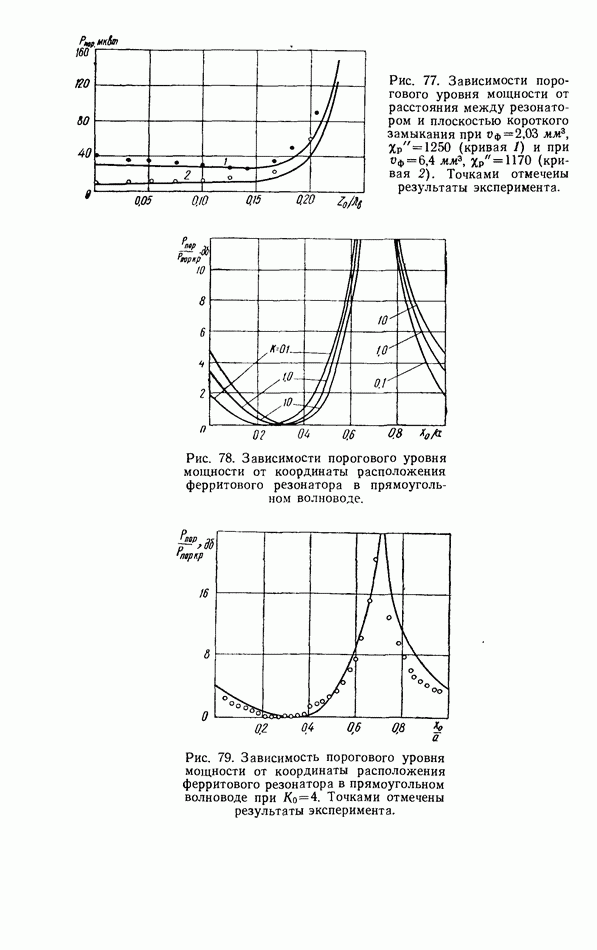
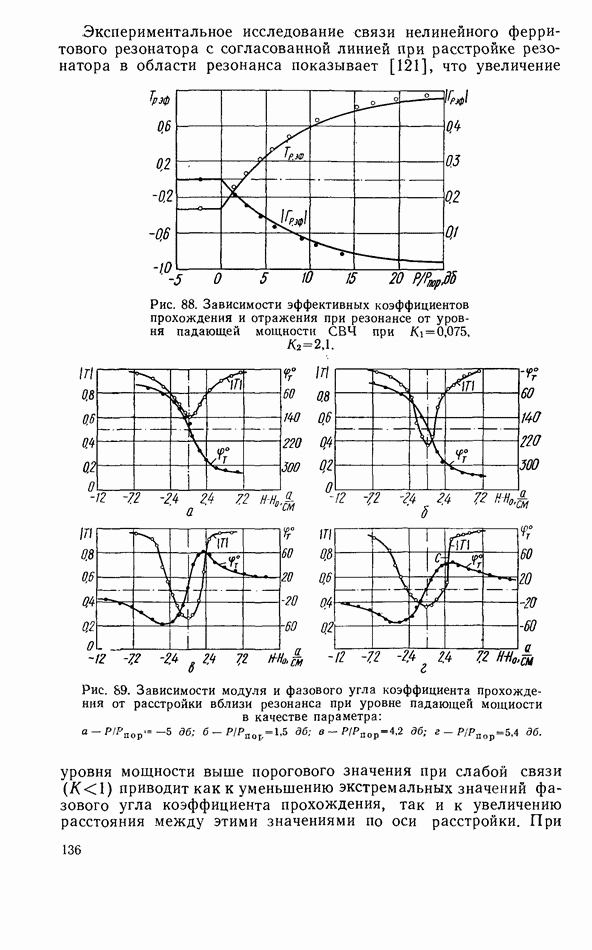
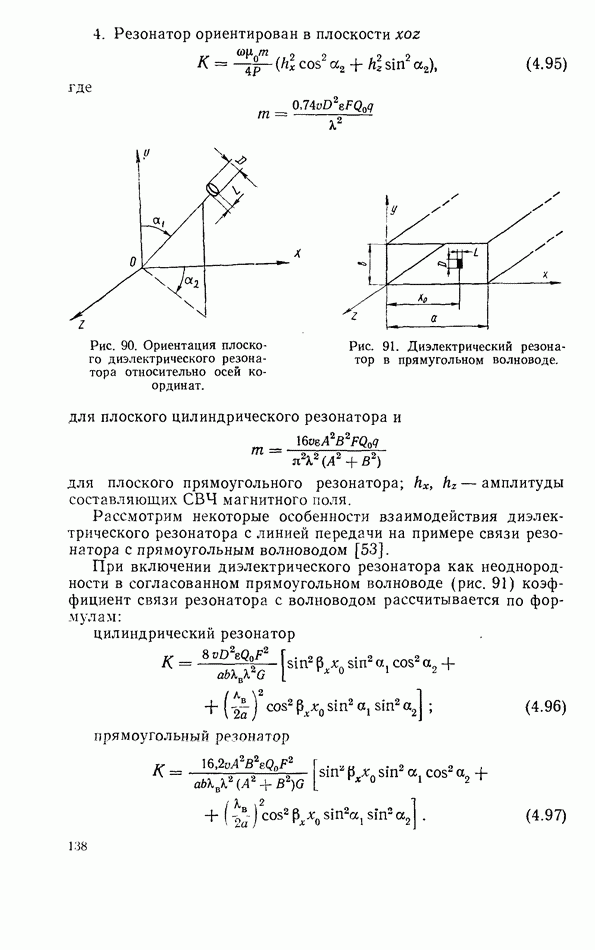
- Ферритовый резонатор в линии передачи при запороговых уровнях мощности
- Нелинейный ферритовый резонатор в короткозамкнутой линии передачи
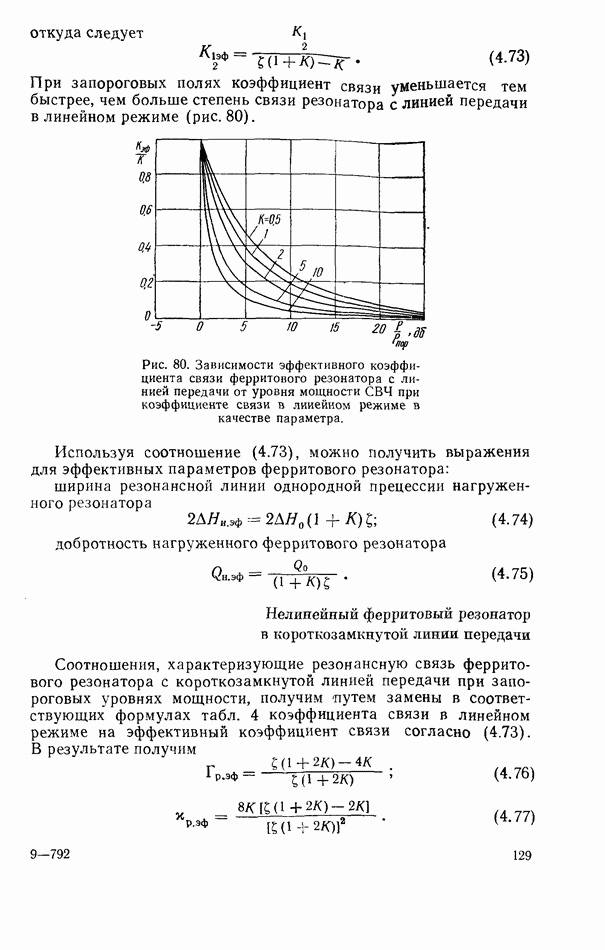
- Связь линий передачи СВЧ при помощи нелинейного ферритового резонатора
- Нелинейный ферритовый резонатор в согласованной линии передачи
- 4.6. СВЯЗЬ ДИЭЛЕКТРИЧЕСКОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ СВЧ
- Глава пятая. ПРИНЦИПЫ ПОСТРОЕНИЯ СВЧ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ И УСТРОЙСТВ НА ОСНОВЕ ТВЕРДОТЕЛЬНЫХ РЕЗОНАТОРОВ
- 5.2. ДАТЧИКИ УРОВНЯ МОЩНОСТИ СВЧ
- Волноводная измерительная головка
- Датчик фиксированного уровня пиковой мощности
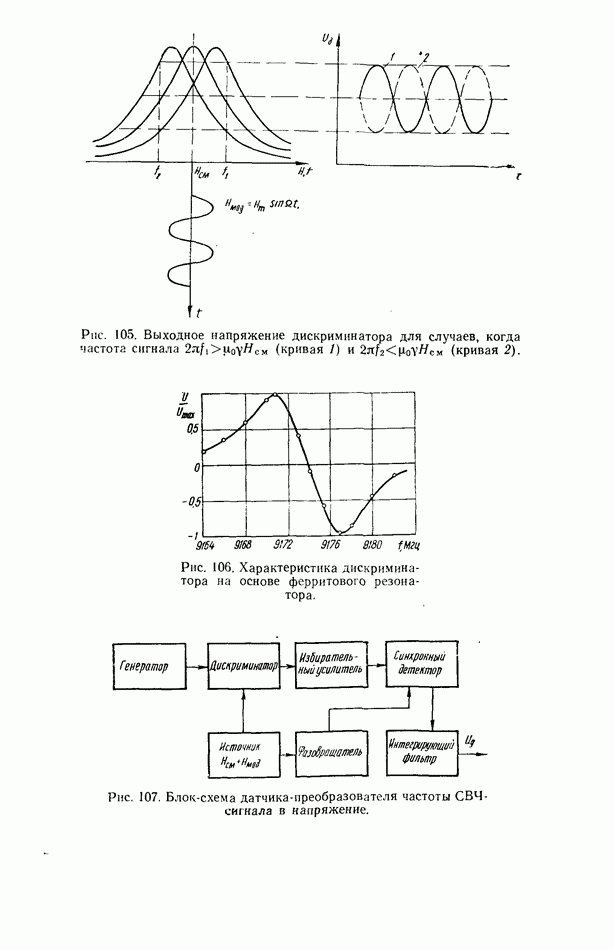
- 5.3. ЧАСТОТНЫЕ ДИСКРИМИНАТОРЫ С МАГНИТНОЙ НАСТРОЙКОЙ
- 5.4. РЕЗОНАНСНЫЕ ФАЗОВРАЩАТЕЛИ
- 5.5. УСТРОЙСТВО ДЛЯ РЕЗОНАНСНОГО ПОВОРОТА ПЛОСКОСТИ ПОЛЯРИЗАЦИИ В ВОЛНОВОДЕ
- 5.6. ФИЛЬТРЫ СВЧ НА ОСНОВЕ ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 5.7. ФЕРРИТОВЫЕ СВЧ-ФИЛЬТРЫ
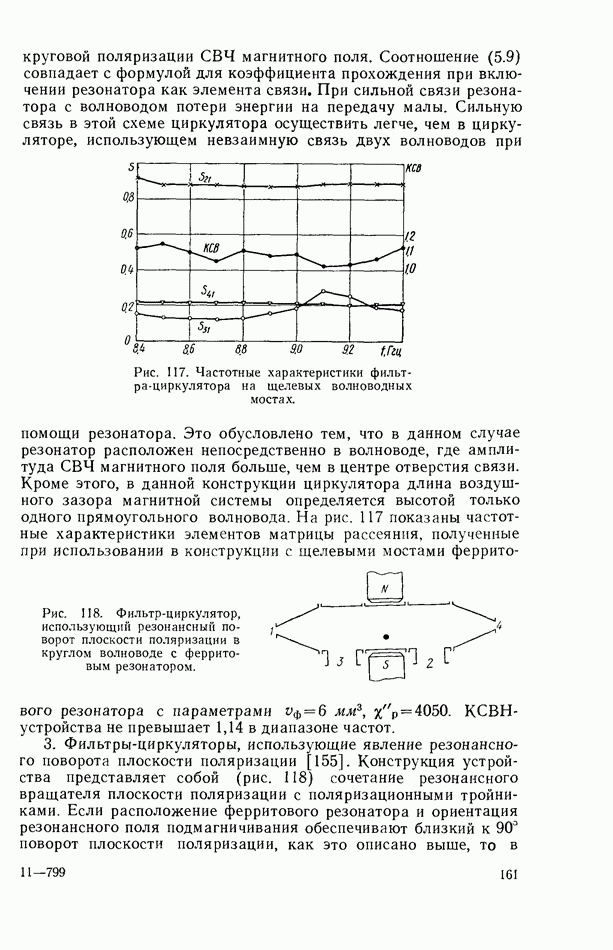
- Многофункциональные фильтры
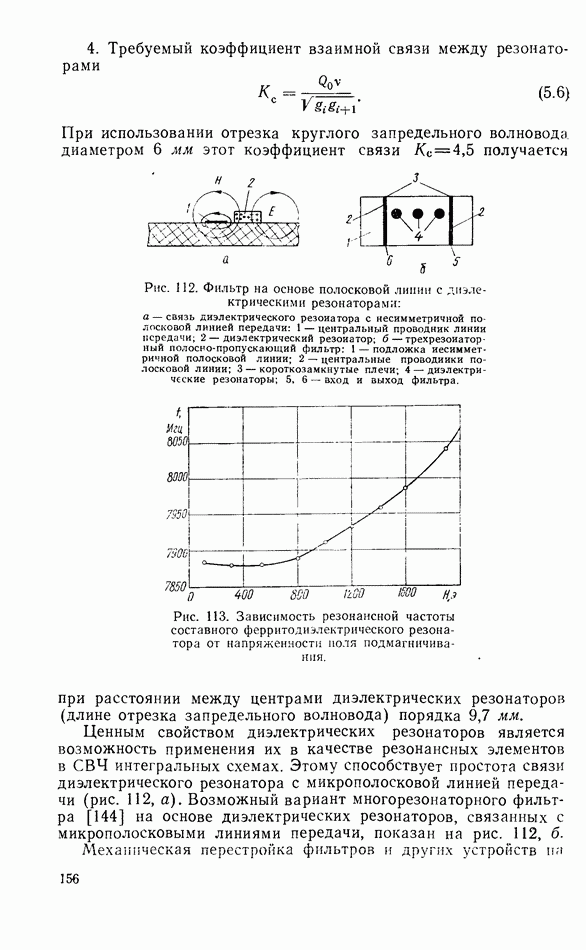
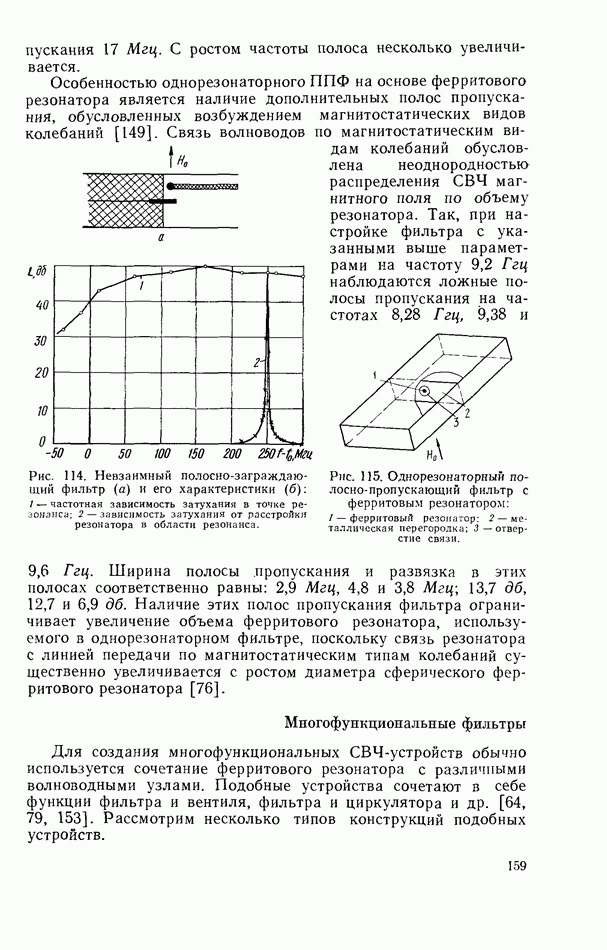
- Многорезонаторные ферритовые фильтры
- 5.8. ЧАСТОТНО-ИЗБИРАТЕЛЬНЫЕ ОГРАНИЧИТЕЛИ МАЛЫХ УРОВНЕЙ МОЩНОСТИ