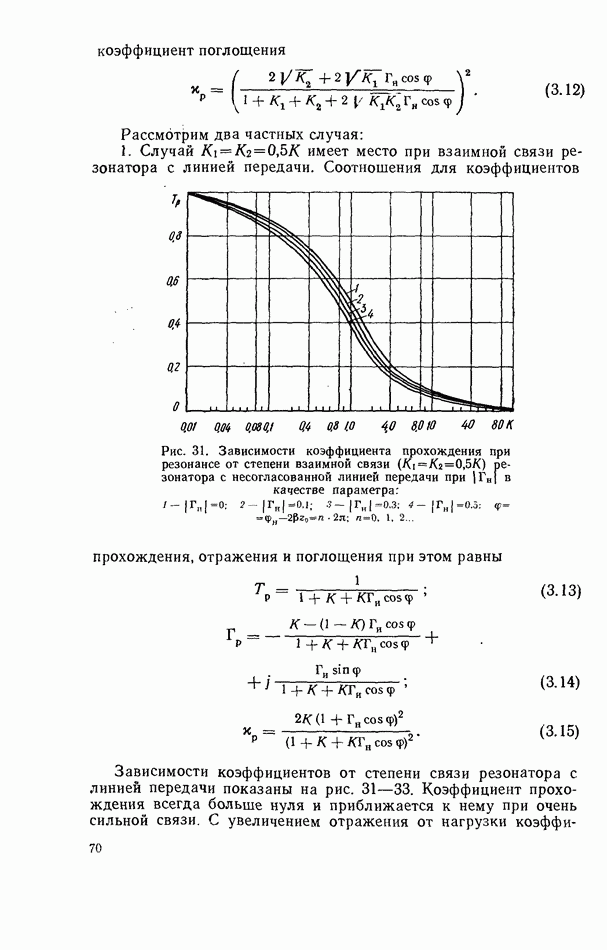
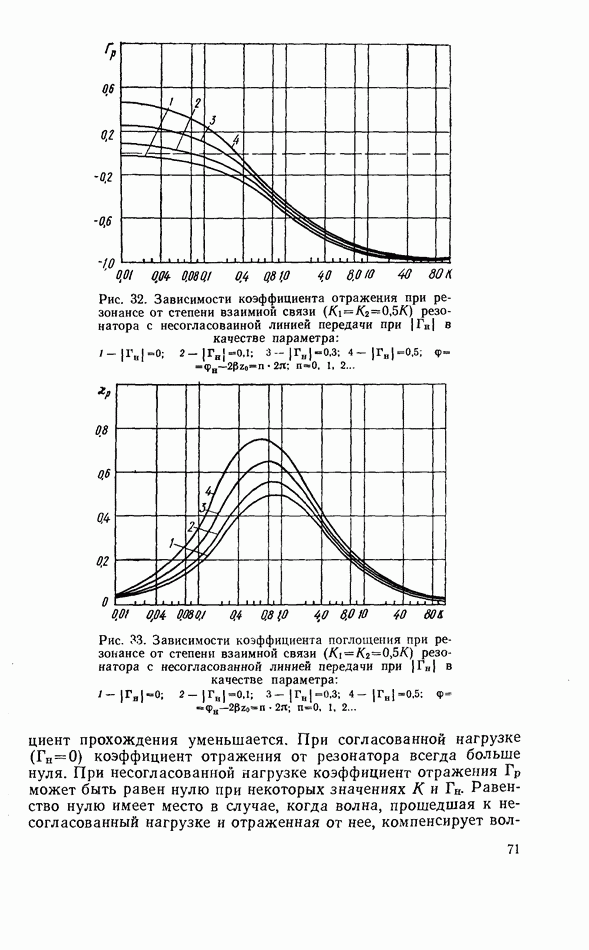
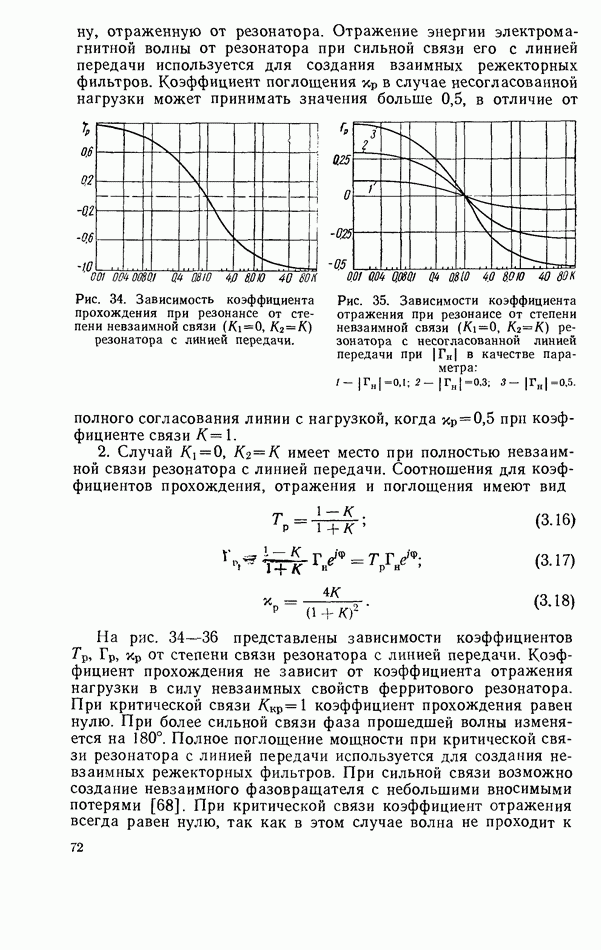
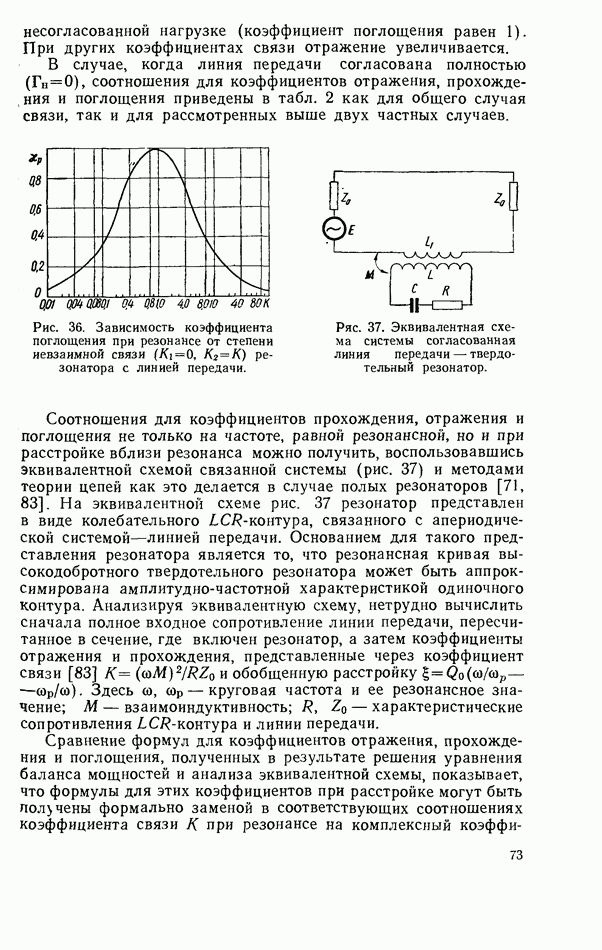
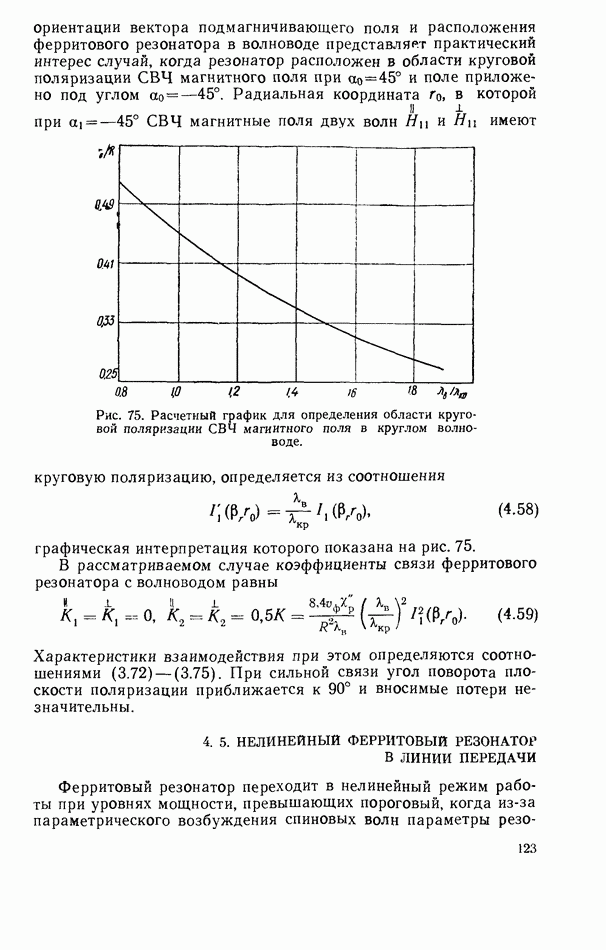
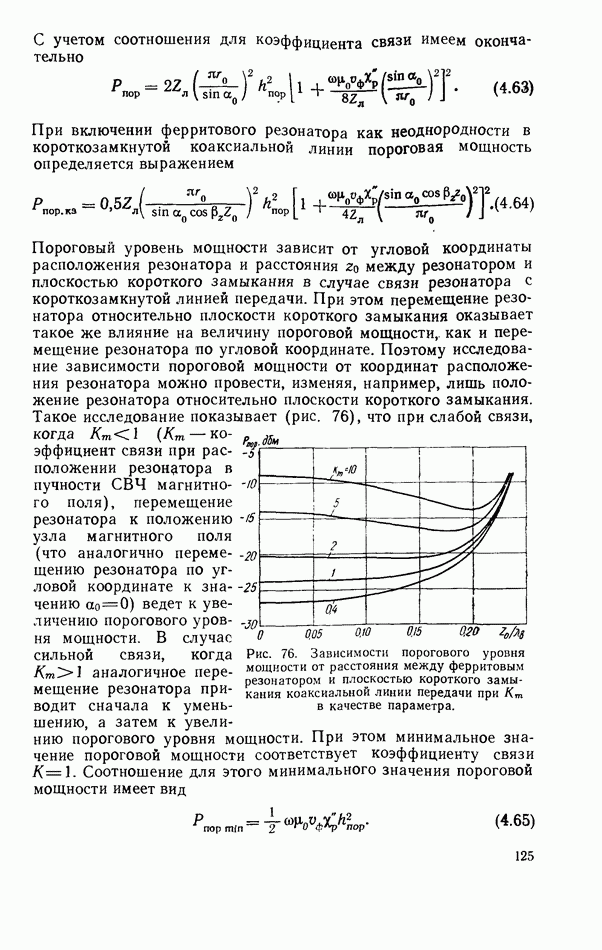
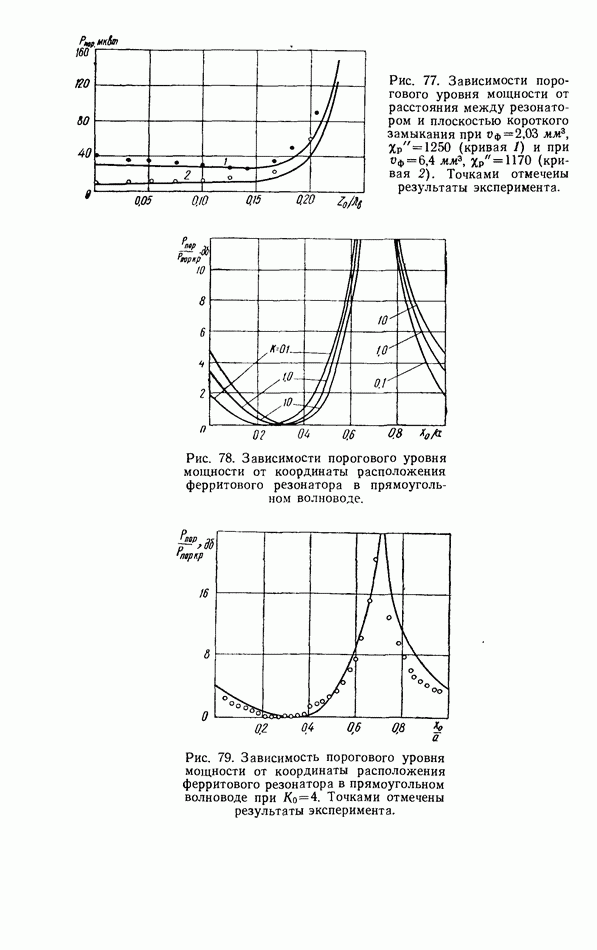
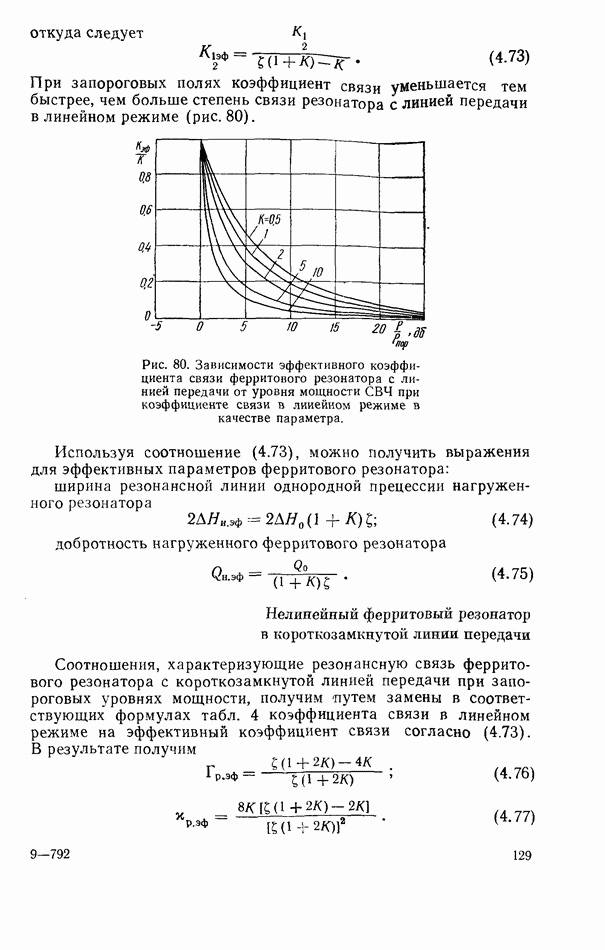
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
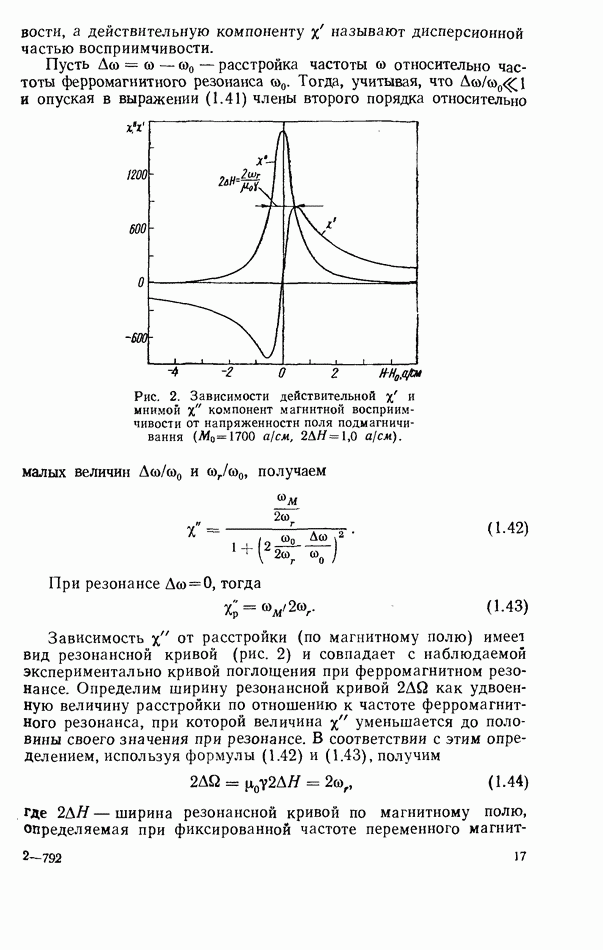
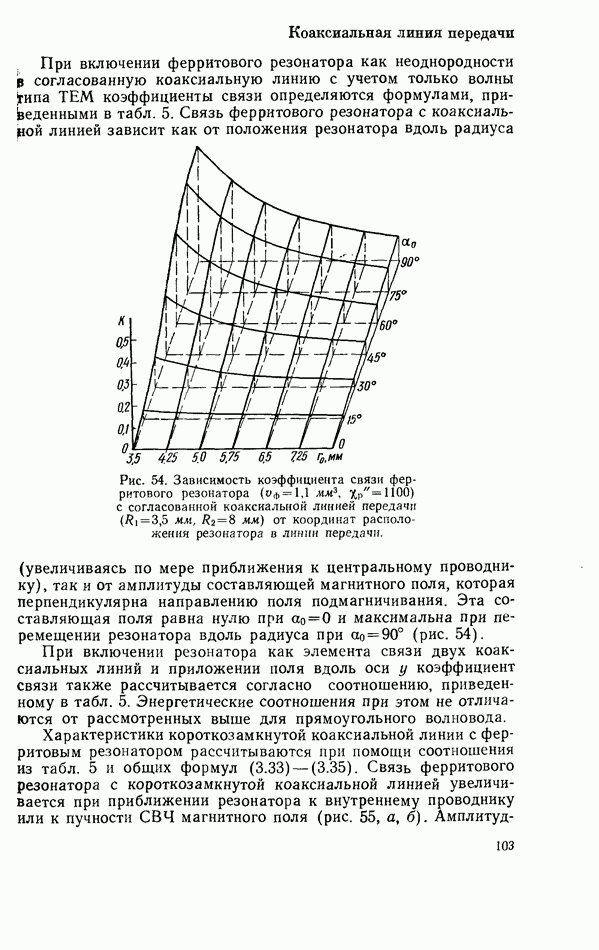
Ферромагнитный резонанс в неограниченной среде без потерь
Важнейшей задачей макроскопической теории ферромагнитного резонанса является установление соотношения между воздействующим на ферритовую среду магнитным полем (сумма постоянного и переменного полей) и возникающим при этом магнитным моментом, отнесенным к единице объема среды, т. е. плотностью намагниченности феррита. Магнитный момент единицы объема является суммой спиновых магнитных моментов электронов в рассматриваемом объеме, и прецессия вектора магнитного момента (прецессия вектора плотности намагниченности) будет такой же, как прецессия вектора спинового магнитного момента электрона. Прецессия вектора плотности намагниченности описывается уравнением движения, которое в 1935 г. было получено Л. Д. Ландау и Е. М. Лифшицем [2] и является основным уравнением квазиклассической теории поведения ферромагнетитов в магнитных полях. Для среды без потерь это уравнение имеет вид [3]

где  вектор плотности намагниченности;
вектор плотности намагниченности;  векторная сумма всех магнитных полей, действующих на спиновые магнитные моменты;
векторная сумма всех магнитных полей, действующих на спиновые магнитные моменты;  - гиромагнитное отношение
- гиромагнитное отношение  заряд,
заряд,  масса электрона);
масса электрона);  магнитная проницаемость вакуума;
магнитная проницаемость вакуума;

Решение уравнения (1.1) легче всего найти, если спроектировать входящие в него векторы на оси декартовой прямоугольной системы координат. Направим ось  системы координат так, чтобы она совпадала с направлением постоянного магнитного поля
системы координат так, чтобы она совпадала с направлением постоянного магнитного поля  внутри феррита (рис. 1) и представим входящие в уравнение (1.1) магнитное поле в виде суммы постоянного поля и переменного поля, изменяющегося по гармоническому закону
внутри феррита (рис. 1) и представим входящие в уравнение (1.1) магнитное поле в виде суммы постоянного поля и переменного поля, изменяющегося по гармоническому закону

Вектор плотности намагниченности определяем в виде

Для линейной теории существенным является предположение, что  и соответственно
и соответственно  где
где  статическая намагниченность, равная намагниченности насыщения.
статическая намагниченность, равная намагниченности насыщения.

Рис. 1. Прецессия магнитного момента электрона  под влиянием постоянного
под влиянием постоянного  и высокочастотного
и высокочастотного  магнитных полей.
магнитных полей.
Если предположение о малости переменного магнитного поля (по сравнению с постоянным) выполняется, то, решая уравнение (1.1) с учетом (1.2) и (1.3) и сохраняя в решении члены только первого порядка относительно малых величин Лит, можно установить линейные соотношения между проекциями векторов высокочастотной намагниченности и переменного магнитного поля

В формулах (1.4)

где

 круговая частота СВЧ магнитного поля.
круговая частота СВЧ магнитного поля.
Соотношения (1.4) могут быть кратко записаны в векторной форме

Здесь  тензор магнитной восприимчивости
тензор магнитной восприимчивости

Тензорный характер магнитной восприимчивости указывает на то, что высокочастотное магнитное поле  приложенное вдоль
приложенное вдоль
оси  порождает составляющие высокочастотной намагниченности как вдоль оси
порождает составляющие высокочастотной намагниченности как вдоль оси  так и вдоль оси у (рис. 1).
так и вдоль оси у (рис. 1).
Из формул (1.5), (1.6) видно, что зависимость компонент тензора восприимчивости от частоты имеет особенность в области частоты  при
при  компоненты тензора обращаются в бесконечность. Это является следствием пренебрежения потерями, которые, конечно, всегда есть в реальной среде. Частота
компоненты тензора обращаются в бесконечность. Это является следствием пренебрежения потерями, которые, конечно, всегда есть в реальной среде. Частота  называется частотой ферромагнитного резонанса. При расчетах чаще всего бывает удобно пользоваться значением циклической частоты, выраженным в мегагерцах; тогда практическая формула для частоты ферромагнитного резонанса имеет вид
называется частотой ферромагнитного резонанса. При расчетах чаще всего бывает удобно пользоваться значением циклической частоты, выраженным в мегагерцах; тогда практическая формула для частоты ферромагнитного резонанса имеет вид

Магнитная восприимчивость по отношению к полю с круговой поляризацией
Волну, магнитная составляющая которой имеет компоненты  и в общем случае эллиптически поляризована, можно представить как суперпозицию волн, магнитные составляющие которых
и в общем случае эллиптически поляризована, можно представить как суперпозицию волн, магнитные составляющие которых  имеют правую и левую круговые поляризации в плоскости
имеют правую и левую круговые поляризации в плоскости 

где  — единичные векторы.
— единичные векторы.
Тогда для составляющих  из выражения (1.11) получаем
из выражения (1.11) получаем

Подставляя (1.12) в (1.4), для компонент высокочастотной намагниченности  и ту находим
и ту находим

Учтено, что при малых расстройках  и соответственно
и соответственно 
Используя выражение (1.13), для амплитуды вектора высокочастотной намагниченности  получаем
получаем

Магнитную восприимчивость по отношению к полю с правой круговой поляризацией определим с помощью соотношения

тогда с учетом (1.11) и (1.15) имеем

Таким образом, в общем случае эллиптической поляризации поля переменная намагниченность, как это следует из выражения (1-14), создается только компонентой поля, имеющей правую круговую поляризацию, причем переменная намагниченность также имеет круговую поляризацию с правым вращением. При этом восприимчивость по отношению к полю с правой круговой поляризацией является скалярной величиной, определяемой выражением (1.16).
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава первая. СВОЙСТВА ФЕРРИТОВЫХ РЕЗОНАТОРОВ
- Ферромагнитный резонанс в неограниченной среде без потерь
- 1.2. РЕЗОНАНСНАЯ ЧАСТОТА
- Зависимость резонансной частоты от формы резонатора
- Влияние кристаллографической анизотропии на резонансную частоту
- 1.3. МАГНИТОСТАТИЧЕСКИЕ ВИДЫ КОЛЕБАНИЙ
- 1.4. УЧЕТ ПОТЕРЬ
- 1.5. ДИПОЛЬНЫЙ МОМЕНТ
- 1.6. НЕЛИНЕЙНЫЕ ЯВЛЕНИЯ
- Спиновые волны
- Пороговая амплитуда высокочастотного магнитного поля
- Восприимчивость при амплитудах поля, превышающих пороговое значение
- 1.7. ПРИМЕНЯЕМЫЕ ДЛЯ ИЗГОТОВЛЕНИЯ МАТЕРИАЛЫ
- 1.8. ТЕМПЕРАТУРНЫЕ ХАРАКТЕРИСТИКИ
- 1.9. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- Глава вторая. СВОЙСТВА ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 2.2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В АНИЗОТРОПНОМ ДИЭЛЕКТРИЧЕСКОМ СТЕРЖНЕ С «МАГНИТНЫМИ» БОКОВЫМИ СТЕНКАМИ
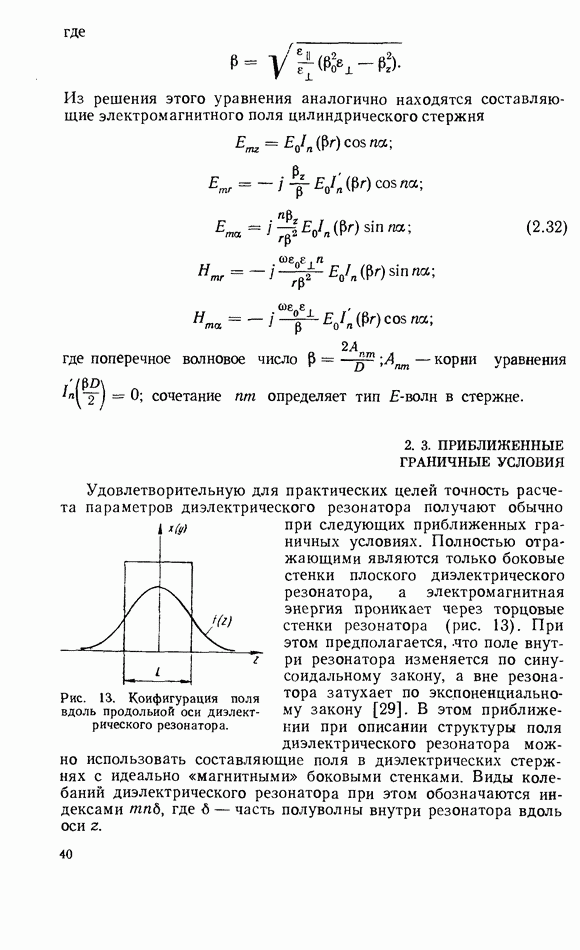
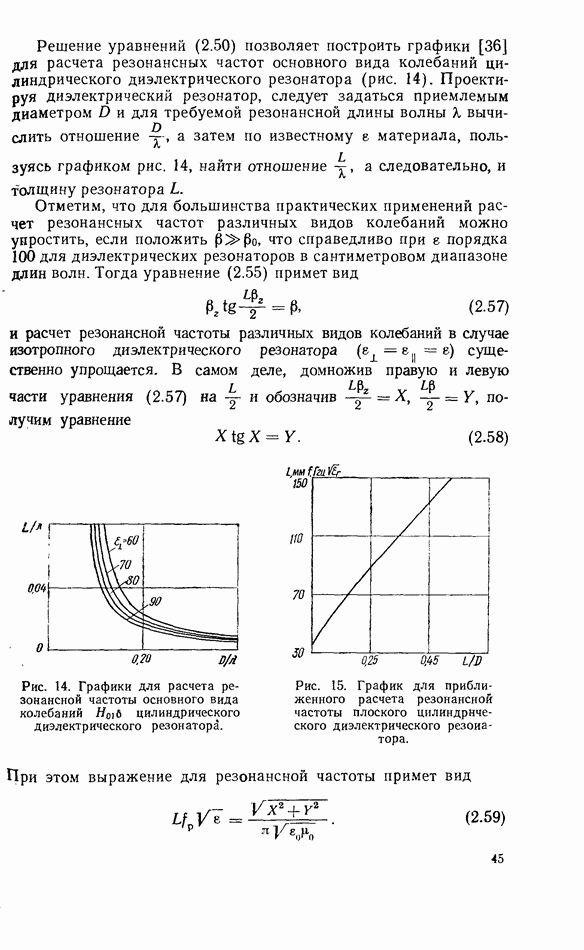
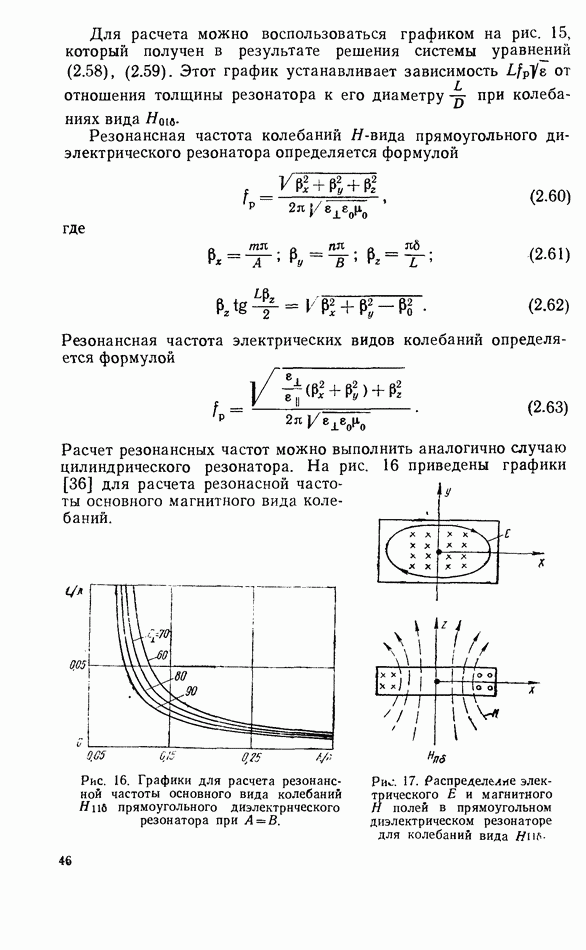
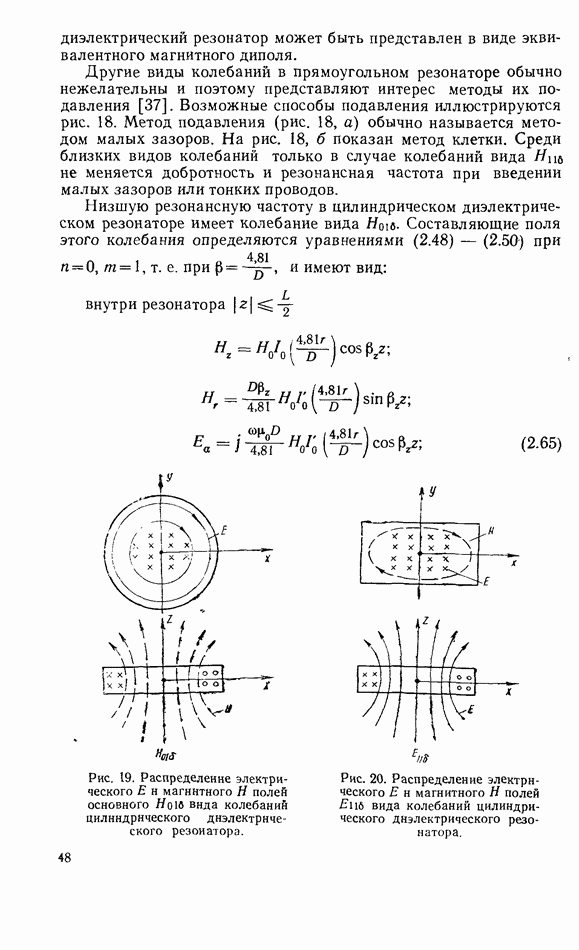
- 2.3. ПРИБЛИЖЕННЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2.5. ОСНОВНЫЕ ВИДЫ КОЛЕБАНИЙ
- 2.6. СФЕРИЧЕСКИЕ ДИЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
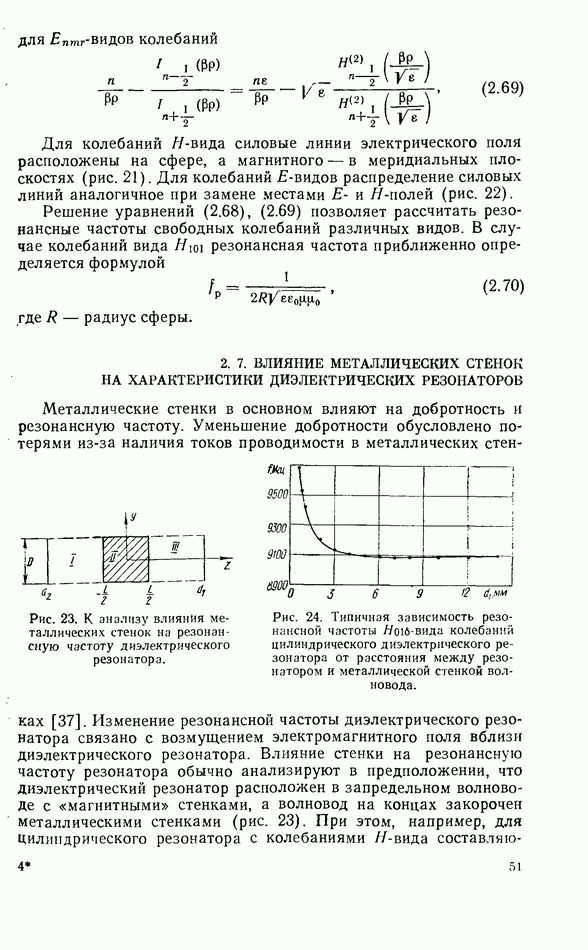
- 2.7. ВЛИЯНИЕ МЕТАЛЛИЧЕСКИХ СТЕНОК НА ХАРАКТЕРИСТИКИ ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 2.8. ДИПОЛЬНЫЙ МОМЕНТ
- 2.9. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ
- 2.10. СООТНОШЕНИЕ МЕЖДУ АМПЛИТУДАМИ СВЧ МАГНИТНОГО ПОЛЯ
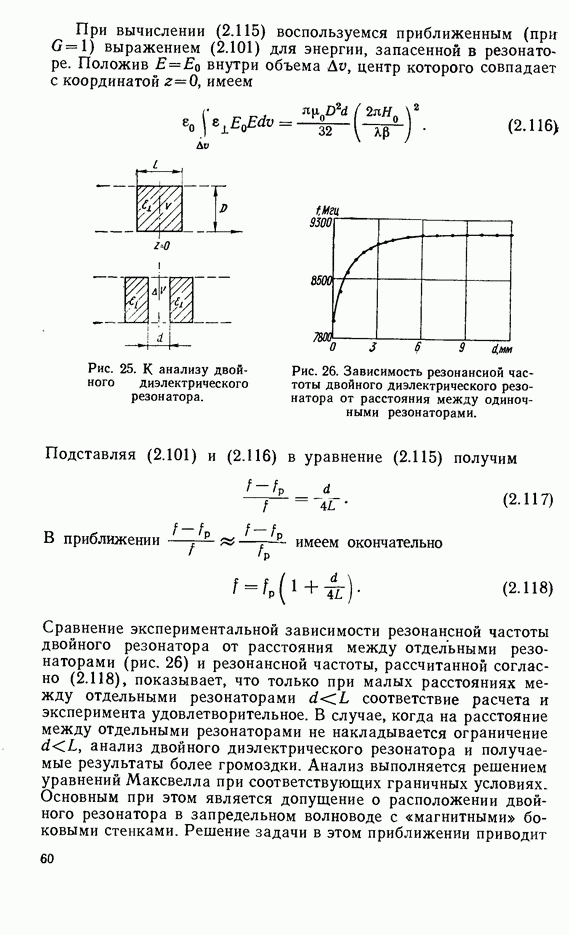
- 2.11. ДВОЙНЫЕ ДИЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
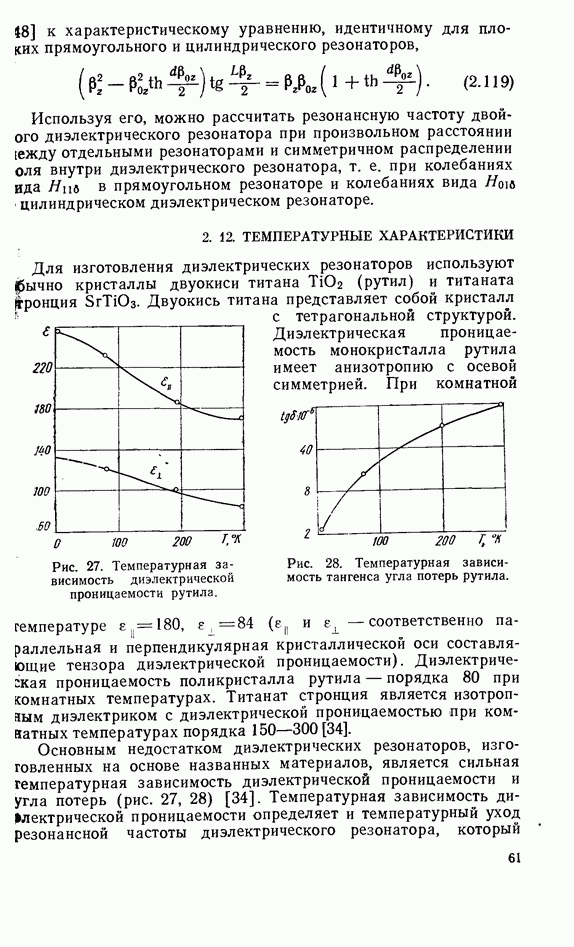
- 2.12. ТЕМПЕРАТУРНЫЕ ХАРАКТЕРИСТИКИ
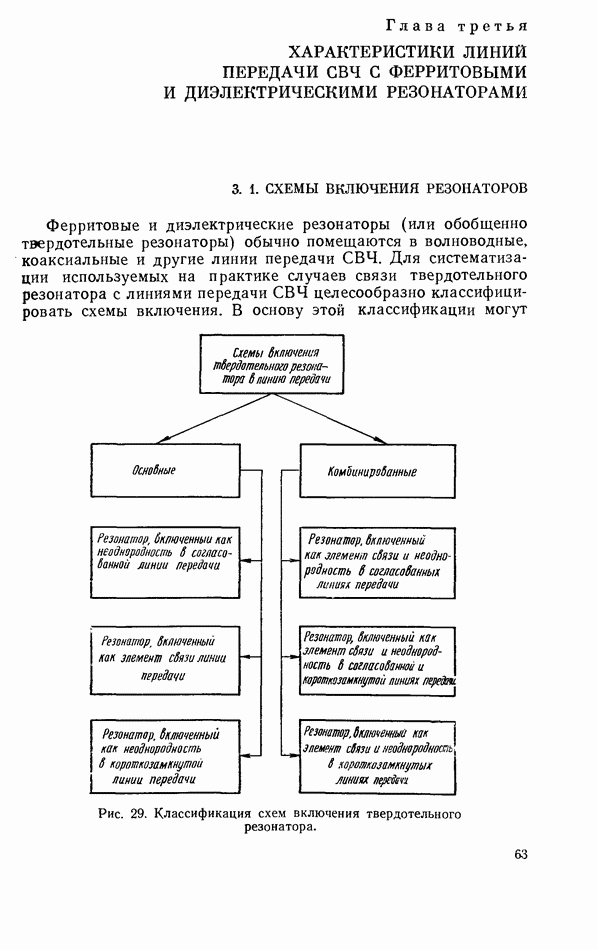
- Глава третья. ХАРАКТЕРИСТИКИ ЛИНИЙ ПЕРЕДАЧИ СВЧ С ФЕРРИТОВЫМИ И ДИЭЛЕКТРИЧЕСКИМИ РЕЗОНАТОРАМИ
- 3.2. МЕТОДЫ РАСЧЕТА СВЧ-СХЕМ С ТВЕРДОТЕЛЬНЫМИ РЕЗОНАТОРАМИ
- 3.3. СВЯЗЬ ТВЕРДОТЕЛЬНОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ СВЧ
- 3.4. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В НЕСОГЛАСОВАННОЙ ЛИНИИ ПЕРЕДАЧИ
- 3.5. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР, ВКЛЮЧЕННЫЙ КАК ЭЛЕМЕНТ СВЯЗИ ЛИНИЙ ПЕРЕДАЧИ
- 3.6. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В КОРОТКОЗАМКНУТОЙ ЛИНИИ ПЕРЕДАЧИ
- 3.7. КОМБИНИРОВАННЫЕ СХЕМЫ ВКЛЮЧЕНИЯ ТВЕРДОТЕЛЬНОГО РЕЗОНАТОРА
- 3.8. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ С НЕСКОЛЬКИМИ РАСПРОСТРАНЯЮЩИМИСЯ ВОЛНАМИ
- Глава четвертая. СВЯЗЬ ТВЕРДОТЕЛЬНЫХ РЕЗОНАТОРОВ С ЛИНИЯМИ ПЕРЕДАЧИ СВЧ
- 4.2. СВЯЗЬ ФЕРРИТОВОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ
- 4.3. ФЕРРИТОВЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ ЗАМЕДЛЕННЫХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
- 4.4. РЕЗОНАНСНЫЙ ПОВОРОТ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ В ВОЛНОВОДЕ С ФЕРРИТОВЫМ РЕЗОНАТОРОМ
- 4.5. НЕЛИНЕЙНЫЙ ФЕРРИТОВЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ
- Ферритовый резонатор в линии передачи при запороговых уровнях мощности
- Нелинейный ферритовый резонатор в короткозамкнутой линии передачи
- Связь линий передачи СВЧ при помощи нелинейного ферритового резонатора
- Нелинейный ферритовый резонатор в согласованной линии передачи
- 4.6. СВЯЗЬ ДИЭЛЕКТРИЧЕСКОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ СВЧ
- Глава пятая. ПРИНЦИПЫ ПОСТРОЕНИЯ СВЧ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ И УСТРОЙСТВ НА ОСНОВЕ ТВЕРДОТЕЛЬНЫХ РЕЗОНАТОРОВ
- 5.2. ДАТЧИКИ УРОВНЯ МОЩНОСТИ СВЧ
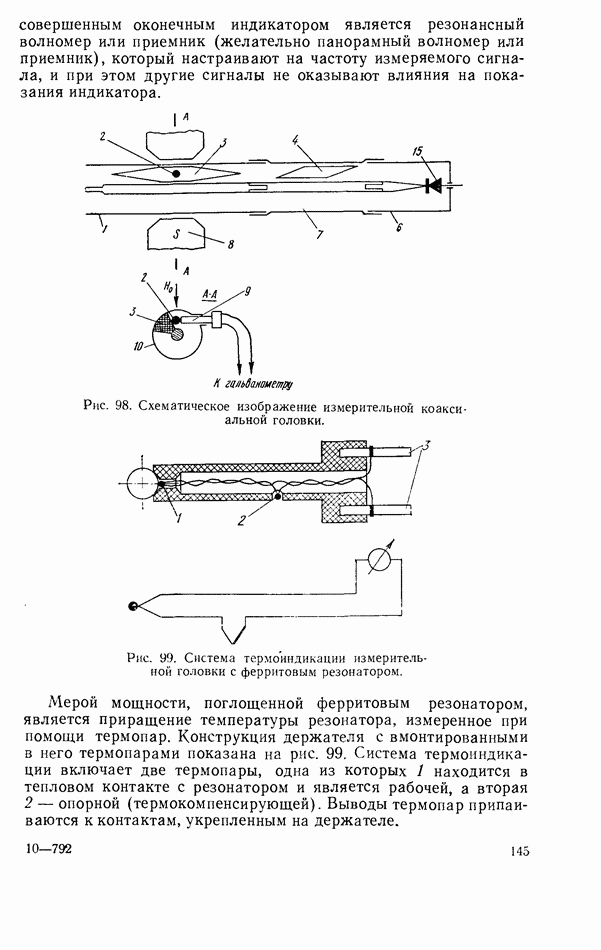
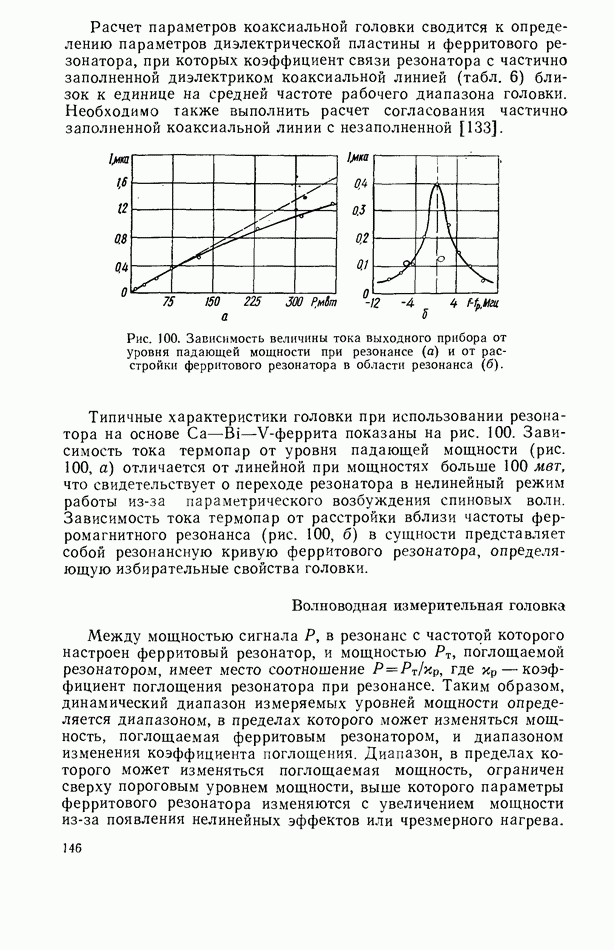
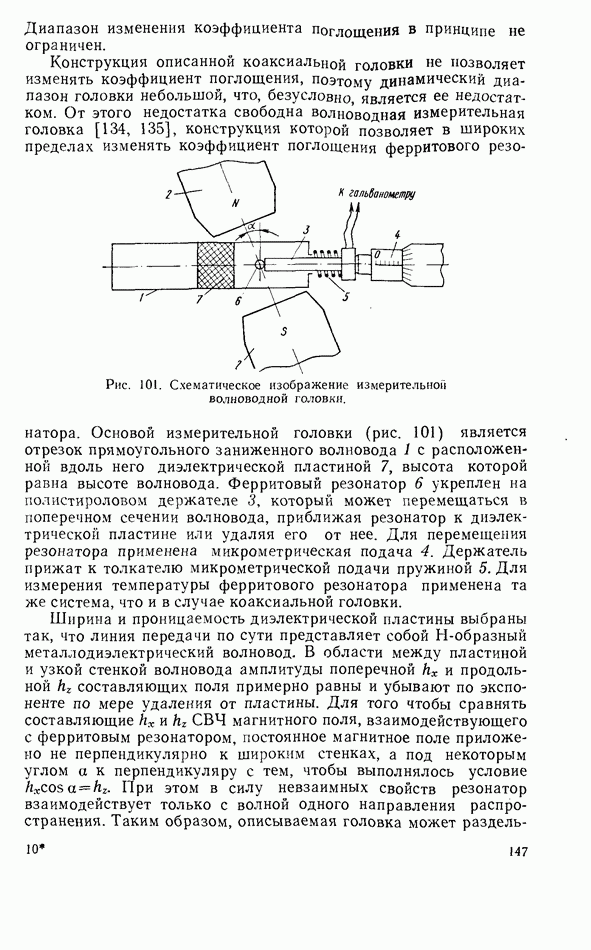
- Волноводная измерительная головка
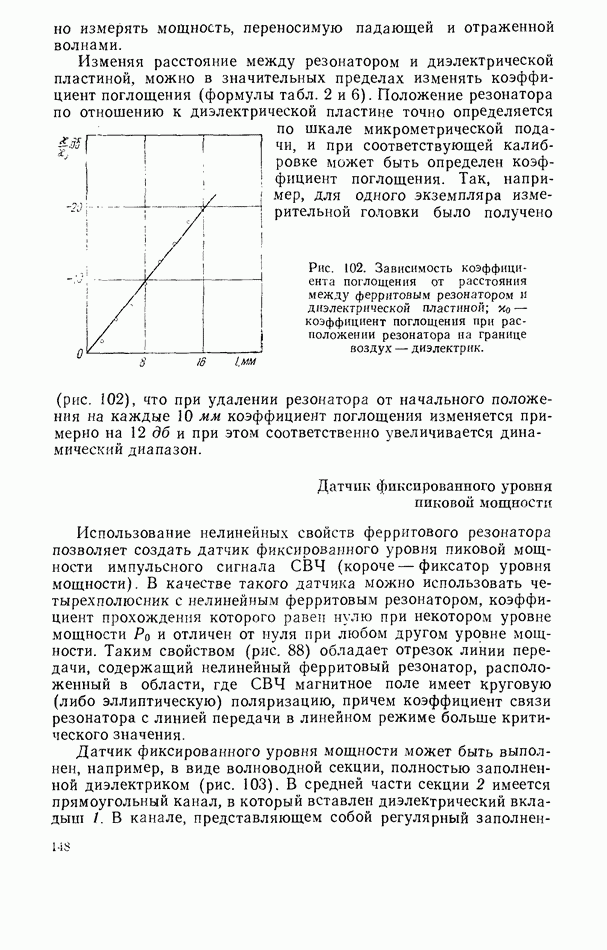
- Датчик фиксированного уровня пиковой мощности
- 5.3. ЧАСТОТНЫЕ ДИСКРИМИНАТОРЫ С МАГНИТНОЙ НАСТРОЙКОЙ
- 5.4. РЕЗОНАНСНЫЕ ФАЗОВРАЩАТЕЛИ
- 5.5. УСТРОЙСТВО ДЛЯ РЕЗОНАНСНОГО ПОВОРОТА ПЛОСКОСТИ ПОЛЯРИЗАЦИИ В ВОЛНОВОДЕ
- 5.6. ФИЛЬТРЫ СВЧ НА ОСНОВЕ ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 5.7. ФЕРРИТОВЫЕ СВЧ-ФИЛЬТРЫ
- Многофункциональные фильтры
- Многорезонаторные ферритовые фильтры
- 5.8. ЧАСТОТНО-ИЗБИРАТЕЛЬНЫЕ ОГРАНИЧИТЕЛИ МАЛЫХ УРОВНЕЙ МОЩНОСТИ