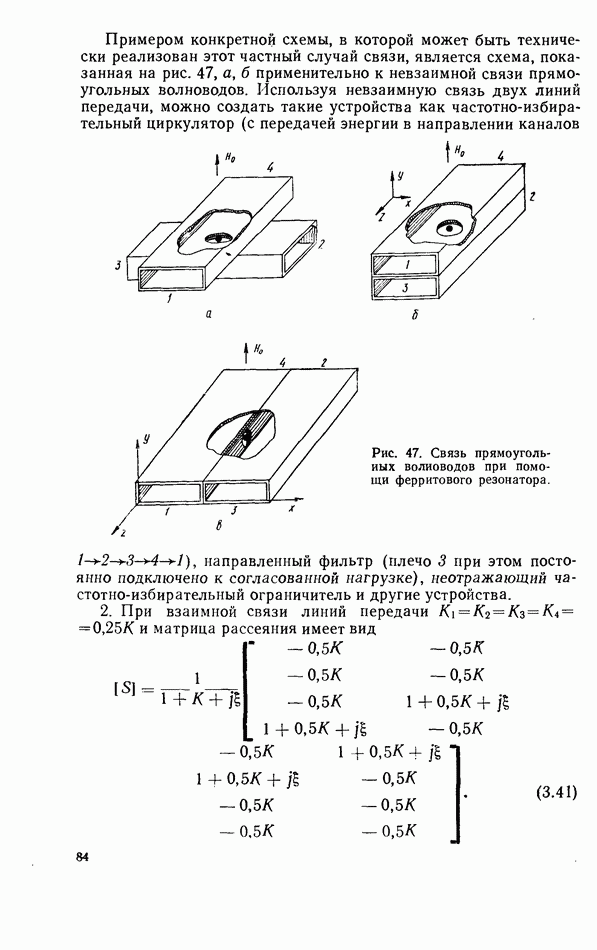
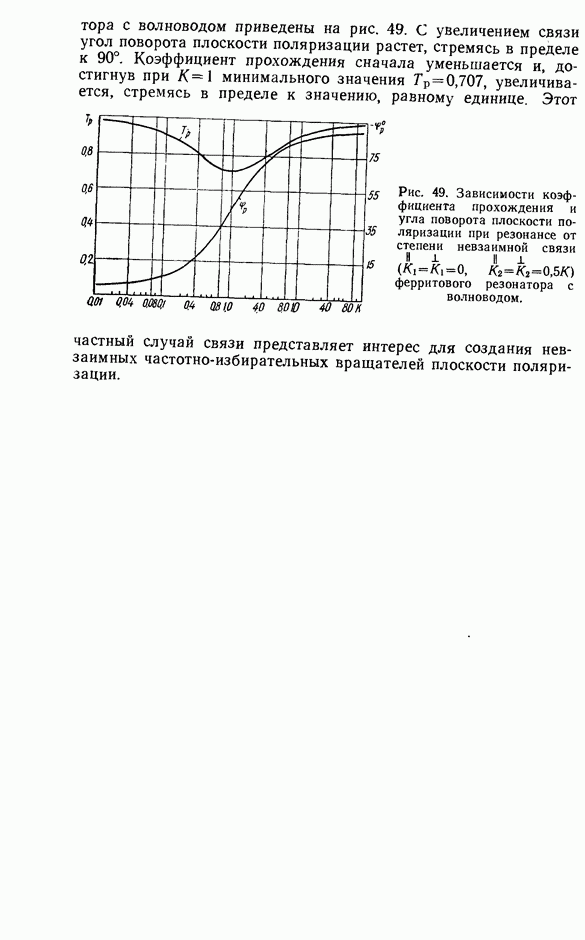
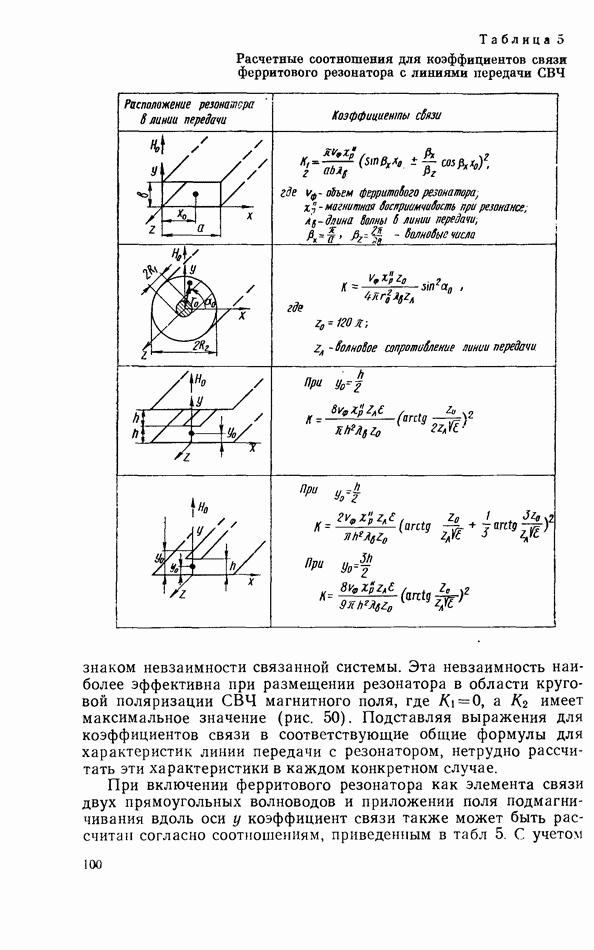
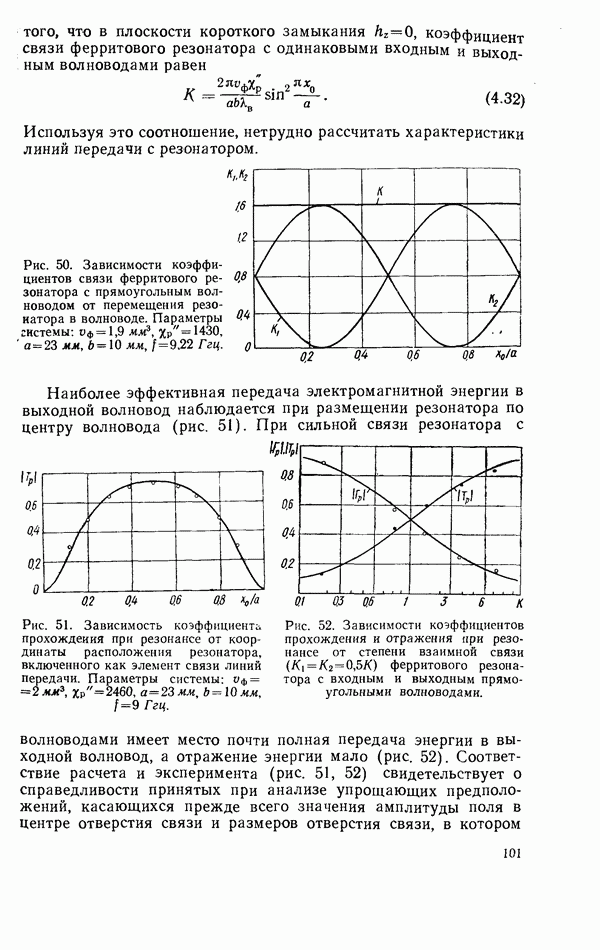
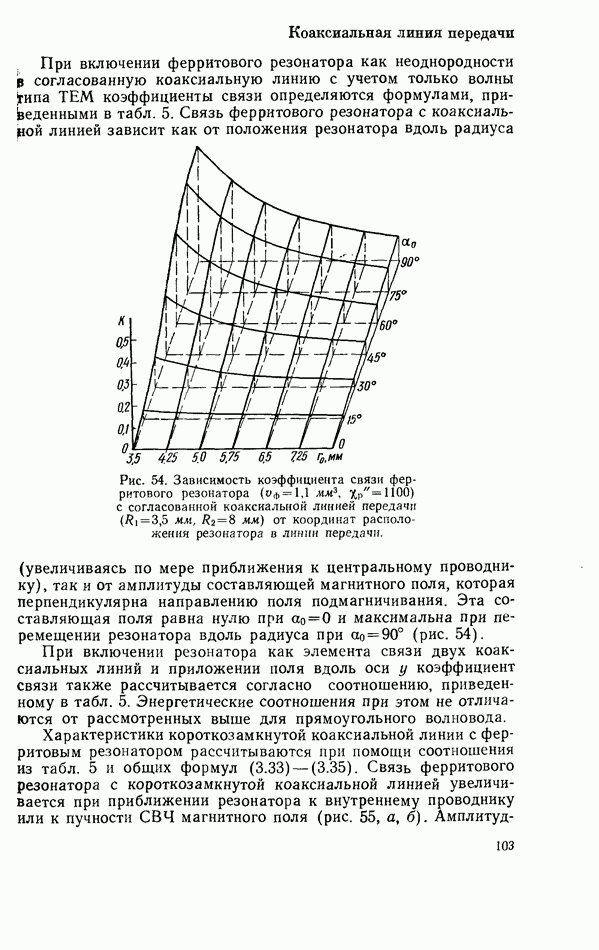
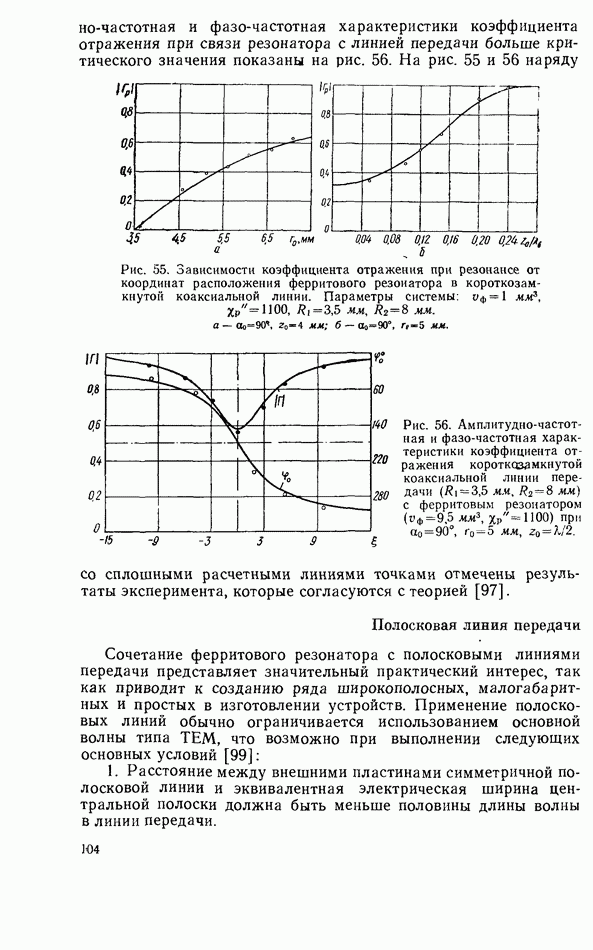
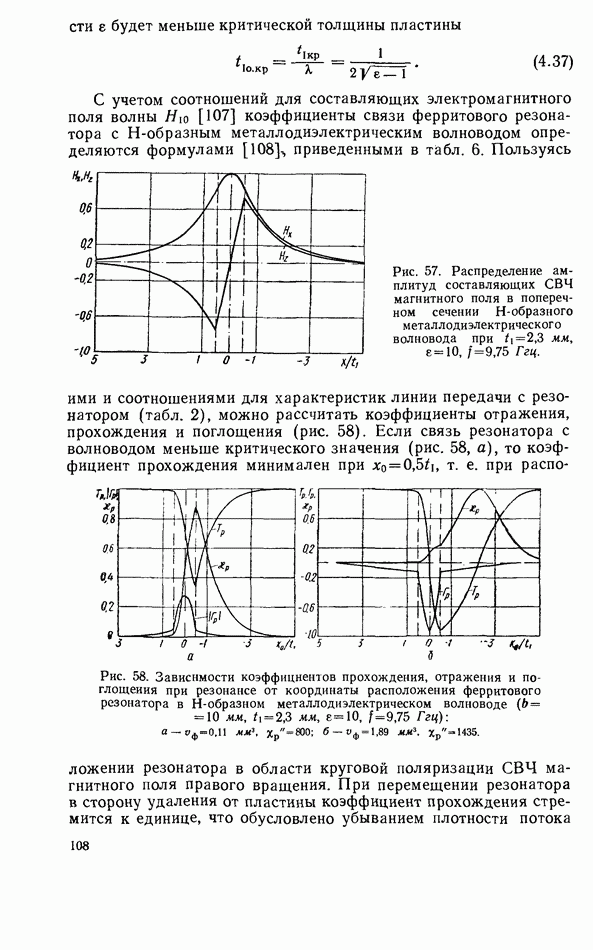
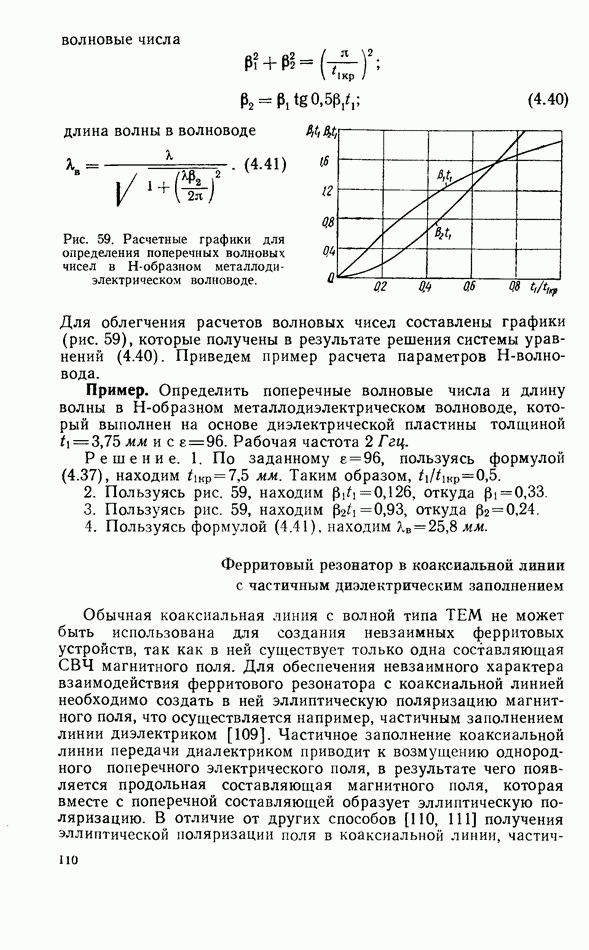
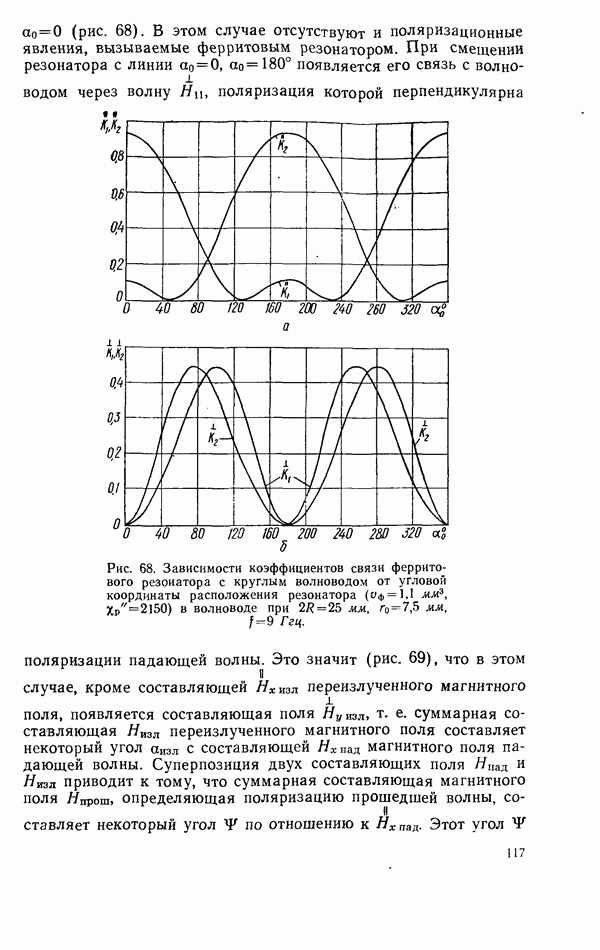
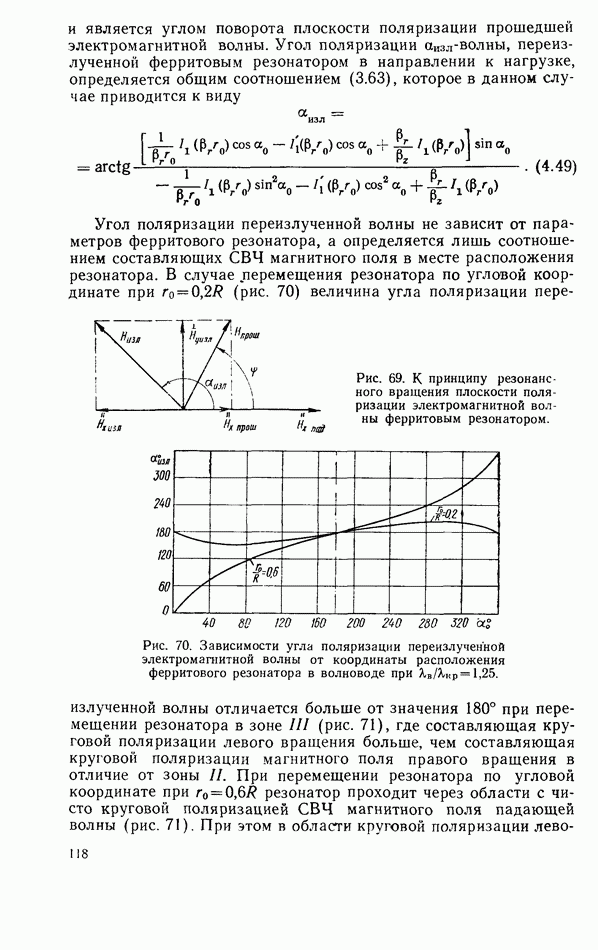
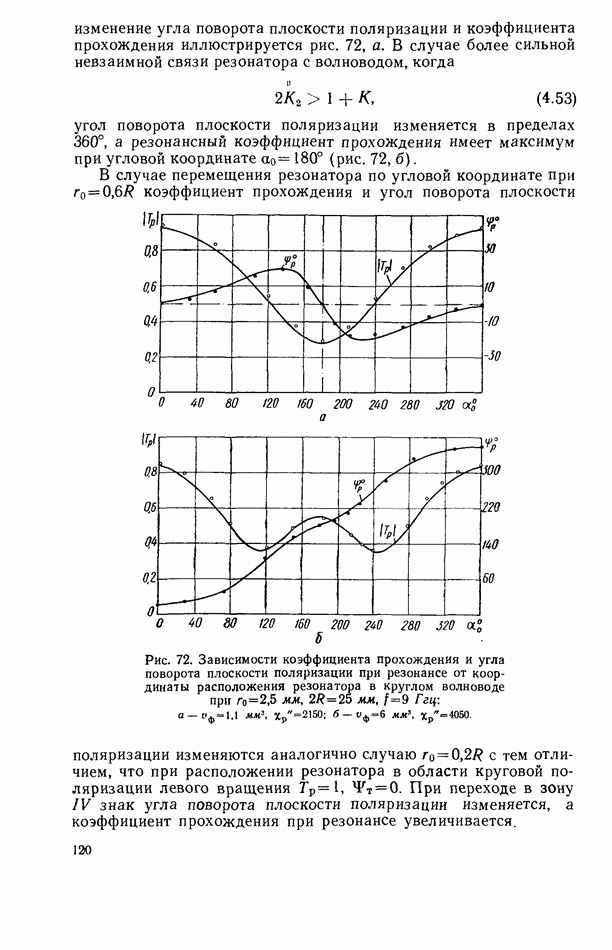
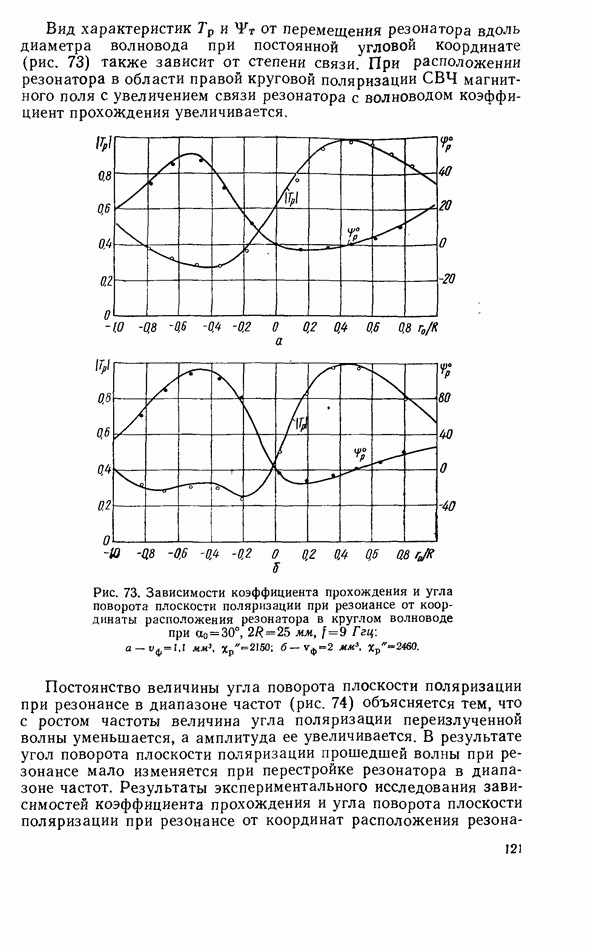
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2.6. СФЕРИЧЕСКИЕ ДИЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
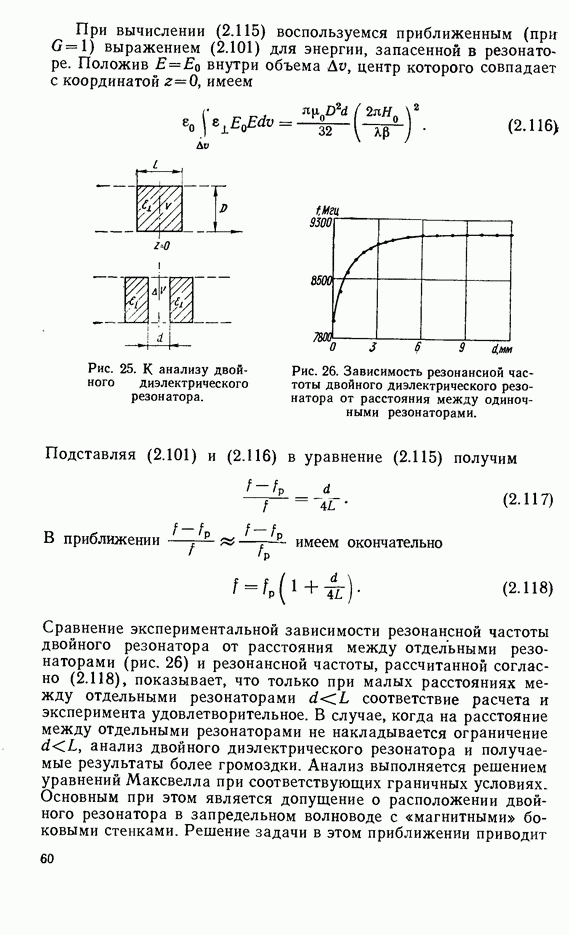
Наряду с плоскими прямоугольными и цилиндрическими резонаторами применяются и сферические диэлектрические резонаторы. Поэтому интересно исследовать вопрос о структуре поля и резонансных частотах возможных видов колебаний сферического диэлектрического резонатора. Такое исследование, проведенное для произвольных значений диэлектрической проницаемости резонатора путем решения уравнений Максвелла в сферической системе координат с тем граничным условием, что энергия резонатора убывает до нулевого значения вдали от диэлектрической сферы, показывает [38], что в изотропной диэлектрической Сфере могут существовать колебания  и
и  -видов. Поля Н-видов внутри резонатора можно записать как
-видов. Поля Н-видов внутри резонатора можно записать как


где  присоединенные функции Лежандра 1-го рода;
присоединенные функции Лежандра 1-го рода;  степень и порядок функции;
степень и порядок функции;  аргумент;
аргумент;  функции Бесселя 1-го рода порядка
функции Бесселя 1-го рода порядка  волновое число в диэлектрическом образце.
волновое число в диэлектрическом образце.
Вне образца выражения для составляющих поля подобны (2.67) при замене функции Бесселя 1-го рода функцией Ганкеля  Компоненты электромагнитного поля
Компоненты электромагнитного поля  -видов колебаний могут быть получены из (2.67) при замене
-видов колебаний могут быть получены из (2.67) при замене  местами и с учетом множителя Из условия непрерывности полей на поверхности раздела диэлектрик — воздух получаются следующие трансцендентные характеристические уравнения: для
местами и с учетом множителя Из условия непрерывности полей на поверхности раздела диэлектрик — воздух получаются следующие трансцендентные характеристические уравнения: для  -видов колебаний
-видов колебаний


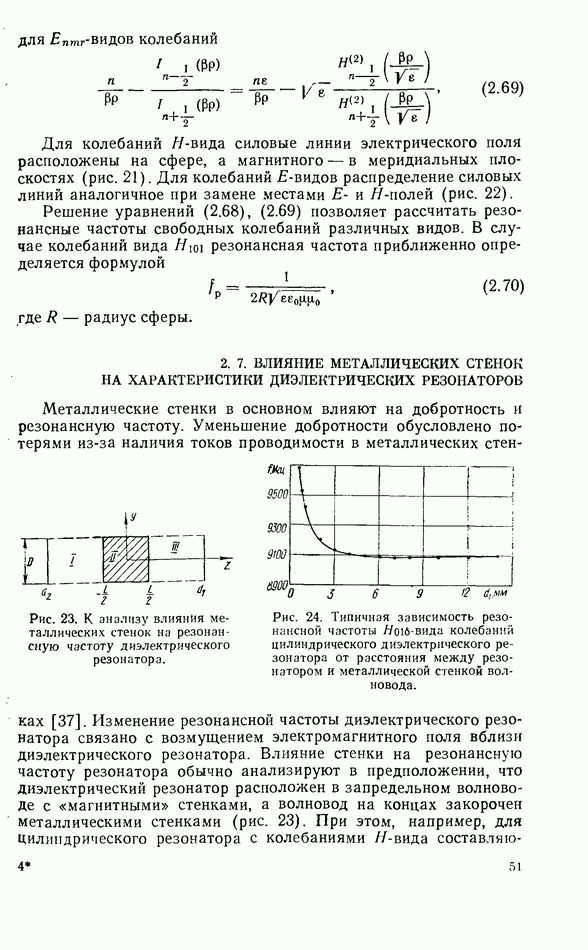
Рис. 21. Распределение магнитного поля  -вида колебаний сферического диэлектрического резонатора.
-вида колебаний сферического диэлектрического резонатора.

Рис. 22. Распределение электрического поля  -вида колебаний сферического диэлектрического резонатора.
-вида колебаний сферического диэлектрического резонатора.
для  видов колебаний
видов колебаний

Для колебаний  -вида силовые линии электрического поля расположены на сфере, а магнитного — в меридиальных плоскостях (рис. 21). Для колебаний
-вида силовые линии электрического поля расположены на сфере, а магнитного — в меридиальных плоскостях (рис. 21). Для колебаний  -видов распределение силовых линий аналогичное при замене местами
-видов распределение силовых линий аналогичное при замене местами  и
и  -полей (рис. 22).
-полей (рис. 22).
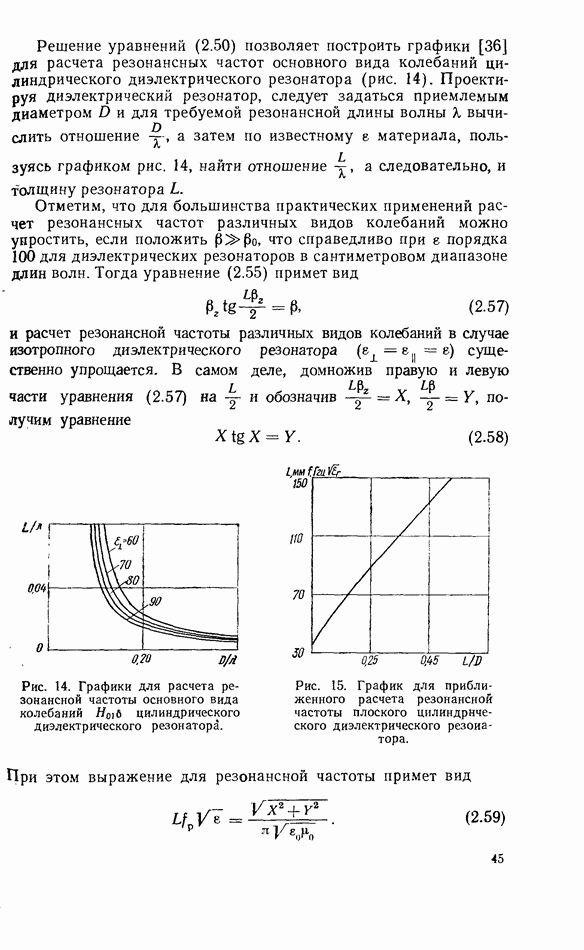
Решение уравнений (2.68), (2.69) позволяет рассчитать резонансные частоты свободных колебаний различных видов. В случае колебаний вида  резонансная частота приближенно определяется формулой
резонансная частота приближенно определяется формулой

где  радиус сферы.
радиус сферы.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- Глава первая. СВОЙСТВА ФЕРРИТОВЫХ РЕЗОНАТОРОВ
- Ферромагнитный резонанс в неограниченной среде без потерь
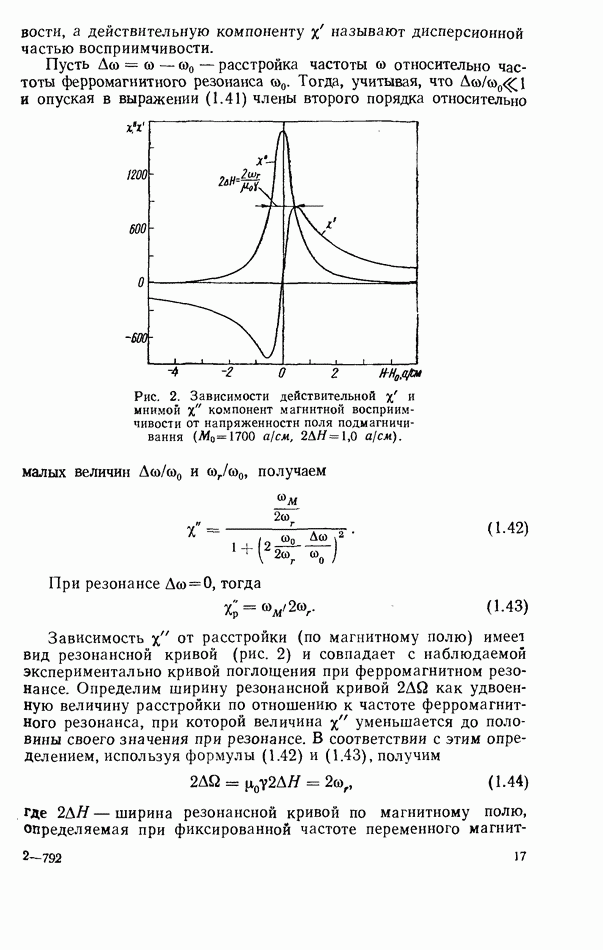
- 1.2. РЕЗОНАНСНАЯ ЧАСТОТА
- Зависимость резонансной частоты от формы резонатора
- Влияние кристаллографической анизотропии на резонансную частоту
- 1.3. МАГНИТОСТАТИЧЕСКИЕ ВИДЫ КОЛЕБАНИЙ
- 1.4. УЧЕТ ПОТЕРЬ
- 1.5. ДИПОЛЬНЫЙ МОМЕНТ
- 1.6. НЕЛИНЕЙНЫЕ ЯВЛЕНИЯ
- Спиновые волны
- Пороговая амплитуда высокочастотного магнитного поля
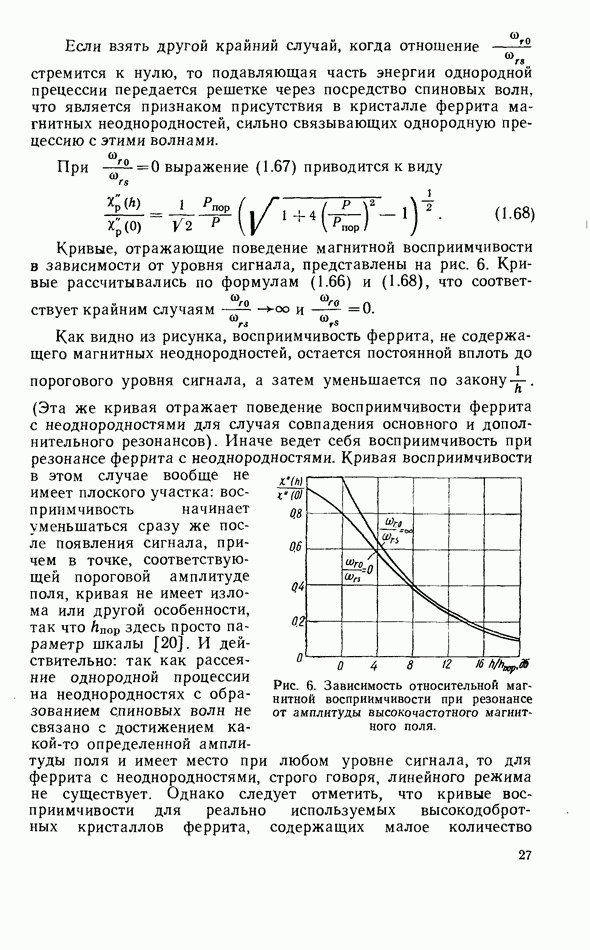
- Восприимчивость при амплитудах поля, превышающих пороговое значение
- 1.7. ПРИМЕНЯЕМЫЕ ДЛЯ ИЗГОТОВЛЕНИЯ МАТЕРИАЛЫ
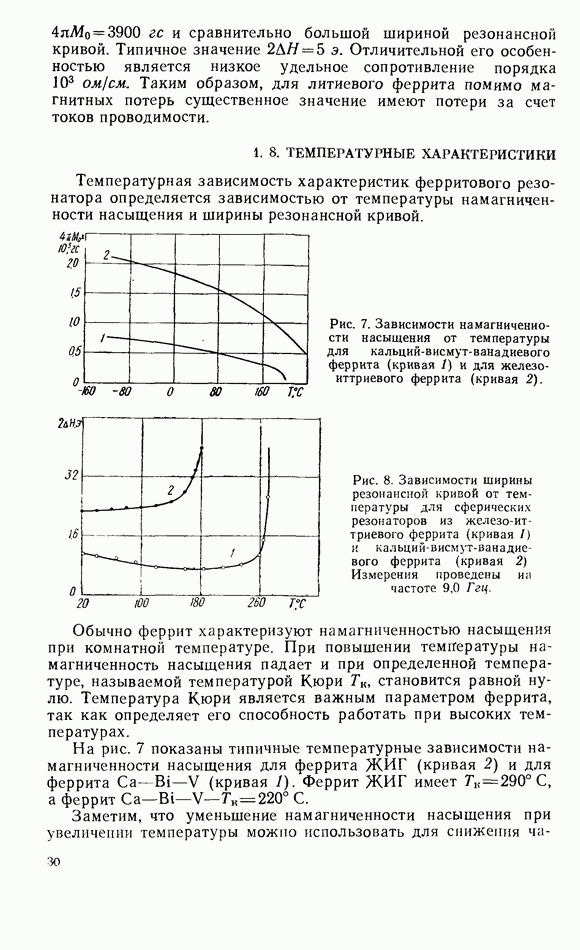
- 1.8. ТЕМПЕРАТУРНЫЕ ХАРАКТЕРИСТИКИ
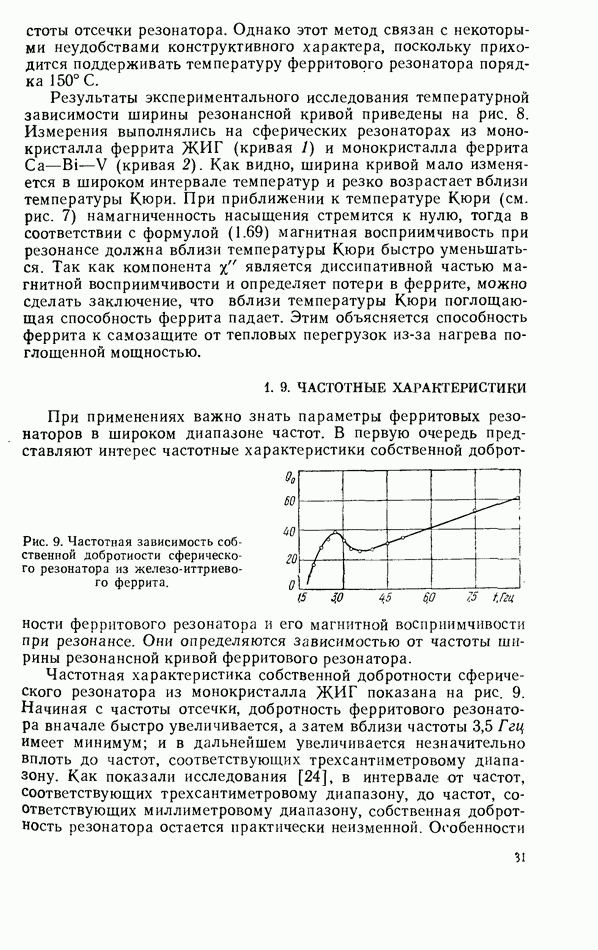
- 1.9. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- Глава вторая. СВОЙСТВА ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 2.2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В АНИЗОТРОПНОМ ДИЭЛЕКТРИЧЕСКОМ СТЕРЖНЕ С «МАГНИТНЫМИ» БОКОВЫМИ СТЕНКАМИ
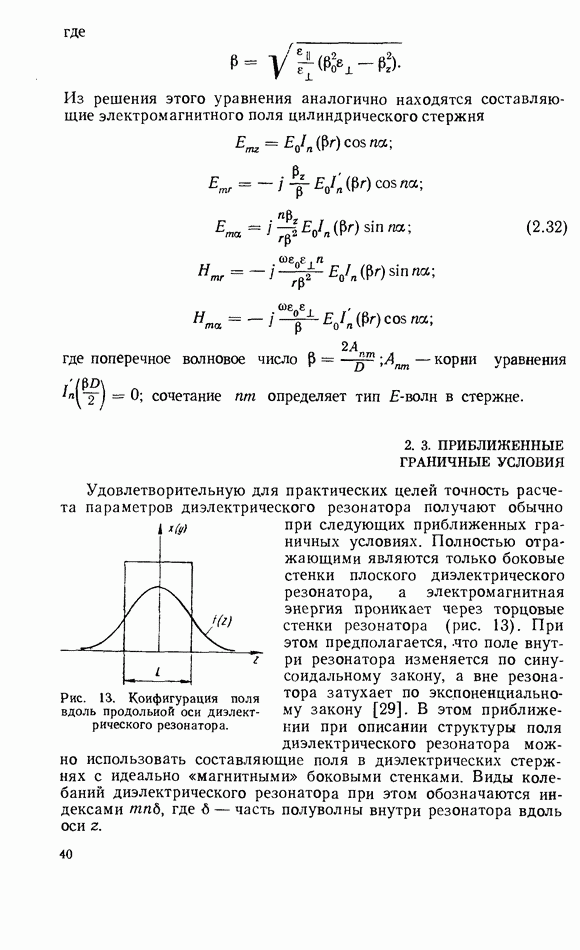
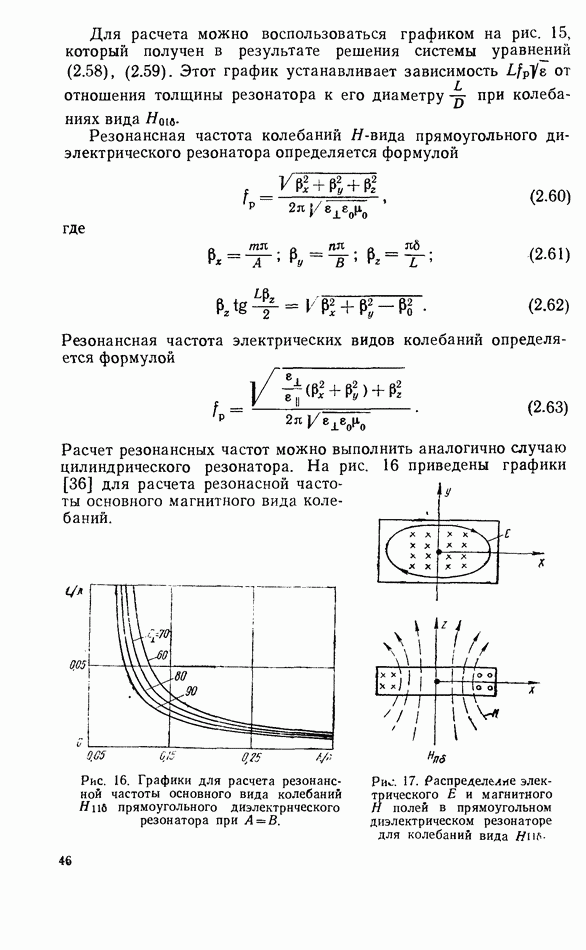
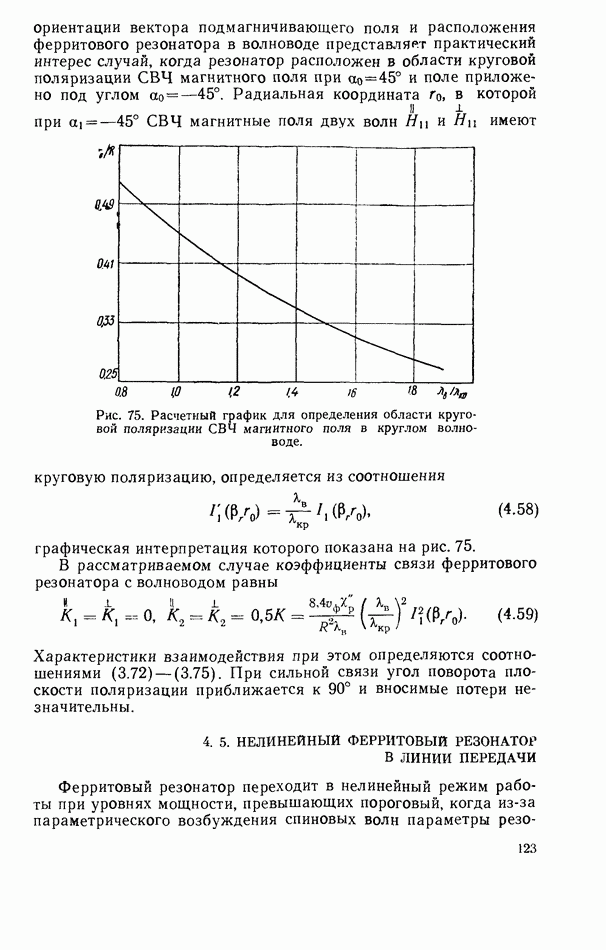
- 2.3. ПРИБЛИЖЕННЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2.5. ОСНОВНЫЕ ВИДЫ КОЛЕБАНИЙ
- 2.6. СФЕРИЧЕСКИЕ ДИЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
- 2.7. ВЛИЯНИЕ МЕТАЛЛИЧЕСКИХ СТЕНОК НА ХАРАКТЕРИСТИКИ ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 2.8. ДИПОЛЬНЫЙ МОМЕНТ
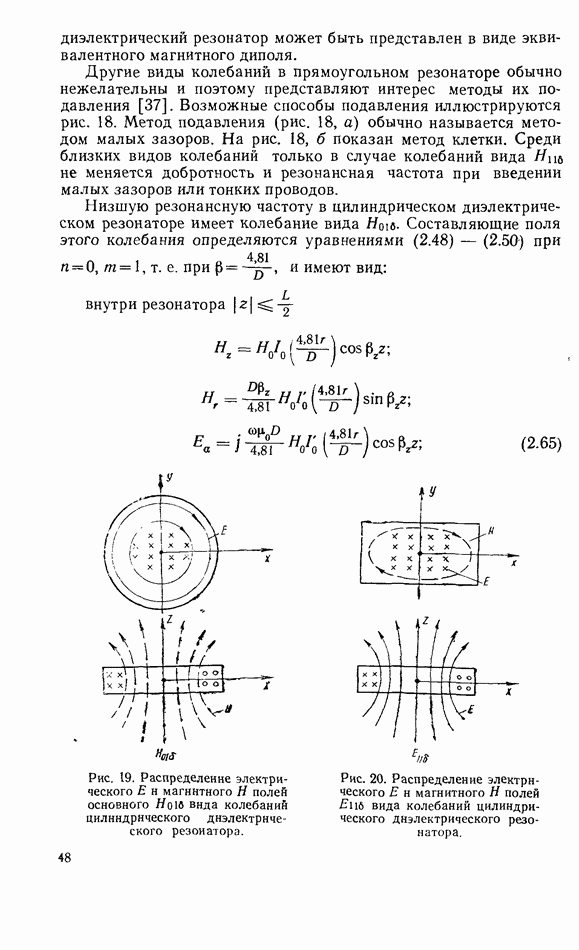
- 2.9. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ
- 2.10. СООТНОШЕНИЕ МЕЖДУ АМПЛИТУДАМИ СВЧ МАГНИТНОГО ПОЛЯ
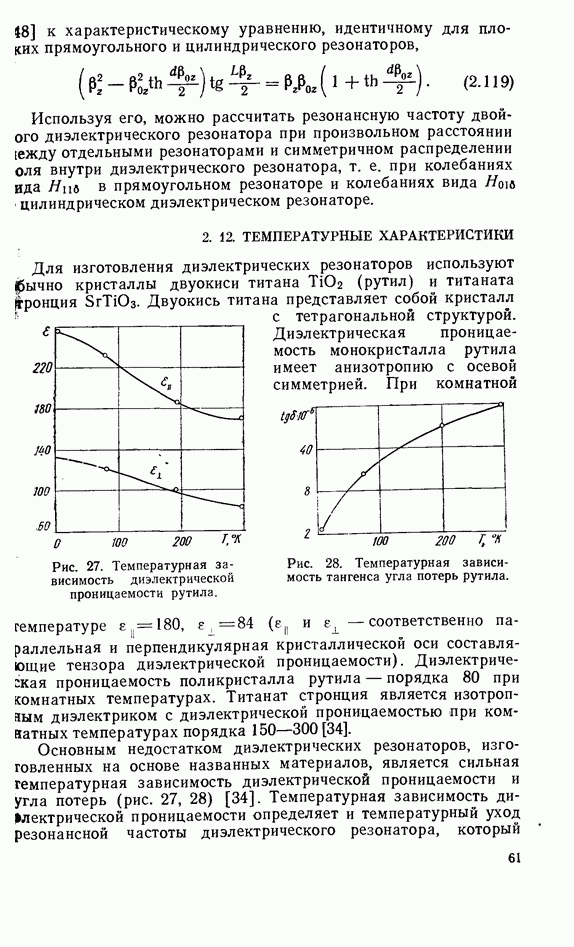
- 2.11. ДВОЙНЫЕ ДИЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
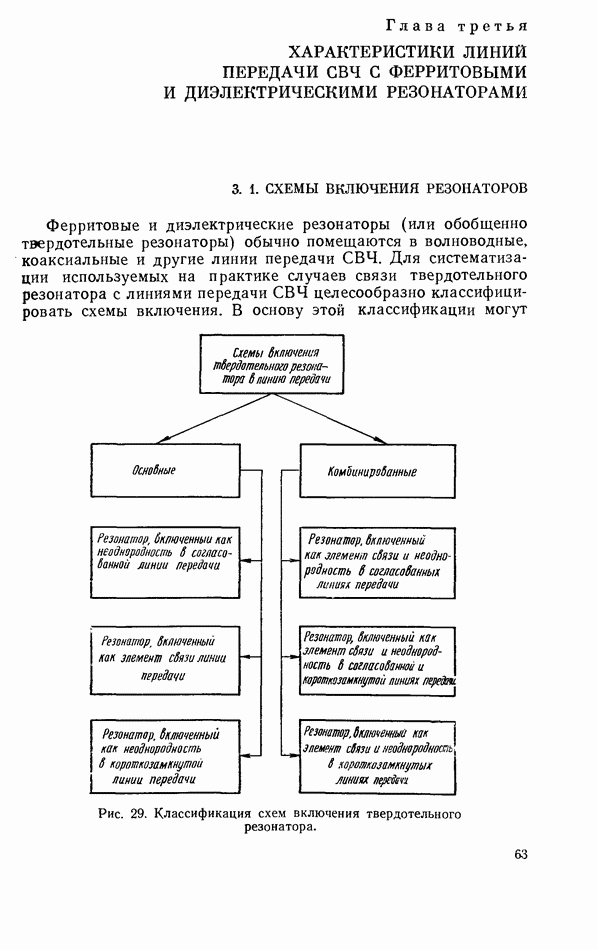
- 2.12. ТЕМПЕРАТУРНЫЕ ХАРАКТЕРИСТИКИ
- Глава третья. ХАРАКТЕРИСТИКИ ЛИНИЙ ПЕРЕДАЧИ СВЧ С ФЕРРИТОВЫМИ И ДИЭЛЕКТРИЧЕСКИМИ РЕЗОНАТОРАМИ
- 3.2. МЕТОДЫ РАСЧЕТА СВЧ-СХЕМ С ТВЕРДОТЕЛЬНЫМИ РЕЗОНАТОРАМИ
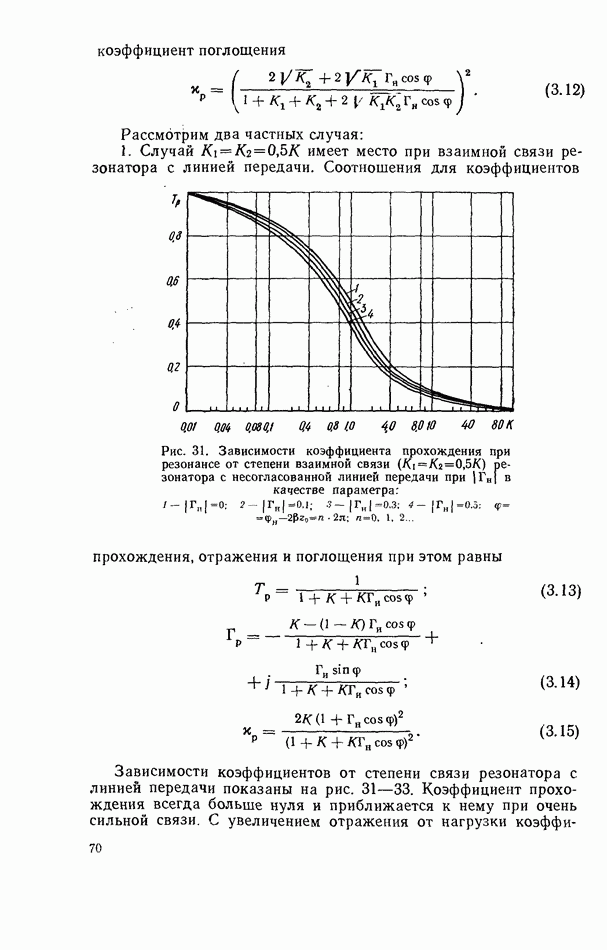
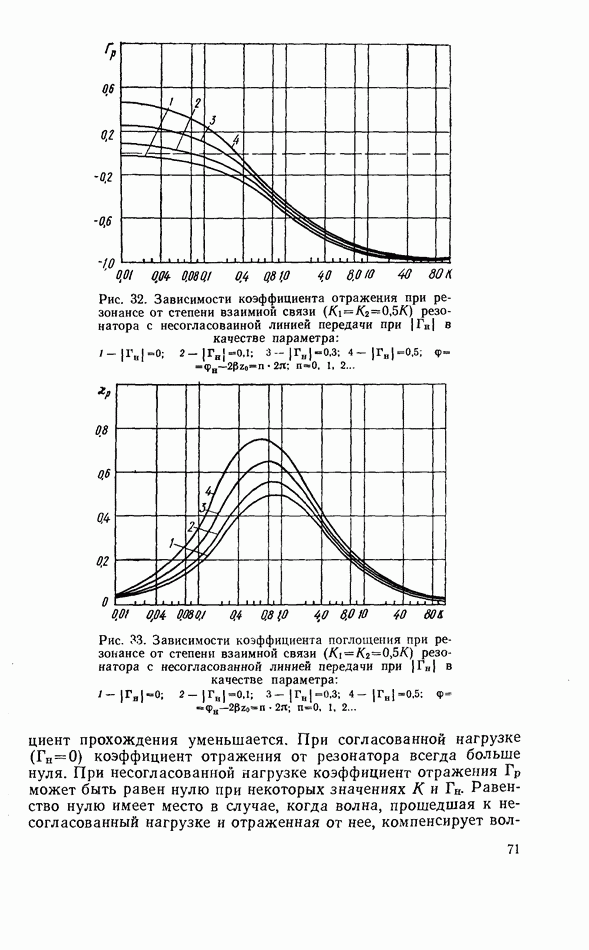
- 3.3. СВЯЗЬ ТВЕРДОТЕЛЬНОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ СВЧ
- 3.4. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В НЕСОГЛАСОВАННОЙ ЛИНИИ ПЕРЕДАЧИ
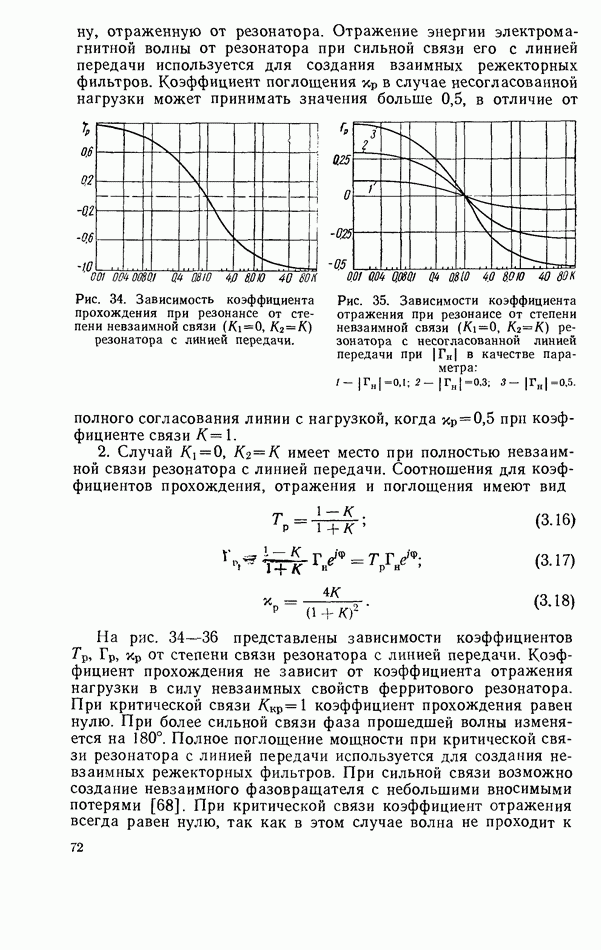
- 3.5. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР, ВКЛЮЧЕННЫЙ КАК ЭЛЕМЕНТ СВЯЗИ ЛИНИЙ ПЕРЕДАЧИ
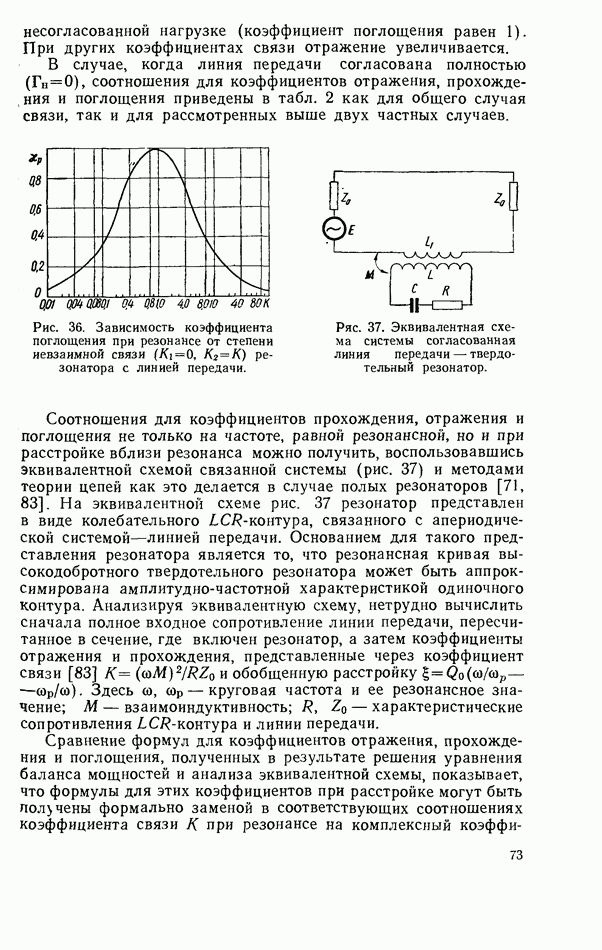
- 3.6. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В КОРОТКОЗАМКНУТОЙ ЛИНИИ ПЕРЕДАЧИ
- 3.7. КОМБИНИРОВАННЫЕ СХЕМЫ ВКЛЮЧЕНИЯ ТВЕРДОТЕЛЬНОГО РЕЗОНАТОРА
- 3.8. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ С НЕСКОЛЬКИМИ РАСПРОСТРАНЯЮЩИМИСЯ ВОЛНАМИ
- Глава четвертая. СВЯЗЬ ТВЕРДОТЕЛЬНЫХ РЕЗОНАТОРОВ С ЛИНИЯМИ ПЕРЕДАЧИ СВЧ
- 4.2. СВЯЗЬ ФЕРРИТОВОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ
- 4.3. ФЕРРИТОВЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ ЗАМЕДЛЕННЫХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
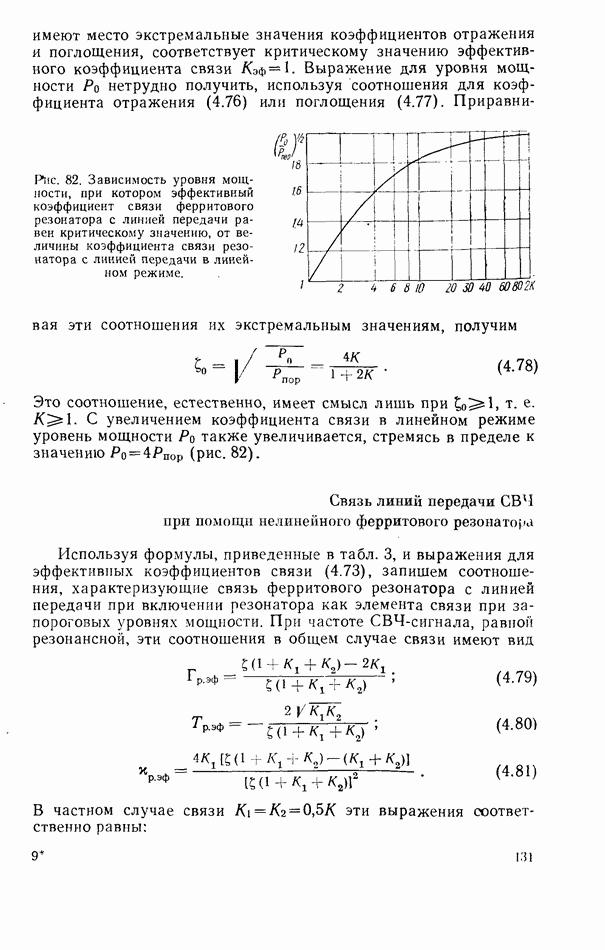
- 4.4. РЕЗОНАНСНЫЙ ПОВОРОТ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ В ВОЛНОВОДЕ С ФЕРРИТОВЫМ РЕЗОНАТОРОМ
- 4.5. НЕЛИНЕЙНЫЙ ФЕРРИТОВЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ
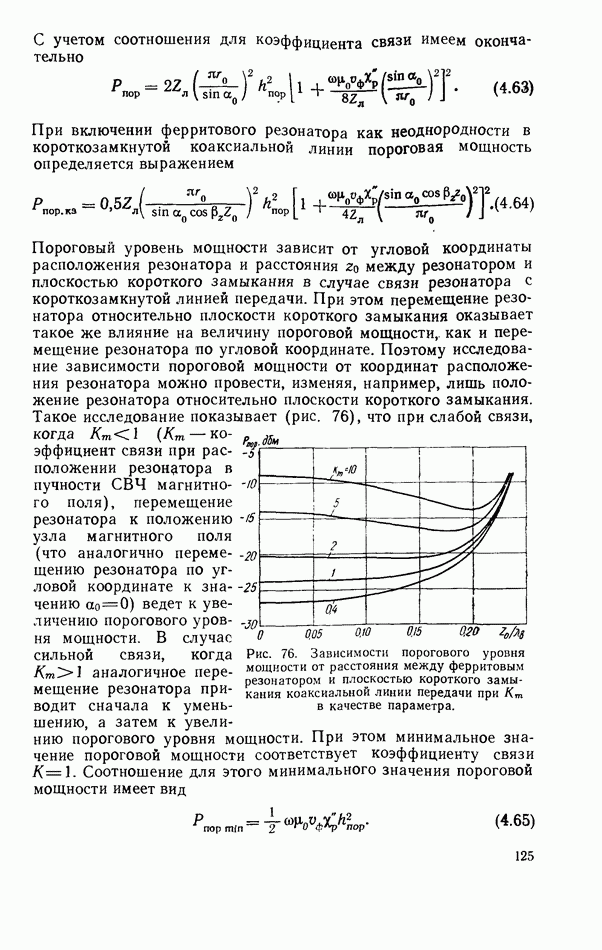
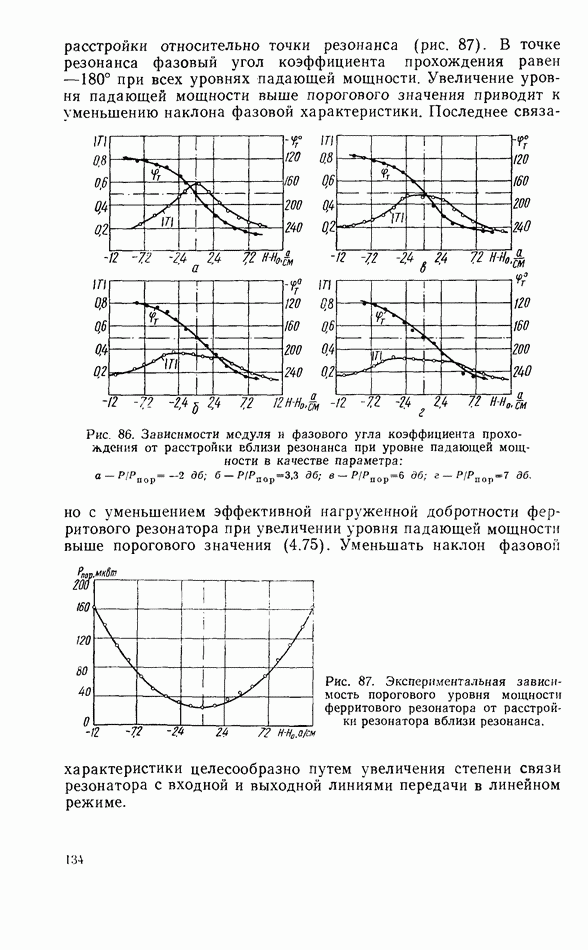
- Ферритовый резонатор в линии передачи при запороговых уровнях мощности
- Нелинейный ферритовый резонатор в короткозамкнутой линии передачи
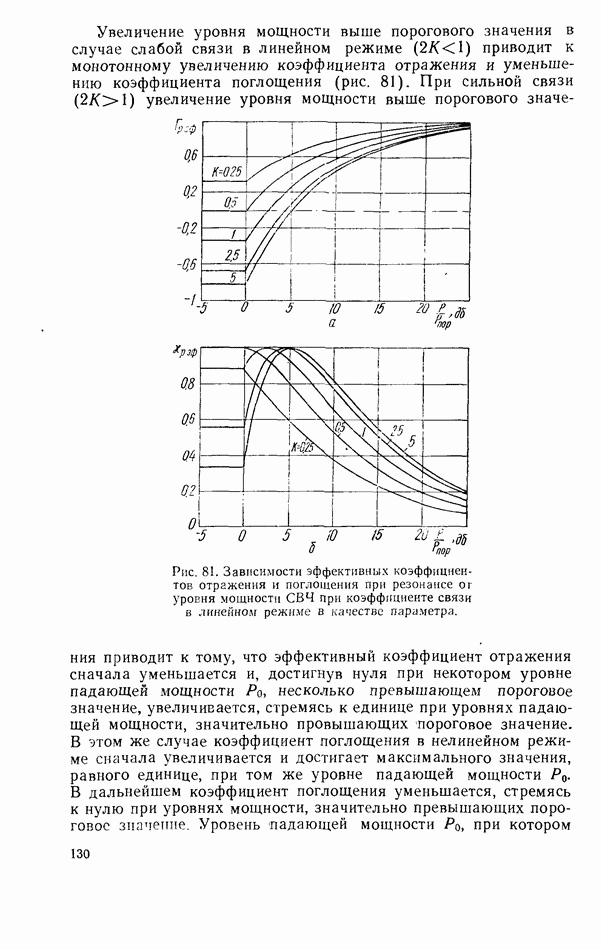
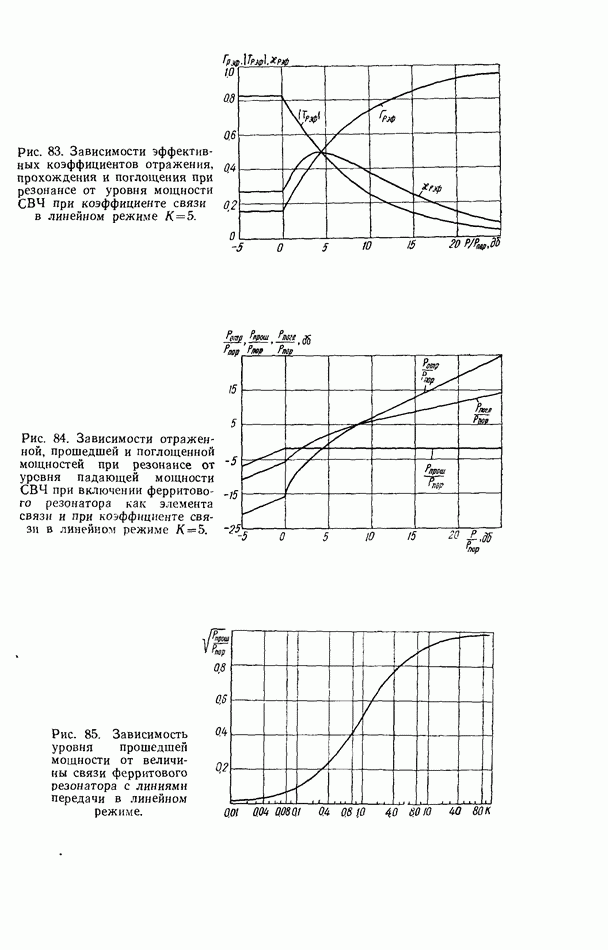
- Связь линий передачи СВЧ при помощи нелинейного ферритового резонатора
- Нелинейный ферритовый резонатор в согласованной линии передачи
- 4.6. СВЯЗЬ ДИЭЛЕКТРИЧЕСКОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ СВЧ
- Глава пятая. ПРИНЦИПЫ ПОСТРОЕНИЯ СВЧ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ И УСТРОЙСТВ НА ОСНОВЕ ТВЕРДОТЕЛЬНЫХ РЕЗОНАТОРОВ
- 5.2. ДАТЧИКИ УРОВНЯ МОЩНОСТИ СВЧ
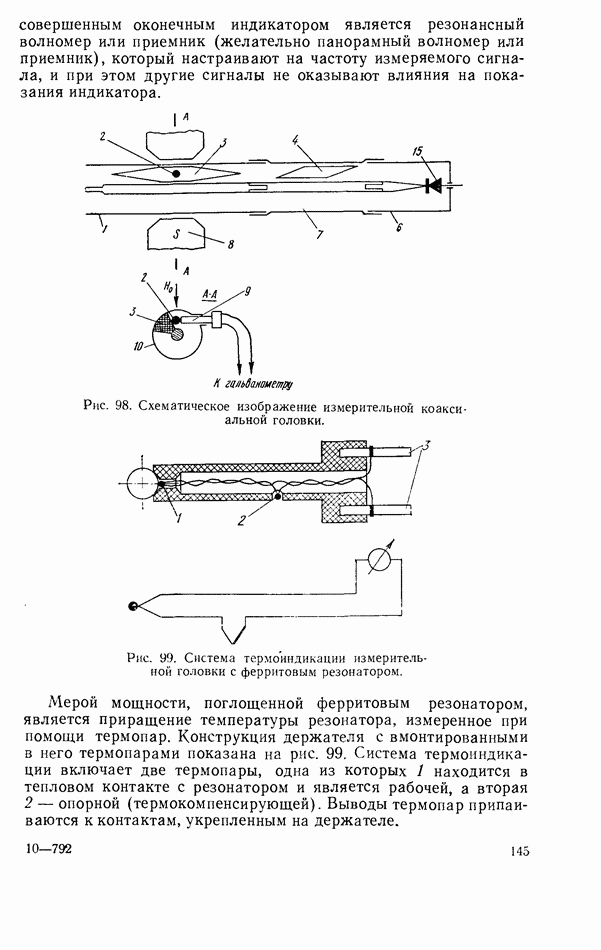
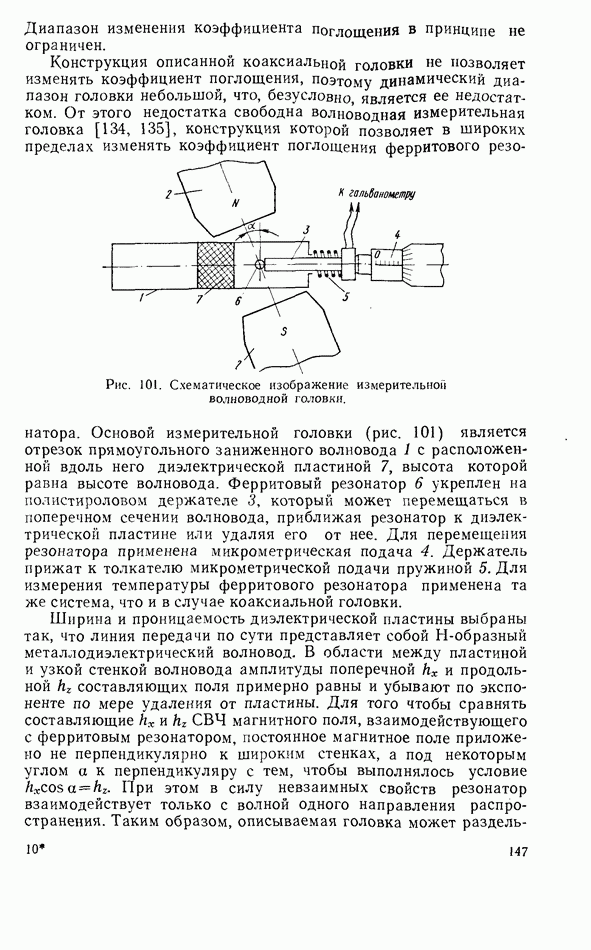
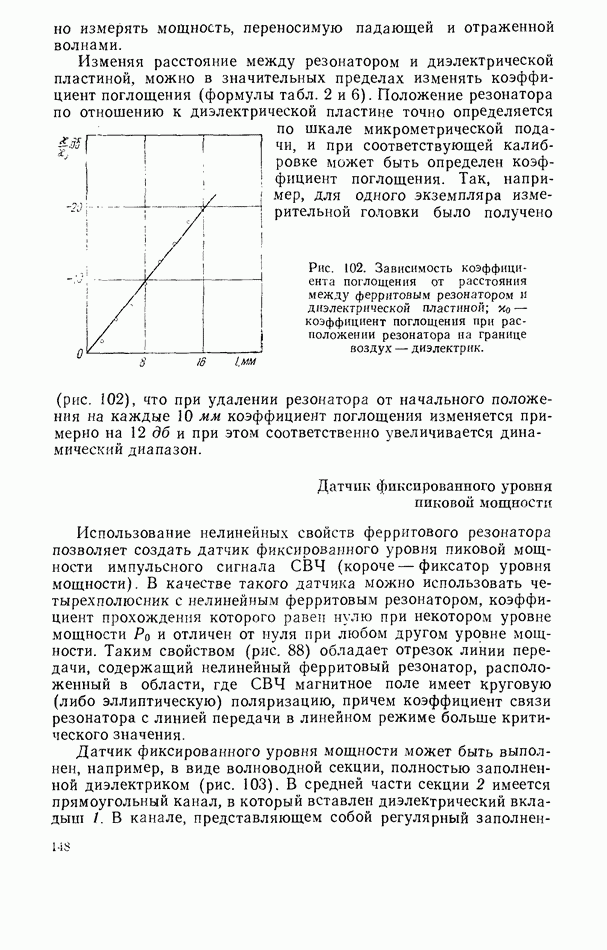
- Волноводная измерительная головка
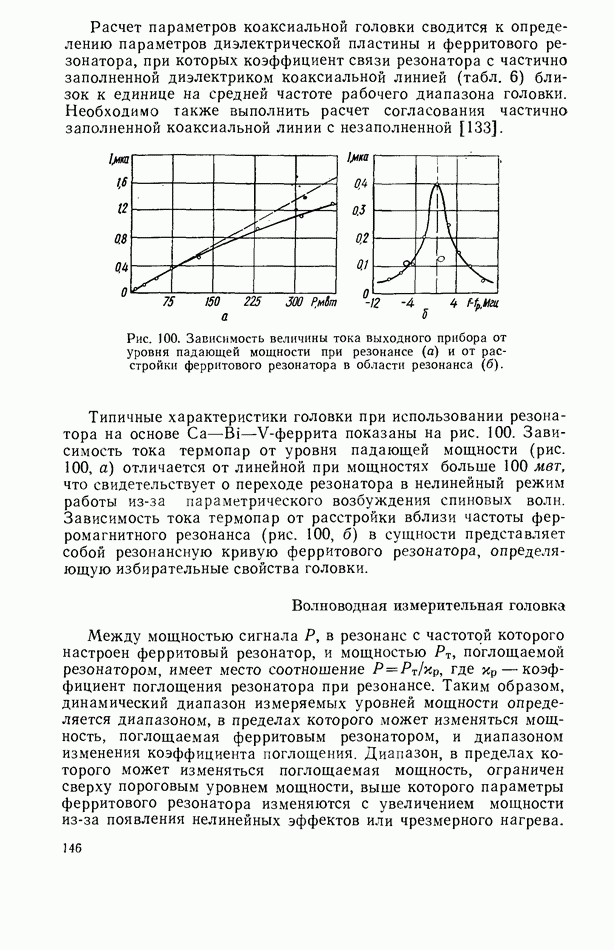
- Датчик фиксированного уровня пиковой мощности
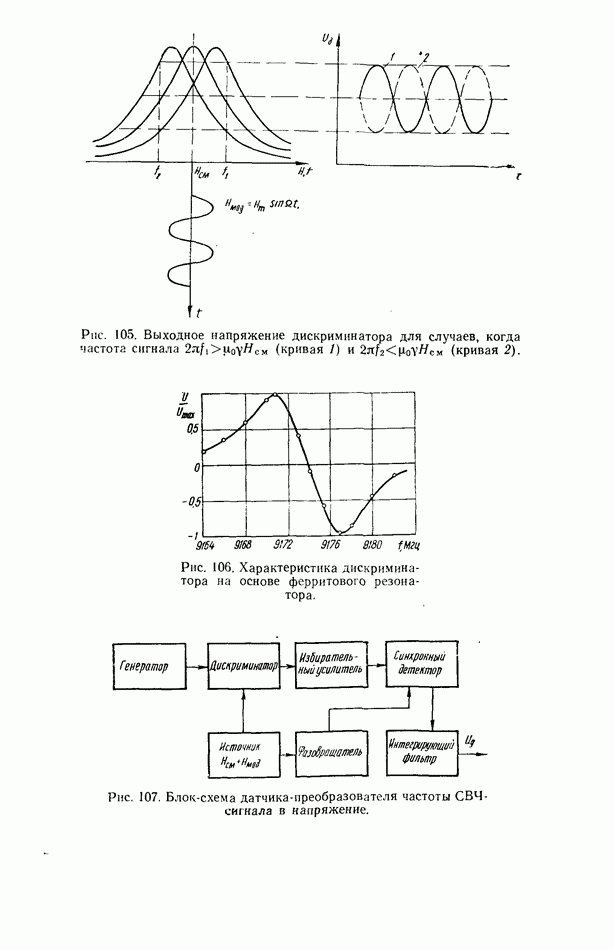
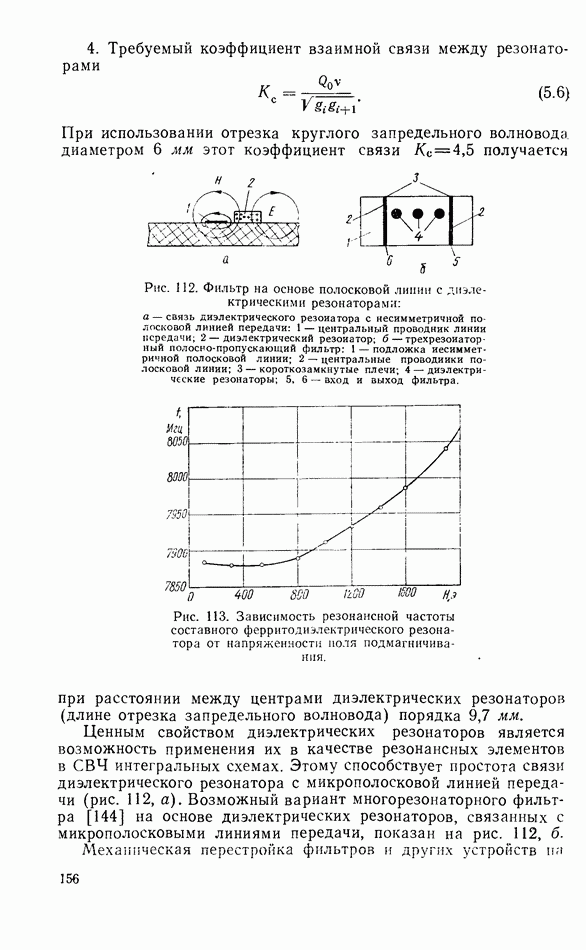
- 5.3. ЧАСТОТНЫЕ ДИСКРИМИНАТОРЫ С МАГНИТНОЙ НАСТРОЙКОЙ
- 5.4. РЕЗОНАНСНЫЕ ФАЗОВРАЩАТЕЛИ
- 5.5. УСТРОЙСТВО ДЛЯ РЕЗОНАНСНОГО ПОВОРОТА ПЛОСКОСТИ ПОЛЯРИЗАЦИИ В ВОЛНОВОДЕ
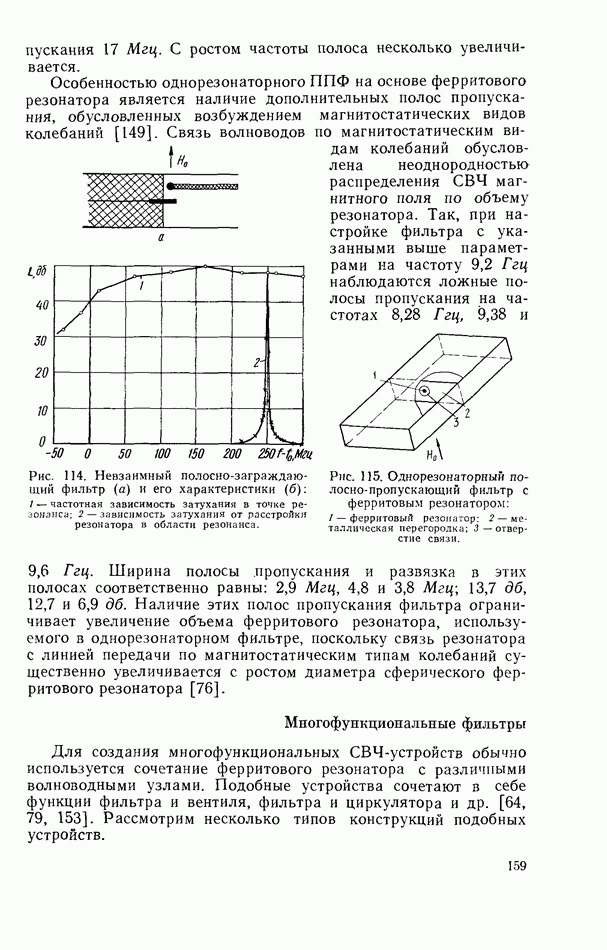
- 5.6. ФИЛЬТРЫ СВЧ НА ОСНОВЕ ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
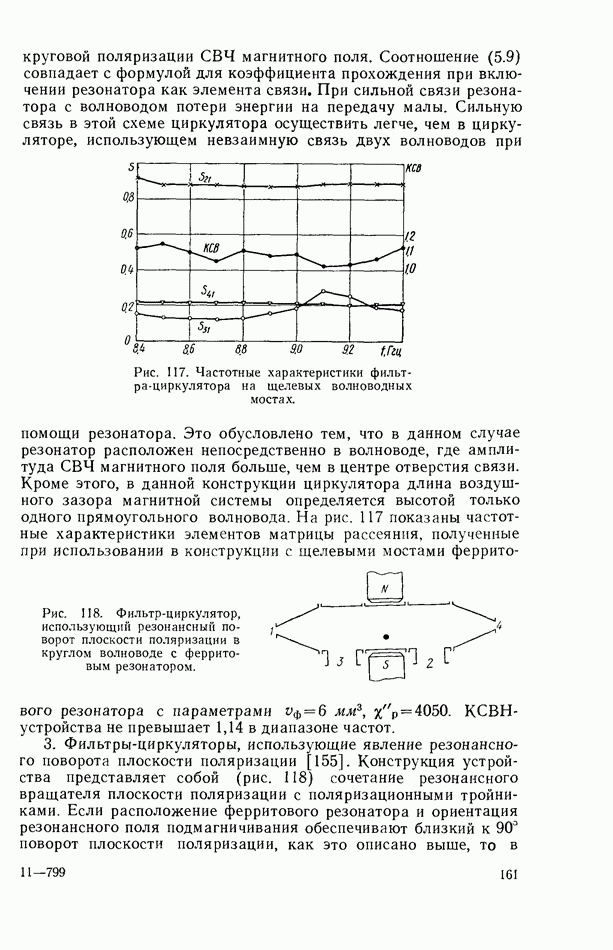
- 5.7. ФЕРРИТОВЫЕ СВЧ-ФИЛЬТРЫ
- Многофункциональные фильтры
- Многорезонаторные ферритовые фильтры
- 5.8. ЧАСТОТНО-ИЗБИРАТЕЛЬНЫЕ ОГРАНИЧИТЕЛИ МАЛЫХ УРОВНЕЙ МОЩНОСТИ