| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
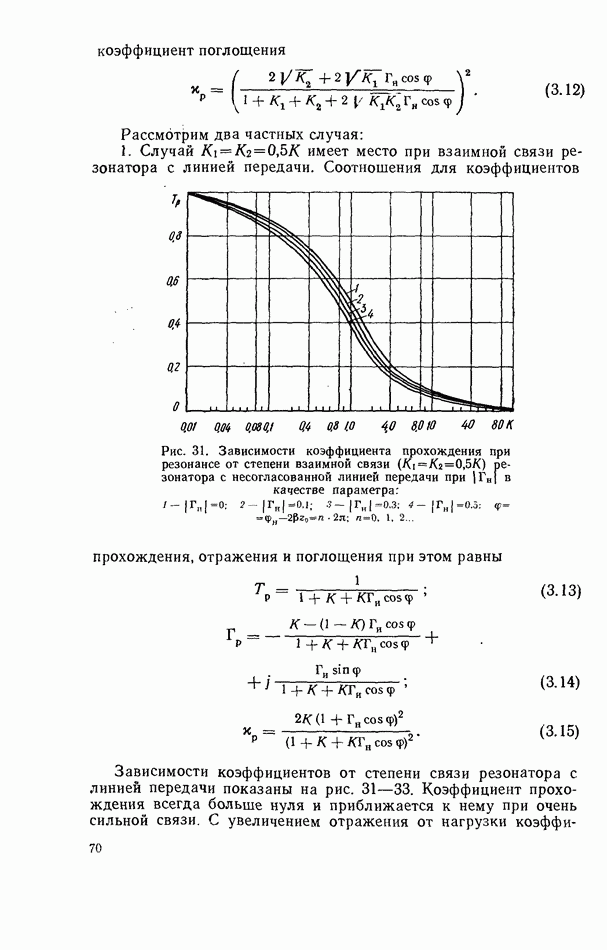
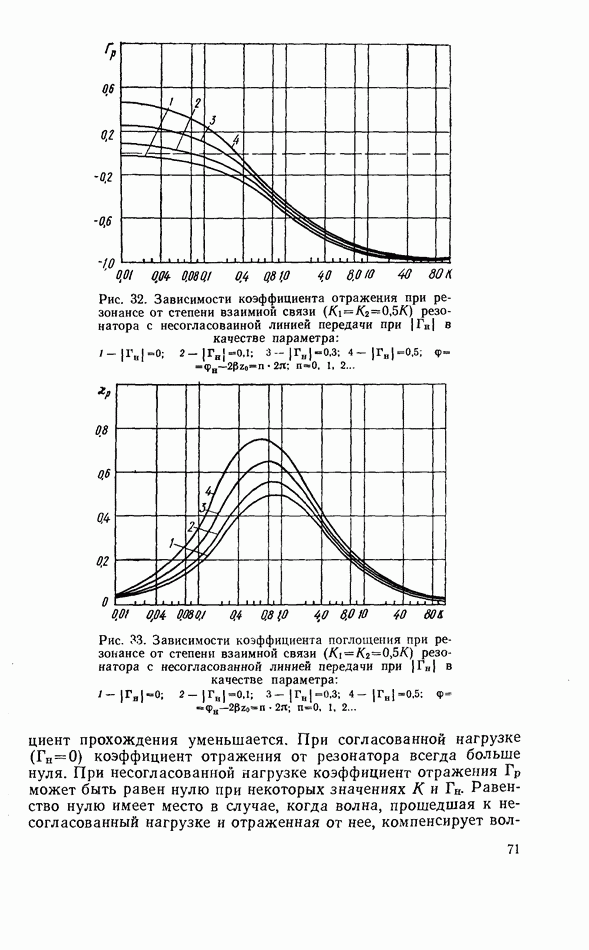
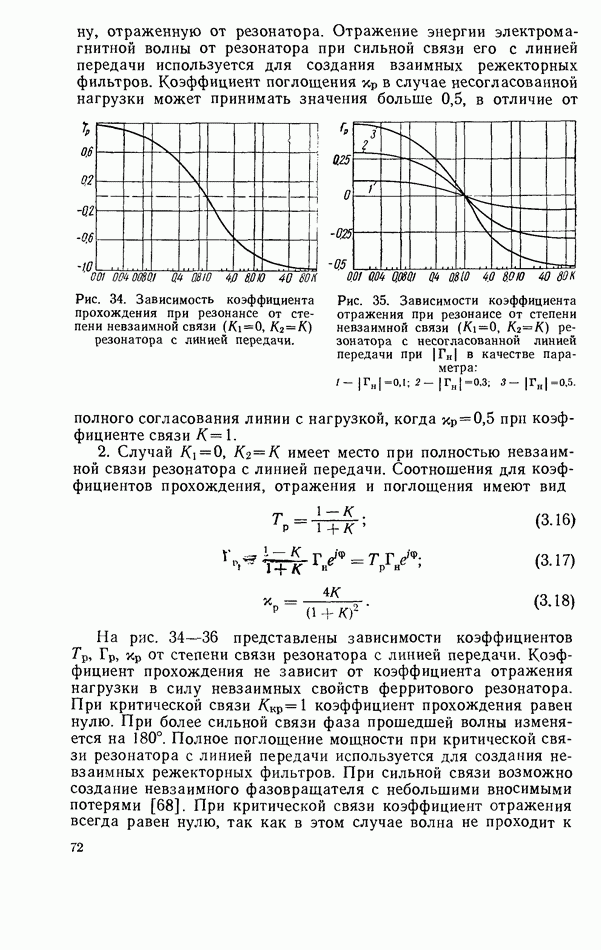
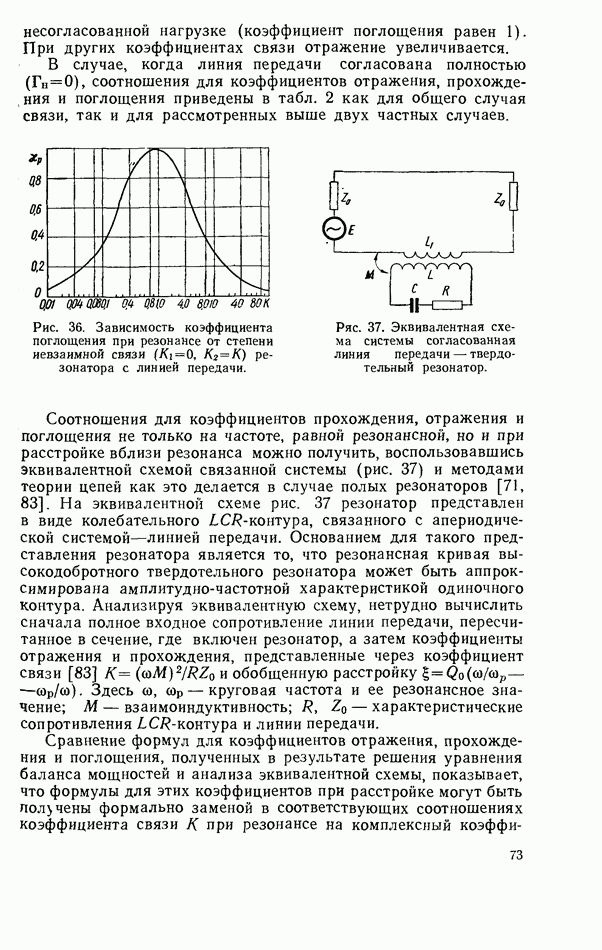
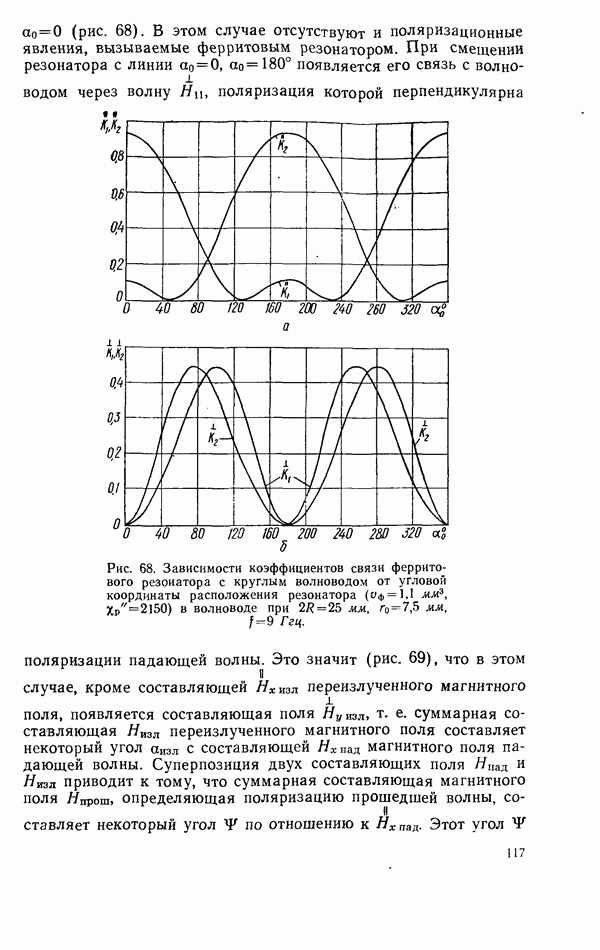
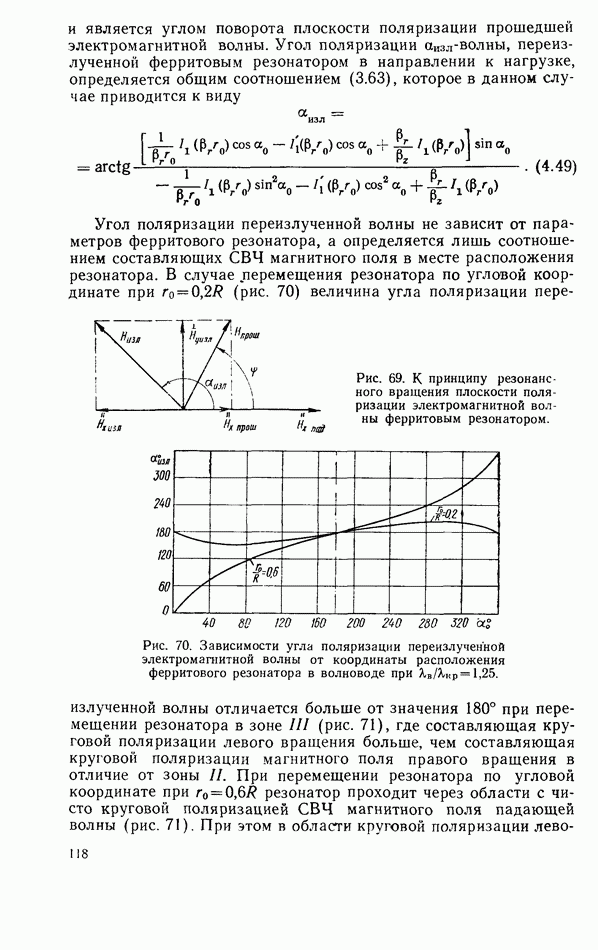
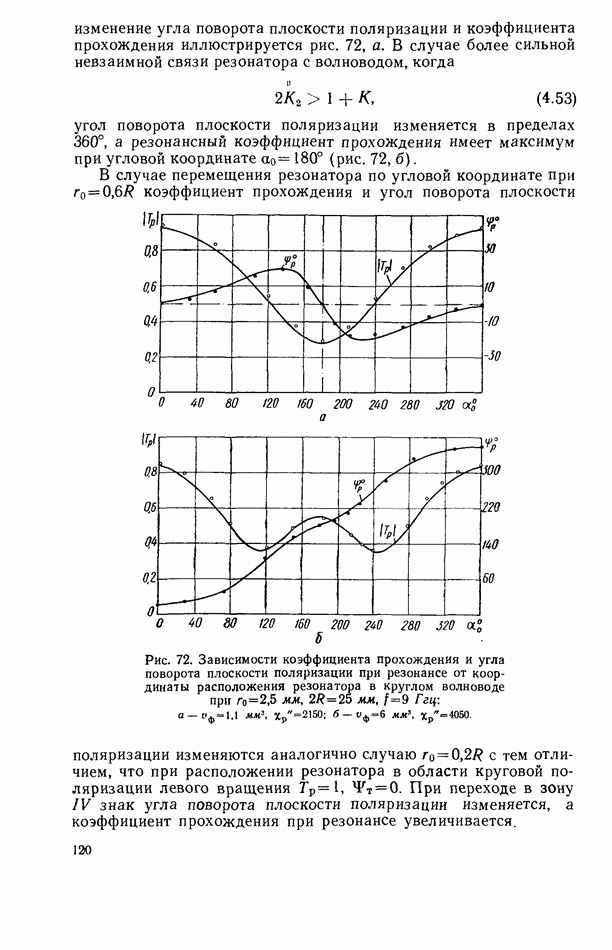
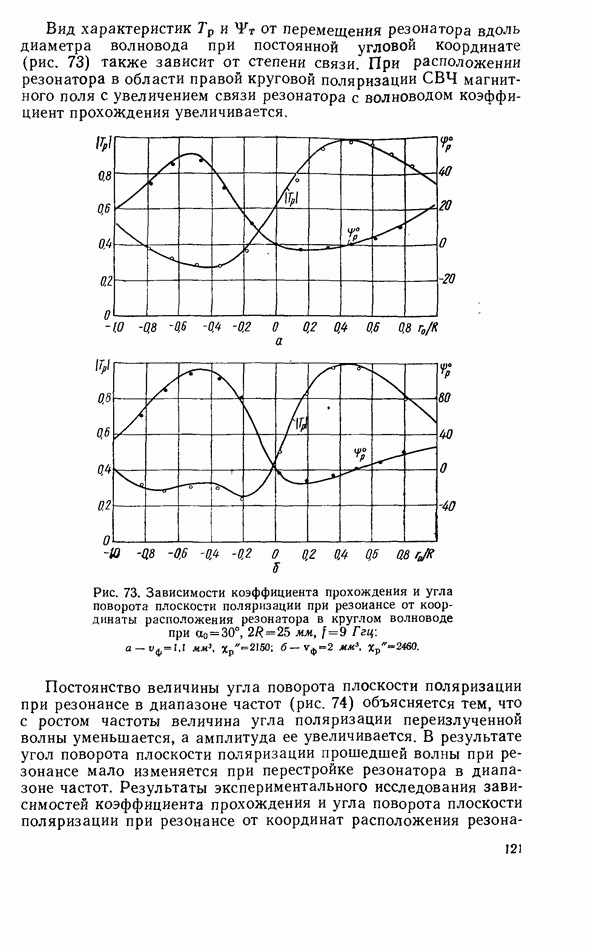
2.9. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ
Диэлектрический резонатор в установившемся режиме вынужденных колебаний можно рассматривать как колебательную систему, обладающую запасом энергии

Добротность такой системы определяется, как обычно [45], в виде

где  мощность, рассеиваемая в колебательной системе. При большой диэлектрической проницаемости резонатора электромагнитные поля в основном ограничены внутри диэлектрического резонатора и вблизи его границ на расстояниях, малых по сравнению с длиной волны в свободном пространстве, затухают до пренебрежимо малых величин. Поэтому рассеяние электромагнитной энергии в металлических экранах (стенках волноводов, проводниках полосковых линий) мало и собственная добротность в основном определяется лишь потерями в диэлектрике. Электрические потери в диэлектрике вычисляются по формуле [43]
мощность, рассеиваемая в колебательной системе. При большой диэлектрической проницаемости резонатора электромагнитные поля в основном ограничены внутри диэлектрического резонатора и вблизи его границ на расстояниях, малых по сравнению с длиной волны в свободном пространстве, затухают до пренебрежимо малых величин. Поэтому рассеяние электромагнитной энергии в металлических экранах (стенках волноводов, проводниках полосковых линий) мало и собственная добротность в основном определяется лишь потерями в диэлектрике. Электрические потери в диэлектрике вычисляются по формуле [43]

где  мнимая часть диэлектрической проницаемости образца. При пренебрежении потерями, обусловленными внешними
мнимая часть диэлектрической проницаемости образца. При пренебрежении потерями, обусловленными внешними
СВЧ-цепями и металлическими экранами, собственная добротность с учетом выражений (2.91) — (2.93) в первом приближении вычисляется по формуле

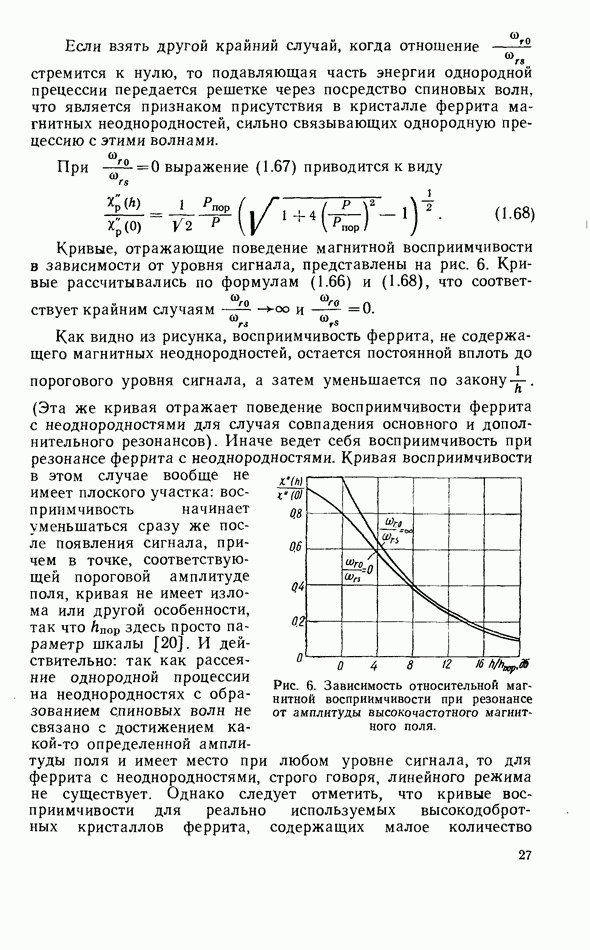
Поскольку типичное значение  для применяемых в настоящее время материалов составляет
для применяемых в настоящее время материалов составляет  то собственная добротность диэлектрического резонатора при комнатных температурах достигает значений 104. В отдельных случаях при температуре жидкого гелия удается получить собственную добротность порядка
то собственная добротность диэлектрического резонатора при комнатных температурах достигает значений 104. В отдельных случаях при температуре жидкого гелия удается получить собственную добротность порядка 
При решении ряда задач необходимо знать энергию, запасаемую диэлектрическим резонатором. Вычислим энергию, запасаемую в диэлектрическом резонаторе при возбуждении в нем  -видов колебаний. В случае прямоугольного резонатора при расчете воспользуемся формулой
-видов колебаний. В случае прямоугольного резонатора при расчете воспользуемся формулой

Подставляя соотношения (2.43), (2.44) для составляющих поля  -видов колебаний прямоугольного резонатора и вычисляя поверхностный интеграл
-видов колебаний прямоугольного резонатора и вычисляя поверхностный интеграл

и интеграл вдоль продольной оси резонатора

где

получим

В случае цилиндрического резонатора энергия, запасаемая  видом колебаний, рассчитывается по формуле
видом колебаний, рассчитывается по формуле

Входящие в это выражение интегралы по поперечному сечению и вдоль продольной оси соответственно равны

где множитель  определяется формулой (2.97). При вычислении интегралов учтено, что
определяется формулой (2.97). При вычислении интегралов учтено, что

Таким образом, энергия, запасаемая в цилиндрическом диэлектрическом резонаторе, равна

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- Глава первая. СВОЙСТВА ФЕРРИТОВЫХ РЕЗОНАТОРОВ
- Ферромагнитный резонанс в неограниченной среде без потерь
- 1.2. РЕЗОНАНСНАЯ ЧАСТОТА
- Зависимость резонансной частоты от формы резонатора
- Влияние кристаллографической анизотропии на резонансную частоту
- 1.3. МАГНИТОСТАТИЧЕСКИЕ ВИДЫ КОЛЕБАНИЙ
- 1.4. УЧЕТ ПОТЕРЬ
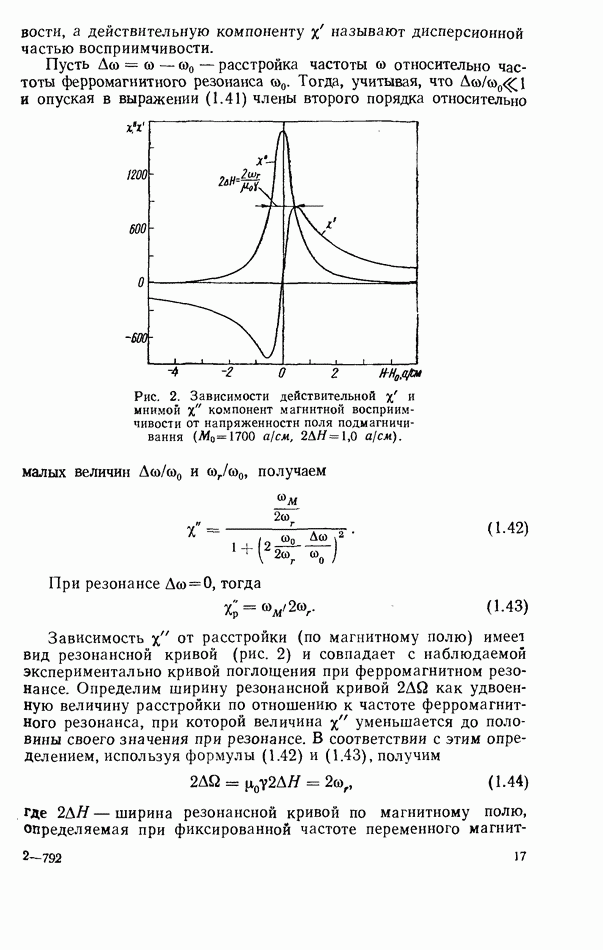
- 1.5. ДИПОЛЬНЫЙ МОМЕНТ
- 1.6. НЕЛИНЕЙНЫЕ ЯВЛЕНИЯ
- Спиновые волны
- Пороговая амплитуда высокочастотного магнитного поля
- Восприимчивость при амплитудах поля, превышающих пороговое значение
- 1.7. ПРИМЕНЯЕМЫЕ ДЛЯ ИЗГОТОВЛЕНИЯ МАТЕРИАЛЫ
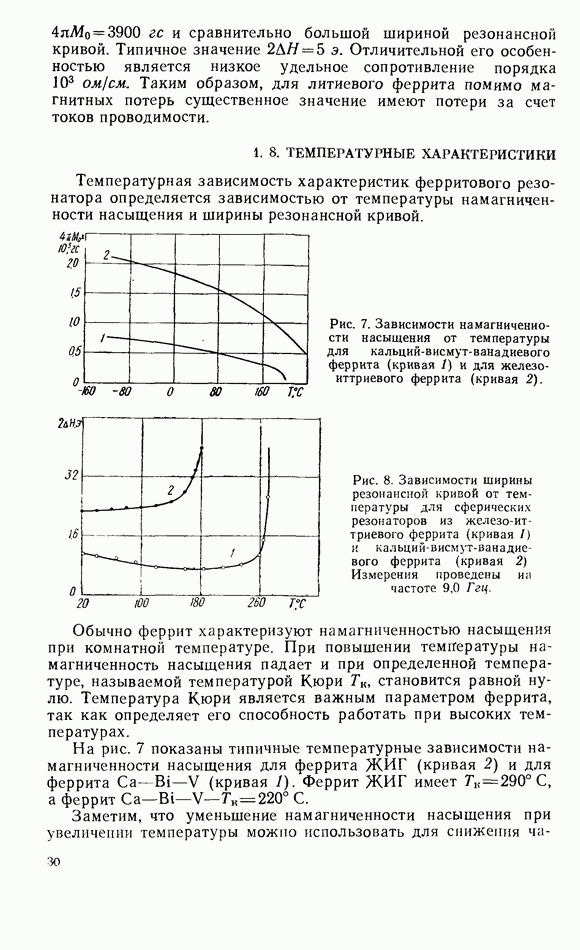
- 1.8. ТЕМПЕРАТУРНЫЕ ХАРАКТЕРИСТИКИ
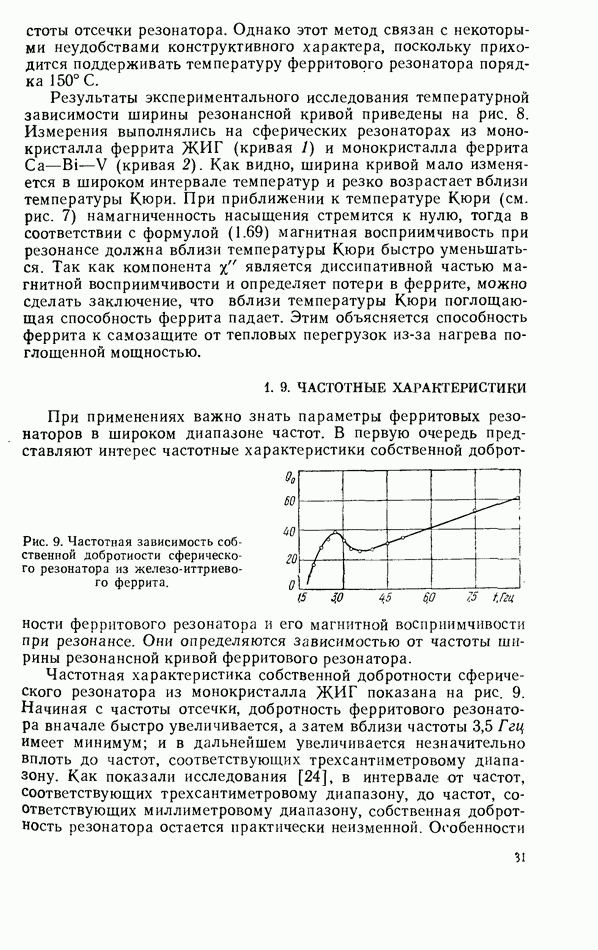
- 1.9. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- Глава вторая. СВОЙСТВА ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 2.2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В АНИЗОТРОПНОМ ДИЭЛЕКТРИЧЕСКОМ СТЕРЖНЕ С «МАГНИТНЫМИ» БОКОВЫМИ СТЕНКАМИ
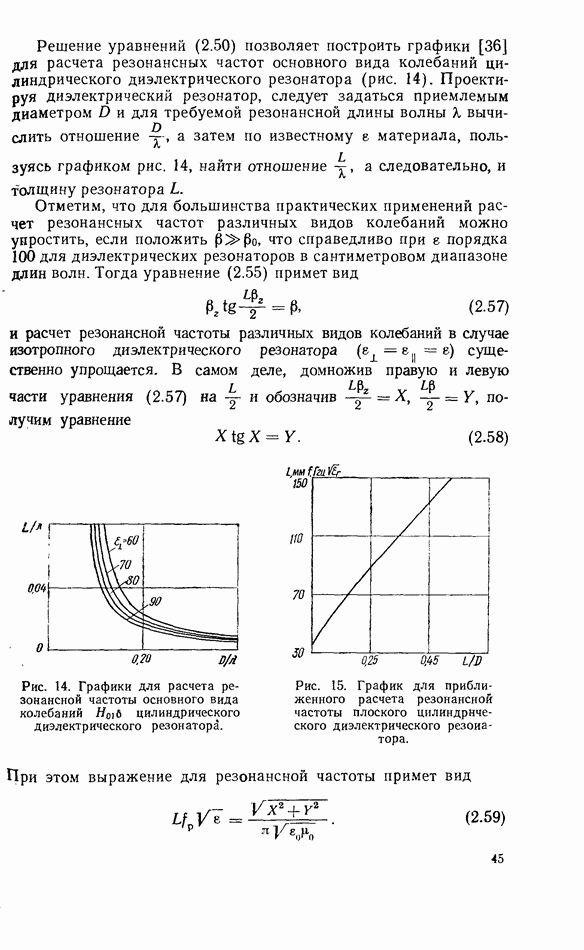
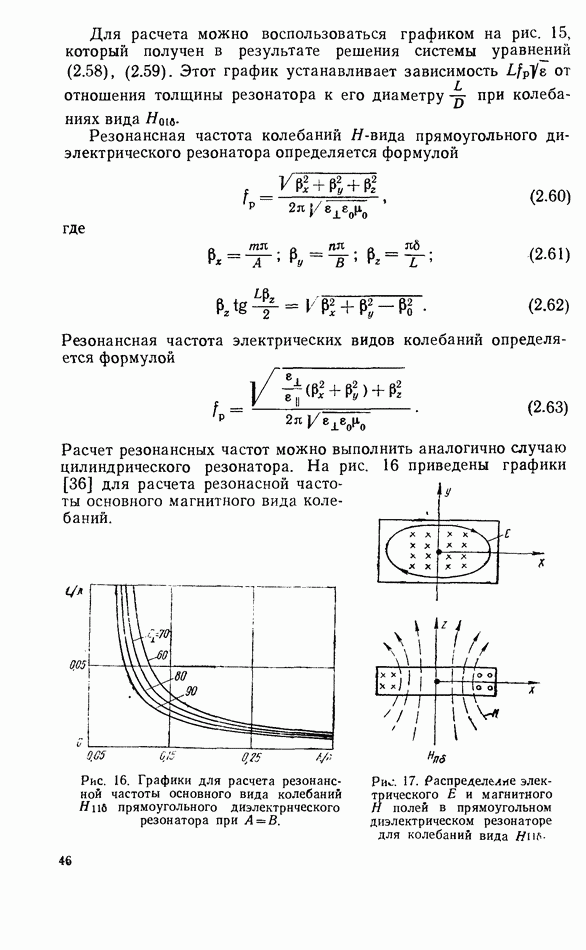
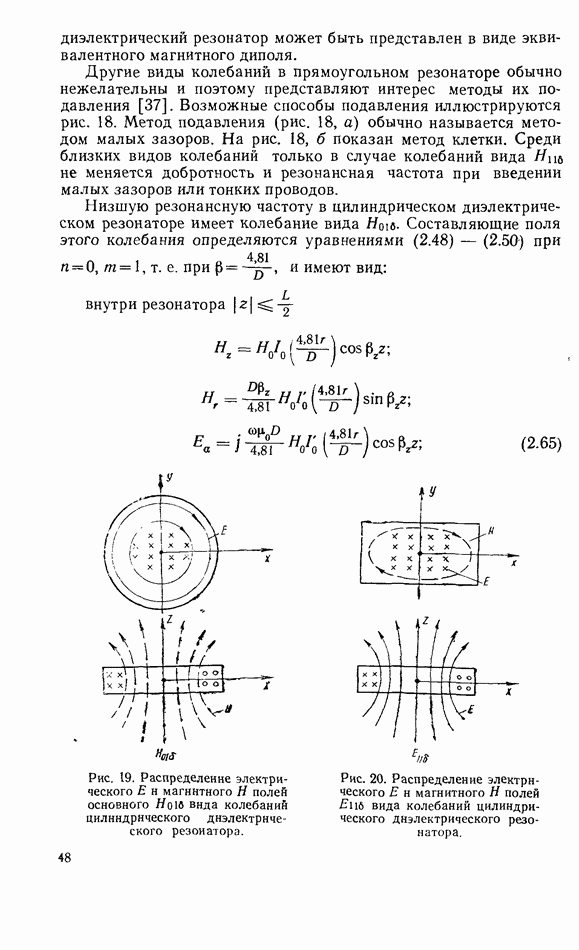
- 2.3. ПРИБЛИЖЕННЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2.5. ОСНОВНЫЕ ВИДЫ КОЛЕБАНИЙ
- 2.6. СФЕРИЧЕСКИЕ ДИЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
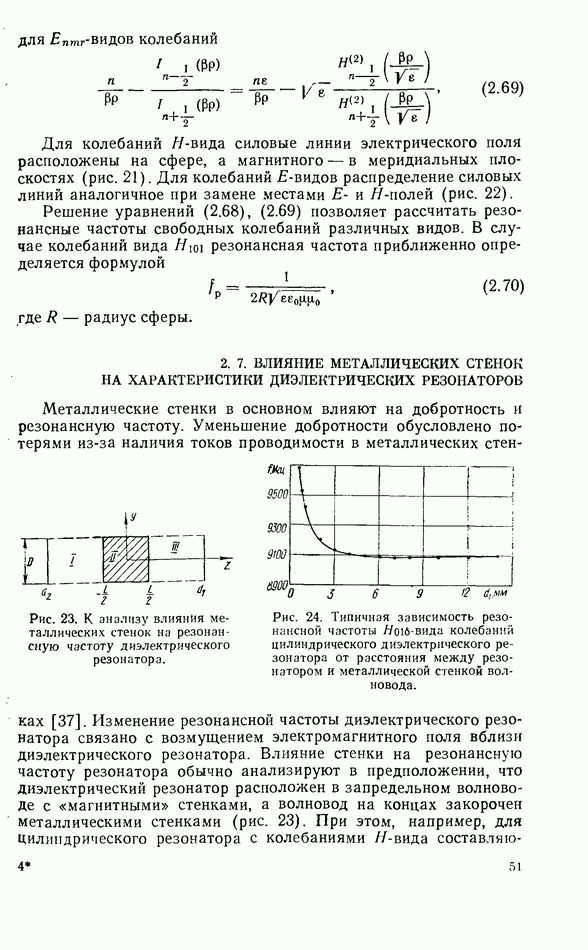
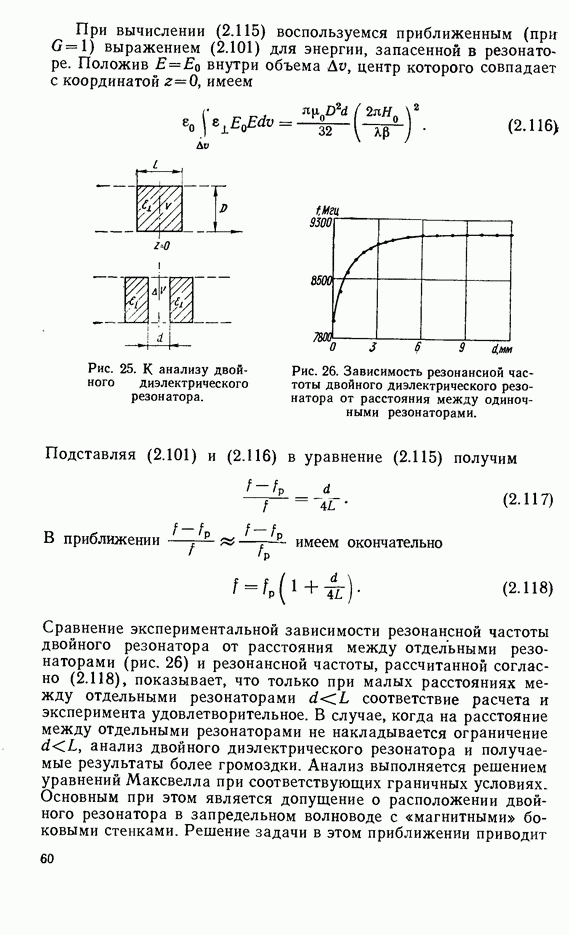
- 2.7. ВЛИЯНИЕ МЕТАЛЛИЧЕСКИХ СТЕНОК НА ХАРАКТЕРИСТИКИ ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 2.8. ДИПОЛЬНЫЙ МОМЕНТ
- 2.9. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ
- 2.10. СООТНОШЕНИЕ МЕЖДУ АМПЛИТУДАМИ СВЧ МАГНИТНОГО ПОЛЯ
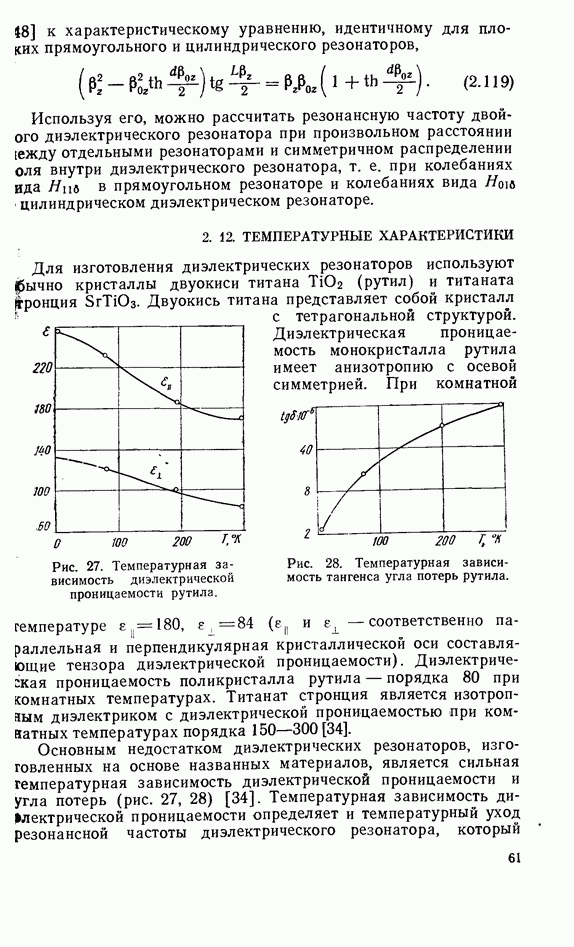
- 2.11. ДВОЙНЫЕ ДИЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
- 2.12. ТЕМПЕРАТУРНЫЕ ХАРАКТЕРИСТИКИ
- Глава третья. ХАРАКТЕРИСТИКИ ЛИНИЙ ПЕРЕДАЧИ СВЧ С ФЕРРИТОВЫМИ И ДИЭЛЕКТРИЧЕСКИМИ РЕЗОНАТОРАМИ
- 3.2. МЕТОДЫ РАСЧЕТА СВЧ-СХЕМ С ТВЕРДОТЕЛЬНЫМИ РЕЗОНАТОРАМИ
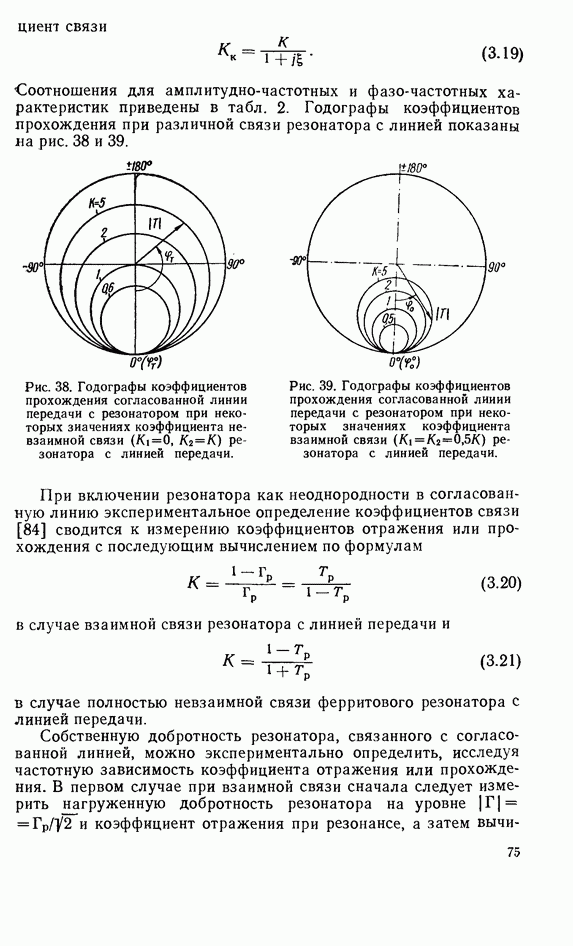
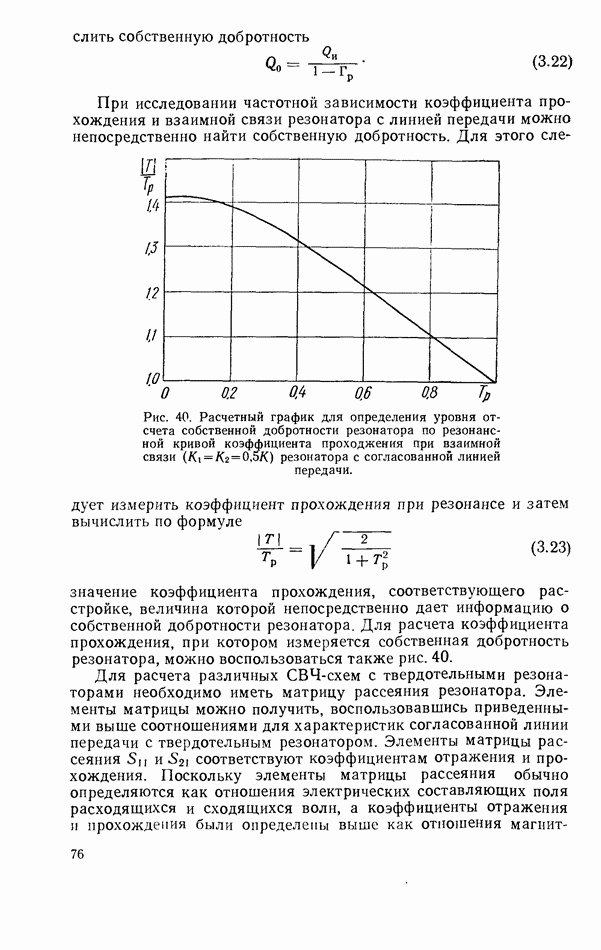
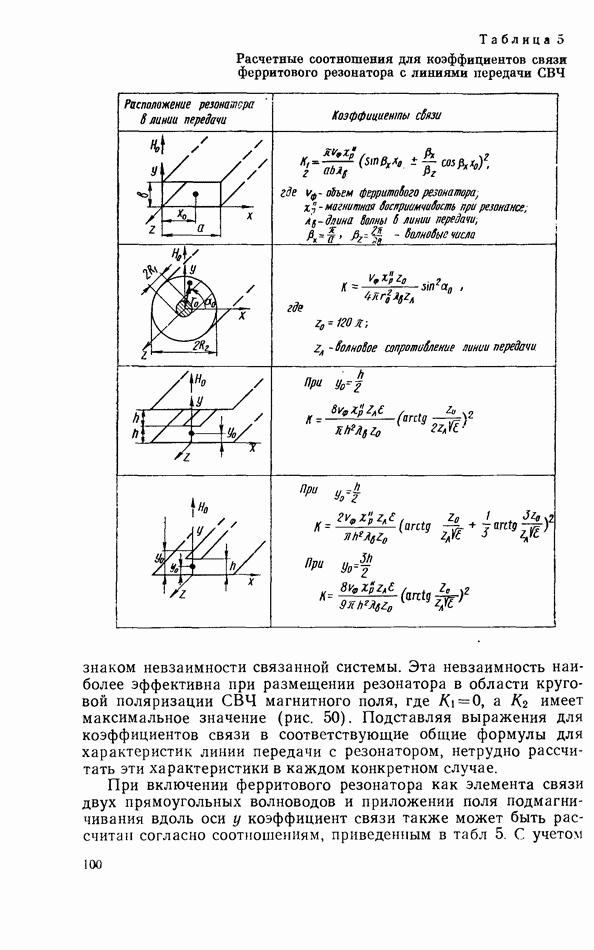
- 3.3. СВЯЗЬ ТВЕРДОТЕЛЬНОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ СВЧ
- 3.4. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В НЕСОГЛАСОВАННОЙ ЛИНИИ ПЕРЕДАЧИ
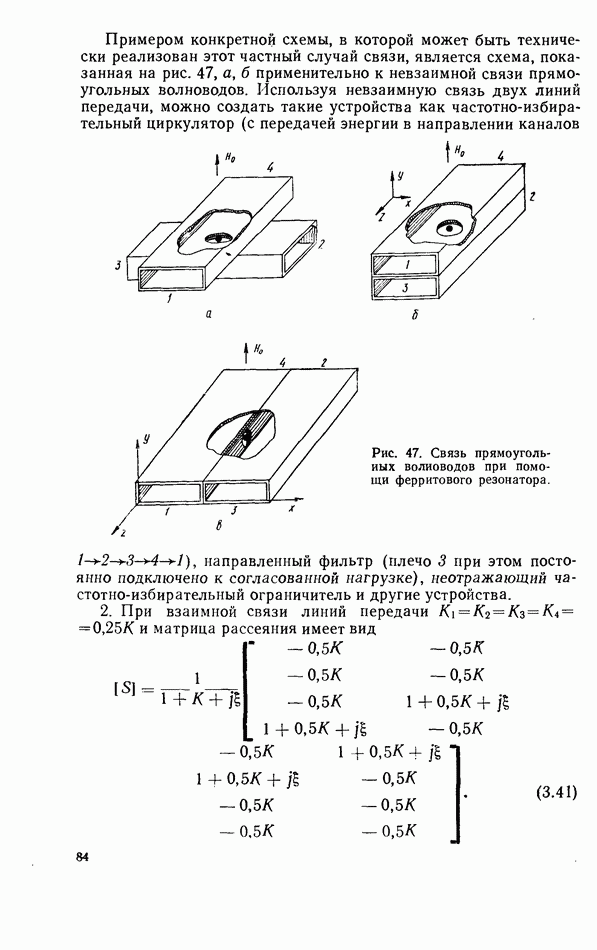
- 3.5. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР, ВКЛЮЧЕННЫЙ КАК ЭЛЕМЕНТ СВЯЗИ ЛИНИЙ ПЕРЕДАЧИ
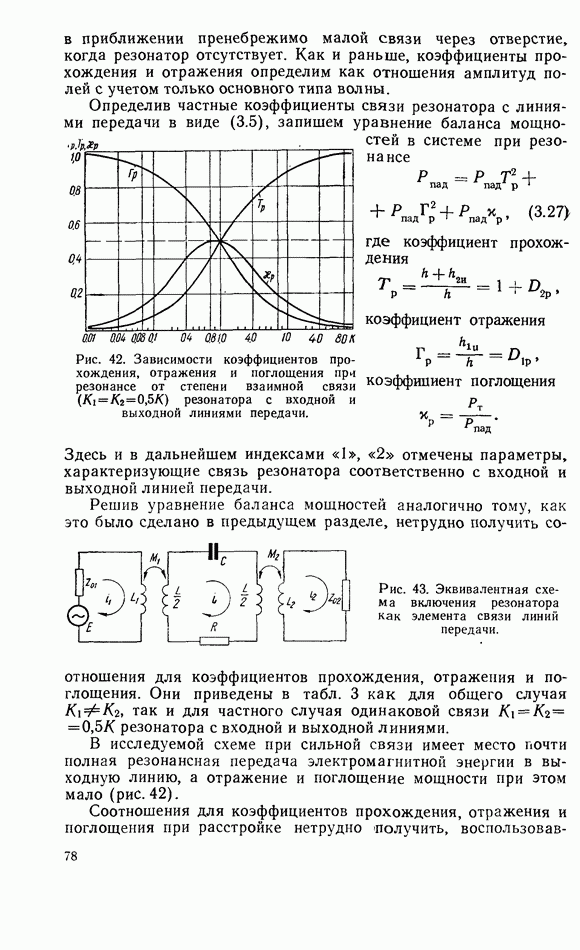
- 3.6. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В КОРОТКОЗАМКНУТОЙ ЛИНИИ ПЕРЕДАЧИ
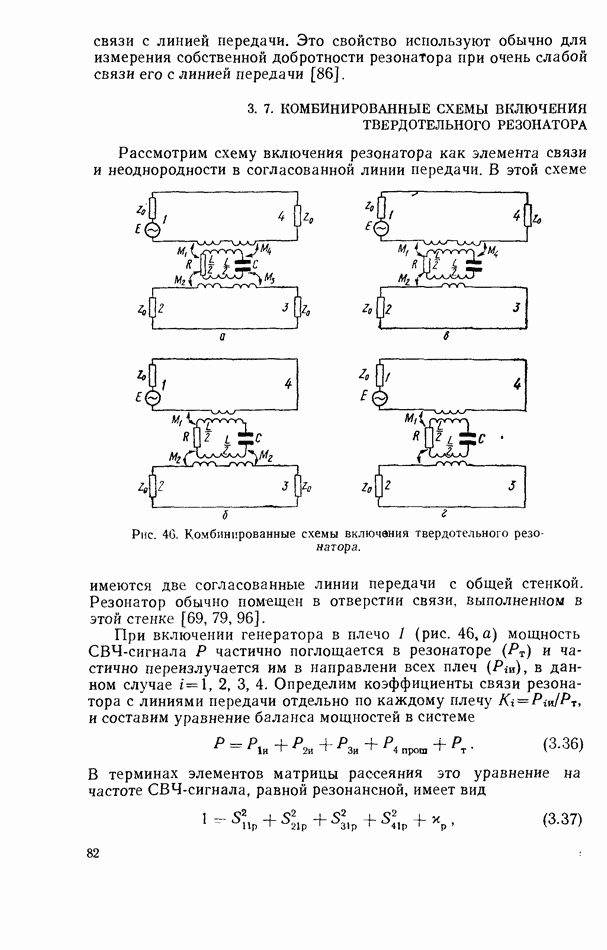
- 3.7. КОМБИНИРОВАННЫЕ СХЕМЫ ВКЛЮЧЕНИЯ ТВЕРДОТЕЛЬНОГО РЕЗОНАТОРА
- 3.8. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ С НЕСКОЛЬКИМИ РАСПРОСТРАНЯЮЩИМИСЯ ВОЛНАМИ
- Глава четвертая. СВЯЗЬ ТВЕРДОТЕЛЬНЫХ РЕЗОНАТОРОВ С ЛИНИЯМИ ПЕРЕДАЧИ СВЧ
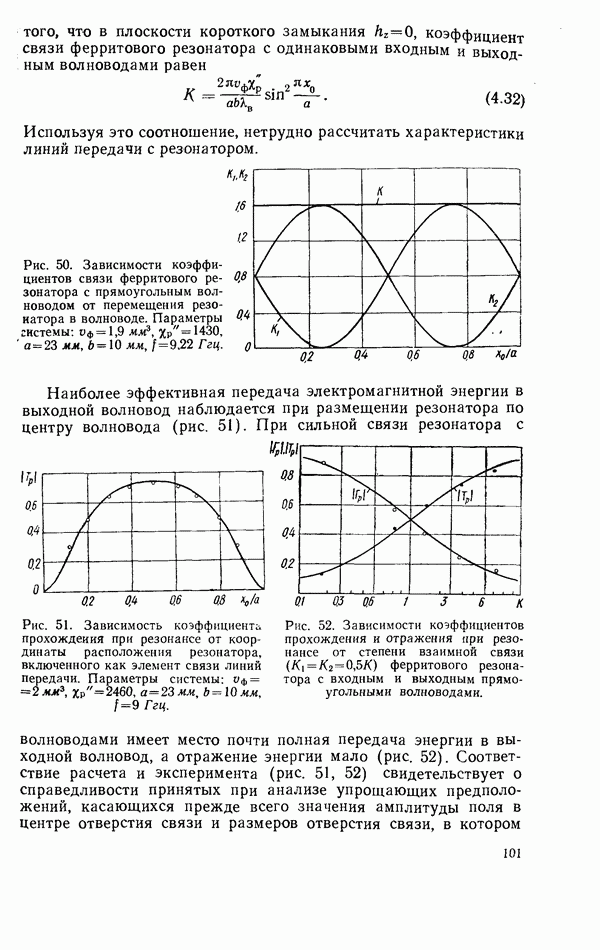
- 4.2. СВЯЗЬ ФЕРРИТОВОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ
- 4.3. ФЕРРИТОВЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ ЗАМЕДЛЕННЫХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
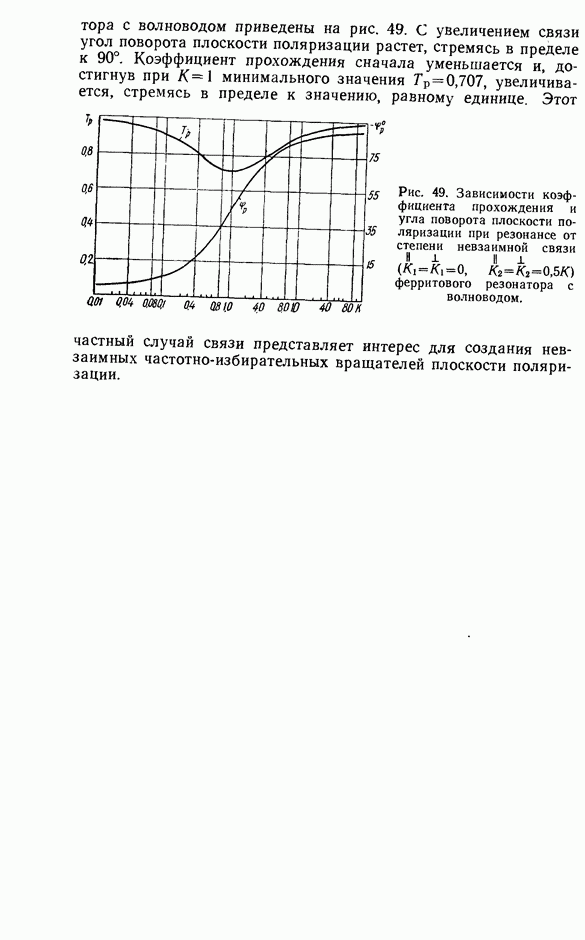
- 4.4. РЕЗОНАНСНЫЙ ПОВОРОТ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ В ВОЛНОВОДЕ С ФЕРРИТОВЫМ РЕЗОНАТОРОМ
- 4.5. НЕЛИНЕЙНЫЙ ФЕРРИТОВЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ
- Ферритовый резонатор в линии передачи при запороговых уровнях мощности
- Нелинейный ферритовый резонатор в короткозамкнутой линии передачи
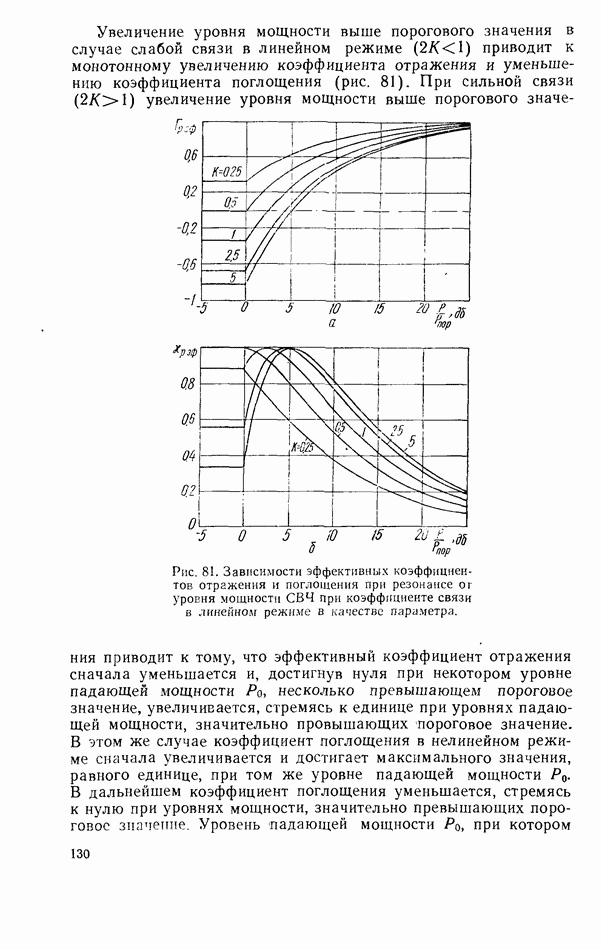
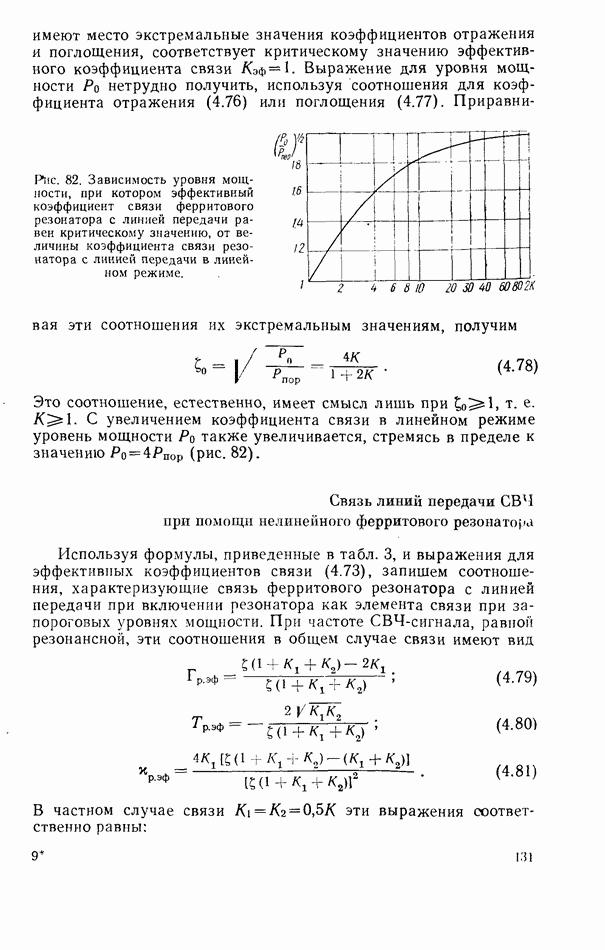
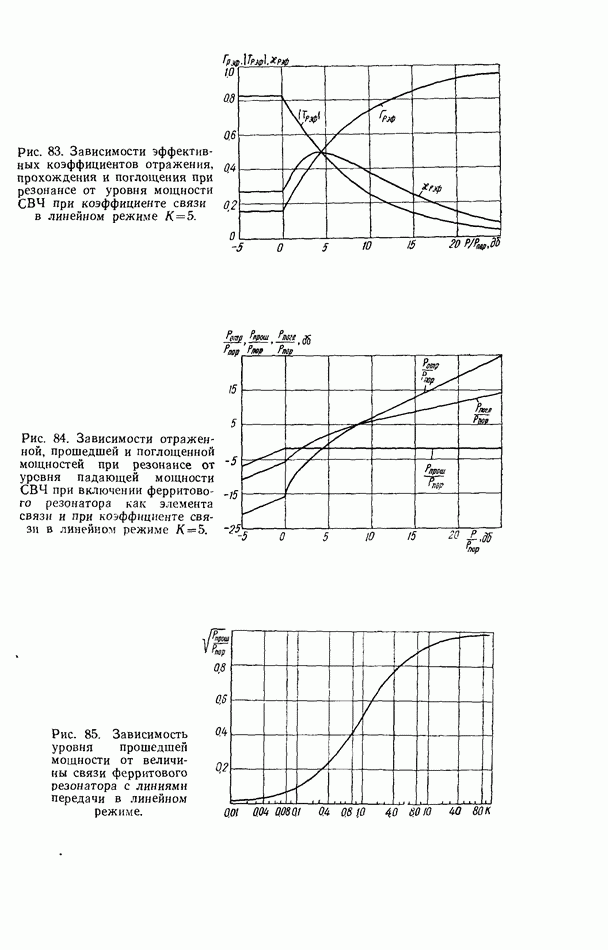
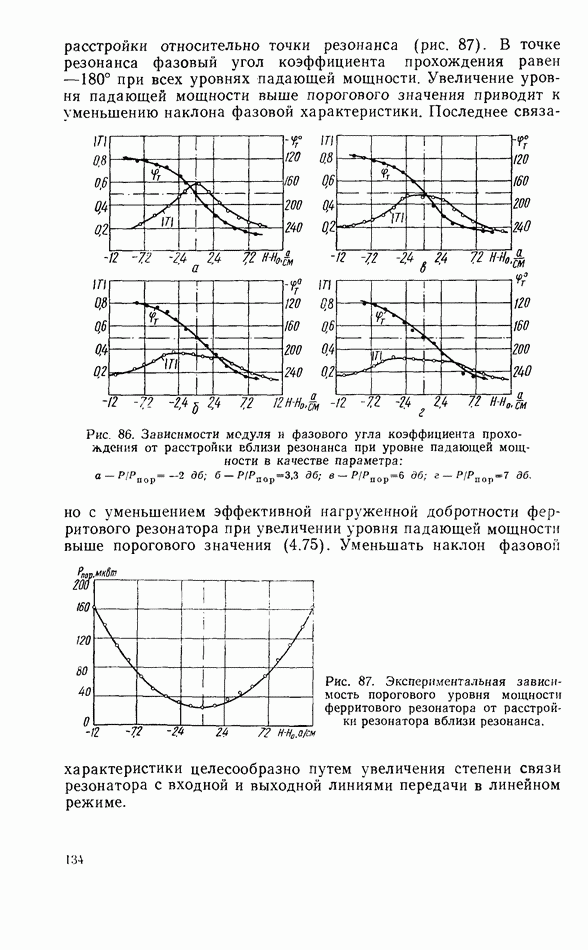
- Связь линий передачи СВЧ при помощи нелинейного ферритового резонатора
- Нелинейный ферритовый резонатор в согласованной линии передачи
- 4.6. СВЯЗЬ ДИЭЛЕКТРИЧЕСКОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ СВЧ
- Глава пятая. ПРИНЦИПЫ ПОСТРОЕНИЯ СВЧ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ И УСТРОЙСТВ НА ОСНОВЕ ТВЕРДОТЕЛЬНЫХ РЕЗОНАТОРОВ
- 5.2. ДАТЧИКИ УРОВНЯ МОЩНОСТИ СВЧ
- Волноводная измерительная головка
- Датчик фиксированного уровня пиковой мощности
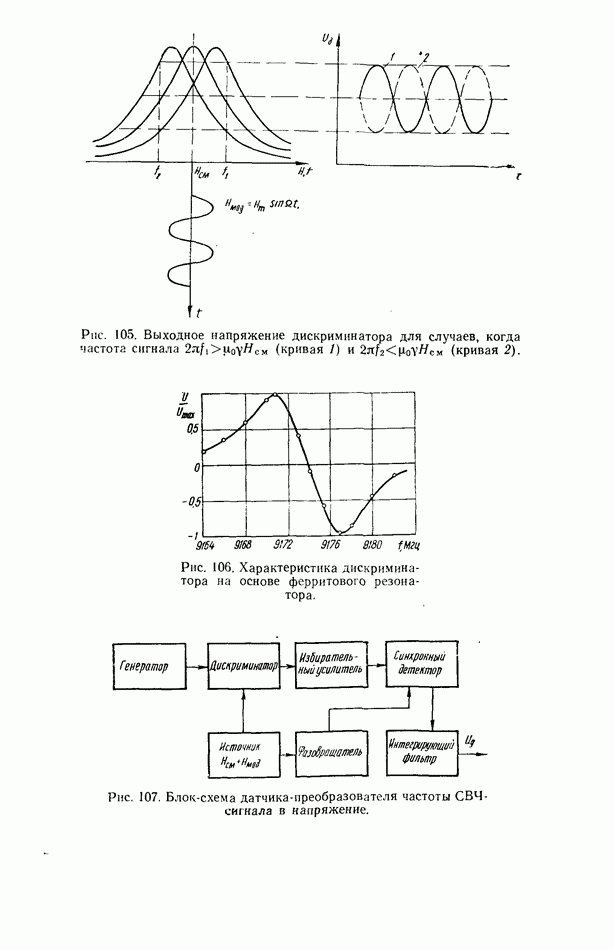
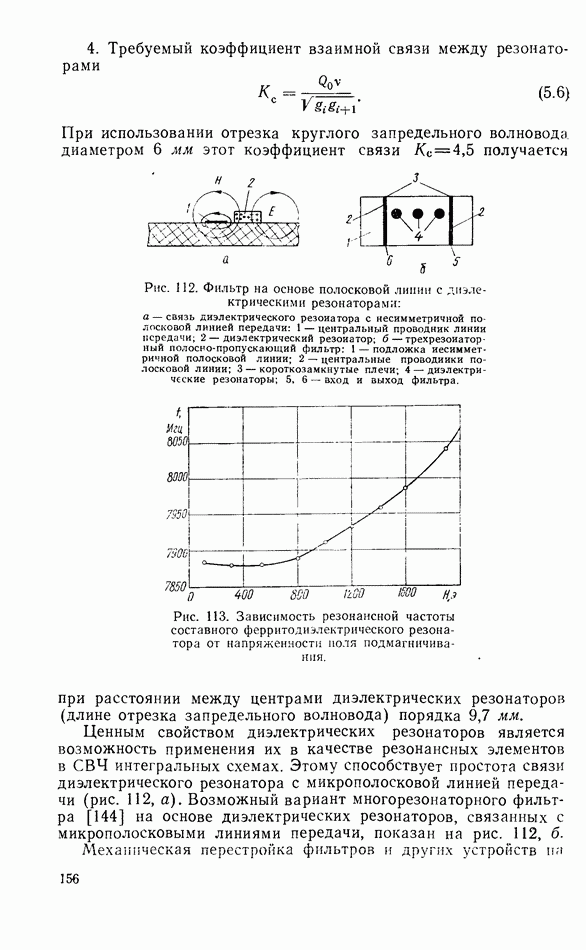
- 5.3. ЧАСТОТНЫЕ ДИСКРИМИНАТОРЫ С МАГНИТНОЙ НАСТРОЙКОЙ
- 5.4. РЕЗОНАНСНЫЕ ФАЗОВРАЩАТЕЛИ
- 5.5. УСТРОЙСТВО ДЛЯ РЕЗОНАНСНОГО ПОВОРОТА ПЛОСКОСТИ ПОЛЯРИЗАЦИИ В ВОЛНОВОДЕ
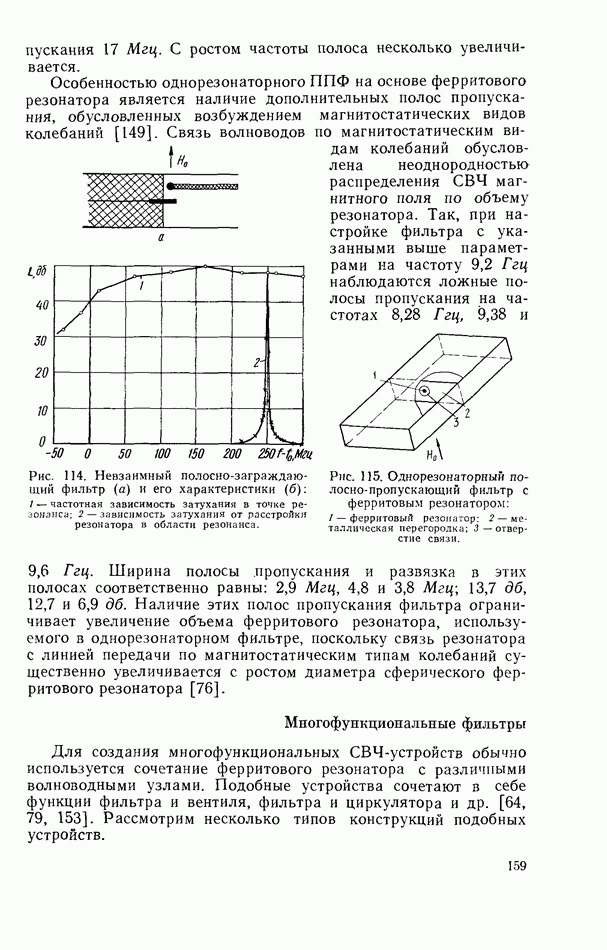
- 5.6. ФИЛЬТРЫ СВЧ НА ОСНОВЕ ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
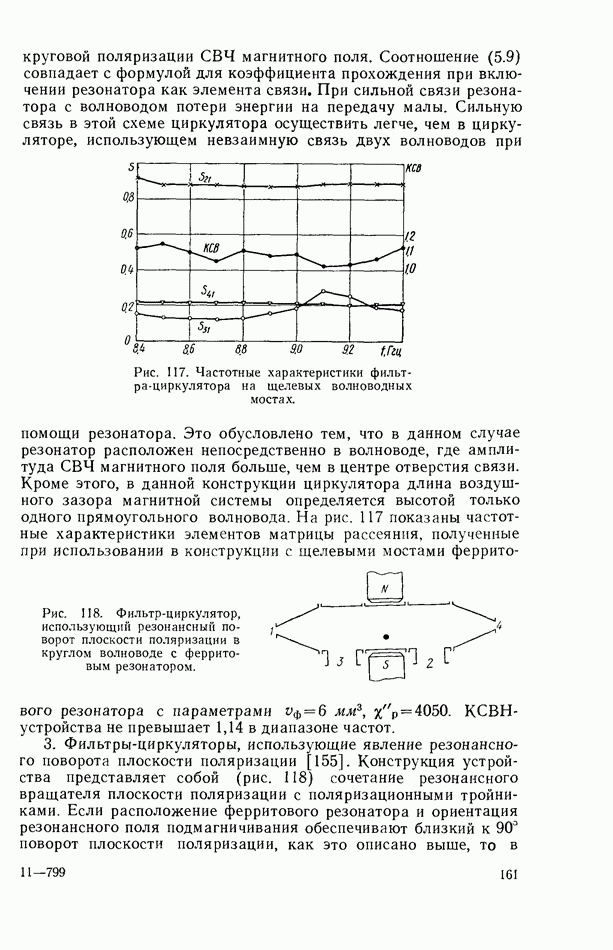
- 5.7. ФЕРРИТОВЫЕ СВЧ-ФИЛЬТРЫ
- Многофункциональные фильтры
- Многорезонаторные ферритовые фильтры
- 5.8. ЧАСТОТНО-ИЗБИРАТЕЛЬНЫЕ ОГРАНИЧИТЕЛИ МАЛЫХ УРОВНЕЙ МОЩНОСТИ