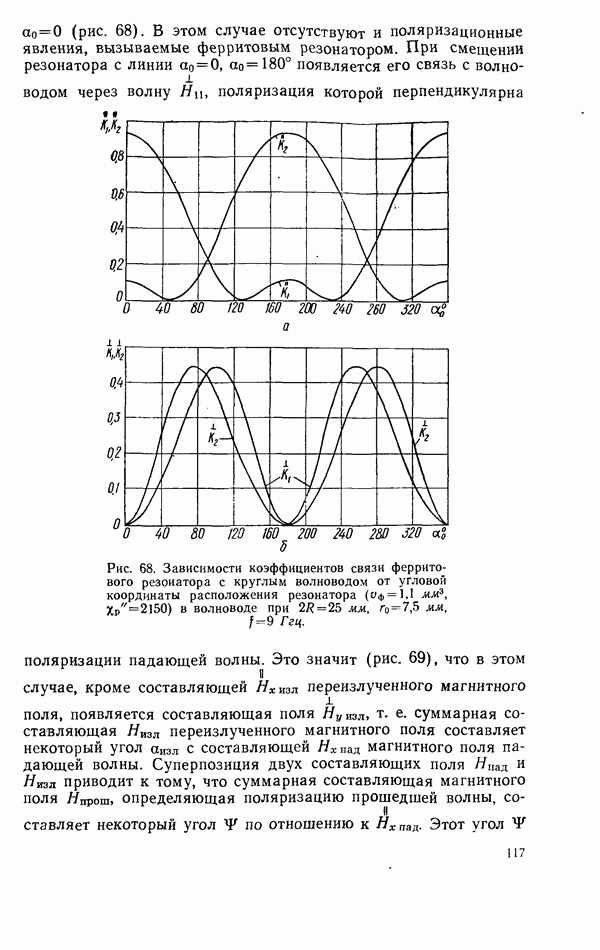
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
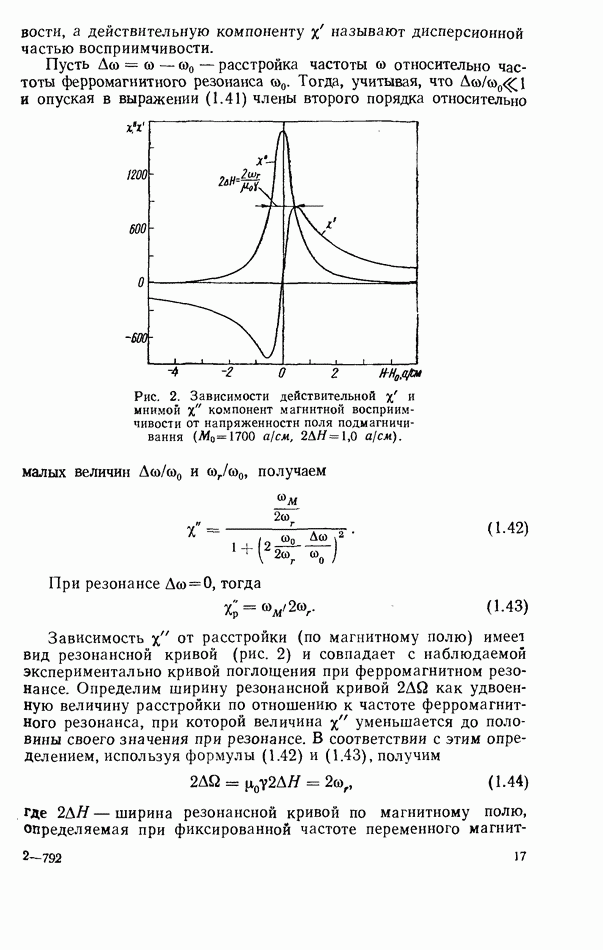
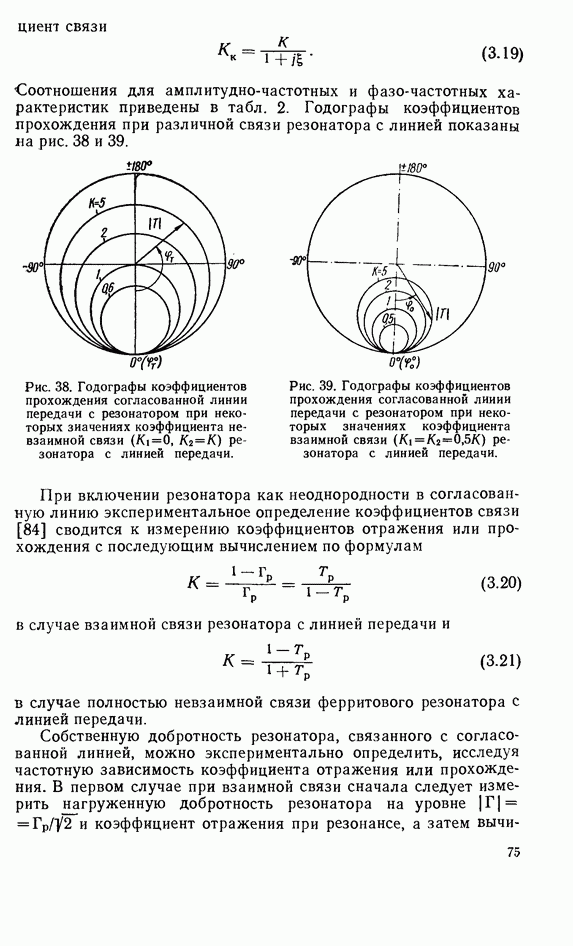
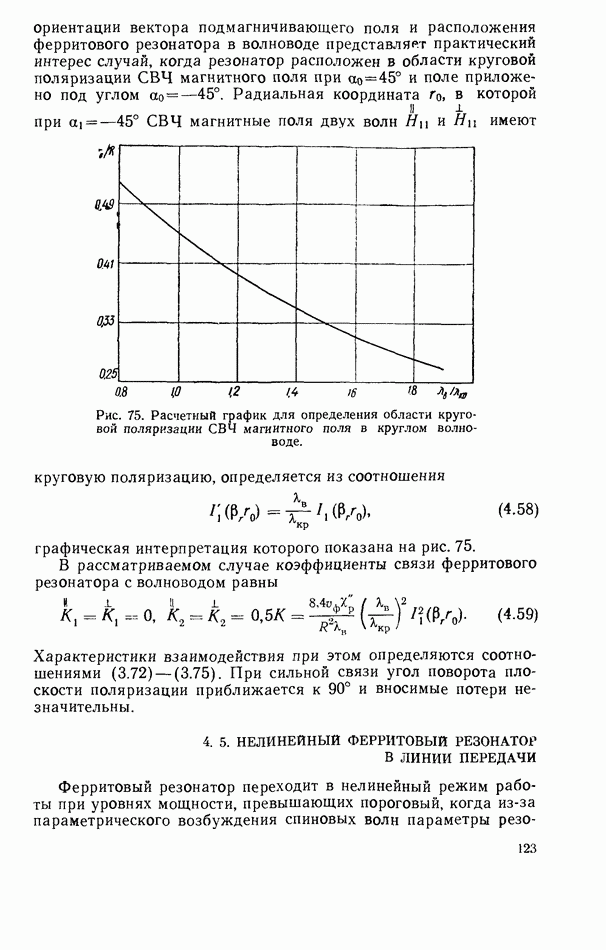
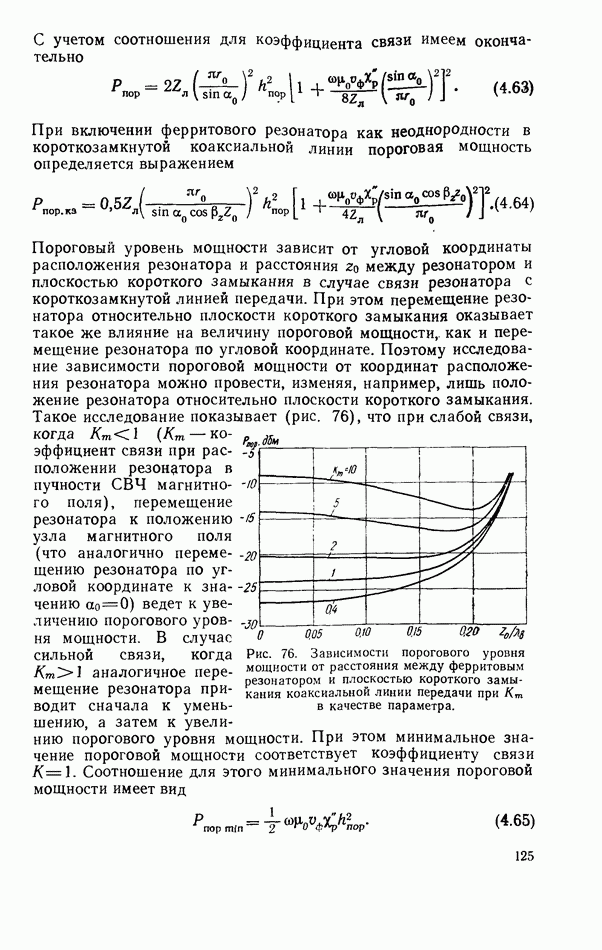
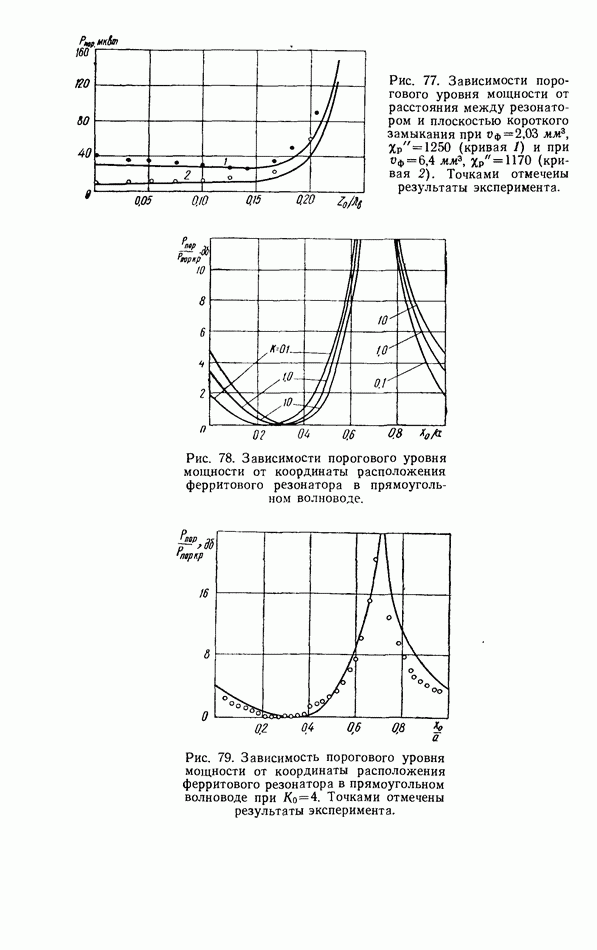
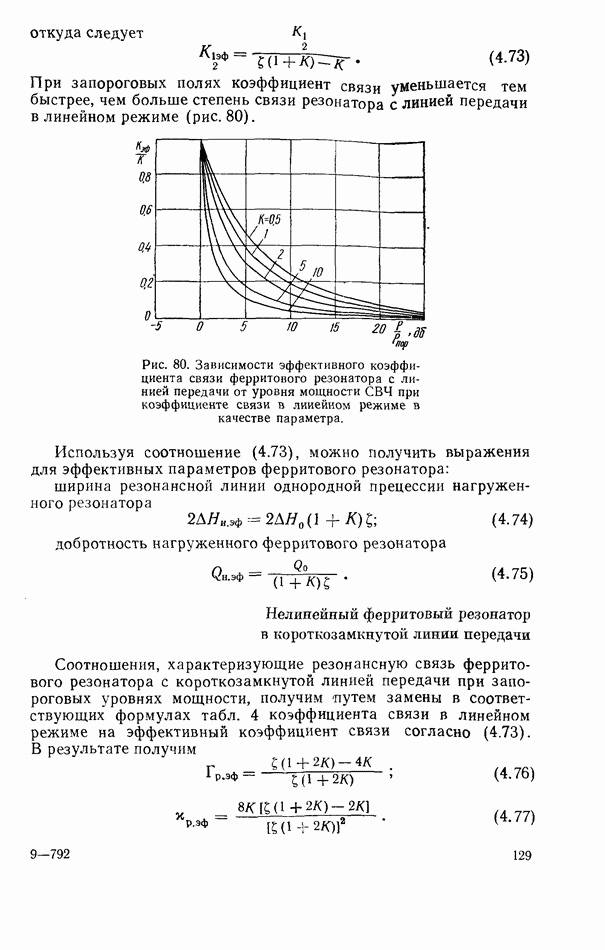
4.3. ФЕРРИТОВЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ ЗАМЕДЛЕННЫХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
Применение линий передачи замедленных электромагнитных волн в технике ферритовых резонаторов представляет практический интерес, поскольку позволяет решить следующие основные задачи:
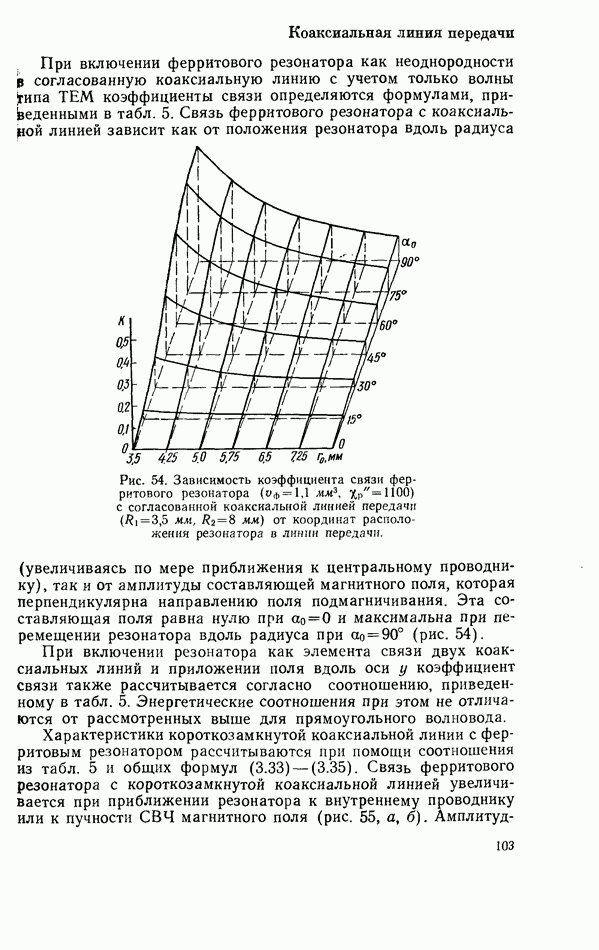
1. Увеличение связи резонатора с линией передачи. Обусловлено оно тем, что коэффициент связи обратно пропорционален длине волны в линии передачи. Решение этой задачи особенно важно при расширении рабочего диапазона частот устройств с ферритовыми резонаторами в сторону дециметровых волн.
2. Поскольку геометрические размеры линий передачи замедленных волн зачастую меньше размеров обычных линий передачи (в том же диапазоне частот), сочетание ферритовых резонаторов с этими линиями позволяет создать малогабаритные устройства.
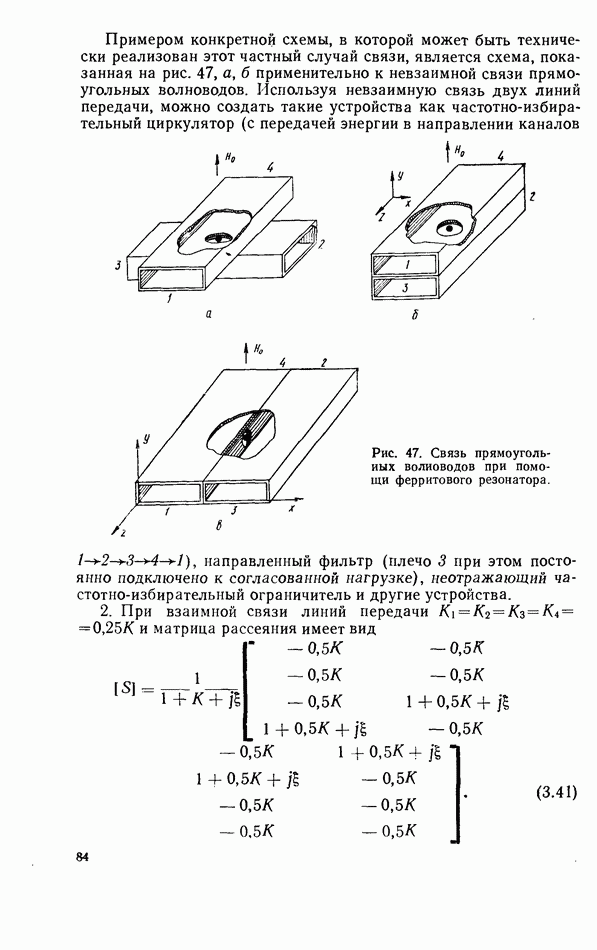
3. Очень часто применение линий передачи замедленных волн позволяет получить невзаимный характер взаимодействия ферритового резонатора с линией передачи, благодаря чему появляется возможность создания невзаимных устройств.
При применении ферритовых резонаторов представляют интерес следующие замедляющие структуры:
1. Передающие линии с периодической структурой. Эти системы наиболее распространены в технике СВЧ электронно-лучевых приборов с протяженным взаимодействием волны с электронным пучком. В последние годы передающие линии с периодической структурой применяются в сочетании с ферритовыми резонаторами [101].
2. Линии передачи, в которых используется заполнение пространства между проводниками линии диэлектриком с  Применение диэлектрических замедляющих систем открывает ряд важных возможностей. Рассмотрим этот вопрос более подробно.
Применение диэлектрических замедляющих систем открывает ряд важных возможностей. Рассмотрим этот вопрос более подробно.
При полном заполнении линии передачи диэлектриком задача анализа взаимодействия резонатора с такой линией не представляет затруднений, поскольку полученные выше соотношения для коэффициентов связи здесь применимы с учетом того, что длина волны в линии передачи, заполненной диэлектриком, уменьшается примерно в  раз. В случае, когда геометрические размеры линии остались такими же, как и до заполнения диэлектриком, и линия передачи осталась одноволновой, все коэффициенты связи резонатора с полностью заполненной линией передачи следует умножить на
раз. В случае, когда геометрические размеры линии остались такими же, как и до заполнения диэлектриком, и линия передачи осталась одноволновой, все коэффициенты связи резонатора с полностью заполненной линией передачи следует умножить на  Если же площадь поперечного сечения линии передачи уменьшена в
Если же площадь поперечного сечения линии передачи уменьшена в  раз, то коэффициенты связи следует увеличить в
раз, то коэффициенты связи следует увеличить в  раз по сравнению с незаполненной линией.
раз по сравнению с незаполненной линией.
При частичном заполнении линии передачи диэлектриком задача анализа взаимодействия ферритового резонатора с линией становится несколько более громоздкой. Однако ее решение представляет интерес в связи с некоторыми возможностями практического применения.
Рассмотрим более подробно особенности связи ферритового резонатора с некоторыми линиями передачи, частично заполненными диэлектриком, а также вопросы инженерного расчета этих систем.
Ферритовый резонатор в Н-образном металлодиэлектрическом волноводе
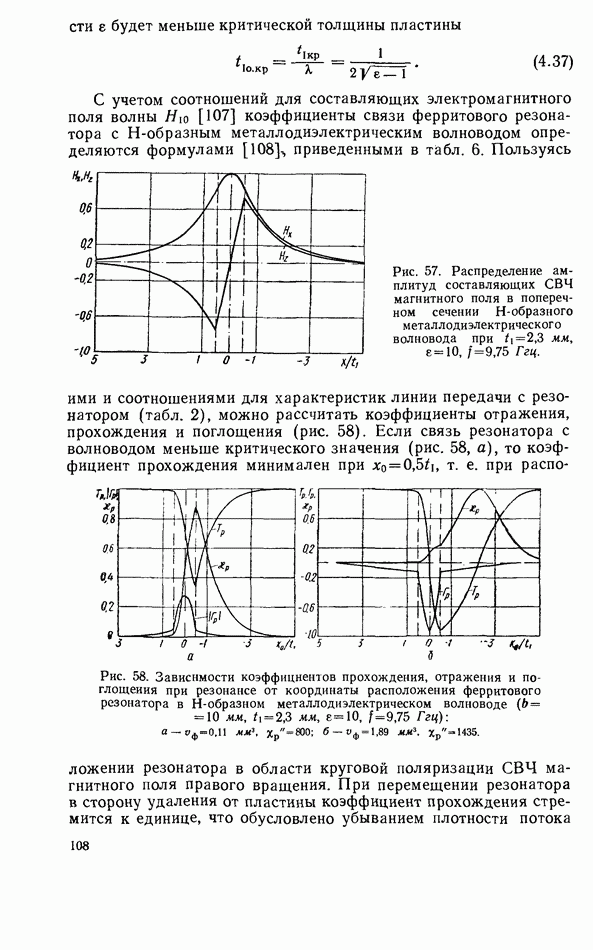
Н-Образный металлодиэлектрический волновод представляет собой плоскопараллельную линию передачи СВЧ с частичным диэлектрическим заполнением (верхний рисунок в табл. 6). Этот волновод был предметом исследования в ряде работ [102—105] и является, вообще говоря, наиболее подходящим для использования в миллиметровом диапазоне волн [104, 105]. Однако если использовать для центральной секции диэлектрик с очень большой диэлектрической проницаемостью, можно получить волновод с весьма малым эффективным поперечным сечением распространения. Такой Н-волновод с малым поперечным сечением пригоден для использования в миниатюрных конструкциях с низкими потерями на низких частотах СВЧ-диапазона [106]. На рис. 57 показано типичное распределение поля в поперечном сечении волновода для основной волны типа  оптимальной для таких трактов. При изменении размеров диэлектрической пластины до
оптимальной для таких трактов. При изменении размеров диэлектрической пластины до  (только воздух) или до
(только воздух) или до  (только диэлектрик) происходит трансформация волны
(только диэлектрик) происходит трансформация волны  в волну типа ТЕМ с длиной волны соответственно
в волну типа ТЕМ с длиной волны соответственно  Ниже будем рассматривать только волну типа
Ниже будем рассматривать только волну типа  соблюдая при этом условия одноволновости волновода, которые сводятся к тому, что расстояние между металлическими плоскостями всегда будет меньше
соблюдая при этом условия одноволновости волновода, которые сводятся к тому, что расстояние между металлическими плоскостями всегда будет меньше  и толщина диэлектрической пластины при заданной проницаемости
и толщина диэлектрической пластины при заданной проницаемости
 будет меньше критической толщины пластины
будет меньше критической толщины пластины

С учетом соотношений для составляющих электромагнитного поля волны  коэффициенты связи ферритового резонатора с Н-образным металлодиэлектрическим волноводом определяются формулами [108], приведенными в табл. 6.
коэффициенты связи ферритового резонатора с Н-образным металлодиэлектрическим волноводом определяются формулами [108], приведенными в табл. 6.

Рис. 57. Распределение амплитуд составляющих СВЧ магнитного поля в поперечном сечении Н-образного металлодиэлектрического волновода при 
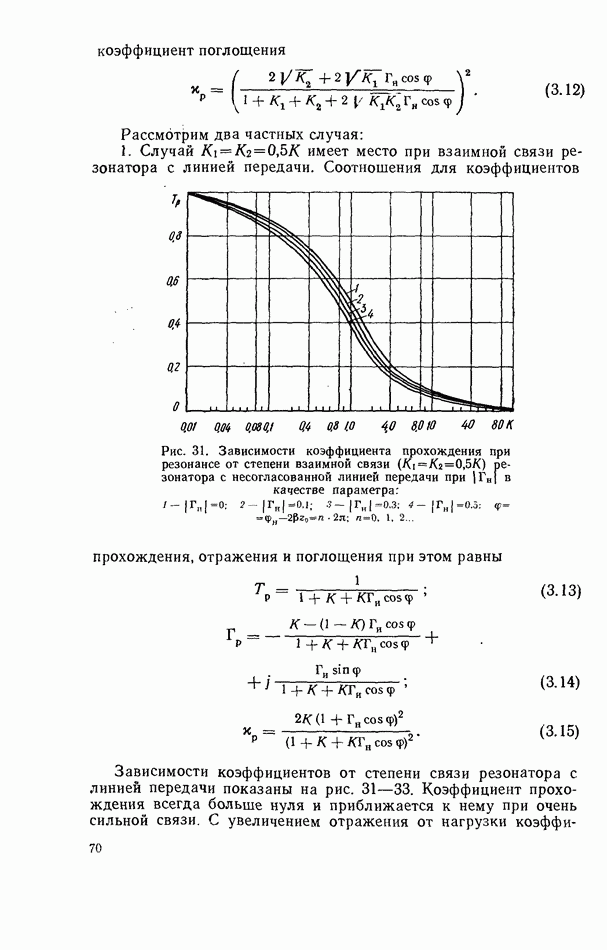
Пользуясь ими и соотношениями для характеристик линии передачи с резонатором (табл. 2), можно рассчитать коэффициенты отражения, прохождения и поглощения (рис. 58). Если связь резонатора с волноводом меньше критического значения (рис. 58, а), то коэффициент прохождения минимален при  т. е. при расположении резонатора в области круговой поляризации СВЧ магнитного поля правого вращения.
т. е. при расположении резонатора в области круговой поляризации СВЧ магнитного поля правого вращения.

Рис. 58. Зависимости коэффициентов прохождения, отражения и поглощения при резонансе от координаты расположения ферритового резонатора в Н-образном металлодиэлектрическом волноводе 
При перемещении резонатора в сторону удаления от пластины коэффициент прохождения стремится к единице, что обусловлено убыванием плотности потока
электромагнитной энергии по мере удаления от пластины. При перемещении резонатора от координаты  в сторону диэлектрической пластины коэффициент прохождения увеличивается, стремясь также к значению, равному 1. Коэффициент поглощения максимален при размещении резонатора в области круговой поляризации
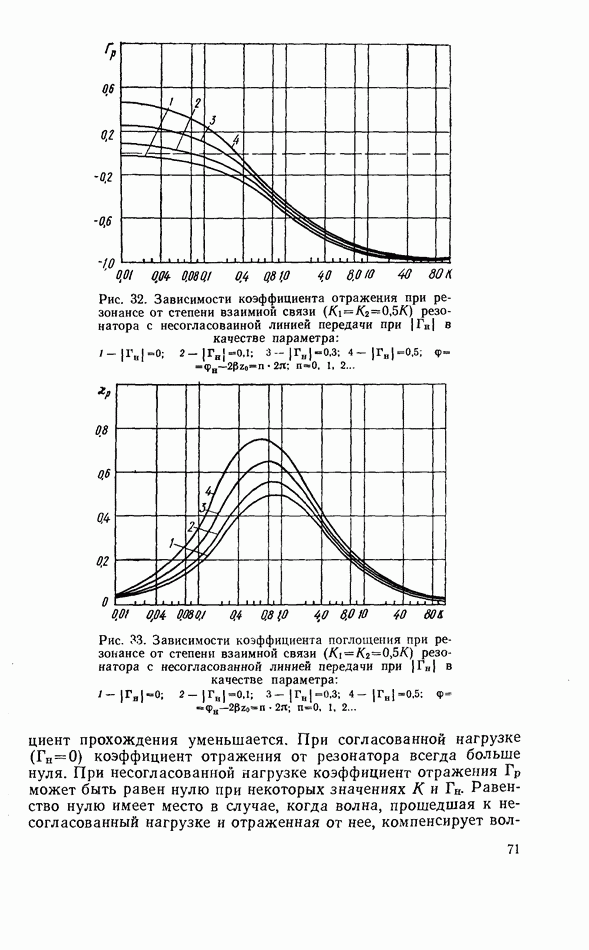
в сторону диэлектрической пластины коэффициент прохождения увеличивается, стремясь также к значению, равному 1. Коэффициент поглощения максимален при размещении резонатора в области круговой поляризации  Коэффициент отражения максимален при расположении резонатора по центру диэлектрической пластины, т. е. в области линейной поляризации СВЧ магнитного поля.
Коэффициент отражения максимален при расположении резонатора по центру диэлектрической пластины, т. е. в области линейной поляризации СВЧ магнитного поля.
В случае, если связь резонатора с волноводом больше критического значения (рис. 58, б), коэффициент прохождения при перемещении резонатора в поперечном сечении волновода равен нулю в двух координатах, где выполняется условие  Между этими координатами коэффициент прохождения изменяет свой знак на противоположный, что обусловлено выбором связи резонатора с линией передачи больше критического значения. Коэффициент поглощения максимален при выполнении условия
Между этими координатами коэффициент прохождения изменяет свой знак на противоположный, что обусловлено выбором связи резонатора с линией передачи больше критического значения. Коэффициент поглощения максимален при выполнении условия  вне диэлектрической пластины.
вне диэлектрической пластины.
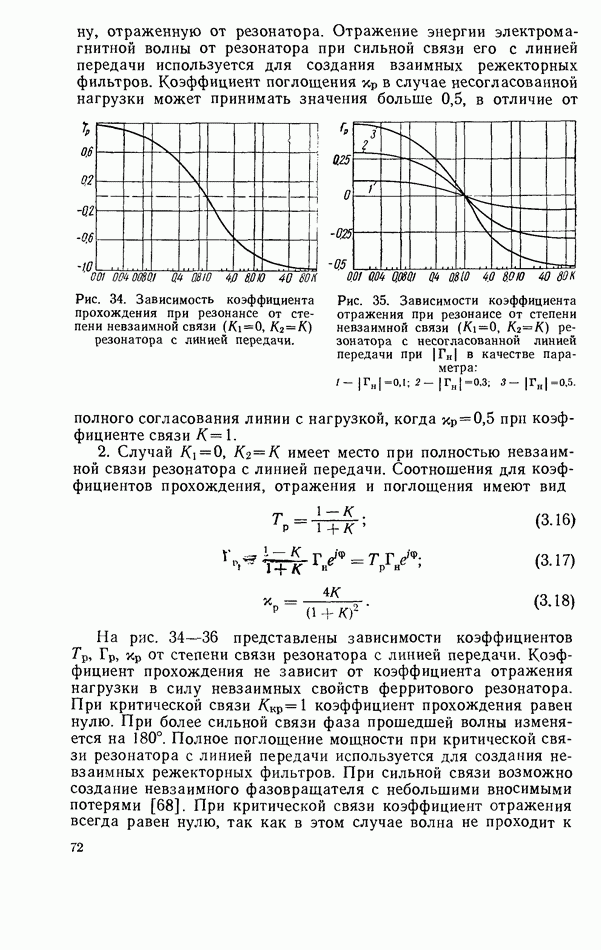
Для ряда практических применений важно отсутствие отражения электромагнитной энергии от резонатора. Известно, что это имеет место при расположении резонатора в области круговой поляризации СВЧ магнитного поля. Из проведенного анализа следует, что в рассматриваемом случае приложения магнитного поля вдоль оси у при расположении резонатора  полностью невзаимная связь достигается при значительном увеличении диэлектрической проницаемости пластины, когда
полностью невзаимная связь достигается при значительном увеличении диэлектрической проницаемости пластины, когда

Осуществление полностью невзаимной связи ферритового резонатора с волноводом для применяемых обычно значений диэлектрической проницаемости пластины возможно при приложении поля подмагничивания под некоторым углом в плоскости  с тем, чтобы величина поперечной составляющей СВЧ магнитного поля, перпендикулярная к направлению поля подмагничивания, стала равной продольной составляющей поля. Оптимальный для осуществления невзаимной связи угол приложения поля подмагничивания определяется соотношением
с тем, чтобы величина поперечной составляющей СВЧ магнитного поля, перпендикулярная к направлению поля подмагничивания, стала равной продольной составляющей поля. Оптимальный для осуществления невзаимной связи угол приложения поля подмагничивания определяется соотношением

В расчетные соотношения для коэффициентов связи входят волновые числа и длина волны в Н-образном металлодиэлектрическом волноводе. Эти параметры определяются следующими соотношениями:
волновые числа

длина волны в волноводе


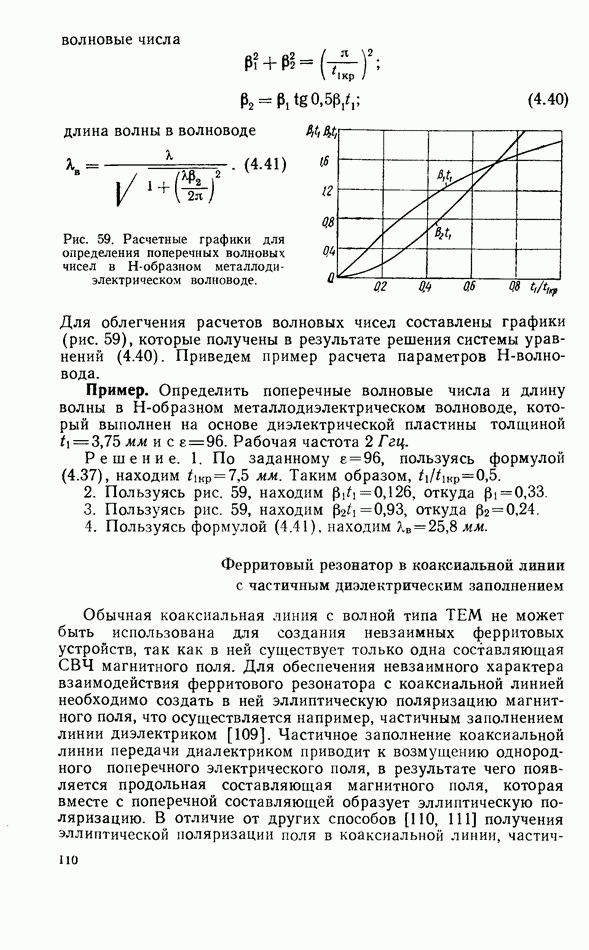
Рис. 59. Расчетные графики для определения поперечных волновых чисел в Н-образном металлодиэлектрическом волноводе.
Для облегчения расчетов волновых чисел составлены графики (рис. 59), которые получены в результате решения системы уравнений (4.40). Приведем пример расчета параметров Н-волно-вода.
Пример. Определить поперечные волновые числа и длину волны в Н-образном металлодиэлектрическом волноводе, который выполнен на основе диэлектрической пластины толщиной  Рабочая частота
Рабочая частота 
Решение. 1. По заданному  пользуясь формулой (4.37), находим
пользуясь формулой (4.37), находим  Таким образом,
Таким образом, 
2. Пользуясь рис. 59, находим  откуда
откуда 
3. Пользуясь рис. 59, находим  откуда
откуда 
4. Пользуясь формулой (4.41), находим 
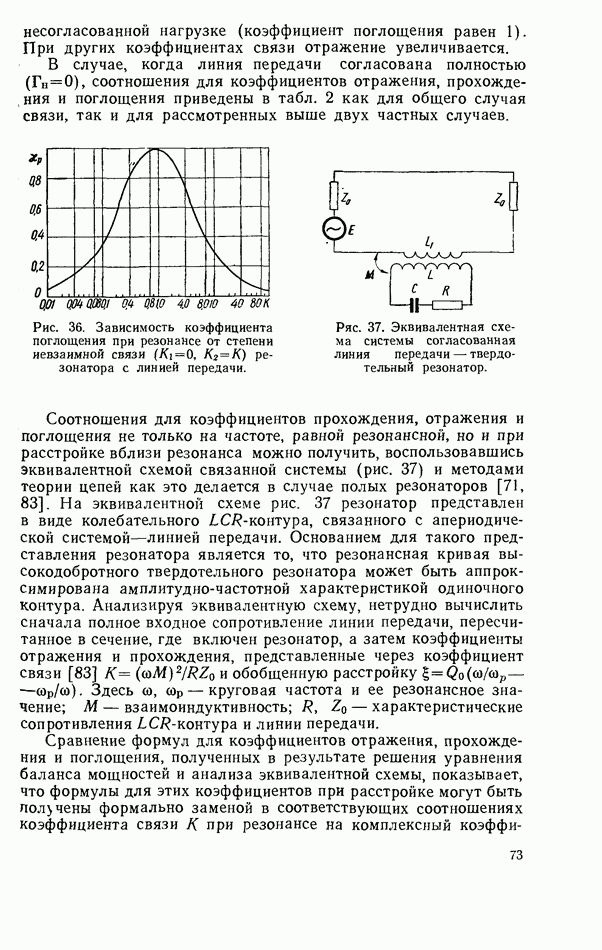
Ферритовый резонатор в коаксиальной линии с частичным диэлектрическим заполнением
Обычная коаксиальная линия с волной типа ТЕМ не может быть использована для создания невзаимных ферритовых устройств, так как в ней существует только одна составляющая СВЧ магнитного поля. Для обеспечения невзаимного характера взаимодействия ферритового резонатора с коаксиальной линией необходимо создать в ней эллиптическую поляризацию магнитного поля, что осуществляется например, частичным заполнением линии диэлектриком [109]. Частичное заполнение коаксиальной линии передачи диэлектриком приводит к возмущению однородного поперечного электрического поля, в результате чего появляется продольная составляющая магнитного поля, которая вместе с поперечной составляющей образует эллиптическую поляризацию. В отличие от других способов  получения эллиптической поляризации поля в коаксиальной линии,
получения эллиптической поляризации поля в коаксиальной линии,
частичное заполнение линии передачи приводит также к замедлению электромагнитной волны и, следовательно, к увеличению связи ферритового резонатора с линией передачи.
При исследовании взаимодействия ферритового резонатора с коаксиальной линией, частично заполненной диэлектриком, удобно представить [112] коаксиальную линию в виде плоско-параллельной линии с периодическим расположением диэлектрических слоев (рис. 60).
При этом период  плоско-параллельного аналога равен длине средней окружности
плоско-параллельного аналога равен длине средней окружности  поперечного сечения коаксиала.
поперечного сечения коаксиала.
Коэффициент заполнения диэлектриком коаксиальной линии и ее аналога равен


Рис. 60. Ферритовый резонатор в коаксиальной линии передачи, частично заполненной диэлектриком (а), и плоско-параллельиый аналог системы: частично заполненная диэлектриком коаксиальная линия — ферритовый резонатор (б).
Из всех возможных типов волн плоско-параллельного аналога [113] будем рассматривать лишь Н-волну основного типа. Используя выражения для составляющих поля этой волны и учитывая, что угловой координате а в коаксиале соответствует величина  в ее аналоге,
в ее аналоге,  , нетрудно получить [114] соотношения для коэффициентов связи резонатора с линией передачи (табл. 6).
, нетрудно получить [114] соотношения для коэффициентов связи резонатора с линией передачи (табл. 6).
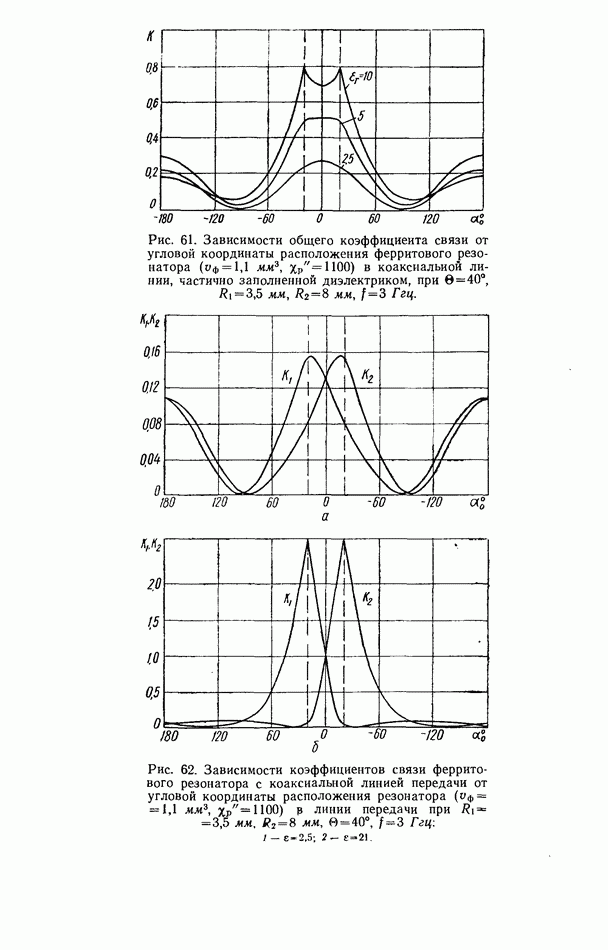
При увеличении  наблюдается увеличение общего коэффициента связи резонатора с линией передачи (рис. 61), определяемое параметрами диэлектрического заполнения
наблюдается увеличение общего коэффициента связи резонатора с линией передачи (рис. 61), определяемое параметрами диэлектрического заполнения  и координатой расположения резонатора в линии передачи.
и координатой расположения резонатора в линии передачи.
Степень невзаимной связи резонатора с коаксиальной линией можно оценить, исследуя зависимости частных коэффициентов связи от перемещения резонатора по угловой координате (рис. 62). Различие коэффициентов связи свидетельствует о невзаимности системы. При  оно незначительно, что обусловлено слабым возмущением электрического поля волны ТЕМ диэлектрическим слоем. В случае, когда диэлектрическая проницаемость слоя равна
оно незначительно, что обусловлено слабым возмущением электрического поля волны ТЕМ диэлектрическим слоем. В случае, когда диэлектрическая проницаемость слоя равна  различие коэффициентов связи значительно сильнее. При этом также имеются координаты, в которых коэффициент связи
различие коэффициентов связи значительно сильнее. При этом также имеются координаты, в которых коэффициент связи  может быть равен нулю при
может быть равен нулю при

(кликните для просмотра скана)
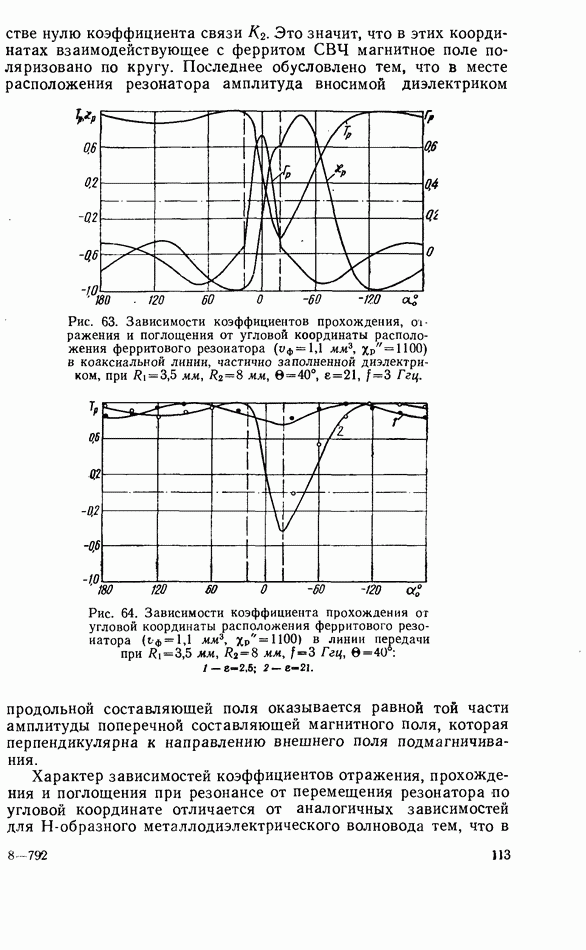
неравенстве нулю коэффициента связи  Это значит, что в этих координатах взаимодействующее с ферритом СВЧ магнитное поле поляризовано по кругу. Последнее обусловлено тем, что в месте расположения резонатора амплитуда вносимой диэлектриком продольной составляющей поля оказывается равной той части амплитуды поперечной составляющей магнитного поля, которая перпендикулярна к направлению внешнего поля подмагничивания.
Это значит, что в этих координатах взаимодействующее с ферритом СВЧ магнитное поле поляризовано по кругу. Последнее обусловлено тем, что в месте расположения резонатора амплитуда вносимой диэлектриком продольной составляющей поля оказывается равной той части амплитуды поперечной составляющей магнитного поля, которая перпендикулярна к направлению внешнего поля подмагничивания.

Рис. 63. Зависимости коэффициентов прохождения, отражения и поглощения от угловой координаты расположения ферритового резонатора  в коаксиальной линии, частично заполненной диэлектриком, при
в коаксиальной линии, частично заполненной диэлектриком, при 

Рис. 64. Зависимости коэффициента прохождения от угловой координаты расположения ферритового резонатора  в линии передачи при
в линии передачи при 
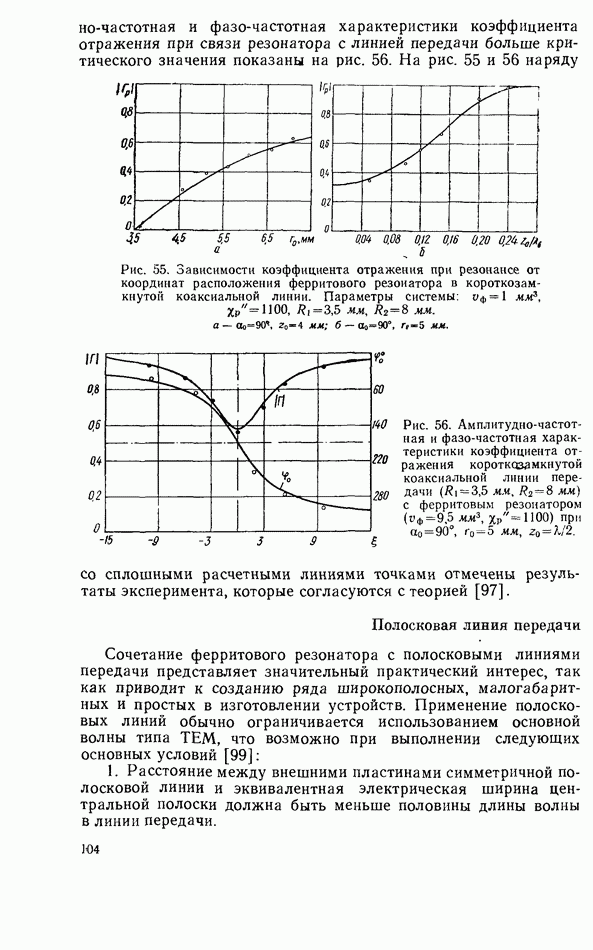
Характер зависимостей коэффициентов отражения, прохождения и поглощения при резонансе от перемещения резонатора по угловой координате отличается от аналогичных зависимостей для Н-образного металлодиэлектрического волновода тем, что в
данном случае существуют координаты, при расположении в которых ферритового резонатора коэффициент отражения равен нулю (рис. 63).
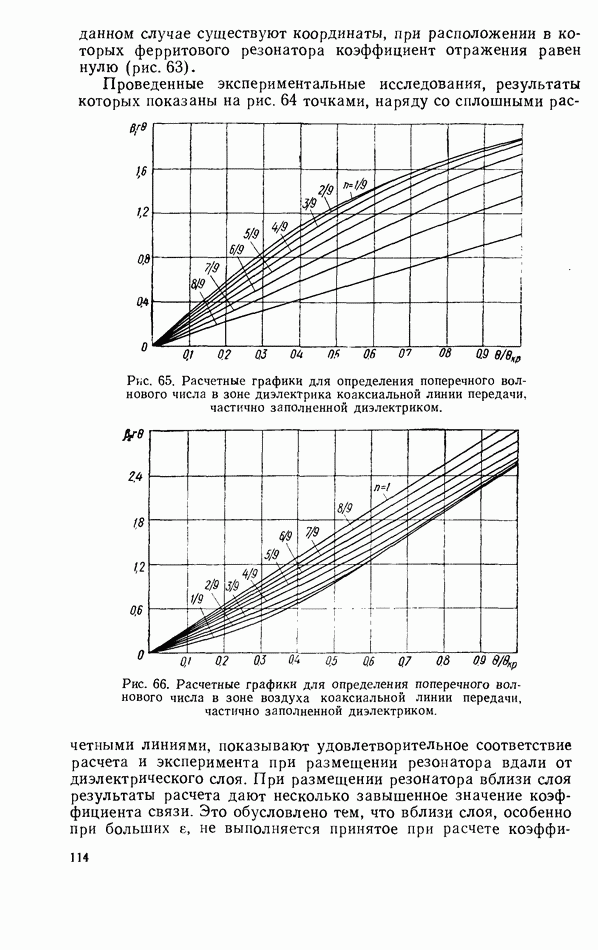
Проведенные экспериментальные исследования, результаты которых показаны на рис. 64 точками, наряду со сплошными расчетными линиями, показывают удовлетворительное соответствие расчета и эксперимента при размещении резонатора вдали от диэлектрического слоя.

Рис. 65. Расчетные графики для определения поперечного волнового числа в зоне диэлектрика коаксиальной линии передачи, частично заполненной диэлектриком.

Рис. 66. Расчетные графики для определения поперечного волнового числа в зоне воздуха коаксиальной линии передачи, частично заполненной диэлектриком.
При размещении резонатора вблизи слоя результаты расчета дают несколько завышенное значение коэффициента связи. Это обусловлено тем, что вблизи слоя, особенно при больших  не выполняется принятое при расчете
не выполняется принятое при расчете
коэффициентов связи предположение, которое касается однородности СВЧ магнитного поля по объему ферритового резонатора. Нарушение однородности поля особенно существенно при больших  и создает условия для возбуждения в резонаторе магнитостатических видов колебаний. В большинстве случаев это в основном и ограничивает увеличение
и создает условия для возбуждения в резонаторе магнитостатических видов колебаний. В большинстве случаев это в основном и ограничивает увеличение 
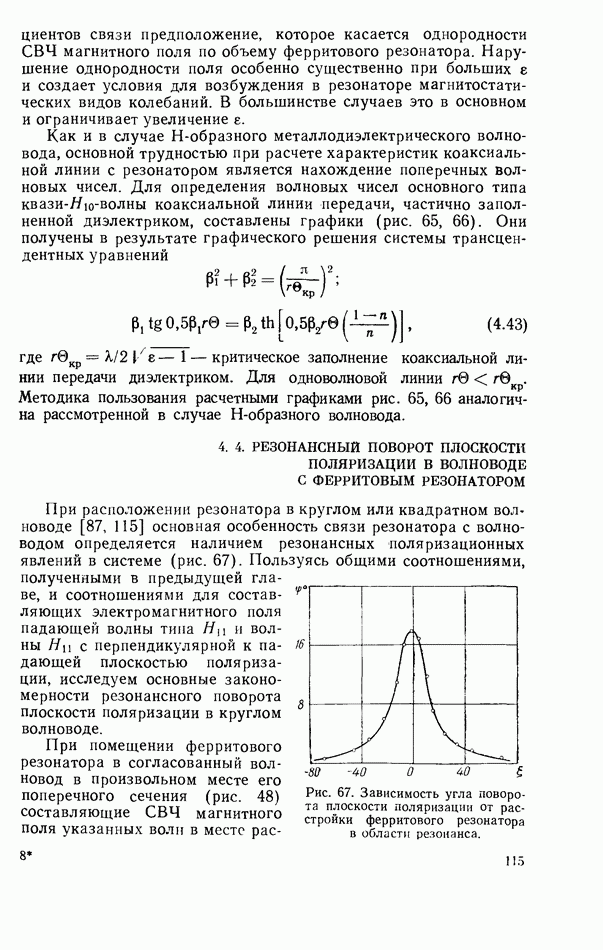
Как и в случае Н-образного металлодиэлектрического волновода, основной трудностью при расчете характеристик коаксиальной линии с резонатором является нахождение поперечных волновых чисел. Для определения волновых чисел основного типа квази-Н-волны коаксиальной линии передачи, частично заполненной диэлектриком, составлены графики (рис. 65, 66). Они получены в результате графического решения системы трансцендентных уравнений

где  критическое заполнение коаксиальной линии передачи диэлектриком. Для одноволновой линии
критическое заполнение коаксиальной линии передачи диэлектриком. Для одноволновой линии  Методика пользования расчетными графиками рис. 65, 66 аналогична рассмотренной в случае Н-образного волновода.
Методика пользования расчетными графиками рис. 65, 66 аналогична рассмотренной в случае Н-образного волновода.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава первая. СВОЙСТВА ФЕРРИТОВЫХ РЕЗОНАТОРОВ
- Ферромагнитный резонанс в неограниченной среде без потерь
- 1.2. РЕЗОНАНСНАЯ ЧАСТОТА
- Зависимость резонансной частоты от формы резонатора
- Влияние кристаллографической анизотропии на резонансную частоту
- 1.3. МАГНИТОСТАТИЧЕСКИЕ ВИДЫ КОЛЕБАНИЙ
- 1.4. УЧЕТ ПОТЕРЬ
- 1.5. ДИПОЛЬНЫЙ МОМЕНТ
- 1.6. НЕЛИНЕЙНЫЕ ЯВЛЕНИЯ
- Спиновые волны
- Пороговая амплитуда высокочастотного магнитного поля
- Восприимчивость при амплитудах поля, превышающих пороговое значение
- 1.7. ПРИМЕНЯЕМЫЕ ДЛЯ ИЗГОТОВЛЕНИЯ МАТЕРИАЛЫ
- 1.8. ТЕМПЕРАТУРНЫЕ ХАРАКТЕРИСТИКИ
- 1.9. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- Глава вторая. СВОЙСТВА ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 2.2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В АНИЗОТРОПНОМ ДИЭЛЕКТРИЧЕСКОМ СТЕРЖНЕ С «МАГНИТНЫМИ» БОКОВЫМИ СТЕНКАМИ
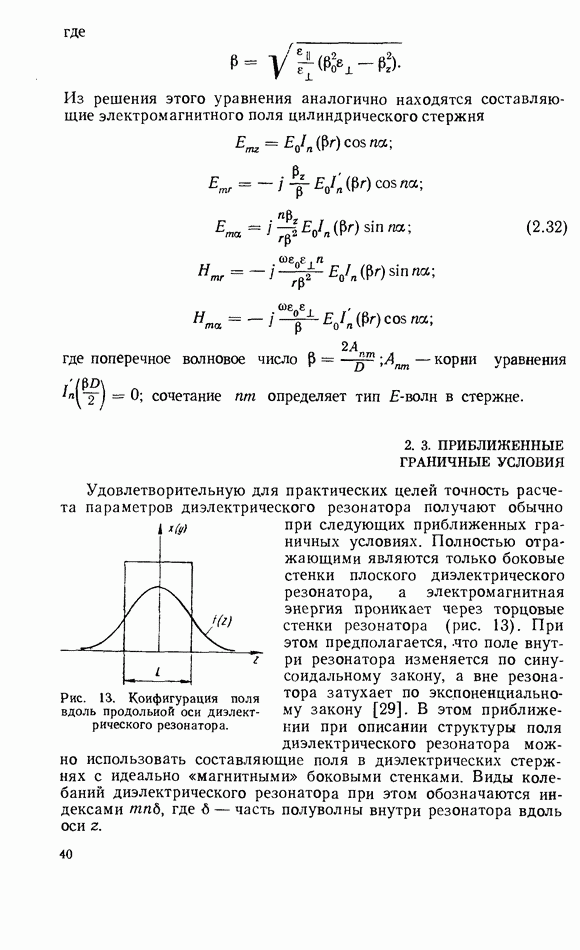
- 2.3. ПРИБЛИЖЕННЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2.5. ОСНОВНЫЕ ВИДЫ КОЛЕБАНИЙ
- 2.6. СФЕРИЧЕСКИЕ ДИЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
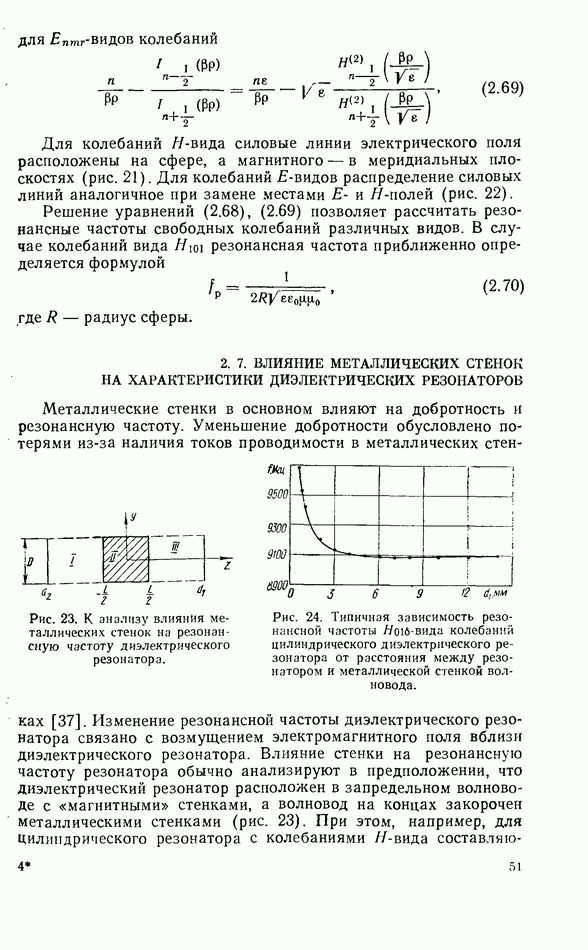
- 2.7. ВЛИЯНИЕ МЕТАЛЛИЧЕСКИХ СТЕНОК НА ХАРАКТЕРИСТИКИ ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 2.8. ДИПОЛЬНЫЙ МОМЕНТ
- 2.9. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ
- 2.10. СООТНОШЕНИЕ МЕЖДУ АМПЛИТУДАМИ СВЧ МАГНИТНОГО ПОЛЯ
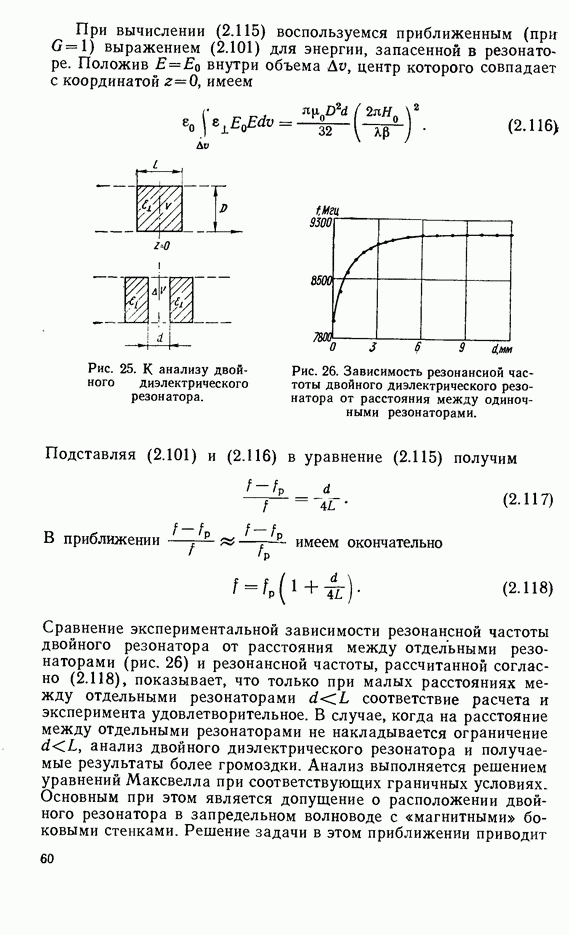
- 2.11. ДВОЙНЫЕ ДИЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
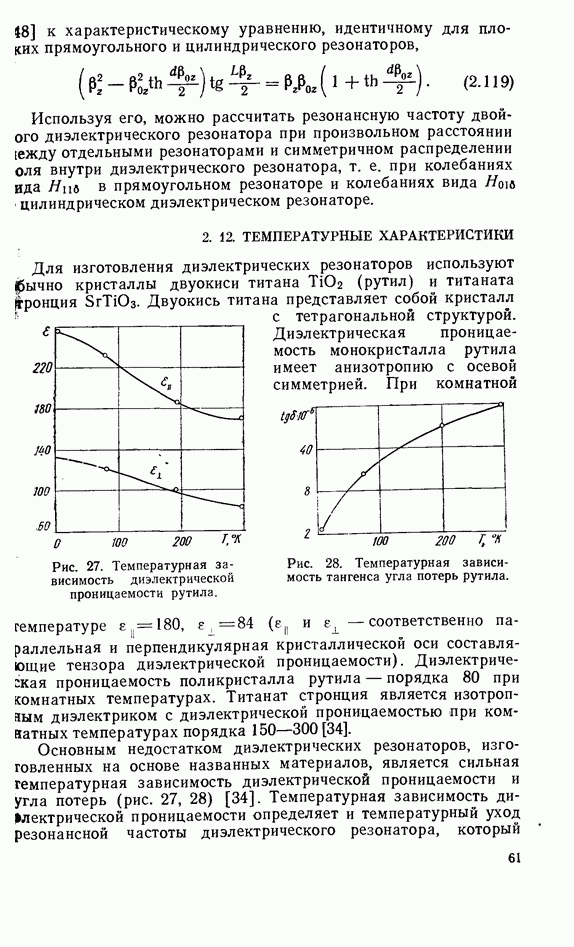
- 2.12. ТЕМПЕРАТУРНЫЕ ХАРАКТЕРИСТИКИ
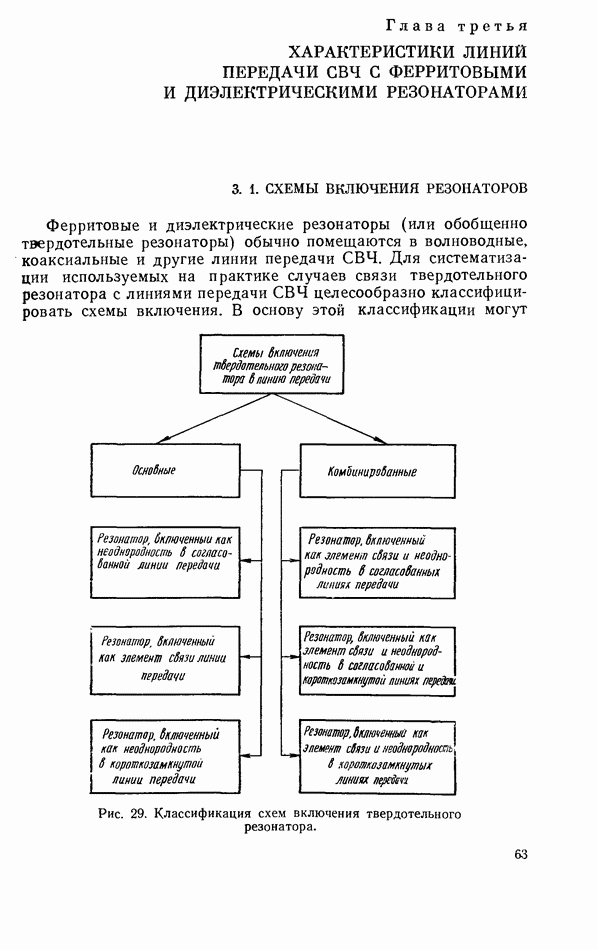
- Глава третья. ХАРАКТЕРИСТИКИ ЛИНИЙ ПЕРЕДАЧИ СВЧ С ФЕРРИТОВЫМИ И ДИЭЛЕКТРИЧЕСКИМИ РЕЗОНАТОРАМИ
- 3.2. МЕТОДЫ РАСЧЕТА СВЧ-СХЕМ С ТВЕРДОТЕЛЬНЫМИ РЕЗОНАТОРАМИ
- 3.3. СВЯЗЬ ТВЕРДОТЕЛЬНОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ СВЧ
- 3.4. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В НЕСОГЛАСОВАННОЙ ЛИНИИ ПЕРЕДАЧИ
- 3.5. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР, ВКЛЮЧЕННЫЙ КАК ЭЛЕМЕНТ СВЯЗИ ЛИНИЙ ПЕРЕДАЧИ
- 3.6. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В КОРОТКОЗАМКНУТОЙ ЛИНИИ ПЕРЕДАЧИ
- 3.7. КОМБИНИРОВАННЫЕ СХЕМЫ ВКЛЮЧЕНИЯ ТВЕРДОТЕЛЬНОГО РЕЗОНАТОРА
- 3.8. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ С НЕСКОЛЬКИМИ РАСПРОСТРАНЯЮЩИМИСЯ ВОЛНАМИ
- Глава четвертая. СВЯЗЬ ТВЕРДОТЕЛЬНЫХ РЕЗОНАТОРОВ С ЛИНИЯМИ ПЕРЕДАЧИ СВЧ
- 4.2. СВЯЗЬ ФЕРРИТОВОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ
- 4.3. ФЕРРИТОВЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ ЗАМЕДЛЕННЫХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
- 4.4. РЕЗОНАНСНЫЙ ПОВОРОТ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ В ВОЛНОВОДЕ С ФЕРРИТОВЫМ РЕЗОНАТОРОМ
- 4.5. НЕЛИНЕЙНЫЙ ФЕРРИТОВЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ
- Ферритовый резонатор в линии передачи при запороговых уровнях мощности
- Нелинейный ферритовый резонатор в короткозамкнутой линии передачи
- Связь линий передачи СВЧ при помощи нелинейного ферритового резонатора
- Нелинейный ферритовый резонатор в согласованной линии передачи
- 4.6. СВЯЗЬ ДИЭЛЕКТРИЧЕСКОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ СВЧ
- Глава пятая. ПРИНЦИПЫ ПОСТРОЕНИЯ СВЧ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ И УСТРОЙСТВ НА ОСНОВЕ ТВЕРДОТЕЛЬНЫХ РЕЗОНАТОРОВ
- 5.2. ДАТЧИКИ УРОВНЯ МОЩНОСТИ СВЧ
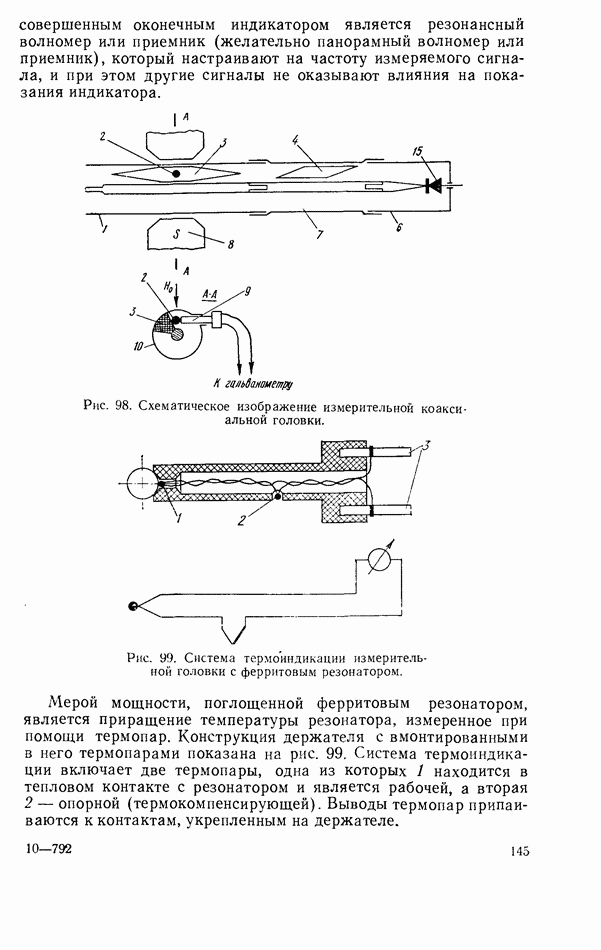
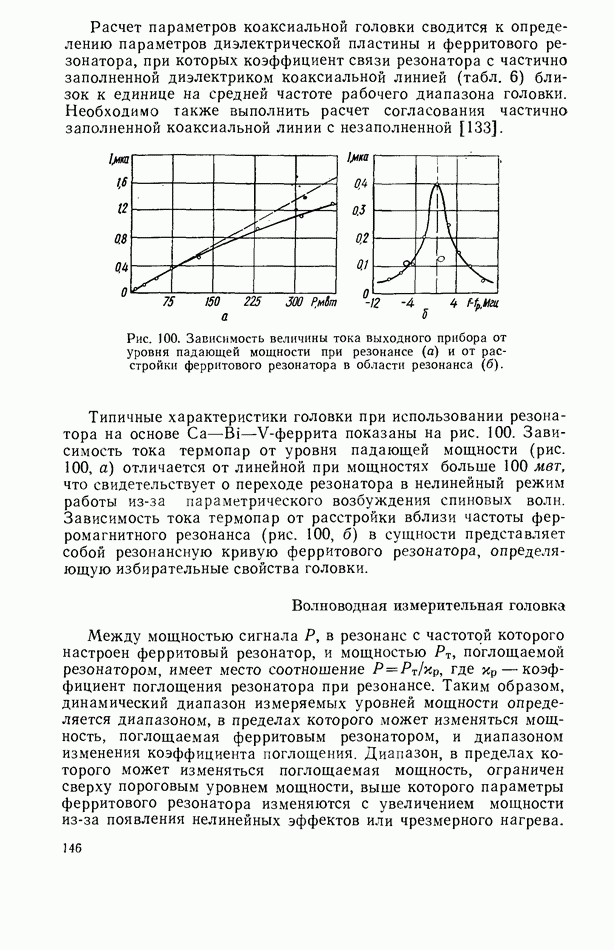
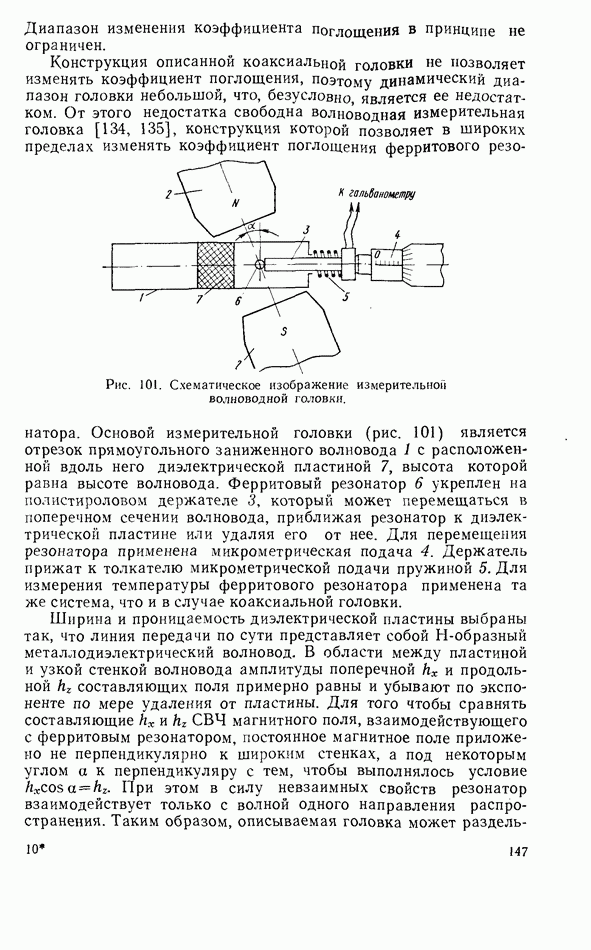
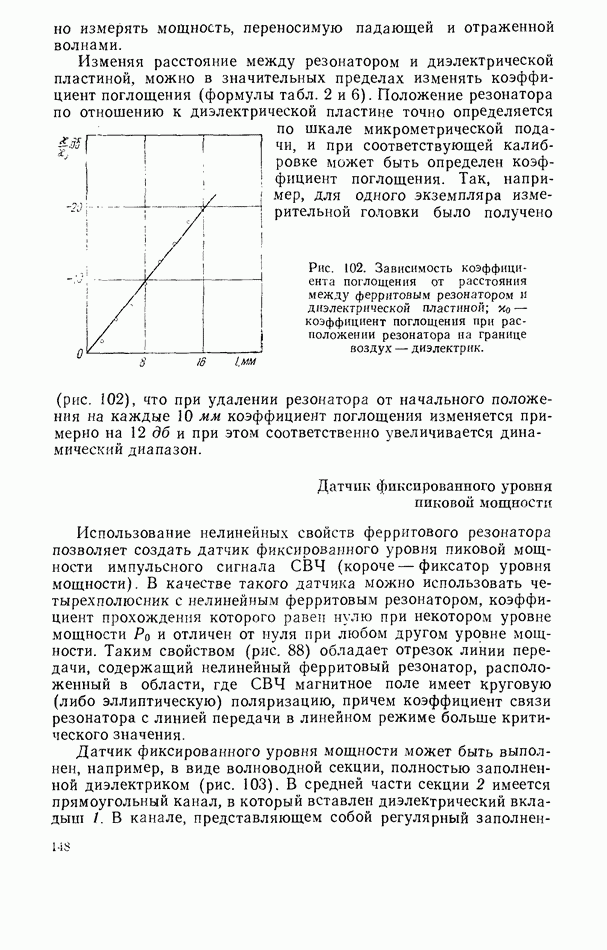
- Волноводная измерительная головка
- Датчик фиксированного уровня пиковой мощности
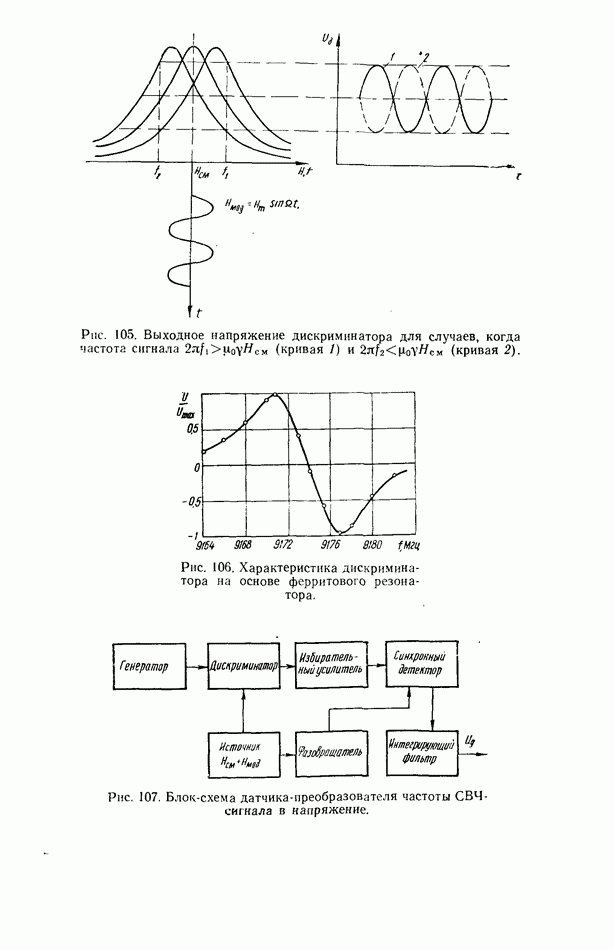
- 5.3. ЧАСТОТНЫЕ ДИСКРИМИНАТОРЫ С МАГНИТНОЙ НАСТРОЙКОЙ
- 5.4. РЕЗОНАНСНЫЕ ФАЗОВРАЩАТЕЛИ
- 5.5. УСТРОЙСТВО ДЛЯ РЕЗОНАНСНОГО ПОВОРОТА ПЛОСКОСТИ ПОЛЯРИЗАЦИИ В ВОЛНОВОДЕ
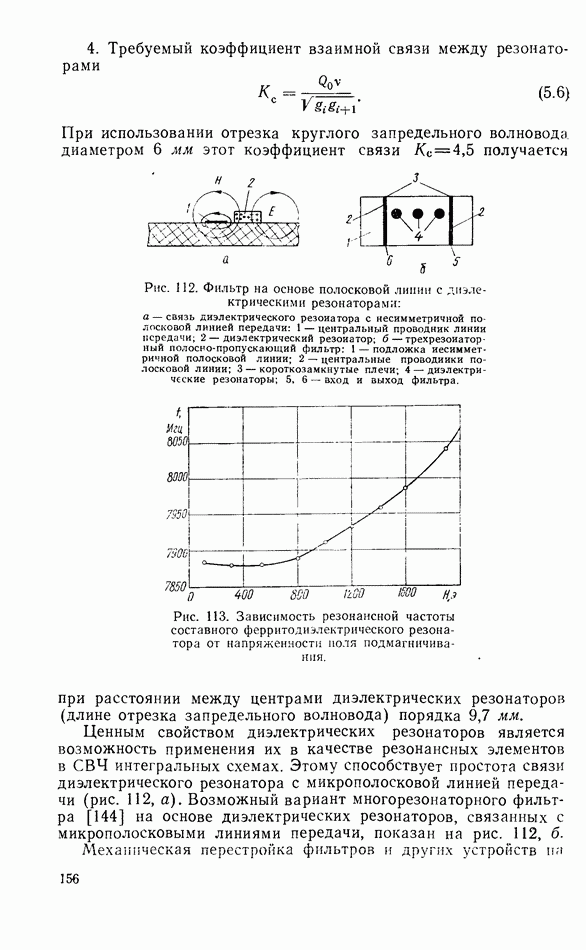
- 5.6. ФИЛЬТРЫ СВЧ НА ОСНОВЕ ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
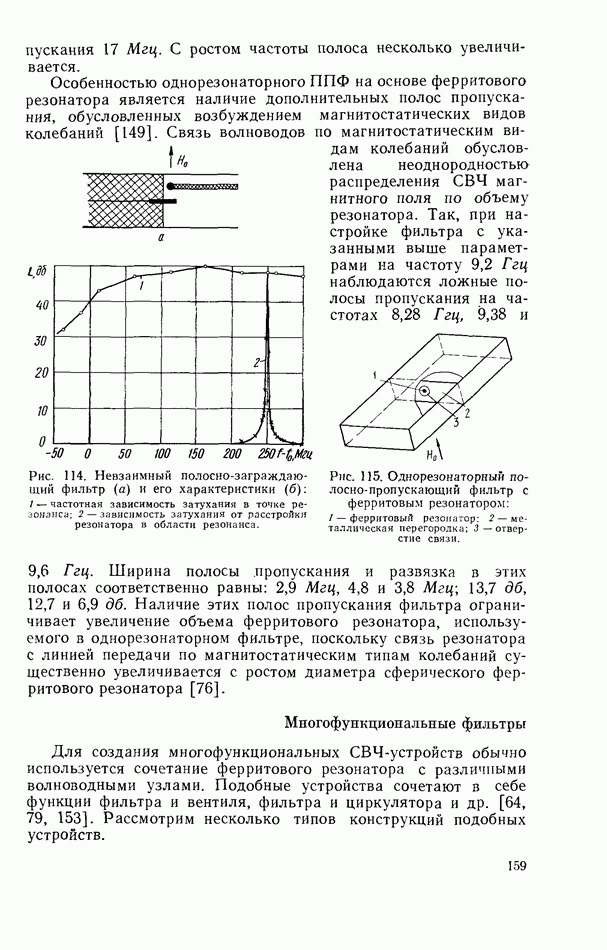
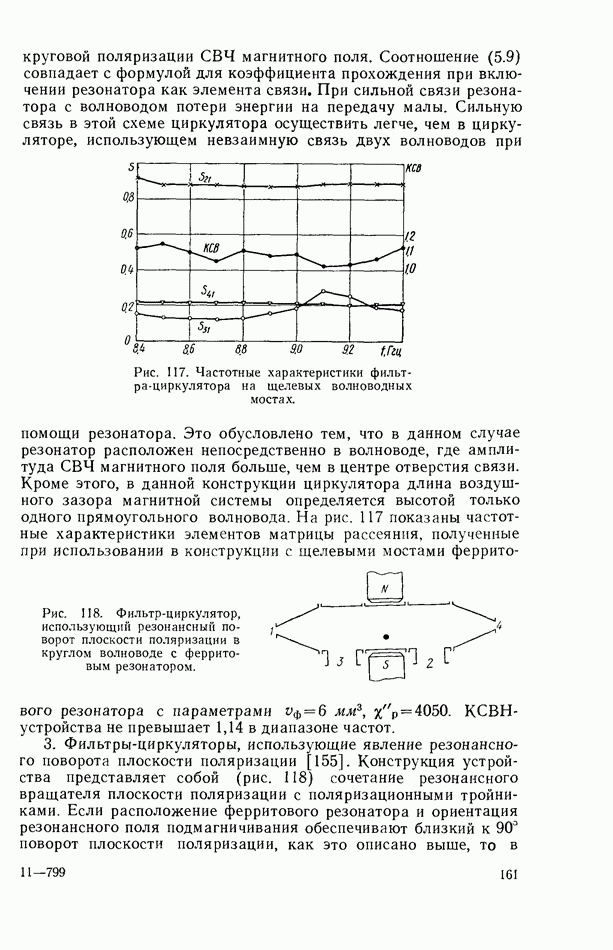
- 5.7. ФЕРРИТОВЫЕ СВЧ-ФИЛЬТРЫ
- Многофункциональные фильтры
- Многорезонаторные ферритовые фильтры
- 5.8. ЧАСТОТНО-ИЗБИРАТЕЛЬНЫЕ ОГРАНИЧИТЕЛИ МАЛЫХ УРОВНЕЙ МОЩНОСТИ