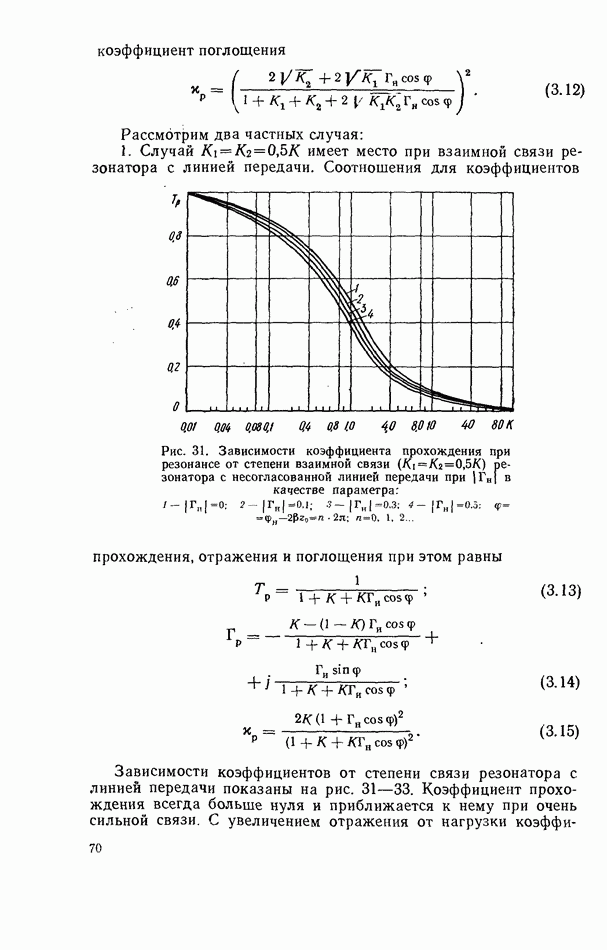
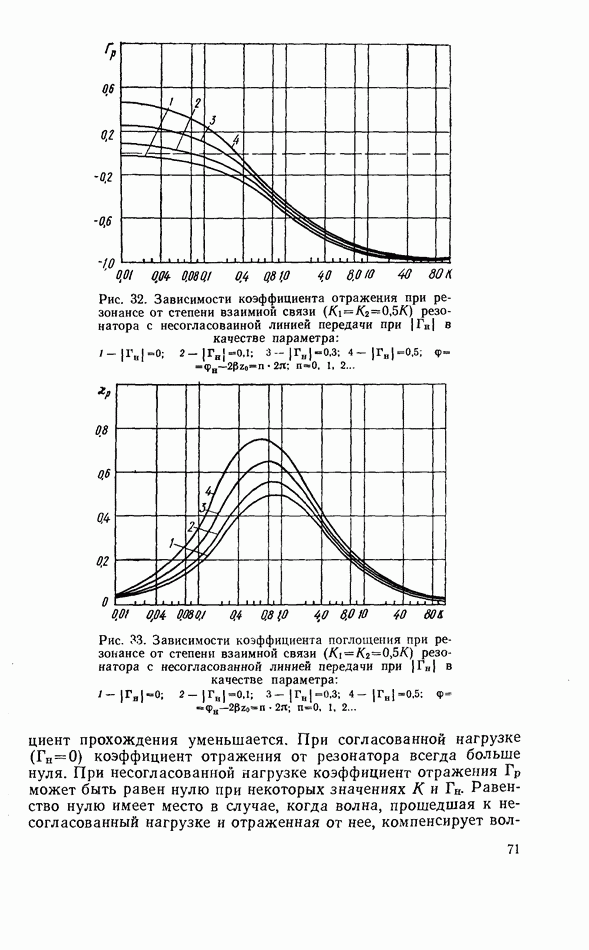
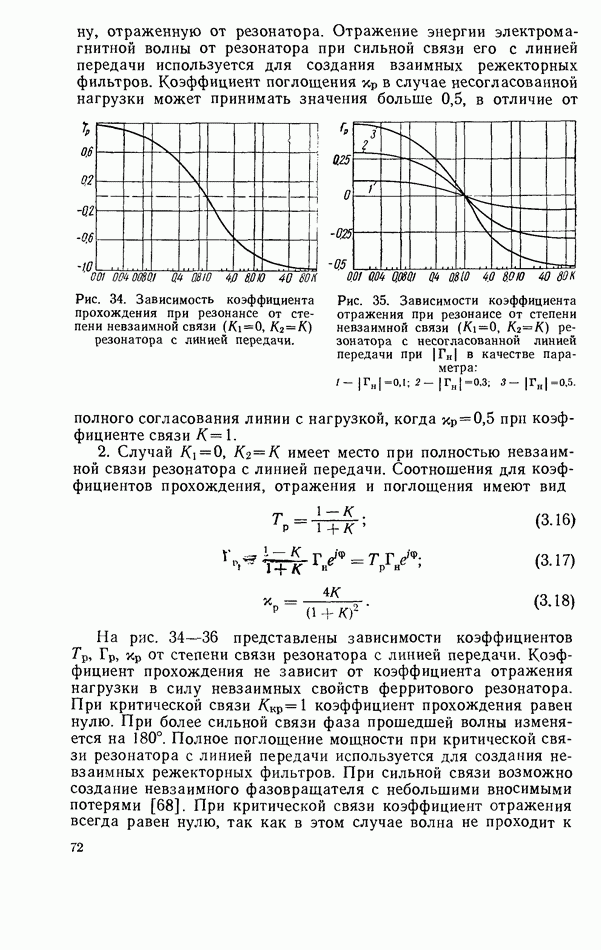
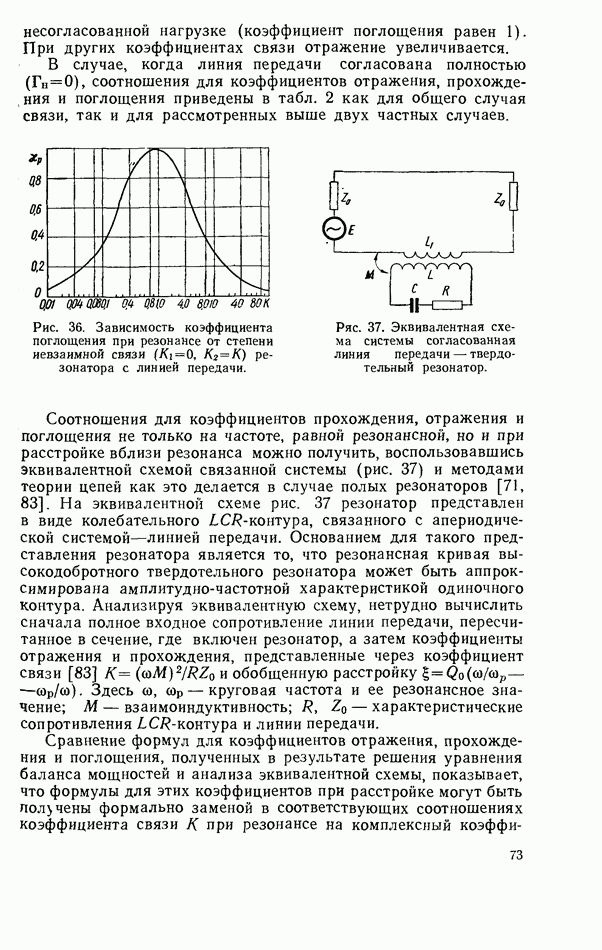
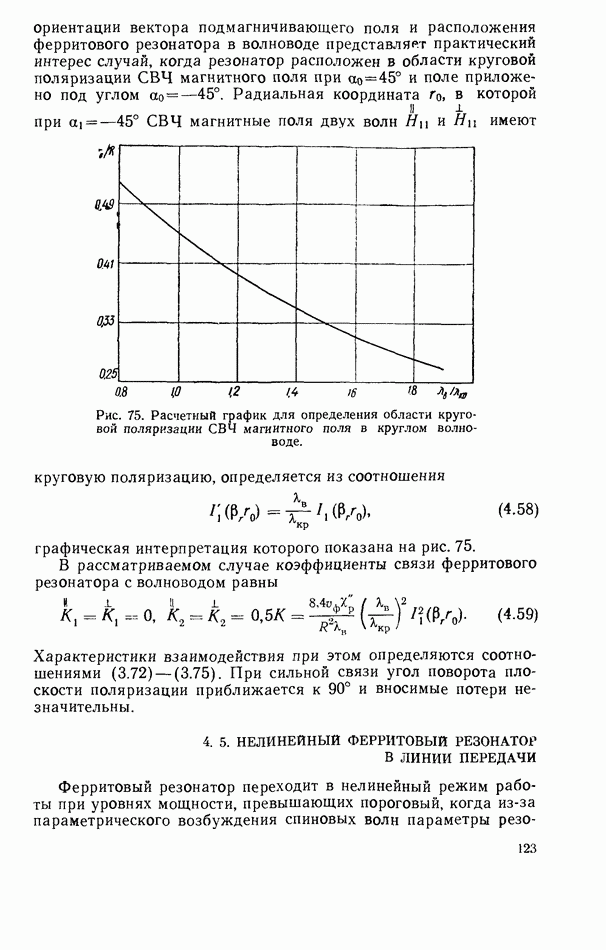
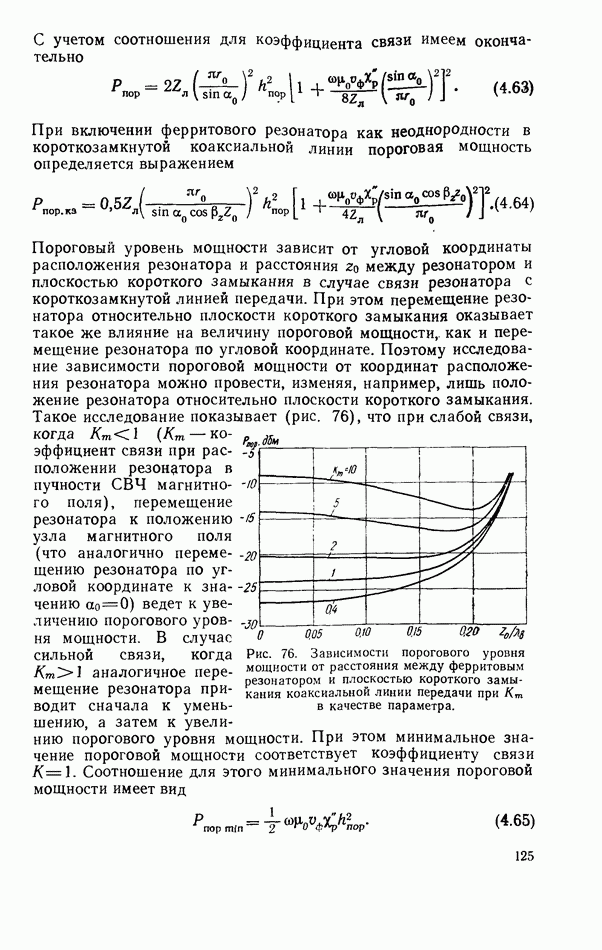
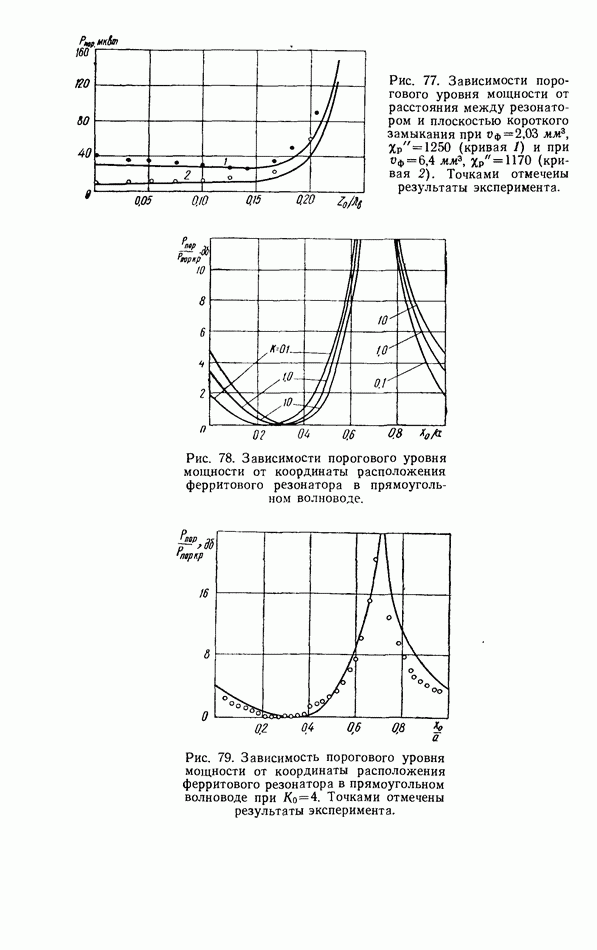
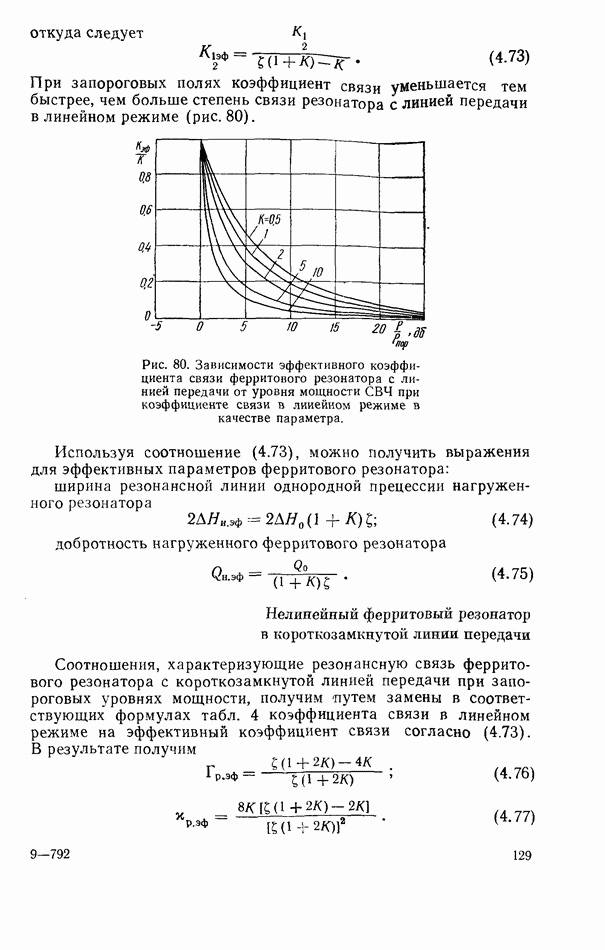
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава четвертая. СВЯЗЬ ТВЕРДОТЕЛЬНЫХ РЕЗОНАТОРОВ С ЛИНИЯМИ ПЕРЕДАЧИ СВЧ
4.1. ОБЩИЕ СООТНОШЕНИЯ ДЛЯ КОЭФФИЦИЕНТОВ СВЯЗИ
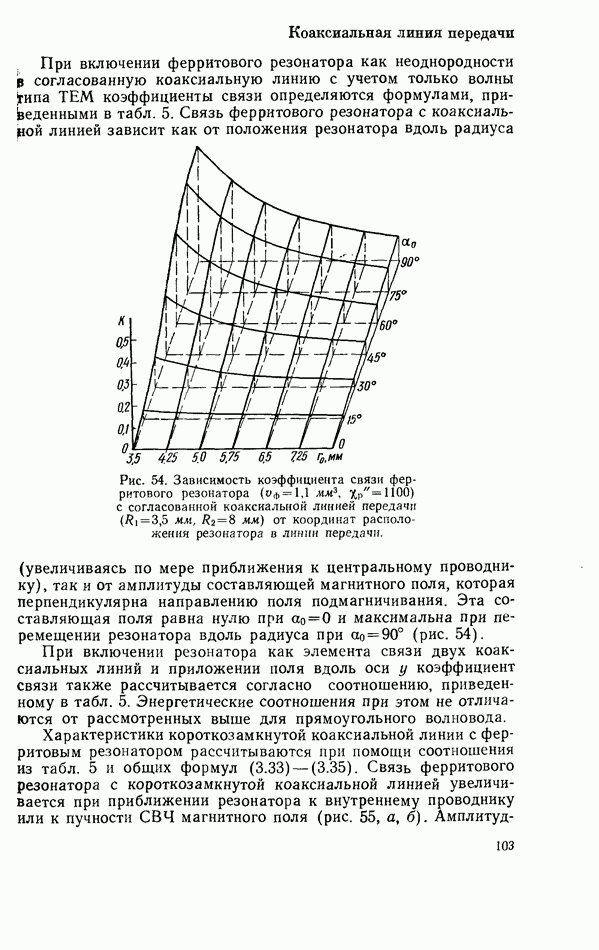
В предыдущей главе получены соотношения для характеристик линий передачи СВЧ с твердотельными резонаторами. Представлены они через коэффициенты связи резонатора с линией передачи СВЧ и через обобщенную расстройку резонатора. Для использования общих соотношений в конкретных случаях необходимо рассчитать коэффициенты связи. Расчет их и результаты исследования особенностей связи резонаторов с наиболее часто применяемыми линиями передачи рассматриваются в настоящей главе.
При вычислении коэффициентов связи учитывается, что размеры резонаторов много меньше длины электромагнитной волны и размеров линии передачи. Это позволяет воспользоваться эквивалентным представлением резонатора в виде диполя, момент которого вычислен выше для ферритового и диэлектрического резонатора. Таким образом, расчет коэффициентов связи сводится к вычислению мощности, поглощаемой и переизлучаемой резонатором, эквивалентный диполь которого известен.
Основными упрощающими допущениями, при которых вычисляется связь резонатора с согласованной линией передачи, являются:
1. Не учитываются нелинейные эффекты из-за нагрева резонатора поглощаемой мощностью, а в случае ферритового резонатора также и нелинейные эффекты из-за параметрического возбуждения спиновых волн.
2. Предполагается, что резонатор размещен на достаточном удалении от металлических стенок линии передачи с тем, чтобы не учитывать влияние последних на параметры и ближние поля резонатора.
Рассчитаем коэффициенты связи резонатора с согласованной линией передачи, поперечное сечение которой не изменяется вдоль продольной координаты z линии передачи. При вычислениях положим, что связь резонатора с линией передачи осуществляется только через один тип  или ТМ-волны.
или ТМ-волны.
Мощность, переносимая волной, переизлучаемой диполем, определяется формулой

где  амплитуды поперечных составляющих волны, переизлучаемой диполем. Эти составляющие можно записать в виде
амплитуды поперечных составляющих волны, переизлучаемой диполем. Эти составляющие можно записать в виде

Здесь а — обобщенный индекс, объединяющий волны типов ТЕ и ТМ одним значком:  где
где  относится к волнам
относится к волнам  к волнам
к волнам  — амплитудные функции, а
— амплитудные функции, а  собственные поперечные векторные функции линии передачи, которые для волн различных типов выражаются через собственные скалярные функции и следующим образом: для волн типа ТЕ
собственные поперечные векторные функции линии передачи, которые для волн различных типов выражаются через собственные скалярные функции и следующим образом: для волн типа ТЕ

для волн типа ТМ

где  собственное значение для линии передачи с рассматриваемым типом волны;
собственное значение для линии передачи с рассматриваемым типом волны;  единичный вектор.
единичный вектор.
Собственные скалярные функции (иначе их называют мембранными функциями) определяются из уравнения Гельмгольца

при следующих граничных условиях на контуре поперечного сечения линии передачи:

где  производная по нормали к контуру поперечного сечения.
производная по нормали к контуру поперечного сечения.
Мембранные функции должны подчиняться условию ортонормировки

где  символ Кронекера
символ Кронекера  при
при  при
при  Подставим электрическую и магнитную составляющие переизлученной волны (4.2) в формулу (4.1)
Подставим электрическую и магнитную составляющие переизлученной волны (4.2) в формулу (4.1)

Амплитудные функции вынесены из-под интеграла, так как они зависят только от продольной координаты 
Вычислим интеграл в выражении (4.8) для волн типа ТЕ. Используя выражения (4.3), запишем

В соответствии с формулой двойного векторного произведения

где учтено, что векторы  ортогональны и их скалярное произведение равно нулю.
ортогональны и их скалярное произведение равно нулю.
С учетом выражений (4.3), (4.10) интеграл (4.9) записывается следующим образом:

Для вычисления интеграла в правой части выражения (4.11) обратимся к уравнению Гельмгольца (4.5), умножив его на  и проинтегрируем по сечению линии передачи
и проинтегрируем по сечению линии передачи

где учтено условие ортонормировки (4.7). Интеграл в последнем выражении преобразуем в соответствии с теоремой Грина

В силу граничных условий (4.6) контурный интеграл в выражении (4.13) равен нулю; тогда, сравнивая (4.12) и (4.13), запишем

Подставляя (4.14) в выражение (4.11), получим

С учетом равенства (4.15) выражение для мощности, переносимой по линии передачи переизлученной волной типа  имеет вид
имеет вид

Для волн типа  выполнив аналогичные расчеты, можно также показать, что
выполнив аналогичные расчеты, можно также показать, что

В результате, обобщенное выражение для переизлученной мощности имеет вид

где  волновое сопротивление линии передачи. Таким образом, задача вычисления переизлученной мощности сводится к вычислению амплитудных функций переизлученных волн.
волновое сопротивление линии передачи. Таким образом, задача вычисления переизлученной мощности сводится к вычислению амплитудных функций переизлученных волн.
Для амплитудных функций волн, переизлученных магнитным диполем в направлении к генератору (индекс 1) и в направлении к нагрузке (индекс 2), справедливы следующие выражения (для упрощения записи обобщенный индекс у амплитудных функций опущен) [91]:

где  дипольный момент;
дипольный момент;  обобщенная собственная магнитная функция волновода, включающая поперечную
обобщенная собственная магнитная функция волновода, включающая поперечную  и продольную
и продольную  векторные функции
векторные функции

Если потери в стенках линии передачи и в среде, заполняющей линию, малы, то постоянная распространения у равна

где  продольное волновое число, а
продольное волновое число, а  длина волны в линии передачи. Тогда
длина волны в линии передачи. Тогда

Собственная магнитная функция (4.21) представляется через мембранные функции линии передачи следующим образом: для волн типа ТЕ

для волн типа ТМ

Подставив выражения (4.19) в формулу (4.18) для переизлучаемой мощности, получим

Для вычисления коэффициентов связи необходимо также определить мощность тепловых потерь в резонаторе. Используя известное выражение для среднего во времени значения мощности потерь в единице объема среды [6] с учетом выражения для дипольного момента резонатора, можно записать соотношение для рассеиваемой мощности

Таким образом, общее выражение для коэффициентов связи резонатора с согласованной линией передачи имеет вид

При расчете коэффициентов связи можно также пользоваться [93] ненормированными собственными векторными функциями, для которых не выполняются условия нормировки (4.15), (4.17). В этом случае в формуле для коэффициентов связи появится нормирующий множитель  где
где  мощность, переносимая по линии передачи волной единичной амплитуды.
мощность, переносимая по линии передачи волной единичной амплитуды.
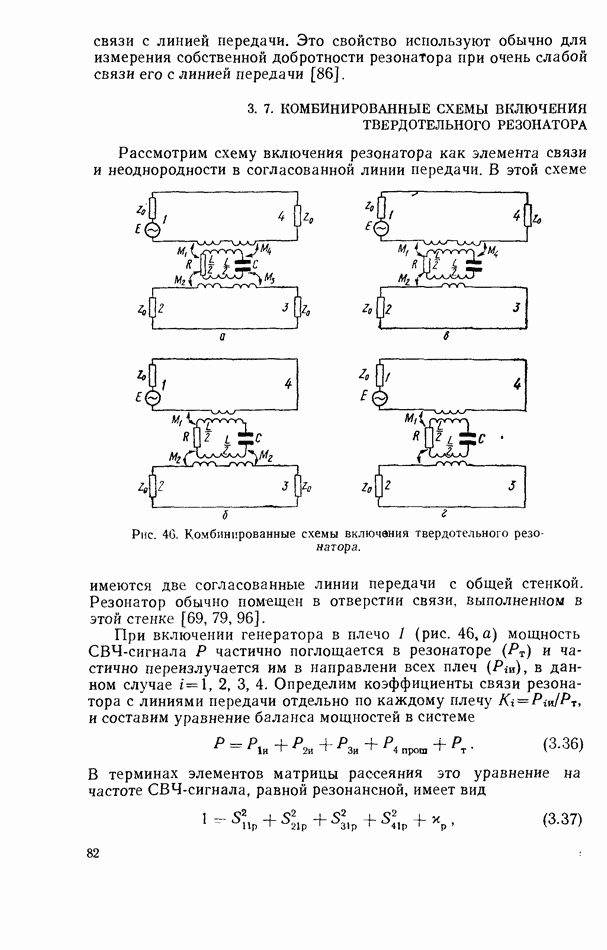
При включении резонатора как элемента связи линий передачи соотношение для коэффициентов связи нетрудно получить при следующих упрощающих предположениях, дополнительных к сформулированным выше для случая согласованной линии передачи.
1. Резонатор расположен симметрично относительно входной и выходной линий передачи в центре отверстия связи.
2. Размеры отверстия связи, в котором расположен резонатор, много меньше длины электромагнитной волны; при этом невозмущенное магнитное поле на месте отверстия связи в первом приближении можно считать однородным.
3. Размеры ферритового резонатора предполагаются много меньшими размеров отверстия связи (по крайней мере в три
раза) с тем, чтобы намагниченность по объему была также однородной. Для диэлектрического резонатора малость размеров резонатора по сравнению с размерами отверстия связи не является обязательной при тонкой перегородке [94]. Как показывают исследования [42], влияние тонкой перегородки на резонансную частоту диэлектрического резонатора не сказывается при размерах отверстия связи, сравнимых с размерами диэлектрического резонатора.
4. Общая стенка линий передачи предполагается тонкой с тем, чтобы напряженность магнитного поля в центре отверстия связи равнялась половине той амплитуды поля, которая была бы там при отсутствии отверстия связи, как это следует из результатов теории Бэтэ [95].
При этих предположениях коэффициенты связи резонатора с входной и выходной линиями передачи могут быть рассчитаны по общей формуле (4.26) для коэффициентов связи резонатора с согласованной линией передачи. Это обусловлено следующим. Коэффициент связи пропорционален квадрату амплитуды магнитного поля в месте расположения резонатора: при этом связь находящегося в пучности СВЧ магнитного поля резонатора с короткозамкнутой линией передачи в четыре раза больше по сравнению с согласованной линией. Наличие отверстия связи в короткозамкнутой стенке приводит к уменьшению амплитуды поля в два раза и уменьшению коэффициента связи в четыре раза. Таким образом, связь резонатора с линиями передачи при включении разонатора как элемента связи при принятых допущениях равна связи резонатора с согласованной линией передачи при включении резонатора как неоднородности. Это позволяет использовать одни и те же соотношения для коэффициентов связи при расчете основных схем включения твердотельного резонатора.
При расчете связи резонатора с линиями передачи в комбинированных схемах включения необходимо учитывать, что коэффициент связи резонатора с короткозамкнутыми плечами линии передачи зависит от расстояния  между центром отверстия связи и короткозамыкающей стенкой линии передачи. При связи резонатора с короткозамкнутым плечом по поперечной составляющей поля связь резонатора с короткозамкнутым плечом определяется соотношением
между центром отверстия связи и короткозамыкающей стенкой линии передачи. При связи резонатора с короткозамкнутым плечом по поперечной составляющей поля связь резонатора с короткозамкнутым плечом определяется соотношением 
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава первая. СВОЙСТВА ФЕРРИТОВЫХ РЕЗОНАТОРОВ
- Ферромагнитный резонанс в неограниченной среде без потерь
- 1.2. РЕЗОНАНСНАЯ ЧАСТОТА
- Зависимость резонансной частоты от формы резонатора
- Влияние кристаллографической анизотропии на резонансную частоту
- 1.3. МАГНИТОСТАТИЧЕСКИЕ ВИДЫ КОЛЕБАНИЙ
- 1.4. УЧЕТ ПОТЕРЬ
- 1.5. ДИПОЛЬНЫЙ МОМЕНТ
- 1.6. НЕЛИНЕЙНЫЕ ЯВЛЕНИЯ
- Спиновые волны
- Пороговая амплитуда высокочастотного магнитного поля
- Восприимчивость при амплитудах поля, превышающих пороговое значение
- 1.7. ПРИМЕНЯЕМЫЕ ДЛЯ ИЗГОТОВЛЕНИЯ МАТЕРИАЛЫ
- 1.8. ТЕМПЕРАТУРНЫЕ ХАРАКТЕРИСТИКИ
- 1.9. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- Глава вторая. СВОЙСТВА ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 2.2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В АНИЗОТРОПНОМ ДИЭЛЕКТРИЧЕСКОМ СТЕРЖНЕ С «МАГНИТНЫМИ» БОКОВЫМИ СТЕНКАМИ
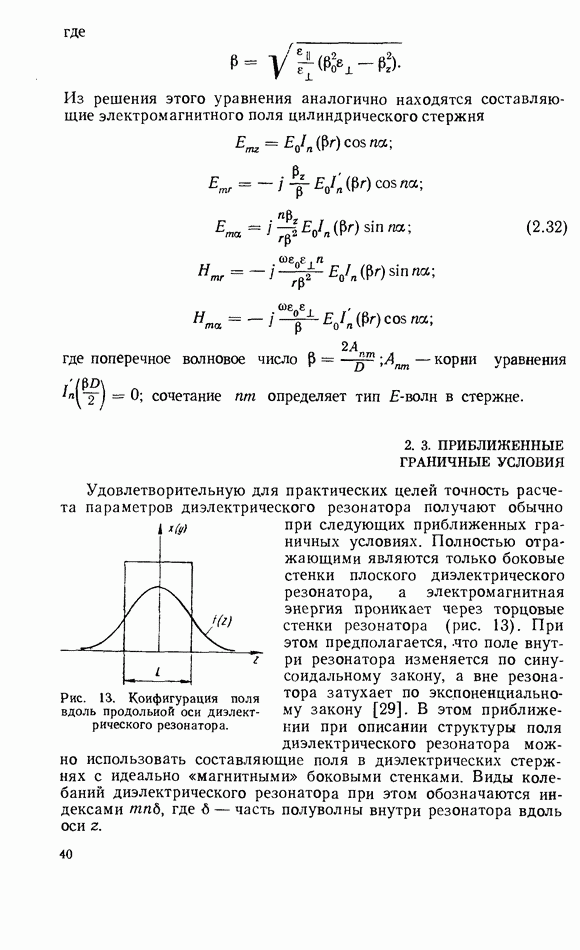
- 2.3. ПРИБЛИЖЕННЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2.5. ОСНОВНЫЕ ВИДЫ КОЛЕБАНИЙ
- 2.6. СФЕРИЧЕСКИЕ ДИЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
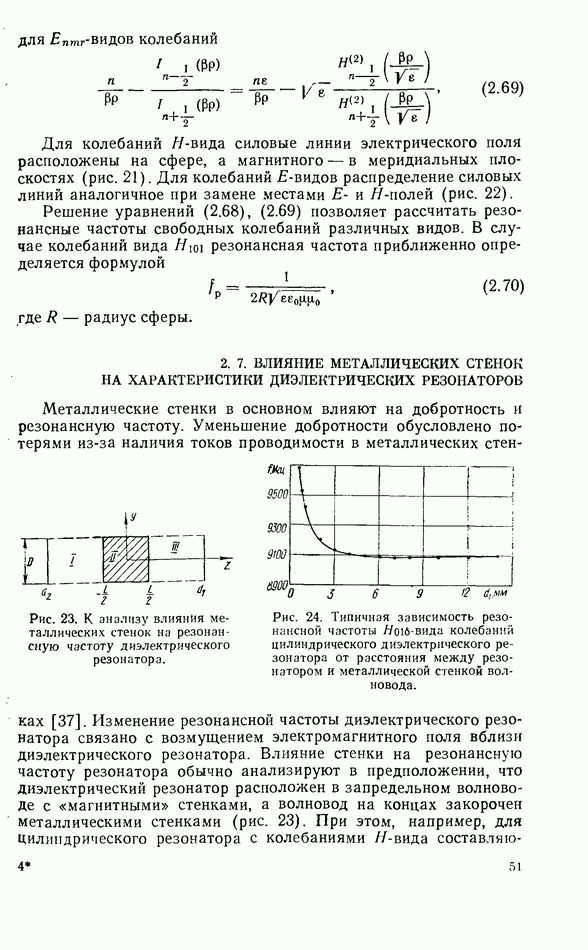
- 2.7. ВЛИЯНИЕ МЕТАЛЛИЧЕСКИХ СТЕНОК НА ХАРАКТЕРИСТИКИ ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 2.8. ДИПОЛЬНЫЙ МОМЕНТ
- 2.9. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ
- 2.10. СООТНОШЕНИЕ МЕЖДУ АМПЛИТУДАМИ СВЧ МАГНИТНОГО ПОЛЯ
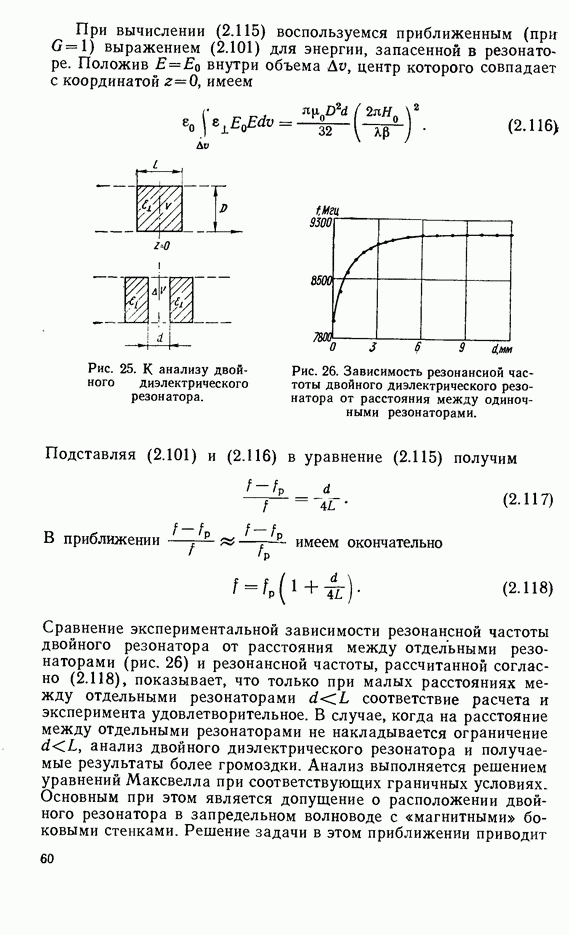
- 2.11. ДВОЙНЫЕ ДИЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
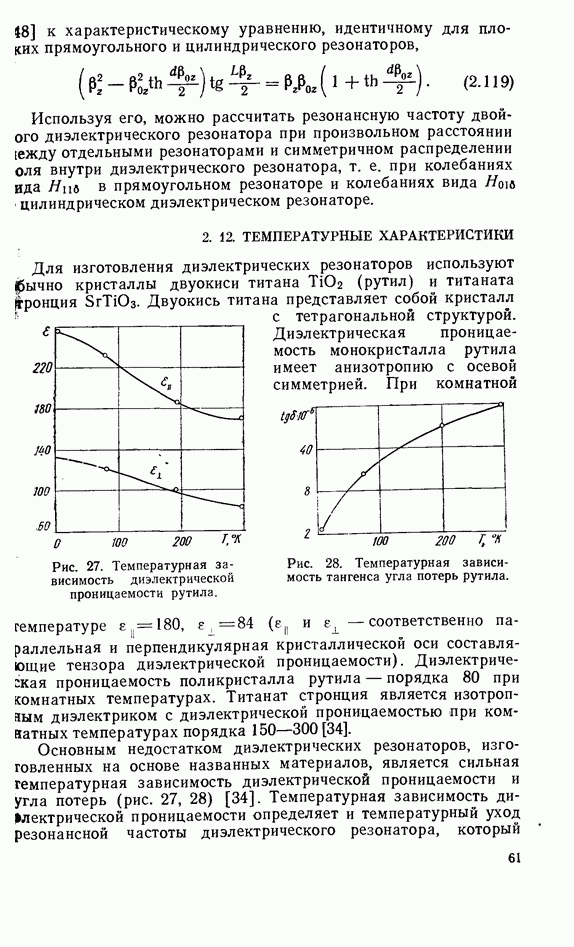
- 2.12. ТЕМПЕРАТУРНЫЕ ХАРАКТЕРИСТИКИ
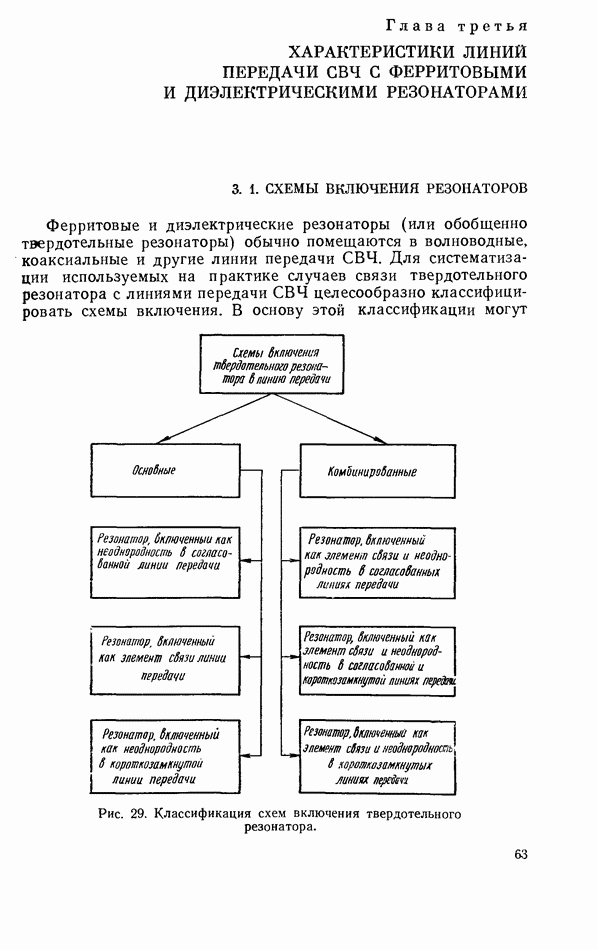
- Глава третья. ХАРАКТЕРИСТИКИ ЛИНИЙ ПЕРЕДАЧИ СВЧ С ФЕРРИТОВЫМИ И ДИЭЛЕКТРИЧЕСКИМИ РЕЗОНАТОРАМИ
- 3.2. МЕТОДЫ РАСЧЕТА СВЧ-СХЕМ С ТВЕРДОТЕЛЬНЫМИ РЕЗОНАТОРАМИ
- 3.3. СВЯЗЬ ТВЕРДОТЕЛЬНОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ СВЧ
- 3.4. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В НЕСОГЛАСОВАННОЙ ЛИНИИ ПЕРЕДАЧИ
- 3.5. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР, ВКЛЮЧЕННЫЙ КАК ЭЛЕМЕНТ СВЯЗИ ЛИНИЙ ПЕРЕДАЧИ
- 3.6. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В КОРОТКОЗАМКНУТОЙ ЛИНИИ ПЕРЕДАЧИ
- 3.7. КОМБИНИРОВАННЫЕ СХЕМЫ ВКЛЮЧЕНИЯ ТВЕРДОТЕЛЬНОГО РЕЗОНАТОРА
- 3.8. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ С НЕСКОЛЬКИМИ РАСПРОСТРАНЯЮЩИМИСЯ ВОЛНАМИ
- Глава четвертая. СВЯЗЬ ТВЕРДОТЕЛЬНЫХ РЕЗОНАТОРОВ С ЛИНИЯМИ ПЕРЕДАЧИ СВЧ
- 4.2. СВЯЗЬ ФЕРРИТОВОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ
- 4.3. ФЕРРИТОВЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ ЗАМЕДЛЕННЫХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
- 4.4. РЕЗОНАНСНЫЙ ПОВОРОТ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ В ВОЛНОВОДЕ С ФЕРРИТОВЫМ РЕЗОНАТОРОМ
- 4.5. НЕЛИНЕЙНЫЙ ФЕРРИТОВЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ
- Ферритовый резонатор в линии передачи при запороговых уровнях мощности
- Нелинейный ферритовый резонатор в короткозамкнутой линии передачи
- Связь линий передачи СВЧ при помощи нелинейного ферритового резонатора
- Нелинейный ферритовый резонатор в согласованной линии передачи
- 4.6. СВЯЗЬ ДИЭЛЕКТРИЧЕСКОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ СВЧ
- Глава пятая. ПРИНЦИПЫ ПОСТРОЕНИЯ СВЧ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ И УСТРОЙСТВ НА ОСНОВЕ ТВЕРДОТЕЛЬНЫХ РЕЗОНАТОРОВ
- 5.2. ДАТЧИКИ УРОВНЯ МОЩНОСТИ СВЧ
- Волноводная измерительная головка
- Датчик фиксированного уровня пиковой мощности
- 5.3. ЧАСТОТНЫЕ ДИСКРИМИНАТОРЫ С МАГНИТНОЙ НАСТРОЙКОЙ
- 5.4. РЕЗОНАНСНЫЕ ФАЗОВРАЩАТЕЛИ
- 5.5. УСТРОЙСТВО ДЛЯ РЕЗОНАНСНОГО ПОВОРОТА ПЛОСКОСТИ ПОЛЯРИЗАЦИИ В ВОЛНОВОДЕ
- 5.6. ФИЛЬТРЫ СВЧ НА ОСНОВЕ ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 5.7. ФЕРРИТОВЫЕ СВЧ-ФИЛЬТРЫ
- Многофункциональные фильтры
- Многорезонаторные ферритовые фильтры
- 5.8. ЧАСТОТНО-ИЗБИРАТЕЛЬНЫЕ ОГРАНИЧИТЕЛИ МАЛЫХ УРОВНЕЙ МОЩНОСТИ