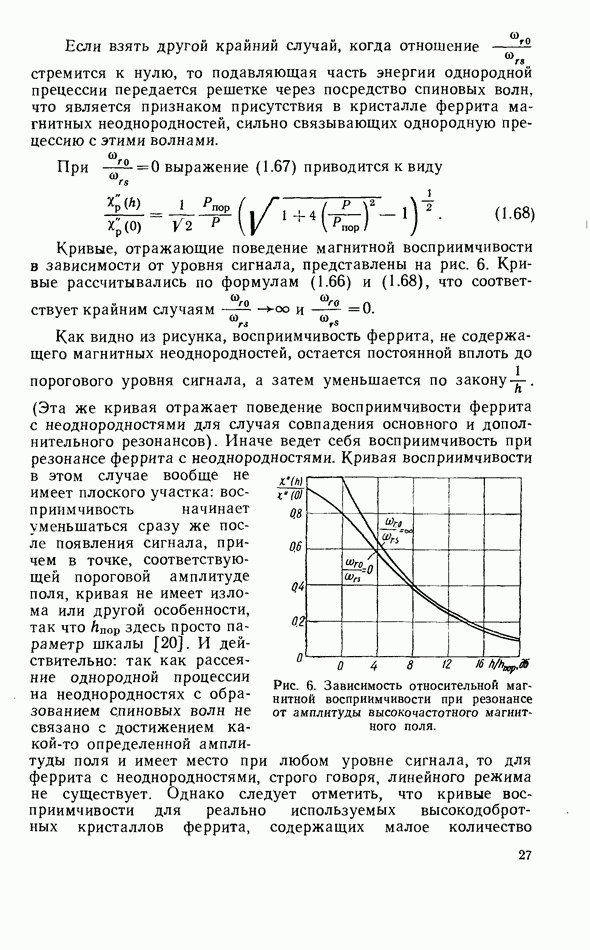
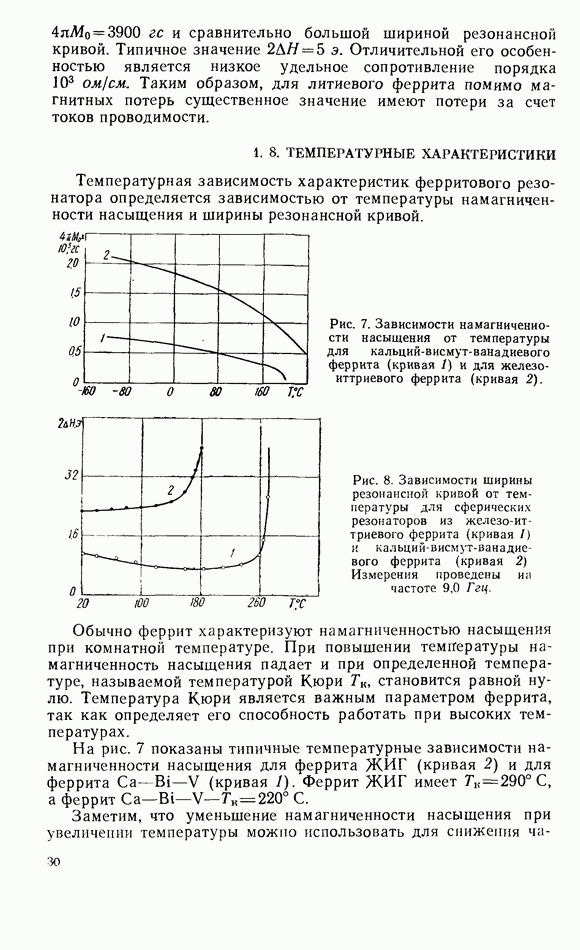
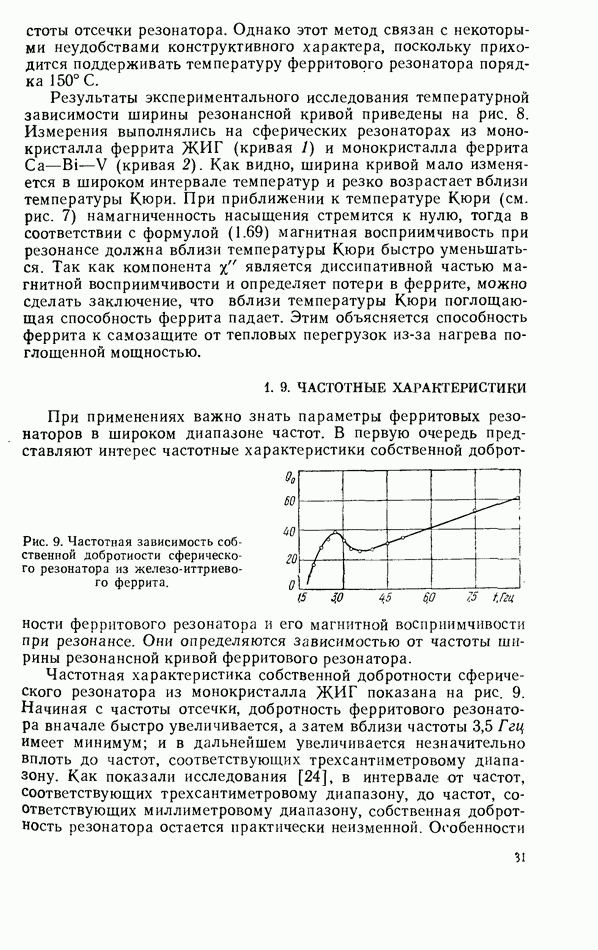
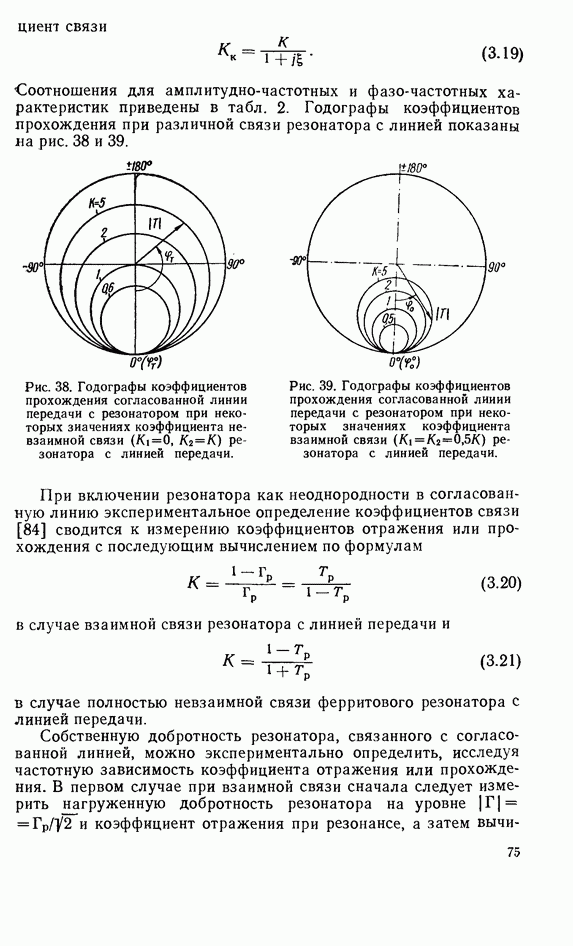
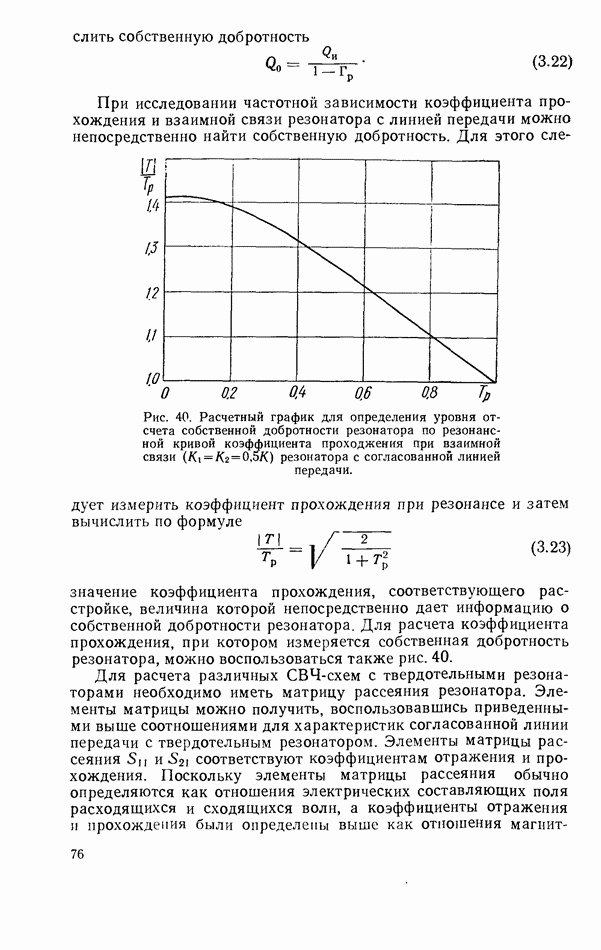
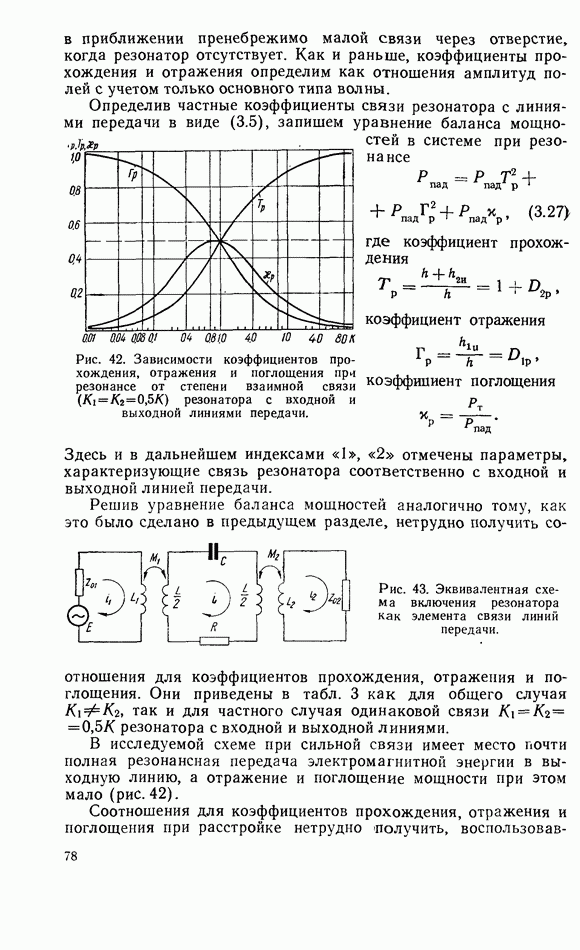
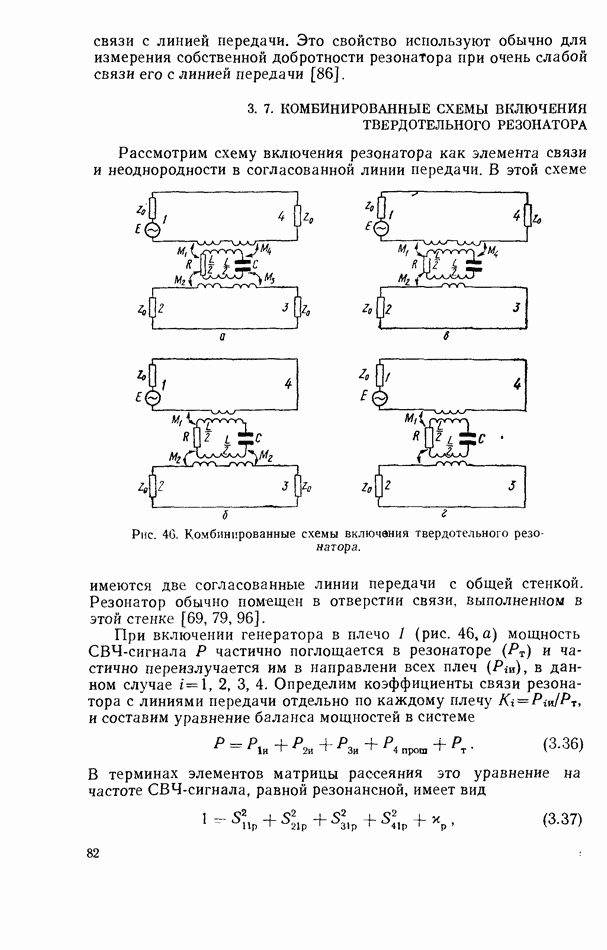
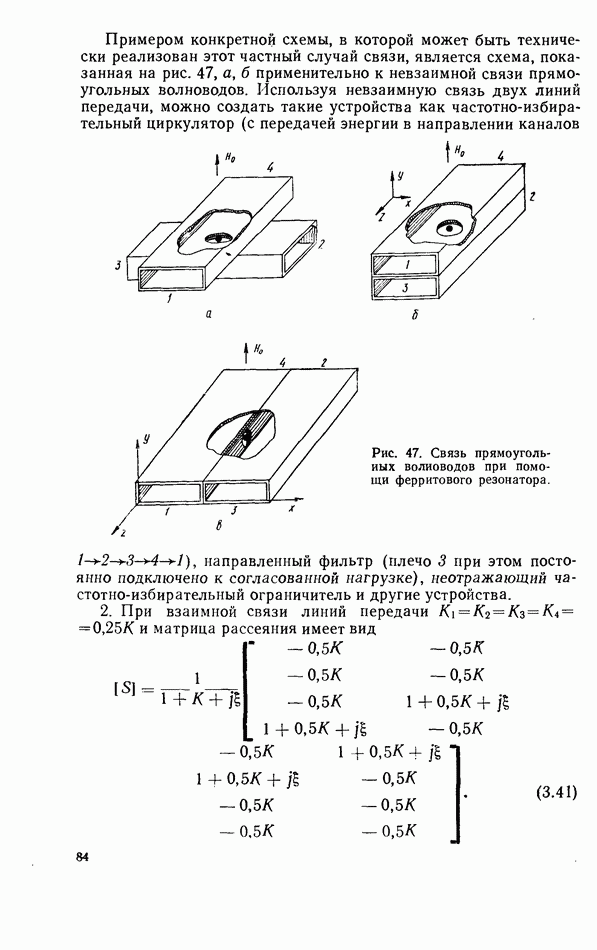
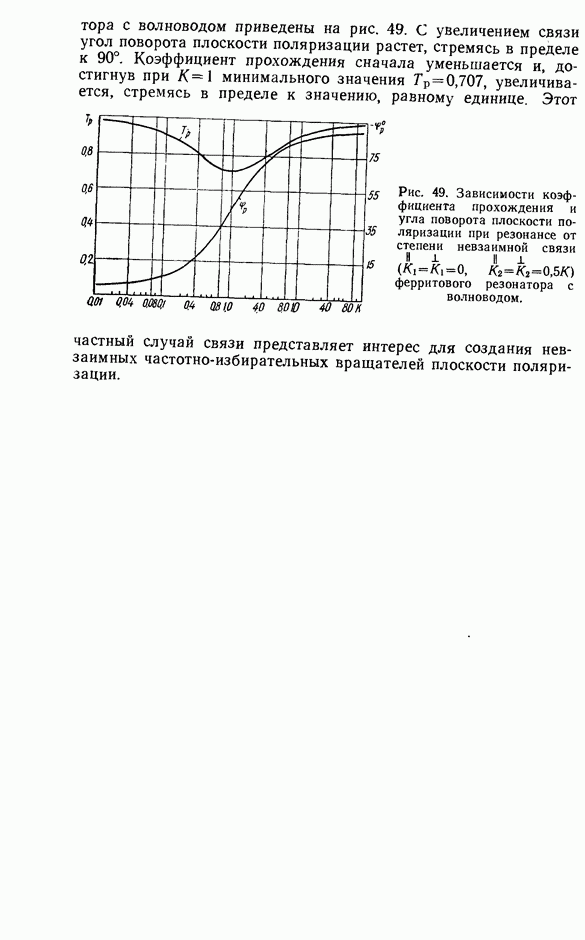
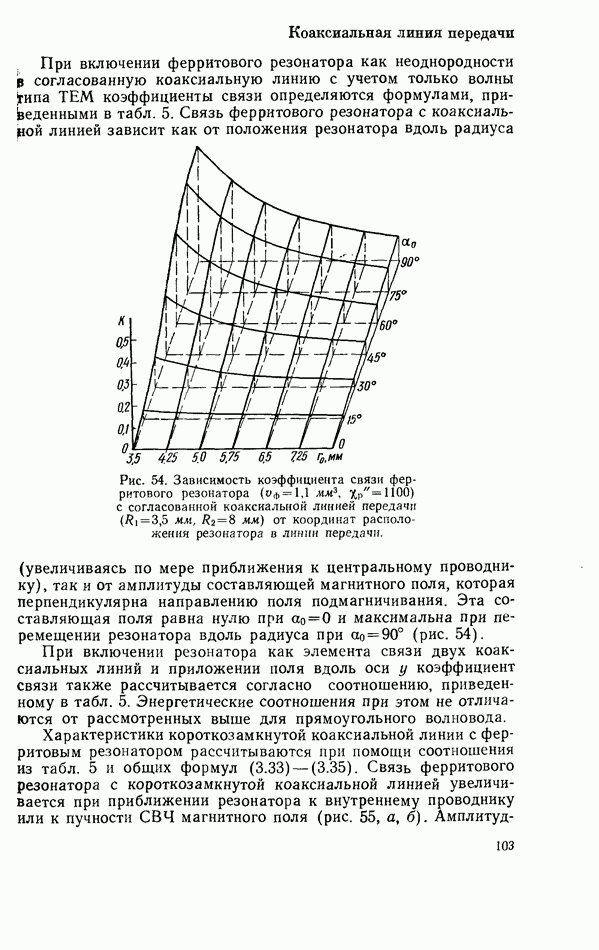
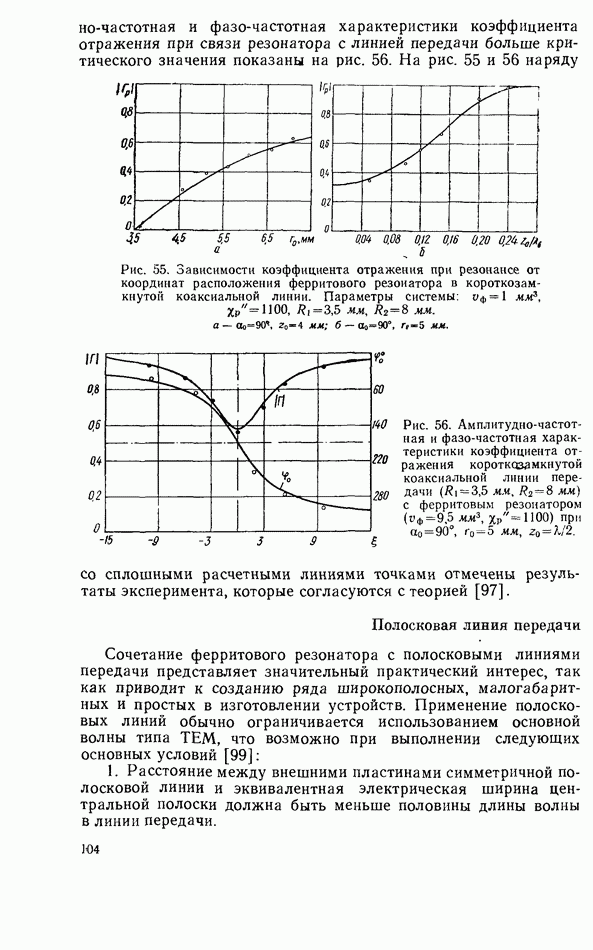
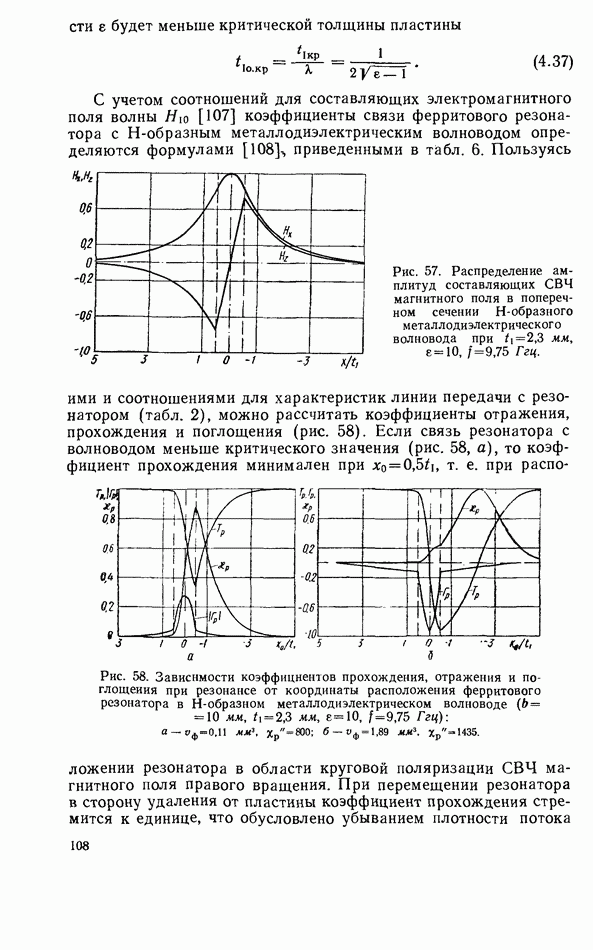
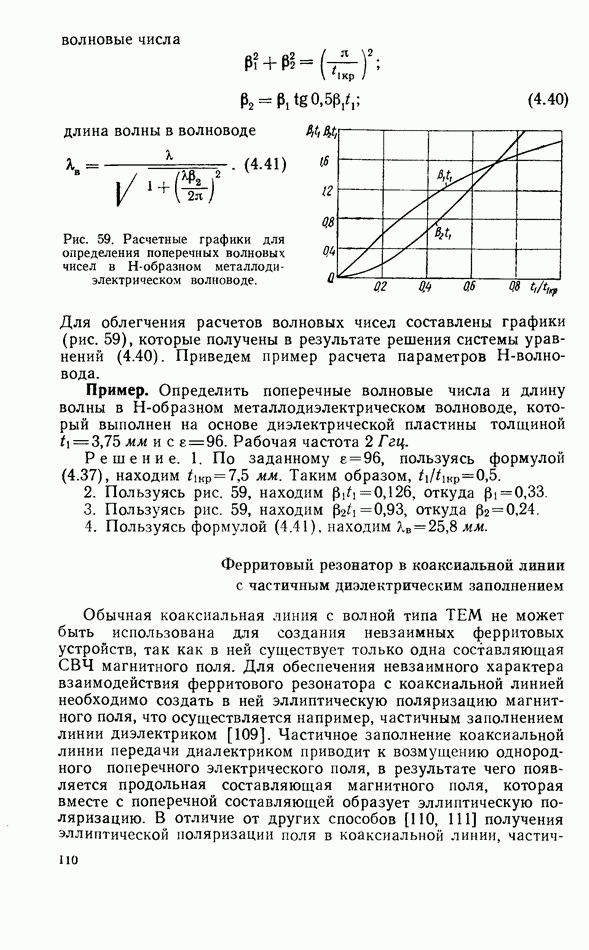
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.4. УЧЕТ ПОТЕРЬ
В реальной ферромагнитной среде всегда есть потери, связанные с преобразованием энергии прецессирующих спиновых магнитных моментов в тепловые колебания кристаллической решетки, т. е. энергия спиновых магнитных моментов частично расходуется на нагрев среды.
Феноменологический учет потерь предполагает добавление в правой части уравнения Ландау-Лифшица диссипативного члена. Уравнение (1.1) с диссипативным членом в форме Гильберта [10] имеет вид

где а — безразмерный параметр, характеризующий потери.
При такой записи видно, что  это единичныи вектор вдоль направления намагниченности и он векторно умножается
это единичныи вектор вдоль направления намагниченности и он векторно умножается  на скорость изменения намагниченности - Таким образом, диссипативный член описывает вектор, величина которого пропорциональна параметру потерь а и скорости изменения намагниченности; он направлен так, что при его добавлении уменьшается отклонение вектора плотности намагниченности от направления постоянного магнитного поля (уменьшается угол или амплитуда прецессии). Вместо параметра а для характеристики потерь часто используют время релаксации
на скорость изменения намагниченности - Таким образом, диссипативный член описывает вектор, величина которого пропорциональна параметру потерь а и скорости изменения намагниченности; он направлен так, что при его добавлении уменьшается отклонение вектора плотности намагниченности от направления постоянного магнитного поля (уменьшается угол или амплитуда прецессии). Вместо параметра а для характеристики потерь часто используют время релаксации  имеющее смысл времени, за которое амплитуда свободных колебаний намагниченности (угол свободной прецессии) убывает в
имеющее смысл времени, за которое амплитуда свободных колебаний намагниченности (угол свободной прецессии) убывает в  раз. Величина, обратная времени релаксации, называется частотой релаксации
раз. Величина, обратная времени релаксации, называется частотой релаксации  Между параметром а, временем релаксации
Между параметром а, временем релаксации  и частотой релаксации
и частотой релаксации  существует соотношение
существует соотношение

Решая уравнение (1.32) с учетом предположения о малости амплитуды высокочастотного магнитного поля, получим выражения для компонент тензора магнитной восприимчивости среды с потерями. В этом случае компоненты тензора восприимчивости будут комплексными величинами, причем, как оказывается, правильные выражения для компонент тензора восприимчивости с
учетом потерь можно получить из выражений для компонент тензора восприимчивости среды без потерь, если применить правило: всюду, где в выражениях встречается частота  Цоее следует заменить на комплексную частоту
Цоее следует заменить на комплексную частоту  Применим это правило к выражениям (1.5), (1.6) и получим для среды с потерями
Применим это правило к выражениям (1.5), (1.6) и получим для среды с потерями

Если ограничиться случаем малых расстроек относительно частоты ферромагнитного резонанса (сошо) и рассматривать только среду с малыми потерями  то можно записать приближенные соотношения
то можно записать приближенные соотношения

С учетом соотношений (1.36) тензор восприимчивости среды с малыми потерями при малых расстройках записывается следующим образом:

где х определяется выражением (1.34), а  тензор вида
тензор вида

Представим выражение (1.34) в виде алгебраической суммы действительной и мнимой частей

Выделяя в (1.34) действительную и мнимую части, получим для 

При уменьшении потерь до нуля частота релаксации стремится к нулю, и должна стремиться к нулю та часть магнитной восприимчивости, которая определяется потерями. Как видно из выражений (1.40) и (1.41), при уменьшении потерь до нуля стремится к нулю мнимая компонента магнитной восприимчивости поэтому ее называют диссипативной частью
восприимчивости, а действительную компоненту  называют дисперсионной частью восприимчивости.
называют дисперсионной частью восприимчивости.
Пусть  расстройка частоты
расстройка частоты  относительно частоты ферромагнитного резонанса
относительно частоты ферромагнитного резонанса 

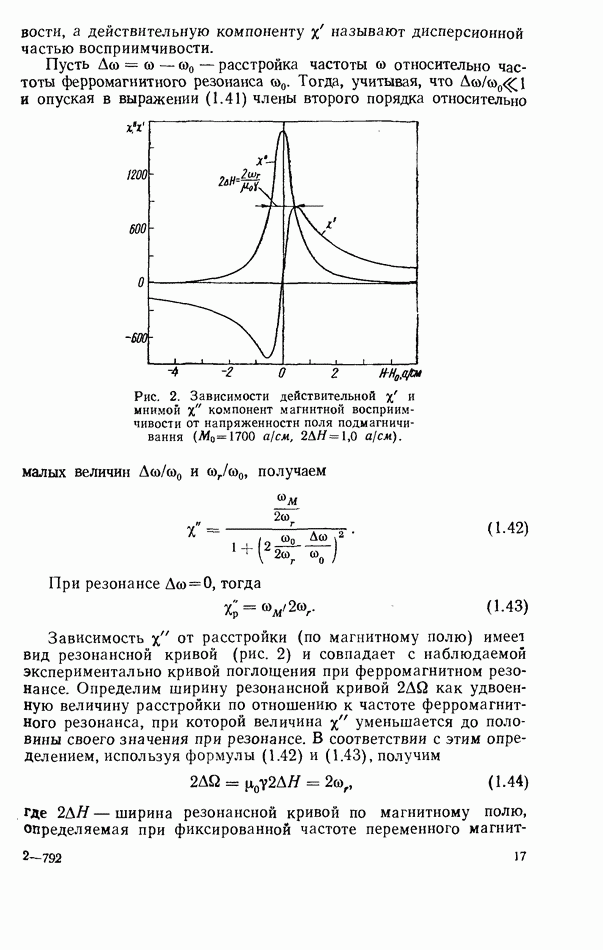
Рис. 2. Зависимости действительной  и мнимой
и мнимой  компонент магнитной восприимчивости от напряженности поля подмагничивання
компонент магнитной восприимчивости от напряженности поля подмагничивання  а/см,
а/см,  а/см).
а/см).
Тогда, учитывая, что  и опуская в выражении (1.41) члены второго порядка относительно малых величин
и опуская в выражении (1.41) члены второго порядка относительно малых величин  получаем
получаем

При резонансе  тогда
тогда

Зависимость  от расстройки (по магнитному полю) имеет вид резонансной кривой (рис. 2) и совпадает с наблюдаемой экспериментально кривой поглощения при ферромагнитном резонансе. Определим ширину резонансной кривой
от расстройки (по магнитному полю) имеет вид резонансной кривой (рис. 2) и совпадает с наблюдаемой экспериментально кривой поглощения при ферромагнитном резонансе. Определим ширину резонансной кривой  как удвоенную величину расстройки по отношению к частоте ферромагнитного резонанса, при которой величина
как удвоенную величину расстройки по отношению к частоте ферромагнитного резонанса, при которой величина  уменьшается до половины своего значения при резонансе. В соответствии с этим определением, используя формулы (1.42) и (1.43), получим
уменьшается до половины своего значения при резонансе. В соответствии с этим определением, используя формулы (1.42) и (1.43), получим

где  ширина резонансной кривой по магнитному полю, определяемая при фиксированной частоте переменного
ширина резонансной кривой по магнитному полю, определяемая при фиксированной частоте переменного
магнитного поля и изменяющейся напряженности постоянного поля, т. е. при изменении частоты ферромагнитного резонанса. Параметр потерь  широко используется в теории и ее приложениях, так как он наиболее нагляден и его легко измерить.
широко используется в теории и ее приложениях, так как он наиболее нагляден и его легко измерить.
Величину  в знаменателе формулы (1.42) можно назвать добротностью ферромагнитного резонанса
в знаменателе формулы (1.42) можно назвать добротностью ферромагнитного резонанса  С учетом соотношений (1.7) и (1.44) формула для добротности записывается следующим образом:
С учетом соотношений (1.7) и (1.44) формула для добротности записывается следующим образом:

Величина в скобках в знаменателе формулы (1.42) может быть названа обобщенной расстройкой  т. е.
т. е.

С учетом последней формулы и формулы (1.43) запишем окончательное выражение для

Сохраняя в выражении (1.40) только члены первого порядка малости, получаем

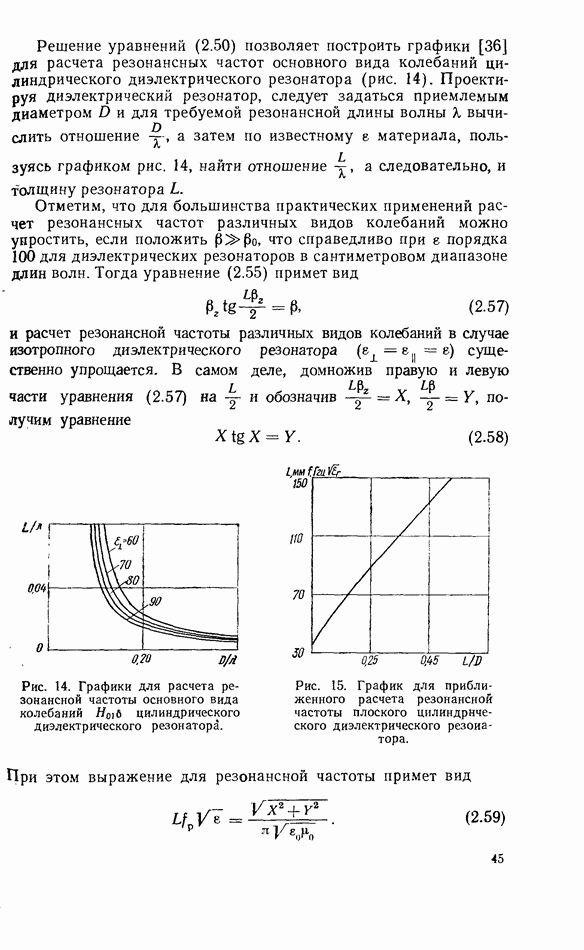
С учетом формулы (1.46) перепишем (1.48) в виде

Формула (1.49) дает правильный знак если фиксировано постоянное магнитное поле (фиксирована резонансная частота) и изменяется частота воздействующего сигнала. Если же, наоборот, частота сигнала остается неизменной, а меняется резонансная, то, как легко видеть, знак расстройки (теперь уже по магнитному полю) нужно изменить. Тогда выражение для  с учетом расстройки по магнитному полю запишется
с учетом расстройки по магнитному полю запишется

где

(здесь  - напряженность постоянного магнитного поля, при которой частота ферромагнитного резонанса совпадает с частотой воздействующего сигнала). На рис. 2 приведена зависимость от расстройки по магнитному полю, рассчитанная по формуле (1.50).
- напряженность постоянного магнитного поля, при которой частота ферромагнитного резонанса совпадает с частотой воздействующего сигнала). На рис. 2 приведена зависимость от расстройки по магнитному полю, рассчитанная по формуле (1.50).
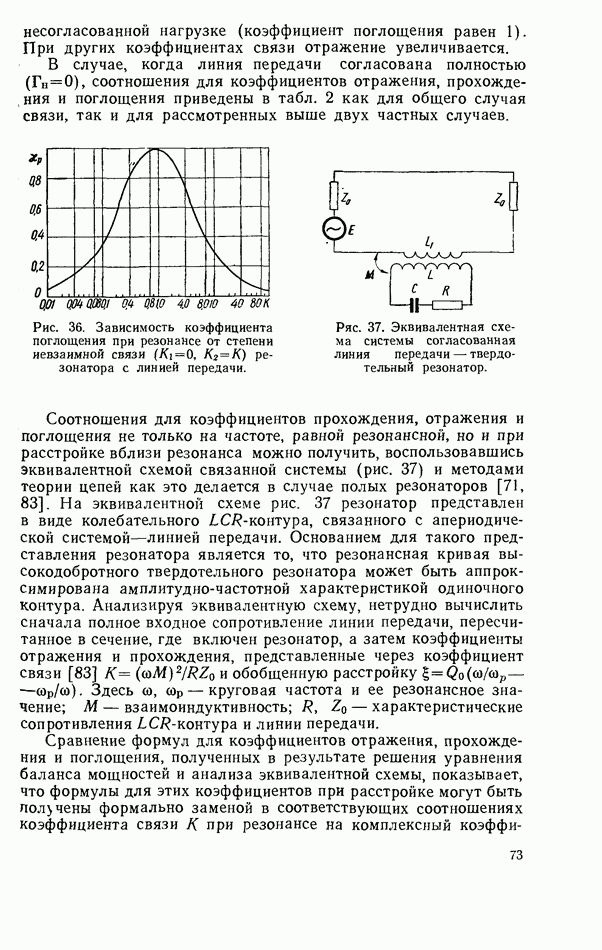
Подставляя выражения (1.47) и (1.49) в формулу (1.39), с учетом (1.37) получим удобное выражение для тензора магнитной восприимчивости среды с потерями

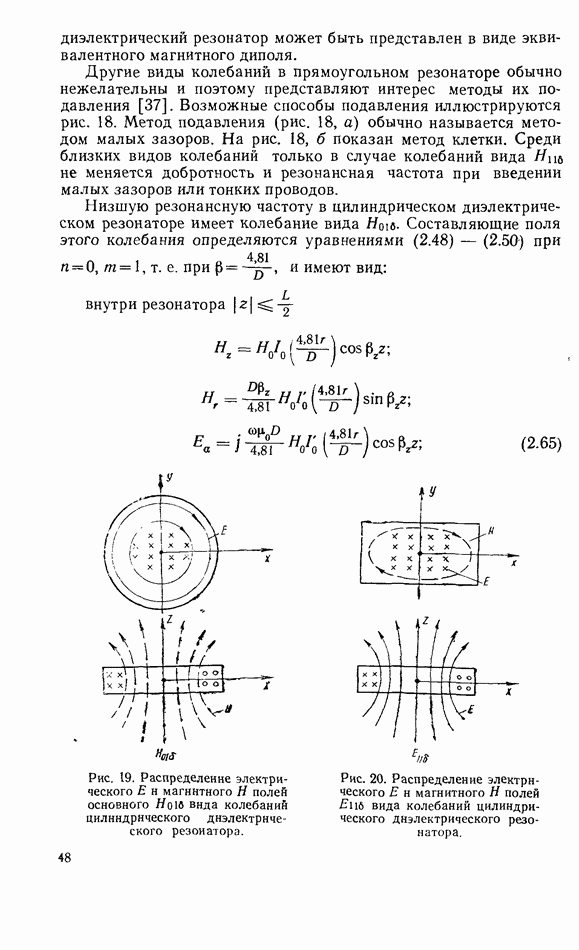
Следует иметь в виду, что допущения, принятые при выводе данного выражения, позволяют использовать его только применительно к резонаторам с малыми потерями (с высокой добротностью) и при малых расстройках относительно частоты ферромагнитного резонанса. В противном случае следует пользоваться общими выражениями (1.9), (1.34), (1.35).
В заключение запишем формулу для ненагруженной добротности ферритового резонатора. Для этого в формулу (1.45) подставим выражение (119) для поля  и получим
и получим

Экспериментальная проверка этой формулы, выполненная Картером и Фламмером [11], показала, что зависимость (1.53) подтверждается.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава первая. СВОЙСТВА ФЕРРИТОВЫХ РЕЗОНАТОРОВ
- Ферромагнитный резонанс в неограниченной среде без потерь
- 1.2. РЕЗОНАНСНАЯ ЧАСТОТА
- Зависимость резонансной частоты от формы резонатора
- Влияние кристаллографической анизотропии на резонансную частоту
- 1.3. МАГНИТОСТАТИЧЕСКИЕ ВИДЫ КОЛЕБАНИЙ
- 1.4. УЧЕТ ПОТЕРЬ
- 1.5. ДИПОЛЬНЫЙ МОМЕНТ
- 1.6. НЕЛИНЕЙНЫЕ ЯВЛЕНИЯ
- Спиновые волны
- Пороговая амплитуда высокочастотного магнитного поля
- Восприимчивость при амплитудах поля, превышающих пороговое значение
- 1.7. ПРИМЕНЯЕМЫЕ ДЛЯ ИЗГОТОВЛЕНИЯ МАТЕРИАЛЫ
- 1.8. ТЕМПЕРАТУРНЫЕ ХАРАКТЕРИСТИКИ
- 1.9. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- Глава вторая. СВОЙСТВА ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 2.2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В АНИЗОТРОПНОМ ДИЭЛЕКТРИЧЕСКОМ СТЕРЖНЕ С «МАГНИТНЫМИ» БОКОВЫМИ СТЕНКАМИ
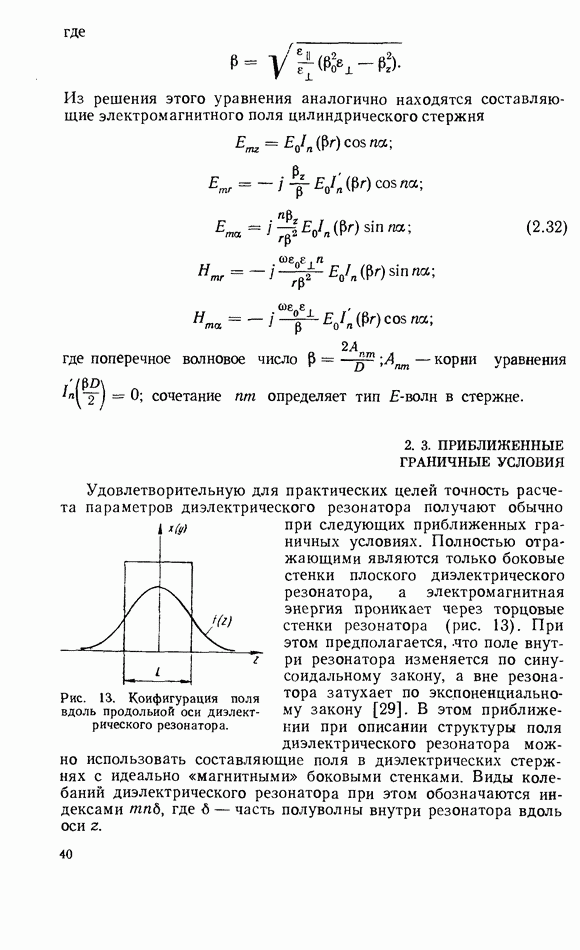
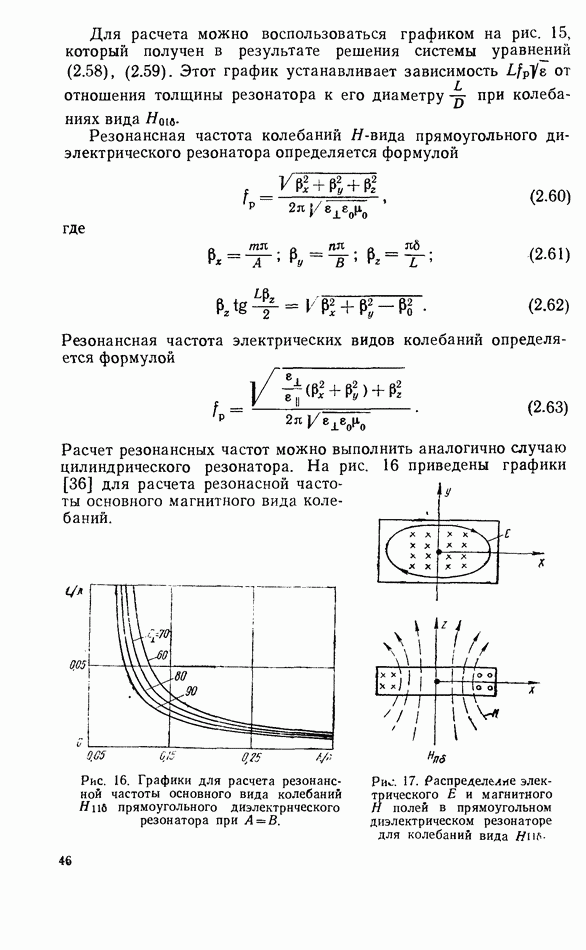
- 2.3. ПРИБЛИЖЕННЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2.5. ОСНОВНЫЕ ВИДЫ КОЛЕБАНИЙ
- 2.6. СФЕРИЧЕСКИЕ ДИЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
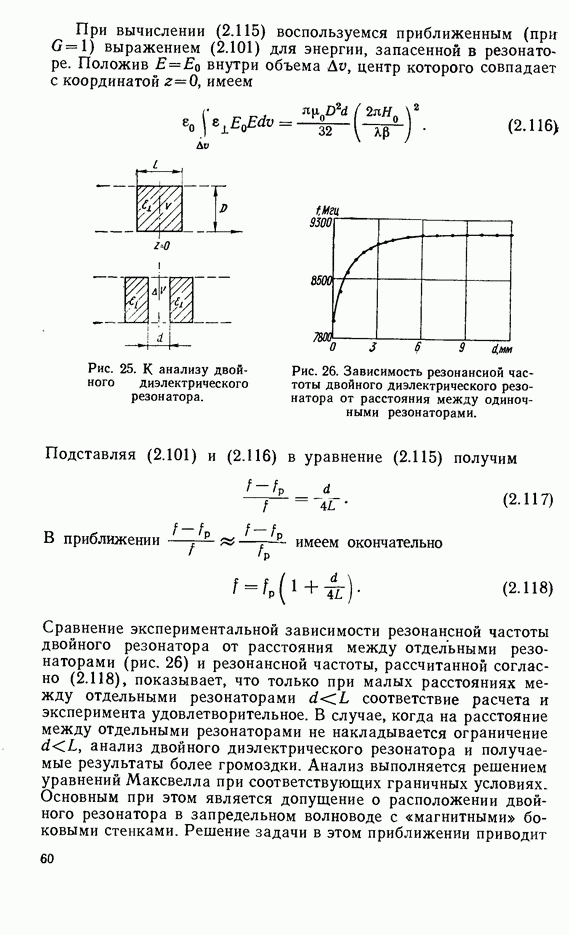
- 2.7. ВЛИЯНИЕ МЕТАЛЛИЧЕСКИХ СТЕНОК НА ХАРАКТЕРИСТИКИ ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 2.8. ДИПОЛЬНЫЙ МОМЕНТ
- 2.9. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ
- 2.10. СООТНОШЕНИЕ МЕЖДУ АМПЛИТУДАМИ СВЧ МАГНИТНОГО ПОЛЯ
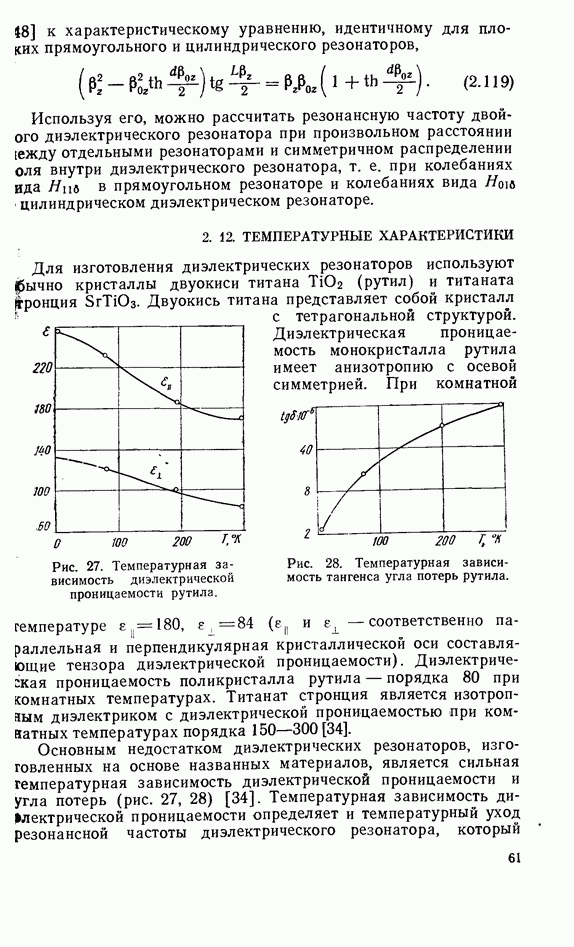
- 2.11. ДВОЙНЫЕ ДИЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
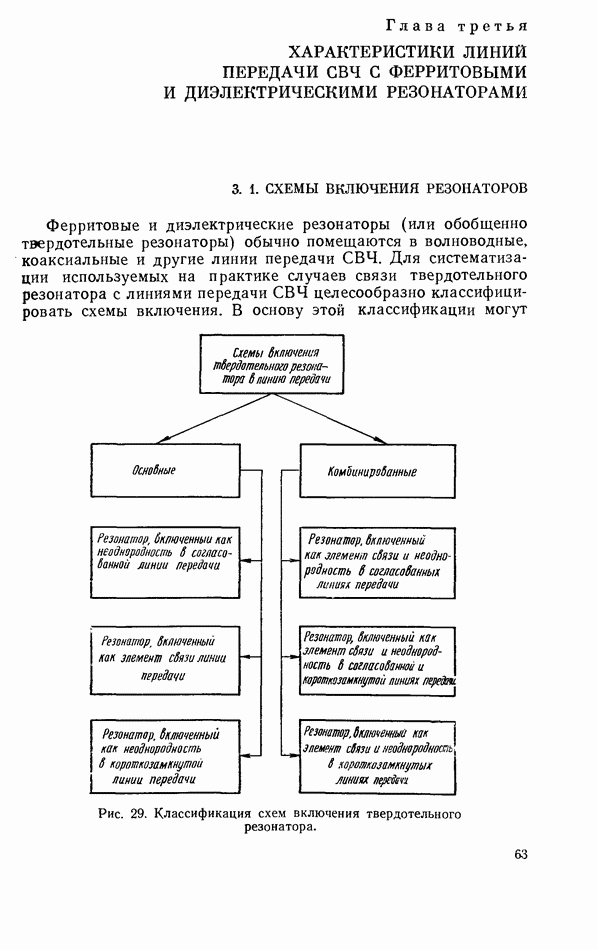
- 2.12. ТЕМПЕРАТУРНЫЕ ХАРАКТЕРИСТИКИ
- Глава третья. ХАРАКТЕРИСТИКИ ЛИНИЙ ПЕРЕДАЧИ СВЧ С ФЕРРИТОВЫМИ И ДИЭЛЕКТРИЧЕСКИМИ РЕЗОНАТОРАМИ
- 3.2. МЕТОДЫ РАСЧЕТА СВЧ-СХЕМ С ТВЕРДОТЕЛЬНЫМИ РЕЗОНАТОРАМИ
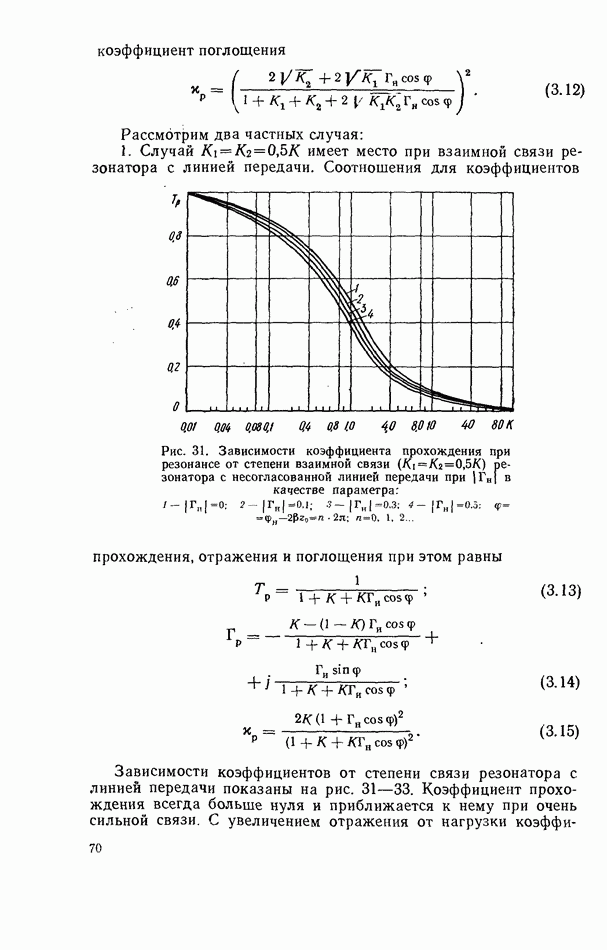
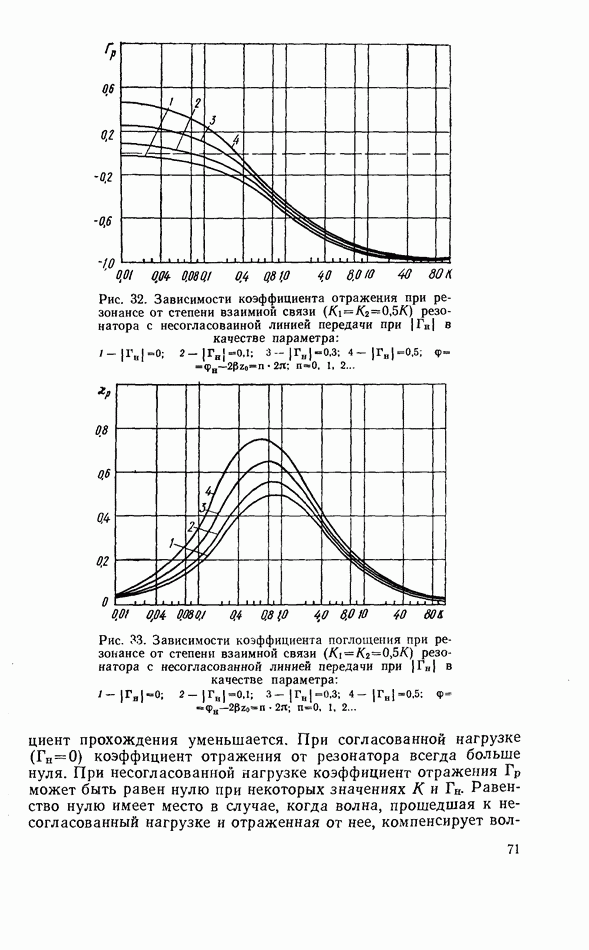
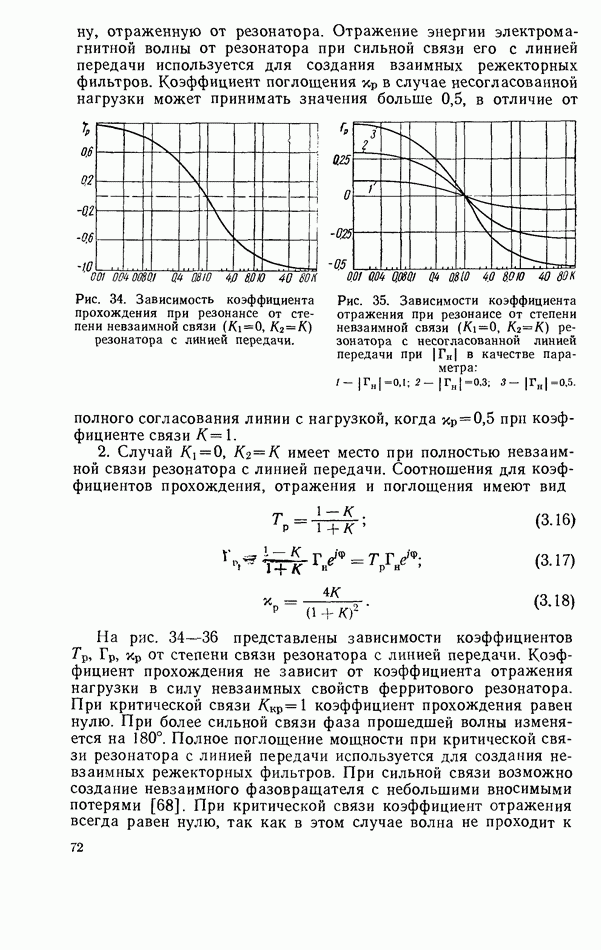
- 3.3. СВЯЗЬ ТВЕРДОТЕЛЬНОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ СВЧ
- 3.4. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В НЕСОГЛАСОВАННОЙ ЛИНИИ ПЕРЕДАЧИ
- 3.5. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР, ВКЛЮЧЕННЫЙ КАК ЭЛЕМЕНТ СВЯЗИ ЛИНИЙ ПЕРЕДАЧИ
- 3.6. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В КОРОТКОЗАМКНУТОЙ ЛИНИИ ПЕРЕДАЧИ
- 3.7. КОМБИНИРОВАННЫЕ СХЕМЫ ВКЛЮЧЕНИЯ ТВЕРДОТЕЛЬНОГО РЕЗОНАТОРА
- 3.8. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ С НЕСКОЛЬКИМИ РАСПРОСТРАНЯЮЩИМИСЯ ВОЛНАМИ
- Глава четвертая. СВЯЗЬ ТВЕРДОТЕЛЬНЫХ РЕЗОНАТОРОВ С ЛИНИЯМИ ПЕРЕДАЧИ СВЧ
- 4.2. СВЯЗЬ ФЕРРИТОВОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ
- 4.3. ФЕРРИТОВЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ ЗАМЕДЛЕННЫХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
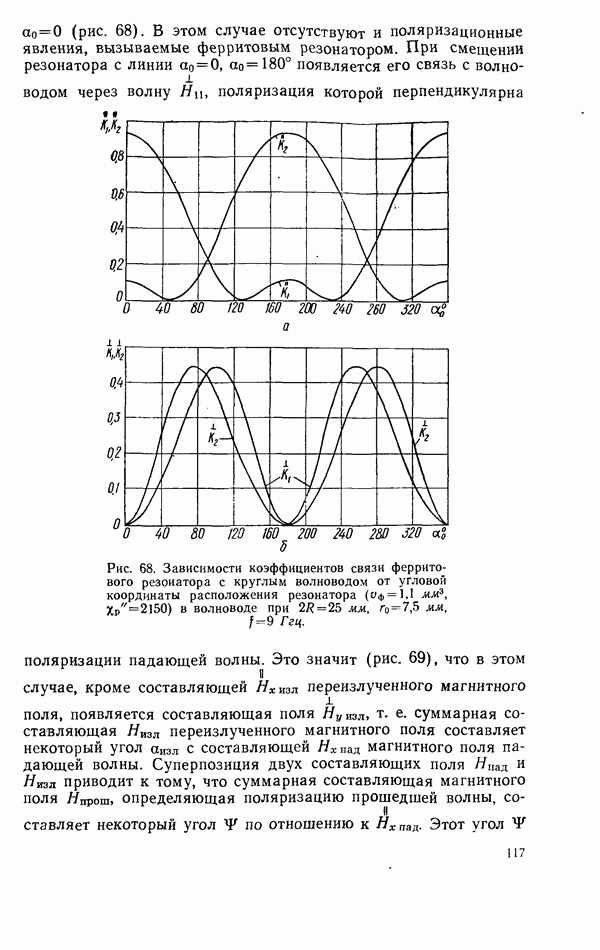
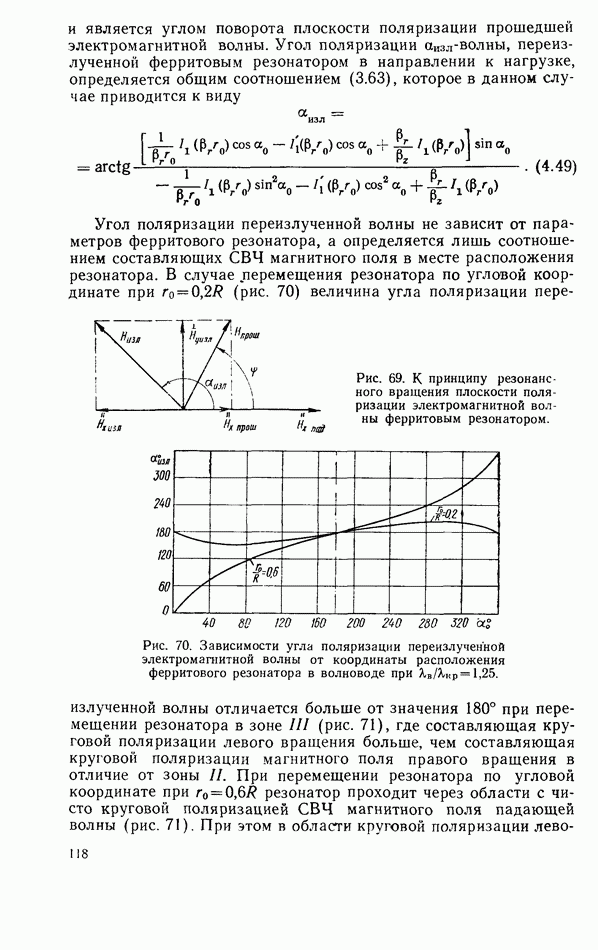
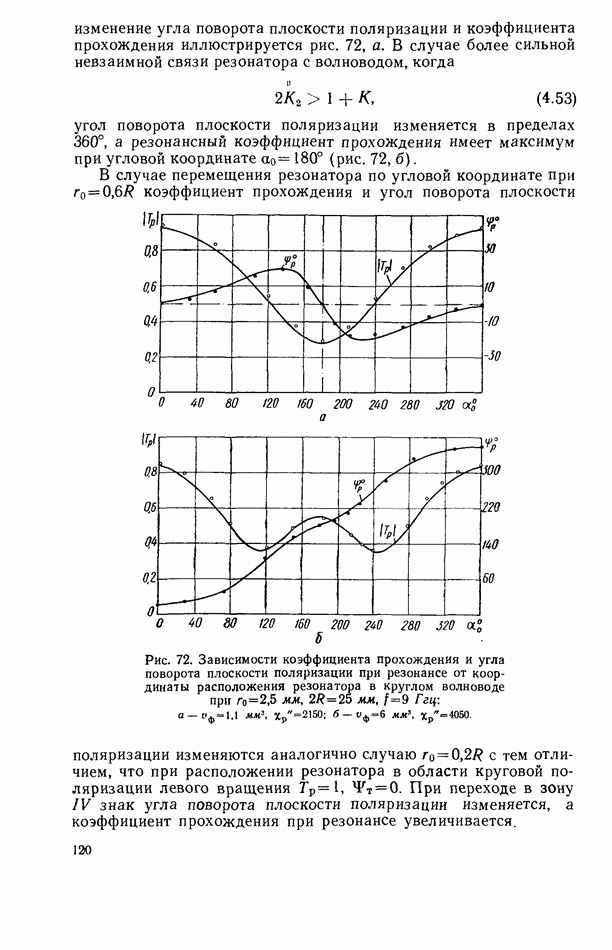
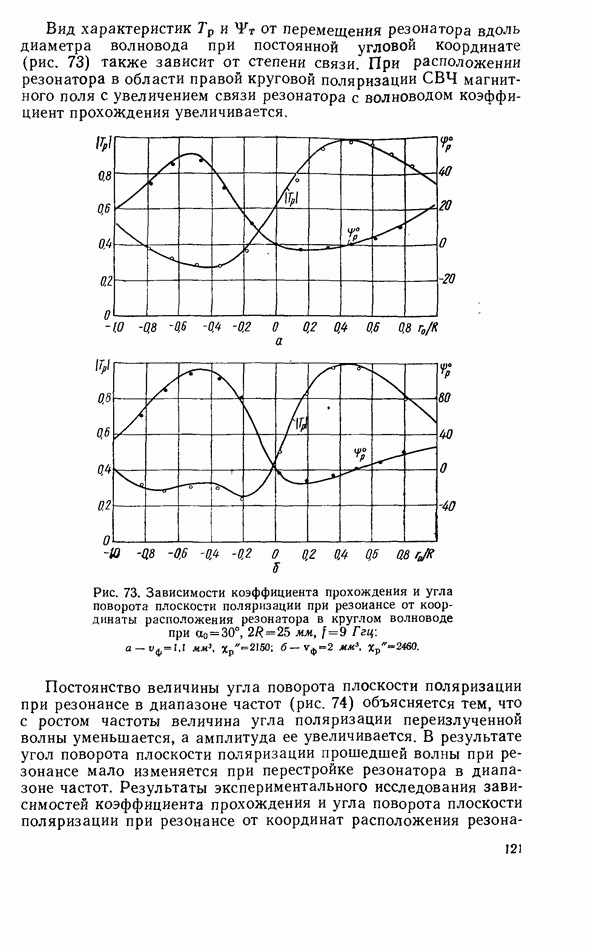
- 4.4. РЕЗОНАНСНЫЙ ПОВОРОТ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ В ВОЛНОВОДЕ С ФЕРРИТОВЫМ РЕЗОНАТОРОМ
- 4.5. НЕЛИНЕЙНЫЙ ФЕРРИТОВЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ
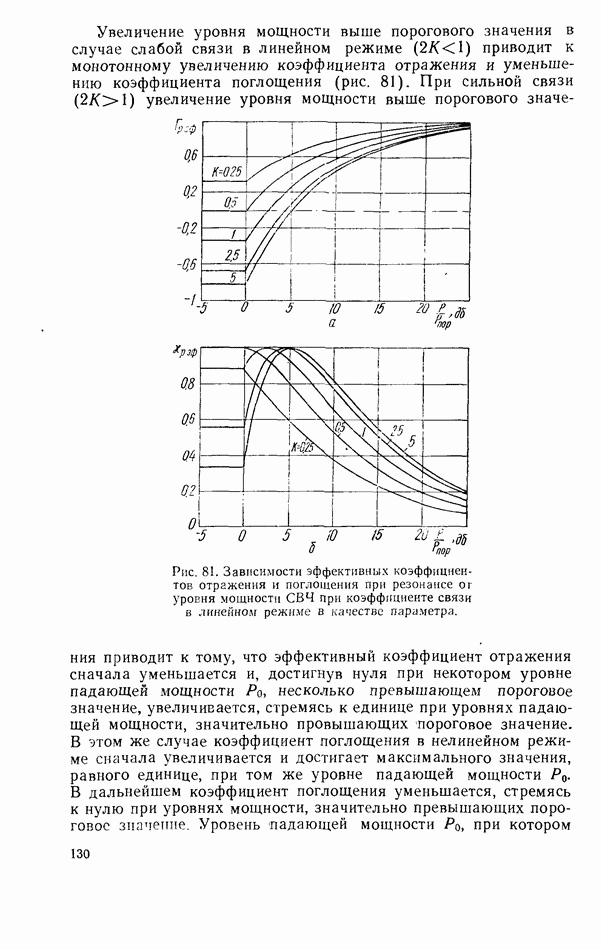
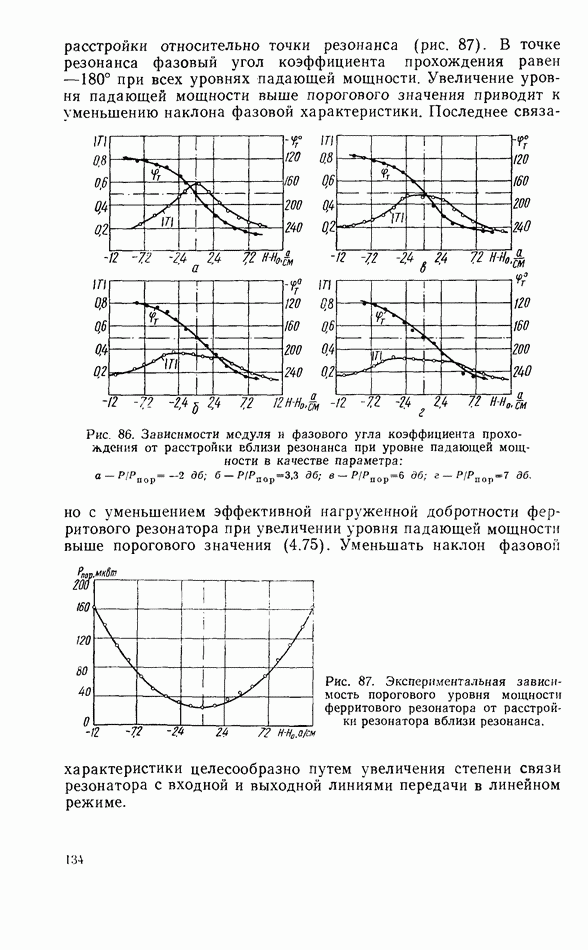
- Ферритовый резонатор в линии передачи при запороговых уровнях мощности
- Нелинейный ферритовый резонатор в короткозамкнутой линии передачи
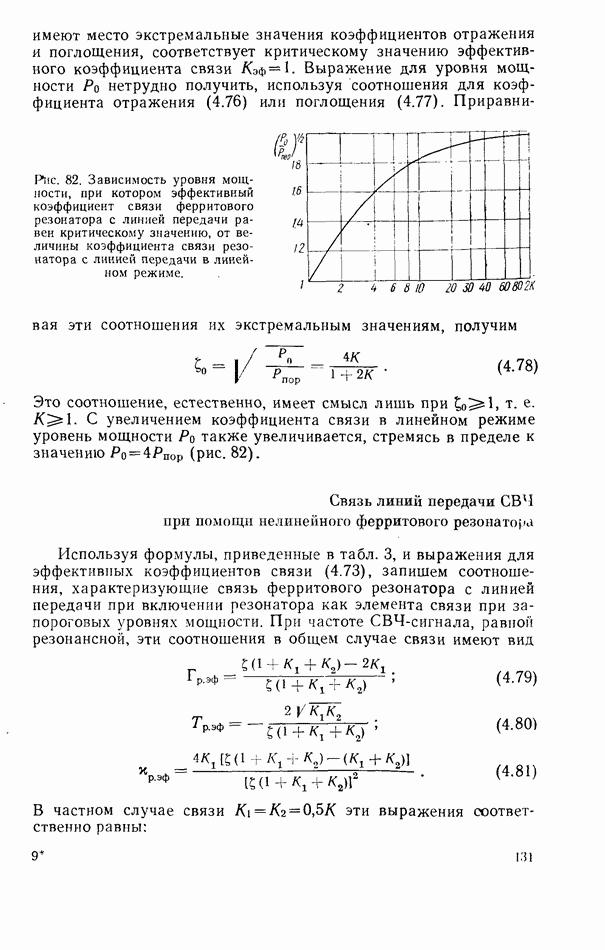
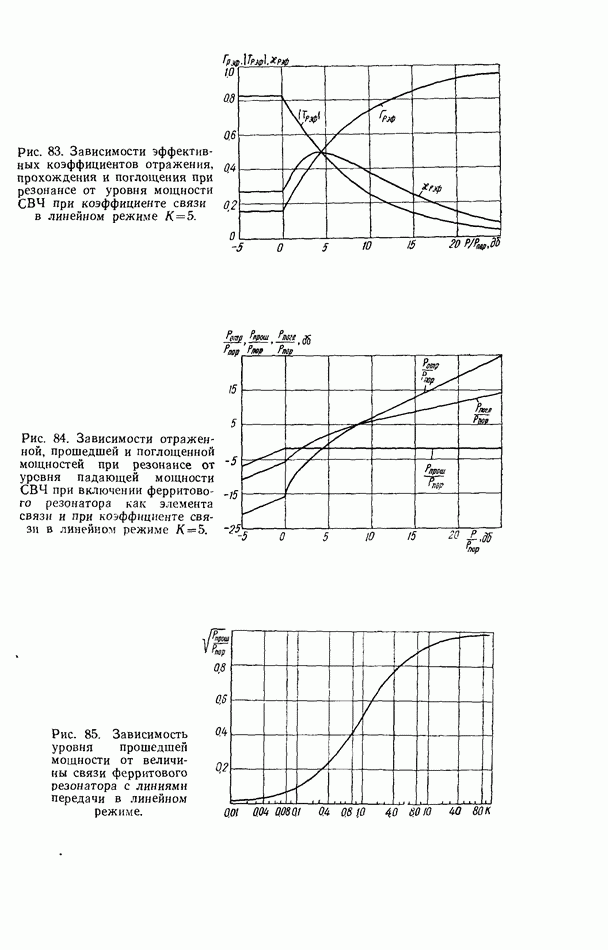
- Связь линий передачи СВЧ при помощи нелинейного ферритового резонатора
- Нелинейный ферритовый резонатор в согласованной линии передачи
- 4.6. СВЯЗЬ ДИЭЛЕКТРИЧЕСКОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ СВЧ
- Глава пятая. ПРИНЦИПЫ ПОСТРОЕНИЯ СВЧ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ И УСТРОЙСТВ НА ОСНОВЕ ТВЕРДОТЕЛЬНЫХ РЕЗОНАТОРОВ
- 5.2. ДАТЧИКИ УРОВНЯ МОЩНОСТИ СВЧ
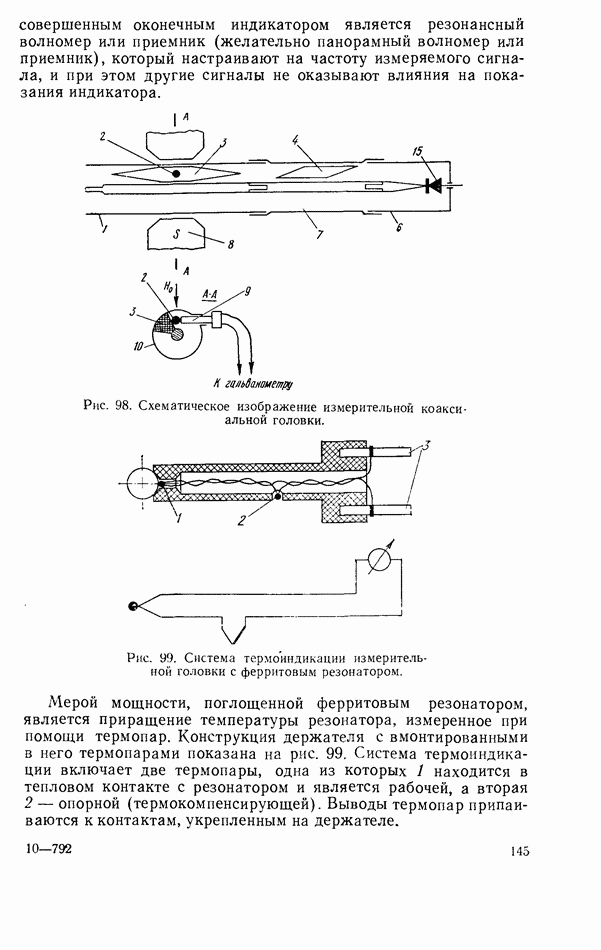
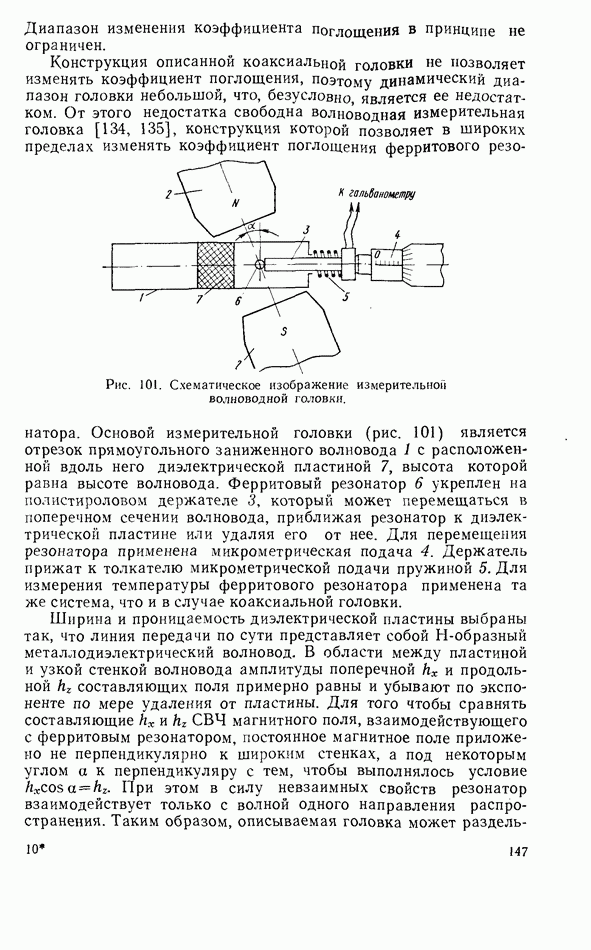
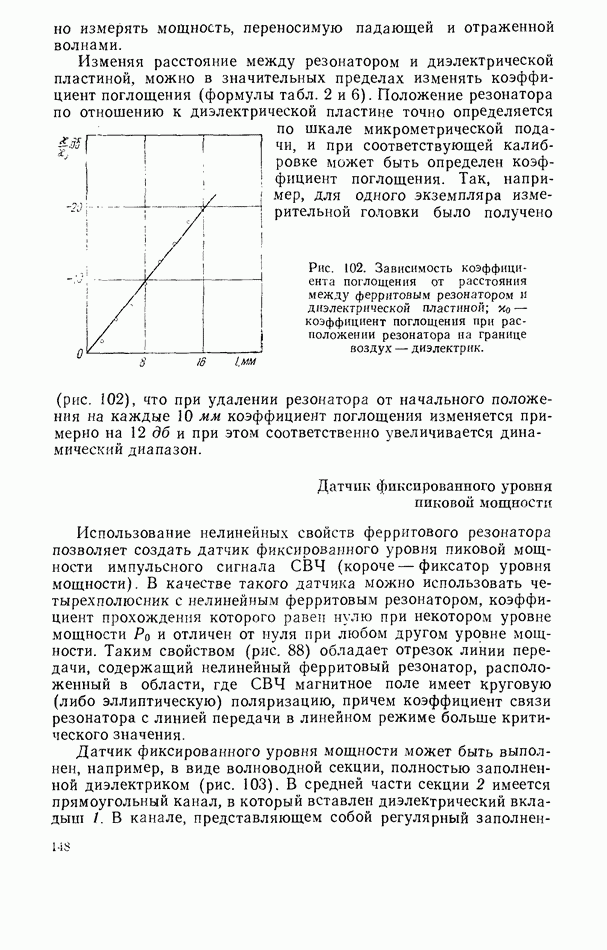
- Волноводная измерительная головка
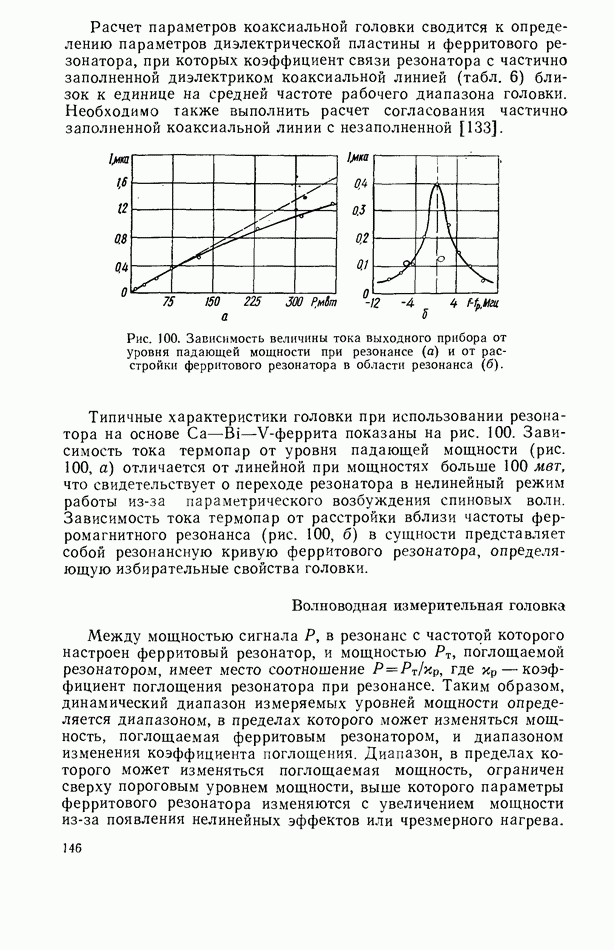
- Датчик фиксированного уровня пиковой мощности
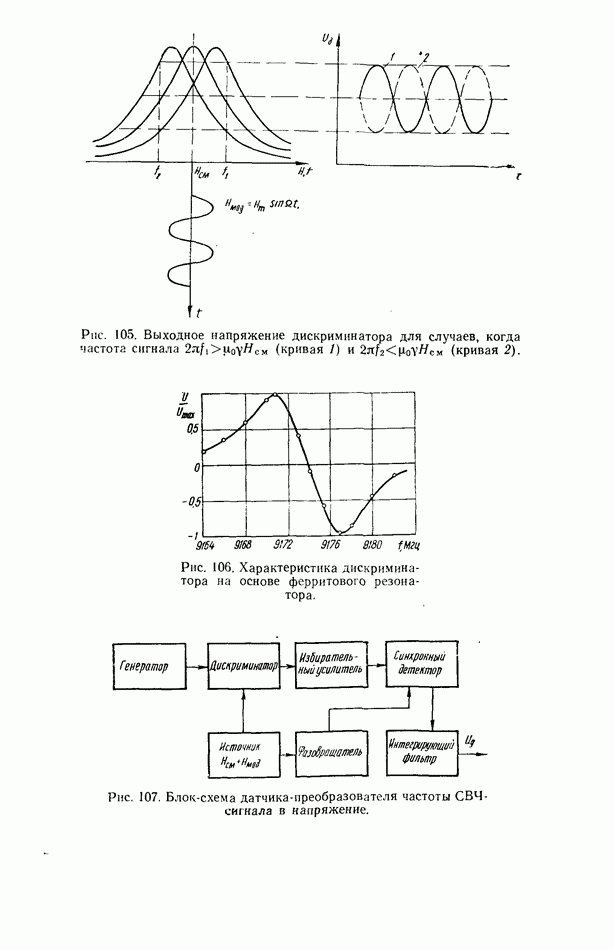
- 5.3. ЧАСТОТНЫЕ ДИСКРИМИНАТОРЫ С МАГНИТНОЙ НАСТРОЙКОЙ
- 5.4. РЕЗОНАНСНЫЕ ФАЗОВРАЩАТЕЛИ
- 5.5. УСТРОЙСТВО ДЛЯ РЕЗОНАНСНОГО ПОВОРОТА ПЛОСКОСТИ ПОЛЯРИЗАЦИИ В ВОЛНОВОДЕ
- 5.6. ФИЛЬТРЫ СВЧ НА ОСНОВЕ ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 5.7. ФЕРРИТОВЫЕ СВЧ-ФИЛЬТРЫ
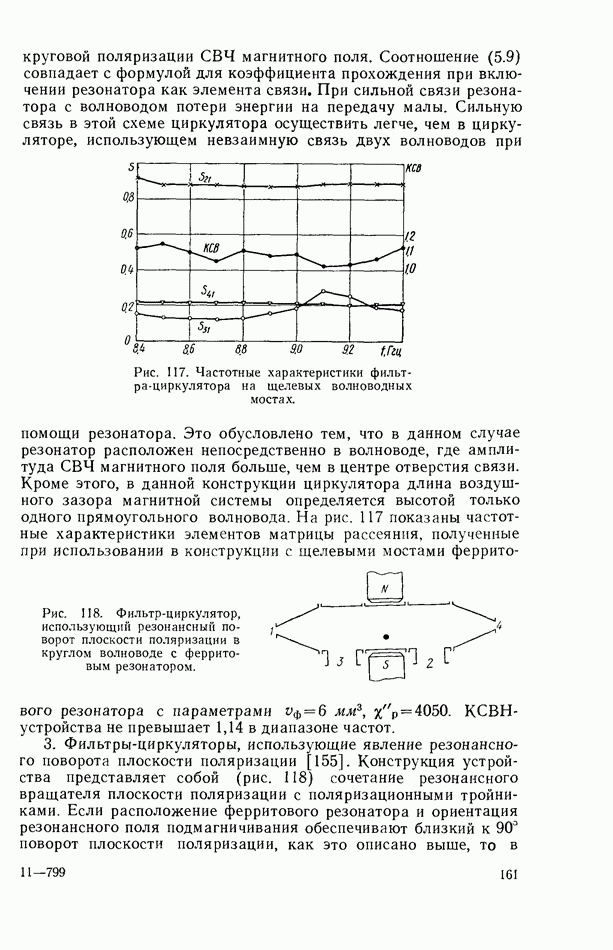
- Многофункциональные фильтры
- Многорезонаторные ферритовые фильтры
- 5.8. ЧАСТОТНО-ИЗБИРАТЕЛЬНЫЕ ОГРАНИЧИТЕЛИ МАЛЫХ УРОВНЕЙ МОЩНОСТИ