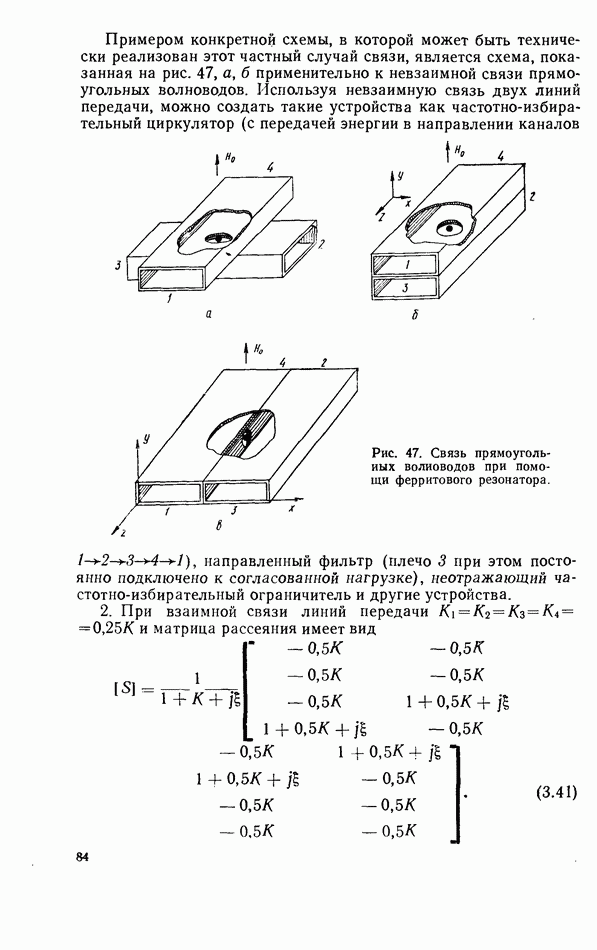
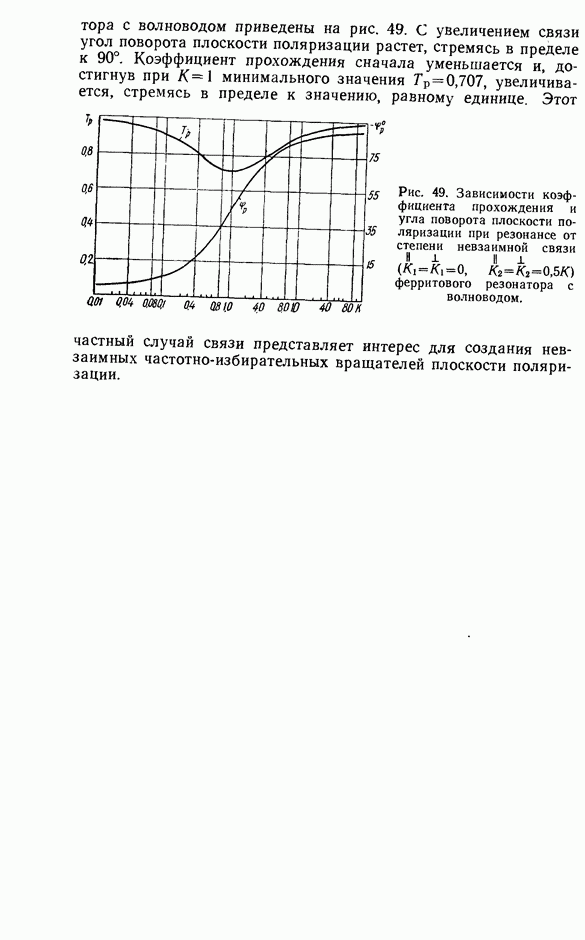
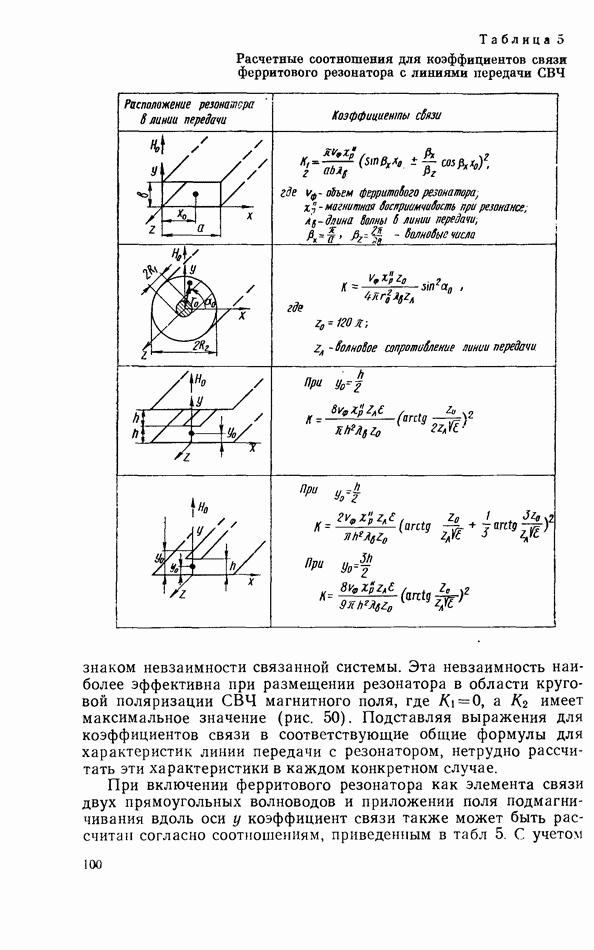
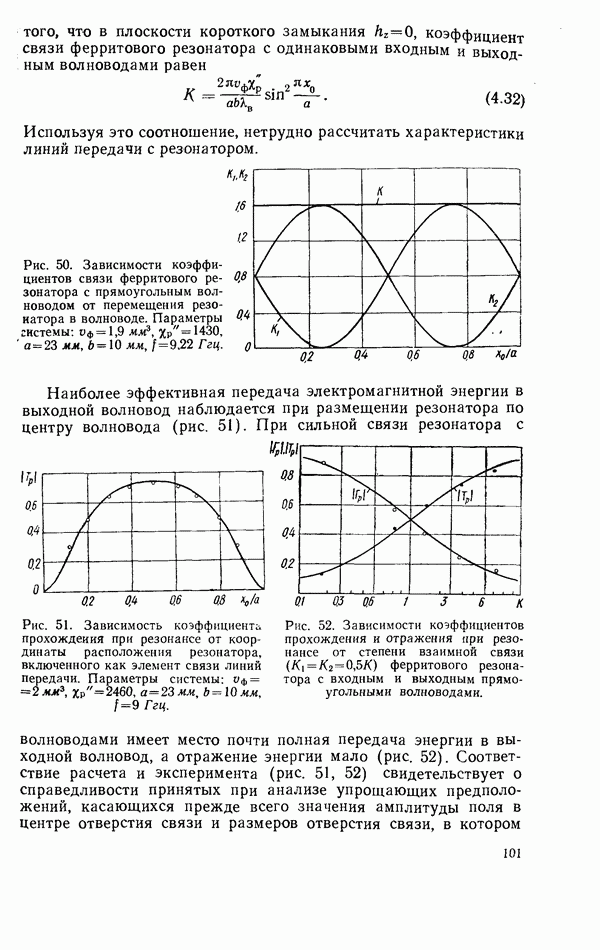
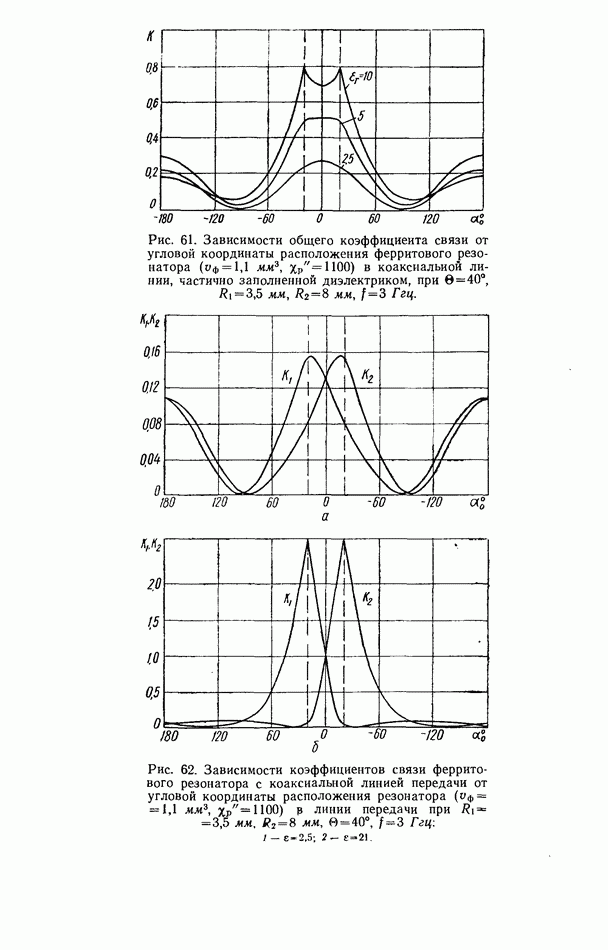
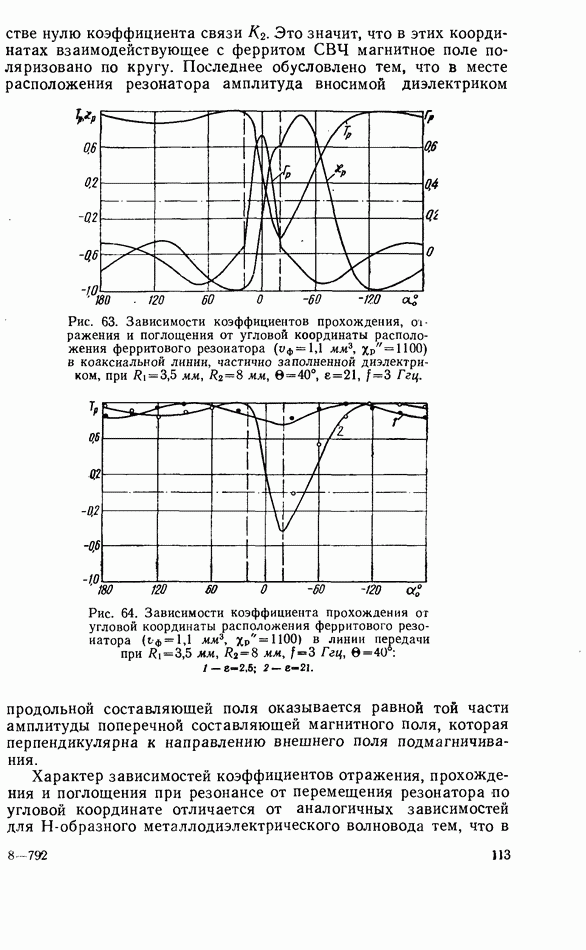
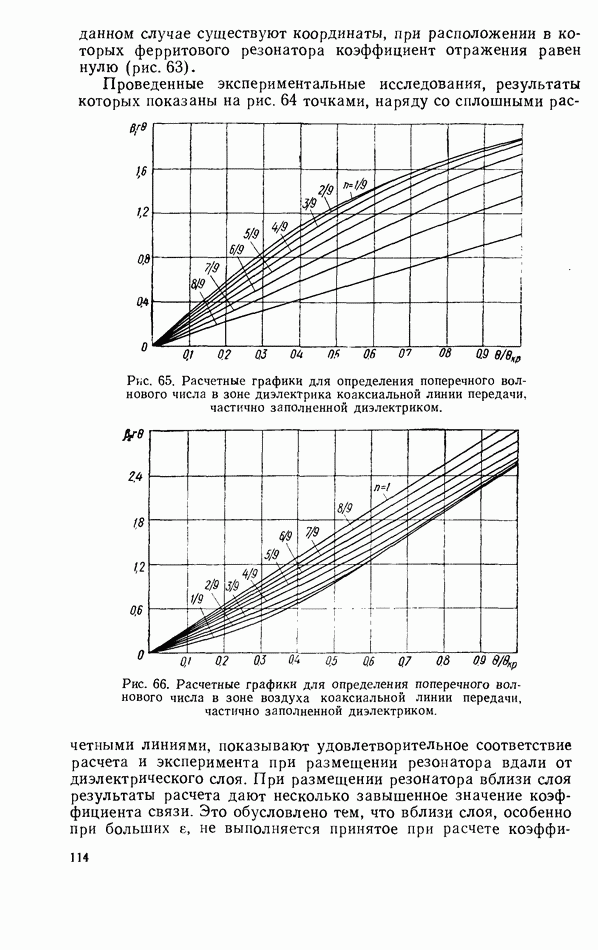
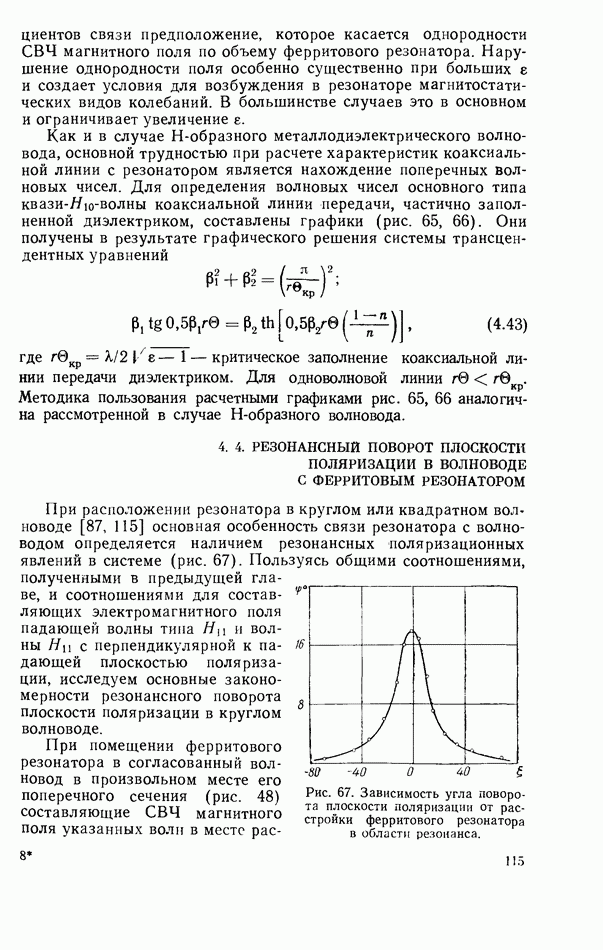
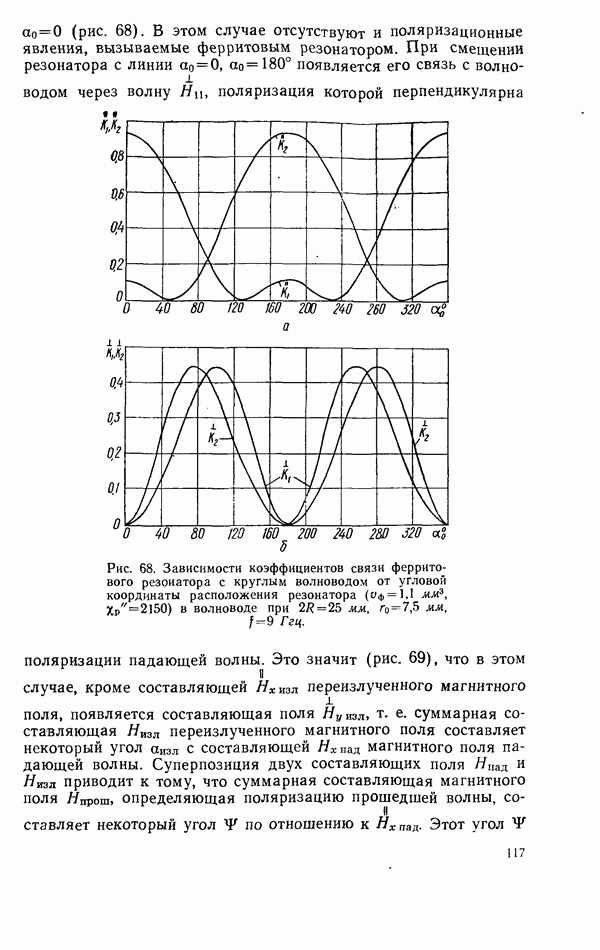
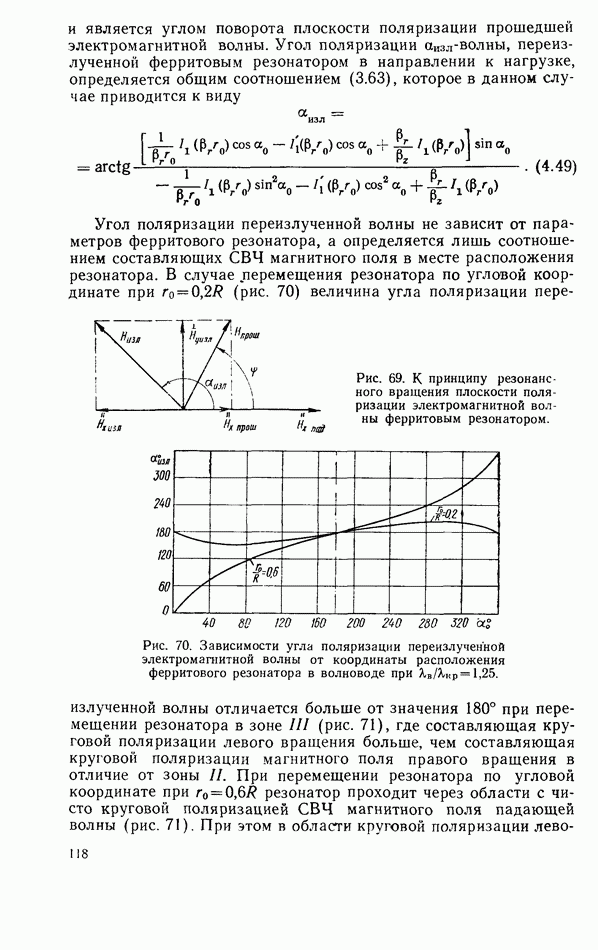
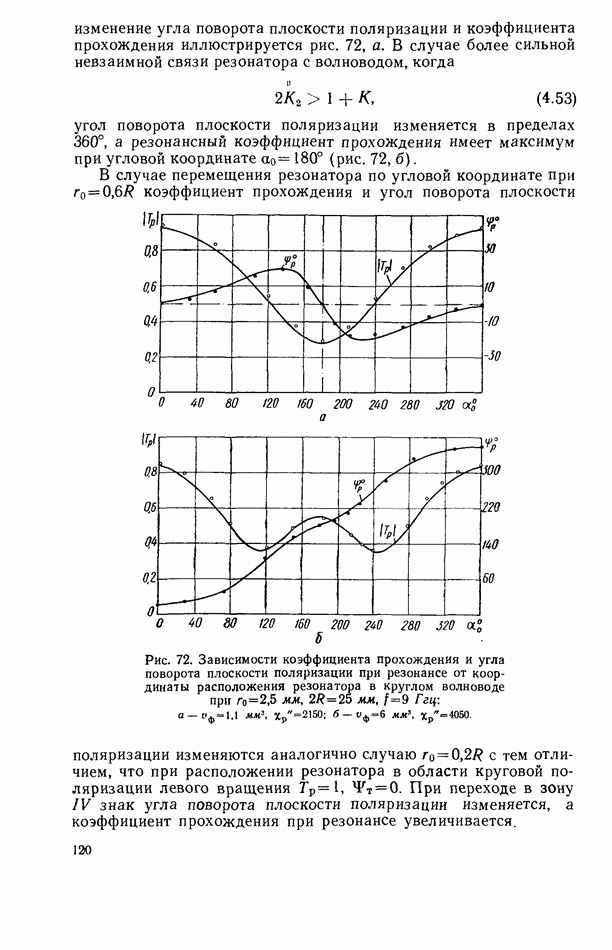
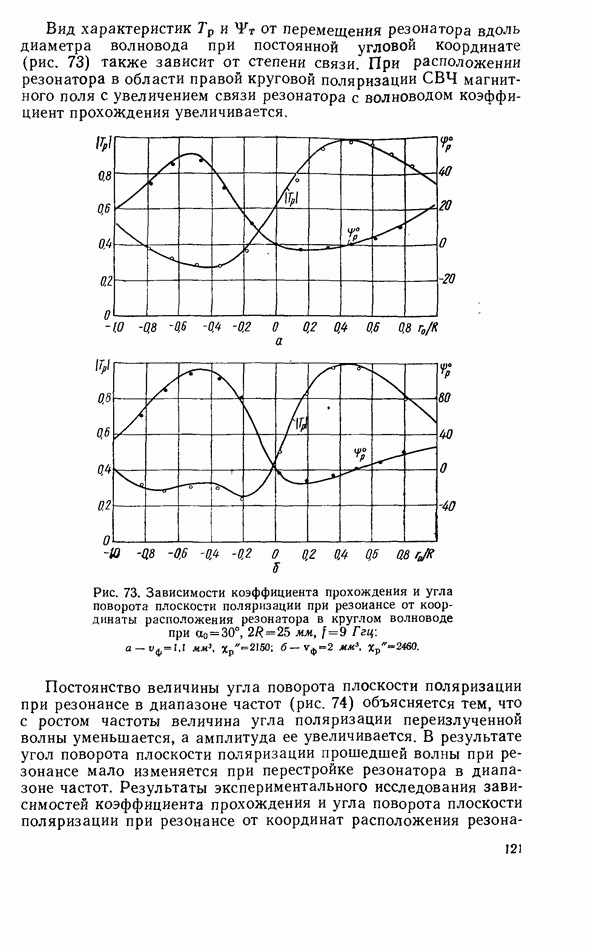
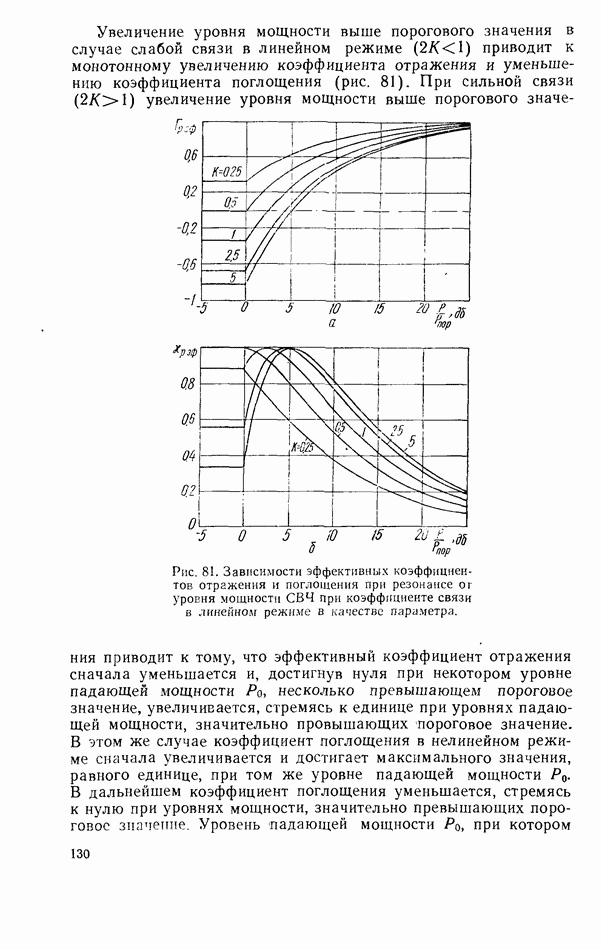
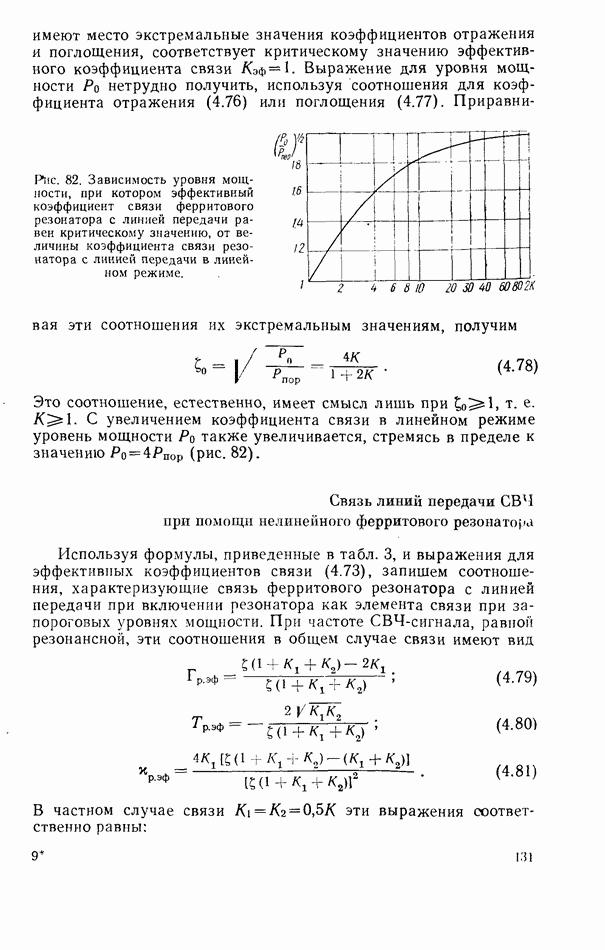
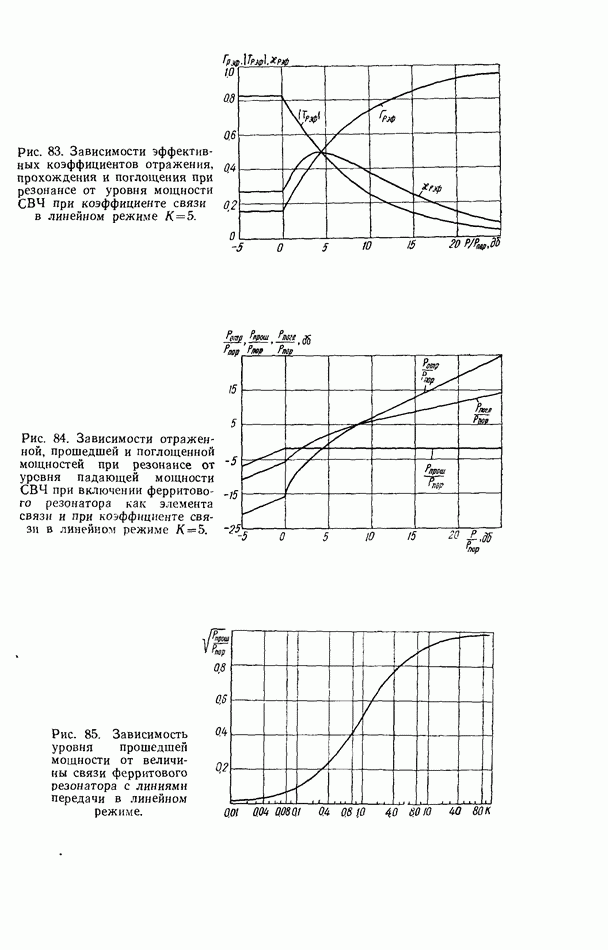
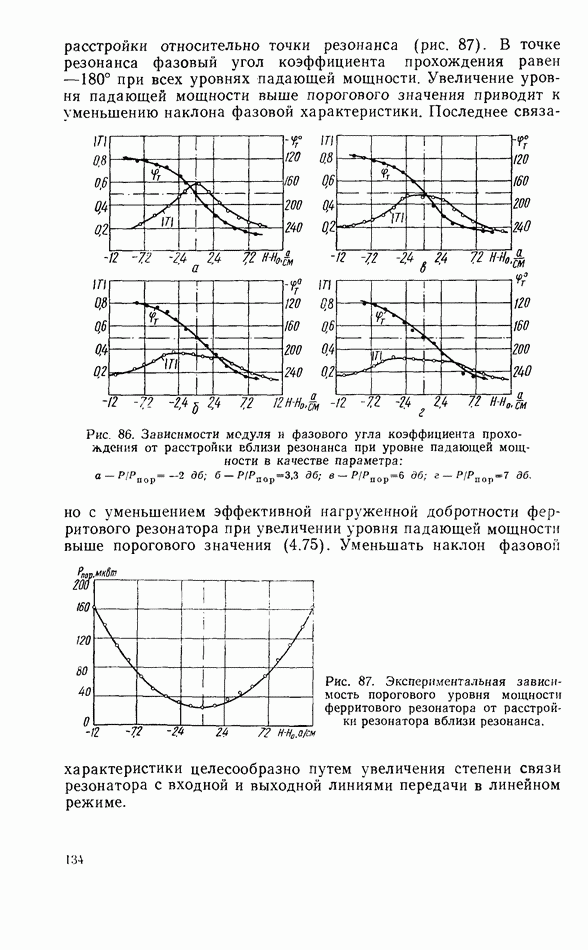
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.3. ПРИБЛИЖЕННЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
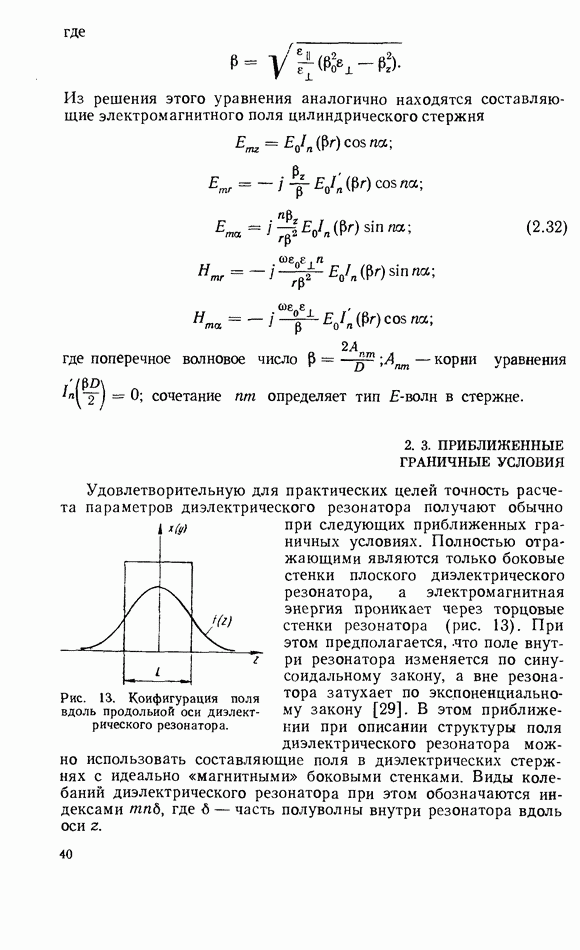
Удовлетворительную для практических целей точность расчета параметров диэлектрического резонатора получают обычно при следующих приближенных граничных условиях. Полностью отражающими являются только боковые стенки плоского диэлектрического резонатора, а электромагнитная энергия проникает через торцовые стенки резонатора (рис. 13). При этом предполагается, что поле внутри резонатора изменяется по синусоидальному закону, а вне резонатора затухает по экспоненциальному закону [29]. В этом приближении при описании структуры поля диэлектрического резонатора можно использовать составляющие поля в диэлектрических стержнях с идеально «магнитными» боковыми стенками. Виды колебаний диэлектрического резонатора при этом обозначаются индексами  где
где  — часть полуволны внутри резонатора вдоль оси
— часть полуволны внутри резонатора вдоль оси 

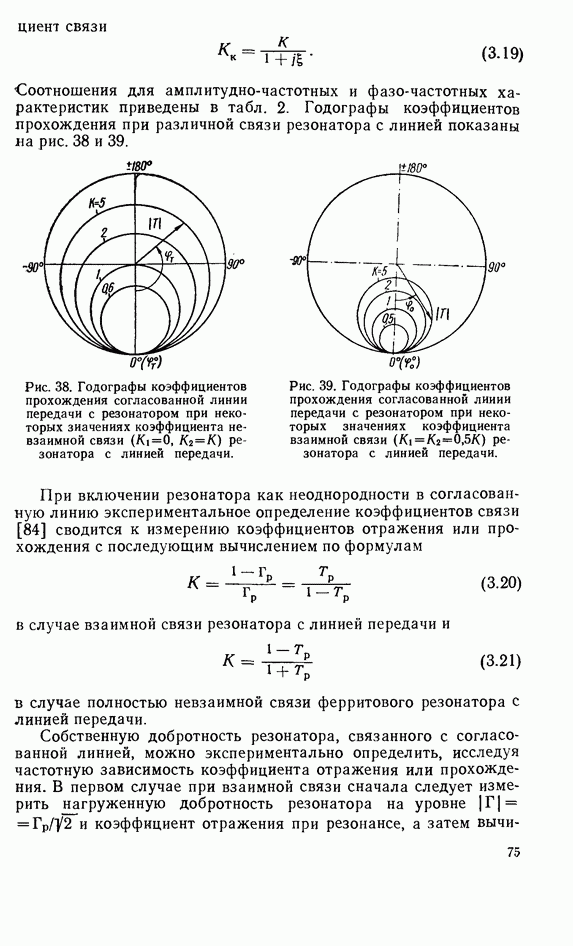
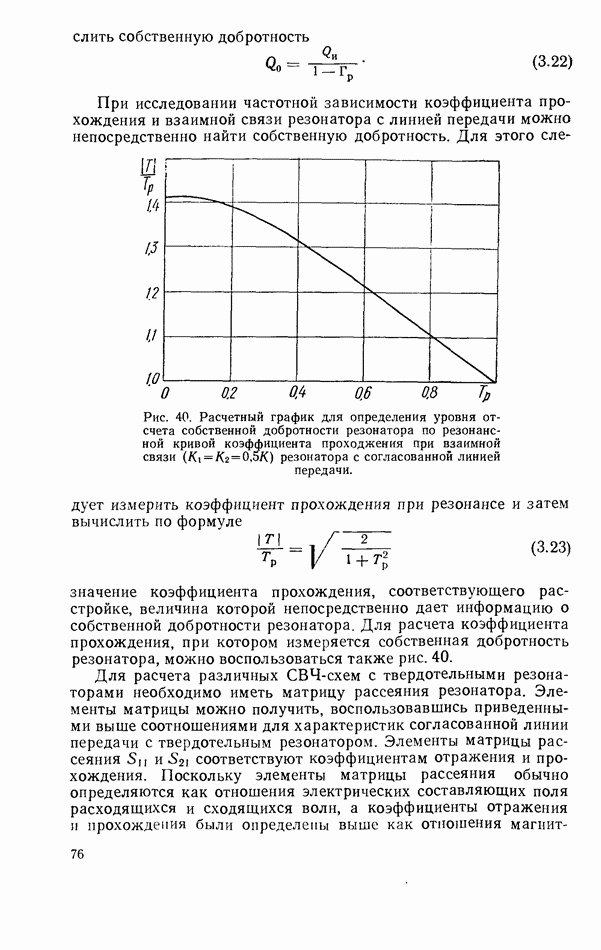
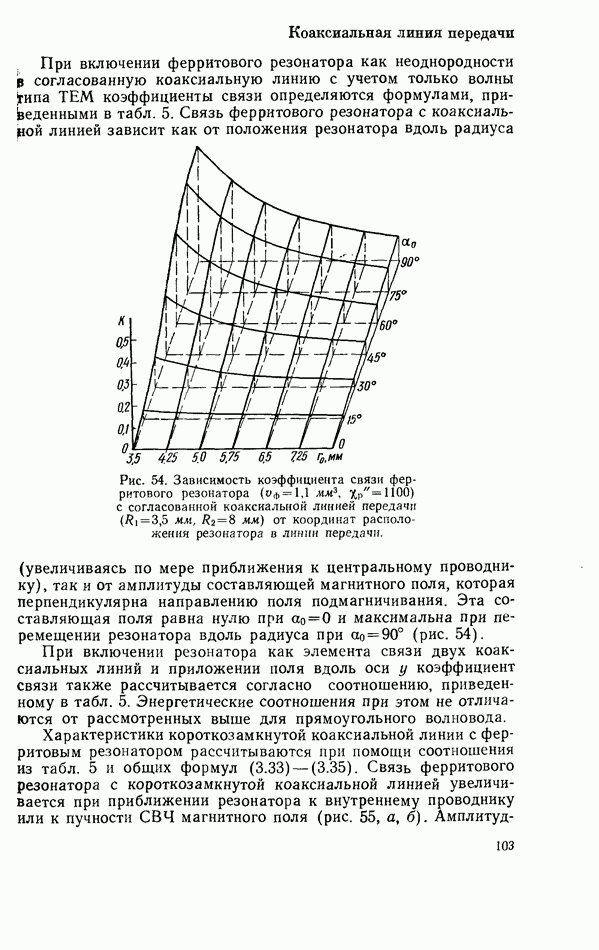
Рис. 13. Конфигурация поля вдоль продольной оси диэлектрического резонатора.
Получим соотношения для составляющих поля при колебаниях  -вида в прямоугольном диэлектрическом резонаторе [34]. Поскольку граничные условия в плоскостях
-вида в прямоугольном диэлектрическом резонаторе [34]. Поскольку граничные условия в плоскостях  не изменились по сравнению со случаем диэлектрического стержня с «магнитными» боковыми стенками, то составляющие электрического поля внутри резонатора можно представить в виде
не изменились по сравнению со случаем диэлектрического стержня с «магнитными» боковыми стенками, то составляющие электрического поля внутри резонатора можно представить в виде

Подставив эти выражения в уравнения Максвелла, получим

Решение этой системы можно представить в виде

где  постоянные.
постоянные.
Подставляя (2.35) в (2.34), получим

откуда

Поле вне резонатора должно быть таким, чтобы внутренние и внешние поля совпадали на плоскости раздела при  толщина резонатора. Таким образом, поля вне резонатора можно записать в виде
толщина резонатора. Таким образом, поля вне резонатора можно записать в виде

Решая аналогично, получим

где

знак «+» соответствует  постоянные числа;
постоянные числа;  постоянная, характеризующая экспоненциальный характер убывания поля вне резонатора.
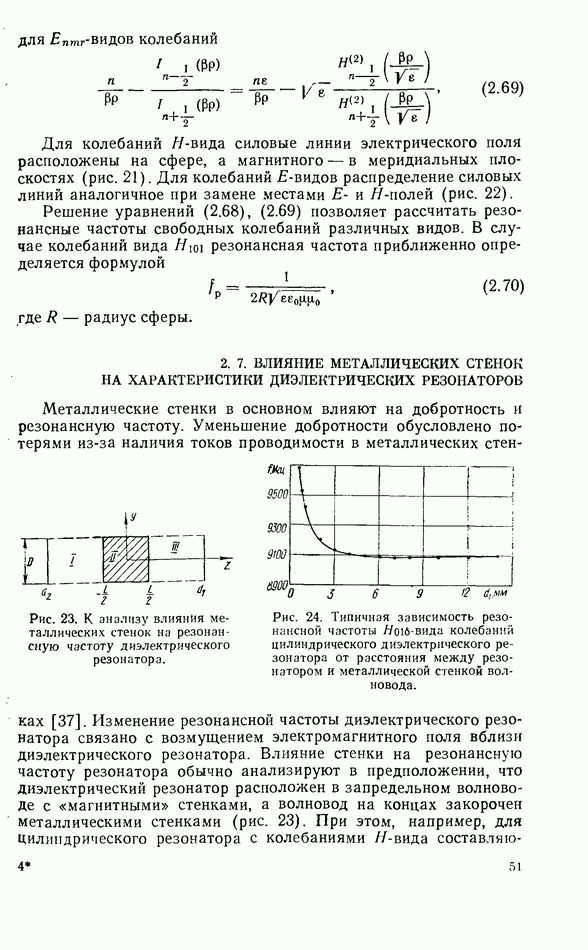
постоянная, характеризующая экспоненциальный характер убывания поля вне резонатора.
Из условия непрерывности касательных составляющих векторов электрического и магнитного поля при 

можно получить уравнение

Составляющие электромагнитного поля нечетных  -видов колебаний прямоугольного диэлектрического резонатора запишем в виде:
-видов колебаний прямоугольного диэлектрического резонатора запишем в виде:
внутри резонатора 

вне резонатора 


где поперечные и продольные волновые числа определяются соотношениями

Составляющие электромагнитного поля колебаний  -вида в цилиндрическом резонаторе определяются аналогично случаю прямоугольного резонатора и имеют вид:
-вида в цилиндрическом резонаторе определяются аналогично случаю прямоугольного резонатора и имеют вид:
внутри резонатора 

вне резонатора 


где

При  -колебаниях волновые числа определяются формулами
-колебаниях волновые числа определяются формулами

2. 4. РЕЗОНАНСНЫЕ ЧАСТОТЫ ПЛОСКИХ ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
Из выражений (2.50) следует, что связь между волновыми числами и резонансной частотой колебаний  -вида определяется соотношением
-вида определяется соотношением

где

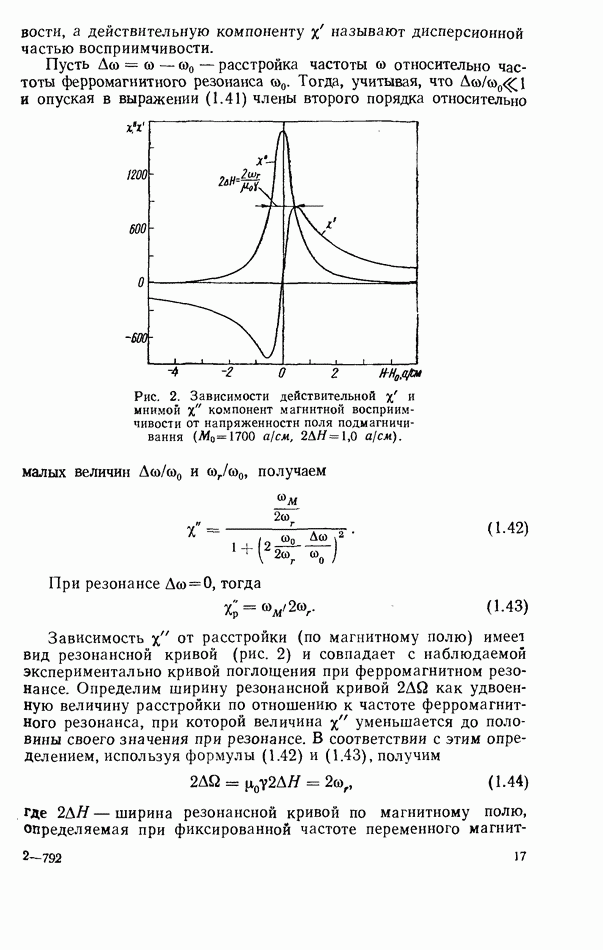
Для колебаний  -вида вместо соотношения (2.54) имеет место уравнение
-вида вместо соотношения (2.54) имеет место уравнение

где

Таким образом, резонансная частота колебаний в диэлектрическом резонаторе при заданных резмерах резонатора, как и в полых металлических резонаторах, определяется видом колебании. При заданных габаритах резонатора наибольшей резонансной длиной волны обладает колебание вида  в случае колебаний электрического вида низшим является колебание
в случае колебаний электрического вида низшим является колебание 
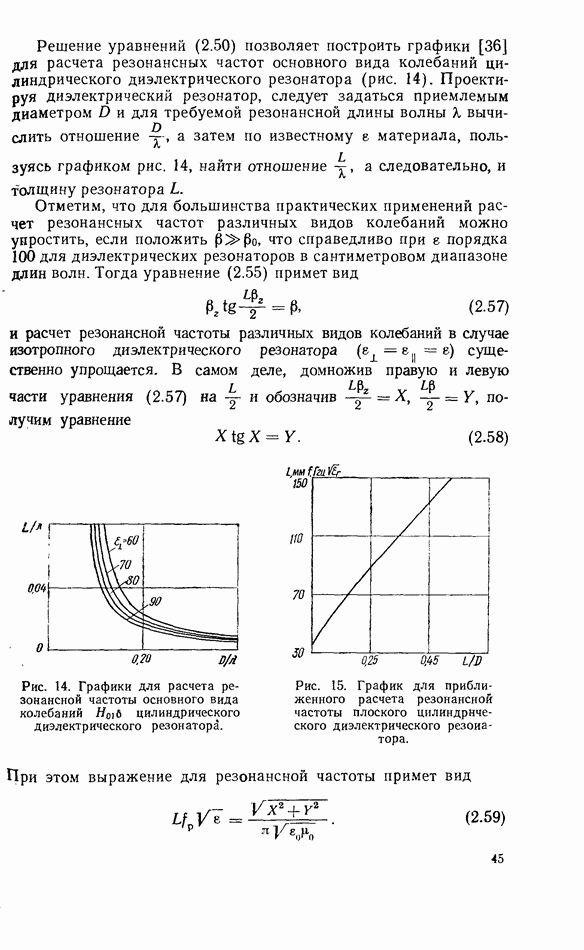
Решение уравнений (2.50) позволяет построить графики [36] для расчета резонансных частот основного вида колебаний цилиндрического диэлектрического резонатора (рис. 14). Проектируя диэлектрический резонатор, следует задаться приемлемым диаметром  и для требуемой резонансной длины волны X вычислить отношение
и для требуемой резонансной длины волны X вычислить отношение  а затем по известному
а затем по известному  материала, пользуясь графиком рис. 14, найти отношение а следовательно, и толщину резонатора
материала, пользуясь графиком рис. 14, найти отношение а следовательно, и толщину резонатора 
Отметим, что для большинства практических применений расчет резонансных частот различных видов колебаний можно упростить, если положить что справедливо при  порядка
порядка
100 для диэлектрических резонаторов в сантиметровом диапазоне длин волн. Тогда уравнение (2.55) примет вид

и расчет резонансной частоты различных видов колебаний в случае изотропного диэлектрического резонатора  существенно упрощается. В самом деле, домножив правую и левую части уравнения (2.57) на
существенно упрощается. В самом деле, домножив правую и левую части уравнения (2.57) на  и обозначив —
и обозначив —  получим уравнение
получим уравнение


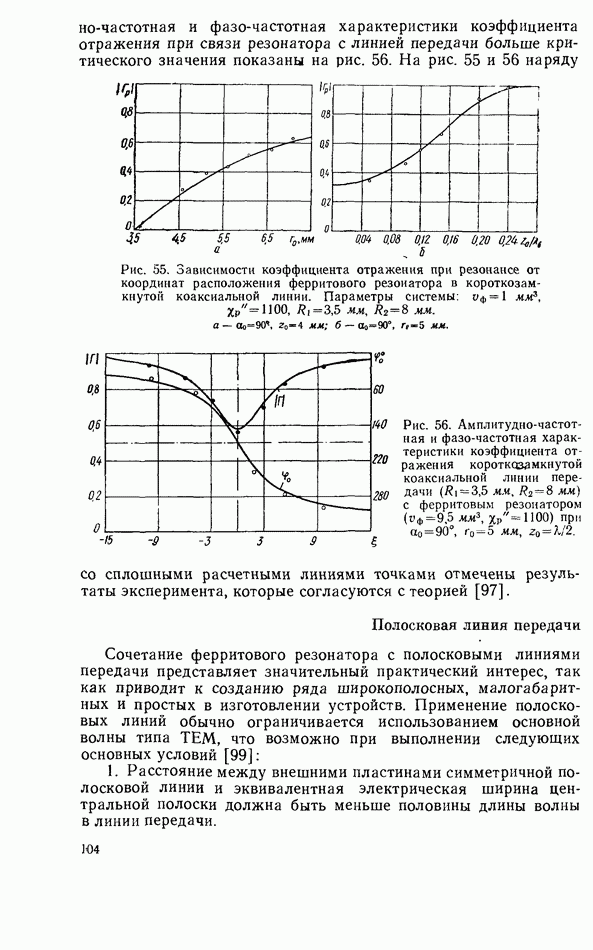
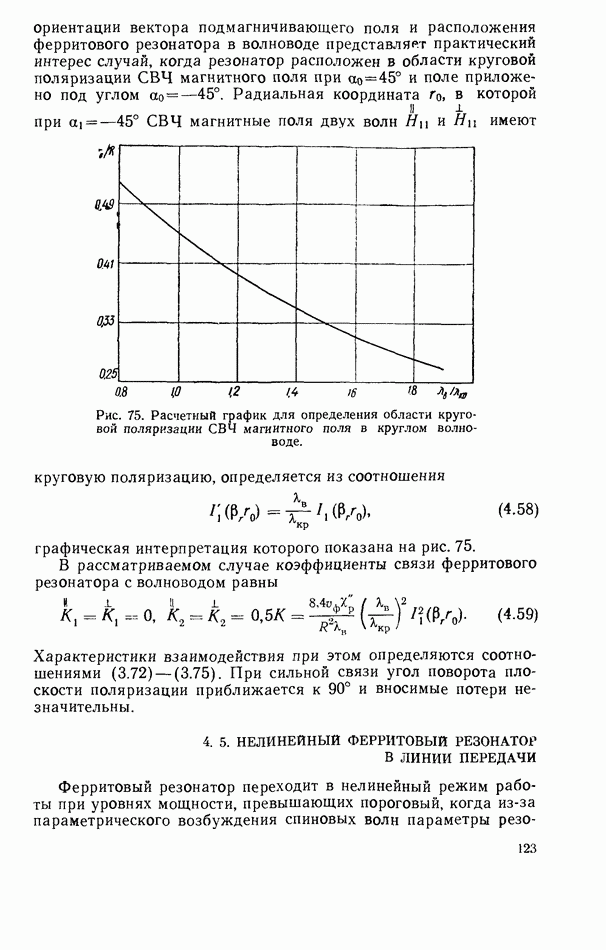
Рис. 14. Графики для расчета резонансной частоты основного вида колебаний  цилиндрического диэлектрического резонатора.
цилиндрического диэлектрического резонатора.

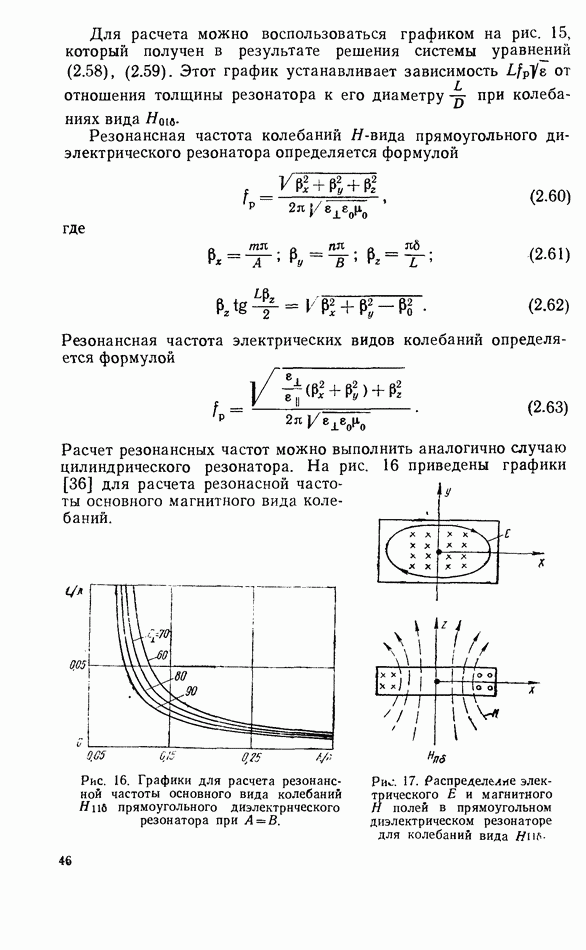
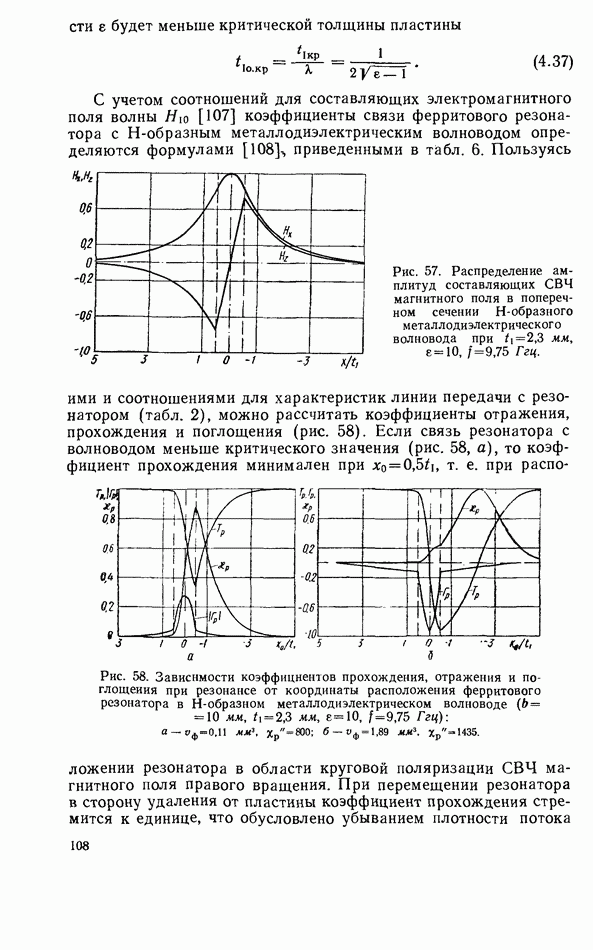
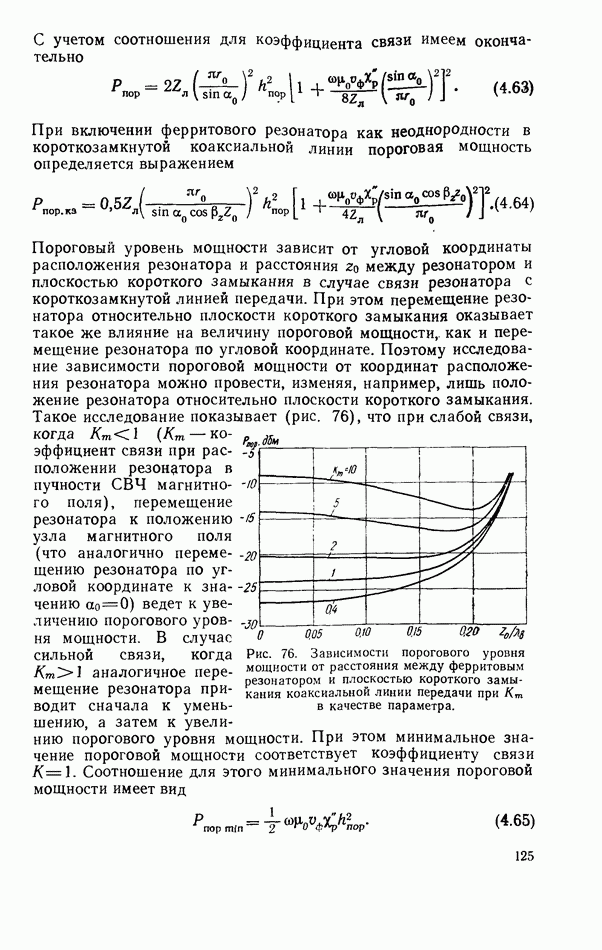
Рис. 15. График для приближенного расчета резонансной частоты плоского цилиндрического диэлектрического резонатора.
При этом выражение для резонансной частоты примет вид

Для расчета можно воспользоваться графиком на рис. 15, который получен в результате решения системы уравнений (2.58), (2.59). Этот график устанавливает зависимость  от отношения толщины резонатора к его диаметру при колебаниях вида
от отношения толщины резонатора к его диаметру при колебаниях вида 
Резонансная частота колебаний Н-вида прямоугольного диэлектрического резонатора определяется формулой

где

Резонансная частота электрических видов колебаний определяется формулой

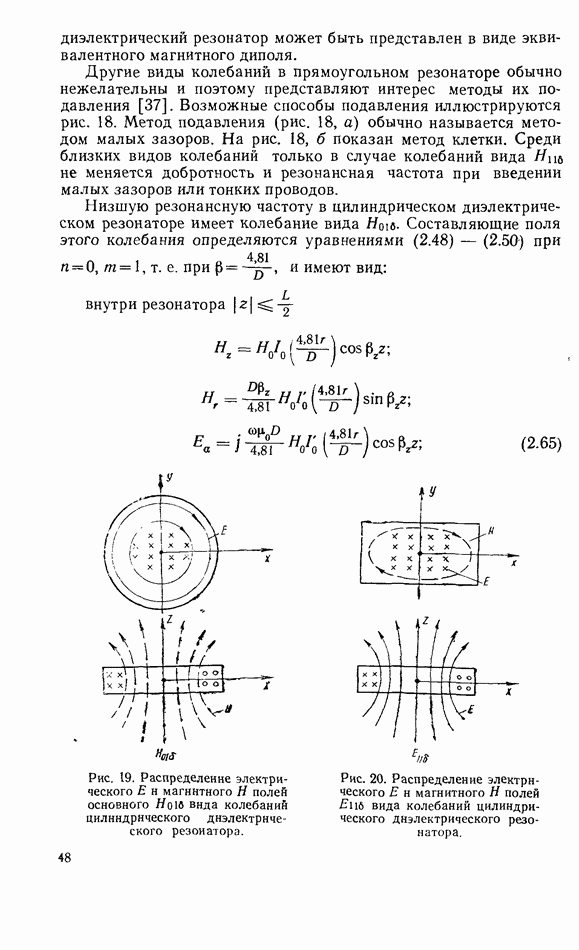
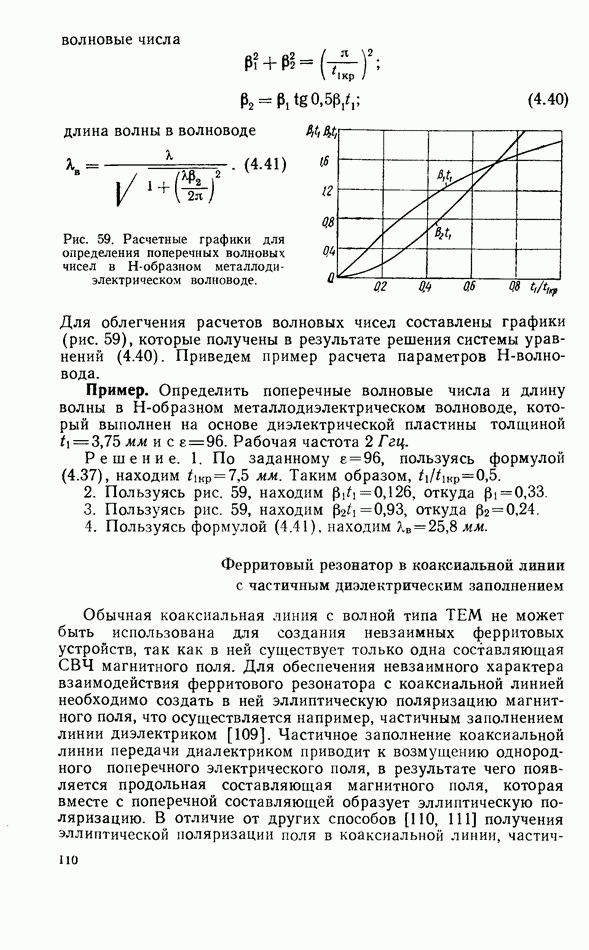
Расчет резонансных частот можно выполнить аналогично случаю цилиндрического резонатора. На рис. 16 приведены графики [36] для расчета резонасной частоты основного магнитного вида колебаний.

Рис. 16. Графики для расчета резонансной частоты основного вида колебаний  прямоугольного диэлектрического резонатора при
прямоугольного диэлектрического резонатора при 

Рис. 17. Распределение электрического  и магнитного Н полей в прямоугольном диэлектрическом резонаторе для колебаний вида
и магнитного Н полей в прямоугольном диэлектрическом резонаторе для колебаний вида 
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава первая. СВОЙСТВА ФЕРРИТОВЫХ РЕЗОНАТОРОВ
- Ферромагнитный резонанс в неограниченной среде без потерь
- 1.2. РЕЗОНАНСНАЯ ЧАСТОТА
- Зависимость резонансной частоты от формы резонатора
- Влияние кристаллографической анизотропии на резонансную частоту
- 1.3. МАГНИТОСТАТИЧЕСКИЕ ВИДЫ КОЛЕБАНИЙ
- 1.4. УЧЕТ ПОТЕРЬ
- 1.5. ДИПОЛЬНЫЙ МОМЕНТ
- 1.6. НЕЛИНЕЙНЫЕ ЯВЛЕНИЯ
- Спиновые волны
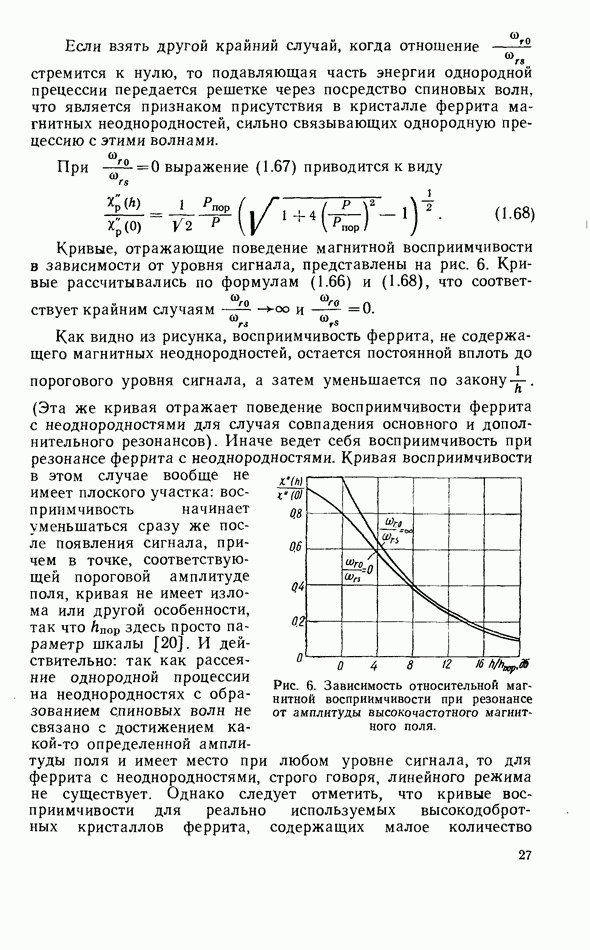
- Пороговая амплитуда высокочастотного магнитного поля
- Восприимчивость при амплитудах поля, превышающих пороговое значение
- 1.7. ПРИМЕНЯЕМЫЕ ДЛЯ ИЗГОТОВЛЕНИЯ МАТЕРИАЛЫ
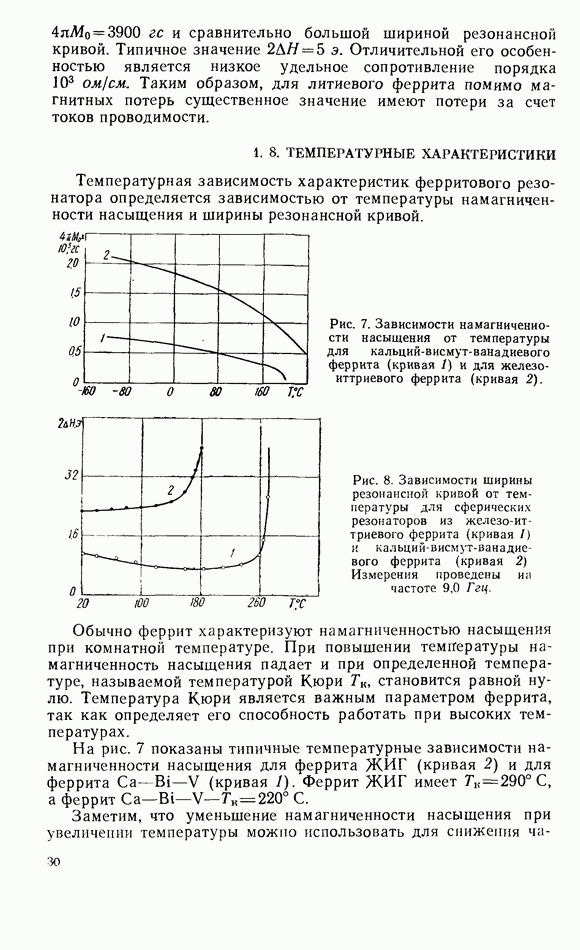
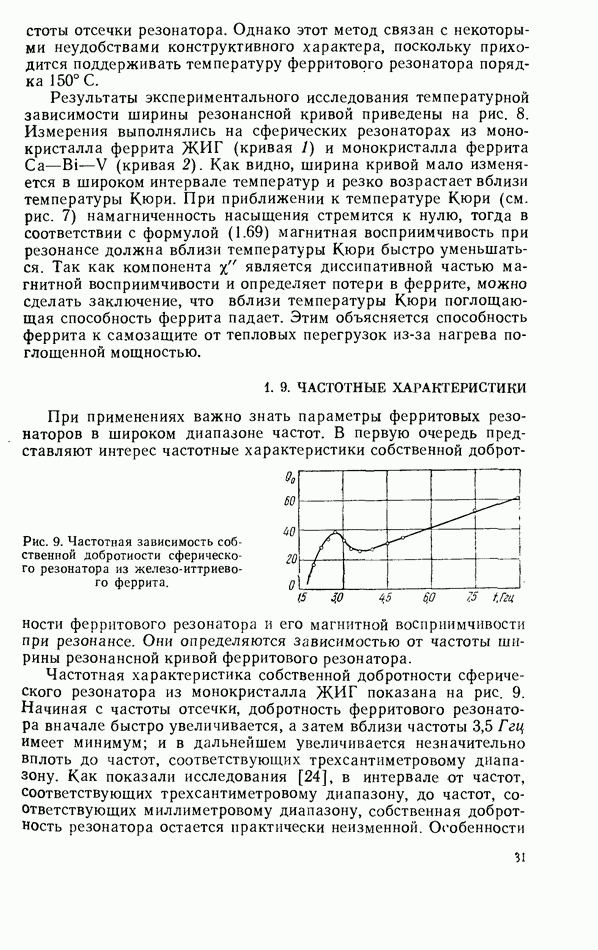
- 1.8. ТЕМПЕРАТУРНЫЕ ХАРАКТЕРИСТИКИ
- 1.9. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- Глава вторая. СВОЙСТВА ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 2.2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В АНИЗОТРОПНОМ ДИЭЛЕКТРИЧЕСКОМ СТЕРЖНЕ С «МАГНИТНЫМИ» БОКОВЫМИ СТЕНКАМИ
- 2.3. ПРИБЛИЖЕННЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2.5. ОСНОВНЫЕ ВИДЫ КОЛЕБАНИЙ
- 2.6. СФЕРИЧЕСКИЕ ДИЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
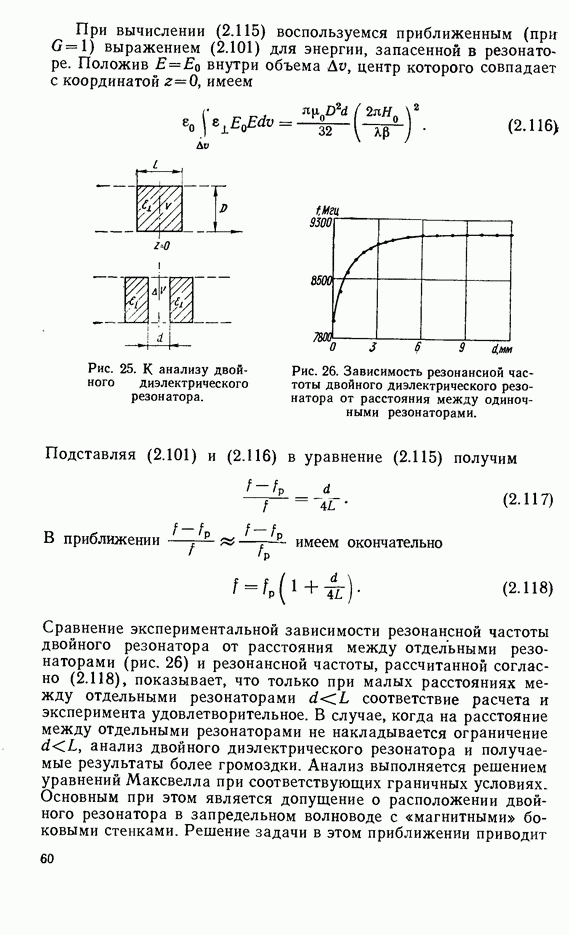
- 2.7. ВЛИЯНИЕ МЕТАЛЛИЧЕСКИХ СТЕНОК НА ХАРАКТЕРИСТИКИ ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 2.8. ДИПОЛЬНЫЙ МОМЕНТ
- 2.9. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ
- 2.10. СООТНОШЕНИЕ МЕЖДУ АМПЛИТУДАМИ СВЧ МАГНИТНОГО ПОЛЯ
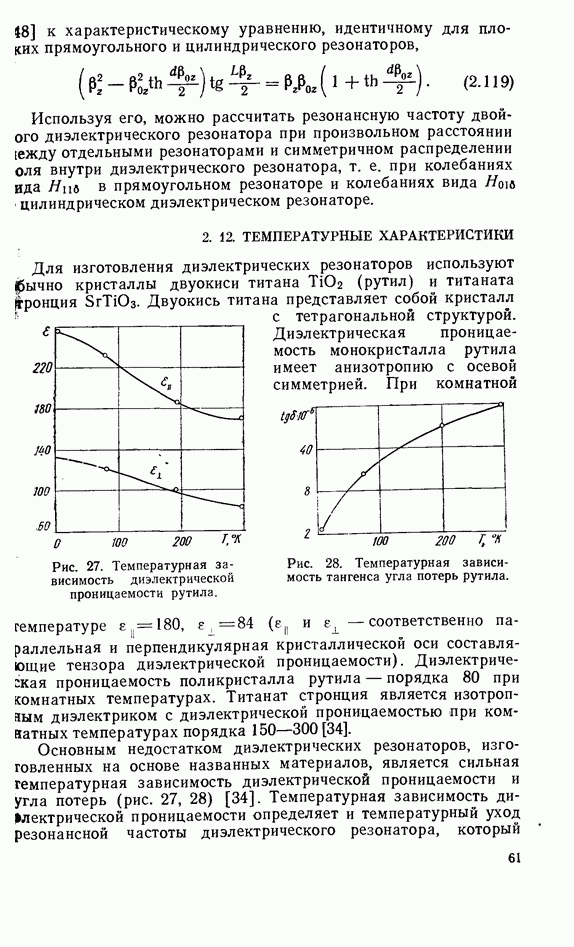
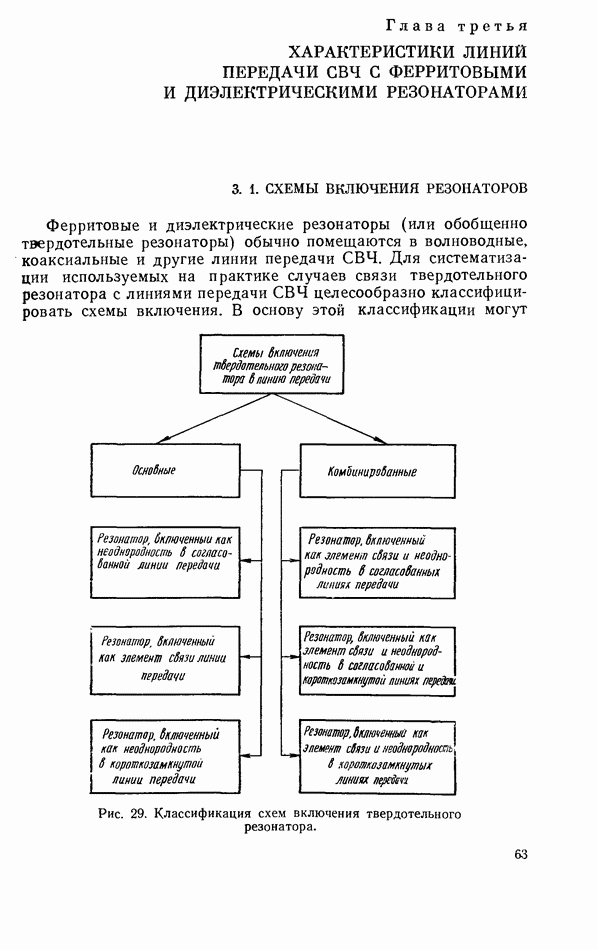
- 2.11. ДВОЙНЫЕ ДИЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
- 2.12. ТЕМПЕРАТУРНЫЕ ХАРАКТЕРИСТИКИ
- Глава третья. ХАРАКТЕРИСТИКИ ЛИНИЙ ПЕРЕДАЧИ СВЧ С ФЕРРИТОВЫМИ И ДИЭЛЕКТРИЧЕСКИМИ РЕЗОНАТОРАМИ
- 3.2. МЕТОДЫ РАСЧЕТА СВЧ-СХЕМ С ТВЕРДОТЕЛЬНЫМИ РЕЗОНАТОРАМИ
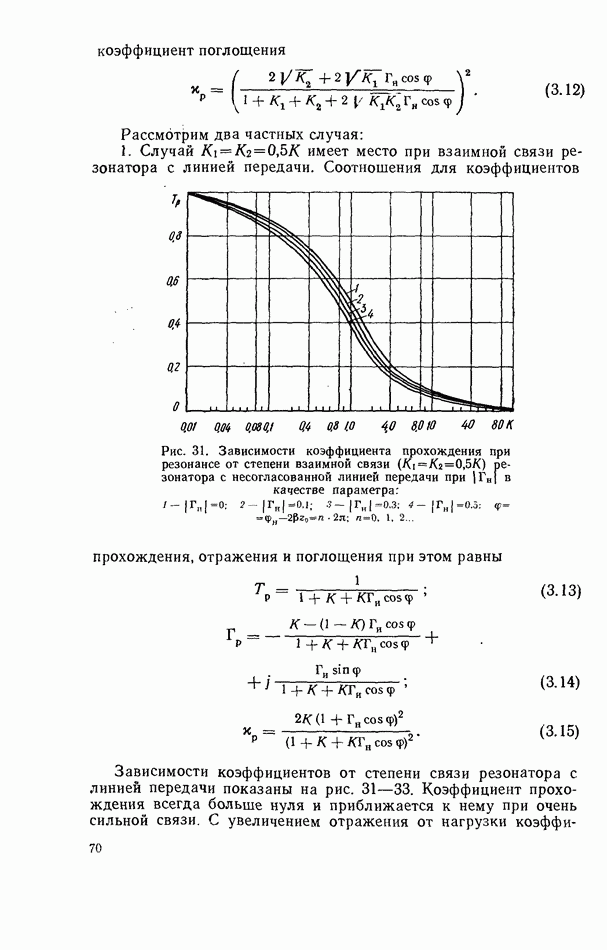
- 3.3. СВЯЗЬ ТВЕРДОТЕЛЬНОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ СВЧ
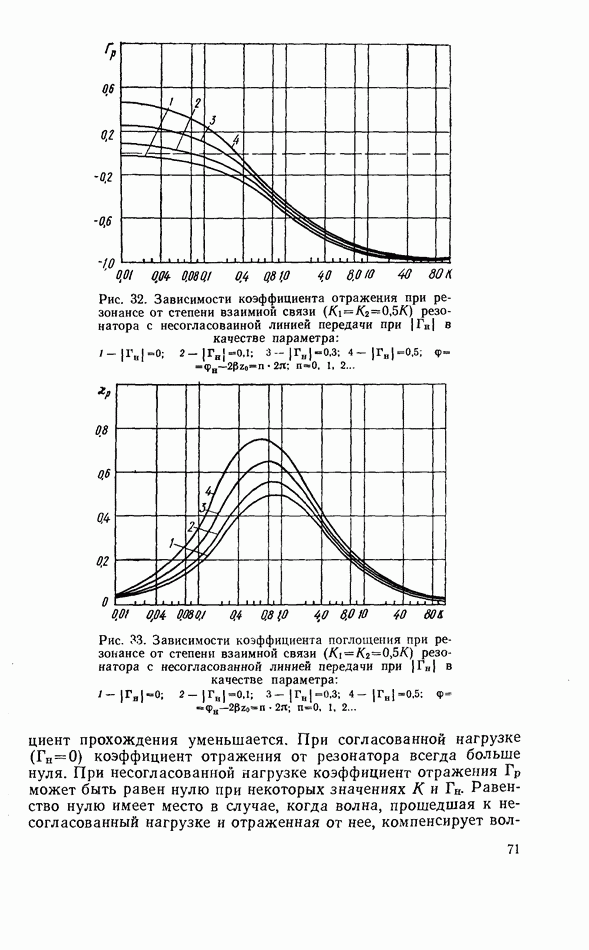
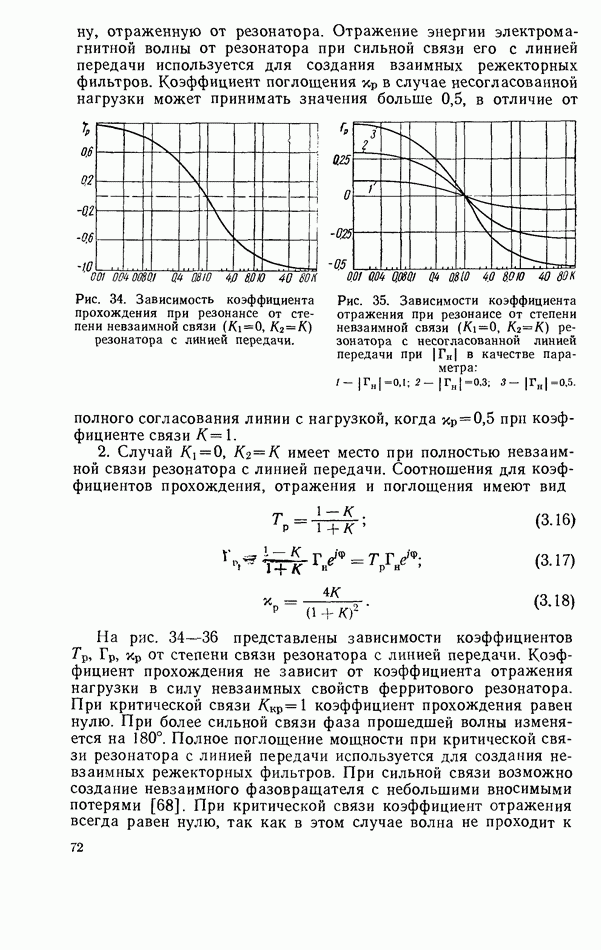
- 3.4. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В НЕСОГЛАСОВАННОЙ ЛИНИИ ПЕРЕДАЧИ
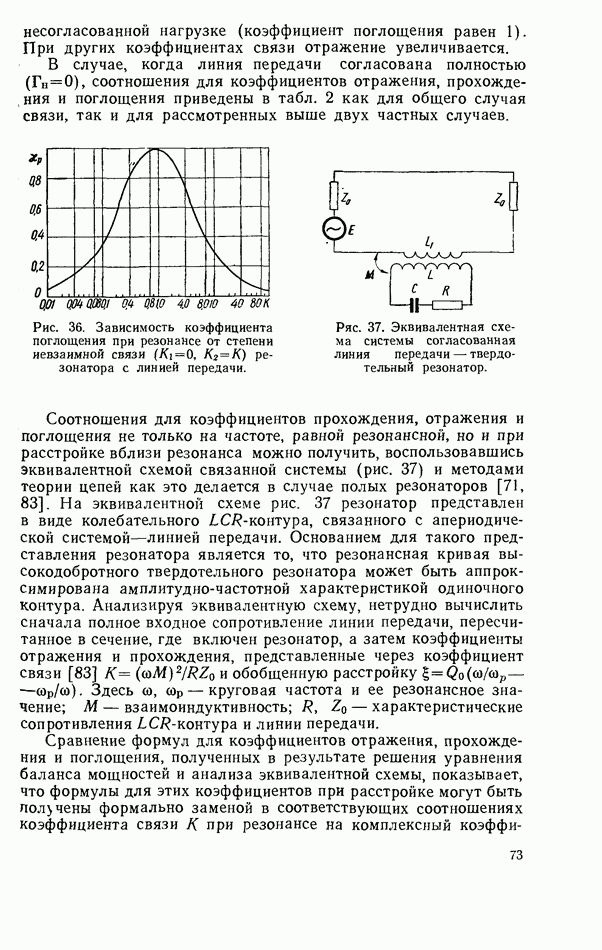
- 3.5. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР, ВКЛЮЧЕННЫЙ КАК ЭЛЕМЕНТ СВЯЗИ ЛИНИЙ ПЕРЕДАЧИ
- 3.6. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В КОРОТКОЗАМКНУТОЙ ЛИНИИ ПЕРЕДАЧИ
- 3.7. КОМБИНИРОВАННЫЕ СХЕМЫ ВКЛЮЧЕНИЯ ТВЕРДОТЕЛЬНОГО РЕЗОНАТОРА
- 3.8. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ С НЕСКОЛЬКИМИ РАСПРОСТРАНЯЮЩИМИСЯ ВОЛНАМИ
- Глава четвертая. СВЯЗЬ ТВЕРДОТЕЛЬНЫХ РЕЗОНАТОРОВ С ЛИНИЯМИ ПЕРЕДАЧИ СВЧ
- 4.2. СВЯЗЬ ФЕРРИТОВОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ
- 4.3. ФЕРРИТОВЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ ЗАМЕДЛЕННЫХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
- 4.4. РЕЗОНАНСНЫЙ ПОВОРОТ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ В ВОЛНОВОДЕ С ФЕРРИТОВЫМ РЕЗОНАТОРОМ
- 4.5. НЕЛИНЕЙНЫЙ ФЕРРИТОВЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ
- Ферритовый резонатор в линии передачи при запороговых уровнях мощности
- Нелинейный ферритовый резонатор в короткозамкнутой линии передачи
- Связь линий передачи СВЧ при помощи нелинейного ферритового резонатора
- Нелинейный ферритовый резонатор в согласованной линии передачи
- 4.6. СВЯЗЬ ДИЭЛЕКТРИЧЕСКОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ СВЧ
- Глава пятая. ПРИНЦИПЫ ПОСТРОЕНИЯ СВЧ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ И УСТРОЙСТВ НА ОСНОВЕ ТВЕРДОТЕЛЬНЫХ РЕЗОНАТОРОВ
- 5.2. ДАТЧИКИ УРОВНЯ МОЩНОСТИ СВЧ
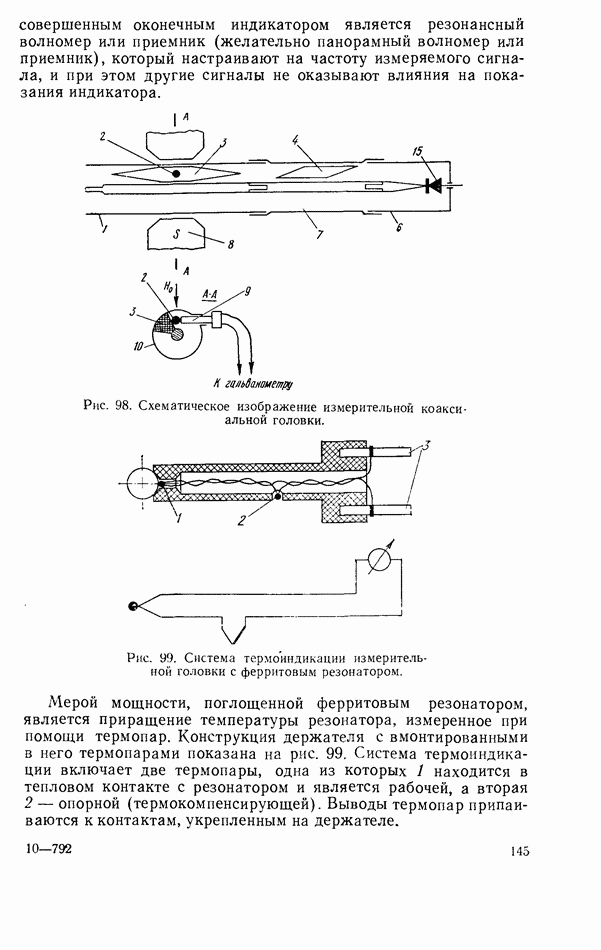
- Волноводная измерительная головка
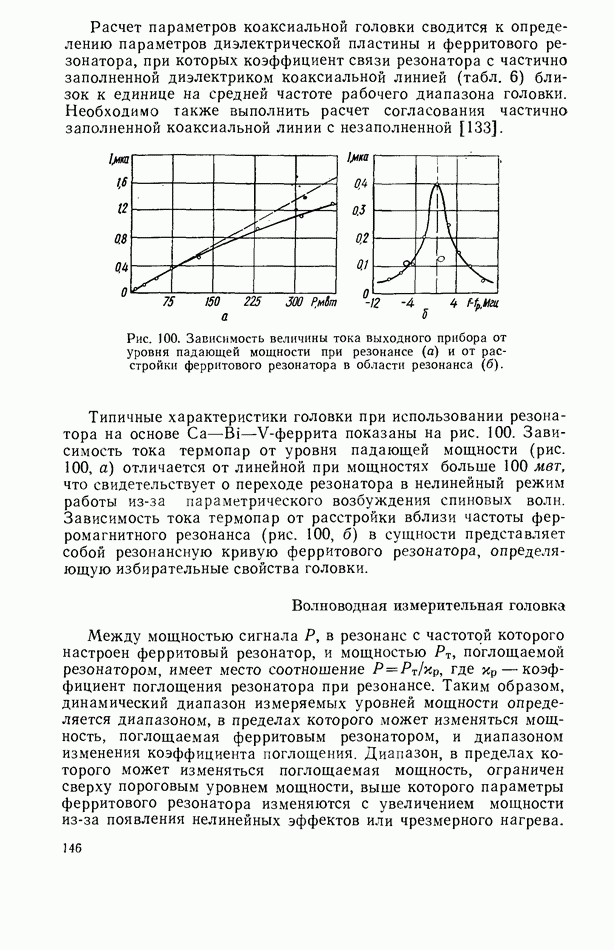
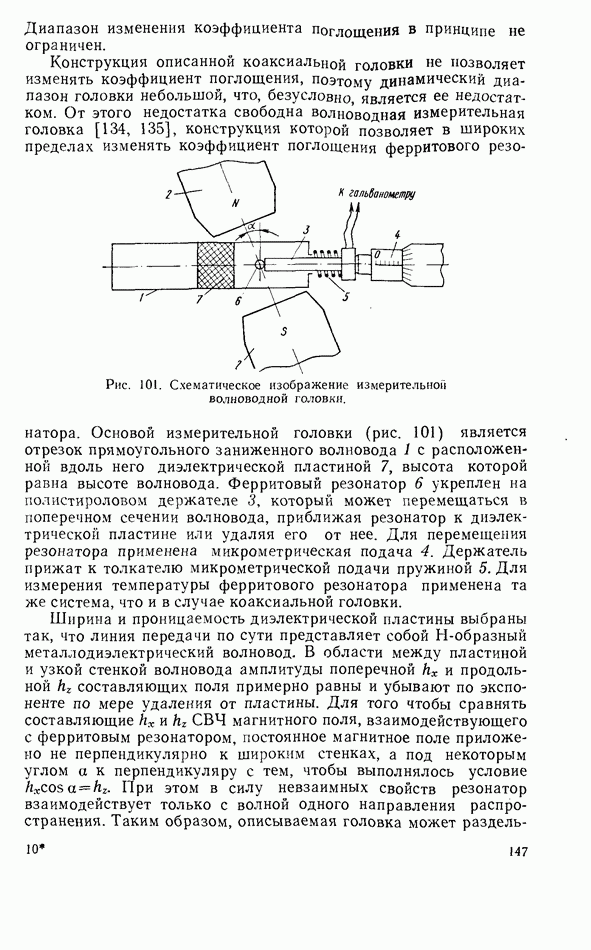
- Датчик фиксированного уровня пиковой мощности
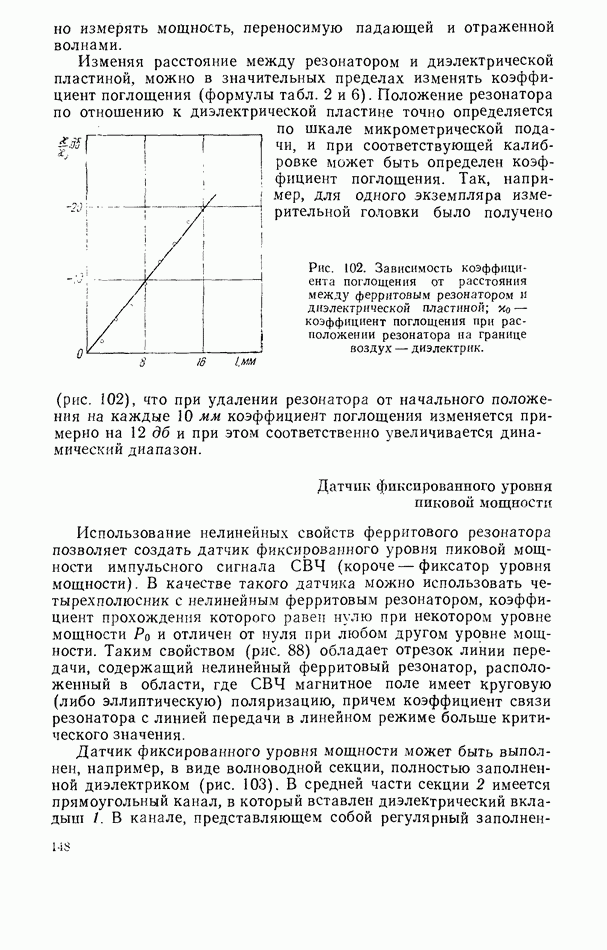
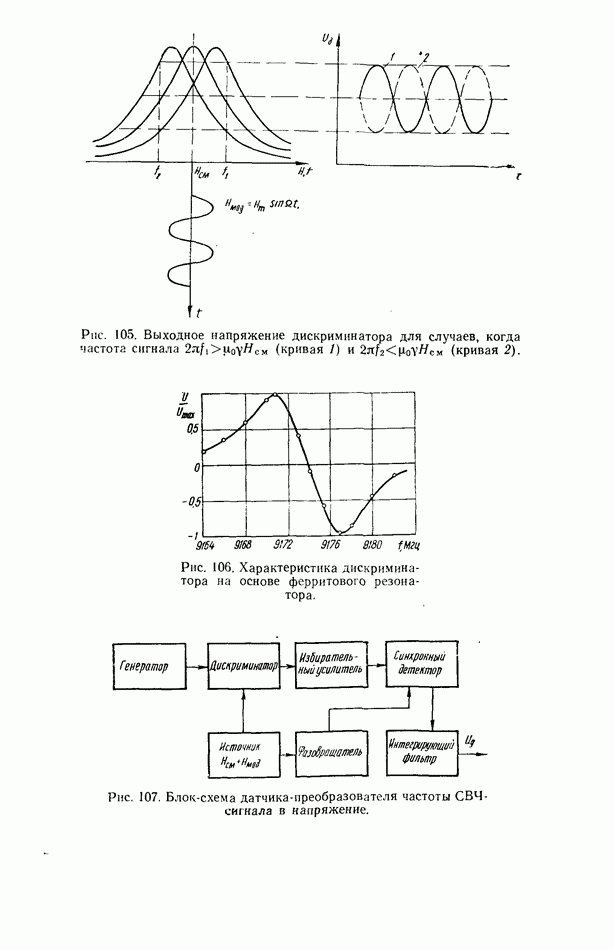
- 5.3. ЧАСТОТНЫЕ ДИСКРИМИНАТОРЫ С МАГНИТНОЙ НАСТРОЙКОЙ
- 5.4. РЕЗОНАНСНЫЕ ФАЗОВРАЩАТЕЛИ
- 5.5. УСТРОЙСТВО ДЛЯ РЕЗОНАНСНОГО ПОВОРОТА ПЛОСКОСТИ ПОЛЯРИЗАЦИИ В ВОЛНОВОДЕ
- 5.6. ФИЛЬТРЫ СВЧ НА ОСНОВЕ ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 5.7. ФЕРРИТОВЫЕ СВЧ-ФИЛЬТРЫ
- Многофункциональные фильтры
- Многорезонаторные ферритовые фильтры
- 5.8. ЧАСТОТНО-ИЗБИРАТЕЛЬНЫЕ ОГРАНИЧИТЕЛИ МАЛЫХ УРОВНЕЙ МОЩНОСТИ