| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
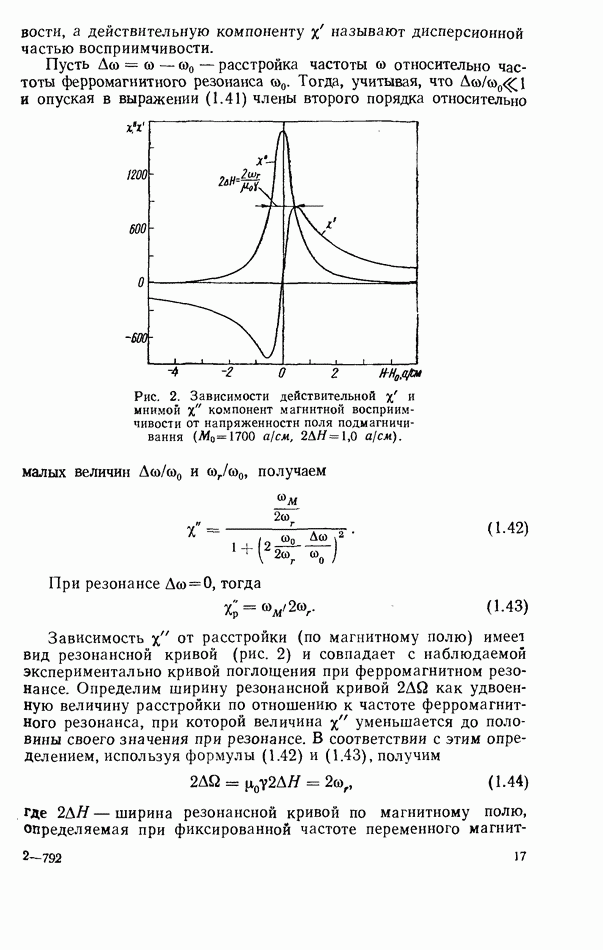
4.2. СВЯЗЬ ФЕРРИТОВОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ
Используя общие расчетные соотношения для коэффициентов связи резонатора с линией передачи, нетрудно рассчитать его связь с конкретной линией передачи, для которой известно математическое описание структуры поля. Составляющие произвольного магнитного поля, изменяющегося по гармоническому закону.
 в случае волны типа ТЕ могут быть записаны в виде
в случае волны типа ТЕ могут быть записаны в виде  амплитуды составляющих магнитного поля в месте расположения резонатора). Если поле подмагничивания приложено к ферритовому резонатору под произвольным углом к осям координат, по которым разложены составляющие СВЧ магнитного поля (рис. 3), то с учетом соотношений
амплитуды составляющих магнитного поля в месте расположения резонатора). Если поле подмагничивания приложено к ферритовому резонатору под произвольным углом к осям координат, по которым разложены составляющие СВЧ магнитного поля (рис. 3), то с учетом соотношений  для дипольного момента ферритового резонатора и общих соотношений (4.26) коэффициенты связи резонатора с согласованной линией передачи можно рассчитать по формулам [93]:
для дипольного момента ферритового резонатора и общих соотношений (4.26) коэффициенты связи резонатора с согласованной линией передачи можно рассчитать по формулам [93]:
1. Магнитное поле приложено вдоль оси у

2. Магнитное поле приложено вдоль оси 

3. Магнитное поле приложено вдоль оси х

4. Магнитное поле приложено в плоскости 

где  мощность, переносимая волной рассматриваемого типа по линии передачи;
мощность, переносимая волной рассматриваемого типа по линии передачи;  объем резонатора.
объем резонатора.
Рассмотрим особенности взаимодействия ферритового резонатора с различными наиболее часто применяющимися на практике линиями передачи СВЧ.
Прямоугольный волновод
При включении ферритового резонатора как неоднородности в согласованный прямоугольный волновод и приложении поля в плоскости  сотношения для коэффициентов связи имеют вид
сотношения для коэффициентов связи имеют вид

В наиболее часто применяемом случае приложения поля вдоль  эти выражения приведены в табл. 5. При размещении резонатора в области линейной поляризации СВЧ магнитного поля
эти выражения приведены в табл. 5. При размещении резонатора в области линейной поляризации СВЧ магнитного поля  при размещении резонатора в области эллиптической поляризации магнитного поля
при размещении резонатора в области эллиптической поляризации магнитного поля  что является
что является
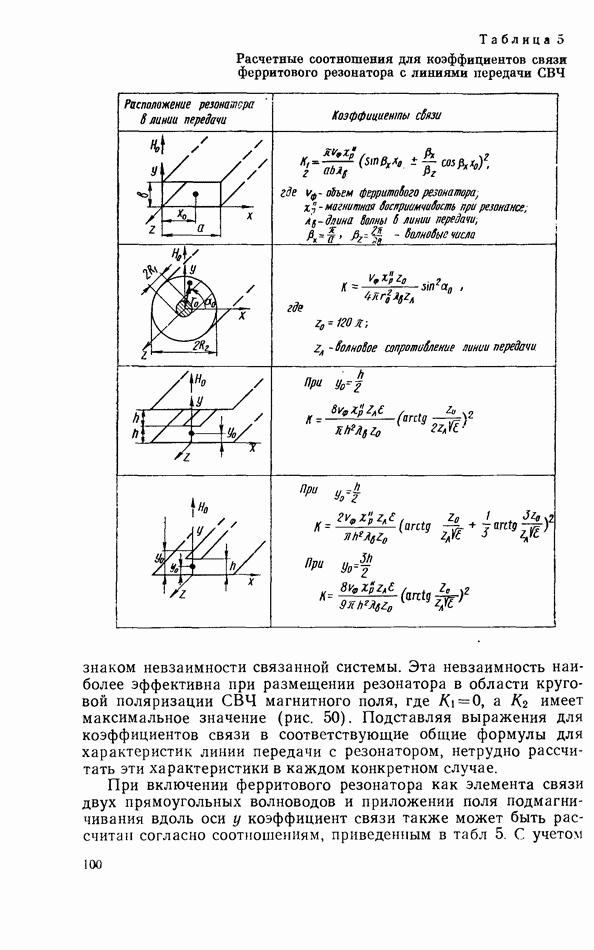
Таблица 5 (см. скан) Расчетные соотношения для коэффициентов связи ферритового резонатора с линиями передачи СВЧ
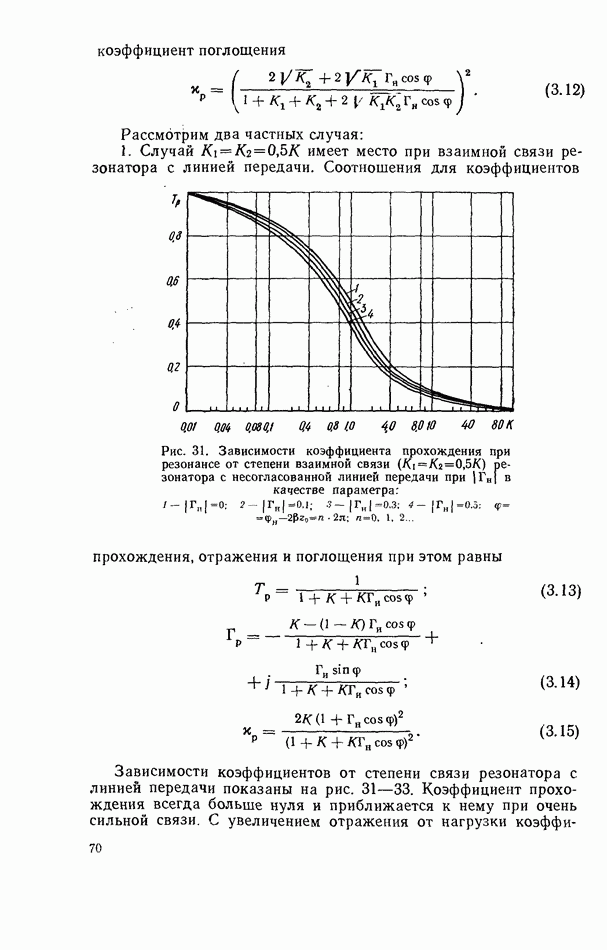
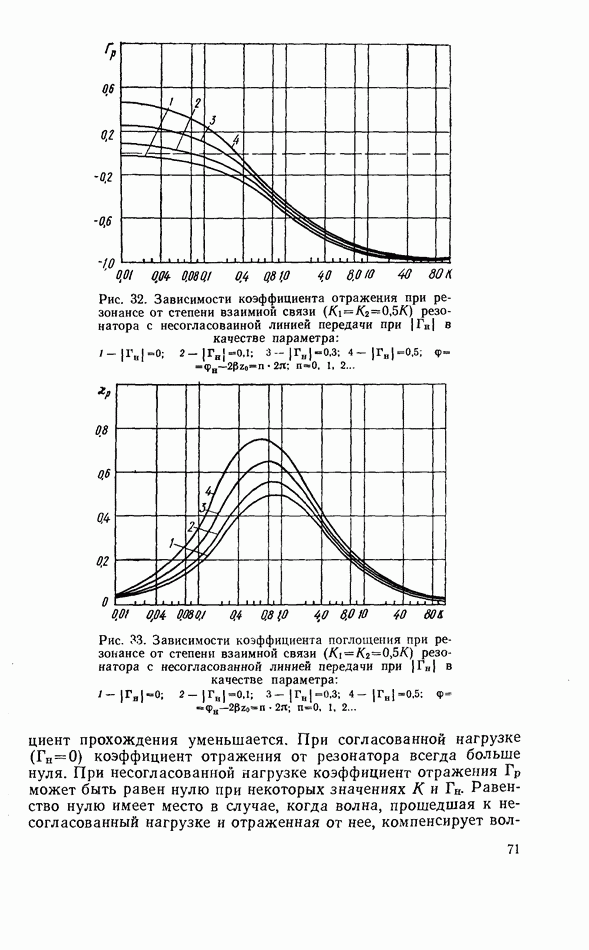
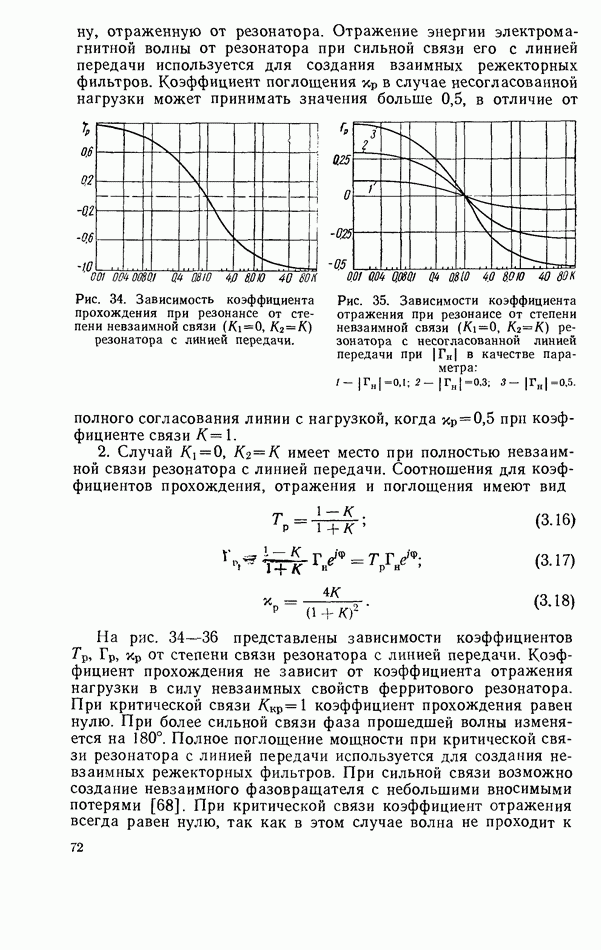
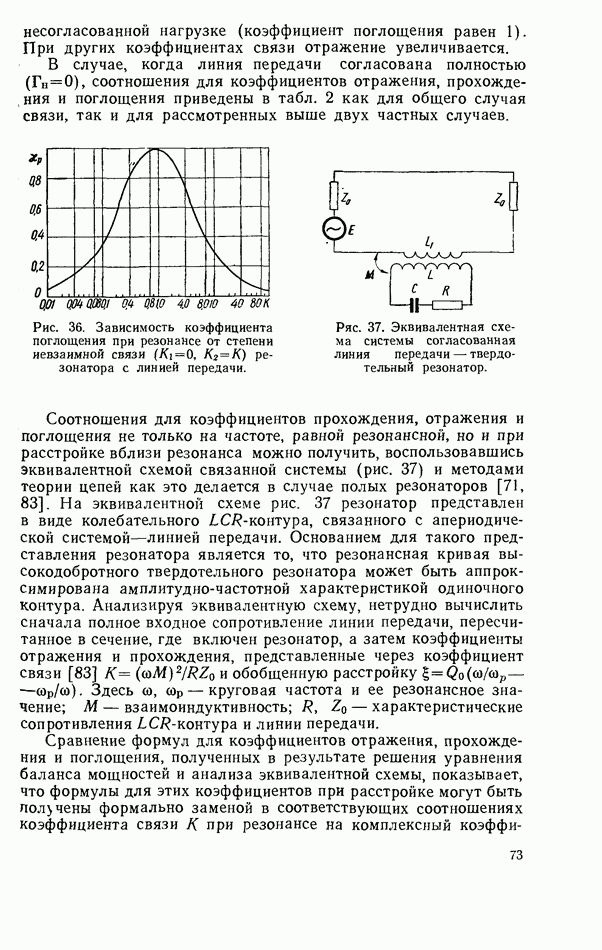
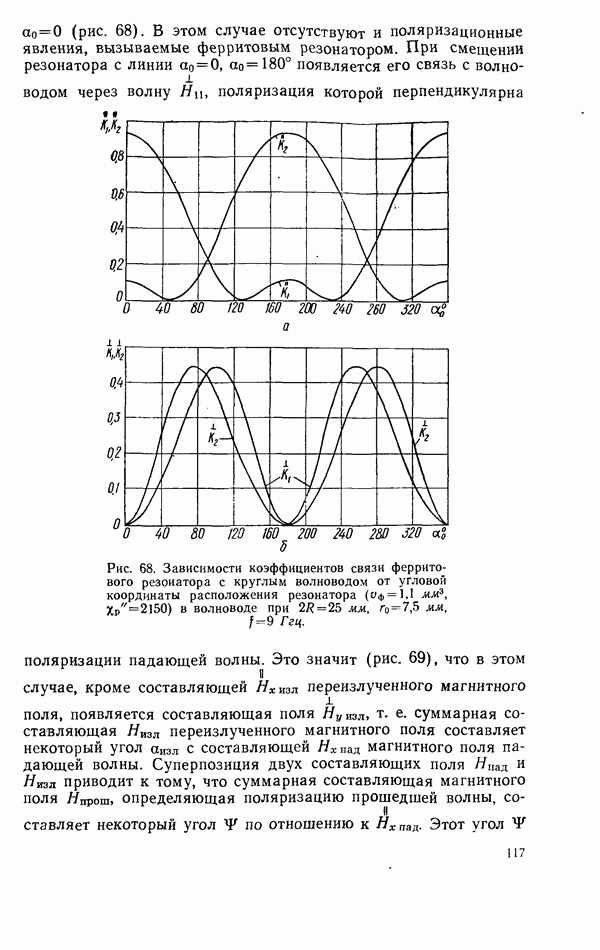
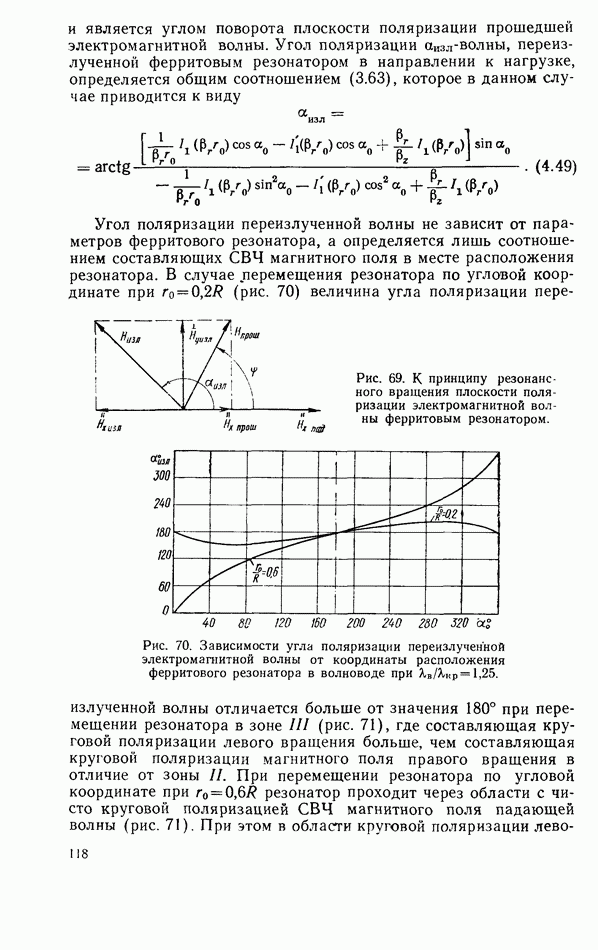
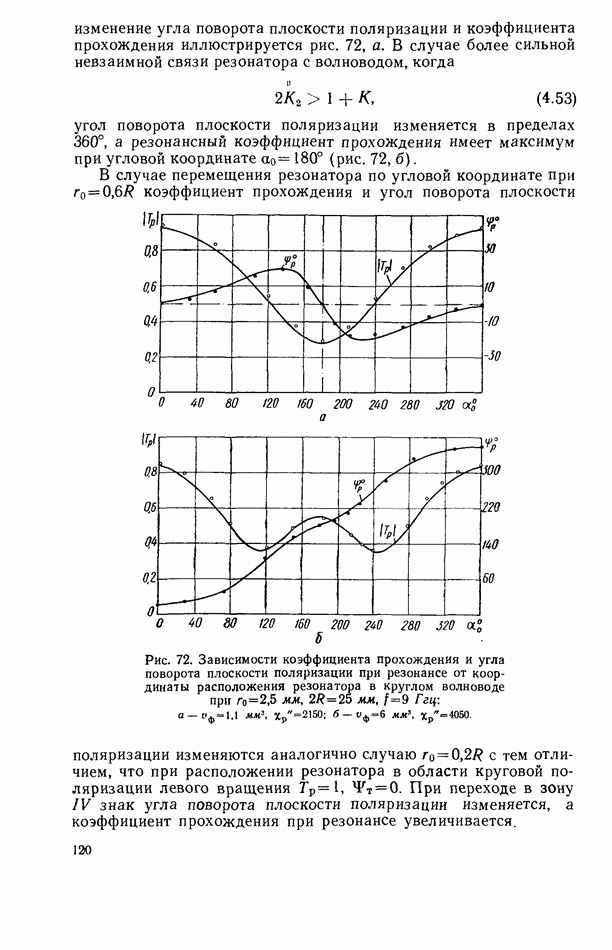
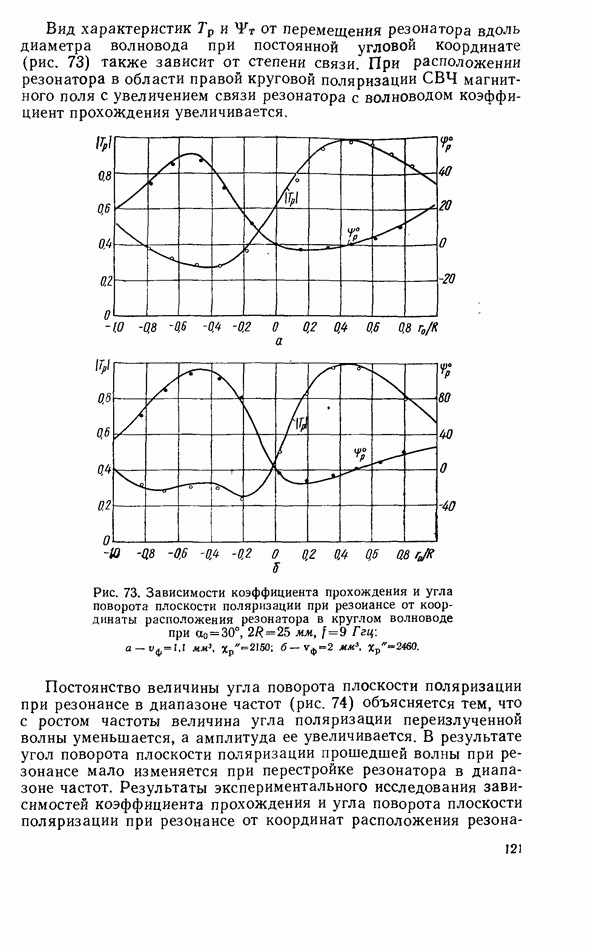
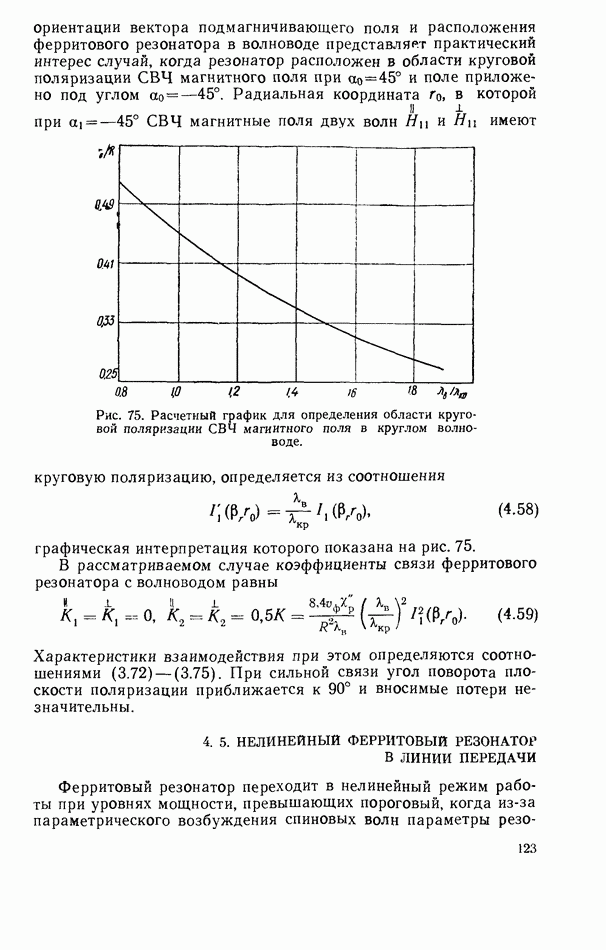
признаком невзаимности связанной системы. Эта невзаимность наиболее эффективна при размещении резонатора в области круговой поляризации СВЧ магнитного поля, где  имеет максимальное значение (рис. 50). Подставляя выражения для коэффициентов связи в соответствующие общие формулы для характеристик линии передачи с резонатором, нетрудно рассчитать эти характеристики в каждом конкретном случае.
имеет максимальное значение (рис. 50). Подставляя выражения для коэффициентов связи в соответствующие общие формулы для характеристик линии передачи с резонатором, нетрудно рассчитать эти характеристики в каждом конкретном случае.
При включении ферритового резонатора как элемента связи двух прямоугольных волноводов и приложении поля подмагничивания вдоль оси у коэффициент связи также может быть рассчитан согласно соотношениям, приведенным в табл 5. С учетом
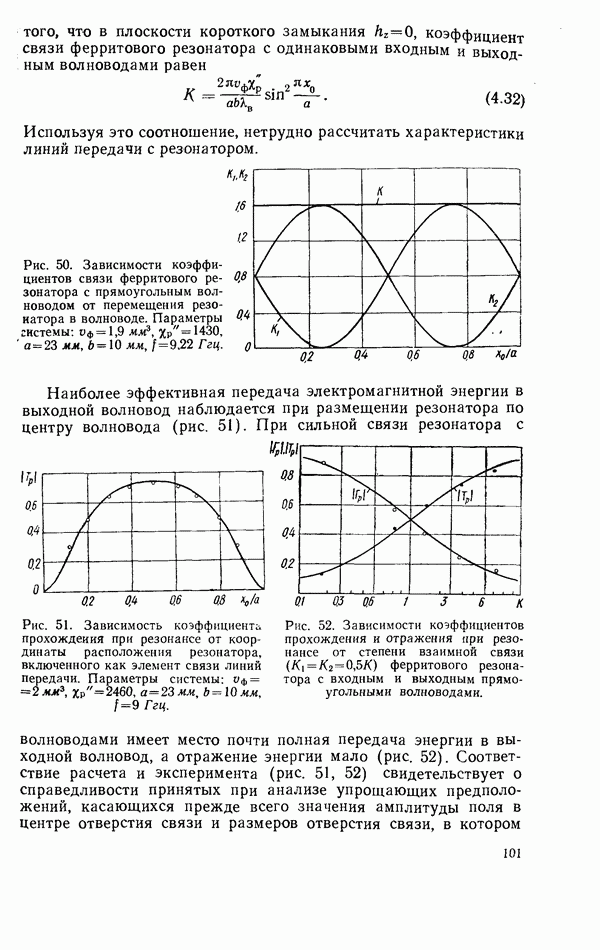
того, что в плоскости короткого замыкания  коэффициент связи ферритового резонатора с одинаковыми входным и выходным волноводами равен
коэффициент связи ферритового резонатора с одинаковыми входным и выходным волноводами равен

Используя это соотношение, нетрудно рассчитать характеристики линий передачи с резонатором.

Рис. 50. Зависимости коэффициентов связи ферритового резонатора с прямоугольным волноводом от перемещения резонатора в волноводе. Параметры системы: 
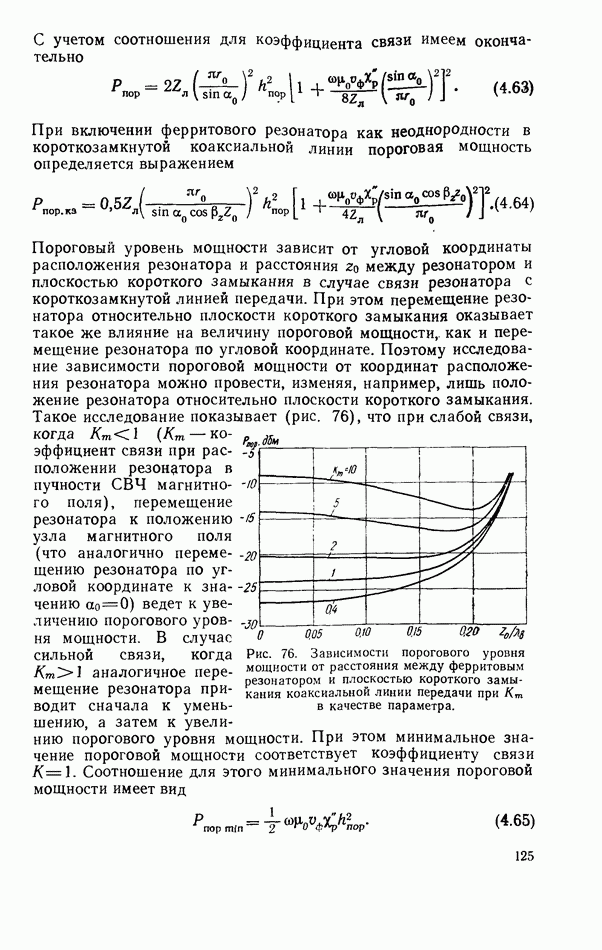
Наиболее эффективная передача электромагнитной энергии в выходной волновод наблюдается при размещении резонатора по центру волновода (рис. 51).

Рис. 51. Зависимость коэффициента прохождения при резонансе от координаты расположения резонатора, включенного как элемент связи линий передачи. Параметры системы: 

Рис. 52. Зависимости коэффициентов прохождения и отражения при резонансе от степени взаимной связи  ферритового резонатора с входным и выходным прямоугольными волноводами.
ферритового резонатора с входным и выходным прямоугольными волноводами.
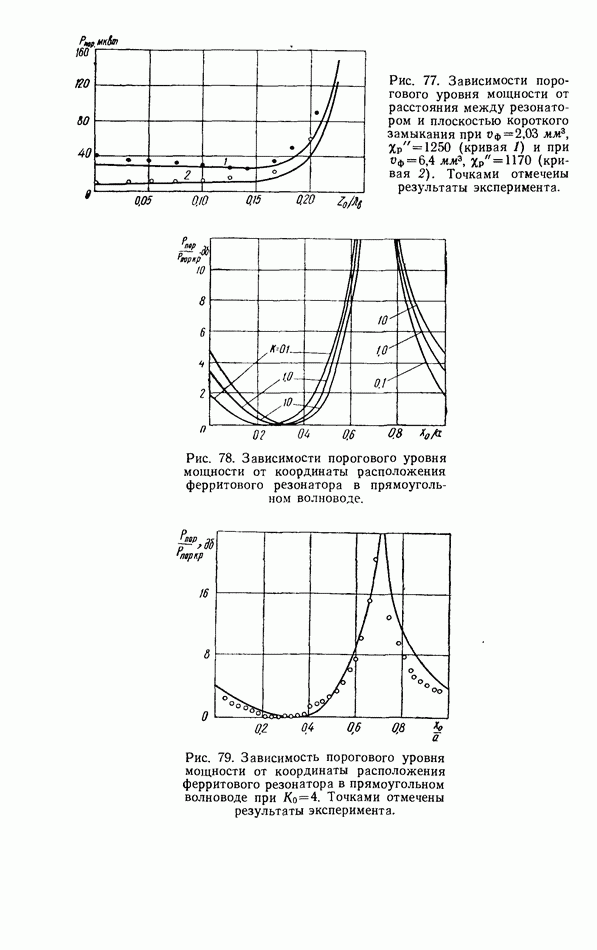
При сильной связи резонатора с волноводами имеет место почти полная передача энергии в выходной волновод, а отражение энергии мало (рис. 52). Соответствие расчета и эксперимента (рис. 51, 52) свидетельствует о справедливости принятых при анализе упрощающих предположений, касающихся прежде всего значения амплитуды поля в центре отверстия связи и размеров отверстия связи, в котором
расположен резонатор. Экспериментальная зависимость коэффициента прохождения от размеров отверстия связи приведена на рис. 53, где штриховой линией показано расчетное значение коэффициента прохождения. Заметное отклонение экспериментальных и теоретических значений коэффициента прохождения сказывается при отношениях диаметра сферического ферритового резонатора к диаметру круглого отверстия связи, больших  . Дальнейшее уменьшение отверстия связи приводит к увеличению вносимых потерь и интенсивному возбуждению магнитостатических типов колебаний ферритового резонатора.
. Дальнейшее уменьшение отверстия связи приводит к увеличению вносимых потерь и интенсивному возбуждению магнитостатических типов колебаний ферритового резонатора.

Рис. 53. Зависимость коэффициента прохождения при резонансе от размеров отверстия связи, в котором расположен ферритовый резонатор. Параметры системы: 
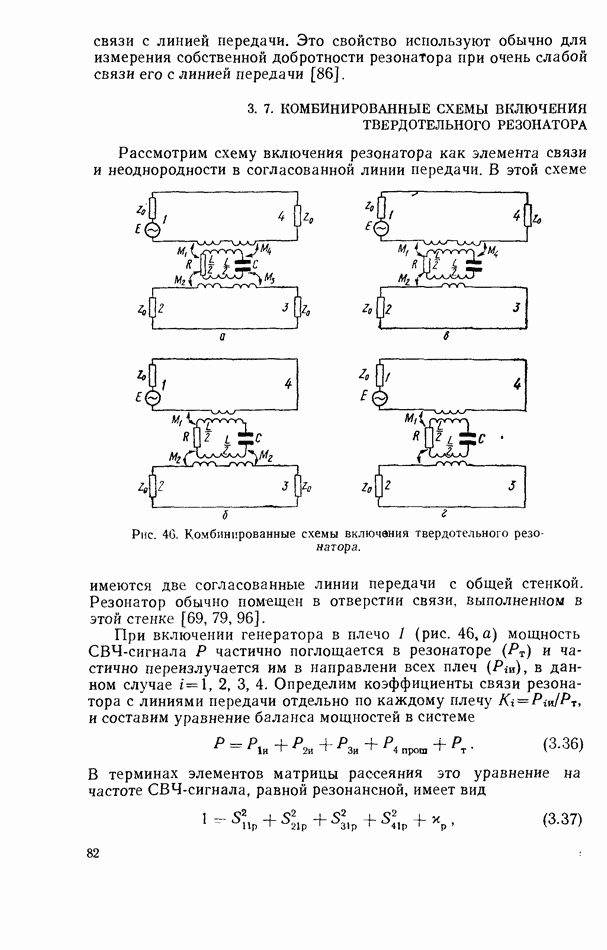
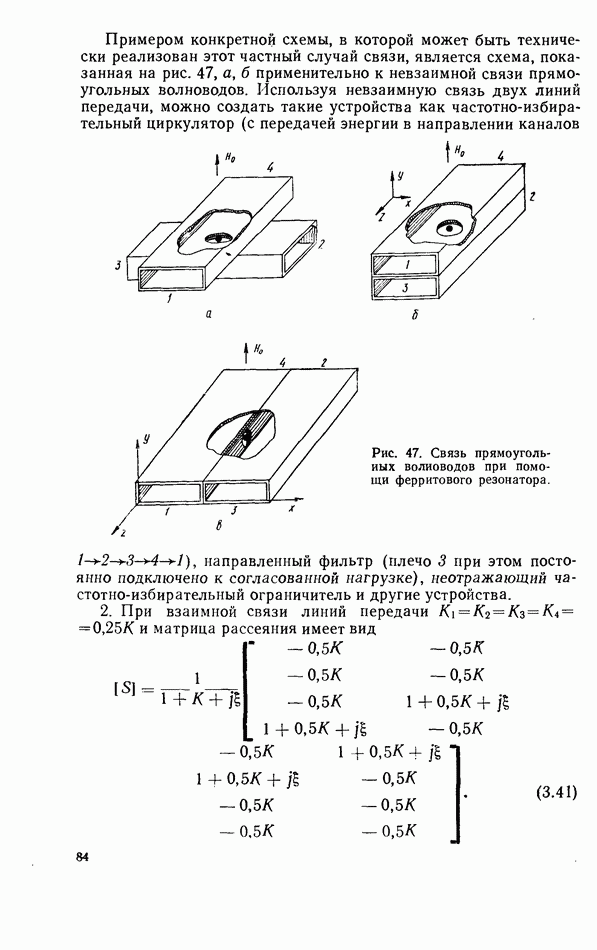
При включении ферритового резонатора как элемента связи и неоднородности в согласованных входном и выходном прямоугольных волноводах (рис. 47) [96] коэффициенты связи резонатора с волноводами определяются соотношениями: для схемы рис. 46, а

для схемы рис. 46, б

для схемы рис. 46, в

В представляющем наибольший практический интерес случае расположения резонатора в области круговой поляризации СВЧ магнитного поля обоих волноводов коэффициенты связи равны

Характеристики системы при этом определяются соотношениями (3.40).
Коаксиальная линия передачи
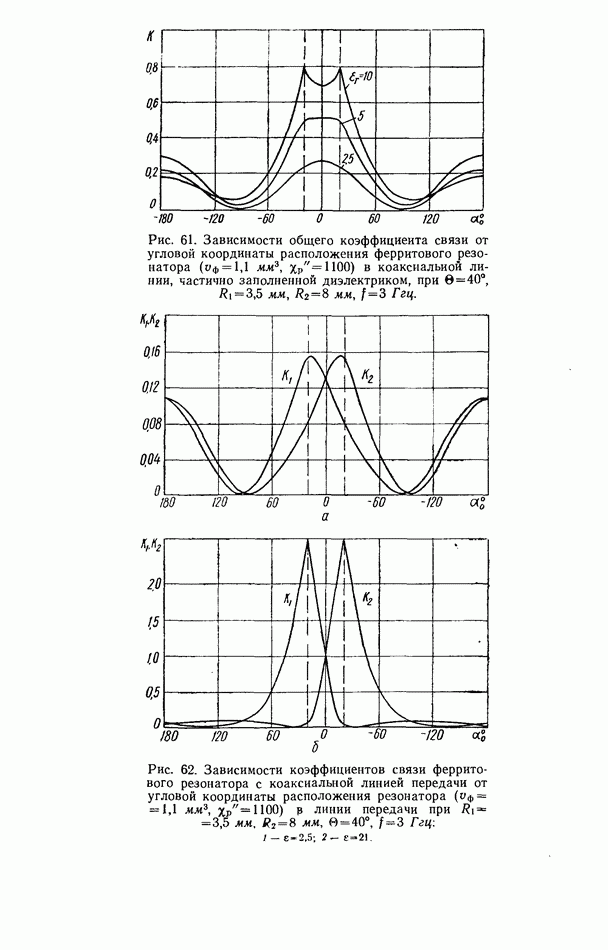
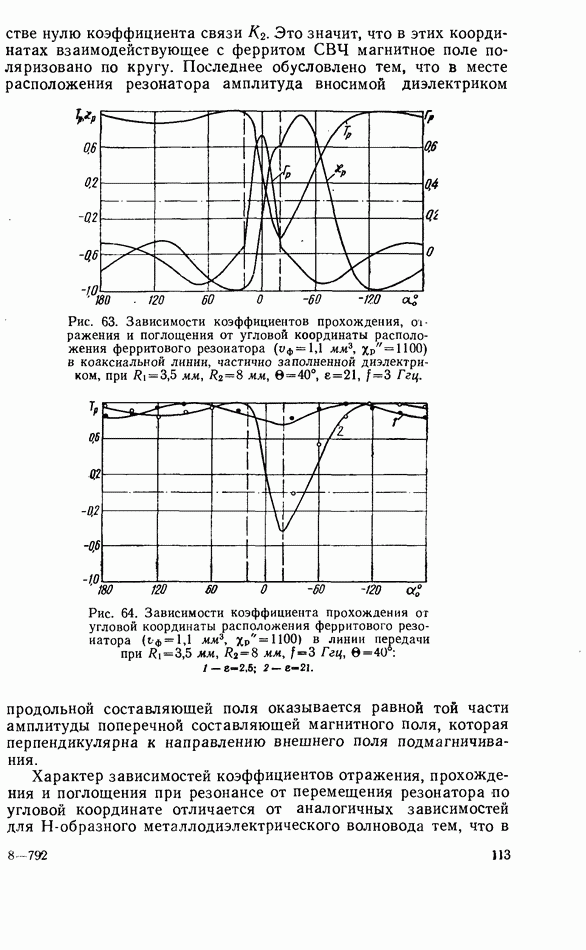
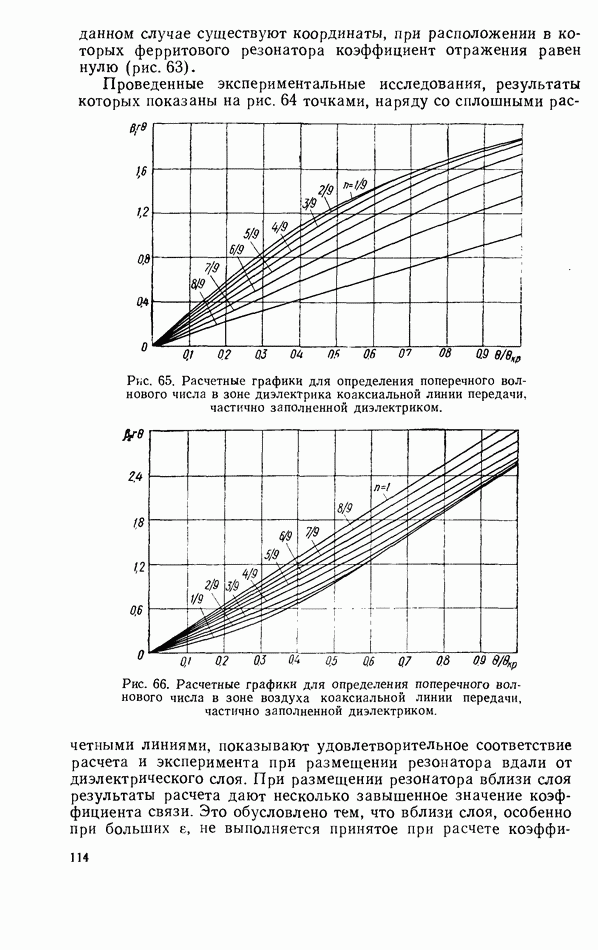
При включении ферритового резонатора как неоднородности  согласованную коаксиальную линию с учетом только волны типа ТЕМ коэффициенты связи определяются формулами, приведенными в табл. 5. Связь ферритового резонатора с коаксиальной линией зависит как от положения резонатора вдоль радиуса (увеличиваясь по мере приближения к центральному проводнику), так и от амплитуды составляющей магнитного поля, которая перпендикулярна направлению поля подмагничивания.
согласованную коаксиальную линию с учетом только волны типа ТЕМ коэффициенты связи определяются формулами, приведенными в табл. 5. Связь ферритового резонатора с коаксиальной линией зависит как от положения резонатора вдоль радиуса (увеличиваясь по мере приближения к центральному проводнику), так и от амплитуды составляющей магнитного поля, которая перпендикулярна направлению поля подмагничивания.

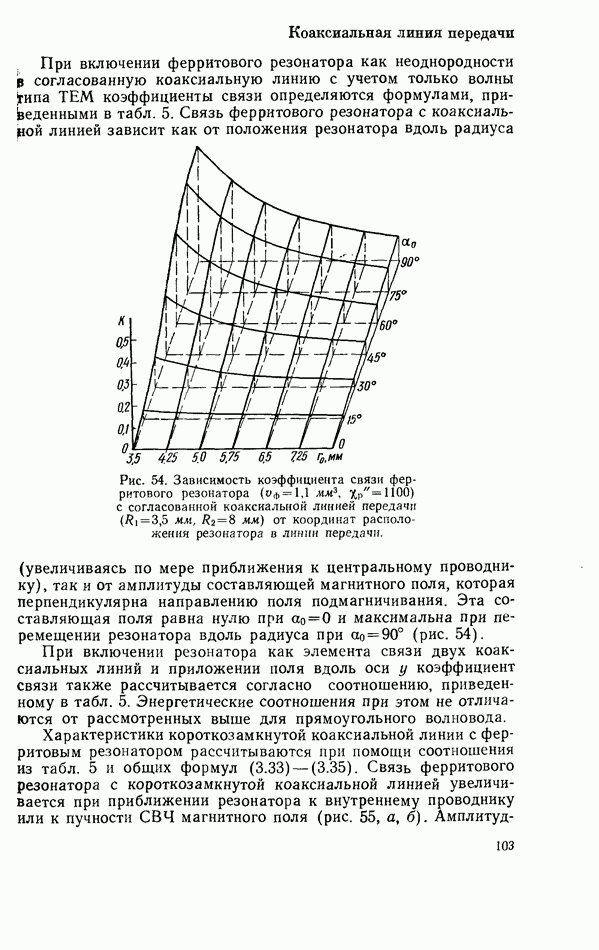
Рис. 54. Зависимость коэффициента связи ферритового резонатора  с согласованной коаксиальной линией передачи
с согласованной коаксиальной линией передачи  от координат расположения резонатора в линии передачи.
от координат расположения резонатора в линии передачи.
Эта составляющая поля равна нулю при  и максимальна при перемещении резонатора вдоль радиуса при
и максимальна при перемещении резонатора вдоль радиуса при  (рис. 54).
(рис. 54).
При включении резонатора как элемента связи двух коаксиальных линий и приложении поля вдоль оси у коэффициент связи также рассчитывается согласно соотношению, приведенному в табл. 5. Энергетические соотношения при этом не отличаются от рассмотренных выше для прямоугольного волновода.
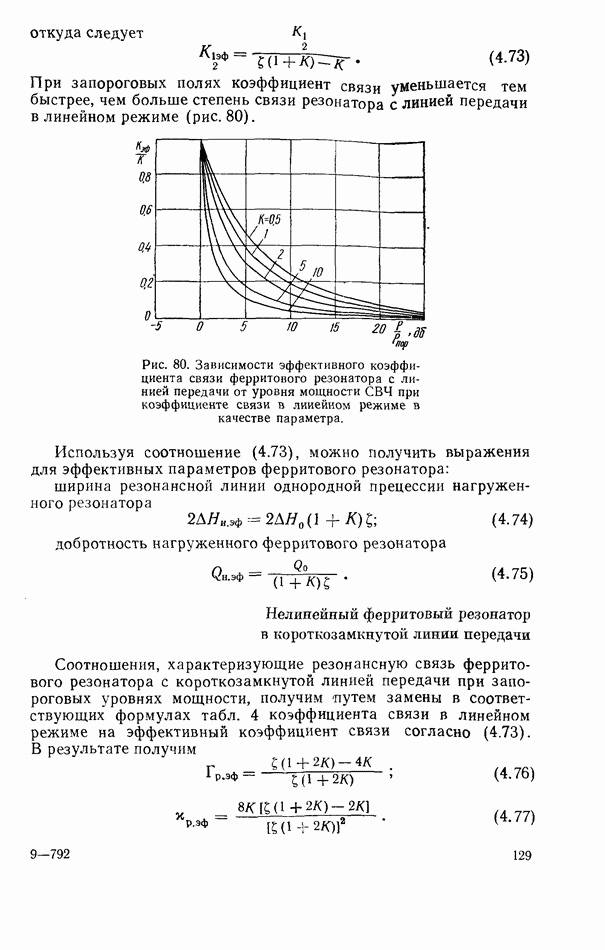
Характеристики короткозамкнутой коаксиальной линии с ферритовым резонатором рассчитываются при помощи соотношения из табл. 5 и общих формул (3.33) — (3.35). Связь ферритового резонатора с короткозамкнутой коаксиальной линией увеличивается при приближении резонатора к внутреннему проводнику или к пучности СВЧ магнитного поля (рис. 55, а, б).
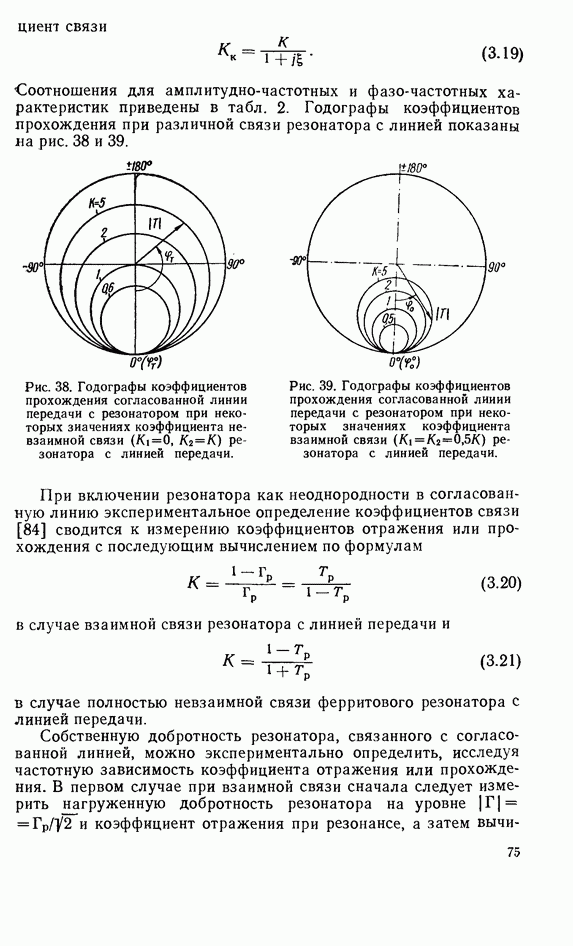
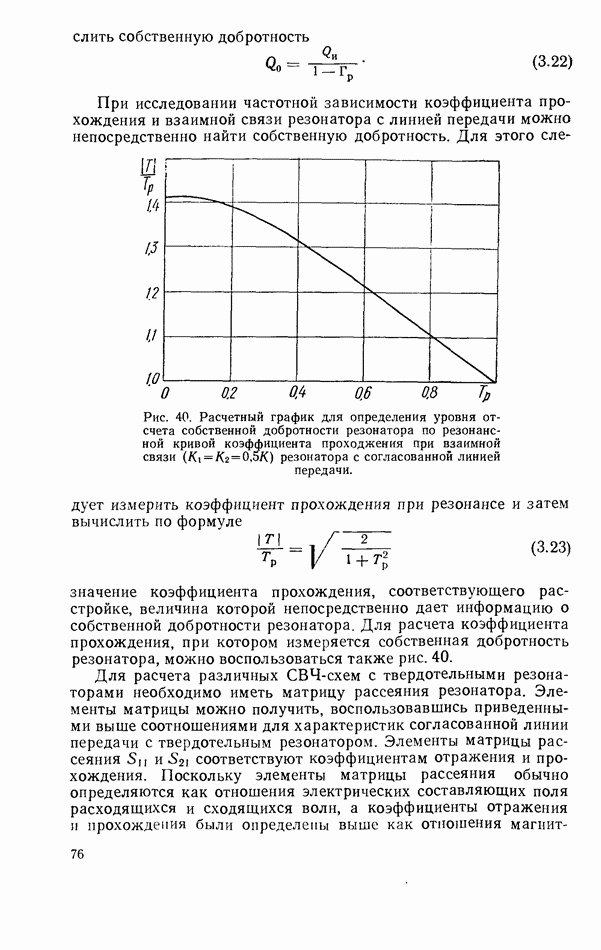
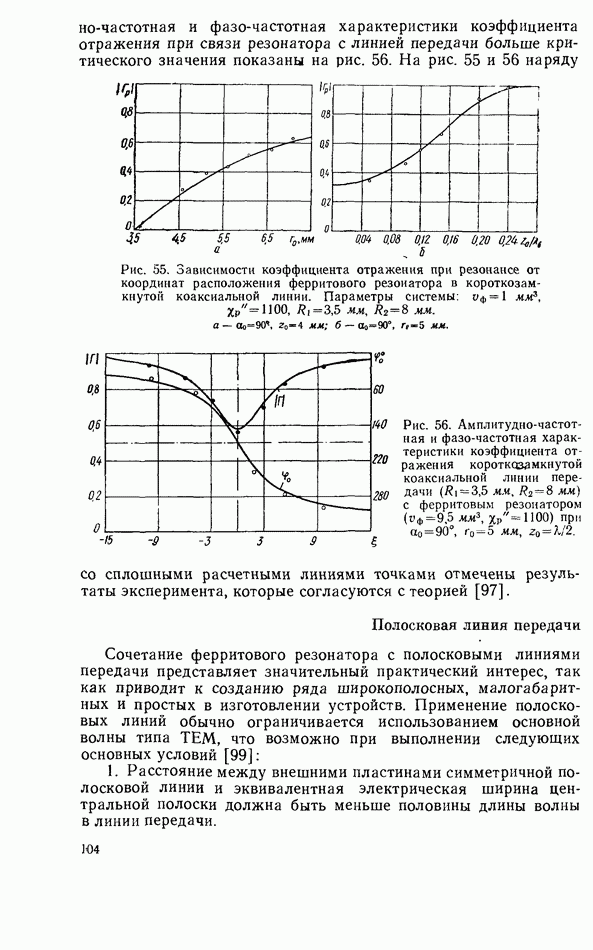
Амплитудно-частотная и фазо-частотная характеристики коэффициента отражения при связи резонатора с линией передачи больше критического значения показаны на рис. 56. На рис. 55 и 56 наряду со сплошными расчетными линиями точками отмечены результаты эксперимента, которые согласуются с теорией [97].

Рис. 55. Зависимости коэффициента отражения при резонансе от координат расположения ферритового резонатора в короткозамкнутой коаксиальной линии. Параметры системы: 

Рис. 56. Амплитудно-частотная и фазо-частотная характеристики коэффициента отражения короткозамкнутой коаксиальной линии передачи  с ферритовым резонатором
с ферритовым резонатором  при
при 
Полосковая линия передачи
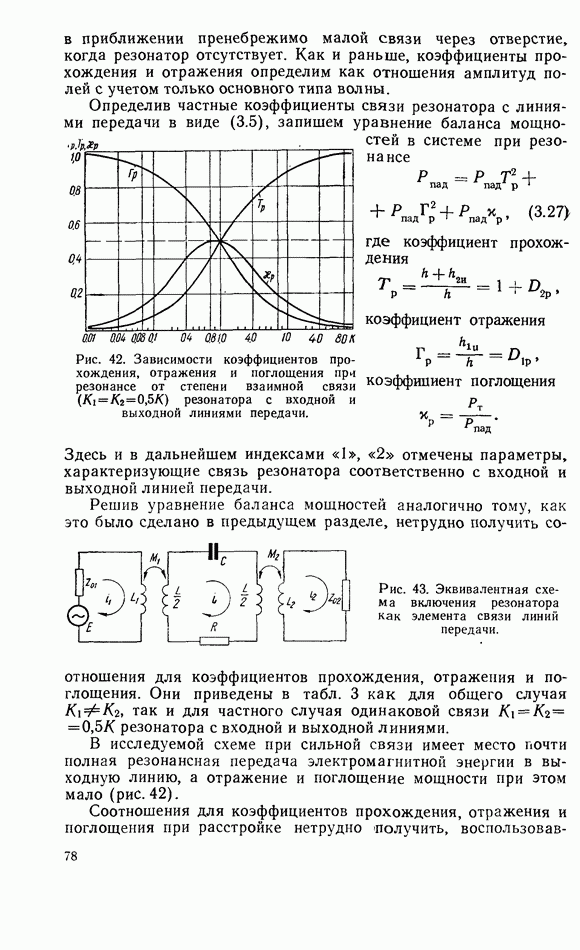
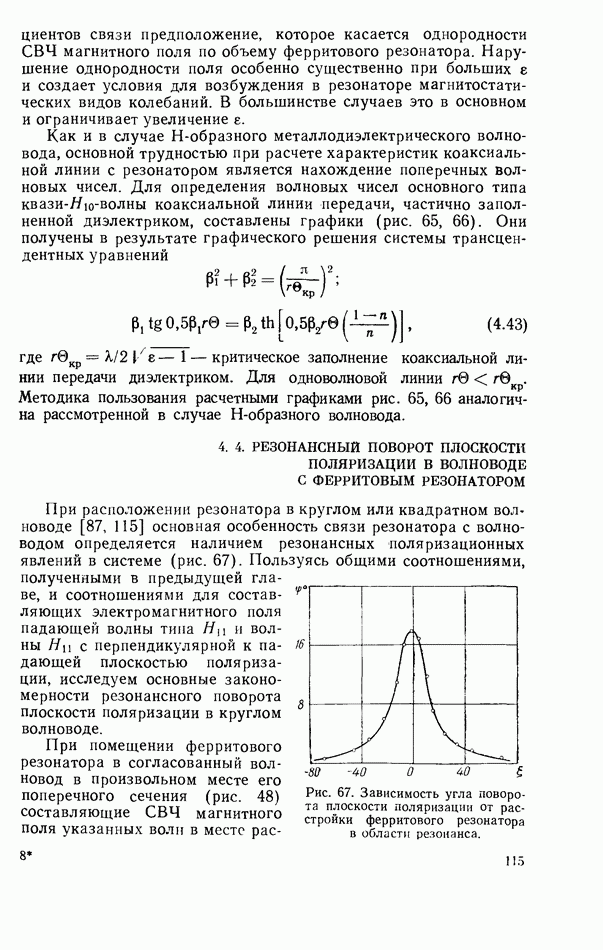
Сочетание ферритового резонатора с полосковыми линиями передачи представляет значительный практический интерес, так как приводит к созданию ряда широкополосных, малогабаритных и простых в изготовлении устройств. Применение полосковых линий обычно ограничивается использованием основной волны типа ТЕМ, что возможно при выполнении следующих основных условий [99]:
1. Расстояние между внешними пластинами симметричной полосковой линии и эквивалентная электрическая ширина центральной полоски должна быть меньше половины длины волны в линии передачи.
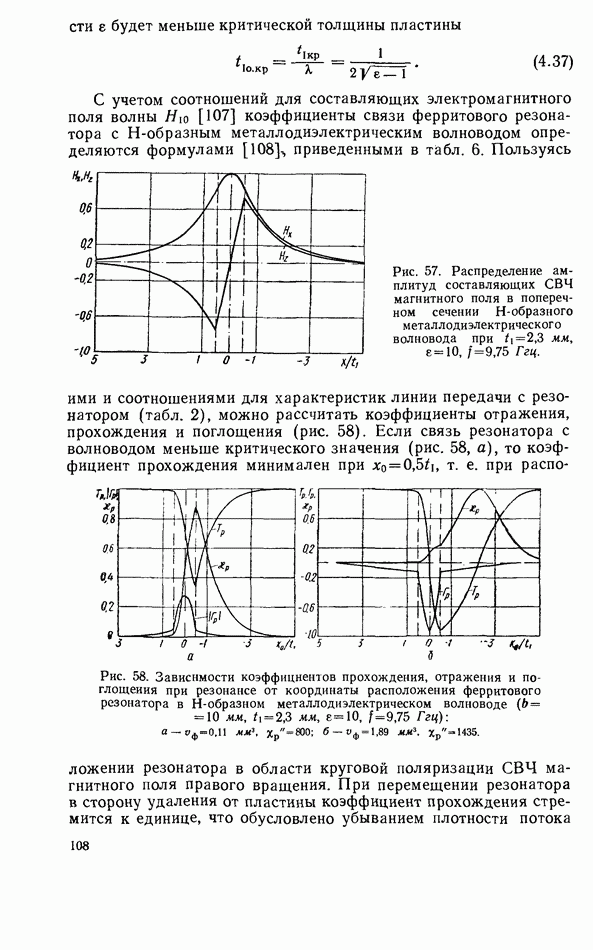
Таблица 6 (см. скан) Расчетные соотношения для коэффициентов связи ферритового резонатора с линиями передачи СВЧ
2. Центральная полоска должна быть, расположена приблизительно в центре между внешними пластинами и параллельно им; ширина внешних пластин должна быть существенно больше ширины центральной полоски.
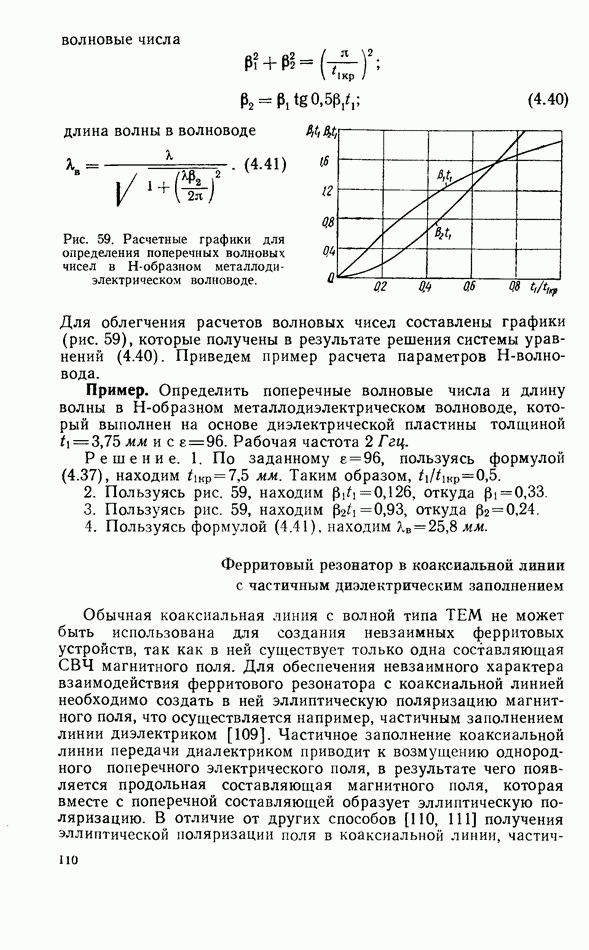
При выполнении этих условий можно принимать, что длина волны в симметричной полосковой линии приблизительно в  раз меньше длины волны в свободном пространстве
раз меньше длины волны в свободном пространстве  относительная диэлектрическая проницаемость среды, заполняющей полосковую линию).
относительная диэлектрическая проницаемость среды, заполняющей полосковую линию).
Наиболее часто применяются полосковые линии с практически нулевой толщиной центральной полоски. В случае, когда ферритовый резонатор расположен в центре между внутренней
полоской и внешней пластиной, соотношение для добротности связи резонатора получено в работе [100]. Используя его, нетрудно рассчитать коэффициент связи ферритового резонатора с симметричной полосковой линией (табл. 5). Соотношения для коэффициентов связи ферритового резонатора с несимметричной (микрополосковой) линией передачи при фиксированном расположении резонатора в линии получены аналогично и приведены в табл. 5. Используя эти выражения для коэффициентов связи и общие формулы для характеристик линии передачи с резонатором, нетрудно рассчитать коэффициенты отражения, прохождения и поглощения для различных схем включения ферритового резонатора.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава первая. СВОЙСТВА ФЕРРИТОВЫХ РЕЗОНАТОРОВ
- Ферромагнитный резонанс в неограниченной среде без потерь
- 1.2. РЕЗОНАНСНАЯ ЧАСТОТА
- Зависимость резонансной частоты от формы резонатора
- Влияние кристаллографической анизотропии на резонансную частоту
- 1.3. МАГНИТОСТАТИЧЕСКИЕ ВИДЫ КОЛЕБАНИЙ
- 1.4. УЧЕТ ПОТЕРЬ
- 1.5. ДИПОЛЬНЫЙ МОМЕНТ
- 1.6. НЕЛИНЕЙНЫЕ ЯВЛЕНИЯ
- Спиновые волны
- Пороговая амплитуда высокочастотного магнитного поля
- Восприимчивость при амплитудах поля, превышающих пороговое значение
- 1.7. ПРИМЕНЯЕМЫЕ ДЛЯ ИЗГОТОВЛЕНИЯ МАТЕРИАЛЫ
- 1.8. ТЕМПЕРАТУРНЫЕ ХАРАКТЕРИСТИКИ
- 1.9. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- Глава вторая. СВОЙСТВА ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 2.2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В АНИЗОТРОПНОМ ДИЭЛЕКТРИЧЕСКОМ СТЕРЖНЕ С «МАГНИТНЫМИ» БОКОВЫМИ СТЕНКАМИ
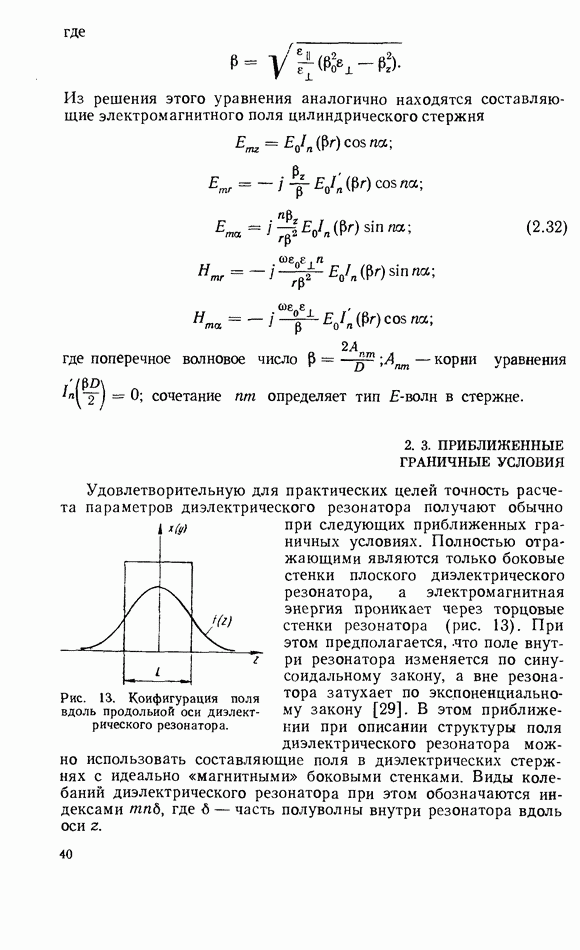
- 2.3. ПРИБЛИЖЕННЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2.5. ОСНОВНЫЕ ВИДЫ КОЛЕБАНИЙ
- 2.6. СФЕРИЧЕСКИЕ ДИЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
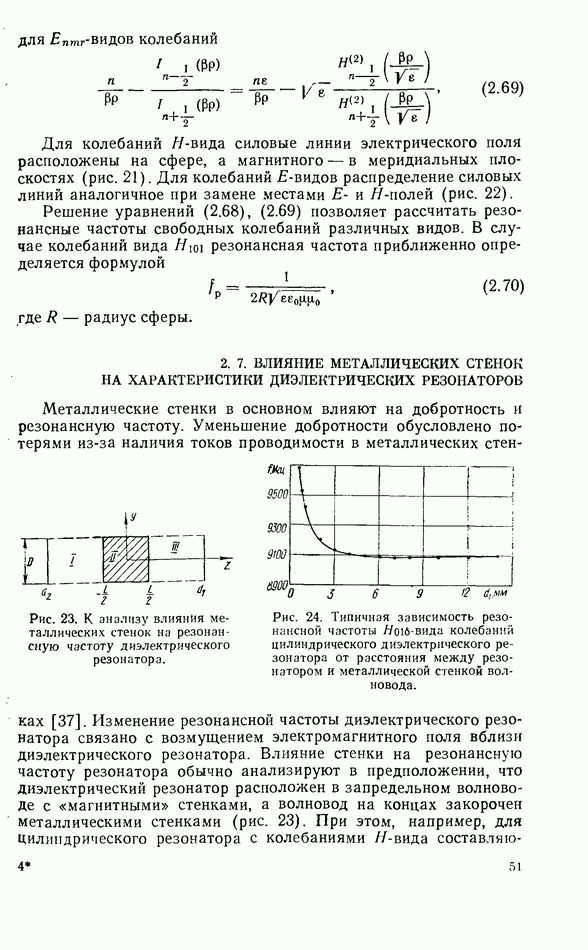
- 2.7. ВЛИЯНИЕ МЕТАЛЛИЧЕСКИХ СТЕНОК НА ХАРАКТЕРИСТИКИ ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 2.8. ДИПОЛЬНЫЙ МОМЕНТ
- 2.9. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ
- 2.10. СООТНОШЕНИЕ МЕЖДУ АМПЛИТУДАМИ СВЧ МАГНИТНОГО ПОЛЯ
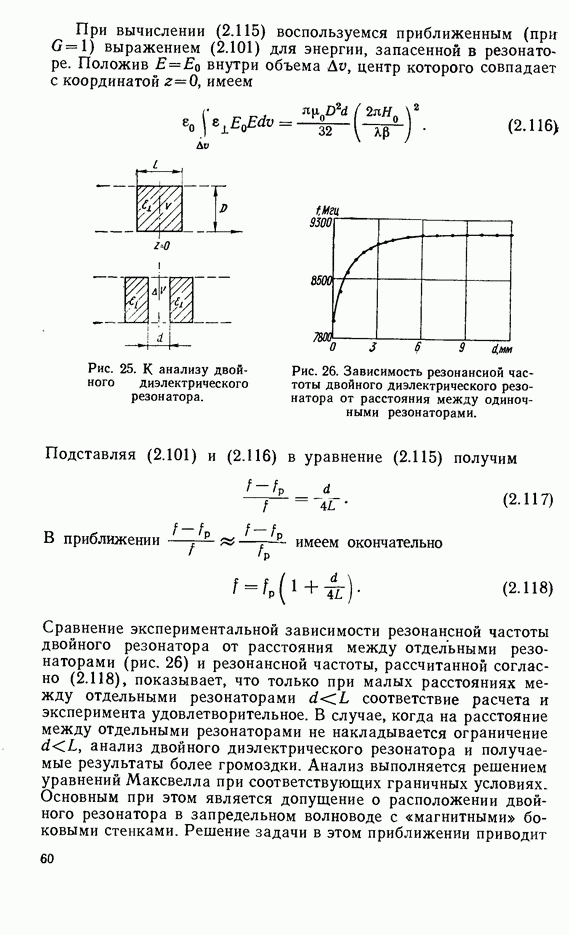
- 2.11. ДВОЙНЫЕ ДИЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
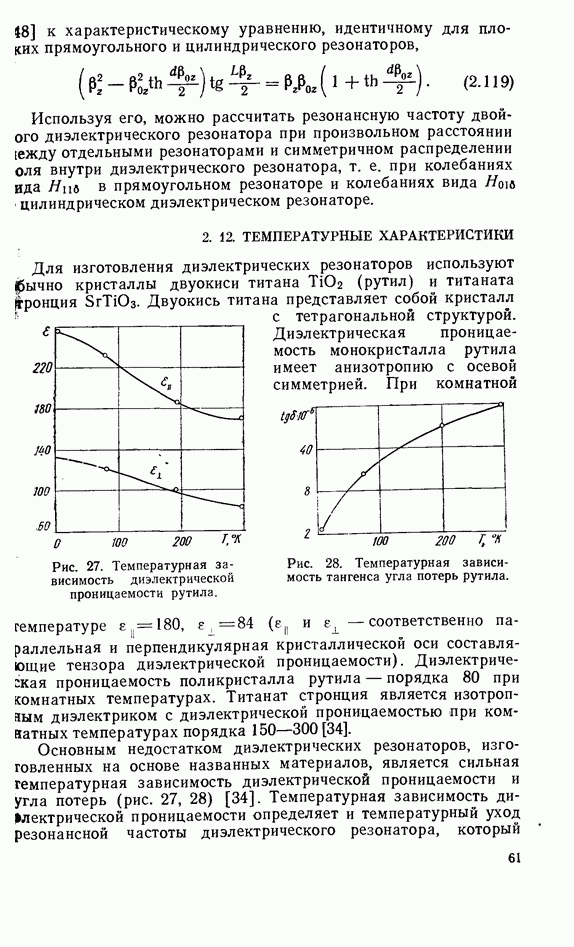
- 2.12. ТЕМПЕРАТУРНЫЕ ХАРАКТЕРИСТИКИ
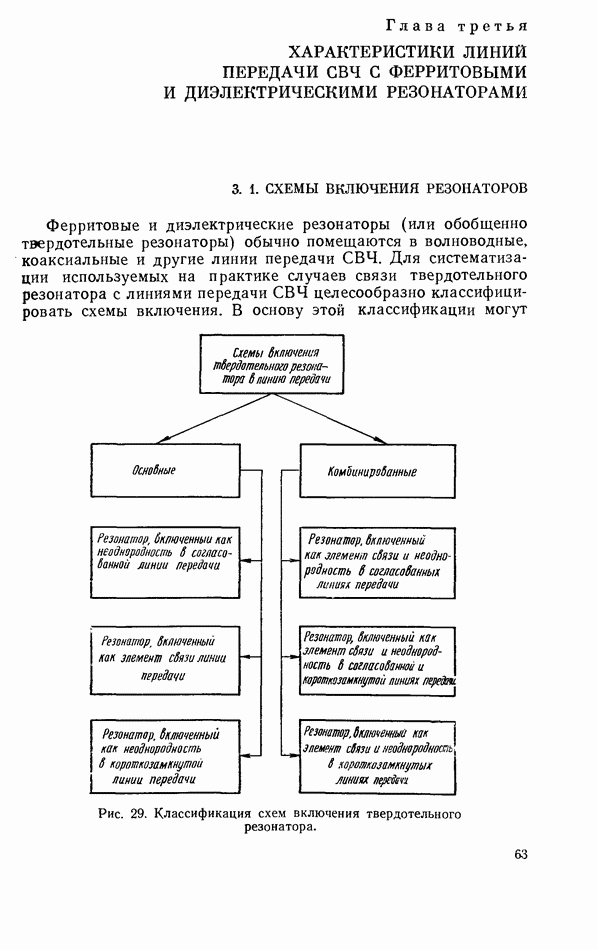
- Глава третья. ХАРАКТЕРИСТИКИ ЛИНИЙ ПЕРЕДАЧИ СВЧ С ФЕРРИТОВЫМИ И ДИЭЛЕКТРИЧЕСКИМИ РЕЗОНАТОРАМИ
- 3.2. МЕТОДЫ РАСЧЕТА СВЧ-СХЕМ С ТВЕРДОТЕЛЬНЫМИ РЕЗОНАТОРАМИ
- 3.3. СВЯЗЬ ТВЕРДОТЕЛЬНОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ СВЧ
- 3.4. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В НЕСОГЛАСОВАННОЙ ЛИНИИ ПЕРЕДАЧИ
- 3.5. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР, ВКЛЮЧЕННЫЙ КАК ЭЛЕМЕНТ СВЯЗИ ЛИНИЙ ПЕРЕДАЧИ
- 3.6. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В КОРОТКОЗАМКНУТОЙ ЛИНИИ ПЕРЕДАЧИ
- 3.7. КОМБИНИРОВАННЫЕ СХЕМЫ ВКЛЮЧЕНИЯ ТВЕРДОТЕЛЬНОГО РЕЗОНАТОРА
- 3.8. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ С НЕСКОЛЬКИМИ РАСПРОСТРАНЯЮЩИМИСЯ ВОЛНАМИ
- Глава четвертая. СВЯЗЬ ТВЕРДОТЕЛЬНЫХ РЕЗОНАТОРОВ С ЛИНИЯМИ ПЕРЕДАЧИ СВЧ
- 4.2. СВЯЗЬ ФЕРРИТОВОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ
- 4.3. ФЕРРИТОВЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ ЗАМЕДЛЕННЫХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
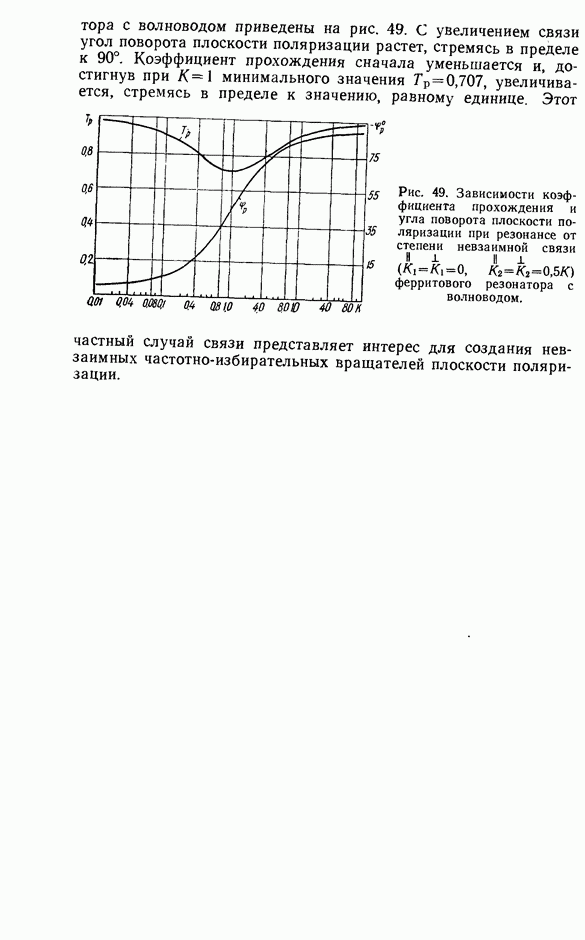
- 4.4. РЕЗОНАНСНЫЙ ПОВОРОТ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ В ВОЛНОВОДЕ С ФЕРРИТОВЫМ РЕЗОНАТОРОМ
- 4.5. НЕЛИНЕЙНЫЙ ФЕРРИТОВЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ
- Ферритовый резонатор в линии передачи при запороговых уровнях мощности
- Нелинейный ферритовый резонатор в короткозамкнутой линии передачи
- Связь линий передачи СВЧ при помощи нелинейного ферритового резонатора
- Нелинейный ферритовый резонатор в согласованной линии передачи
- 4.6. СВЯЗЬ ДИЭЛЕКТРИЧЕСКОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ СВЧ
- Глава пятая. ПРИНЦИПЫ ПОСТРОЕНИЯ СВЧ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ И УСТРОЙСТВ НА ОСНОВЕ ТВЕРДОТЕЛЬНЫХ РЕЗОНАТОРОВ
- 5.2. ДАТЧИКИ УРОВНЯ МОЩНОСТИ СВЧ
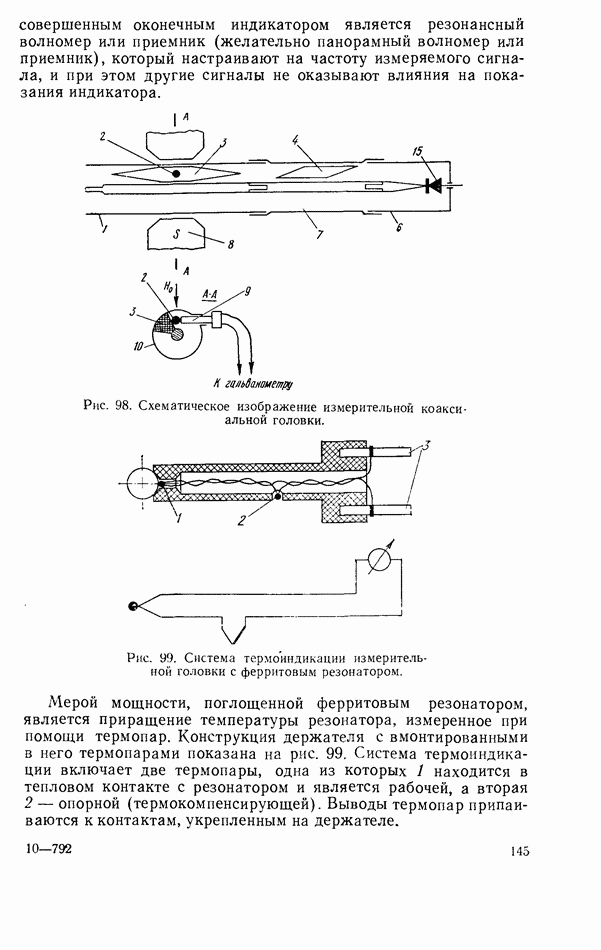
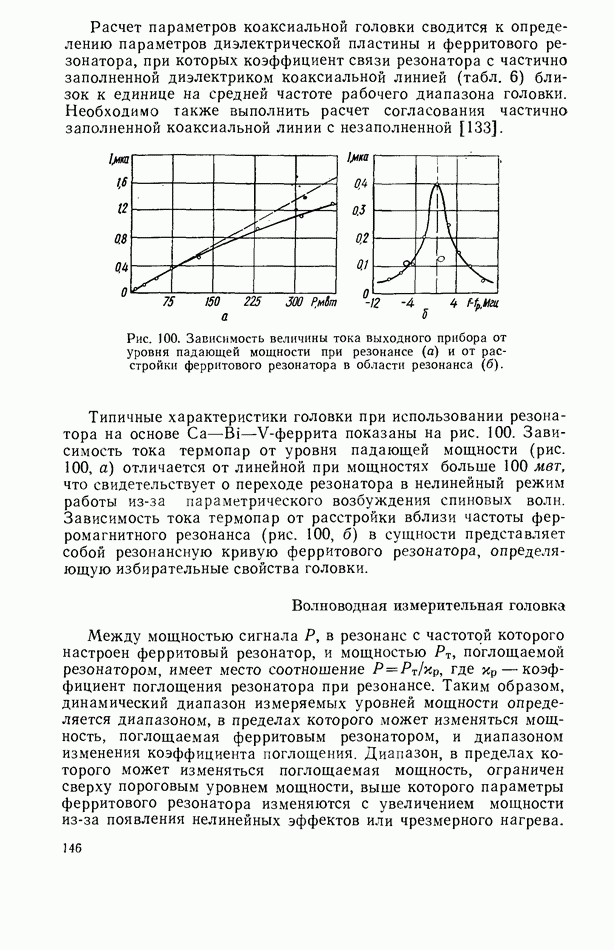
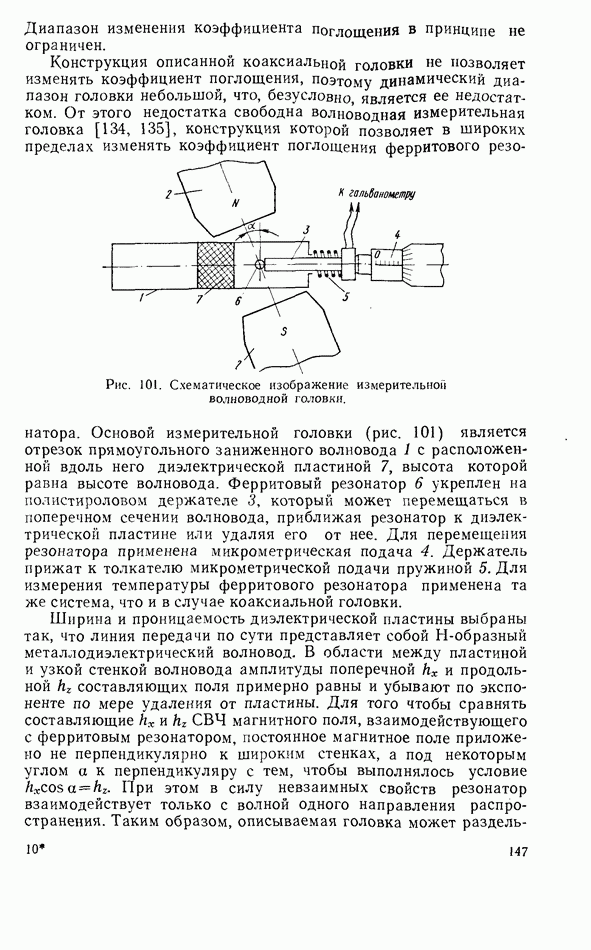
- Волноводная измерительная головка
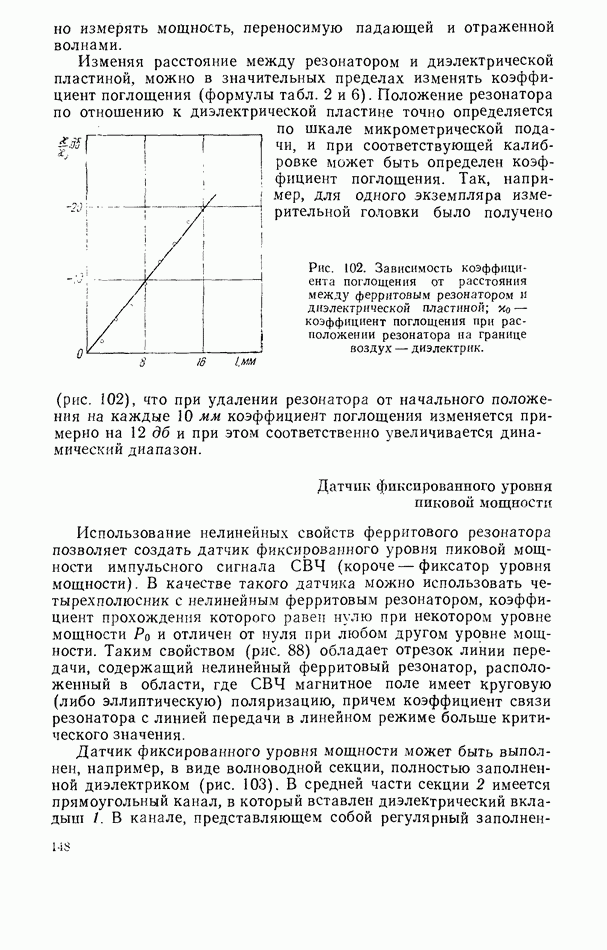
- Датчик фиксированного уровня пиковой мощности
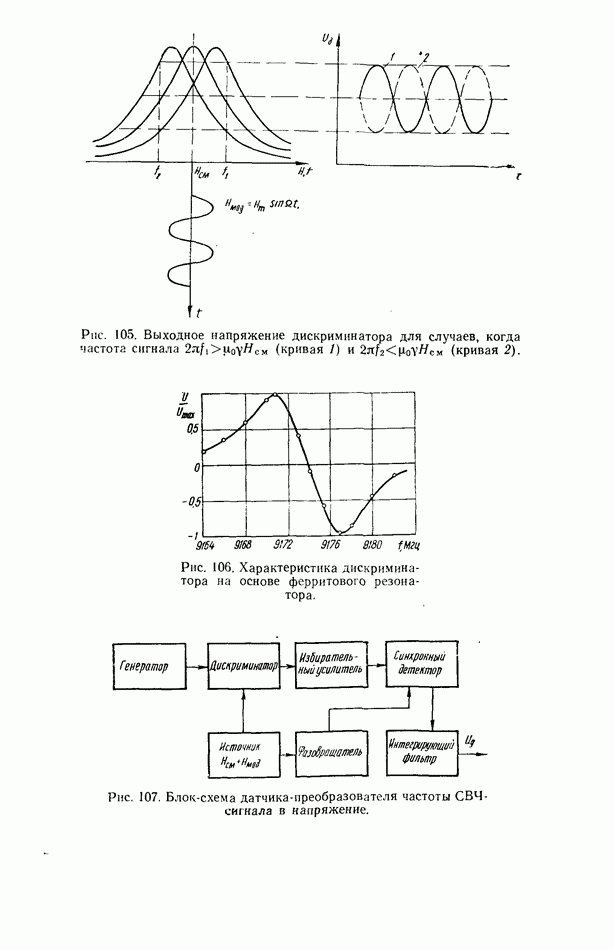
- 5.3. ЧАСТОТНЫЕ ДИСКРИМИНАТОРЫ С МАГНИТНОЙ НАСТРОЙКОЙ
- 5.4. РЕЗОНАНСНЫЕ ФАЗОВРАЩАТЕЛИ
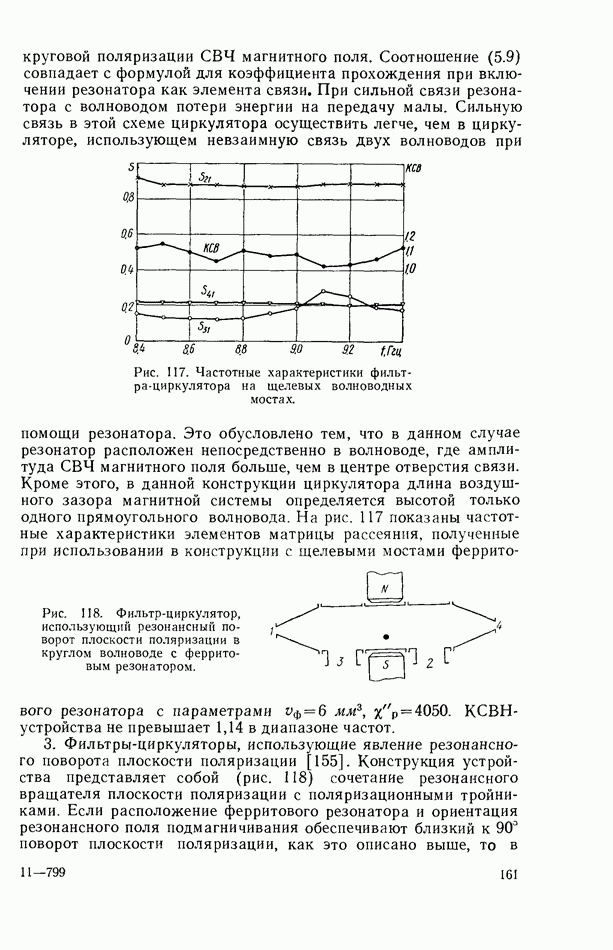
- 5.5. УСТРОЙСТВО ДЛЯ РЕЗОНАНСНОГО ПОВОРОТА ПЛОСКОСТИ ПОЛЯРИЗАЦИИ В ВОЛНОВОДЕ
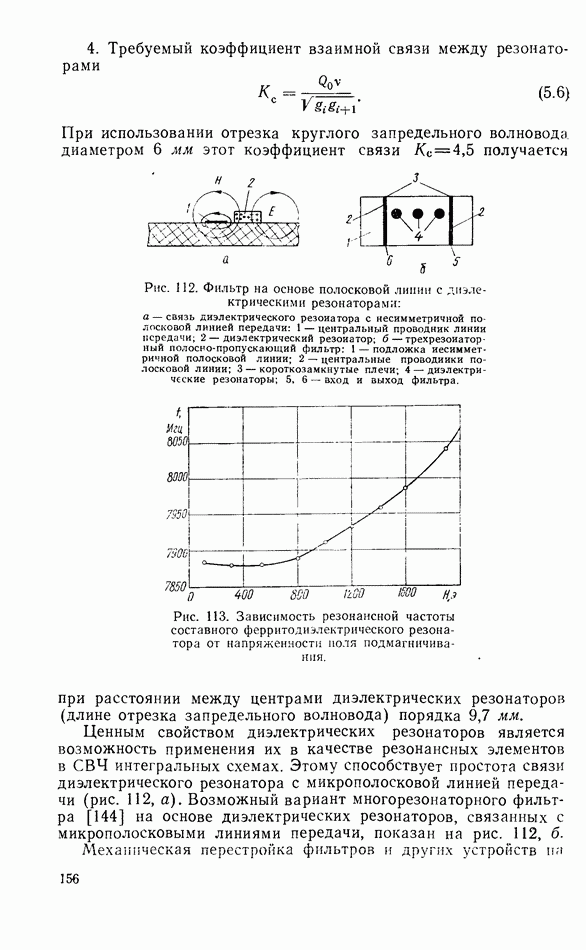
- 5.6. ФИЛЬТРЫ СВЧ НА ОСНОВЕ ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
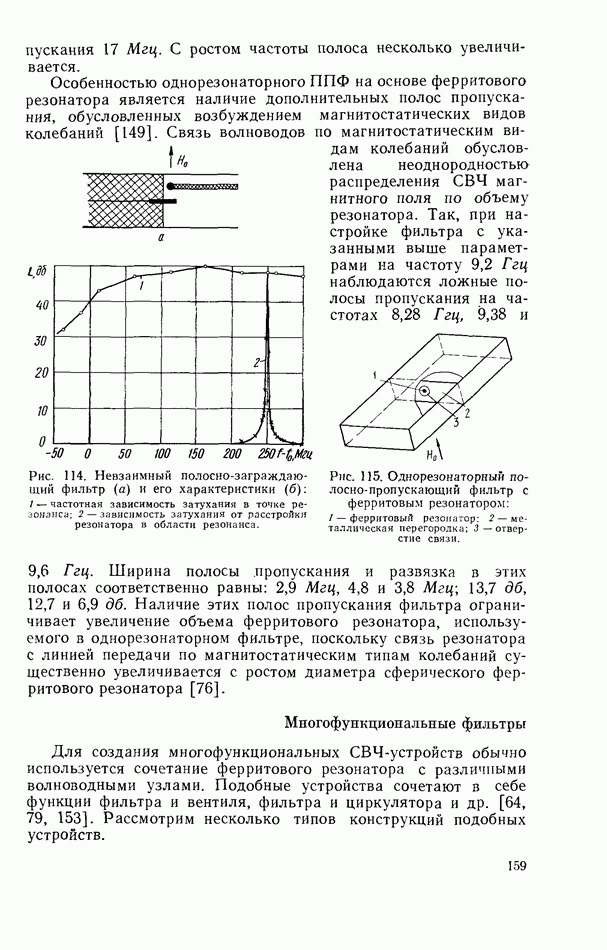
- 5.7. ФЕРРИТОВЫЕ СВЧ-ФИЛЬТРЫ
- Многофункциональные фильтры
- Многорезонаторные ферритовые фильтры
- 5.8. ЧАСТОТНО-ИЗБИРАТЕЛЬНЫЕ ОГРАНИЧИТЕЛИ МАЛЫХ УРОВНЕЙ МОЩНОСТИ