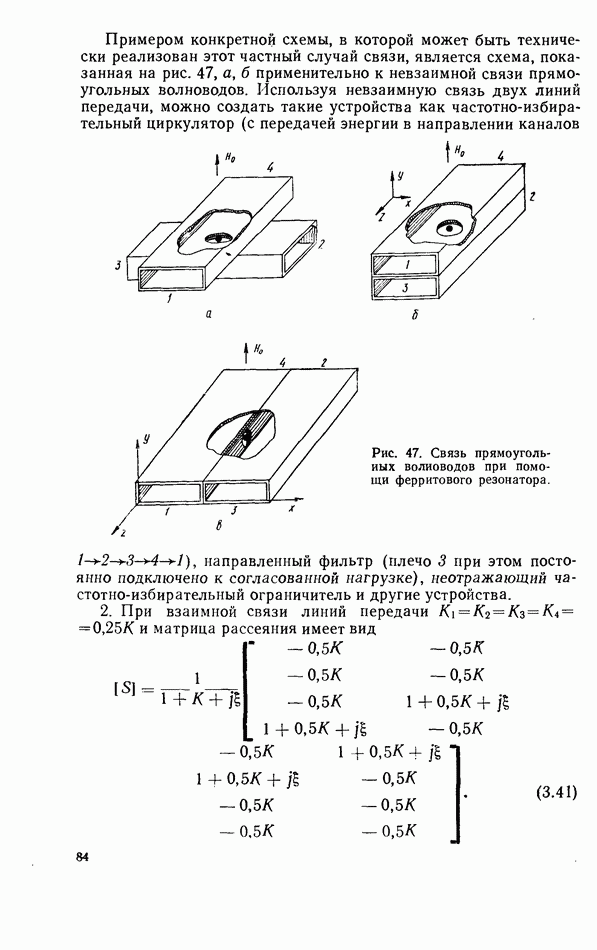
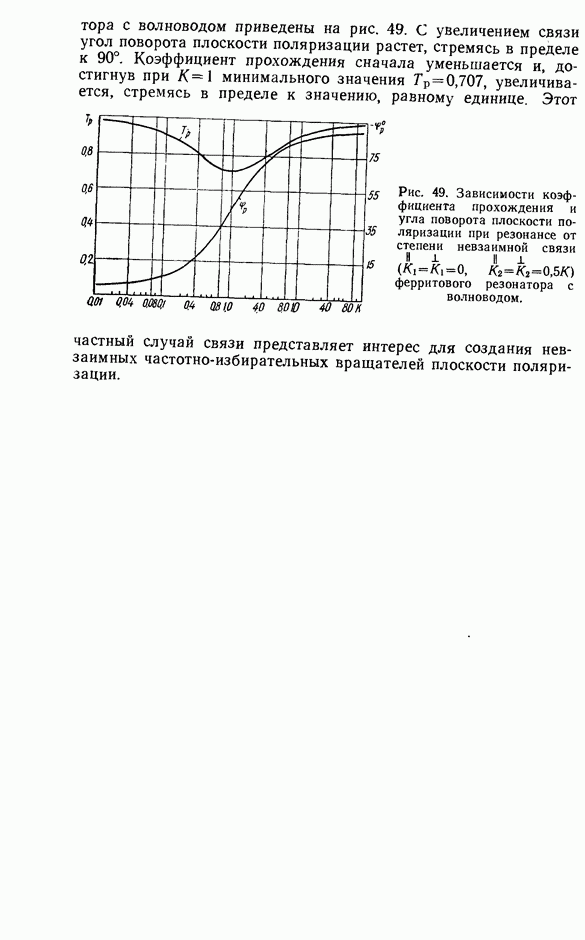
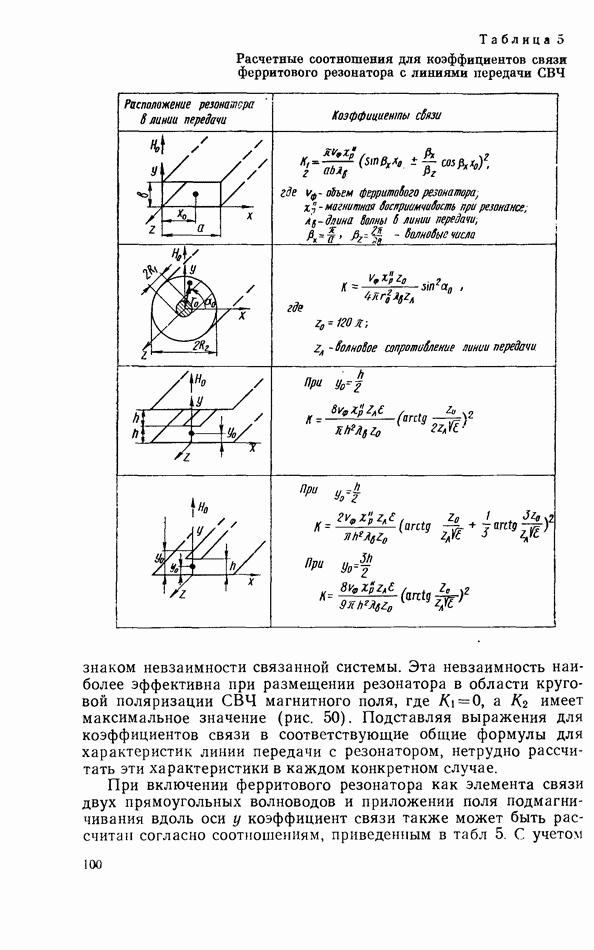
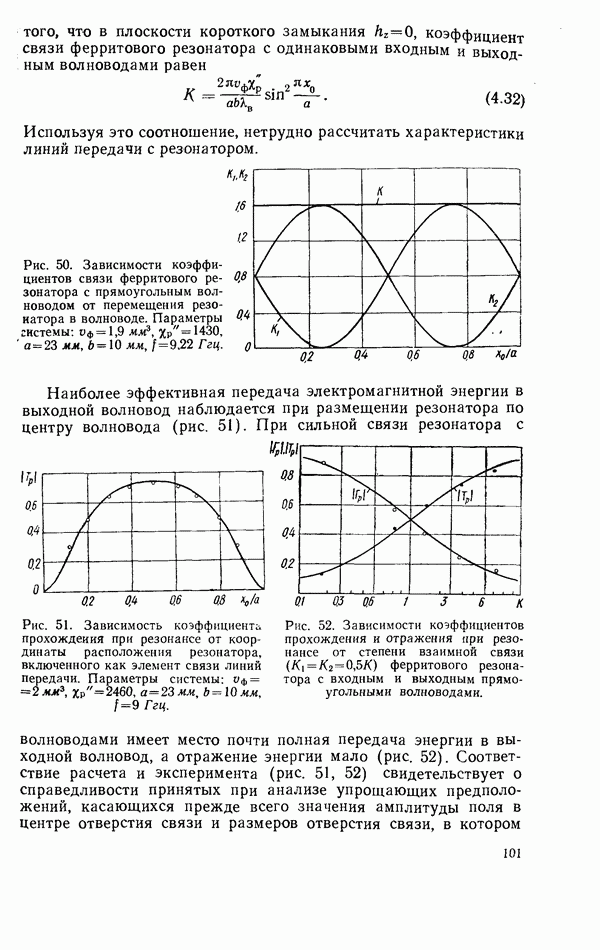
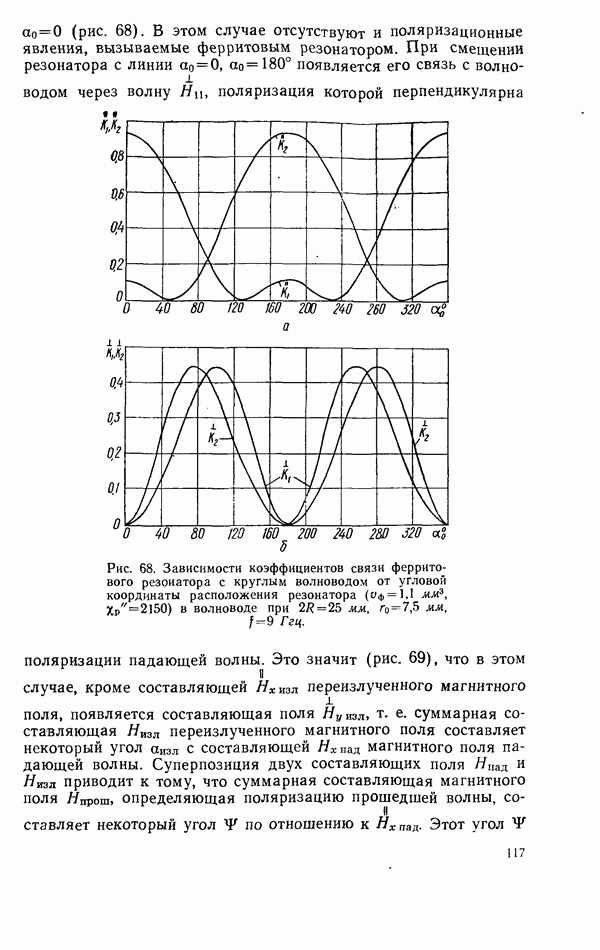
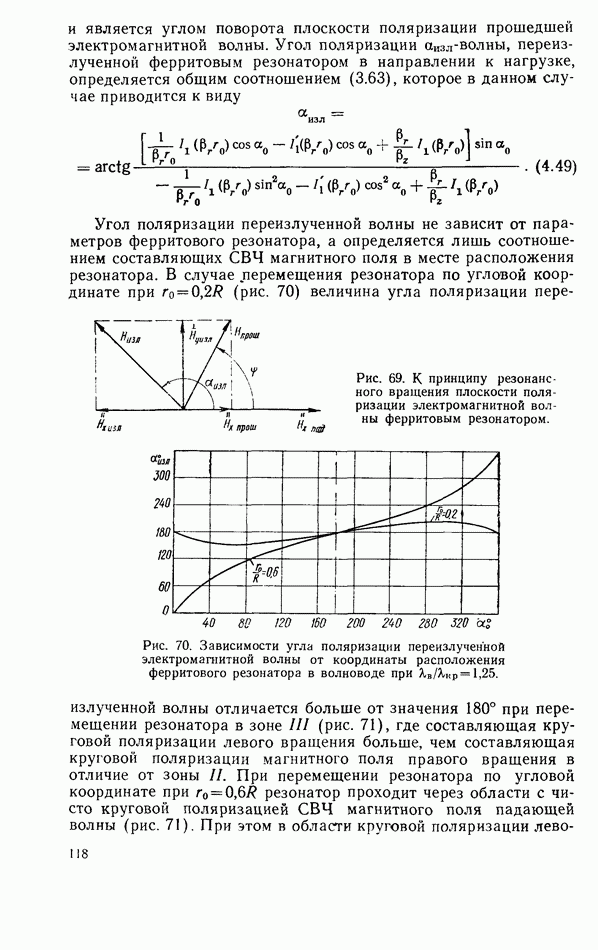
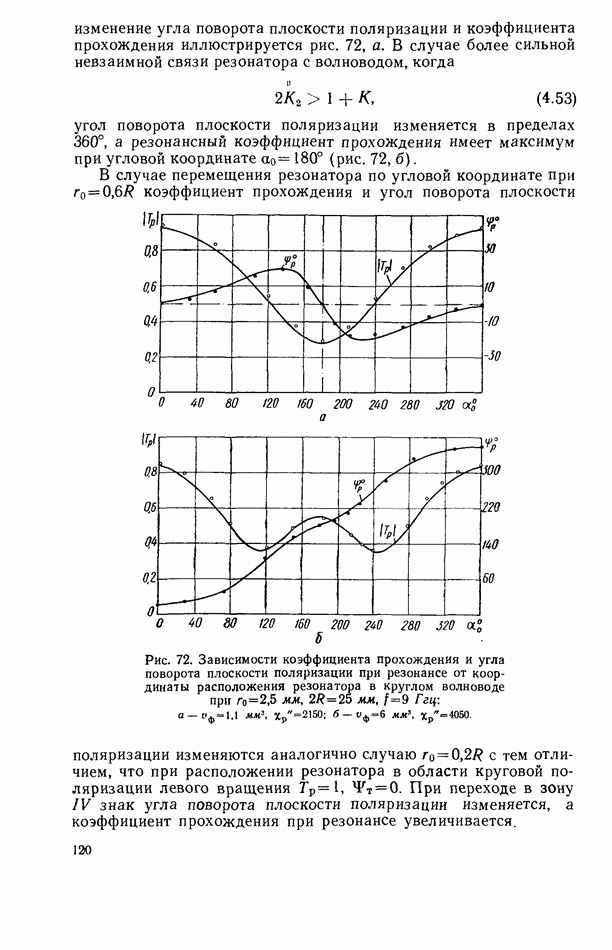
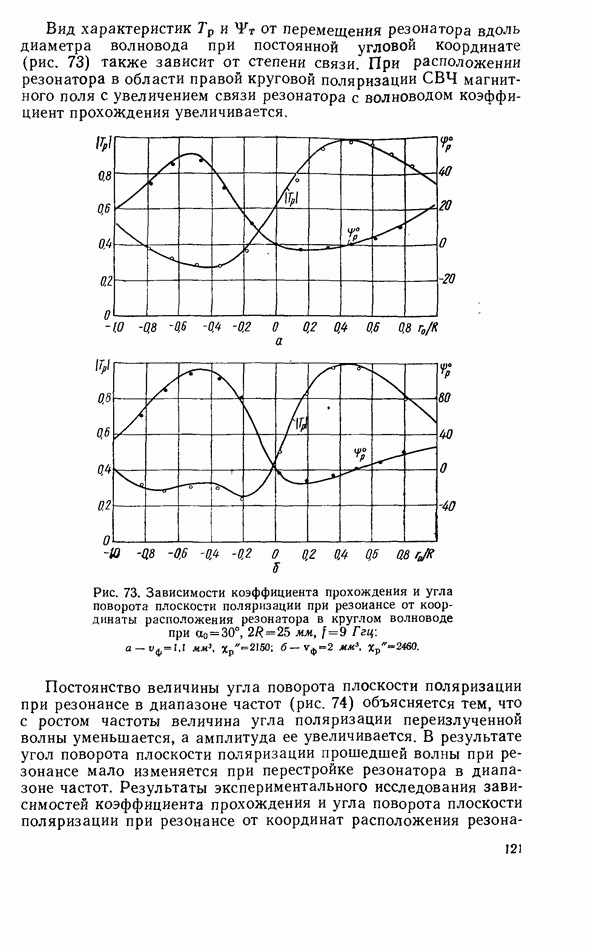
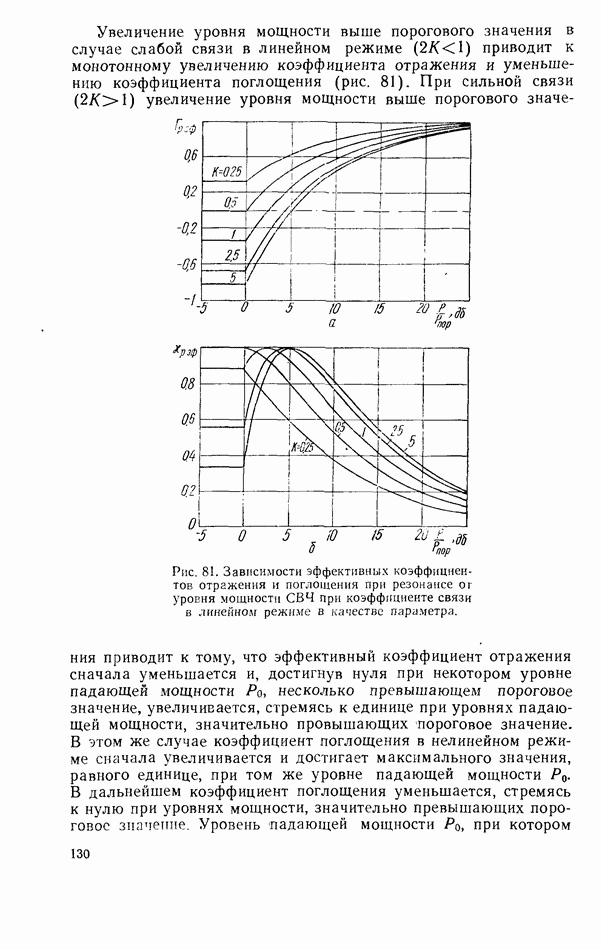
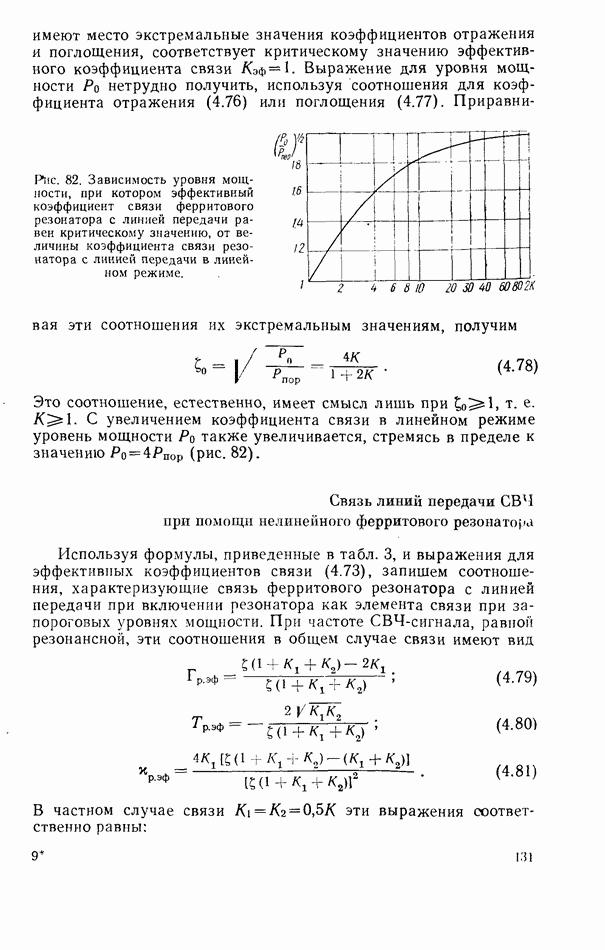
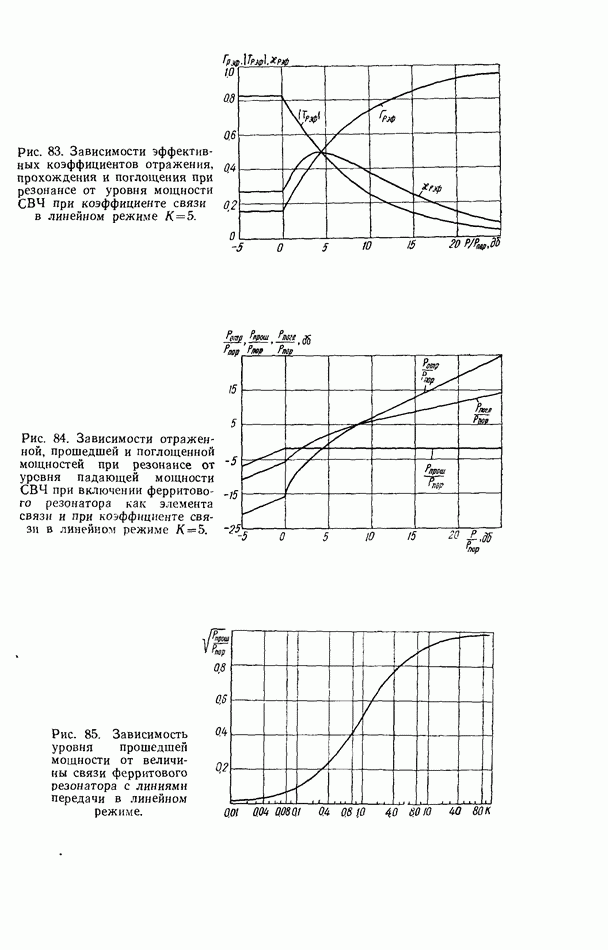
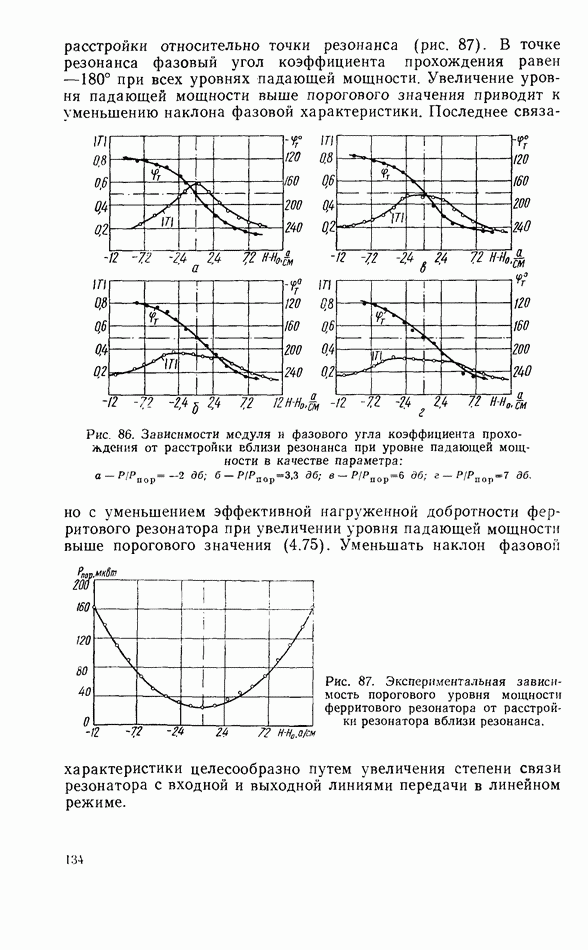
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.2. РЕЗОНАНСНАЯ ЧАСТОТА
Зависимость резонансной частоты от формы резонатора
Рассмотрим ферритовый резонатор, на который воздействуют внешние магнитные поля, при этом магнитные поля внутри резонатора отличаются от внешних. Этому отличию внешних и внутренних полей можно дать следующее объяснение.
При помещении ферритового резонатора в магнитное поле магнитные моменты как внутри резонатора, так и на его поверхности ориентируются вдоль направления поля. Ориентированные магнитные моменты на поверхности резонатора как бы являются магнитными зарядами, между которыми создается размагничивающее поле, направленное навстречу внешнему магнитному полю.
Строгий учет поверхностных эффектов требует решения соответствующей граничной электродинамической задачи. Однако если резонатор ограничен поверхностью второго порядка — эллипсоидом, то, как известно из магнитостатики [4], магнитное поле внутри такого эллипсоида, помещенного в однородное постоянное поле, также однородно. Размагничивающее поле пропорционально намагниченности феррита, поэтому для внутреннего поля ферритового эллипсоида будет справедливо выражение

где  — внешнее постоянное магнитное поле;
— внешнее постоянное магнитное поле;  коэффициент, который называют размагничивающим фактором.
коэффициент, который называют размагничивающим фактором.
Так как ферритовый резонатор имеет малые размеры по сравнению с длиной электромагнитной волны, можно воспользоваться квазистатическим приближением и записать для внутренних высокочастотных полей соотношения типа (1.17). Тогда для суммы постоянного и высокочастотного полей внутри резонатора будет справедливо векторное выражение

где  тензор размагничивающих факторов.
тензор размагничивающих факторов.
Если оси эллипсоида совместить с осями системы координат, то  будет диагональным тензором, т. е. для установления соотношений между внутренними и внешними полями необходимо знать только три размагничивающих фактора. Пусть, например, постоянное магнитное поле направлено вдоль оси
будет диагональным тензором, т. е. для установления соотношений между внутренними и внешними полями необходимо знать только три размагничивающих фактора. Пусть, например, постоянное магнитное поле направлено вдоль оси  (и с ней совмещена ось эллипсоида), а высокочастотное магнитное поле действует в плоскости
(и с ней совмещена ось эллипсоида), а высокочастотное магнитное поле действует в плоскости  (с осями х и у совпадают две другие оси эллипсоида). В этом случае магнитные поля внутри эллипсоида описываются системой равенств
(с осями х и у совпадают две другие оси эллипсоида). В этом случае магнитные поля внутри эллипсоида описываются системой равенств

где  размагничивающие факторы по соответствующим. осям. Если рассматривается эллипсоид вращения и постоянное, магнитное поле направлено вдоль оси вращения, например оси
размагничивающие факторы по соответствующим. осям. Если рассматривается эллипсоид вращения и постоянное, магнитное поле направлено вдоль оси вращения, например оси  то в силу осевой симметрии
то в силу осевой симметрии  где
где  -поперечный размагничивающий фактор.
-поперечный размагничивающий фактор.
Резонансную частоту ферритового резонатора определим как частоту свободной прецессии в отсутствие магнитного поля СВЧ. Полагая  в выражении (1.18), подставим значение суммарного внутреннего магнитного поля в уравнение Ландау-Лифшица (1.1) и после простых преобразований получим
в выражении (1.18), подставим значение суммарного внутреннего магнитного поля в уравнение Ландау-Лифшица (1.1) и после простых преобразований получим

Здесь учтено, что 
Проектируя уравнение (1.20) на оси декартовой системы координат, запишем систему уравнений

Из условия совместности системы, т. е. из условия равенства нулю ее определителя, находим выражение для резонансной частоты

С учетом выражения (1.17) для поля  получим формулу резонансной частоты, известную как формула Киттеля [5]
получим формулу резонансной частоты, известную как формула Киттеля [5]

Таблица 1 (см. скан) Размагничивающие факторы и резонансные частоты ферритовых резонаторов
Для ферритового резонатора в форме эллипсоида вращения 

Частным случаем эллипсоида, у которого все три оси равны между собой, является сфера, а так как размагничивающие факторы определяются соотношениями осей эллипсоида, то для сферы размагничивающие факторы равны, т. е.  тогда формула Киттеля для сферы принимает вид
тогда формула Киттеля для сферы принимает вид

Значения размагничивающих факторов для образцов в форме тонкой пластины, сферы, длинного цилиндра и тонкого диска приведены в табл. 1. Если сфера, как отмечалось, является частным случаем эллипсоида, то пластину, цилиндр и диск можно рассматривать как предельные случаи эллипсоида, поэтому на них распространяется решение, полученное с помощью размагничивающих факторов.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава первая. СВОЙСТВА ФЕРРИТОВЫХ РЕЗОНАТОРОВ
- Ферромагнитный резонанс в неограниченной среде без потерь
- 1.2. РЕЗОНАНСНАЯ ЧАСТОТА
- Зависимость резонансной частоты от формы резонатора
- Влияние кристаллографической анизотропии на резонансную частоту
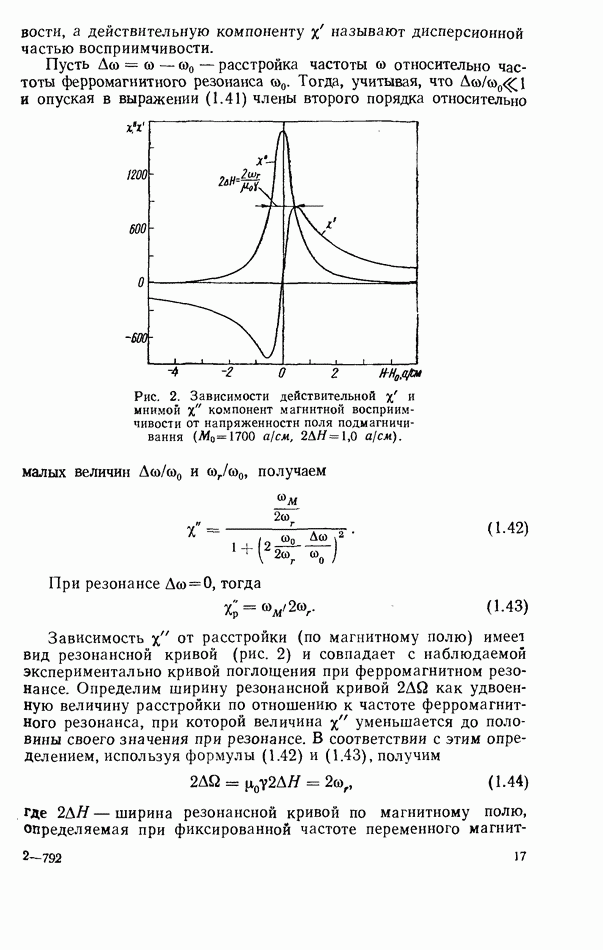
- 1.3. МАГНИТОСТАТИЧЕСКИЕ ВИДЫ КОЛЕБАНИЙ
- 1.4. УЧЕТ ПОТЕРЬ
- 1.5. ДИПОЛЬНЫЙ МОМЕНТ
- 1.6. НЕЛИНЕЙНЫЕ ЯВЛЕНИЯ
- Спиновые волны
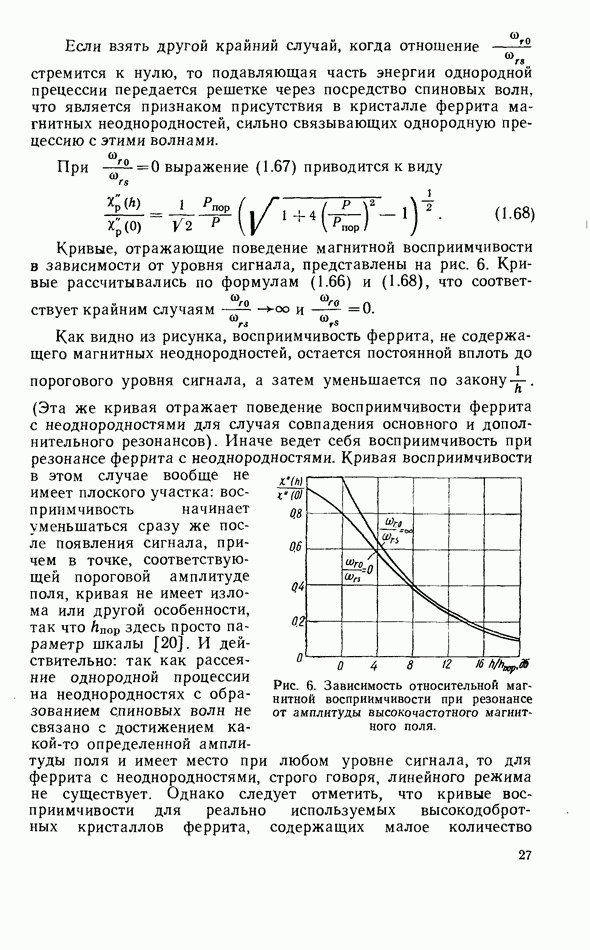
- Пороговая амплитуда высокочастотного магнитного поля
- Восприимчивость при амплитудах поля, превышающих пороговое значение
- 1.7. ПРИМЕНЯЕМЫЕ ДЛЯ ИЗГОТОВЛЕНИЯ МАТЕРИАЛЫ
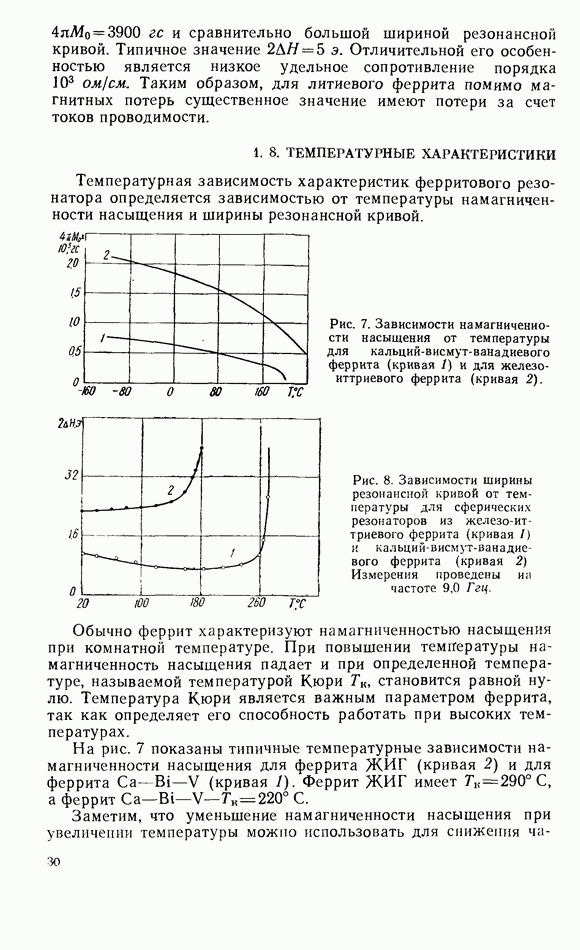
- 1.8. ТЕМПЕРАТУРНЫЕ ХАРАКТЕРИСТИКИ
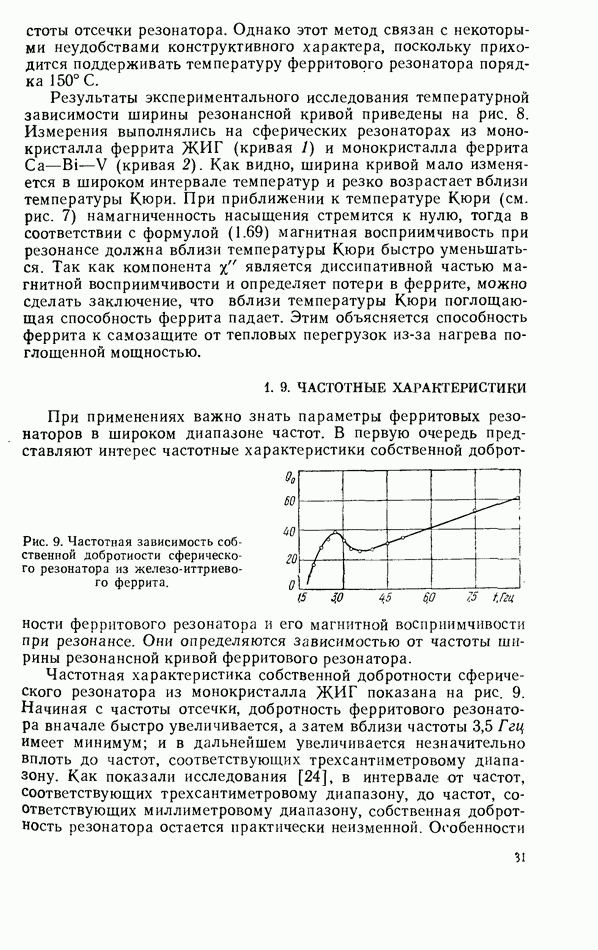
- 1.9. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- Глава вторая. СВОЙСТВА ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 2.2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В АНИЗОТРОПНОМ ДИЭЛЕКТРИЧЕСКОМ СТЕРЖНЕ С «МАГНИТНЫМИ» БОКОВЫМИ СТЕНКАМИ
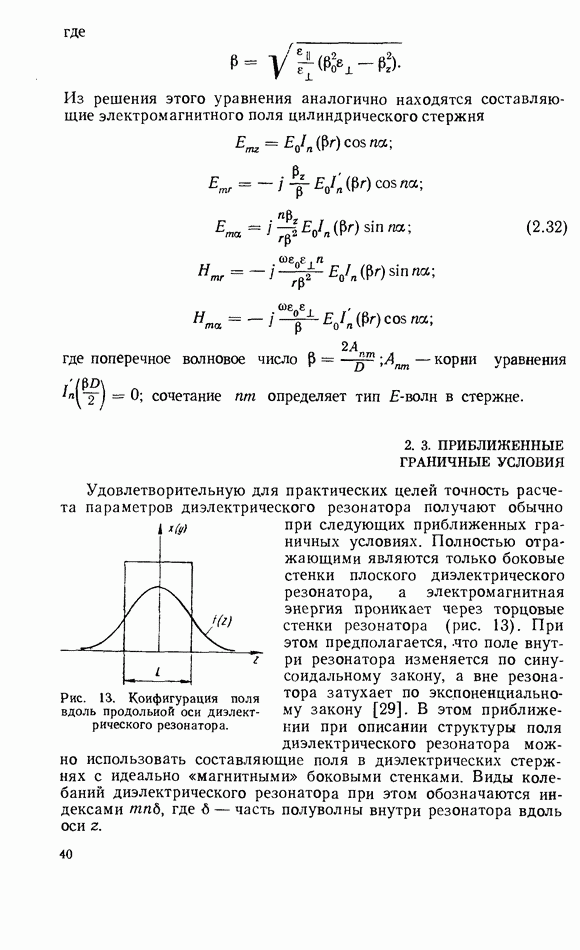
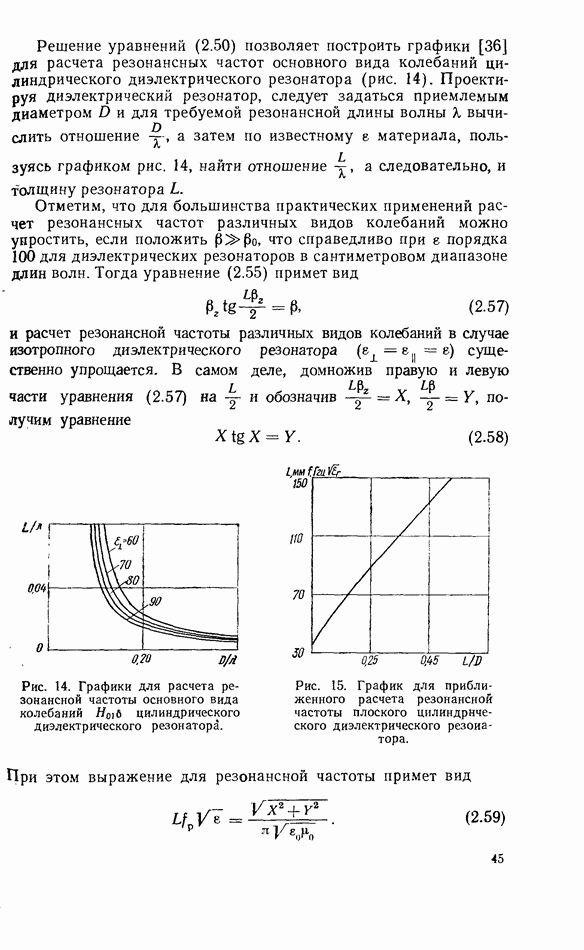
- 2.3. ПРИБЛИЖЕННЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2.5. ОСНОВНЫЕ ВИДЫ КОЛЕБАНИЙ
- 2.6. СФЕРИЧЕСКИЕ ДИЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
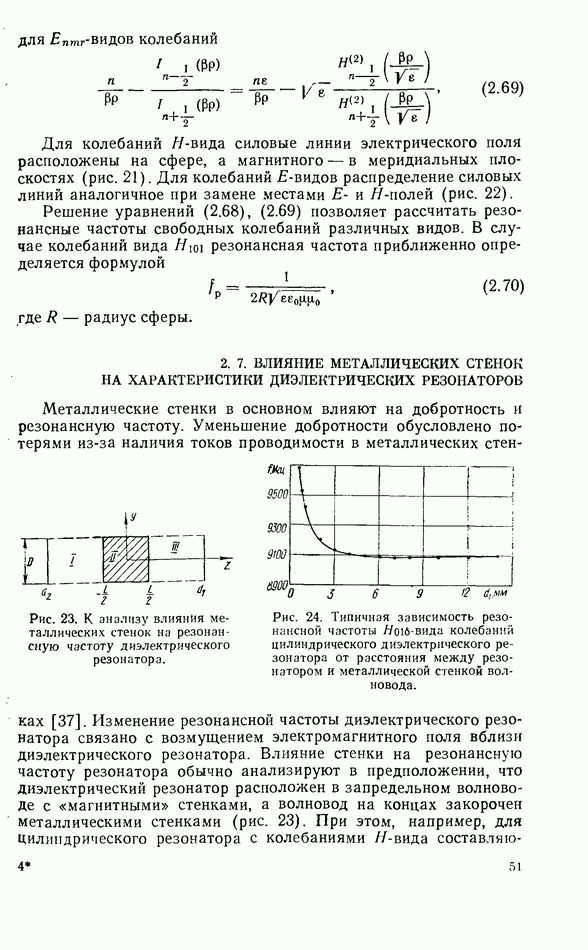
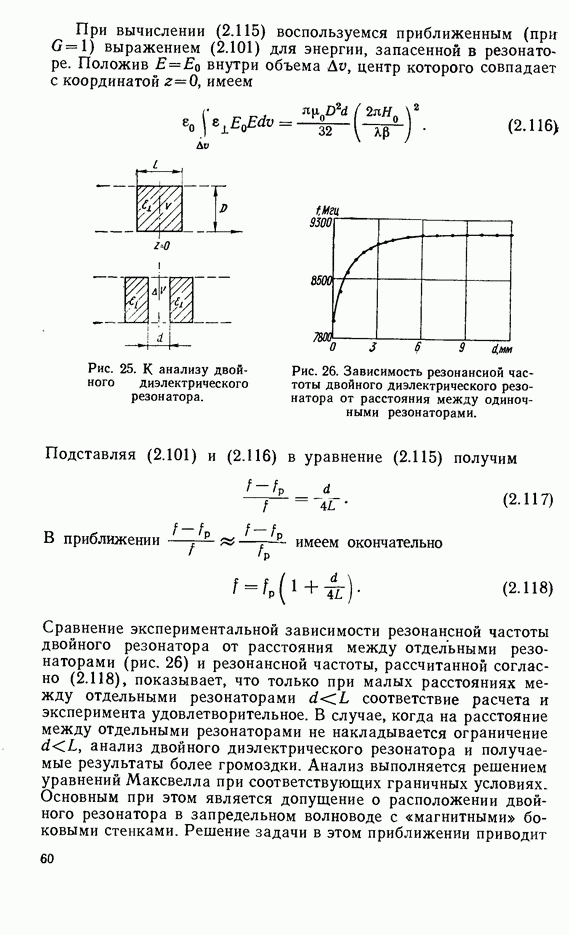
- 2.7. ВЛИЯНИЕ МЕТАЛЛИЧЕСКИХ СТЕНОК НА ХАРАКТЕРИСТИКИ ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
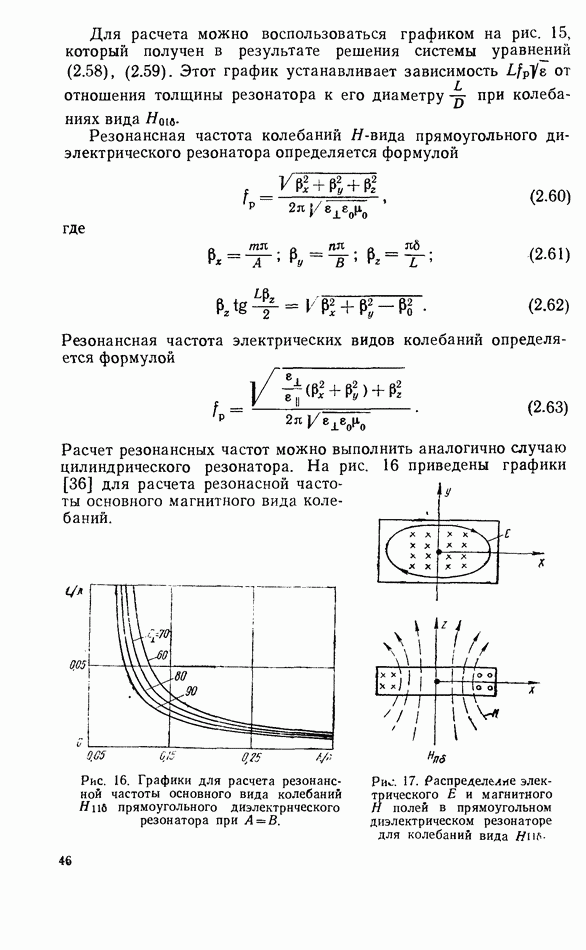
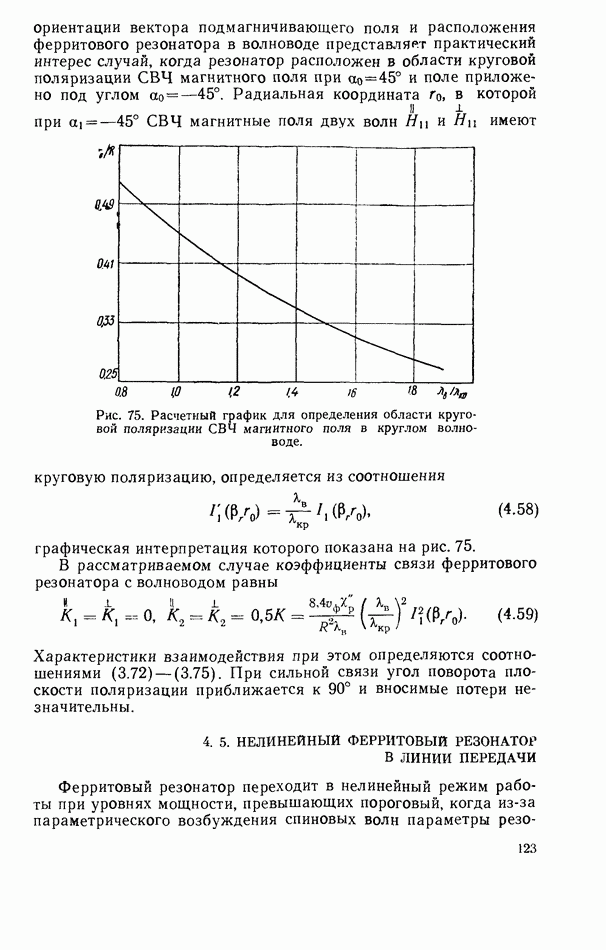
- 2.8. ДИПОЛЬНЫЙ МОМЕНТ
- 2.9. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ
- 2.10. СООТНОШЕНИЕ МЕЖДУ АМПЛИТУДАМИ СВЧ МАГНИТНОГО ПОЛЯ
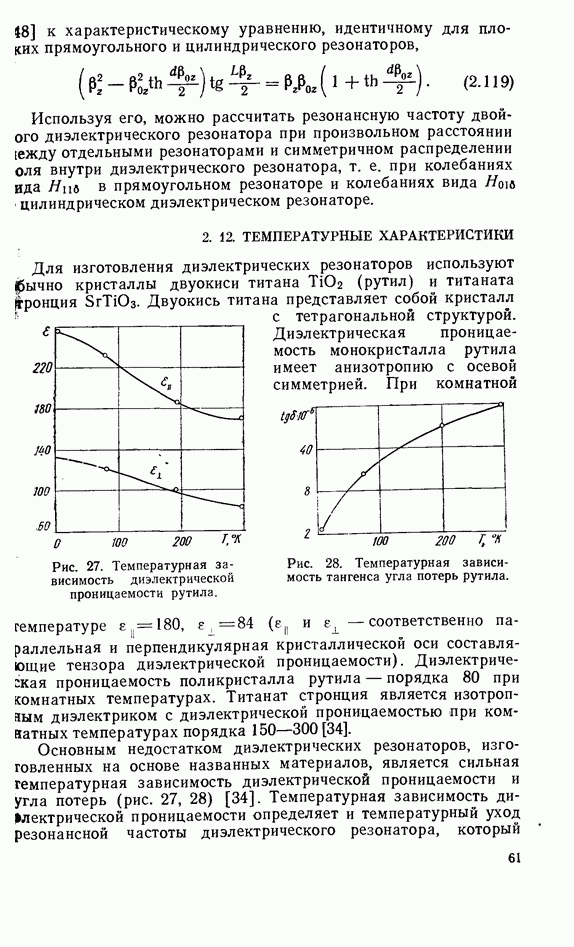
- 2.11. ДВОЙНЫЕ ДИЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
- 2.12. ТЕМПЕРАТУРНЫЕ ХАРАКТЕРИСТИКИ
- Глава третья. ХАРАКТЕРИСТИКИ ЛИНИЙ ПЕРЕДАЧИ СВЧ С ФЕРРИТОВЫМИ И ДИЭЛЕКТРИЧЕСКИМИ РЕЗОНАТОРАМИ
- 3.2. МЕТОДЫ РАСЧЕТА СВЧ-СХЕМ С ТВЕРДОТЕЛЬНЫМИ РЕЗОНАТОРАМИ
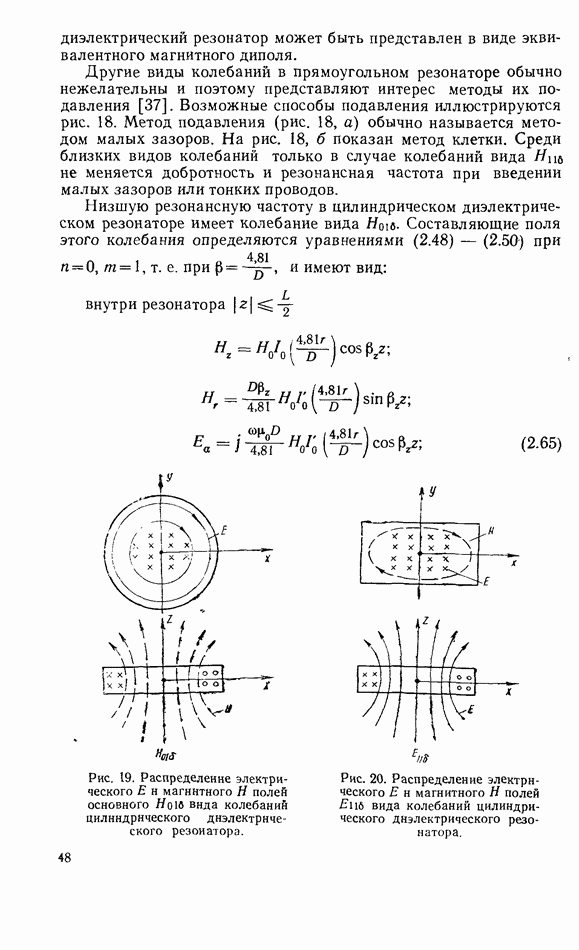
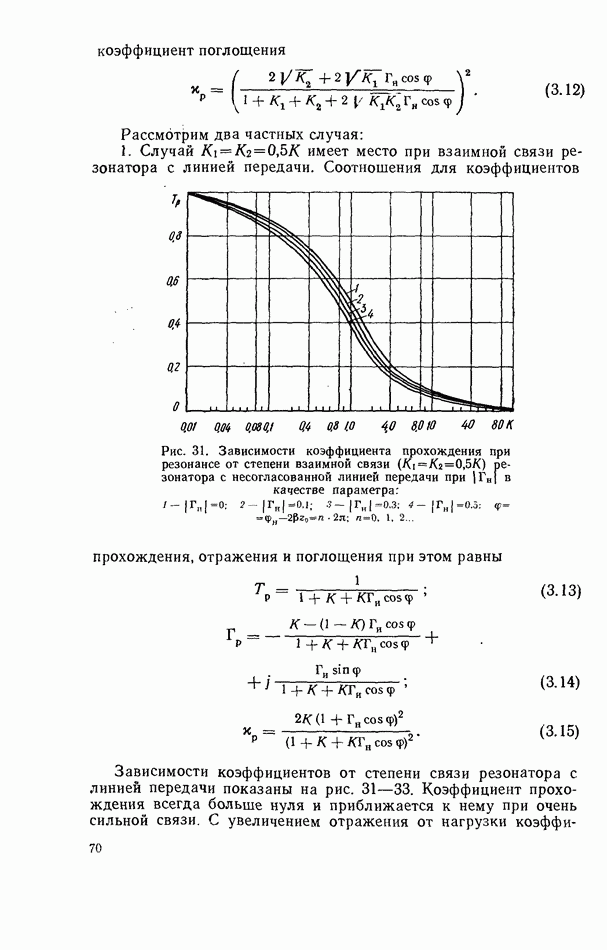
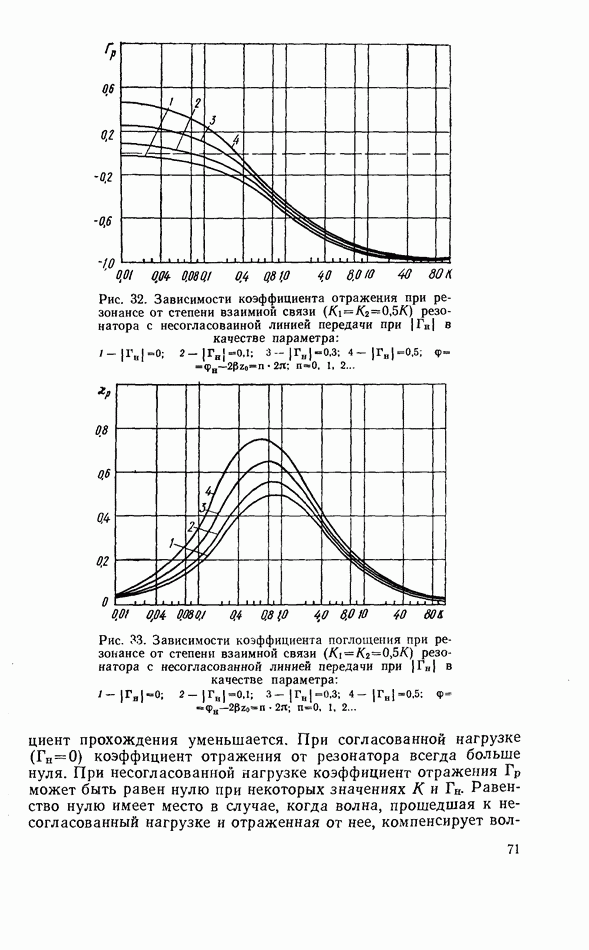
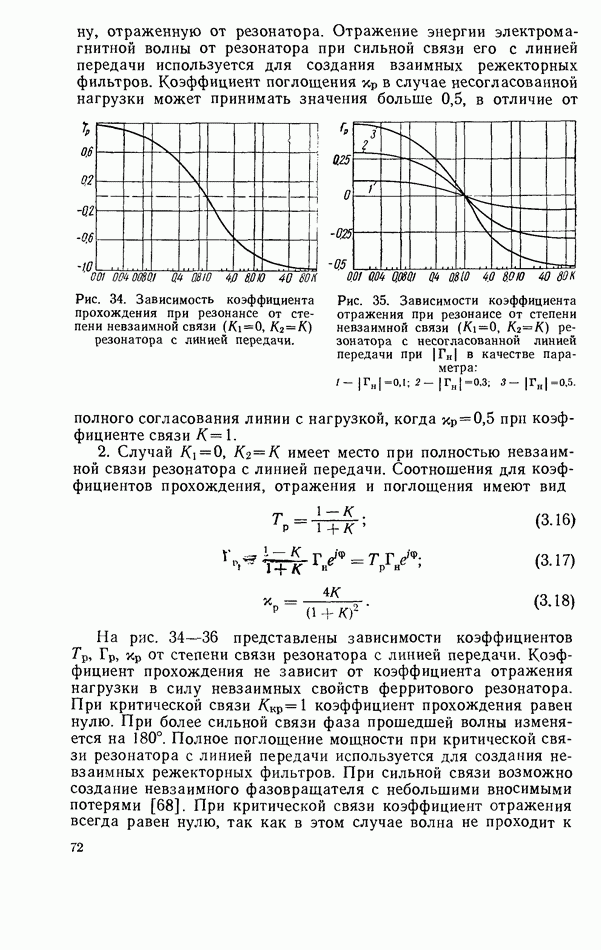
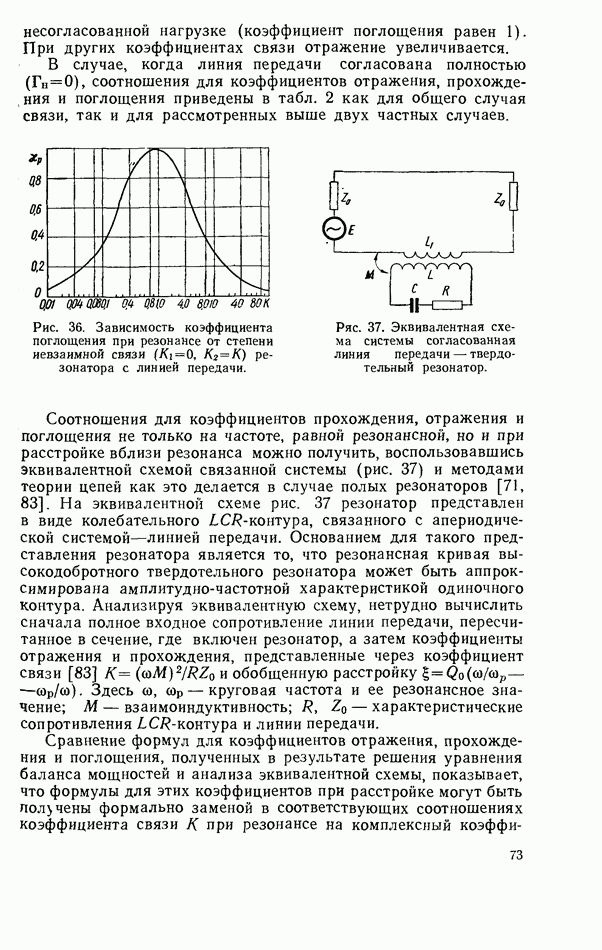
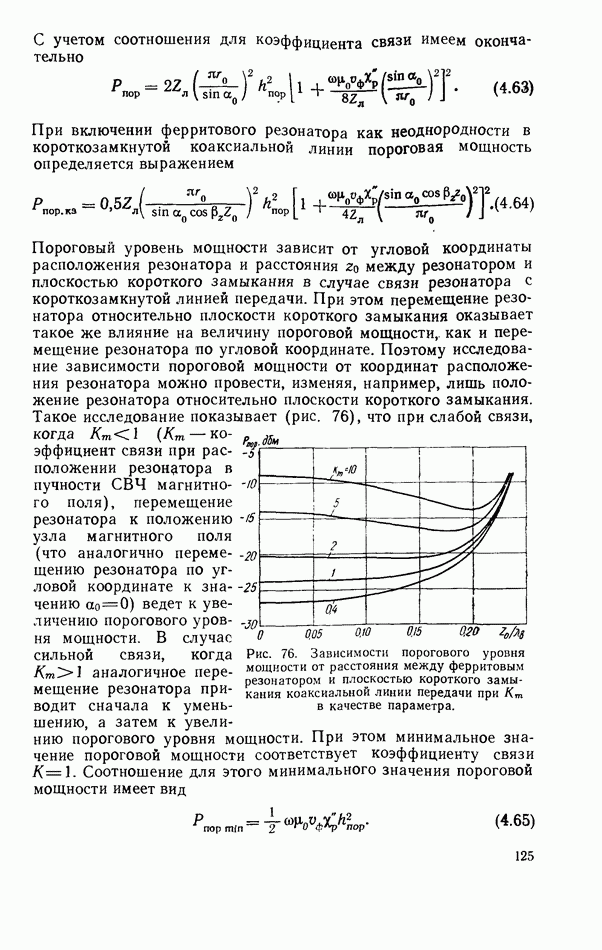
- 3.3. СВЯЗЬ ТВЕРДОТЕЛЬНОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ СВЧ
- 3.4. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В НЕСОГЛАСОВАННОЙ ЛИНИИ ПЕРЕДАЧИ
- 3.5. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР, ВКЛЮЧЕННЫЙ КАК ЭЛЕМЕНТ СВЯЗИ ЛИНИЙ ПЕРЕДАЧИ
- 3.6. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В КОРОТКОЗАМКНУТОЙ ЛИНИИ ПЕРЕДАЧИ
- 3.7. КОМБИНИРОВАННЫЕ СХЕМЫ ВКЛЮЧЕНИЯ ТВЕРДОТЕЛЬНОГО РЕЗОНАТОРА
- 3.8. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ С НЕСКОЛЬКИМИ РАСПРОСТРАНЯЮЩИМИСЯ ВОЛНАМИ
- Глава четвертая. СВЯЗЬ ТВЕРДОТЕЛЬНЫХ РЕЗОНАТОРОВ С ЛИНИЯМИ ПЕРЕДАЧИ СВЧ
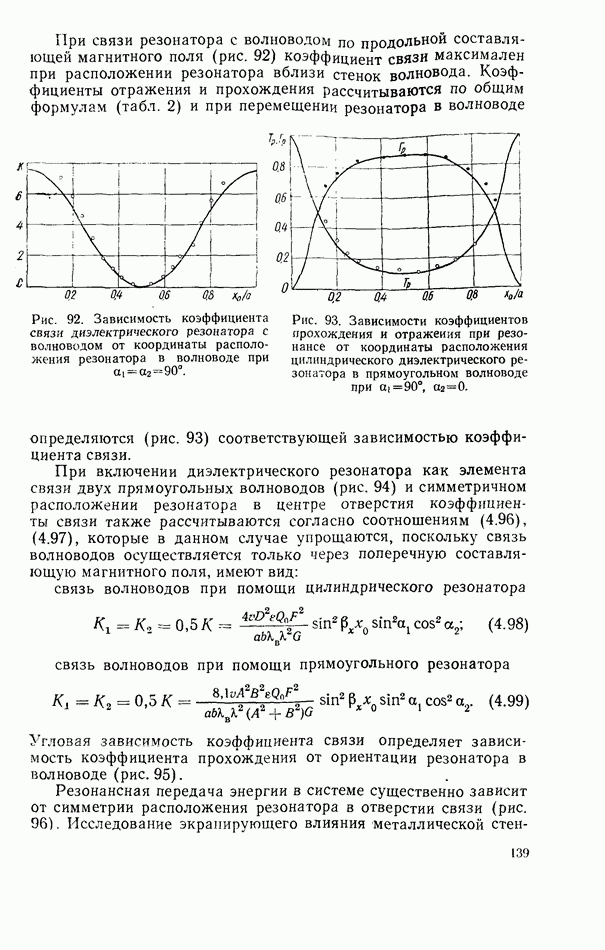
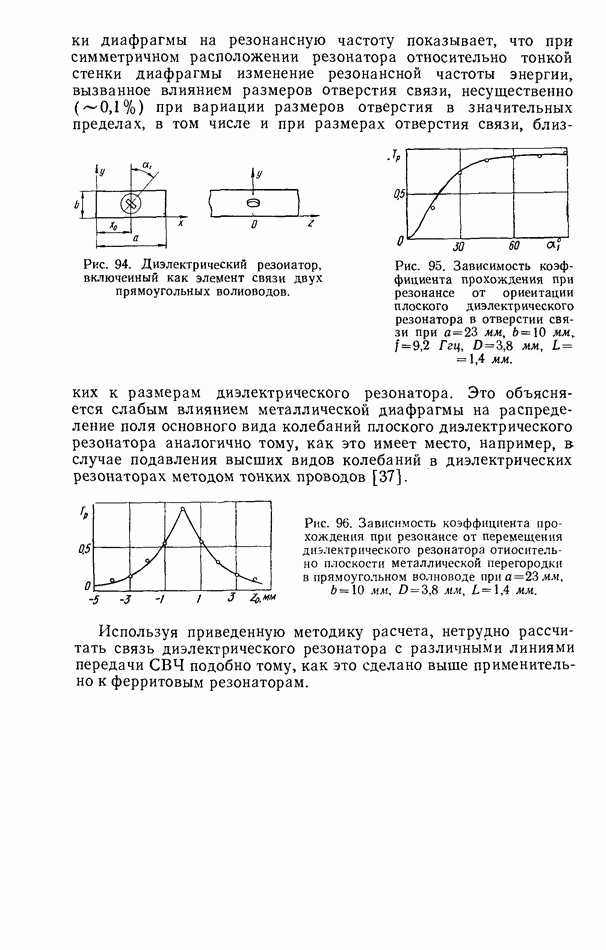
- 4.2. СВЯЗЬ ФЕРРИТОВОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ
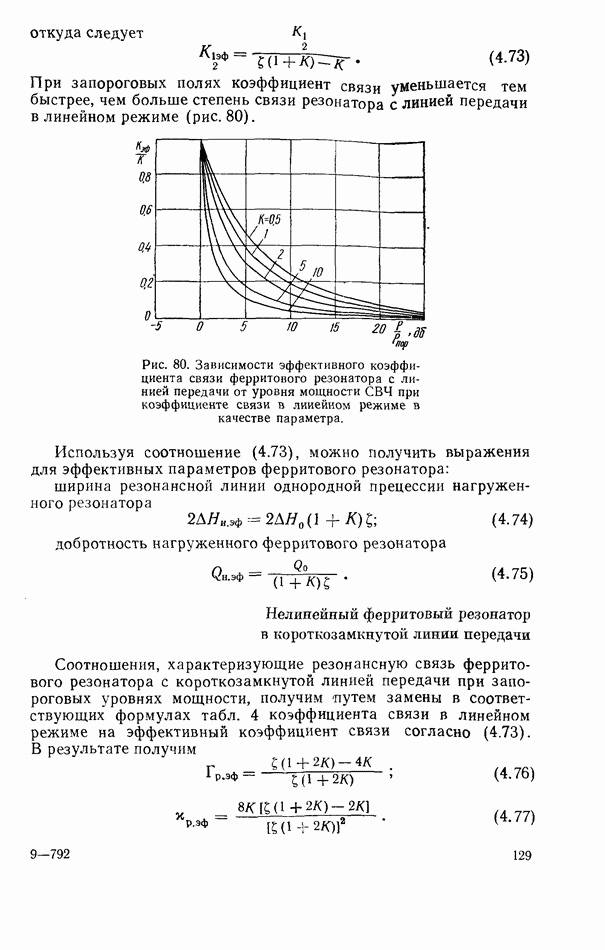
- 4.3. ФЕРРИТОВЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ ЗАМЕДЛЕННЫХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
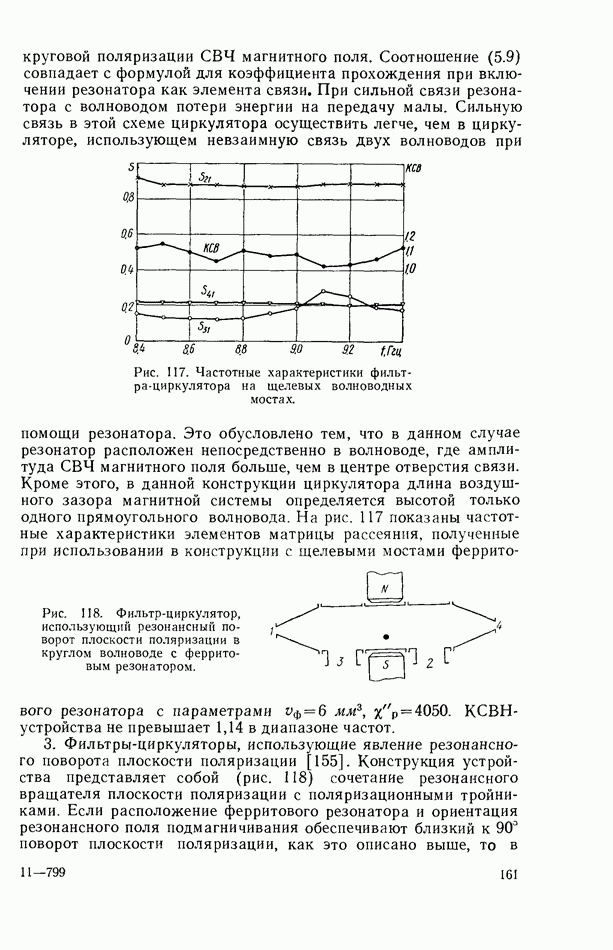
- 4.4. РЕЗОНАНСНЫЙ ПОВОРОТ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ В ВОЛНОВОДЕ С ФЕРРИТОВЫМ РЕЗОНАТОРОМ
- 4.5. НЕЛИНЕЙНЫЙ ФЕРРИТОВЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ
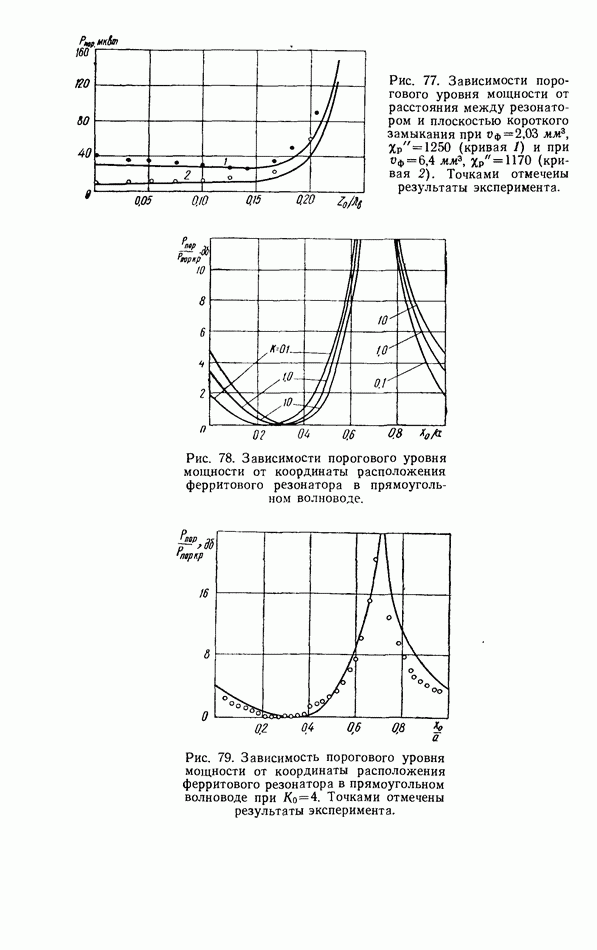
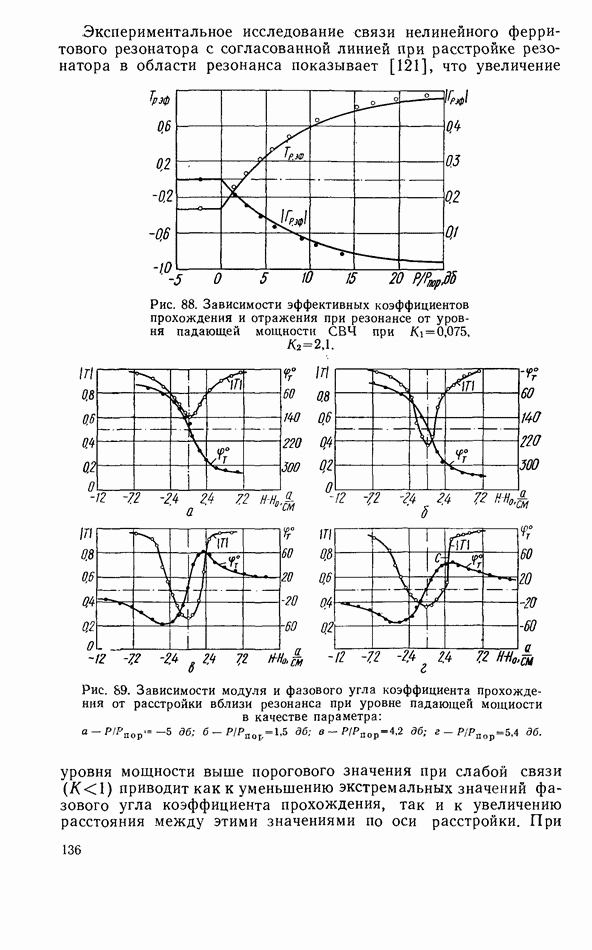
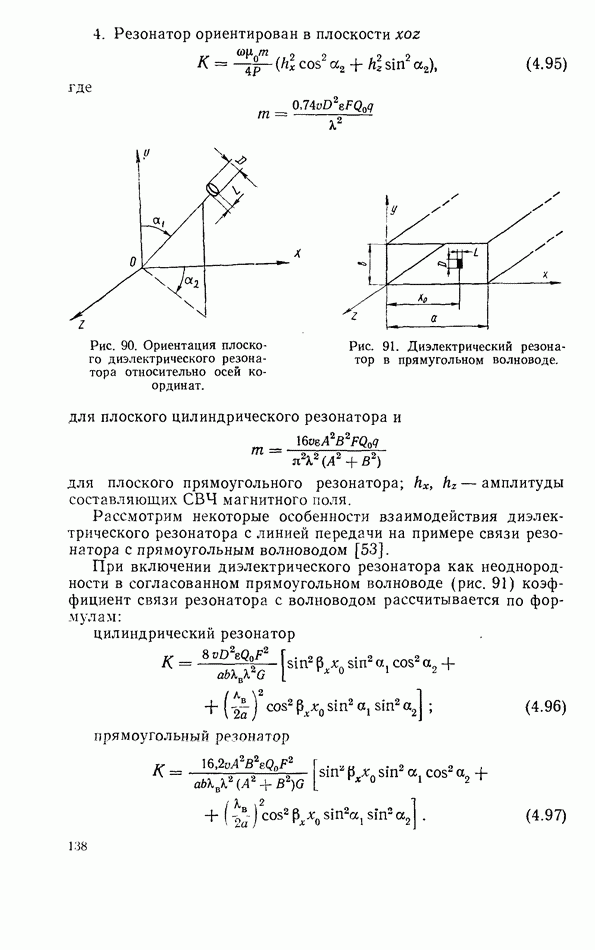
- Ферритовый резонатор в линии передачи при запороговых уровнях мощности
- Нелинейный ферритовый резонатор в короткозамкнутой линии передачи
- Связь линий передачи СВЧ при помощи нелинейного ферритового резонатора
- Нелинейный ферритовый резонатор в согласованной линии передачи
- 4.6. СВЯЗЬ ДИЭЛЕКТРИЧЕСКОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ СВЧ
- Глава пятая. ПРИНЦИПЫ ПОСТРОЕНИЯ СВЧ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ И УСТРОЙСТВ НА ОСНОВЕ ТВЕРДОТЕЛЬНЫХ РЕЗОНАТОРОВ
- 5.2. ДАТЧИКИ УРОВНЯ МОЩНОСТИ СВЧ
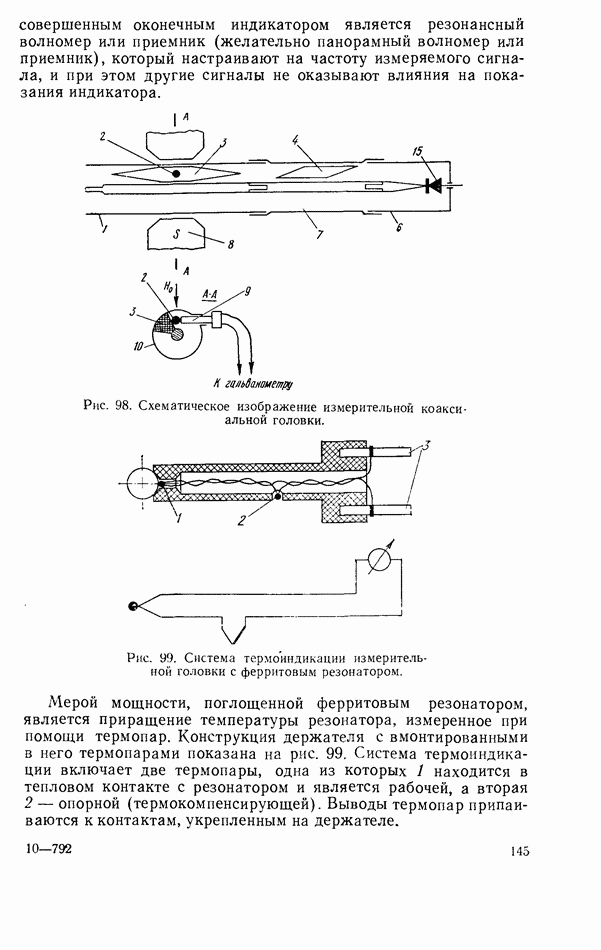
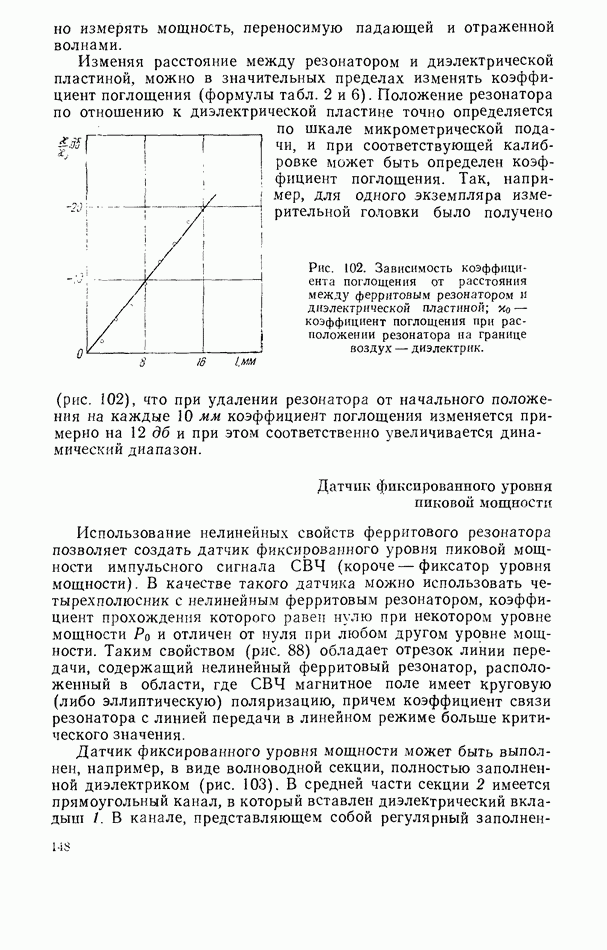
- Волноводная измерительная головка
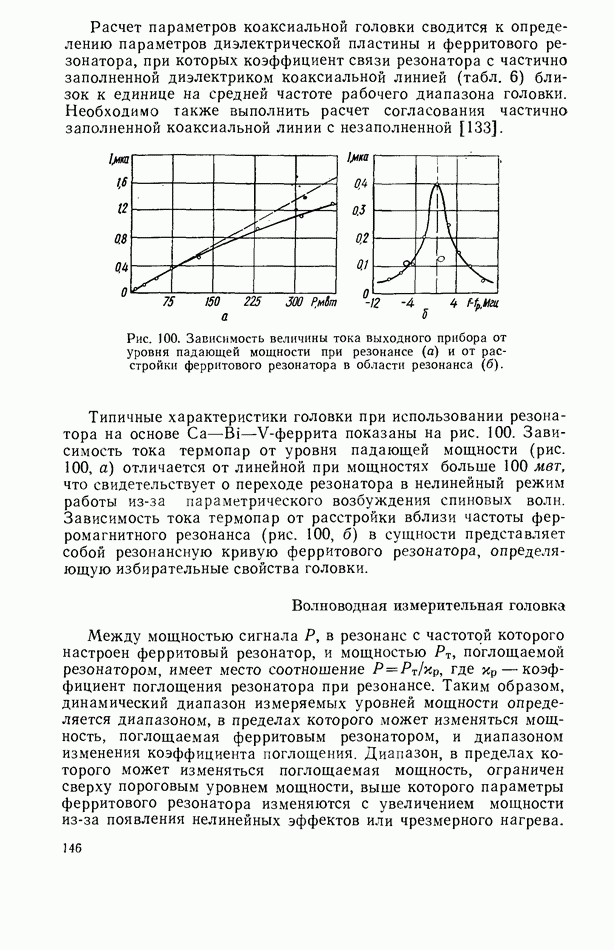
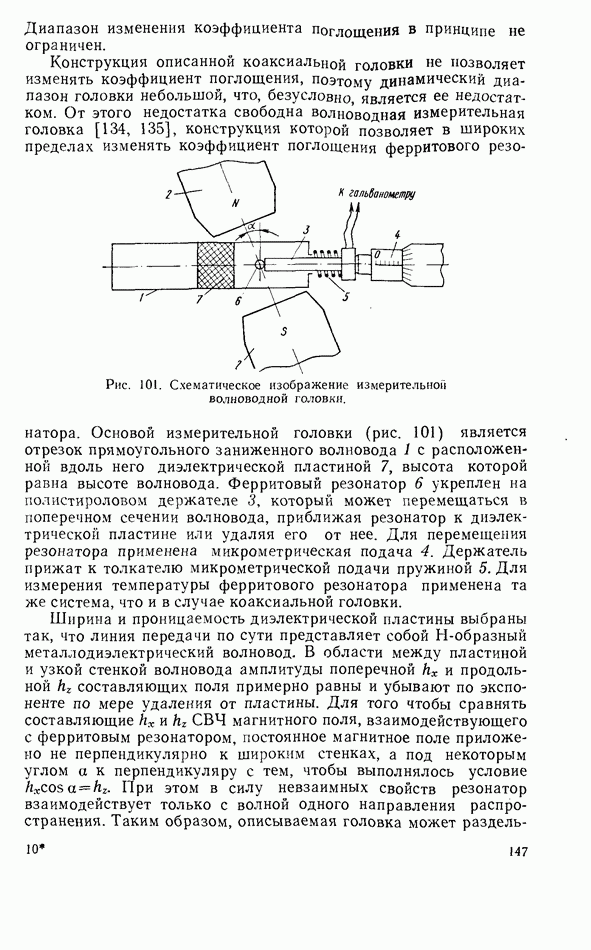
- Датчик фиксированного уровня пиковой мощности
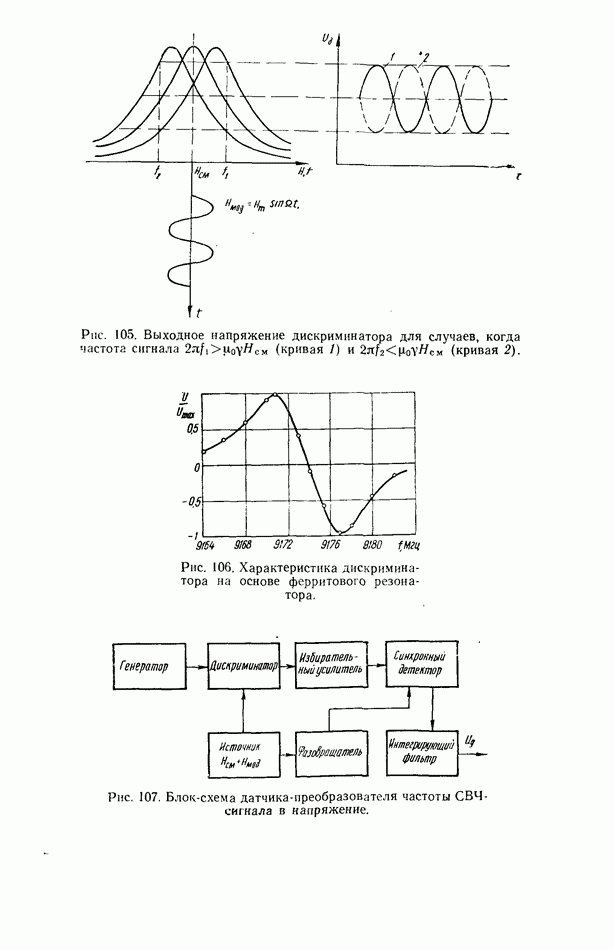
- 5.3. ЧАСТОТНЫЕ ДИСКРИМИНАТОРЫ С МАГНИТНОЙ НАСТРОЙКОЙ
- 5.4. РЕЗОНАНСНЫЕ ФАЗОВРАЩАТЕЛИ
- 5.5. УСТРОЙСТВО ДЛЯ РЕЗОНАНСНОГО ПОВОРОТА ПЛОСКОСТИ ПОЛЯРИЗАЦИИ В ВОЛНОВОДЕ
- 5.6. ФИЛЬТРЫ СВЧ НА ОСНОВЕ ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 5.7. ФЕРРИТОВЫЕ СВЧ-ФИЛЬТРЫ
- Многофункциональные фильтры
- Многорезонаторные ферритовые фильтры
- 5.8. ЧАСТОТНО-ИЗБИРАТЕЛЬНЫЕ ОГРАНИЧИТЕЛИ МАЛЫХ УРОВНЕЙ МОЩНОСТИ