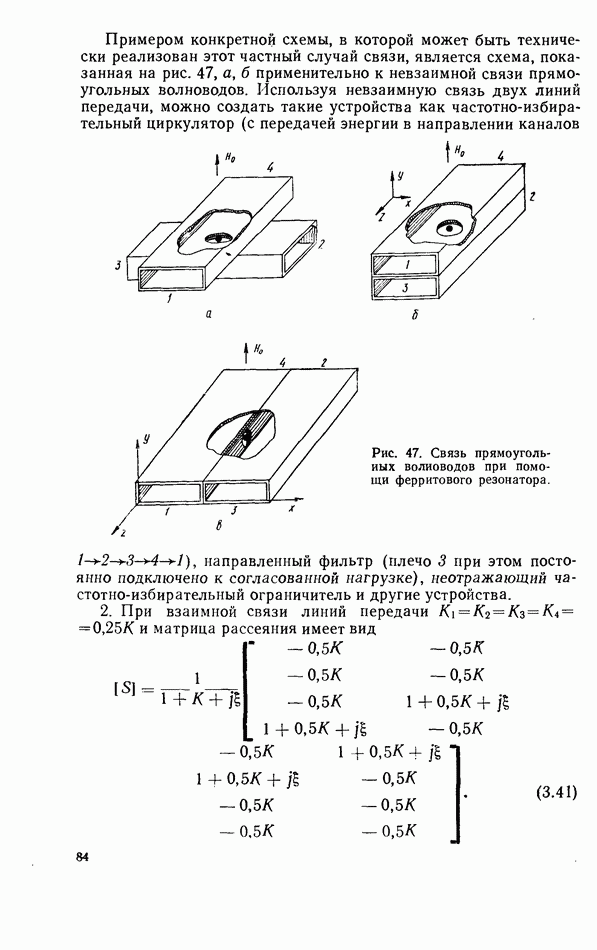
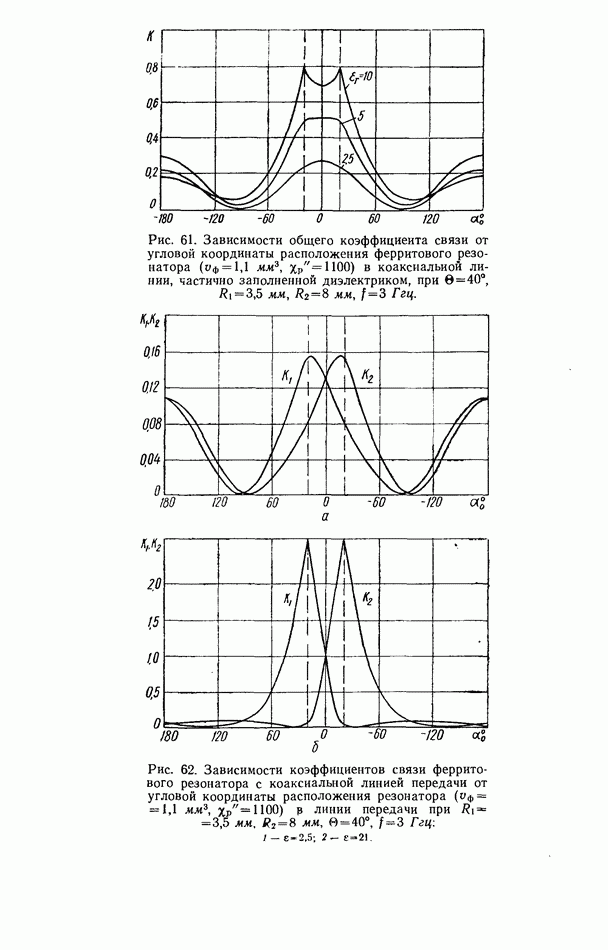
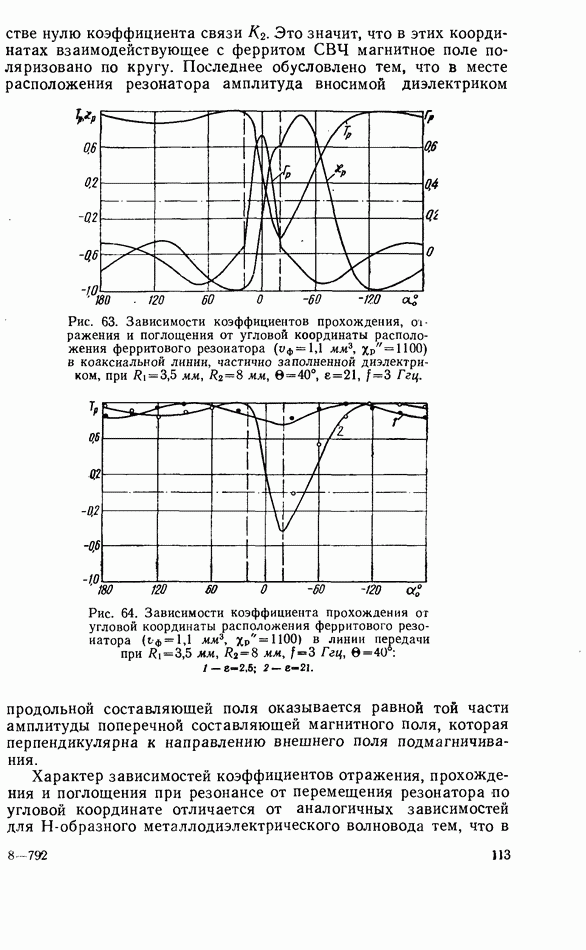
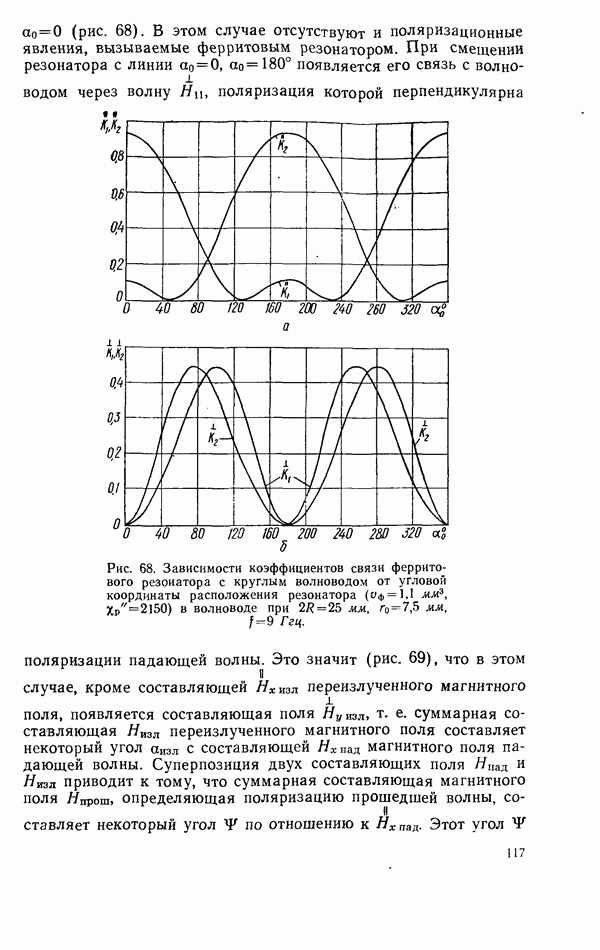
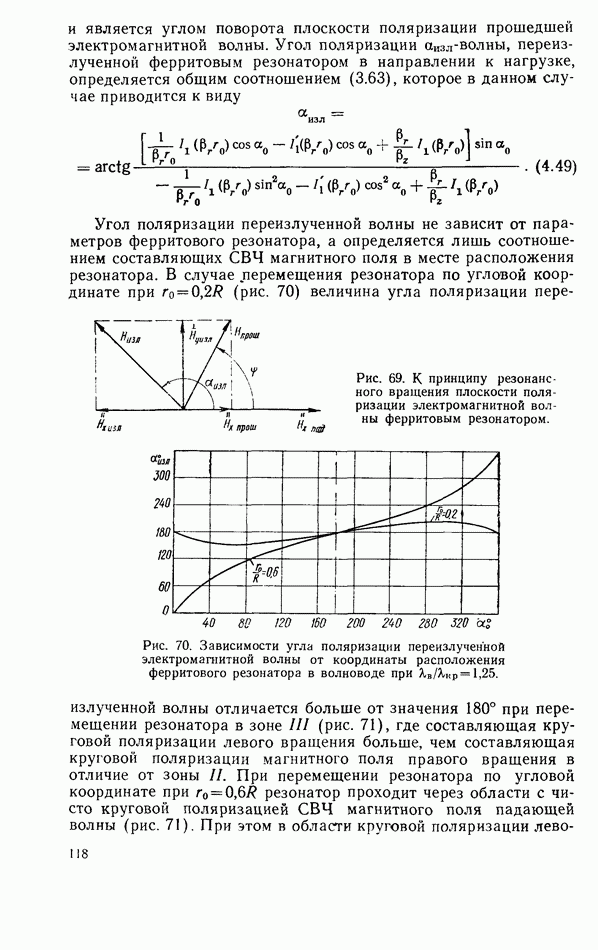
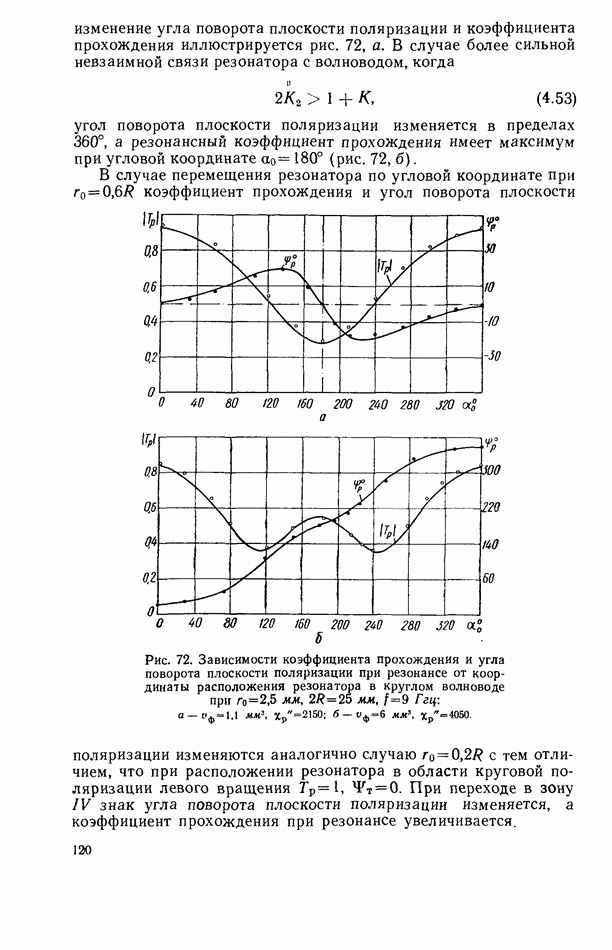
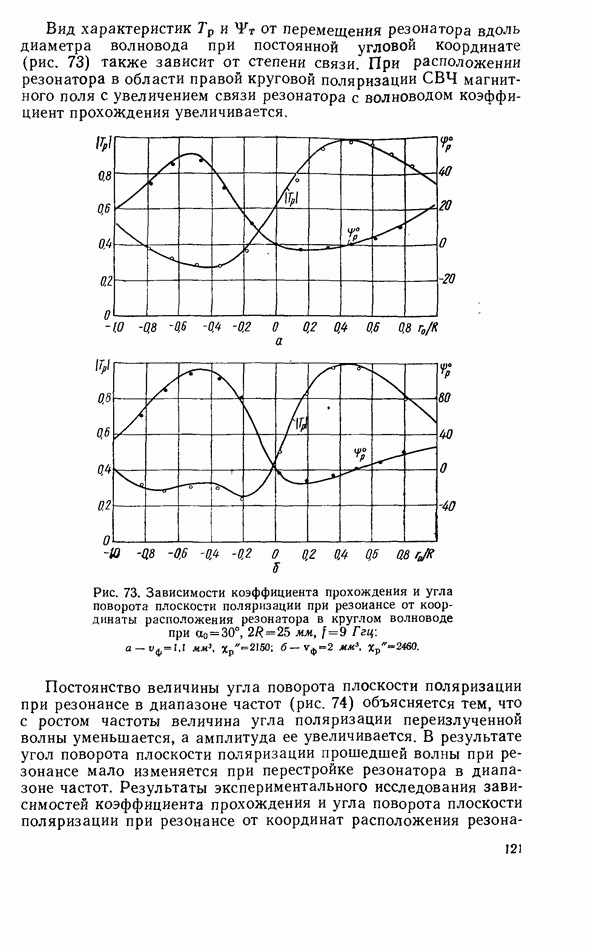
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.4. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В НЕСОГЛАСОВАННОЙ ЛИНИИ ПЕРЕДАЧИ
Рассчитаем коэффициенты отражения, прохождения и поглощения при включении твердотельного резонатора как неоднородности в линии передачи. Будем полагать, что на выходе линии передачи включена реальная нагрузка с комплексным коэффициентом отражения  [81]. Анализируя, примем основные допущения:
[81]. Анализируя, примем основные допущения:
1. Размеры резонатора вдоль оси линии передачи незначительны по сравнению с длиной электромагнитной волны. Соотношения между падающей и отраженной волнами определим с учетом только волны основного типа на значительном расстоянии от резонатора, где нераспространяющиеся волны затухают до пренебрежимо малых значений.
2. В уравнение баланса мощностей введем мощность, переносимую волной, отраженной от нагрузки, хотя взаимодействие резонатора с полем этой волны учитывать не будем. Это приближение в случае взаимной связи резонатора с линией передачи даст ошибку порядка  где
где  коэффициент прохождения. Численная оценка показывает, что при КСВН нагрузки, равном
коэффициент прохождения. Численная оценка показывает, что при КСВН нагрузки, равном
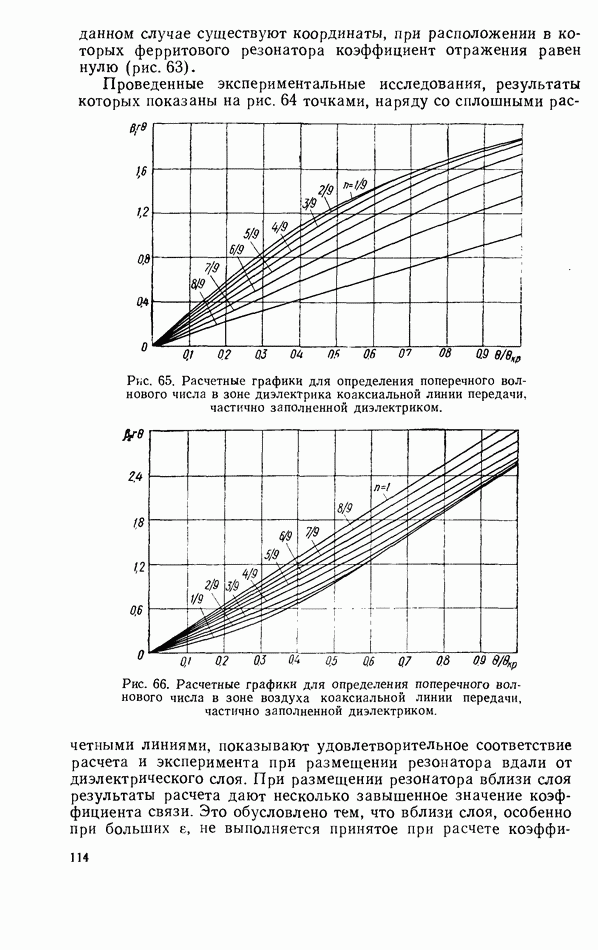
3, ошибка в определении коэффициентов отражения, прохождения и поглощения не превысит 20—25%. Поэтому использование йолученных результатов должно быть ограничено небольшими КСВН нагрузки, за исключением случая полностью невзаимной связи ферритового резонатора с линией передачи, когда СВЧ Магнитное поле, взаимодействующее с резонатором, имеет правую круговую поляризацию, и ошибка исключается в силу невзамных свойств этого резонатора. Если взаимодействующее с ферритовым резонатором СВЧ магнитное поле имеет левую
круговую поляризацию, то формальное применение соотношений, полученных в результате приближенного решения задачи, невозможно.
Пусть резонатор расположен в произвольном месте поперечного сечения линии передачи (рис. 30) на расстоянии  от несогласованной нагрузки с комплексным коэффициентом отражения по магнитному полю
от несогласованной нагрузки с комплексным коэффициентом отражения по магнитному полю  Коэффициент отражения нагрузки, пересчитанный в сечение
Коэффициент отражения нагрузки, пересчитанный в сечение  где расположен резонатор, обозначим
где расположен резонатор, обозначим

где  соответственно модуль и фазовый угол коэффициента отражения нагрузки;
соответственно модуль и фазовый угол коэффициента отражения нагрузки;  продольное волновое число.
продольное волновое число.

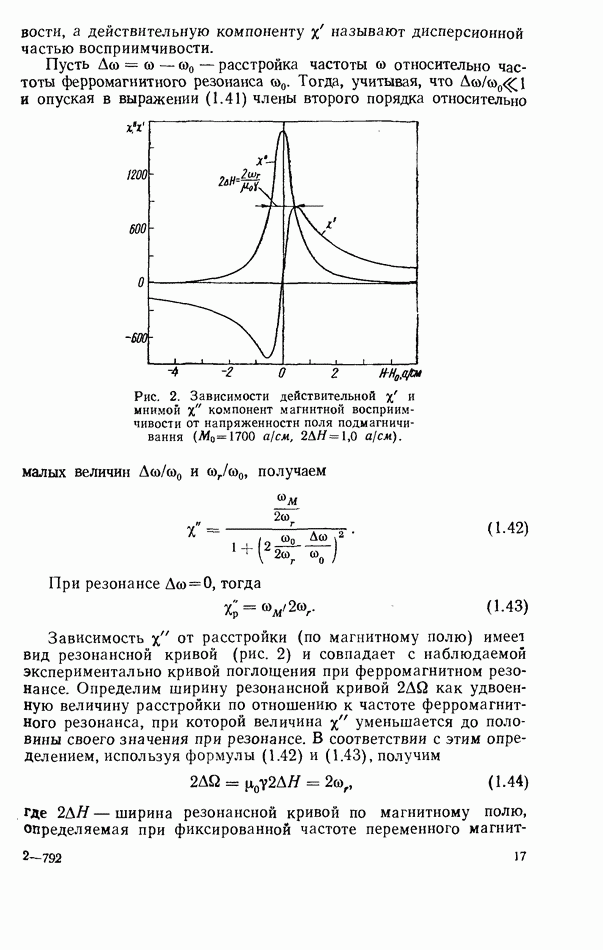
Рис. 30. Твердотельный резонатор в несогласованной лннин передачи.
Определим частные коэффициенты связи резонатора с линией передачи в виде

где  соответственно входная и выходная внешние добротности резонатора;
соответственно входная и выходная внешние добротности резонатора;  мощности, переносимые по линии передачи волнами, переизлученными резонатором соответственно в направлении к генератору (индекс
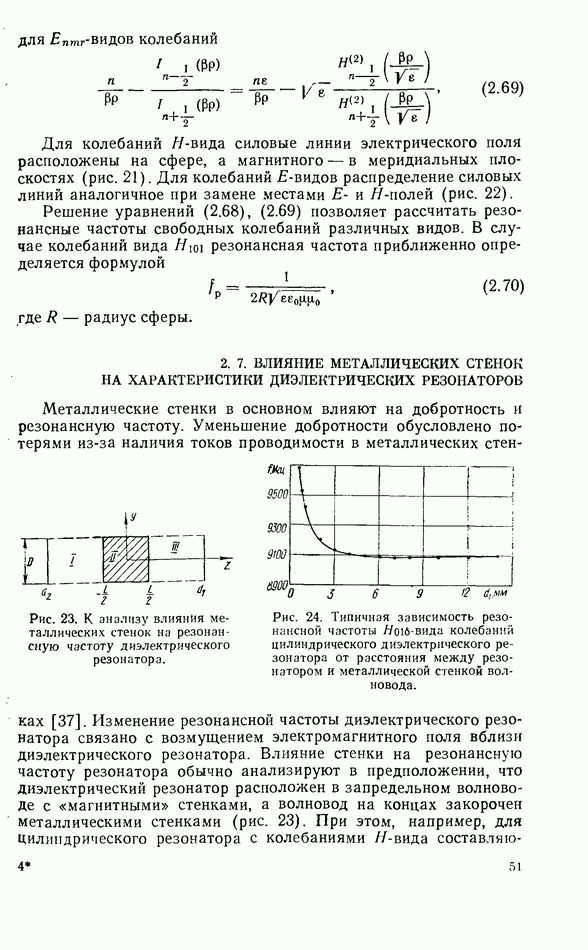
мощности, переносимые по линии передачи волнами, переизлученными резонатором соответственно в направлении к генератору (индекс  и в направлении к нагрузке (индекс
и в направлении к нагрузке (индекс  Полный коэффициент связи резонатора с линией передачи равен сумме частных коэффициентов
Полный коэффициент связи резонатора с линией передачи равен сумме частных коэффициентов 
Составим уравнение баланса мощностей [81] в несогласованной линии с резонатором, для чего просуммируем мощности, входящие в объем волновода, расположенный между сечениями 1—1 и 2—2, и приравняем их сумме, состоящей из мощностей, расходящихся от указанного объема, и мощности, поглощенной резонатором. Уравнение баланса мощностей имеет вид

где  — мощность падающей волны;
— мощность падающей волны;  мощность волны, отраженной от нагрузки;
мощность волны, отраженной от нагрузки;  мощность волны, отраженной от резонатора;
мощность волны, отраженной от резонатора;  мощность прошедшей волны;
мощность прошедшей волны;  мощность, поглощенная в резонаторе.
мощность, поглощенная в резонаторе.
Представим эти мощности через  и коэффициенты отражения
и коэффициенты отражения  прохождения
прохождения  и поглощения к,
и поглощения к,

После подстановки (3.7) в уравнение (3.6) имеем

Вычислим коэффициенты отражения, прохождения и поглощения на частоте, равной резонансной, и определим их по магнитному полю в виде

где  амплитуда магнитной составляющей падающей волны;
амплитуда магнитной составляющей падающей волны;  амплитуда волны, отраженной от нагрузки;
амплитуда волны, отраженной от нагрузки;  амплитуды волн, переизлученных резонатором;
амплитуды волн, переизлученных резонатором;  нормированные по амплитуде падающей волны коэффициенты переизлучения. (В последующих формулах
нормированные по амплитуде падающей волны коэффициенты переизлучения. (В последующих формулах  модуль коэффициента отражения).
модуль коэффициента отражения).
Из соотношения (3.8) имеем

откуда с учетом того, что

нетрудно получить сначала

а затем и соотношения для коэффициентов прохождения, отражения и поглощения на частоте, равной резонансной: коэффициент прохождения

коэффициент отражения

коэффициент поглощения

Рассмотрим два частных случая:
1. Случай  имеет место при взаимной связи резонатора с линией передачи.
имеет место при взаимной связи резонатора с линией передачи.

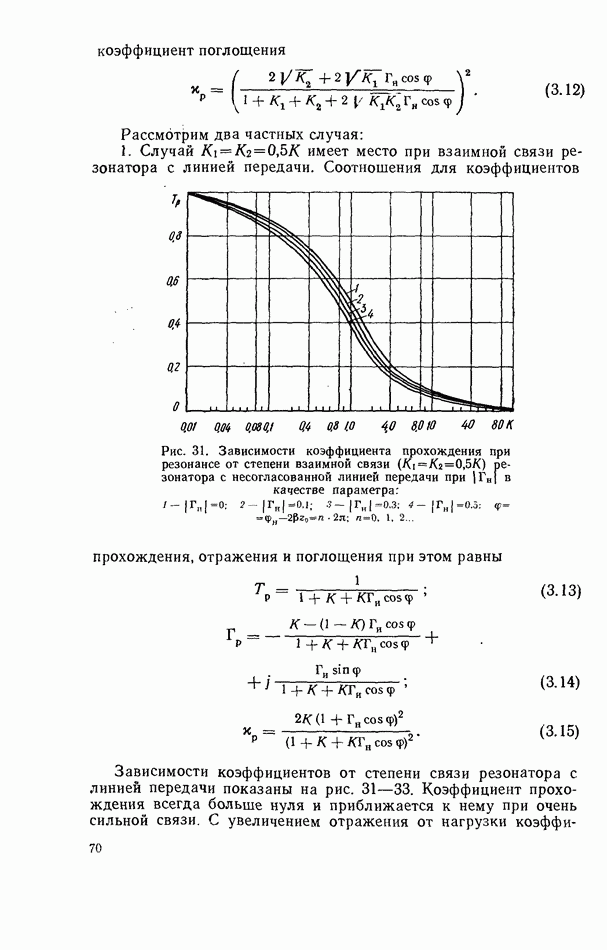
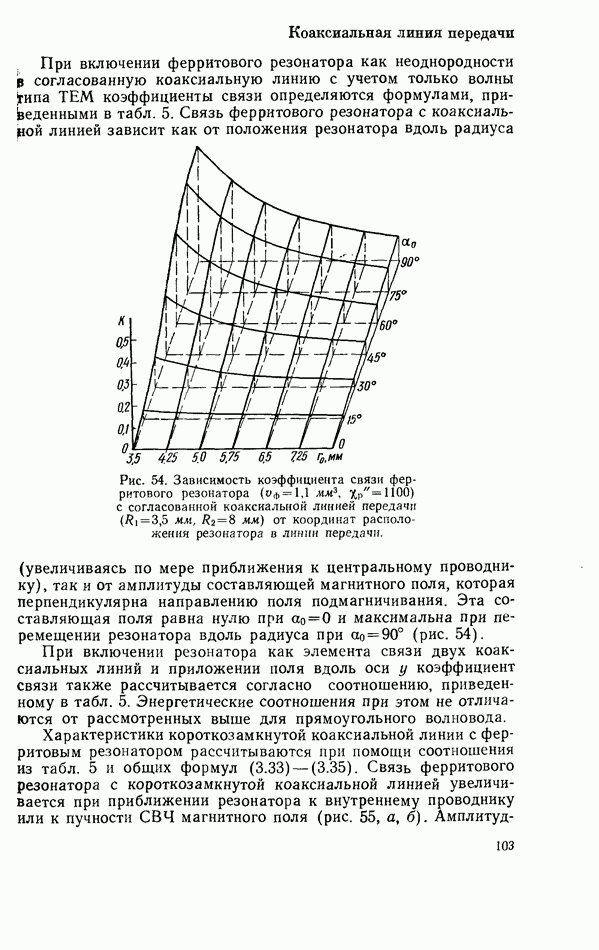
Рис. 31. Зависимости коэффициента прохождения при резонансе от степени взаимной связи  резонатора с несогласованной линией передачи при
резонатора с несогласованной линией передачи при  в качестве параметра:
в качестве параметра: 
Соотношения для коэффициентов прохождения, отражения и поглощения при этом равны

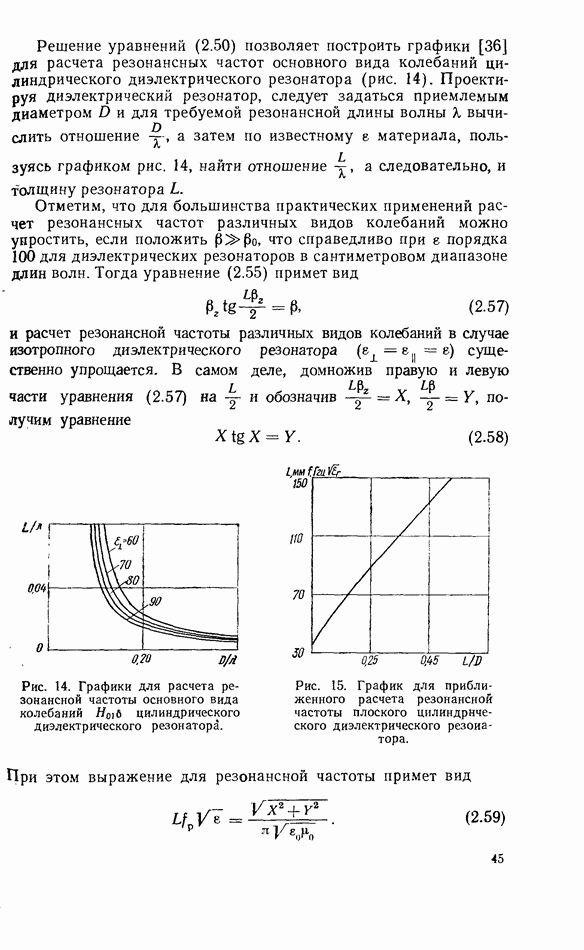
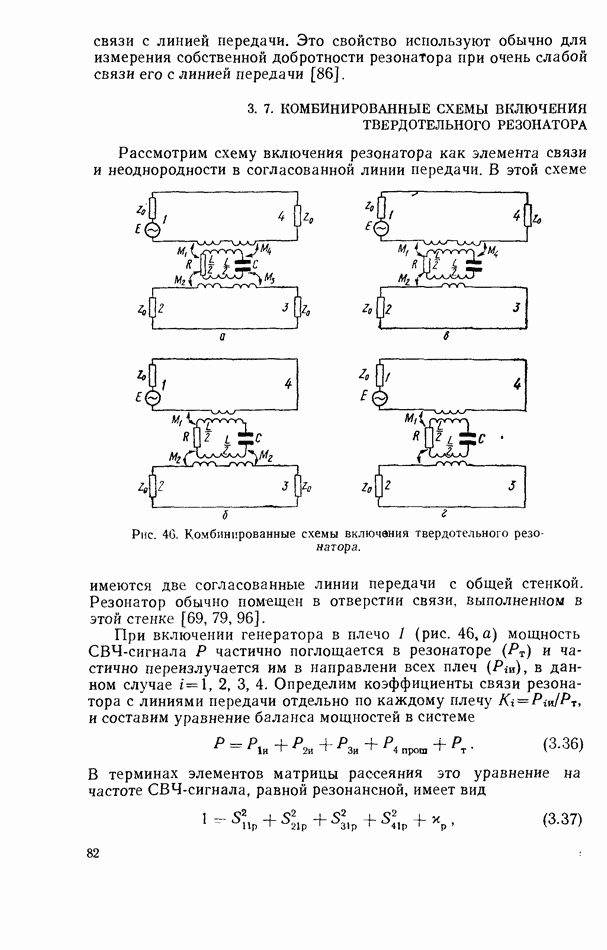
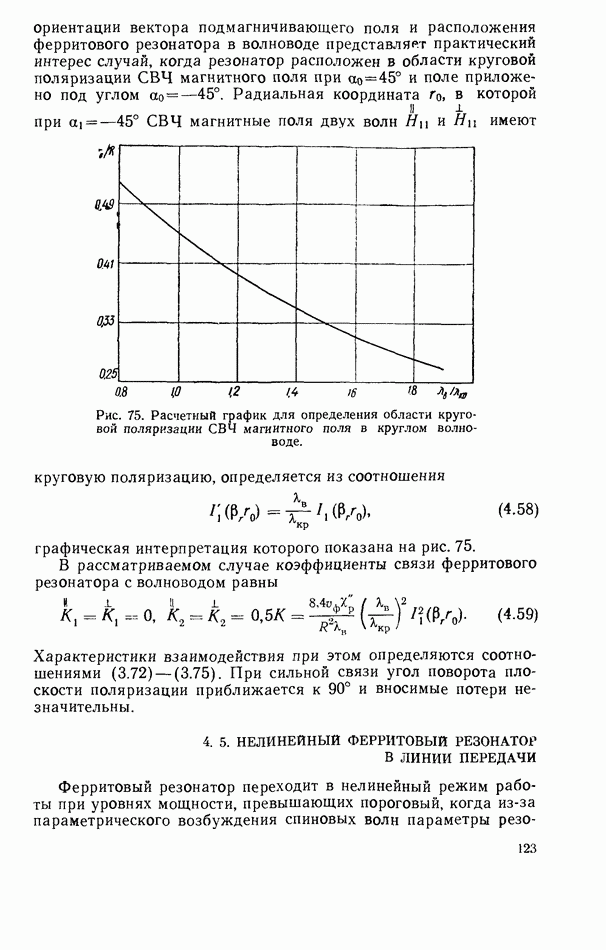
Зависимости коэффициентов от степени связи резонатора с линией передачи показаны на рис. 31—33. Коэффициент прохождения всегда больше нуля и приближается к нему при очень сильной связи. С увеличением отражения от нагрузки

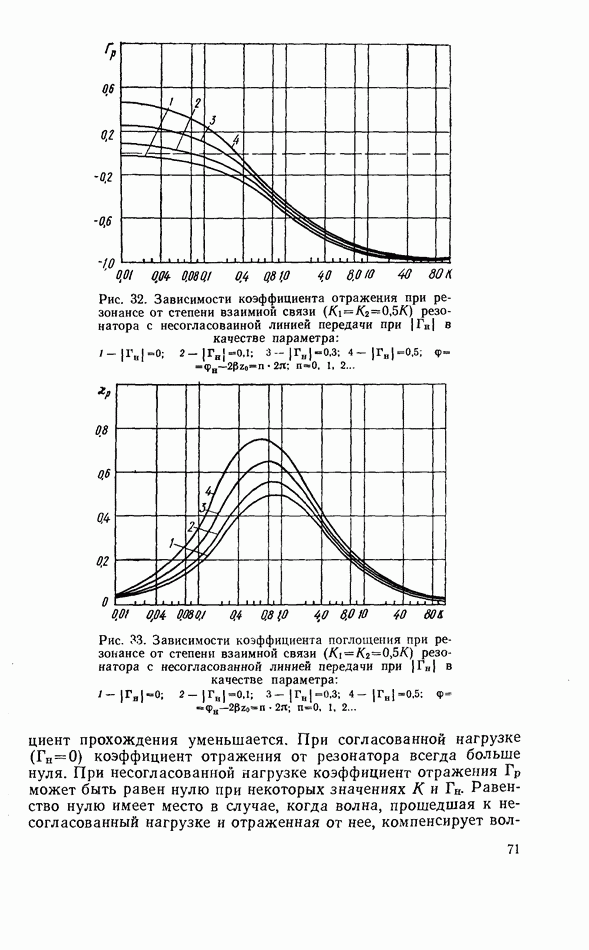
Рис. 32. Зависимости коэффициента отражения при резонансе от степени взаимной связи  резонатора с несогласованной линией передачи при
резонатора с несогласованной линией передачи при  в качестве параметра:
в качестве параметра: 

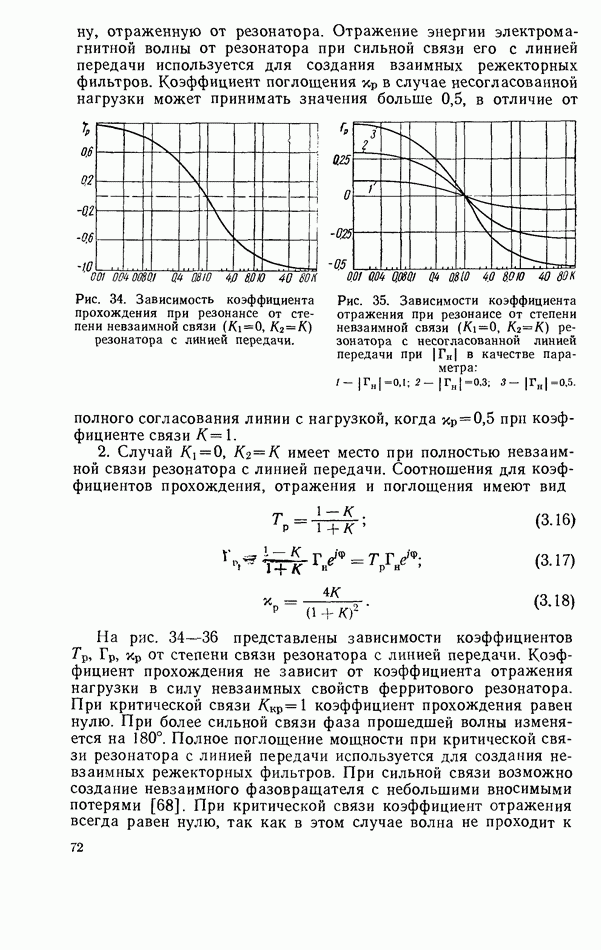
Рис. 33. Зависимости коэффициента поглощения при резонансе от степени взаимной связи  резонатора с несогласованной линией передачи при
резонатора с несогласованной линией передачи при  в качестве параметра:
в качестве параметра: 
коэффициент прохождения уменьшается. При согласованной нагрузке  коэффициент отражения от резонатора всегда больше нуля. При несогласованной нагрузке коэффициент отражения
коэффициент отражения от резонатора всегда больше нуля. При несогласованной нагрузке коэффициент отражения  может быть равен нулю при некоторых значениях
может быть равен нулю при некоторых значениях  Равенство нулю имеет место в случае, когда волна, прошедшая к несогласованный нагрузке и отраженная от нее, компенсирует
Равенство нулю имеет место в случае, когда волна, прошедшая к несогласованный нагрузке и отраженная от нее, компенсирует
волну, отраженную от резонатора. Отражение энергии электромагнитной волны от резонатора при сильной связи его с линией передачи используется для создания взаимных режекторных фильтров. Коэффициент поглощения  в случае несогласованной нагрузки может принимать значения больше 0,5, в отличие от полного согласования линии с нагрузкой, когда
в случае несогласованной нагрузки может принимать значения больше 0,5, в отличие от полного согласования линии с нагрузкой, когда  при коэффициенте связи
при коэффициенте связи 

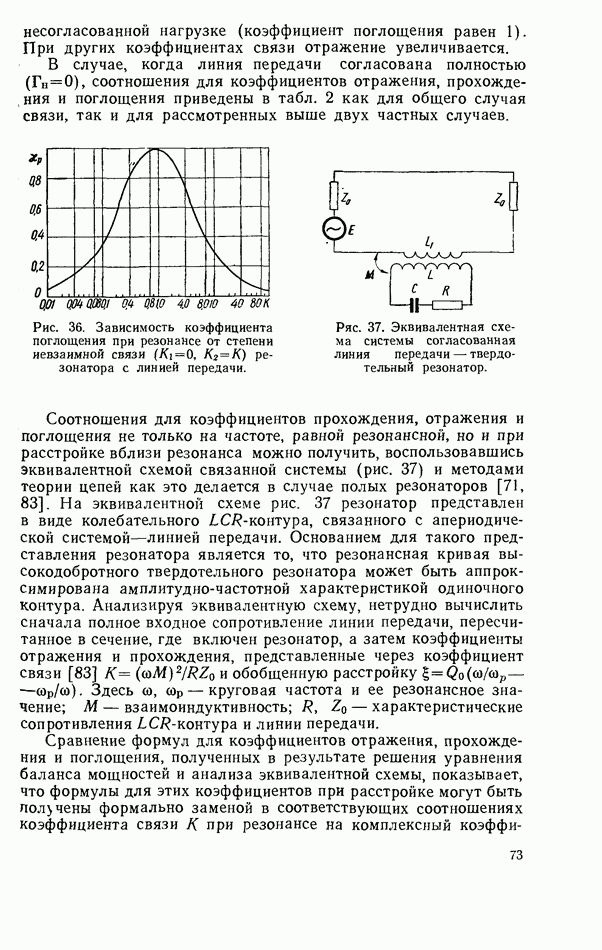
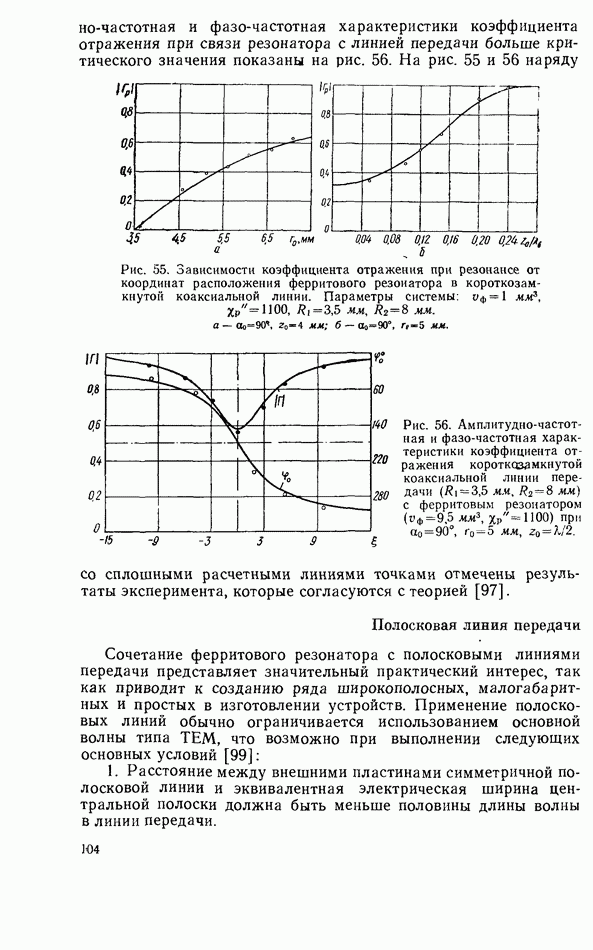
Рис. 34. Зависимость коэффициента прохождения при резонансе от степени невзаимной связи  резонатора с линией передачи.
резонатора с линией передачи.

Рис. 35. Зависимости коэффициента отражения при резонансе от степени невзаимной связи  резонатора с несогласованной линией передачи при
резонатора с несогласованной линией передачи при  в качестве параметра:
в качестве параметра: 
2. Случай  имеет место при полностью невзаимной связи резонатора с линией передачи. Соотношения для коэффициентов прохождения, отражения и поглощения имеют вид
имеет место при полностью невзаимной связи резонатора с линией передачи. Соотношения для коэффициентов прохождения, отражения и поглощения имеют вид

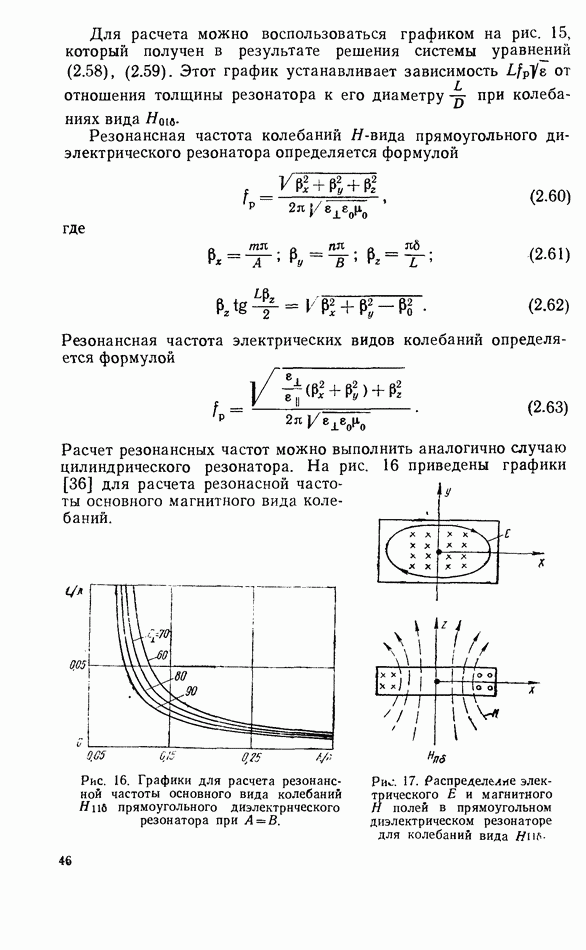
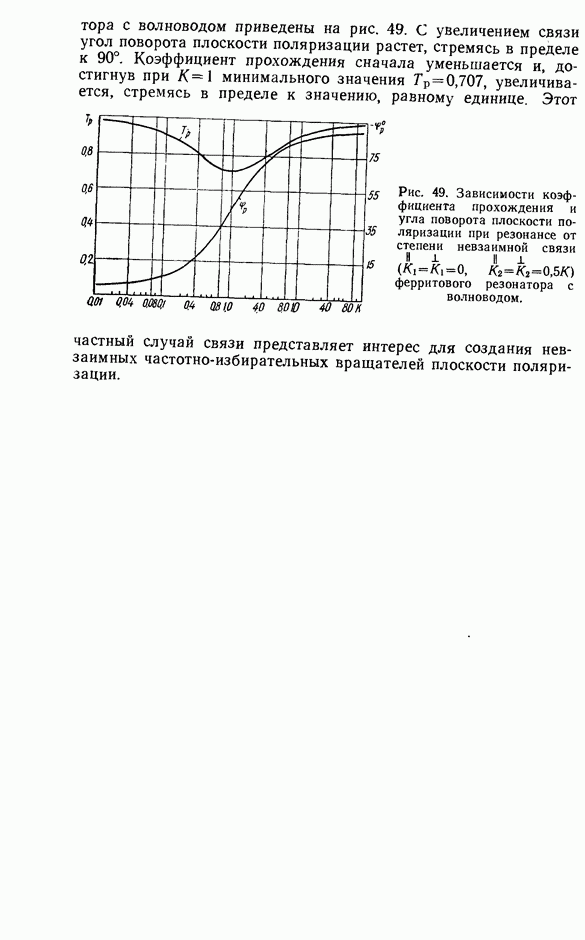
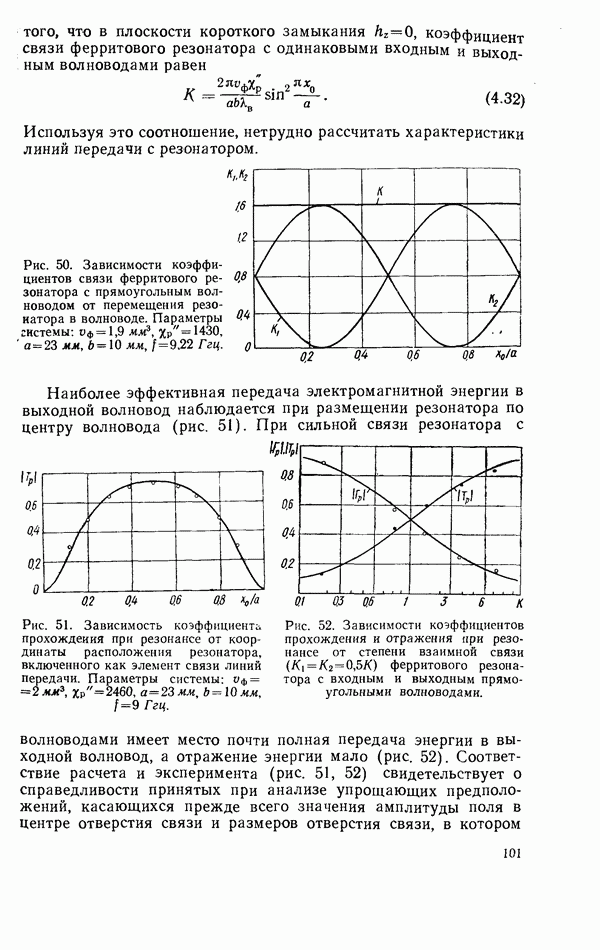
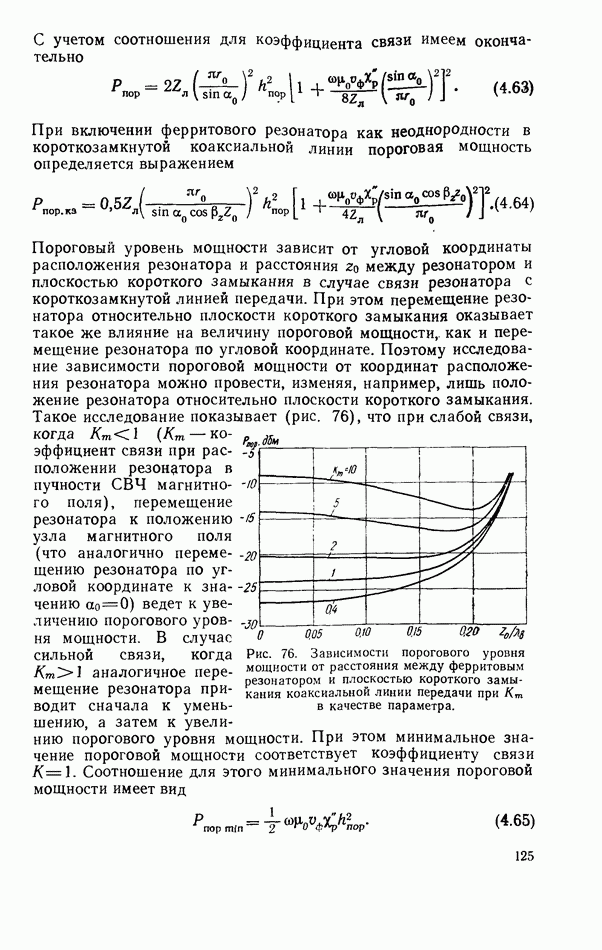
На рис. 34—36 представлены зависимости коэффициентов  от степени связи резонатора с линией передачи. Коэффициент прохождения не зависит от коэффициента отражения нагрузки в силу невзаимных свойств ферритового резонатора. При критической связи
от степени связи резонатора с линией передачи. Коэффициент прохождения не зависит от коэффициента отражения нагрузки в силу невзаимных свойств ферритового резонатора. При критической связи  коэффициент прохождения равен нулю. При более сильной связи фаза прошедшей волны изменяется на 180°. Полное поглощение мощности при критической связи резонатора с линией передачи используется для создания невзаимных режекторных фильтров. При сильной связи возможно создание невзаимного фазовращателя с небольшими вносимыми потерями [68]. При критической связи коэффициент отражения всегда равен нулю, так как в этом случае волна не проходит к
коэффициент прохождения равен нулю. При более сильной связи фаза прошедшей волны изменяется на 180°. Полное поглощение мощности при критической связи резонатора с линией передачи используется для создания невзаимных режекторных фильтров. При сильной связи возможно создание невзаимного фазовращателя с небольшими вносимыми потерями [68]. При критической связи коэффициент отражения всегда равен нулю, так как в этом случае волна не проходит к
несогласованной нагрузке (коэффициент поглощения равен 1). При других коэффициентах связи отражение увеличивается.
В случае, когда линия передачи согласована полностью  соотношения для коэффициентов отражения, прохождения и поглощения приведены в табл. 2 как для общего случая связи, так и для рассмотренных выше двух частных случаев.
соотношения для коэффициентов отражения, прохождения и поглощения приведены в табл. 2 как для общего случая связи, так и для рассмотренных выше двух частных случаев.

Рис. 36. Зависимость коэффициента поглощения при резонансе от степени иевзаимной связи  резонатора с линией передачи.
резонатора с линией передачи.

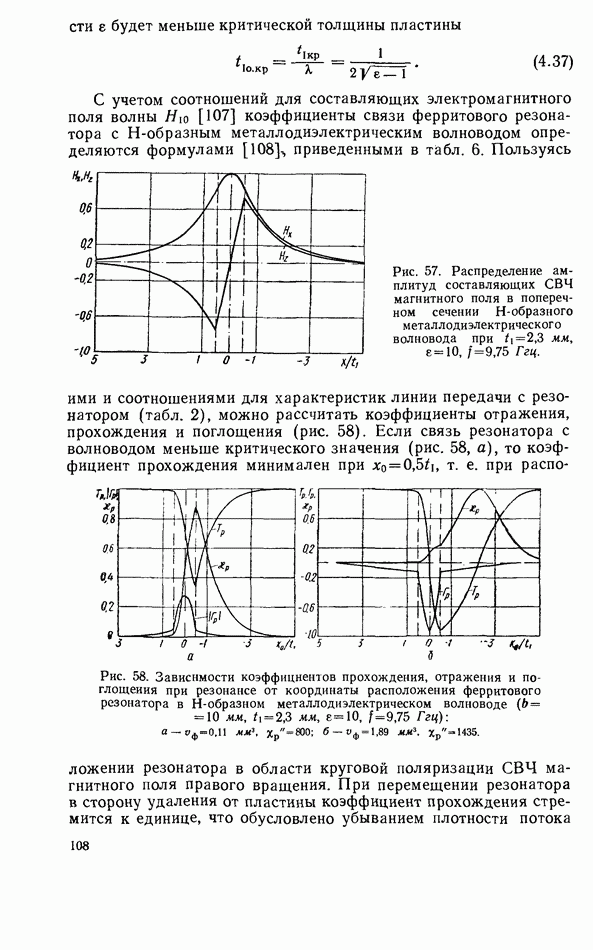
Рис. 37. Эквивалентная схема системы согласованная линия передачи — твердотельный резонатор.
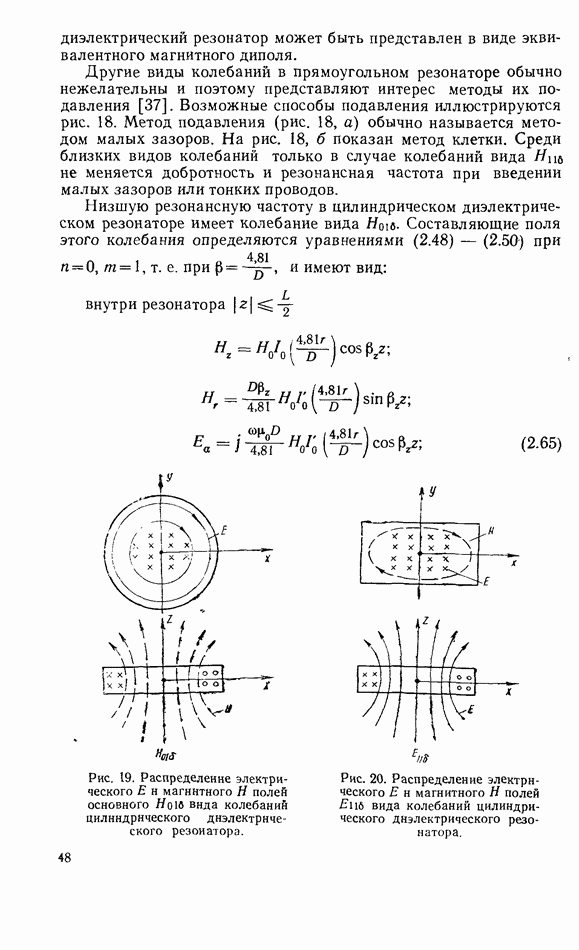
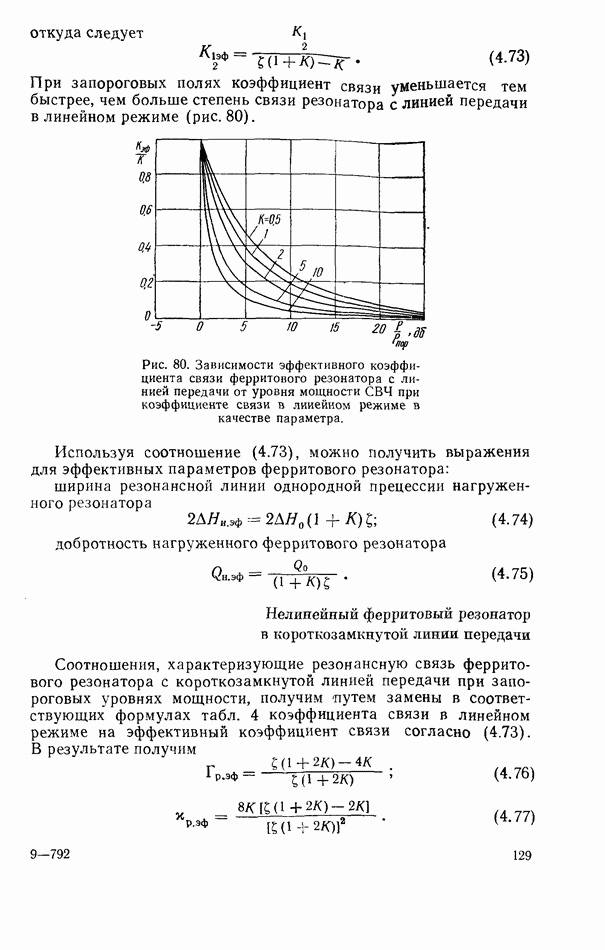
Соотношения для коэффициентов прохождения, отражения и поглощения не только на частоте, равной резонансной, но и при расстройке вблизи резонанса можно получить, воспользовавшись Эквивалентной схемой связанной системы (рис. 37) и методами теории цепей как это делается в случае полых резонаторов [71, 83]. На эквивалентной схеме рис. 37 резонатор представлен в виде колебательного  -контура, связанного с апериодической системой—линией передачи. Основанием для такого представления резонатора является то, что резонансная кривая высокодобротного твердотельного резонатора может быть аппроксимирована амплитудно-частотной характеристикой одиночного контура. Анализируя эквивалентную схему, нетрудно вычислить сначала полное входное сопротивление линии передачи, пересчитанное в сечение, где включен резонатор, а затем коэффициенты отражения и прохождения, представленные через коэффициент связи [83]
-контура, связанного с апериодической системой—линией передачи. Основанием для такого представления резонатора является то, что резонансная кривая высокодобротного твердотельного резонатора может быть аппроксимирована амплитудно-частотной характеристикой одиночного контура. Анализируя эквивалентную схему, нетрудно вычислить сначала полное входное сопротивление линии передачи, пересчитанное в сечение, где включен резонатор, а затем коэффициенты отражения и прохождения, представленные через коэффициент связи [83]  и обобщенную расстройку
и обобщенную расстройку  . Здесь
. Здесь  — круговая частота и ее резонансное значение;
— круговая частота и ее резонансное значение;  взаимоиндуктивность;
взаимоиндуктивность;  характеристические сопротивления LCR-контура и линии передачи.
характеристические сопротивления LCR-контура и линии передачи.
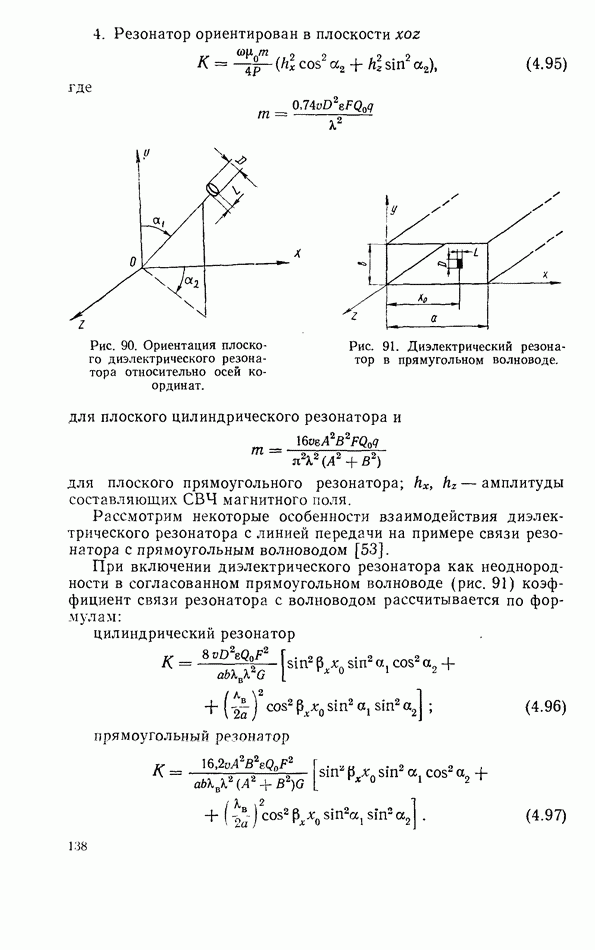
Сравнение формул для коэффициентов отражения, прохождения и поглощения, полученных в результате решения уравнения баланса мощностей и анализа эквивалентной схемы, показывает, что формулы для этих коэффициентов при расстройке могут быть полечены формально заменой в соответствующих соотношениях коэффициента связи К при резонансе на комплексный
(см. скан)
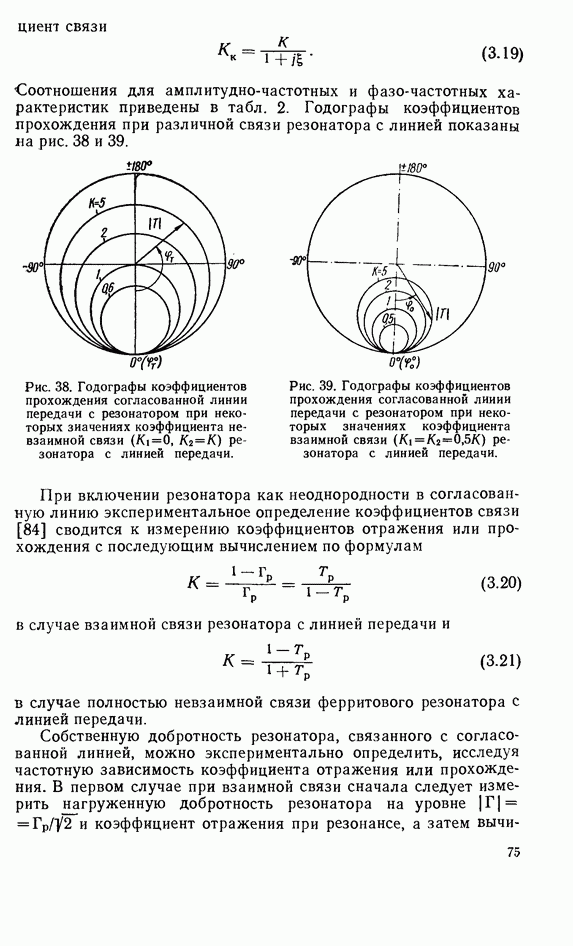
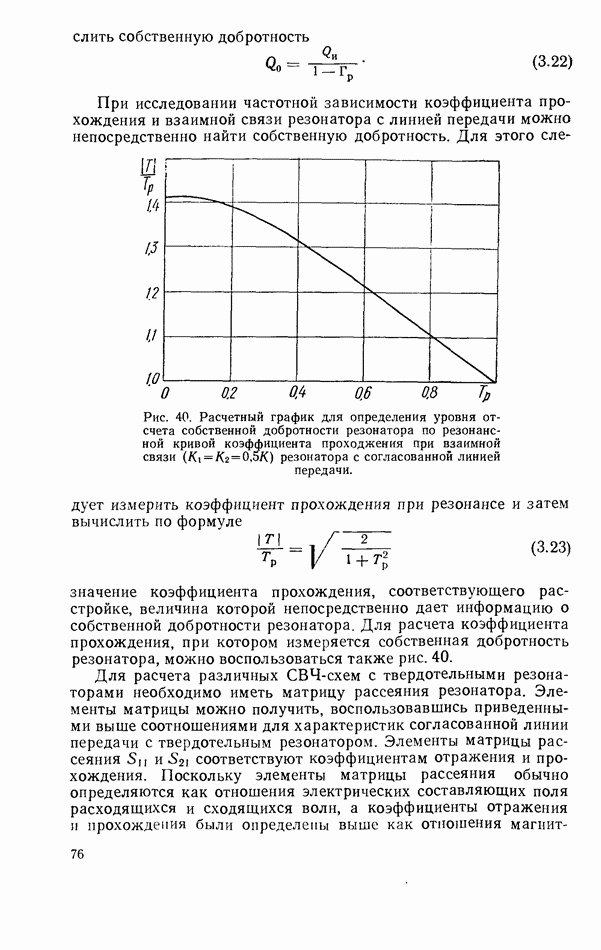
коэффициент связи

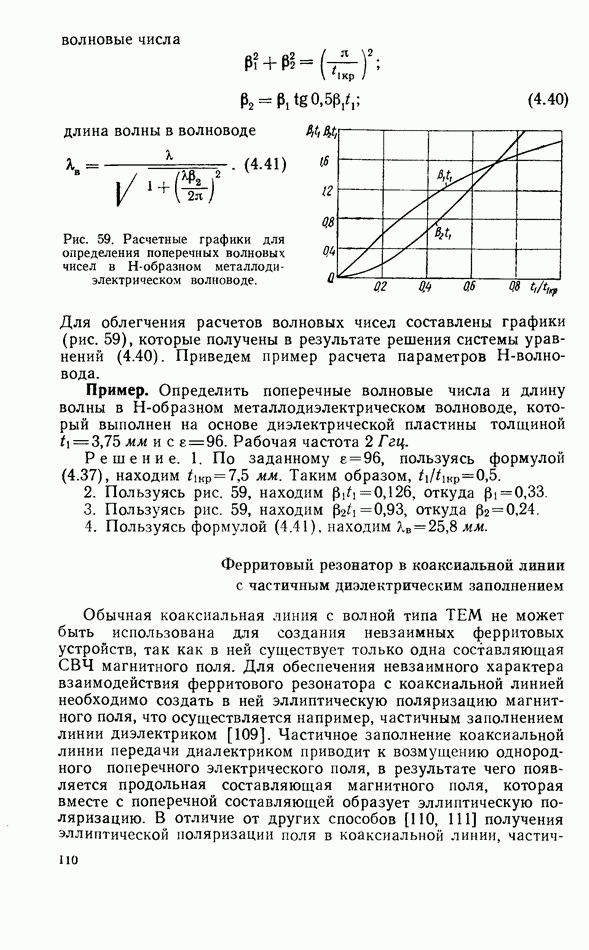
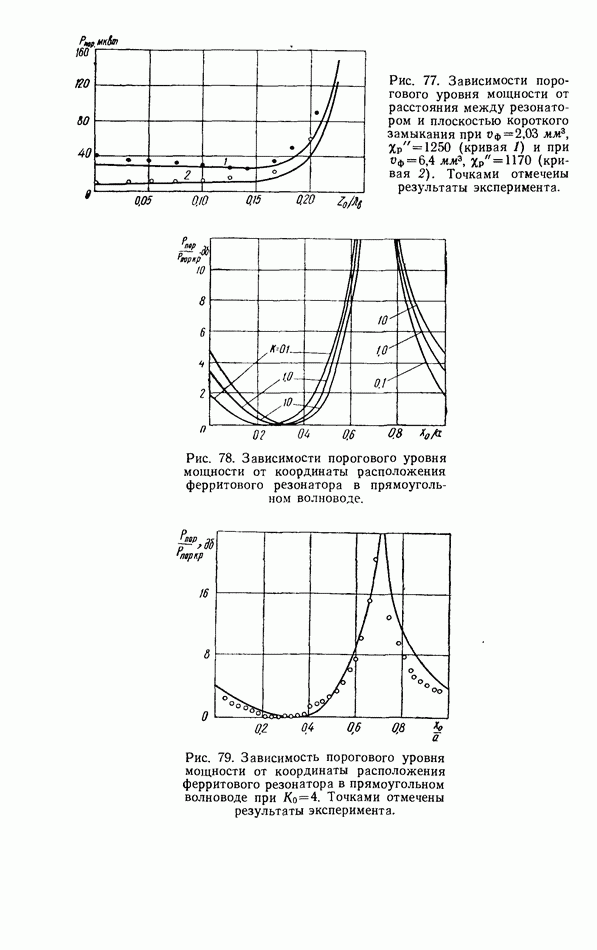
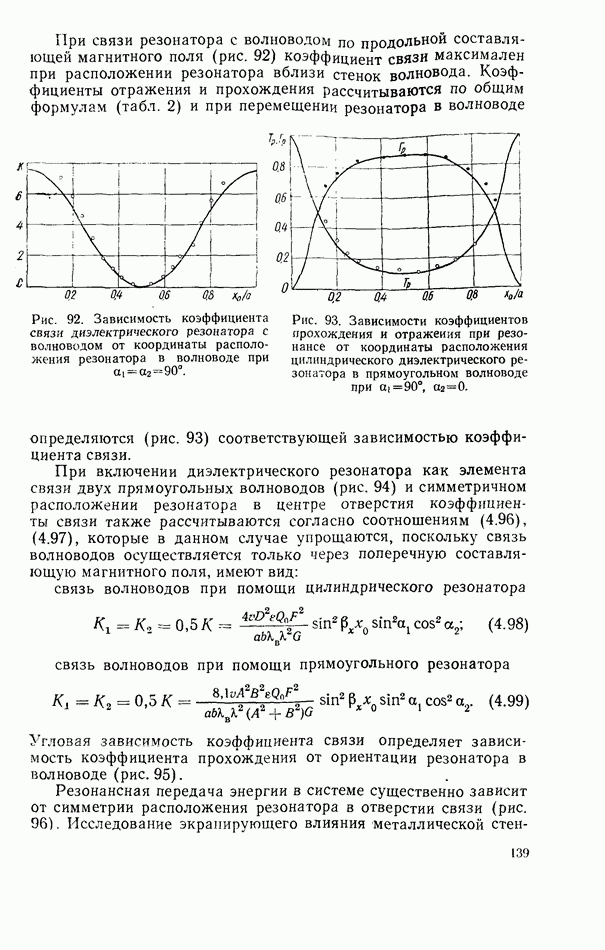
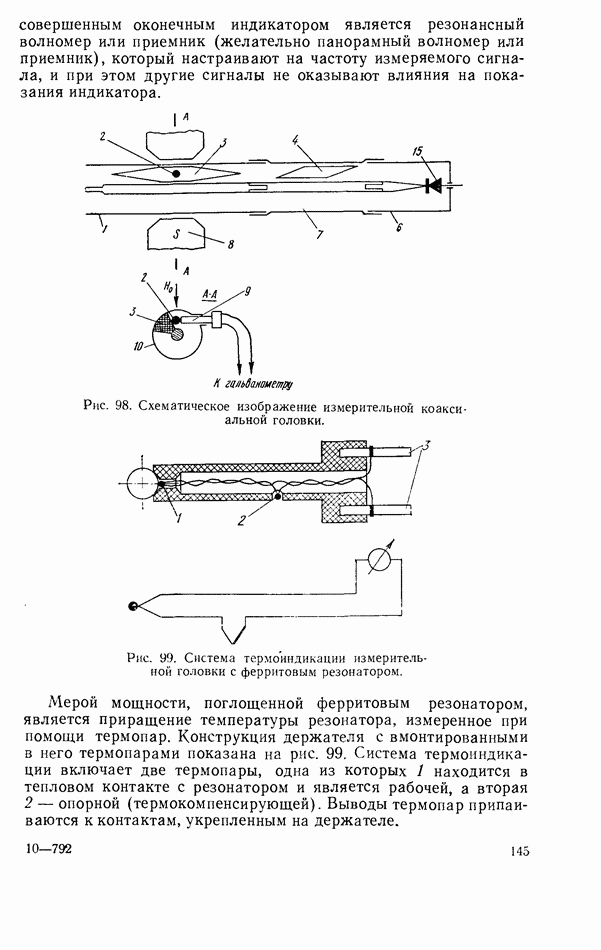
Соотношения для амплитудно-частотных и фазо-частотных характеристик приведены в табл. 2. Годографы коэффициентов прохождения при различной связи резонатора с линией показаны на рис. 38 и 39.

Рис. 38. Годографы коэффициентов прохождения согласованной линии передачи с резонатором при некоторых значениях коэффициента невзаимной связи  резонатора с линией передачи.
резонатора с линией передачи.

Рис. 39. Годографы коэффициентов прохождения согласованной линии передачи с резонатором при некоторых значениях коэффициента взаимной связи  резонатора с линией передачи.
резонатора с линией передачи.
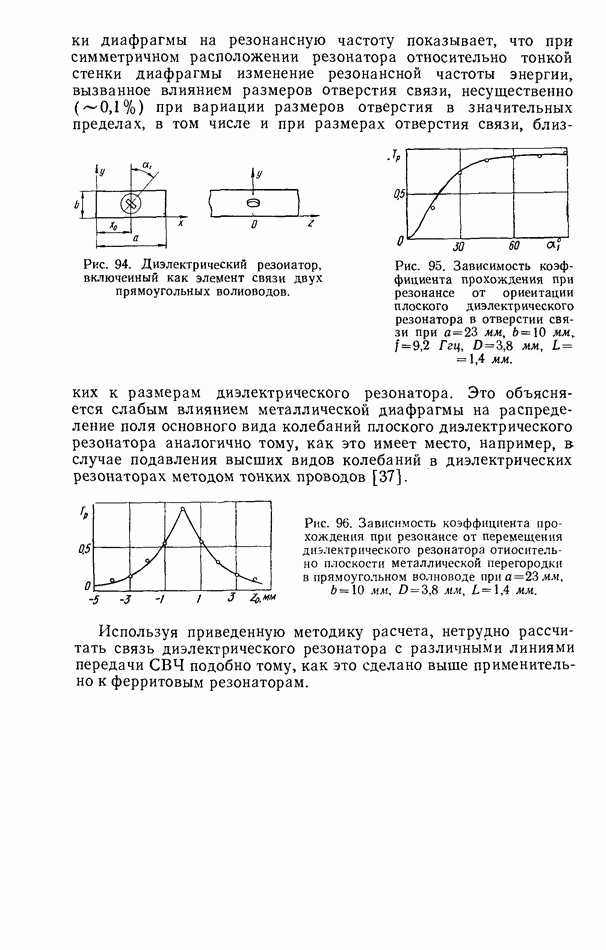
При включении резонатора как неоднородности в согласованную линию экспериментальное определение коэффициентов связи [84] сводится к измерению коэффициентов отражения или прохождения с последующим вычислением по формулам

в случае взаимной связи резонатора с линией передачи и

в случае полностью невзаимной связи ферритового резонатора с линией передачи.
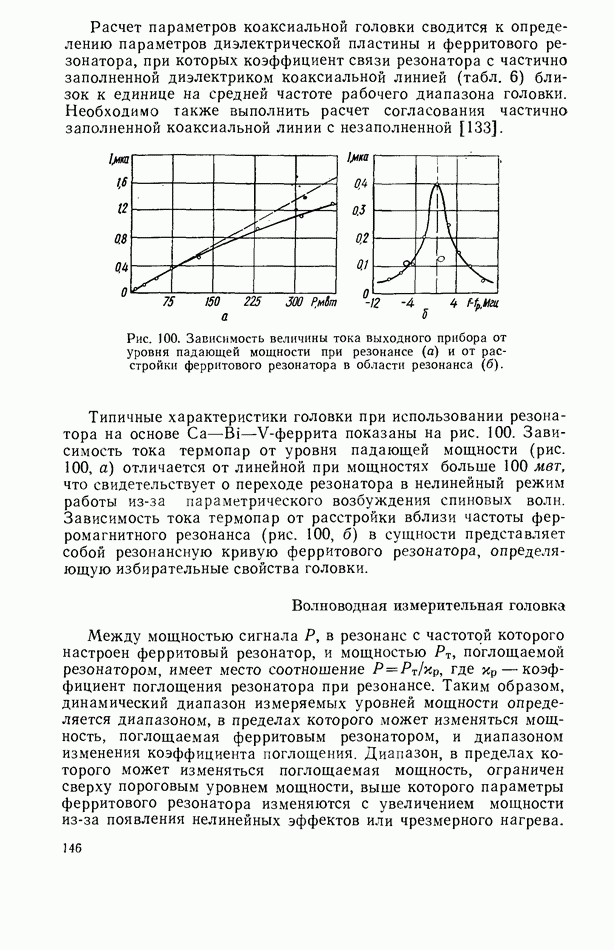
Собственную добротность резонатора, связанного с согласованной линией, можно экспериментально определить, исследуя частотную зависимость коэффициента отражения или прохождения. В первом случае при взаимной связи сначала следует измерить нагруженную добротность резонатора на уровне  и коэффициент отражения при резонансе, а затем
и коэффициент отражения при резонансе, а затем
вычислить собственную добротность

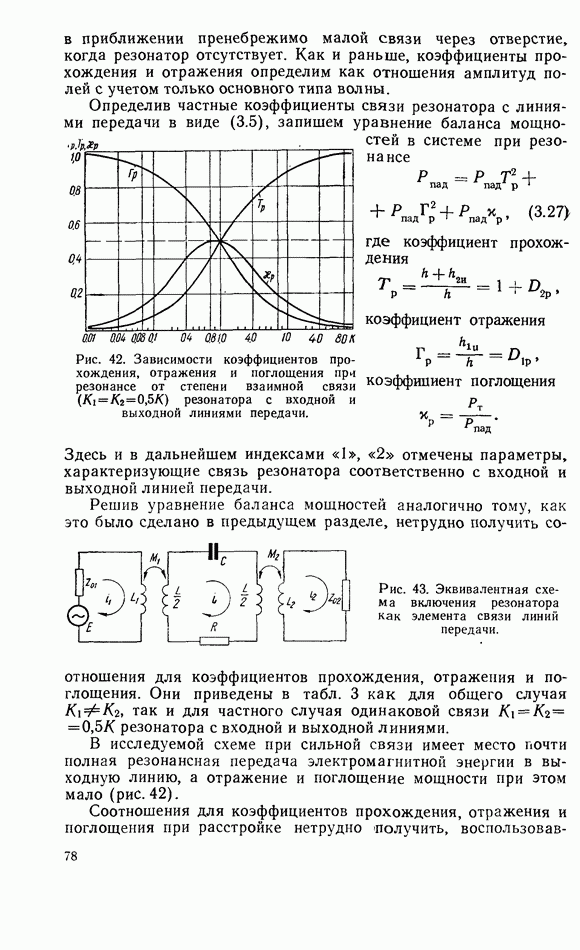
При исследовании частотной зависимости коэффициента прохождения и взаимной связи резонатора с линией передачи можно непосредственно найти собственную добротность.

Рис. 40. Расчетный график для определения уровня отсчета собственной добротности резонатора по резонансной кривой коэффициента проходжения при взаимной связи  резонатора с согласованной линией передачи.
резонатора с согласованной линией передачи.
Для этого следует измерить коэффициент прохождения при резонансе и затем вычислить по формуле

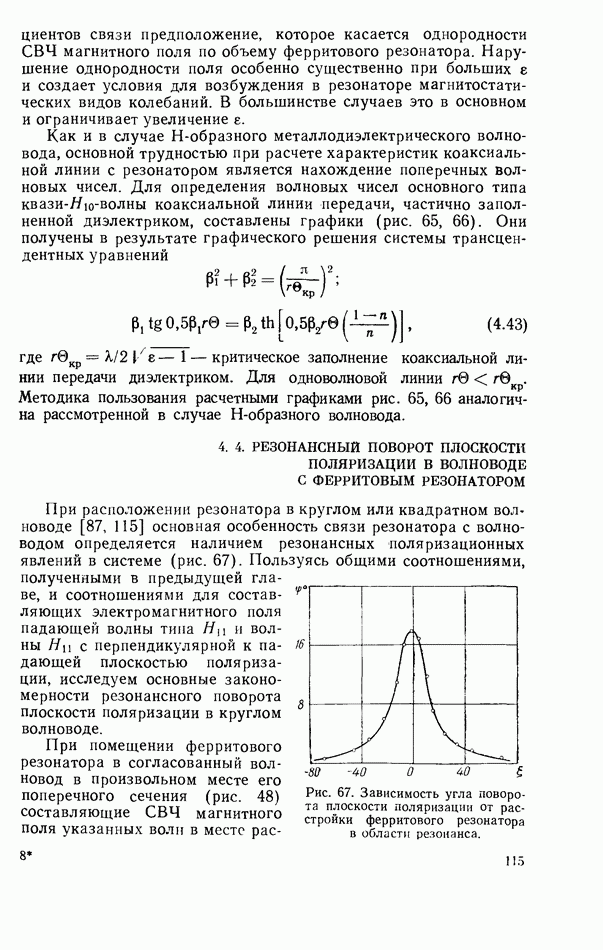
значение коэффициента прохождения, соответствующего расстройке, величина которой непосредственно дает информацию о собственной добротности резонатора. Для расчета коэффициента прохождения, при котором измеряется собственная добротность резонатора, можно воспользоваться также рис. 40.
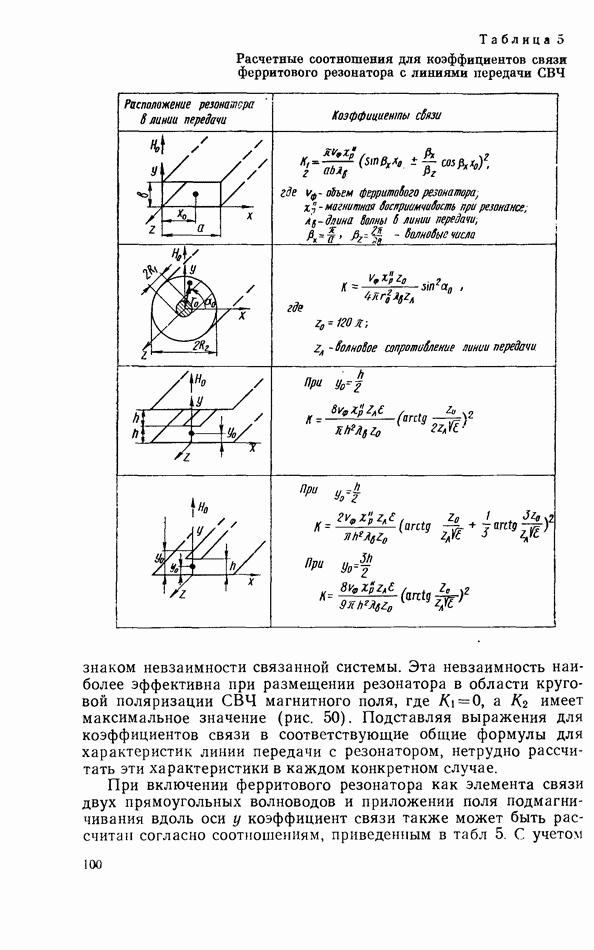
Для расчета различных СВЧ-схем с твердотельными резонаторами необходимо иметь матрицу рассеяния резонатора. Элементы матрицы можно получить, воспользовавшись приведенными выше соотношениями для характеристик согласованной линии передачи с твердотельным резонатором. Элементы матрицы рассеяния  соответствуют коэффициентам отражения и прохождения. Поскольку элементы матрицы рассеяния обычно определяются как отношения электрических составляющих поля расходящихся и сходящихся волн, а коэффициенты отражения и прохождения были определены выше как отношения
соответствуют коэффициентам отражения и прохождения. Поскольку элементы матрицы рассеяния обычно определяются как отношения электрических составляющих поля расходящихся и сходящихся волн, а коэффициенты отражения и прохождения были определены выше как отношения
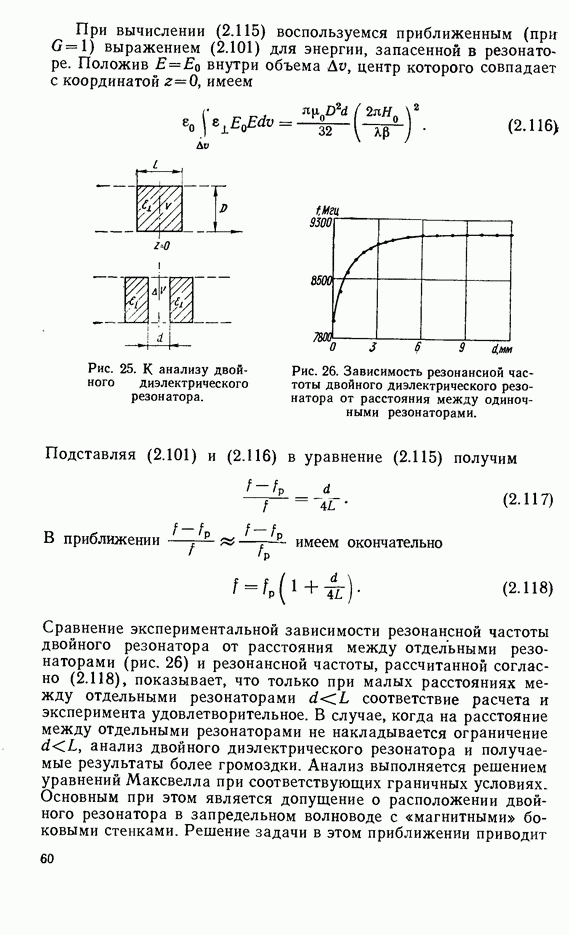
магнитных составляющих поля, то при переходе от коэффициента отражения  к элементу матрицы рассеяния
к элементу матрицы рассеяния  необходимо изменить знак. Для получения коэффициентов рассеяния
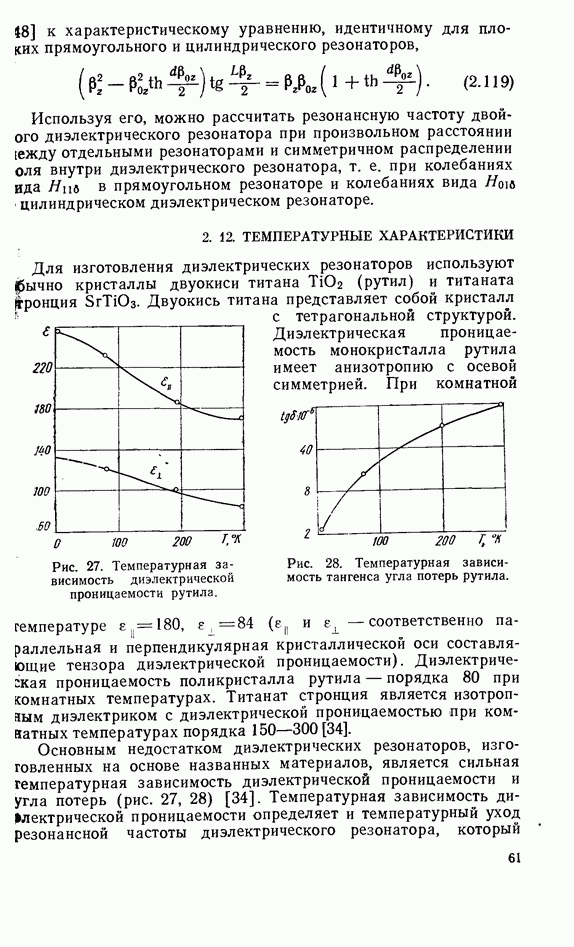
необходимо изменить знак. Для получения коэффициентов рассеяния  можно также воспользоваться соотношениями для
можно также воспользоваться соотношениями для  и поменять местами индексы у коэффициентов связи, так как волна, переизлучаемая резонатором в направлении к генератору, распространяется в том же направлении, что и волна, приходящая с выхода линии передачи, а волна, переизлучаемая в направлении к нагрузке, распространяется навстречу волне, приходящей с выхода линии передачи. С учетом этих значений матрицу рассеяния твердотельного резонатора можно записать в виде
и поменять местами индексы у коэффициентов связи, так как волна, переизлучаемая резонатором в направлении к генератору, распространяется в том же направлении, что и волна, приходящая с выхода линии передачи, а волна, переизлучаемая в направлении к нагрузке, распространяется навстречу волне, приходящей с выхода линии передачи. С учетом этих значений матрицу рассеяния твердотельного резонатора можно записать в виде

В частном случае взаимной связи резонатора с линией передачи матрица рассеяния равна

В частном случае невзаимной связи ферритового резонатора с линией передачи матрица рассеяния равна

| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава первая. СВОЙСТВА ФЕРРИТОВЫХ РЕЗОНАТОРОВ
- Ферромагнитный резонанс в неограниченной среде без потерь
- 1.2. РЕЗОНАНСНАЯ ЧАСТОТА
- Зависимость резонансной частоты от формы резонатора
- Влияние кристаллографической анизотропии на резонансную частоту
- 1.3. МАГНИТОСТАТИЧЕСКИЕ ВИДЫ КОЛЕБАНИЙ
- 1.4. УЧЕТ ПОТЕРЬ
- 1.5. ДИПОЛЬНЫЙ МОМЕНТ
- 1.6. НЕЛИНЕЙНЫЕ ЯВЛЕНИЯ
- Спиновые волны
- Пороговая амплитуда высокочастотного магнитного поля
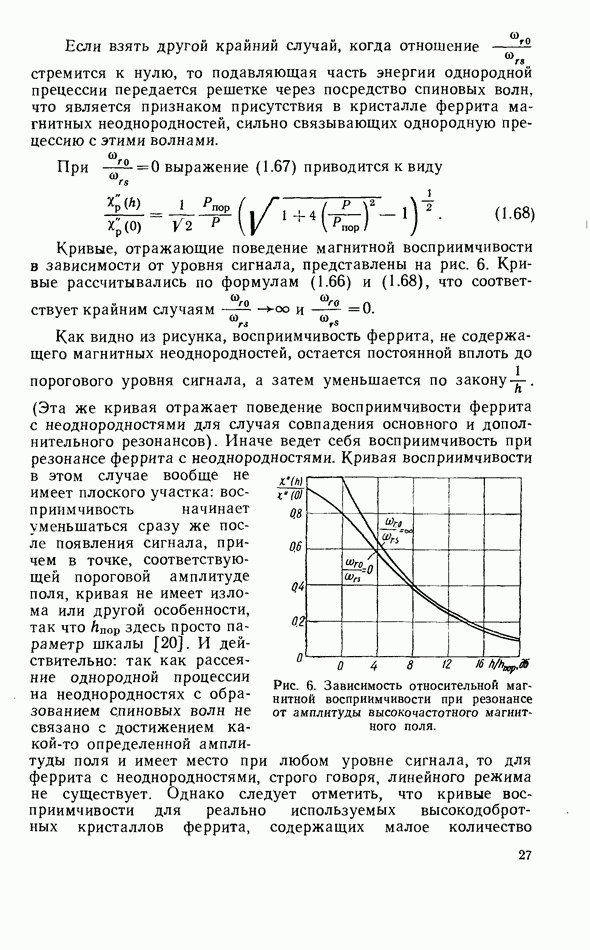
- Восприимчивость при амплитудах поля, превышающих пороговое значение
- 1.7. ПРИМЕНЯЕМЫЕ ДЛЯ ИЗГОТОВЛЕНИЯ МАТЕРИАЛЫ
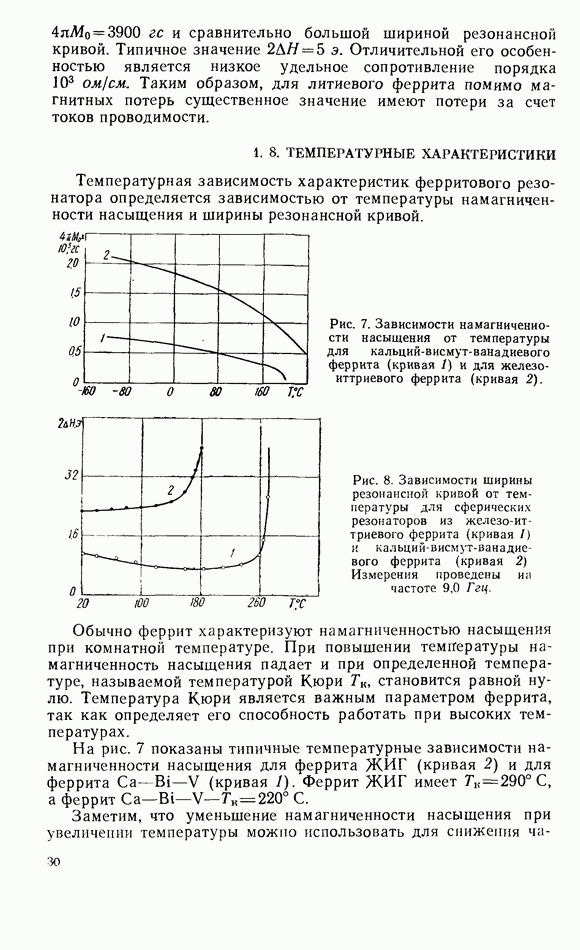
- 1.8. ТЕМПЕРАТУРНЫЕ ХАРАКТЕРИСТИКИ
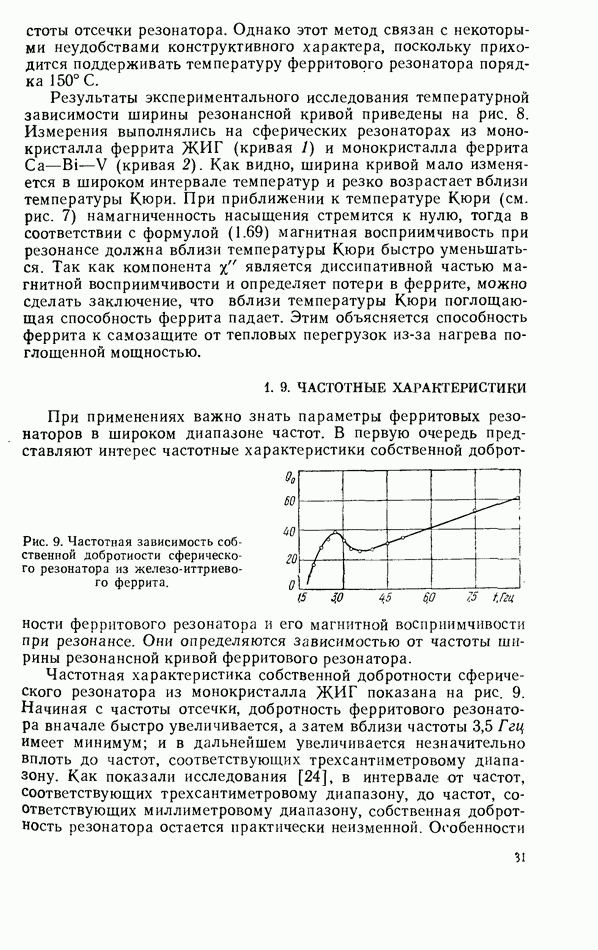
- 1.9. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- Глава вторая. СВОЙСТВА ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 2.2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В АНИЗОТРОПНОМ ДИЭЛЕКТРИЧЕСКОМ СТЕРЖНЕ С «МАГНИТНЫМИ» БОКОВЫМИ СТЕНКАМИ
- 2.3. ПРИБЛИЖЕННЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2.5. ОСНОВНЫЕ ВИДЫ КОЛЕБАНИЙ
- 2.6. СФЕРИЧЕСКИЕ ДИЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
- 2.7. ВЛИЯНИЕ МЕТАЛЛИЧЕСКИХ СТЕНОК НА ХАРАКТЕРИСТИКИ ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 2.8. ДИПОЛЬНЫЙ МОМЕНТ
- 2.9. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ
- 2.10. СООТНОШЕНИЕ МЕЖДУ АМПЛИТУДАМИ СВЧ МАГНИТНОГО ПОЛЯ
- 2.11. ДВОЙНЫЕ ДИЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
- 2.12. ТЕМПЕРАТУРНЫЕ ХАРАКТЕРИСТИКИ
- Глава третья. ХАРАКТЕРИСТИКИ ЛИНИЙ ПЕРЕДАЧИ СВЧ С ФЕРРИТОВЫМИ И ДИЭЛЕКТРИЧЕСКИМИ РЕЗОНАТОРАМИ
- 3.2. МЕТОДЫ РАСЧЕТА СВЧ-СХЕМ С ТВЕРДОТЕЛЬНЫМИ РЕЗОНАТОРАМИ
- 3.3. СВЯЗЬ ТВЕРДОТЕЛЬНОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ СВЧ
- 3.4. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В НЕСОГЛАСОВАННОЙ ЛИНИИ ПЕРЕДАЧИ
- 3.5. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР, ВКЛЮЧЕННЫЙ КАК ЭЛЕМЕНТ СВЯЗИ ЛИНИЙ ПЕРЕДАЧИ
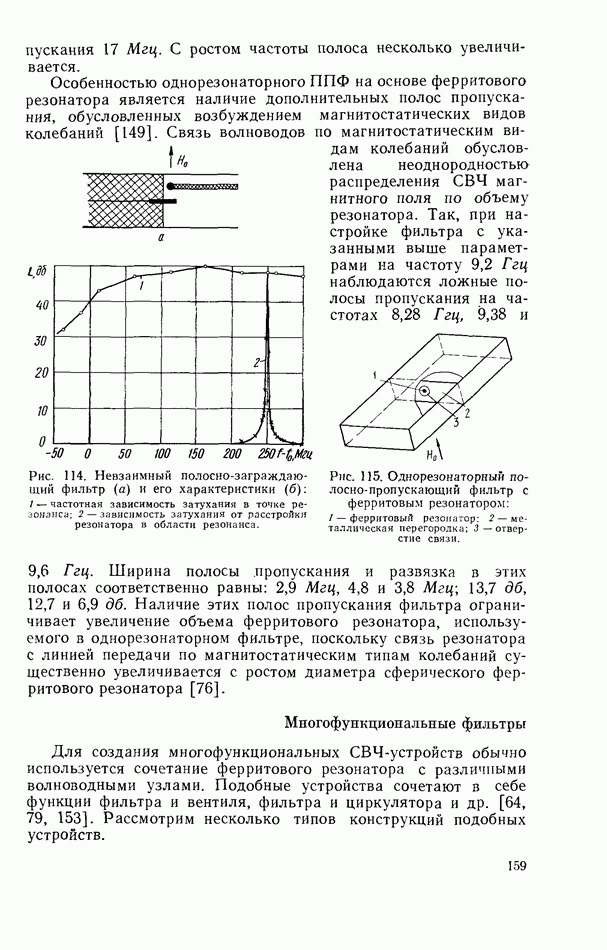
- 3.6. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В КОРОТКОЗАМКНУТОЙ ЛИНИИ ПЕРЕДАЧИ
- 3.7. КОМБИНИРОВАННЫЕ СХЕМЫ ВКЛЮЧЕНИЯ ТВЕРДОТЕЛЬНОГО РЕЗОНАТОРА
- 3.8. ТВЕРДОТЕЛЬНЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ С НЕСКОЛЬКИМИ РАСПРОСТРАНЯЮЩИМИСЯ ВОЛНАМИ
- Глава четвертая. СВЯЗЬ ТВЕРДОТЕЛЬНЫХ РЕЗОНАТОРОВ С ЛИНИЯМИ ПЕРЕДАЧИ СВЧ
- 4.2. СВЯЗЬ ФЕРРИТОВОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ
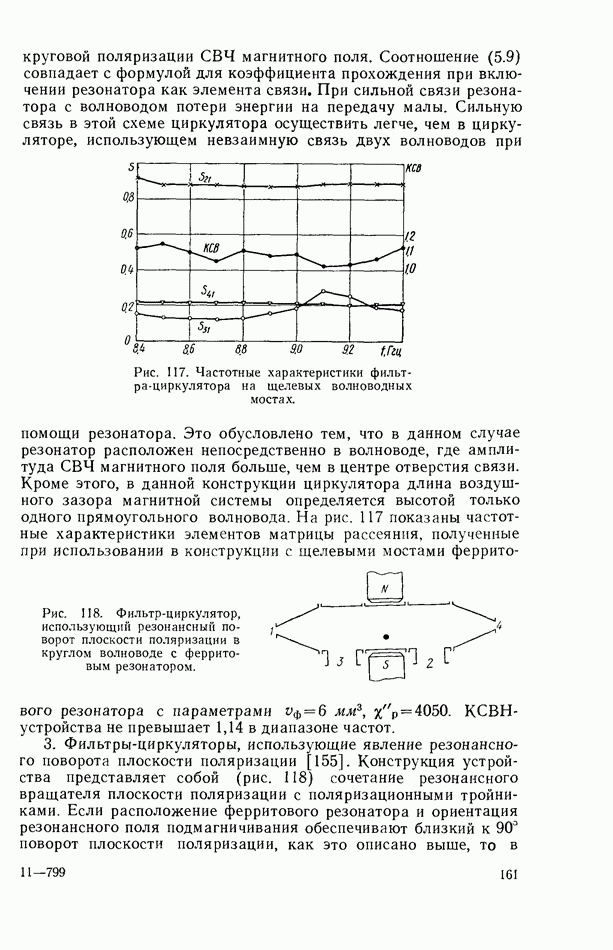
- 4.3. ФЕРРИТОВЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ ЗАМЕДЛЕННЫХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
- 4.4. РЕЗОНАНСНЫЙ ПОВОРОТ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ В ВОЛНОВОДЕ С ФЕРРИТОВЫМ РЕЗОНАТОРОМ
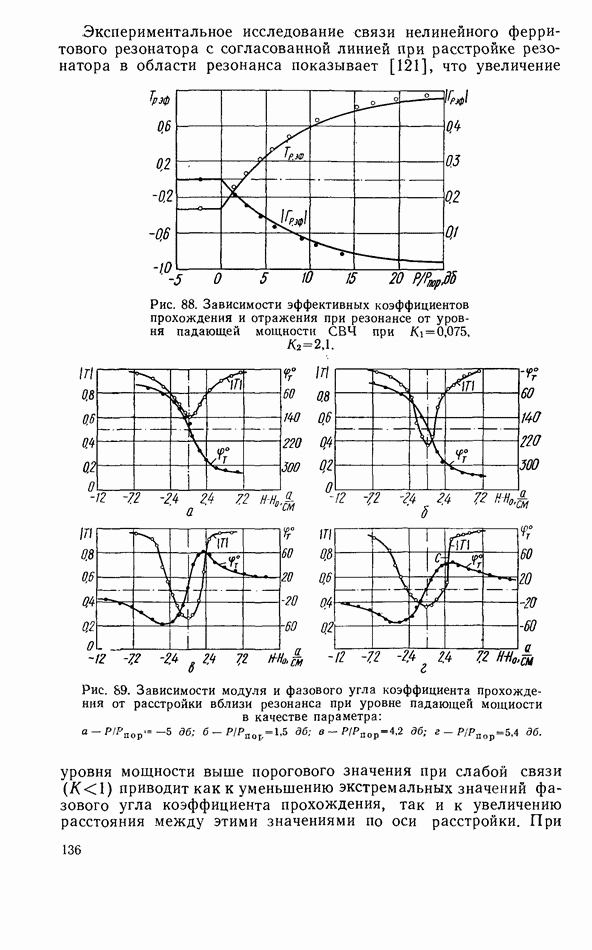
- 4.5. НЕЛИНЕЙНЫЙ ФЕРРИТОВЫЙ РЕЗОНАТОР В ЛИНИИ ПЕРЕДАЧИ
- Ферритовый резонатор в линии передачи при запороговых уровнях мощности
- Нелинейный ферритовый резонатор в короткозамкнутой линии передачи
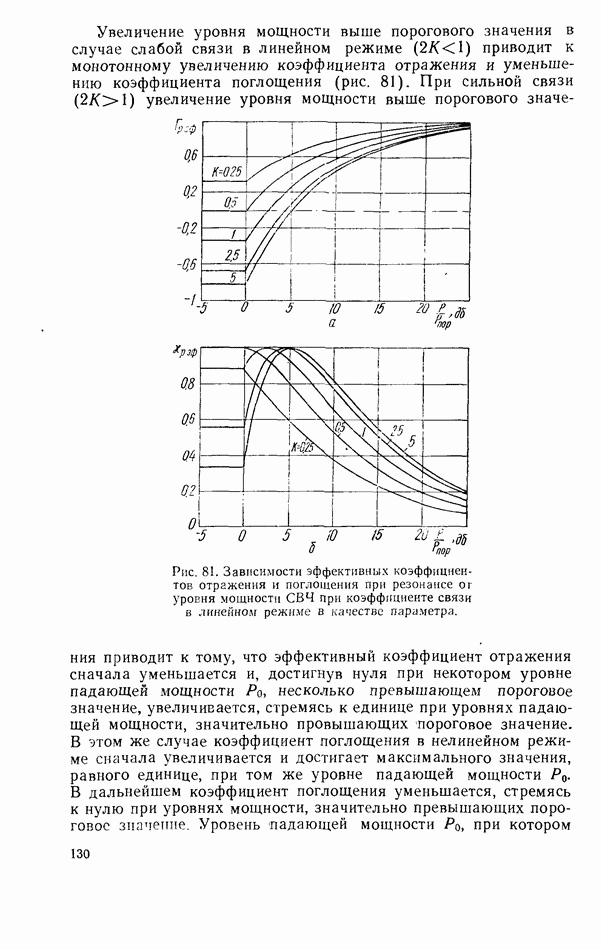
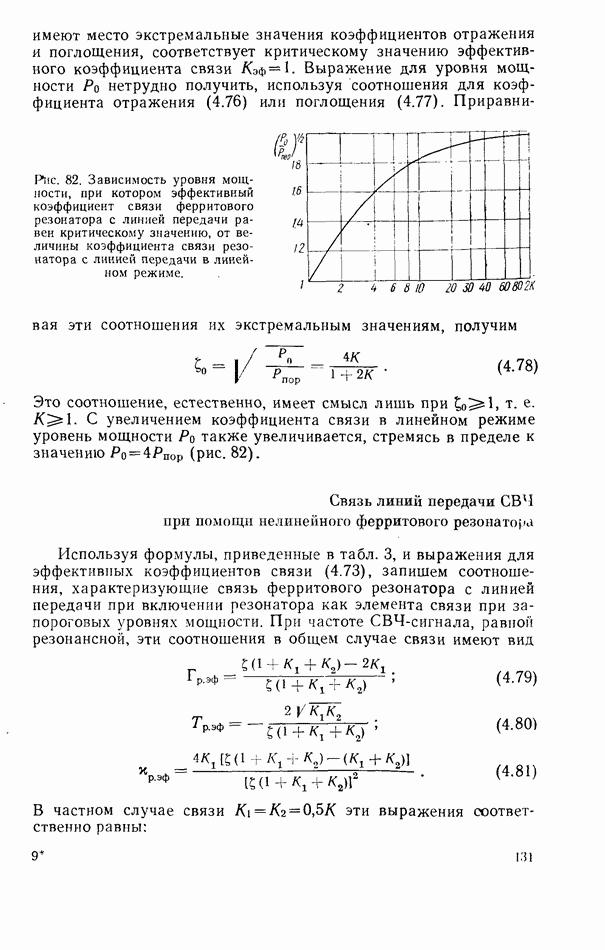
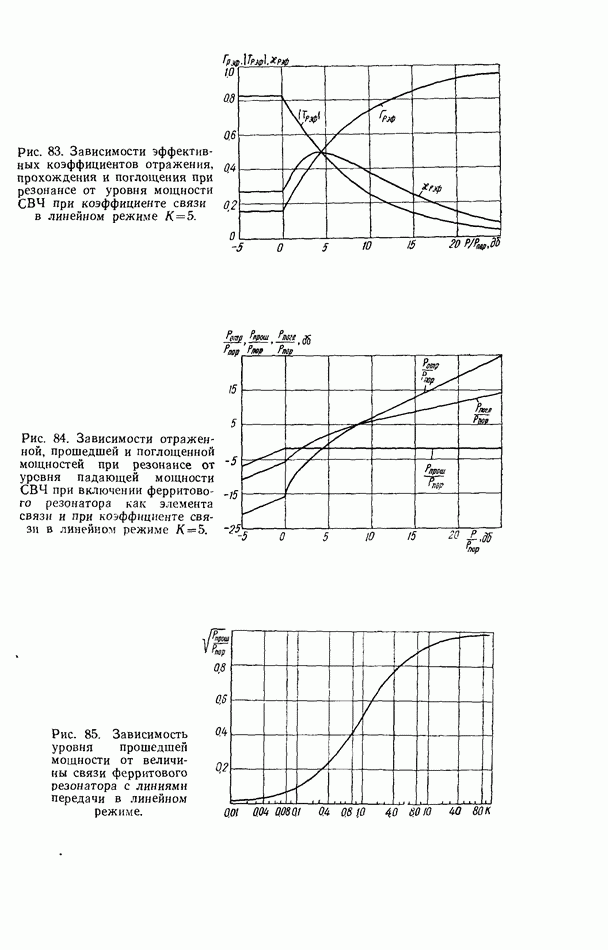
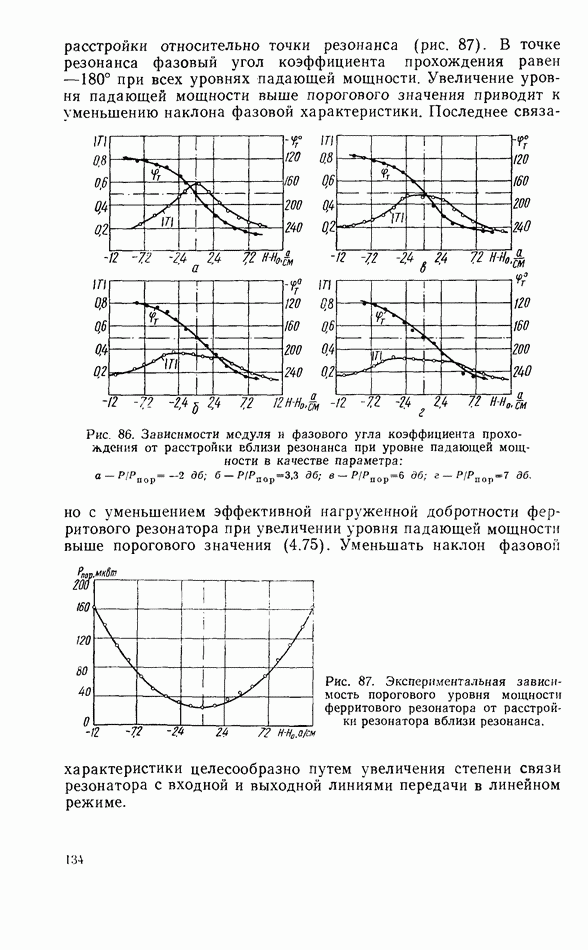
- Связь линий передачи СВЧ при помощи нелинейного ферритового резонатора
- Нелинейный ферритовый резонатор в согласованной линии передачи
- 4.6. СВЯЗЬ ДИЭЛЕКТРИЧЕСКОГО РЕЗОНАТОРА С ЛИНИЕЙ ПЕРЕДАЧИ СВЧ
- Глава пятая. ПРИНЦИПЫ ПОСТРОЕНИЯ СВЧ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ И УСТРОЙСТВ НА ОСНОВЕ ТВЕРДОТЕЛЬНЫХ РЕЗОНАТОРОВ
- 5.2. ДАТЧИКИ УРОВНЯ МОЩНОСТИ СВЧ
- Волноводная измерительная головка
- Датчик фиксированного уровня пиковой мощности
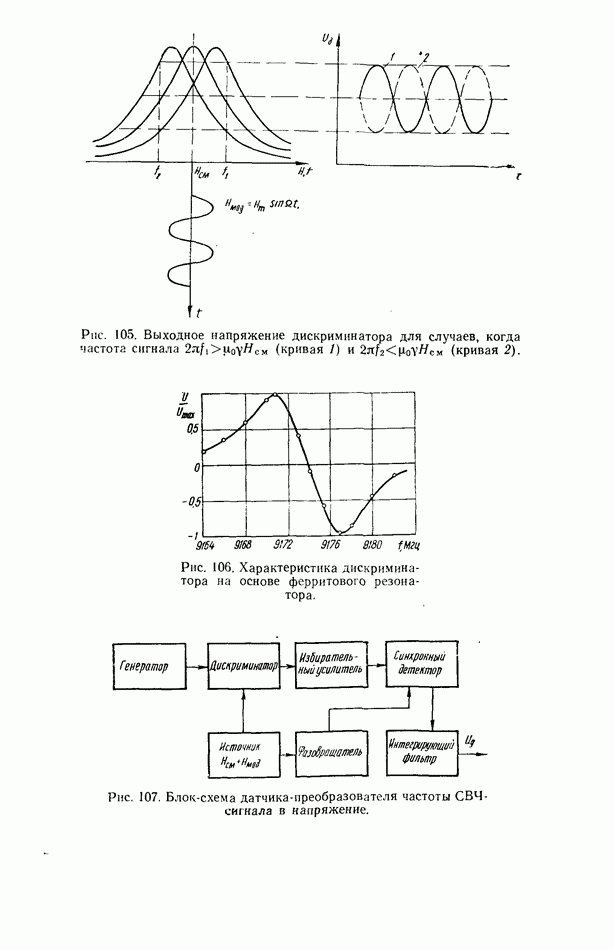
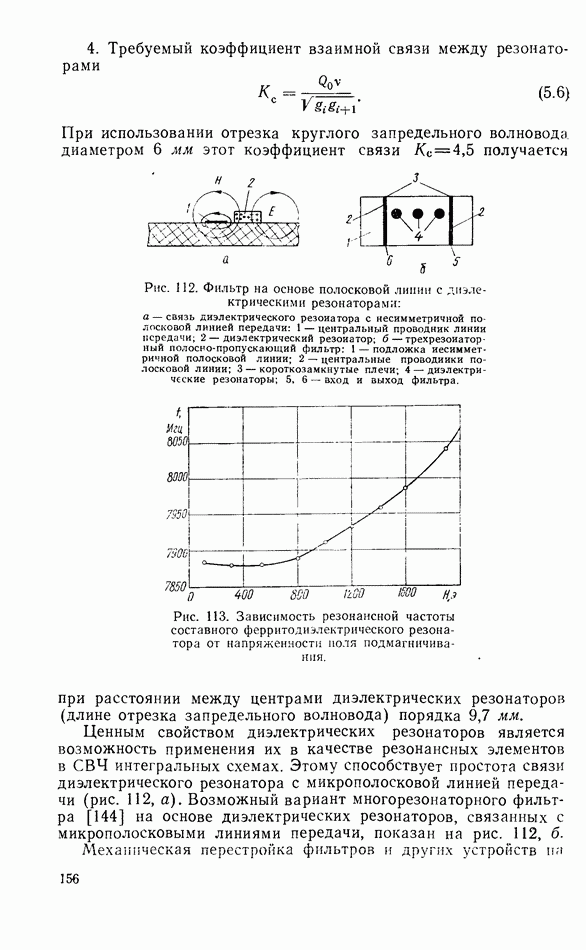
- 5.3. ЧАСТОТНЫЕ ДИСКРИМИНАТОРЫ С МАГНИТНОЙ НАСТРОЙКОЙ
- 5.4. РЕЗОНАНСНЫЕ ФАЗОВРАЩАТЕЛИ
- 5.5. УСТРОЙСТВО ДЛЯ РЕЗОНАНСНОГО ПОВОРОТА ПЛОСКОСТИ ПОЛЯРИЗАЦИИ В ВОЛНОВОДЕ
- 5.6. ФИЛЬТРЫ СВЧ НА ОСНОВЕ ДИЭЛЕКТРИЧЕСКИХ РЕЗОНАТОРОВ
- 5.7. ФЕРРИТОВЫЕ СВЧ-ФИЛЬТРЫ
- Многофункциональные фильтры
- Многорезонаторные ферритовые фильтры
- 5.8. ЧАСТОТНО-ИЗБИРАТЕЛЬНЫЕ ОГРАНИЧИТЕЛИ МАЛЫХ УРОВНЕЙ МОЩНОСТИ