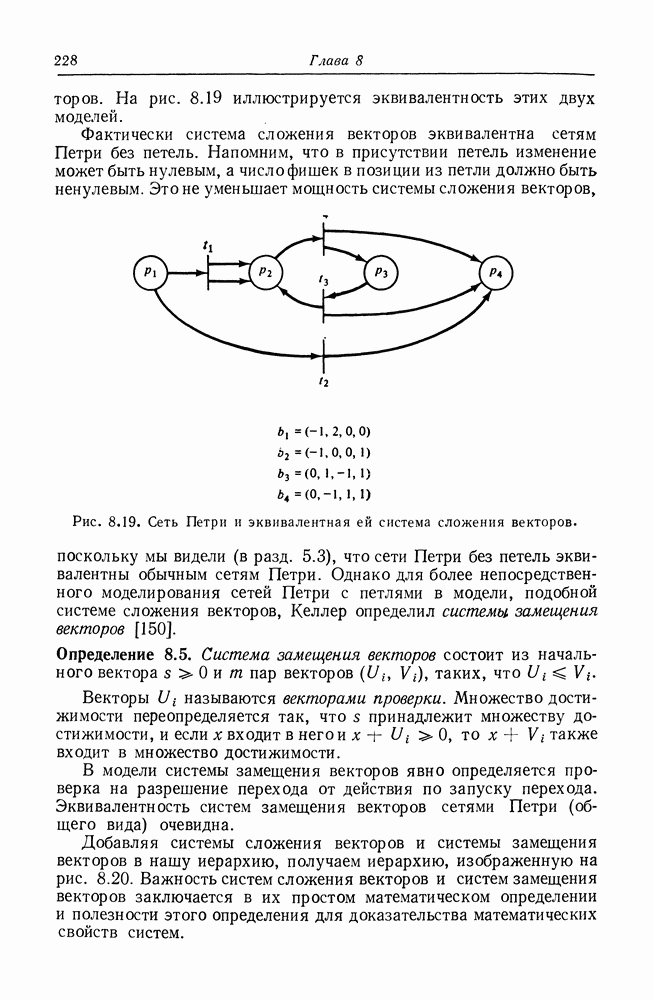
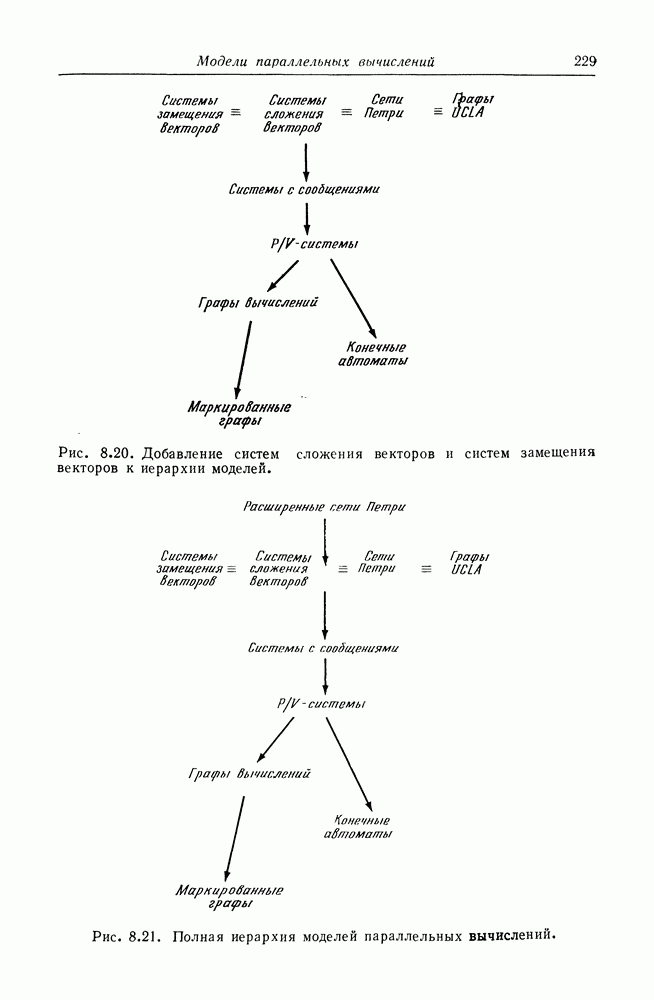
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.4. Программное обеспечение ЭВМ
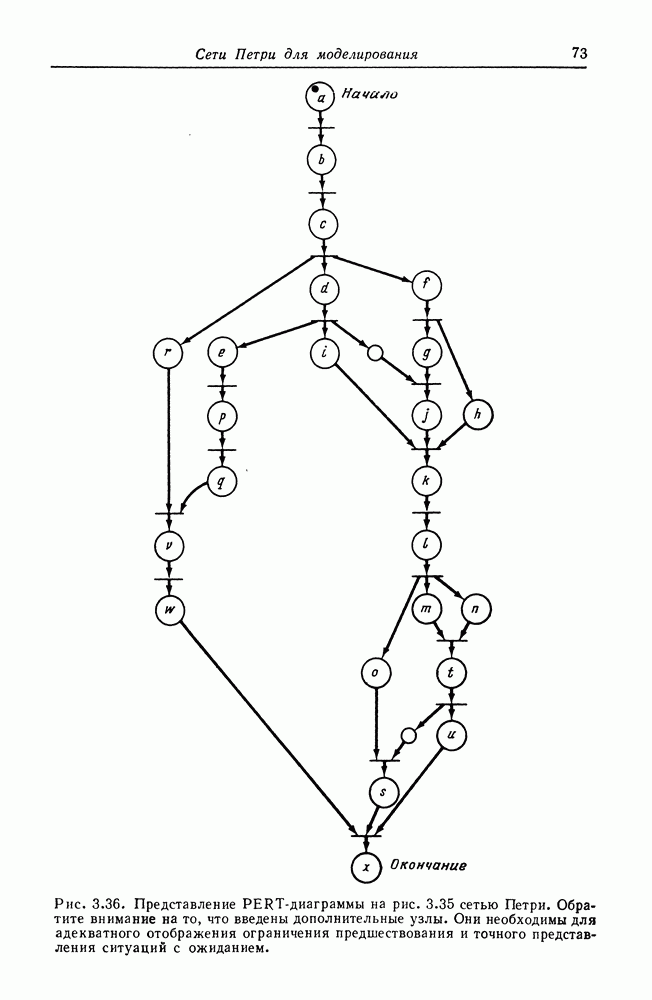
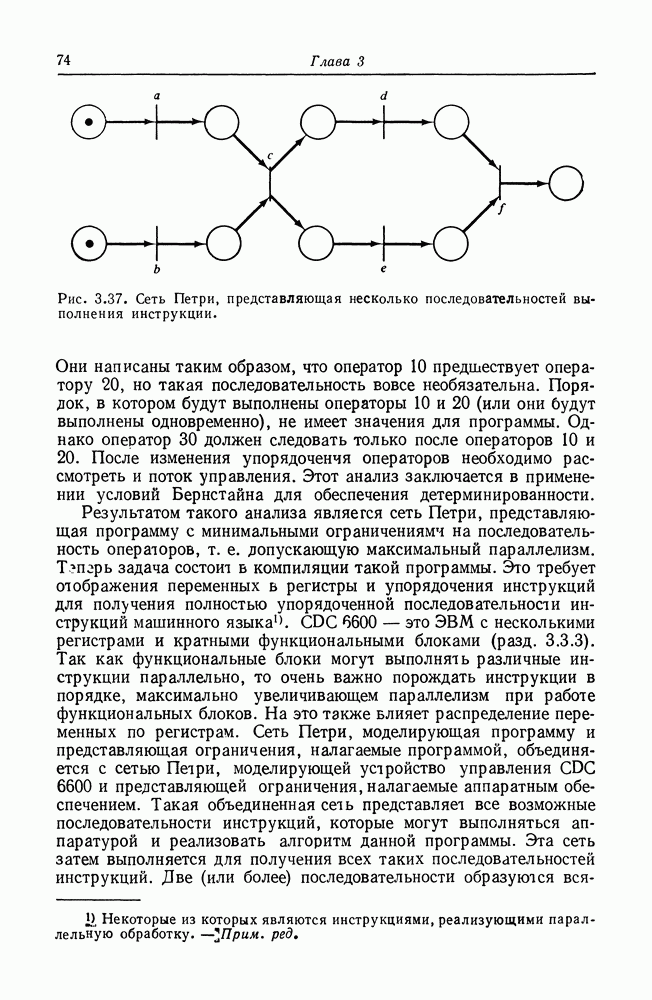
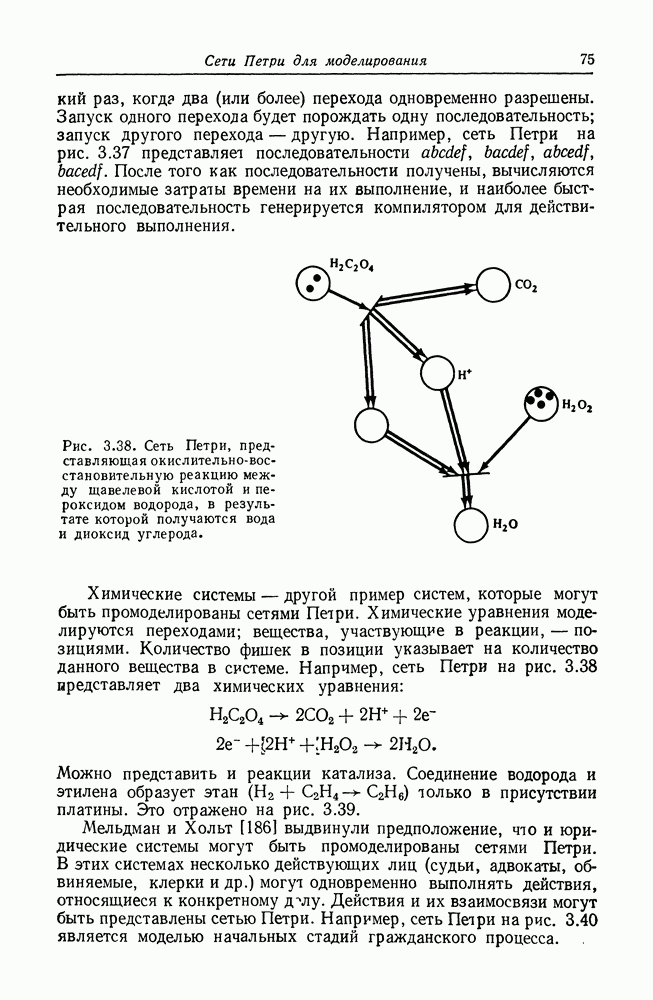
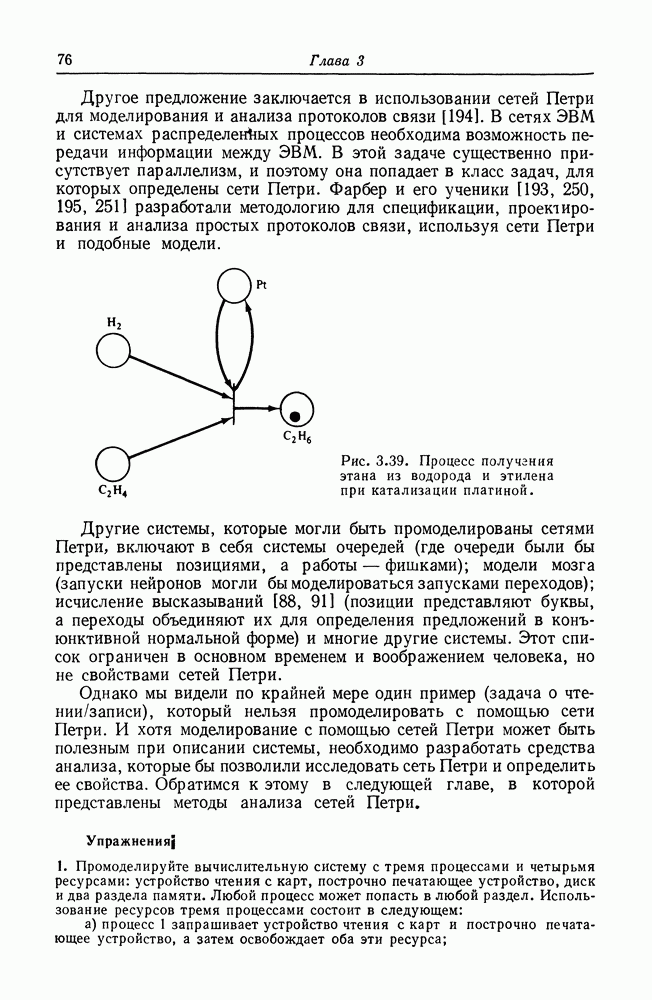
В дополнение к аппаратному обеспечению ЭВМ сетями Петри можно моделировать и программное обеспечение. Чаще всего сети Петри используются именно для этого, и здесь они имеют
наибольшие возможности для практического применения. В течение длительного времени разрабатывались системы для описания и моделирования аппаратного обеспечения ЭВМ, но только в последние годы такие попытки предприняты для формального моделирования программного обеспечения ЭВМ. Большинство этих усилий связано с анализом, спецификацией и описанием последовательных программ; системы параллельных процессов до сих пор остаются важной исследовательской проблемой. В этом разделе мы покажем, как сети Петри могут моделировать различные системы параллельных взаимодействующих процессов.
3.4.1. Блок-схемы
Вырожденным случаем параллельной системы обработки является система с одним процессом. Сначала рассмотрим, как сетью Петри может быть представлен отдельный процесс, а затем путем комбинации сетей Петри, представляющих несколько процессов, получим систему параллельных процессов.
Отдельный процесс описывается программой. Эта программа может быть написана на многих языках, но для удобства примем общецелевой язык, такой, как Алгол, Фортран, PL/1, Кобол, Паскаль, Бэйсик или даже язык ассемблера. Программа представляет два различных аспекта процесса: вычисление и управление. Вычисление связано с текущими арифметическими и логическими операциями, вводом и выводом, обычными манипуляциями над участками памяти и их содержимым. Управление же связано не со значениями или выполняемыми вычислениями, а только с порядком их выполнения.
Сети Петри удачно представляют структуру управления программ. Сети Петри предназначены для моделирования упорядочения инструкций и потока информации, но не для действительного вычисления самих значений. Модель системы по своей природе является абстракцией моделируемой системы. Поэтому она игнорирует все возможные специфические детали. Если бы моделировались все детали, тогда модель была бы дубликатом моделируемой системы, а не абстракцией.
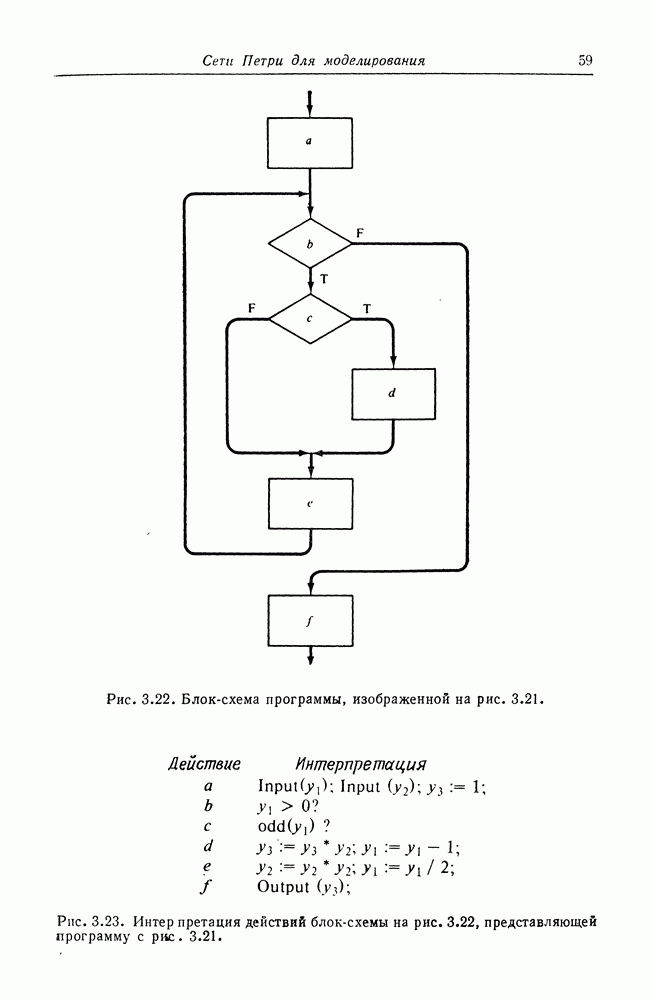
Стандартный способ представления структуры управления программ — это блок-схемы. Блок-схема представляет поток управления в программе. Например, программа на рис. 3.21 представляется блок-схемой на рис. 3.22. Заметим, что блок-схема на рис. 3.22 не указывает конкретные вычисления, которые надо произвести, а только определяет структуру программы. Такая блок-схема является абстрактной. Рис. 3.23 показывает, как можно проинтерпретировать блок-схему (рис. 3.22) программы, представленной на рис. 3.21. Каждая последовательная программа может быть представлена в виде блок-схемы. Таким образом, показывая, как

Рис. 3.21. Простая программа. Эта программа представлена блок-схемой на рис. 3.22 и сетью Петри на рис. 3.25.
блок-схема может быть представлена сетью Петри, мы дадим представление сетью Петри программы.
Оказывается блок-схема во многом подобна сети Петри: блок-схема представима в виде узлов двух типов (принятия решения, показанные ромбами, и вычисления, показанные прямоугольниками) и дуг между ними. Удобный способ выполнения блок-схемы — введение фишки, которая представляет текущую инструкцию. По мере выполнения инструкций фишка передвигается по блок-схеме. Из сходства между графическими представлениями программы и сети Петри может показаться, что для получения эквивалентной сети Петри можно заменить узлы блок-схемы на позиции, а дуги — на переходы. Такой подход использовался для превращения конечного автомата в сеть Петри (разд. 3.3.1).
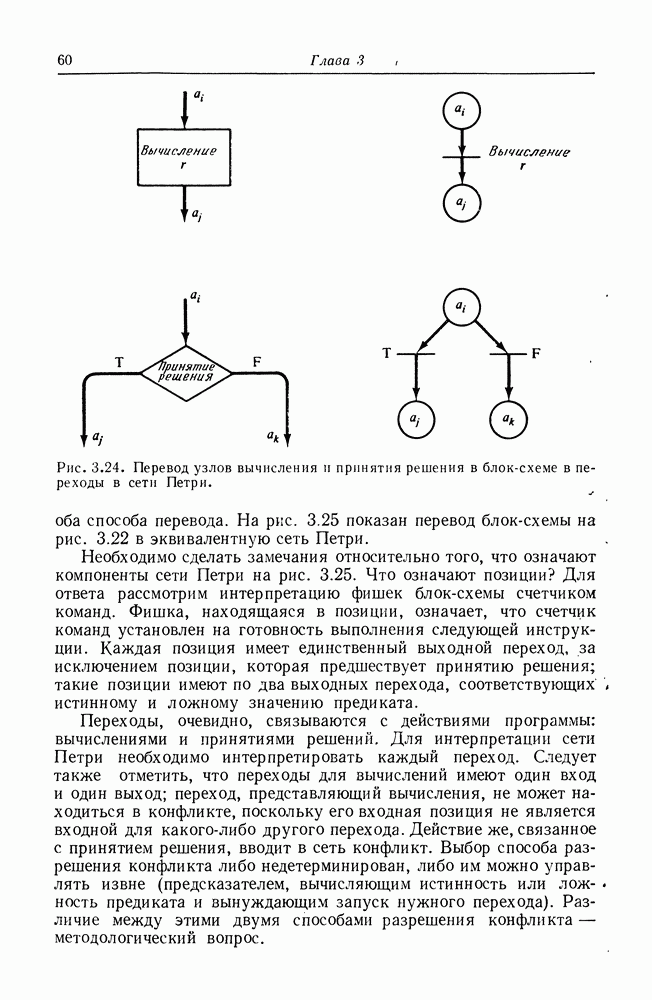
Однако заметим, что в сети Петри действия моделируются переходами, тогда как в блок-схеме действия моделируются узлами. Кроме того, если движение нашей фишки текущей инструкции в блок-схеме нужно приостановить, это делается между узлами, на дугах, а не внутри блока. Таким образом, правильный перевод блок-схемы в сеть Петри заменяет узлы блок-схемы на переходы сети Петри, а дуги блок-схемы — на позиции сети Петри. Каждая дуга блок-схемы соответствует точно одной позиции в сети Петри. Узлы блок-схемы представляются по-разному в зависимости от типа узла: вычисления или принятия решения. На рис. 3.24 иллюстрируются

(кликните для просмотра скана)

Рис. 3.24. Перевод узлов вычисления и принятия решения в блок-схеме в переходы в сети Петри.
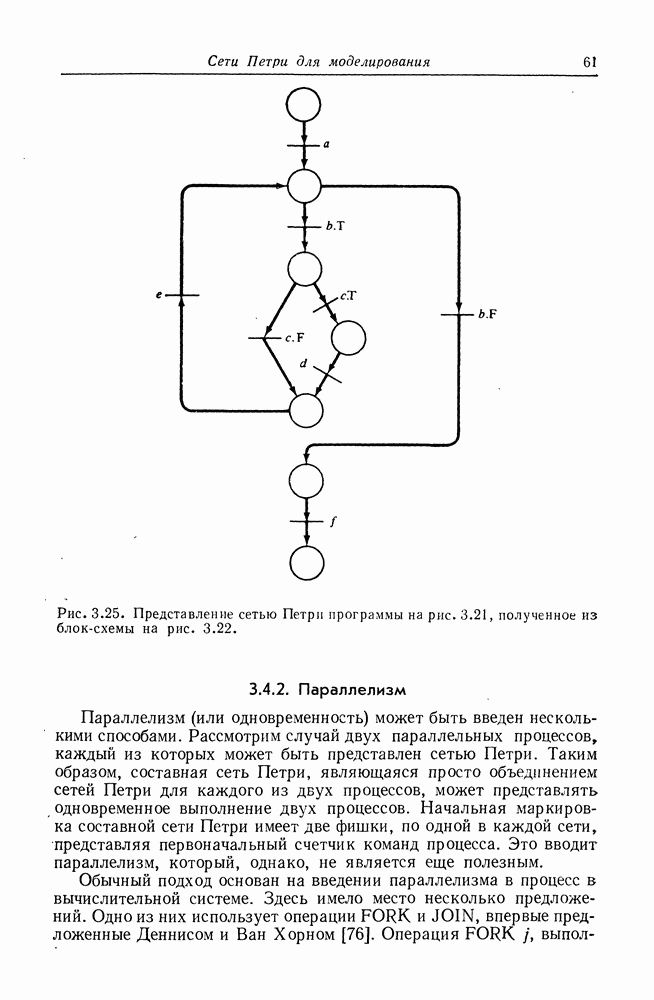
оба способа перевода. На рис. 3.25 показан перевод блок-схемы на рис. 3.22 в эквивалентную сеть Петри.
Необходимо сделать замечания относительно того, что означают компоненты сети Петри на рис. 3.25. Что означают позиции? Для ответа рассмотрим интерпретацию фишек блок-схемы счетчиком команд. Фишка, находящаяся в позиции, означает, что счетчик команд установлен на готовность выполнения следующей инструкции. Каждая позиция имеет единственный выходной переход, за исключением позиции, которая предшествует принятию решения; такие позиции имеют по два выходных перехода, соответствующих истинному и ложному значению предиката.
Переходы, очевидно, связываются с действиями программы: вычислениями и принятиями решений. Для интерпретации сети Петри необходимо интерпретировать каждый переход. Следует также отметить, что переходы для вычислений имеют один вход и один выход; переход, представляющий вычисления, не может находиться в конфликте, поскольку его входная позиция не является входной для какого-либо другого перехода. Действие же, связанное с принятием решения, вводит в сеть конфликт. Выбор способа разрешения конфликта либо недетерминирован, либо им можно управлять извне (предсказателем, вычисляющим истинность или ложность предиката и вынуждающим запуск нужного перехода). Различие между этими двумя способами разрешения конфликта — методологический вопрос.
Рис. 3.25. (см. скан) Представление сетью Петри программы на рис. 3.21, полученное из блок-схемы на рис. 3.22.
3.4.2. Параллелизм
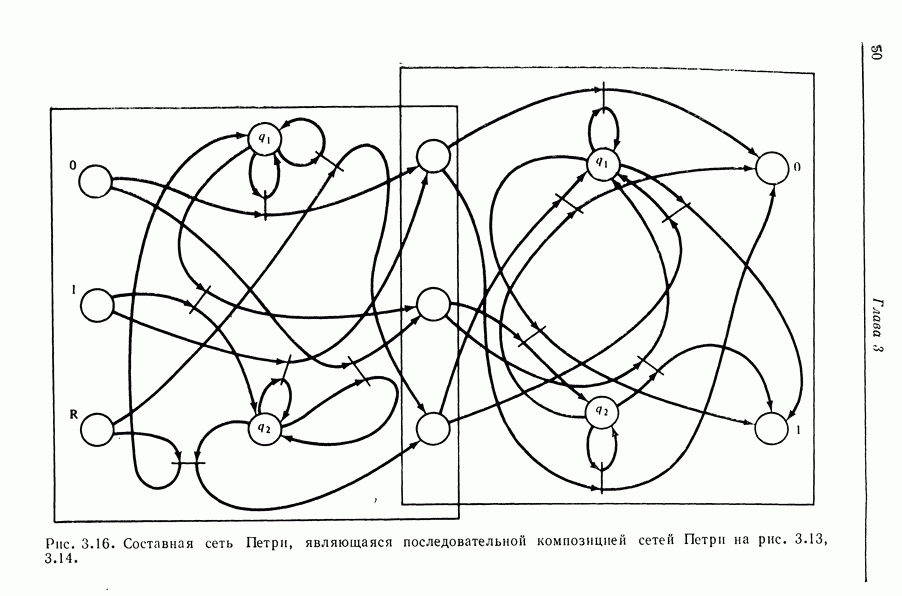
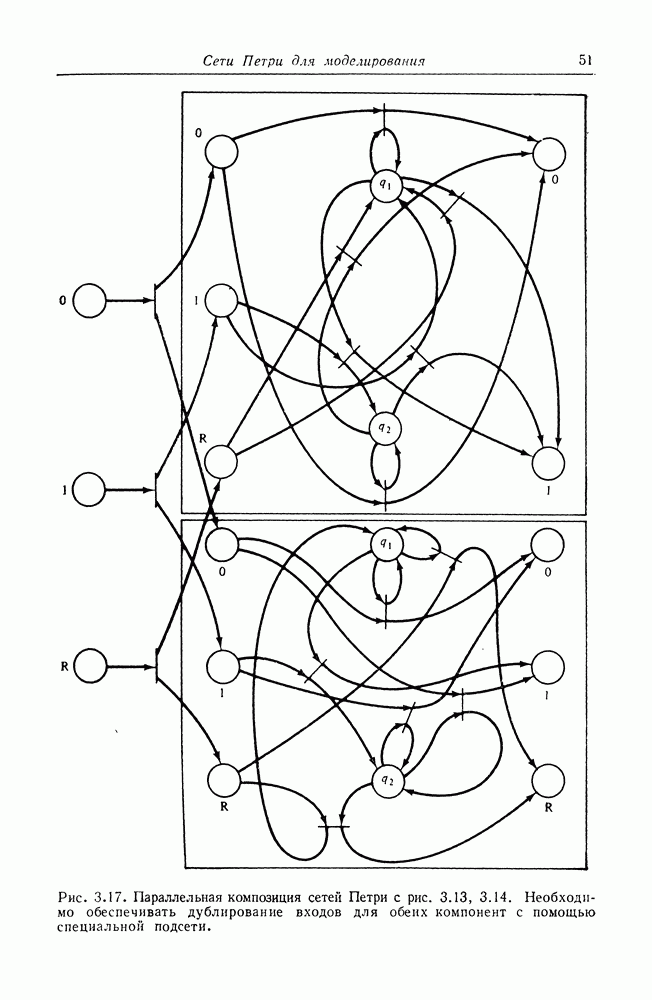
Параллелизм (или одновременность) может быть введен несколькими способами. Рассмотрим случай двух параллельных процессов, каждый из которых может быть представлен сетью Петри. Таким образом, составная сеть Петри, являющаяся просто объединением сетей Петри для каждого из двух процессов, может представлять одновременное выполнение двух процессов. Начальная маркировка составной сети Петри имеет две фишки, по одной в каждой сети, представляя первоначальный счетчик команд процесса. Это вводит параллелизм, который, однако, не является еще полезным.
Обычный подход основан на введении параллелизма в процесс в вычислительной системе. Здесь имело место несколько предложений. Одно из них использует операции  и
и  впервые предложенные Деннисом и Ван Хорном [76]. Операция
впервые предложенные Деннисом и Ван Хорном [76]. Операция 

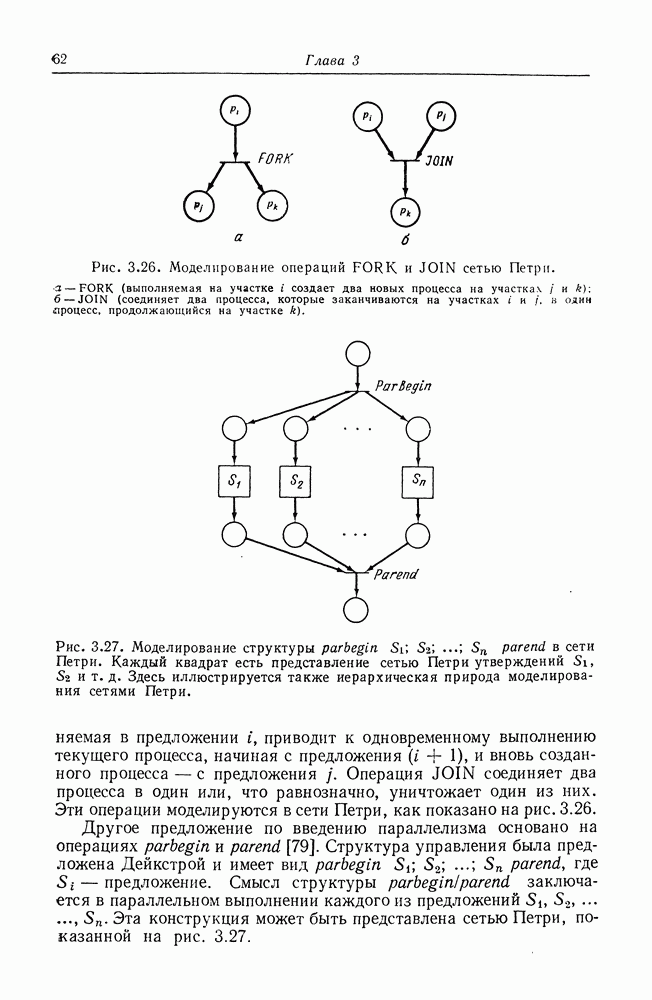
Рис. 3.26. Моделирование операций  и
и  сетью Петри.
сетью Петри.  (выполняемая на участке
(выполняемая на участке  создает два новых процесса на участках
создает два новых процесса на участках  (соединяет два процесса, которые заканчиваются на участках
(соединяет два процесса, которые заканчиваются на участках  в один «процесс, продолжающийся на участке
в один «процесс, продолжающийся на участке 

Рис. 3.27. Моделирование структуры  в сети Петри. Каждый квадрат есть представление сетью Петри утверждений
в сети Петри. Каждый квадрат есть представление сетью Петри утверждений  и т. д. Здесь иллюстрируется также иерархическая природа моделирования сетями Петри.
и т. д. Здесь иллюстрируется также иерархическая природа моделирования сетями Петри.
выполняемая в предложении  приводит к одновременному выполнению текущего процесса, начиная с предложения
приводит к одновременному выполнению текущего процесса, начиная с предложения  и вновь созданного процесса — с предложения
и вновь созданного процесса — с предложения  Операция
Операция  соединяет два процесса в один или, что равнозначно, уничтожает один из них. Эти операции моделируются в сети Петри, как показано на рис. 3.26.
соединяет два процесса в один или, что равнозначно, уничтожает один из них. Эти операции моделируются в сети Петри, как показано на рис. 3.26.
Другое предложение по введению параллелизма основано на операциях  и
и  [79]. Структура управления была предложена Дейкстрой и имеет вид
[79]. Структура управления была предложена Дейкстрой и имеет вид  где
где  предложение. Смысл структуры
предложение. Смысл структуры  заключается в параллельном выполнении каждого из предложений
заключается в параллельном выполнении каждого из предложений  Эта конструкция может быть представлена сетью Петри, показанной на рис. 3.27.
Эта конструкция может быть представлена сетью Петри, показанной на рис. 3.27.
3.4.3. Синхронизация
Введение параллелизма полезно только в том случае, когда компоненты процессов могут взаимодействовать при получении решения задачи. Такое взаимодействие требует распределения ресурсов между процессами. Для гарантии правильности работы системы в целом распределением необходимо управлять. Проблемы синхронизации, возникающие при взаимодействии процессов, иллюстрируются многочисленными примерами, приведенными в литературе. Среди задач синхронизации: задача о взаимном исключении [78], производителе/потребителе [79], обедающих мудрецах [79], чтении/записи [58] и др.
Эти задачи стали классическими в области синхронизации; каждое новое предлржение по механизму синхронизации должно решать их. И хотя сети Петри представляют собой схему моделирования, а не механизм синхронизации, они определенно способны моделировать механизмы синхронизации. Мы представляем здесь некоторые решения в виде сетей Петри. Такое представление основана частично на работе [56].
3.4.4. Задача о взаимном исключении
Предположим, что несколько процессов разделяют общую переменную, запись, файл или другой элемент данных. Этот разделяемый элемент данных может использоваться процессами различными способами, упрощенно их можно классифицировать как чтение значения элемента данных или запись нового значения. Эти две операции являются часто единственными примитивными операциями. Это означает, что для обновления разделяемого элемента данных процесс должен сначала считать старое значение, затем вычислить новое и, наконец, записать его на то же место. Если два процесса в одно и то же время пытаются выполнить такую последовательность действий, то могут возникнуть трудности. Возможна следующая последовательность:
1. Первый процесс считывает значение х из разделяемого объекта;
2. Второй процесс считывает значение х из разделяемого объекта;
3. Первый процесс вычисляет новое значение 
4. Второй процесс вычисляет новое значение 
5. Первый процесс записывает х в разделяемый объект;
6. Второй процесс записывает  в разделяемый объект, уничтожая значение х.
в разделяемый объект, уничтожая значение х.
Результат вычисления первого процесса потерян, так как теперь значением разделяемого объекта является  в то время как им должно быть либо
в то время как им должно быть либо  либо
либо  (Представьте себе,
(Представьте себе,  «снять со счета
«снять со счета  «поместить на счет
«поместить на счет  а процессы 1 и 2 — банковские операции.)
а процессы 1 и 2 — банковские операции.)

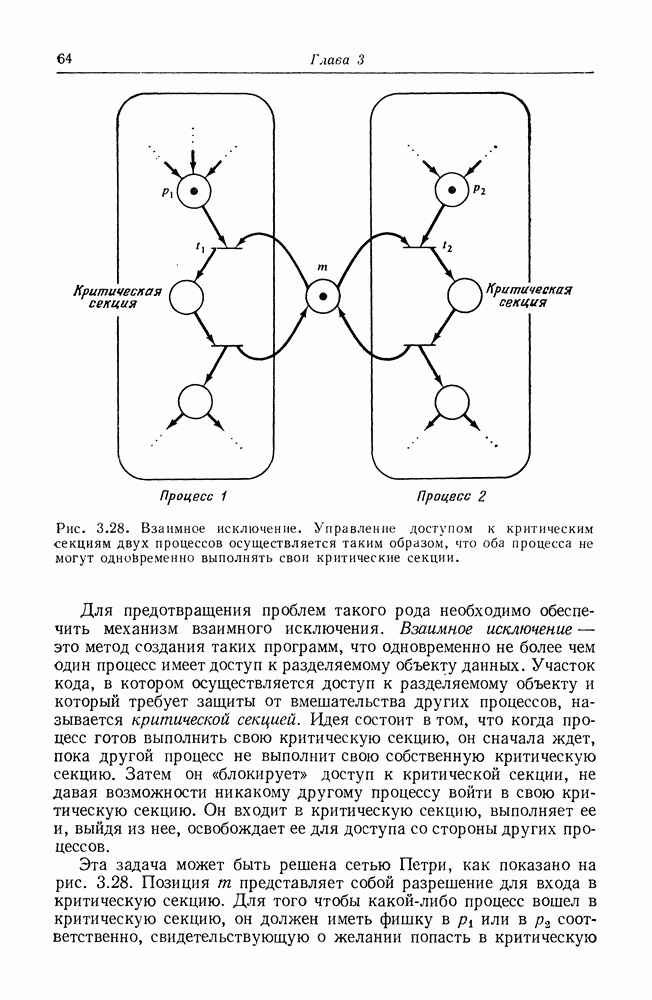
Рис. 3.28. Взаимное исключение. Управление доступом к критическим секциям двух процессов осуществляется таким образом, что оба процесса не могут одновременно выполнять свои критические секции.
Для предотвращения проблем такого рода необходимо обеспечить механизм взаимного исключения. Взаимное исключение — это метод создания таких программ, что одновременно не более чем один процесс имеет доступ к разделяемому объекту данных. Участок кода, в котором осуществляется доступ к разделяемому объекту и который требует защиты от вмешательства других процессов, называется критической секцией. Идея состоит в том, что когда процесс готов выполнить свою критическую секцию, он сначала ждет, пока другой процесс не выполнит свою собственную критическую секцию. Затем он «блокирует» доступ к критической секции, не давая возможности никакому другому процессу войти в свою критическую секцию. Он входит в критическую секцию, выполняет ее и, выйдя из нее, освобождает ее для доступа со стороны других процессов.
Эта задача может быть решена сетью Петри, как показано на рис. 3.28. Позиция  представляет собой разрешение для входа в критическую секцию. Для того чтобы какой-либо процесс вошел в критическую секцию, он должен иметь фишку в
представляет собой разрешение для входа в критическую секцию. Для того чтобы какой-либо процесс вошел в критическую секцию, он должен иметь фишку в  или в
или в  соответственно, свидетельствующую о желании попасть в критическую
соответственно, свидетельствующую о желании попасть в критическую
секцию, а также должна существовать фишка в  дающая разрешение на вход. Если оба процесса пытаются войти в критическую секцию одновременно, то переходы
дающая разрешение на вход. Если оба процесса пытаются войти в критическую секцию одновременно, то переходы  вступят в конфликт, и только один из них сможет запуститься. Запуск запретит переход
вступят в конфликт, и только один из них сможет запуститься. Запуск запретит переход  вынуждая процесс 2 ждать, пока первый процесс выйдет из своей критической секции и возвратит фишку обратно в позицию
вынуждая процесс 2 ждать, пока первый процесс выйдет из своей критической секции и возвратит фишку обратно в позицию 
3.4.5. Задача о производителе/потребителе
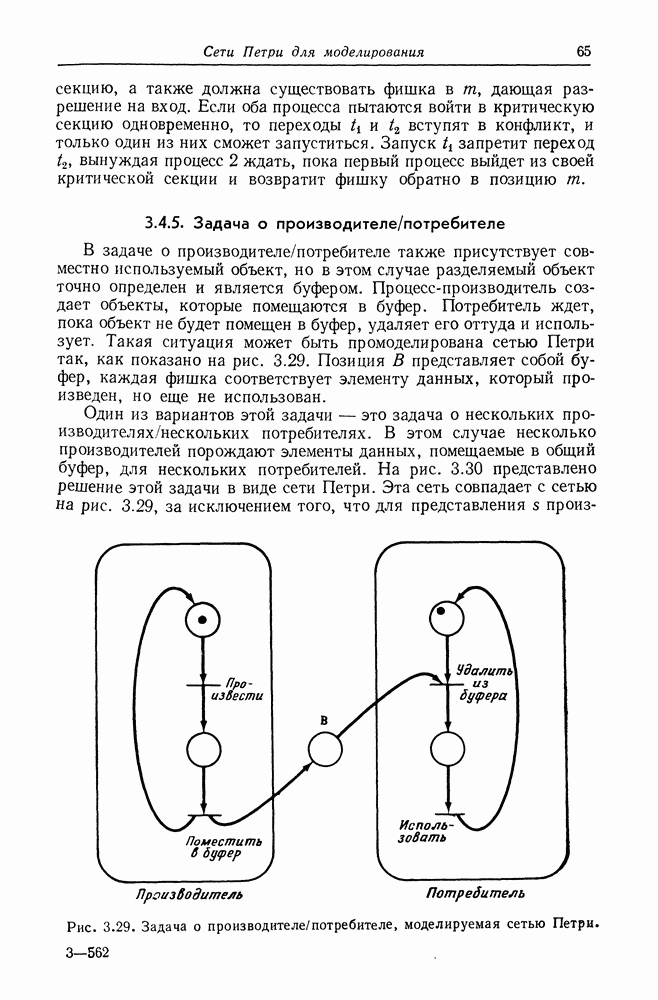
В задаче о производителе/потребителе также присутствует совместно используемый объект, но в этом случае разделяемый объект точно определен и является буфером. Процесс-производитель создает объекты, которые помещаются в буфер. Потребитель ждет, пока объект не будет помещен в буфер, удаляет его оттуда и использует. Такая ситуация может быть промоделирована сетью Петри так, как показано на рис. 3.29. Позиция В представляет собой буфер, каждая фишка соответствует элементу данных, который произведен, но еще не использован.
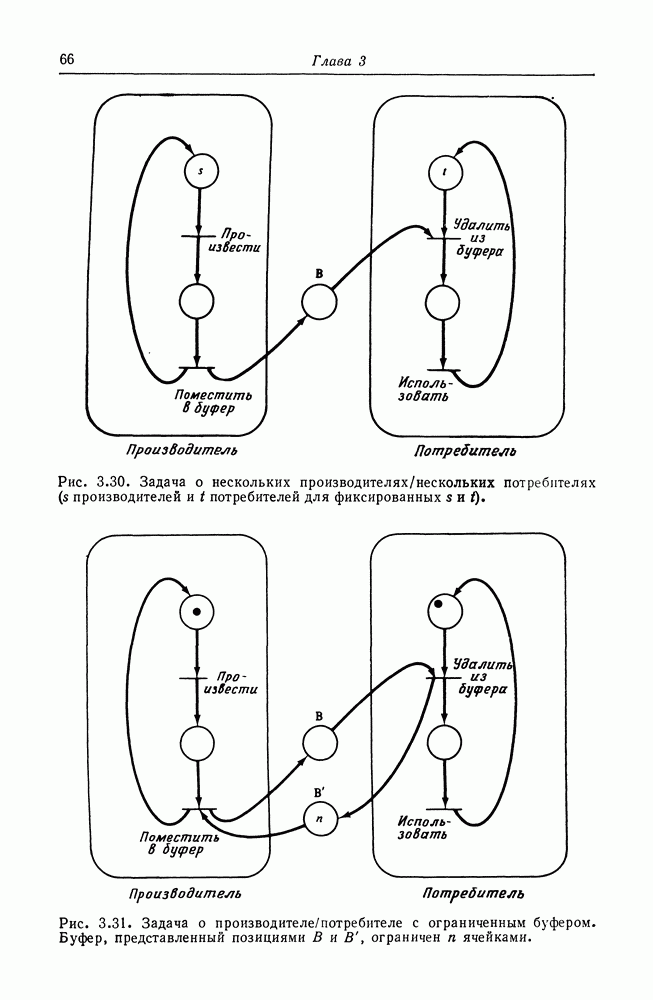
Один из вариантов этой задачи — это задача о нескольких производителях/нескольких потребителях. В этом случае несколько производителей порождают элементы данных, помещаемые в общий буфер, для нескольких потребителей. На рис. 3.30 представлено решение этой задачи в виде сети Петри. Эта сеть совпадает с сетью на рис. 3.29, за исключением того, что для представления 

Рис. 3.29. Задача о производителе/потребителе, моделируемая сетью Петри.

(кликните для просмотра скана)
производителей и  потребителей мы начали выполнение сети с
потребителей мы начали выполнение сети с  фишками в начальной позиции процесса-производителя и
фишками в начальной позиции процесса-производителя и  фишками в начальной позиции процесса-потребителя. Таким образом мы представляем
фишками в начальной позиции процесса-потребителя. Таким образом мы представляем  производителей и
производителей и  потребителей, реализуемых реентерабельными совместно используемыми программами. Альтернативой было бы дублирование программного кода для процессов производителя и потребителя, однако результатом этого при том же самом поведении была бы гораздо большая сеть.
потребителей, реализуемых реентерабельными совместно используемыми программами. Альтернативой было бы дублирование программного кода для процессов производителя и потребителя, однако результатом этого при том же самом поведении была бы гораздо большая сеть.
В другом варианте задачи о производителе/потребителе используется буфер ограниченного размера. При такой постановке задачи буфер между производителем и потребителем ограничен, т. е. имеет только  ячеек для элементов данных. Следовательно, производитель не может постоянно работать с той скоростью, которая ему нужна, а вынужден ждать, если потребитель работает медленно и буфер заполнен. На рис. 3.31 показано решение этой проблемы. Ограниченному буферу сопоставляются две позиции: В представляет количество элементов данных, которые произведены, но еще не использованы (число заполненных ячеек), В — количество пустых ячеек в буфере. Первоначально В имеет
ячеек для элементов данных. Следовательно, производитель не может постоянно работать с той скоростью, которая ему нужна, а вынужден ждать, если потребитель работает медленно и буфер заполнен. На рис. 3.31 показано решение этой проблемы. Ограниченному буферу сопоставляются две позиции: В представляет количество элементов данных, которые произведены, но еще не использованы (число заполненных ячеек), В — количество пустых ячеек в буфере. Первоначально В имеет  фишек, а В фишек не имеет. Если буфер заполнен, то В фишек не имеет, а В имеет
фишек, а В фишек не имеет. Если буфер заполнен, то В фишек не имеет, а В имеет  фишек. Если теперь производитель попытается поместить еще один элемент данных в буфер, то он будет остановлен, так как в В нет фишки, делающей этот переход разрешенным.
фишек. Если теперь производитель попытается поместить еще один элемент данных в буфер, то он будет остановлен, так как в В нет фишки, делающей этот переход разрешенным.
3.4.6. Задача об обедающих мудрецах
Задача об обедающих мудрецах была предложена Дейкстрой в [79] и связана с пятью мудрецами, которые попеременно то думали, то ели. Мудрецы сидят за большим круглым столом, на котором много блюд китайской кухни. Между соседями лежит одна палочка для еды. Однако для приема китайской пищи необходимо две палочки, следовательно, каждый мудрец должен взять палочку слева и палочку справа: проблема, конечно, заключается в том, что если все мудрецы возьмут палочки слева и затем будут ждать, когда освободятся палочки с правой стороны, то они будут ждать вечно и умрут от голода (состояние тупика).
На рис. 3.32 показано решение этой задачи с помощью сети Петри. Позиции  представляют палочки для еды, и так как каждая из них первоначально свободна, то в начальной маркировке в каждой из этих позиций имеется фишка. Каждый мудрец представлен двумя позициями
представляют палочки для еды, и так как каждая из них первоначально свободна, то в начальной маркировке в каждой из этих позиций имеется фишка. Каждый мудрец представлен двумя позициями  для состояний размышления и принятия пищи соответственно. Для того чтобы мудрец перешел из состояния размышления в состояние принятия пищи, обе палочки (слева и справа) должны быть свободны. Это легко моделируется сетью Петри.
для состояний размышления и принятия пищи соответственно. Для того чтобы мудрец перешел из состояния размышления в состояние принятия пищи, обе палочки (слева и справа) должны быть свободны. Это легко моделируется сетью Петри.

Рис. 3.32. Задача об обедающих мудрецах. Каждый мудрец представлен двумя позициями: размышление  принятие пищи
принятие пищи 
3.4.7. Задача о чтении/записи
Существует несколько вариантов задачи о чтении/записи [58], однако основная структура их остается неизменной. Имеются процессы двух типов: процессы чтения и процессы записи. Все процессы совместно используют общий файл или переменную или элемент данных. Процессы чтения не изменяют объект в отличие от процессов записи. Таким образом, процессы записи должны взаимно исключать все другие процессы чтения и записи, в то время как несколько процессов чтения могут иметь доступ к разделяемым данным одновременно. Задача состоит в определении структуры управления, которая не приведет к тупику и не допустит нарушения критерия взаимного исключения.
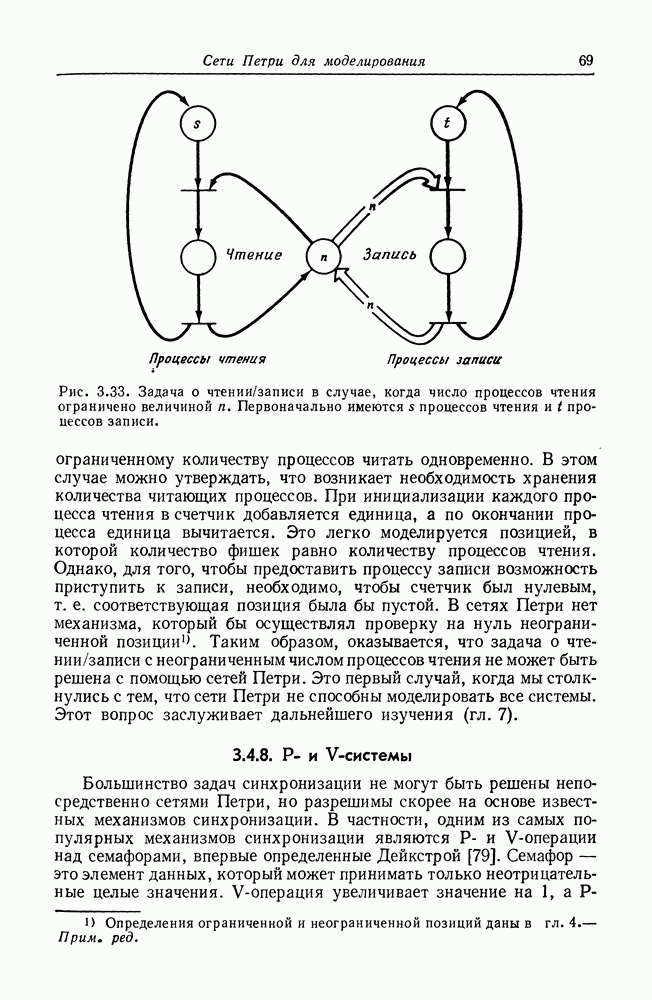
На рис. 3.33 иллюстрируется решение задачи в том случае, когда количество процессов чтения ограничено величиной  Если в системе количество процессов чтения не ограничено, то только
Если в системе количество процессов чтения не ограничено, то только  процессов могут выполняться в одно и то же время.
процессов могут выполняться в одно и то же время.
Проблема возникает в том случае, если количество процессов чтения не ограничено и мы хотим предоставить возможность

Рис. 3.33. Задача о чтении/записи в случае, когда число процессов чтения ограничено величиной  Первоначально имеются
Первоначально имеются  процессов чтения и
процессов чтения и  процессов записи.
процессов записи.
неограниченному количеству процессов читать одновременно. В этом случае можно утверждать, что возникает необходимость хранения количества читающих процессов. При инициализации каждого процесса чтения в счетчик добавляется единица, а по окончании процесса единица вычитается. Это легко моделируется позицией, в которой количество фишек равно количеству процессов чтения. Однако, для того, чтобы предоставить процессу записи возможность приступить к записи, необходимо, чтобы счетчик был нулевым, т. е. соответствующая позиция была бы пустой. В сетях Петри нет механизма, который бы осуществлял проверку на нуль неограниченной позиции. Таким образом, оказывается, что задача о чтении/записи с неограниченным числом процессов чтения не может быть решена с помощью сетей Петри. Это первый случай, когда мы столкнулись с тем, что сети Петри не способны моделировать все системы. Этот вопрос заслуживает дальнейшего изучения 
3.4.8. Р- и V-системы
Большинство задач синхронизации не могут быть решены непосредственно сетями Петри, но разрешимы скорее на основе известных механизмов синхронизации. В частности, одним из самых популярных механизмов синхронизации являются Р- и V-операции над семафорами, впервые определенные Дейкстрой [79]. Семафор — это элемент данных, который может принимать только неотрицательные целые значения. V-операция увеличивает значение на 1, а
Р-операция уменьшает его на  -операцию можно применять только в том случае, когда значение семафора останется в результате неотрицательным; если же значение семафора равно 0, то
-операцию можно применять только в том случае, когда значение семафора останется в результате неотрицательным; если же значение семафора равно 0, то  -операция должна ждать, пока какой-нибудь другой процесс не выполнит V-операцию. Р- и V-операции определены как примитивные, т. е. никакая другая операция не может изменять значение семафора одновременно с ними.
-операция должна ждать, пока какой-нибудь другой процесс не выполнит V-операцию. Р- и V-операции определены как примитивные, т. е. никакая другая операция не может изменять значение семафора одновременно с ними.

Рис. 3.34. Моделирование  -операций над семафором
-операций над семафором 
Такие операции легко моделируются сетью Петри, как показано на рис. 3.34. Каждый семафор моделируется позицией, количество фишек в позиции показывает значение семафора.  -операция использует позицию семафора в качестве входа, V-операция — в качестве выхода.
-операция использует позицию семафора в качестве входа, V-операция — в качестве выхода.
Преимущество этого заключается в том, что многие системы проектируются и описываются с помощью  и V-операций. Например, в операционной системе Venus [179] Р- и V-операции являются основным механизмом связи между процессами. Такие системы, следовательно, можно промоделировать сетями Петри.
и V-операций. Например, в операционной системе Venus [179] Р- и V-операции являются основным механизмом связи между процессами. Такие системы, следовательно, можно промоделировать сетями Петри.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ГЛАВА 1. ВВЕДЕНИЕ
- ГЛАВА 2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
- 2.1. Структура сети Петри
- 2.2. Графы сетей Петри
- 2.3. Маркировка сетей Петри
- 2.4. Правила выполнения сетей Петри
- 2.5. Пространство состояний сети Петри
- 2.6. Альтернативные формы определения сетей Петри
- ГЛАВА 3. СЕТИ ПЕТРИ ДЛЯ МОДЕЛИРОВАНИЯ
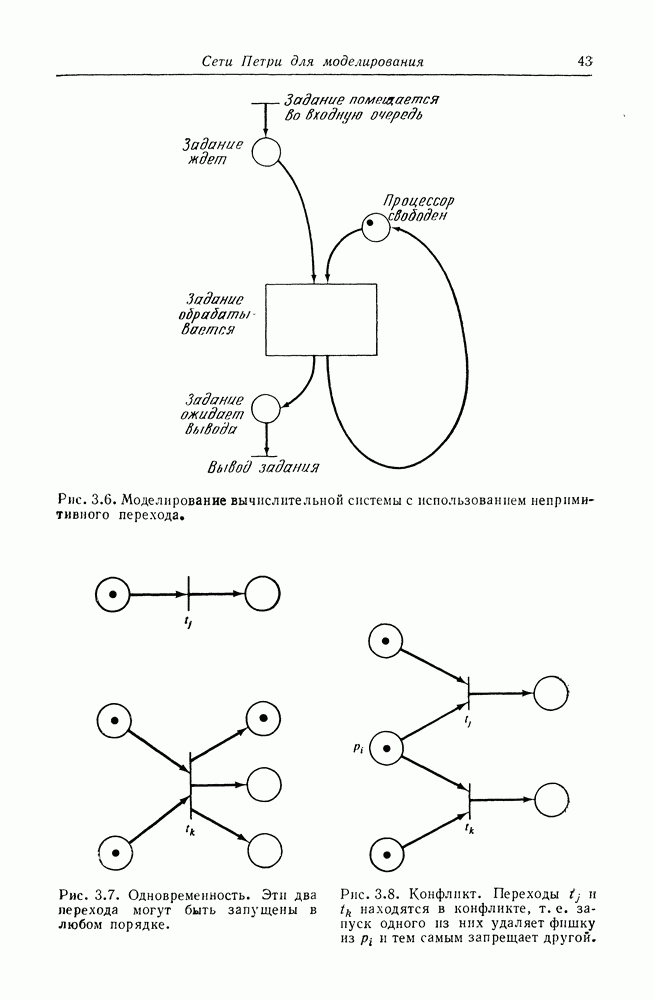
- 3.2. Одновременность и конфликт
- 3.3. Аппаратное обеспечение ЭВМ
- 3.4. Программное обеспечение ЭВМ
- 3.5. Другие системы
- ГЛАВА 4. АНАЛИЗ СЕТЕЙ ПЕТРИ
- 4.1. Задачи анализа сетей Петри
- 4.2. Методы анализа
- ГЛАВА 5. СЛОЖНОСТЬ И РАЗРЕШИМОСТЬ
- 5.1. Сводимость задач анализа
- 5.2. Задачи достижимости
- 5.3. Сети Петри с ограничениями
- 5.4. Активность и достижимость
- 5.5. Неразрешимые задачи
- 5.6. Сложность задачи достижимости
- ГЛАВА 6. ЯЗЫКИ СЕТЕЙ ПЕТРИ
- 6.2. Некоторые понятия теории формальных языков
- 6.3. Определения языков сетей Петри
- 6.4. Свойства языков сетей Петри
- 6.5. Свойства замкнутости
- 6.6. Языки сетей Петри и другие классы языков
- ГЛАВА 7. РАСШИРЕННЫЕ И ОГРАНИЧЕННЫЕ МОДЕЛИ СЕТЕЙ ПЕТРИ
- 7.1. Границы возможностей моделирования с помощью сетей Петри
- 7.2. Расширения
- 7.3. Расширенные сети Петри и регистровые машины
- 7.4. Подклассы сетей Петри
- ГЛАВА 8. МОДЕЛИ ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ
- 8.2. Маркированные графы
- 8.3. Графы вычислений
- 8.4. P/V-системы
- 8.5. Системы передачи сообщений
- 8.6. Графы UCLA
- 8.7. Системы замещения и сложения векторов
- 8.8. Расширенные модели сетей Петри
- ОБЗОР ТЕОРИИ КОМПЛЕКТОВ
- АННОТИРОВАННАЯ БИБЛИОГРАФИЯ