| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.2. Задачи достижимости
Задача достижимости — одна из самых важных задач анализа сетей Петри. Она до сих пор еще не решена для различных вариаций ее определения. Были поставлены следующие четыре задачи достижимости для сети Петри  с начальной маркировкой
с начальной маркировкой 
Определение 5.3. Задача достижимости. Выполняется ли для данной 
Определение 5.4. Задача достижимости подмаркировки. Для подмножества  и маркировки
и маркировки  существует ли
существует ли  такая, что
такая, что  Для всех
Для всех 
Определение 5.5. Задача достижимости нуля. Выполняется ли  где
где  для всех
для всех 
Определение 5.6. Задача достижимости нуля в одной позиции. Для данной позиции  существует ли
существует ли 
Задача достижимости подмаркировки ограничивает задачу достижимости до рассмотрения только подмножества позиций, не принимая во внимание маркировки других позиций. Задача достижимости нуля выясняет, является ли достижимой частная маркировка с нулем фишек во всех позициях. Задача достижимости нуля в одной позиции выясняет, возможно ли удалить все фишки из данной позиции.
Хотя эти четыре задачи различны, все они эквивалентны. Определенные взаимосвязи очевидны сразу. Задача достижимости нуля сводится к задаче достижимости; просто в задаче достижимости устанавливается  Аналогично задача достижимости сводится к задаче достижимости подмаркировки путем установки
Аналогично задача достижимости сводится к задаче достижимости подмаркировки путем установки  Задача достижимости нуля в одной позиции сводится к задаче достижимости подмаркировки установкой
Задача достижимости нуля в одной позиции сводится к задаче достижимости подмаркировки установкой  Сложнее показать, что задача достижимости подмаркировки сводится к задаче достижимости нуля и что задача достижимости нуля
Сложнее показать, что задача достижимости подмаркировки сводится к задаче достижимости нуля и что задача достижимости нуля
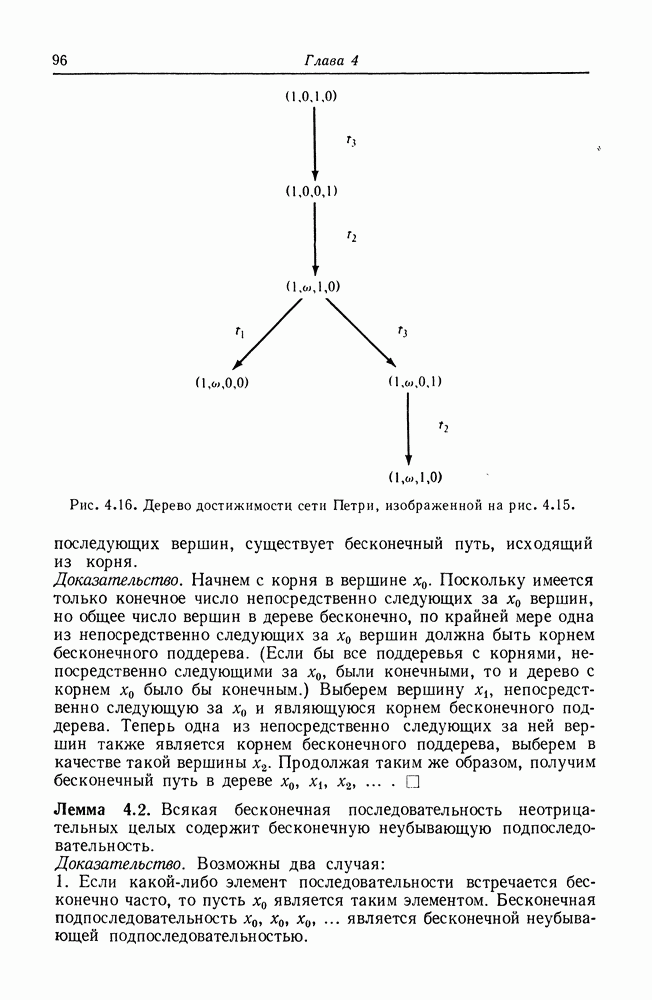
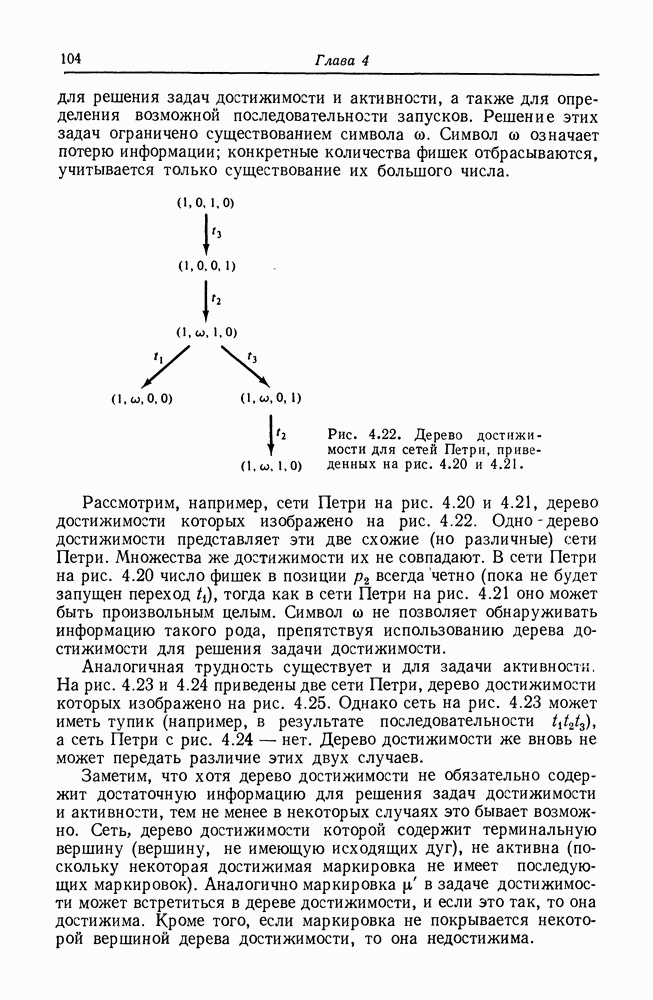
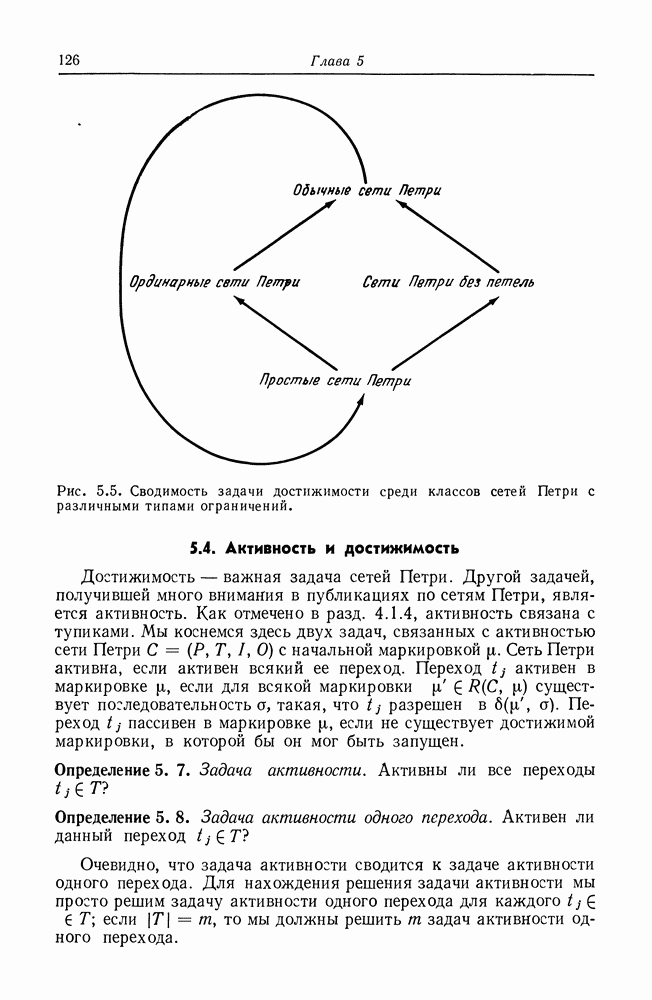
сводится к задаче достижимости нуля в одной позиции. Все множество взаимосвязей представлено на рис. 5.1.
Сначала покажем, что задача достижимости подмаркировки сводится к задаче достижимости нуля. Пусть даны сеть Петри  с начальной маркировкой
с начальной маркировкой  подмножество
подмножество  и маркировка
и маркировка  Мы хотим узнать, существует ли
Мы хотим узнать, существует ли  Для всех
Для всех 

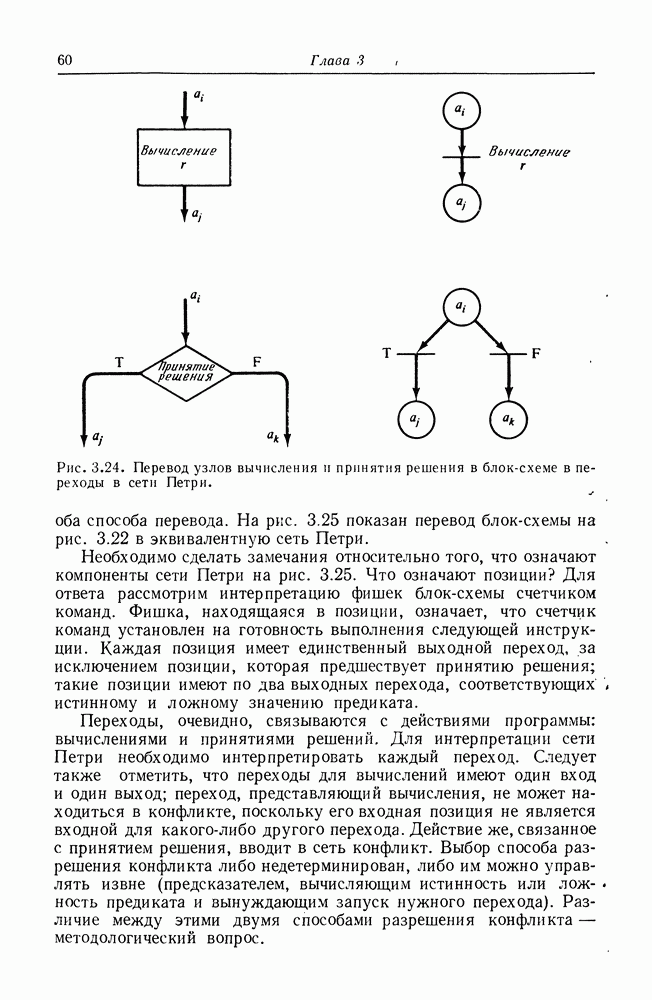
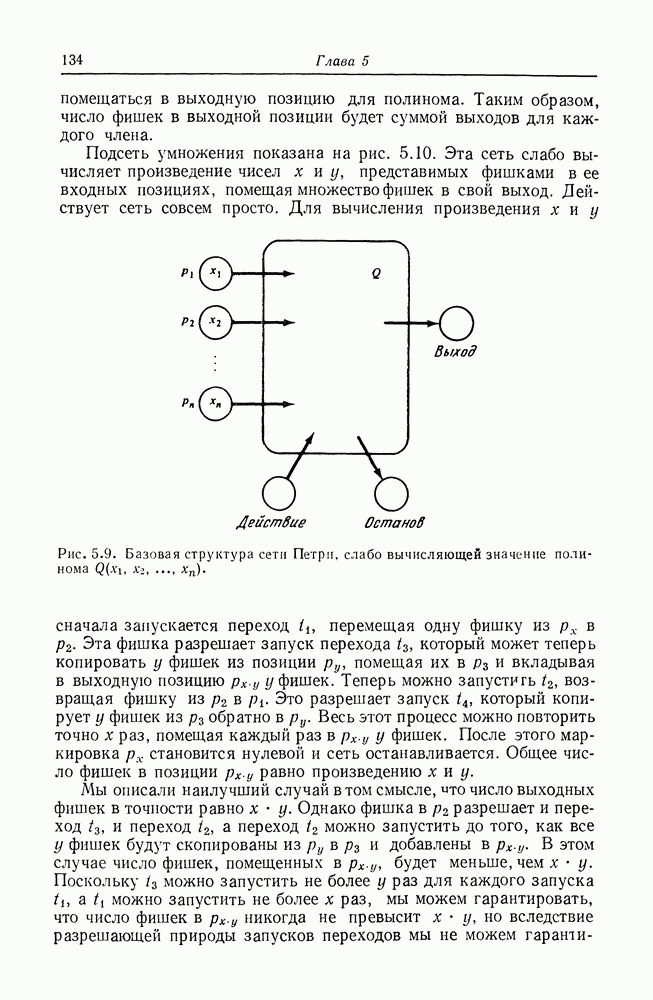
Рис. 5.1. Сводимость задач достижимости. Дуга от одной задачи к другой означает, что первая сводится ко второй.
Наш подход заключается в построении новой сети Петри  с начальной маркировкой
с начальной маркировкой  такой, что маркировка
такой, что маркировка  для всех
для всех  существует тогда и только тогда, когда
существует тогда и только тогда, когда 
Построение  из
из  осуществляется исключительно просто. Начнем с 62, совпадающей с
осуществляется исключительно просто. Начнем с 62, совпадающей с  Для того чтобы позволить всякой позиции
Для того чтобы позволить всякой позиции  вне
вне  стать пустой, введем переход
стать пустой, введем переход  с входом
с входом  и пустым выходом. Этот переход можно запускать всякий раз, когда в
и пустым выходом. Этот переход можно запускать всякий раз, когда в  имеются фишки, чтобы изъять их, что позволяет достичь нулевой маркировки и тем самым игнорировать такие позиции.
имеются фишки, чтобы изъять их, что позволяет достичь нулевой маркировки и тем самым игнорировать такие позиции.
Относительно  в
в  необходимо иметь уверенность, что в
необходимо иметь уверенность, что в  точно
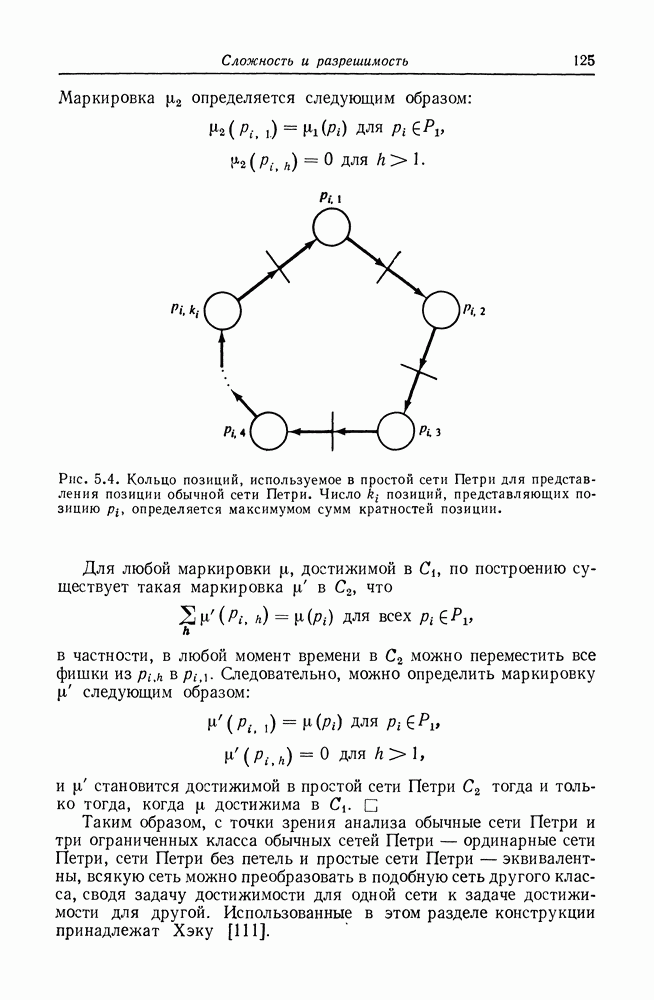
точно  фишек. Для этого построим новые позиции
фишек. Для этого построим новые позиции  для каждой
для каждой  с начальной маркировкой
с начальной маркировкой  фишек и переход
фишек и переход  с входом
с входом  и пустым выходом. Если в
и пустым выходом. Если в  точно
точно  фишек, то этот переход можно запустить точно
фишек, то этот переход можно запустить точно  раз, сокращая маркировки
раз, сокращая маркировки  до нуля. Если число фишек в
до нуля. Если число фишек в  отлично от
отлично от  то переход
то переход  можно запустить только минимальное из двух маркировок число раз, и поэтому либо в
можно запустить только минимальное из двух маркировок число раз, и поэтому либо в  либо в
либо в  останутся фишки, препятствующие достижению нулевой маркировки.
останутся фишки, препятствующие достижению нулевой маркировки.

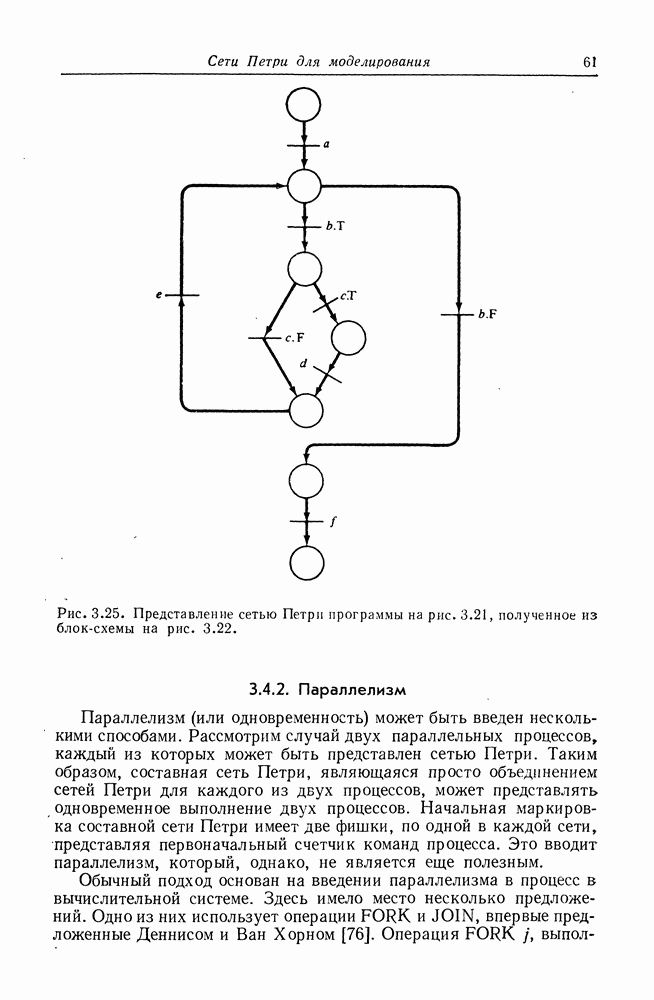
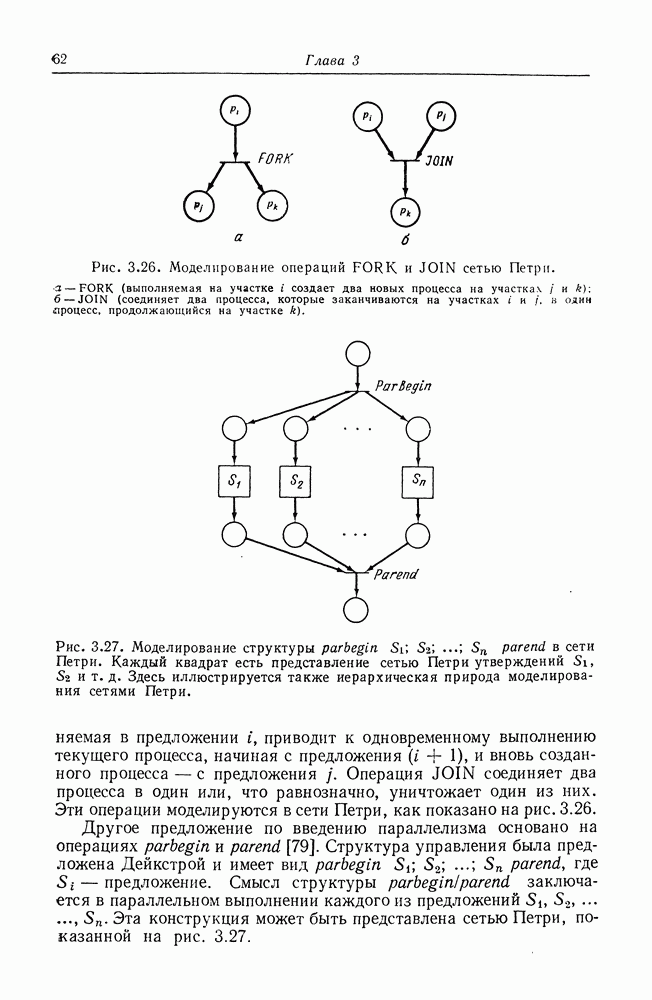
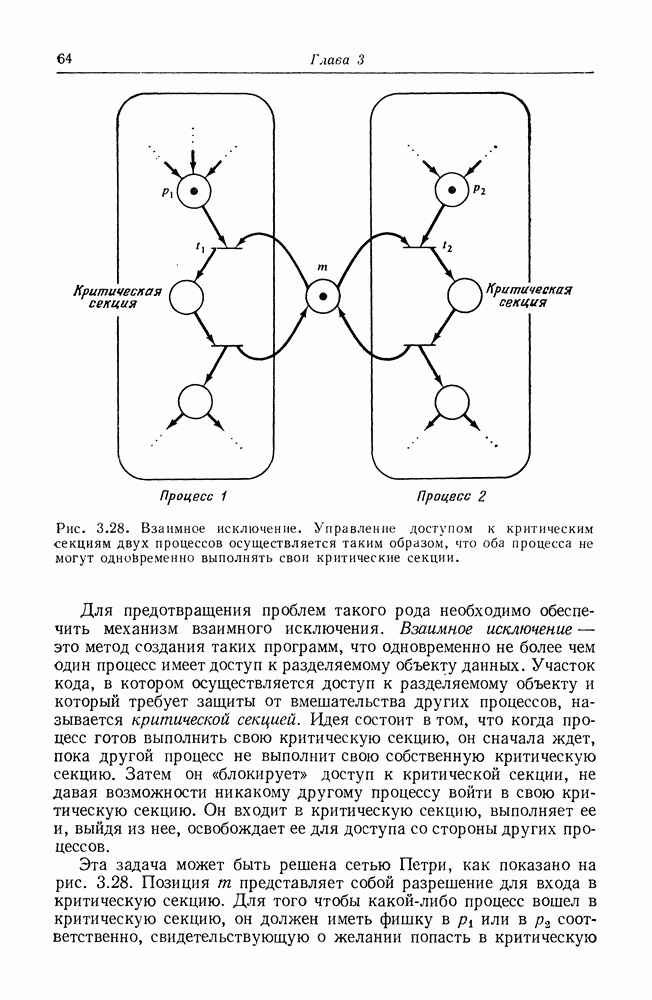
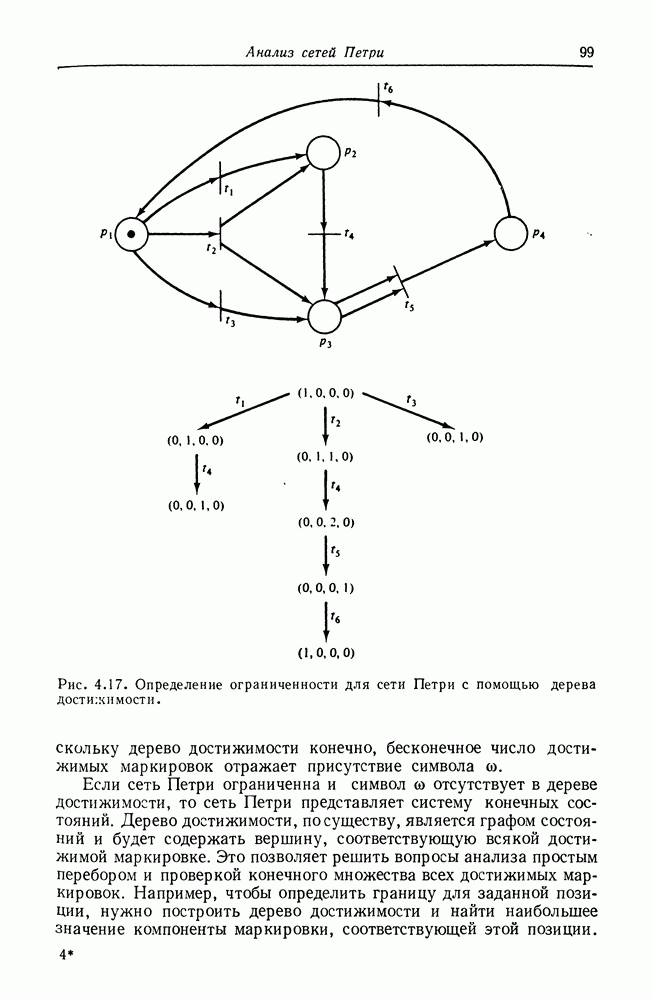
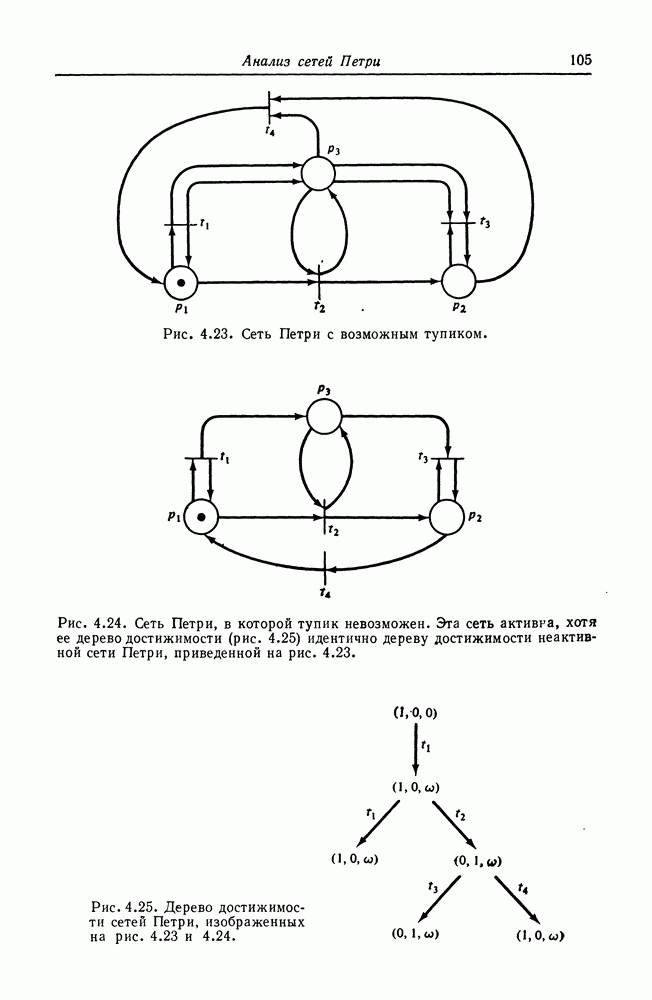
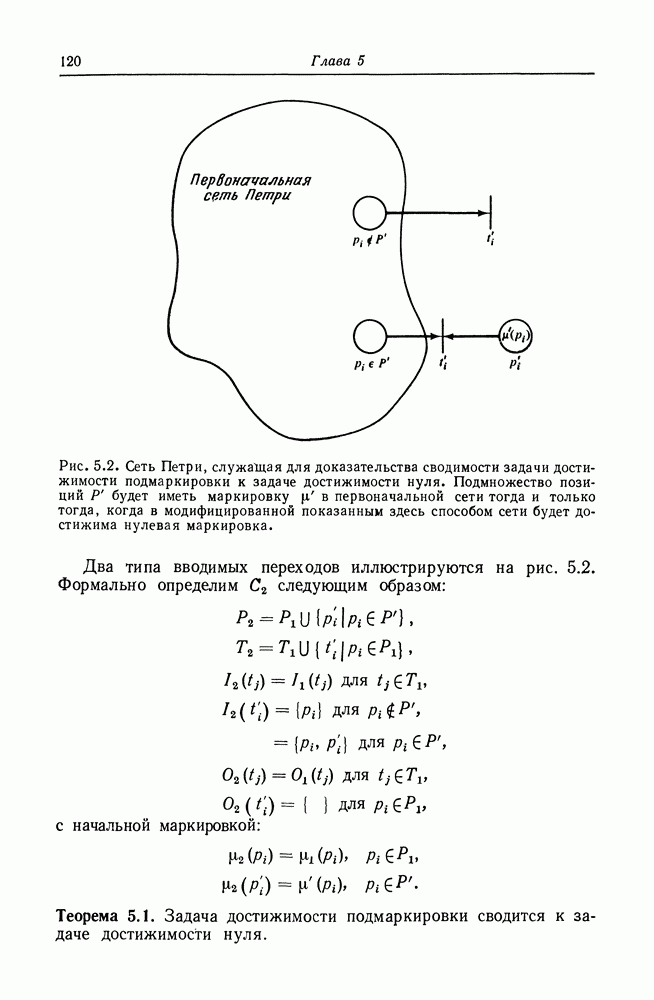
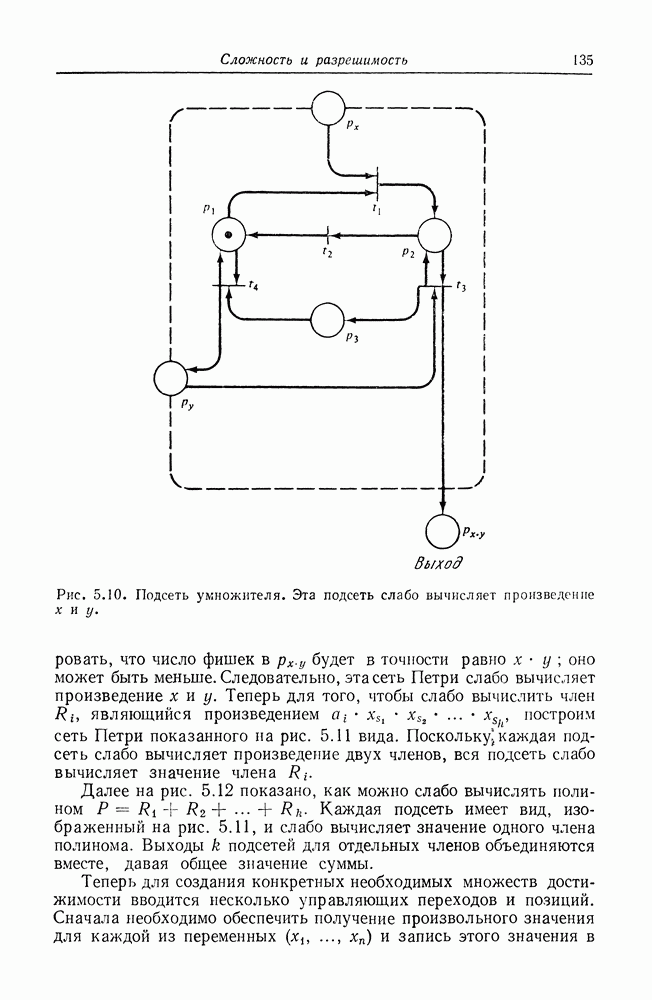
Рис. 5.2. Сеть Петри, служащая для доказательства сводимости задачи достижимости подмаркировки к задаче достижимости нуля. Подмножество позиций  будет иметь маркировку
будет иметь маркировку  в первоначальной сети тогда и только тогда, когда в модифицированной показанным здесь способом сети будет достижима нулевая маркировка.
в первоначальной сети тогда и только тогда, когда в модифицированной показанным здесь способом сети будет достижима нулевая маркировка.
Два типа вводимых переходов иллюстрируются на рис. 5.2. Формально определим  следующим образом:
следующим образом:

с начальной маркировкой:

Теорема 5.1. Задача достижимости подмаркировки сводится к задаче достижимости нуля.
Доказательство. Покажем, что для сети Петри  построенной из
построенной из  вышеописанным способом,
вышеописанным способом,  тогда и только тогда, когда
тогда и только тогда, когда  для всех
для всех 
Для того чтобы показать, что  тогда и только тогда, когда существует
тогда и только тогда, когда существует  для
для  допустим сначала, что
допустим сначала, что  присутствует в
присутствует в  . Тогда в
. Тогда в  также можно достичь маркировки
также можно достичь маркировки  в позициях
в позициях  запуском только переходов из
запуском только переходов из  Сейчас для каждой позиции
Сейчас для каждой позиции  можно запустить
можно запустить  точно
точно  раз, сокращая маркировку и
раз, сокращая маркировку и  до нуля. Затем можно запустить
до нуля. Затем можно запустить  для каждой
для каждой  столько раз, сколько необходимо для приведения маркировки этих позиций к нулю, поэтому
столько раз, сколько необходимо для приведения маркировки этих позиций к нулю, поэтому 
Теперь предположим, что  тогда существует последовательность запусков переходов
тогда существует последовательность запусков переходов  переводящая
переводящая  в 0. Эта последовательность будет содержать точно
в 0. Эта последовательность будет содержать точно  запусков
запусков  для
для  (для удаления фишек из
(для удаления фишек из  и некоторое число запусков
и некоторое число запусков  для
для  Заметим, что запуски этих переходов только удаляют фишки из
Заметим, что запуски этих переходов только удаляют фишки из  и поскольку
и поскольку  определено там, где определено
определено там, где определено  для
для  (лишние фишки не могут повредить запуску переходов), последовательность
(лишние фишки не могут повредить запуску переходов), последовательность  после удаления из нее всех запусков
после удаления из нее всех запусков  останется действительной и будет приводить к маркировке
останется действительной и будет приводить к маркировке  с точно
с точно  фишками в
фишками в  для
для  Таким образом, если
Таким образом, если  то
то  для
для 
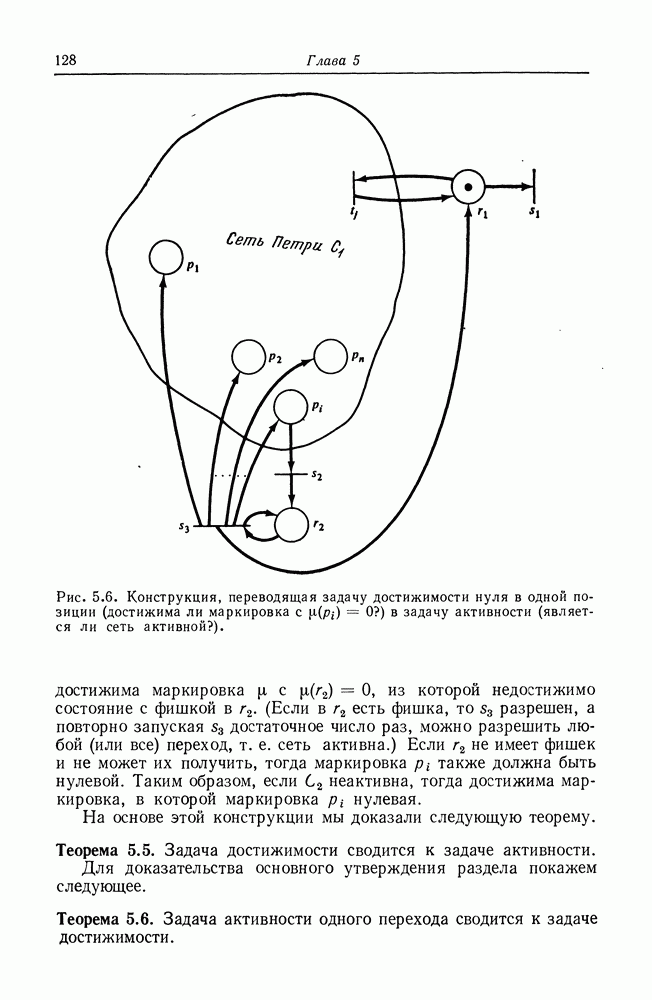
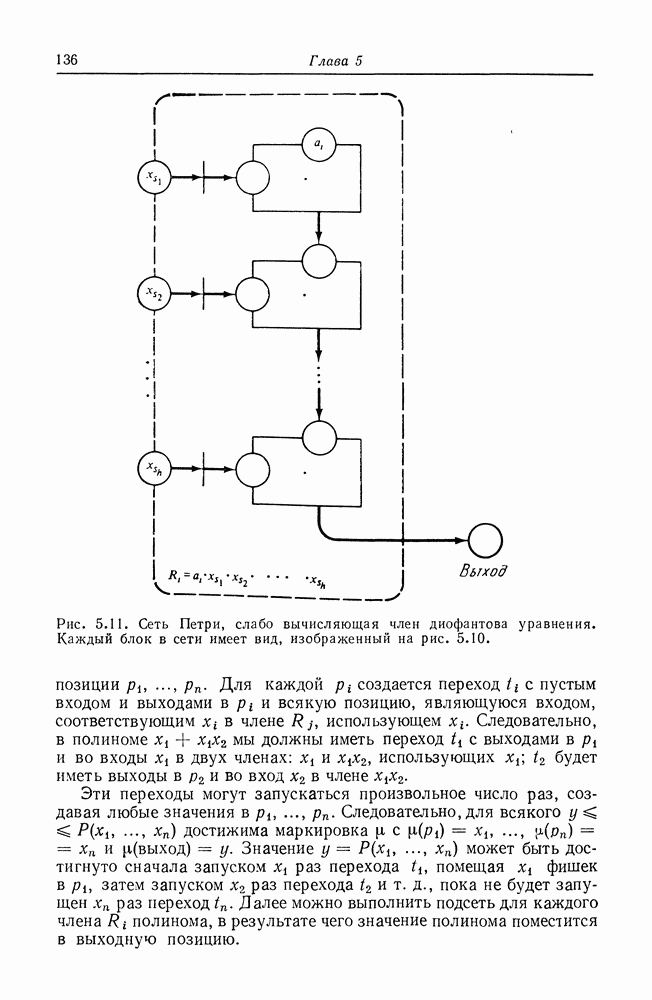
Наша следующая задача — показать, что задача достижимости нуля сводится к задаче достижимости нуля в одной позиции. Доказательство этого утверждения также основано на вспомогательном построении. Пусть дана сеть Петри  с начальной маркировкой
с начальной маркировкой  мы хотим определить, выполняется ли
мы хотим определить, выполняется ли  Построим из
Построим из  новую сеть Петри
новую сеть Петри  с дополнительной позицией
с дополнительной позицией  такой, что маркировка
такой, что маркировка  существует тогда и только тогда, когда
существует тогда и только тогда, когда 
Построение  определяет
определяет  так, что всякий раз число фишек в
так, что всякий раз число фишек в  равно сумме числа фишек в позициях
равно сумме числа фишек в позициях  Следовательно, если
Следовательно, если  то в позициях
то в позициях  нет фишек, и наоборот. Определим начальную маркировку
нет фишек, и наоборот. Определим начальную маркировку  следующим образом:
следующим образом:

Далее для каждого перехода  будет тот же переход, но с добавленными дугами к позиции
будет тот же переход, но с добавленными дугами к позиции  Определим
Определим

Тогда  это разность числа фишек после запуска перехода
это разность числа фишек после запуска перехода  и числа фишек до запуска
и числа фишек до запуска  Теперь, если
Теперь, если  то
то  фишек должно быть добавлено в позицию
фишек должно быть добавлено в позицию  поэтому введем
поэтому введем  дуг из
дуг из  если
если  то удалим
то удалим  фишек из
фишек из  введением
введением  дуг из
дуг из 
Если  то
то 
Если  , то
, то 
Если  , то
, то 
При таком построении любая последовательность запусков переходов, приводящая к маркировке 0, приведет  к маркировке
к маркировке  (а также
(а также  и наоборот.
и наоборот.
Теорема 5.2. Задача достижимости нуля сводится к задаче достижимости нуля в одной позиции.
Доказательство. Формальное доказательство, основанное на описанной конструкции, оставляем читателю. 
На основе этих двух теорем и очевидных выводов можно заключить следующее:
Теорема 5.3. Следующие задачи достижимости эквивалентны:
1. Задача достижимости.
2. Задача достижимости нуля.
3. Задача достижимости подмаркировки.
4. Задача достижимости нуля в одной позиции.
Эти теоремы и их доказательства принадлежат главным образом Хэку [116].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ГЛАВА 1. ВВЕДЕНИЕ
- ГЛАВА 2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
- 2.1. Структура сети Петри
- 2.2. Графы сетей Петри
- 2.3. Маркировка сетей Петри
- 2.4. Правила выполнения сетей Петри
- 2.5. Пространство состояний сети Петри
- 2.6. Альтернативные формы определения сетей Петри
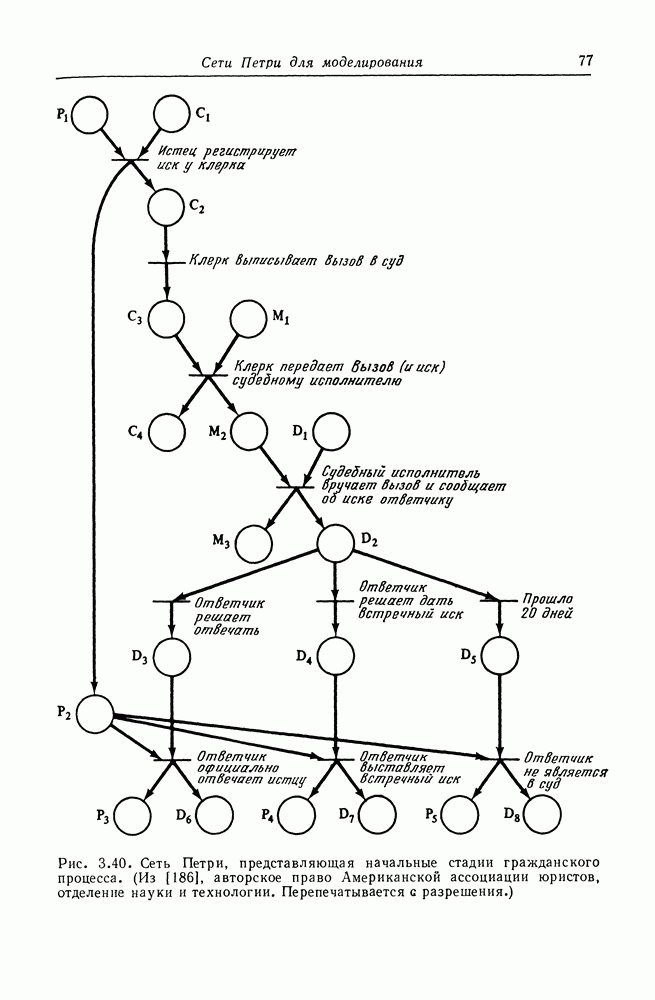
- ГЛАВА 3. СЕТИ ПЕТРИ ДЛЯ МОДЕЛИРОВАНИЯ
- 3.2. Одновременность и конфликт
- 3.3. Аппаратное обеспечение ЭВМ
- 3.4. Программное обеспечение ЭВМ
- 3.5. Другие системы
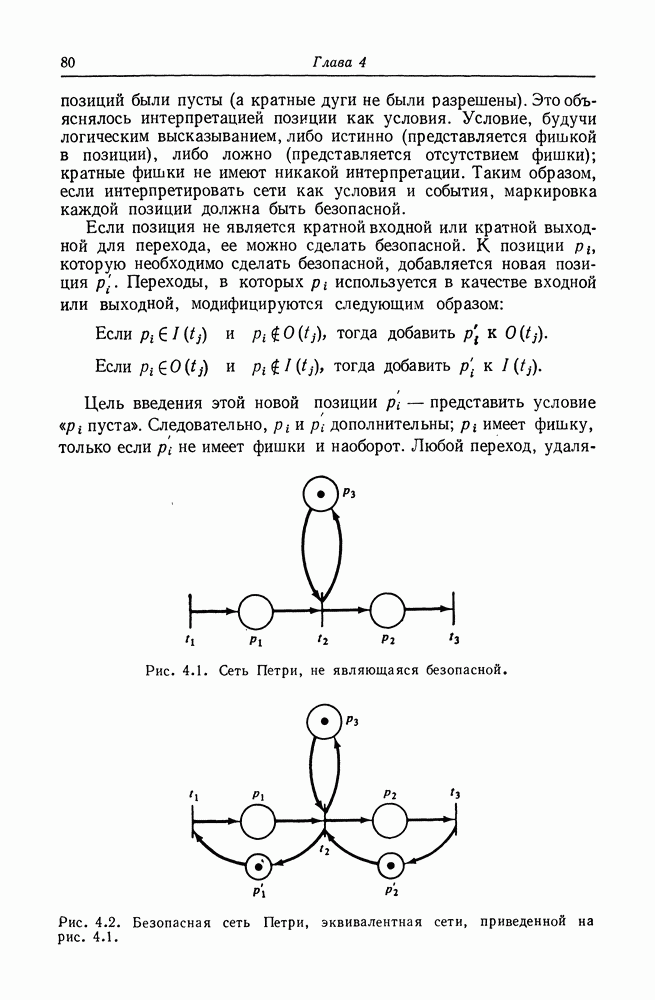
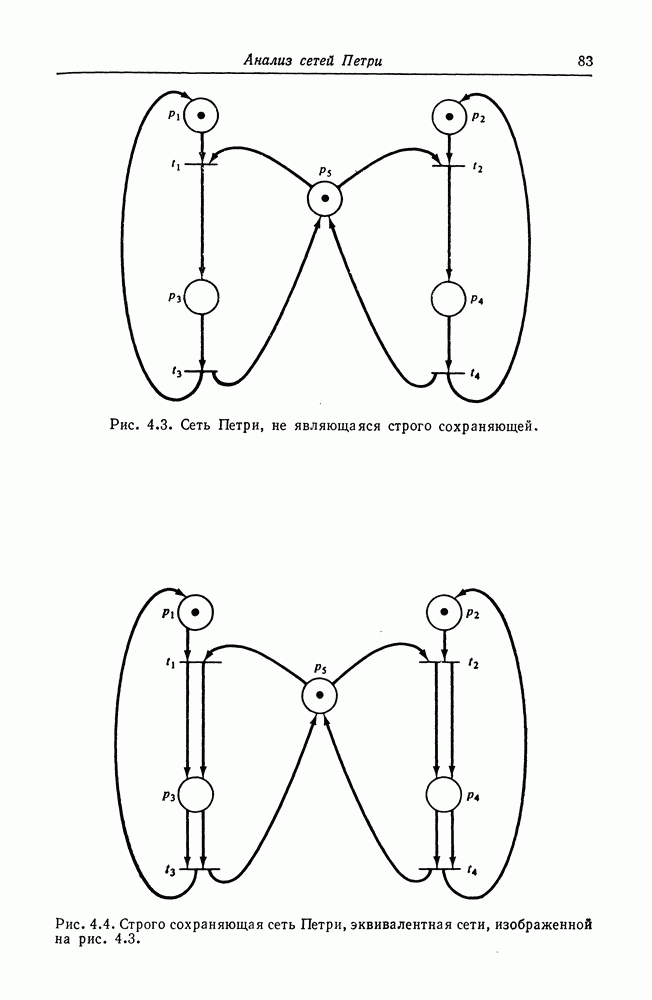
- ГЛАВА 4. АНАЛИЗ СЕТЕЙ ПЕТРИ
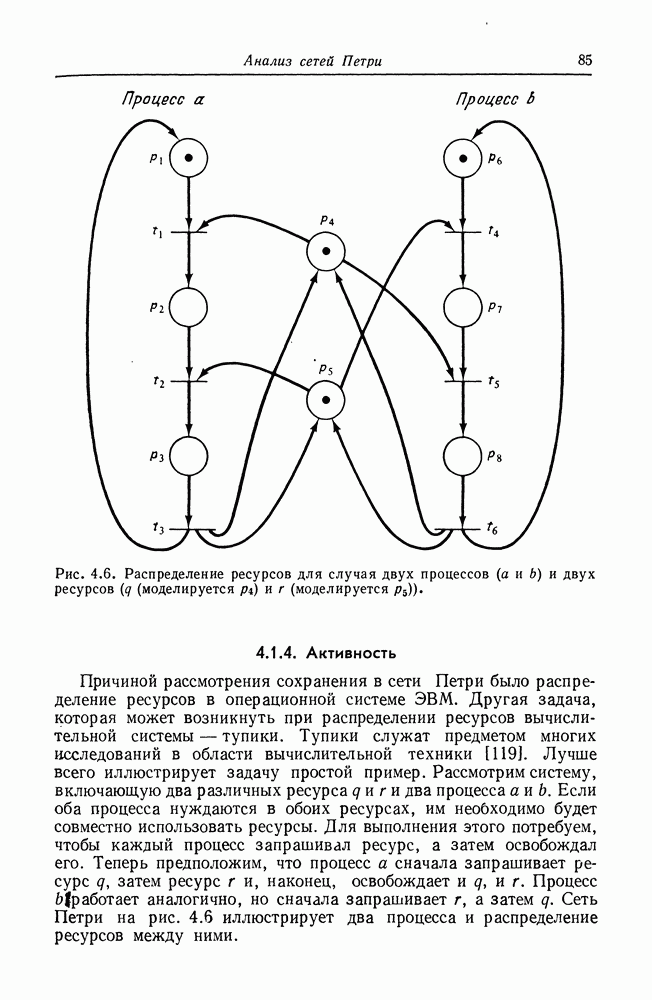
- 4.1. Задачи анализа сетей Петри
- 4.2. Методы анализа
- ГЛАВА 5. СЛОЖНОСТЬ И РАЗРЕШИМОСТЬ
- 5.1. Сводимость задач анализа
- 5.2. Задачи достижимости
- 5.3. Сети Петри с ограничениями
- 5.4. Активность и достижимость
- 5.5. Неразрешимые задачи
- 5.6. Сложность задачи достижимости
- ГЛАВА 6. ЯЗЫКИ СЕТЕЙ ПЕТРИ
- 6.2. Некоторые понятия теории формальных языков
- 6.3. Определения языков сетей Петри
- 6.4. Свойства языков сетей Петри
- 6.5. Свойства замкнутости
- 6.6. Языки сетей Петри и другие классы языков
- ГЛАВА 7. РАСШИРЕННЫЕ И ОГРАНИЧЕННЫЕ МОДЕЛИ СЕТЕЙ ПЕТРИ
- 7.1. Границы возможностей моделирования с помощью сетей Петри
- 7.2. Расширения
- 7.3. Расширенные сети Петри и регистровые машины
- 7.4. Подклассы сетей Петри
- ГЛАВА 8. МОДЕЛИ ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ
- 8.2. Маркированные графы
- 8.3. Графы вычислений
- 8.4. P/V-системы
- 8.5. Системы передачи сообщений
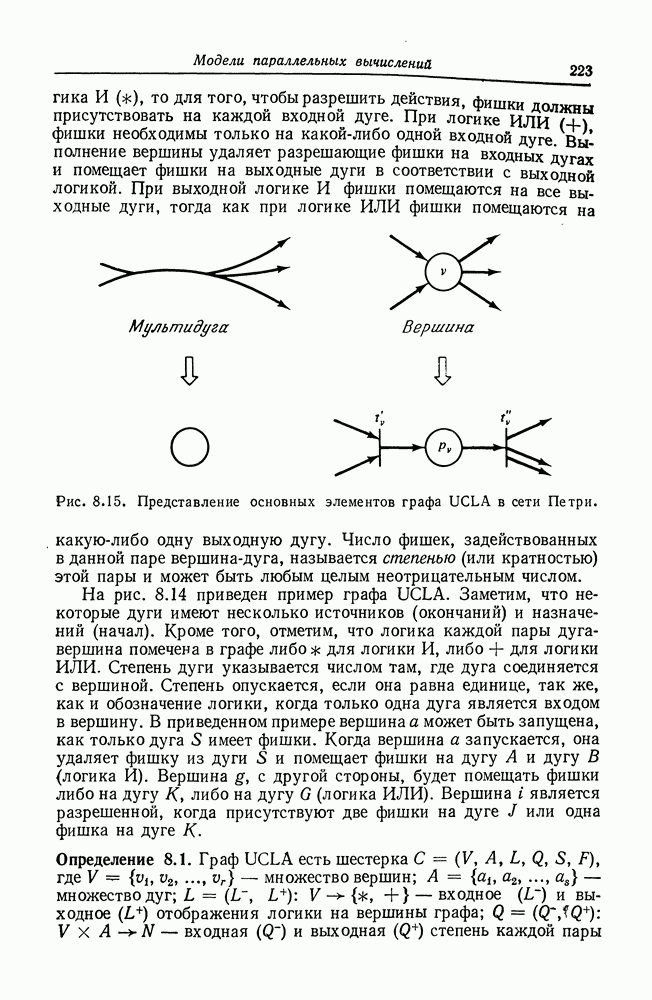
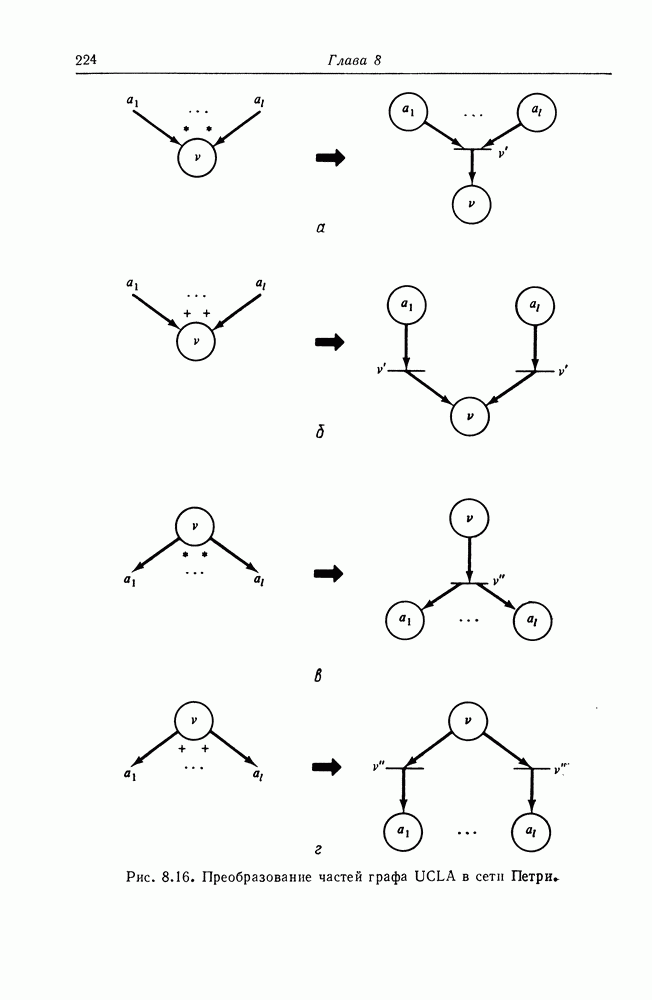
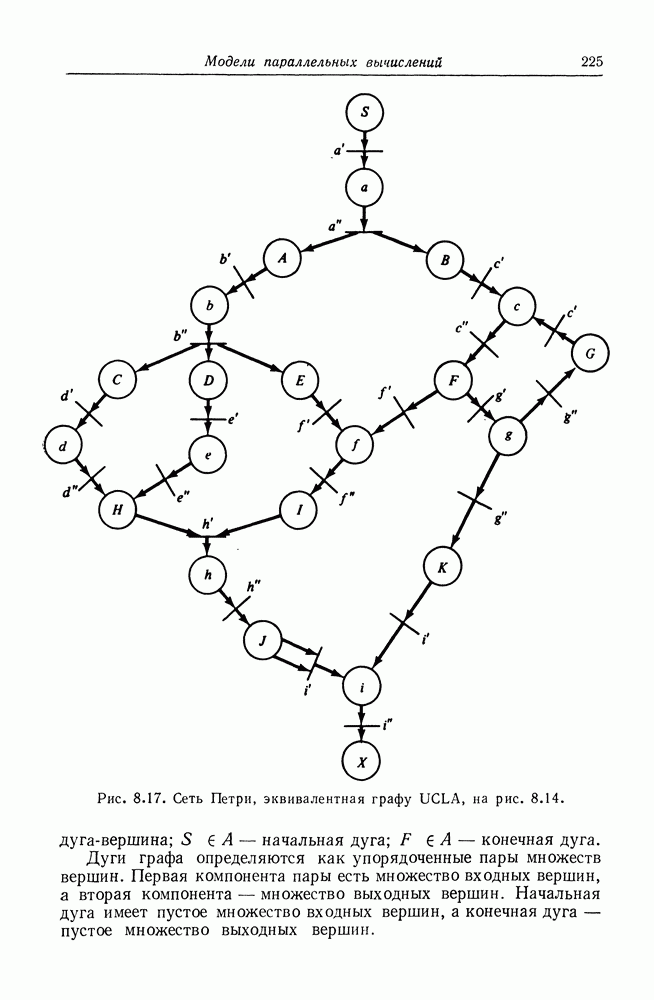
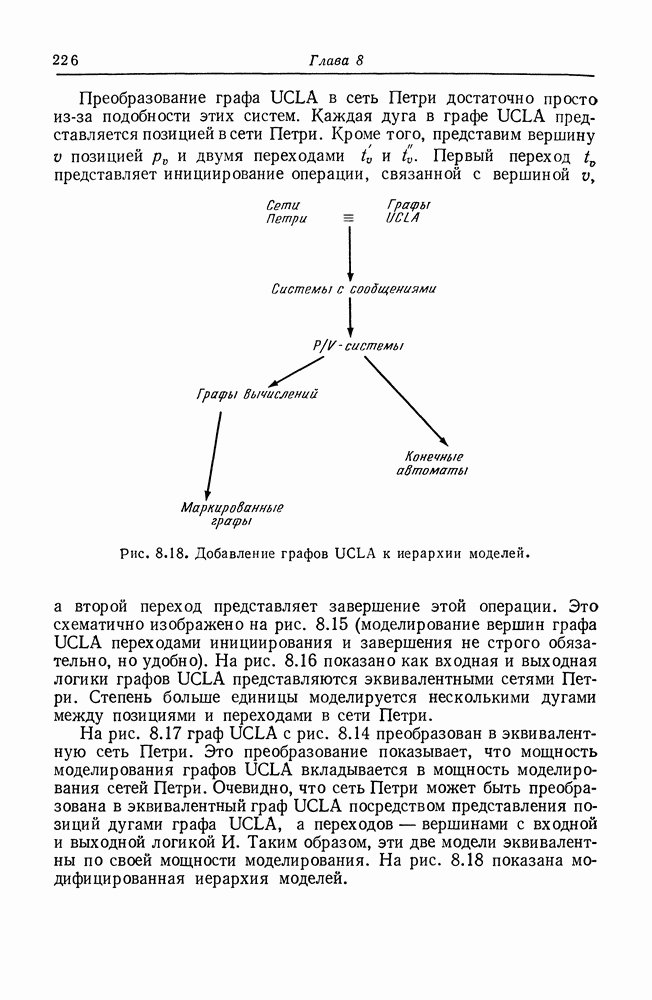
- 8.6. Графы UCLA
- 8.7. Системы замещения и сложения векторов
- 8.8. Расширенные модели сетей Петри
- ОБЗОР ТЕОРИИ КОМПЛЕКТОВ
- АННОТИРОВАННАЯ БИБЛИОГРАФИЯ