| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.3. Сети Петри с ограничениями
В первых работах по сетям Петри, а также в некоторых современных работах сети Петри определяются в несколько более ограниченной форме, чем в определении, данном в гл. 2. В частности, иногда принимаются следующие два ограничения:
Ограничение 5.1. Кратность любой позиции равна  или 1. Иначе говоря,
или 1. Иначе говоря,  для всех
для всех  Это ограничивает входные и выходные комплекты до множеств.
Это ограничивает входные и выходные комплекты до множеств.
Ограничение 5.2. Никакая позиция не может быть одновременно входом и выходом одного и того же перехода.  Это часто формулируется как
Это часто формулируется как  для всех
для всех 
Сети Петри, удовлетворяющие ограничению 5.1, называются ординарными. Сети Петри, удовлетворяющие ограничению 5.2, называются сетями Петри без петель, или нерефлексивными сетями. Сети Петри, удовлетворяющие обоим ограничениям,
называются простыми сетями Петри. Эти классы сетей Петри соотносятся так, как показано на рис. 5.3.
Подклассы модели обычных сетей Петри рассматривались по нескольким причинам. Основная причина заключается в том, что введение понятий сетей Петри в начале развития теории было неформальным. Необходимость в кратных дугах и петлях при моделировании тогда отсутствовала.

Рис. 5.3. Взаимосвязи между классами сетей Петри. Дуга означает включение; дуги сводимости будут ориентированы в противоположном направлении.
Кроме того, вероятно, казалось, что теория без этих усложнений будет проще. По мере развития теории стало ясно, что работать с более общими определениями не труднее. Использование моделей с этими ограничениями в современных работах объясняется стремлением исследователя к более простому и лаконичному изложению.
Однако эти ограничения не добавляют ничего к способности анализировать сети Петри. Рассмотрим для этих классов сетей задачу достижимости. Для того чтобы показать эквивалентность всех четырех классов сетей Петри, докажем следующее:
Теорема 5.4. Задача достижимости эквивалентна для следующих классов сетей Петри:
1. Обычные сети Петри.
2. Ординарные сети Петри.
3. Сети Петри без петель.
4. Простые сети Петри.
Доказательство. Из определений очевидны следующие сведения:
1. Задача достижимости для ординарных сетей Петри сводится к задаче достижимости для обычных сетей Петри.
2. Задача достижимости для сетей Петри без петель сводится к задаче достижимости для обычных сетей Петри.
3. Задача достижимости для простых сетей Петри сводится и к задаче достижимости для ординарных сетей Петри, и к задаче достижимости для сетей Петри без петель.
Покажем, что обычные сети Петри можно преобразовать в простые сети Петри таким образом, чтобы свести задачу достижимости для обычных сетей Петри к задаче достижимости для простых сетей Петри. Это покажет, что все четыре задачи достижимости эквивалентны.
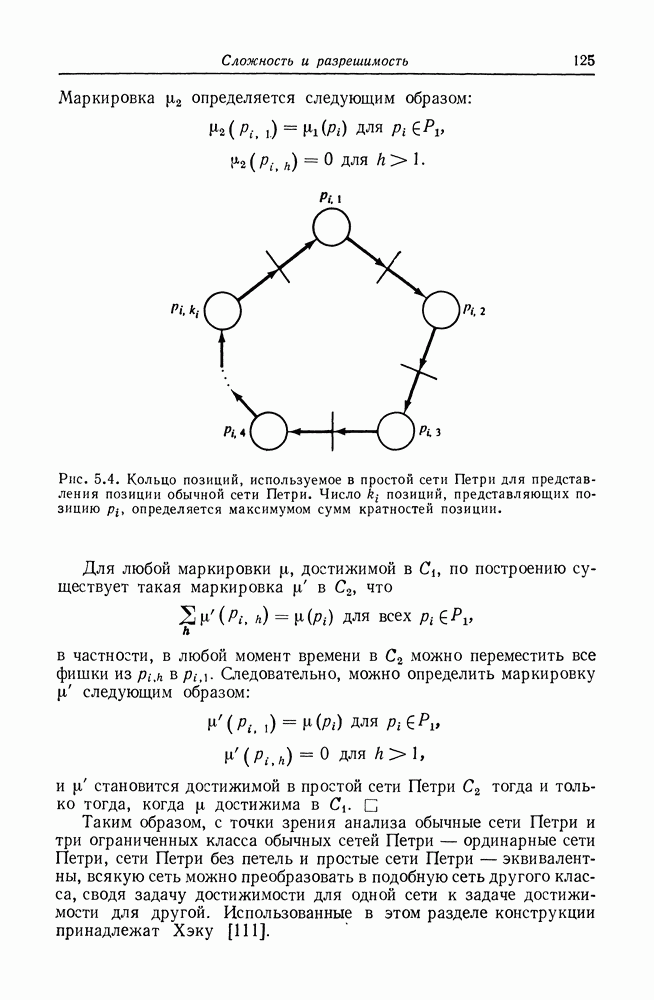
Для преобразования обычной сети Петри в простую сеть Петри используем следующий подход. Каждая позиция в обычной сети Петри заменяется кольцом позиций в простой сети Петри. На рис. 5.4 показан общий вид кольца позиций. Заметим, что набор фишек, помещенных в кольцо, может свободно двигаться по кольцу к любой позиции в любой момент времени; все они могут сгруппироваться в позиции  или равномерно распределиться, покрывая все
или равномерно распределиться, покрывая все  позиций кольца. Поэтому переход, для запуска которого необходимы три фишки из позиции
позиций кольца. Поэтому переход, для запуска которого необходимы три фишки из позиции  может выбрать вместо всех трех из
может выбрать вместо всех трех из  по одной из
по одной из  Аналогично переход, использующий
Аналогично переход, использующий  в качестве входа и в качестве выхода (петля), может иметь вход в
в качестве входа и в качестве выхода (петля), может иметь вход в  а выход в
а выход в  тем самым устраняя петлю.
тем самым устраняя петлю.
Формально для обычной сети Петри  с маркировкой
с маркировкой  определим простую сеть Петри
определим простую сеть Петри  с маркировкой
с маркировкой  следующим образом. Сначала для каждой позиции
следующим образом. Сначала для каждой позиции  определим целое
определим целое 

Сеть Петри с ограничениями  определяется
определяется 

Входная и выходная функции для «нормальных» переходов определяются так, что

а для «кольцевых» переходов

Маркировка  определяется следующим образом:
определяется следующим образом:


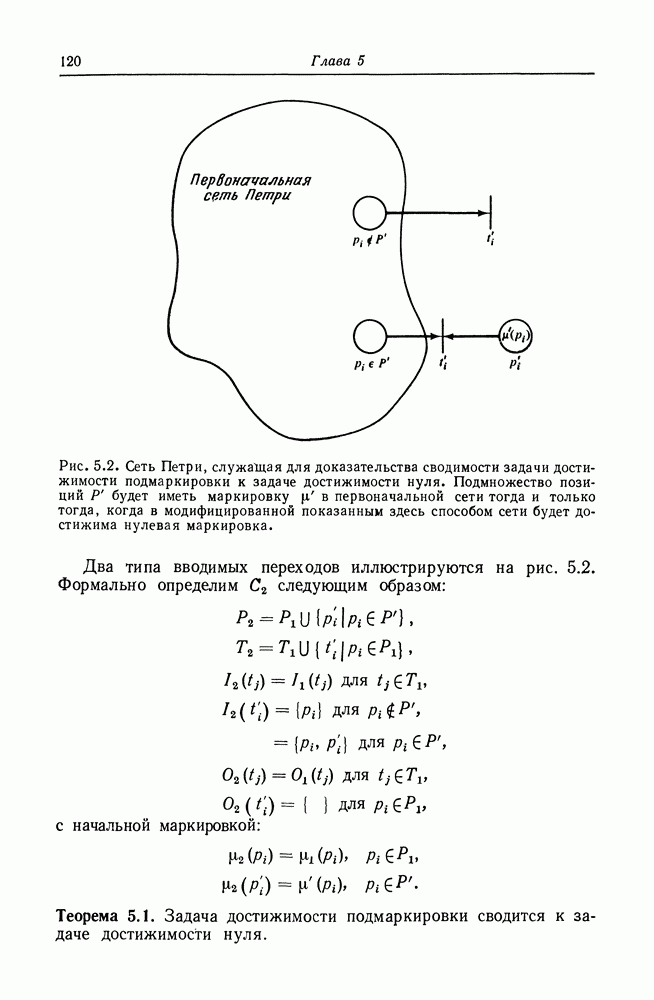
Рис. 5.4. Кольцо позиций, используемое в простой сети Петри для представления позиции обычной сети Петри. Число  позиций, представляющих позицию
позиций, представляющих позицию  определяется максимумом сумм кратностей позиции.
определяется максимумом сумм кратностей позиции.
Для любой маркировки  достижимой в
достижимой в  по построению существует такая маркировка
по построению существует такая маркировка  что
что

в частности, в любой момент времени в  можно переместить все фишки из
можно переместить все фишки из  в
в  Следовательно, можно определить маркировку
Следовательно, можно определить маркировку  следующим образом:
следующим образом:

 становится достижимой в простой сети Петри
становится достижимой в простой сети Петри  тогда и только тогда, когда
тогда и только тогда, когда  достижима в
достижима в  .
.
Таким образом, с точки зрения анализа обычные сети Петри и три ограниченных класса обычных сетей Петри — ординарные сети Петри, сети Петри без петель и простые сети Петри — эквивалентны, всякую сеть можно преобразовать в подобную сеть другого класса, сводя задачу достижимости для одной сети к задаче достижимости для другой. Использованные в этом разделе конструкции принадлежат Хэку [111].

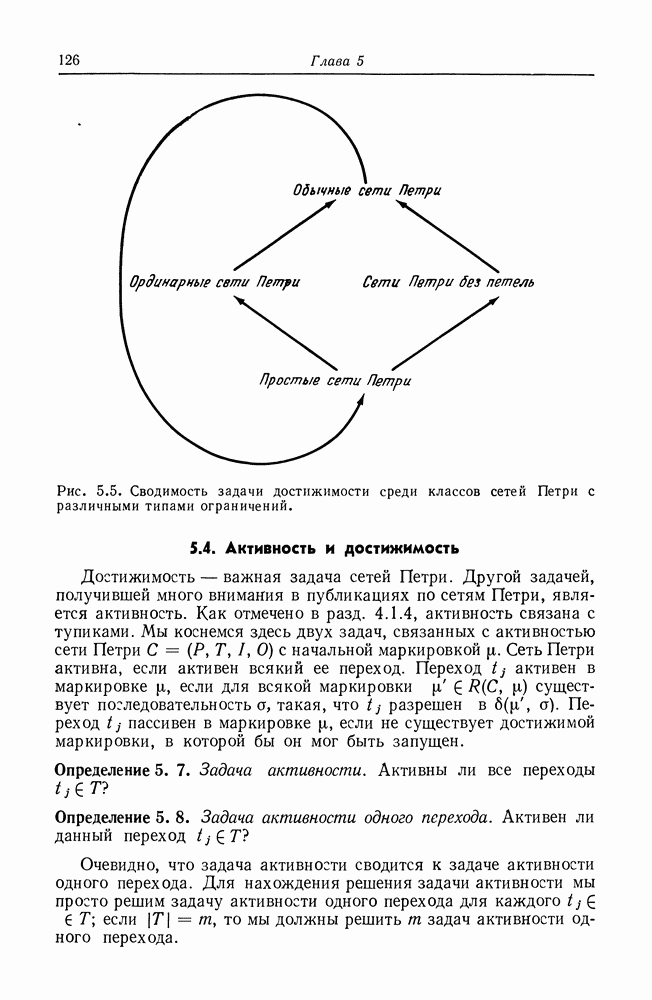
Рис. 5.5. Сводимость задачи достижимости среди классов сетей Петри с различными типами ограничений.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ГЛАВА 1. ВВЕДЕНИЕ
- ГЛАВА 2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
- 2.1. Структура сети Петри
- 2.2. Графы сетей Петри
- 2.3. Маркировка сетей Петри
- 2.4. Правила выполнения сетей Петри
- 2.5. Пространство состояний сети Петри
- 2.6. Альтернативные формы определения сетей Петри
- ГЛАВА 3. СЕТИ ПЕТРИ ДЛЯ МОДЕЛИРОВАНИЯ
- 3.2. Одновременность и конфликт
- 3.3. Аппаратное обеспечение ЭВМ
- 3.4. Программное обеспечение ЭВМ
- 3.5. Другие системы
- ГЛАВА 4. АНАЛИЗ СЕТЕЙ ПЕТРИ
- 4.1. Задачи анализа сетей Петри
- 4.2. Методы анализа
- ГЛАВА 5. СЛОЖНОСТЬ И РАЗРЕШИМОСТЬ
- 5.1. Сводимость задач анализа
- 5.2. Задачи достижимости
- 5.3. Сети Петри с ограничениями
- 5.4. Активность и достижимость
- 5.5. Неразрешимые задачи
- 5.6. Сложность задачи достижимости
- ГЛАВА 6. ЯЗЫКИ СЕТЕЙ ПЕТРИ
- 6.2. Некоторые понятия теории формальных языков
- 6.3. Определения языков сетей Петри
- 6.4. Свойства языков сетей Петри
- 6.5. Свойства замкнутости
- 6.6. Языки сетей Петри и другие классы языков
- ГЛАВА 7. РАСШИРЕННЫЕ И ОГРАНИЧЕННЫЕ МОДЕЛИ СЕТЕЙ ПЕТРИ
- 7.1. Границы возможностей моделирования с помощью сетей Петри
- 7.2. Расширения
- 7.3. Расширенные сети Петри и регистровые машины
- 7.4. Подклассы сетей Петри
- ГЛАВА 8. МОДЕЛИ ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ
- 8.2. Маркированные графы
- 8.3. Графы вычислений
- 8.4. P/V-системы
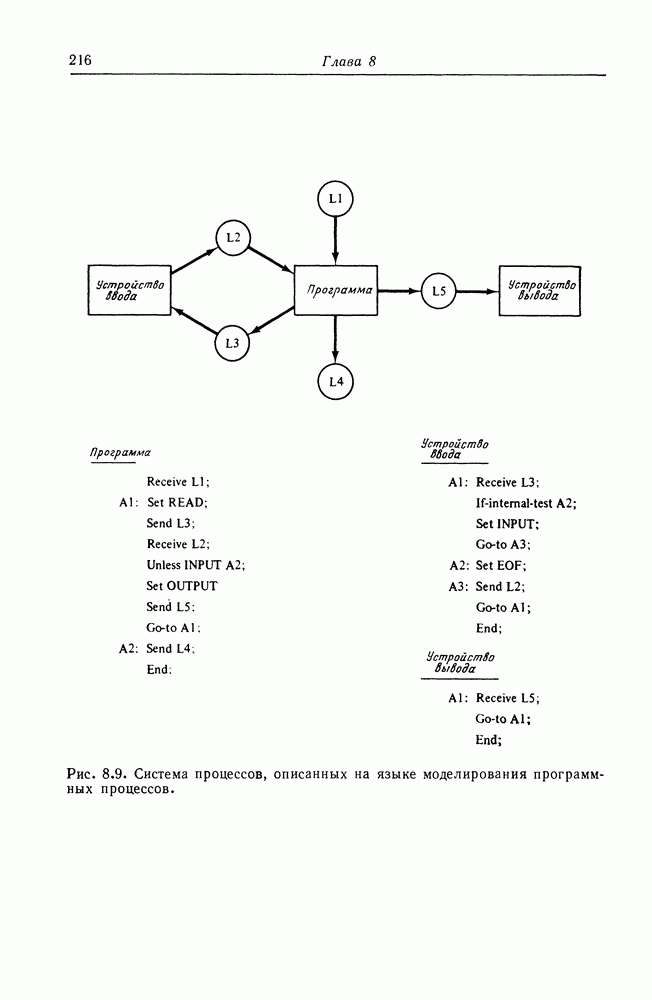
- 8.5. Системы передачи сообщений
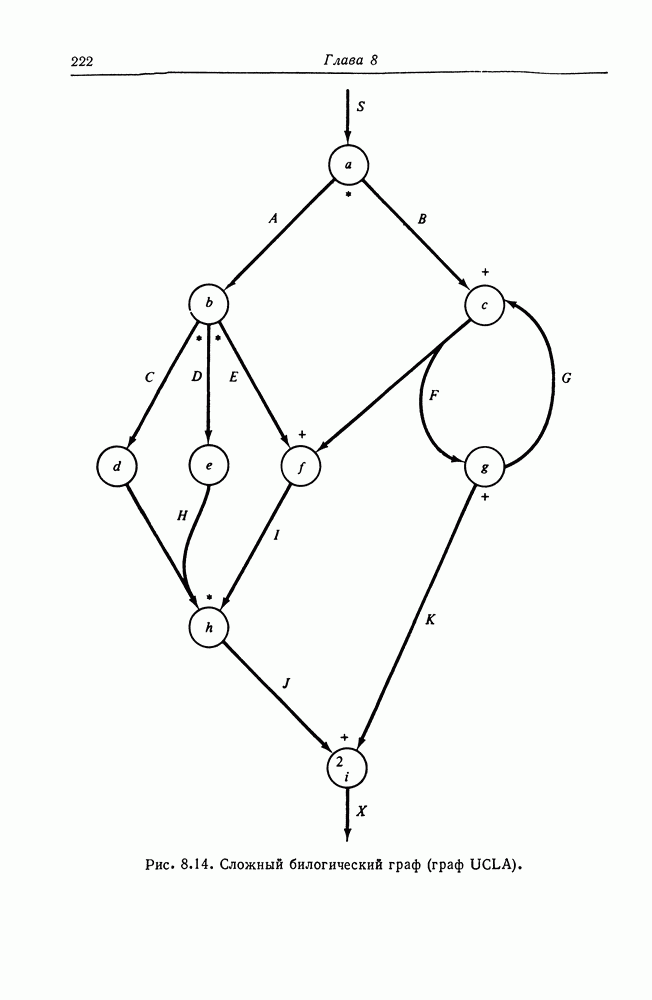
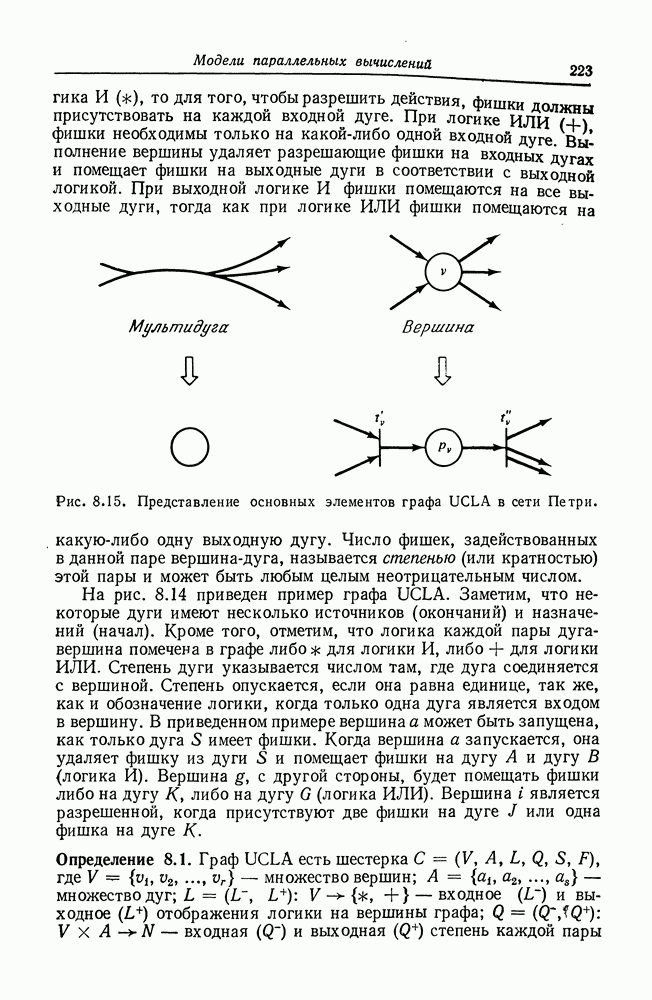
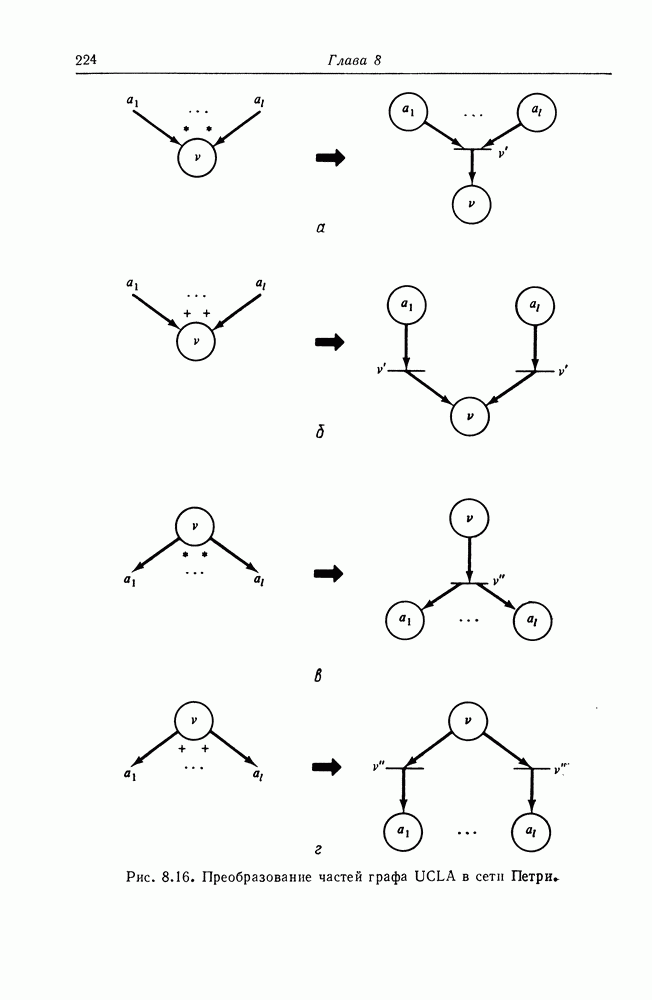
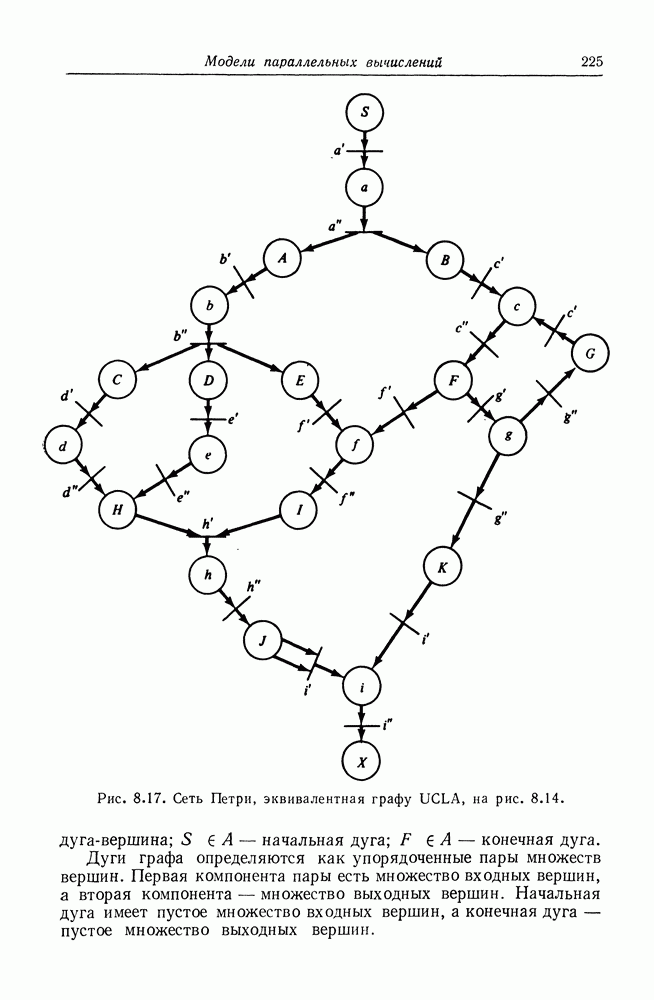
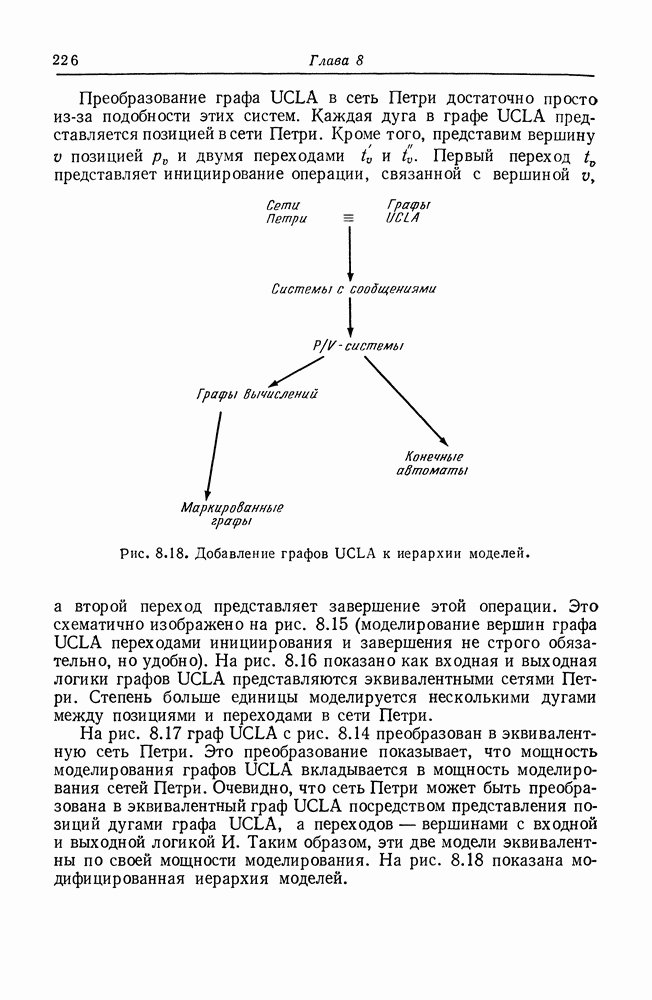
- 8.6. Графы UCLA
- 8.7. Системы замещения и сложения векторов
- 8.8. Расширенные модели сетей Петри
- ОБЗОР ТЕОРИИ КОМПЛЕКТОВ
- АННОТИРОВАННАЯ БИБЛИОГРАФИЯ