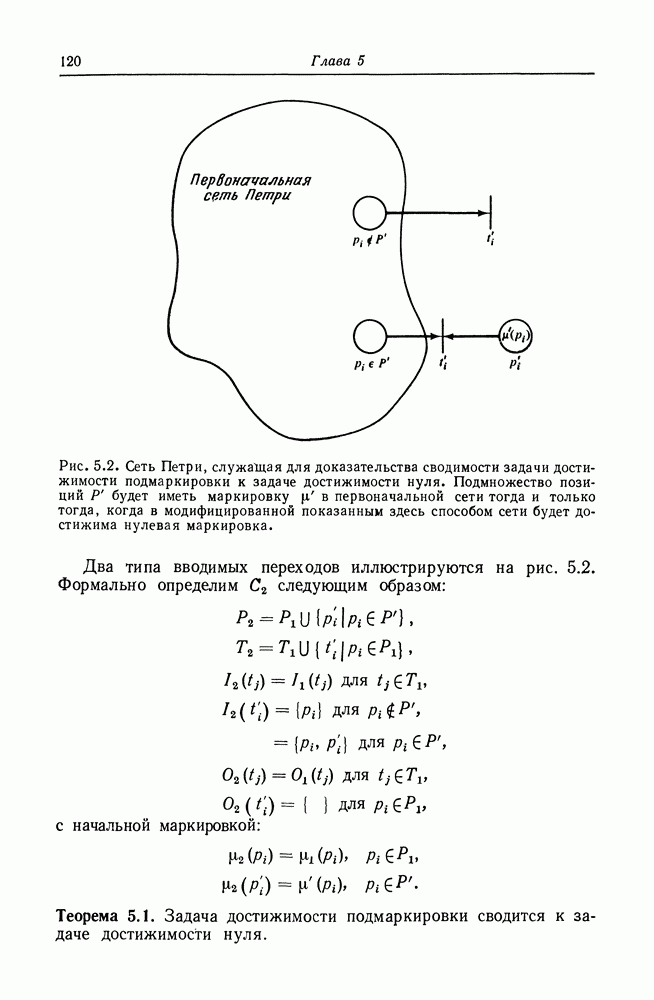
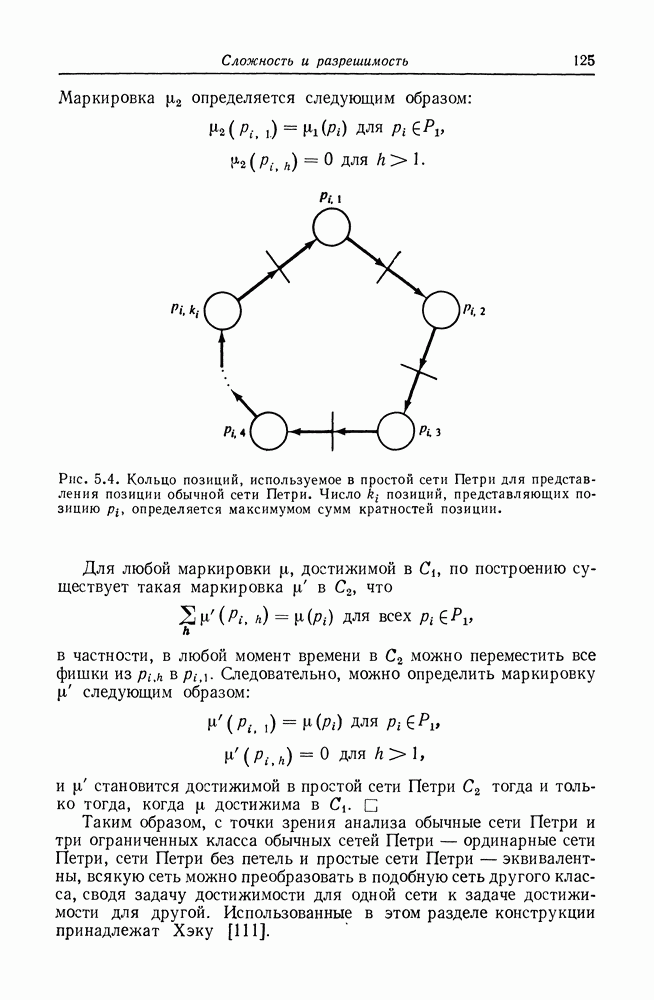
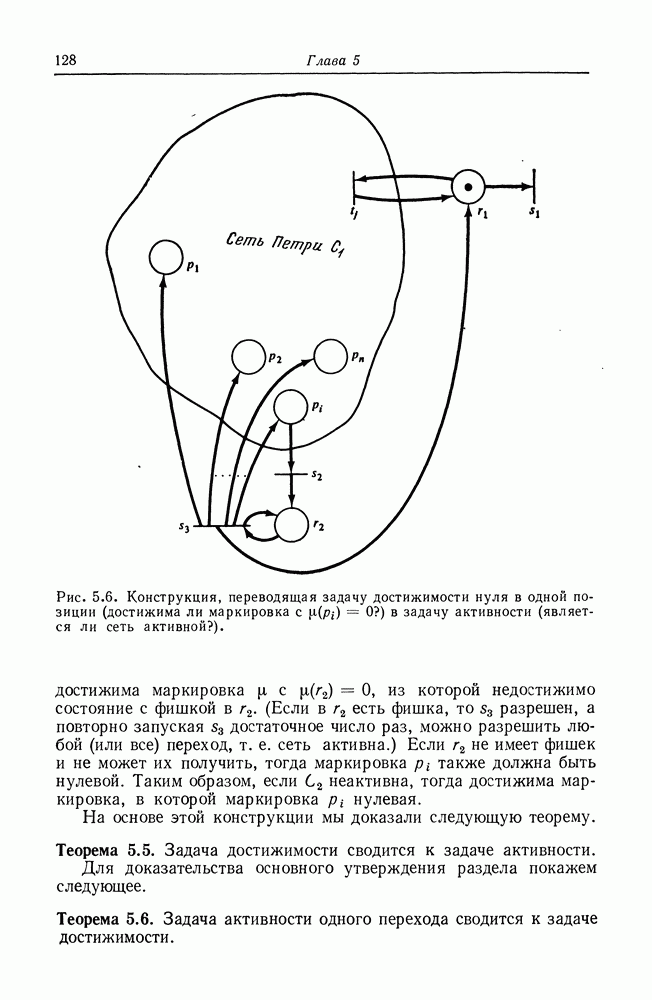
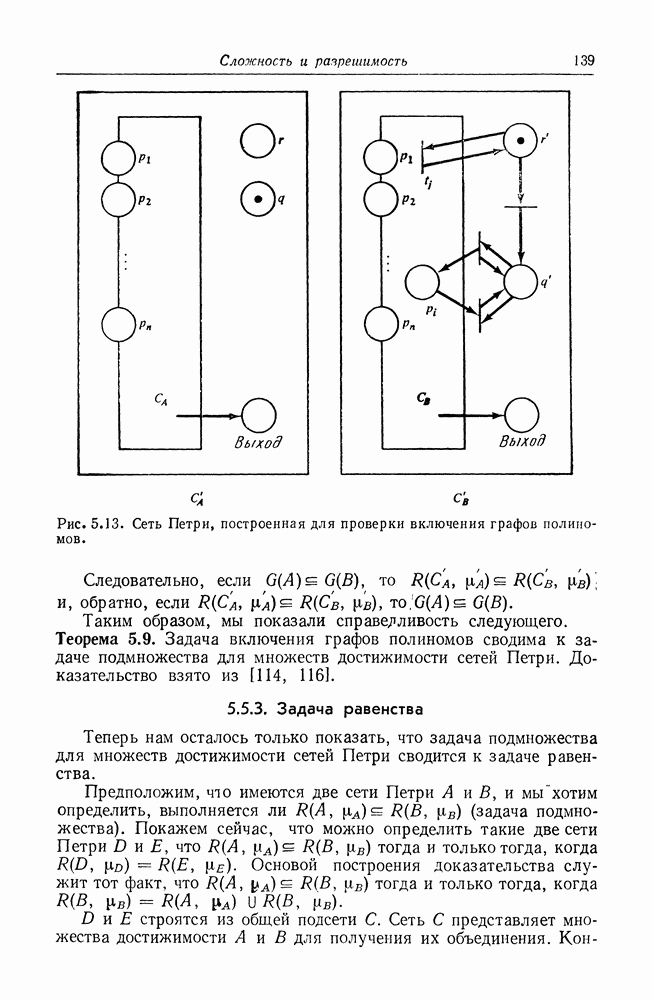
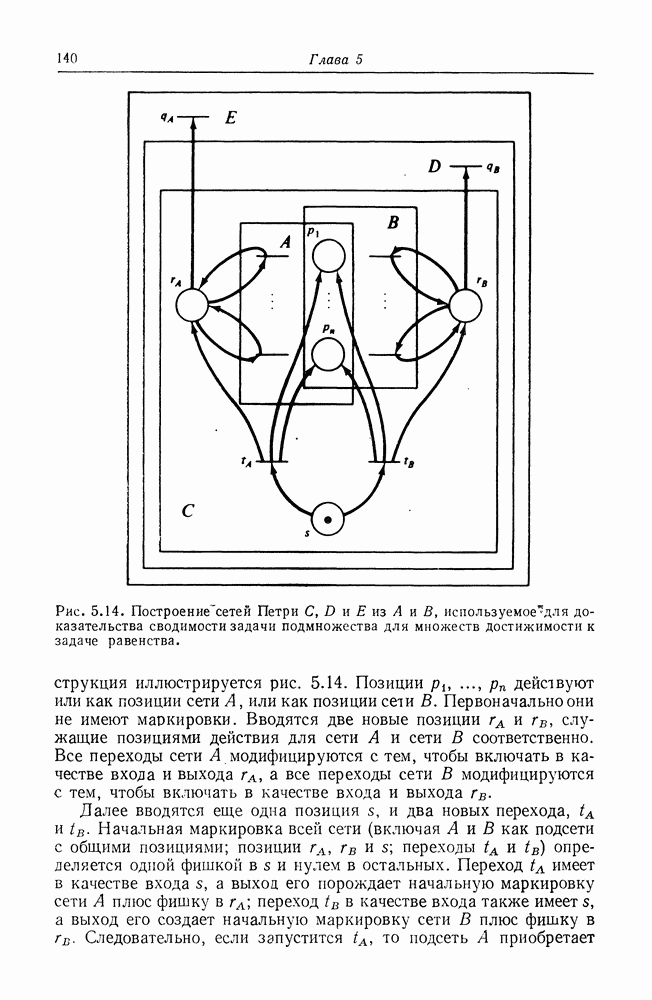
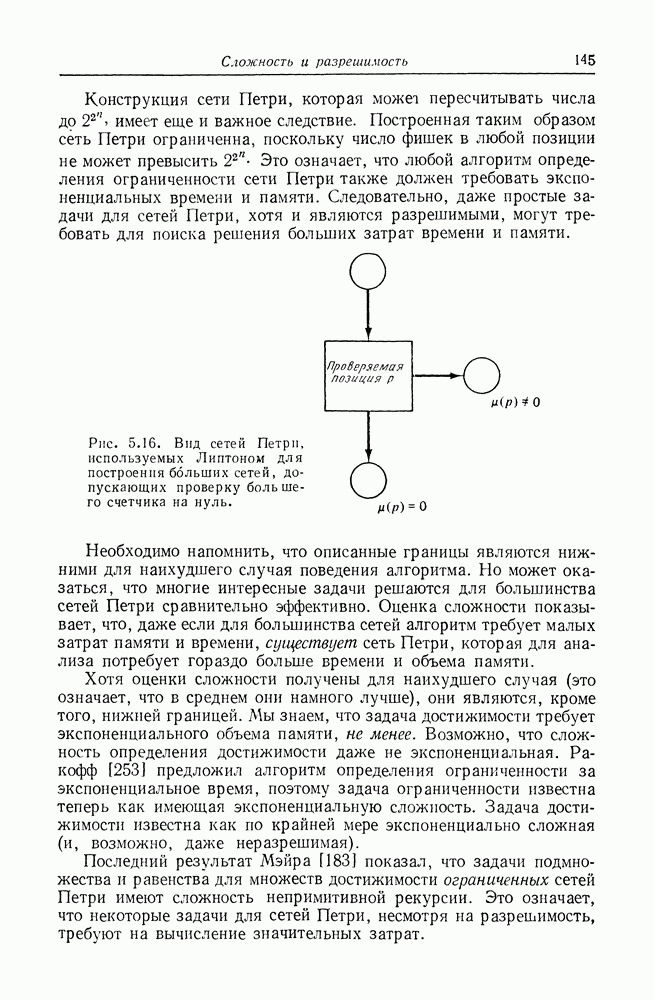
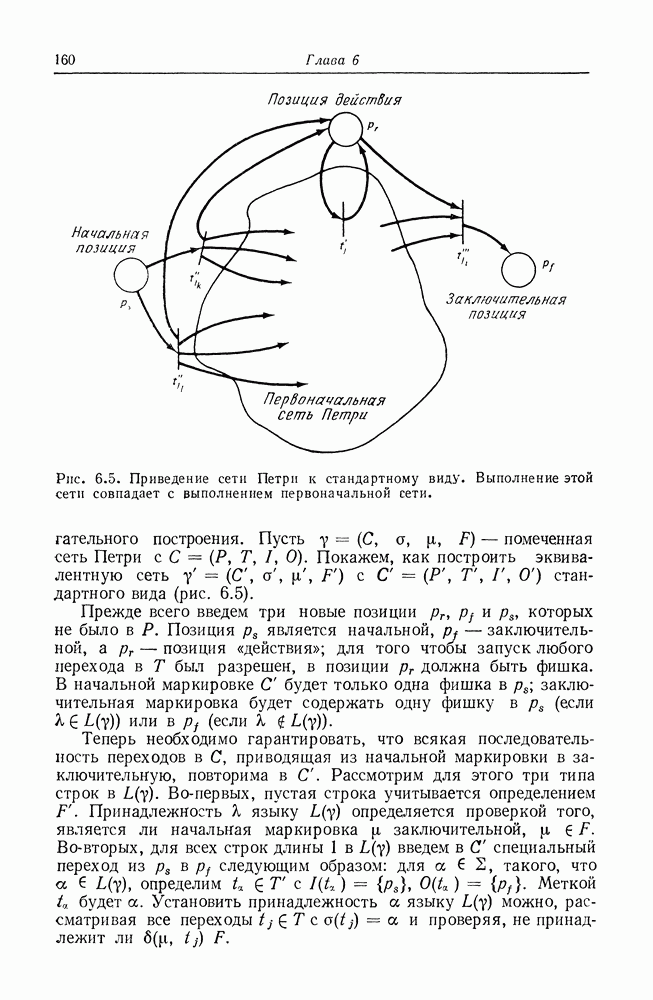
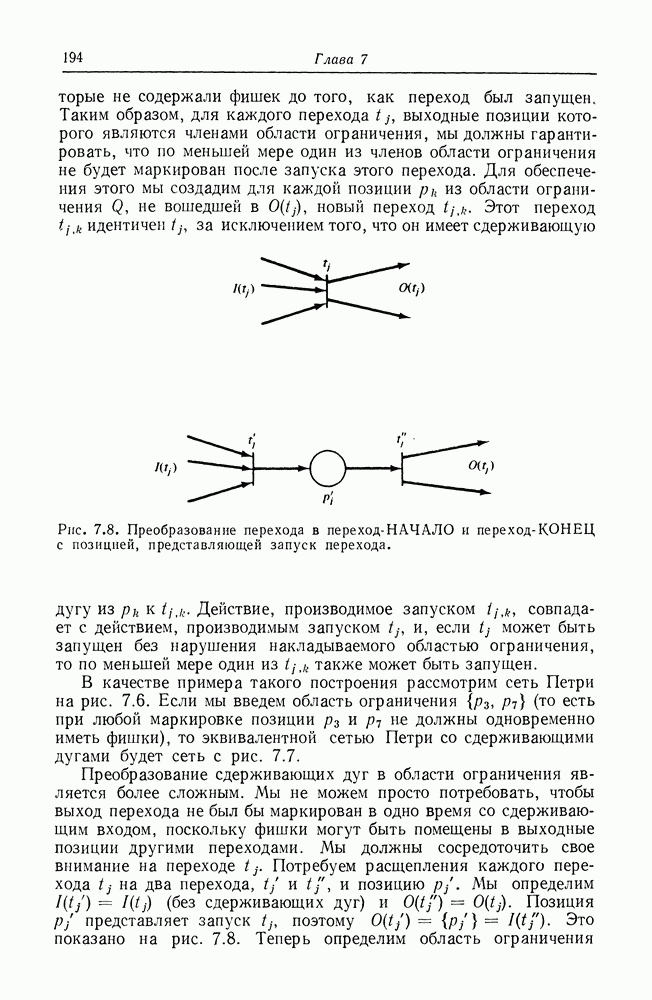
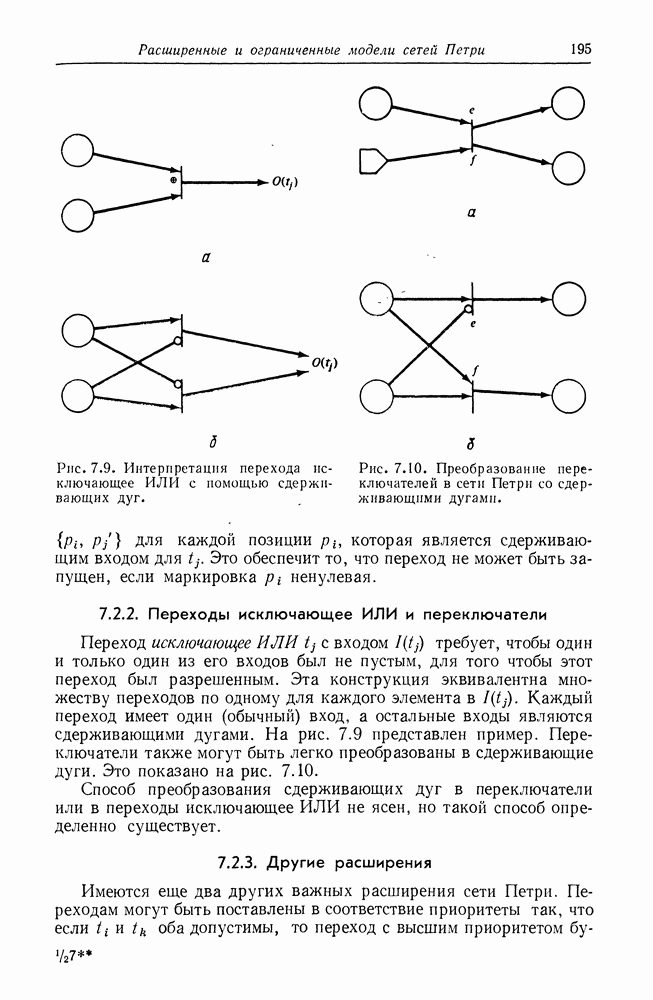
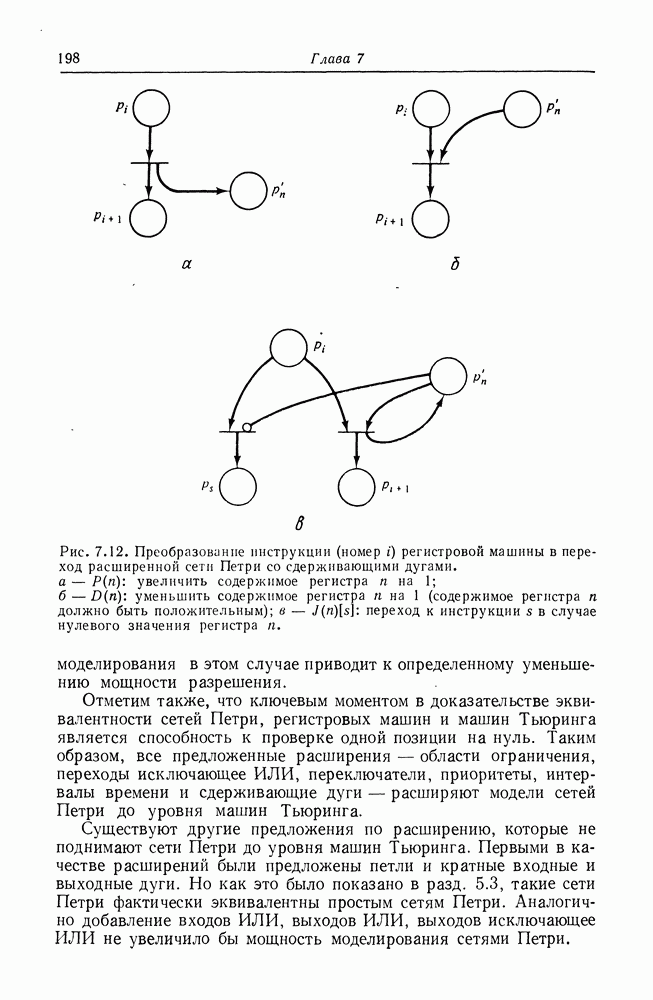
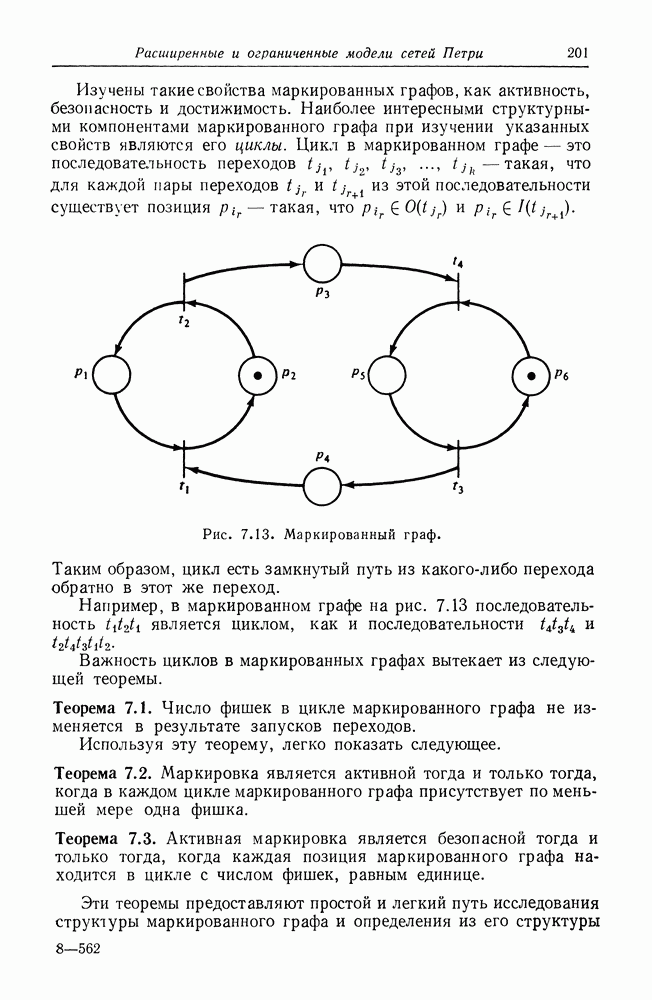
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.6. Альтернативные формы определения сетей Петри
Теория сетей Петри разрабатывалась рядом авторов. У них были различные мотивы и предпосылки. Вследствие такого разнообразия многие фундаментальные понятия были определены по-разному. Дадим некоторые из этих альтернативных определений, чтобы показать, что между ними нет существенных различий, и чтобы подготовить читателя к тем разнообразным представлениям, которые могут встретиться в литературе.
Например, оригинальные сети Петри [241] не разрешают существование кратных дуг между позициями и переходами. Это эквивалентно определению входов и выходов переходов как множеств (а не как комплектов) позиций. Далее, правило запуска было ограничено следующим требованием: фишка есть в каждой входной позиции для перехода, и нет ни одной фишки в выходных позициях. Переход запускается путем удаления фишек из его входов (которые теперь становятся пустыми) и размещением фишек в (ранее пустых) выходах (которые теперь заполняются). Переход не может быть запущен, если фишка уже принадлежит выходной позиции. Таким образом, маркировка каждой позиции присваивает либо  фишек, либо 1 фишку,
фишек, либо 1 фишку,  Теперь становится очевидным тот факт, что сеть с
Теперь становится очевидным тот факт, что сеть с  позициями имеет точно
позициями имеет точно  возможных маркировок, т. е. конечное число состояний.
возможных маркировок, т. е. конечное число состояний.
Ранние разработки Хольта по проекту теории информационных систем [128] использовали эти же определения, но по мере продвижения исследований была обнаружена ограниченность такой модели. В работе Хольта и Коммонера, представленной на конференции в Вудс Холле [127], класс маркировок и правила запуска распространены на произвольные маркировки,  Таким образом была создана базовая модель сетей Петри в том виде, в каком она определена сегодня (за исключением возможности кратных дуг).
Таким образом была создана базовая модель сетей Петри в том виде, в каком она определена сегодня (за исключением возможности кратных дуг).
Многие из первых исследователей не давали формального определения своих моделей, а описывали неформально относящиеся к их работе компоненты, такие, как позиции, переходы, фишки и правило запуска. Одно из первых формальных определений было дано Патилом [231] в его докторской диссертации, в которой сеть Петри определялась в виде четверки  где
где  множество переходов, А — множество дуг,
множество переходов, А — множество дуг,  множество позиций и В — начальная маркировка. Дуги множества А соединяли либо позицию с переходом, либо переход с позицией. Таким образом,
множество позиций и В — начальная маркировка. Дуги множества А соединяли либо позицию с переходом, либо переход с позицией. Таким образом,  Многие статьи по сетям Петри основываются
Многие статьи по сетям Петри основываются
на этом определении и определяют сеть Петри как тройку  с выделенной функцией маркировки.
с выделенной функцией маркировки.
Преобразование из формы  к определению с выделением входной и выходной функциями сравнительно просто. Множества дуг А разбивается на множество входных дуг
к определению с выделением входной и выходной функциями сравнительно просто. Множества дуг А разбивается на множество входных дуг  и выходных дуг
и выходных дуг  Эта форма непосредственно приводит к обобщению, допускающему кратные входы и выходы. Необходимо только указывать кратность для каждой входной и выходной дуги.
Эта форма непосредственно приводит к обобщению, допускающему кратные входы и выходы. Необходимо только указывать кратность для каждой входной и выходной дуги.
Хэк [116] в конце концов остановился на определении сетей Петри в виде четверки  где, как обычно,
где, как обычно,  множество позиций,
множество позиций,  множество переходов,
множество переходов,  функции, ставящие в соответствие позициям и переходам количество фишек, необходимых для входа
функции, ставящие в соответствие позициям и переходам количество фишек, необходимых для входа  или образованных для выхода
или образованных для выхода  Следовательно, переход
Следовательно, переход  можно запустить только в том случае, если по крайней мере
можно запустить только в том случае, если по крайней мере  фишек находятся в каждой позиции
фишек находятся в каждой позиции  Переход запускается путем удаления
Переход запускается путем удаления  фишек из каждой входной позиции и помещения
фишек из каждой входной позиции и помещения  фишек в каждую выходную позицию. Функции
фишек в каждую выходную позицию. Функции  могут быть представлены матрицами.
могут быть представлены матрицами.
Питерсон в своей диссертации [236] попытался объединить переходы и их входы и выходы, определяя переход как упорядоченную пару комплектов позиций:  Первая компонента пары — комплект входов перехода; вторая — комплект выходов перехода. Это сводит множество примитивных понятий теории к позициям и фишкам, так как переходы являются структурами, составленными из позиций. Такой подход особенно полезен для простого определения переходов при построении сети Петри.
Первая компонента пары — комплект входов перехода; вторая — комплект выходов перехода. Это сводит множество примитивных понятий теории к позициям и фишкам, так как переходы являются структурами, составленными из позиций. Такой подход особенно полезен для простого определения переходов при построении сети Петри.
Эти определения отличаются от представленных здесь только разницей в обозначениях. В большинстве работ по сетям Петри именно это имеет место: различие в определениях проявляется только в обозначениях. Однако в некоторых случаях определения могут ограничивать класс сетей Петри тем, что не допускаются кратные входные и выходные дуги или существует ограничение на форму переходов, т. е. требуется, чтобы переходы имели непустые множества входных и выходных позиций или входные и выходные позиции перехода не должны совпадать (без петель). Но, как мы покажем в гл. 5, даже эти различия не имеют большого значения.
Упражнения
(см. скан)
2.7. Замечания к литературе
Для дальнейшего знакомства с сетями Петри, вероятно, лучше всего начать с обзоров [20, 238] в Computing Surveys. Почти в любой работе несколько первых разделов посвящены основным определениям и обозначениям, поэтому, чтобы найти различия в определениях, достаточно бегло просмотреть начала некоторых из перечисленных в библиографии. Например: [128, 127, 111, 115, 116, 152, 201, 208, 290].
2.8. Темы для дальнейшего изучения
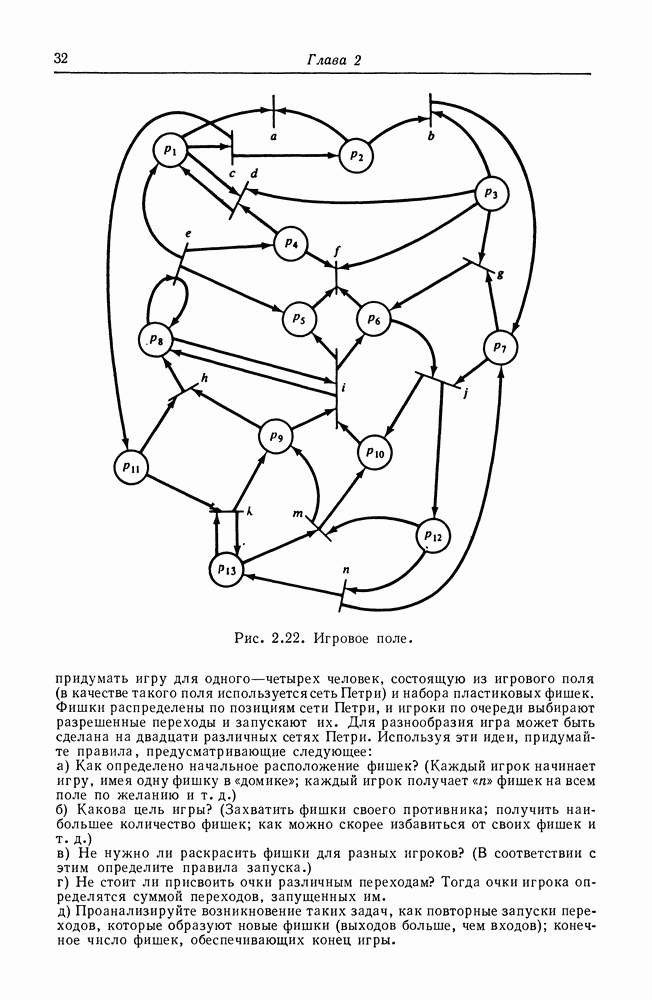
1. Разработайте теорию сетей Петри, разрешающую существование окрашенных фишек. Рассмотрите различия в определениях разрешенных переходов и запусков переходов. Существует по меньшей мере три разумных способа обобщения сетей Петри в случае окрашенных фишек. Укажите те, которые вы сможете предложить, и оцените степень их полезности.
2. Разработайте представление теории сети Петри для научных работников, не связанных с вычислительной техникой. Сравните ваше представление с представлением Хольта [123] и Мельдмана [184, 185].
3. Постройте систему моделирования на ЭВМ для выполнения сети Петри. Для удобного интерфейса пользователя с программой используйте стирающий графический дисплей (с электронно-лучевой трубкой или плазменный) для изображения запусков переходов и последовательного передвижения фишек. Это потребует решения множества вспомогательных задач.
а) Определить язык, имеющий средства вариантов задания для задания сети Петри, ее маркировок.
б) Разработать внутреннее представление сети Петри, ее маркировки и необходимые алгоритмы для моделирования.
в) Обеспечить графическую выдачу. Главная проблема здесь в достижении планарного представления сети (до разумной степени). Следует также подумать о представлении динамических свойств сети (движение фишек).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ГЛАВА 1. ВВЕДЕНИЕ
- ГЛАВА 2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
- 2.1. Структура сети Петри
- 2.2. Графы сетей Петри
- 2.3. Маркировка сетей Петри
- 2.4. Правила выполнения сетей Петри
- 2.5. Пространство состояний сети Петри
- 2.6. Альтернативные формы определения сетей Петри
- ГЛАВА 3. СЕТИ ПЕТРИ ДЛЯ МОДЕЛИРОВАНИЯ
- 3.2. Одновременность и конфликт
- 3.3. Аппаратное обеспечение ЭВМ
- 3.4. Программное обеспечение ЭВМ
- 3.5. Другие системы
- ГЛАВА 4. АНАЛИЗ СЕТЕЙ ПЕТРИ
- 4.1. Задачи анализа сетей Петри
- 4.2. Методы анализа
- ГЛАВА 5. СЛОЖНОСТЬ И РАЗРЕШИМОСТЬ
- 5.1. Сводимость задач анализа
- 5.2. Задачи достижимости
- 5.3. Сети Петри с ограничениями
- 5.4. Активность и достижимость
- 5.5. Неразрешимые задачи
- 5.6. Сложность задачи достижимости
- ГЛАВА 6. ЯЗЫКИ СЕТЕЙ ПЕТРИ
- 6.2. Некоторые понятия теории формальных языков
- 6.3. Определения языков сетей Петри
- 6.4. Свойства языков сетей Петри
- 6.5. Свойства замкнутости
- 6.6. Языки сетей Петри и другие классы языков
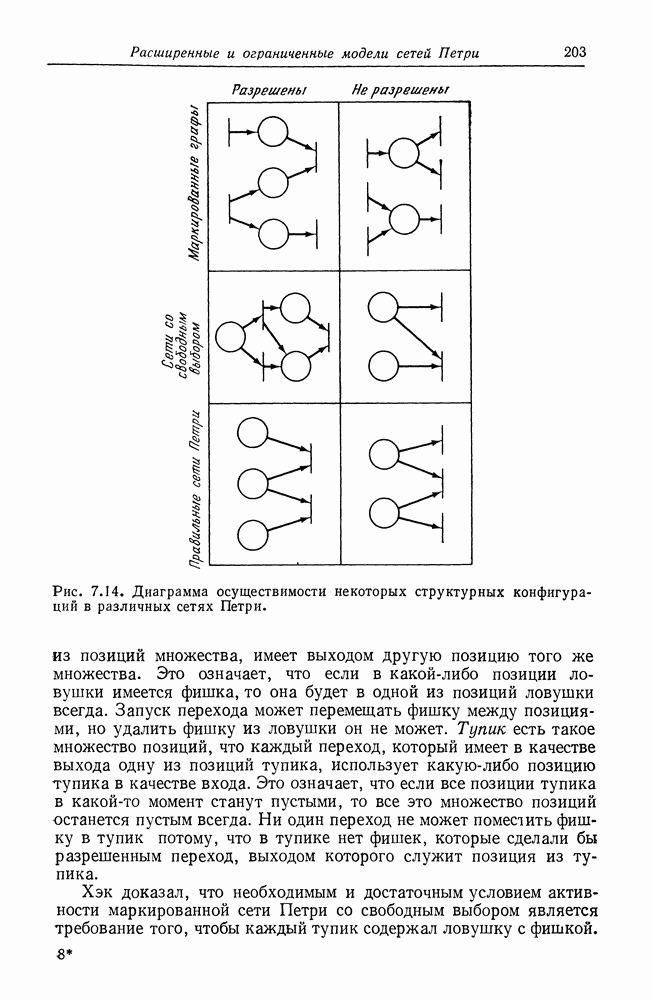
- ГЛАВА 7. РАСШИРЕННЫЕ И ОГРАНИЧЕННЫЕ МОДЕЛИ СЕТЕЙ ПЕТРИ
- 7.1. Границы возможностей моделирования с помощью сетей Петри
- 7.2. Расширения
- 7.3. Расширенные сети Петри и регистровые машины
- 7.4. Подклассы сетей Петри
- ГЛАВА 8. МОДЕЛИ ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ
- 8.2. Маркированные графы
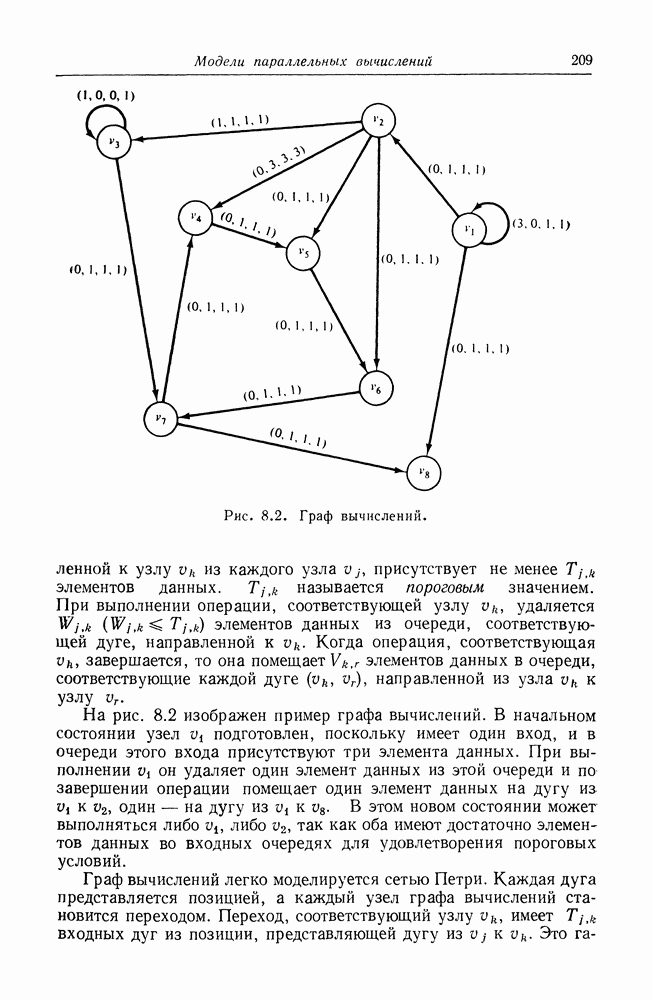
- 8.3. Графы вычислений
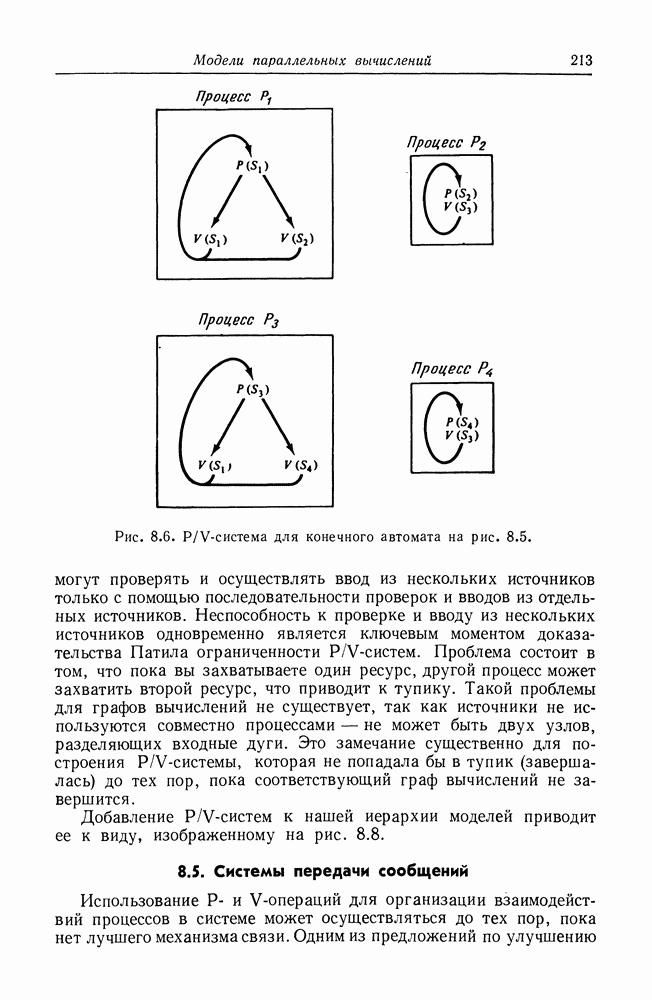
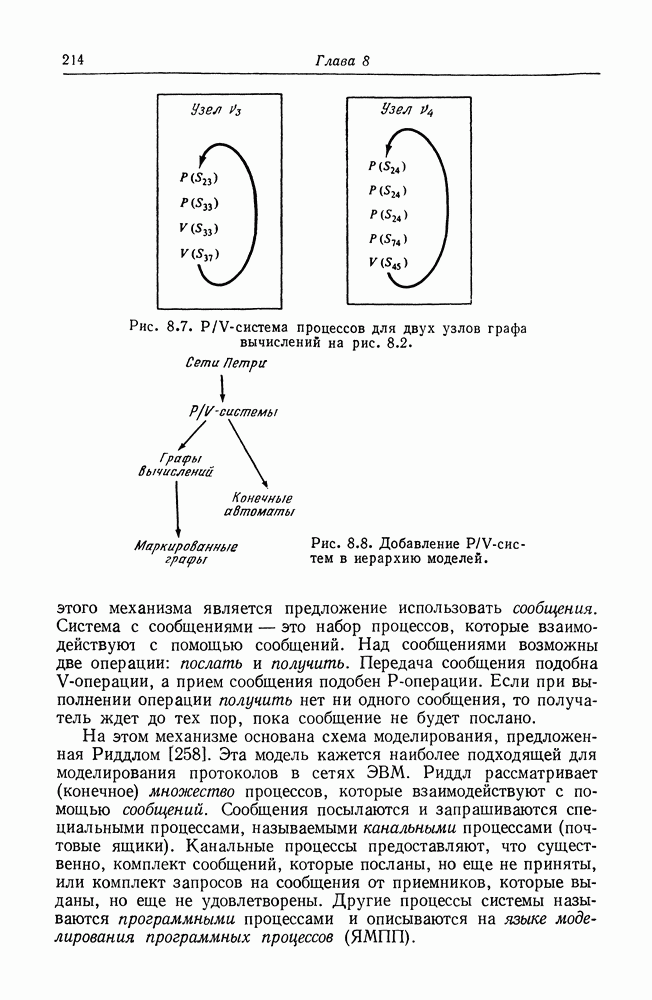
- 8.4. P/V-системы
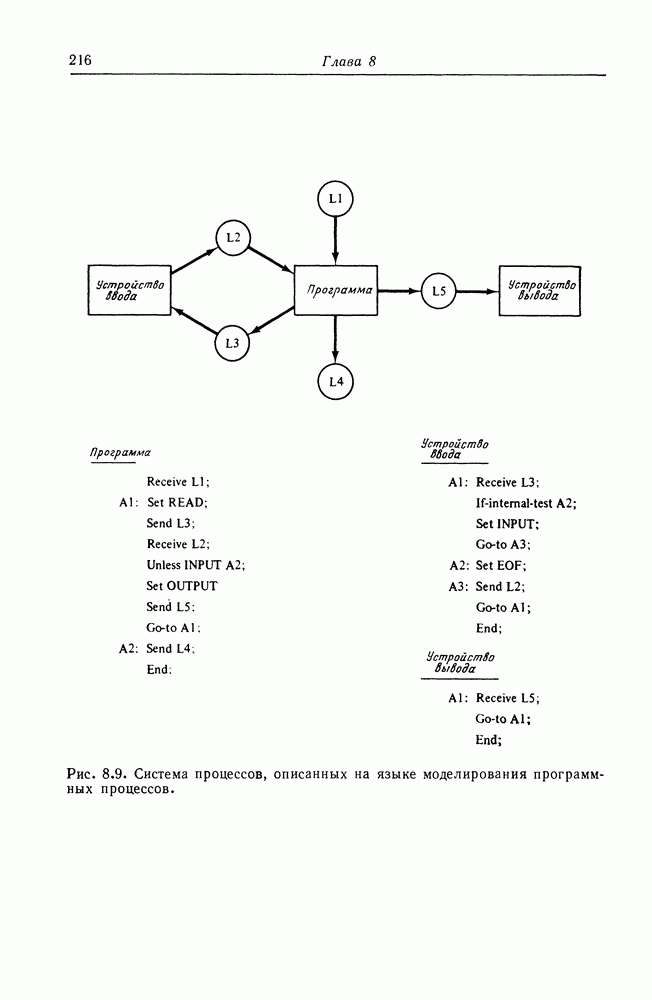
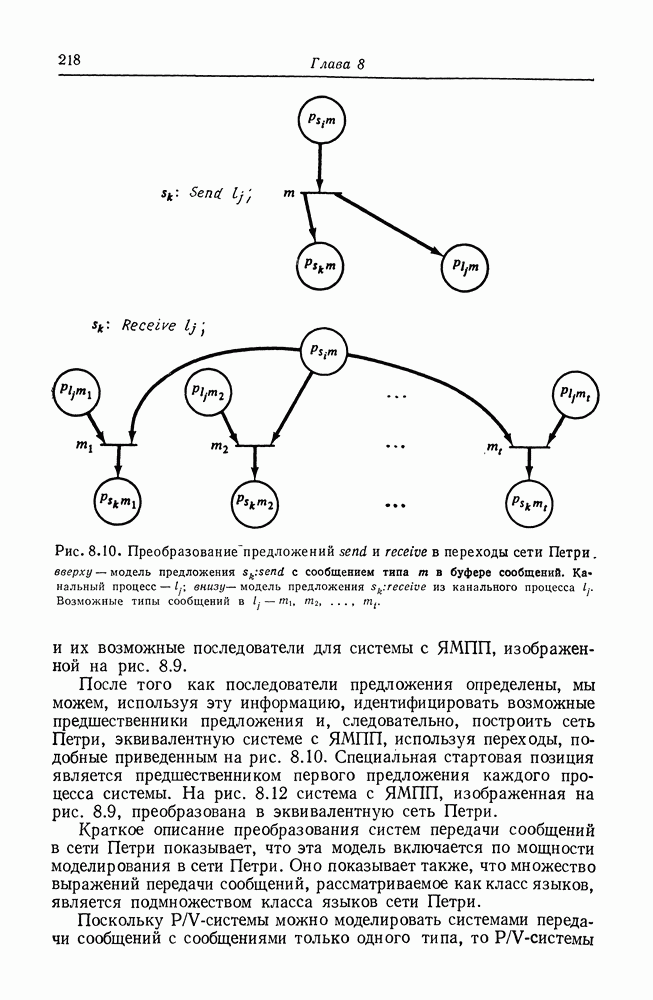
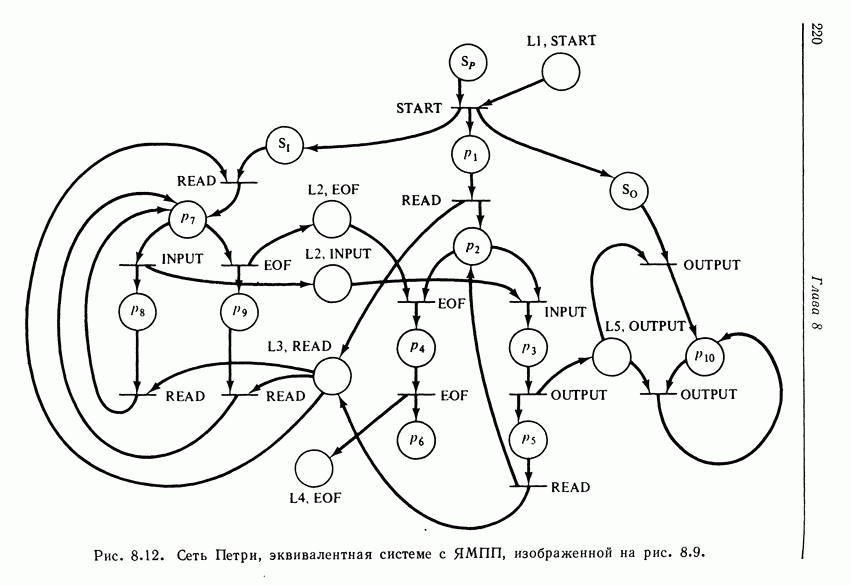
- 8.5. Системы передачи сообщений
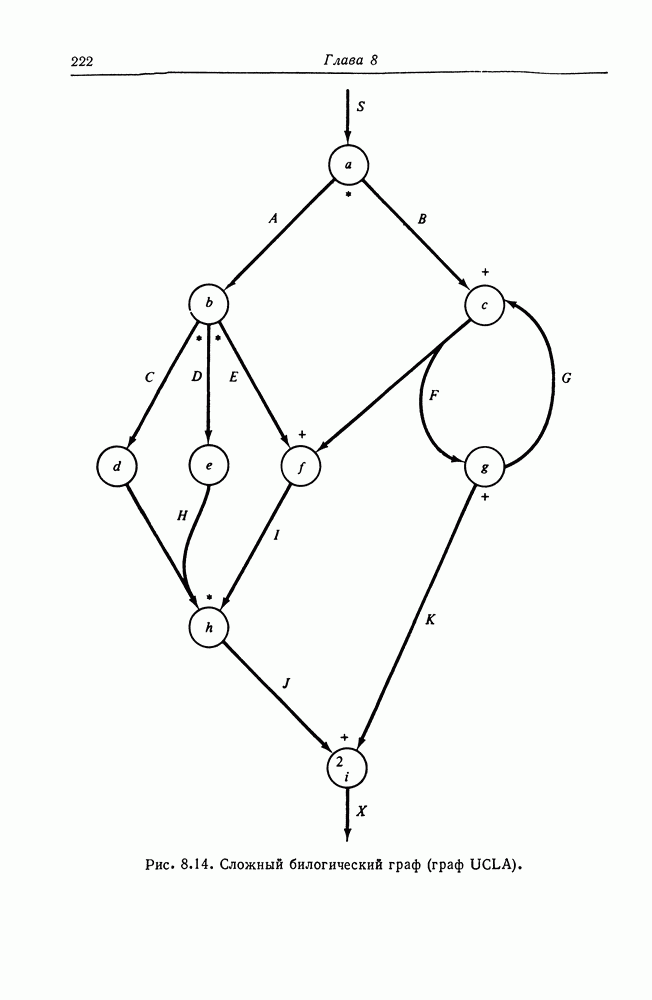
- 8.6. Графы UCLA
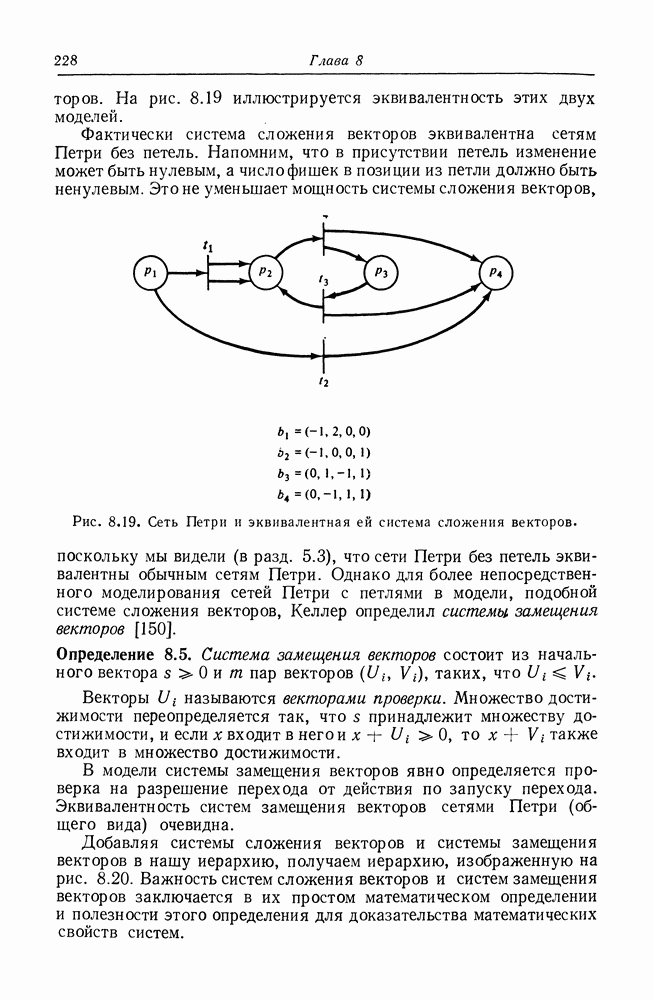
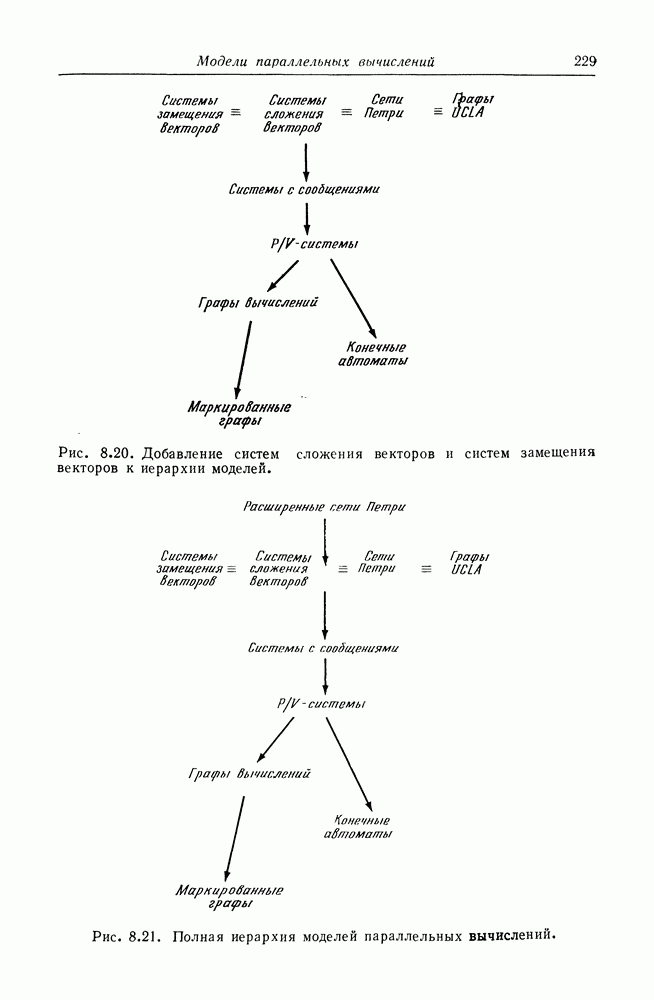
- 8.7. Системы замещения и сложения векторов
- 8.8. Расширенные модели сетей Петри
- ОБЗОР ТЕОРИИ КОМПЛЕКТОВ
- АННОТИРОВАННАЯ БИБЛИОГРАФИЯ