ГЛАВА 8. МОДЕЛИ ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ

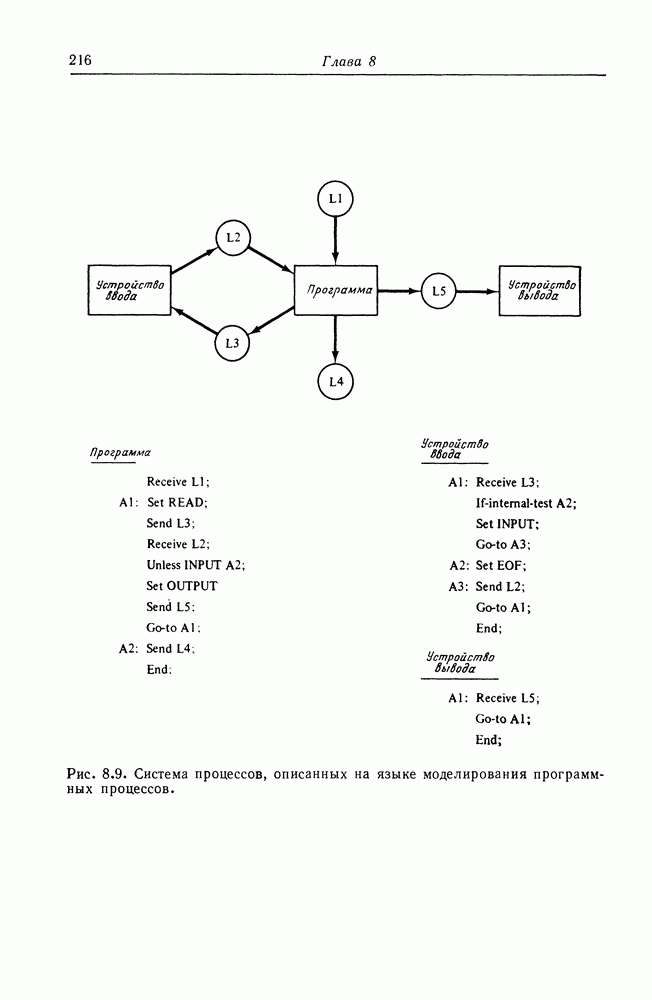
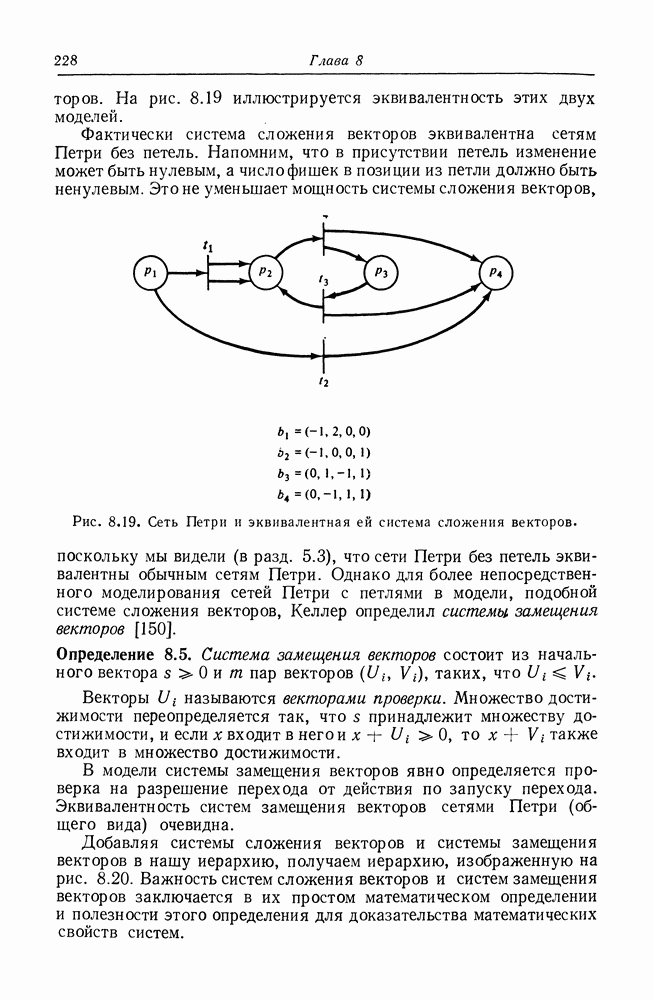
Сети Петри определены как модели систем с параллельными действиями. И, как мы видели, сети Петри имеют хорошие возможности моделирования, с их помощью можно моделировать большое число систем. Однако сети Петри — не единственная модель параллельных вычислений. Предложено, исследуется и используется множество других моделей. В этой главе мы представим некоторые из этих моделей и исследуем их взаимосвязь с сетями Петри. Целью этой главы является определение моделей, которые могут использоваться в системах моделирования, и их сравнительной мощности моделирования.

Основной задачей, проистекающей из намерения соотнести различные модели друг с другом, является задача установления соответствующего метода сравнения моделей параллельных вычислений. Мы хотели бы иметь возможность доказывать, что модель А является «менее мощной», чем модель В, или что модель А «эквивалентна» модели В. Понятия эквивалентности и включения имеют в данном случае особую важность.

Некоторые исследования по соотнесению различных моделей уже проведены. Обзоры [20, 41, 197] помогли собрать воедино описания нескольких моделей. В частности, в [41] дано общее определение управляющей структуры, которое позволяет определять единым образом различные модели. Это привело к работам [236, 240], в которых сравниваются различные модели для получения иерархии моделей, соотнесенных по их мощности моделирования. Независимый результат получен в [5], где сравнивается большое число моделей и строится другая иерархия с подобной структурой.

Оба результата — и в [240] и в [5] — получены с помощью использования языков моделей для их сравнения. Класс моделей А определяет класс языков Два класса моделей, будут эквивалентны по определению, если Это на чает, что для любого определенного экземпляра а класса моделей А с языком должен существовать экземпляр класса В с идентичным языком Если языки правильно характеризуют эти модели, то они являются искомым средством для сравнения двух классов моделей.

Однако, как мы видели, не вполне ясно, как определить язык для моделей параллельных вычислений. Исследования в области определения языков сетей Петри привели к по меньшей мере 12 различным определениям языков, большинство из них, очевидно, различны. Различия в этих языках могут привести к различиям в соотношениях эквивалентности и включения между моделями. С другой стороны, если различия между моделями действительно существенны, то они могут быть не чувствительны к (незначительным) изменениям в определениях эквивалентности исключения. Таким образом, подобность результатов, полученныхв [5] и [240], весьма важна из-за того, что в этих работах использовались различные определения эквивалентности и включения.

Однако нельзя утверждать, что эти результаты бесспорны. Авторы [178] также сравнили большое число моделей параллельных вычислений и пришли к другим выводам. Их "сравнение основывается на очень детальном анализе структуры и пространства состояний отдельных представителей классов моделей. Этим объясняется значительное отличие результатов [178] от результатов [5] и [240].

Итак, установлено, что существуют различия в мнениях исследователей по вопросам о том, какие модели должны сравниваться, как их сравнивать? Сравнение, проводимое в этой главе, основано как на структурных характеристиках, так и на характеристиках поведения. Мы будем говорить, что класс моделей А является меньшим или равным по мощности моделирования (включается в) классу если для любого данного экземпляра а класса А существует алгоритм построения экземпляра класса В, для которого верно, что:

1. Каждая структурная компонента модели а представляется (небольшим) различимым множеством компонент модели Размер модели (число элементов) отличается в худшем случае на мультипликативную константу от размера модели а, причем константа определяется классами моделей А и В, а не конкретными экземплярами

2. Любая последова ельность действий в а может быть промоделирована последовательностью в , с длиной последовательности в , отличающейся не более чем на мультипликативную константу от длины последовательности в а.

3. Модель заходит в тупик только тогда, когда заходит в тупик модель Модель заходит в тупик, если все ее действия становятся невозможными.

Цели введения этих ограничений очевидны. Первое ограничение устанавливает структурное подобие двух моделей; второе ограничение гарантирует, что две модели ведут себя одинаково. Однако мы не требуем абсолютного соответствия между двумя моделями. Мы допускаем представление действия в одной модели (короткой) последовательностью действий в другой модели или представление компоненты (подобной позиции или переходу) набором (небольшим) компонент. Следовательно, действие в одной модели может моделироваться последовательностью из двух действий в другой модели. Последнее ограничение требует, чтобы более мощная модель не совершала ошибок, когда их не совершает менее мощная. Это исключает возможность построения модели, которая недетерминированно выбирает одно из нескольких действий и останавливается, если оказывается, что был сделан неверный выбор.

Две модели эквивалентны, если они включают друг друга. Это предполагает, что любой экземпляр какой-либо модели преобразуется в экземпляр другой.

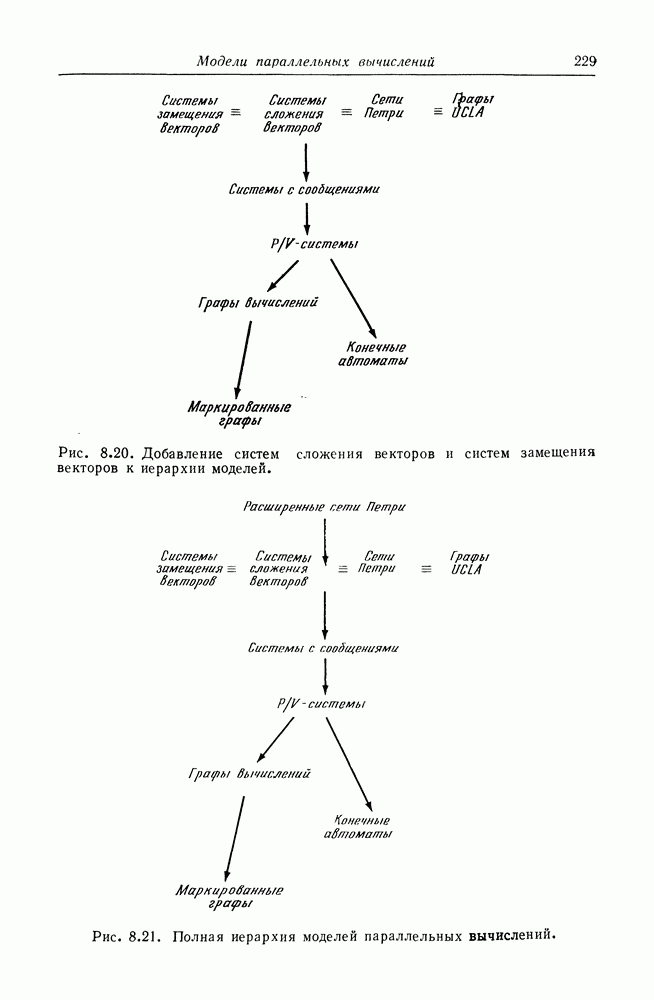
С учетом сказанного выше, рассмотрим соотношения между следующими моделями параллельных вычислений:

1. Конечные автоматы [42, 97, 129].

2. Маркированные графы [54].

3. Графы вычислений [147].

5. Системы с сообщениями [258].

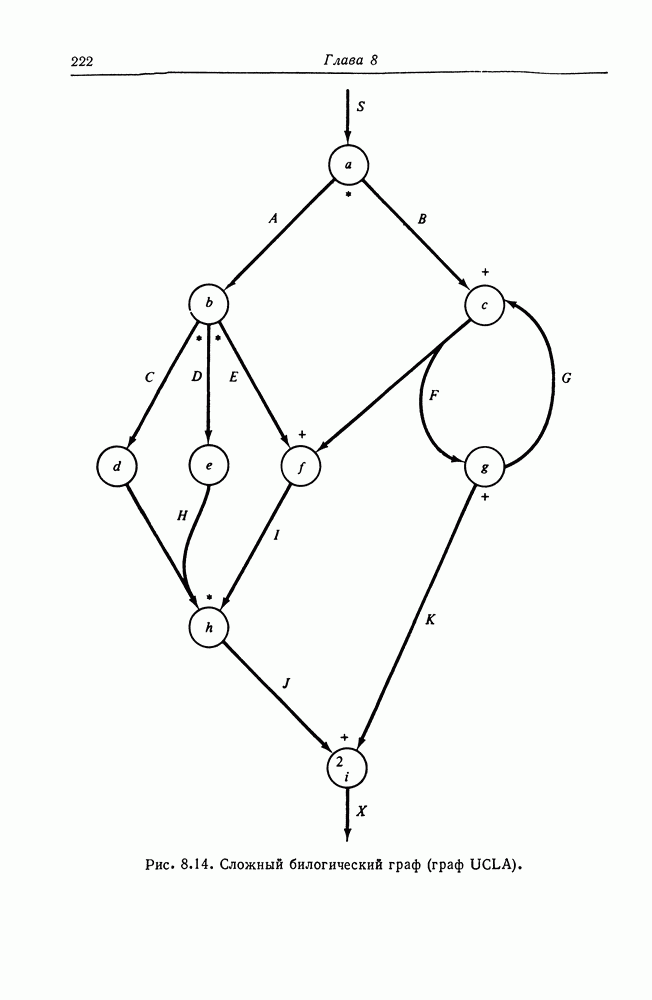
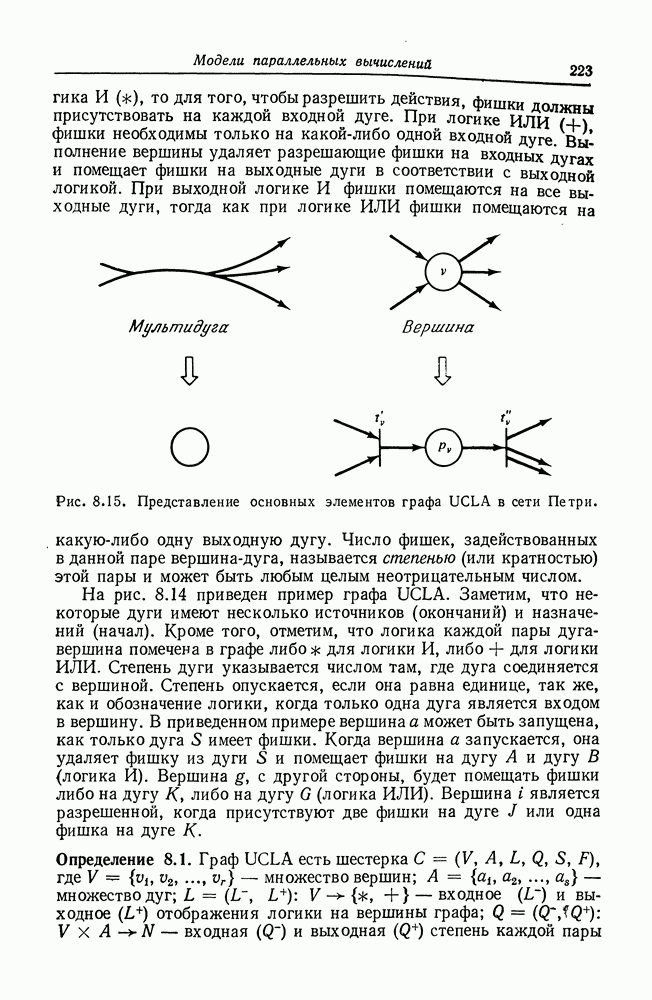
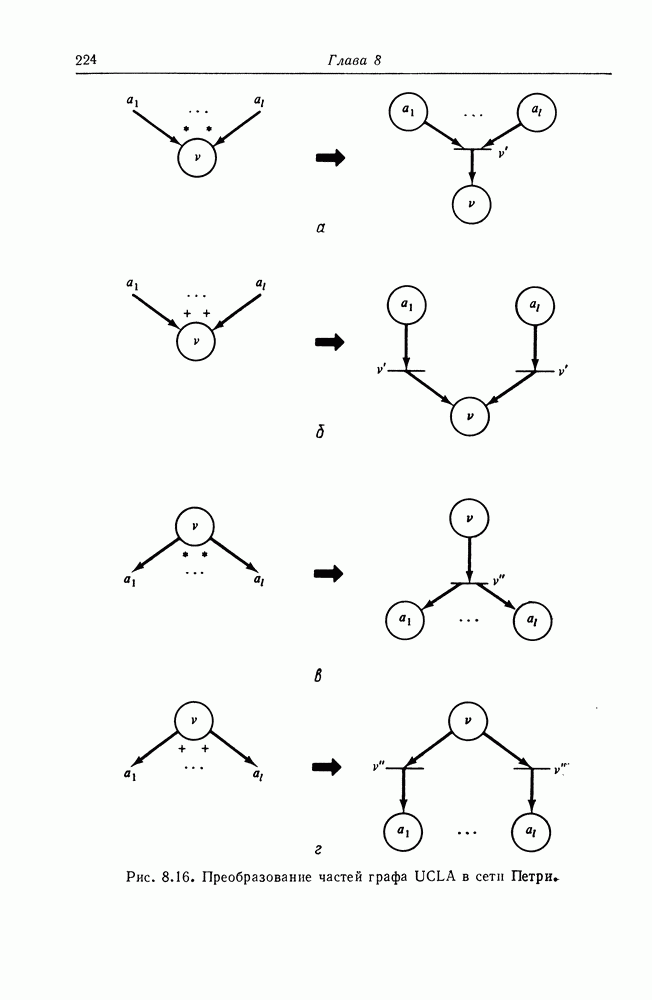
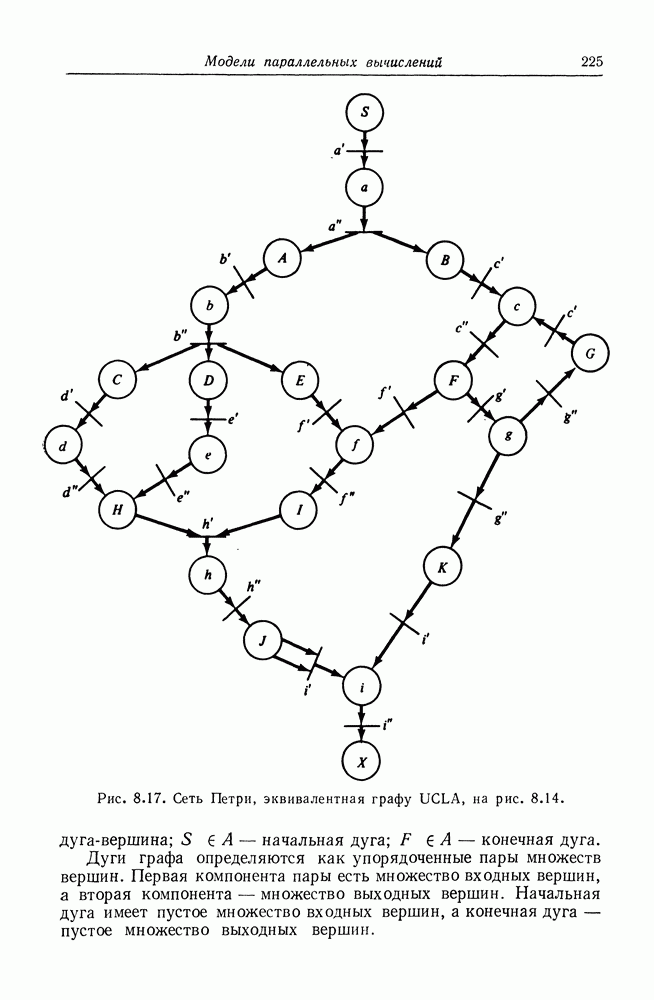
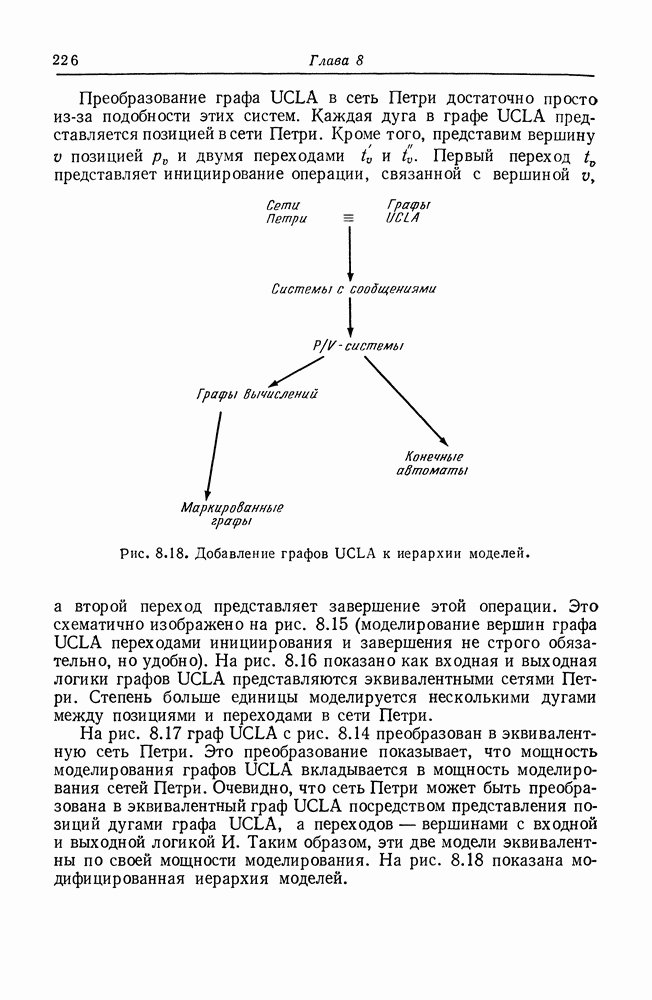
6. Графы UCLA [49, 50, 51, 104].

7. Системы сложения векторов [148].

8. Системы замещения векторов [150].

9. Расширенные сети Петри

Для каждого класса моделей вначале определим модель и приведем пример. Затем обсудим связь ее с другими моделями параллельных вычислений.

8.1. Конечные автоматы

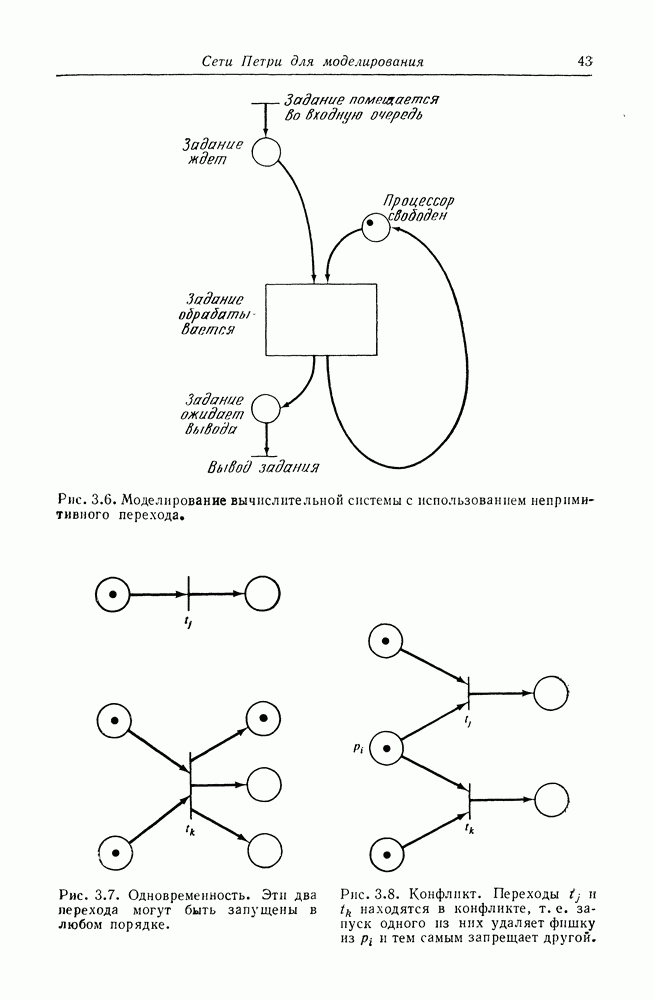
В разд. 3.3.1 и 7.4.1 показано, что конечные автоматы легко преобразуются в сети Петри. Конечные автоматы использовались несколькими исследователями в качестве модели параллельных вычислений. Бредт [42] определил модель, основанную на концепциях, вложенных в аппаратуру ЭВМ. Каждый процессор

моделируется конечным автоматом с входными и выходными каналами, которые связывают один процессор с другим. Состоянием каждого входного и выходного канала является либо 0, либо 1. Поскольку каждый выходной канал одного процессора является входным каналом другого процессора, и существует конечное число процессоров и конечное число каналов, каждый с конечным числом состояний, то и вся система имеет конечное число состояний.

Гильберт и Чандлер [97] использовали модель с общей памятью, а не каналы связи. Это означает, что их модель в большей степени, чем модель аппаратуры Бредта, направлена на моделирование программных процессов с совместно используемой памятью, но все же является не чем иным, как моделью с конечным числом состояний, и, следовательно, включена в модель сети Петри.