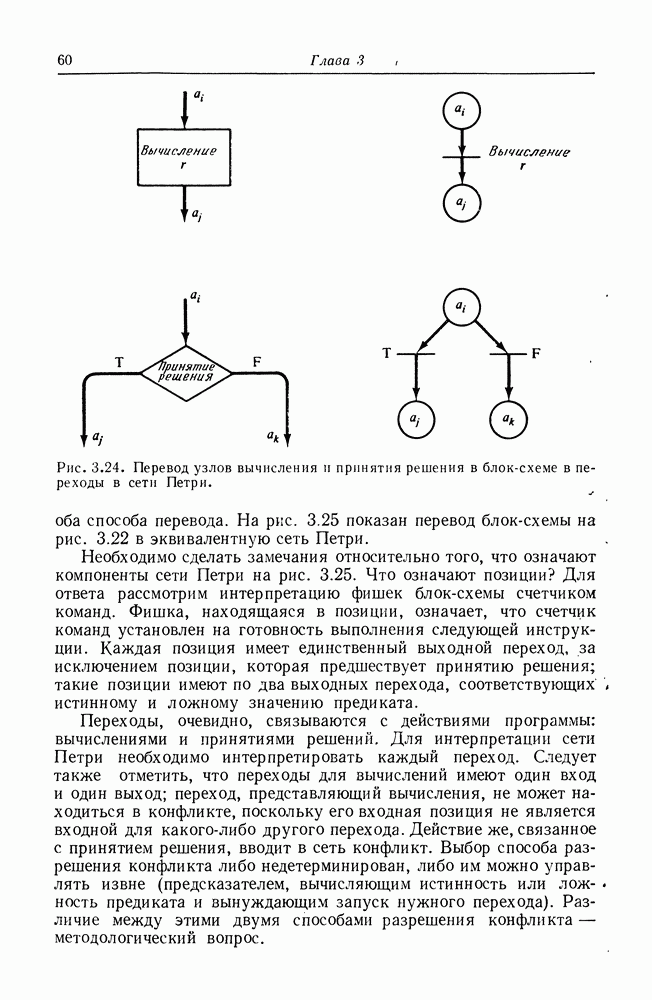
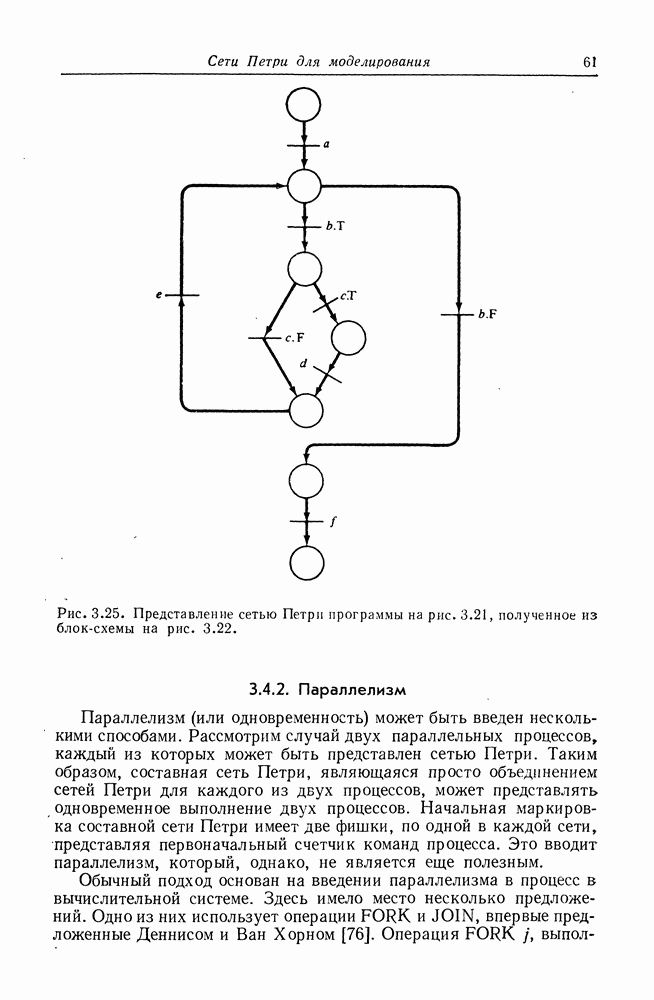
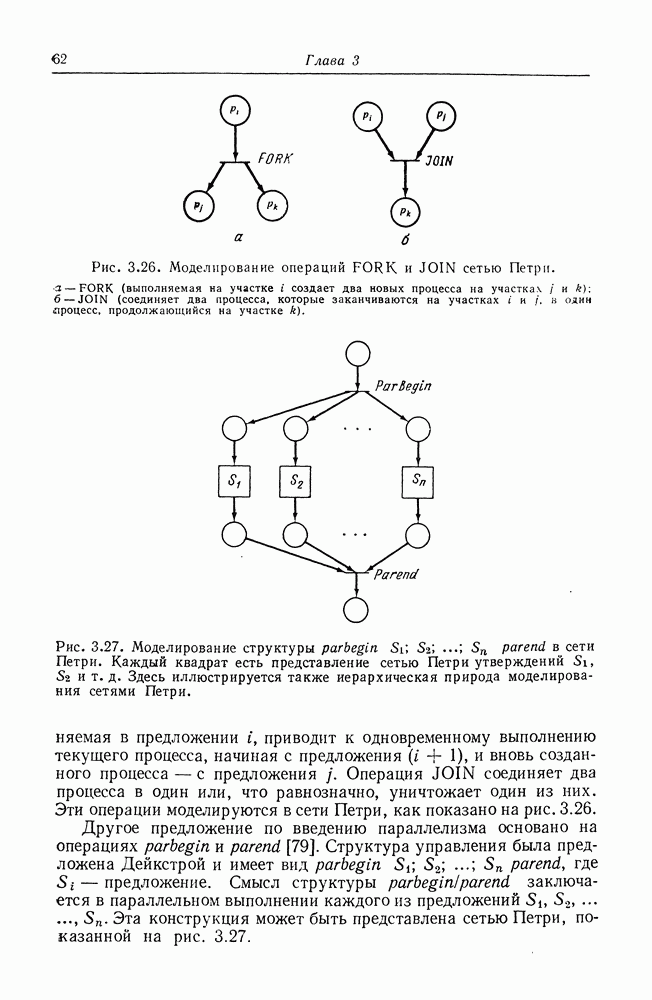
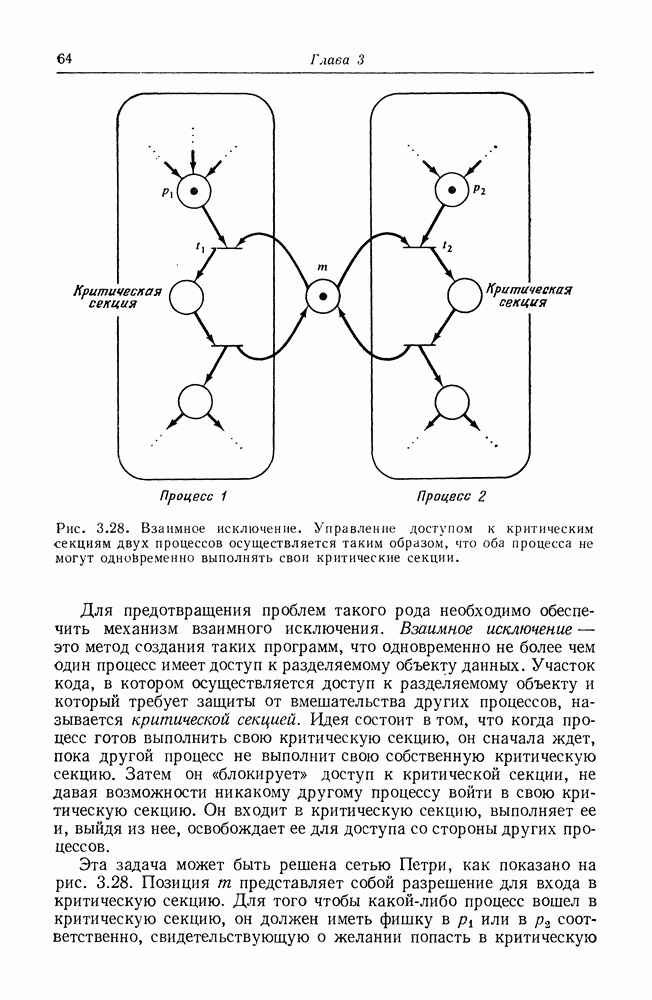
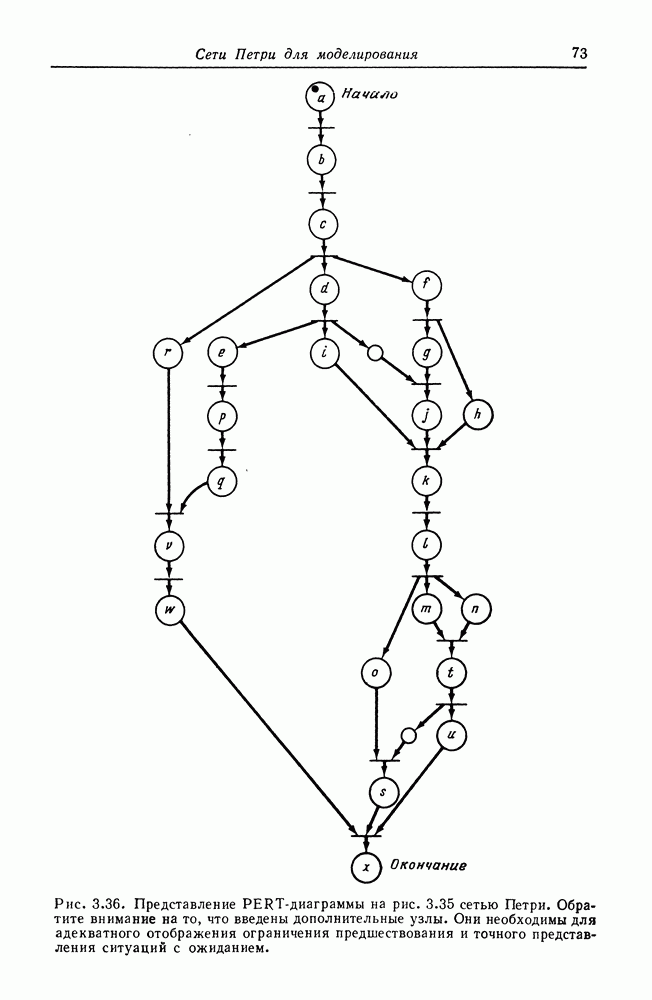
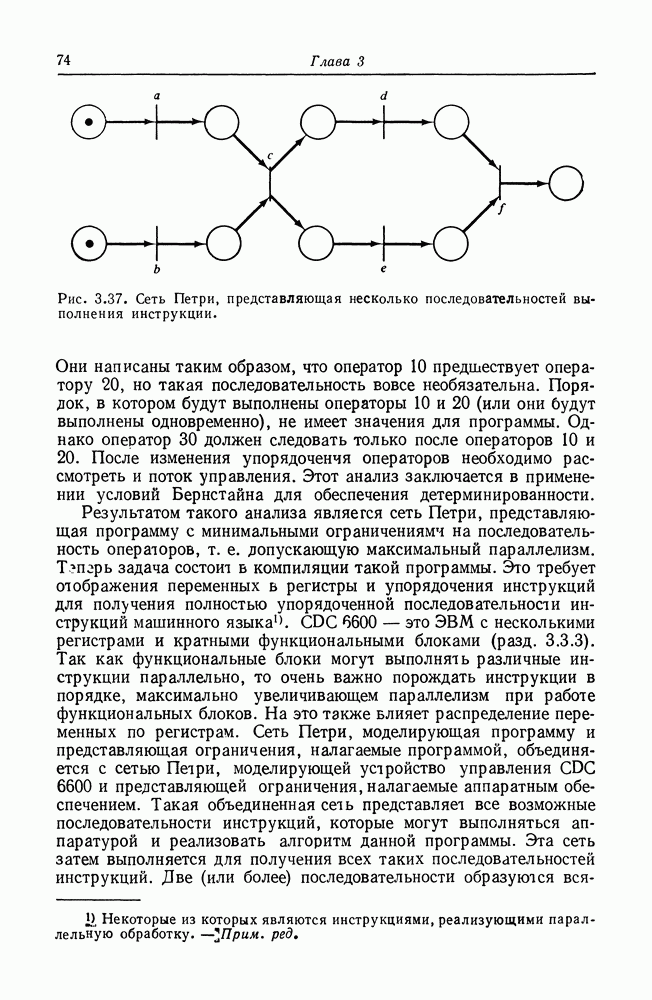
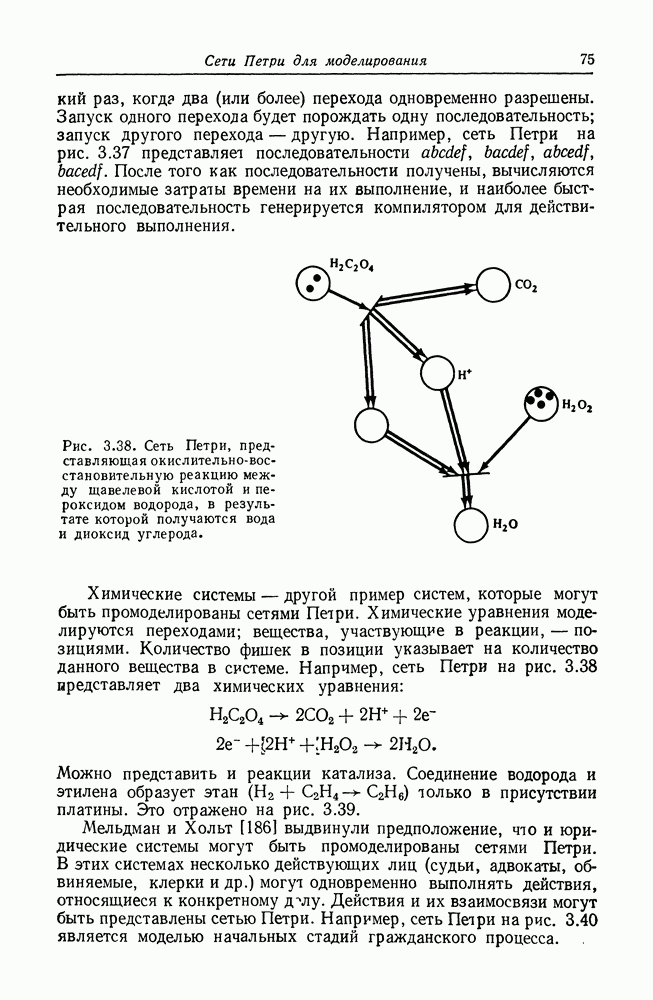
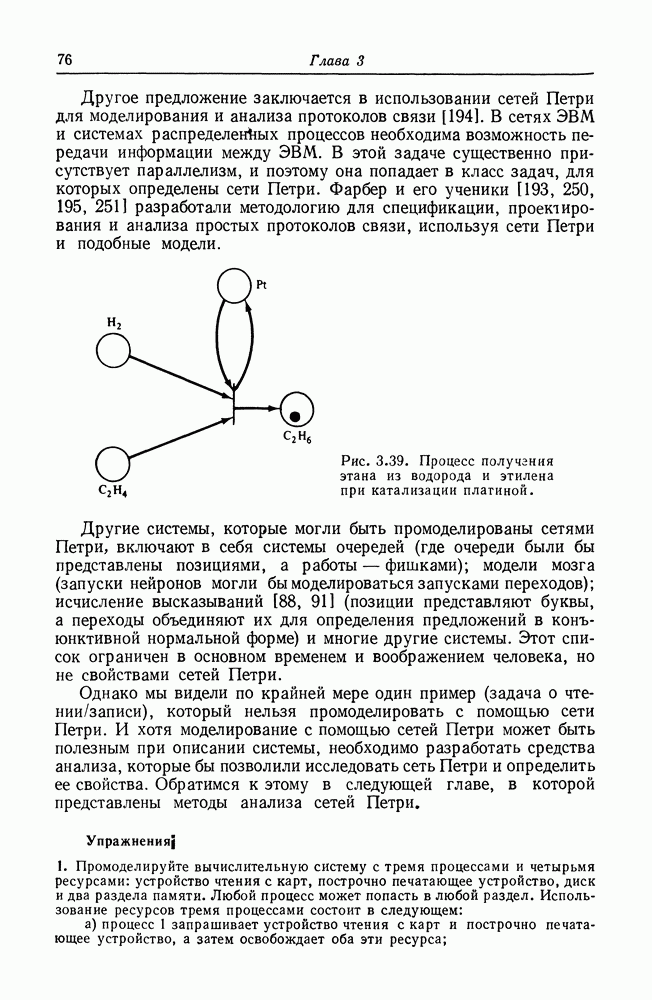
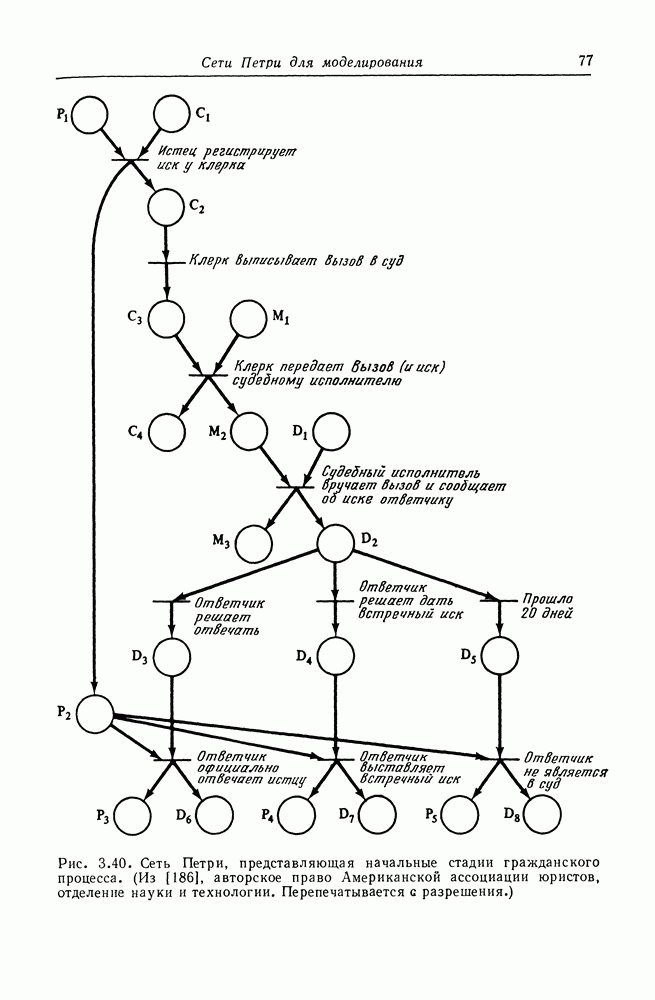
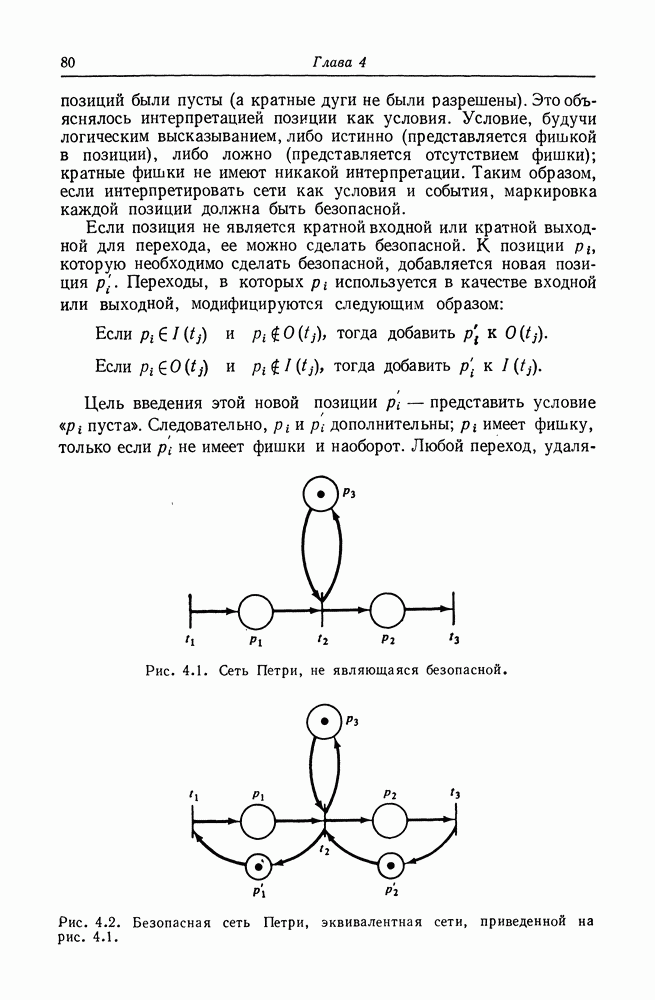
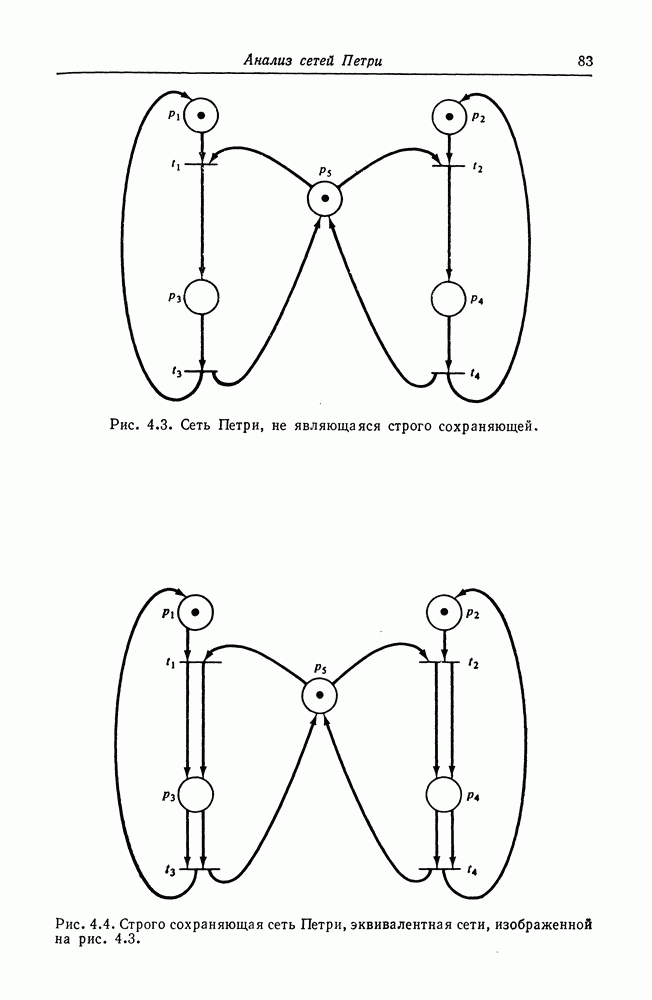
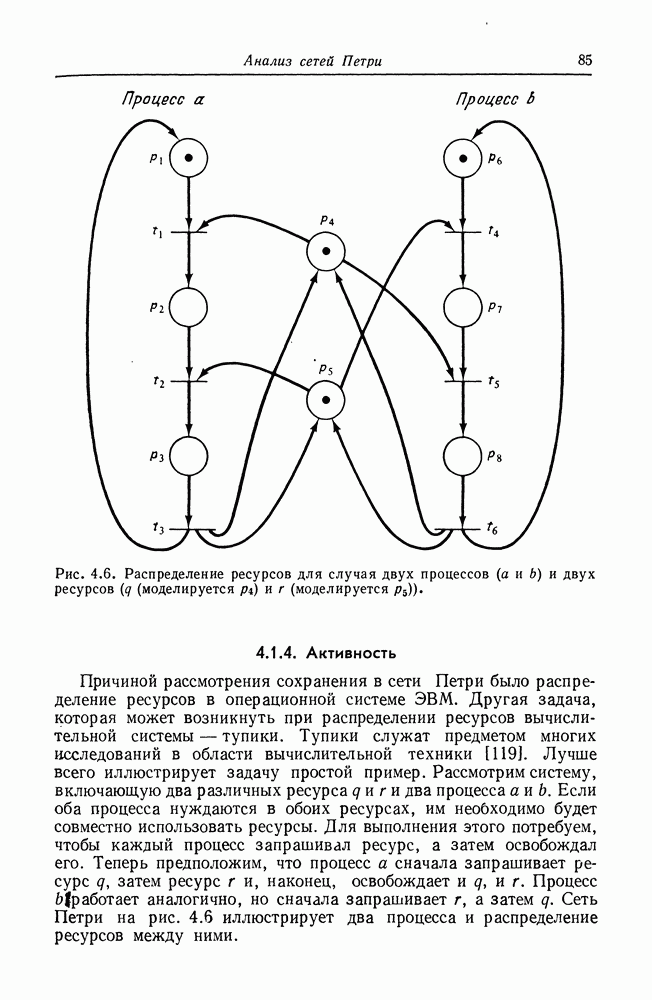
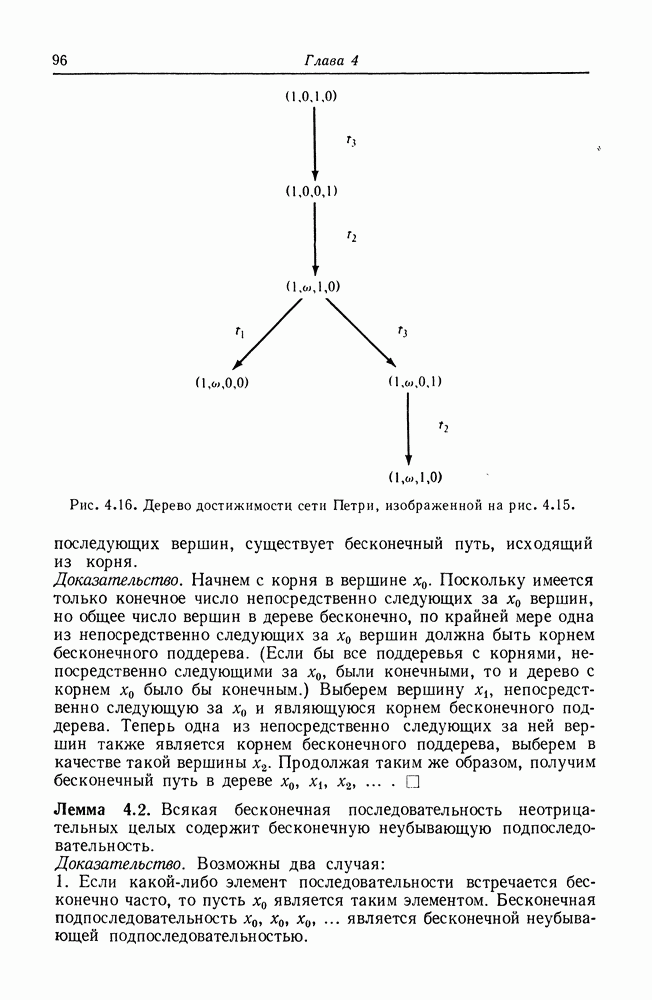
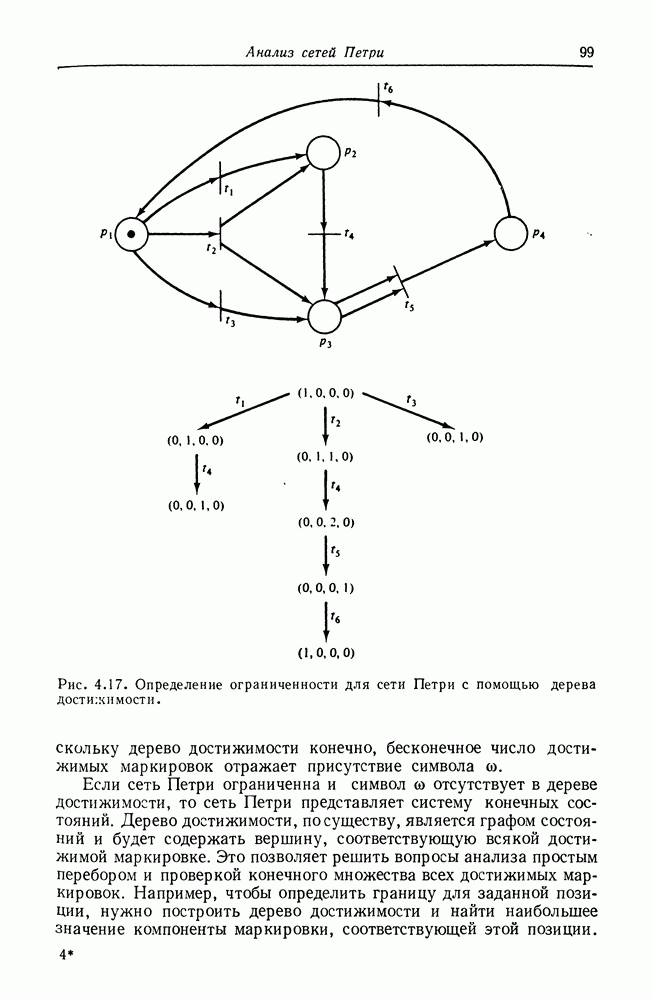
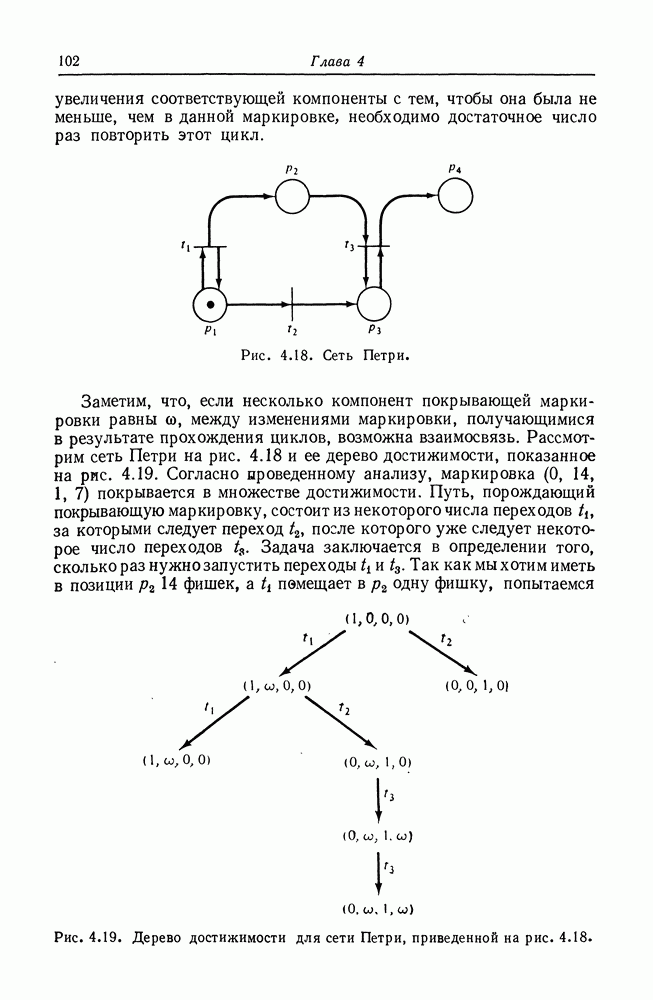
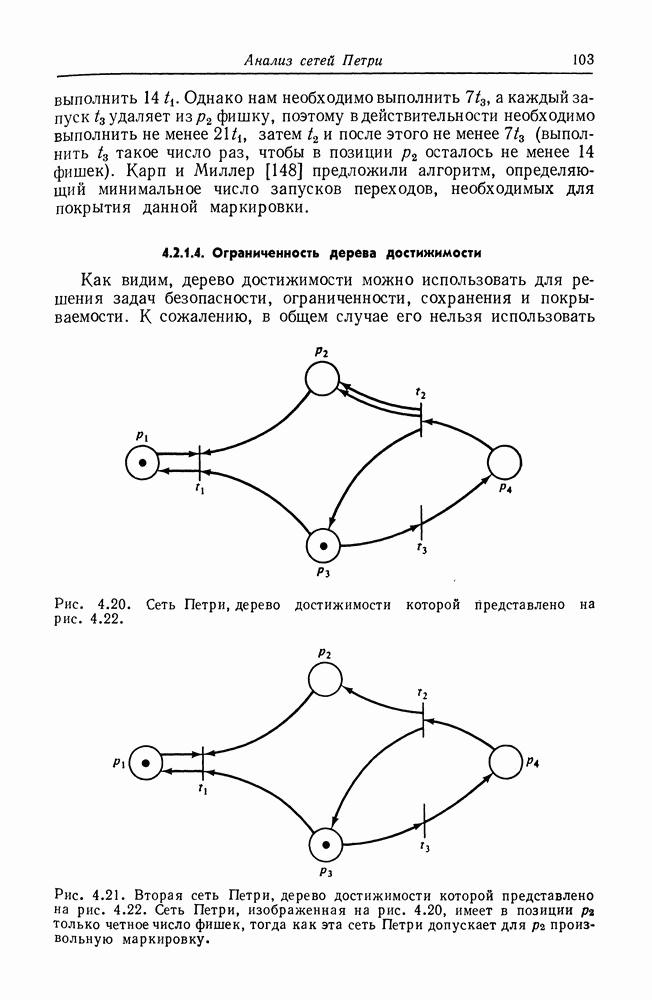
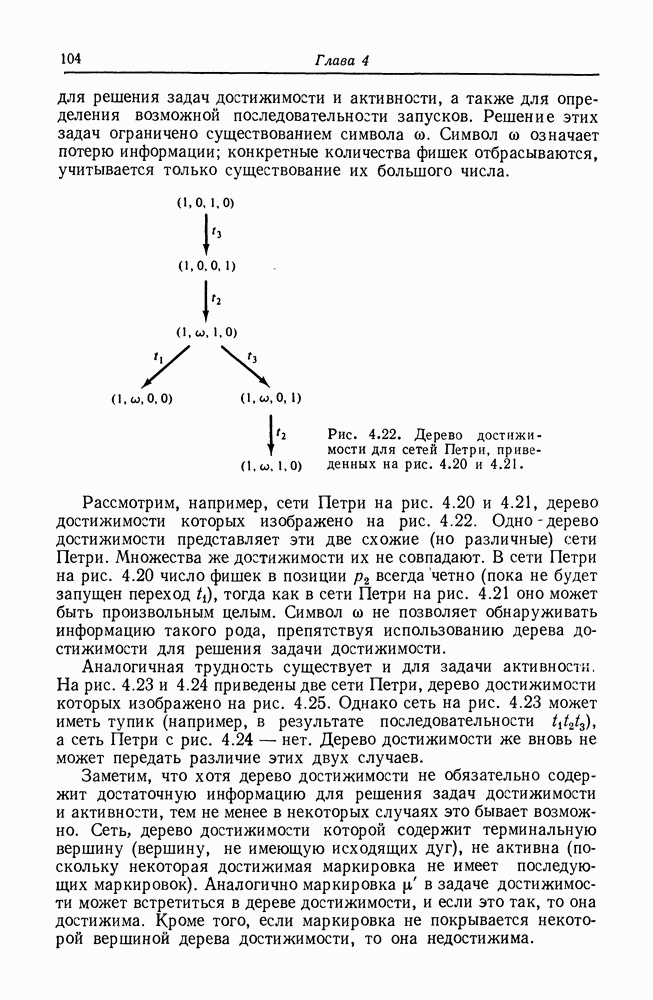
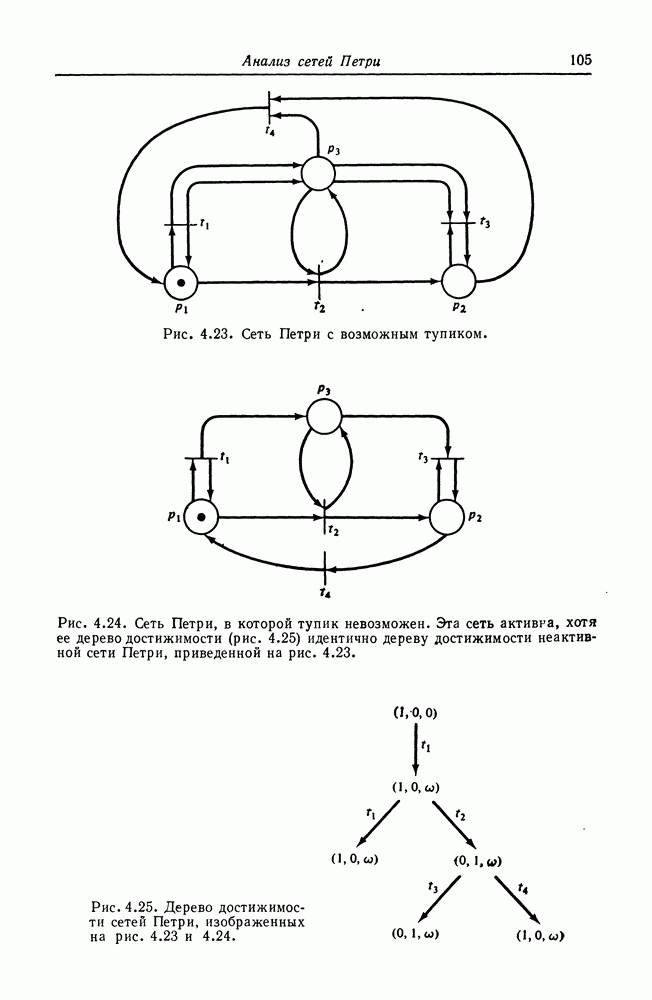
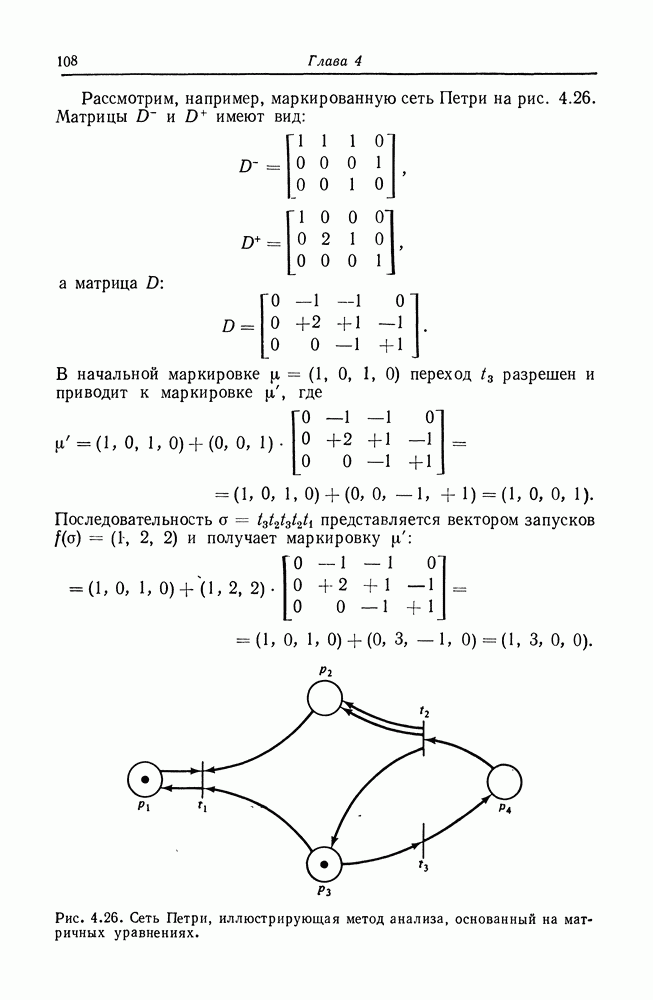
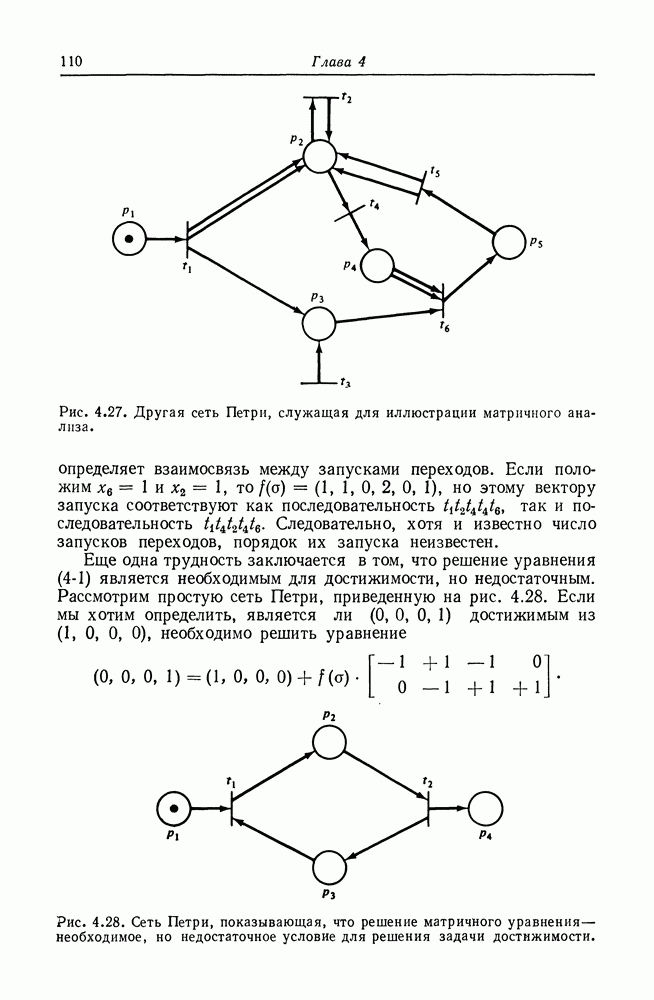
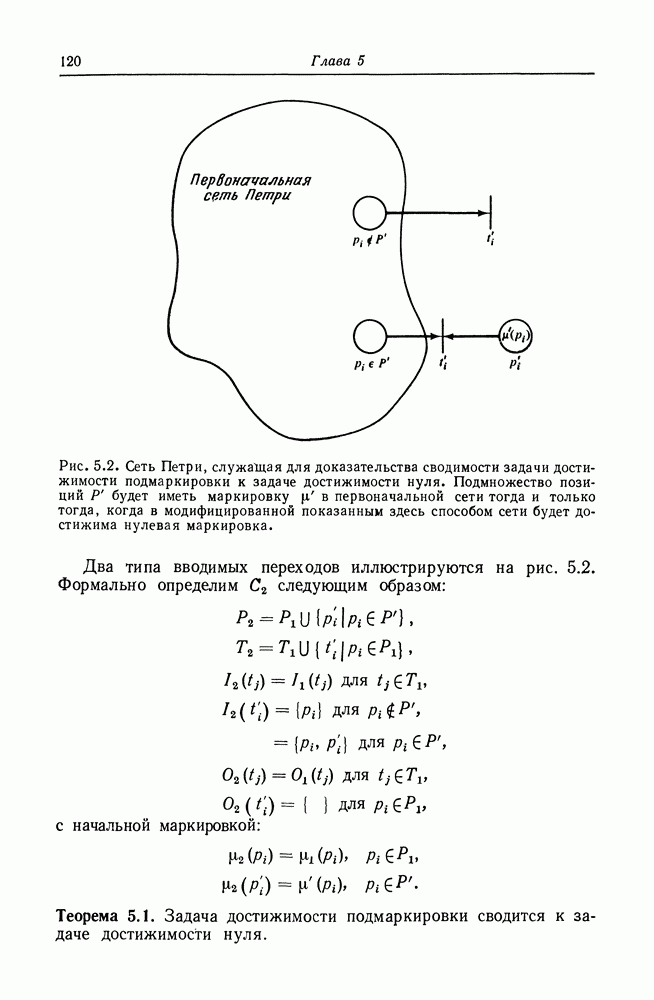
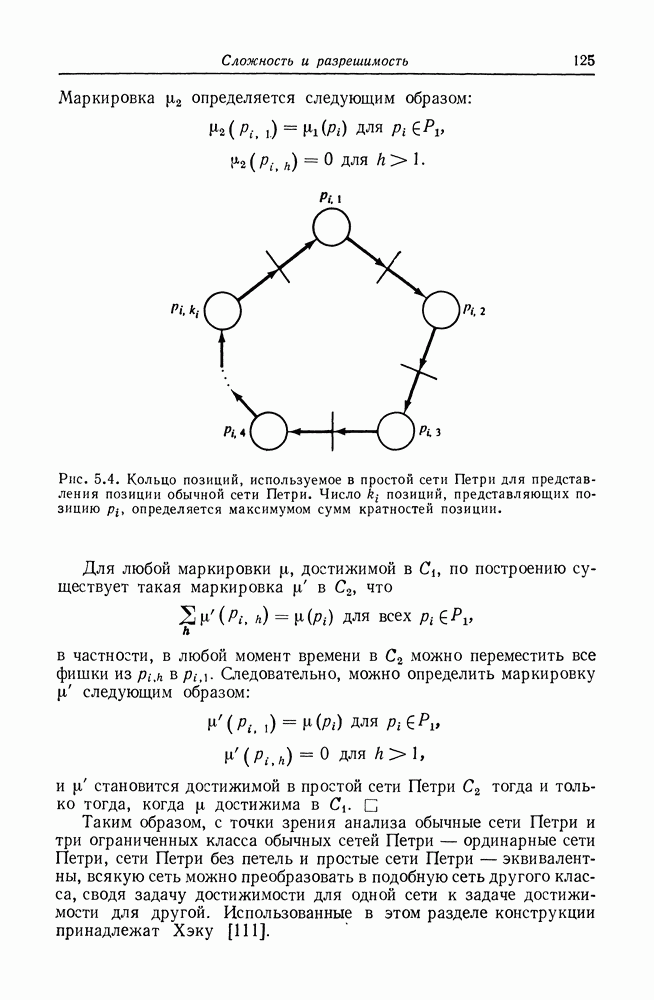
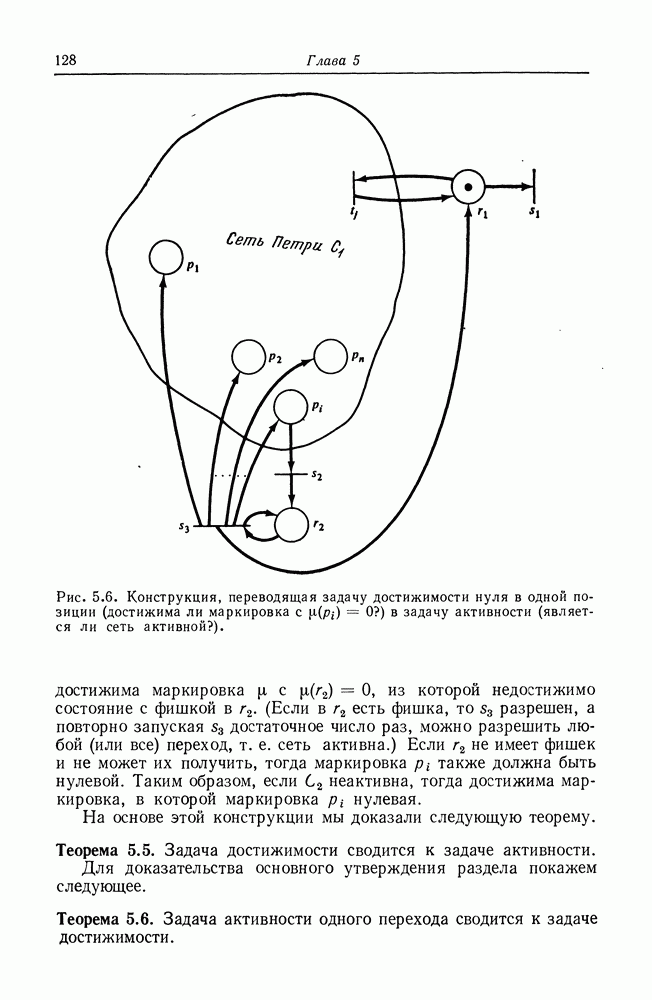
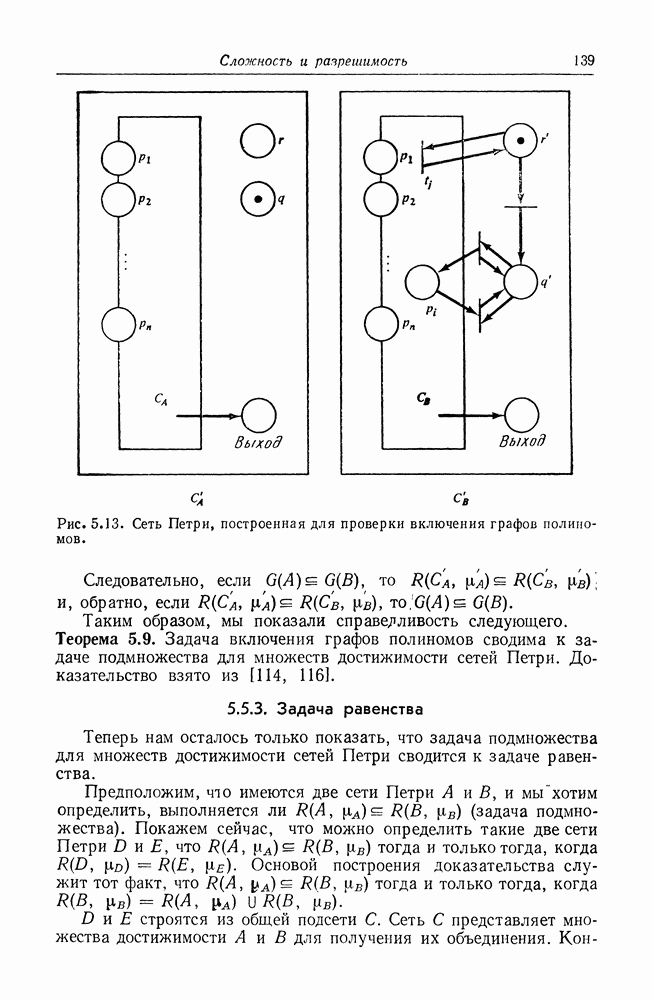
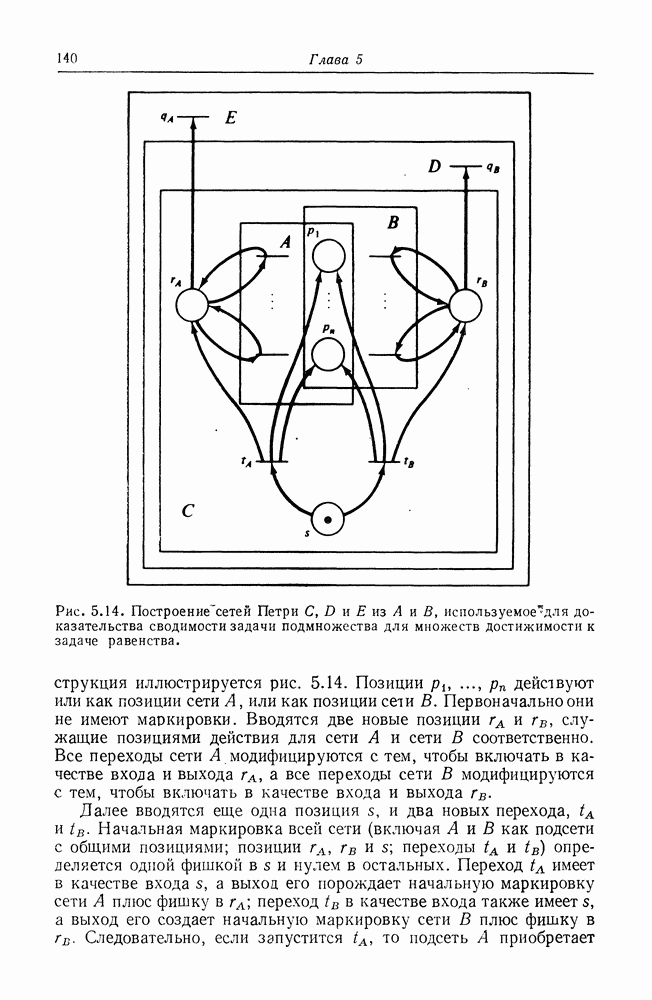
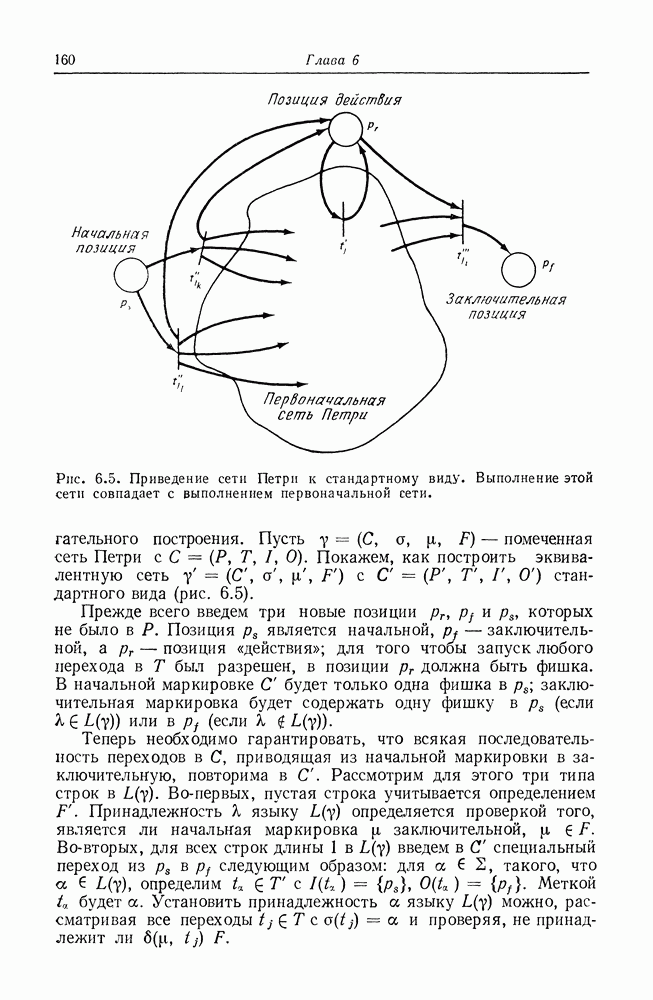
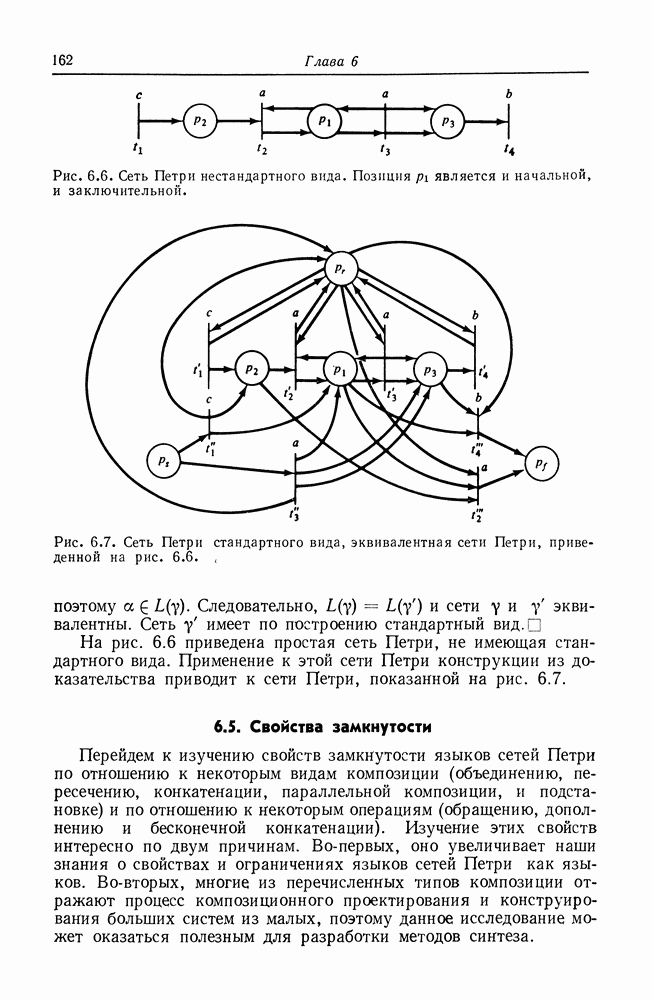
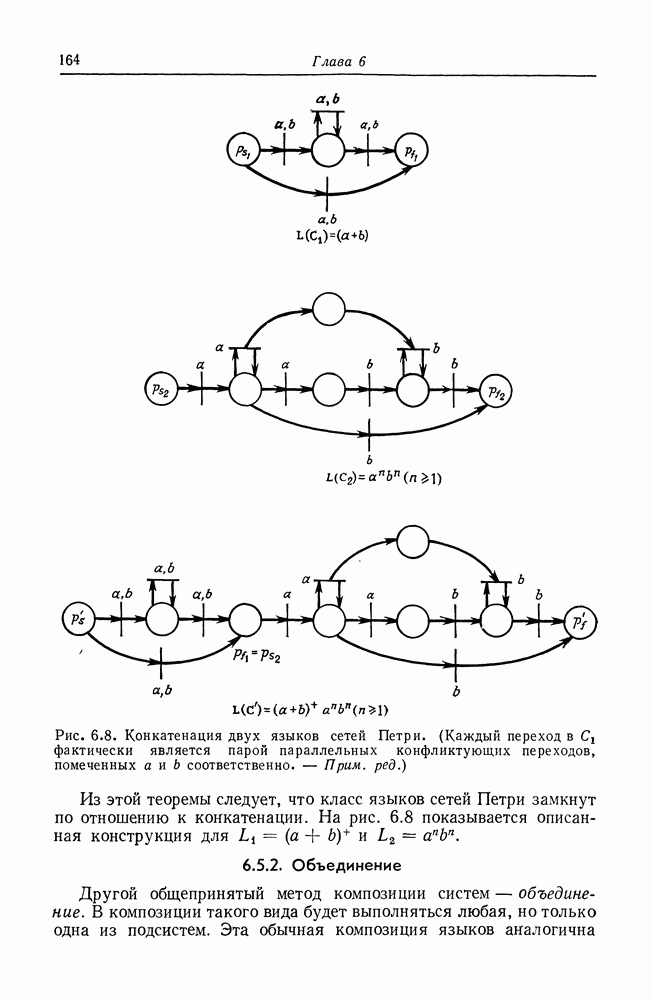
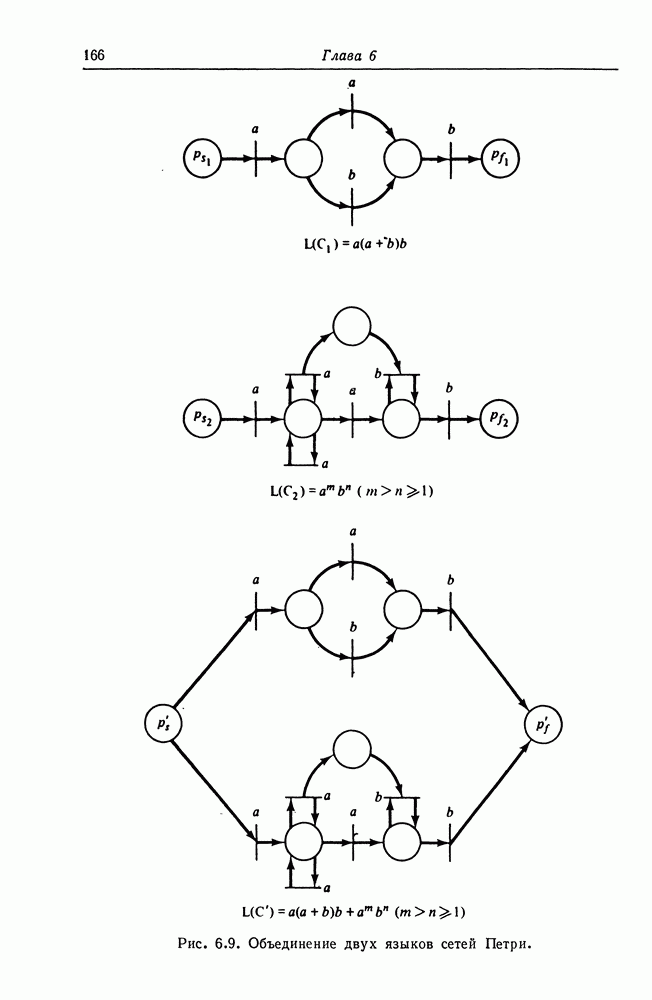
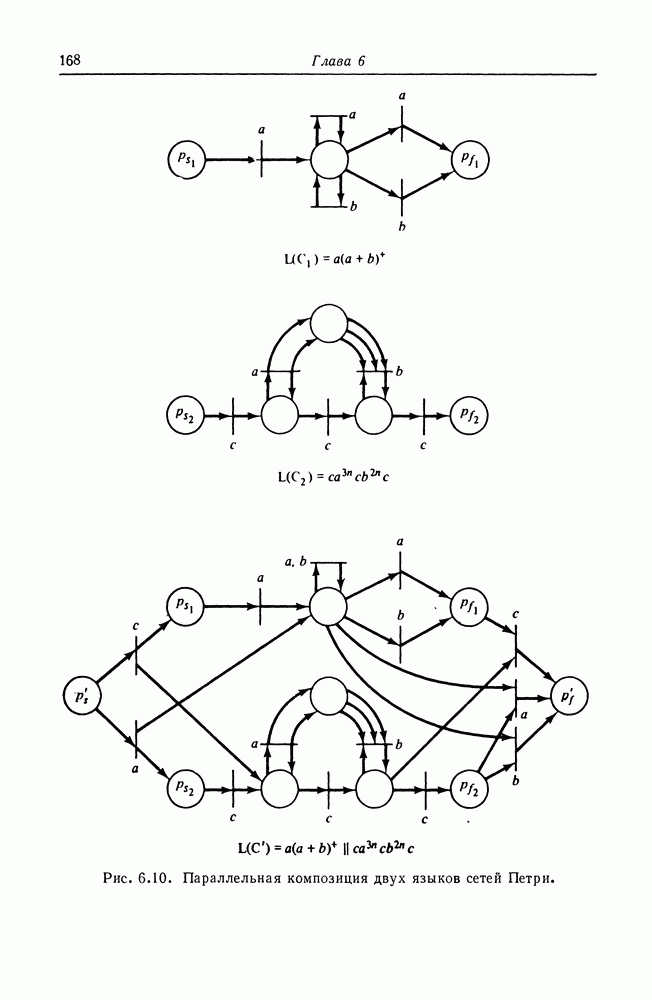
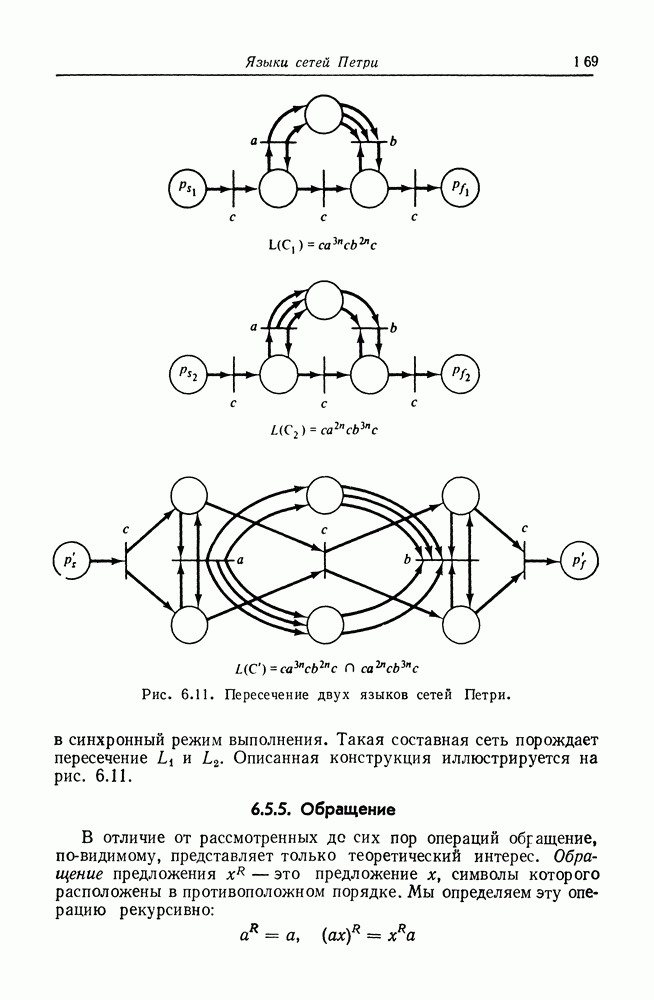
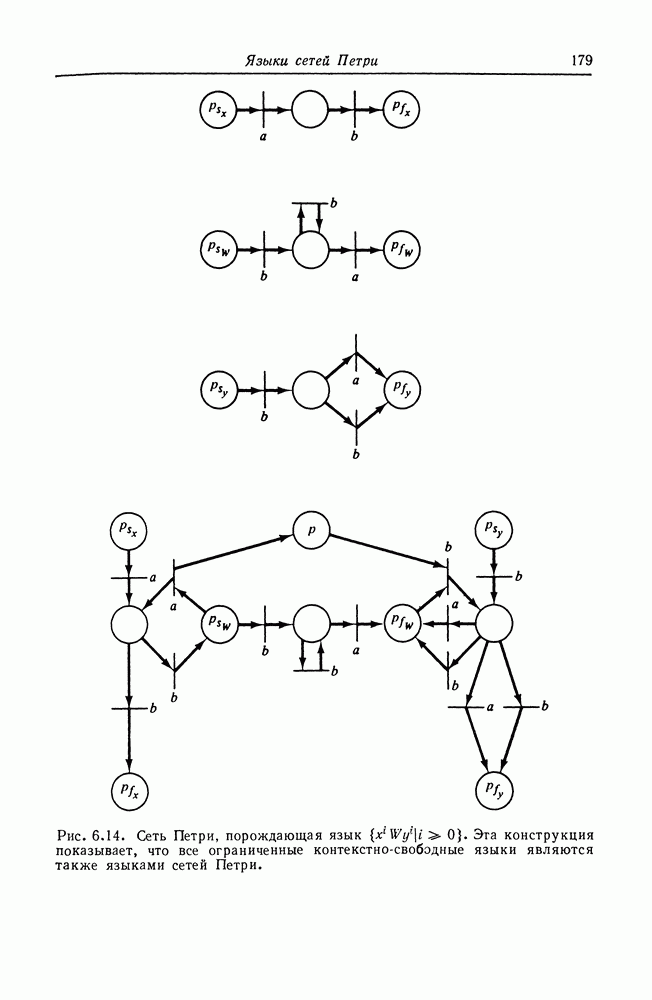
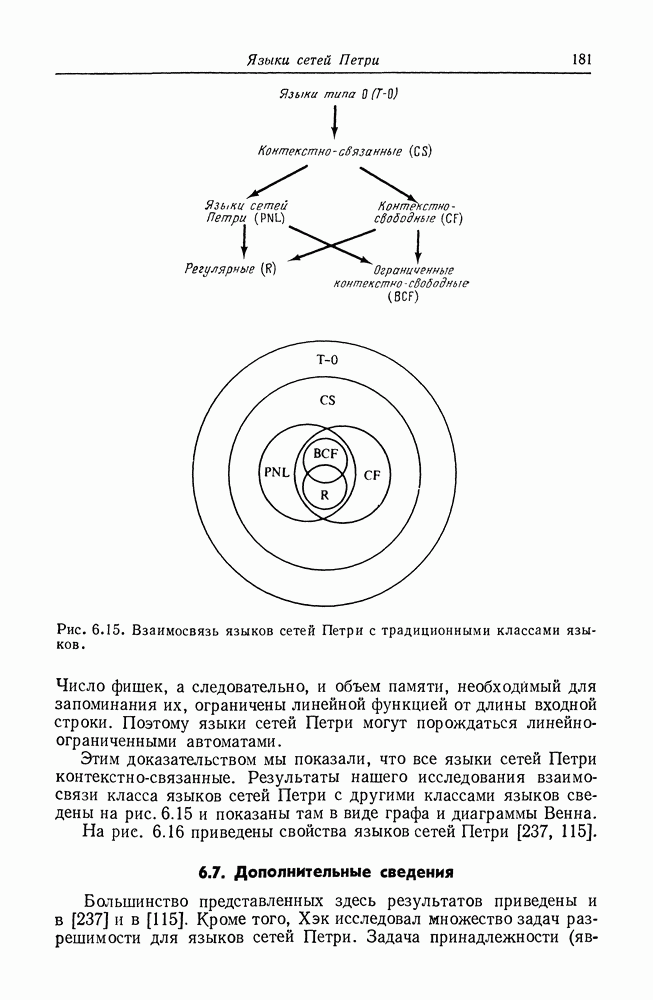
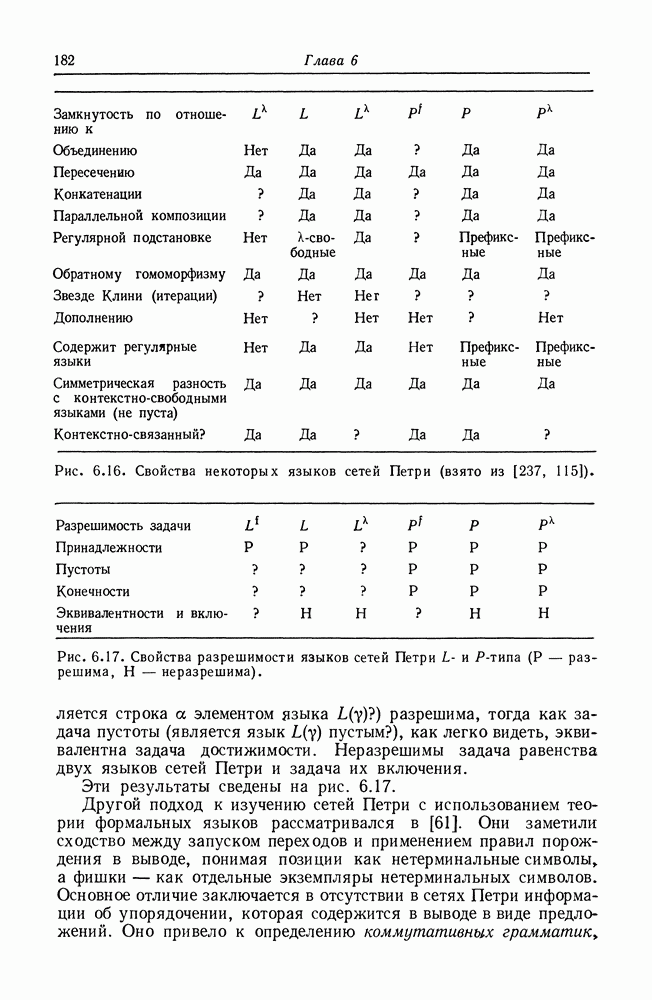
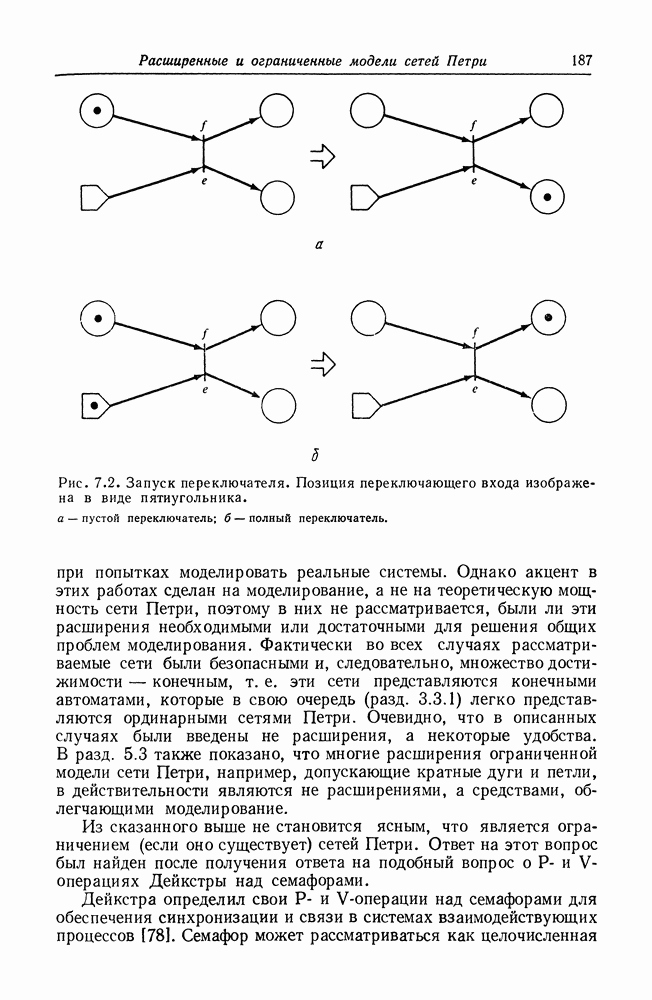
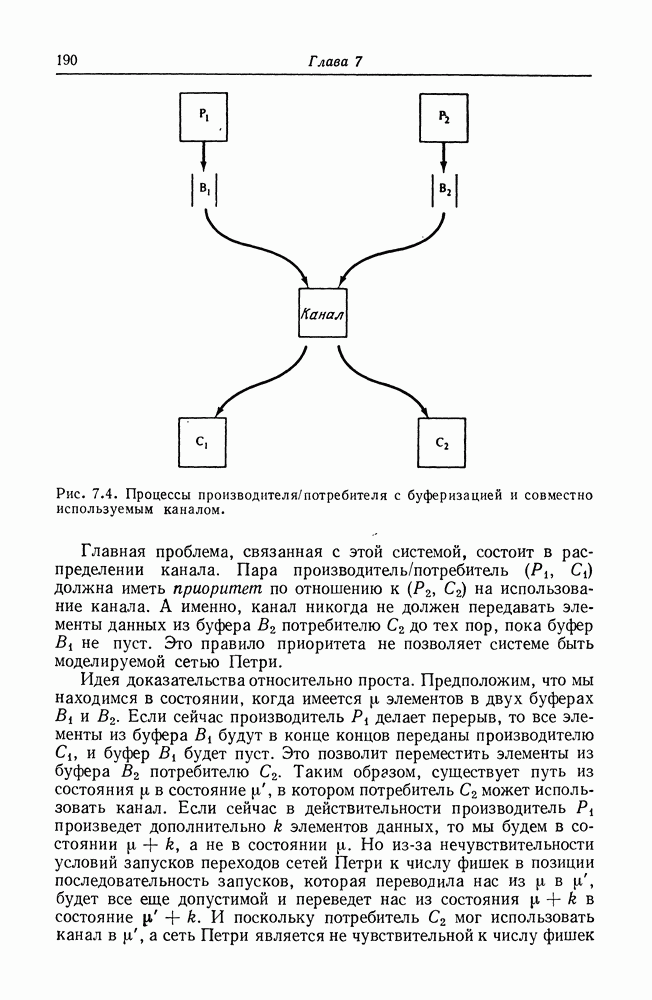
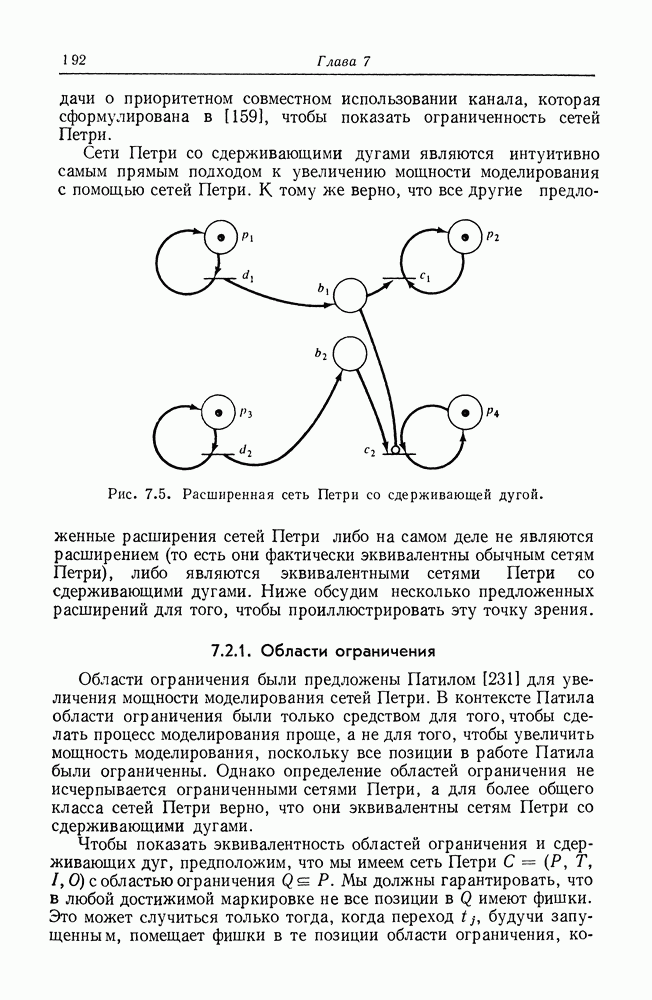
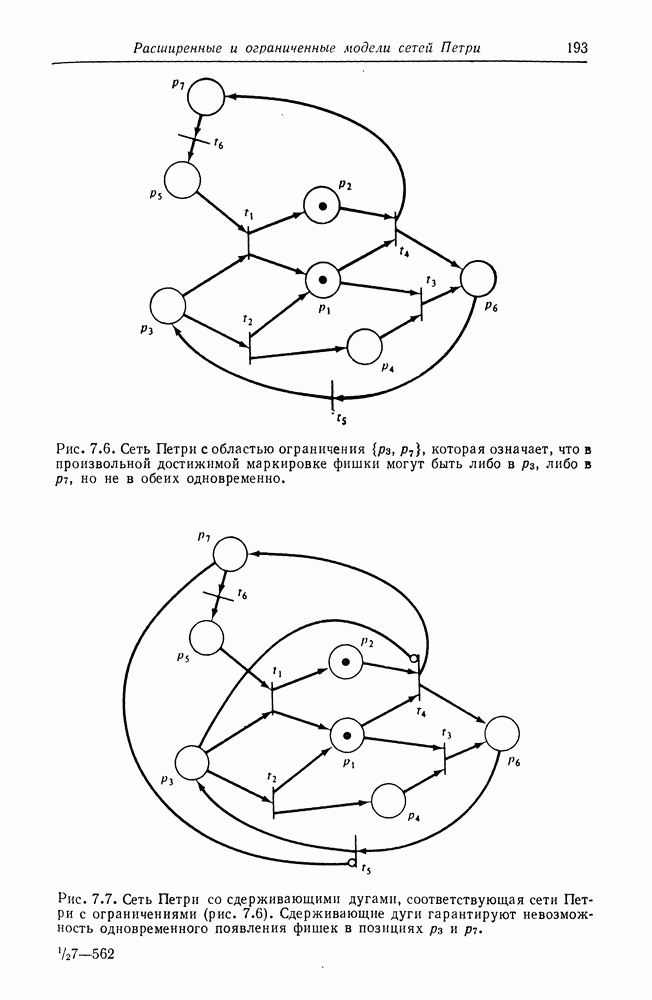
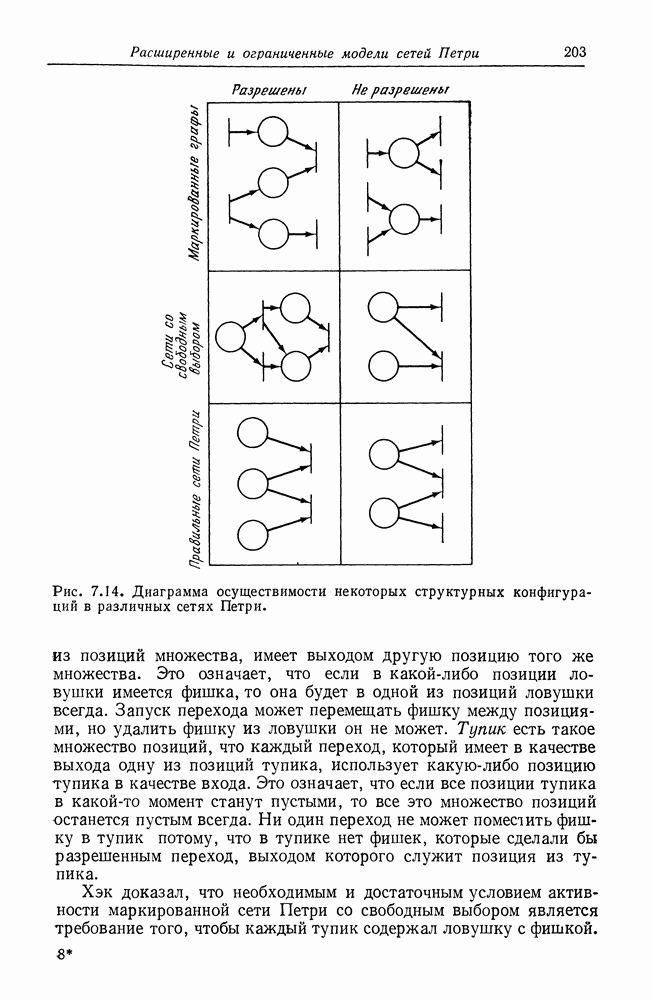
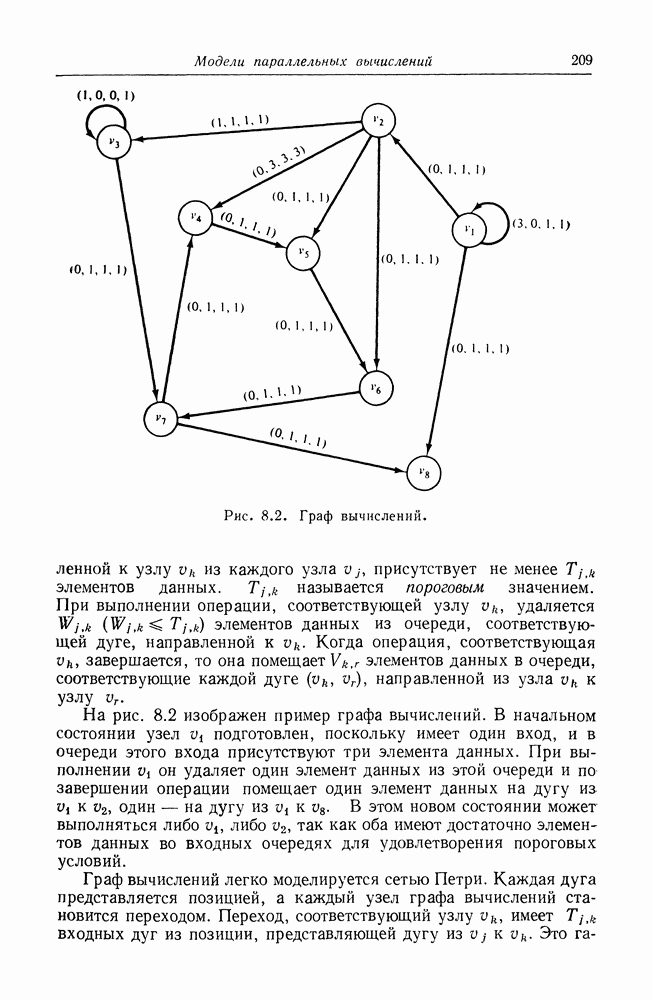
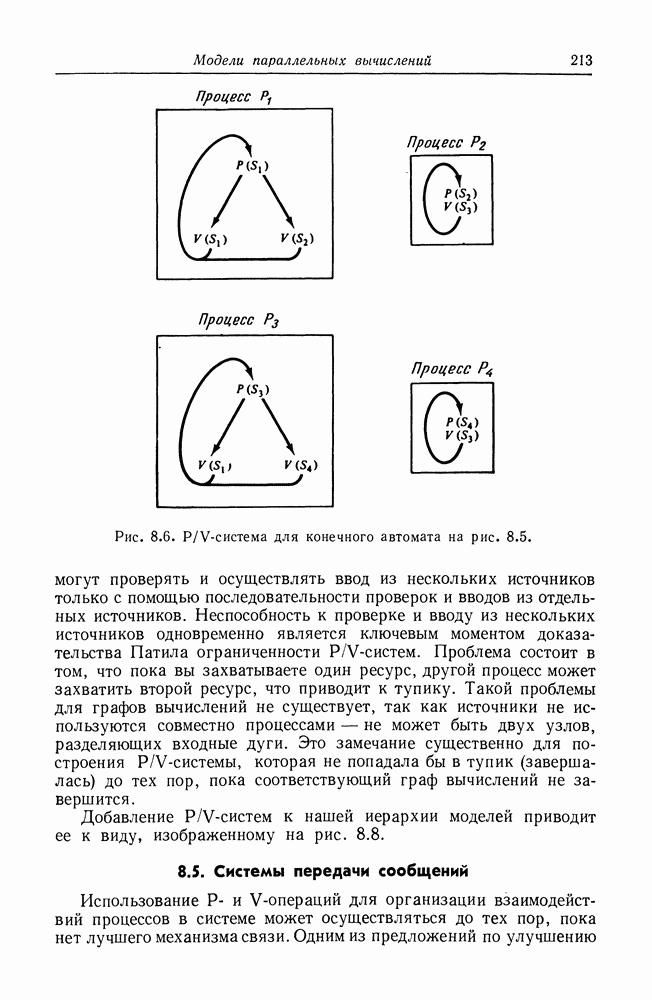
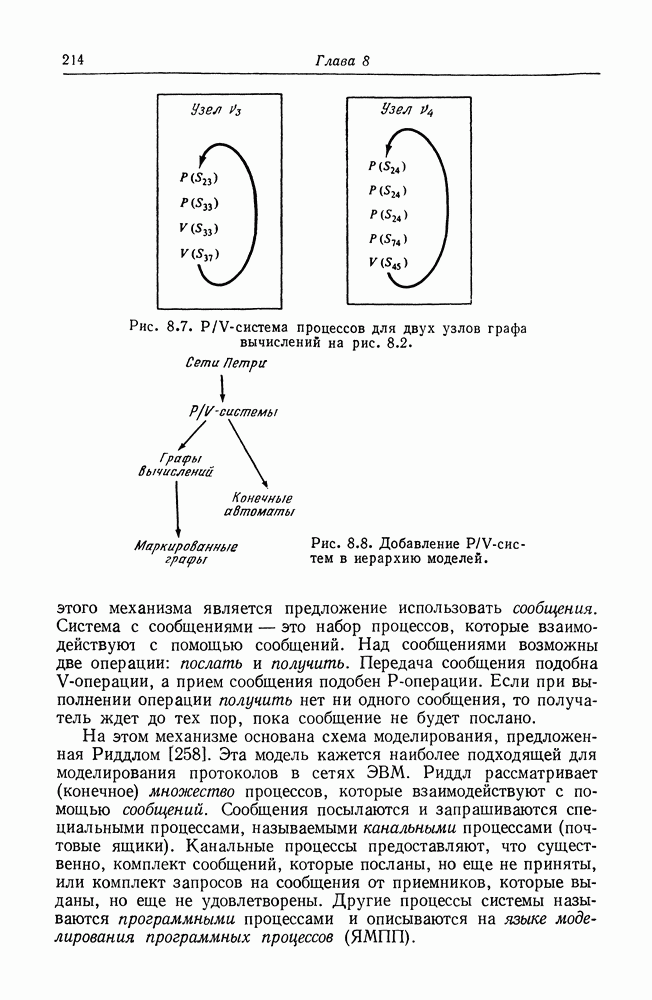
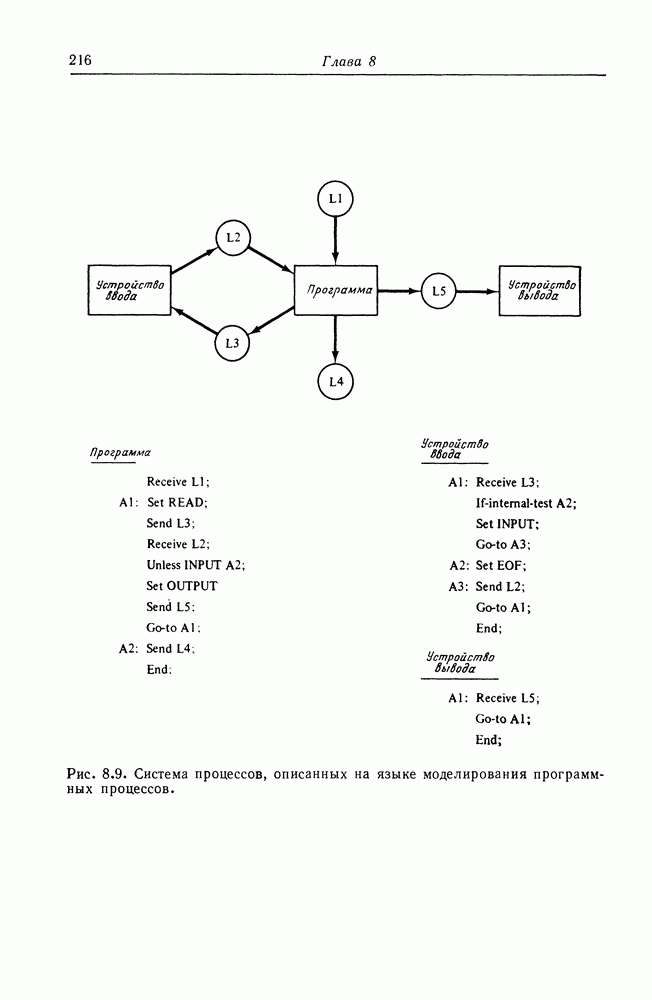
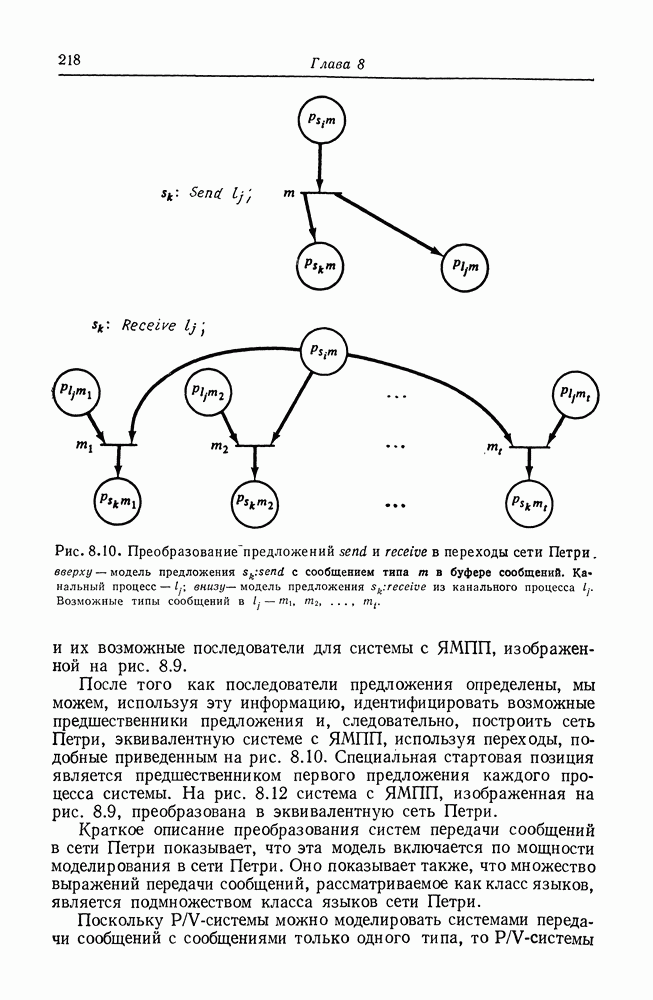
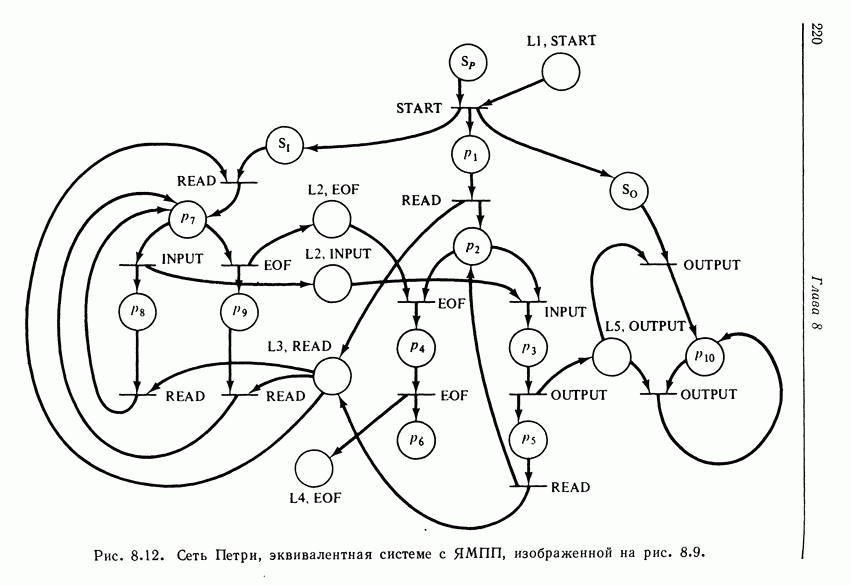
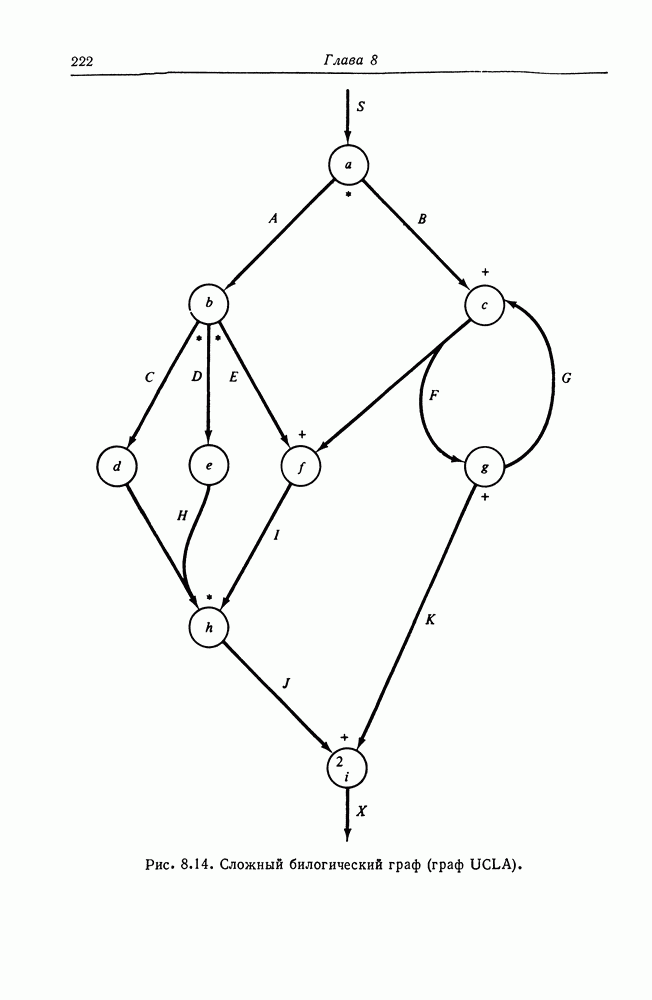
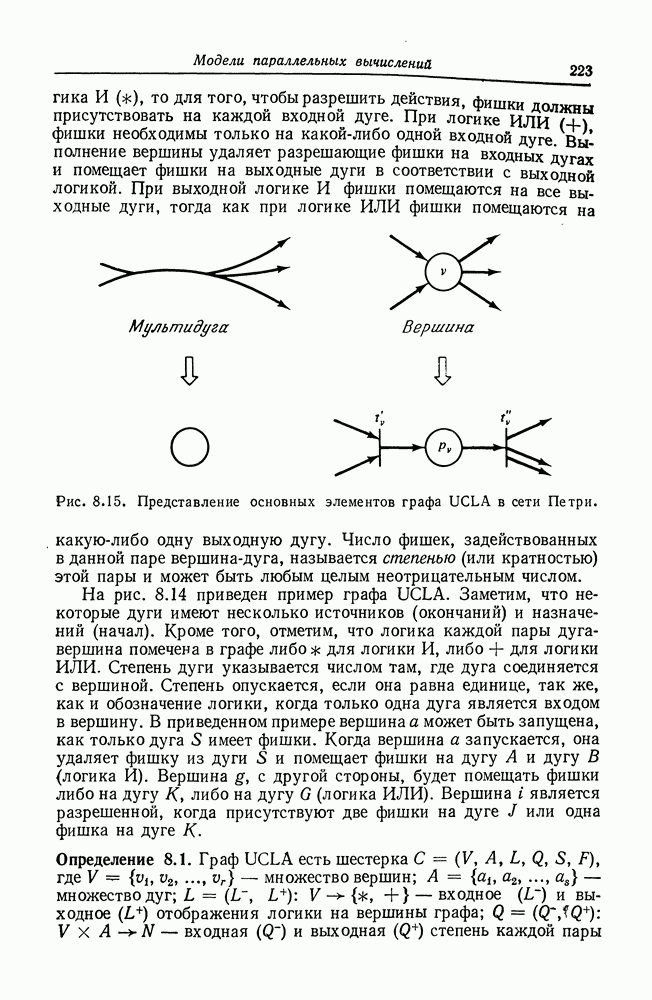
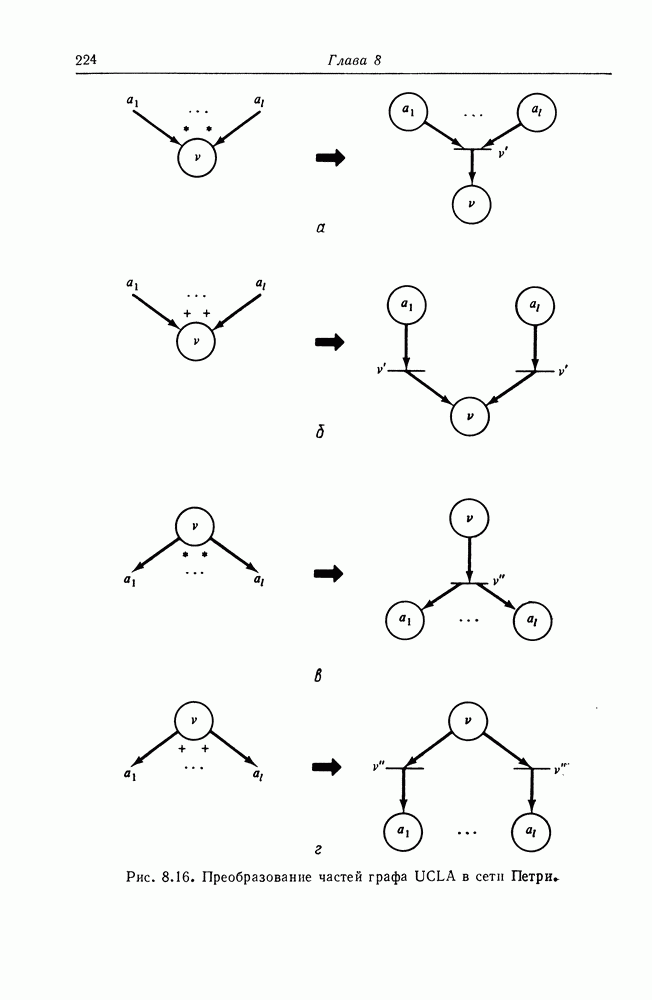
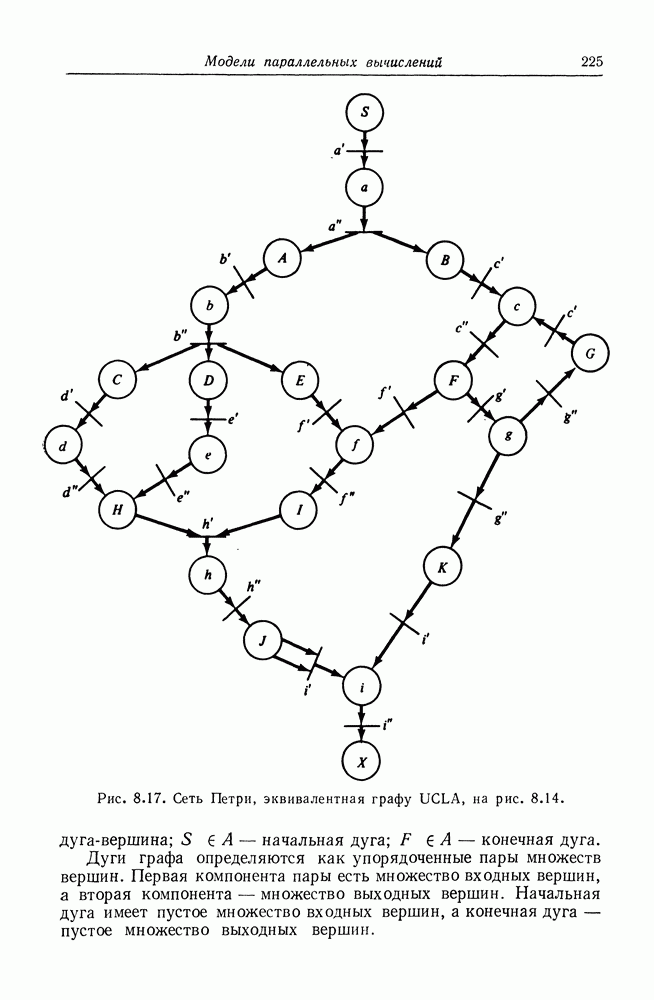
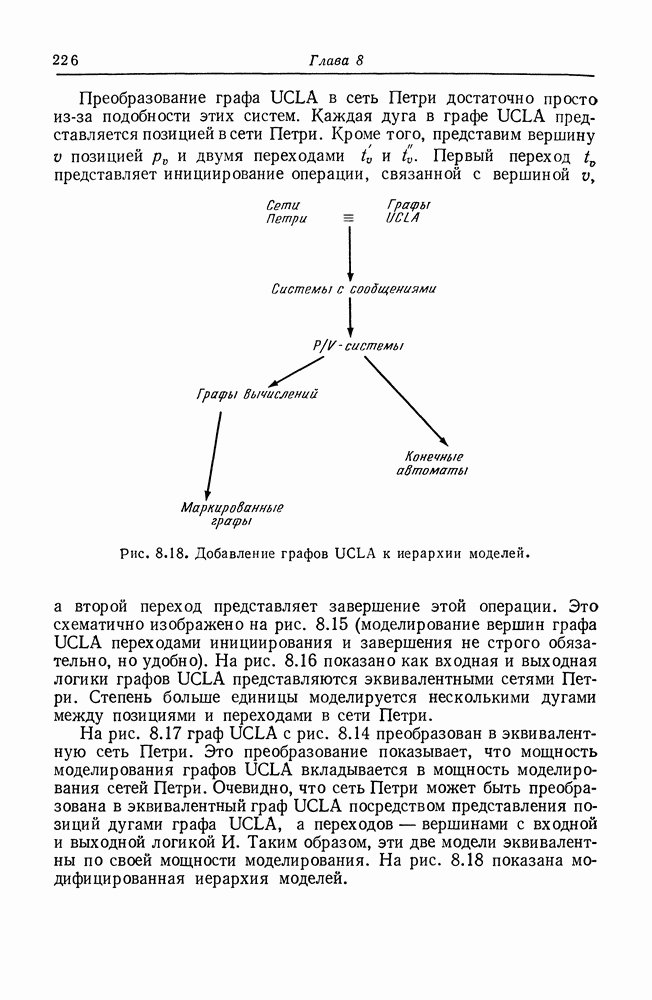
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7.3. Расширенные сети Петри и регистровые машины
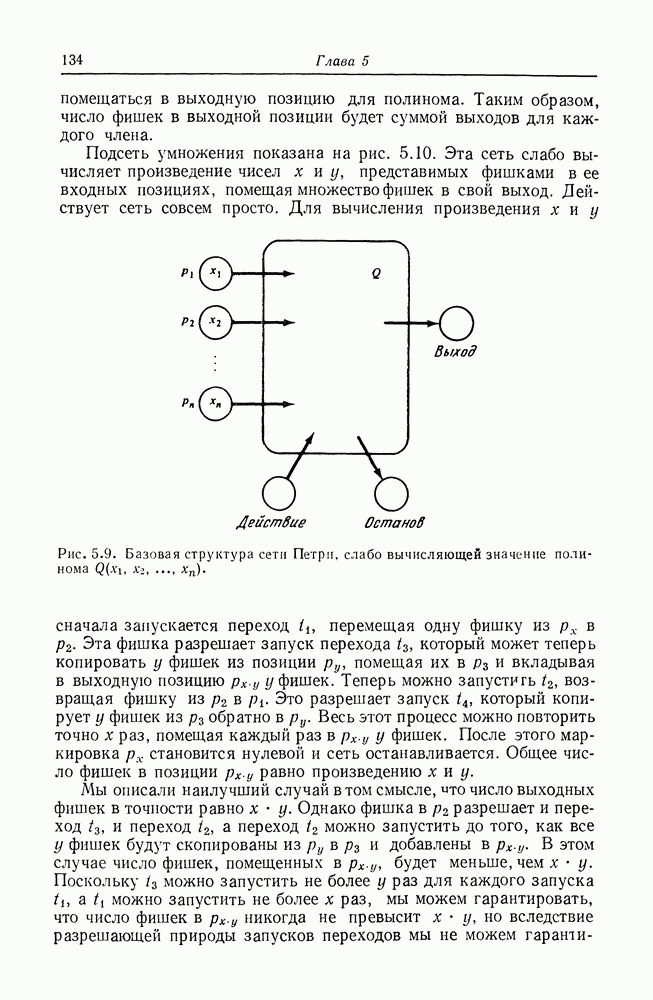
Мы показали, что все предложенные расширения модели сетей Петри допускают возможность проверки позиции на нуль. Насколько это важно по отношению к мощности разрешения сетей Петри? Влияет ли это на возможность анализа сетей Петри?
Проверка на нуль уменьшает мощность разрешения сети Петри. Агервала [4], Хэк [115], Томас [290] и др. показали, что появление способности проверки на нуль у модели сетей Петри позволяет
сетям Петри моделировать машину Тьюринга. Таким образом, сети Петри с проверкой на нуль дают схему моделирования, с помощью которой можно моделировать любую систему. Однако почти все вопросы анализа сетей Петри становятся неразрешимыми, поскольку они неразрешимы для машин Тьюринга.
Доказательство эквивалентности расширенных сетей Петри и машин Тьюринга относительно просто. Легче всего его представить в терминах регистровых машин Шепардсона и Стургиса [276] или программных машин Минского [200].
Регистровая машина есть абстрактная модель ЭВМ с несколькими регистрами, которые используются для хранения произвольно больших чисел. Для манипулирования этими регистрами пишется программа. Программа есть последовательность инструкций вида «увеличить регистр  на 1», «уменьшить регистр
на 1», «уменьшить регистр  на 1 (только если регистр
на 1 (только если регистр  не равен
не равен  «перейти к предложению
«перейти к предложению  если регистр
если регистр  не равен нулю», и т. д. Ниже представлена программа сложения содержимого регистра 2 с регистром 1.
не равен нулю», и т. д. Ниже представлена программа сложения содержимого регистра 2 с регистром 1.
1. Если регистр 2 равен нулю, то идти к инструкции 5.
2. Вычесть 1 из регистра 2.
3. Прибавить 1 к регистру 1.
4. Идти к инструкции 1.
5. Стоп.
Шепардсон и Стургис показали, что регистровая машина со следующими инструкциями эквивалентна машине Тьюринга.
1.  увеличить регистр
увеличить регистр  на 1.
на 1.
2.  уменьшить регистр
уменьшить регистр  на 1 (регистр
на 1 (регистр  не равен нулю).
не равен нулю).
3.  перейти к предложению
перейти к предложению  если регистр
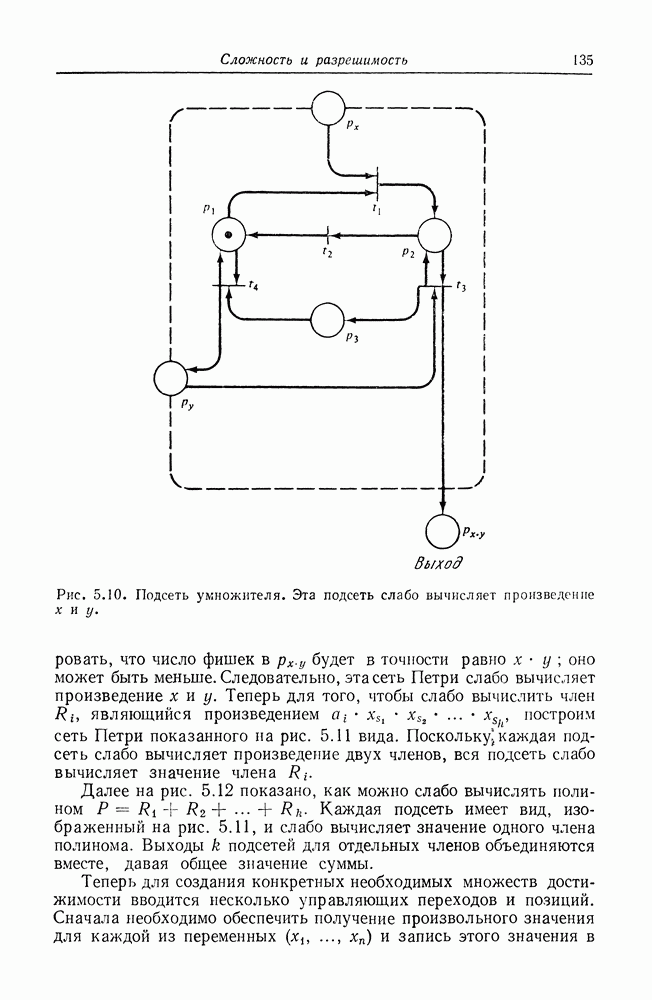
если регистр  равен нулю. Таким образом, если регистровая машина может быть преобразована в эквивалентную сеть Петри, то тем самым будет показано, что расширенные сети Петри эквивалентны регистровым машинам. Это преобразование относительно просто.
равен нулю. Таким образом, если регистровая машина может быть преобразована в эквивалентную сеть Петри, то тем самым будет показано, что расширенные сети Петри эквивалентны регистровым машинам. Это преобразование относительно просто.
Для представления регистровой машины расширенной сетью Петри представим  регистров, используемых в программе,
регистров, используемых в программе,  позициями
позициями  Мы также используем
Мы также используем  позицию для представления положения счетчика инструкций либо перед предложением 1 (начальная маркировка), либо после предложения
позицию для представления положения счетчика инструкций либо перед предложением 1 (начальная маркировка), либо после предложения  для
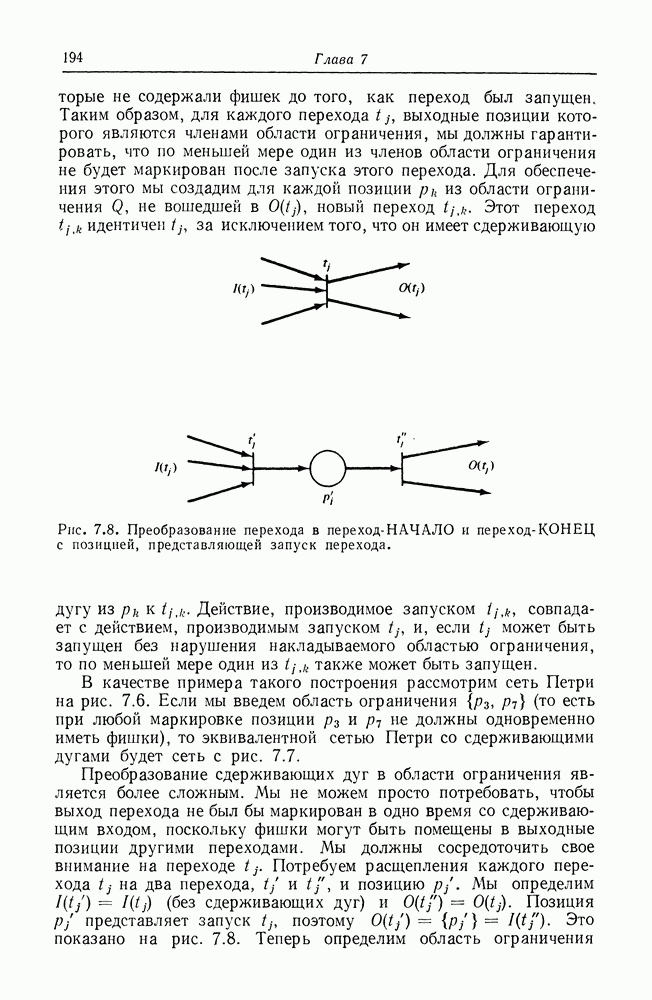
для  В программе из
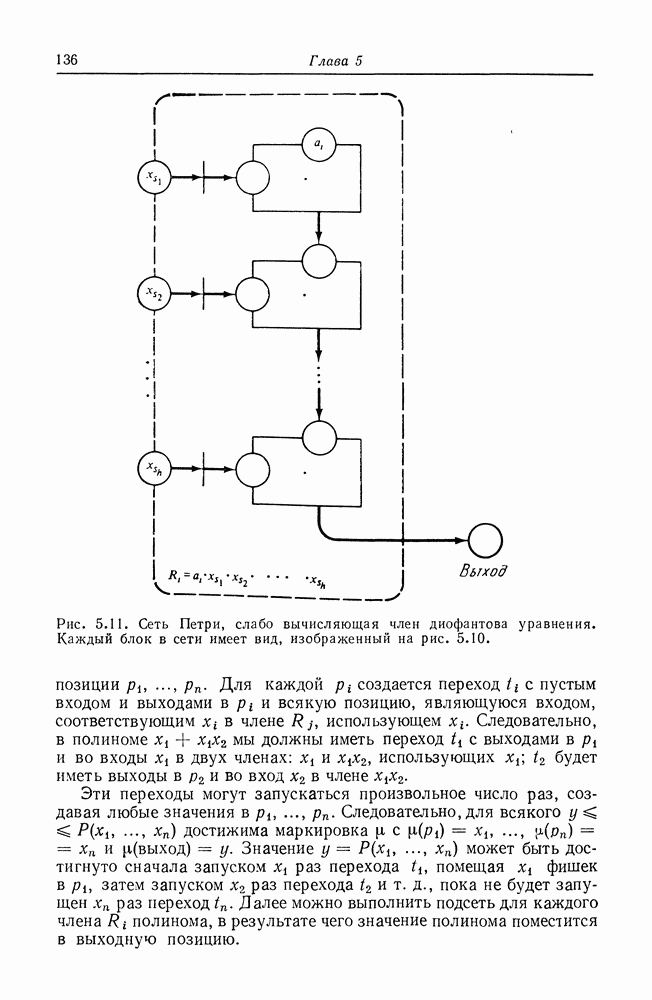
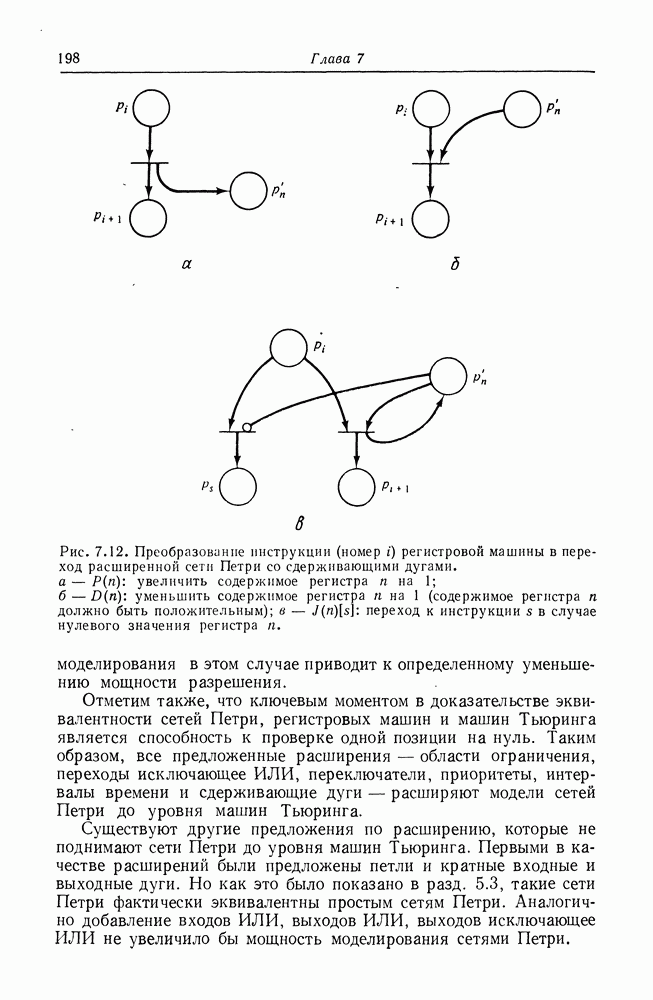
В программе из  предложений. Каждая инструкция в программе представляется переходом. На рис. 7.12 показано, как каждая из трех вышеприведенных инструкций представляется переходом в расширенной сети Петри. Из этого видно, что регистровая машина может быть преобразована в расширенную сеть Петри, и, следовательно, расширенная сеть Петри эквивалентна машине Тьюринга. Эта эквивалентность машине Тьюринга разрушает все надежды на возможность анализа расширенных сетей Петри. Однако это же доказывает, что расширенные сети Петри могут моделировать любую систему (или по крайней мере любую вычислимую систему). Таким образом, мы видим, что увеличение мощности
предложений. Каждая инструкция в программе представляется переходом. На рис. 7.12 показано, как каждая из трех вышеприведенных инструкций представляется переходом в расширенной сети Петри. Из этого видно, что регистровая машина может быть преобразована в расширенную сеть Петри, и, следовательно, расширенная сеть Петри эквивалентна машине Тьюринга. Эта эквивалентность машине Тьюринга разрушает все надежды на возможность анализа расширенных сетей Петри. Однако это же доказывает, что расширенные сети Петри могут моделировать любую систему (или по крайней мере любую вычислимую систему). Таким образом, мы видим, что увеличение мощности
Рис. 7.12. (см. скан) Преобразование инструкции  регистровой машины в переход расширенной сети Петри со сдерживающими дугами. а
регистровой машины в переход расширенной сети Петри со сдерживающими дугами. а  увеличить содержимое регистра
увеличить содержимое регистра  на 1;
на 1;  уменьшить содержимое регистра
уменьшить содержимое регистра  на 1 (содержимое регистра
на 1 (содержимое регистра  должно быть положительным); в —
должно быть положительным); в —  переход к инструкции
переход к инструкции  в случае нулевого значения регистра
в случае нулевого значения регистра 
моделирования в этом случае приводит к определенному уменьшению мощности разрешения.
Отметим также, что ключевым моментом в доказательстве эквивалентности сетей Петри, регистровых машин и машин Тьюринга является способность к проверке одной позиции на нуль. Таким образом, все предложенные расширения — области ограничения, переходы исключающее ИЛИ, переключатели, приоритеты, интервалы времени и сдерживающие дуги — расширяют модели сетей Петри до уровня машин Тьюринга.
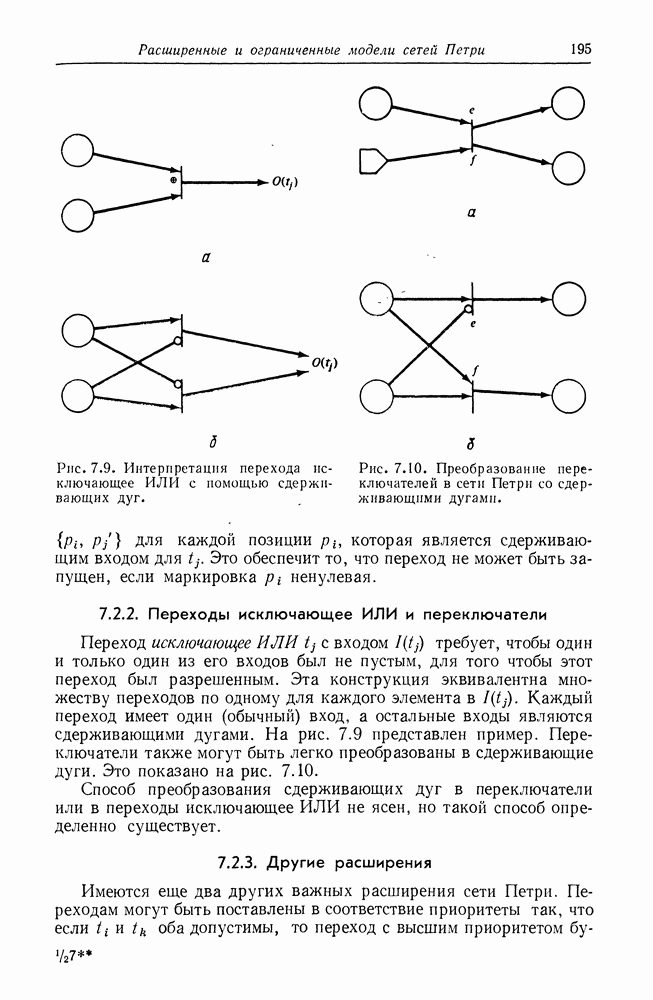
Существуют другие предложения по расширению, которые не поднимают сети Петри до уровня машин Тьюринга. Первыми в качестве расширений были предложены петли и кратные входные и выходные дуги. Но как это было показано в разд. 5.3, такие сети Петри фактически эквивалентны простым сетям Петри. Аналогично добавление входов ИЛИ, выходов ИЛИ, выходов исключающее ИЛИ не увеличило бы мощность моделирования сетями Петри.
Вообще, кажется, что любое расширение, которое не позволяет проверку на нуль, в действительности не увеличивает мощность моделирования (или не уменьшает мощность разрешения) сетей Петри, но приводит просто к другой эквивалентной формулировке модели сети Петри (может возрасти удобство моделирования). В то же самое время любое расширение, которое разрешает проверку на нуль, увеличивает мощность моделирования до уровня машин Тьюринга и сводит мощность разрешения к нулю.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ГЛАВА 1. ВВЕДЕНИЕ
- ГЛАВА 2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
- 2.1. Структура сети Петри
- 2.2. Графы сетей Петри
- 2.3. Маркировка сетей Петри
- 2.4. Правила выполнения сетей Петри
- 2.5. Пространство состояний сети Петри
- 2.6. Альтернативные формы определения сетей Петри
- ГЛАВА 3. СЕТИ ПЕТРИ ДЛЯ МОДЕЛИРОВАНИЯ
- 3.2. Одновременность и конфликт
- 3.3. Аппаратное обеспечение ЭВМ
- 3.4. Программное обеспечение ЭВМ
- 3.5. Другие системы
- ГЛАВА 4. АНАЛИЗ СЕТЕЙ ПЕТРИ
- 4.1. Задачи анализа сетей Петри
- 4.2. Методы анализа
- ГЛАВА 5. СЛОЖНОСТЬ И РАЗРЕШИМОСТЬ
- 5.1. Сводимость задач анализа
- 5.2. Задачи достижимости
- 5.3. Сети Петри с ограничениями
- 5.4. Активность и достижимость
- 5.5. Неразрешимые задачи
- 5.6. Сложность задачи достижимости
- ГЛАВА 6. ЯЗЫКИ СЕТЕЙ ПЕТРИ
- 6.2. Некоторые понятия теории формальных языков
- 6.3. Определения языков сетей Петри
- 6.4. Свойства языков сетей Петри
- 6.5. Свойства замкнутости
- 6.6. Языки сетей Петри и другие классы языков
- ГЛАВА 7. РАСШИРЕННЫЕ И ОГРАНИЧЕННЫЕ МОДЕЛИ СЕТЕЙ ПЕТРИ
- 7.1. Границы возможностей моделирования с помощью сетей Петри
- 7.2. Расширения
- 7.3. Расширенные сети Петри и регистровые машины
- 7.4. Подклассы сетей Петри
- ГЛАВА 8. МОДЕЛИ ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ
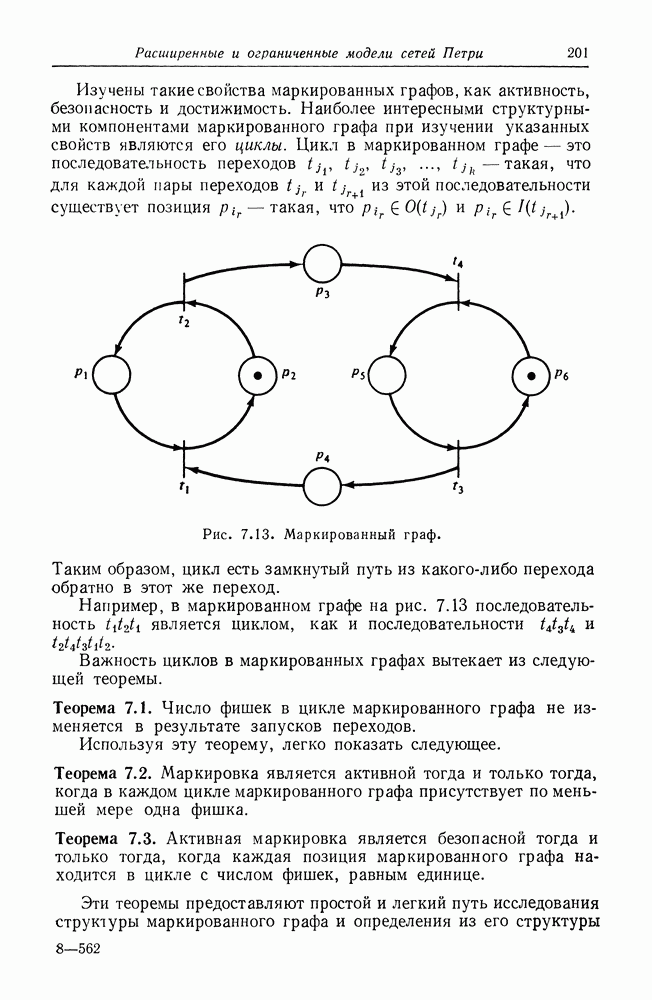
- 8.2. Маркированные графы
- 8.3. Графы вычислений
- 8.4. P/V-системы
- 8.5. Системы передачи сообщений
- 8.6. Графы UCLA
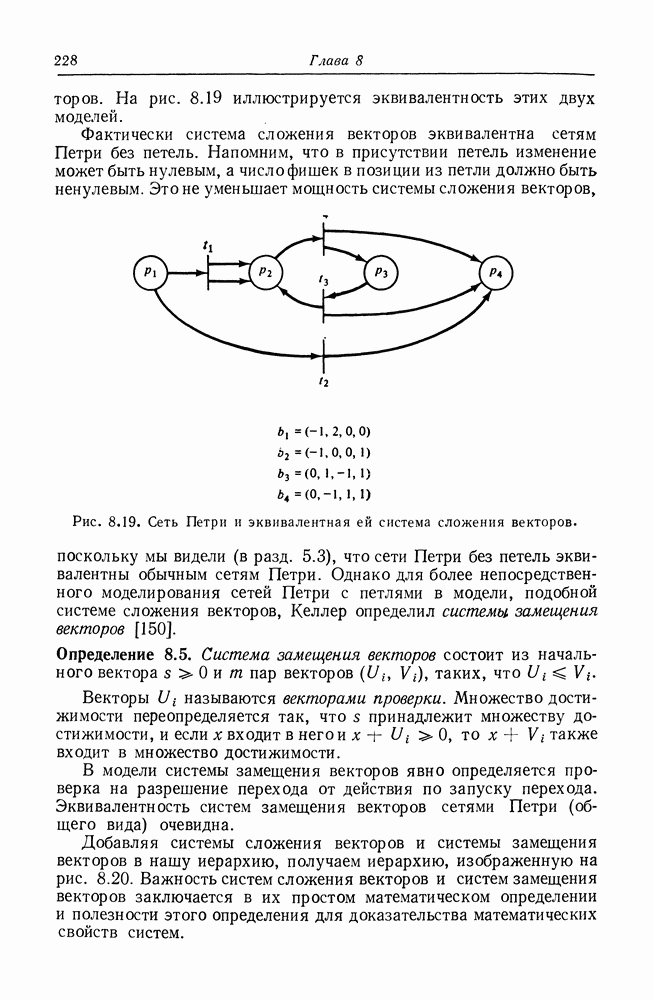
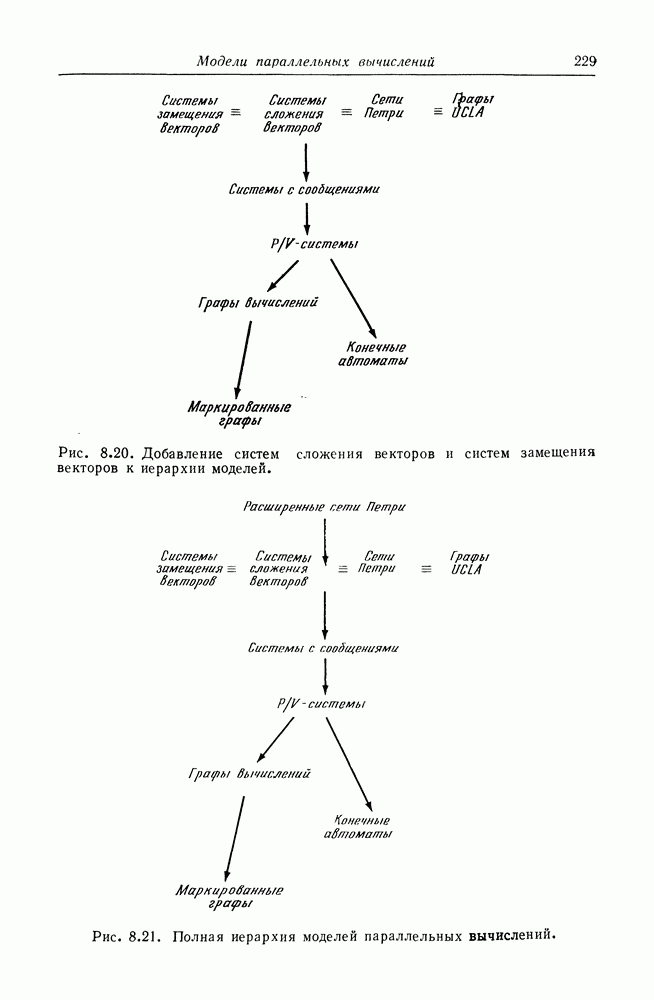
- 8.7. Системы замещения и сложения векторов
- 8.8. Расширенные модели сетей Петри
- ОБЗОР ТЕОРИИ КОМПЛЕКТОВ
- АННОТИРОВАННАЯ БИБЛИОГРАФИЯ