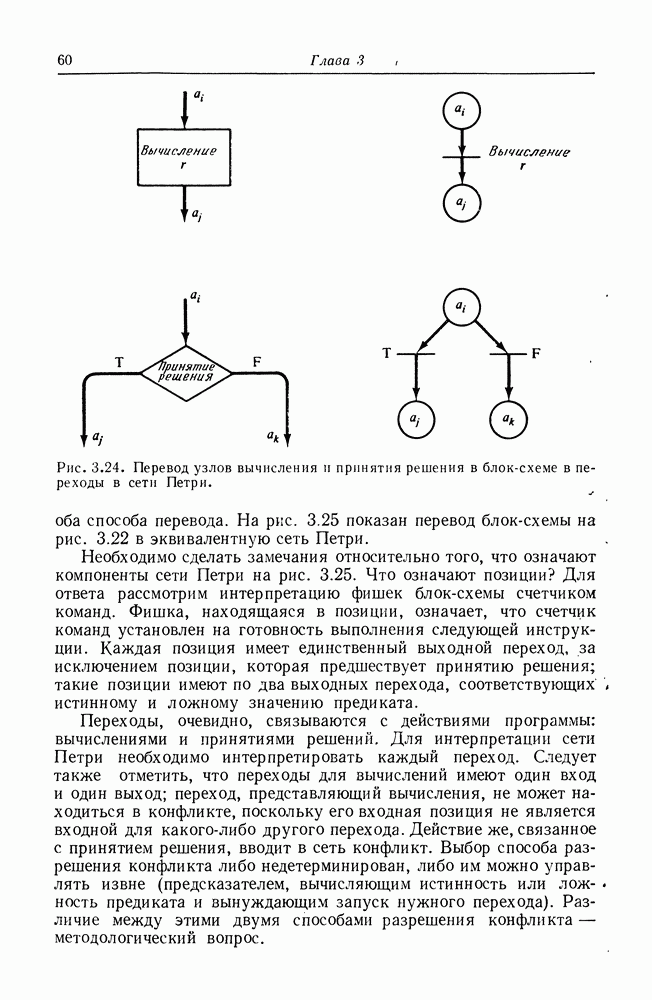
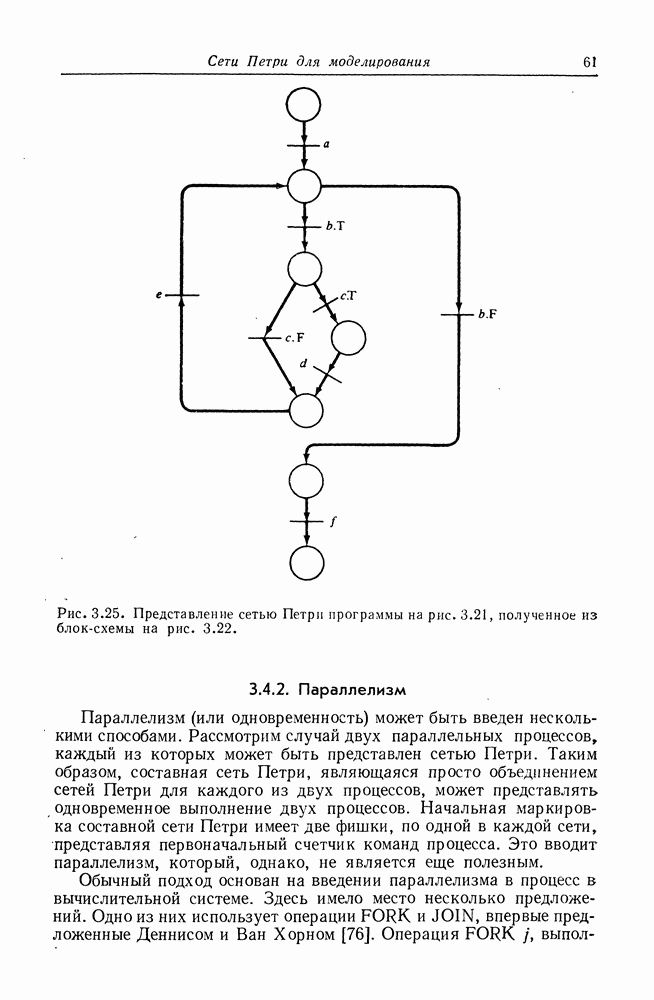
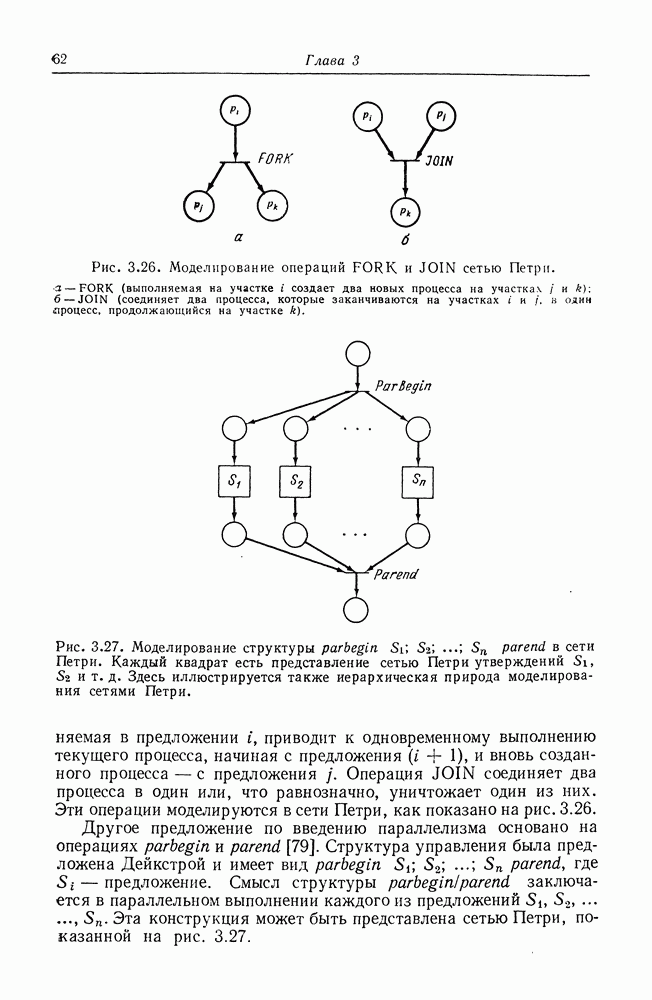
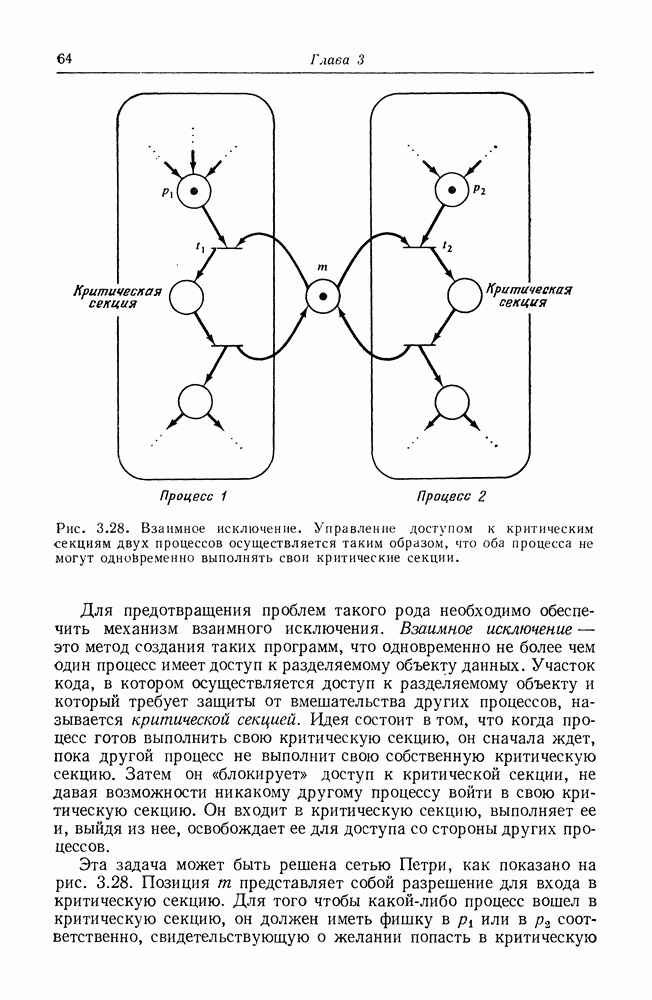
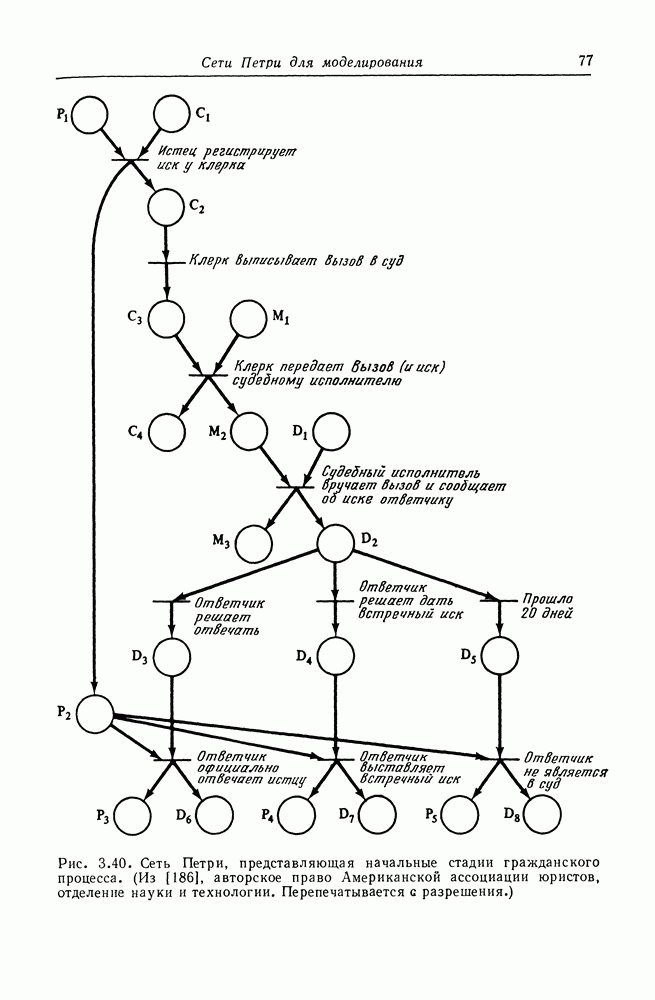
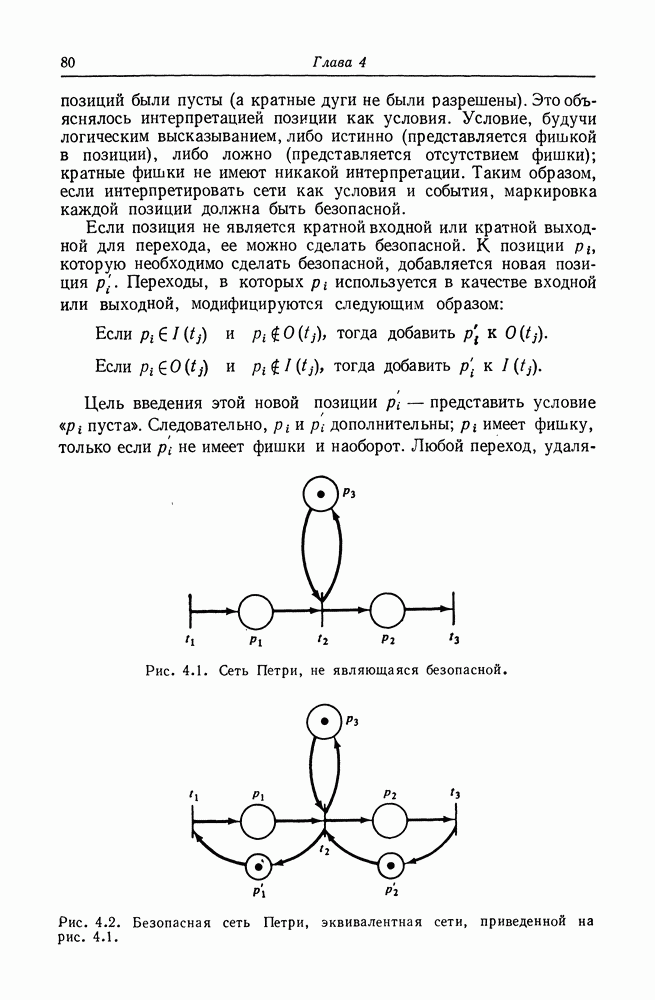
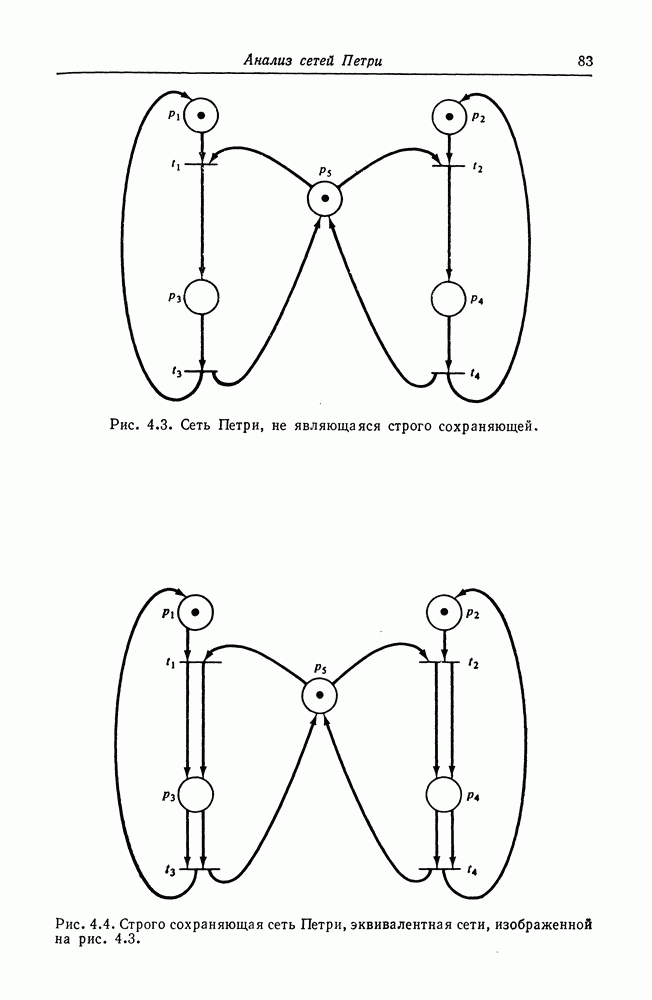
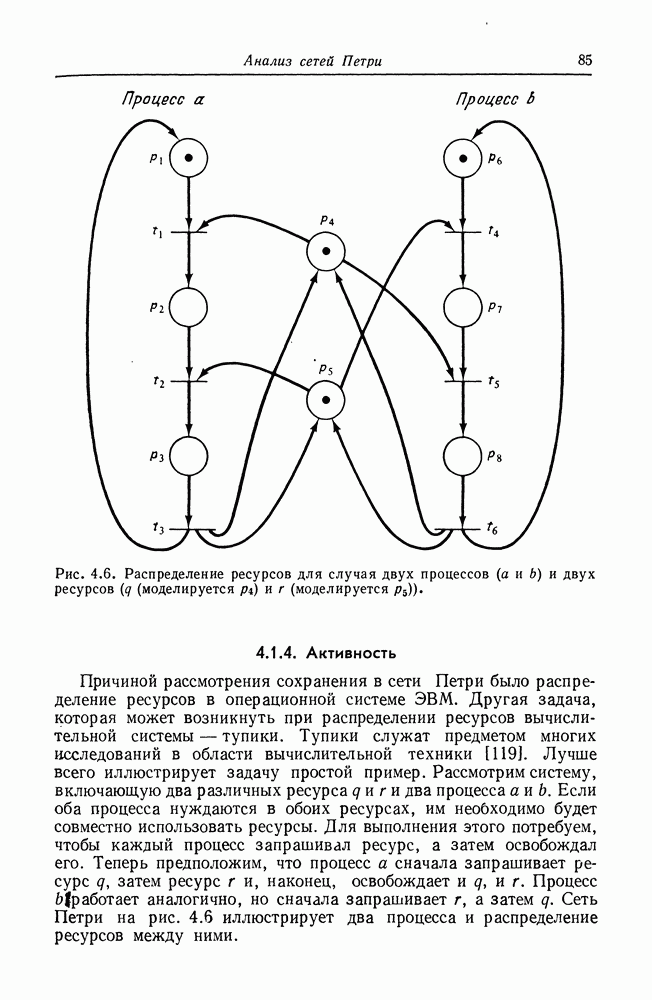
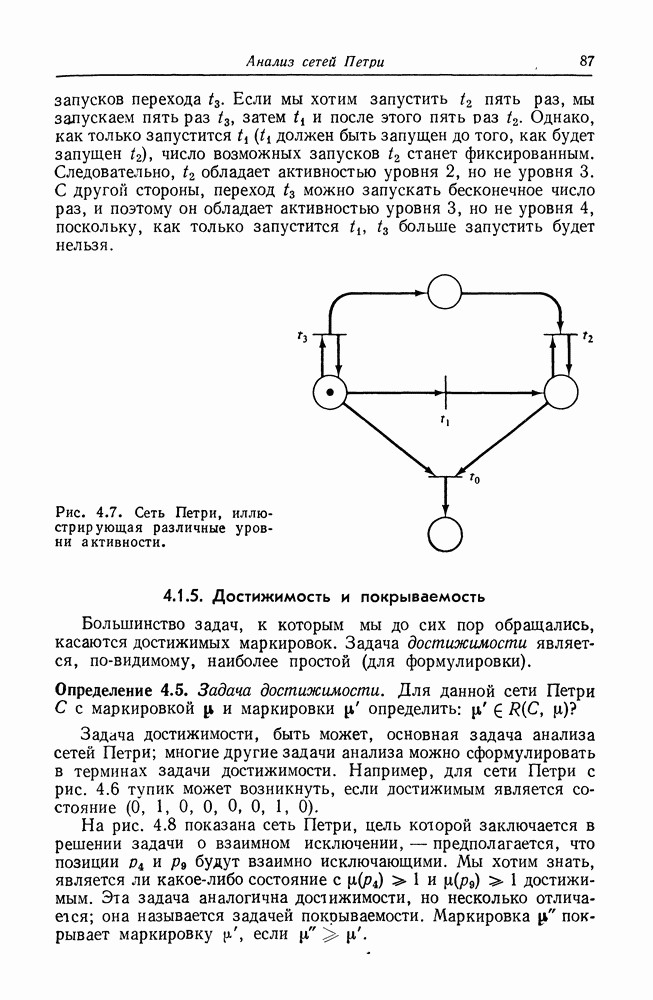
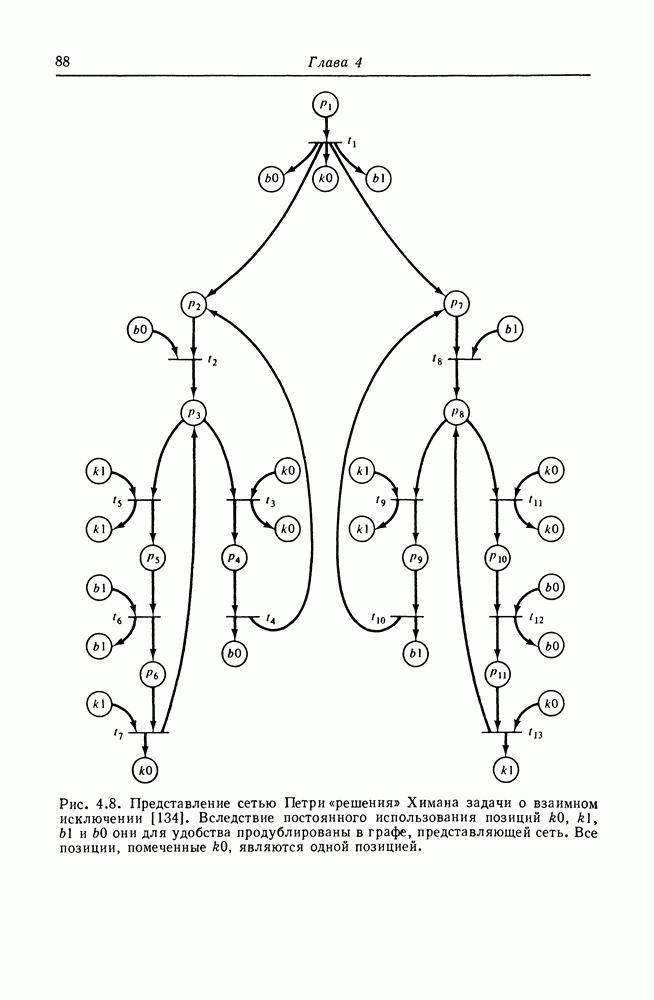
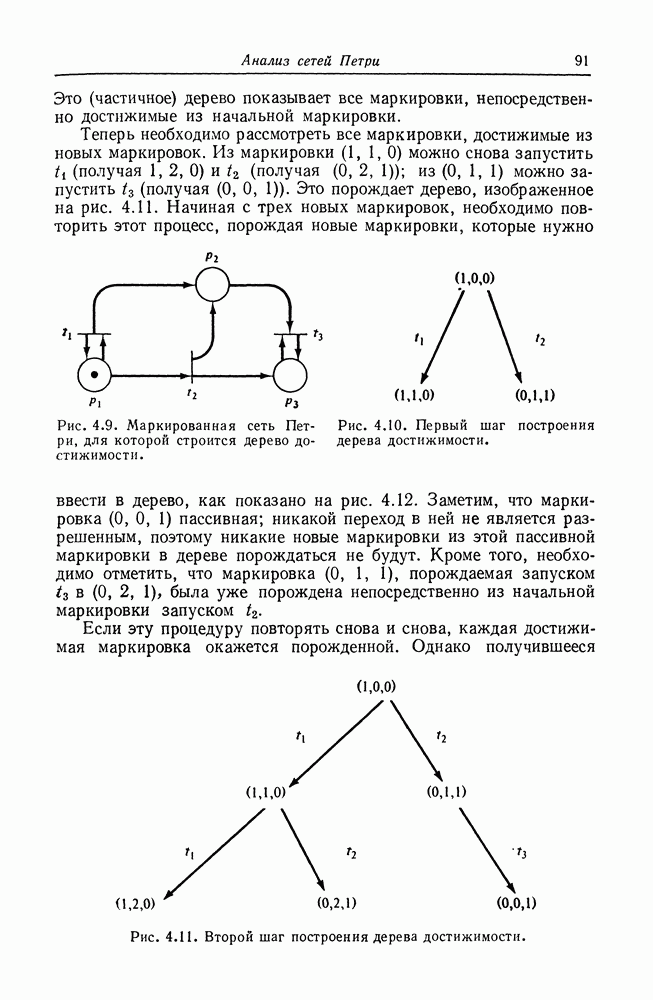
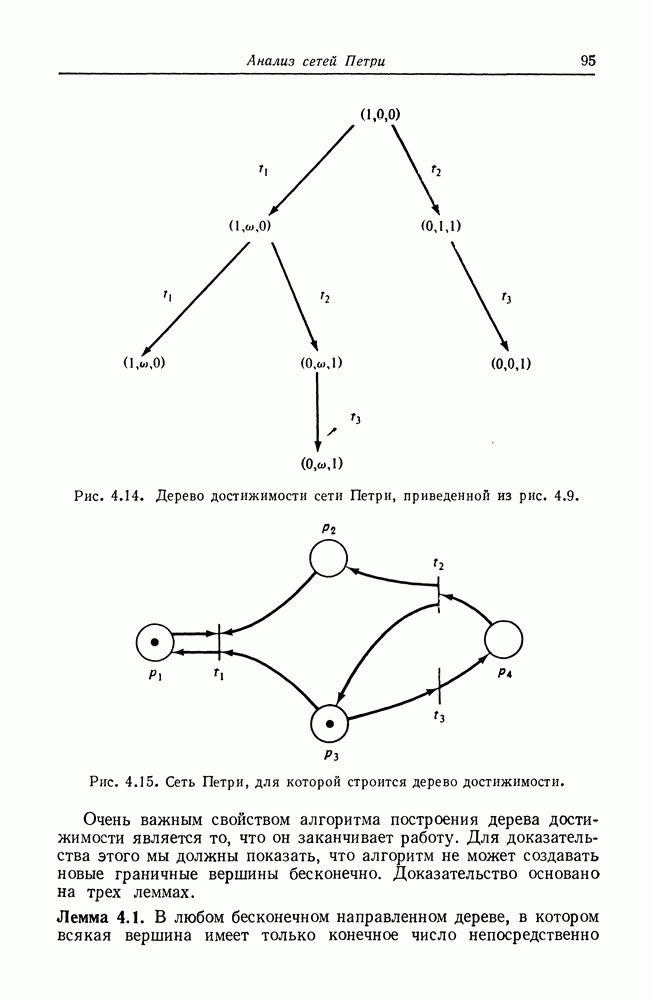
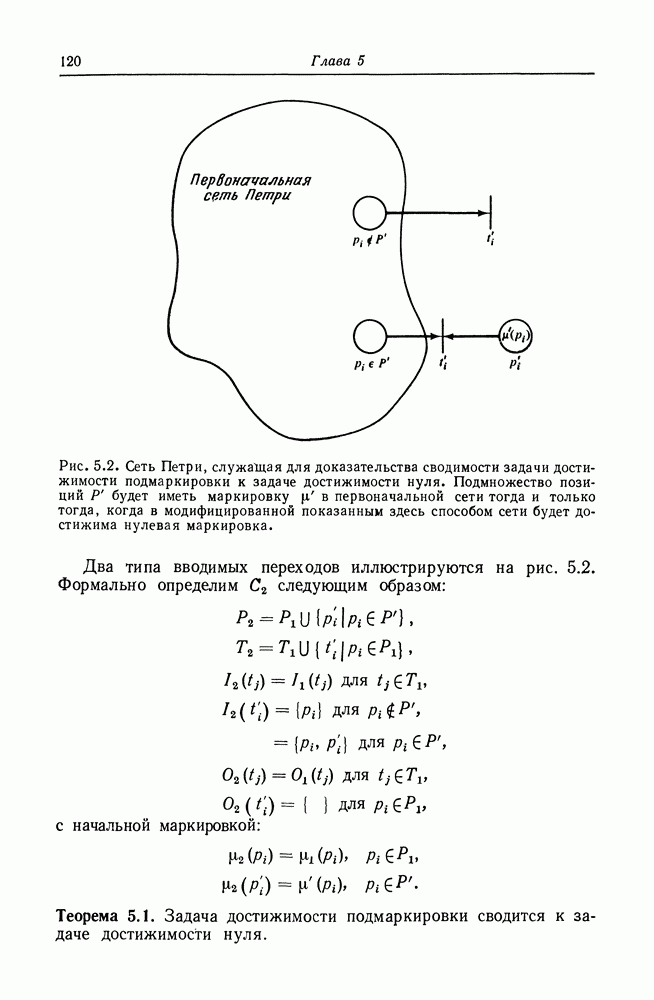
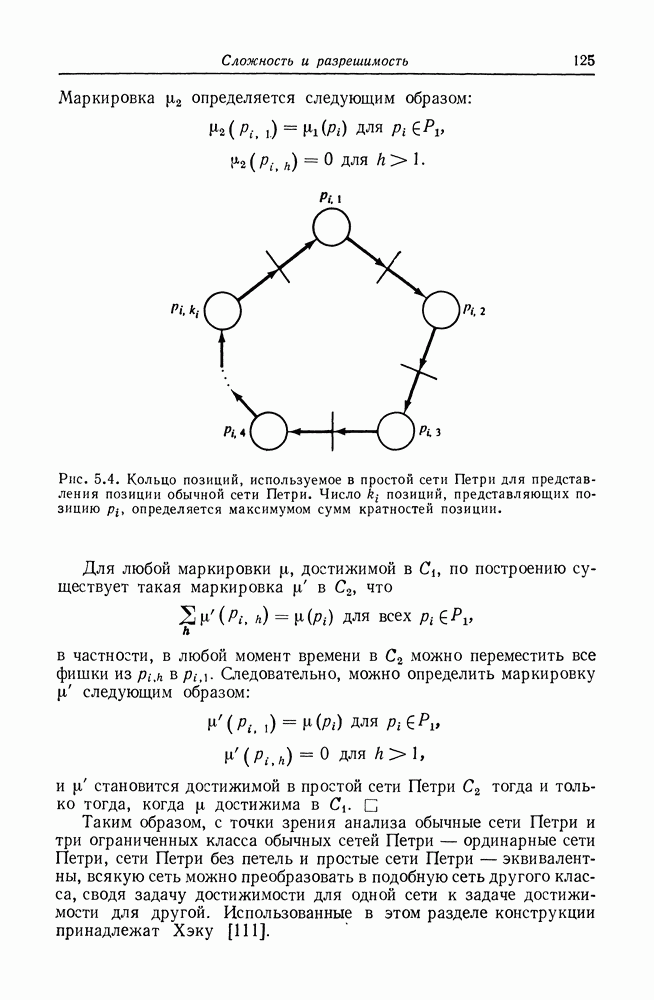
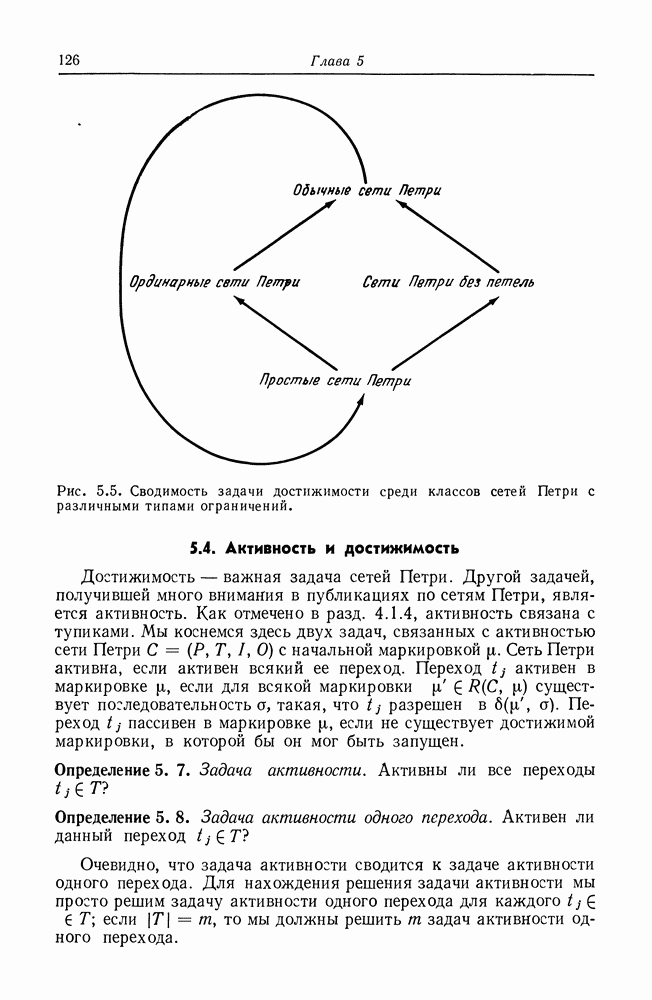
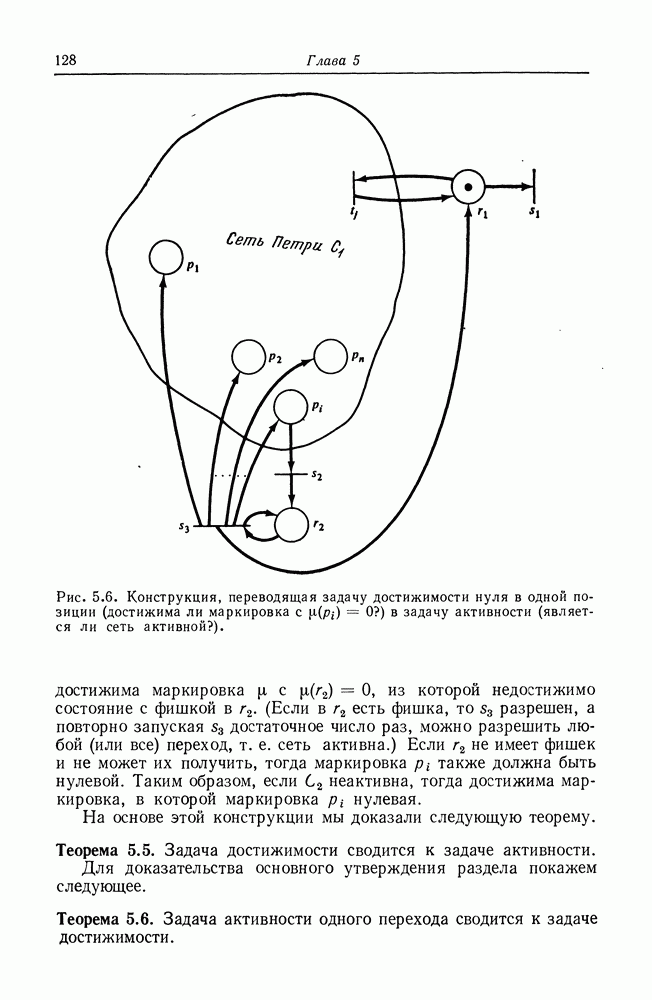
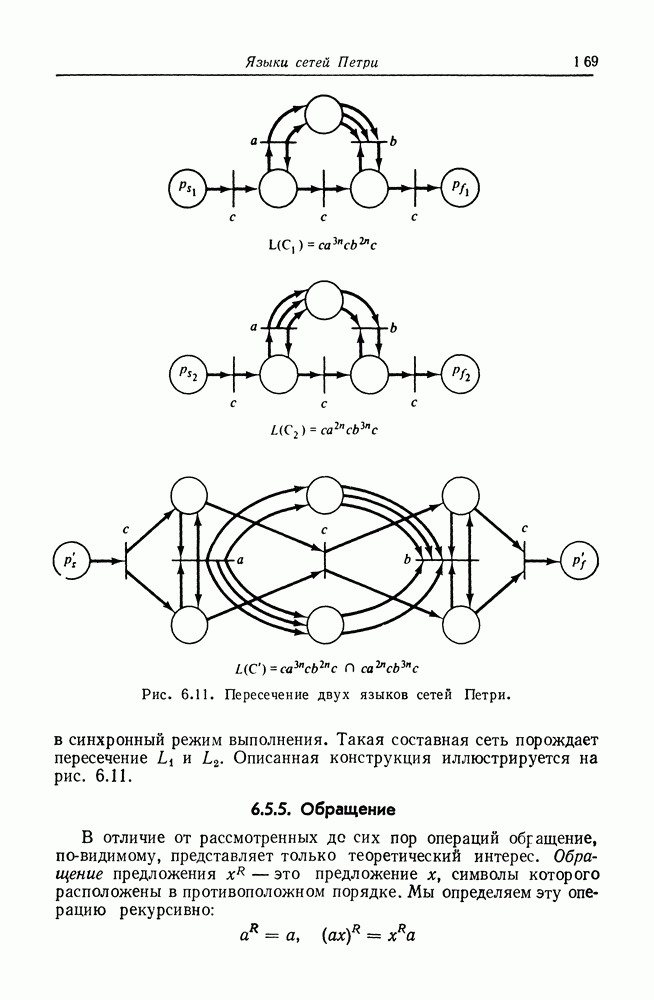
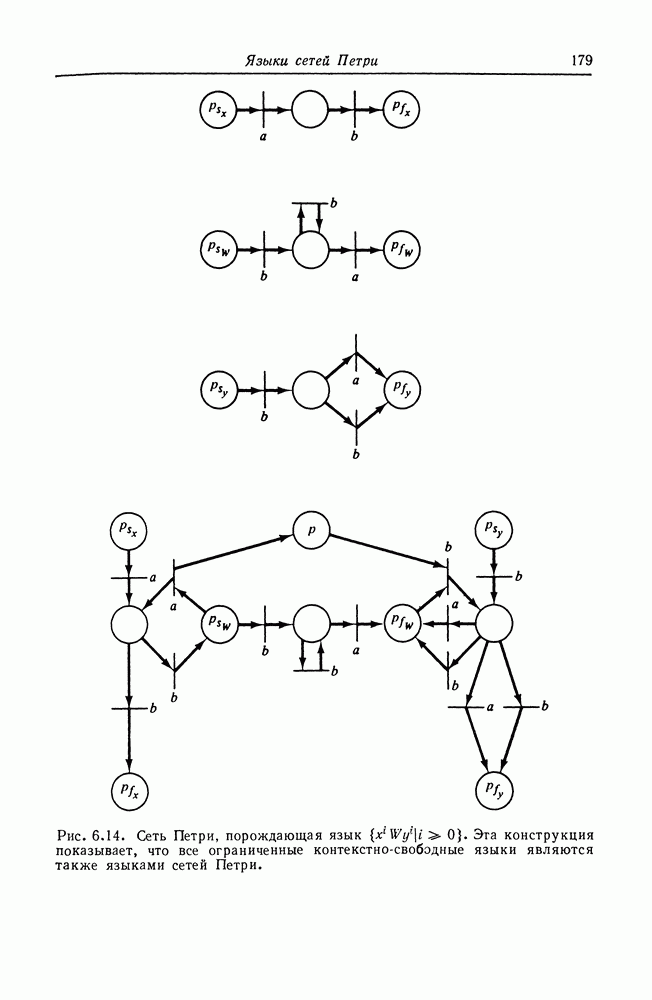
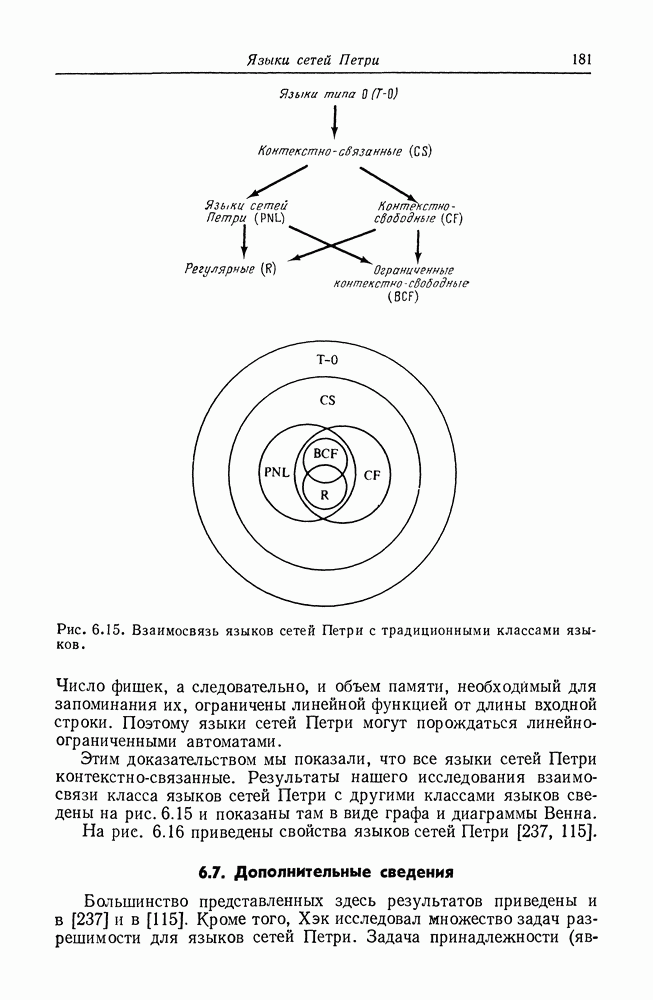
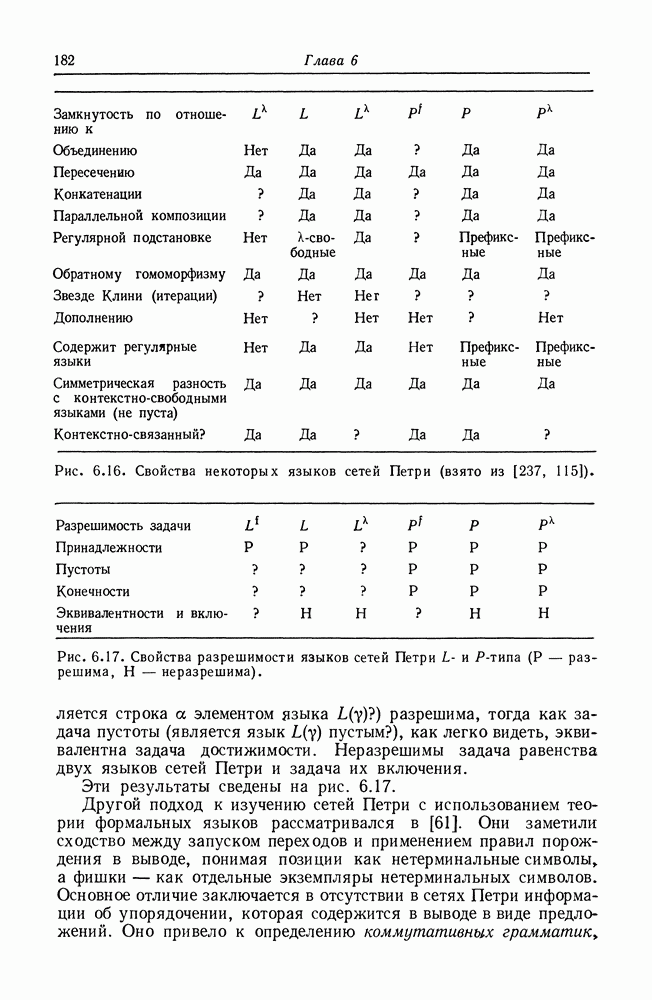
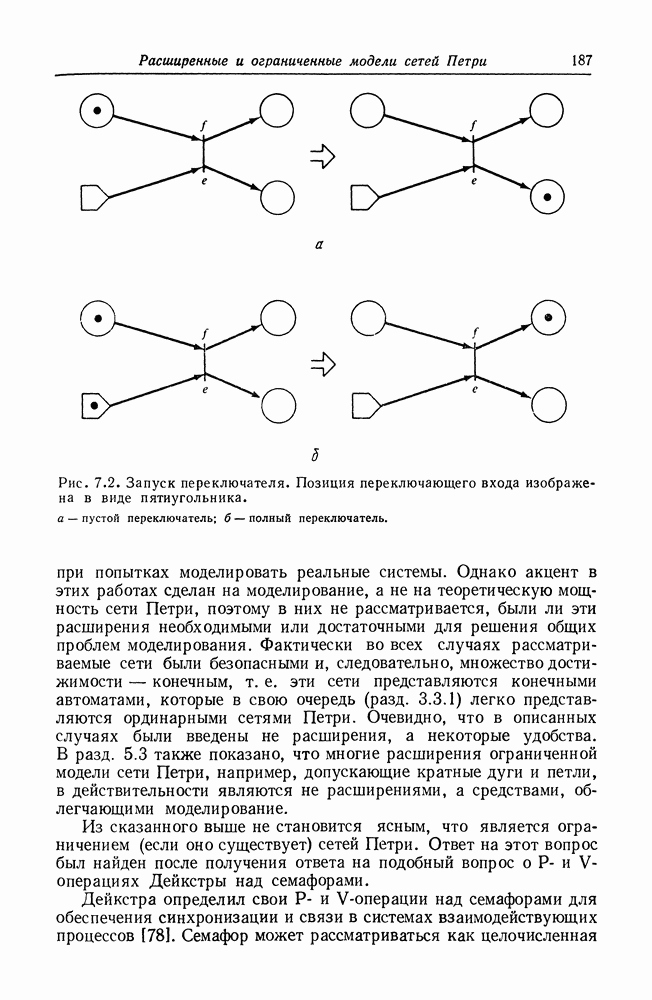
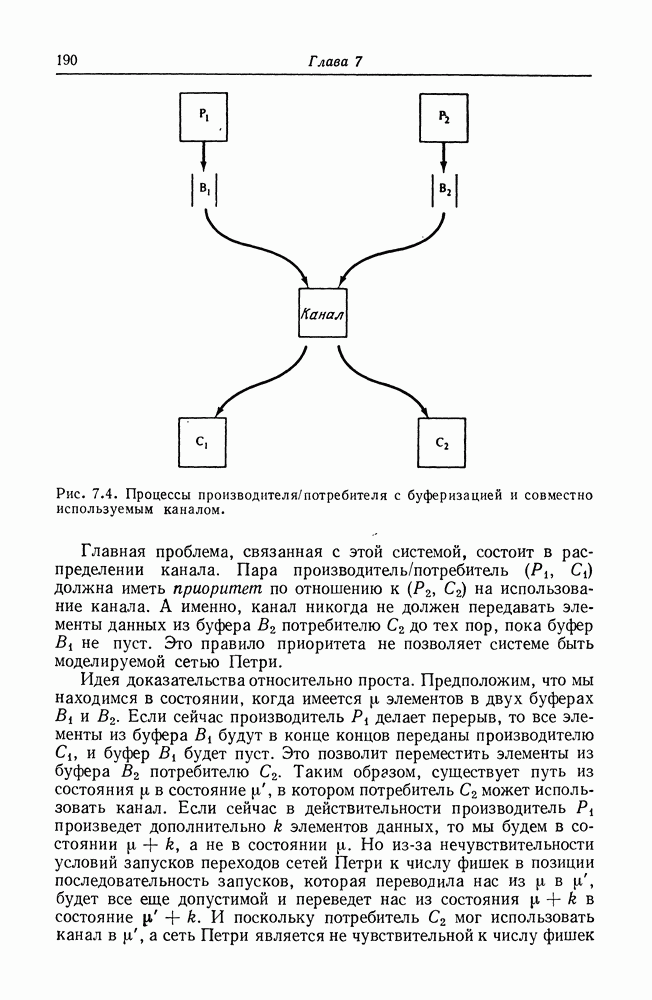
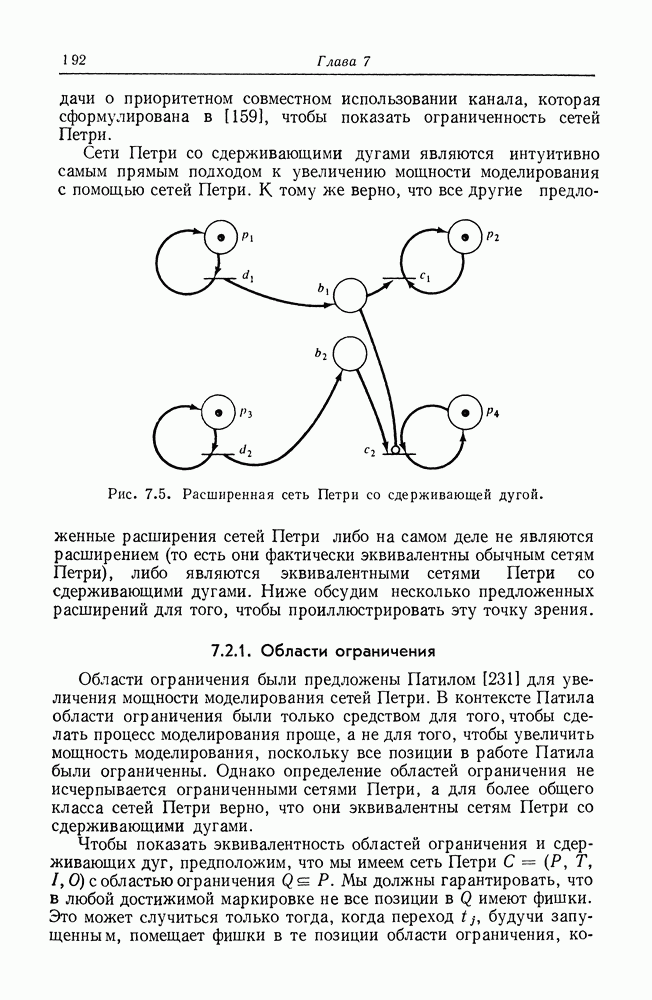
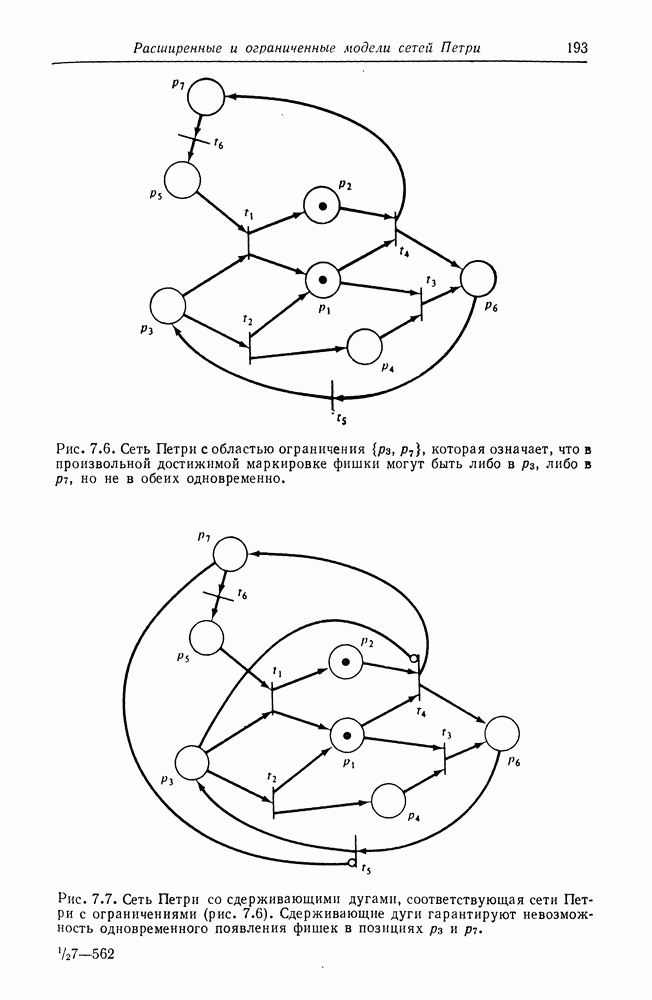
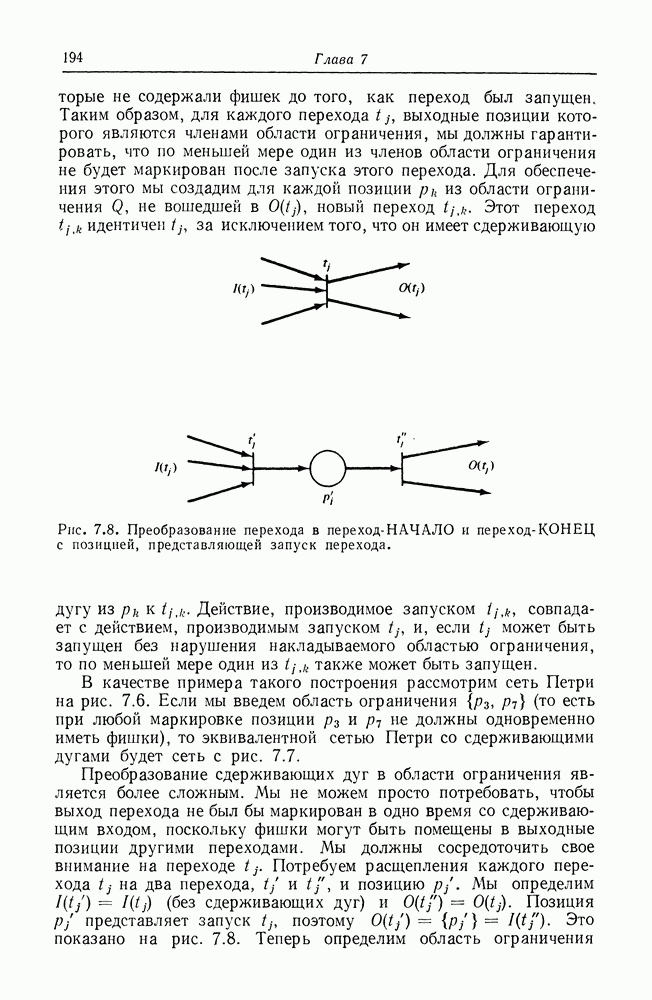
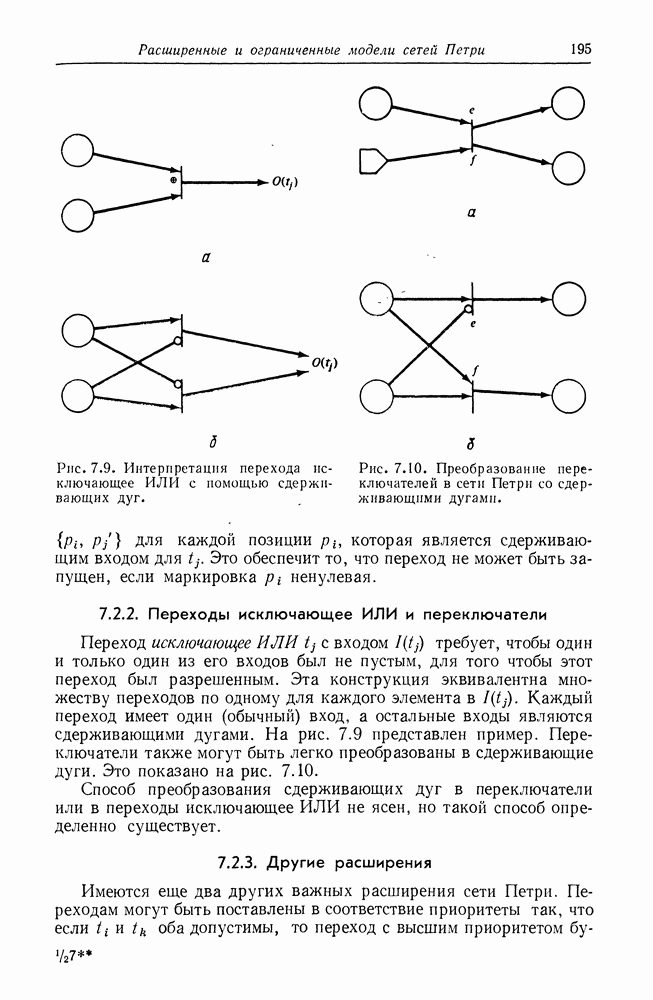
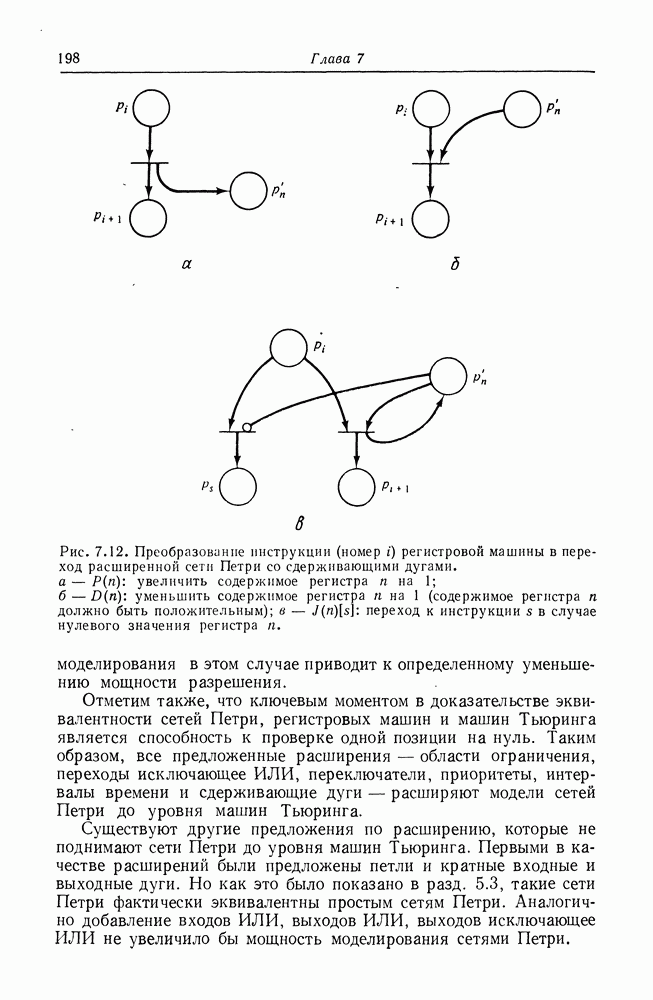
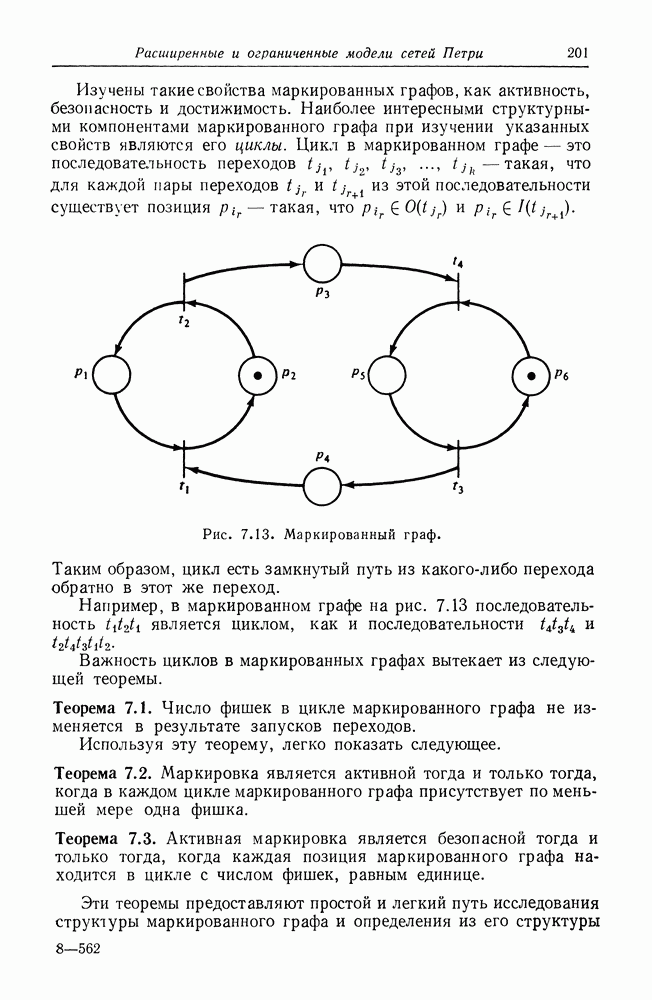
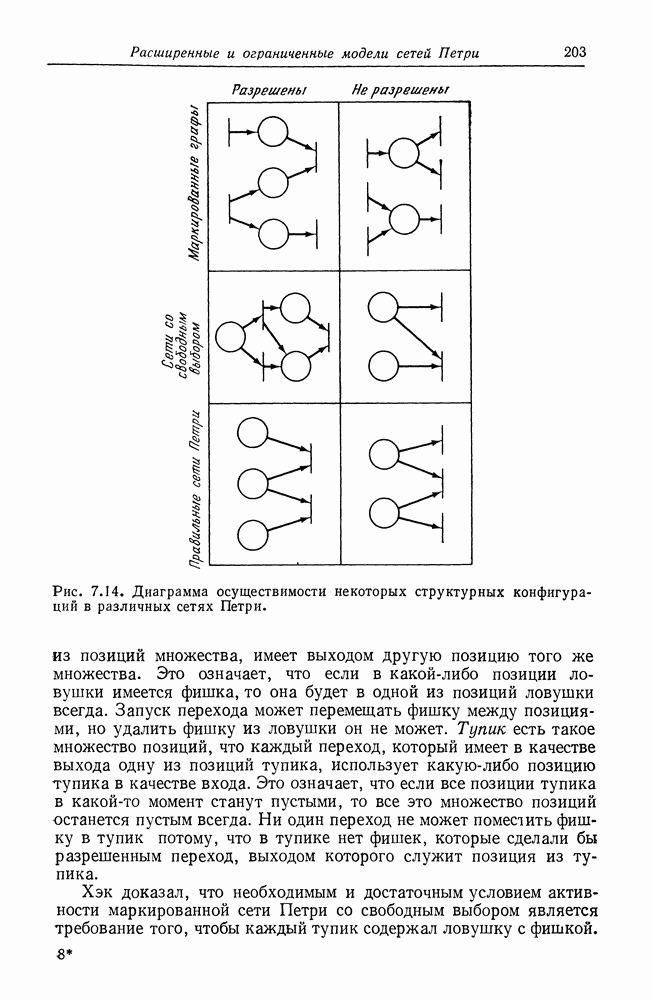
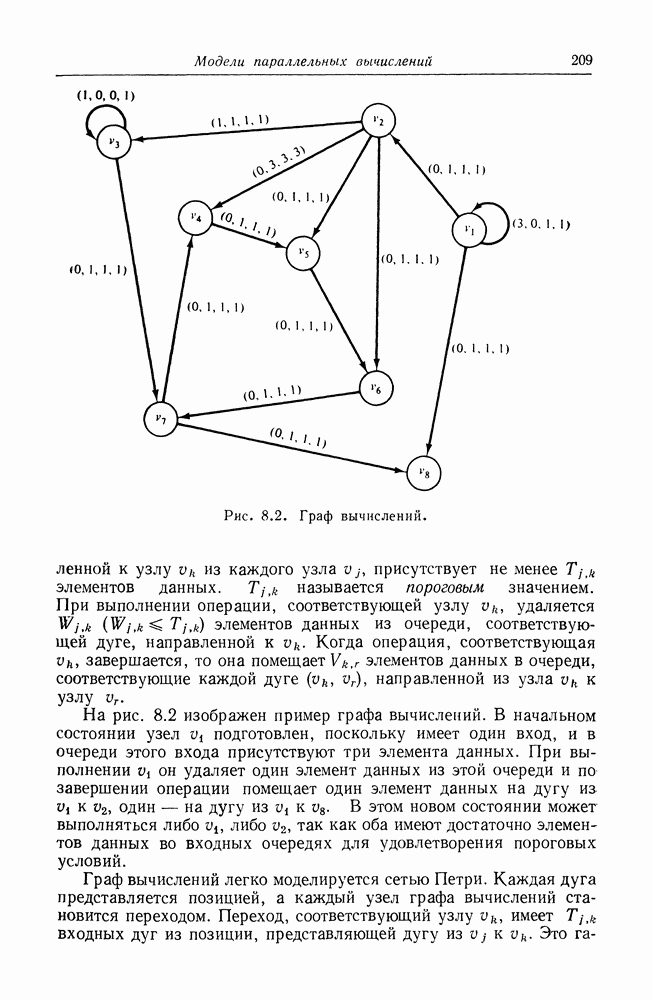
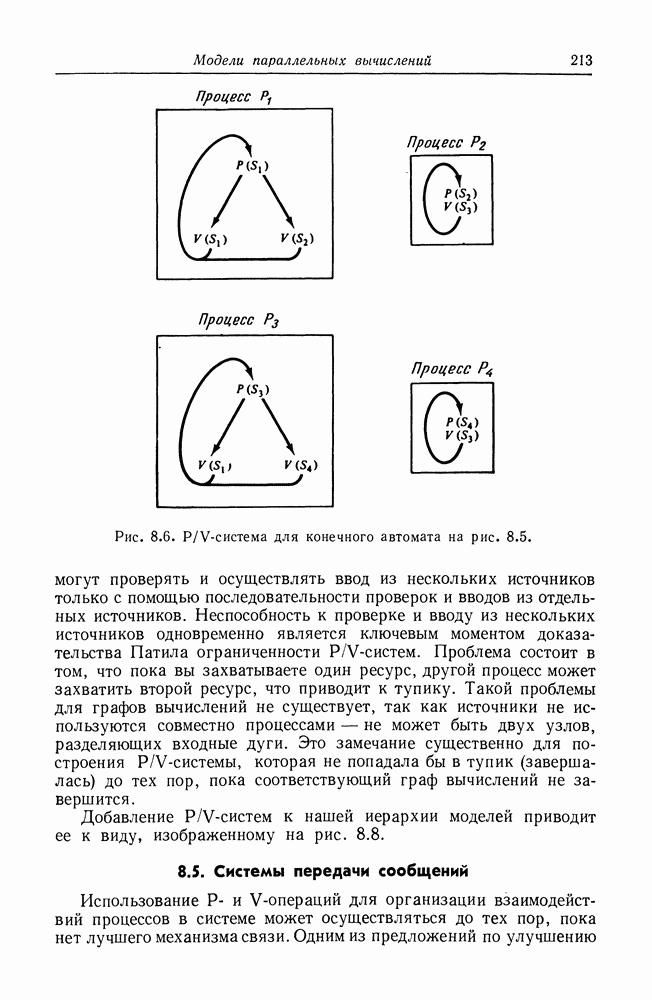
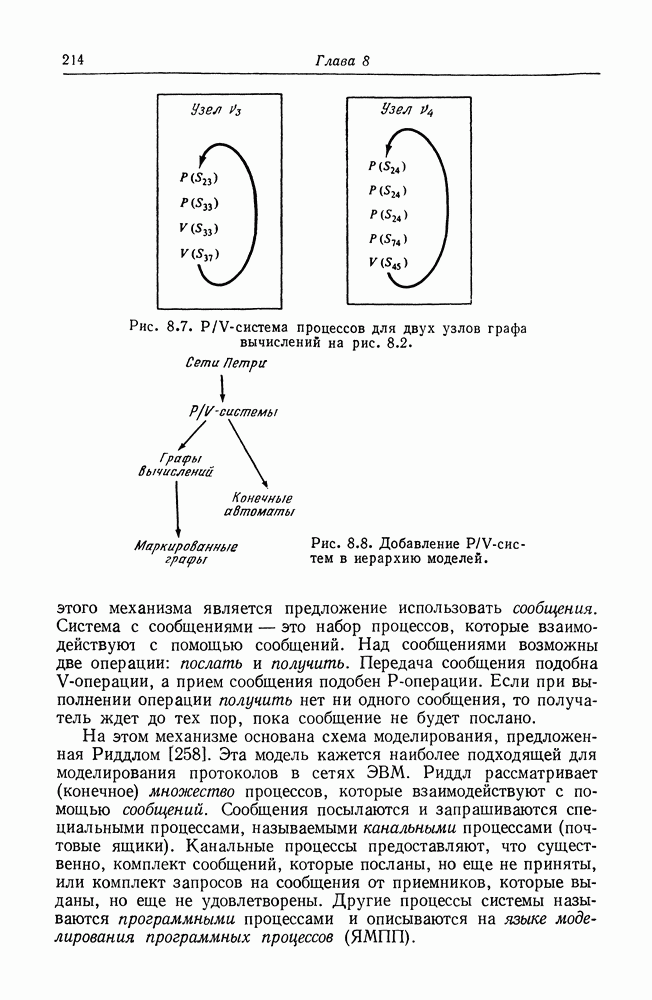
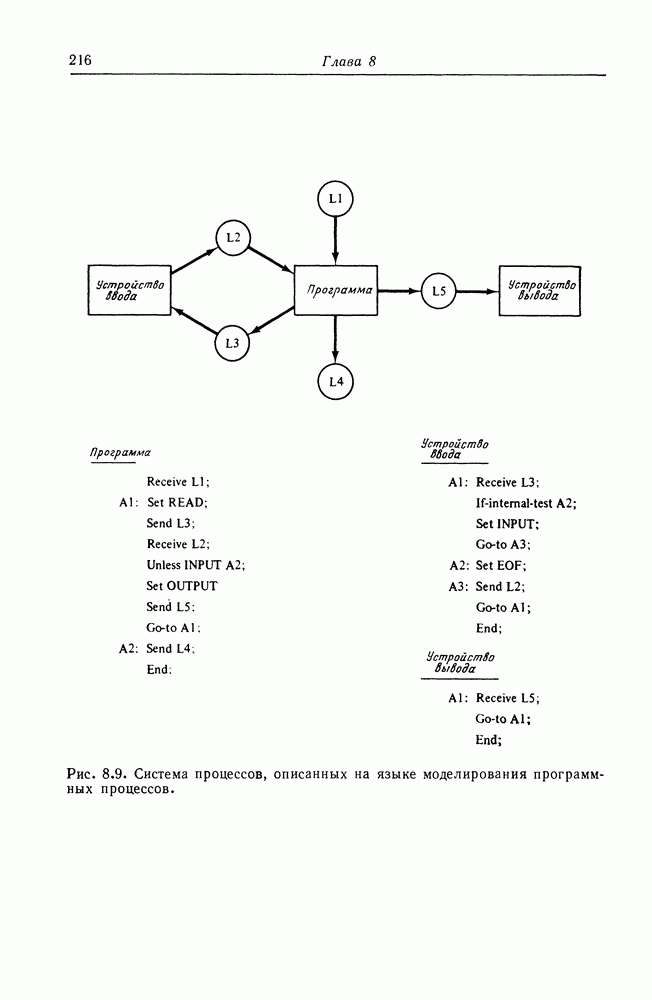
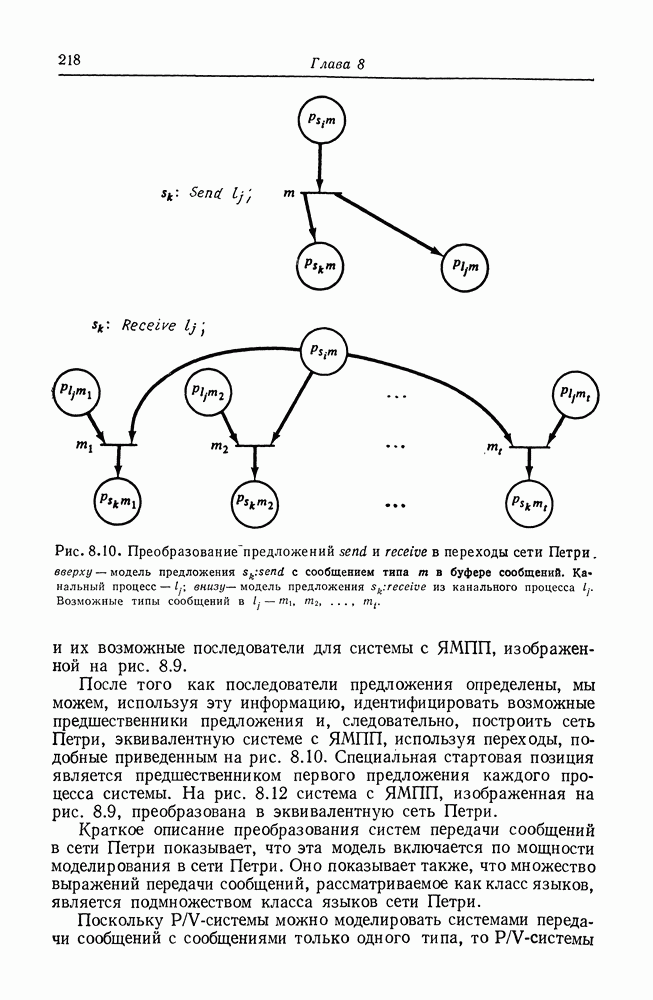
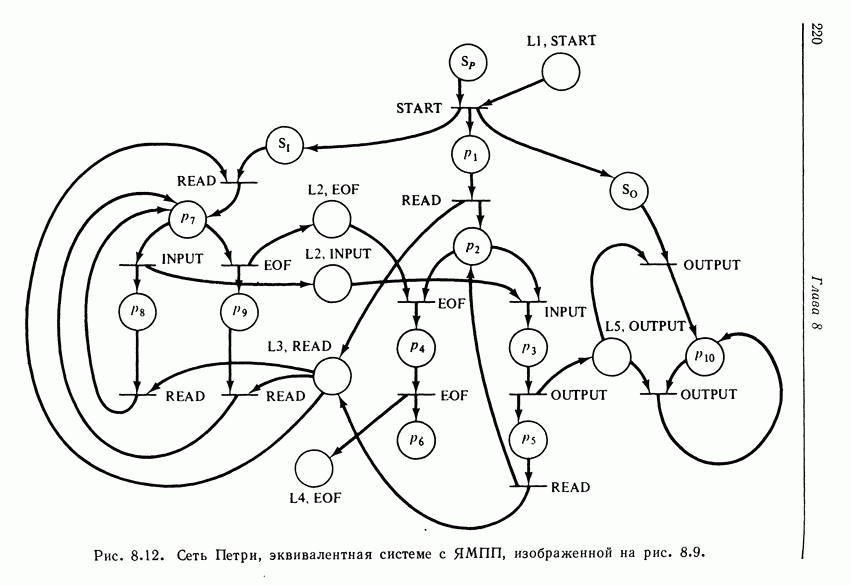
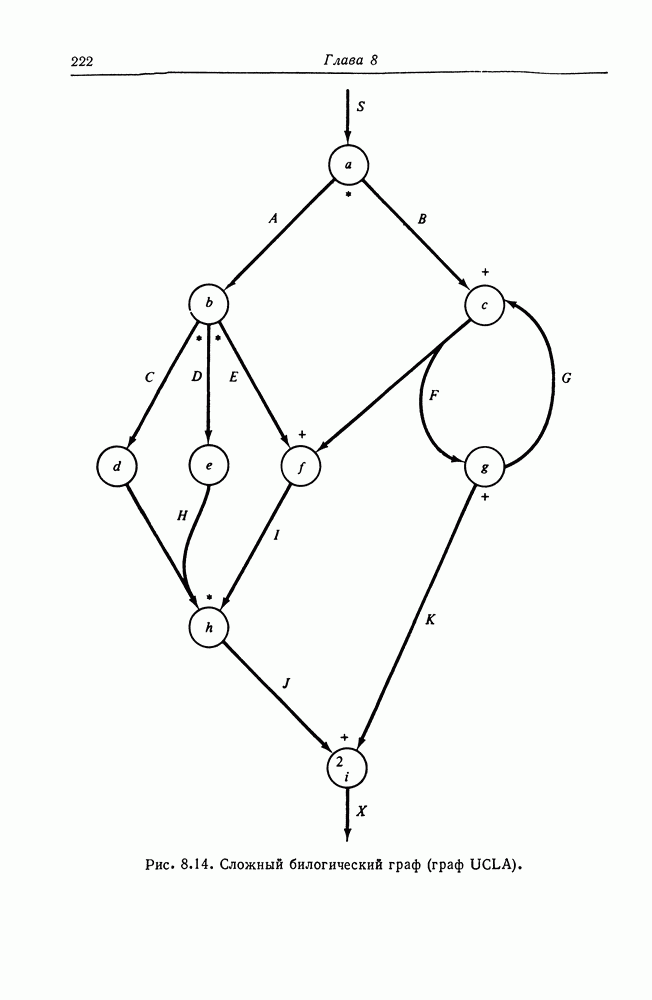
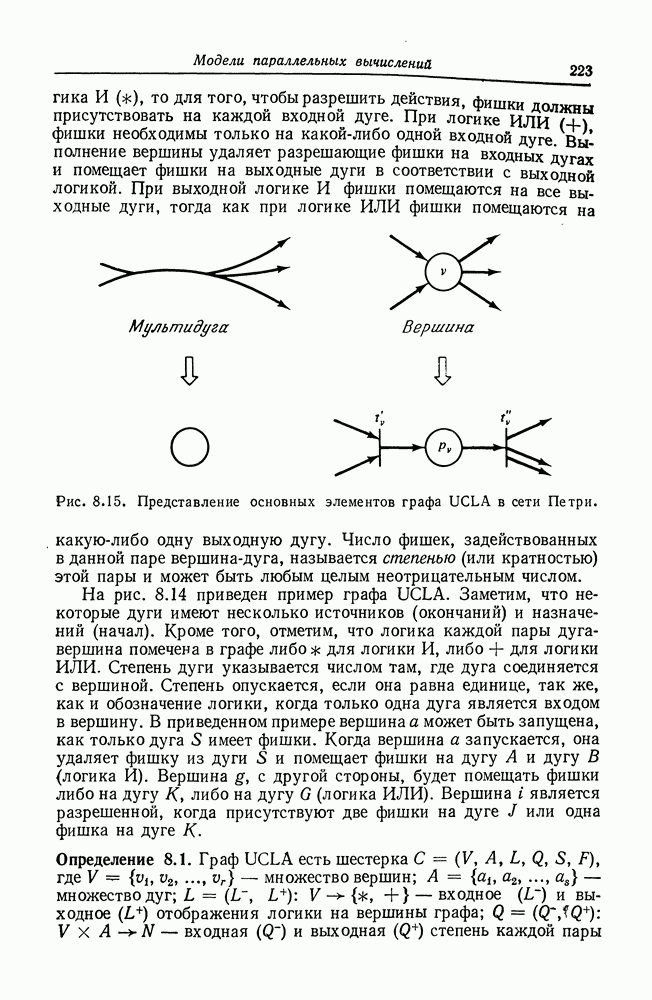
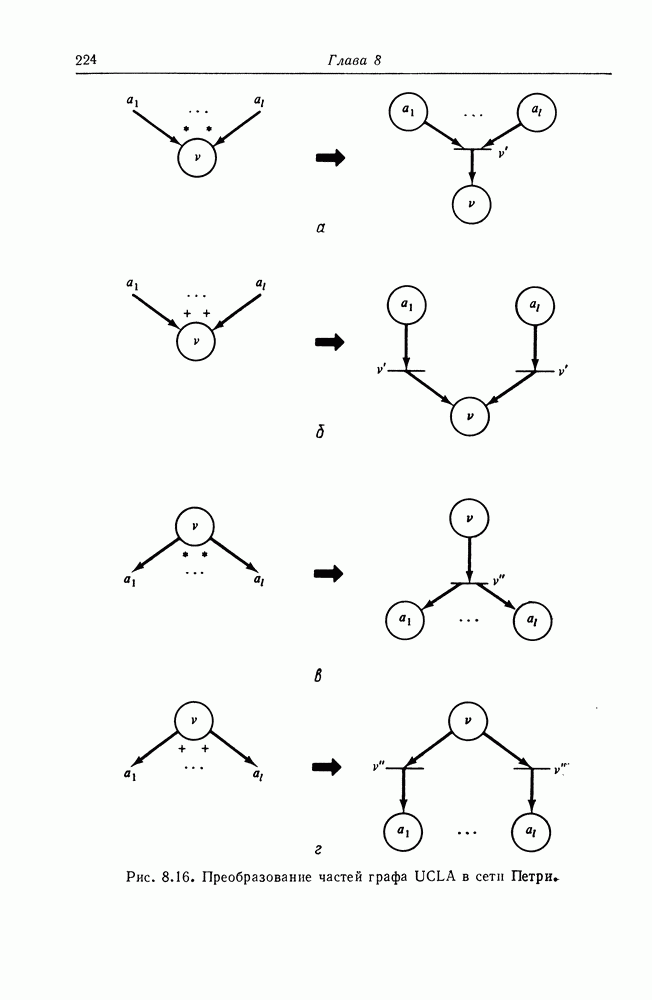
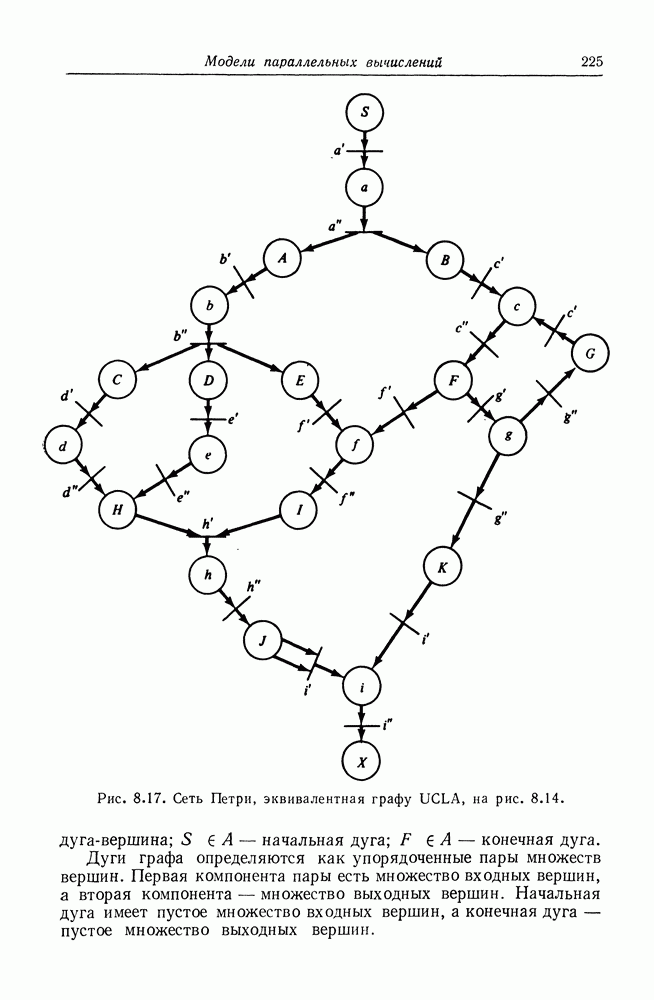
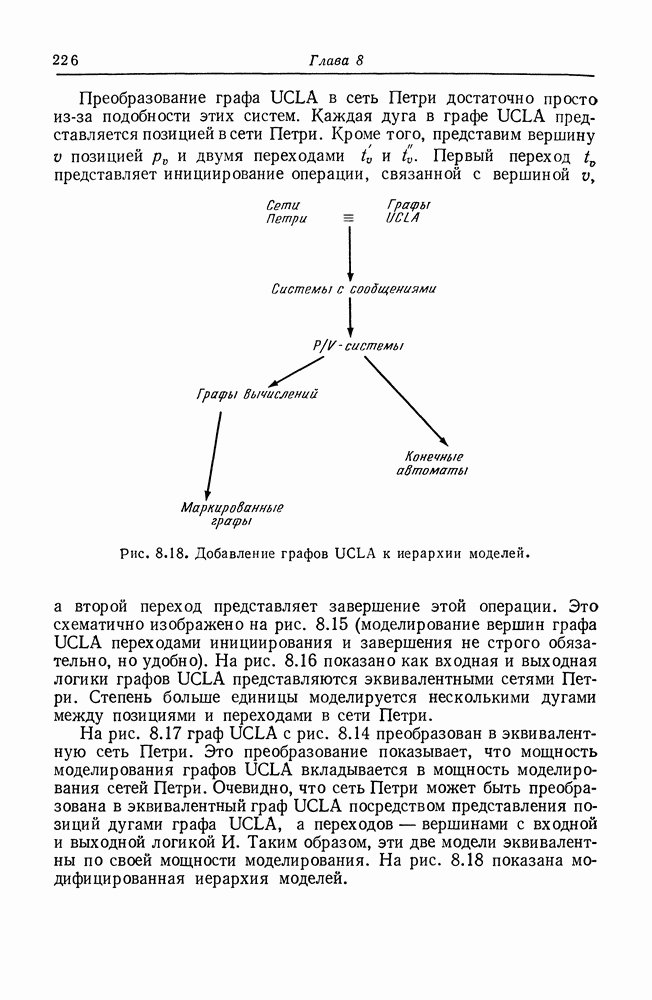
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.5. Неразрешимые задачи
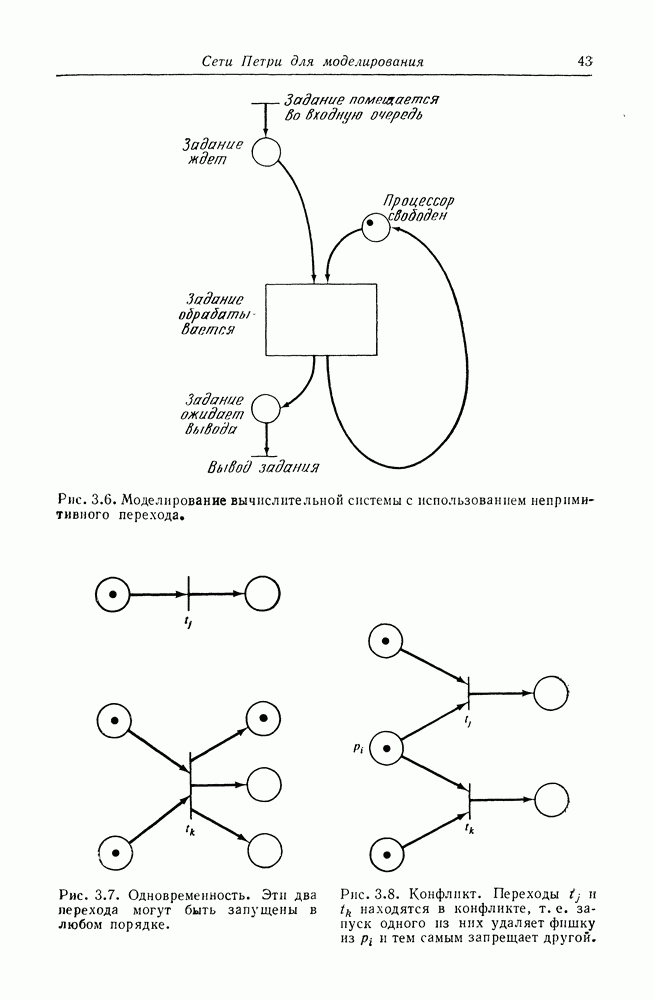
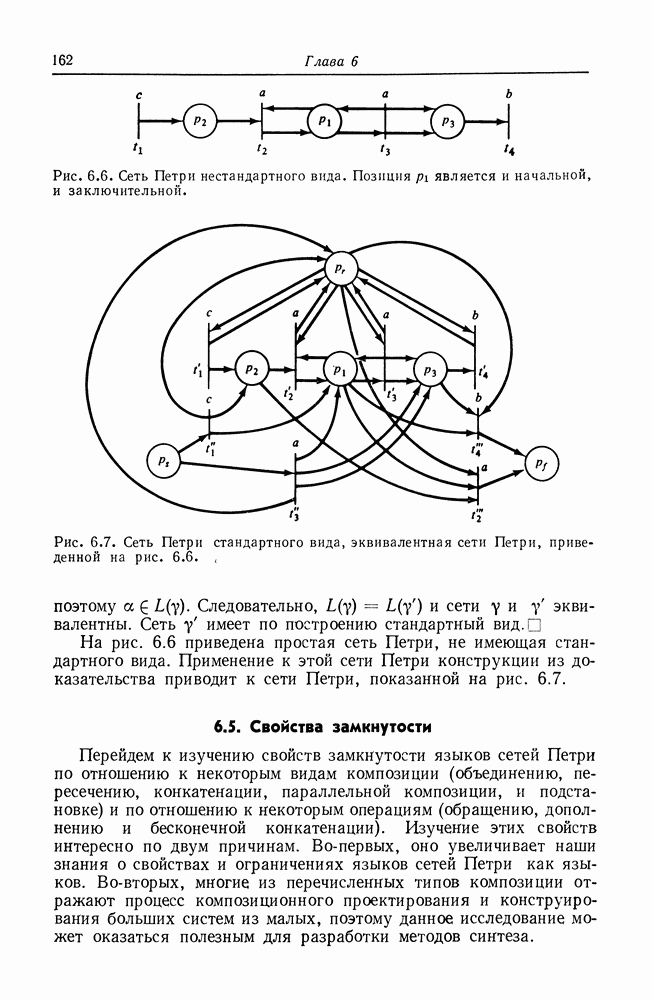
В предыдущем разделе мы показали, что многие задачи достижимости и активности эквивалентны, но никакого результата относительно разрешимости этих задач еще не получили. Для того чтобы показать разрешимость, необходимо свести задачу для сетей Петри к задаче с известным решением, а для того, чтобы показать неразрешимость, нужно свести задачу, которая известна как неразрешимая, к задаче для сетей Петри. Первый важный результат такого рода был получен Рабином [26]. Он показал неразрешимость задачи: выполняется ли  для двух сетей Петри —
для двух сетей Петри —  с маркировкой
с маркировкой  с маркировкой
с маркировкой  Позднее Хэк [114] показал, что неразрешимой является и задача: выполняется ли
Позднее Хэк [114] показал, что неразрешимой является и задача: выполняется ли  Доказательство этих утверждений основано на десятой проблеме Гильберта.
Доказательство этих утверждений основано на десятой проблеме Гильберта.  Гильберт на конференции математиков в 1900 г. поставил 23 проблемы, и та, на которую опирался
Гильберт на конференции математиков в 1900 г. поставил 23 проблемы, и та, на которую опирался  была десятой в списке.)
была десятой в списке.)
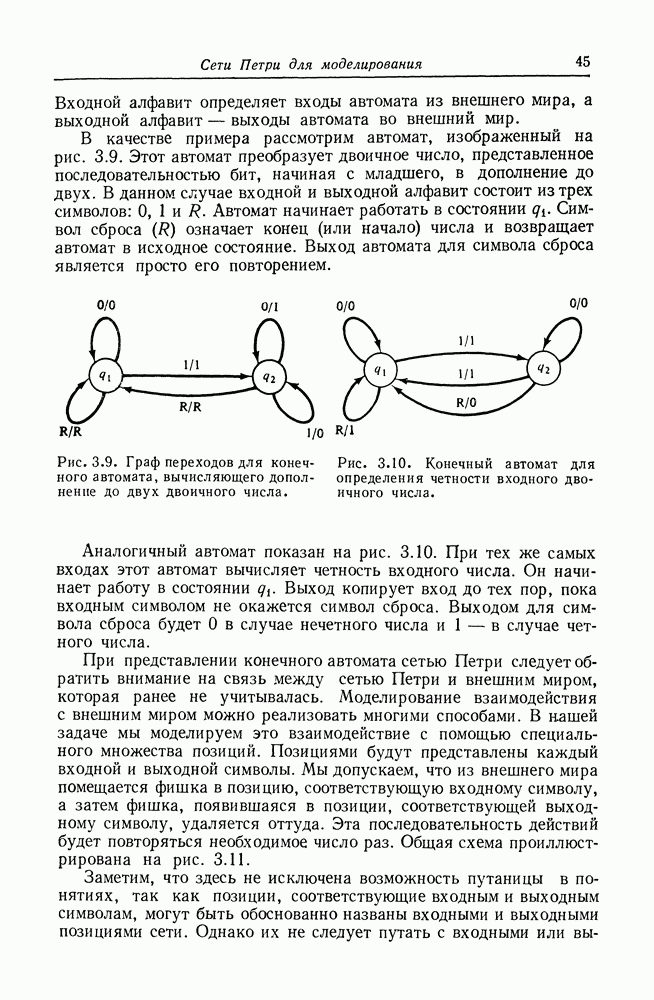
Определение 5.9. Дан полином  от
от  переменных с целыми коэффициентами; существует ли такой вектор целых
переменных с целыми коэффициентами; существует ли такой вектор целых  что
что  Уравнение
Уравнение  называется диофантовым.
называется диофантовым.
В общем оно представляет собой сумму членов:


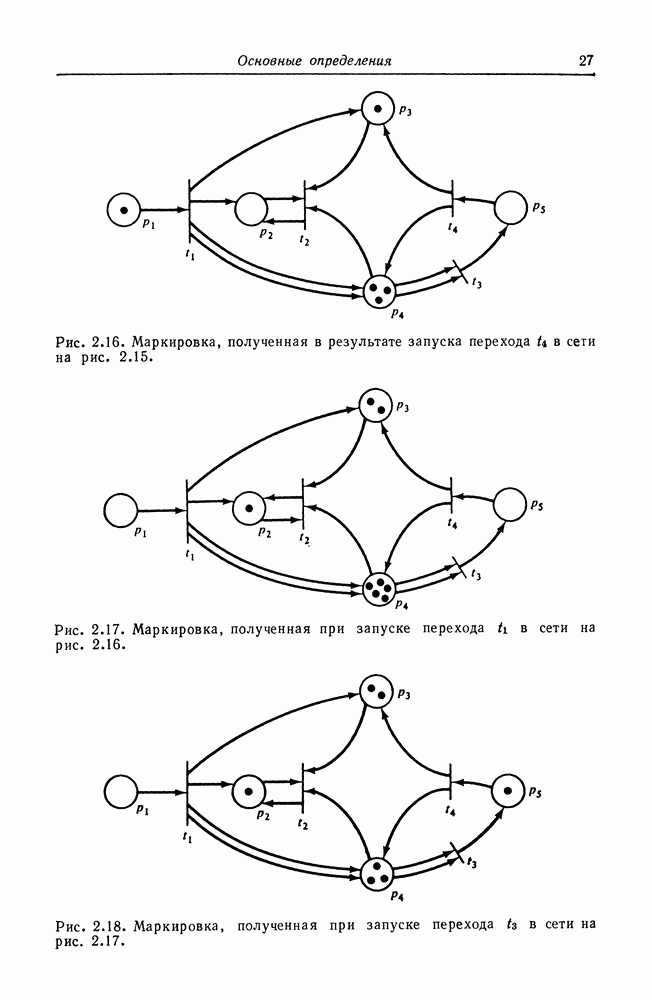
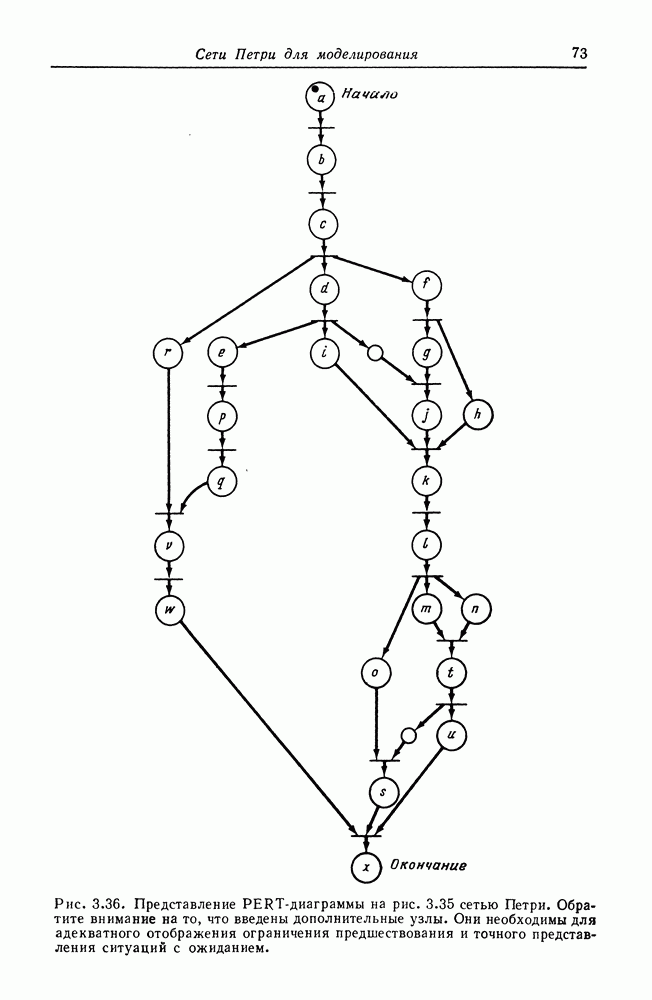
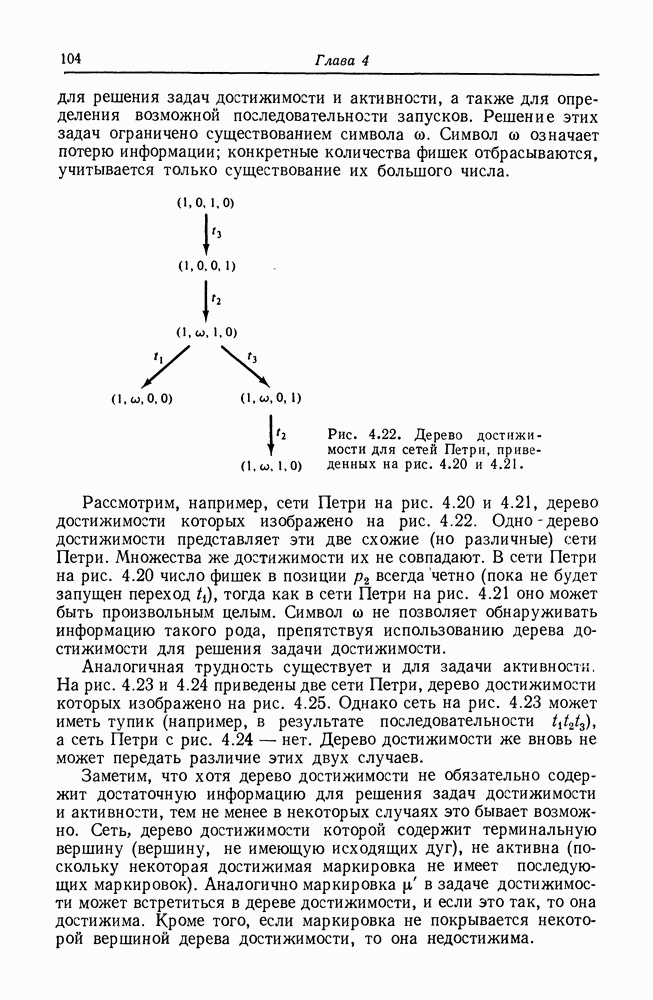
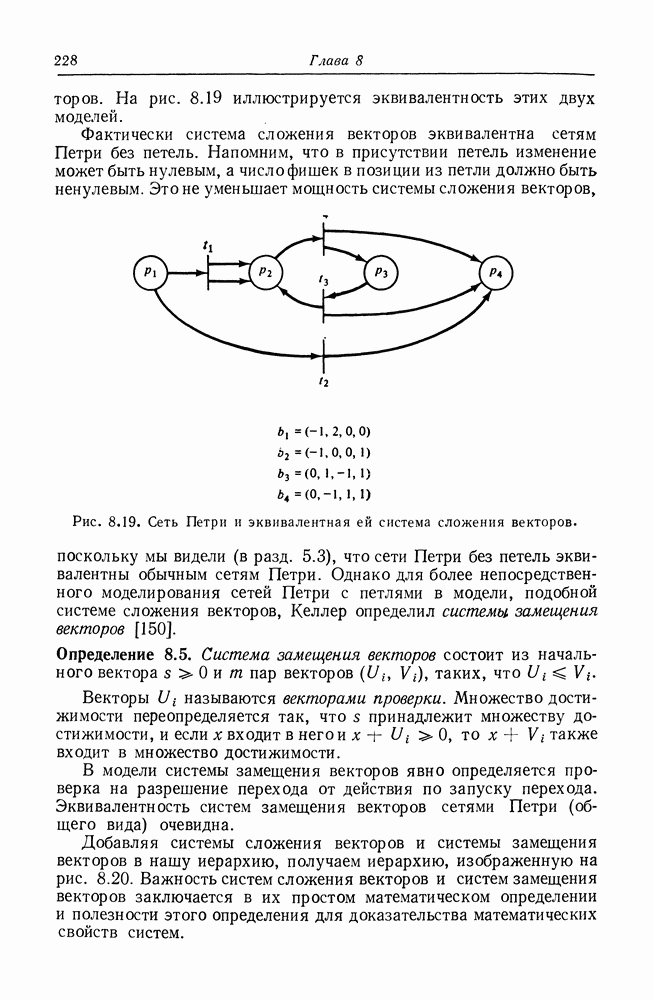
Рис. 5.8. Сведения, показывающие, что задача равенства (и подмножества) длямножеств достижимости сетей Петри неразрешима.
Диофантовыми уравнениями являются 
В 1970 г. Матиясевич доказал, что десятая проблема Гильберта неразрешима [70, 711: не существует общего алгоритма, определяющего, имеет ли произвольное диофантово уравнение корень (набор значений, для которых полином равен нулю). Этот результат служит основой доказательства того, что задача равенства множеств достижимости сетей Петри неразрешима. Стратегия его заключается в построении для диофантова полинома сети Петри, которая (в определенном смысле) вычисляет все значения полинома.
5.5.1. Задача включения графов полиномов
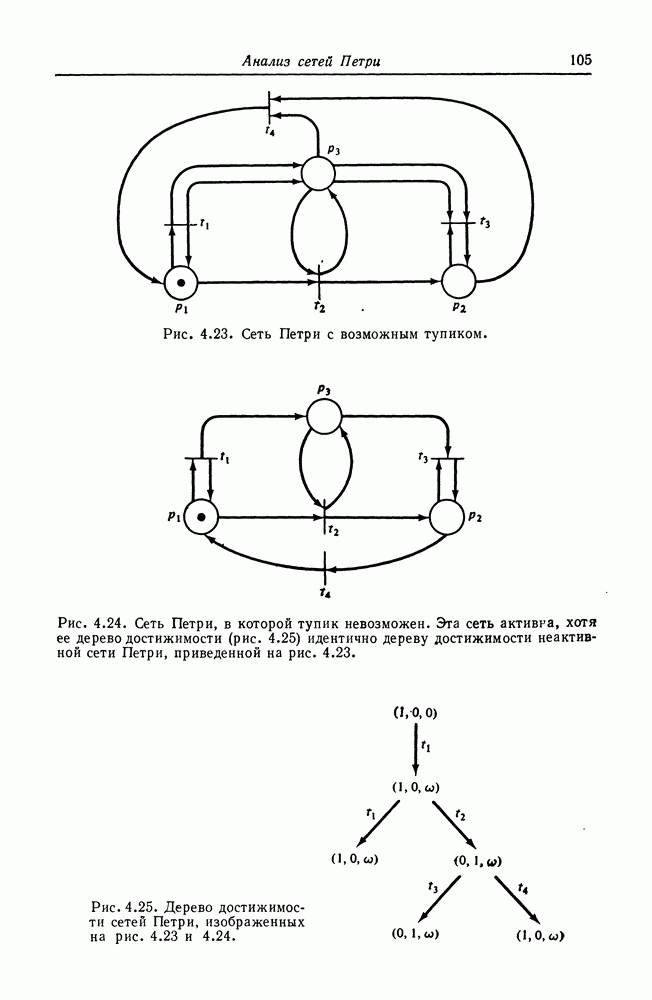
Доказательство неразрешимости задачи равенства состоит из трех частей (рис. 5.8). Сначала десятая проблема Гильберта сводится к задаче включения графов полиномов. Затем задача включения
графов полиномов сводится к задаче подмножества для множеств достижимости сетей Петри. Наконец, задача подмножества для множеств достижимости сетей Петри сводится к задаче равенства множеств достижимости сетей Петри. Это показывает, что десятая проблема Гильберта, известная как неразрешимая, сводится к задаче равенства, которая поэтому также должна быть неразрешимой.
Определение 5.10. Граф  диофантова полинома
диофантова полинома  с неотрицательными коэффициентами — это множество
с неотрицательными коэффициентами — это множество

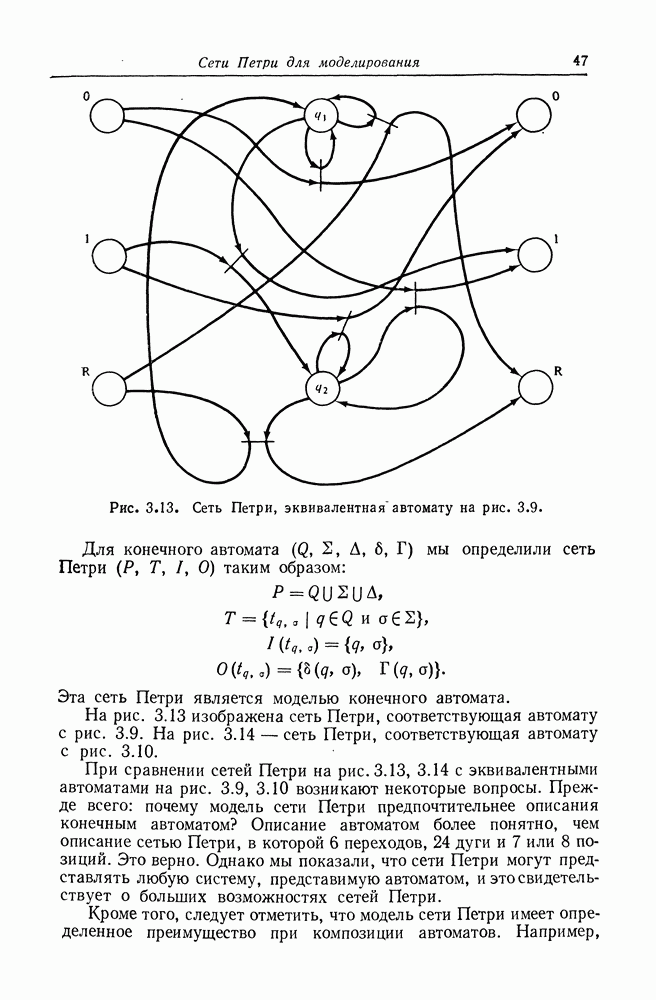
Определение 5.11. Задача включения графов полиномов заключается в определении для двух диофантовых полиномов  выполняется ли
выполняется ли 
Покажем сначала, что десятая проблема Гильберта сводится к задаче включения графов полиномов.
Теорема 5.8. Задача включения графов полиномов неразрешима. Доказательство:
1. Ограничим наше доказательство задачами с неотрицательными решениями. Если  -решение для
-решение для  то
то  решение для
решение для  Следовательно, для определения того, является ли
Следовательно, для определения того, является ли  решением произвольного полинома, необходимо только проверить каждый из
решением произвольного полинома, необходимо только проверить каждый из  полиномов, получающихся в результате изменения знака у некоторого подмножества переменных для неотрицательного решения.
полиномов, получающихся в результате изменения знака у некоторого подмножества переменных для неотрицательного решения.
2. Аналогично, поскольку  тогда и только тогда, когда
тогда и только тогда, когда  необходимо рассматривать только полиномы, значения которых неотрицательны.
необходимо рассматривать только полиномы, значения которых неотрицательны.
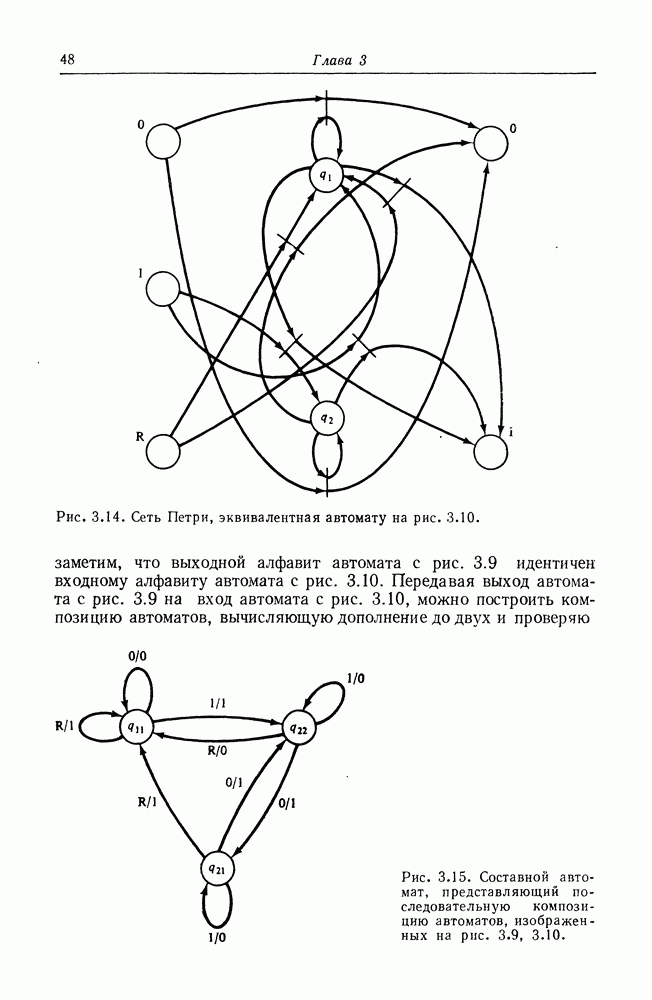
3. Сейчас можно разбить любой полином  на Два полинома,
на Два полинома,  такие, что
такие, что  помещая все члены с положительными коэффициентами в
помещая все члены с положительными коэффициентами в  а все члены с отрицательными коэффициентами в
а все члены с отрицательными коэффициентами в  Далее, поскольку
Далее, поскольку  (по п. 2), имеем, что
(по п. 2), имеем, что  тогда и только тогда, когда
тогда и только тогда, когда 
4. Рассмотрим два графа полиномов:

Теперь  тогда и только тогда, когда для всех неотрицательных
тогда и только тогда, когда для всех неотрицательных  из
из  следует, что
следует, что  Это справедливо тогда и только тогдакогда не существует
Это справедливо тогда и только тогдакогда не существует  таких, что
таких, что

Но из п. 3 следует, что  поэтому
поэтому  а поскольку все величины целые,
а поскольку все величины целые,

что справедливо тогда и только  Таким образом, мы убедились в том, что
Таким образом, мы убедились в том, что  тогда и только тогда, когда не существует таких
тогда и только тогда, когда не существует таких  которых
которых 

5. Итак, для определения того, что уравнение  имеет решение, необходимо показать только, что не выполняется
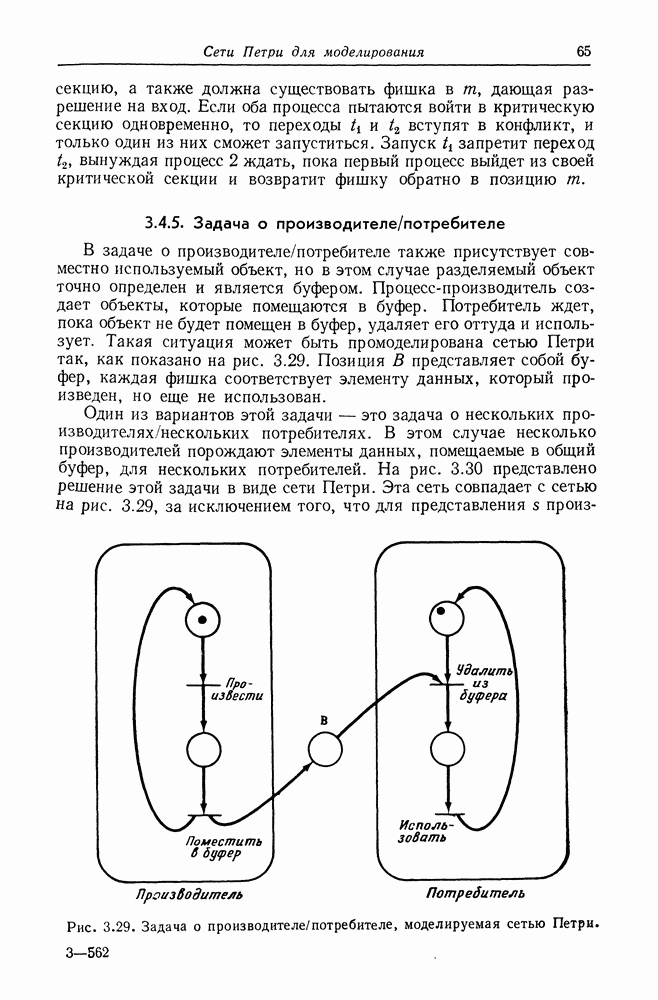
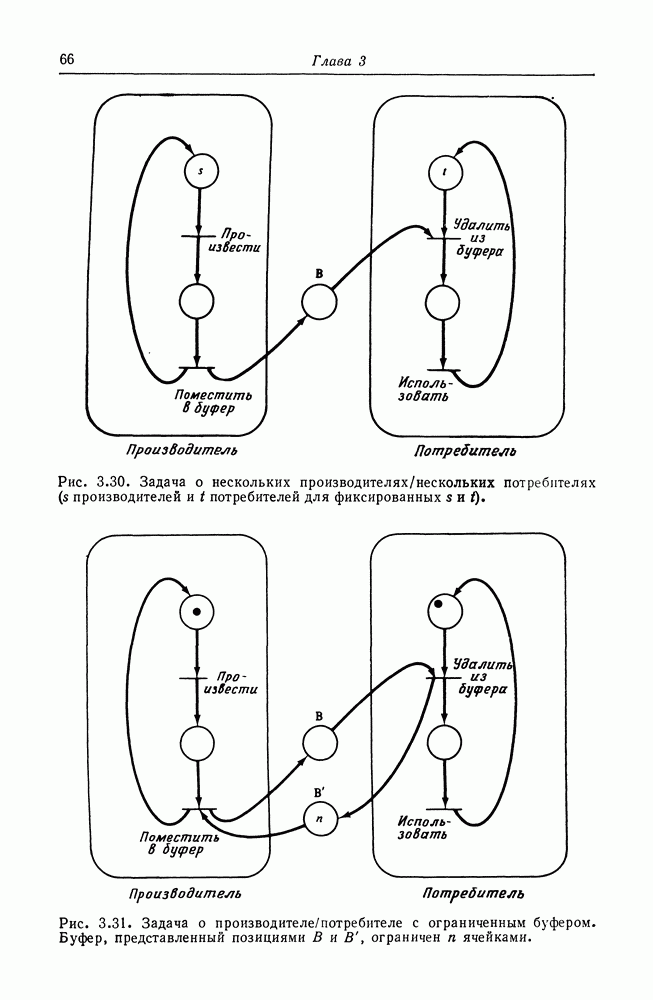
имеет решение, необходимо показать только, что не выполняется 
5.5.2. Слабое вычисление
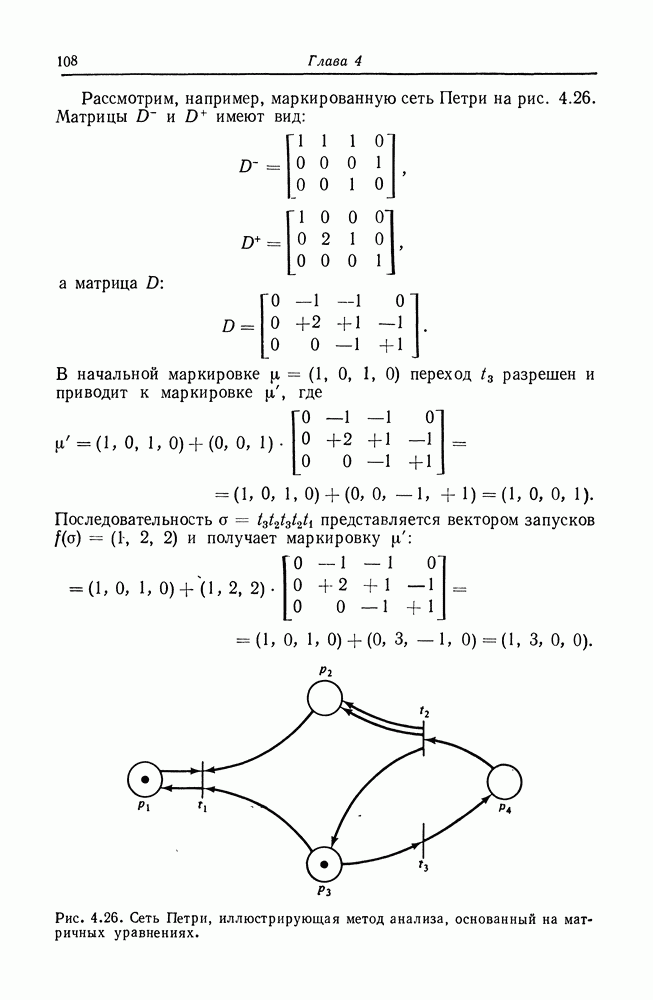
Теперь нам необходимо показать, что сети Петри могут (в определенном смысле) вычислять значение полинома  Мы осмотрительно ограничили полином
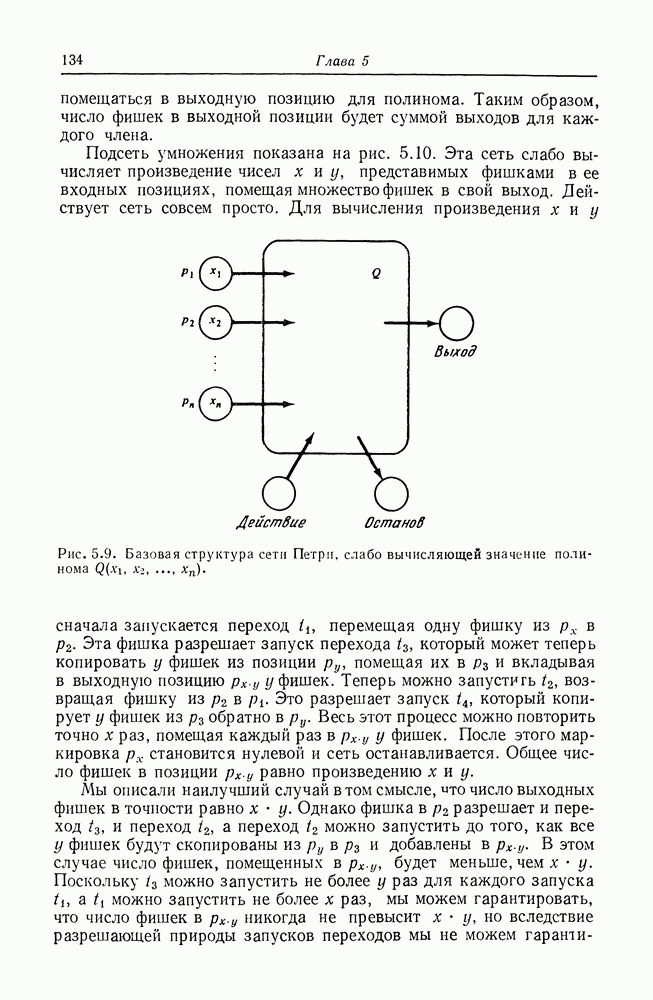
Мы осмотрительно ограничили полином  до неотрицательных значений полинома, неотрицательных коэффициентов и неотрицательных значений переменных. Это позволяет нам представить значения переменных и значение полинома числом фишек в позициях сети Петри. Общая схема показана на рис. 5.9. Входные значения
до неотрицательных значений полинома, неотрицательных коэффициентов и неотрицательных значений переменных. Это позволяет нам представить значения переменных и значение полинома числом фишек в позициях сети Петри. Общая схема показана на рис. 5.9. Входные значения  представляются
представляются  фишками в
фишками в  для
для  Первоначально фишка помещается также в позицию «действия». Выполнение сети будет закончено помещением фишки в позицию останова. В это время «выходная» позиция будет иметь у фишек, где
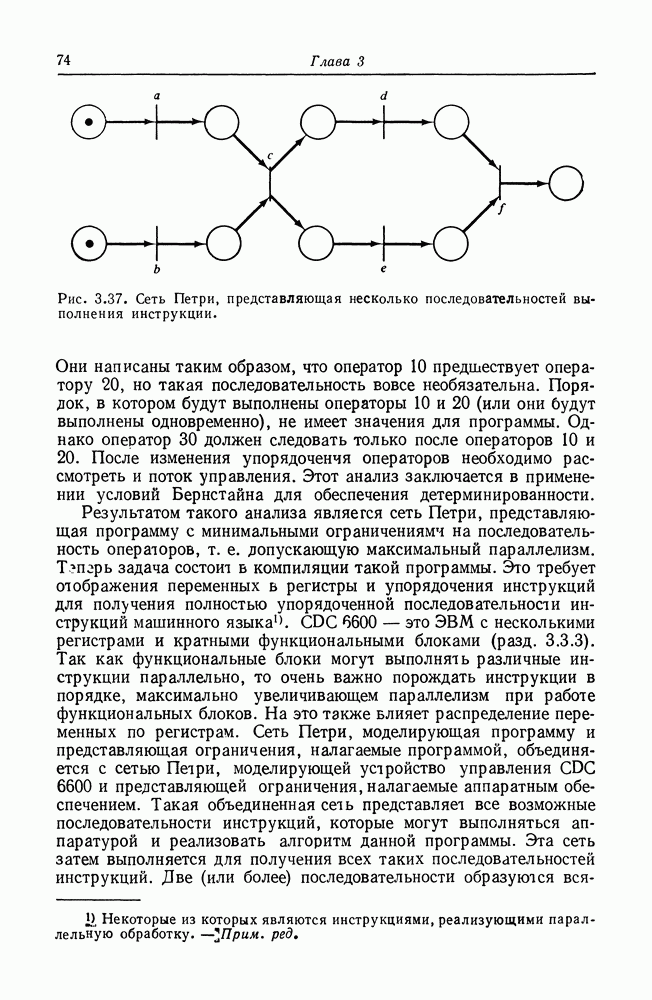
Первоначально фишка помещается также в позицию «действия». Выполнение сети будет закончено помещением фишки в позицию останова. В это время «выходная» позиция будет иметь у фишек, где 
Эта сеть Петри слабо вычисляет значение  Слабое вычисление означает, что вычисленное значение не будет превышать
Слабое вычисление означает, что вычисленное значение не будет превышать  но может быть любым (неотрицательным) значением, меньшим
но может быть любым (неотрицательным) значением, меньшим  Слабое вычисление обязательно для сетей Петри вследствие разрешающей природы запусков переходов: сеть Петри нельзя заставить остановиться. При определении графа полинома
Слабое вычисление обязательно для сетей Петри вследствие разрешающей природы запусков переходов: сеть Петри нельзя заставить остановиться. При определении графа полинома  это особенно учитывалось.
это особенно учитывалось.
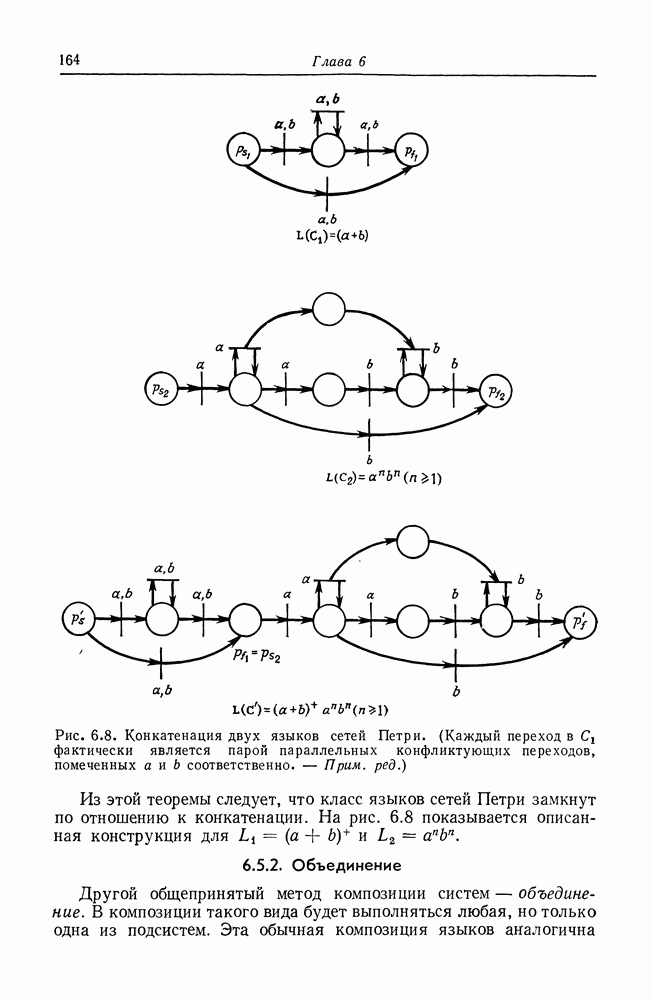
Сейчас мы хотим показать, что можно построить подсеть, слабо вычисляющую функцию умножения (двух чисел). На ее основе мы можем построить составную сеть, которая слабо вычисляет значение каждого члена полинома путем последовательной композиции подсетей умножения. Выход подсети для каждого члена будет
помещаться в выходную позицию для полинома. Таким образом, число фишек в выходной позиции будет суммой выходов для каждого члена.
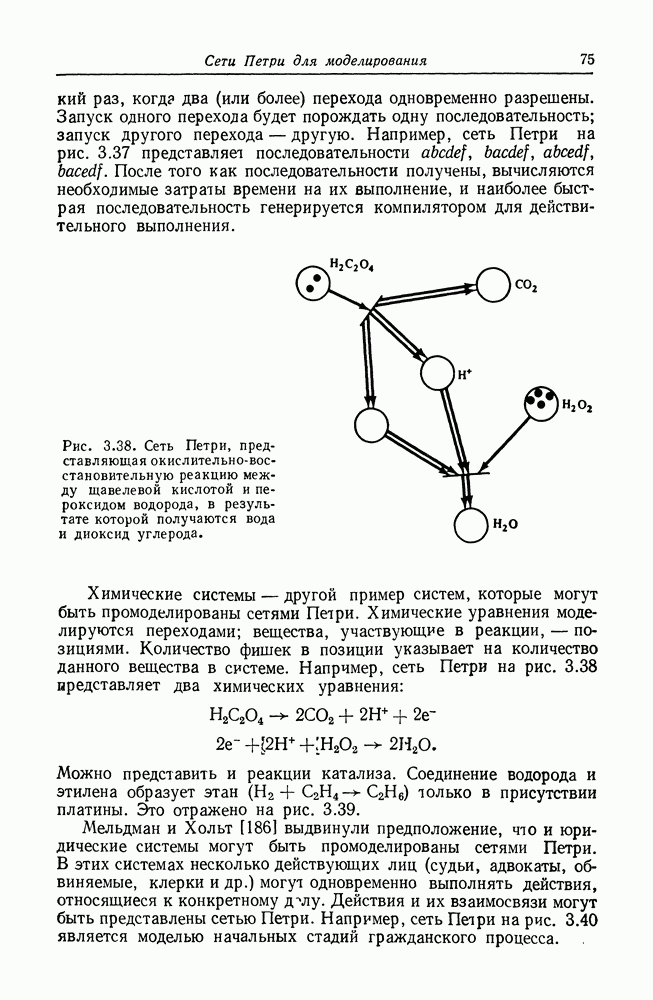
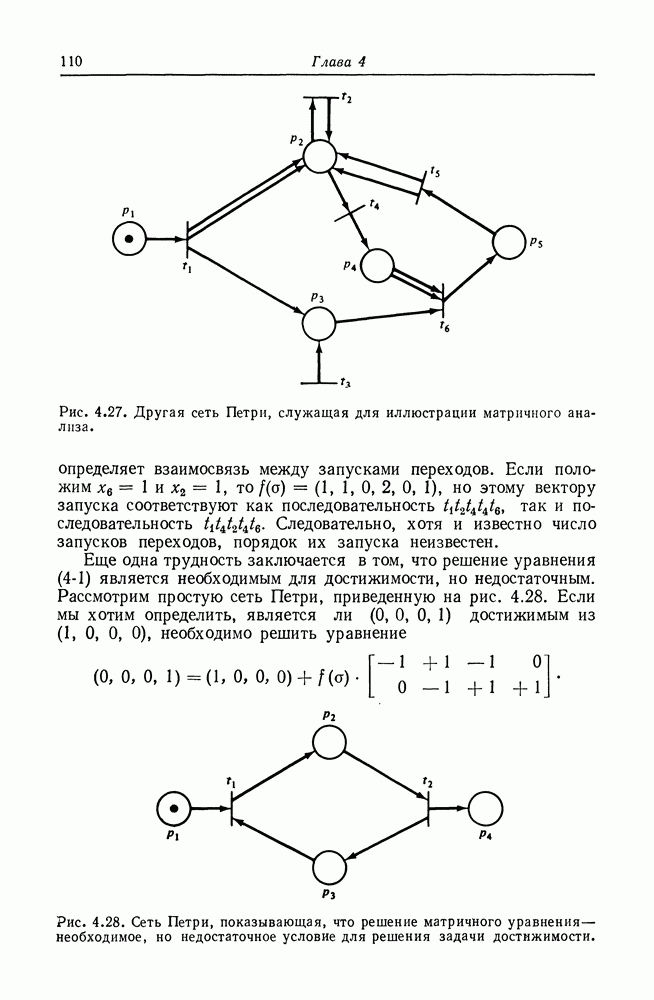
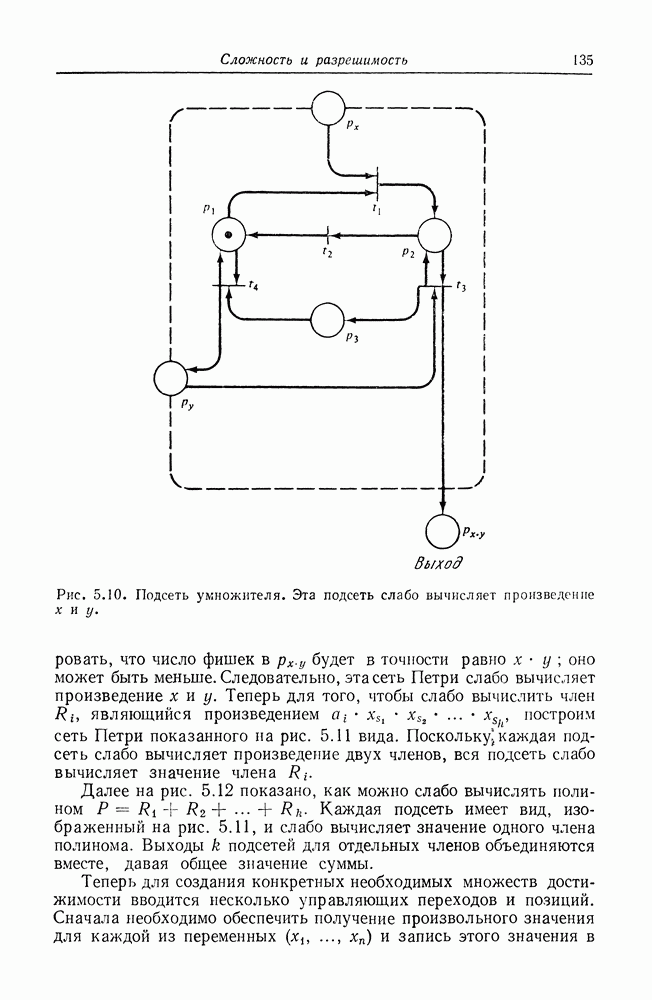
Подсеть умножения показана на рис. 5.10. Эта сеть слабо вычисляет произведение чисел х и у, представимых фишками в ее входных позициях, помещая множество фишек в свой выход. Действует сеть совсем просто.

Рис. 5.9. Базовая структура сети Петри, слабо вычисляющей значение полинома 
Для вычисления произведения х и у сначала запускается переход  перемещая одну фишку из
перемещая одну фишку из  Эта фишка разрешает запуск перехода
Эта фишка разрешает запуск перехода  который может теперь копировать у фишек из позиции
который может теперь копировать у фишек из позиции  помещая их в
помещая их в  и вкладывая в выходную позицию
и вкладывая в выходную позицию  фишек. Теперь можно запустить
фишек. Теперь можно запустить  возвращая фишку из
возвращая фишку из  Это разрешает запуск
Это разрешает запуск  который копирует у фишек из
который копирует у фишек из  обратно в
обратно в  Весь этот процесс можно повторить точно х раз, помещая каждый раз в
Весь этот процесс можно повторить точно х раз, помещая каждый раз в  фишек. После этого маркировка
фишек. После этого маркировка  становится нулевой и сеть останавливается. Общее число фишек в позиции
становится нулевой и сеть останавливается. Общее число фишек в позиции  равно произведению х и у.
равно произведению х и у.
Мы описали наилучший случай в том смысле, что число выходных фишек в точности равно  Однако фишка в
Однако фишка в  разрешает и переход
разрешает и переход  и переход а переход
и переход а переход  можно запустить до того, как все у фишек будут скопированы из
можно запустить до того, как все у фишек будут скопированы из  и добавлены в
и добавлены в  В этом случае число фишек, помещенных в
В этом случае число фишек, помещенных в  будет меньше, чем
будет меньше, чем  Поскольку
Поскольку  можно запустить не более у раз для каждого запуска
можно запустить не более у раз для каждого запуска  можно запустить не более х раз, мы можем гарантировать, что число фишек в
можно запустить не более х раз, мы можем гарантировать, что число фишек в  никогда не превысит
никогда не превысит  но вследствие разрешающей природы запусков переходов мы не можем
но вследствие разрешающей природы запусков переходов мы не можем
Рис. 5.10. (см. скан) Подсеть умножителя. Эта подсеть слабо вычисляет произведение х и у.
гарантировать, что число фишек в  будет в точности равно
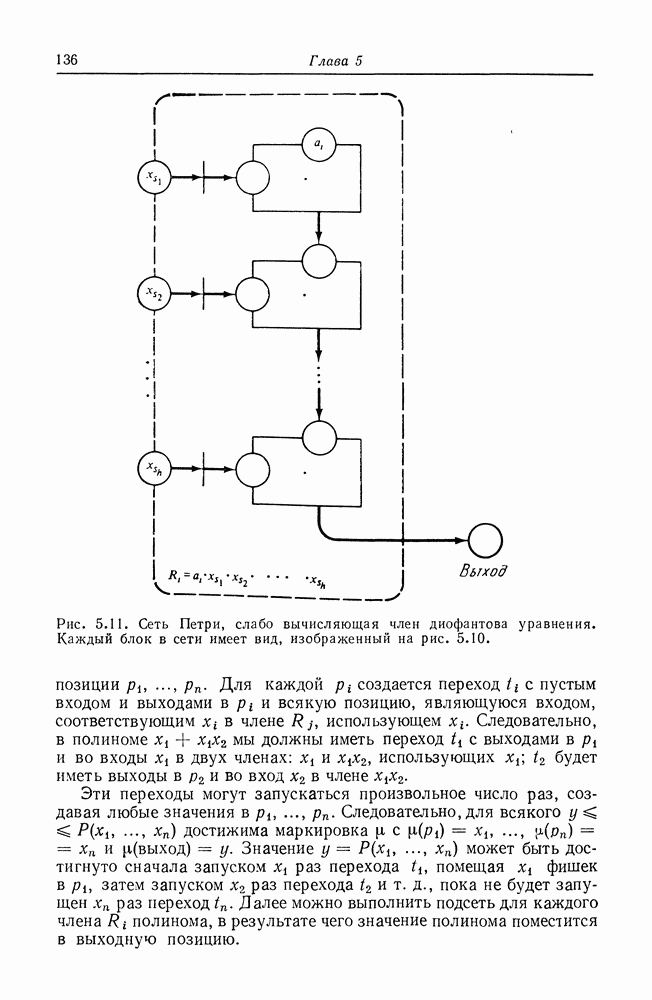
будет в точности равно  оно может быть меньше. Следовательно, эта сеть Петри слабо вычисляет произведение х и у. Теперь для того, чтобы слабо вычислить член
оно может быть меньше. Следовательно, эта сеть Петри слабо вычисляет произведение х и у. Теперь для того, чтобы слабо вычислить член  являющийся произведением
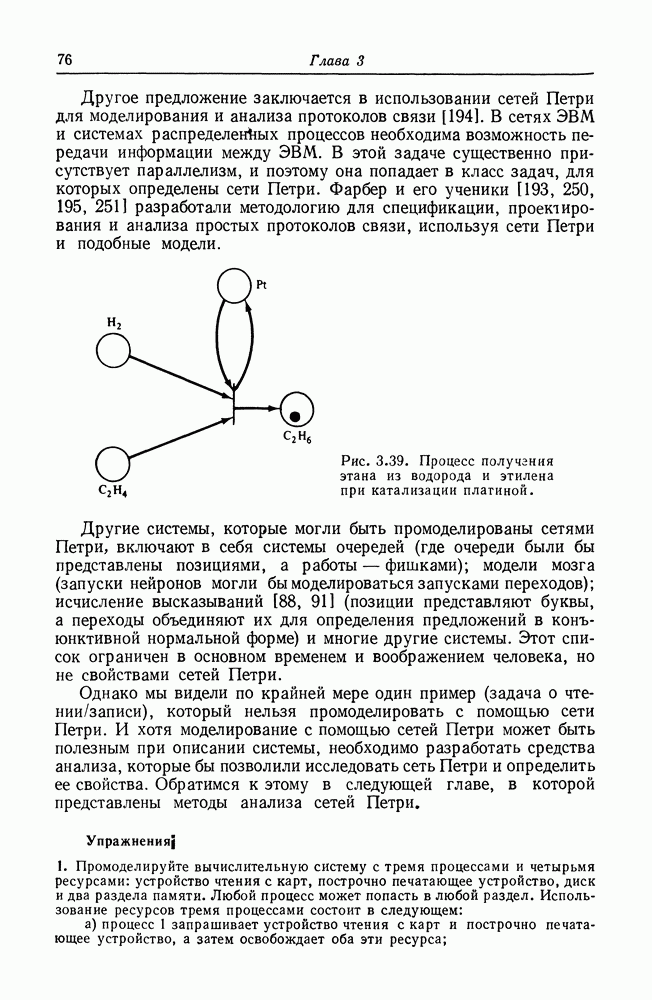
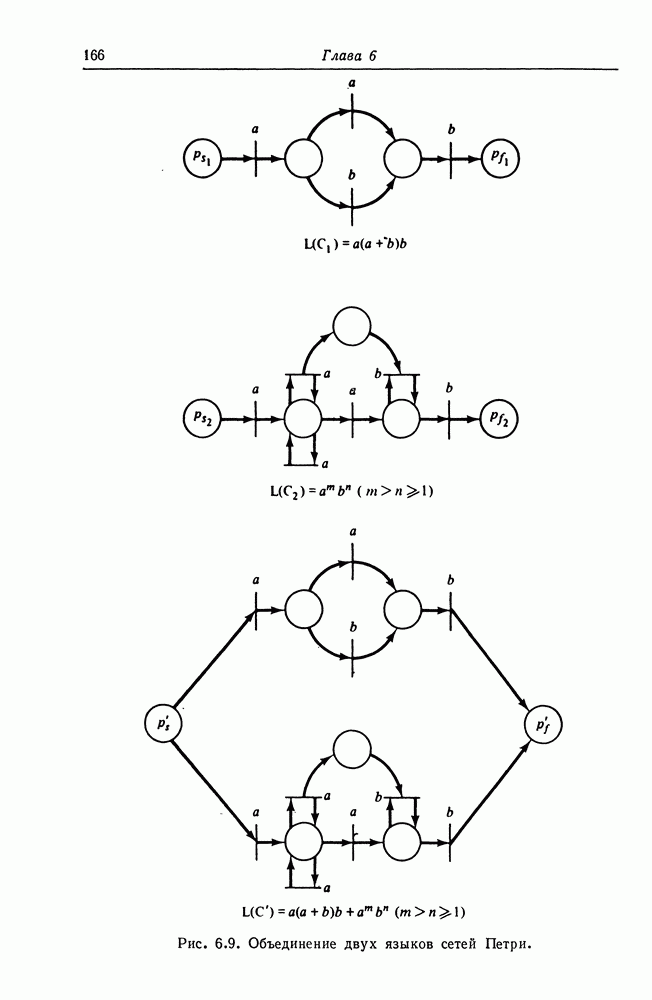
являющийся произведением  построим сеть Петри показанного на рис. 5.11 вида. Поскольку каждая подсеть слабо вычисляет произведение двух членов, вся подсеть слабо вычисляет значение члена
построим сеть Петри показанного на рис. 5.11 вида. Поскольку каждая подсеть слабо вычисляет произведение двух членов, вся подсеть слабо вычисляет значение члена 
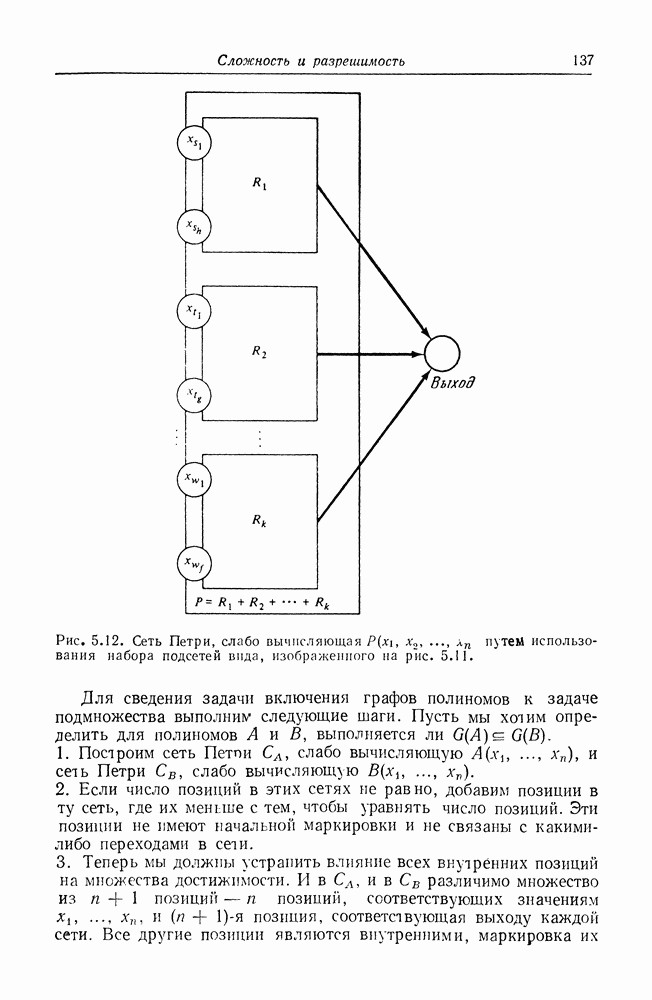
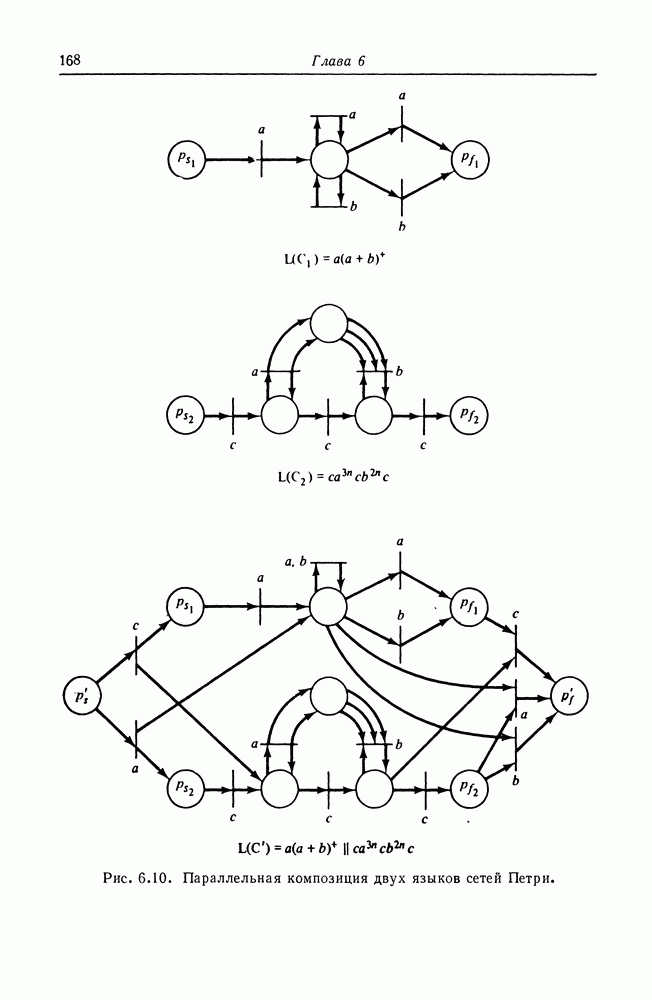
Далее на рис. 5.12 показано, как можно слабо вычислять полином  Каждая подсеть имеет вид, изображенный на рис. 5.11, и слабо вычисляет значение одного члена полинома. Выходы
Каждая подсеть имеет вид, изображенный на рис. 5.11, и слабо вычисляет значение одного члена полинома. Выходы  подсетей для отдельных членов объединяются вместе, давая общее значение суммы.
подсетей для отдельных членов объединяются вместе, давая общее значение суммы.
Теперь для создания конкретных необходимых множеств достижимости вводится несколько управляющих переходов и позиций. Сначала необходимо обеспечить получение произвольного значения для каждой из переменных  и запись этого значения в
и запись этого значения в
Рис. 5.11. (см. скан) Сеть Петри, слабо вычисляющая член диофантова уравнения.
Каждый блок в сети имеет вид, изображенный на рис. 5.10.
позиции  Для каждой
Для каждой  создается переход с пустым входом и выходами в
создается переход с пустым входом и выходами в  и всякую позицию, являющуюся входом, соответствующим
и всякую позицию, являющуюся входом, соответствующим  в члене
в члене  использующем
использующем  Следовательно, в полиноме
Следовательно, в полиноме  мы должны иметь переход
мы должны иметь переход  с выходами в
с выходами в  и во входы
и во входы  в двух членах:
в двух членах:  использующих
использующих  будет иметь выходы в
будет иметь выходы в  и во вход
и во вход  в члене
в члене 
Эти переходы могут запускаться произвольное число раз, создавая любые значения в  Следовательно, для всякого
Следовательно, для всякого  достижима маркировка
достижима маркировка  (выход)
(выход)  Значение
Значение  может быть достигнуто сначала запуском
может быть достигнуто сначала запуском  раз перехода
раз перехода  помещая
помещая  фишек в
фишек в  затем запуском
затем запуском  Раз перехода
Раз перехода  пока не будет запущен
пока не будет запущен  раз переход
раз переход  Далее можно выполнить подсеть для каждого члена
Далее можно выполнить подсеть для каждого члена  полинома, в результате чего значение полинома поместится в выходную позицию.
полинома, в результате чего значение полинома поместится в выходную позицию.
Рис. 5.12. (см. скан) Сеть Петри, слабо вычисляющая  путем использования набора подсетей вида, изображенного на рис. 5.11.
путем использования набора подсетей вида, изображенного на рис. 5.11.
Для сведения задачи включения графов полиномов к задаче подмножества выполним следующие шаги. Пусть мы хотим определить для полиномов А и 5, выполняется ли 
1. Построим сеть Петли  слабо вычисляющую
слабо вычисляющую  и сеть Петри
и сеть Петри  слабо вычисляющую
слабо вычисляющую 
2. Если число позиций в этих сетях не равно, добавим позиции в ту сеть, где их меньше с тем, чтобы уравнять число позиций. Эти позиции не имеют начальной маркировки и не связаны с какими-либо переходами в сети.
3. Теперь мы должны устранить влияние всех внутренних позиций на множества достижимости. И в  различимо множество из
различимо множество из  позиций —
позиций —  позиний, соответствующих значениям
позиний, соответствующих значениям  позиция, соответствующая выходу каждой сети. Все другие позиции являются внутренними, маркировка их
позиция, соответствующая выходу каждой сети. Все другие позиции являются внутренними, маркировка их
неважна. Однако может оказаться, что для внутренней позиции  в
в  и соответствующей позиции
и соответствующей позиции  существуют неравные маркировки
существуют неравные маркировки  поскольку
поскольку  для всех
для всех  в
в 
Для того чтобы обойти это препятствие, введем по две новые позиции:  в
в  (получая
(получая  ) и
) и  (получая
(получая  ) В
) В  позиции
позиции  не связаны с переходами и первоначально
не связаны с переходами и первоначально  пуста,
пуста,  имеет одну фишку. Позиция
имеет одну фишку. Позиция  служит позицией «действия». Она получает начальную маркировку, а каждый переход модифицируется с тем, чтобы включать
служит позицией «действия». Она получает начальную маркировку, а каждый переход модифицируется с тем, чтобы включать  в качестве входа и в качестве выхода. Следовательно, пока фишка остается в
в качестве входа и в качестве выхода. Следовательно, пока фишка остается в  сеть
сеть  может функционировать, как и прежде. Введем в
может функционировать, как и прежде. Введем в  новый переход, переводящий разрешающую фишку из
новый переход, переводящий разрешающую фишку из  запрещая все переходы
запрещая все переходы  и «замораживая» маркировку. Теперь для каждой внутренней позиции введем по два новых перехода.
и «замораживая» маркировку. Теперь для каждой внутренней позиции введем по два новых перехода.
Один из этих переходов, вводимых для каждой внутренней позиции  маркировка которой неважна, имеет в качестве входов позиции
маркировка которой неважна, имеет в качестве входов позиции  а в качестве выхода — только
а в качестве выхода — только  (уменьшая при запуске на 1 маркировку в
(уменьшая при запуске на 1 маркировку в  другой переход в качестве входа имеет
другой переход в качестве входа имеет  а в качестве выхода
а в качестве выхода  и (увеличивая при запуске на 1 маркировку в
и (увеличивая при запуске на 1 маркировку в  Эти переходы благодаря соответствующей последовательности прибавляющих или убавляющих запусков обеспечивают каждой внутренней позиции возможность иметь произвольную маркировку.
Эти переходы благодаря соответствующей последовательности прибавляющих или убавляющих запусков обеспечивают каждой внутренней позиции возможность иметь произвольную маркировку.
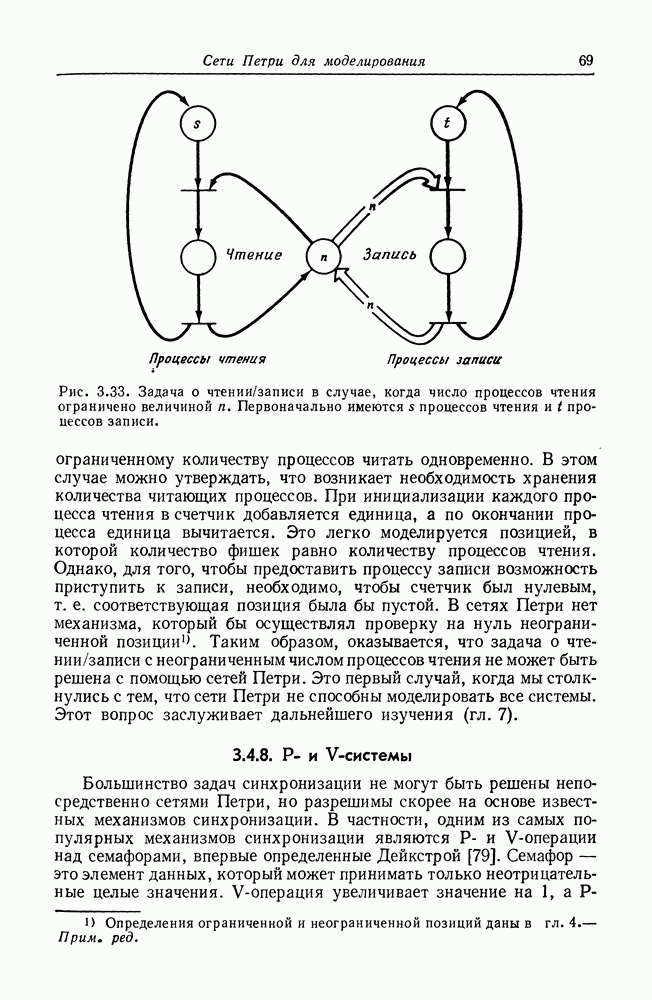
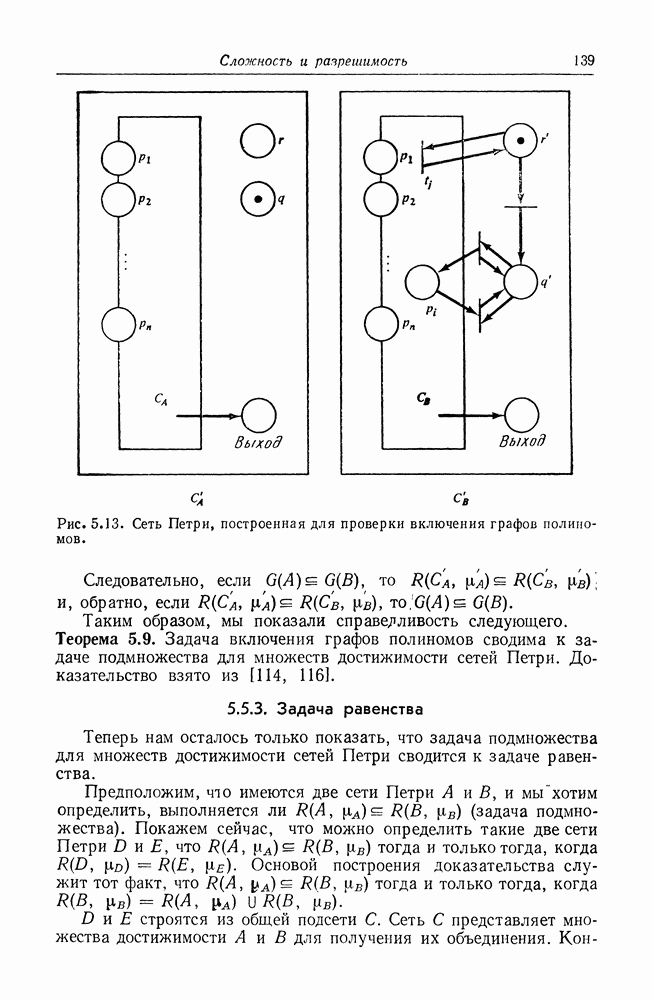
4. Описанная конструкция показана на рис. 5.13. Для двух сетей Петри  с начальной маркировкой
с начальной маркировкой  соответственно,
соответственно,  тогда и только тогда, когда
тогда и только тогда, когда  имеют следующие множества достижимости:
имеют следующие множества достижимости:


Рис. 5.13. Сеть Петри, построенная для проверки включения графов полиномов.
Следовательно, если  то
то  и, обратно, если
и, обратно, если 
Таким образом, мы показали справедливость следующего. Теорема 5.9. Задача включения графов полиномов сводима к задаче подмножества для множеств достижимости сетей Петри. Доказательство взято из [114, 116].
5.5.3. Задача равенства
Теперь нам осталось только показать, что задача подмножества для множеств достижимости сетей Петри сводится к задаче равенства.
Предположим, что имеются две сети Петри А и 5, и  определить, выполняется ли
определить, выполняется ли  (задача подмножества). Покажем сейчас, что можно определить такие две сети Петри
(задача подмножества). Покажем сейчас, что можно определить такие две сети Петри  что
что  тогда и только тогда, когда
тогда и только тогда, когда  Основой построения доказательства служит тот факт, что
Основой построения доказательства служит тот факт, что  тогда и только тогда, когда
тогда и только тогда, когда  строятся из общей подсети С. Сеть С представляет множества достижимости
строятся из общей подсети С. Сеть С представляет множества достижимости  для получения их объединения.
для получения их объединения.
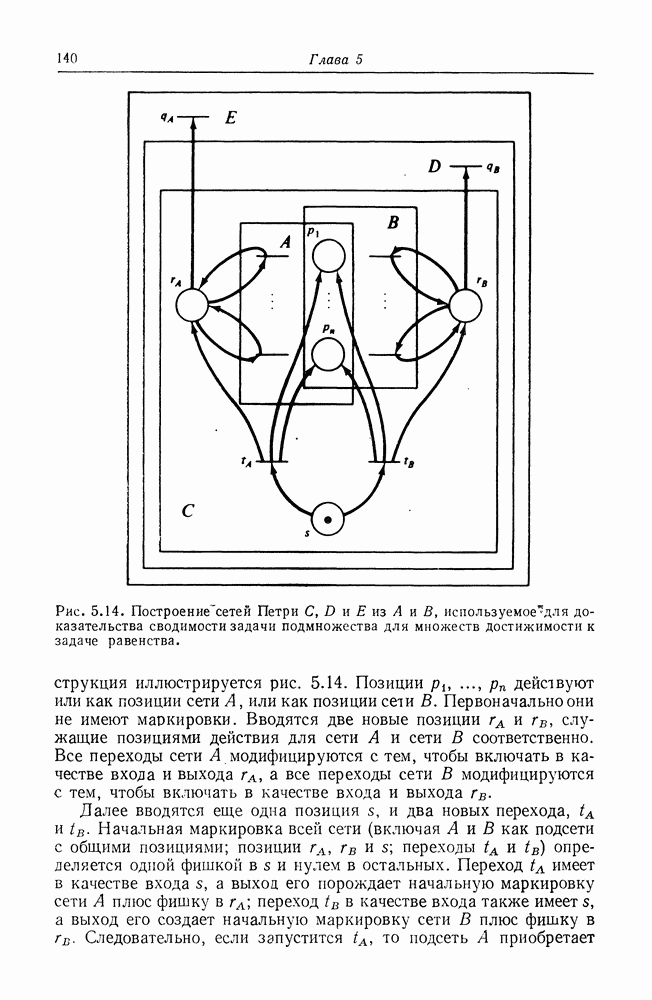
Рис. 5.14. (см. скан) Построение сетей Петри  из
из  используемое для доказательства сводимости задачи подмножества для множеств достижимости к задаче равенства.
используемое для доказательства сводимости задачи подмножества для множеств достижимости к задаче равенства.
Конструкция иллюстрируется рис. 5.14. Позиции  действуют или как позиции сети А, или как позиции сети В. Первоначально они не имеют маркировки. Вводятся две новые позиции гл и
действуют или как позиции сети А, или как позиции сети В. Первоначально они не имеют маркировки. Вводятся две новые позиции гл и  служащие позициями действия для сети А и сети В соответственно. Все переходы сети
служащие позициями действия для сети А и сети В соответственно. Все переходы сети  модифицируются с тем, чтобы включать в качестве входа и выхода
модифицируются с тем, чтобы включать в качестве входа и выхода  а все переходы сети В модифицируются с тем, чтобы включать в качестве входа и выхода
а все переходы сети В модифицируются с тем, чтобы включать в качестве входа и выхода 
Далее вводятся еще одна позиция  и два новых перехода,
и два новых перехода,  Начальная маркировка всей сети (включая
Начальная маркировка всей сети (включая  как подсети с общими позициями; позиции
как подсети с общими позициями; позиции  переходы
переходы  определяется одной фишкой в
определяется одной фишкой в  и нулем в остальных. Переход
и нулем в остальных. Переход  имеет в качестве входа
имеет в качестве входа  а выход его порождает начальную маркировку сети А плюс фишку в
а выход его порождает начальную маркировку сети А плюс фишку в  переход
переход  в качестве входа также имеет
в качестве входа также имеет  а выход его создает начальную маркировку сети В плюс фишку в
а выход его создает начальную маркировку сети В плюс фишку в  Следовательно, если запустится
Следовательно, если запустится  то подсеть А приобретает
то подсеть А приобретает
свою начальную маркировку, и все ее переходы могут запускаться, как обычно, поскольку в  имеется фишка. Подсеть
имеется фишка. Подсеть  однако, полностью запрещена, поскольку фишки в
однако, полностью запрещена, поскольку фишки в  нет. Если первым запустится
нет. Если первым запустится  то сможет действовать подсеть В, а подсеть А будет запрещена. Тогда множество последовательностей для С — это любая последовательность вида
то сможет действовать подсеть В, а подсеть А будет запрещена. Тогда множество последовательностей для С — это любая последовательность вида

или любая последовательность вида

Сеть  получается из С введением одного нового перехода
получается из С введением одного нового перехода  имеет в качестве входа позицию
имеет в качестве входа позицию  выход его пуст. Заметим, что
выход его пуст. Заметим, что  может запуститься, только если первым был запущен переход
может запуститься, только если первым был запущен переход  если же первым запустится переход
если же первым запустится переход  то
то  будет пустой и
будет пустой и  не сможет запуститься.
не сможет запуститься.
Сеть  строится из
строится из  добавлением нового перехода
добавлением нового перехода  Он в качестве входа имеет позицию
Он в качестве входа имеет позицию  выхода не имеет. Переход может запуститься, только если первым был запущен
выхода не имеет. Переход может запуститься, только если первым был запущен  Подчеркнем, что сеть
Подчеркнем, что сеть  строится из
строится из  а не (непосредственно) из С. Поэтому
а не (непосредственно) из С. Поэтому  имеет и переход
имеет и переход  и переход
и переход 
Рассмотрим теперь множества достижимости сетей Петри  Множество достижимости С — это все маркировки вида:
Множество достижимости С — это все маркировки вида:

Сеть Петри  добавляет к этому множеству один новый класс маркировок:
добавляет к этому множеству один новый класс маркировок:

Сеть Петри  добавляет еще один класс:
добавляет еще один класс:

Теперь, если  то последний класс в
то последний класс в  (маркировки вида
(маркировки вида  где
где  включен в последний класс
включен в последний класс  (маркировки вида
(маркировки вида  ), где
), где  Поскольку все другие маркировки совпадают, то
Поскольку все другие маркировки совпадают, то  если
если  Аналогично, если
Аналогично, если  так как для всякой маркировки
так как для всякой маркировки  где
где  должна существовать такая же маркировка в
должна существовать такая же маркировка в  Но все маркировки с
Но все маркировки с  имеют вид
имеют вид  где
где  поэтому
поэтому 
Таким образом, на основе этой конструкции доказано следующее.
Теорема 5.10. Задача подмножества для множеств достижимости сетей Петри сводима к задаче равенства для множеств достижимости сетей Петри.
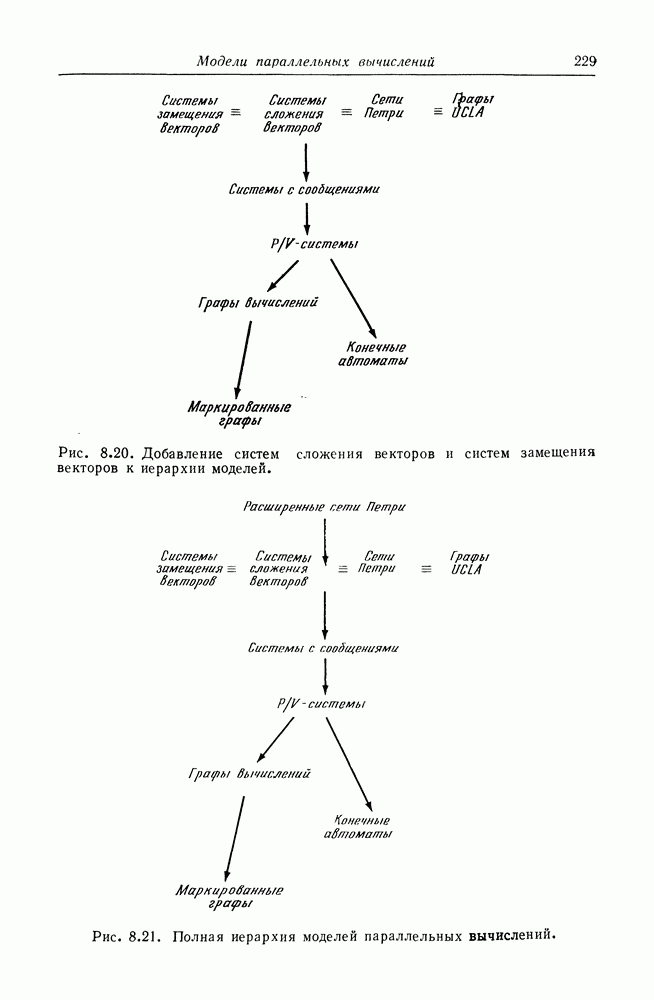
Последние три теоремы приводят к следующему результату.
Теорема 5.11. Следующие задачи неразрешимы:
1. Задача включения графов полиномов.
2. Задача подмножества для множеств достижимости сетей Петри.
3. Задача равенства для множеств достижимости сетей Петри.
Эти теоремы и их доказательства принадлежат Хэку [114, 116].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ГЛАВА 1. ВВЕДЕНИЕ
- ГЛАВА 2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
- 2.1. Структура сети Петри
- 2.2. Графы сетей Петри
- 2.3. Маркировка сетей Петри
- 2.4. Правила выполнения сетей Петри
- 2.5. Пространство состояний сети Петри
- 2.6. Альтернативные формы определения сетей Петри
- ГЛАВА 3. СЕТИ ПЕТРИ ДЛЯ МОДЕЛИРОВАНИЯ
- 3.2. Одновременность и конфликт
- 3.3. Аппаратное обеспечение ЭВМ
- 3.4. Программное обеспечение ЭВМ
- 3.5. Другие системы
- ГЛАВА 4. АНАЛИЗ СЕТЕЙ ПЕТРИ
- 4.1. Задачи анализа сетей Петри
- 4.2. Методы анализа
- ГЛАВА 5. СЛОЖНОСТЬ И РАЗРЕШИМОСТЬ
- 5.1. Сводимость задач анализа
- 5.2. Задачи достижимости
- 5.3. Сети Петри с ограничениями
- 5.4. Активность и достижимость
- 5.5. Неразрешимые задачи
- 5.6. Сложность задачи достижимости
- ГЛАВА 6. ЯЗЫКИ СЕТЕЙ ПЕТРИ
- 6.2. Некоторые понятия теории формальных языков
- 6.3. Определения языков сетей Петри
- 6.4. Свойства языков сетей Петри
- 6.5. Свойства замкнутости
- 6.6. Языки сетей Петри и другие классы языков
- ГЛАВА 7. РАСШИРЕННЫЕ И ОГРАНИЧЕННЫЕ МОДЕЛИ СЕТЕЙ ПЕТРИ
- 7.1. Границы возможностей моделирования с помощью сетей Петри
- 7.2. Расширения
- 7.3. Расширенные сети Петри и регистровые машины
- 7.4. Подклассы сетей Петри
- ГЛАВА 8. МОДЕЛИ ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ
- 8.2. Маркированные графы
- 8.3. Графы вычислений
- 8.4. P/V-системы
- 8.5. Системы передачи сообщений
- 8.6. Графы UCLA
- 8.7. Системы замещения и сложения векторов
- 8.8. Расширенные модели сетей Петри
- ОБЗОР ТЕОРИИ КОМПЛЕКТОВ
- АННОТИРОВАННАЯ БИБЛИОГРАФИЯ