| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.3. Маркировка сетей Петри
Маркировка  есть присвоение фишек позициям сети Петри. Фишка — это примитивное понятие сетей Петри (подобно позициям и переходам). Фишки присваиваются (можно считать, что они принадлежат) позициям. Количество и положение фишек при выполнении сети Петри могут изменяться. Фишки используются для определения выполнения сети Петри.
есть присвоение фишек позициям сети Петри. Фишка — это примитивное понятие сетей Петри (подобно позициям и переходам). Фишки присваиваются (можно считать, что они принадлежат) позициям. Количество и положение фишек при выполнении сети Петри могут изменяться. Фишки используются для определения выполнения сети Петри.
Определение 2.5. Маркировка  сети Петри
сети Петри  есть функция отображающая множество позиций
есть функция отображающая множество позиций  в множество неотрицательных целых чисел
в множество неотрицательных целых чисел 

Маркировка  может быть также определена как
может быть также определена как  -вектор
-вектор  где
где  и каждое
и каждое 

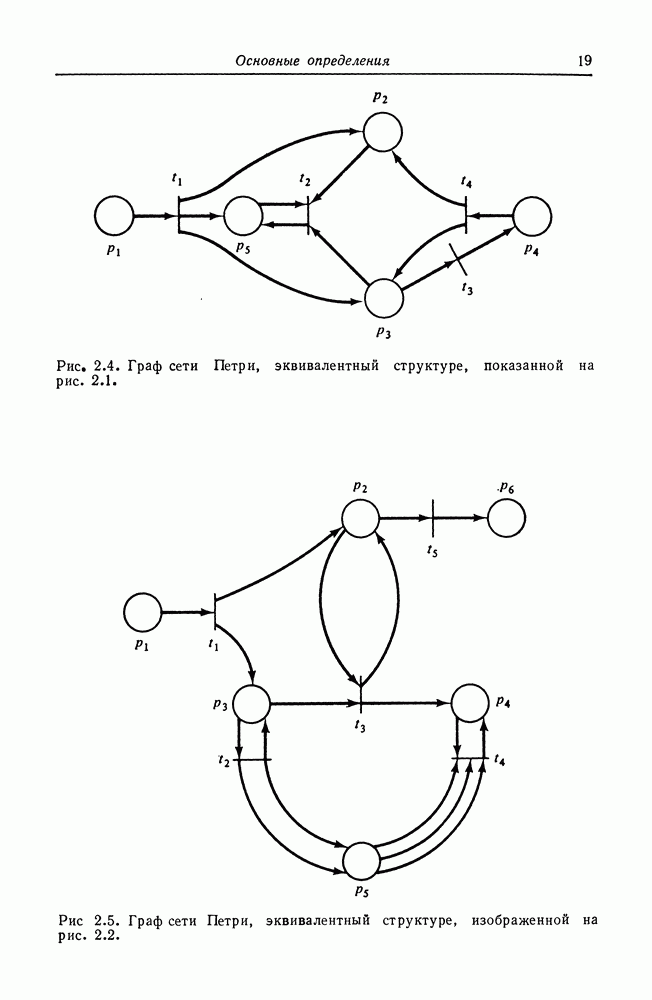
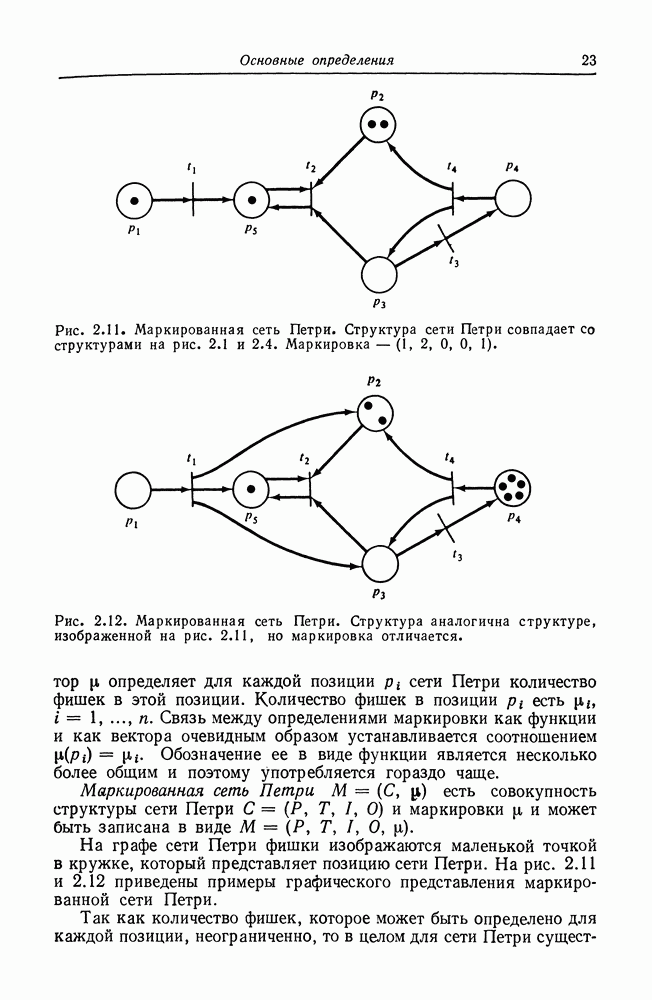
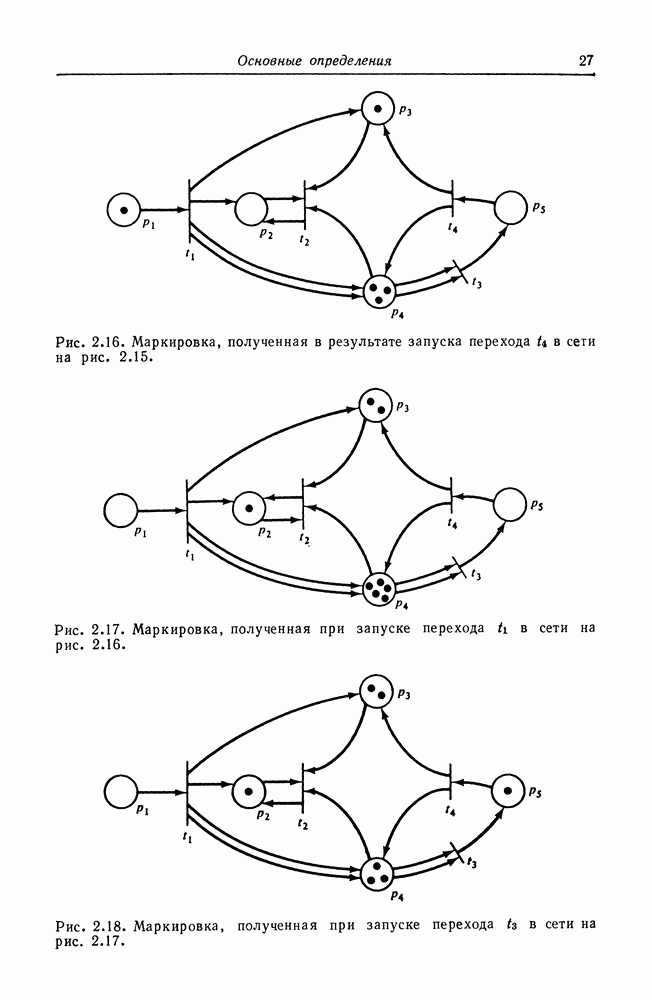
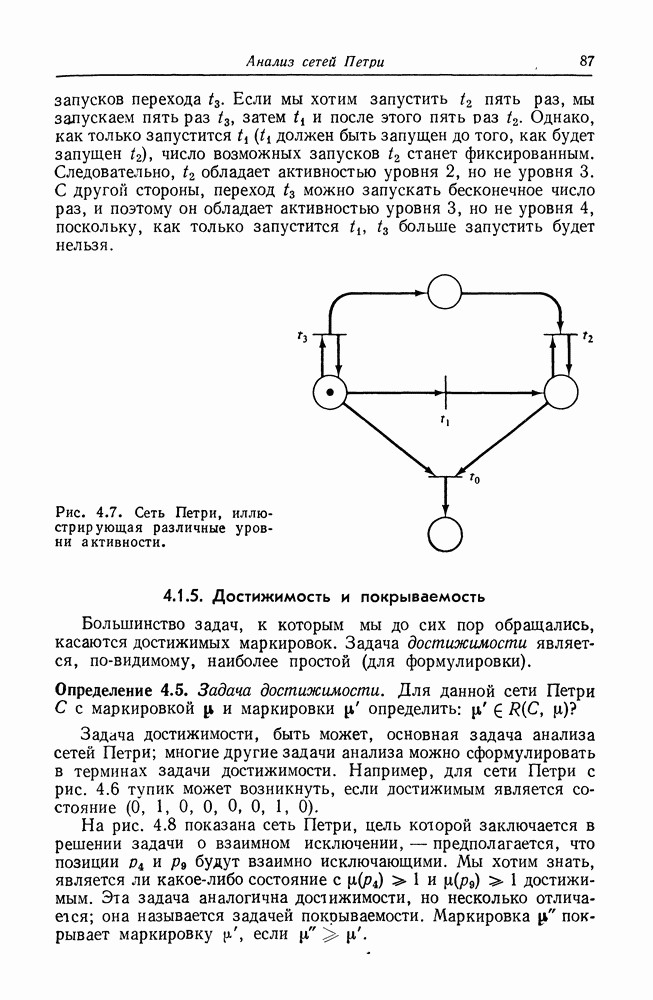
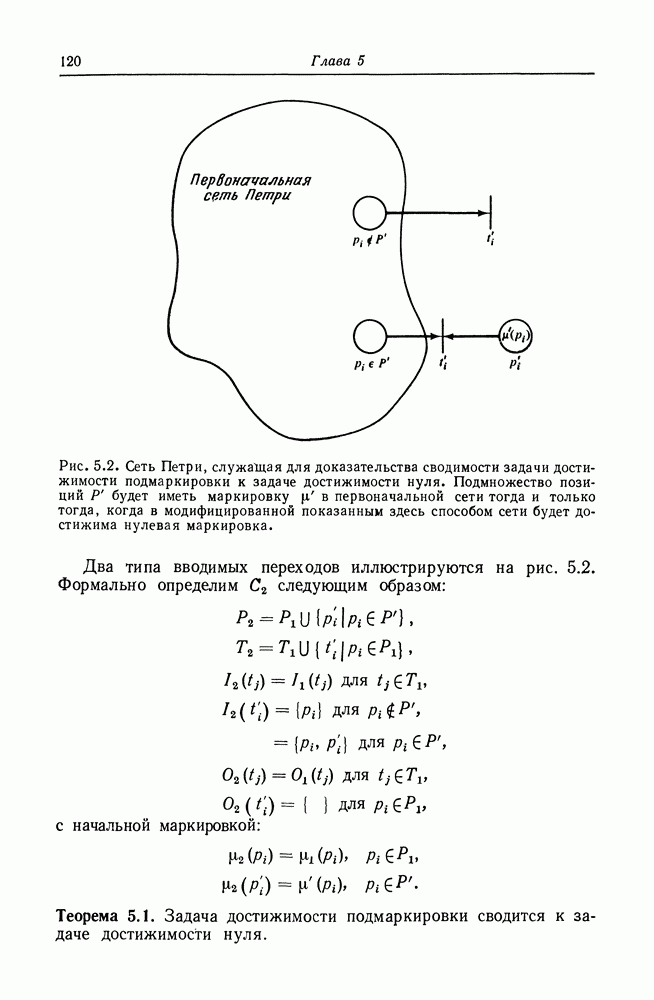
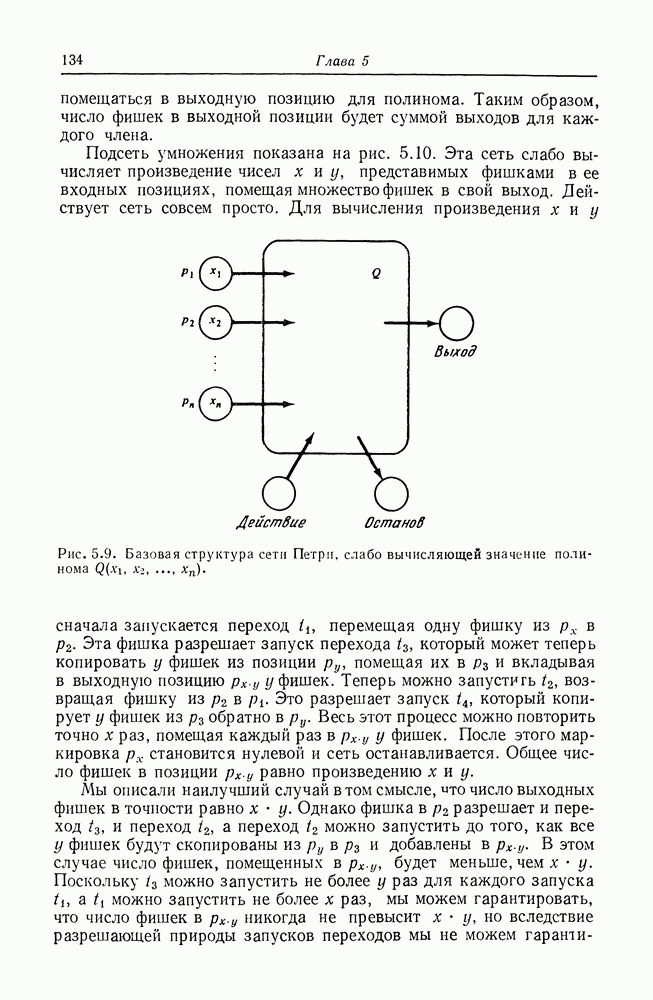
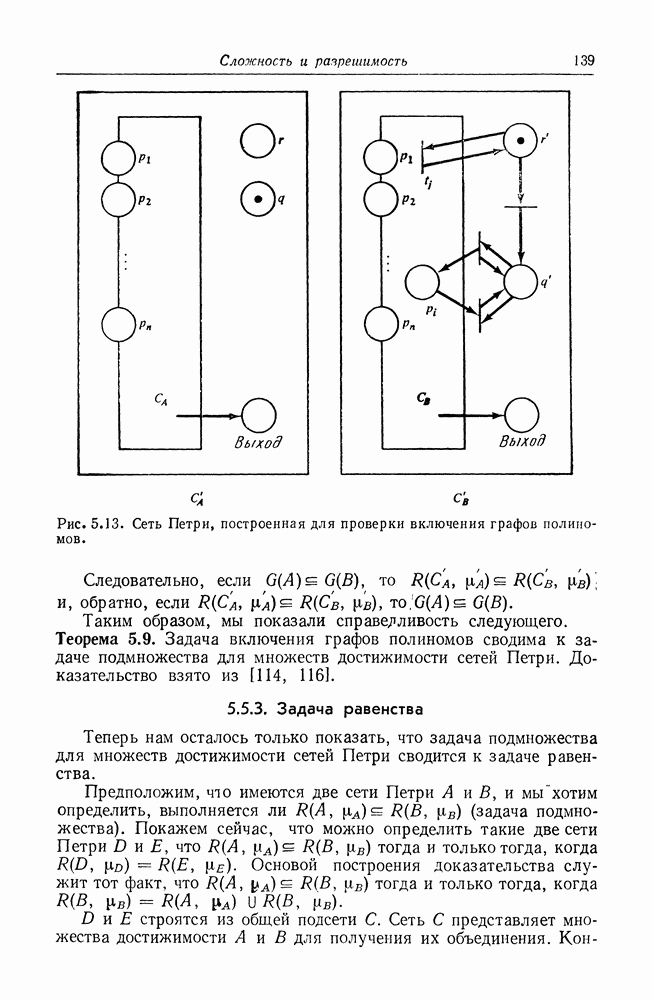
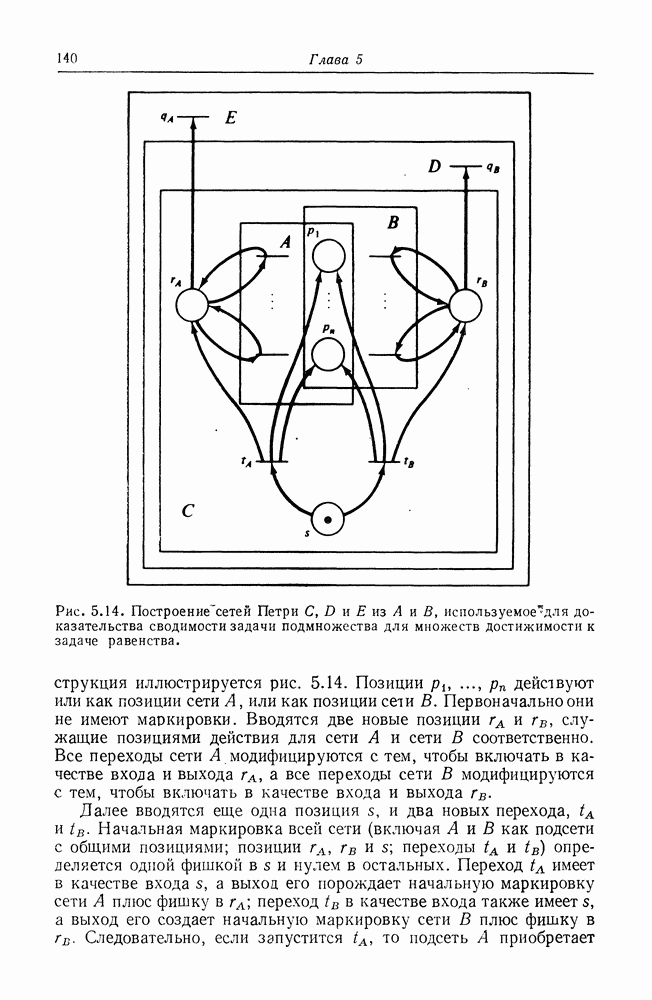
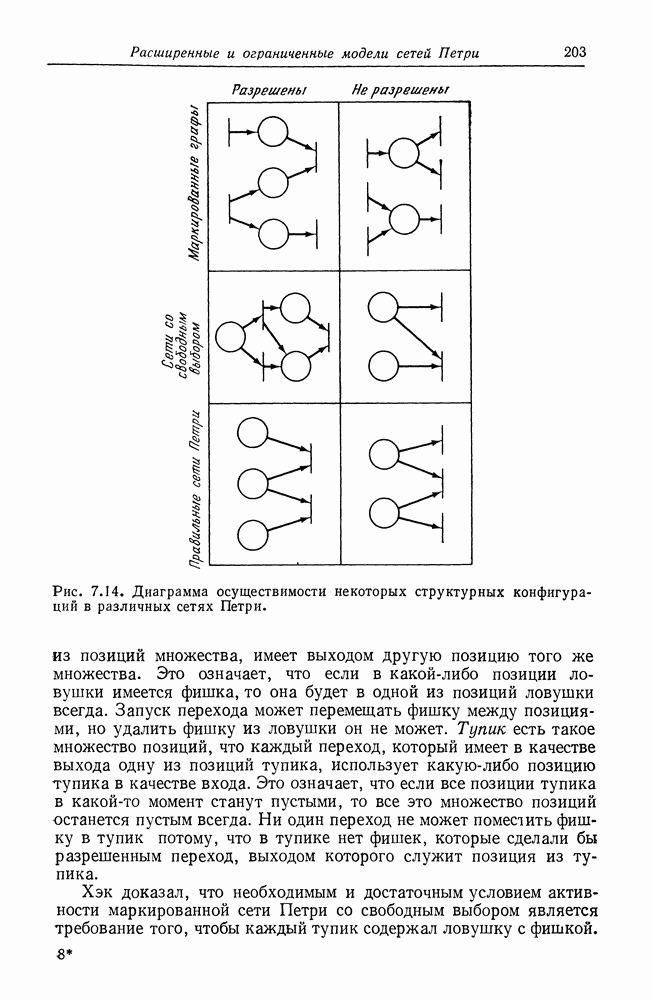
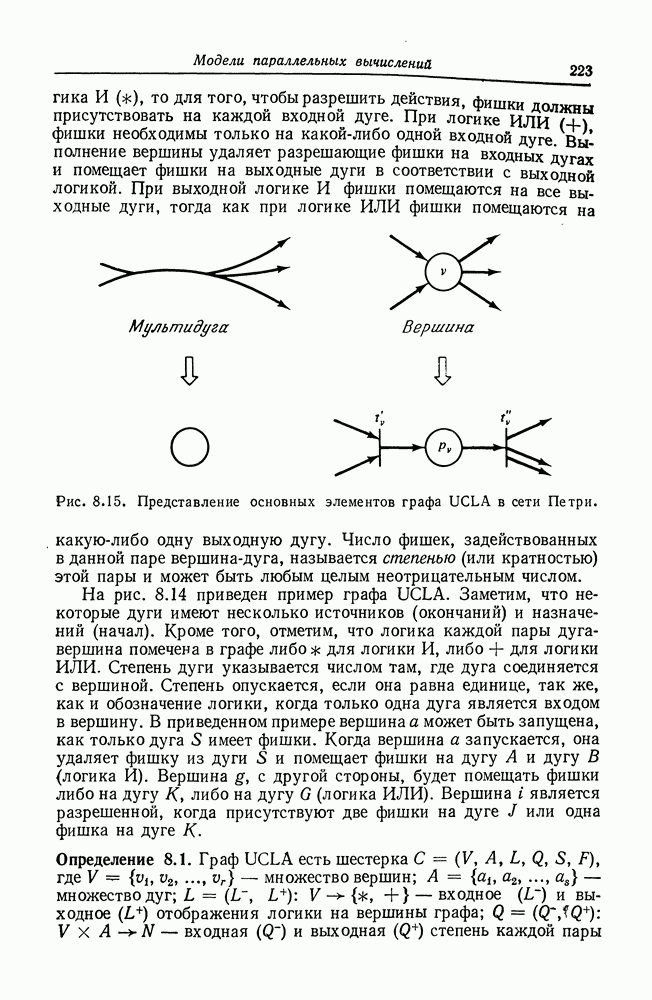
Рис. 2.11. Маркированная сеть Петри. Структура сети Петри совпадает со структурами на рис. 2.1 и 2.4. Маркировка 

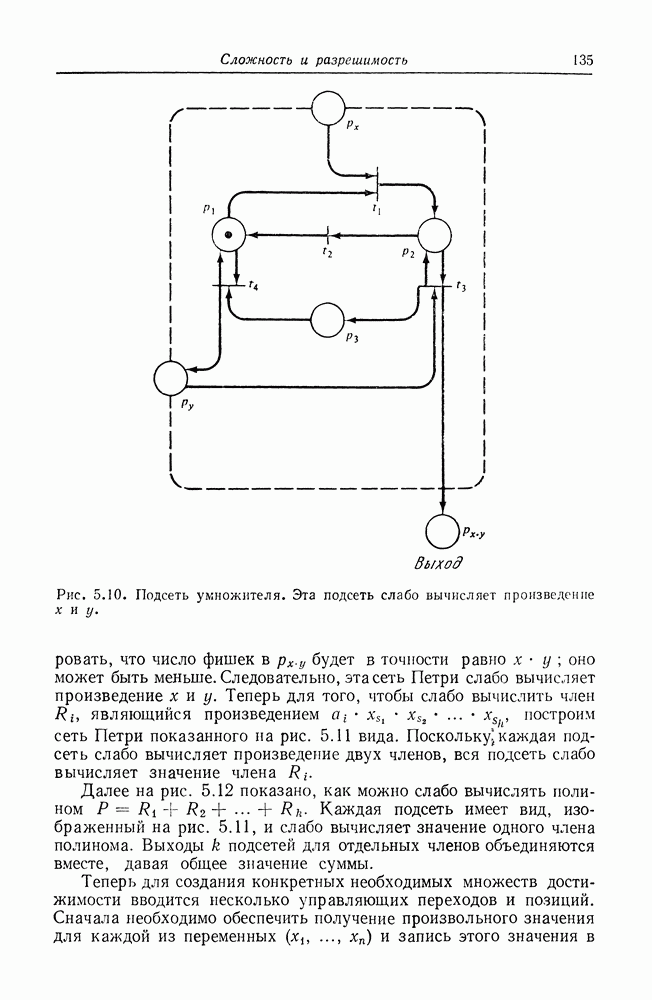
Рис. 2.12. Маркированная сеть Петри. Структура аналогична структуре, изображенной на рис. 2.11, но маркировка отличается.
Вектор  определяет для каждой позиции
определяет для каждой позиции  сети Петри количество фишек в этой позиции. Количество фишек в позиции
сети Петри количество фишек в этой позиции. Количество фишек в позиции  есть
есть 
Связь между определениями маркировки как функции и как вектора очевидным образом устанавливается соотношением  Обозначение ее в виде функции является несколько более общим и поэтому употребляется гораздо чаще.
Обозначение ее в виде функции является несколько более общим и поэтому употребляется гораздо чаще.
Маркированная сеть Петри  есть совокупность структуры сети Петри
есть совокупность структуры сети Петри  и маркировки
и маркировки  и может быть записана в виде
и может быть записана в виде 
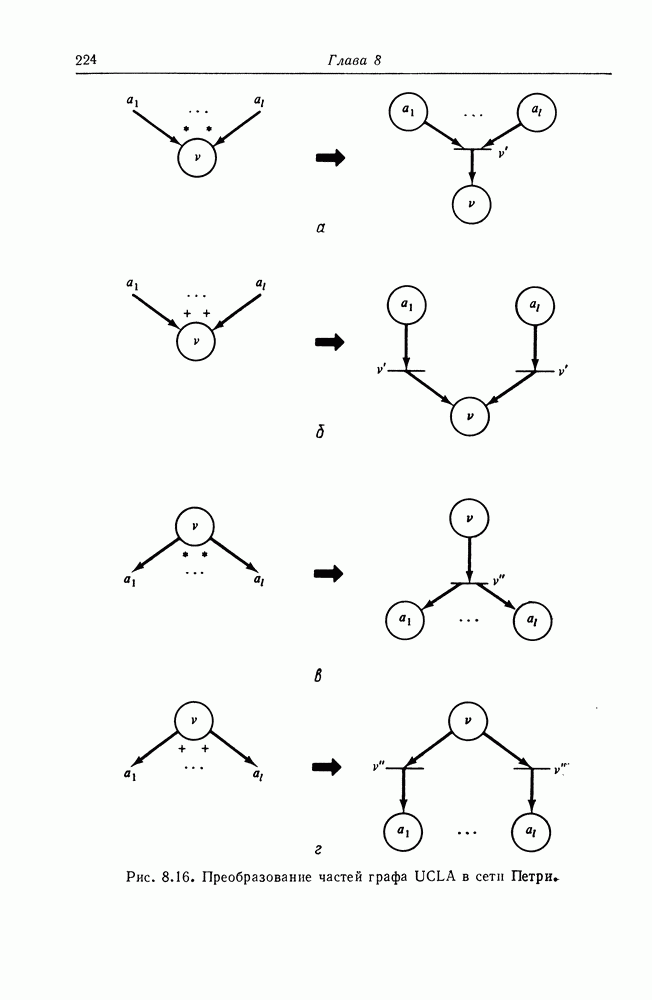
На графе сети Петри фишки изображаются маленькой точкой в кружке, который представляет позицию сети Петри. На рис. 2.11 и 2.12 приведены примеры графического представления маркированной сети Петри.
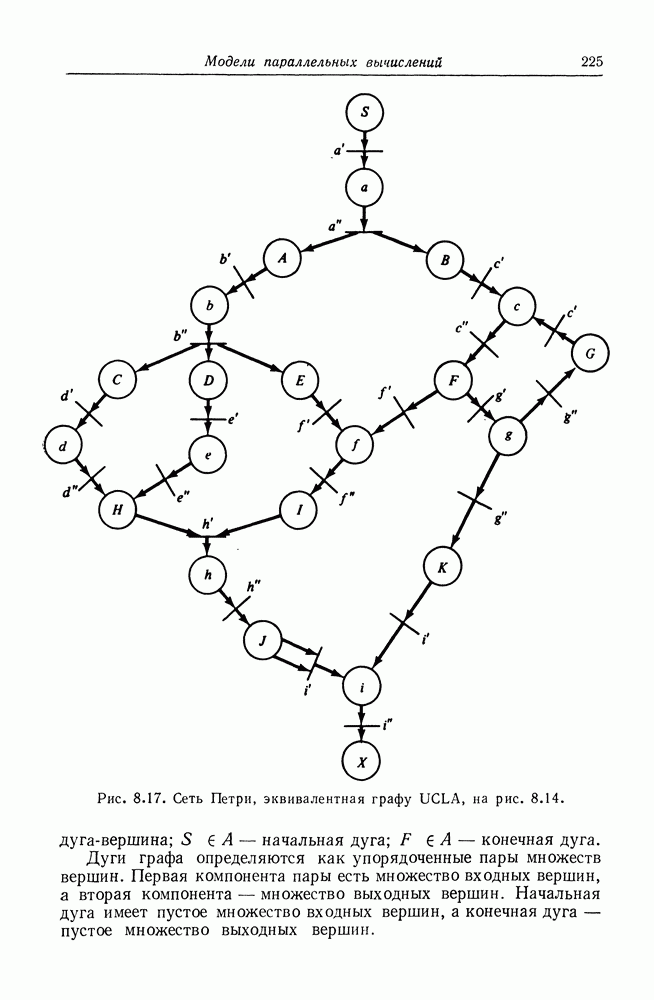
Так как количество фишек, которое может быть определено для каждой позиции, неограниченно, то в целом для сети Петри

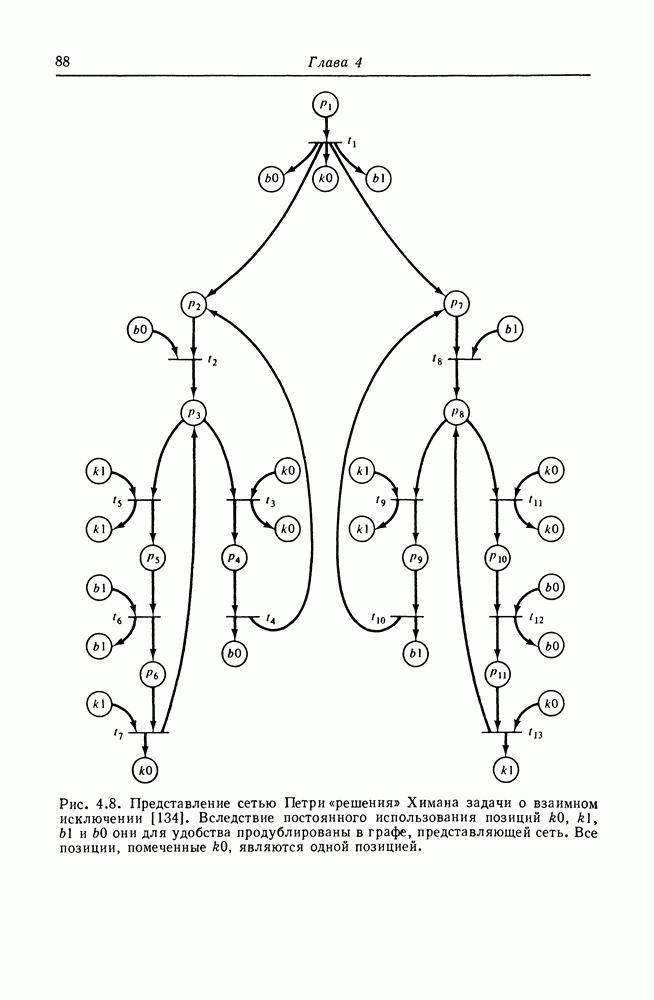
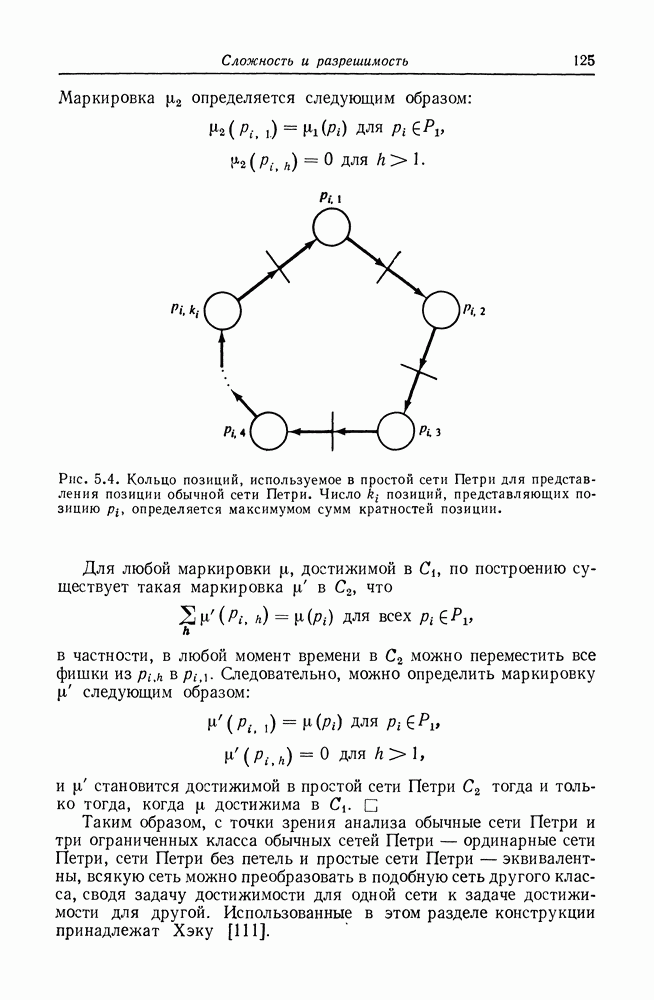
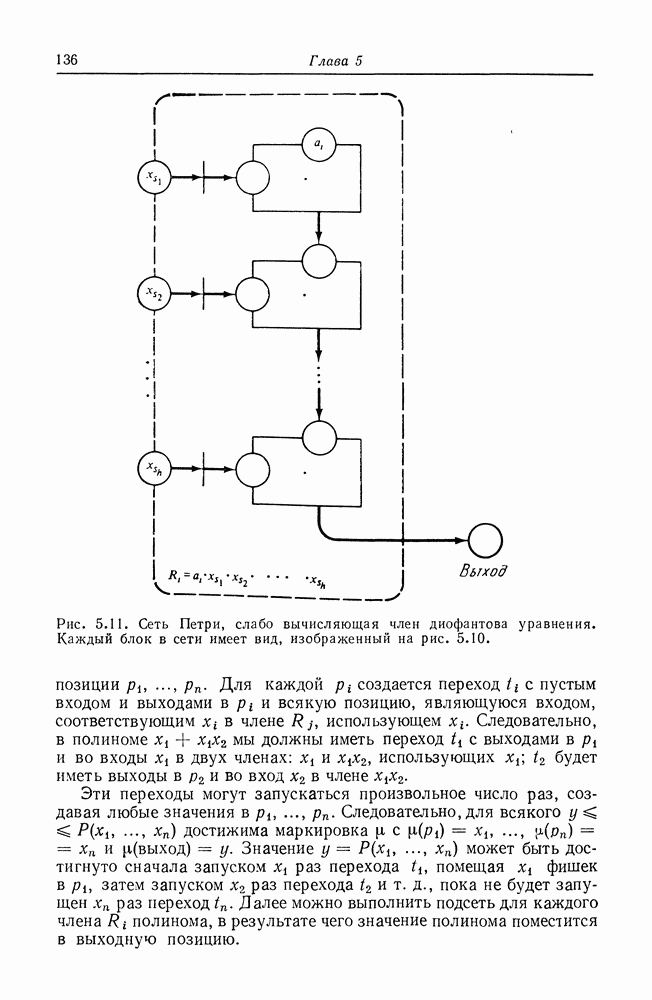
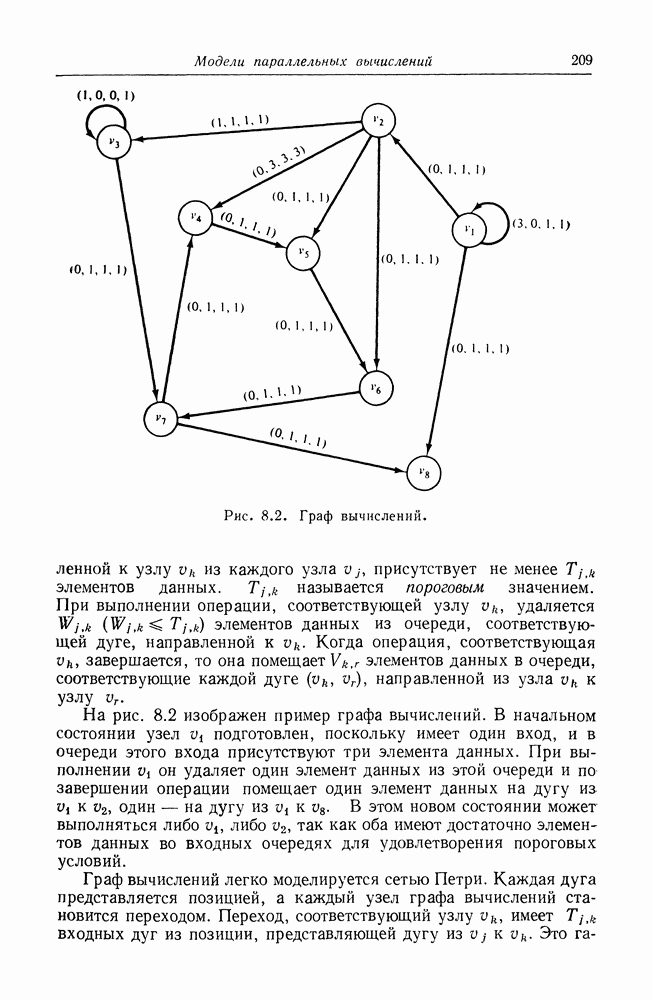
Рис. 2.13. Граф сети Петри с очень большой маркировкой (47, 13, 7, 42),
существует бесконечно много маркировок. Множество всех маркировок сети Петри, обладающей  позициями, есть множество всех
позициями, есть множество всех  -векторов,
-векторов,  Это множество, хотя и бесконечно, является счетным.
Это множество, хотя и бесконечно, является счетным.
Упражнения
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ГЛАВА 1. ВВЕДЕНИЕ
- ГЛАВА 2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
- 2.1. Структура сети Петри
- 2.2. Графы сетей Петри
- 2.3. Маркировка сетей Петри
- 2.4. Правила выполнения сетей Петри
- 2.5. Пространство состояний сети Петри
- 2.6. Альтернативные формы определения сетей Петри
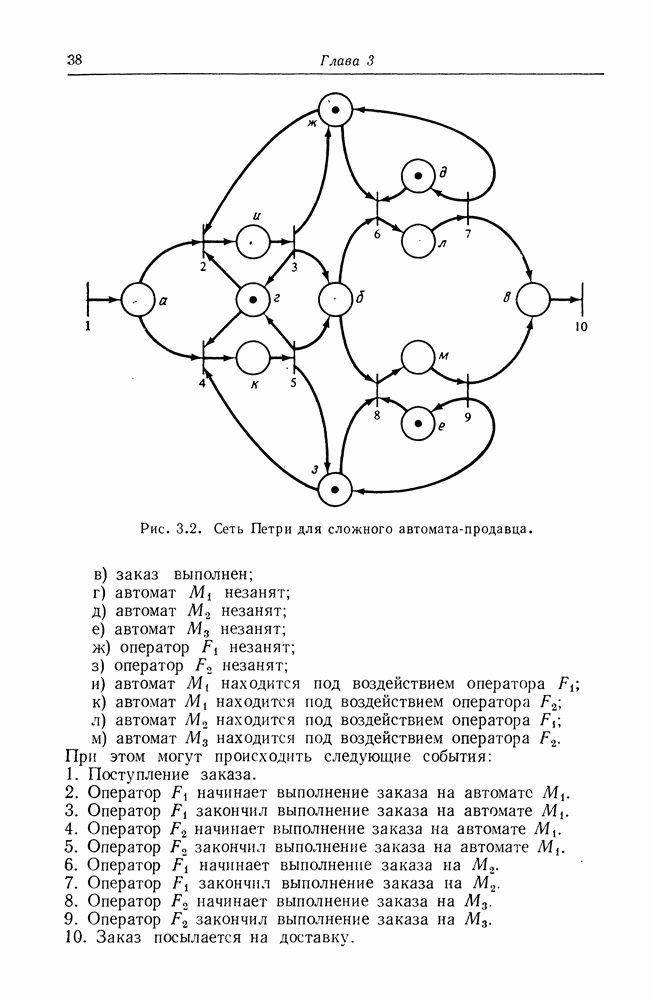
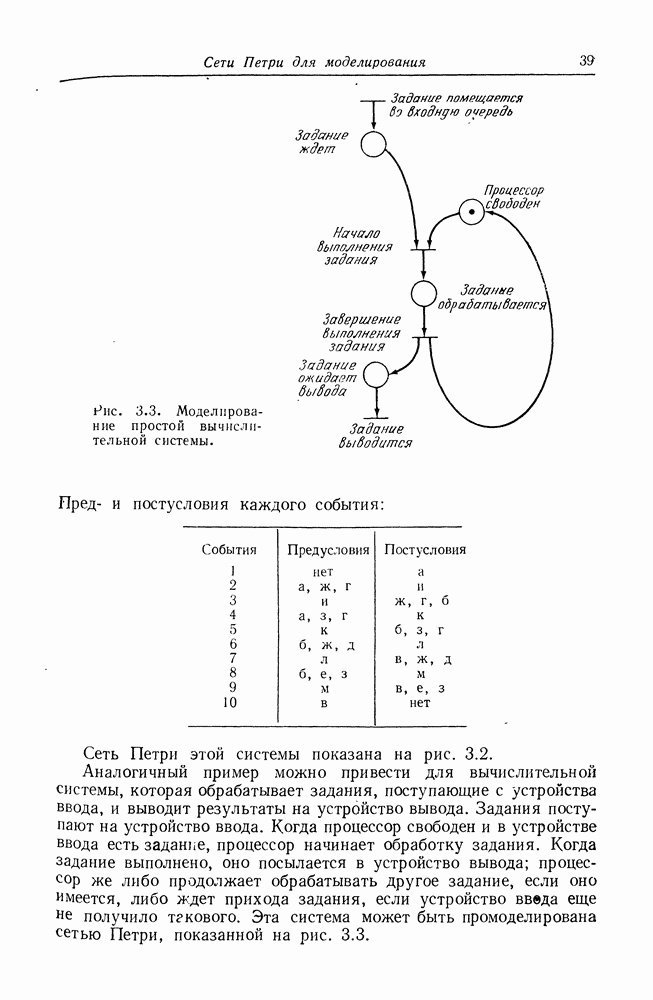
- ГЛАВА 3. СЕТИ ПЕТРИ ДЛЯ МОДЕЛИРОВАНИЯ
- 3.2. Одновременность и конфликт
- 3.3. Аппаратное обеспечение ЭВМ
- 3.4. Программное обеспечение ЭВМ
- 3.5. Другие системы
- ГЛАВА 4. АНАЛИЗ СЕТЕЙ ПЕТРИ
- 4.1. Задачи анализа сетей Петри
- 4.2. Методы анализа
- ГЛАВА 5. СЛОЖНОСТЬ И РАЗРЕШИМОСТЬ
- 5.1. Сводимость задач анализа
- 5.2. Задачи достижимости
- 5.3. Сети Петри с ограничениями
- 5.4. Активность и достижимость
- 5.5. Неразрешимые задачи
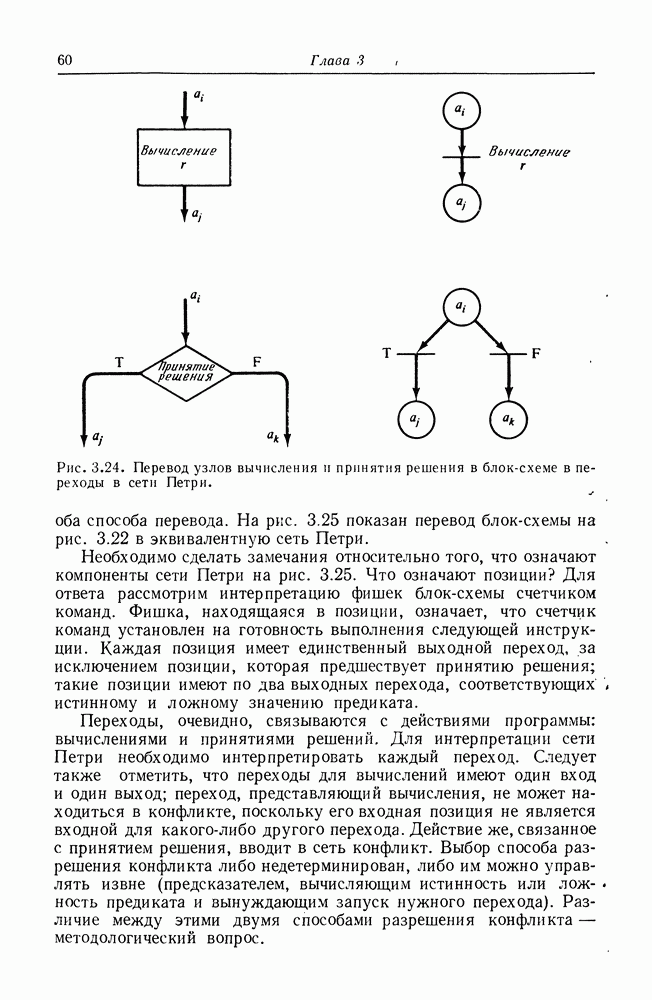
- 5.6. Сложность задачи достижимости
- ГЛАВА 6. ЯЗЫКИ СЕТЕЙ ПЕТРИ
- 6.2. Некоторые понятия теории формальных языков
- 6.3. Определения языков сетей Петри
- 6.4. Свойства языков сетей Петри
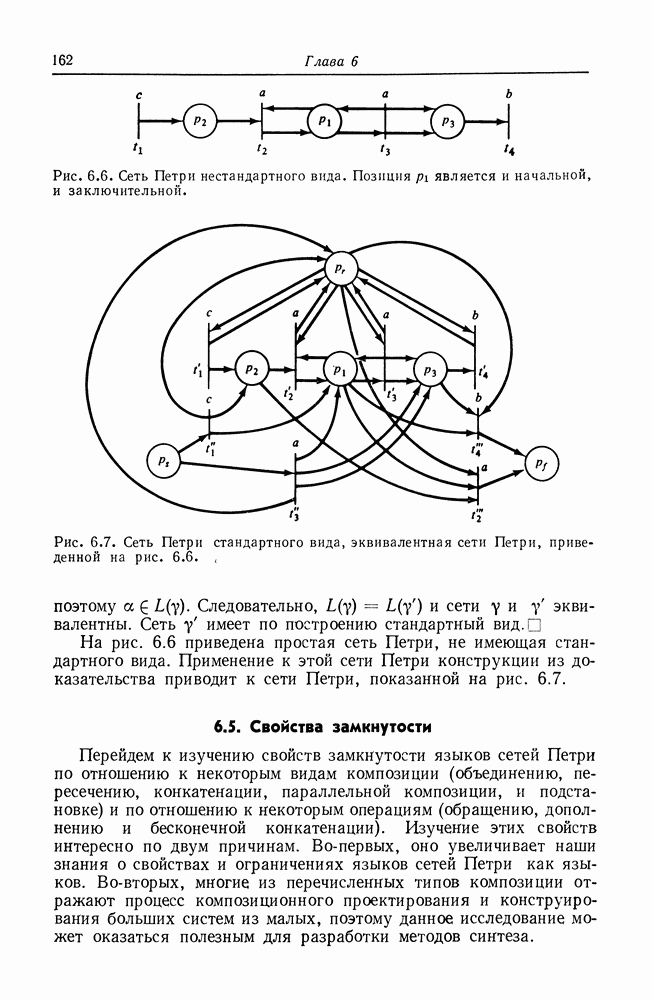
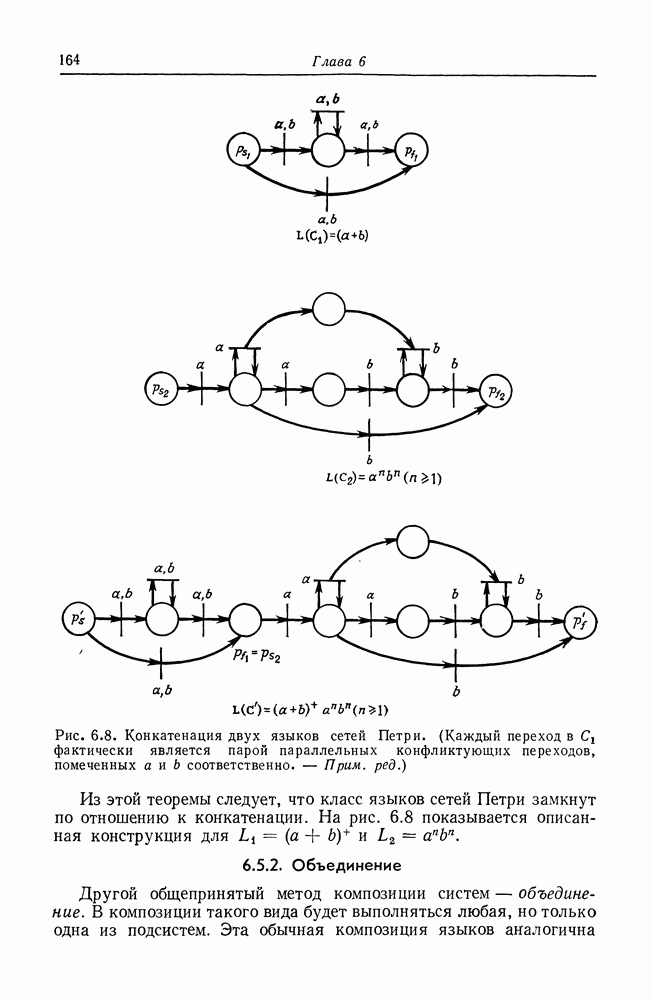
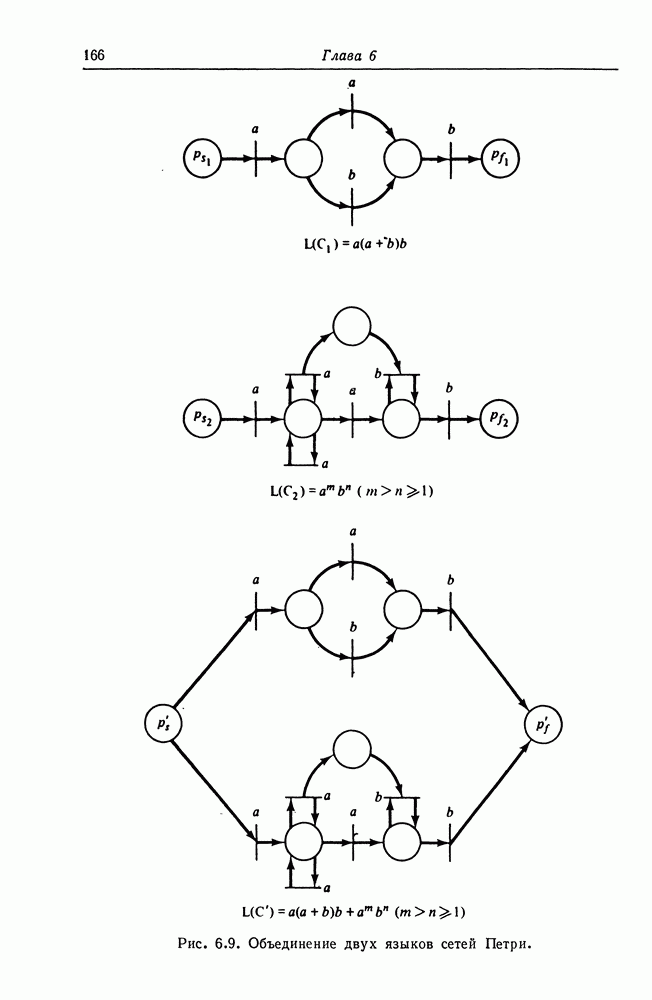
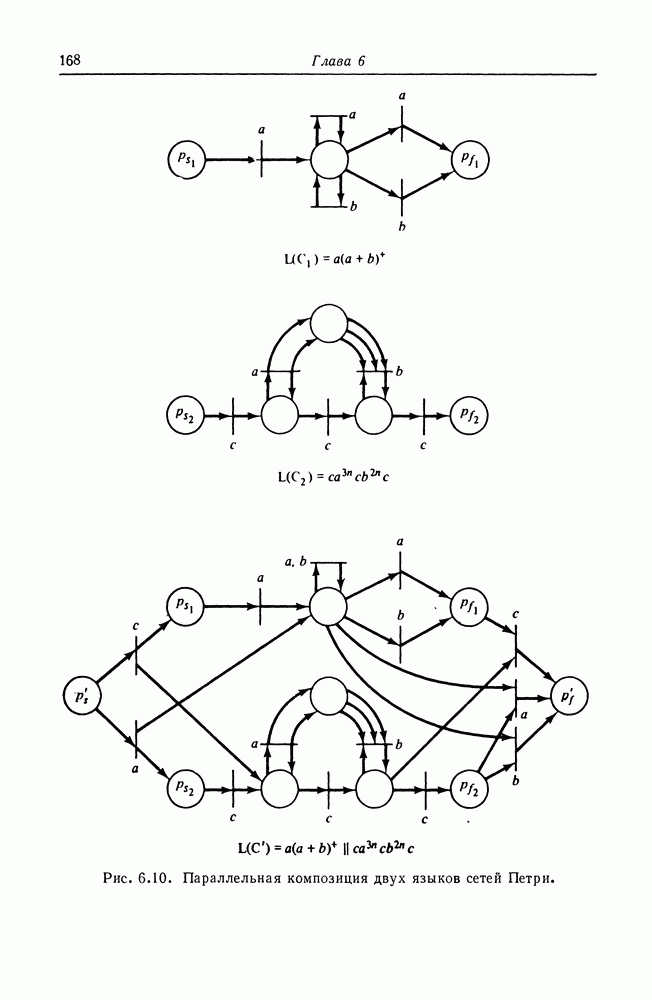
- 6.5. Свойства замкнутости
- 6.6. Языки сетей Петри и другие классы языков
- ГЛАВА 7. РАСШИРЕННЫЕ И ОГРАНИЧЕННЫЕ МОДЕЛИ СЕТЕЙ ПЕТРИ
- 7.1. Границы возможностей моделирования с помощью сетей Петри
- 7.2. Расширения
- 7.3. Расширенные сети Петри и регистровые машины
- 7.4. Подклассы сетей Петри
- ГЛАВА 8. МОДЕЛИ ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ
- 8.2. Маркированные графы
- 8.3. Графы вычислений
- 8.4. P/V-системы
- 8.5. Системы передачи сообщений
- 8.6. Графы UCLA
- 8.7. Системы замещения и сложения векторов
- 8.8. Расширенные модели сетей Петри
- ОБЗОР ТЕОРИИ КОМПЛЕКТОВ
- АННОТИРОВАННАЯ БИБЛИОГРАФИЯ