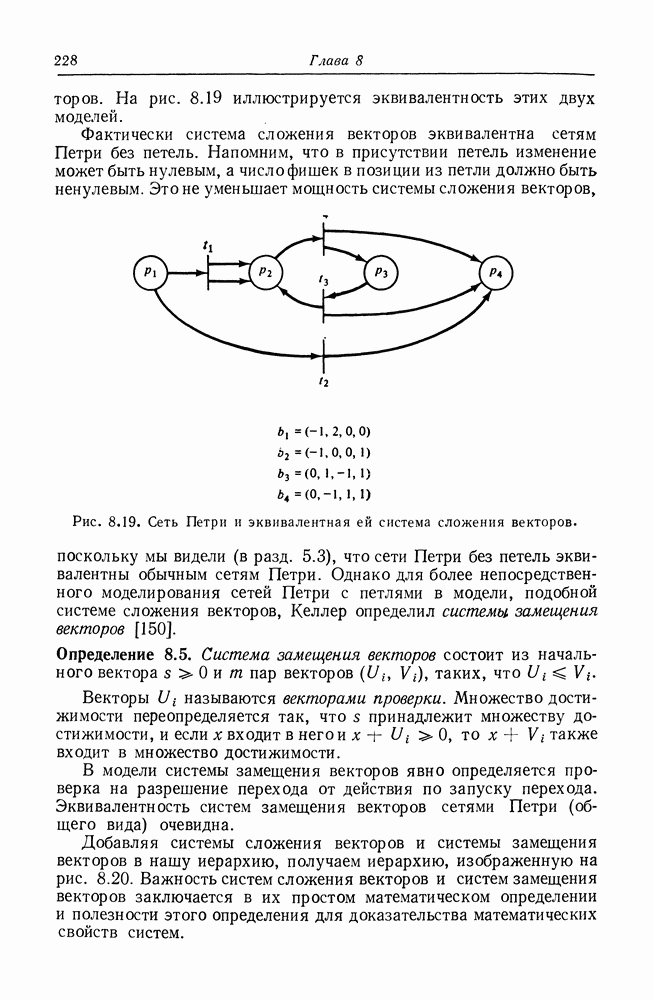
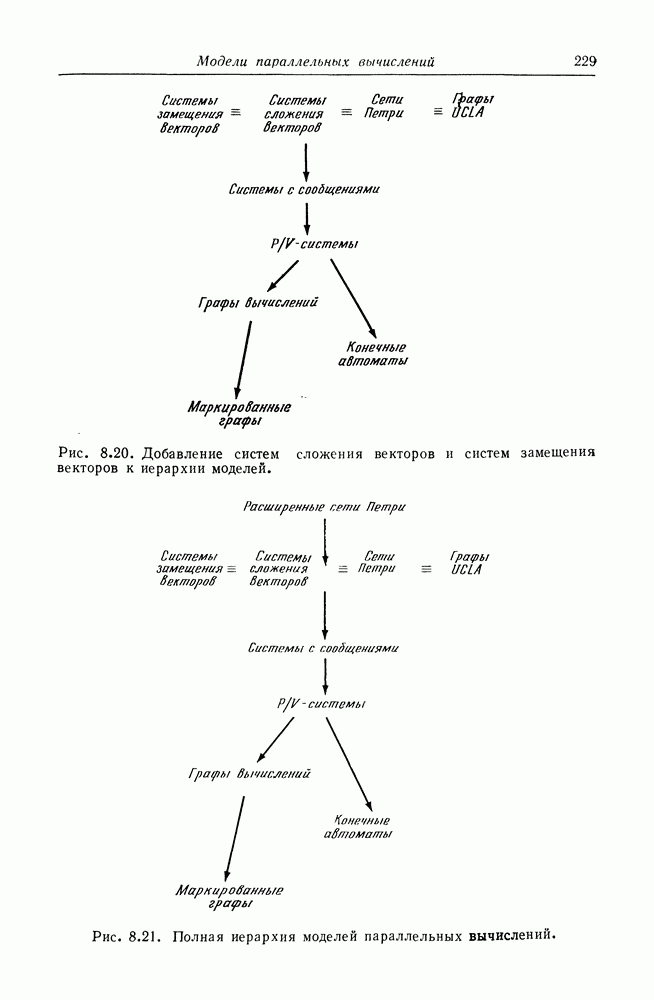
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА 2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
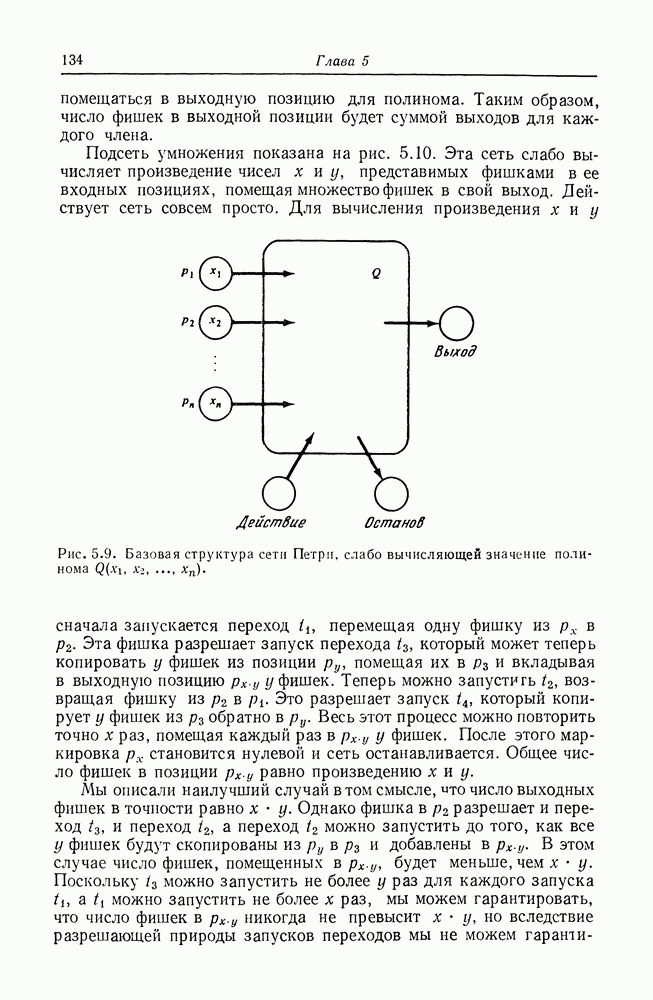
В этой главе мы дадим формальные определения основных понятий сетей Петри. Основные понятия используются на протяжении всей книги и являются необходимыми для правильного понимания.
Наш формализм основывается на теории комплектов, являющейся обобщением теории множеств. Если вы не знакомы близко с теорией комплектов, предлагаем вам прочитать приложение.
Определения, данныэ здесь, по стилю подобны определениям теории автоматов [130], т. е. определен новый класс машин — автоматная сеть Петри. Как мы увидим позднее (гл. 5—8), такая точка зрейия может привести к некоторым интересным результатам в теории формальных языков и теории автоматов.
2.1. Структура сети Петри
Сеть Петри состоит из четырех элементов: множество позиций  множество переходов 7, входная функция I и выходная функция О. Входная и выходная функции связаны с переходами и позициями. Входная функция I отображает переход
множество переходов 7, входная функция I и выходная функция О. Входная и выходная функции связаны с переходами и позициями. Входная функция I отображает переход  в множество позиций
в множество позиций  называемых входными позициями перехода. Выходная функция О отображает переход
называемых входными позициями перехода. Выходная функция О отображает переход  в множество позиций
в множество позиций  называемых выходными позициями перехода.
называемых выходными позициями перехода.
Структура сети Петри определяется ее позициями, переходами, входной и выходной функциями.
Определение 2.1. Сеть Петри С является четверкой,  конечное множество позиций,
конечное множество позиций,  конечное множество переходов,
конечное множество переходов,  Множество позиций и множество переходов не пересекаются,
Множество позиций и множество переходов не пересекаются,  является входной функцией — отображением из переходов в комплекты позиций.
является входной функцией — отображением из переходов в комплекты позиций.  есть выходная функция — отображение из переходов в комплекты позиций.
есть выходная функция — отображение из переходов в комплекты позиций.
Мощность множества  есть число
есть число  а мощность множества
а мощность множества  есть число
есть число  Произвольный элемент
Произвольный элемент  обозначается символом
обозначается символом  а произвольный элемент
а произвольный элемент  символом
символом 
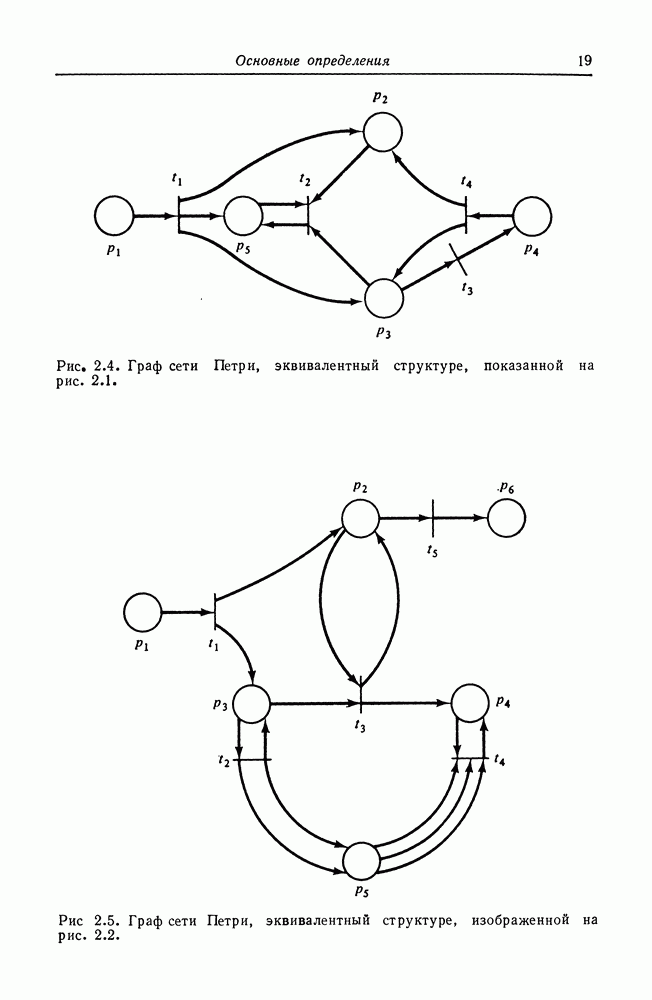
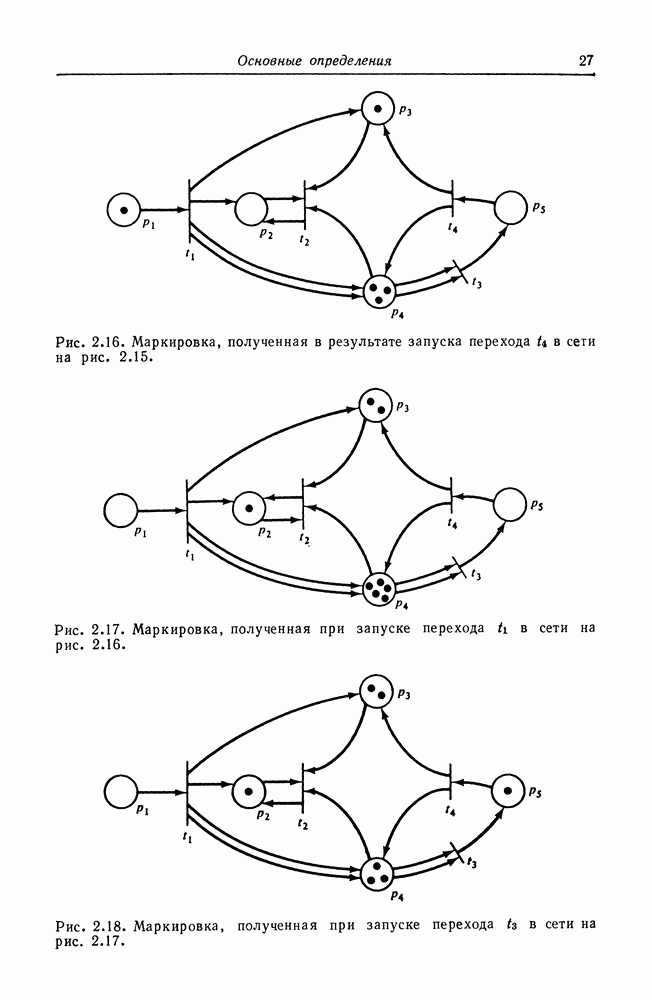
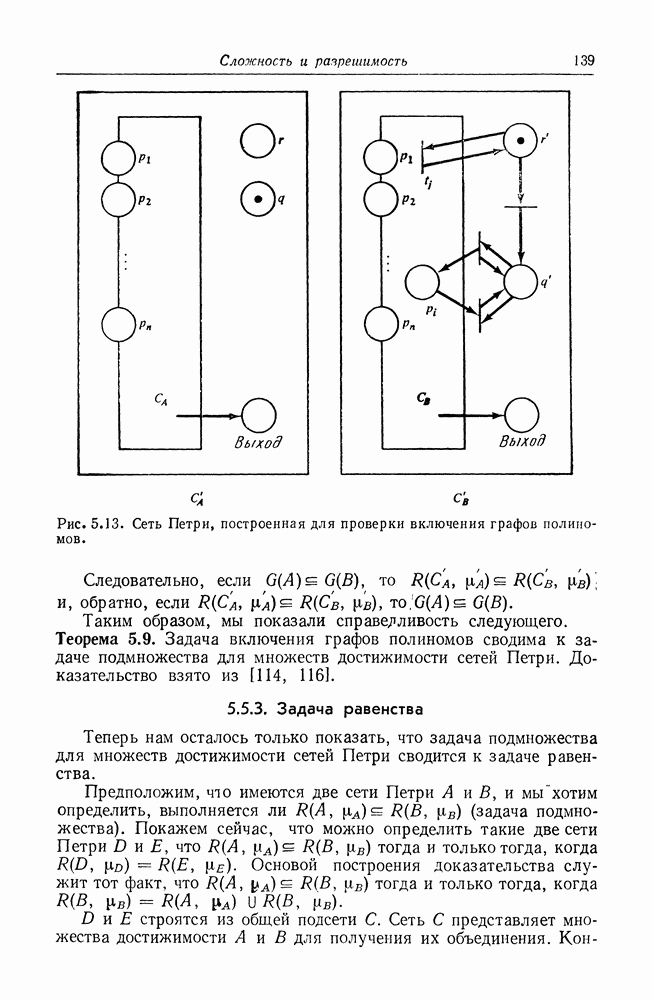
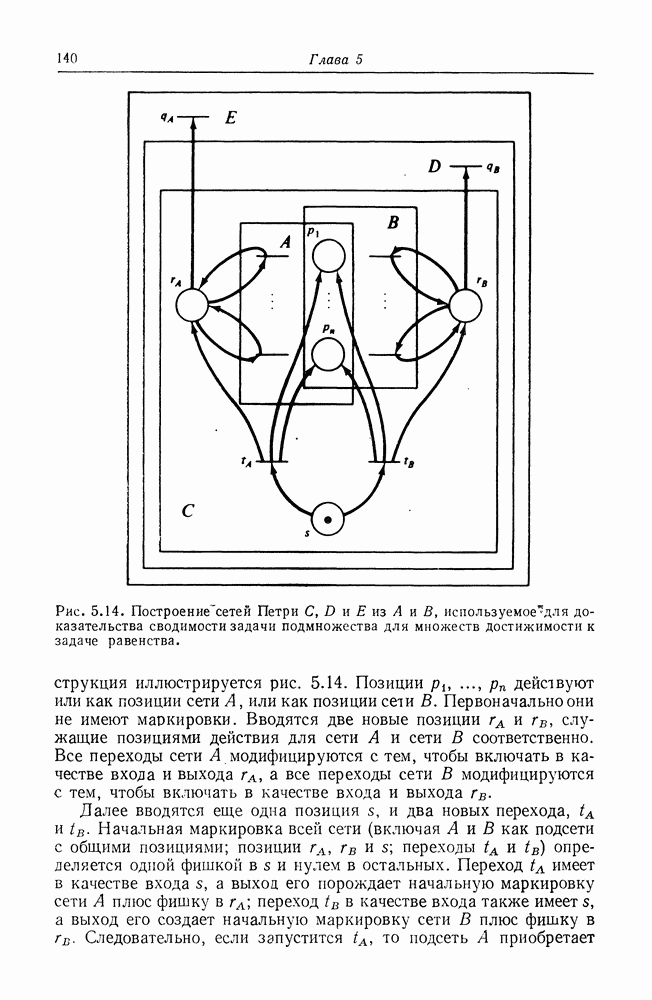
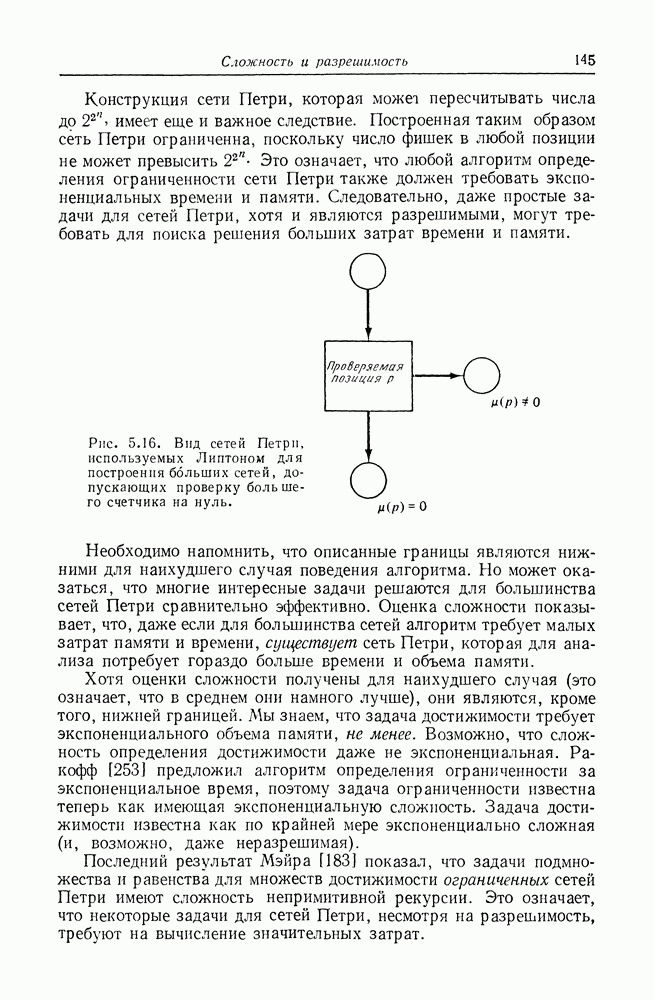
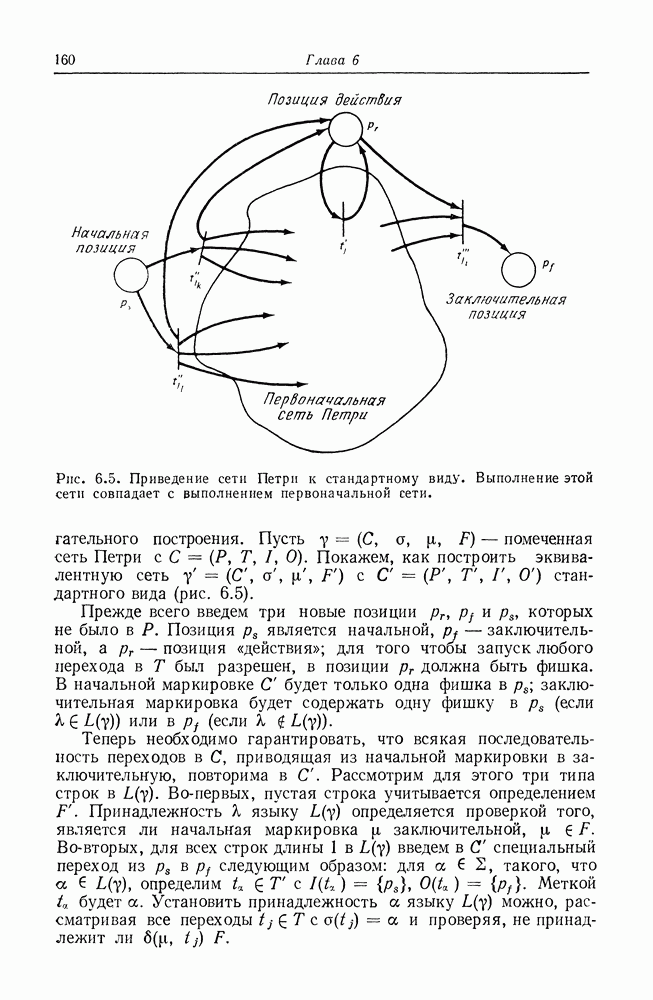
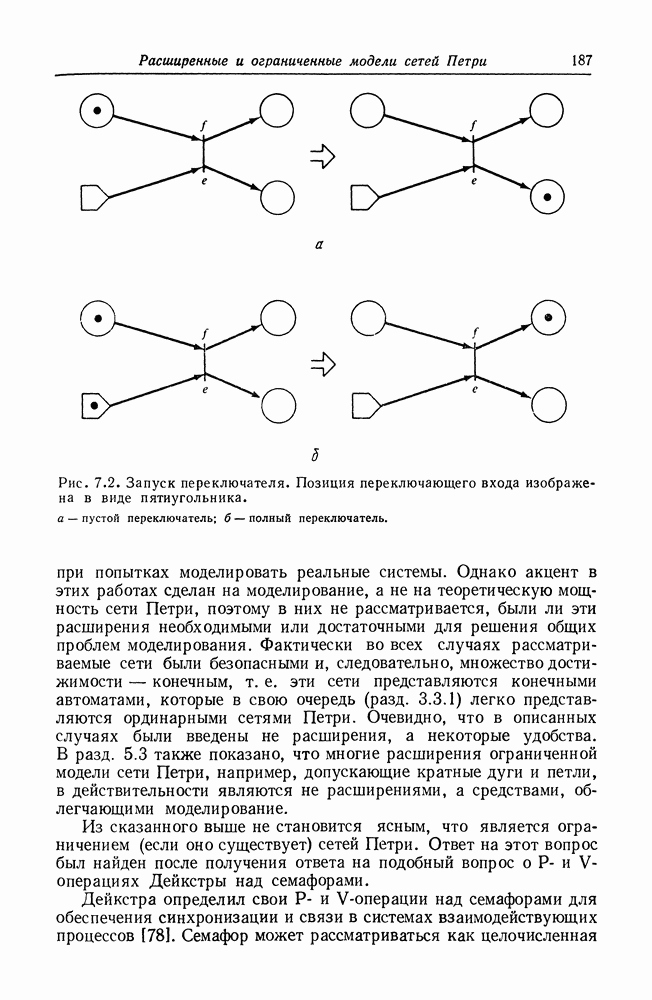
Примеры сетей Петри даны на рис. 2.1-2.3.
Позиция  является входной позицией перехода
является входной позицией перехода  в том случае, если
в том случае, если  является выходной позицией, если
является выходной позицией, если  Входы и выходы переходов представляют собой комплекты позиций. Комплект является обобщением множества, в которое
Входы и выходы переходов представляют собой комплекты позиций. Комплект является обобщением множества, в которое
включены многократно повторяющиеся элементы — тиражированные элементы. В приложении содержится описание теории комплектов. Использование комплектов, а не множеств для входов и выходов перехода позволяет позиции быть кратным входом либо кратным выходом перехода. Кратность входной позиции  для перехода
для перехода  есть число появлений позиции во входном комплекте перехода,
есть число появлений позиции во входном комплекте перехода,  Аналогично кратность выходной позиции
Аналогично кратность выходной позиции  для перехода
для перехода  есть число появлений позиции в выходном комплекте перехода,
есть число появлений позиции в выходном комплекте перехода,  Если входная и выходная функции являются множествами (а не комплектами), то кратность каждой позиции есть либо 0, либо 1.
Если входная и выходная функции являются множествами (а не комплектами), то кратность каждой позиции есть либо 0, либо 1.
Входные и выходные функции используются для отображения позиций в комплекты переходов, а также их можно использовать для отображения переходов в комплекты позиций. Определим, что переход  является входом позиции
является входом позиции  если
если  есть выход
есть выход  Переход
Переход  есть выход позиции
есть выход позиции  если
если  есть вход
есть вход 
Определение 2.2. Определим расширенную входную функцию I и выходную функцию

таким образом, что

Для сети Петри на рис. 2.1 расширенными входной и выходной функциями являются:

Рис. 2.1. Структура сети Петри представлена в виде четверки, которая состоит из множества позиций  множества переходов
множества переходов  входной функции
входной функции  и выходной функции
и выходной функции 

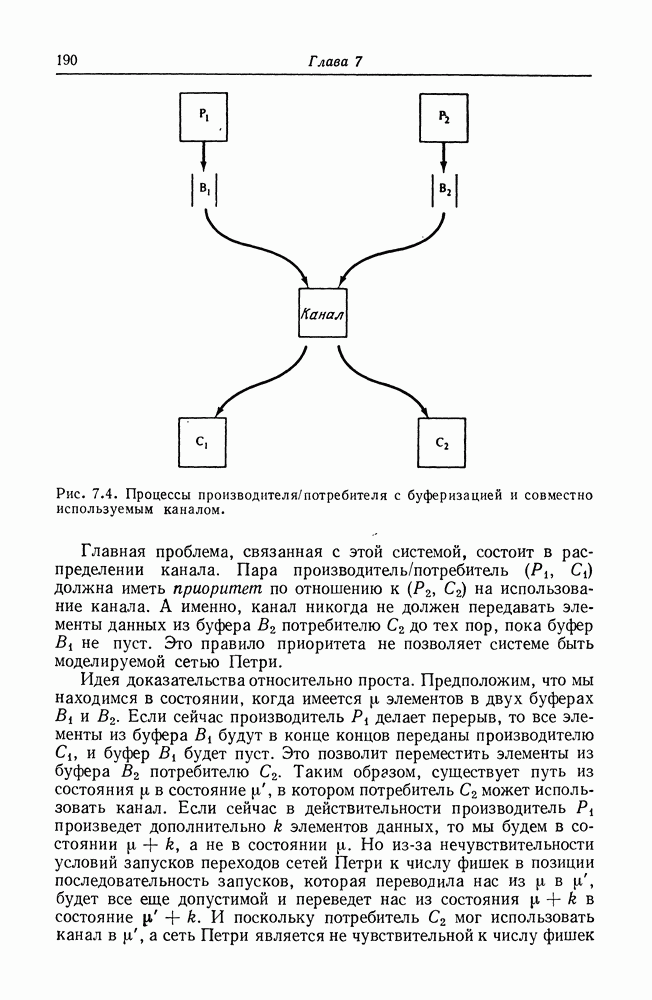
Рис. 2.2. Структура сети Петри.

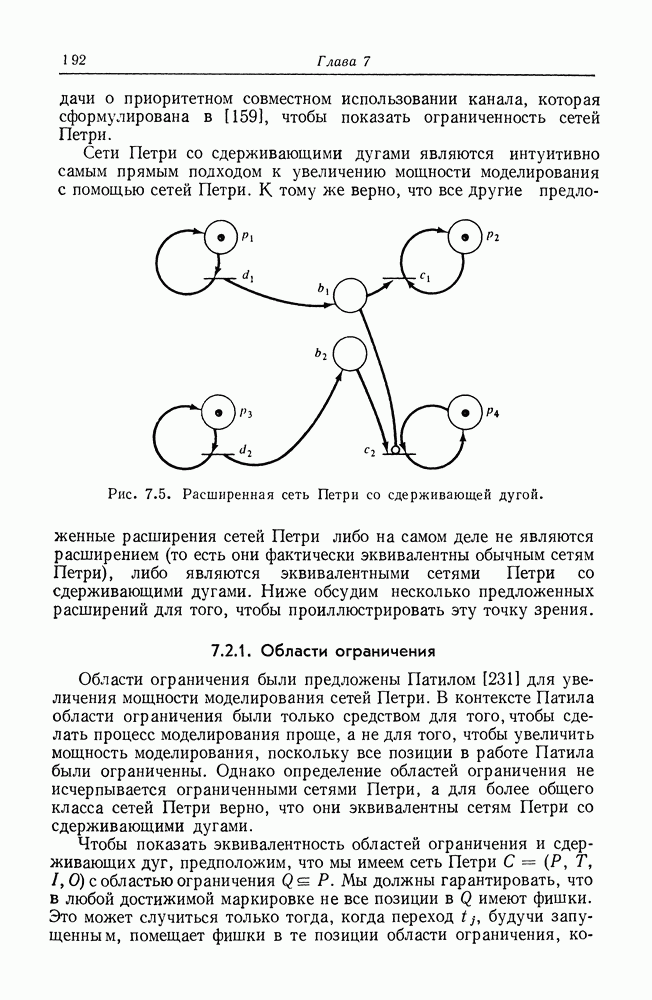
Рис. 2.3. Структура сети Петри.
Упражнения.
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ГЛАВА 1. ВВЕДЕНИЕ
- ГЛАВА 2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
- 2.1. Структура сети Петри
- 2.2. Графы сетей Петри
- 2.3. Маркировка сетей Петри
- 2.4. Правила выполнения сетей Петри
- 2.5. Пространство состояний сети Петри
- 2.6. Альтернативные формы определения сетей Петри
- ГЛАВА 3. СЕТИ ПЕТРИ ДЛЯ МОДЕЛИРОВАНИЯ
- 3.2. Одновременность и конфликт
- 3.3. Аппаратное обеспечение ЭВМ
- 3.4. Программное обеспечение ЭВМ
- 3.5. Другие системы
- ГЛАВА 4. АНАЛИЗ СЕТЕЙ ПЕТРИ
- 4.1. Задачи анализа сетей Петри
- 4.2. Методы анализа
- ГЛАВА 5. СЛОЖНОСТЬ И РАЗРЕШИМОСТЬ
- 5.1. Сводимость задач анализа
- 5.2. Задачи достижимости
- 5.3. Сети Петри с ограничениями
- 5.4. Активность и достижимость
- 5.5. Неразрешимые задачи
- 5.6. Сложность задачи достижимости
- ГЛАВА 6. ЯЗЫКИ СЕТЕЙ ПЕТРИ
- 6.2. Некоторые понятия теории формальных языков
- 6.3. Определения языков сетей Петри
- 6.4. Свойства языков сетей Петри
- 6.5. Свойства замкнутости
- 6.6. Языки сетей Петри и другие классы языков
- ГЛАВА 7. РАСШИРЕННЫЕ И ОГРАНИЧЕННЫЕ МОДЕЛИ СЕТЕЙ ПЕТРИ
- 7.1. Границы возможностей моделирования с помощью сетей Петри
- 7.2. Расширения
- 7.3. Расширенные сети Петри и регистровые машины
- 7.4. Подклассы сетей Петри
- ГЛАВА 8. МОДЕЛИ ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ
- 8.2. Маркированные графы
- 8.3. Графы вычислений
- 8.4. P/V-системы
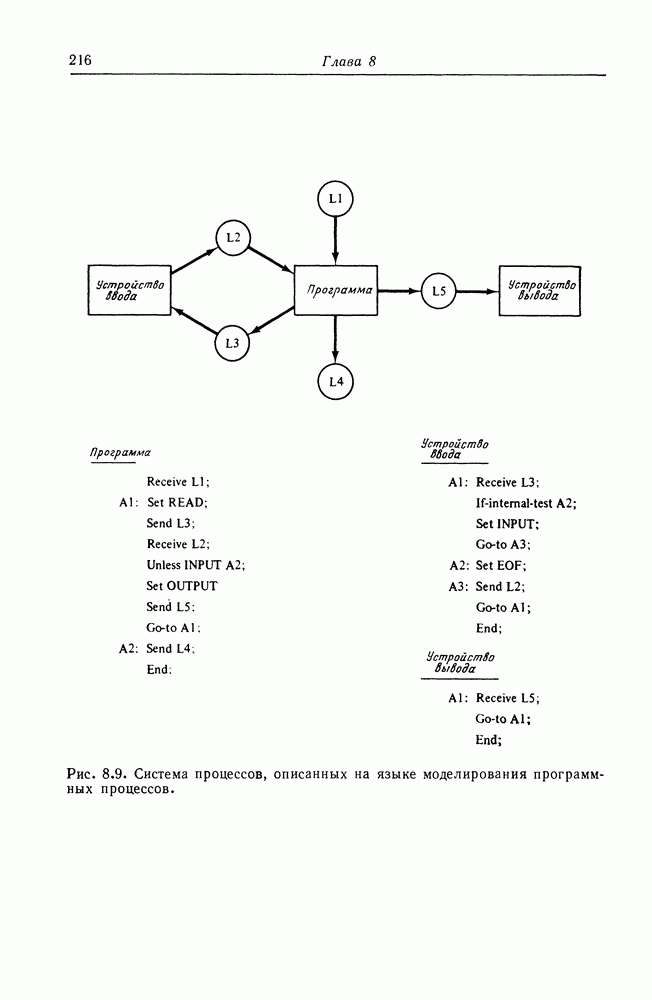
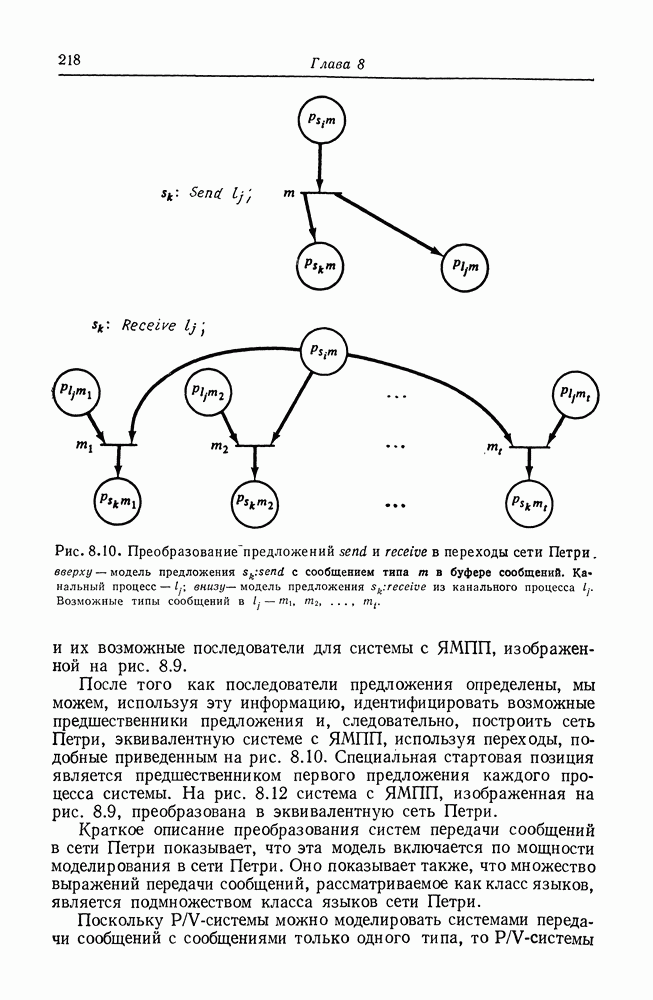
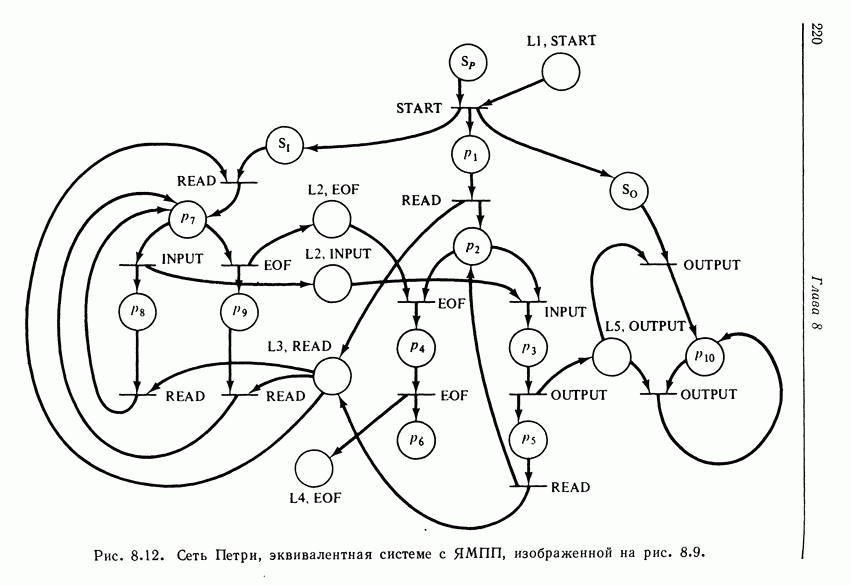
- 8.5. Системы передачи сообщений
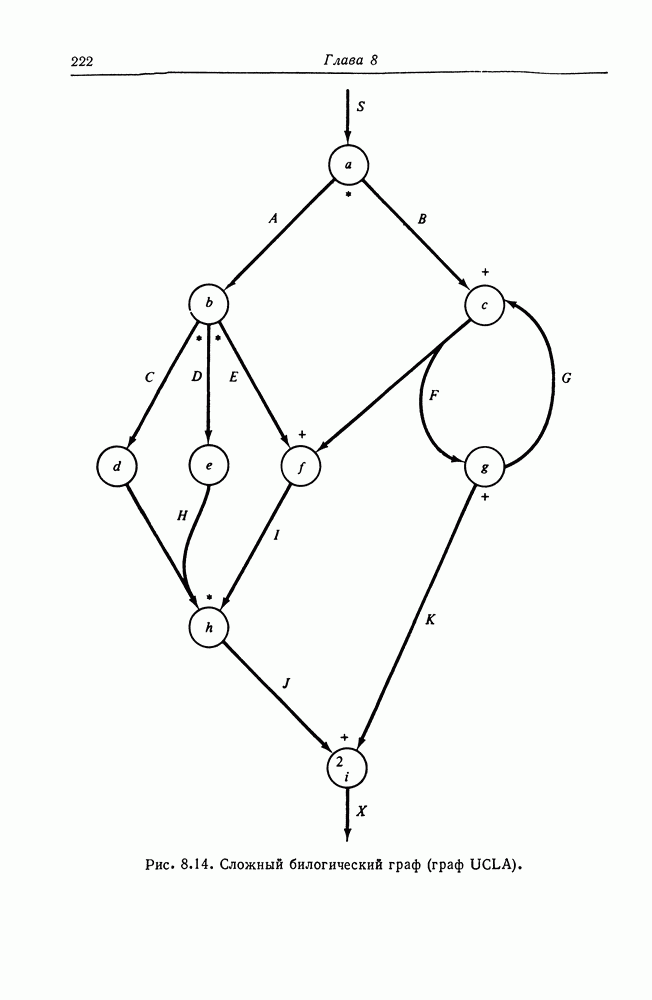
- 8.6. Графы UCLA
- 8.7. Системы замещения и сложения векторов
- 8.8. Расширенные модели сетей Петри
- ОБЗОР ТЕОРИИ КОМПЛЕКТОВ
- АННОТИРОВАННАЯ БИБЛИОГРАФИЯ