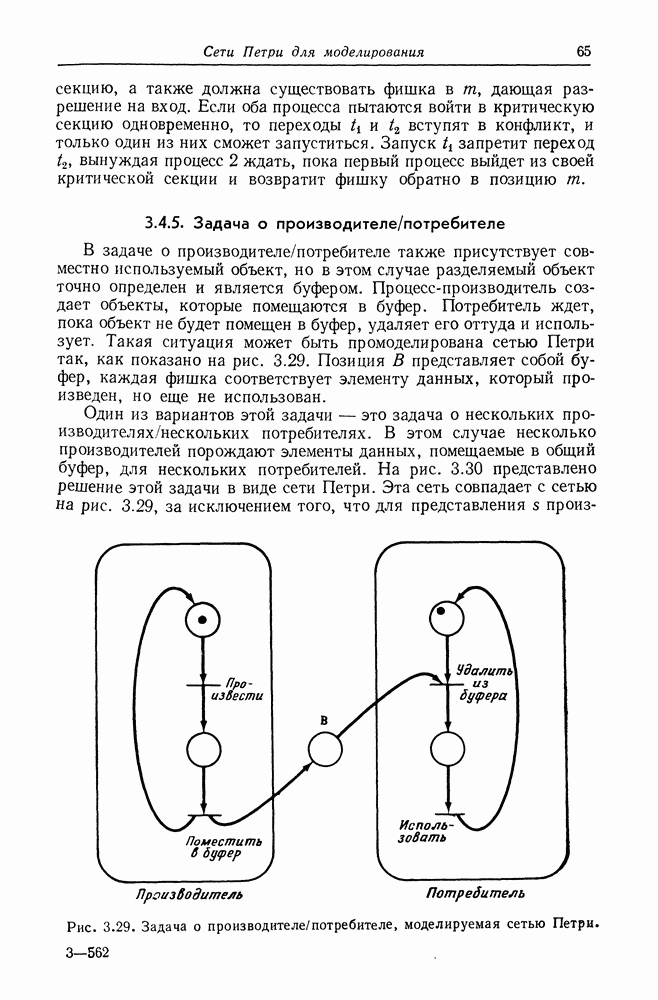
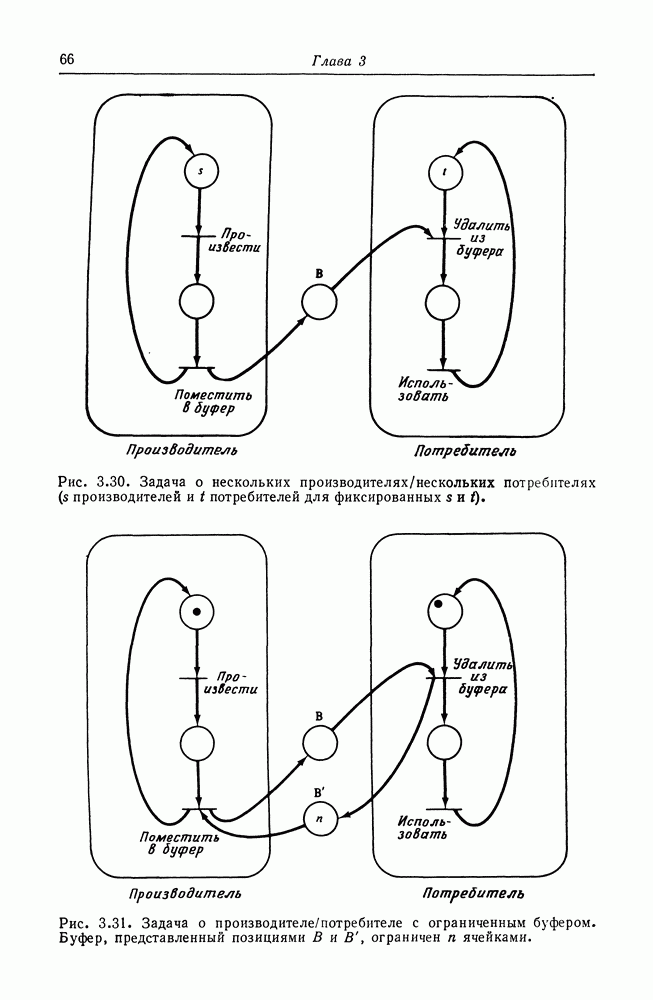
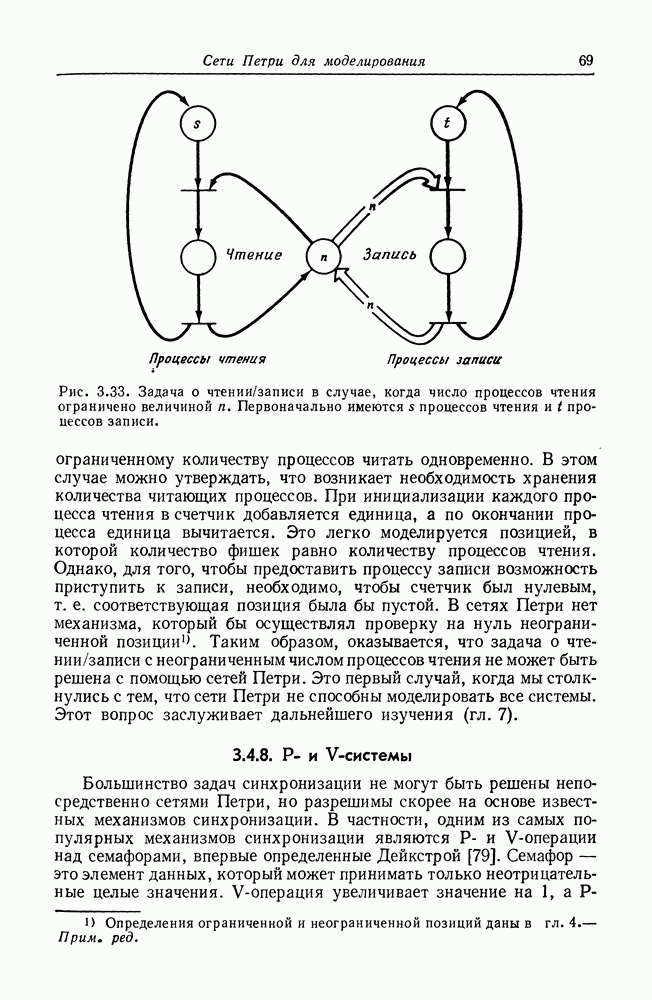
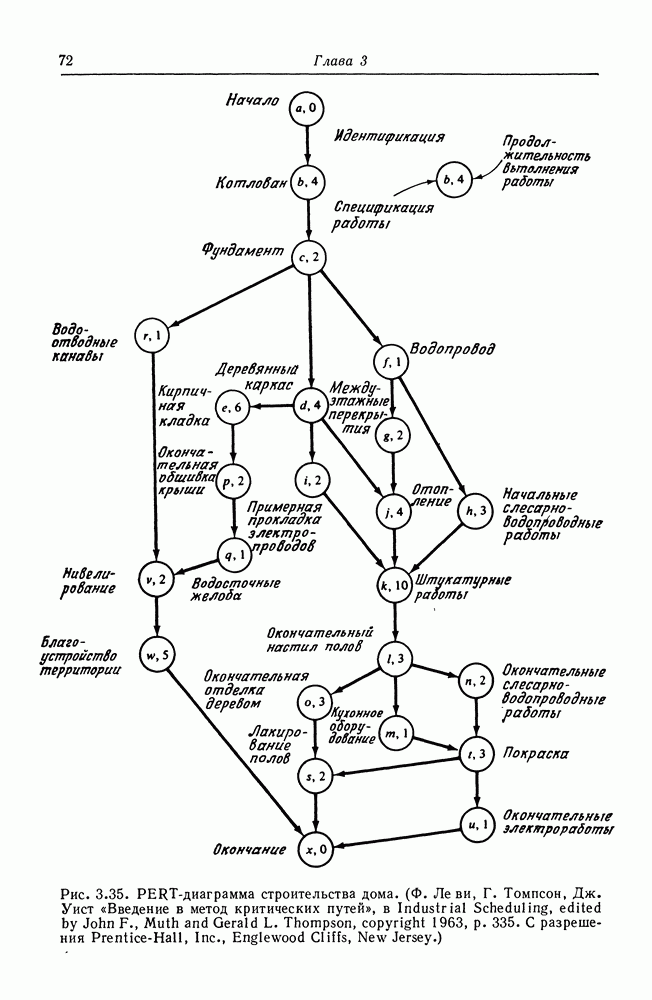
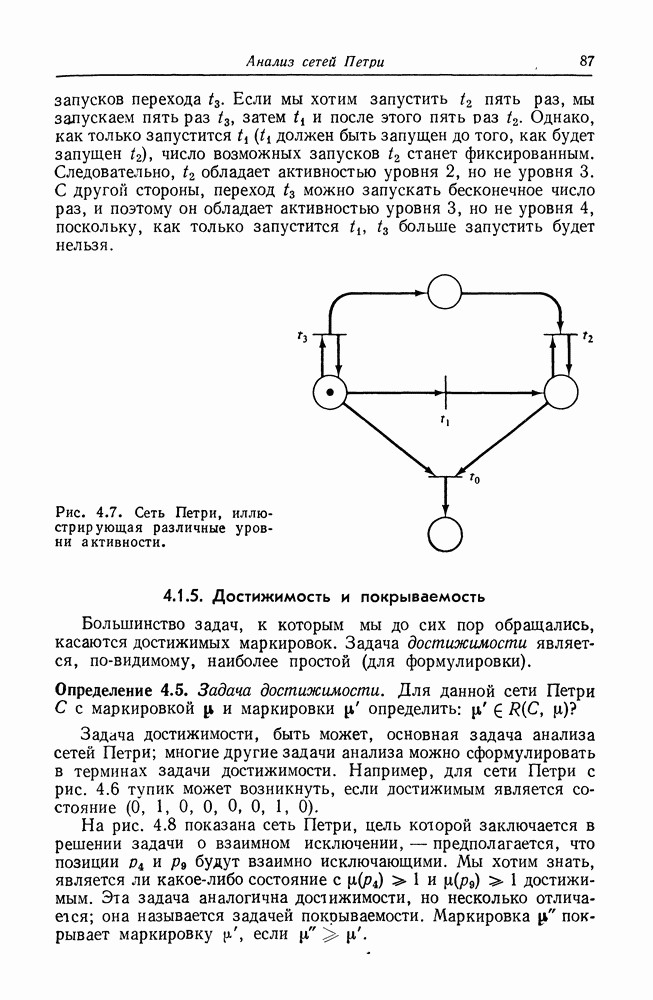
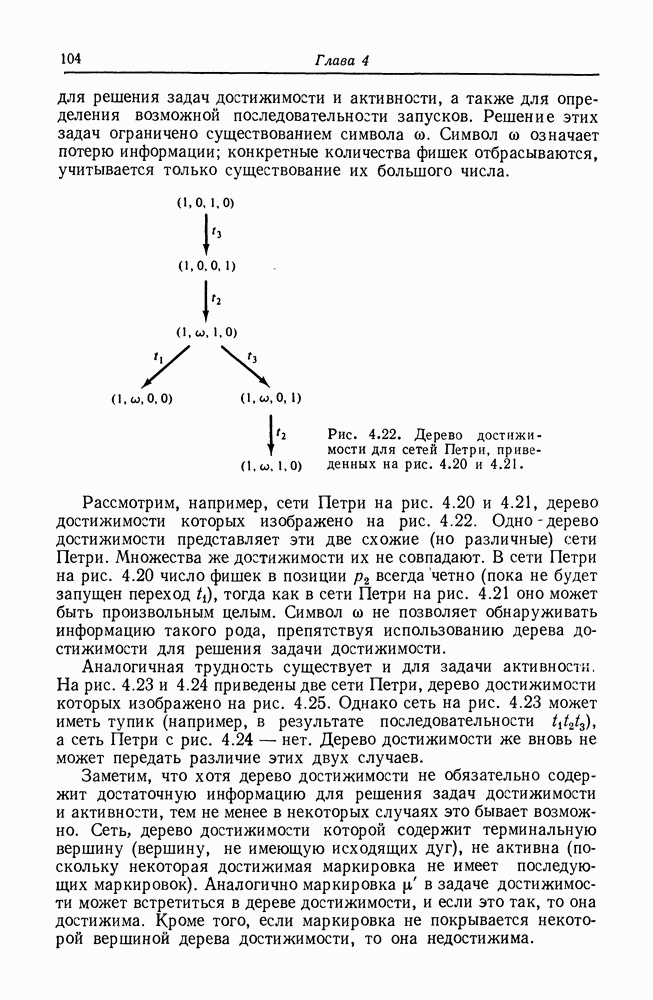
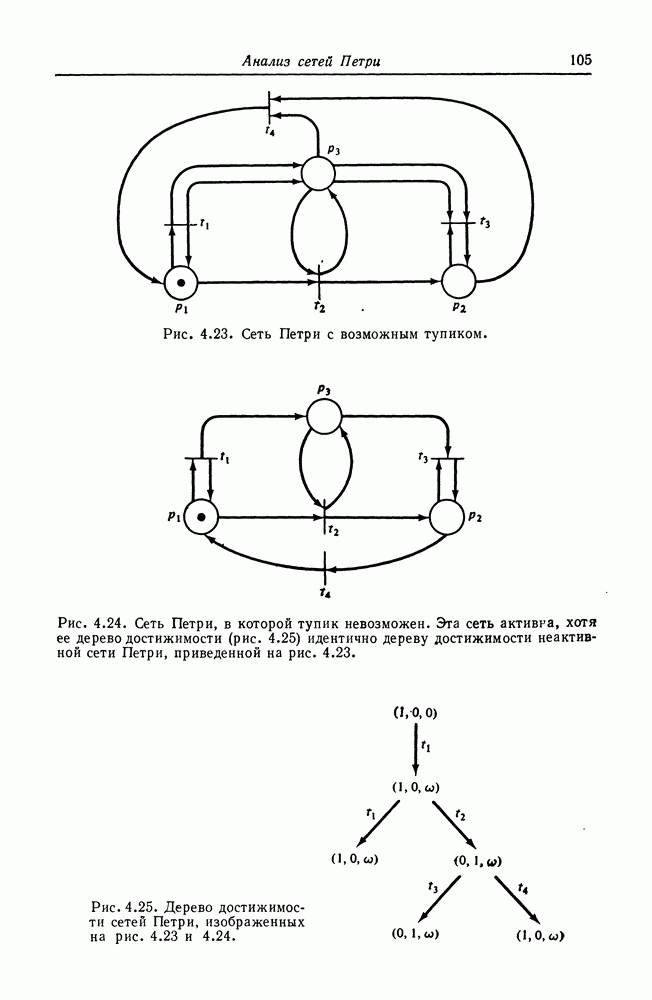
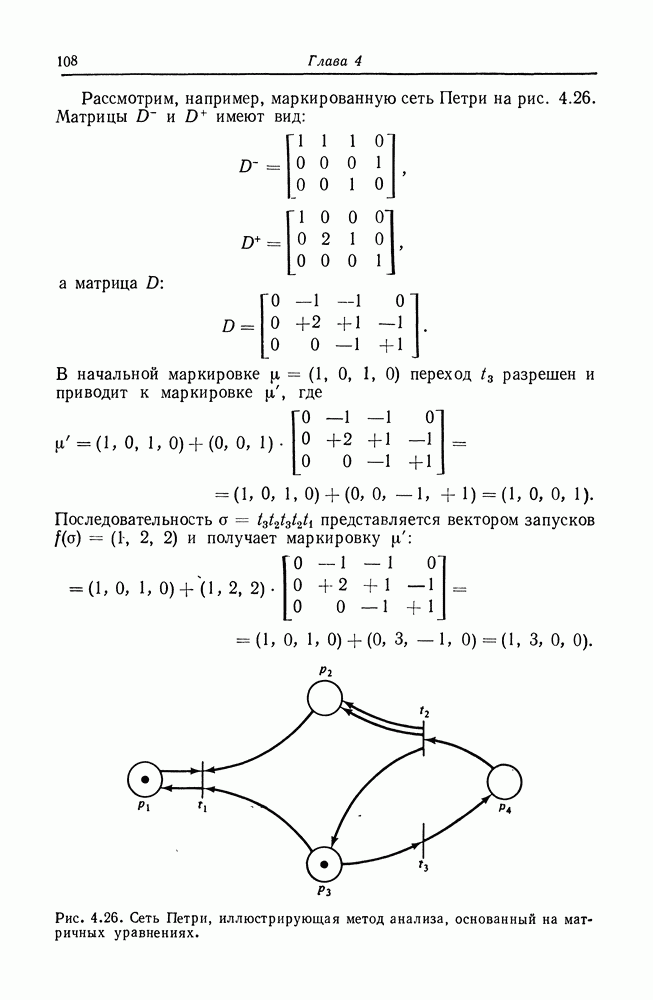
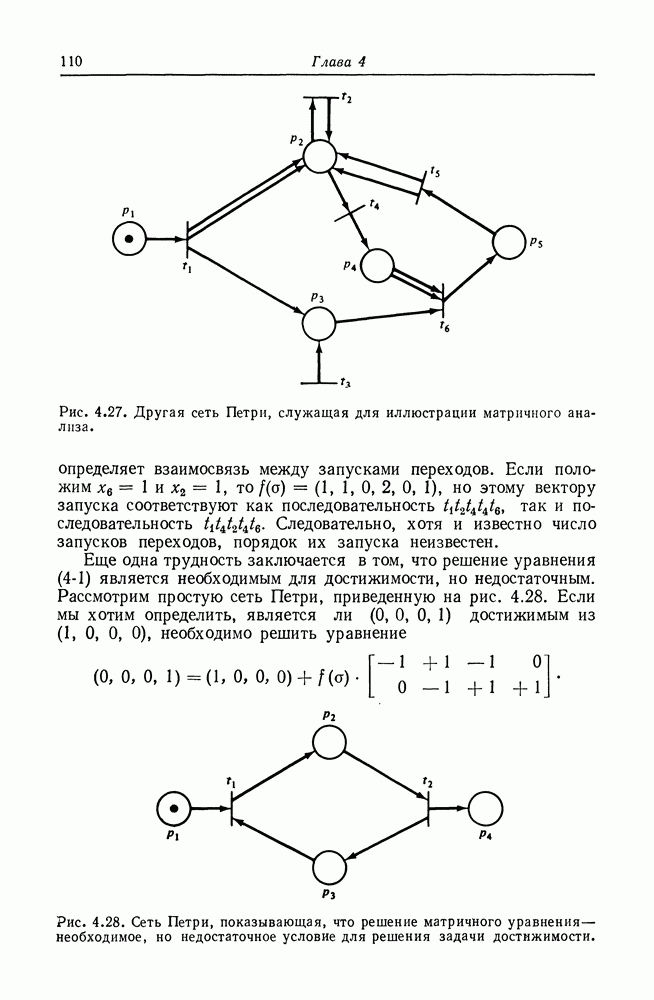
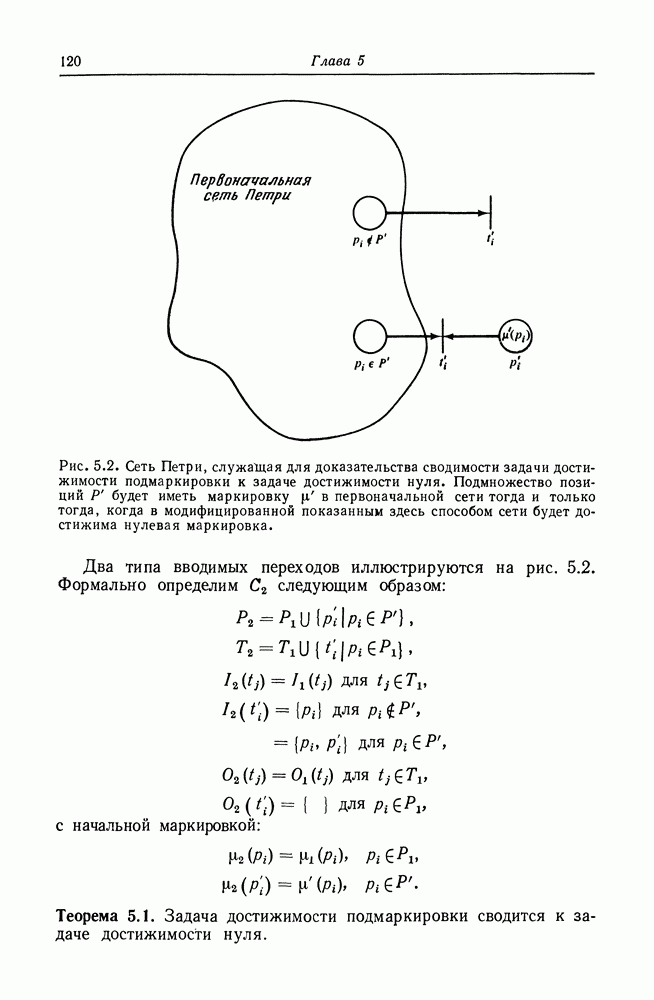
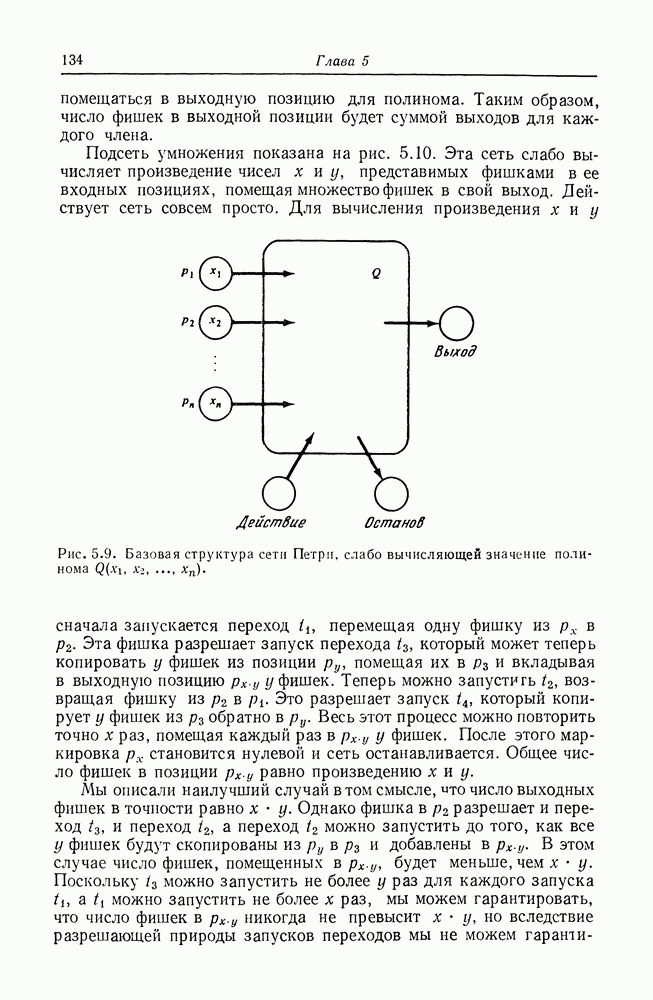
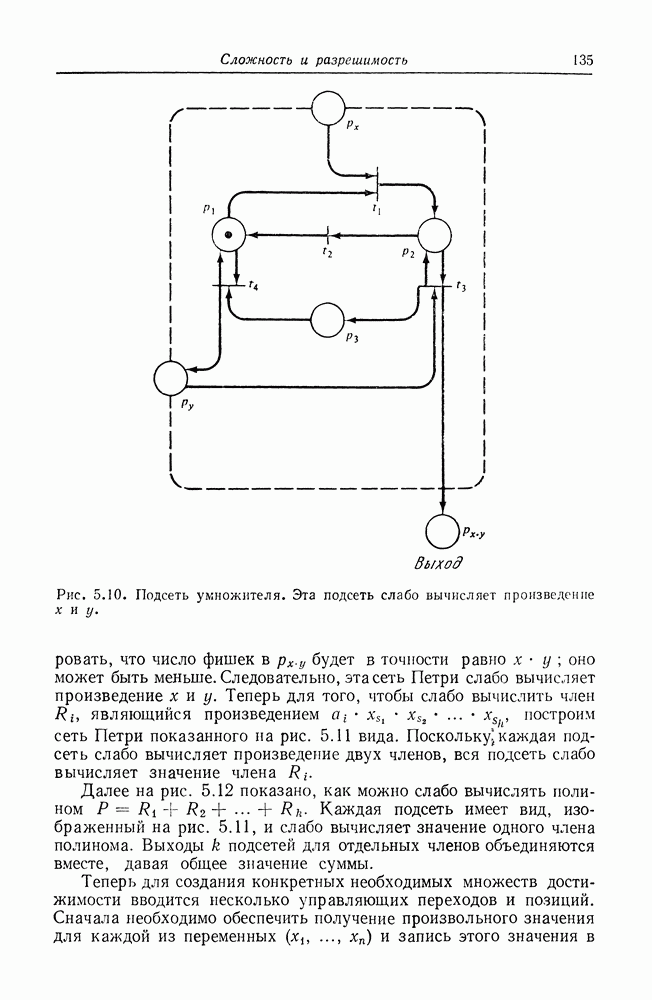
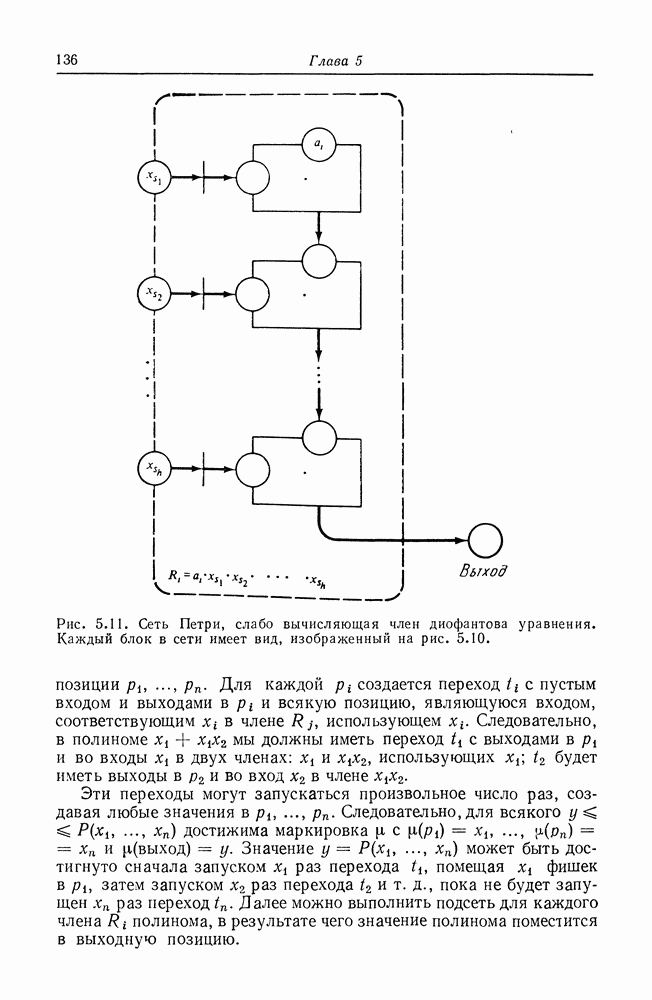
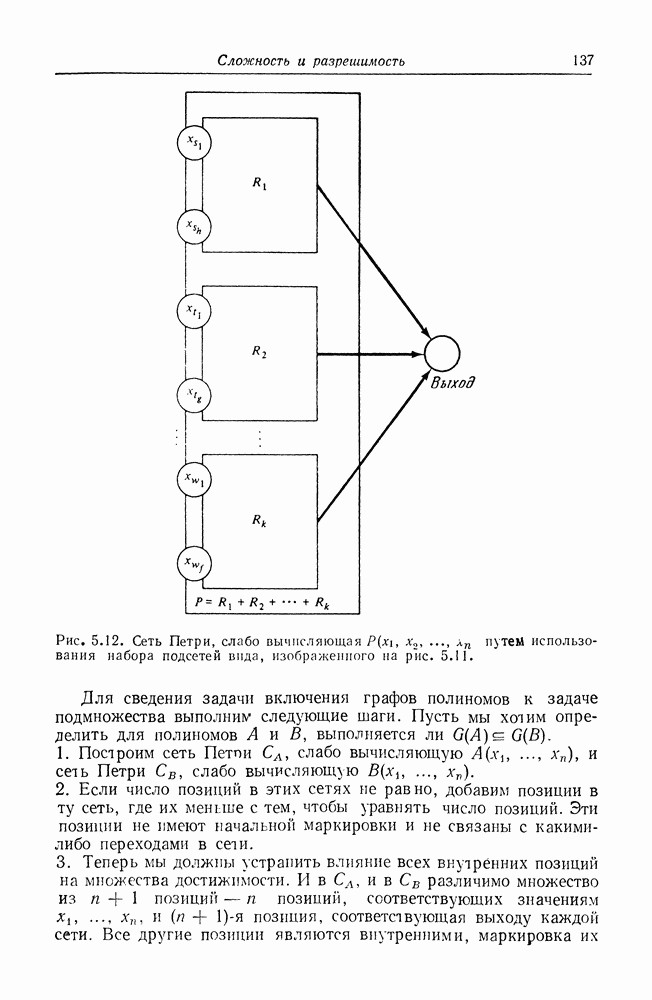
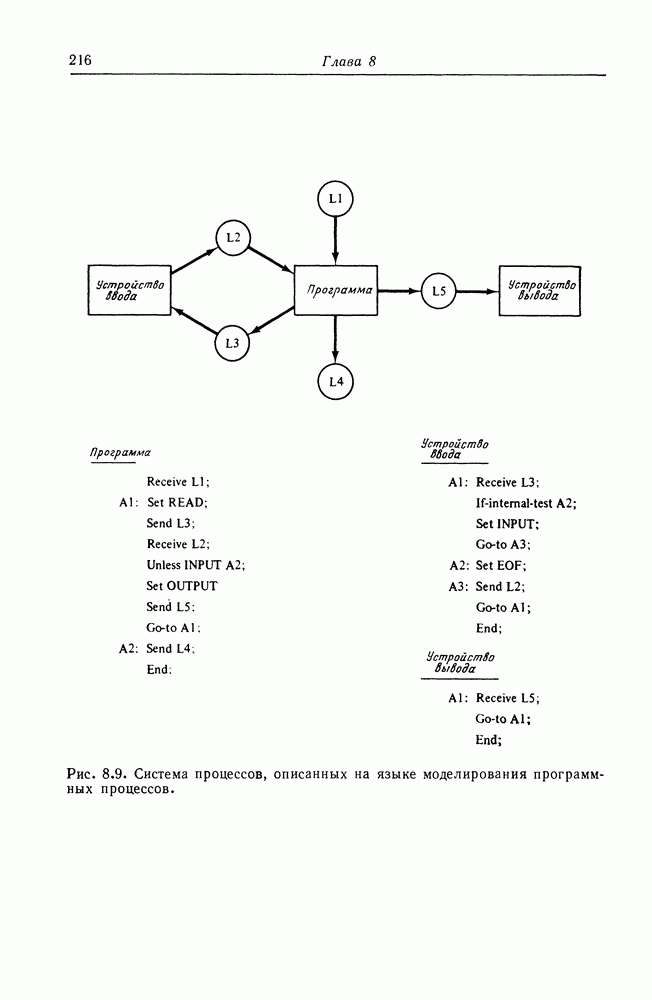
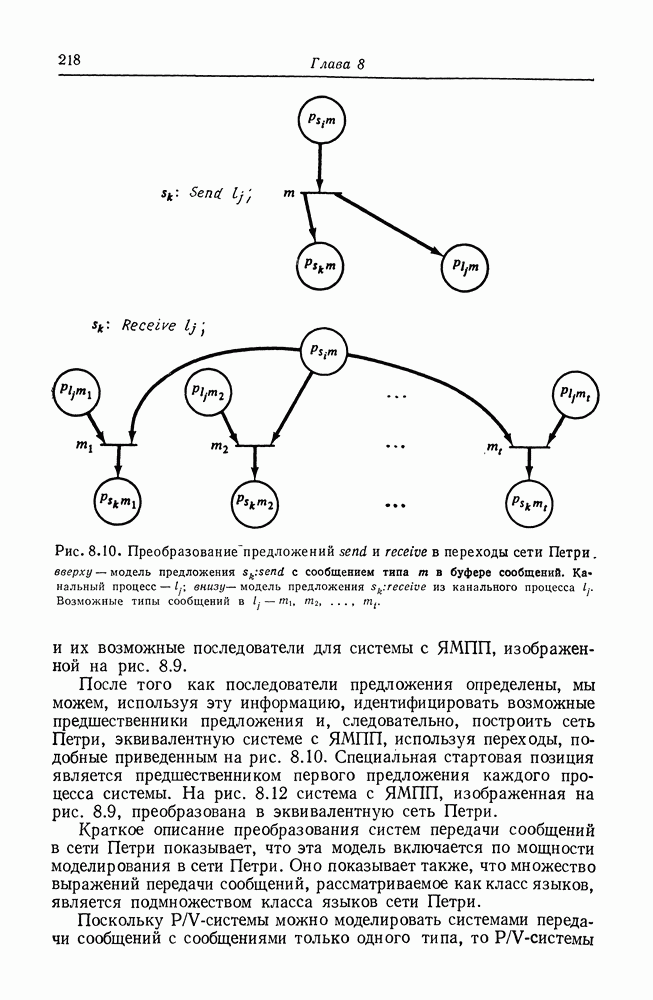
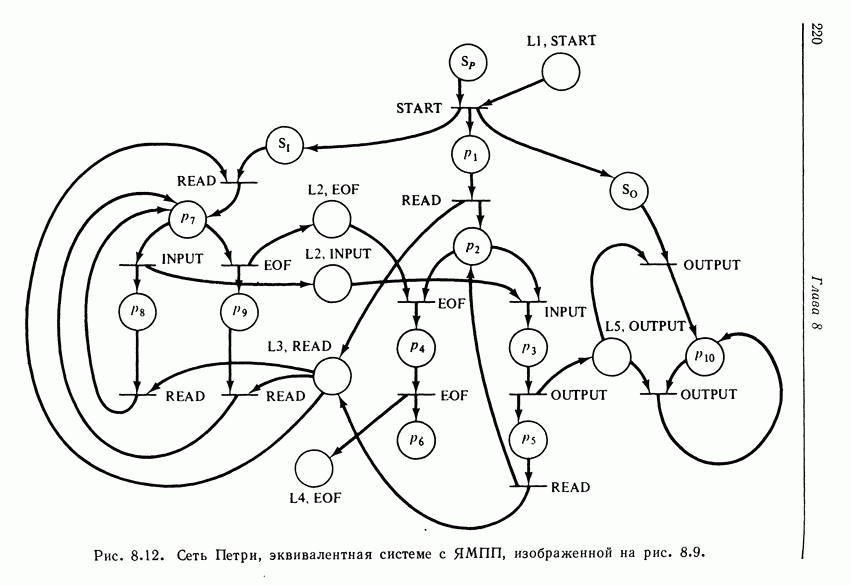
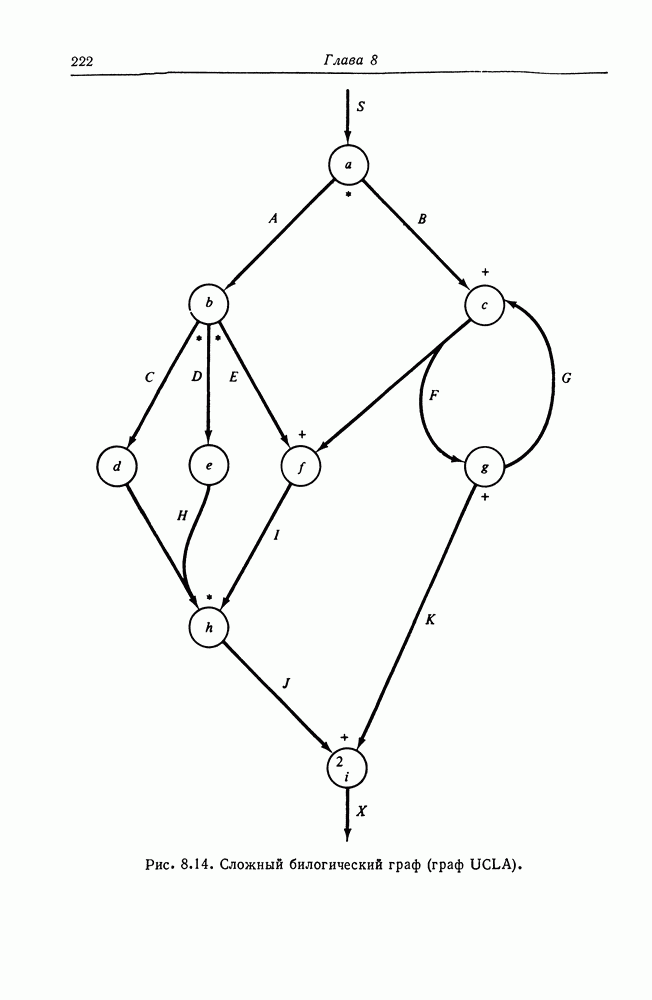
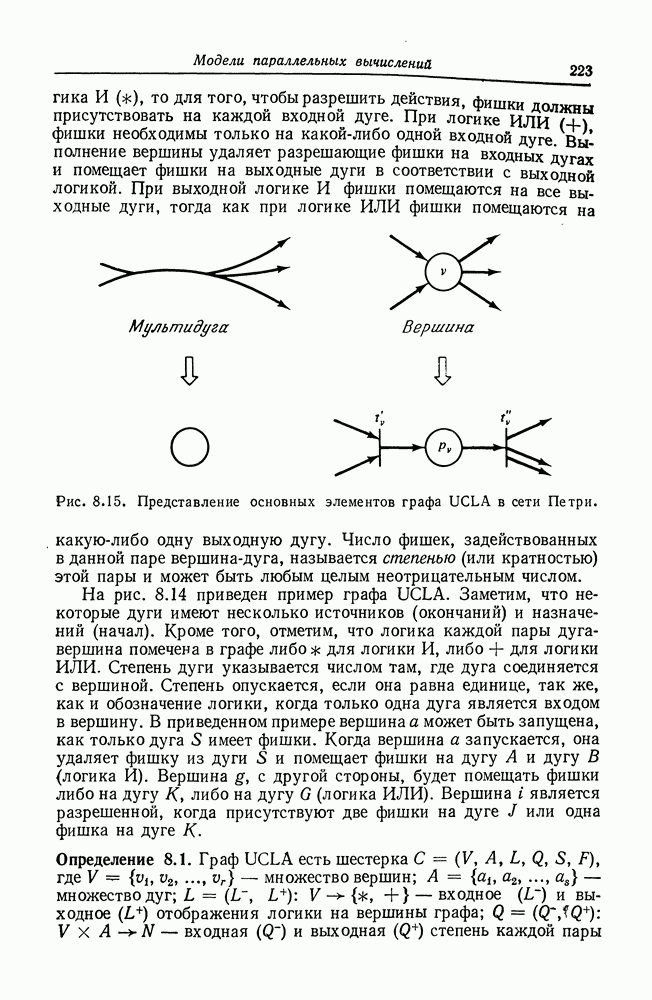
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.4. Свойства языков сетей Петри
Исследование языков сетей Петри только начинается, и в настоящий момент сведения о свойствах этих недавно определенных классов языков ограниченны. Сила сетей Петри отражается в разнообразии классов языков сетей Петри. Новизна исследований объясняет нашу неспособность показать все взаимосвязи между этими языками или обосновать важность только некоторых из классов. Это приводит к широте области исследований, необходимости определения свойств 12 различных классов языков.
Очевидно, что все 12 классов языков исследовать в этой книге невозможно, поэтому мы ограничимся рассмотрением здесь только одного класса языков сетей Петри, а именно языков  -типа. Основными причинами такого решения являются ограниченность объема монографии и то, что этот язык уже исследовался в литературе [236, 115]. Некоторые результаты были получены Хэком [115] и для префиксных языков (т. е.
-типа. Основными причинами такого решения являются ограниченность объема монографии и то, что этот язык уже исследовался в литературе [236, 115]. Некоторые результаты были получены Хэком [115] и для префиксных языков (т. е.  -типа) и будут представлены в нашем заключении. Языки
-типа) и будут представлены в нашем заключении. Языки  и
и  -типа были определены, но никакой работы по их развитию не проводилось. Напомним, что класс языков
-типа были определены, но никакой работы по их развитию не проводилось. Напомним, что класс языков  -типа включает классы языков
-типа включает классы языков  и
и  -типа. Таким образом, языки
-типа. Таким образом, языки  -типа в некотором смысле образуют наибольший класс языков сетей Петри, и поэтому понятно, почему они исследовались первыми.
-типа в некотором смысле образуют наибольший класс языков сетей Петри, и поэтому понятно, почему они исследовались первыми.
При изучении свойств языков сетей Петри  -типа обратимся к двум аспектам. Сначала представим свойства замкнутости сетей Петри]) по отношению к некоторым обычным операциям:
-типа обратимся к двум аспектам. Сначала представим свойства замкнутости сетей Петри]) по отношению к некоторым обычным операциям:
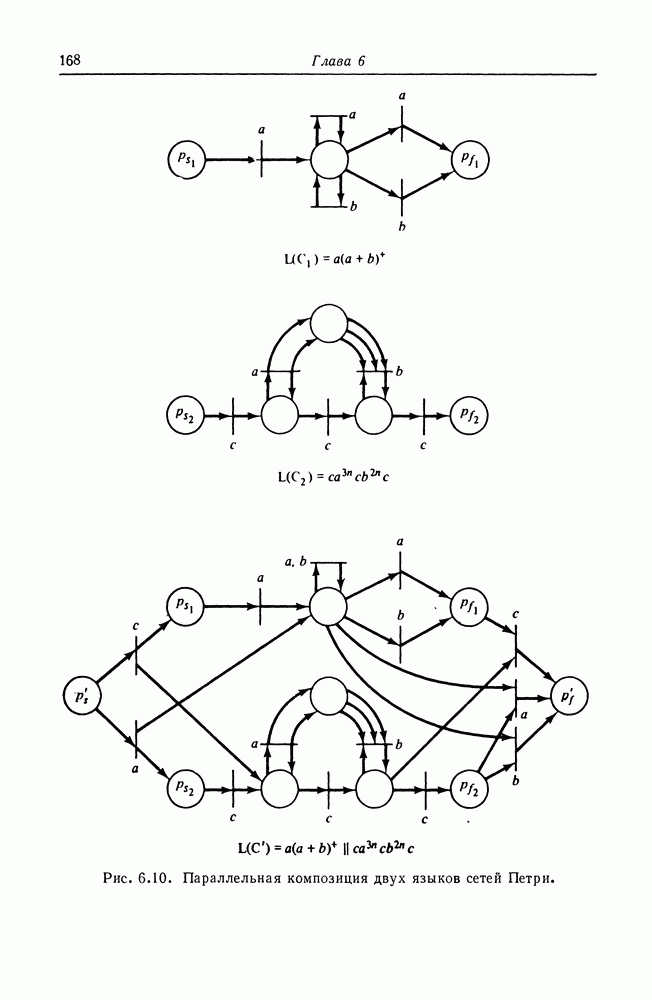
конкатенации, объединению, параллельной композиции, пересечению, обращению, дополнению, бесконечной конкатенации и подстановке. Затем рассмотрим взаимосвязь между языками сетей Петри и классическими формальными языками: регулярными, контекстно-свободными, контекстно-связанными и типа 0. Это позволит оценить силу и ограниченность языков сетей Петри  -типа), а также покажет, как можно исследовать другие классы языков сетей Петри.
-типа), а также покажет, как можно исследовать другие классы языков сетей Петри.
Хотя нас интересует весь класс языков сетей Петри  -типа, ограничимся рассмотрением только множества сетей Петри стандартного вида. Это ограничение вводится для того, чтобы облегчить доказательства и конструкции; оно не ограничивает класс языков сетей Петри. Всякий язык сетей Петри может порождаться множеством сетей; выберем для работы только сети, обладающие определенными свойствами. Для доказательства того, что это не сокращает множество языков, покажем, что для всякого языка сети Петри
-типа, ограничимся рассмотрением только множества сетей Петри стандартного вида. Это ограничение вводится для того, чтобы облегчить доказательства и конструкции; оно не ограничивает класс языков сетей Петри. Всякий язык сетей Петри может порождаться множеством сетей; выберем для работы только сети, обладающие определенными свойствами. Для доказательства того, что это не сокращает множество языков, покажем, что для всякого языка сети Петри  -типа существует сеть Петри стандартного вида, порождающая его.
-типа существует сеть Петри стандартного вида, порождающая его.
Определение 6.5. Помеченная сеть Петри  с языком
с языком  имеющая стандартный вид, удовлетворяет следующим условиям:
имеющая стандартный вид, удовлетворяет следующим условиям:
1. Начальная маркировка  состоит точно из одной фишки в начальной позиции
состоит точно из одной фишки в начальной позиции  и не имеет фишек в других позициях.
и не имеет фишек в других позициях. 
2. Существует позиция  такая, что
такая, что

в)  не определено для всех
не определено для всех  имеющих в
имеющих в  фишку (т. е.
фишку (т. е. 
Выполнение сети Петри стандартного вида начинается с одной фишки в начальной позиции. Первый запускаемый переход удаляет эту фишку из начальной позиции, после чего начальная позиция остается уже до конца выполнения пустой. Сеть Петри останавливается, если фишка помещается в заключительную позицию.
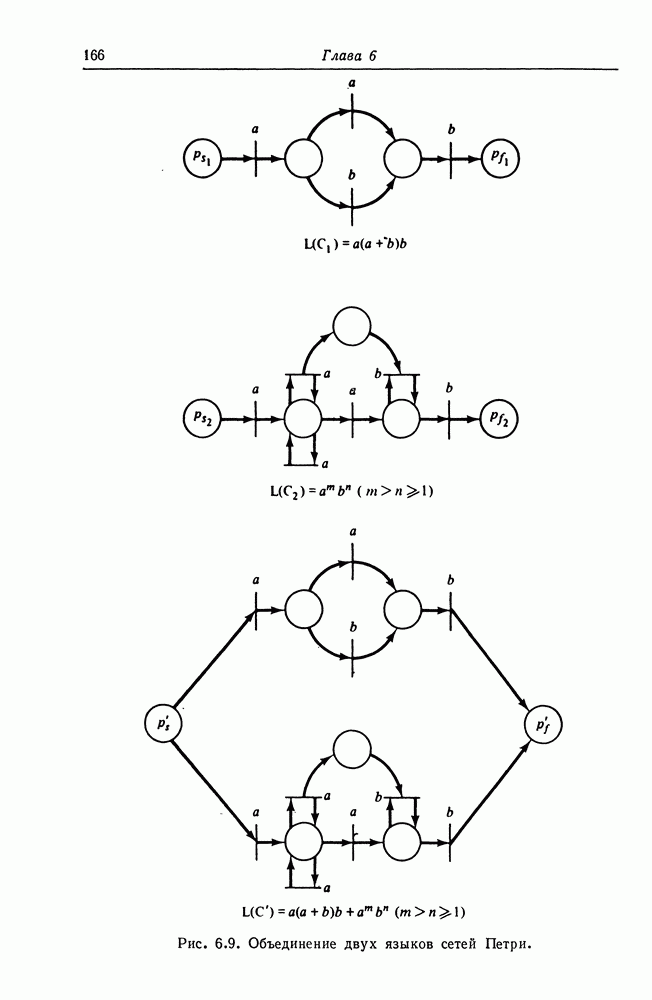
Эту фишку нельзя удалить из заключительной позиции потому, что, во-первых, никакой переход не имеет заключительной позиции в качестве входной, а, во-вторых, все переходы не разрешены. Таким образом, выполнение сети Петри стандартного вида достаточно просто. Это очень полезно при построении композиций из сетей Петри. Для того чтобы показать, что сети стандартного вида не менее мощны, чем обычные сети Петри, докажем следующую теорему.
Теорема 6.1. Всякая сеть Петри эквивалентна сети Петри стандартного вида.
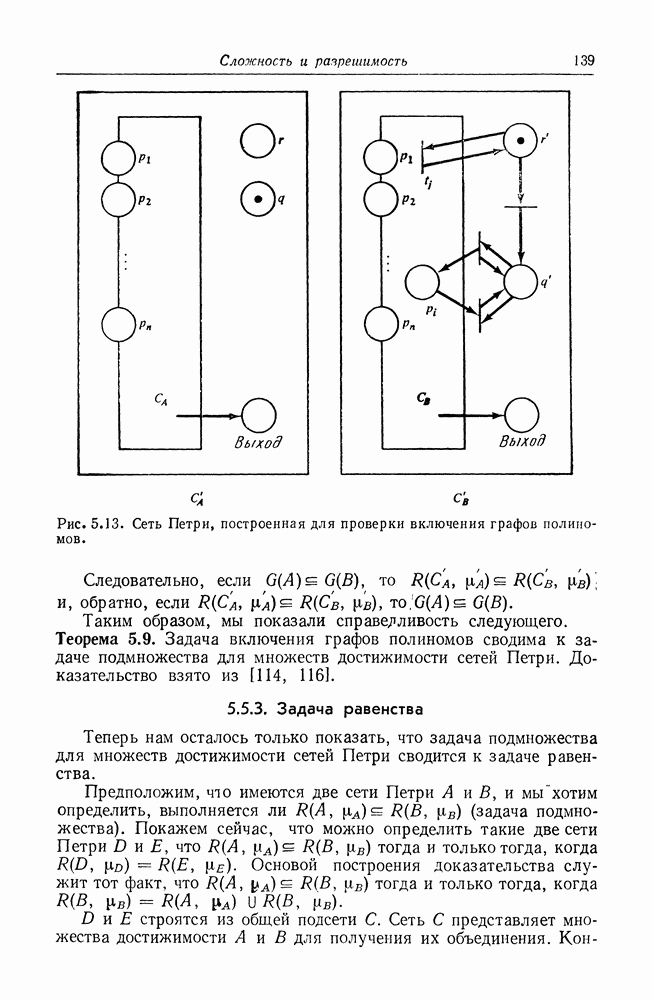
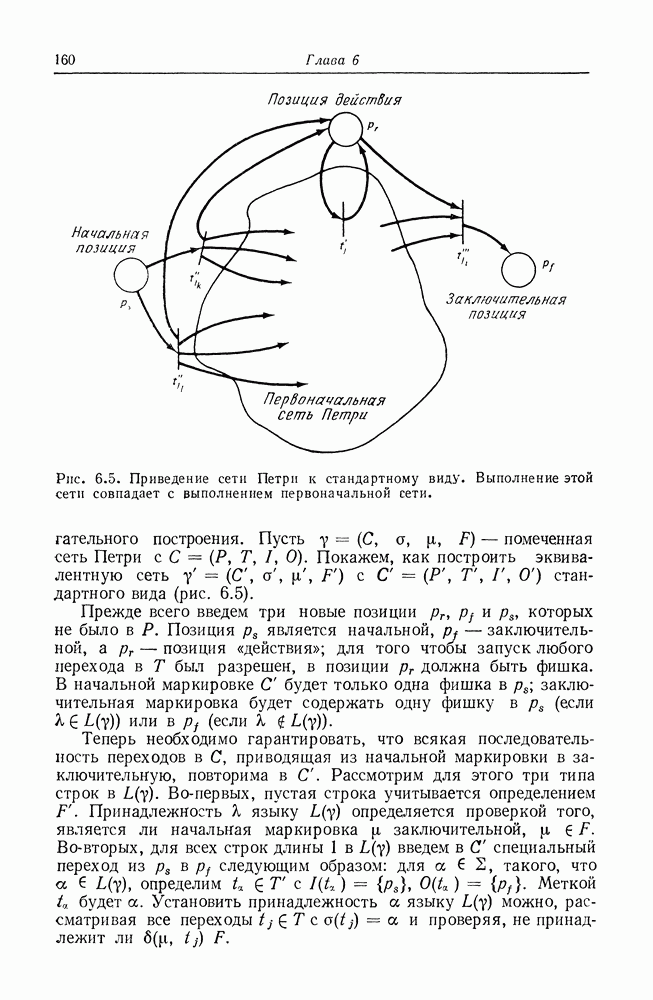
Доказательство. Доказательство проведем с помощью

Рис. 6.5. Приведение сети Петри к стандартному виду. Выполнение этой сети совпадает с выполнением первоначальной сети.
вспомогательного построения. Пусть  помеченная сеть Петри с
помеченная сеть Петри с  Покажем, как построить эквивалентную сеть
Покажем, как построить эквивалентную сеть  стандартного вида (рис. 6.5).
стандартного вида (рис. 6.5).
Прежде всего введем три новые позиции  которых не было в
которых не было в  Позиция
Позиция  является начальной,
является начальной,  заключительной, а
заключительной, а  позиция «действия»; для того чтобы запуск любого перехода в
позиция «действия»; для того чтобы запуск любого перехода в  был разрешен, в позиции
был разрешен, в позиции  должна быть фишка. В начальной маркировке С будет только одна фишка в
должна быть фишка. В начальной маркировке С будет только одна фишка в  заключительная маркировка будет содержать одну фишку в
заключительная маркировка будет содержать одну фишку в  (если
(если  или в
или в  (если
(если 
Теперь необходимо гарантировать, что всякая последовательность переходов в С, приводящая из начальной маркировки в заключительную, повторима в С. Рассмотрим для этого три типа строк в  Во-первых, пустая строка учитывается определением
Во-первых, пустая строка учитывается определением  Принадлежность
Принадлежность  языку
языку  определяется проверкой того, является ли начальная маркировка
определяется проверкой того, является ли начальная маркировка  заключительной,
заключительной,  Во-вторых, для всех строк длины 1 в
Во-вторых, для всех строк длины 1 в  введем в С специальный переход из
введем в С специальный переход из  следующим образом: для а
следующим образом: для а  такого, что а
такого, что а  определим
определим  Меткой 4 будет а. Установить принадлежность а языку
Меткой 4 будет а. Установить принадлежность а языку  можно, рассматривая все переходы
можно, рассматривая все переходы  и проверяя, не принадлежит ли
и проверяя, не принадлежит ли 
Наконец, рассмотрим все строки длины больше 1. Эти строки получаются в результате запуска последовательности  переходов
переходов  Нам бы хотелось определить последовательность
Нам бы хотелось определить последовательность  с новыми переходами
с новыми переходами  Переход а будет брать фишку из
Переход а будет брать фишку из  и порождать начальную маркировку
и порождать начальную маркировку  сети С плюс фишку в
сети С плюс фишку в  Каждый переход
Каждый переход  в
в  идентичен переходу
идентичен переходу  в
в  за исключением того, что
за исключением того, что  является для него входной и выходной. Это позволит нам запретить все переходы в
является для него входной и выходной. Это позволит нам запретить все переходы в  путем удаления фишки из
путем удаления фишки из  Переход
Переход  будет удалять фишку из
будет удалять фишку из  уничтожать заключительную маркировку С и помещать фишку в
уничтожать заключительную маркировку С и помещать фишку в  При таком построении фишка будет перемещаться из начальной позиции в заключительную только в результате последовательности
При таком построении фишка будет перемещаться из начальной позиции в заключительную только в результате последовательности  соответствующей последовательности
соответствующей последовательности  которая переводит
которая переводит  в заключительную маркировку в С.
в заключительную маркировку в С.
К сожалению, поскольку в С, но не в С будут присутствовать лишние символы, соответствующие переходам  полученная последовательность окажется длиннее. Выходом из такого положения явилось бы пустое помечение
полученная последовательность окажется длиннее. Выходом из такого положения явилось бы пустое помечение  но в языках
но в языках  -типа оно неразрешено. Для обхода этой трудности мы вынуждены «слить» переходы
-типа оно неразрешено. Для обхода этой трудности мы вынуждены «слить» переходы  в один переход
в один переход  а переходы
а переходы  в переход
в переход  Переход в
Переход в  для всякого
для всякого  определяется следующим образом:
определяется следующим образом:
1. Вводим в 
2. Если  входы в
входы в  образуют подмножество начальной маркировки, вследствие чего
образуют подмножество начальной маркировки, вследствие чего  может быть первым запускаемым в С переходом), вводим в
может быть первым запускаемым в С переходом), вводим в  переход
переход 
3. Если  для некоторой
для некоторой  может быть последним переходом, запуск которого приводит к заключительной маркировке), вводим переход
может быть последним переходом, запуск которого приводит к заключительной маркировке), вводим переход 
Помечение  определяется следующим образом:
определяется следующим образом:

Любая строка а  порождается по определению последовательностью
порождается по определению последовательностью  такой, что
такой, что  По построению
По построению


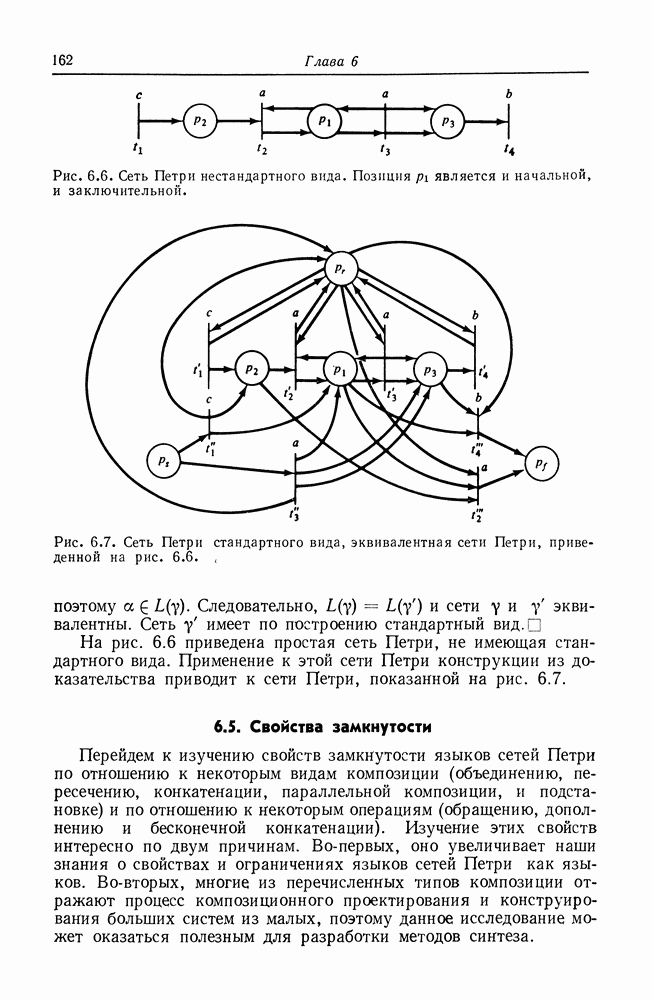
Рис. 6.6. Сеть Петри нестандартного вида. Позиция  является и начальной, и заключительной.
является и начальной, и заключительной.

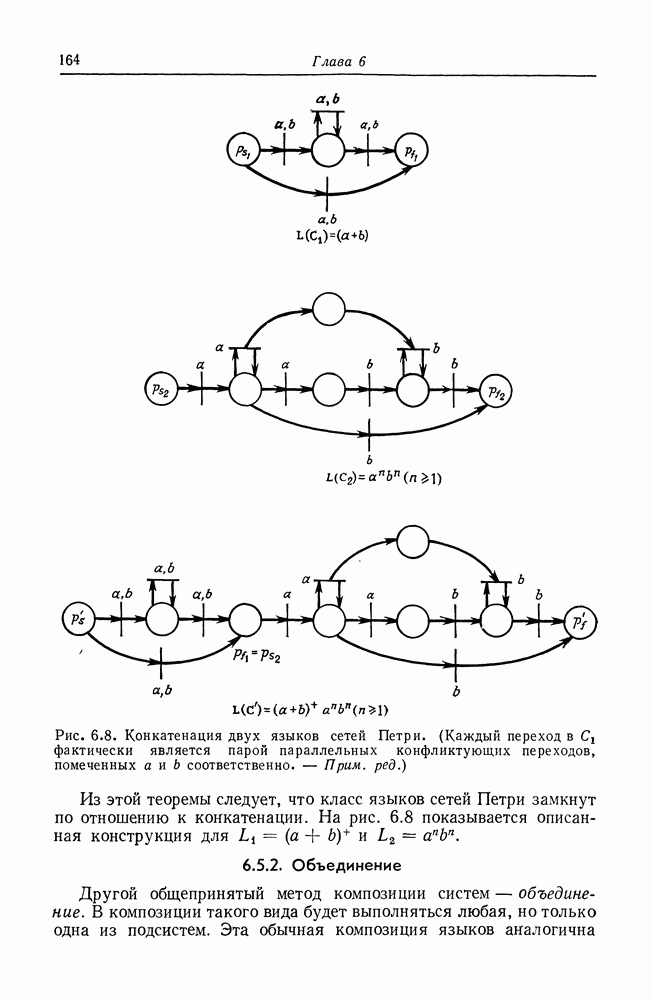
Рис. 6.7. Сеть Петри стандартного вида, эквивалентная сети Петри, приведенной на рис. 6.6. t
поэтому а  Следовательно,
Следовательно,  и сети
и сети  эквивалентны. Сеть у имеет по построению стандартный вид.
эквивалентны. Сеть у имеет по построению стандартный вид.
На рис. 6.6 приведена простая сеть Петри, не имеющая стандартного вида. Применение к этой сети Петри конструкции из доказательства приводит к сети Петри, показанной на рис. 6.7.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ГЛАВА 1. ВВЕДЕНИЕ
- ГЛАВА 2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
- 2.1. Структура сети Петри
- 2.2. Графы сетей Петри
- 2.3. Маркировка сетей Петри
- 2.4. Правила выполнения сетей Петри
- 2.5. Пространство состояний сети Петри
- 2.6. Альтернативные формы определения сетей Петри
- ГЛАВА 3. СЕТИ ПЕТРИ ДЛЯ МОДЕЛИРОВАНИЯ
- 3.2. Одновременность и конфликт
- 3.3. Аппаратное обеспечение ЭВМ
- 3.4. Программное обеспечение ЭВМ
- 3.5. Другие системы
- ГЛАВА 4. АНАЛИЗ СЕТЕЙ ПЕТРИ
- 4.1. Задачи анализа сетей Петри
- 4.2. Методы анализа
- ГЛАВА 5. СЛОЖНОСТЬ И РАЗРЕШИМОСТЬ
- 5.1. Сводимость задач анализа
- 5.2. Задачи достижимости
- 5.3. Сети Петри с ограничениями
- 5.4. Активность и достижимость
- 5.5. Неразрешимые задачи
- 5.6. Сложность задачи достижимости
- ГЛАВА 6. ЯЗЫКИ СЕТЕЙ ПЕТРИ
- 6.2. Некоторые понятия теории формальных языков
- 6.3. Определения языков сетей Петри
- 6.4. Свойства языков сетей Петри
- 6.5. Свойства замкнутости
- 6.6. Языки сетей Петри и другие классы языков
- ГЛАВА 7. РАСШИРЕННЫЕ И ОГРАНИЧЕННЫЕ МОДЕЛИ СЕТЕЙ ПЕТРИ
- 7.1. Границы возможностей моделирования с помощью сетей Петри
- 7.2. Расширения
- 7.3. Расширенные сети Петри и регистровые машины
- 7.4. Подклассы сетей Петри
- ГЛАВА 8. МОДЕЛИ ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ
- 8.2. Маркированные графы
- 8.3. Графы вычислений
- 8.4. P/V-системы
- 8.5. Системы передачи сообщений
- 8.6. Графы UCLA
- 8.7. Системы замещения и сложения векторов
- 8.8. Расширенные модели сетей Петри
- ОБЗОР ТЕОРИИ КОМПЛЕКТОВ
- АННОТИРОВАННАЯ БИБЛИОГРАФИЯ