| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
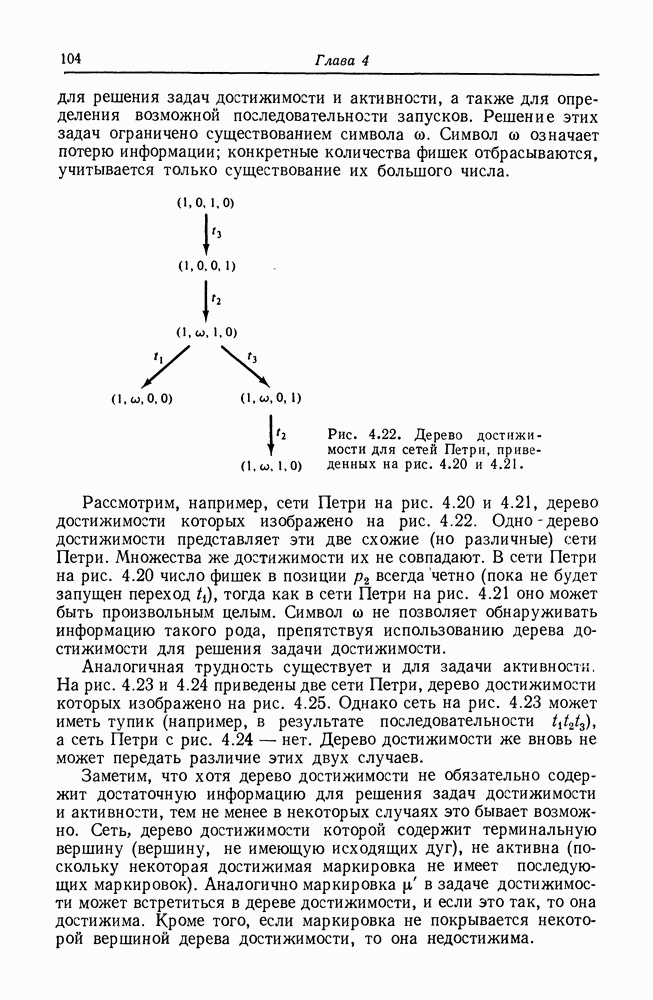
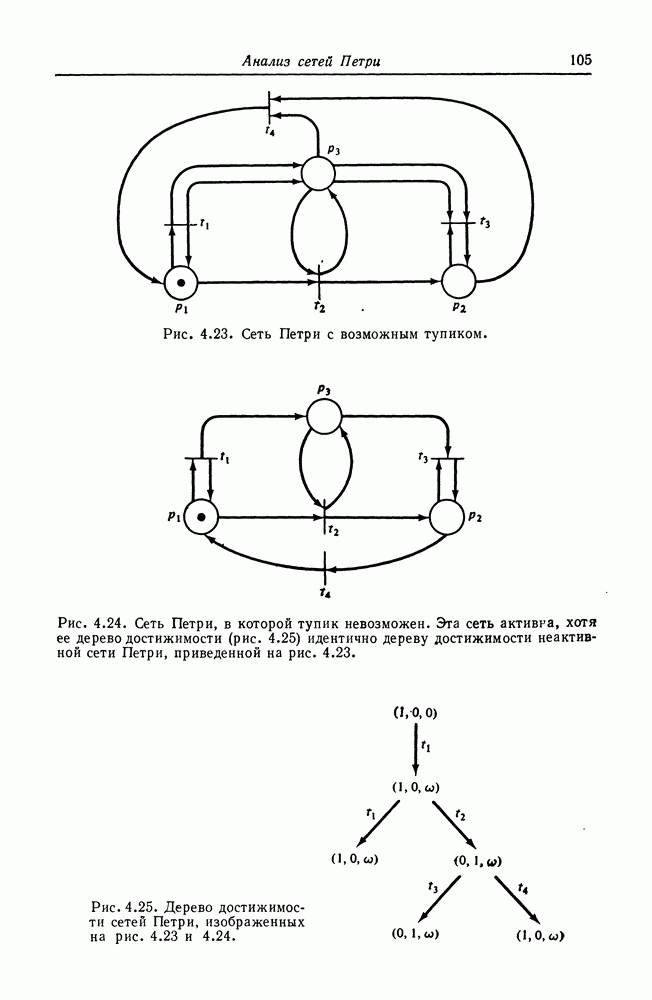
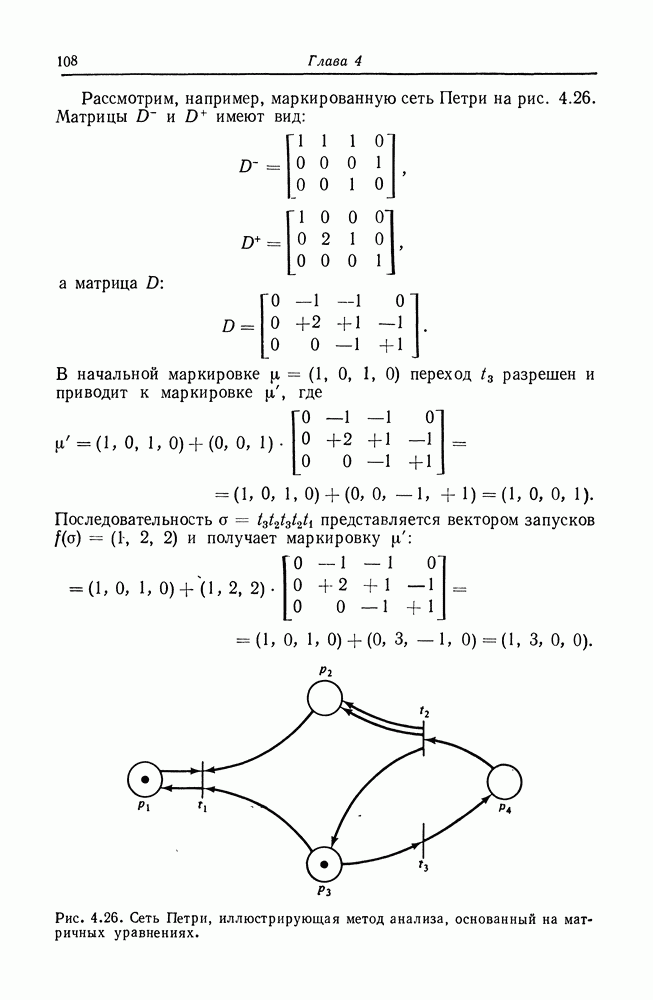
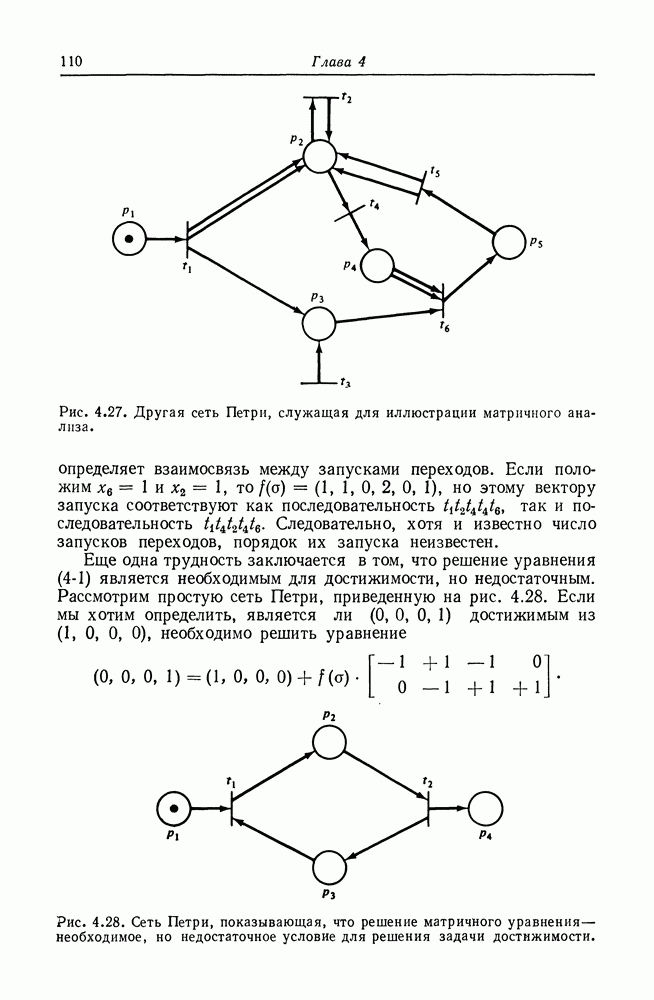
8.6. Графы UCLA
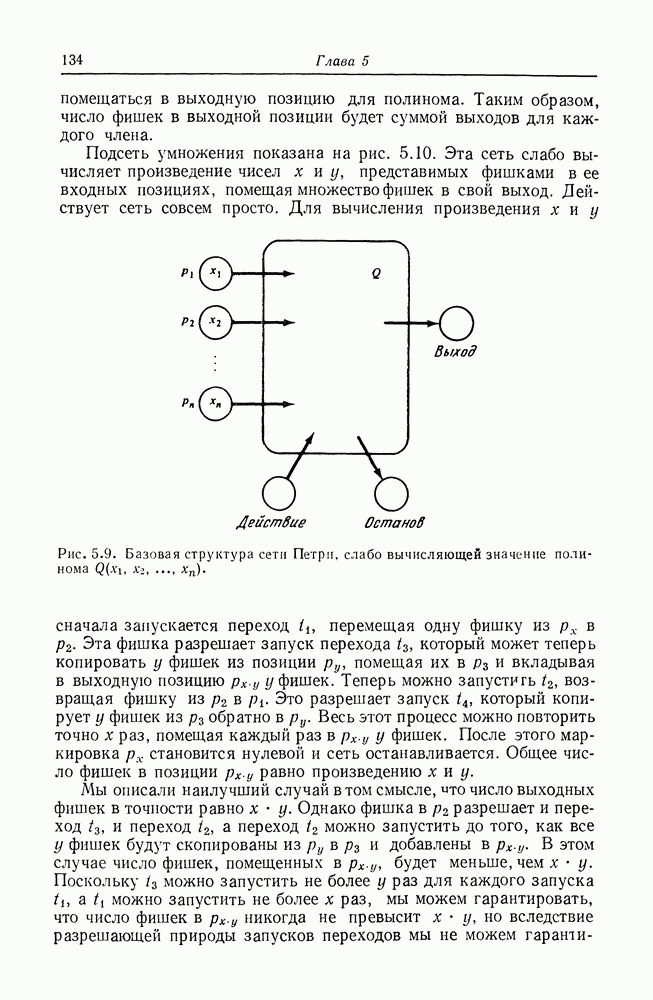
Сеть Петри является графовой моделью параллельных вычислений. Другая графовая модель разработана в Калифорнийском университете в Лос-Анджелесе под руководством профессора Эстрина. Эта модель является сложной билогической графовой моделью вычислений (или графовой моделью UCLA) [19, 23, 302, 105, 49]. В этой модели системы представляются графом со сложными ориентированными дугами. Сложная дуга — это дуга с (потенциально) многими источниками и назначениями.
Комбинационная логика управляет последовательностью операций в вершинах. Если входной логикой вершины является

(кликните для просмотра скана)
логика  то для того, чтобы разрешить действия, фишки должны присутствовать на каждой входной дуге. При логике ИЛИ {-И фишки необходимы только на какой-либо одной входной дуге
то для того, чтобы разрешить действия, фишки должны присутствовать на каждой входной дуге. При логике ИЛИ {-И фишки необходимы только на какой-либо одной входной дуге  полнение вершины удаляет разрешающие фишки на входных дугах и помещает фишки на выходные дуги в соответствии с выходной логикой. При выходной логике И фишки помещаются на все выходные дуги, тогда как при логике ИЛИ фишки помещаются на какую-либо одну выходную дугу.
полнение вершины удаляет разрешающие фишки на входных дугах и помещает фишки на выходные дуги в соответствии с выходной логикой. При выходной логике И фишки помещаются на все выходные дуги, тогда как при логике ИЛИ фишки помещаются на какую-либо одну выходную дугу.

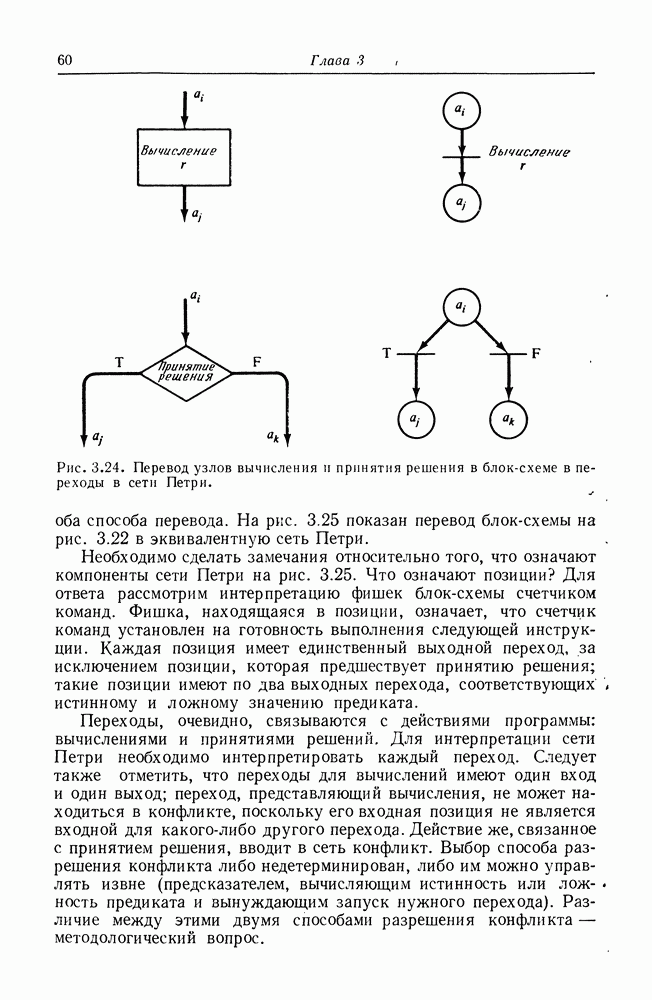
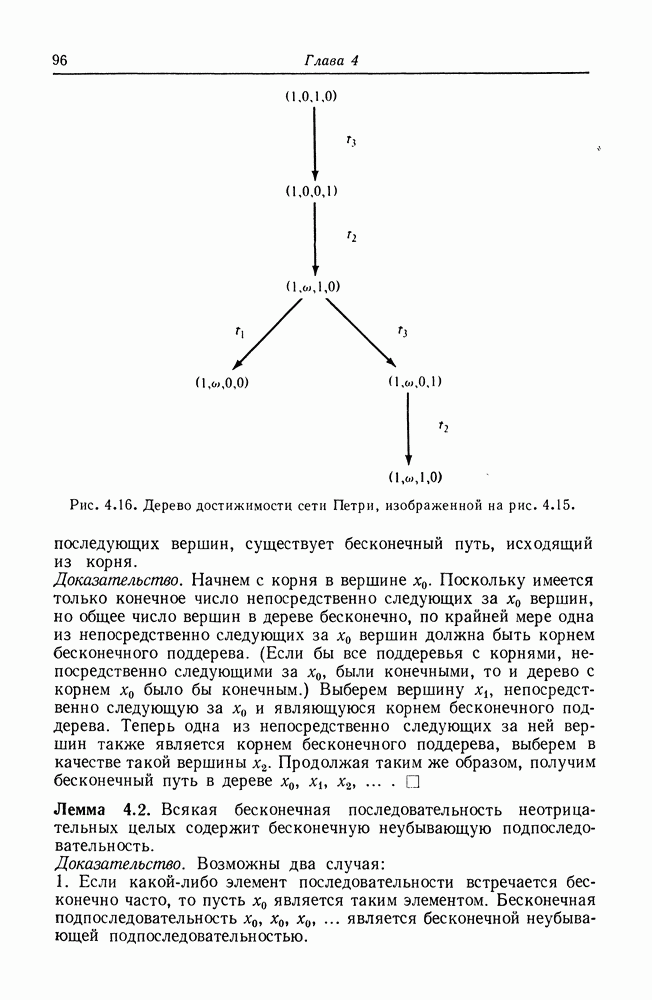
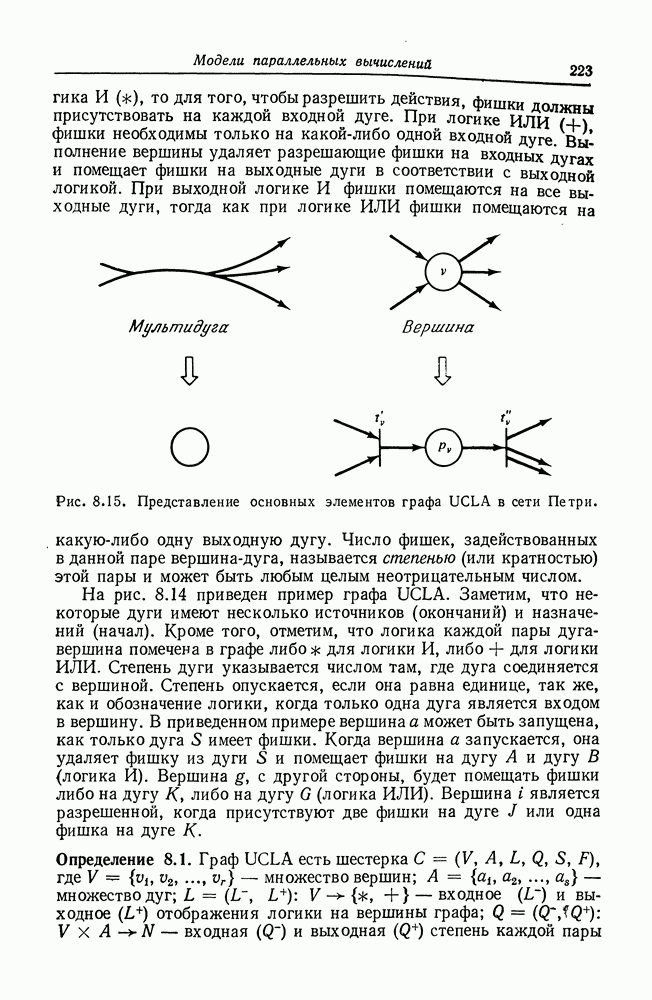
Рис. 8.15. Представление основных элементов графа UCLA в сети Петри.
Число фишек, задействованных в данной паре вершина-дуга, называется степенью (или кратностью) этой пары и может быть любым целым неотрицательным числом.
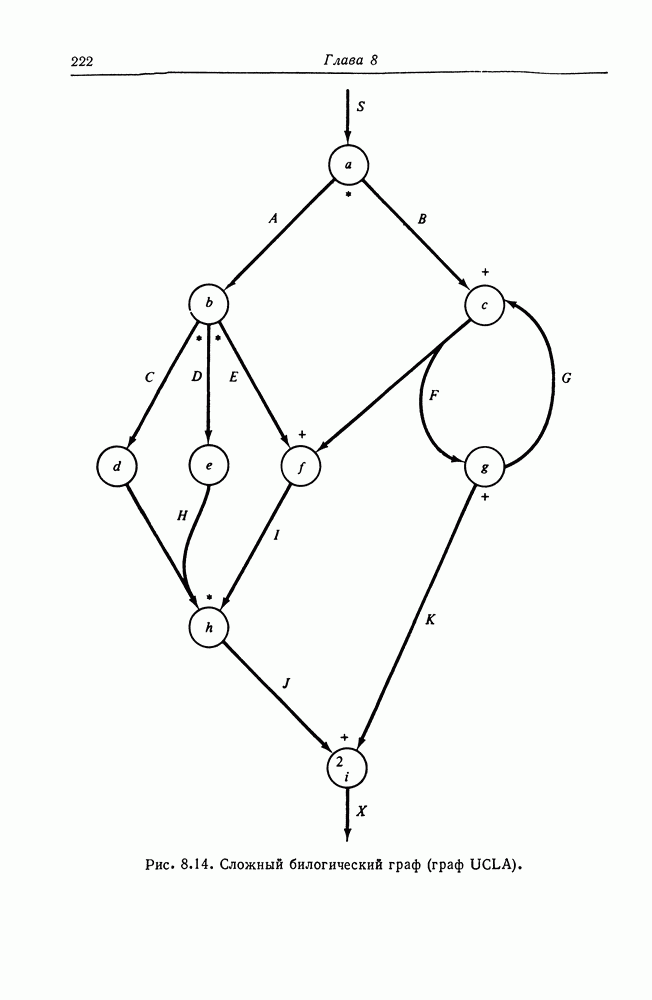
На рис. 8.14 приведен пример графа UCLA. Заметим, что некоторые дуги имеют несколько источников (окончаний) и назначений (начал). Кроме того, отметим, что логика каждой пары дуга-вершина помечена в графе либо для логики И, либо  для логики ИЛИ. Степень дуги указывается числом там, где дуга соединяется с вершиной. Степень опускается, если она равна единице, так же, как и обозначение логики, когда только одна дуга является входом в вершину. В приведенном примере вершина а может быть запущена, как только дуга 5 имеет фишки. Когда вершина а запускается, она удаляет фишку из дуги
для логики ИЛИ. Степень дуги указывается числом там, где дуга соединяется с вершиной. Степень опускается, если она равна единице, так же, как и обозначение логики, когда только одна дуга является входом в вершину. В приведенном примере вершина а может быть запущена, как только дуга 5 имеет фишки. Когда вершина а запускается, она удаляет фишку из дуги  и помещает фишки на дугу А и дугу В (логика И). Вершина
и помещает фишки на дугу А и дугу В (логика И). Вершина  с другой стороны, будет помещать фишки либо на дугу
с другой стороны, будет помещать фишки либо на дугу  либо на дугу
либо на дугу  (логика ИЛИ). Вершина
(логика ИЛИ). Вершина  является разрешенной, когда присутствуют две фишки на дуге
является разрешенной, когда присутствуют две фишки на дуге  или одна фишка на дуге К.
или одна фишка на дуге К.
Определение 8.1. Граф UCLA есть шестерка  где
где  множество вершин;
множество вершин;  множество дуг;
множество дуг;  входное
входное  и выходное
и выходное  отображения логики на вершины графа;
отображения логики на вершины графа;  входная
входная  и выходная
и выходная  степень каждой пары
степень каждой пары

(кликните для просмотра скана)
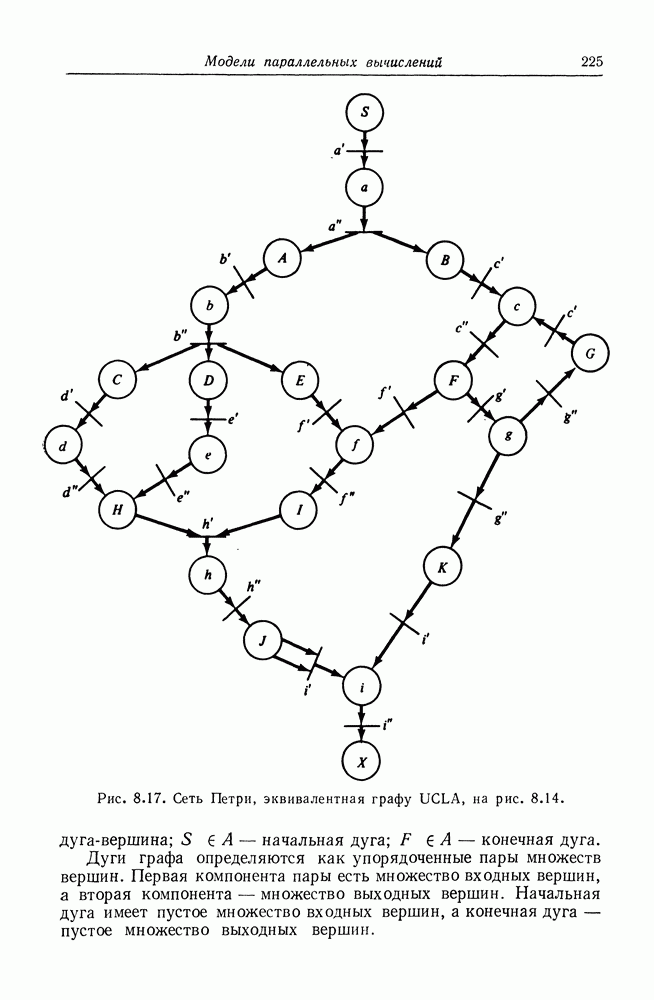
Рис. 8.17. (см. скан) Сеть Петри, эквивалентная графу UCLA, на рис. 8.14.
дуга-вершина;  начальная дуга;
начальная дуга;  конечная дуга.
конечная дуга.
Дуги графа определяются как упорядоченные пары множеств вершин. Первая компонента пары есть множество входных вершин, а вторая компонента — множество выходных вершин. Начальная дуга имеет пустое множество входных вершин, а конечная дуга — пустое множество выходных вершин.
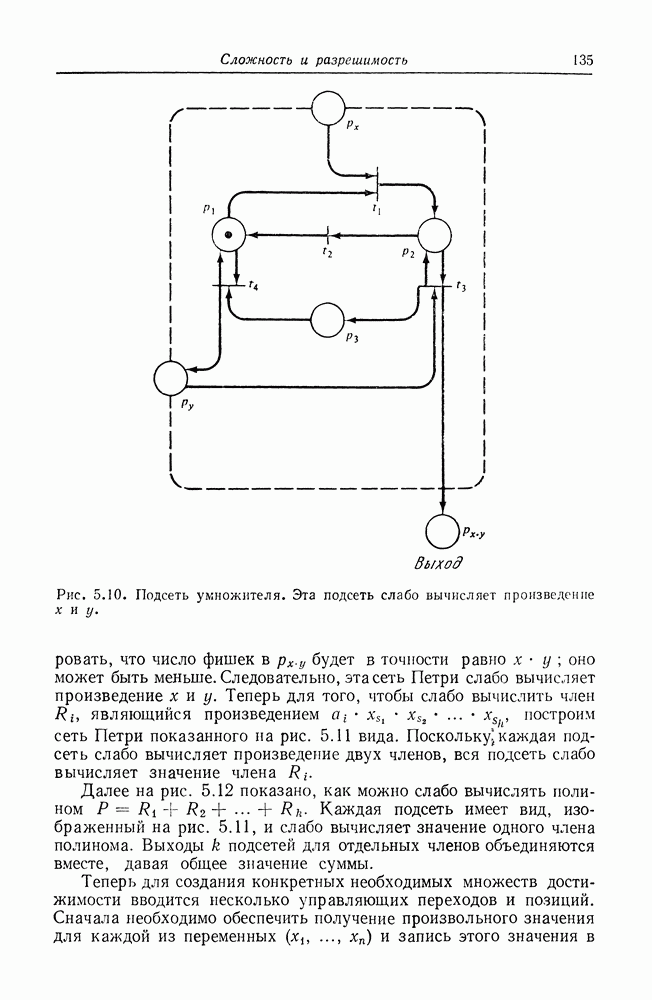
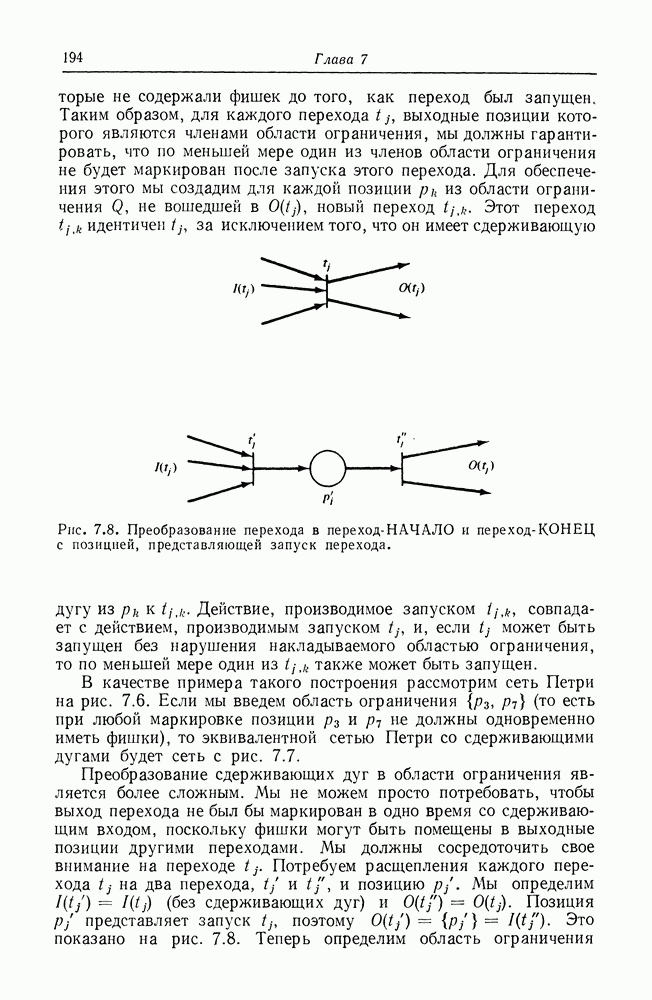
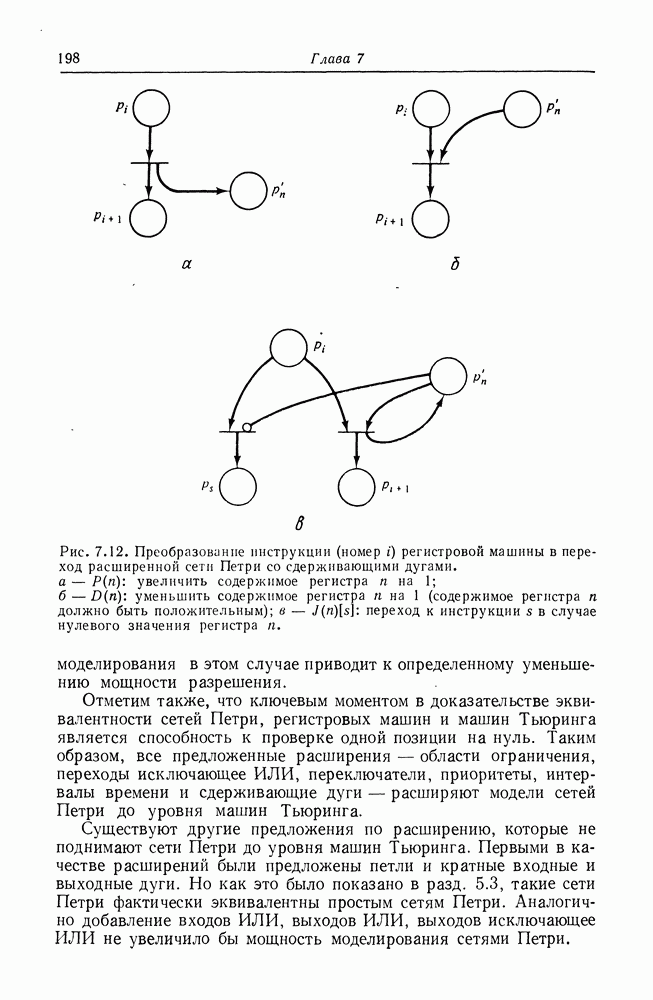
Преобразование графа UCLA в сеть Петри достаточно просто из-за подобности этих систем. Каждая дуга в графе UCLA представляется позицией в сети Петри. Кроме того, представим вершину и позицией  и двумя переходами
и двумя переходами  и
и  Первый переход
Первый переход  представляет инициирование операции, связанной с вершиной
представляет инициирование операции, связанной с вершиной  а второй переход представляет завершение этой операции.
а второй переход представляет завершение этой операции.

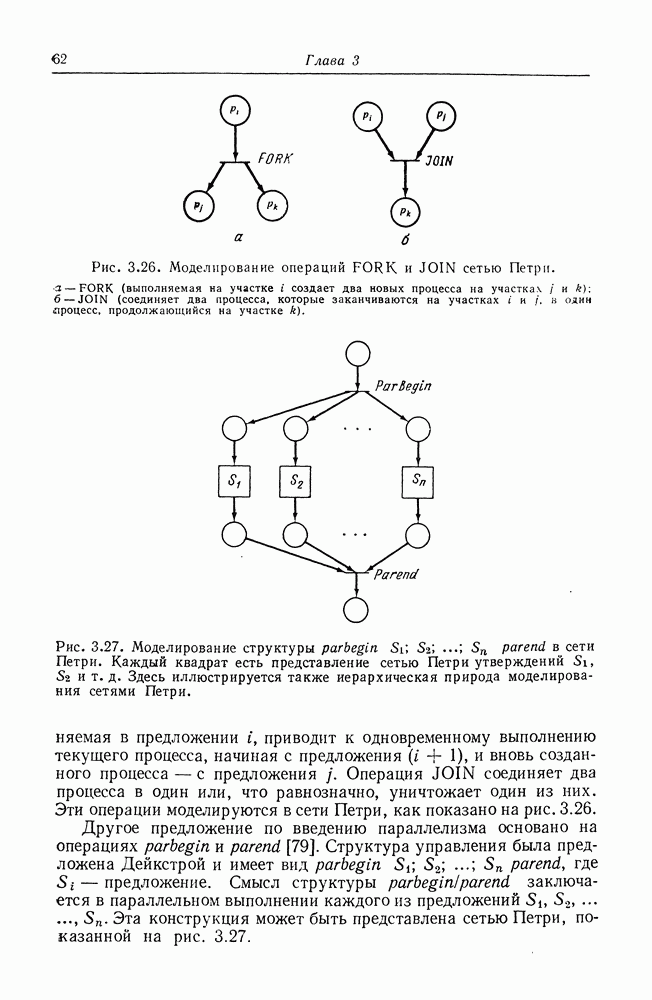
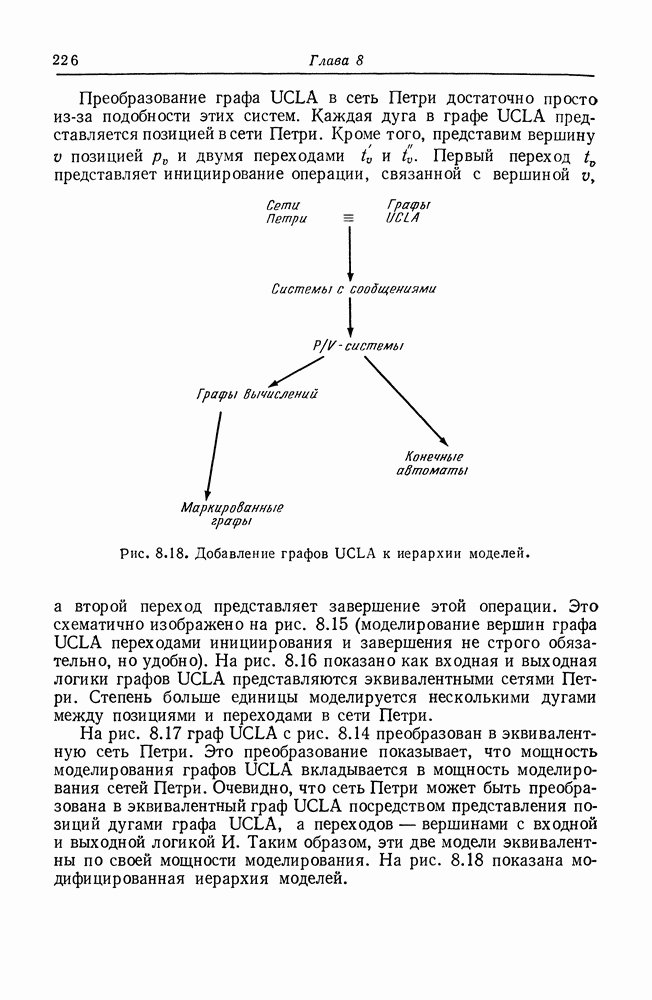
Рис. 8.18. Добавление графов UCLA к иерархии моделей.
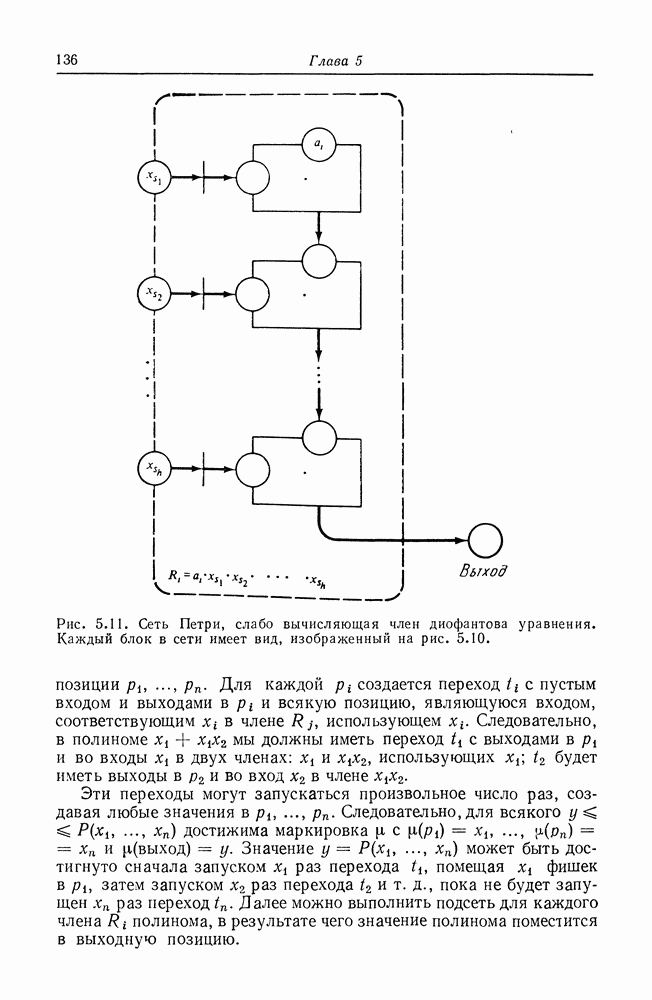
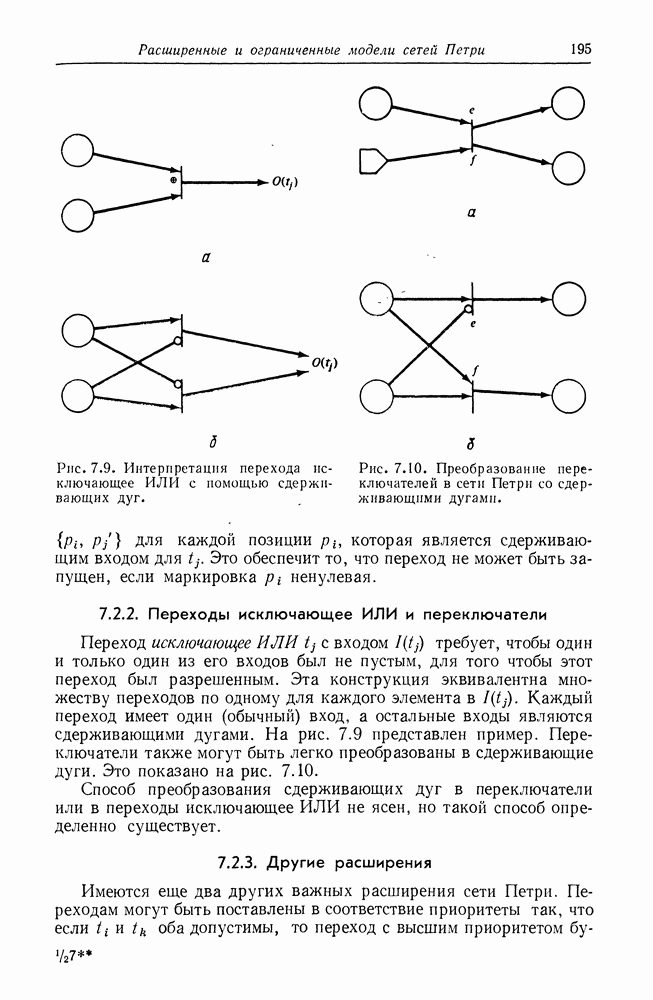
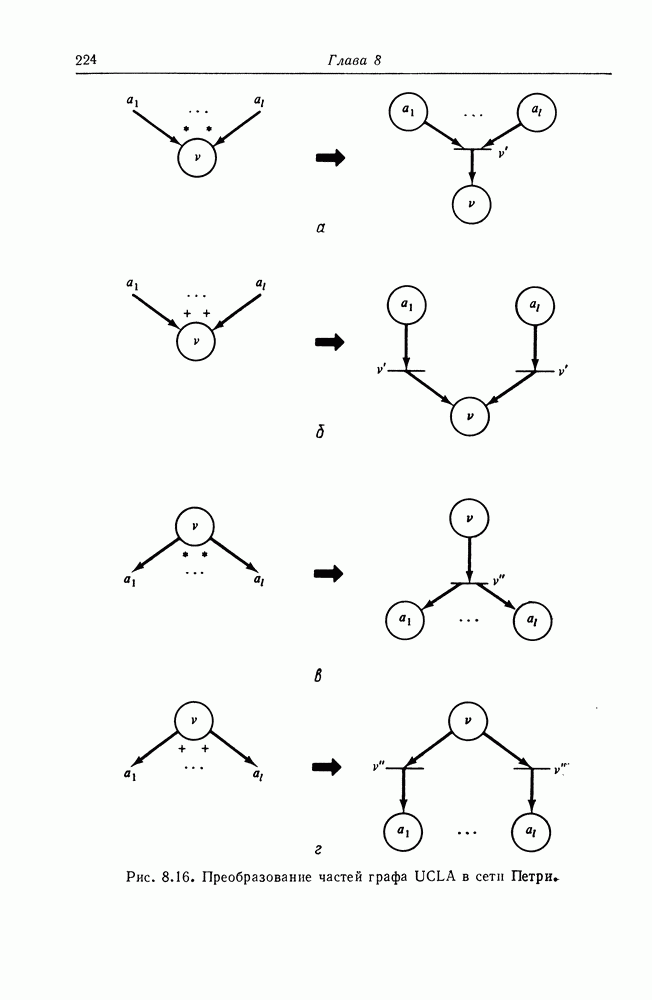
Это схематично изображено на рис. 8.15 (моделирование вершин графа UCLA переходами инициирования и завершения не строго обязательно, но удобно). На рис. 8.16 показано как входная и выходная логики графов UCLA представляются эквивалентными сетями Петри. Степень больше единицы моделируется несколькими дугами между позициями и переходами в сети Петри.
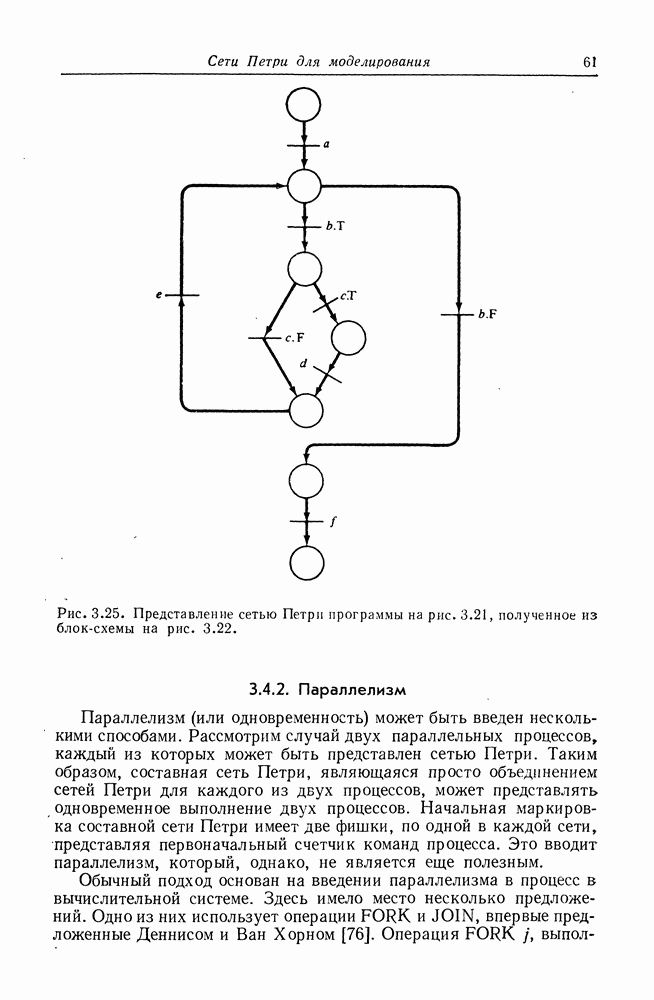
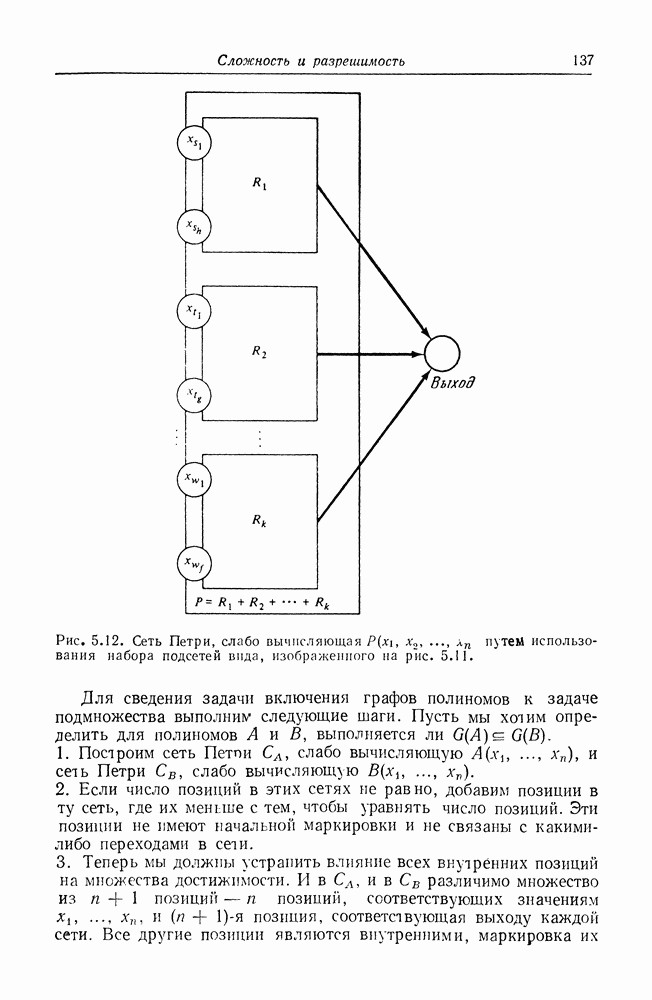
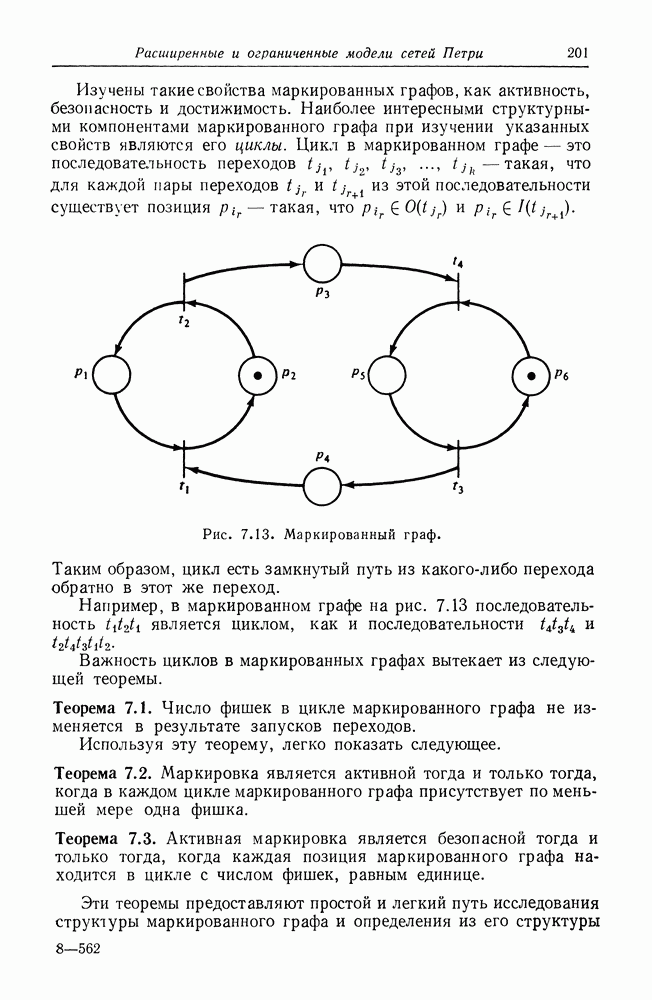
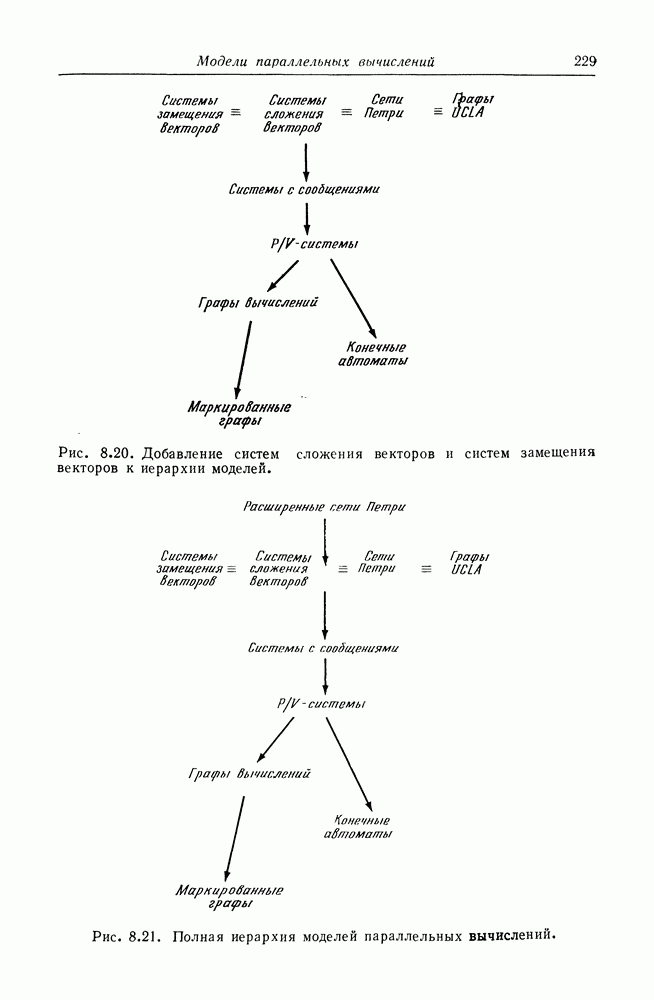
На рис. 8.17 граф UCLA с рис. 8.14 преобразован в эквивалентную сеть Петри. Это преобразование показывает, что мощность моделирования графов UCLA вкладывается в мощность моделирования сетей Петри. Очевидно, что сеть Петри может быть преобразована в эквивалентный граф UCLA посредством представления позиций дугами графа UCLA, а переходов — вершинами с входной и выходной логикой И. Таким образом, эти две модели эквивалентны по своей мощности моделирования. На рис. 8.18 показана модифицированная иерархия моделей.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ГЛАВА 1. ВВЕДЕНИЕ
- ГЛАВА 2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
- 2.1. Структура сети Петри
- 2.2. Графы сетей Петри
- 2.3. Маркировка сетей Петри
- 2.4. Правила выполнения сетей Петри
- 2.5. Пространство состояний сети Петри
- 2.6. Альтернативные формы определения сетей Петри
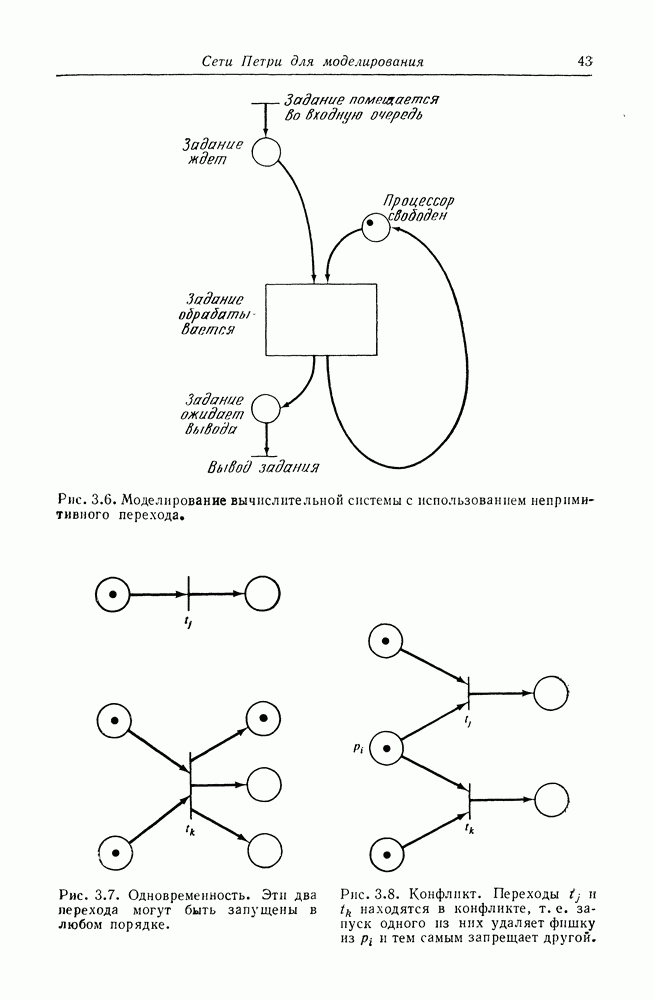
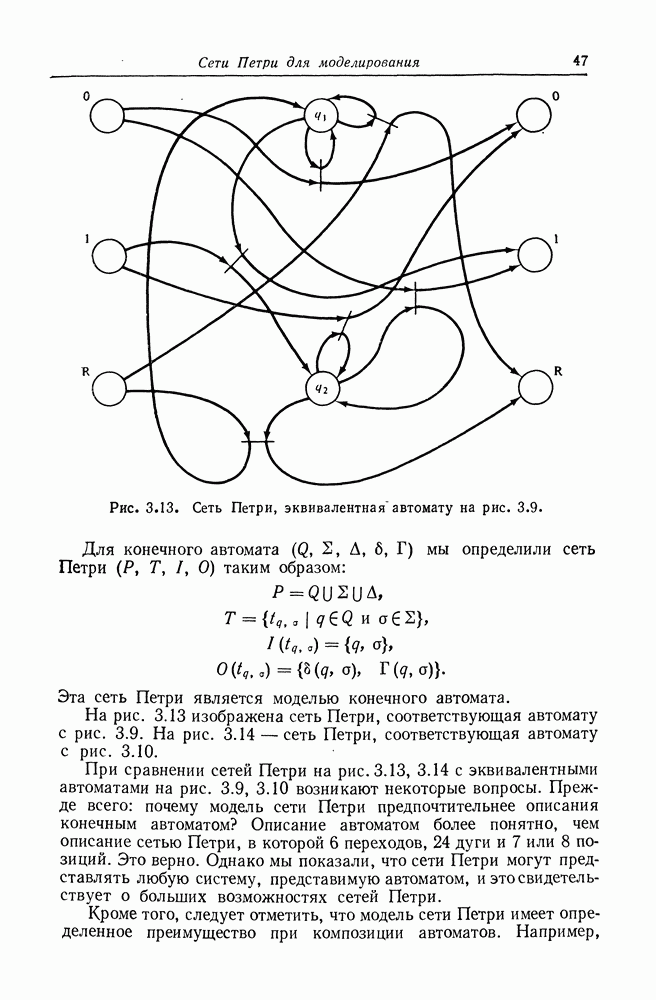
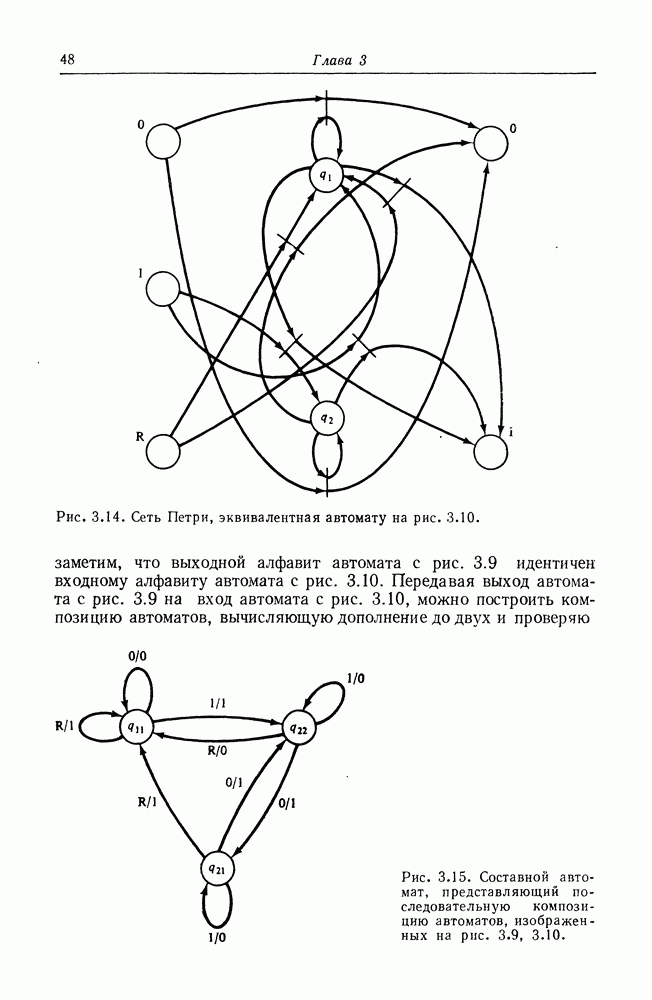
- ГЛАВА 3. СЕТИ ПЕТРИ ДЛЯ МОДЕЛИРОВАНИЯ
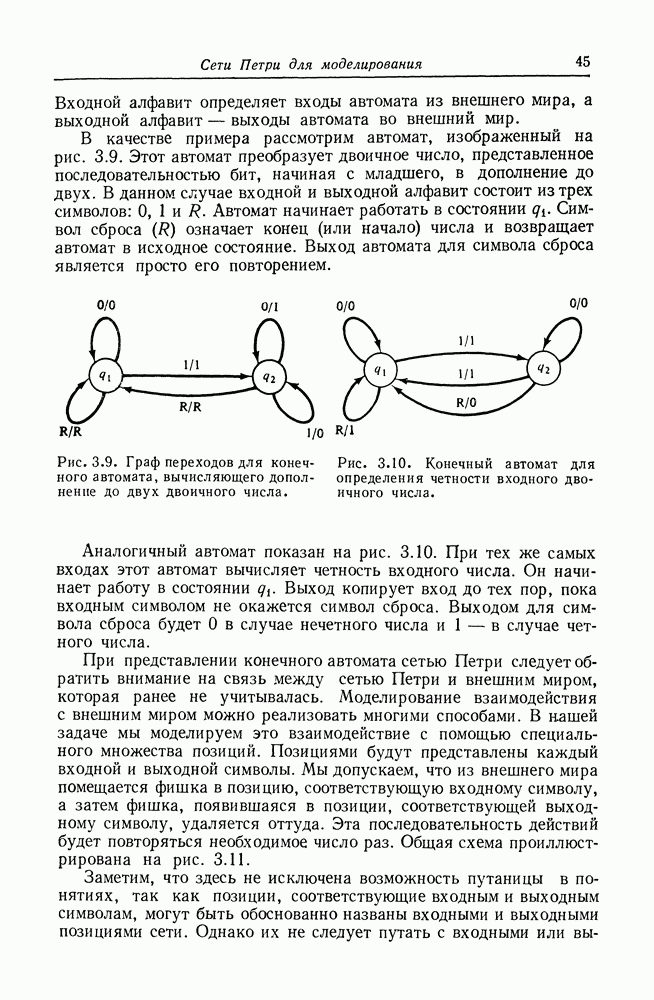
- 3.2. Одновременность и конфликт
- 3.3. Аппаратное обеспечение ЭВМ
- 3.4. Программное обеспечение ЭВМ
- 3.5. Другие системы
- ГЛАВА 4. АНАЛИЗ СЕТЕЙ ПЕТРИ
- 4.1. Задачи анализа сетей Петри
- 4.2. Методы анализа
- ГЛАВА 5. СЛОЖНОСТЬ И РАЗРЕШИМОСТЬ
- 5.1. Сводимость задач анализа
- 5.2. Задачи достижимости
- 5.3. Сети Петри с ограничениями
- 5.4. Активность и достижимость
- 5.5. Неразрешимые задачи
- 5.6. Сложность задачи достижимости
- ГЛАВА 6. ЯЗЫКИ СЕТЕЙ ПЕТРИ
- 6.2. Некоторые понятия теории формальных языков
- 6.3. Определения языков сетей Петри
- 6.4. Свойства языков сетей Петри
- 6.5. Свойства замкнутости
- 6.6. Языки сетей Петри и другие классы языков
- ГЛАВА 7. РАСШИРЕННЫЕ И ОГРАНИЧЕННЫЕ МОДЕЛИ СЕТЕЙ ПЕТРИ
- 7.1. Границы возможностей моделирования с помощью сетей Петри
- 7.2. Расширения
- 7.3. Расширенные сети Петри и регистровые машины
- 7.4. Подклассы сетей Петри
- ГЛАВА 8. МОДЕЛИ ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ
- 8.2. Маркированные графы
- 8.3. Графы вычислений
- 8.4. P/V-системы
- 8.5. Системы передачи сообщений
- 8.6. Графы UCLA
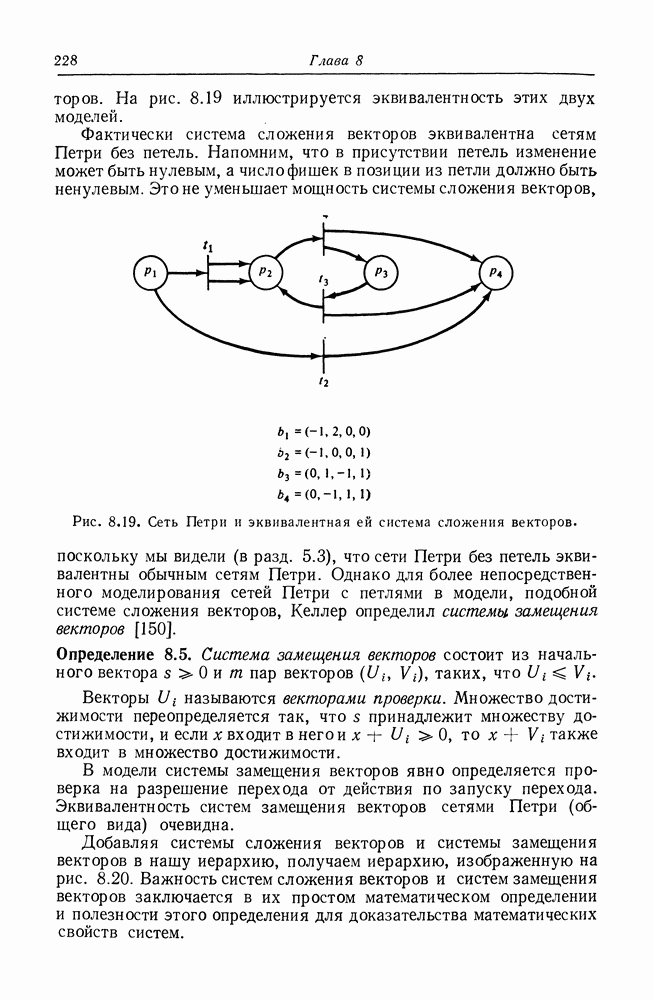
- 8.7. Системы замещения и сложения векторов
- 8.8. Расширенные модели сетей Петри
- ОБЗОР ТЕОРИИ КОМПЛЕКТОВ
- АННОТИРОВАННАЯ БИБЛИОГРАФИЯ