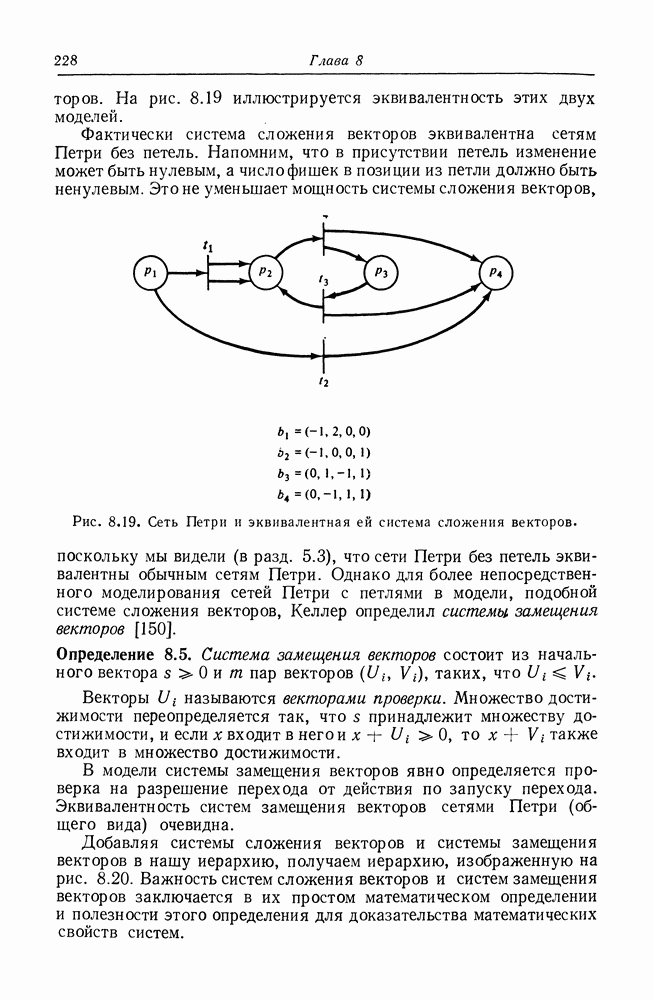
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8.3. Графы вычислений
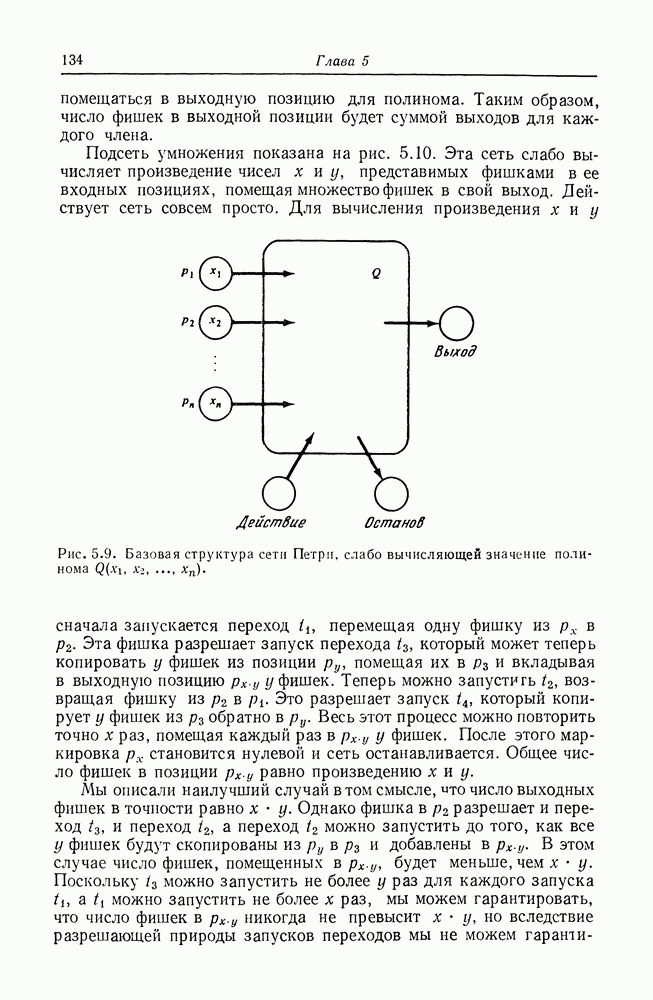
Одной из наиболее ранних моделей параллельных вычислений была модель графов вычислений [147]. Ее предложили главным образом для представления параллельного выполнения программ, вычисляющих арифметические выражения.
Граф вычислений  определяется как ориентированный граф
определяется как ориентированный граф  где
где  множество узлов;
множество узлов;  множество дуг.
множество дуг.
Каждая дуга  есть упорядоченная пара узлов
есть упорядоченная пара узлов  представляющая дугу из
представляющая дугу из  Каждой дуге
Каждой дуге  сопоставлена четверка
сопоставлена четверка  Каждая дуга представляет очередь элементов данных, полученных процессором в узле
Каждая дуга представляет очередь элементов данных, полученных процессором в узле  и используемых процессором в узле
и используемых процессором в узле  есть число элементов данных, находящихся первоначально в очереди, соответствующей дуге из
есть число элементов данных, находящихся первоначально в очереди, соответствующей дуге из  Узел
Узел  подготовлен, если на каждой дуге,
подготовлен, если на каждой дуге,

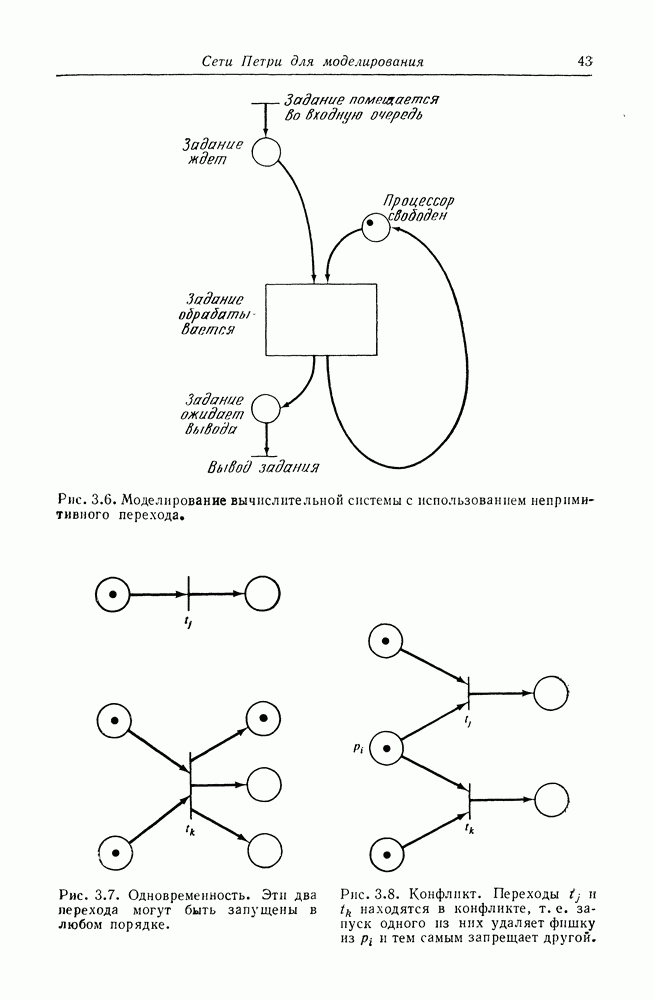
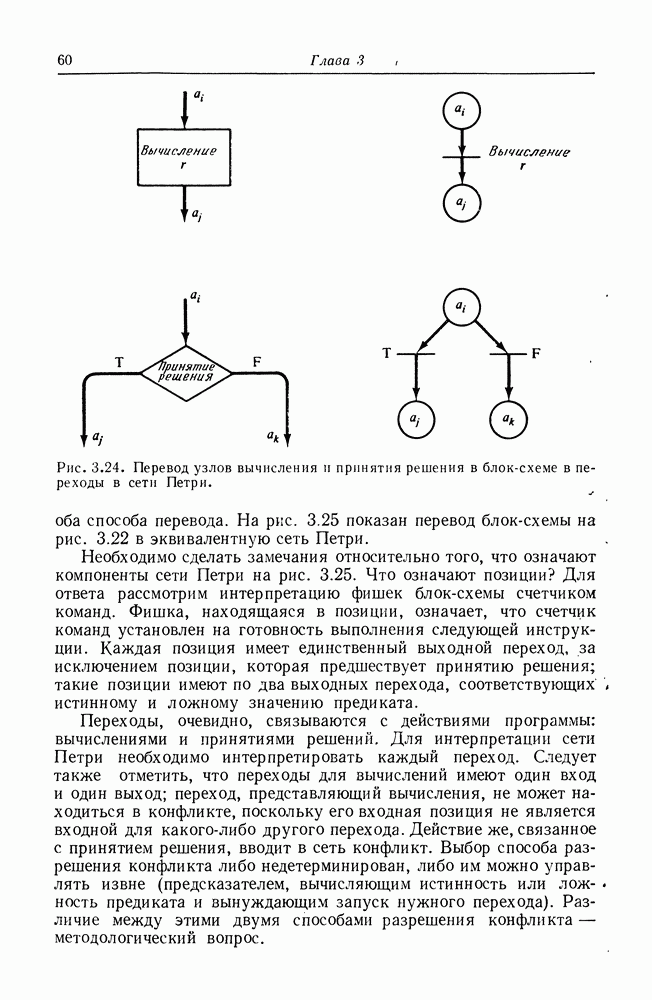
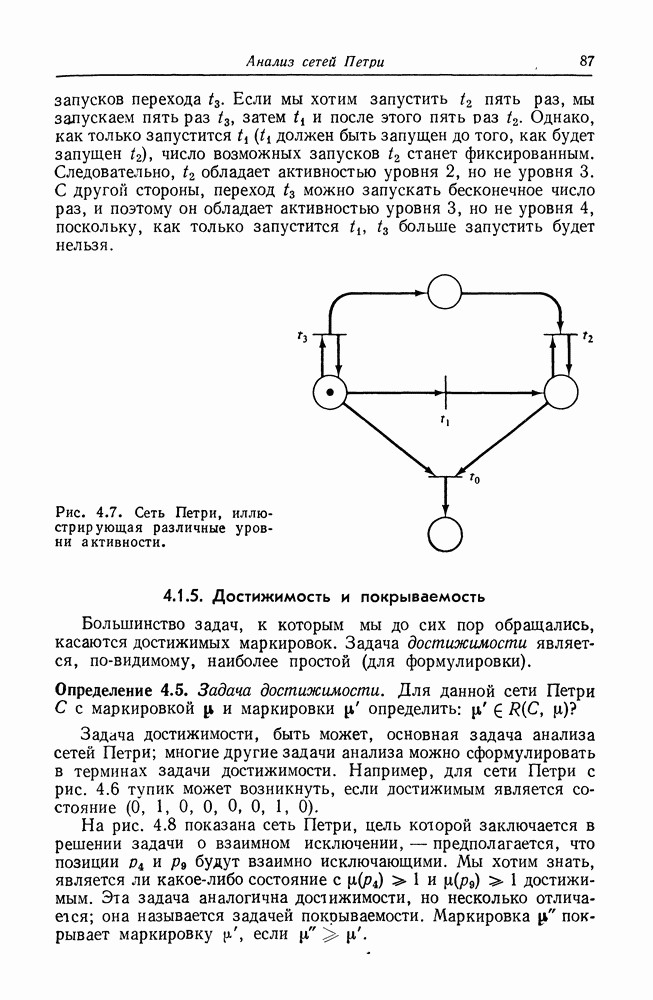
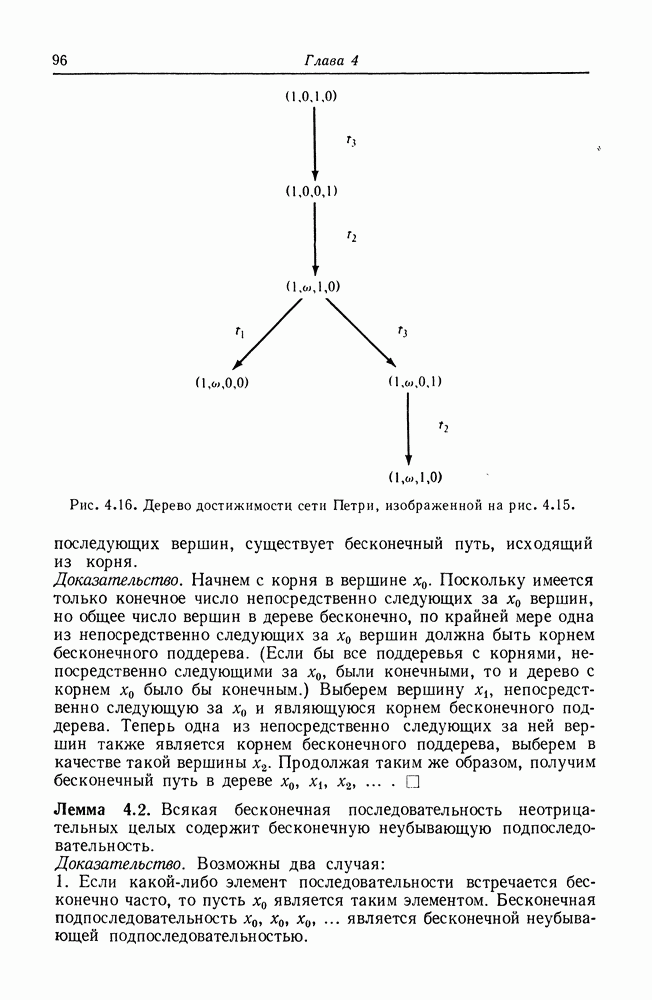
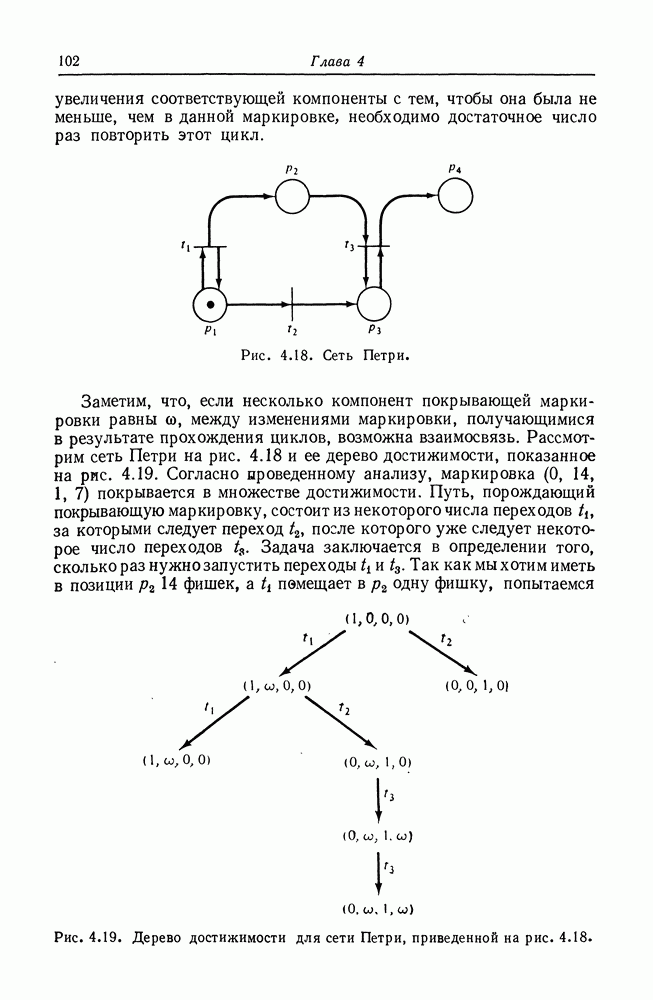
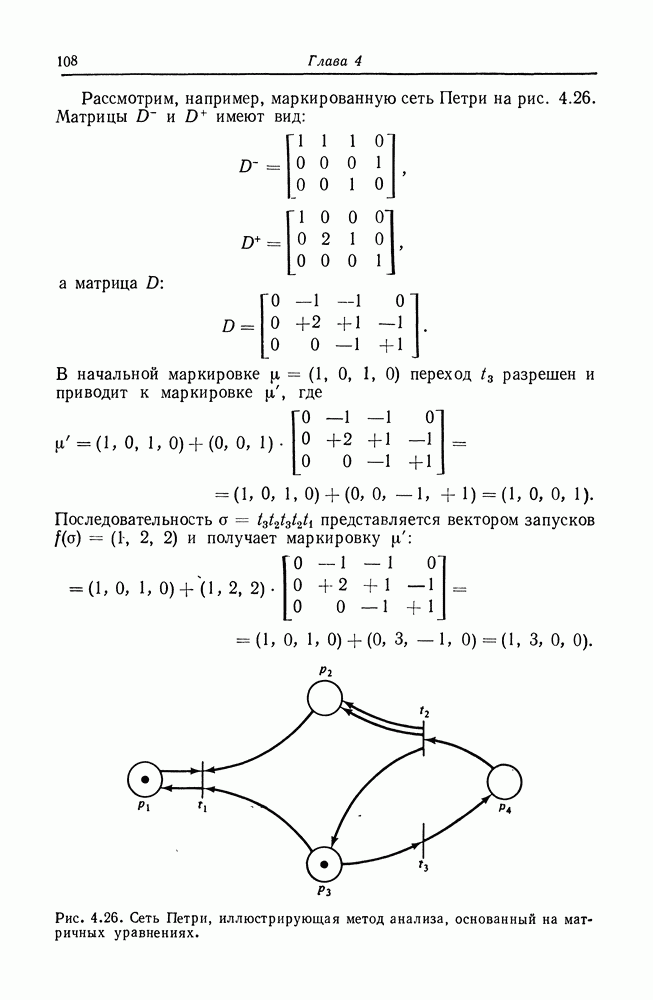
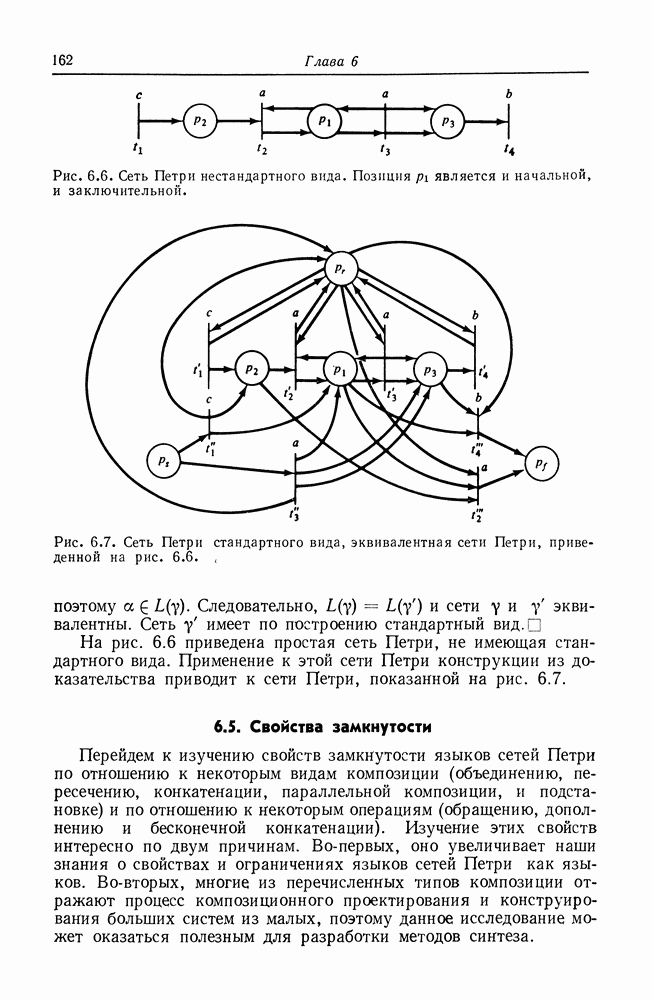
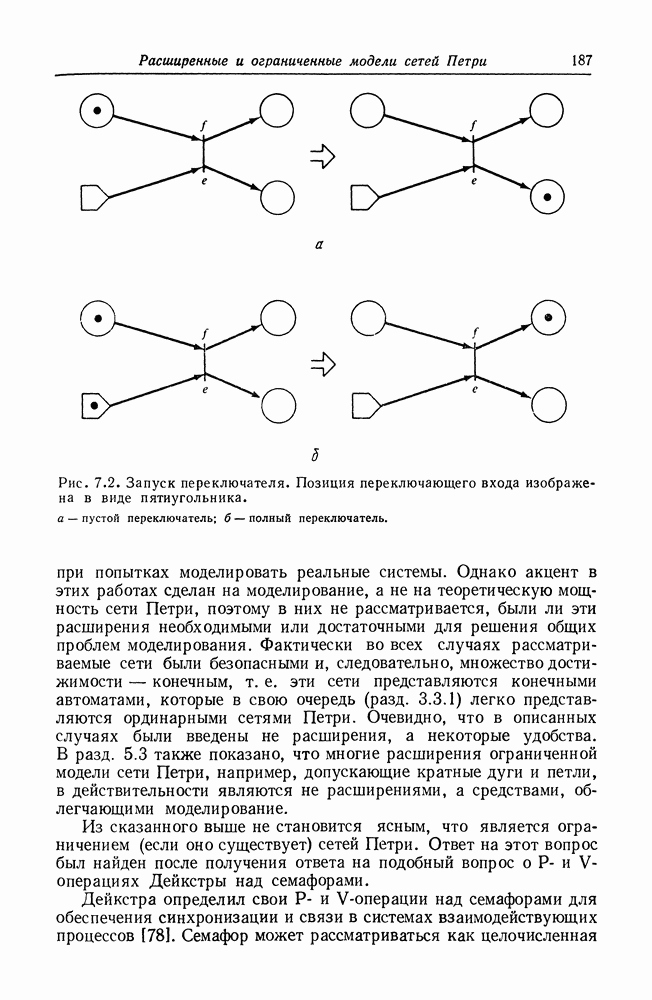
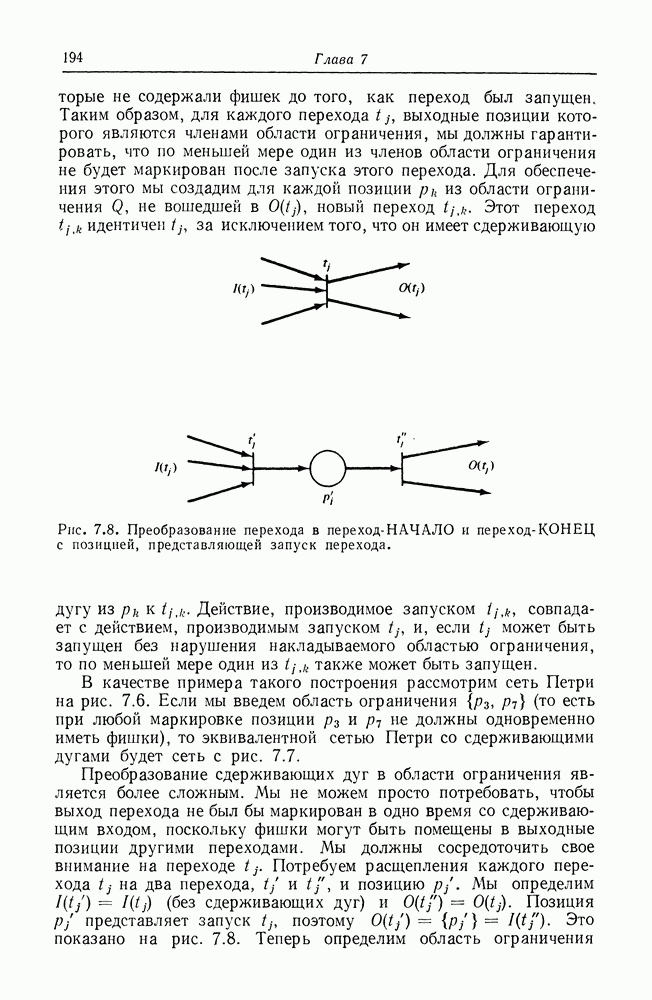
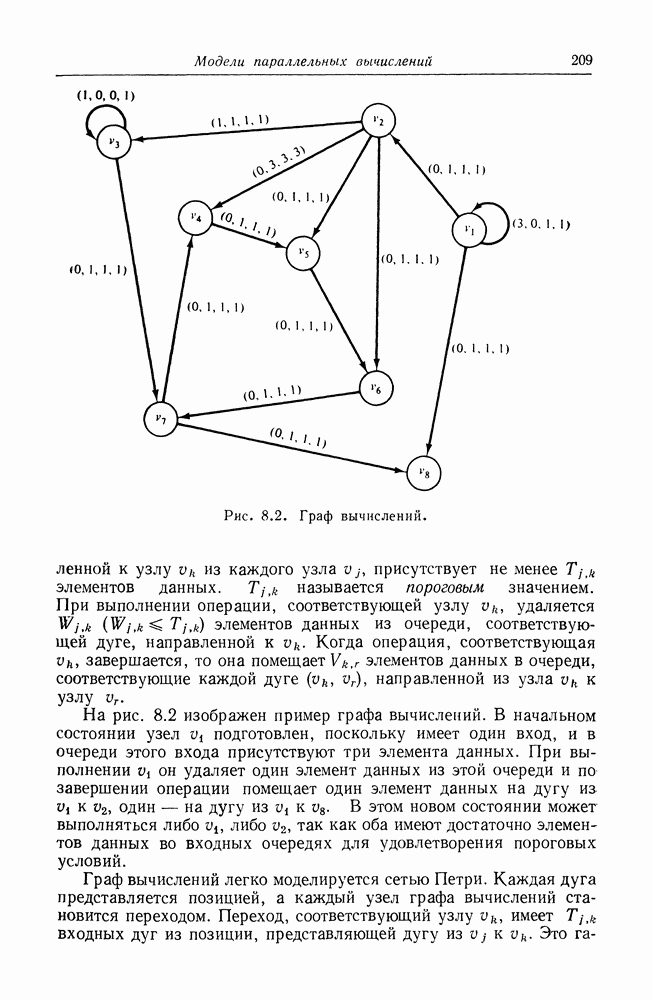
Рис. 8.2. Граф вычислений.
направленной к узлу  из каждого узла
из каждого узла  присутствует не менее
присутствует не менее  элементов данных.
элементов данных.  называется пороговым значением. При выполнении операции, соответствующей узлу
называется пороговым значением. При выполнении операции, соответствующей узлу  удаляется
удаляется  элементов данных из очереди, соответствующей дуге, направленной к
элементов данных из очереди, соответствующей дуге, направленной к  Когда операция, соответствующая
Когда операция, соответствующая  завершается, то она помещает
завершается, то она помещает  элементов данных в очереди, соответствующие каждой дуге
элементов данных в очереди, соответствующие каждой дуге  направленной из узла
направленной из узла  к узлу
к узлу 
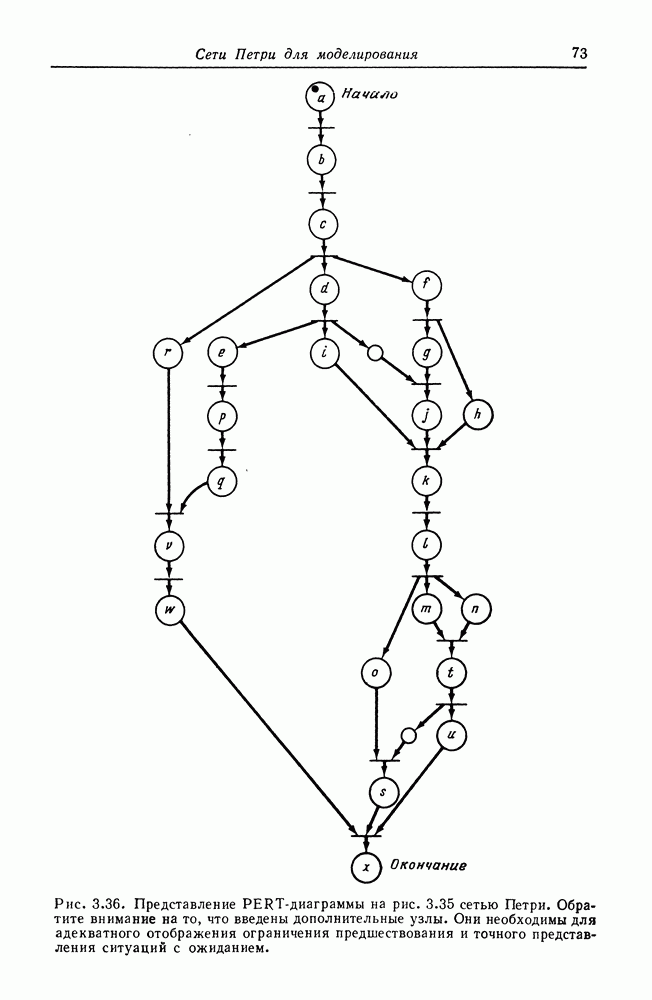
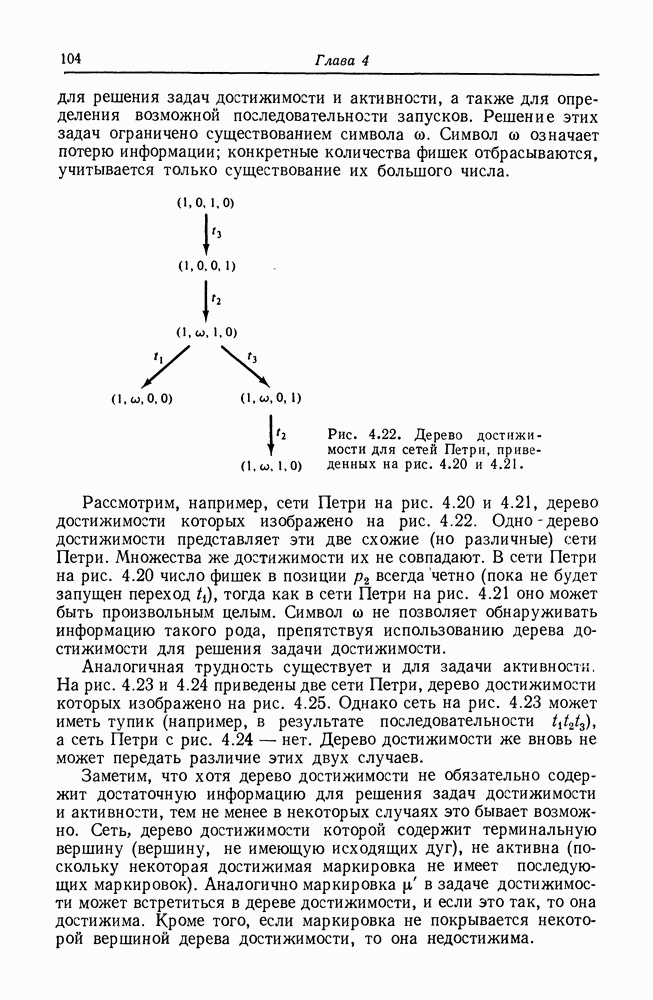
На рис. 8.2 изображен пример графа вычислений. В начальном состоянии узел  подготовлен, поскольку имеет один вход, и в очереди этого входа присутствуют три элемента данных. При выполнении он удаляет один элемент данных из этой очереди и по завершении операции помещает один элемент данных на дугу из
подготовлен, поскольку имеет один вход, и в очереди этого входа присутствуют три элемента данных. При выполнении он удаляет один элемент данных из этой очереди и по завершении операции помещает один элемент данных на дугу из  один — на дугу из к
один — на дугу из к  В этом новом состоянии может выполняться либо
В этом новом состоянии может выполняться либо  либо
либо  так как оба имеют достаточно элементов данных во входных очередях для удовлетворения пороговых условий.
так как оба имеют достаточно элементов данных во входных очередях для удовлетворения пороговых условий.
Граф вычислений легко моделируется сетью Петри. Каждая дуга представляется позицией, а каждый узел графа вычислений становится переходом. Переход, соответствующий узлу  имеет
имеет  входных дуг из позиции, представляющей дугу из
входных дуг из позиции, представляющей дугу из  Это
Это

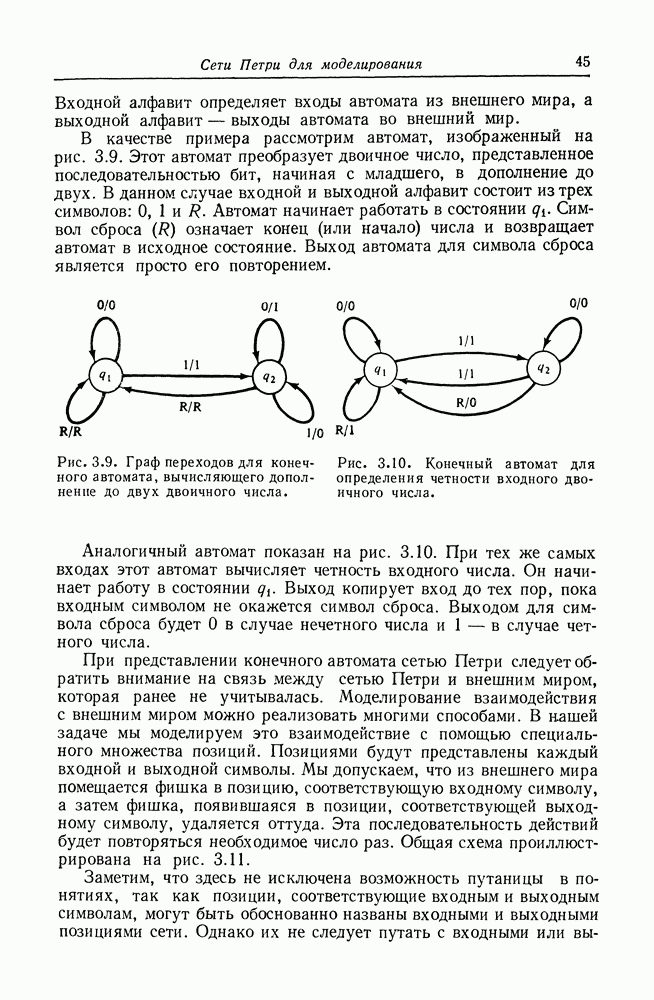
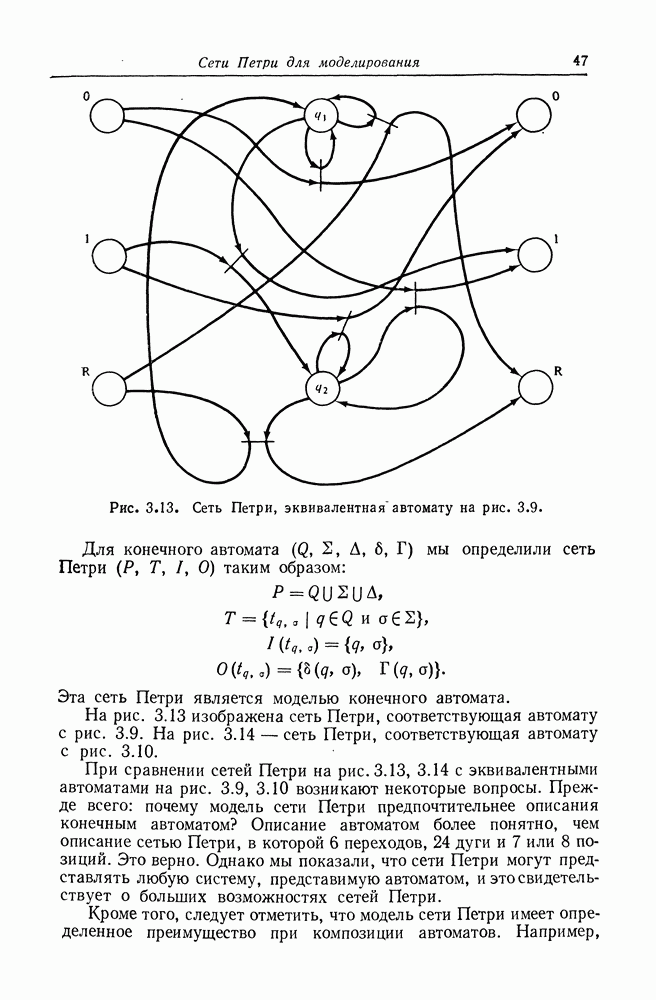
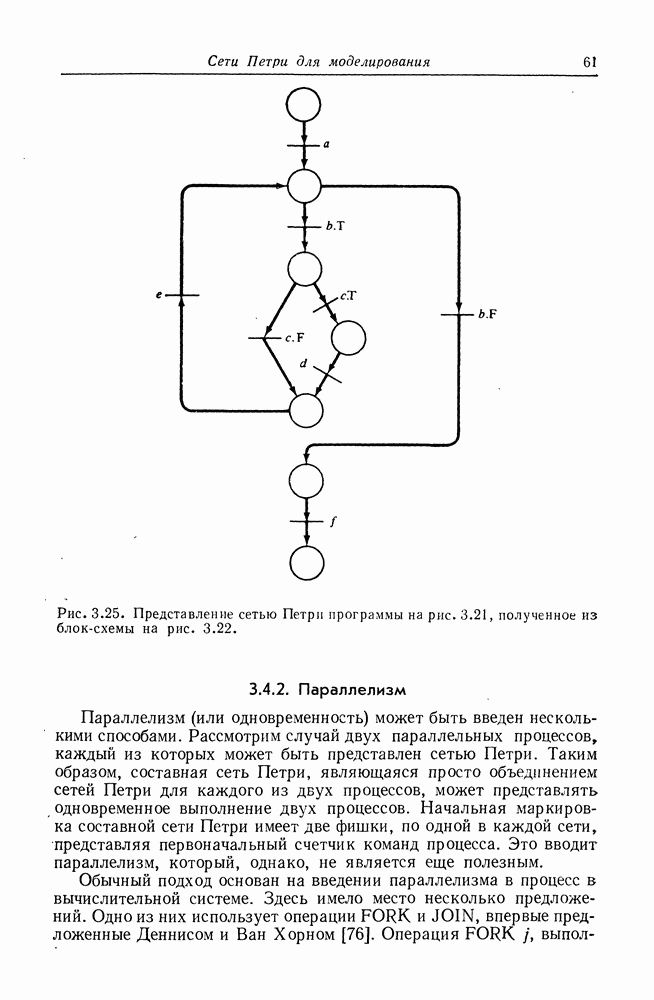
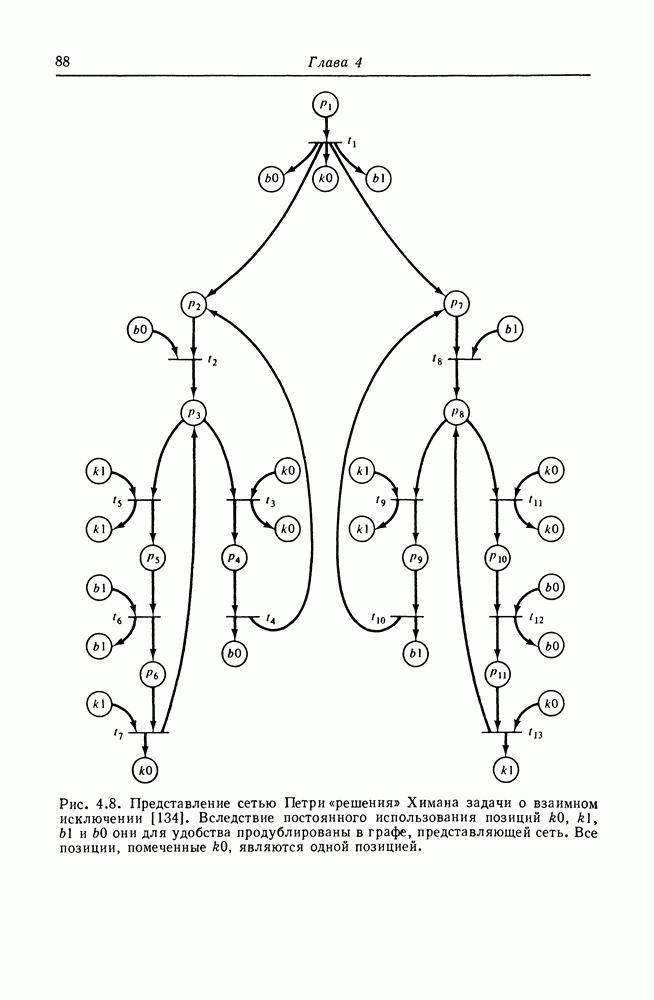
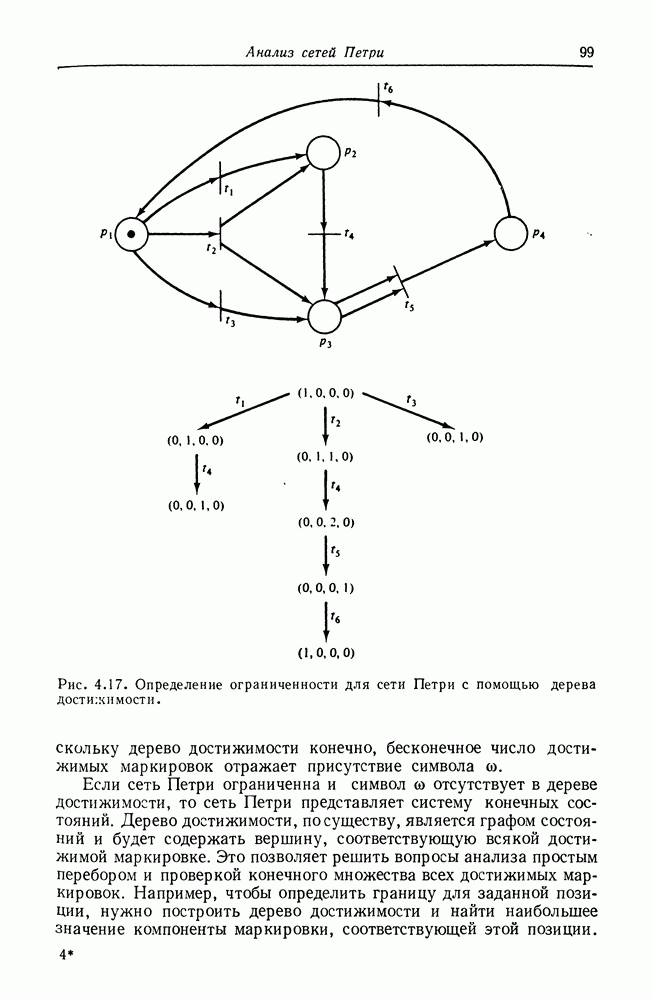
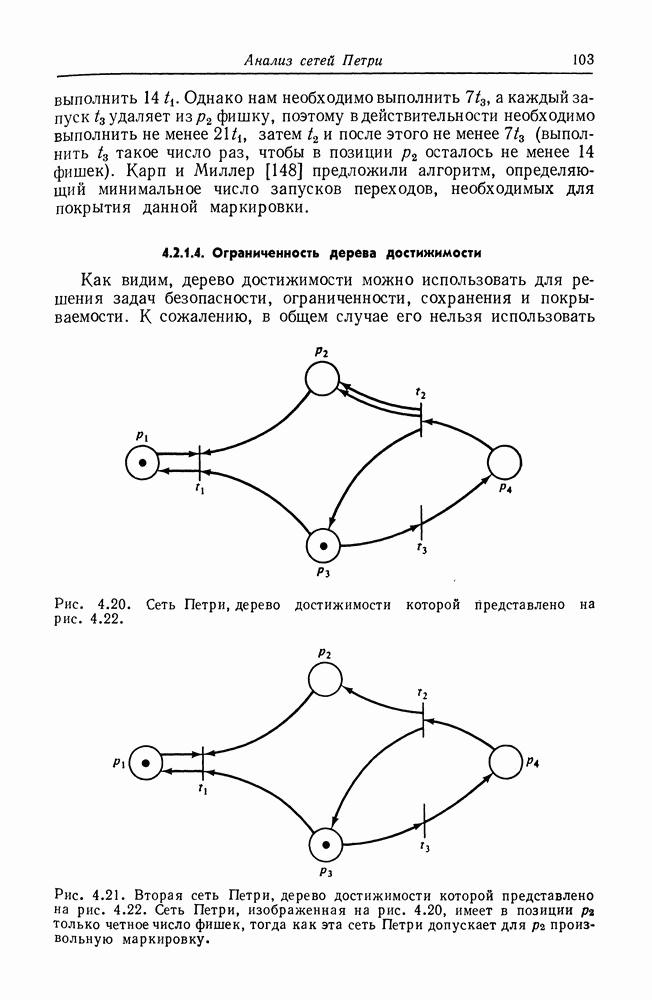
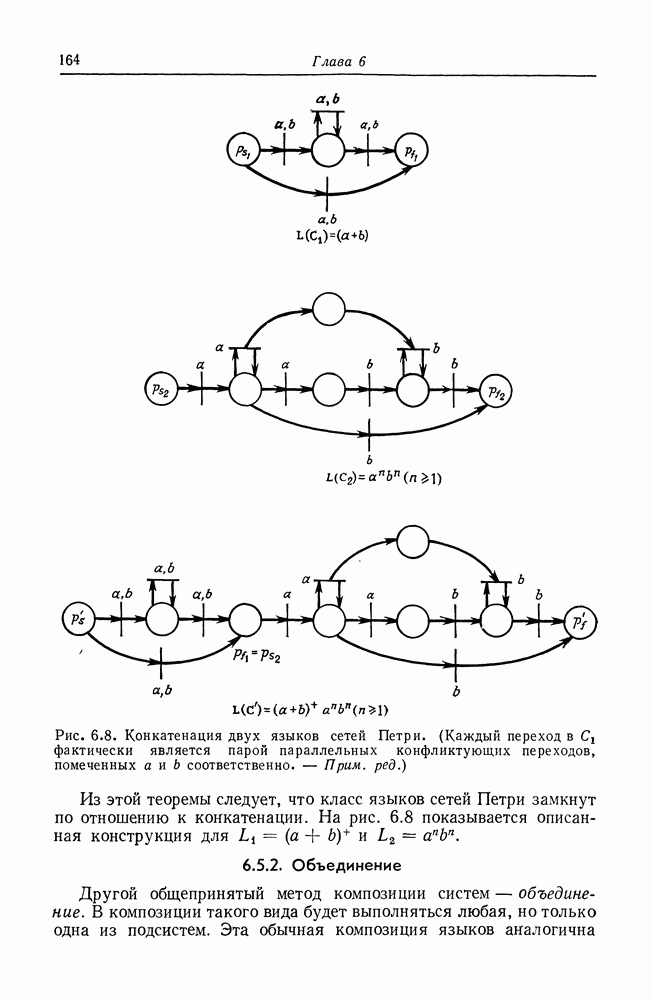
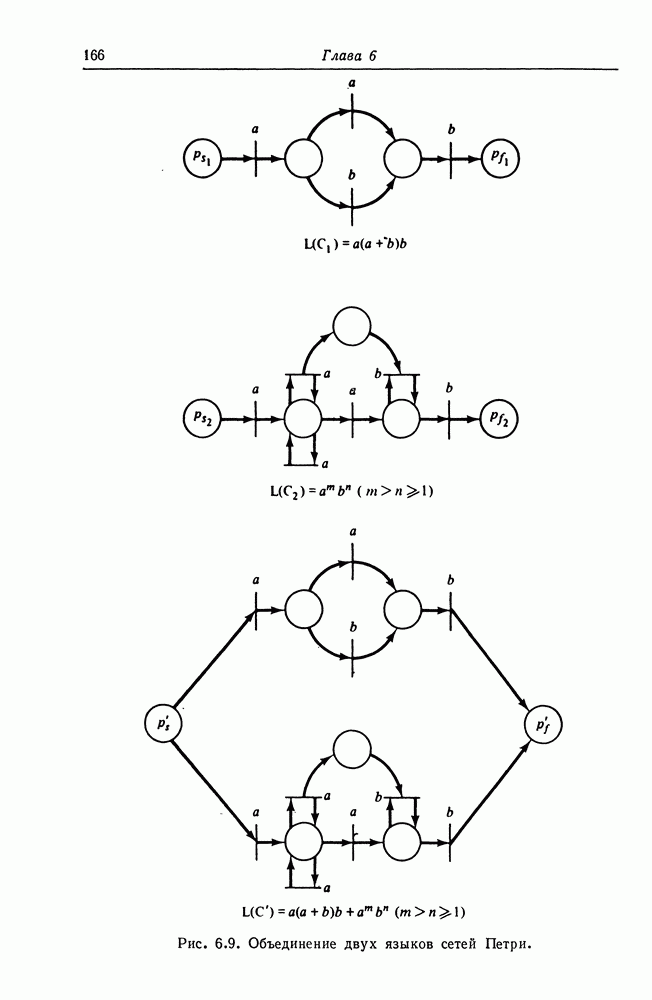
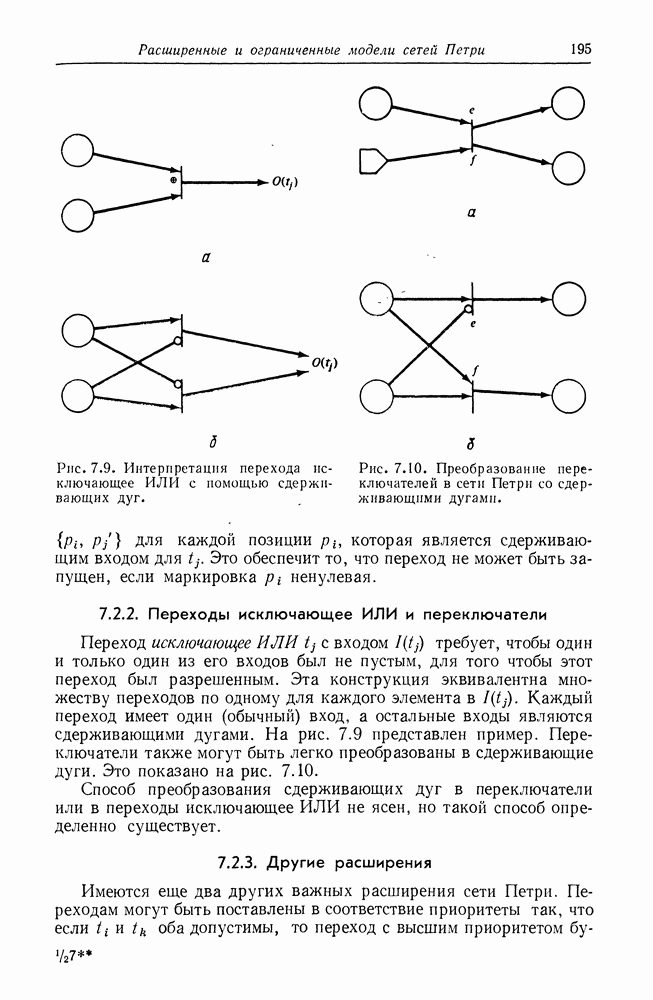
Рис. 8.3. Сеть Петри, эквивалентная графу вычислений, изображенному на рис. 8.2.
гарантирует то, что переход будет подготовленным только тогда, когда пороговое условие выполнено. Однако, когда переход запущен, он может удалить только  фишек, поэтому дуг направляются обратно от перехода
фишек, поэтому дуг направляются обратно от перехода  к позиции, представляющей дугу из
к позиции, представляющей дугу из  Кроме того,
Кроме того,  меток помещаются в позицию, представляющую дугу из
меток помещаются в позицию, представляющую дугу из  Начальная маркировка определяется значениями
Начальная маркировка определяется значениями 
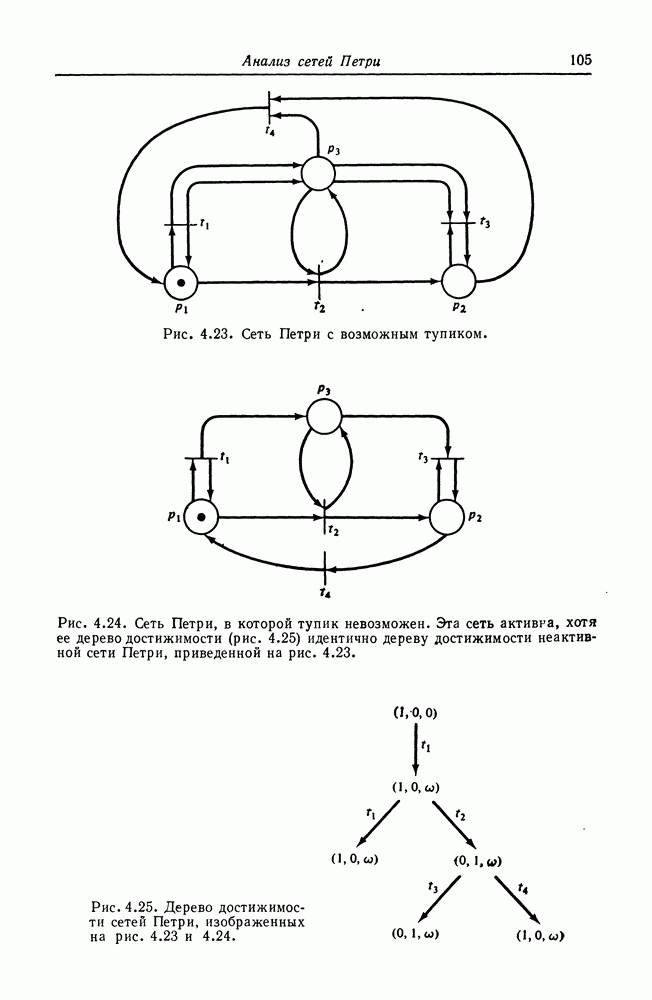
На рис. 8.3 изображена сеть Петри, построенная описанным выше способом для графа вычислений на рис. 8.2.
Легко показывается, что маркированные графы могут быть промоделированы графами вычислений, для которых  для всех узлов
для всех узлов  Однако графы вычислений являются более мощным средством, чем маркированные графы, благодаря возможности моделировать ситуации с
Однако графы вычислений являются более мощным средством, чем маркированные графы, благодаря возможности моделировать ситуации с 
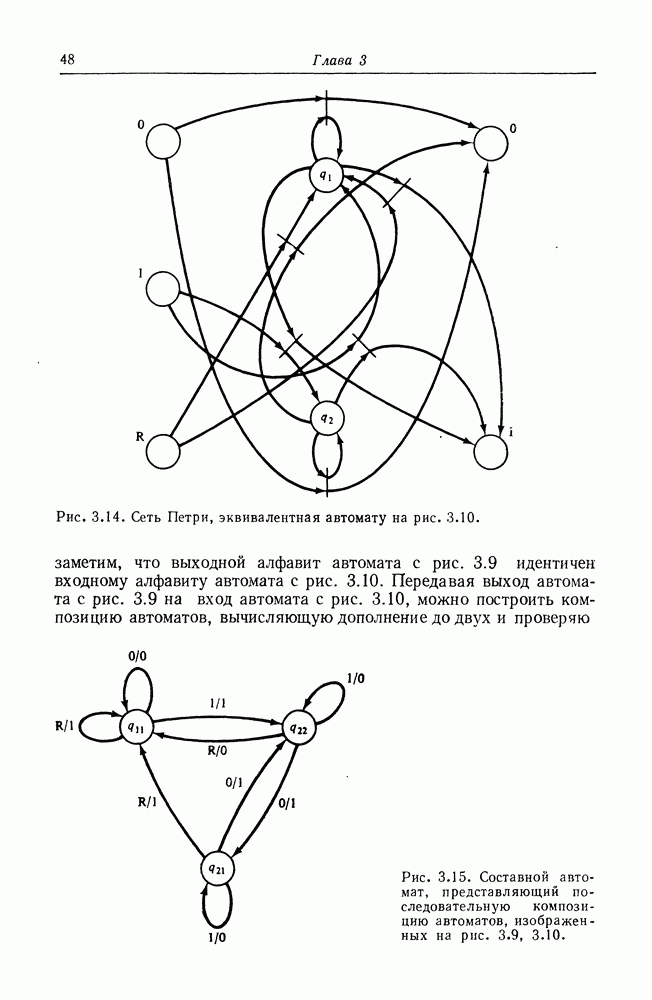
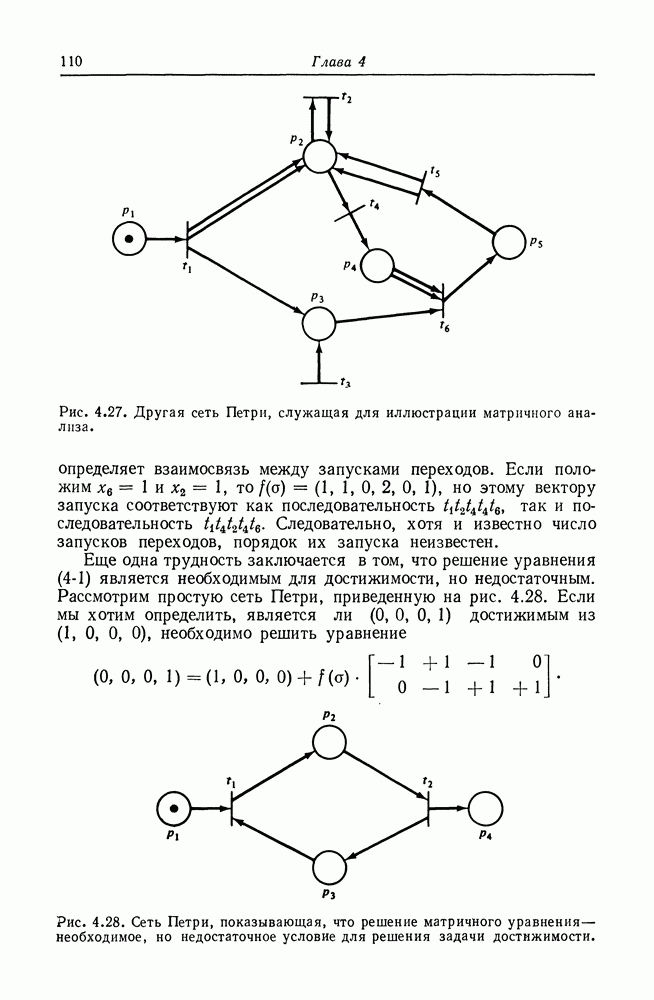
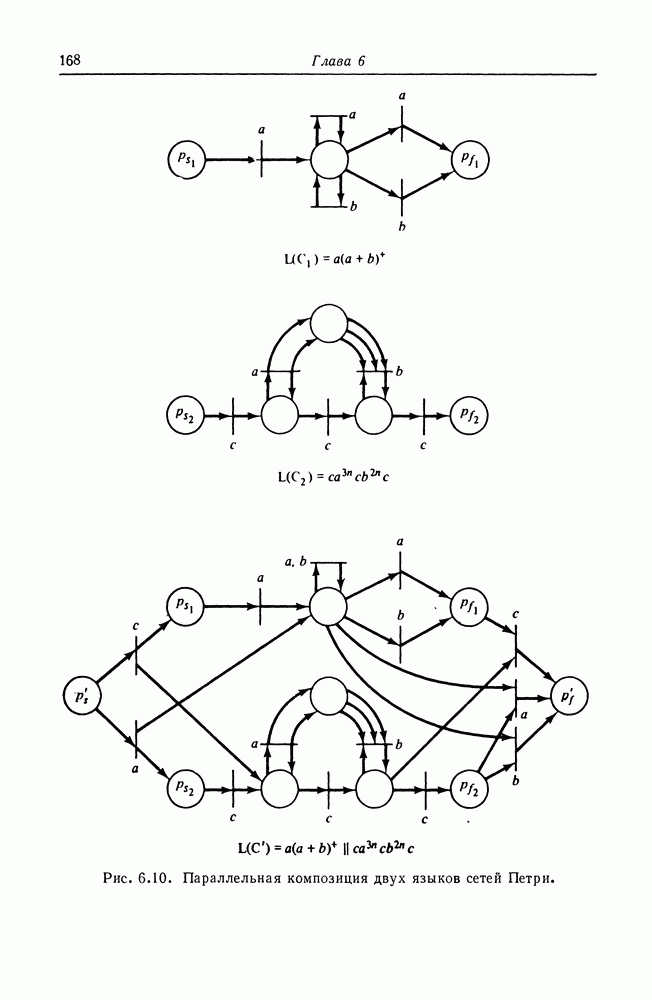
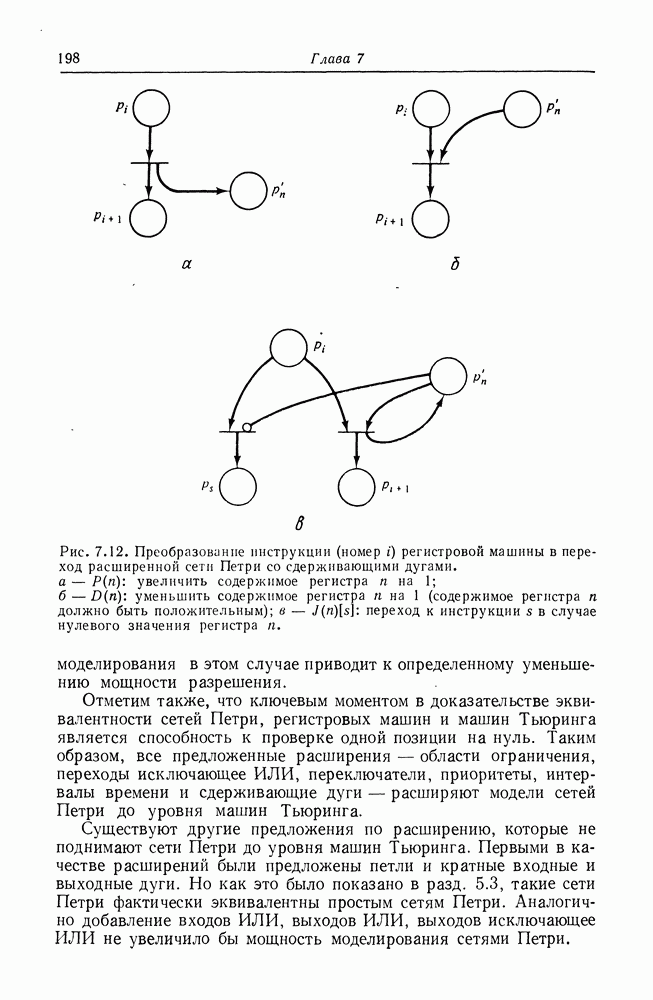
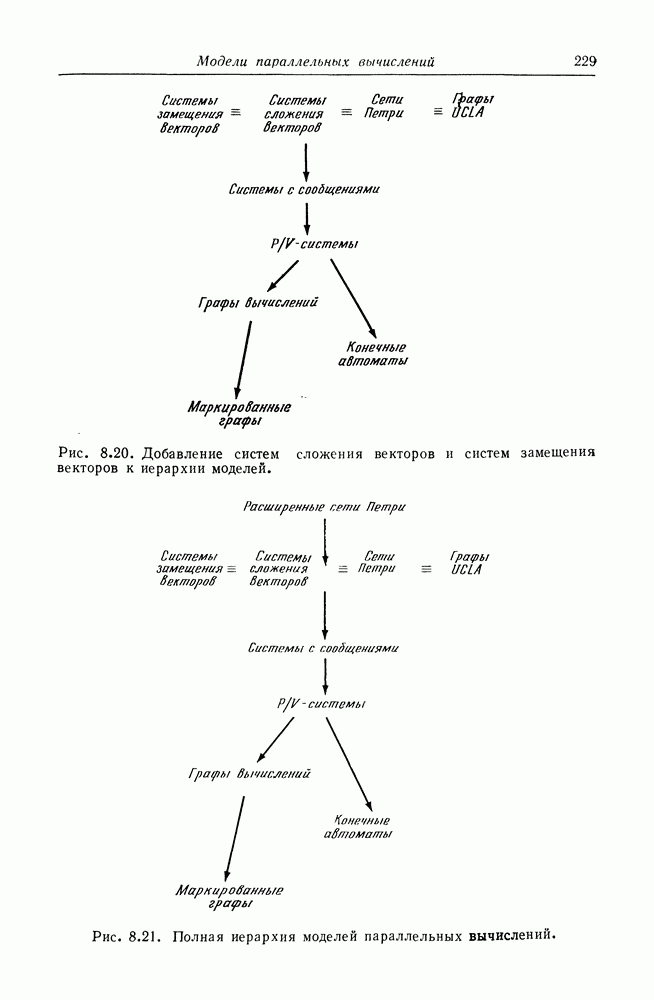
С другой стороны, графы вычислений и конечные автоматы не сопоставимы, как маркированные графы и конечные автоматы. Графы вычислений не могут моделировать принятие решений или условное выполнение — это ограничение справедливо и для маркированных графов. Таким образом, наша иерархия моделей принимает вид, показанный на рис. 8.4.
Карп и Миллер [147] подробно исследовали графы вычислений, особенно проблемы активности и безопасности. В действительности
их интересовало обеспечение и определение условий завершенности графа вычислений (т. е. условия неактивности). Так как дуги (позиции) представляют очереди данных, то исследования ограниченности, проводимые Карпом и Миллером, были направлены на определение максимальной длины очереди. Эти различия в обозначениях и целях, а также отличия в определении моделей между графами вычислений и маркированными графами послужили причиной того, что никто не попытался соотнести результаты и алгоритмы Карпа и Миллера [147] по графам вычислений с работой [54] по маркированным графам.

Рис. 8.4. Добавление графов вычислений к иерархии моделей.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ГЛАВА 1. ВВЕДЕНИЕ
- ГЛАВА 2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
- 2.1. Структура сети Петри
- 2.2. Графы сетей Петри
- 2.3. Маркировка сетей Петри
- 2.4. Правила выполнения сетей Петри
- 2.5. Пространство состояний сети Петри
- 2.6. Альтернативные формы определения сетей Петри
- ГЛАВА 3. СЕТИ ПЕТРИ ДЛЯ МОДЕЛИРОВАНИЯ
- 3.2. Одновременность и конфликт
- 3.3. Аппаратное обеспечение ЭВМ
- 3.4. Программное обеспечение ЭВМ
- 3.5. Другие системы
- ГЛАВА 4. АНАЛИЗ СЕТЕЙ ПЕТРИ
- 4.1. Задачи анализа сетей Петри
- 4.2. Методы анализа
- ГЛАВА 5. СЛОЖНОСТЬ И РАЗРЕШИМОСТЬ
- 5.1. Сводимость задач анализа
- 5.2. Задачи достижимости
- 5.3. Сети Петри с ограничениями
- 5.4. Активность и достижимость
- 5.5. Неразрешимые задачи
- 5.6. Сложность задачи достижимости
- ГЛАВА 6. ЯЗЫКИ СЕТЕЙ ПЕТРИ
- 6.2. Некоторые понятия теории формальных языков
- 6.3. Определения языков сетей Петри
- 6.4. Свойства языков сетей Петри
- 6.5. Свойства замкнутости
- 6.6. Языки сетей Петри и другие классы языков
- ГЛАВА 7. РАСШИРЕННЫЕ И ОГРАНИЧЕННЫЕ МОДЕЛИ СЕТЕЙ ПЕТРИ
- 7.1. Границы возможностей моделирования с помощью сетей Петри
- 7.2. Расширения
- 7.3. Расширенные сети Петри и регистровые машины
- 7.4. Подклассы сетей Петри
- ГЛАВА 8. МОДЕЛИ ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ
- 8.2. Маркированные графы
- 8.3. Графы вычислений
- 8.4. P/V-системы
- 8.5. Системы передачи сообщений
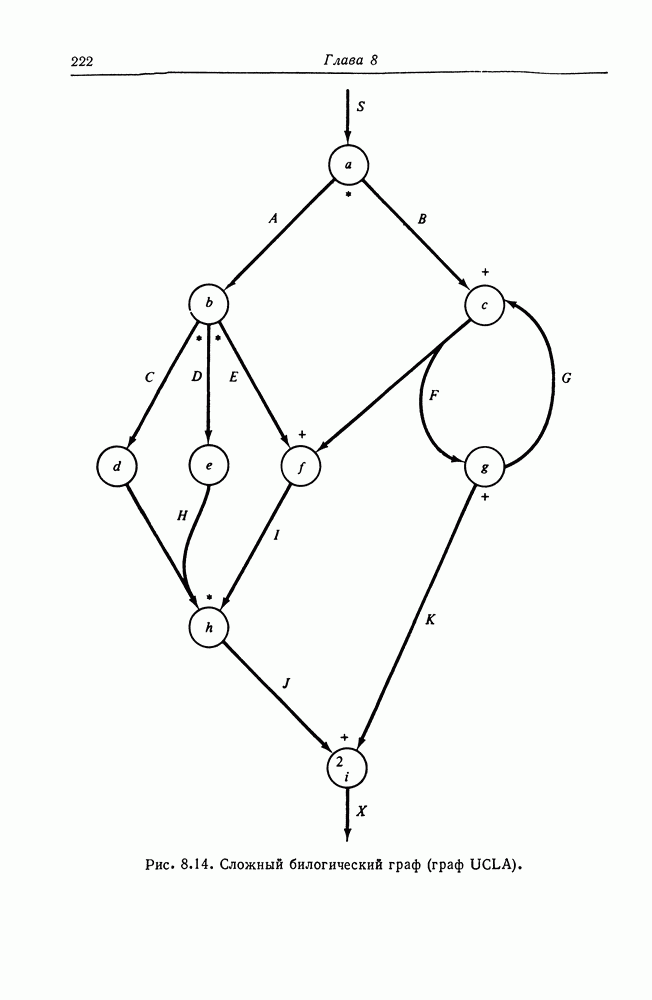
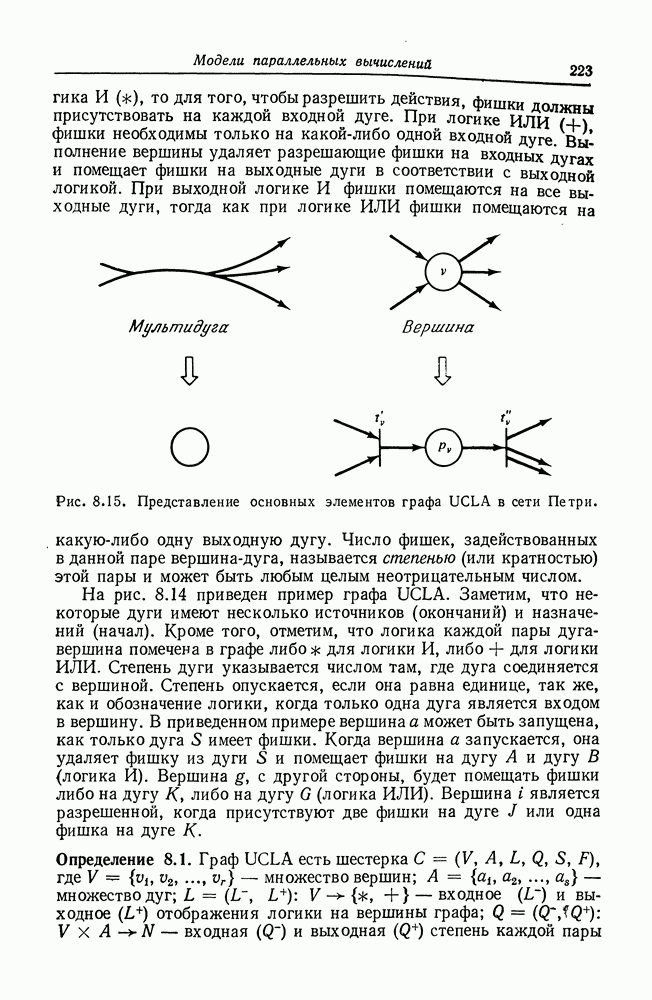
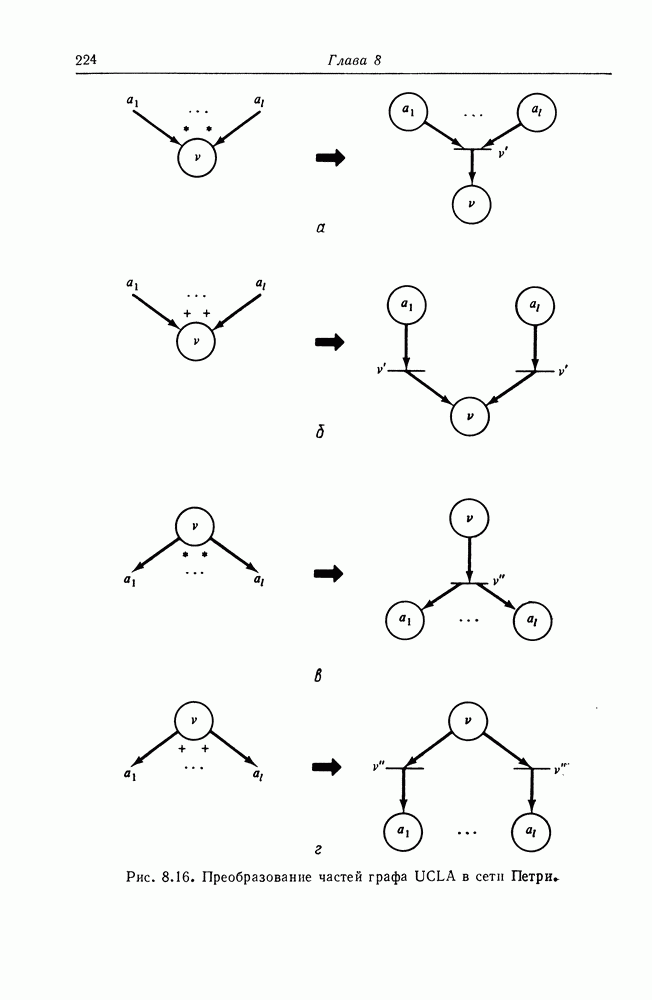
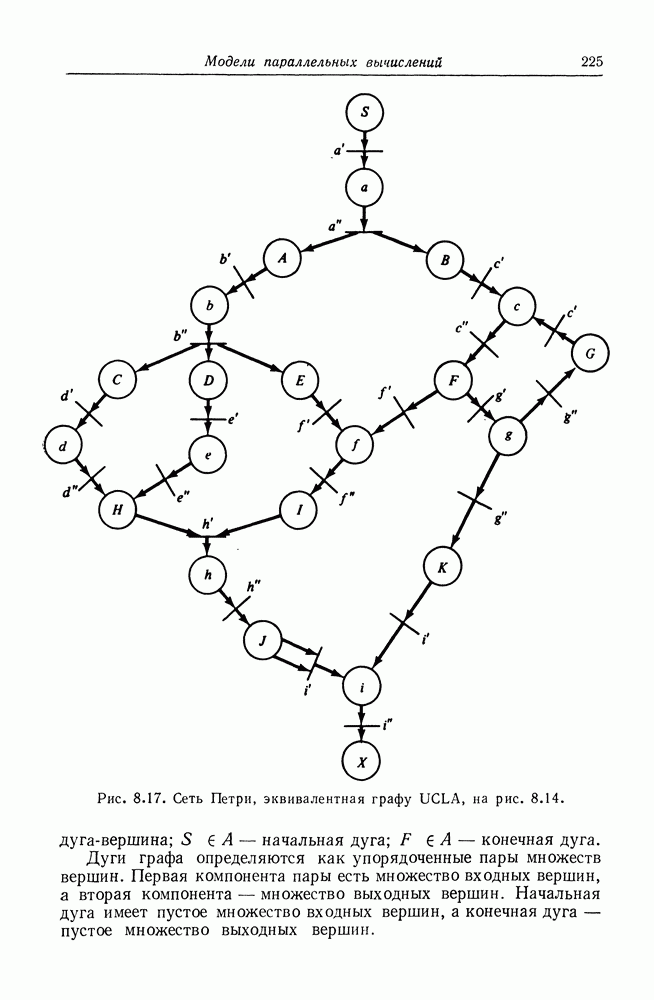
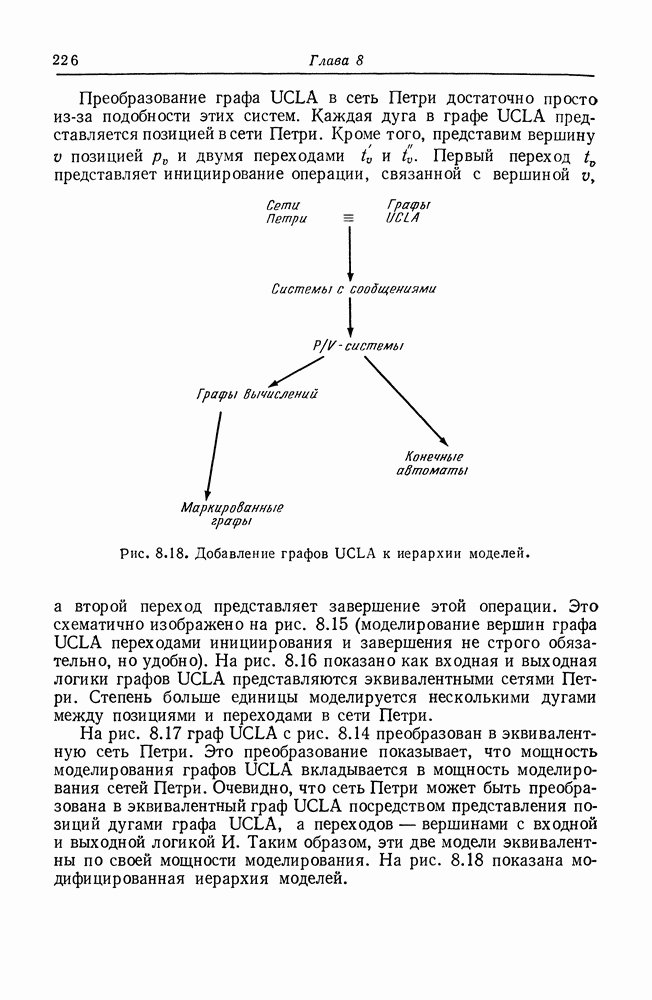
- 8.6. Графы UCLA
- 8.7. Системы замещения и сложения векторов
- 8.8. Расширенные модели сетей Петри
- ОБЗОР ТЕОРИИ КОМПЛЕКТОВ
- АННОТИРОВАННАЯ БИБЛИОГРАФИЯ