| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.5. Пространство состояний сети Петри
Состояние сети Петри определяется ее маркировкой. Запуск перехода изменяет состояние сети Петри посредством изменения маркировки сети. Пространство состояний сети Петри, обладающей  позициями, есть множество всех маркировок, т. е.
позициями, есть множество всех маркировок, т. е.  Изменение в состоянии, вызванное запуском перехода, определяется функцией изменения
Изменение в состоянии, вызванное запуском перехода, определяется функцией изменения  которую мы назовем функцией следующего состояния. Когда эта функция применяется к маркировке
которую мы назовем функцией следующего состояния. Когда эта функция применяется к маркировке  (состоянию) и переходу
(состоянию) и переходу  она образует новую маркировку (состояние), которая получается при запуске перехода
она образует новую маркировку (состояние), которая получается при запуске перехода  в маркировке
в маркировке  Так как
Так как  может быть запущен только в том случае, когда он разрешен, то функция
может быть запущен только в том случае, когда он разрешен, то функция  не определена, если
не определена, если  не разрешен в
не разрешен в
маркировке  Если же
Если же  разрешен, то
разрешен, то  где
где  есть маркировка, полученная в результате удаления фишек из входов
есть маркировка, полученная в результате удаления фишек из входов  и добавления фишек в выходы
и добавления фишек в выходы 
Определение 2.8. Функция <ледующего состояния  для сети Петри
для сети Петри  с маркировкой
с маркировкой  и переходом
и переходом  определена тогда и только тогда, когда
определена тогда и только тогда, когда  для всех
для всех  Если
Если  определена, то
определена, то  где
где  для всех
для всех 
Пусть дана сеть Петри  с начальной маркировкой
с начальной маркировкой  Эта сеть может быть выполнена последовательными запусками переходов. Запуск разрешенного перехода
Эта сеть может быть выполнена последовательными запусками переходов. Запуск разрешенного перехода  в начальной маркировке образует новую маркировку
в начальной маркировке образует новую маркировку  В этой новой маркировке можно запустить любой другой разрешенный переход, например
В этой новой маркировке можно запустить любой другой разрешенный переход, например  образующий новую маркировку
образующий новую маркировку  Этот процесс будет продолжаться до тех пор, пока в маркировке будет существовать хотя бы один разрешенный переход. Если же получена маркировка, в которой ни один переход не разрешен, то никакой переход не может быть запущен, функция следующего состояния не определена для всех переходов, и выполнение сети должно быть закончено.
Этот процесс будет продолжаться до тех пор, пока в маркировке будет существовать хотя бы один разрешенный переход. Если же получена маркировка, в которой ни один переход не разрешен, то никакой переход не может быть запущен, функция следующего состояния не определена для всех переходов, и выполнение сети должно быть закончено.
При выполнении сети Петри получаются две последовательности: последовательность маркировок  и последовательность переходов которые были запущены
и последовательность переходов которые были запущены  Эти две последовательности связаны следующим соотношением:
Эти две последовательности связаны следующим соотношением:  для
для  Имея последовательность переходов и
Имея последовательность переходов и  легко получить последовательность маркировок сети Петри, а имея последовательность маркировок, легко получить последовательность переходов, за исключением нескольких вырожденных случаев. Таким образом, обе эти последовательности представляют описание выполнения сети Петри.
легко получить последовательность маркировок сети Петри, а имея последовательность маркировок, легко получить последовательность переходов, за исключением нескольких вырожденных случаев. Таким образом, обе эти последовательности представляют описание выполнения сети Петри.
Пусть некоторый переход в маркировке  разрешен и, следовательно, может быть запущен. Результат запуска перехода в маркировке
разрешен и, следовательно, может быть запущен. Результат запуска перехода в маркировке  есть новая маркировка
есть новая маркировка  Говорят, что
Говорят, что  является непосредственно достижимой из маркировки
является непосредственно достижимой из маркировки  иными словами, состояние
иными словами, состояние  непосредственно получается из состояния
непосредственно получается из состояния 
Определение 2.9. Для сети Петри  с маркировкой
с маркировкой  маркировка
маркировка  называется непосредственно достижимой из
называется непосредственно достижимой из  если существует переход
если существует переход  такой, что
такой, что 
Можно распространить это понятие на определение множества достижимых маркировок данной маркированной сети Петри. Если  непосредственно достижима из
непосредственно достижима из  а
а  из
из  говорят,
говорят,  достижима из
достижима из  Определим множество достижимости
Определим множество достижимости 
сети Петри С с маркировкой  как множество всех маркировок, достижимых из
как множество всех маркировок, достижимых из  Маркировка
Маркировка  принадлежит
принадлежит  если существует какая-либо последовательность запусков переходов, изменяющих
если существует какая-либо последовательность запусков переходов, изменяющих  на
на  Отношение «достижимости» является рефлексивным, транзитивным замыканием отношения «непосредственной достижимости».
Отношение «достижимости» является рефлексивным, транзитивным замыканием отношения «непосредственной достижимости».
Определение 2.10. Множество достижимости  для сети Петри
для сети Петри  с маркировкой
с маркировкой  есть наименьшее множество маркировок, определенных следующим образом:
есть наименьшее множество маркировок, определенных следующим образом:

2. Если  для некоторого
для некоторого  то
то 
Для сети Петри, изображенной на рис. 2.20, и маркировки  ) непосредственно достижимыми являются две маркировки: (0, 1, 0) и (1, 0, 1). Из (0, 1, 0) нельзя достичь ни одной маркировки, так как ни один переход не разрешен. Из (1, 0, 1) можно получить (0, 1, 1) и (1, 0, 2). Пользуясь методами, разработанными в гл. 4, можно показать, что множество достижимости
) непосредственно достижимыми являются две маркировки: (0, 1, 0) и (1, 0, 1). Из (0, 1, 0) нельзя достичь ни одной маркировки, так как ни один переход не разрешен. Из (1, 0, 1) можно получить (0, 1, 1) и (1, 0, 2). Пользуясь методами, разработанными в гл. 4, можно показать, что множество достижимости  имеет следующий вид:
имеет следующий вид: 

Рис. 2.20. Маркированная сеть Петри.
Удобно распространить функцию следующего состояния на отображение маркировки и последовательности переходов в новую маркировку. Для последовательности переходов  и маркировки
и маркировки  маркировка
маркировка  есть результат запусков: сначала —
есть результат запусков: сначала —  затем —
затем —  до
до  (Такая операция, конечно, возможна только в том случае, если каждый переход к моменту его запуска разрешен.)
(Такая операция, конечно, возможна только в том случае, если каждый переход к моменту его запуска разрешен.)
Определение 2.11. Расширенная функция следующего состояния определяется для маркировки  и последовательности переходов
и последовательности переходов  следующими соотношениями:
следующими соотношениями: 
Обычно мы применяем эту расширенную функцию.
Рис. 2.21. (см. скан) Маркированная сеть Петри.
Упражнения
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ГЛАВА 1. ВВЕДЕНИЕ
- ГЛАВА 2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
- 2.1. Структура сети Петри
- 2.2. Графы сетей Петри
- 2.3. Маркировка сетей Петри
- 2.4. Правила выполнения сетей Петри
- 2.5. Пространство состояний сети Петри
- 2.6. Альтернативные формы определения сетей Петри
- ГЛАВА 3. СЕТИ ПЕТРИ ДЛЯ МОДЕЛИРОВАНИЯ
- 3.2. Одновременность и конфликт
- 3.3. Аппаратное обеспечение ЭВМ
- 3.4. Программное обеспечение ЭВМ
- 3.5. Другие системы
- ГЛАВА 4. АНАЛИЗ СЕТЕЙ ПЕТРИ
- 4.1. Задачи анализа сетей Петри
- 4.2. Методы анализа
- ГЛАВА 5. СЛОЖНОСТЬ И РАЗРЕШИМОСТЬ
- 5.1. Сводимость задач анализа
- 5.2. Задачи достижимости
- 5.3. Сети Петри с ограничениями
- 5.4. Активность и достижимость
- 5.5. Неразрешимые задачи
- 5.6. Сложность задачи достижимости
- ГЛАВА 6. ЯЗЫКИ СЕТЕЙ ПЕТРИ
- 6.2. Некоторые понятия теории формальных языков
- 6.3. Определения языков сетей Петри
- 6.4. Свойства языков сетей Петри
- 6.5. Свойства замкнутости
- 6.6. Языки сетей Петри и другие классы языков
- ГЛАВА 7. РАСШИРЕННЫЕ И ОГРАНИЧЕННЫЕ МОДЕЛИ СЕТЕЙ ПЕТРИ
- 7.1. Границы возможностей моделирования с помощью сетей Петри
- 7.2. Расширения
- 7.3. Расширенные сети Петри и регистровые машины
- 7.4. Подклассы сетей Петри
- ГЛАВА 8. МОДЕЛИ ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ
- 8.2. Маркированные графы
- 8.3. Графы вычислений
- 8.4. P/V-системы
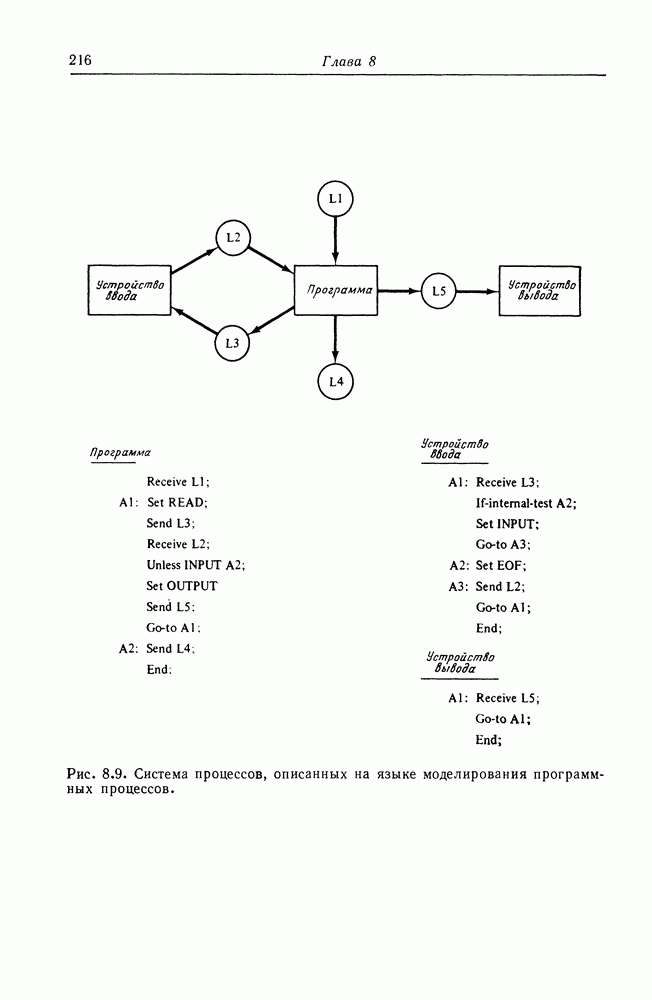
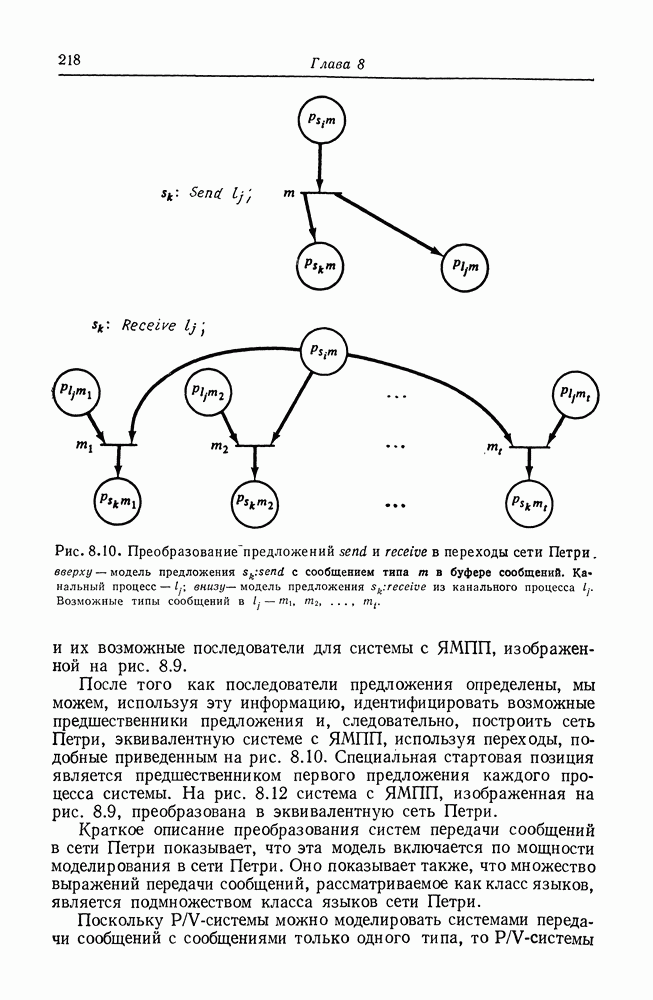
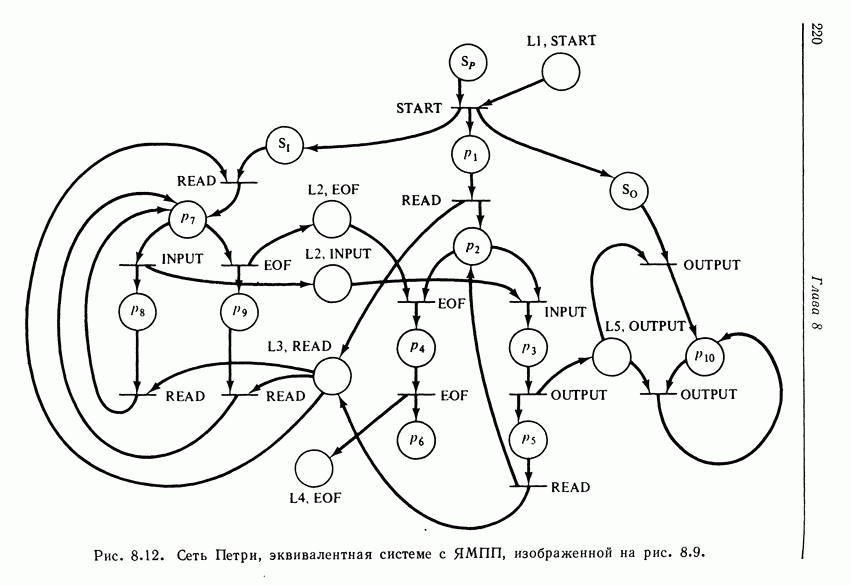
- 8.5. Системы передачи сообщений
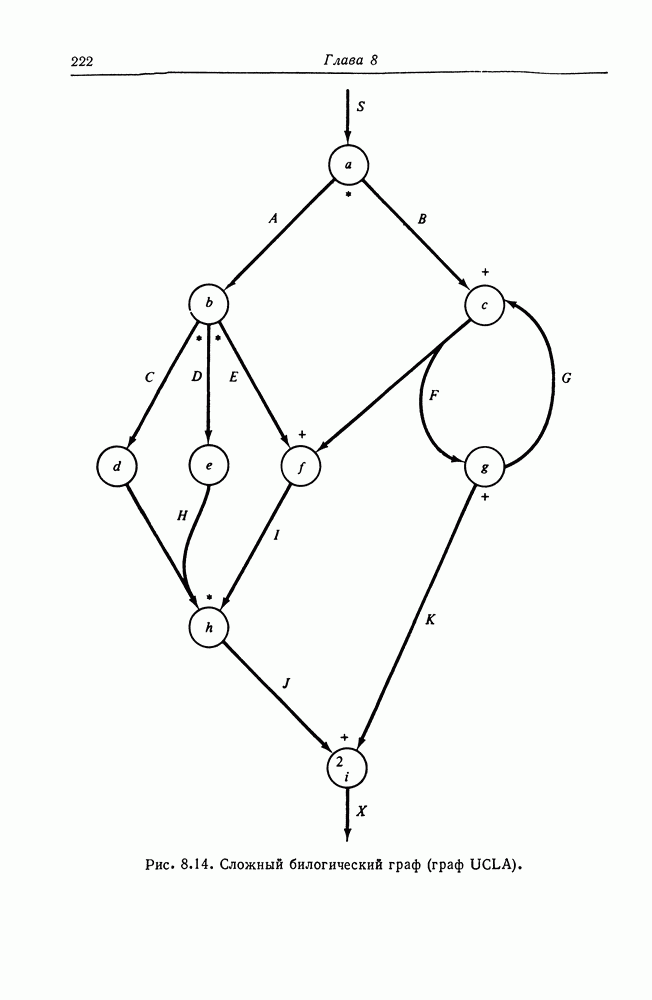
- 8.6. Графы UCLA
- 8.7. Системы замещения и сложения векторов
- 8.8. Расширенные модели сетей Петри
- ОБЗОР ТЕОРИИ КОМПЛЕКТОВ
- АННОТИРОВАННАЯ БИБЛИОГРАФИЯ