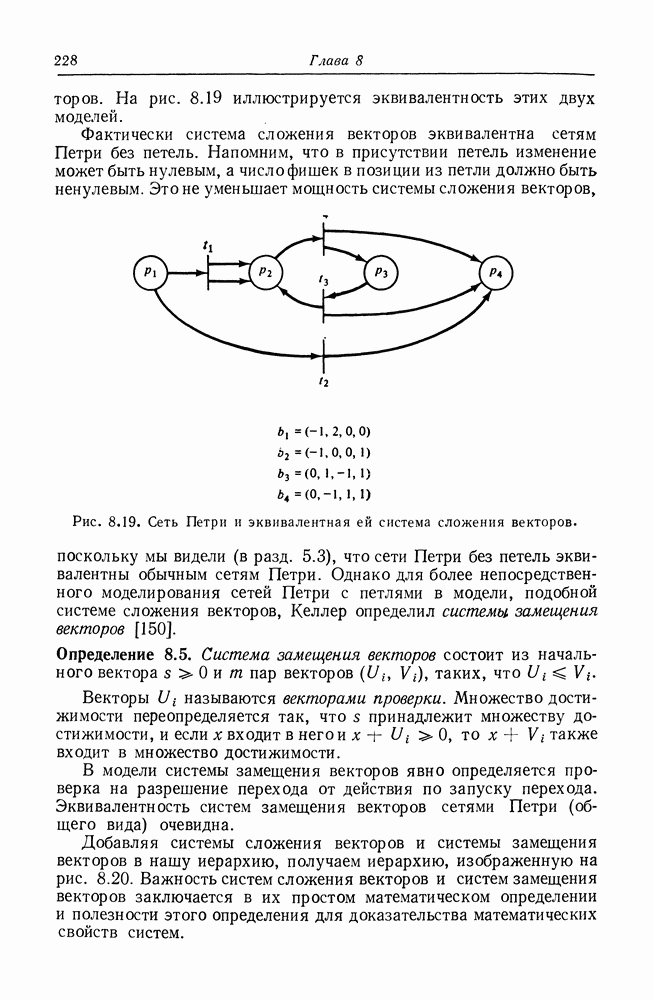
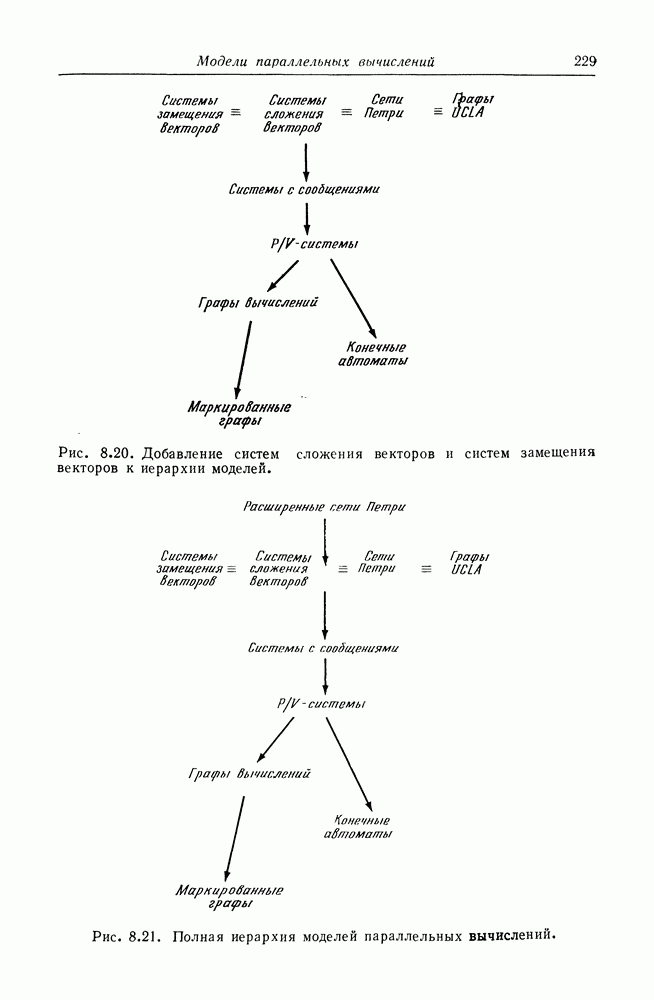
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.2. Методы анализа
Задачи, которые были представлены здесь, являются наиболее общими, тем не менее существует множество других задач, решение которых может потребоваться для сетей Петри. Можно ли разработать методы анализа сетей Петри для решения этих задач? Причем нас интересуют особенно те методы, которые легко реализовались бы на ЭВМ, что важно для осуществления автоматического анализа моделируемых систем.
В этом разделе мы представим два основных метода анализа сетей Петри, которые описывают механизмы решения некоторых из уже перечисленных задач. Первый метод анализа, используемый для сетей Петри, — это дерево достижимости, второй метод связан с матричными уравнениями. Обсудим каждый из них.
4.2.1. Дерево достижимости
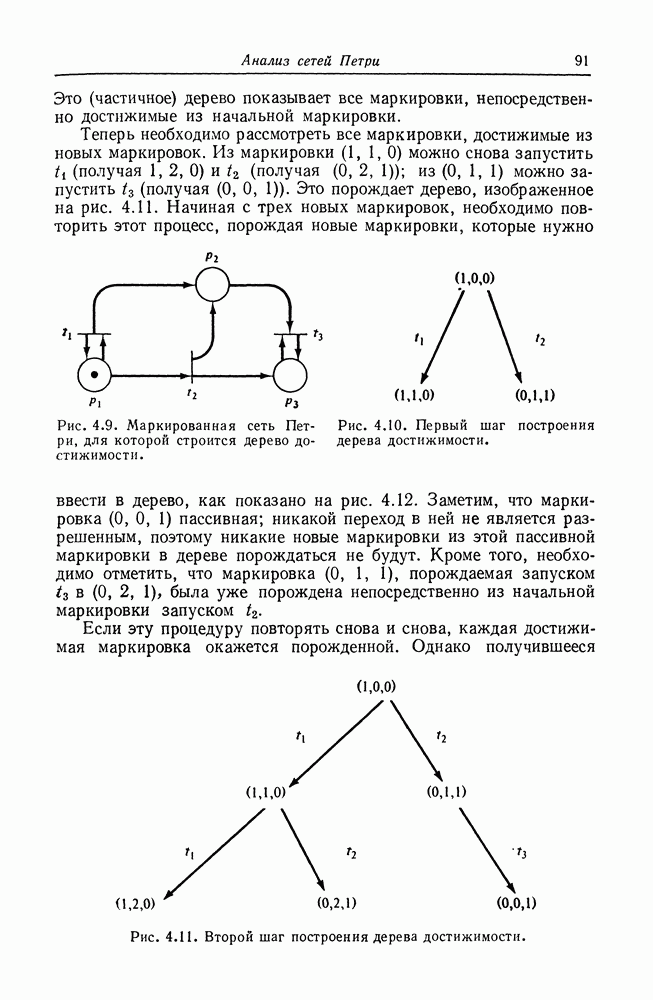
Дерево достижимости представляет множество достижимости сети Петри. Рассмотрим, например, маркированную сеть Петри на рис. 4.9. Начальная маркировка ее  этой начальной маркировке разрешены два перехода:
этой начальной маркировке разрешены два перехода:  Поскольку мы хотим рассмотреть все множества достижимости, определим новые вершины в дереве достижимости для (достижимых) маркировок, получающихся в результате запуска каждого из этих двух переходов. Дуга, помеченная запускаемым переходом, приводит из начальной маркировки к каждой из новых маркировок (рис. 4.10).
Поскольку мы хотим рассмотреть все множества достижимости, определим новые вершины в дереве достижимости для (достижимых) маркировок, получающихся в результате запуска каждого из этих двух переходов. Дуга, помеченная запускаемым переходом, приводит из начальной маркировки к каждой из новых маркировок (рис. 4.10).
Это (частичное) дерево показывает все маркировки, непосредственно достижимые из начальной маркировки.
Теперь необходимо рассмотреть все маркировки, достижимые из новых маркировок. Из маркировки (1, 1,0) можно снова запустить  (получая 1, 2, 0) и
(получая 1, 2, 0) и  (получая
(получая  из (0, 1, 1) можно запустить
из (0, 1, 1) можно запустить  (получая (0, 0, 1)). Это порождает дерево, изображенное на рис. 4.11.
(получая (0, 0, 1)). Это порождает дерево, изображенное на рис. 4.11.

Рис. 4.9. Маркированная сеть Петри, для которой строится дерево достижимости.

Рис. 4.10. Первый шаг построения дерева достижимости.
Начиная с трех новых маркировок, необходимо повторить этот процесс, порождая новые маркировки, которые нужно ввести в дерево, как показано на рис. 4.12. Заметим, что маркировка (0, 0, 1) пассивная; никакой переход в ней не является разрешенным, поэтому никакие новые маркировки из этой пассивной маркировки в дереве порождаться не будут. Кроме того, необходимо отметить, что маркировка (0, 1, 1), порождаемая запуском  в (0, 2, 1), была уже порождена непосредственно из начальной маркировки запуском
в (0, 2, 1), была уже порождена непосредственно из начальной маркировки запуском 
Если эту процедуру повторять снова и снова, каждая достижимая маркировка окажется порожденной. Однако получившееся

Рис. 4.11. Второй шаг построения дерева достижимости.

Рис. 4.12. Третий шаг построения дерева достижимости.
дерево достижимости может оказаться бесконечным. Будет порождена каждая маркировка из множества достижимости, поэтому для любой сети Петри с бесконечным множеством достижимости соответствующее дерево также должно быть бесконечным. Даже сеть Петри с конечным множеством достижимости может иметь бесконечное дерево (рис. 4.13). Дерево представляет все возможные последовательности запусков переходов. Всякий путь в дереве, начинающийся в корне, соответствует допустимой последовательности переходов. Для превращения дерева в полезный инструмент анализа необходимо найти средства ограничения его до конечного размера. (Заметим, что если какое-то представление бесконечного множества конечно, то бесконечное множество маркировок должно отображаться в такое представление. В общем случае это приведет к потере информации и, возможно, к тому, что некоторые свойства сетей Петри определить будет нельзя, но все зависит от того, как представление было получено.)
Приведение к конечному представлению осуществляется несколькими способами. Нам необходимо найти те средства, которые ограничивают введение новых маркировок (называемых граничными вершинами) на каждом шаге. Здесь могут помочь пассивные маркировки — маркировки, в которых нет разрешенных переходов. Эти пассивные маркировки называются терминальными вершинами. Другой класс маркировок — это маркировки, ранее
встречавшиеся в дереве. Такие дублирующие маркировки называются дублирующими вершинами; никакие последующие маркировки рассматривать нет нужды — все они будут порождены из места первого появления дублирующей маркировки в дереве.

Рис. 4.13. Простая сеть Петри с бесконечным деревом достижимости.
Таким образом, в дереве на рис. 4.12 маркировка (0, 1, 1), получившаяся в результате выполнения последовательности  не будет порождать какие-либо новые вершины в дереве, поскольку она ранее встречалась в дереве в результате выполнения последовательности
не будет порождать какие-либо новые вершины в дереве, поскольку она ранее встречалась в дереве в результате выполнения последовательности  из начальной маркировки.
из начальной маркировки.
Для сведения дерева достижимости к конечному представлению используется еще одно средство. Рассмотрим последовательность запусков переходов  начинающуюся в начальной маркировке
начинающуюся в начальной маркировке  и кончающуюся в маркировке
и кончающуюся в маркировке  Маркировка
Маркировка  совпадает с маркировкой
совпадает с маркировкой  за исключением того, что имеет некоторые «дополнительные» фишки в некоторых позициях, т. е.
за исключением того, что имеет некоторые «дополнительные» фишки в некоторых позициях, т. е. 
Теперь, поскольку на запуски переходов лишние фишки не влияют, последовательность  можно запустить снова, начиная в
можно запустить снова, начиная в  приходя к маркировке
приходя к маркировке  Так как действие последовательности переходов
Так как действие последовательности переходов  добавило
добавило  фишек к маркировке
фишек к маркировке  она добавит также
она добавит также  фишек и к маркировке
фишек и к маркировке  поэтому
поэтому  или
или  В общем можно запустить последовательность
В общем можно запустить последовательность  раз, получив в результате маркировку
раз, получив в результате маркировку  Следовательно, для тех позиций, которые увеличивают число фишек последовательностью
Следовательно, для тех позиций, которые увеличивают число фишек последовательностью  можно создать произвольно большое число фишек, просто повторяя последовательность
можно создать произвольно большое число фишек, просто повторяя последовательность  столько, сколько это нужно. В сети Петри на
столько, сколько это нужно. В сети Петри на
рис. 4.9, например, можно запустить переход  столько раз, сколько необходимо для того, чтобы получить произвольное число фишек в
столько раз, сколько необходимо для того, чтобы получить произвольное число фишек в 
Представим бесконечное число маркировок, получающихся из циклов такого типа, с помощью специального символа  который обозначает «бесконечность». Для любого постоянного а определим
который обозначает «бесконечность». Для любого постоянного а определим

Для построения дерева достижимости необходимы только эти операции над 
Теперь можно точно сформулировать действительный алгоритм построения дерева достижимости. Каждая вершина  дерева связывается с расширенной маркировкой
дерева связывается с расширенной маркировкой  в расширенной маркировке число фишек в позиции может быть либо неотрицательным целым, либо
в расширенной маркировке число фишек в позиции может быть либо неотрицательным целым, либо  Каждая вершина классифицируется или как граничная вершина, терминальная вершина, дублирующая вершина, или как внутренняя вершина. Граничными являются вершины, которые еще не обработаны алгоритмом; алгоритм превратит их в терминальные, дублирующие или внутренние вершины.
Каждая вершина классифицируется или как граничная вершина, терминальная вершина, дублирующая вершина, или как внутренняя вершина. Граничными являются вершины, которые еще не обработаны алгоритмом; алгоритм превратит их в терминальные, дублирующие или внутренние вершины.
Алгоритм начинает с определения начальной маркировки корнем дерева, т. е. граничной вершиной. До тех пор пока имеются граничные вершины, они обрабатываются алгоритмом.
Пусть  граничная вершина, которую необходимо обработать.
граничная вершина, которую необходимо обработать.
1. Если в дереве имеется другая вершина у, не являющаяся граничной, и с ней связана та же маркировка,  то вершина
то вершина  дублирующая.
дублирующая.
2. Если для маркировки  ни один из переходов не разрешен (т. е.
ни один из переходов не разрешен (т. е.  не определено для всех
не определено для всех  то
то  терминальная вершина.
терминальная вершина.
3. Для всякого перехода  разрешенного в
разрешенного в  (т. е.
(т. е.  определено), создать новую вершину
определено), создать новую вершину  дерева достижимости. Маркировка
дерева достижимости. Маркировка  связанная с этой вершиной, определяется для каждой позиции
связанная с этой вершиной, определяется для каждой позиции  следующим образом:
следующим образом:

б) Если на пути от корневой вершины к х существует вершина 
в) В противном случае 
Дуга, помеченная  направлена от вершины х к вершине
направлена от вершины х к вершине  Вершина х переопределяется как внутренняя, вершина
Вершина х переопределяется как внутренняя, вершина  становится граничной.
становится граничной.
Когда все вершины дерева — терминальные, дублирующие или внутренние, алгоритм останавливается.
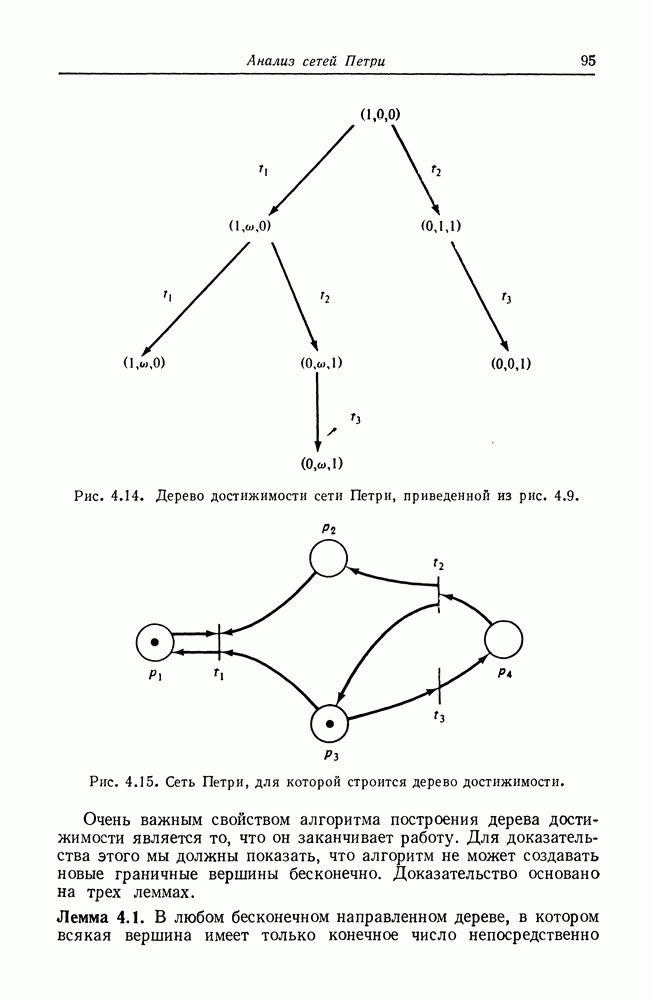
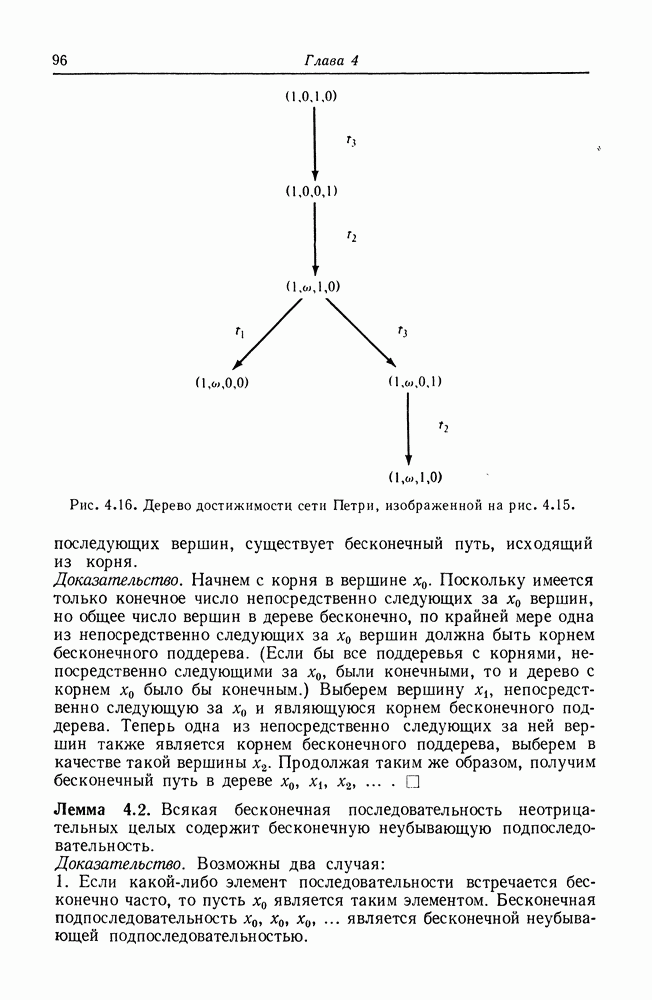
На рис. 4.14 представлено дерево достижимости для сети Петри на рис. 4.9. Дерево достижимости сети Петри с рис. 4.15 изображено на рис. 4.16.

Рис. 4.14. Дерево достижимости сети Петри, приведенной из рис. 4.9.

Рис. 4.15. Сеть Петри, для которой строится дерево достижимости.
Очень важным свойством алгоритма построения дерева достижимости является то, что он заканчивает работу. Для доказательства этого мы должны показать, что алгоритм не может создавать новые граничные вершины бесконечно. Доказательство основано на трех леммах.
Лемма 4.1. В любом бесконечном направленном дереве, в котором всякая вершина имеет только конечное число непосредственно

Рис. 4.16. Дерево достижимости сети Петри, изображенной на рис. 4.15.
последующих вершин, существует бесконечный путь, исходящий из корня.
Доказательство. Начнем с корня в вершине  Поскольку имеется только конечное число непосредственно следующих за
Поскольку имеется только конечное число непосредственно следующих за  вершин, но общее число вершин в дереве бесконечно, по крайней мере одна из непосредственно следующих за
вершин, но общее число вершин в дереве бесконечно, по крайней мере одна из непосредственно следующих за  вершин должна быть корнем бесконечного поддерева. (Если бы все поддеревья с корнями, непосредственно следующими за
вершин должна быть корнем бесконечного поддерева. (Если бы все поддеревья с корнями, непосредственно следующими за  были конечными, то и дерево с корнем
были конечными, то и дерево с корнем  было бы конечным.) Выберем вершину
было бы конечным.) Выберем вершину  непосредственно следующую за
непосредственно следующую за  и являющуюся корнем бесконечного поддерева. Теперь одна из непосредственно следующих за ней вершин также является корнем бесконечного поддерева, выберем в качестве такой вершины
и являющуюся корнем бесконечного поддерева. Теперь одна из непосредственно следующих за ней вершин также является корнем бесконечного поддерева, выберем в качестве такой вершины  Продолжая таким же образом, получим бесконечный путь в дереве
Продолжая таким же образом, получим бесконечный путь в дереве 
Лемма 4.2. Всякая бесконечная последовательность неотрицательных целых содержит бесконечную неубывающую подпоследовательность.
Доказательство. Возможны два случая:
1. Если какой-либо элемент последовательности встречается бесконечно часто, то пусть  является таким элементом. Бесконечная подпоследовательность
является таким элементом. Бесконечная подпоследовательность  является бесконечной неубывающей подпоследовательностью.
является бесконечной неубывающей подпоследовательностью.
2. Если никакой элемент не встречается бесконечно часто, тогда всякий элемент встречается только конечное число раз. Пусть  произвольный элемент последовательности. Существует самое большее
произвольный элемент последовательности. Существует самое большее  целых, неотрицательных и меньших, чем
целых, неотрицательных и меньших, чем  причем каждый из них присутствует в последовательности только конечное число раз. Следовательно, продвигаясь достаточно долго по последовательности, мы должны встретить элемент
причем каждый из них присутствует в последовательности только конечное число раз. Следовательно, продвигаясь достаточно долго по последовательности, мы должны встретить элемент  Аналогично должен существовать в последовательности
Аналогично должен существовать в последовательности  Это определяет бесконечную неубывающую подпоследовательность
Это определяет бесконечную неубывающую подпоследовательность 
В обоих случаях бесконечная неубывающая последовательность существует. 
Лемма 4.3. Всякая бесконечная последовательность  -векторов над расширенными неотрицательными целыми (неотрицательные целые плюс символ
-векторов над расширенными неотрицательными целыми (неотрицательные целые плюс символ  содержит бесконечную неубывающую подпоследовательность.
содержит бесконечную неубывающую подпоследовательность.
Доказательство. Доказываем индукцией по  где
где  размерность векторного пространства.
размерность векторного пространства.
1. Базовый случай  Если в последовательности имеется бесконечное число векторов
Если в последовательности имеется бесконечное число векторов  то они образуют бесконечную неубывающую последовательность. В противном случае бесконечная последовательность, образованная удалением конечного числа векторов
то они образуют бесконечную неубывающую последовательность. В противном случае бесконечная последовательность, образованная удалением конечного числа векторов  имеет по лемме 4.2 бесконечную неубывающую подпоследовательность.
имеет по лемме 4.2 бесконечную неубывающую подпоследовательность.
2. Индуктивное предположение. (Допустим, что лемма верна для  докажем ее справедливость для
докажем ее справедливость для  Рассмотрим первую координату. Если существует бесконечно много векторов, имеющих в качестве первой координаты
Рассмотрим первую координату. Если существует бесконечно много векторов, имеющих в качестве первой координаты  тогда выберем эту бесконечную подпоследовательность, которая не убывает (постоянна) по первой координате. Если только конечное число векторов имеют
тогда выберем эту бесконечную подпоследовательность, которая не убывает (постоянна) по первой координате. Если только конечное число векторов имеют  в качестве первой координаты, то рассмотрим бесконечную последовательность целых, являющихся значениями первых координат. По лемме 4.2 эта последовательность имеет бесконечную неубывающую подпоследовательность. Она определяет бесконечную подпоследовательность векторов, которые не убывают по своей пер в ой к оорди нате.
в качестве первой координаты, то рассмотрим бесконечную последовательность целых, являющихся значениями первых координат. По лемме 4.2 эта последовательность имеет бесконечную неубывающую подпоследовательность. Она определяет бесконечную подпоследовательность векторов, которые не убывают по своей пер в ой к оорди нате.
В любом случае мы имеем последовательность векторов, неубывающих по первой координате. Применим индуктивное предположение к последовательности  -векторов, которая получается в результате отбрасывания первой компоненты
-векторов, которая получается в результате отбрасывания первой компоненты  -векторов. Полученная таким образом бесконечная подпоследовательность является неубывающей по каждой координате.
-векторов. Полученная таким образом бесконечная подпоследовательность является неубывающей по каждой координате. 
Докажем следующую теорему.
Теорема 4.1. Дерево достижимости сети Петри конечно. Доказательство. Доказательство проводим от противного. Допустим, что существует бесконечное дерево достижимости. Тогда
по лемме 4.1 в нем имеется бесконечный путь  исходящий из корня
исходящий из корня  . (Число вершин, следующих за каждой вершиной в дереве, ограничено числом переходов
. (Число вершин, следующих за каждой вершиной в дереве, ограничено числом переходов  Тогда
Тогда  бесконечная последовательность
бесконечная последовательность  -векторов над
-векторов над  а по лемме 4.3 она имеет бесконечную неубывающую подпоследовательность
а по лемме 4.3 она имеет бесконечную неубывающую подпоследовательность  Но по построению мы не можем иметь
Но по построению мы не можем иметь  поскольку тогда одна из вершин была бы дублирующей и не имела следующих за собой вершин. Следовательно, мы имеем бесконечную строго убывающую последовательность
поскольку тогда одна из вершин была бы дублирующей и не имела следующих за собой вершин. Следовательно, мы имеем бесконечную строго убывающую последовательность  Но по построению, так как
Но по построению, так как  нам следовало бы заменить по крайней мере одну компоненту
нам следовало бы заменить по крайней мере одну компоненту  не являющуюся
не являющуюся  на
на  Таким образом,
Таким образом,  имеет по крайней мере одну компоненту, являющуюся
имеет по крайней мере одну компоненту, являющуюся  имеет по крайней мере две
имеет по крайней мере две  -компоненты, а
-компоненты, а  имеет по крайней мере
имеет по крайней мере  Поскольку маркировки n-мерные,
Поскольку маркировки n-мерные,  имеет во всех компонентах
имеет во всех компонентах  Но тогда
Но тогда  не может быть больше
не может быть больше  Пришли к противоречию, что доказывает, что наше допущение относительно существования бесконечного дерева достижимости неверно.
Пришли к противоречию, что доказывает, что наше допущение относительно существования бесконечного дерева достижимости неверно. 
Построение дерева достижимости было впервые описано Карпом и Миллером [148]. Используемый здесь вариант алгоритма был предложен Келлером [150]. Доказательство конечности, данное здесь, взято у Хэка [111], который принял за основу доказательство Карпа и Миллера [148].
Дерево достижимости — очень полезный инструмент анализа сетей Петри. В последующих разделах мы покажем, как его можно использовать для решения некоторых задач, представленных в разд. 4.1.
4.2.1.1. Безопасность и ограниченность
Сеть Петри безопасна, если число фишек в каждой позиции не может превысить 1; сеть Петри ограниченна, если существует такое целое  что число фишек в любой позиции не может превысить
что число фишек в любой позиции не может превысить  Оба этих свойства можно проверить с помощью дерева достижимости. Сеть Петри ограниченна тогда и только тогда, когда символ
Оба этих свойства можно проверить с помощью дерева достижимости. Сеть Петри ограниченна тогда и только тогда, когда символ  отсутствует в ее дереве достижимости. Присутствие символа
отсутствует в ее дереве достижимости. Присутствие символа  в дереве достижимости означает, что число фишек потенциально не ограничено; существует последовательность запусков переходов, которую можно повторить произвольное число раз, увеличивая количество фишек до произвольно большого числа. Таким образом, если имеется символ
в дереве достижимости означает, что число фишек потенциально не ограничено; существует последовательность запусков переходов, которую можно повторить произвольное число раз, увеличивая количество фишек до произвольно большого числа. Таким образом, если имеется символ  сеть неограниченна. Кроме того, положение символа
сеть неограниченна. Кроме того, положение символа  показывает, какие позиции неограниченны.
показывает, какие позиции неограниченны.
Обратное утверждение также является верным, если сеть Петри неограниченна, то число достижимых маркировок бесконечно.
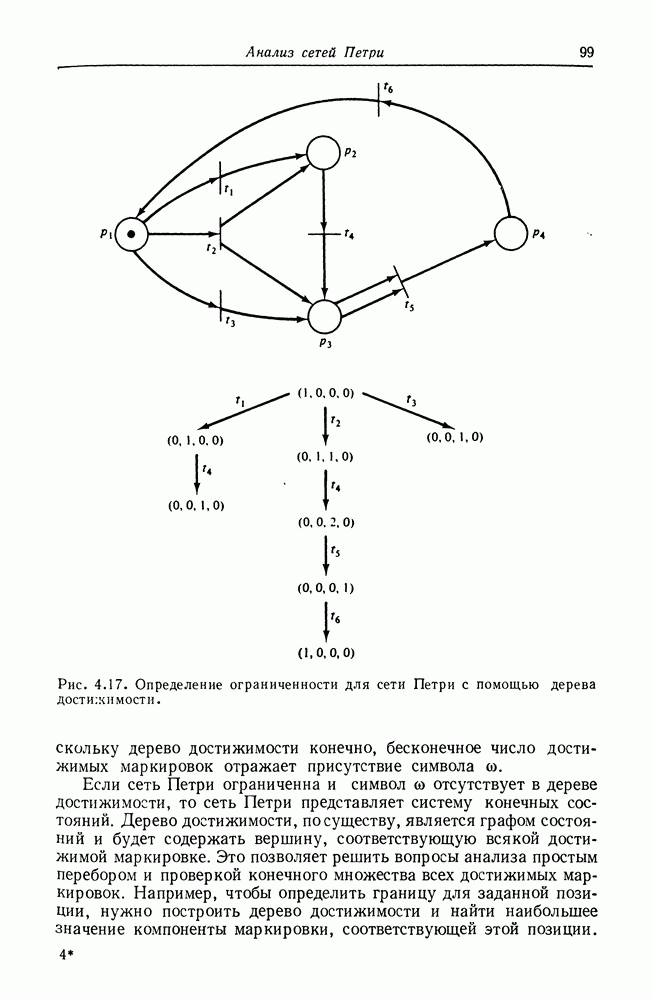
Рис. 4.17. (см. скан) Определение ограниченности для сети Петри с помощью дерева  мости.
мости.
Поскольку дерево достижимости конечно, бесконечное число достижимых маркировок отражает присутствие символа 
Если сеть Петри ограниченна и символ  отсутствует в дереве достижимости, то сеть Петри представляет систему конечных состояний. Дерево достижимости, по существу, является графом состояний и будет содержать вершину, соответствующую всякой достижимой маркировке. Это позволяет решить вопросы анализа простым перебором и проверкой конечного множества всех достижимых маркировок. Например, чтобы определить границу для заданной позиции, нужно построить дерево достижимости и найти наибольшее значение компоненты маркировки, соответствующей этой позиции.
отсутствует в дереве достижимости, то сеть Петри представляет систему конечных состояний. Дерево достижимости, по существу, является графом состояний и будет содержать вершину, соответствующую всякой достижимой маркировке. Это позволяет решить вопросы анализа простым перебором и проверкой конечного множества всех достижимых маркировок. Например, чтобы определить границу для заданной позиции, нужно построить дерево достижимости и найти наибольшее значение компоненты маркировки, соответствующей этой позиции.
Найденное значение является границей числа фишек для заданной позиции. Если граница для всех позиций равна I, сеть безопасна.
На рис. 4.17 демонстрируется использование дерева достижимости для определения ограниченности.
Отметим, что по дереву достижимости даже для сетей Петри, не являющихся ограниченными (вследствие неограниченности некоторой позиции), можно определить границы для тех позиций, которые являются ограниченными. Таким образом, дерево достижимости позволяет эффективно решить задачи анализа сетей Петри по определению ограниченности и безопасности для отдельных позиций и целых сетей.
4.2.1.2. Сохранение
Сеть Петри является сохраняющей, если она не теряет и не порождает фишки, а просто передвигает их. Поскольку две фишки можно закодировать как одну фишку, которая позже вызовет запуск перехода, создающего две фишки, значение фишки в каждой позиции определяет вектор взвешивания, веса неотрицательны. Сеть Петри является сохраняющей по отношению к вектору взвешивания, если взвешенная сумма фишек постоянна для всех достижимых маркировок.
Свойство сохранения эффективно проверяется с помощью дерева достижимости. Так как дерево достижимости конечно, для каждой маркировки можно вычислить взвешенную сумму. Если сумма одинакова для каждой достижимой маркировки, сеть — сохраняющая по отношению к данному весу. Если суммы не равны, сеть — несохраняющая.
При оценке сохранения необходимо быть внимательным с символом  Если маркировка имеет
Если маркировка имеет  в качестве маркировки позиции
в качестве маркировки позиции  тогда для того, чтобы сеть была сохраняющей, вес этой позиции должен быть равным 0. Напомним, что символ
тогда для того, чтобы сеть была сохраняющей, вес этой позиции должен быть равным 0. Напомним, что символ  представляет бесконечное множество значений. Так как все веса неотрицательны, вес должен равняться либо нулю (тем самым означая, что число фишек в данной позиции не важно), либо быть положительным. Если вес положителен, то сумма будет разной для двух маркировок, различающихся в своей
представляет бесконечное множество значений. Так как все веса неотрицательны, вес должен равняться либо нулю (тем самым означая, что число фишек в данной позиции не важно), либо быть положительным. Если вес положителен, то сумма будет разной для двух маркировок, различающихся в своей  -компоненте. Следовательно, если какая-либо маркировка с ненулевым весом равна
-компоненте. Следовательно, если какая-либо маркировка с ненулевым весом равна  сеть — несохраняющая.
сеть — несохраняющая.
Эти рассуждения относятся к сохранению по отношению к определенному взвешиванию. Сеть Петри является сохраняющей, если она сохраняющая по отношению к некоторому вектору  Дерево достижимости можно использовать для определения того, является сеть сохраняющей или нет, путем нахождения вектора весов
Дерево достижимости можно использовать для определения того, является сеть сохраняющей или нет, путем нахождения вектора весов  (если он существует). Заметим прежде всего, что для того,
(если он существует). Заметим прежде всего, что для того,
чтобы сеть Петри была сохраняющей по отношению к положительному вектору весов, она должна быть ограниченной. Как было указано выше, неограниченная позиция должна иметь нулевой вес, что недопустимо в сети с положительным вектором весов. (Если мы хотим допустить нулевые компоненты, нужно просто установить веса всех неограниченных позиций равными нулю и рассматривать после этого только оставшиеся компоненты.) Теперь, если сеть сохраняющая, существуют взвешенная сумма, обозначим ее 5, и вектор весов  Для каждой маркировки
Для каждой маркировки  дерева достижимости имеем
дерева достижимости имеем

Это равенство определяет для  вершин дерева достижимости совокупность из
вершин дерева достижимости совокупность из  линейных уравнений с
линейных уравнений с  неизвестными. Добавим к ним ограничения:
неизвестными. Добавим к ним ограничения:  в результате чего определим ограничения для вектора весов.
в результате чего определим ограничения для вектора весов.
Решение этой системы линейных уравнений — хорошо известная задача, имеющая множество алгоритмов решения. Можно рассматривать ее как задачу линейного программирования или просто как систему линейных уравнений. В любом случае, если решение существует, оно будет вычислено. (Решения, получаемые этими методами, будут, как правило, рациональными, не целыми, но веса можно умножить на общее кратное для получения целого решения.)
Если ограничения, накладываемые на веса, являются чрезмерно жесткими и, следовательно, вектора взвешиваний не существует, это будет определено. В любом случае можно определить, является или нет сеть Петри сохраняющей, и если это так, получить вектор весов.
4.2.1.3. Покрываемость
Последняя задача, которую можно решить с помощью дерева достижимости, — задача покрываемости. В задаче покрываемости мы хотим для данной маркировки  определить, достижима ли маркировка
определить, достижима ли маркировка  Данная задача решается проверкой дерева достижимости. Строим для начальной маркировки
Данная задача решается проверкой дерева достижимости. Строим для начальной маркировки  дерево достижимости. Затем ищем любую вершину
дерево достижимости. Затем ищем любую вершину  Если такой вершины не существует, маркировка
Если такой вершины не существует, маркировка  не покрывается никакой достижимой маркировкой; если она найдена,
не покрывается никакой достижимой маркировкой; если она найдена,  дает достижимую маркировку, покрывающую
дает достижимую маркировку, покрывающую 
Путь от корня к покрывающей маркировке определяет последовательность переходов, которые приводят из начальной маркировки к покрывающей маркировке, а маркировка, связанная с этой вершиной, определяет покрывающую маркировку. Символ  вновь должен рассматриваться как обозначение бесконечного множества значений. Если компонента покрывающей маркировки —
вновь должен рассматриваться как обозначение бесконечного множества значений. Если компонента покрывающей маркировки —  то в пути от корня к покрывающей маркировке имеется «цикл». Для
то в пути от корня к покрывающей маркировке имеется «цикл». Для
увеличения соответствующей компоненты с тем, чтобы она была не меньше, чем в данной маркировке, необходимо достаточное число раз повторить этот цикл.

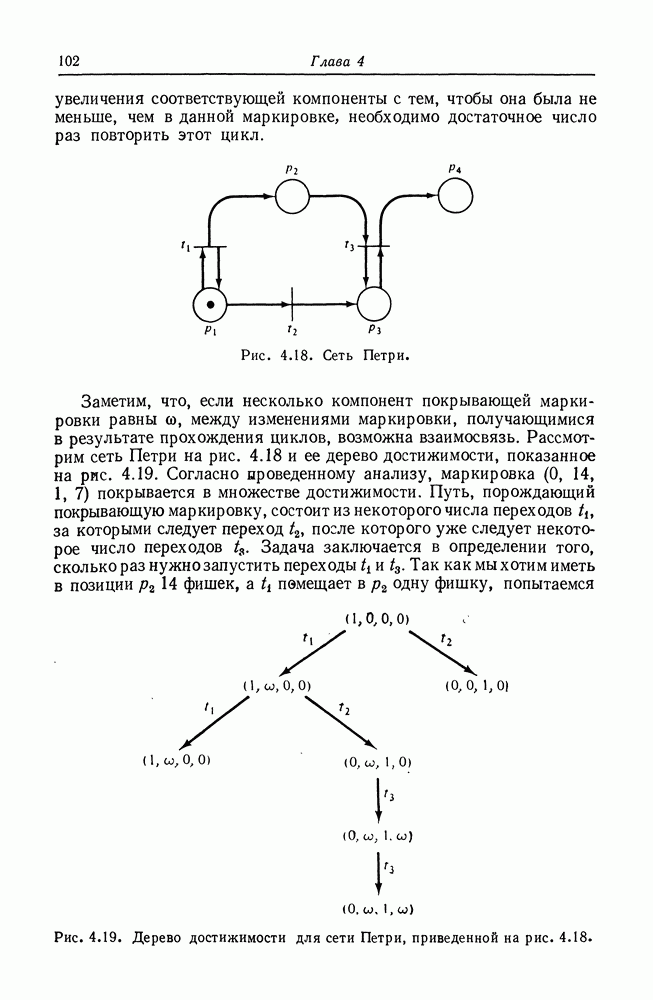
Рис. 4.18. Сеть Петри.
Заметим, что, если несколько компонент покрывающей маркировки равны  между изменениями маркировки, получающимися в результате прохождения циклов, возможна взаимосвязь. Рассмотрим сеть Петри на рис. 4.18 и ее дерево достижимости, показанное на рис. 4.19. Согласно проведенному анализу, маркировка (0, 14,
между изменениями маркировки, получающимися в результате прохождения циклов, возможна взаимосвязь. Рассмотрим сеть Петри на рис. 4.18 и ее дерево достижимости, показанное на рис. 4.19. Согласно проведенному анализу, маркировка (0, 14,
1, 7) покрывается в множестве достижимости. Путь, порождающий покрывающую маркировку, состоит из некоторого числа переходов  за которыми следует переход
за которыми следует переход  после которого уже следует некоторое число переходов
после которого уже следует некоторое число переходов  Задача заключается в определении того, сколько раз нужно запустить переходы
Задача заключается в определении того, сколько раз нужно запустить переходы  Так как мы хотим иметь в позиции
Так как мы хотим иметь в позиции  фишек,
фишек,  вмещает в
вмещает в  одну фишку, попытаемся
одну фишку, попытаемся

Рис. 4.19. Дерево достижимости для сети Петри, приведенной на рис. 4.18.
выполнить  Однако нам необходимо выполнить 7/3, а каждый запуск
Однако нам необходимо выполнить 7/3, а каждый запуск  удаляет из
удаляет из  фишку, поэтому в действительности необходимо выполнить не менее
фишку, поэтому в действительности необходимо выполнить не менее  затем
затем  и после этого не менее 7/3 (выполнить 4 такое число раз, чтобы в позиции
и после этого не менее 7/3 (выполнить 4 такое число раз, чтобы в позиции  осталось не менее 14 фишек). Карп и Миллер [148] предложили алгоритм, определяющий минимальное число запусков переходов, необходимых для покрытия данной маркировки.
осталось не менее 14 фишек). Карп и Миллер [148] предложили алгоритм, определяющий минимальное число запусков переходов, необходимых для покрытия данной маркировки.
4.2.1.4. Ограниченность дерева достижимости
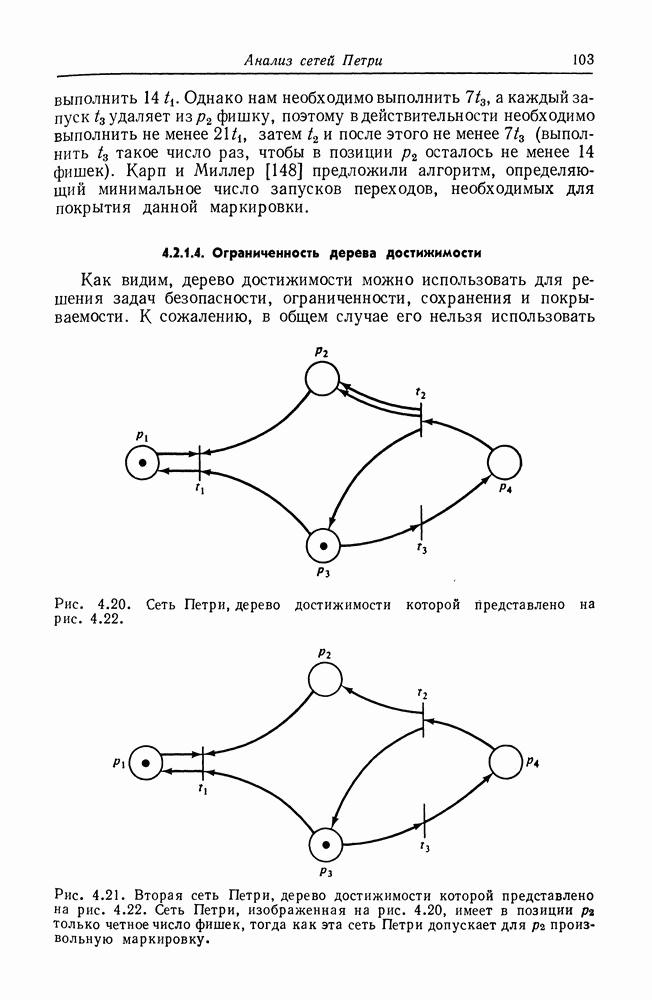
Как видим, дерево достижимости можно использовать для решения задач безопасности, ограниченности, сохранения и покрываемости. К сожалению, в общем случае его нельзя использовать

Рис. 4.20. Сеть Петри, дерево достижимости которой представлено на рис. 4.22.

Рис. 4.21. Вторая сеть Петри, дерево достижимости которой представлено на рис. 4.22. Сеть Петри, изображенная на рис. 4.20, имеет в позиции  только четное число фишек, тогда как эта сеть Петри допускает для
только четное число фишек, тогда как эта сеть Петри допускает для  произвольную маркировку.
произвольную маркировку.
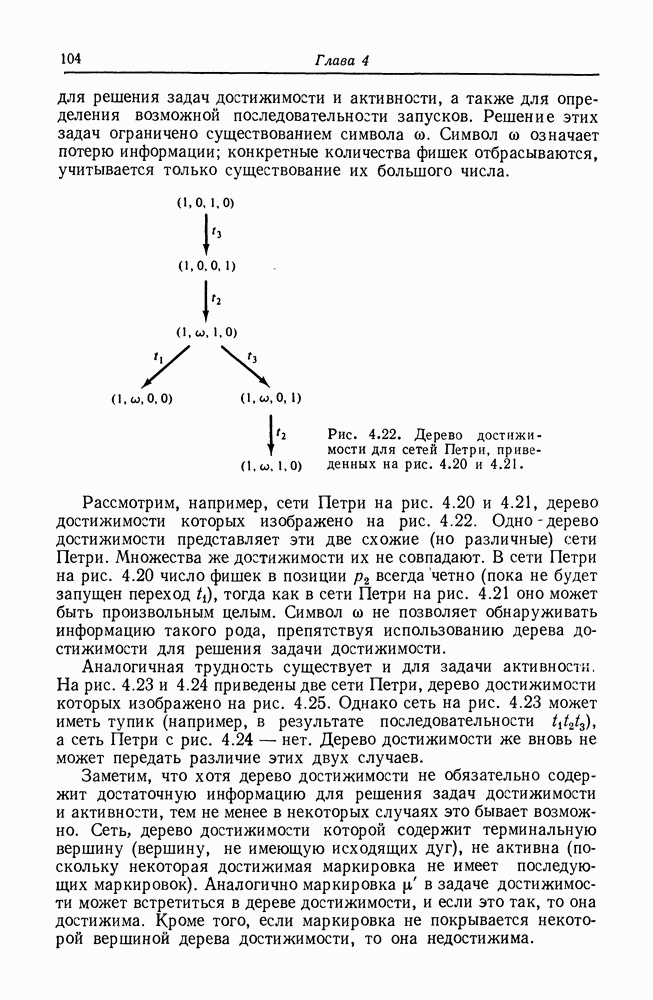
для решения задач достижимости и активности, а также для определения возможной последовательности запусков. Решение этих задач ограничено существованием символа  Символ
Символ  означает потерю информации; конкретные количества фишек отбрасываются, учитывается только существование их большого числа.
означает потерю информации; конкретные количества фишек отбрасываются, учитывается только существование их большого числа.

Рис. 4.22. Дерево достижимости для сетей Петри, приведенных на рис. 4.20 и 4.21.
Рассмотрим, например, сети Петри на рис. 4.20 и 4.21, дерево достижимости которых изображено на рис. 4.22. Одно дерево достижимости представляет эти две схожие (но различные) сети Петри. Множества же достижимости их не совпадают. В сети Петри на рис. 4.20 число фишек в позиции  всегда четно (пока не будет запущен переход
всегда четно (пока не будет запущен переход  тогда как в сети Петри на рис. 4.21 оно может быть произвольным целым. Символ
тогда как в сети Петри на рис. 4.21 оно может быть произвольным целым. Символ  не позволяет обнаруживать информацию такого рода, препятствуя использованию дерева достижимости для решения задачи достижимости.
не позволяет обнаруживать информацию такого рода, препятствуя использованию дерева достижимости для решения задачи достижимости.
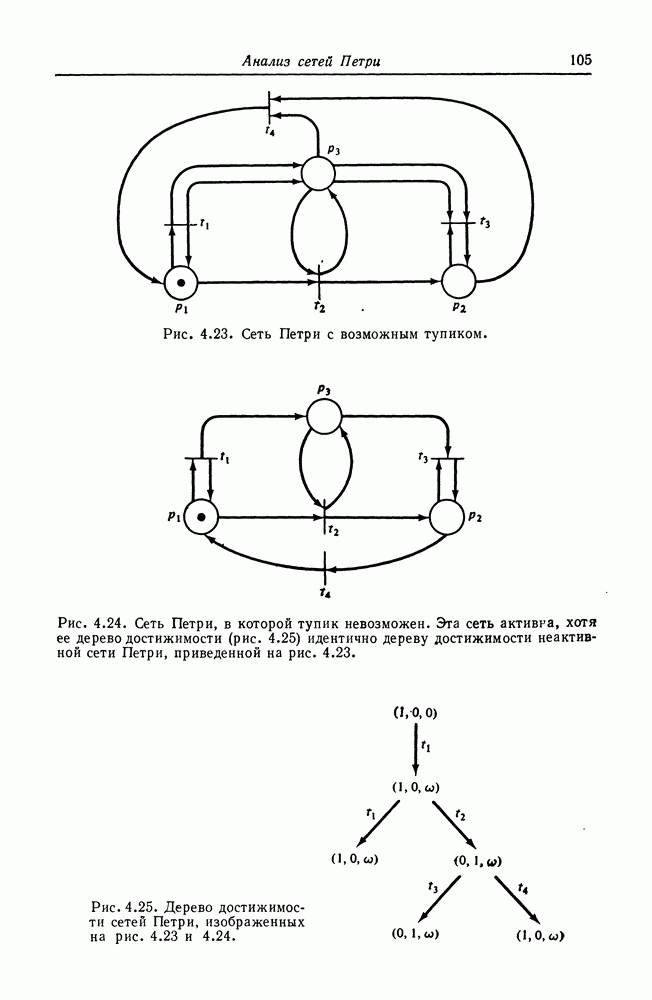
Аналогичная трудность существует и для задачи активности. На рис. 4.23 и 4.24 приведены две сети Петри, дерево достижимости которых изображено на рис. 4.25. Однако сеть на рис. 4.23 может иметь тупик (например, в результате последовательности а сеть Петри с рис. 4.24 — нет. Дерево достижимости же вновь не может передать различие этих двух случаев.
Заметим, что хотя дерево достижимости не обязательно содержит достаточную информацию для решения задач достижимости и активности, тем не менее в некоторых случаях это бывает возможно. Сеть, дерево достижимости которой содержит терминальную вершину (вершину, не имеющую исходящих дуг), не активна (поскольку некоторая достижимая маркировка не имеет последующих маркировок). Аналогично маркировка  в задаче достижимости может встретиться в дереве достижимости, и если это так, то она достижима. Кроме того, если маркировка не покрывается некоторой вершиной дерева достижимости, то она недостижима.
в задаче достижимости может встретиться в дереве достижимости, и если это так, то она достижима. Кроме того, если маркировка не покрывается некоторой вершиной дерева достижимости, то она недостижима.

(кликните для просмотра скана)
Эти условия достаточны для решения некоторых задач достижимости и активности, но они не решают эти задачи в общем. Следовательно, для решения этих двух задач необходимы другие подходы.
Упражнения
(см. скан)
4.2.2. Матричные уравнения
Второй подход к анализу сетей Петри основан на матричном представлении сетей Петри. Альтернативным по отношению к определению сети Петри в виде  является определение двух матриц
является определение двух матриц  представляющих входную и выходную функции. (Они эквивалентны функциям
представляющих входную и выходную функции. (Они эквивалентны функциям  определения Хэка сетей Петри, см. разд. 2.6.) Каждая матрица имеет
определения Хэка сетей Петри, см. разд. 2.6.) Каждая матрица имеет  строк (по одной на переход) и
строк (по одной на переход) и  столбцов (по одному на позицию). Определим
столбцов (по одному на позицию). Определим  определяет входы в переходы,
определяет входы в переходы,  выходы.
выходы.
Матричная форма определения сети Петри  эквивалентна стандартной форме, используемой нами, но позволяет дать определения в терминах векторов и матриц. Пусть
эквивалентна стандартной форме, используемой нами, но позволяет дать определения в терминах векторов и матриц. Пусть  -вектор, содержащий нули везде, за исключением
-вектор, содержащий нули везде, за исключением  компоненты. Переход
компоненты. Переход  представляется
представляется  -вектором
-вектором 
Теперь переход  в маркировке
в маркировке  разрешен, если
разрешен, если  а результат запуска перехода
а результат запуска перехода  в маркировке
в маркировке  записывается как
записывается как

где  составная матрица изменений.
составная матрица изменений.
Тогда для последовательности запусков переходов  имеем
имеем

Вектор  называется вектором запусков последовательности
называется вектором запусков последовательности  элемент вектора
элемент вектора  это число запусков перехода
это число запусков перехода  в последовательности
в последовательности  Вектор запусков, следовательно, является вектором с неотрицательными целыми компонентами. (Вектор
Вектор запусков, следовательно, является вектором с неотрицательными целыми компонентами. (Вектор  это отображение Париха последовательности
это отображение Париха последовательности 
Для того чтобы показать полезность такого матричного подхода к сетям Петри, рассмотрим, например, задачу сохранения: является ли данная маркированная сеть Петри сохраняющей? Для того чтобы показать сохранение, необходимо найти (ненулевой) вектор взвешивания, для которого взвешенная сумма по всем достижимым маркировкам постоянна. Пусть  вектор-столбец. Тогда, если
вектор-столбец. Тогда, если  начальная маркировка,
начальная маркировка,  произвольная достижимая маркировка, необходимо, чтобы
произвольная достижимая маркировка, необходимо, чтобы  Теперь, поскольку
Теперь, поскольку  достижима, существует последовательность запусков переходов
достижима, существует последовательность запусков переходов  которая переводит сеть из
которая переводит сеть из  в
в  Поэтому
Поэтому

Следовательно,  поэтому
поэтому 
Поскольку это должно быть верно для всех  имеем
имеем

Таким образом, сеть Петри является сохраняющей тогда и только тогда, когда существует такой положительный вектор  что
что  Это обеспечивает простой алгоритм проверки сохранения, а также позволяет получать вектор взвешивания
Это обеспечивает простой алгоритм проверки сохранения, а также позволяет получать вектор взвешивания 
Развитая матричная теория сетей Петри является инструментом для решения проблемы достижимости. Предположим, что маркировка  достижима из маркировки
достижима из маркировки  Тогда существует последовательность (возможно, пустая) запусков переходов
Тогда существует последовательность (возможно, пустая) запусков переходов  которая приводит из
которая приводит из  к
к  Это означает, что
Это означает, что  является неотрицательным целым решением следующего матричного уравнения для
является неотрицательным целым решением следующего матричного уравнения для 

Следовательно, если  достижима из
достижима из  тогда уравнение
тогда уравнение  имеет решение в неотрицательных целых; если уравнение
имеет решение в неотрицательных целых; если уравнение  не имеет решения, тогда
не имеет решения, тогда  недостижима из
недостижима из 
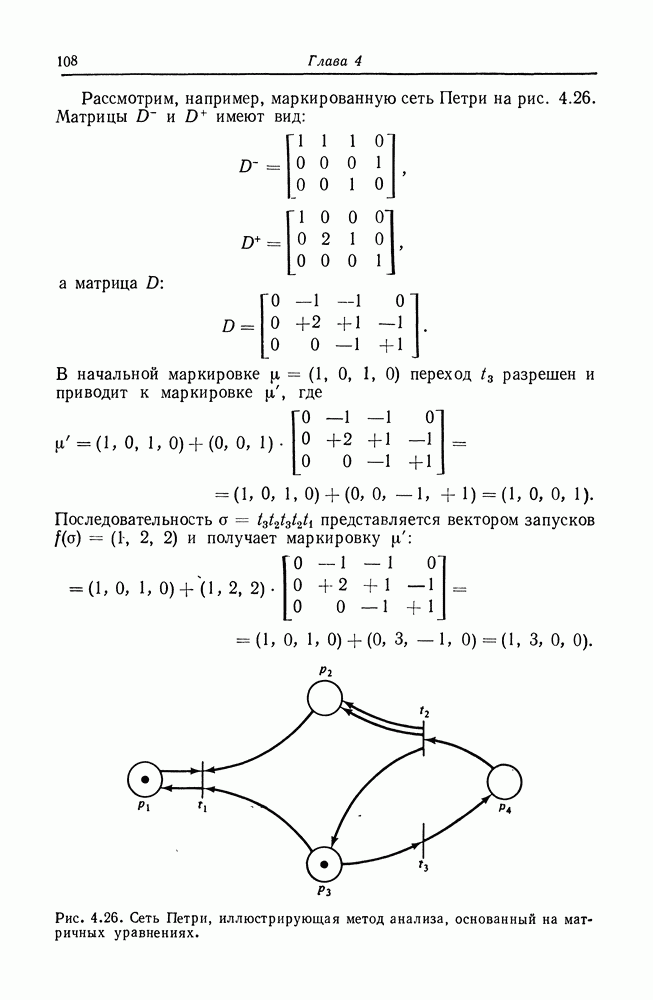
Рассмотрим, например, маркированную сеть Петри на рис. 4.26. Матрицы  имеют вид:
имеют вид:

а матрица 

В начальной маркировке  ) переход
) переход  разрешен и приводит к маркировке
разрешен и приводит к маркировке  где
где

Последовательность  представляется вектором запусков
представляется вектором запусков  ) и получает маркировку
) и получает маркировку  :
:


Рис. 4.26. Сеть Петри, иллюстрирующая метод анализа, основанный на матричных уравнениях.
Для определения того, является ли маркировка (1, 8, 0, 1) достижимой из маркировки (1, 0, 1, 0), имеем уравнение

которое имеет решение  ). Это соответствует последовательности
). Это соответствует последовательности 
Далее мы можем показать, что маркировка (1, 7, 0, 1) недостижима из маркировки (1, 0, 1, 0), поскольку матричное уравнение

не имеет решения.
Матричный подход к анализу сетей Петри очень перспективен, но имеет и некоторые трудности. Заметим прежде всего, что матрица  сама по себе не полностью отражает структуру сети Петри. Переходы, имеющие как входы, так и выходы из одной позиции (петли), представляются соответствующими элементами матриц
сама по себе не полностью отражает структуру сети Петри. Переходы, имеющие как входы, так и выходы из одной позиции (петли), представляются соответствующими элементами матриц  но затем взаимно уничтожаются в матрице
но затем взаимно уничтожаются в матрице  Это отражено в предыдущем примере позицией
Это отражено в предыдущем примере позицией  и переходом Другая проблема — это отсутствие информации о последовательности в векторе запуска. Рассмотрим сеть Петри на рис. 4.27. Предположим, мы хотим определить, является ли маркировка (0, 0, 0, 0, 1) достижимой из (1, 0, 0, 0, 0). Тогда имеем уравнение
и переходом Другая проблема — это отсутствие информации о последовательности в векторе запуска. Рассмотрим сеть Петри на рис. 4.27. Предположим, мы хотим определить, является ли маркировка (0, 0, 0, 0, 1) достижимой из (1, 0, 0, 0, 0). Тогда имеем уравнение

Это уравнение не имеет однозначного решения, но сводится к множеству решений  Оно
Оно

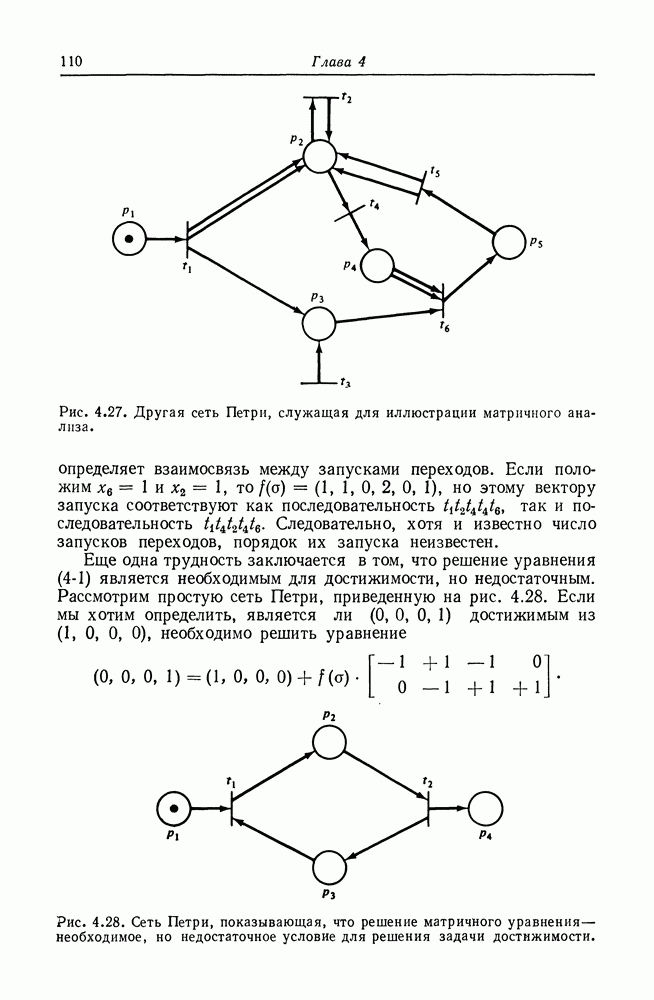
Рис. 4.27. Другая сеть Петри, служащая для иллюстрации матричного анализа.
определяет взаимосвязь между запусками переходов. Если положим  то
то  , но этому вектору запуска соответствуют как последовательность так и последовательность
, но этому вектору запуска соответствуют как последовательность так и последовательность  Следовательно, хотя и известно число запусков переходов, порядок их запуска неизвестен.
Следовательно, хотя и известно число запусков переходов, порядок их запуска неизвестен.
Еще одна трудность заключается в том, что решение уравнения  является необходимым для достижимости, но недостаточным. Рассмотрим простую сеть Петри, приведенную на рис. 4.28. Если мы хотим определить, является ли (0, 0, 0, 1) достижимым из (1, 0, 0, 0), необходимо решить уравнение
является необходимым для достижимости, но недостаточным. Рассмотрим простую сеть Петри, приведенную на рис. 4.28. Если мы хотим определить, является ли (0, 0, 0, 1) достижимым из (1, 0, 0, 0), необходимо решить уравнение


Рис. 4.28. Сеть Петри, показывающая, что решение матричного уравнения — необходимое, но недостаточное условие для решения задачи достижимости.
Это уравнение имеет решение  соответствующее двум последовательностям:
соответствующее двум последовательностям:  Но ни одна из этих двух последовательностей переходов невозможна, поскольку в (1,0, 0, 0) ни
Но ни одна из этих двух последовательностей переходов невозможна, поскольку в (1,0, 0, 0) ни  ни 4 не разрешены. Таким образом, решения уравнения
ни 4 не разрешены. Таким образом, решения уравнения  недостаточно для доказательства достижимости.
недостаточно для доказательства достижимости.
Возможность недействительных решений уравнения  (решений, которые не соответствуют возможным последовательностям переходов) стала причиной только ограниченного исследования матричного представления сетей Петри. Лучшее исследование этого подхода проведено Муратой [206, 208, 209].
(решений, которые не соответствуют возможным последовательностям переходов) стала причиной только ограниченного исследования матричного представления сетей Петри. Лучшее исследование этого подхода проведено Муратой [206, 208, 209].
4.3. Замечания к литературе
В публикациях Хольта и др. [128] и Хольта и Коммонера [127] определены некоторые из первых задач анализа сетей Петри — активность и безопасность, которые продолжают считаться основными задачами анализа. Активность изучалась Коммонером [53], Лаутенбахом [167] и Льеном [173]. Келлер [150] вместе с другими задачами рассматривал также и активность. Льен [173] определил задачу сохранения.
Карп и Миллер [128] впервые описали построение дерева достижимости и доказали его конечность. Задачи покрываемости и достижимости были определены ими как если бы это были задачи эквивалентности и включения. Последние задачи явились предг метом изучения в [26]. В [213] дана краткая формулировка задачи достижимости. Хэк [111] рассмотрел большинство этих задач вместе и показал, как дерево достижимости можно использовать для решения некоторых из них.
Матричный подход рассматривался Питерсоном [236], но, как оказалось, возможности его ограничены. Мурата, имеющий большую квалификацию в линейной алгебре, достиг чуть большего в этом подходе в [210, 206, 212, 208, 209].
4.4. Темы для дальнейшего изучения
1. Рассмотрите построение не дерева, а графа достижимости. Если вершина  порождает последующую вершину
порождает последующую вершину  для некоторой неграничной вершины
для некоторой неграничной вершины  просто введите помеченную соответствующим образом дугу из и у. Заметим, что путь из корня в вершину перестает быть единственным. Опишите алгоритм построения графа достижимости, покажите, что он сходится, и исследуйте его свойства, сравнивая с алгоритмом построения дерева достижимости.
просто введите помеченную соответствующим образом дугу из и у. Заметим, что путь из корня в вершину перестает быть единственным. Опишите алгоритм построения графа достижимости, покажите, что он сходится, и исследуйте его свойства, сравнивая с алгоритмом построения дерева достижимости.
2. Дерево достижимости нельзя использовать для решения проблемы достижимости вследствие потери информации, порождаемой символом  Он вводится, когда мы приходим к маркировке
Он вводится, когда мы приходим к маркировке  и на пути от корня к
и на пути от корня к  имеется такая маркировка
имеется такая маркировка  что
что  В этом
В этом
случае можно получить все маркировки вида  Исследуйте возможность использования выражения а
Исследуйте возможность использования выражения а  вместо
вместо  для того чтобы представить значения компонент. Если вы сможете определить дерево достижимости, в котором все векторы маркировок представляются выражениями, тогда решение задачи достижимости определяется просто решением системы уравнений.
для того чтобы представить значения компонент. Если вы сможете определить дерево достижимости, в котором все векторы маркировок представляются выражениями, тогда решение задачи достижимости определяется просто решением системы уравнений.
3. Обобщите определение сохранения, разрешая отрицательные веса. Что можно было бы считать разумной интерпретацией отрицательного веса? Является ли разрешимой задача определения сохранения сети Петри, если разрешены отрицательные веса?
4. Разработайте с помощью матричного подхода к анализу алгоритм определения ограниченности сети Петри [61].
5. Основная проблема матричного анализа — отсутствие информации о последовательности и существование недействительных решений. Однако задача достижимости является самой существенной для сетей Петри, поэтому важно показать, что она разрешима, даже если решения вычислительно дороги. Если задача разрешима, можно будет искать более эффективные методы решения, но сначала необходимо показать, что метод решения существует.
Для обоснования этого обозначим через сумму вектора запуска  по всем компонентам. Иначе говоря, если
по всем компонентам. Иначе говоря, если  Далее, если существует последовательность
Далее, если существует последовательность  переводящая сеть Петри из маркировки
переводящая сеть Петри из маркировки  в маркировку
в маркировку  тогда уравнение
тогда уравнение  имеет решение, являющееся вектором запуска
имеет решение, являющееся вектором запуска  для
для  Последовательность
Последовательность  можно определить из вектора запуска
можно определить из вектора запуска  простым перебором всех возможных последовательностей длины
простым перебором всех возможных последовательностей длины  стараясь, чтобы каждая из них 1) была действительной и 2) приводила от
стараясь, чтобы каждая из них 1) была действительной и 2) приводила от  к
к  Для сети Петри с
Для сети Петри с  переходами возможно самое большое
переходами возможно самое большое  последовательностей длины
последовательностей длины  На самом деле это число можно сократить. Поскольку нам известно, сколько раз запускается переход
На самом деле это число можно сократить. Поскольку нам известно, сколько раз запускается переход  сколько раз запускается
сколько раз запускается  то необходимо проверять не более чем
то необходимо проверять не более чем  возможных упорядочений из
возможных упорядочений из  запусков перехода
запусков перехода  запусков перехода
запусков перехода 
Это, казалось бы, обеспечивает процедуру решения задачи определения, является ли  достижимой из
достижимой из  Сначала решаем матричное уравнение
Сначала решаем матричное уравнение  Если решения не существует,
Если решения не существует,  недостижима из
недостижима из  Если решение
Если решение  существует, проверяем все
существует, проверяем все  возможных упорядочений переходов. Если какая-нибудь из этих последовательностей действительна, то
возможных упорядочений переходов. Если какая-нибудь из этих последовательностей действительна, то  достижима из
достижима из  и мы имеем последовательность переходов, переводящую из
и мы имеем последовательность переходов, переводящую из  в
в 
Имеется только одно препятствие. Решение  может быть не однозначным, а (бесконечным) множеством векторов запусков, представленным множеством выражений (как показано выше для примера анализа сети Петри на рис. 4.27). Для определения возможности доказательства достижимости в этом случае необходимы исследования. В простейшем случае может оказаться, что или все решения
может быть не однозначным, а (бесконечным) множеством векторов запусков, представленным множеством выражений (как показано выше для примера анализа сети Петри на рис. 4.27). Для определения возможности доказательства достижимости в этом случае необходимы исследования. В простейшем случае может оказаться, что или все решения
представляются выражением вектора запуска, соответствующим действительным решениям, или ни одно. В этом случае мы просто выбираем любое решение и выполняем описанную процедуру проверки всех возможных упорядочений. Более вероятно, однако, что некоторые решения будут работать, тогда как другие — нет. Так как мы не можем испытать все решения (из, возможно, бесконечного множества их), необходимы исследования, для того чтобы можно было определить, какие решения необходимо проверять.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ГЛАВА 1. ВВЕДЕНИЕ
- ГЛАВА 2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
- 2.1. Структура сети Петри
- 2.2. Графы сетей Петри
- 2.3. Маркировка сетей Петри
- 2.4. Правила выполнения сетей Петри
- 2.5. Пространство состояний сети Петри
- 2.6. Альтернативные формы определения сетей Петри
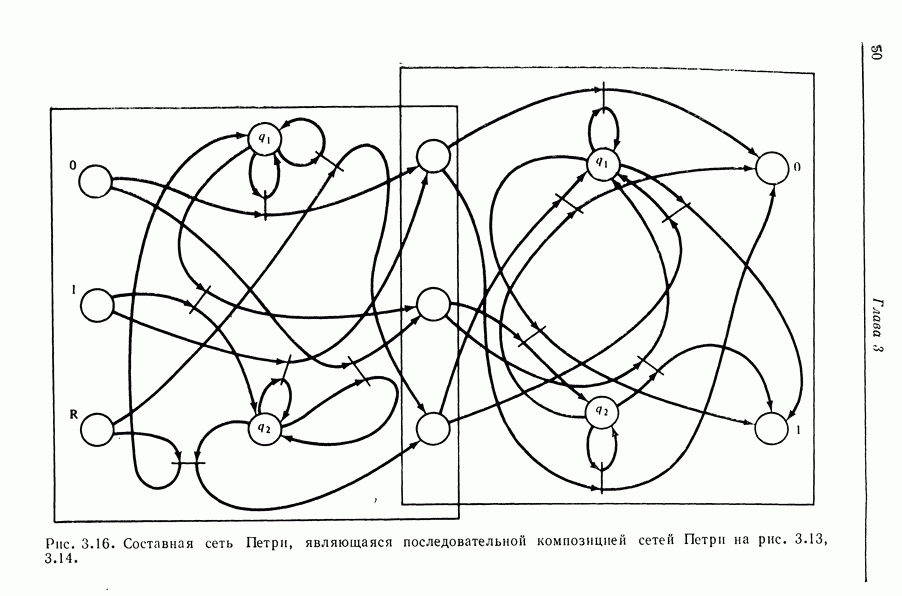
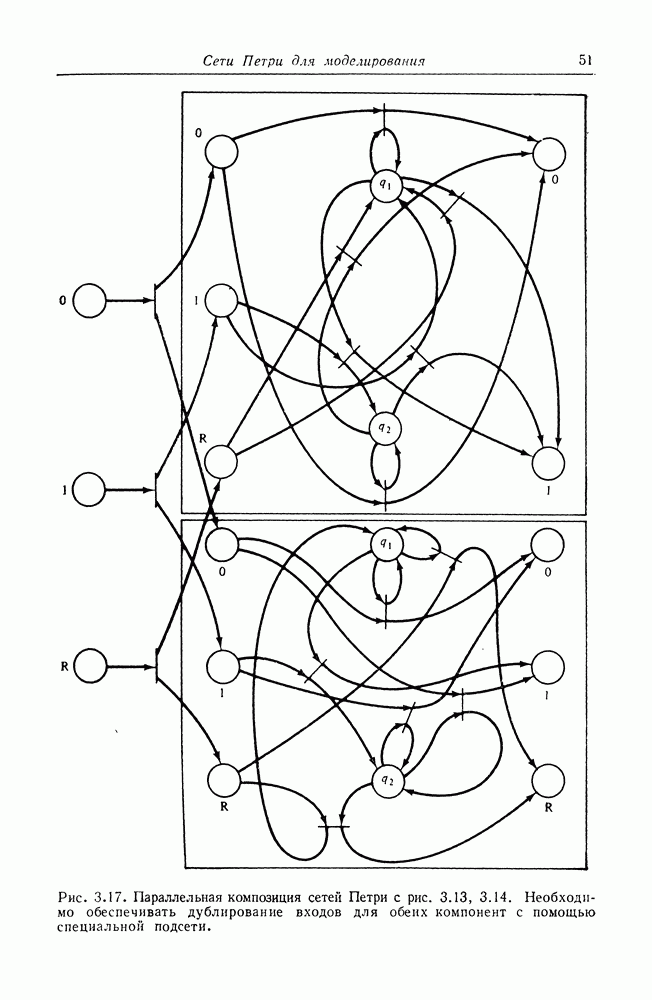
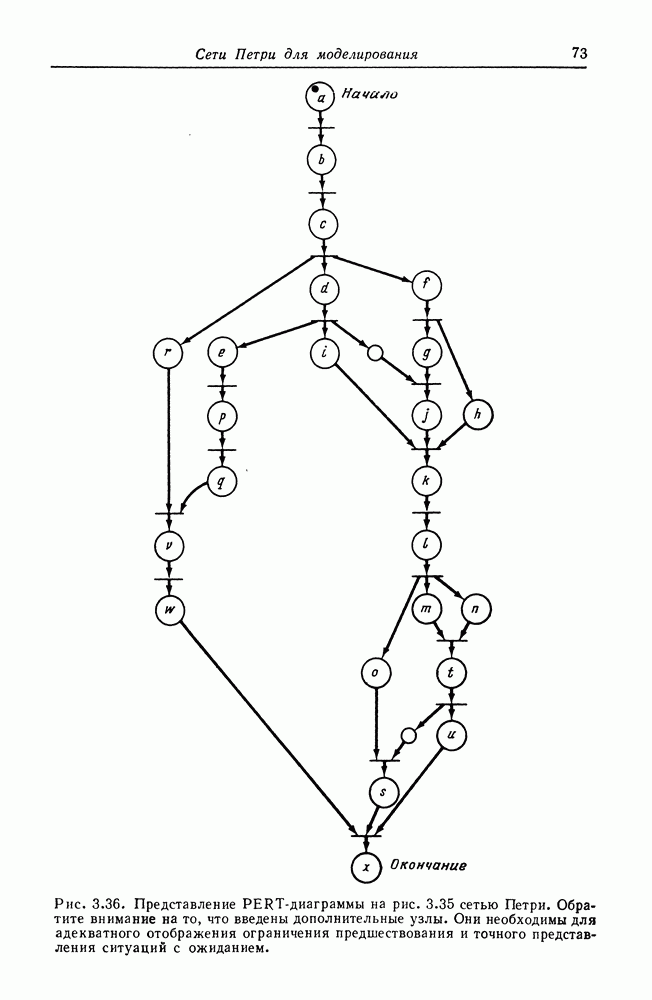
- ГЛАВА 3. СЕТИ ПЕТРИ ДЛЯ МОДЕЛИРОВАНИЯ
- 3.2. Одновременность и конфликт
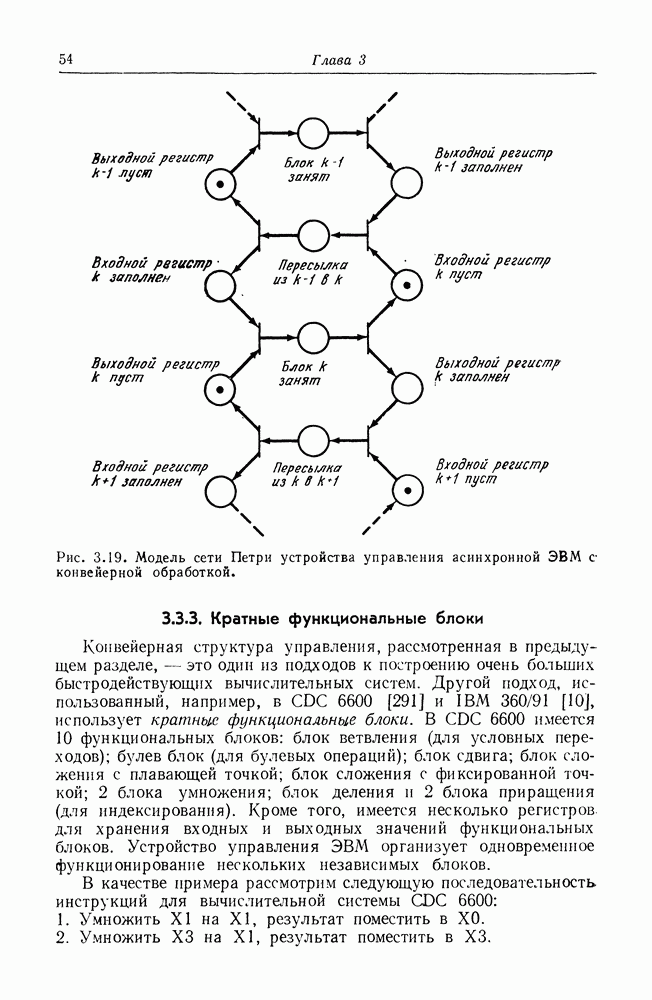
- 3.3. Аппаратное обеспечение ЭВМ
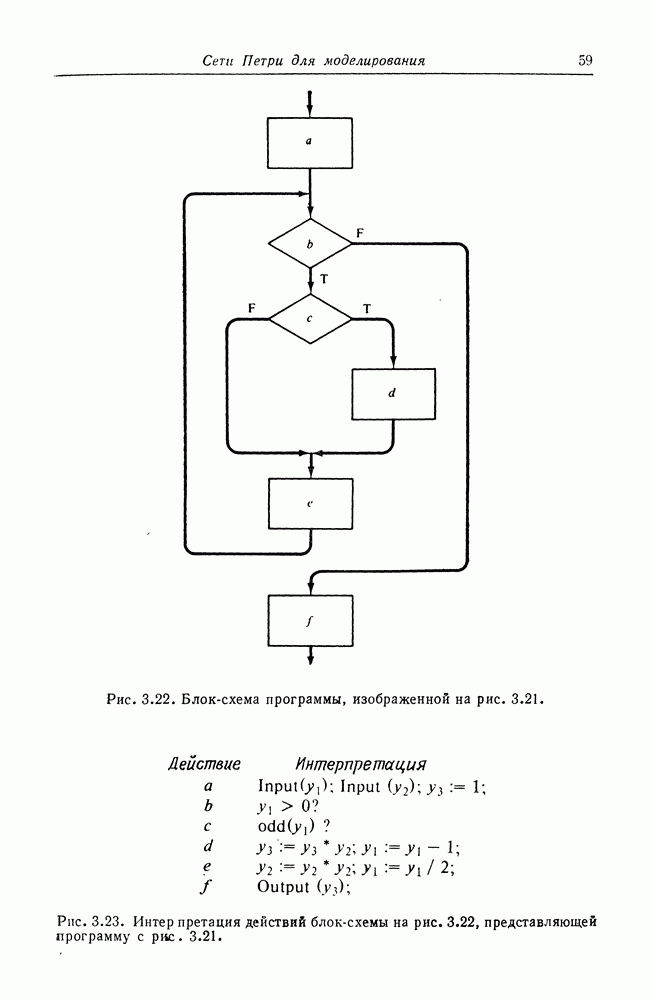
- 3.4. Программное обеспечение ЭВМ
- 3.5. Другие системы
- ГЛАВА 4. АНАЛИЗ СЕТЕЙ ПЕТРИ
- 4.1. Задачи анализа сетей Петри
- 4.2. Методы анализа
- ГЛАВА 5. СЛОЖНОСТЬ И РАЗРЕШИМОСТЬ
- 5.1. Сводимость задач анализа
- 5.2. Задачи достижимости
- 5.3. Сети Петри с ограничениями
- 5.4. Активность и достижимость
- 5.5. Неразрешимые задачи
- 5.6. Сложность задачи достижимости
- ГЛАВА 6. ЯЗЫКИ СЕТЕЙ ПЕТРИ
- 6.2. Некоторые понятия теории формальных языков
- 6.3. Определения языков сетей Петри
- 6.4. Свойства языков сетей Петри
- 6.5. Свойства замкнутости
- 6.6. Языки сетей Петри и другие классы языков
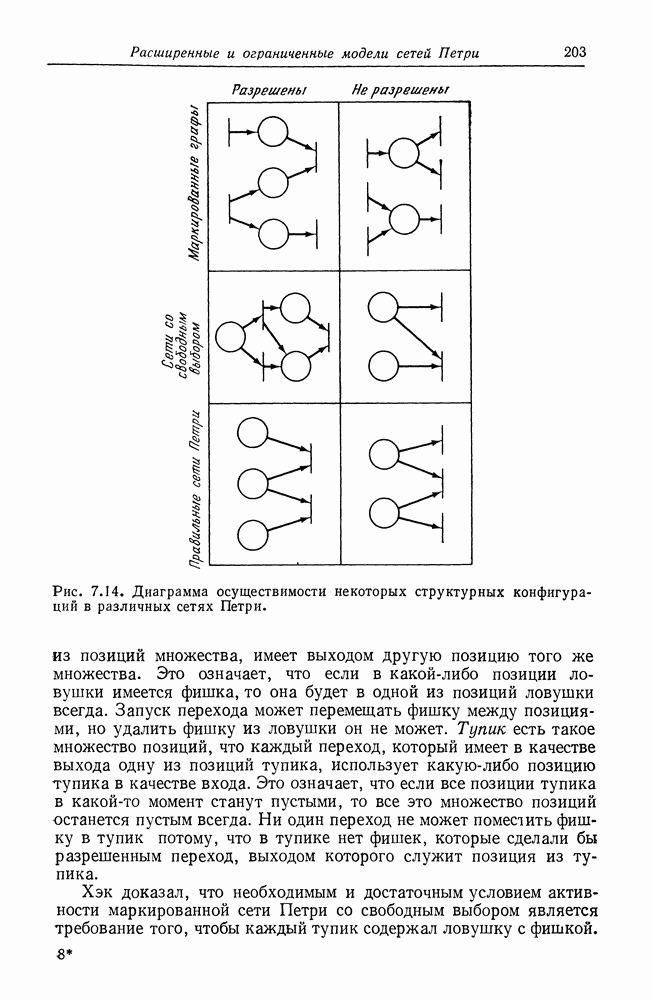
- ГЛАВА 7. РАСШИРЕННЫЕ И ОГРАНИЧЕННЫЕ МОДЕЛИ СЕТЕЙ ПЕТРИ
- 7.1. Границы возможностей моделирования с помощью сетей Петри
- 7.2. Расширения
- 7.3. Расширенные сети Петри и регистровые машины
- 7.4. Подклассы сетей Петри
- ГЛАВА 8. МОДЕЛИ ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ
- 8.2. Маркированные графы
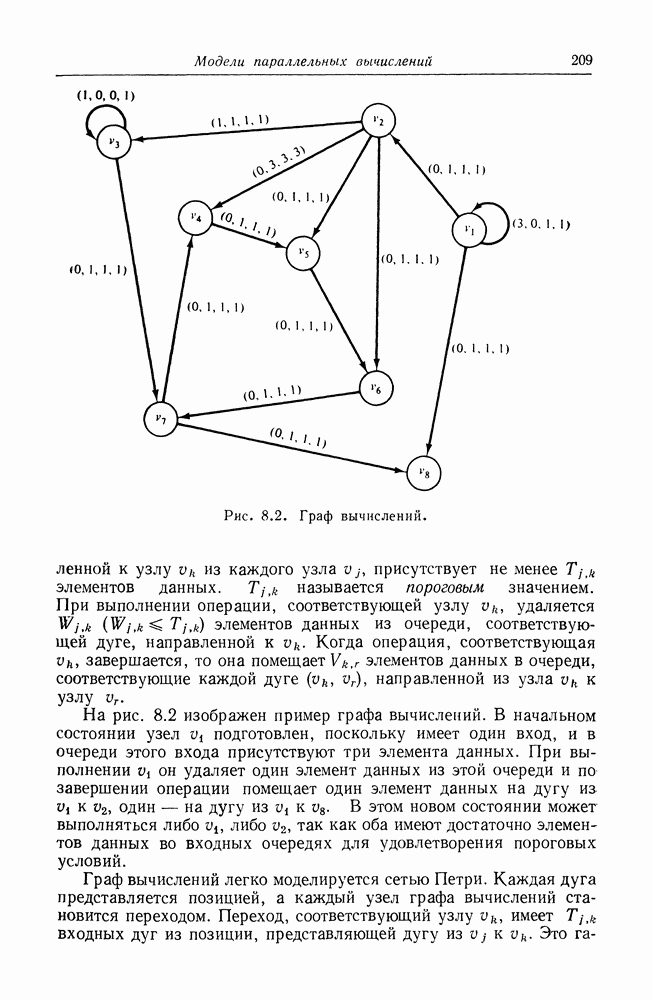
- 8.3. Графы вычислений
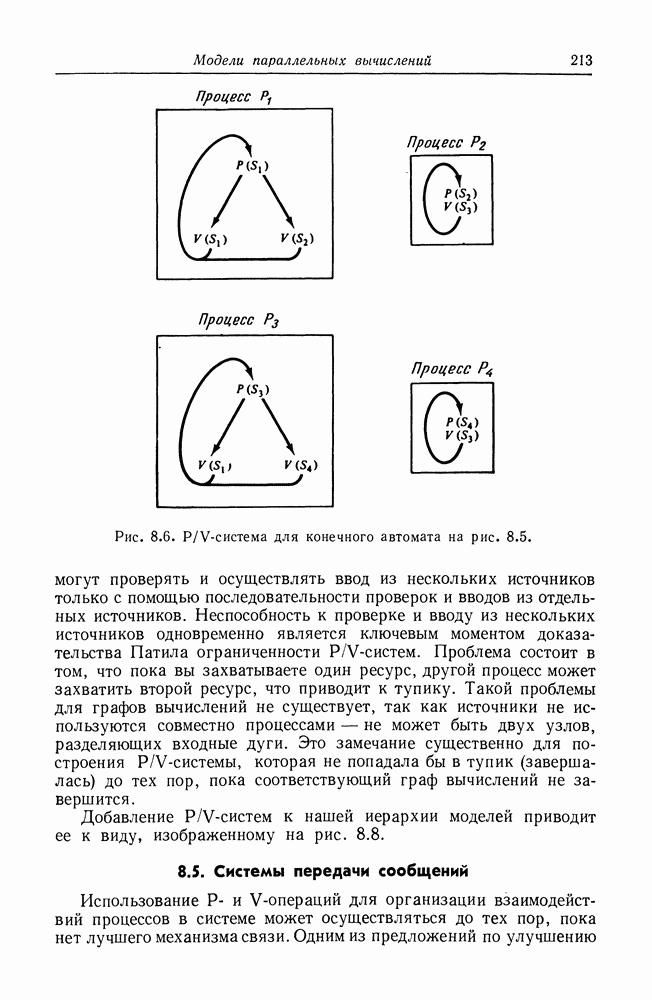
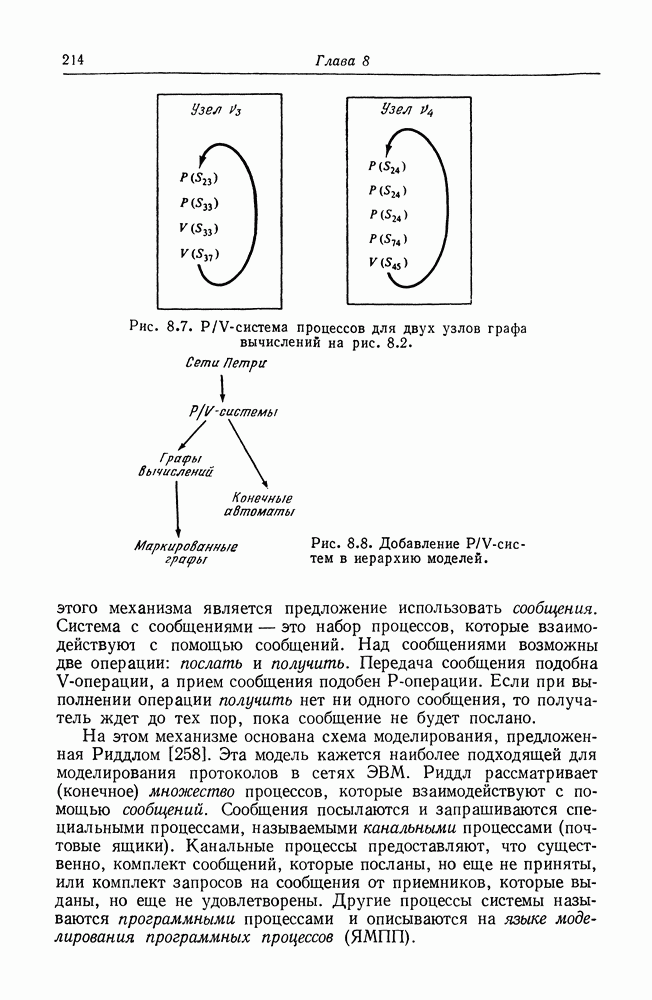
- 8.4. P/V-системы
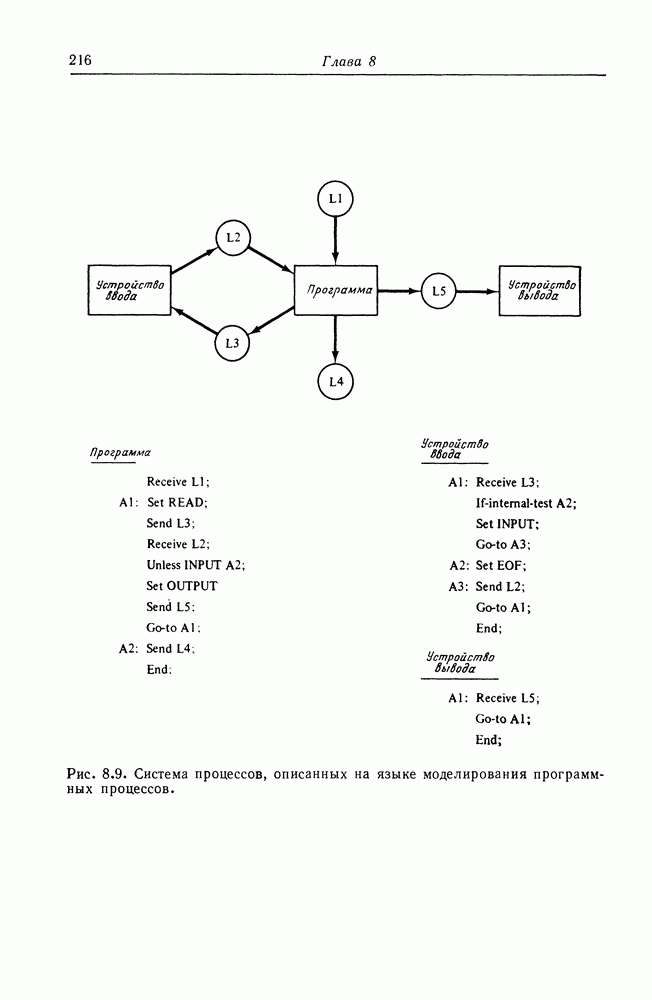
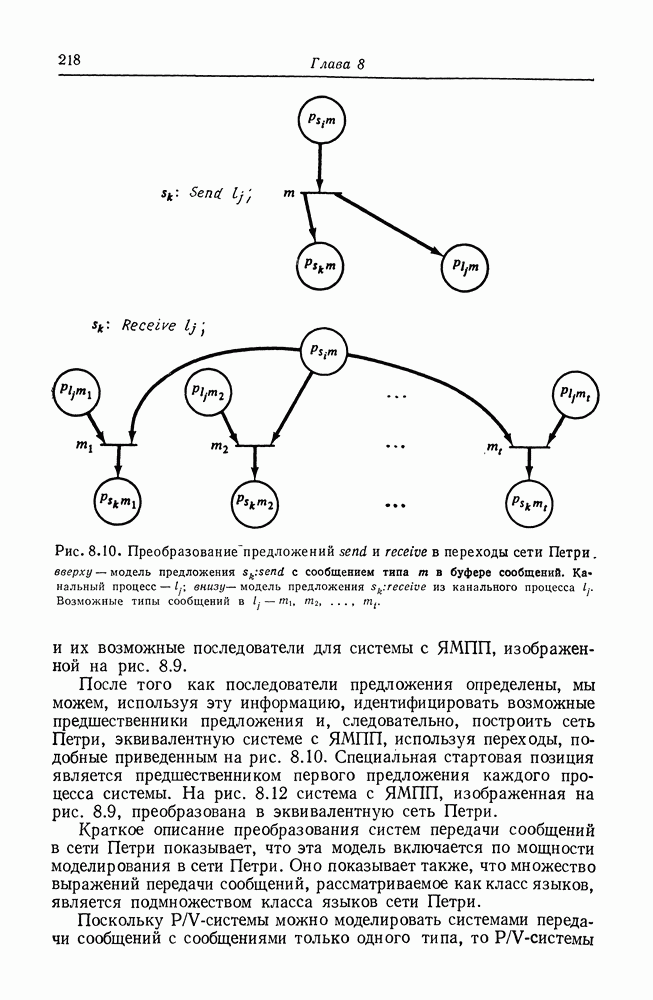
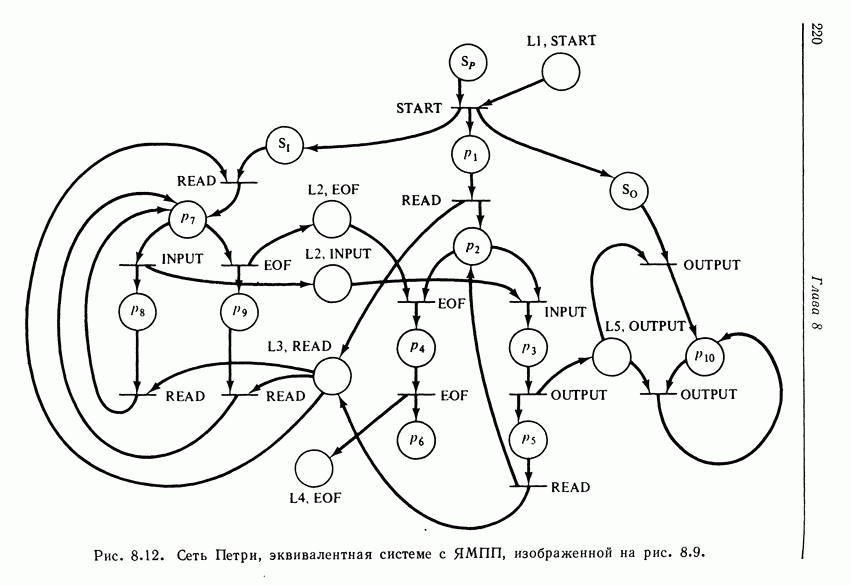
- 8.5. Системы передачи сообщений
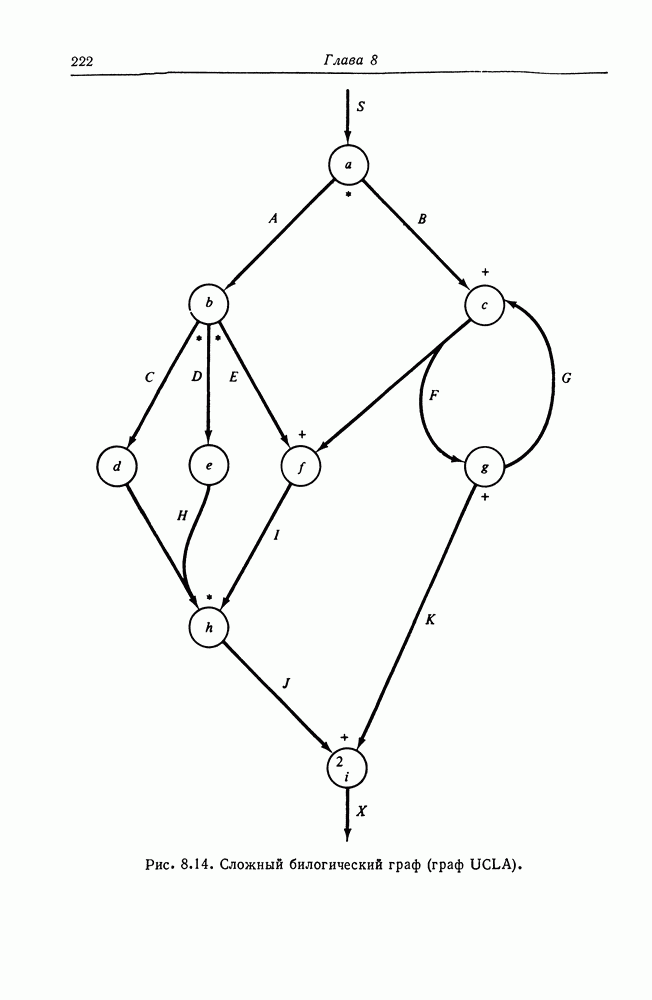
- 8.6. Графы UCLA
- 8.7. Системы замещения и сложения векторов
- 8.8. Расширенные модели сетей Петри
- ОБЗОР ТЕОРИИ КОМПЛЕКТОВ
- АННОТИРОВАННАЯ БИБЛИОГРАФИЯ