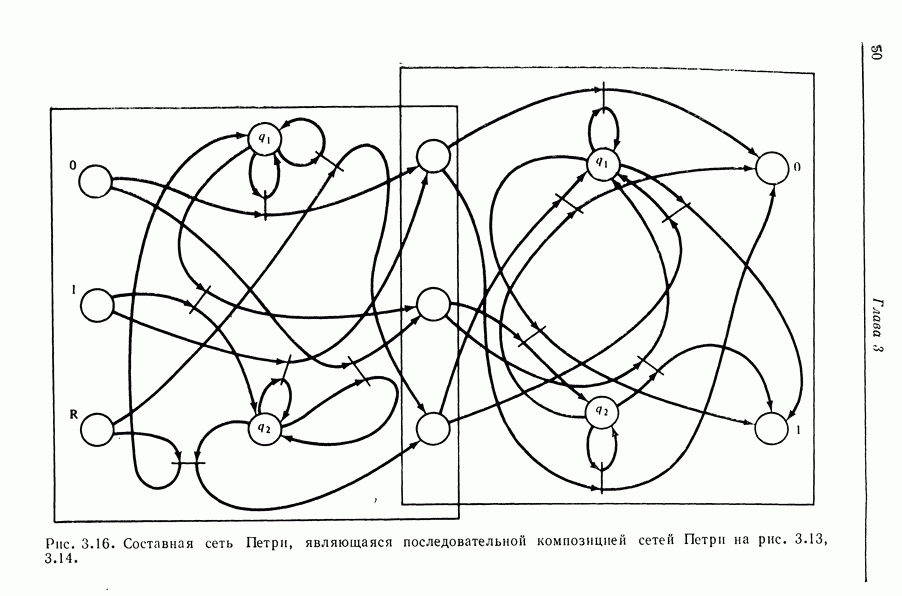
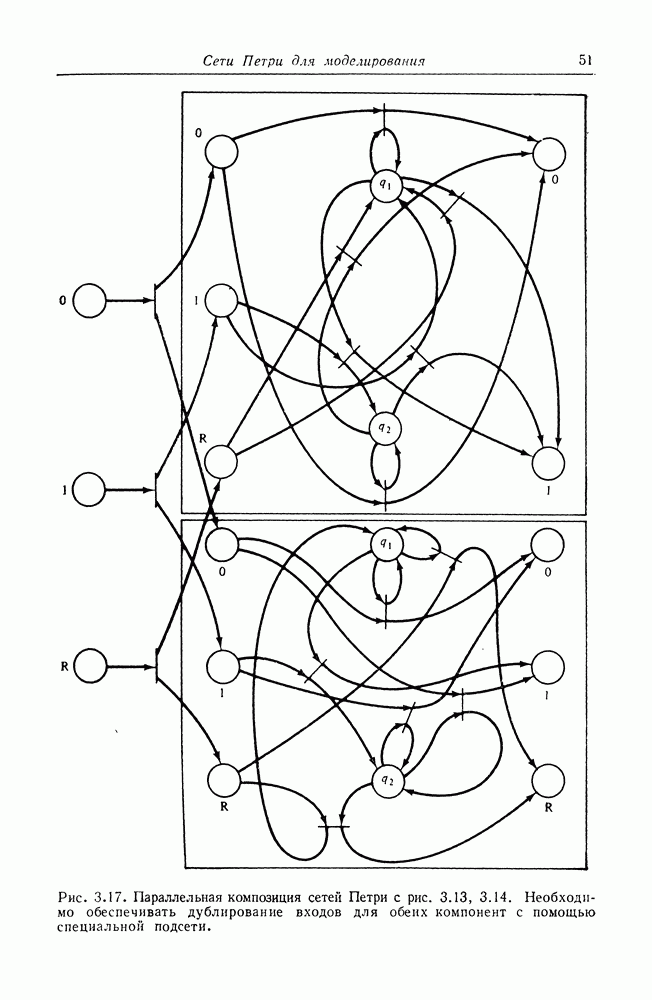
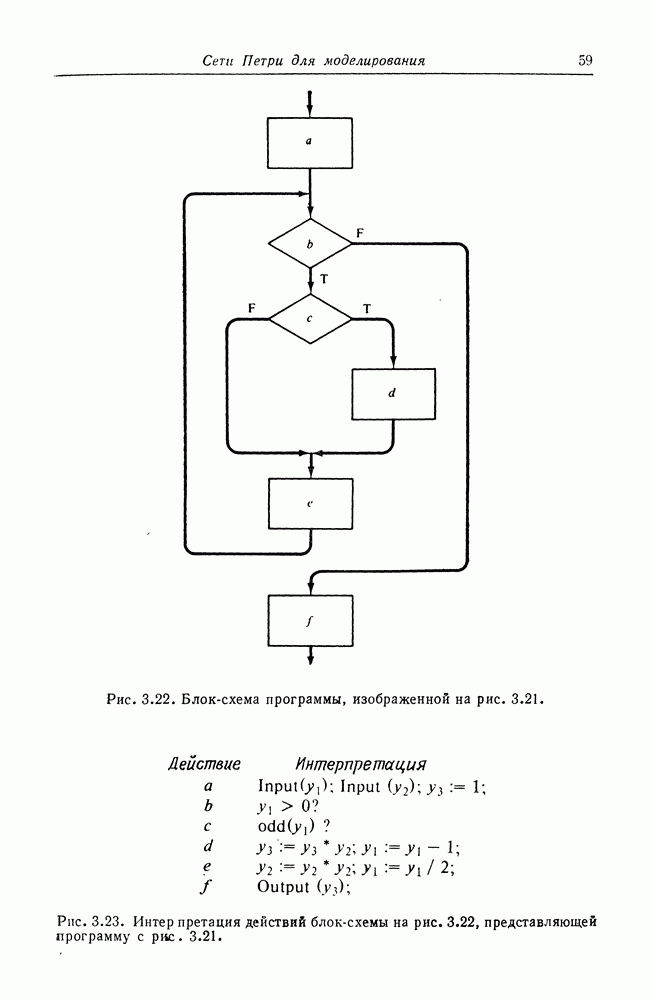
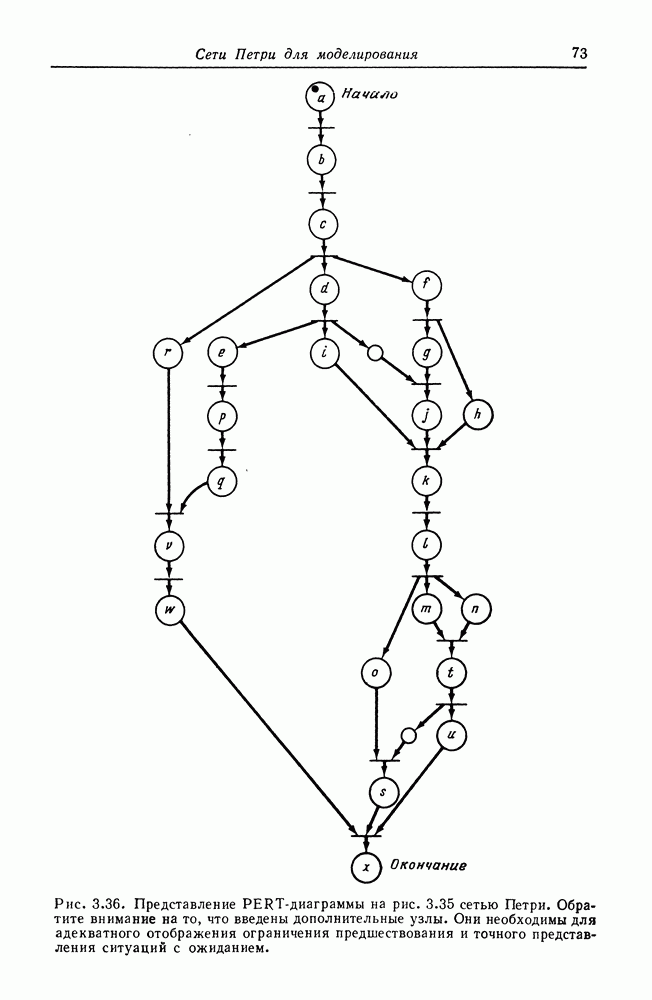
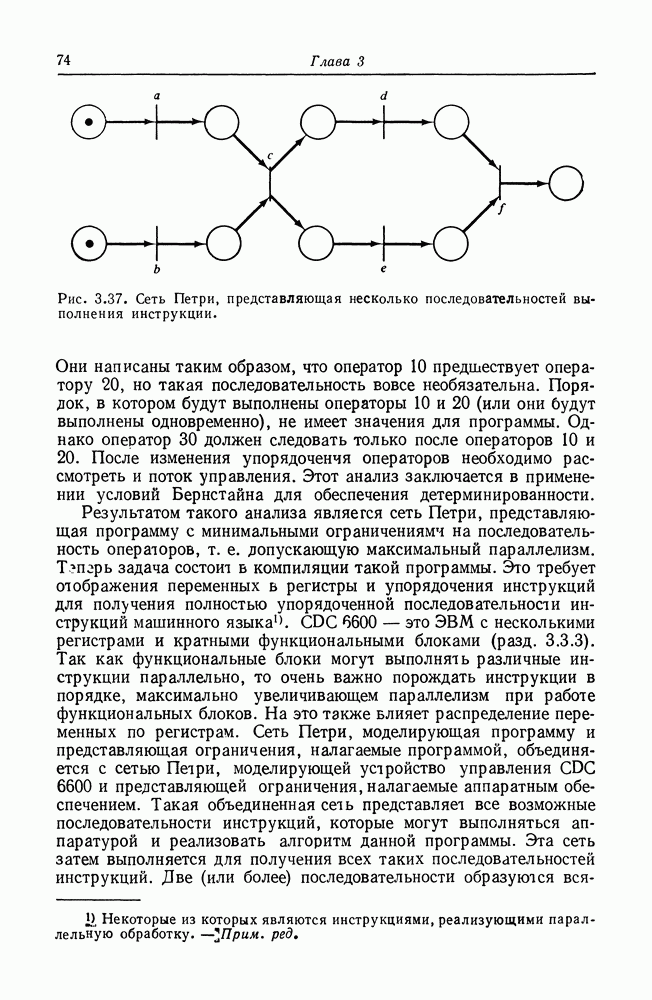
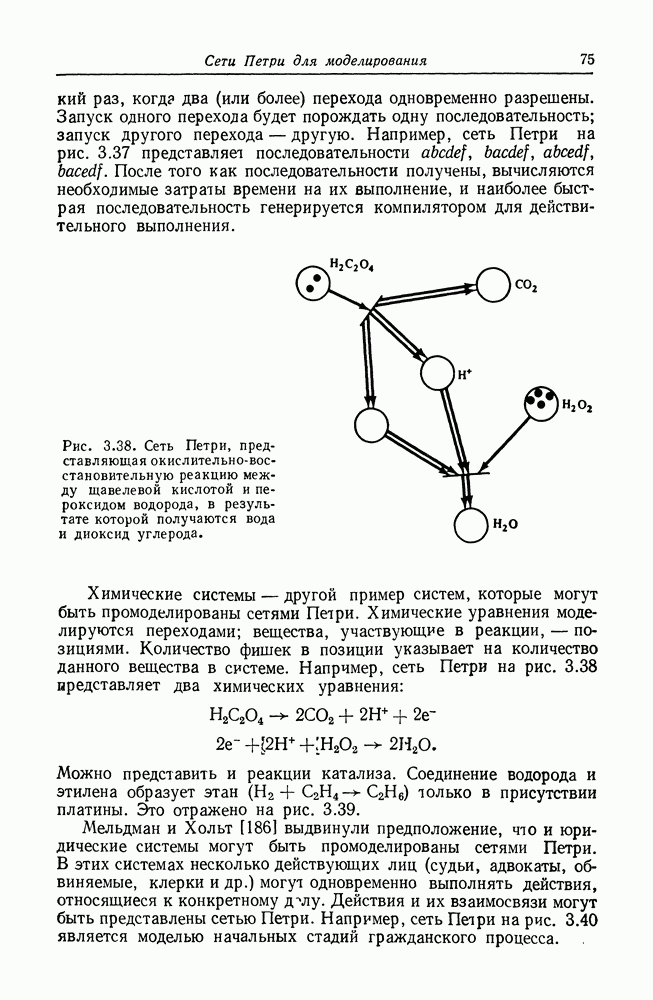
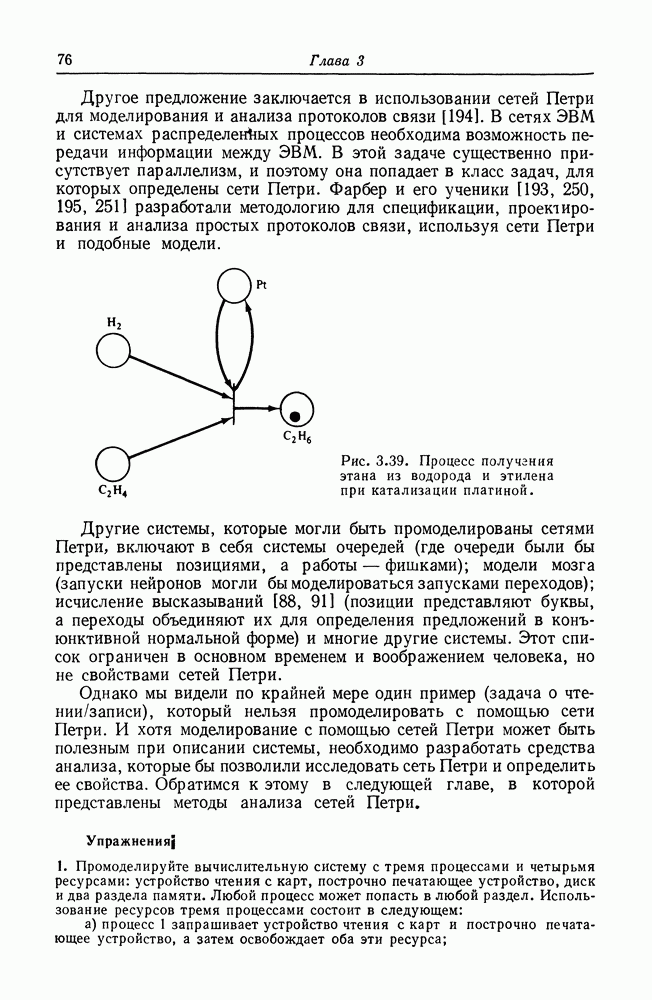
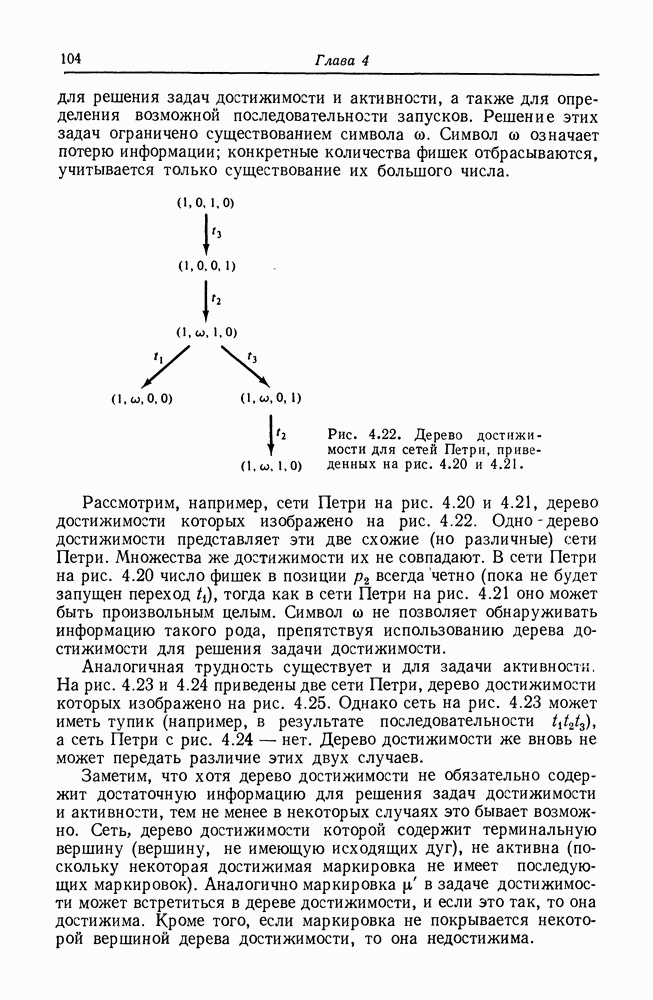
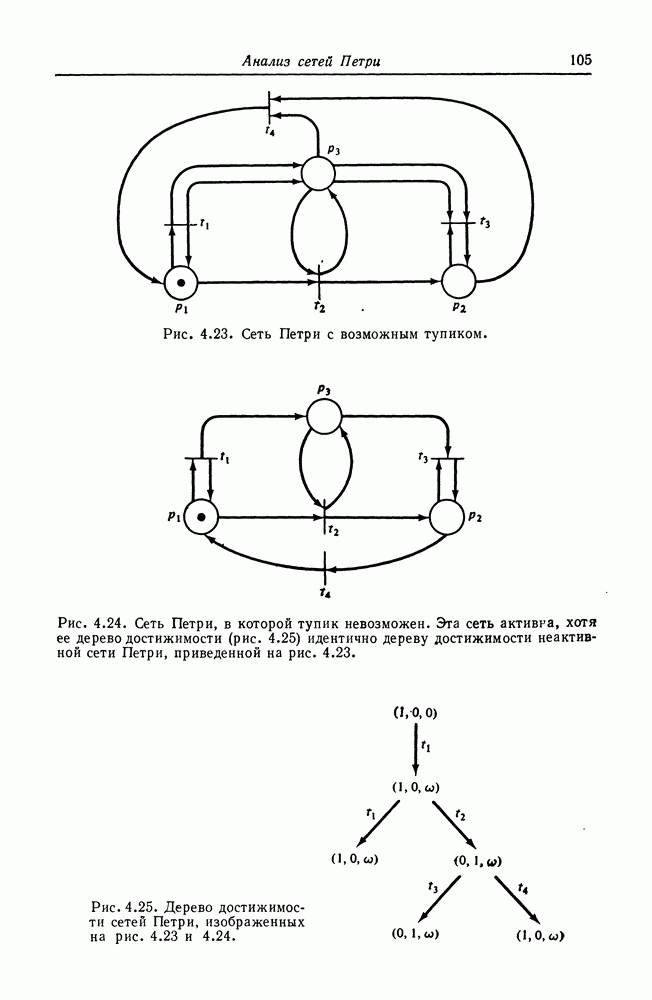
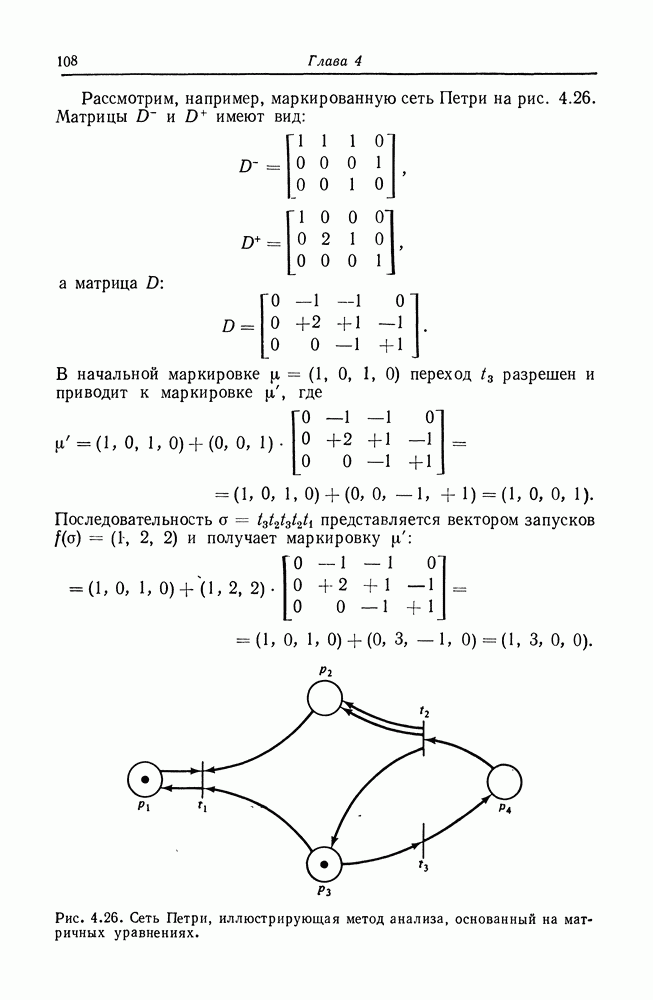
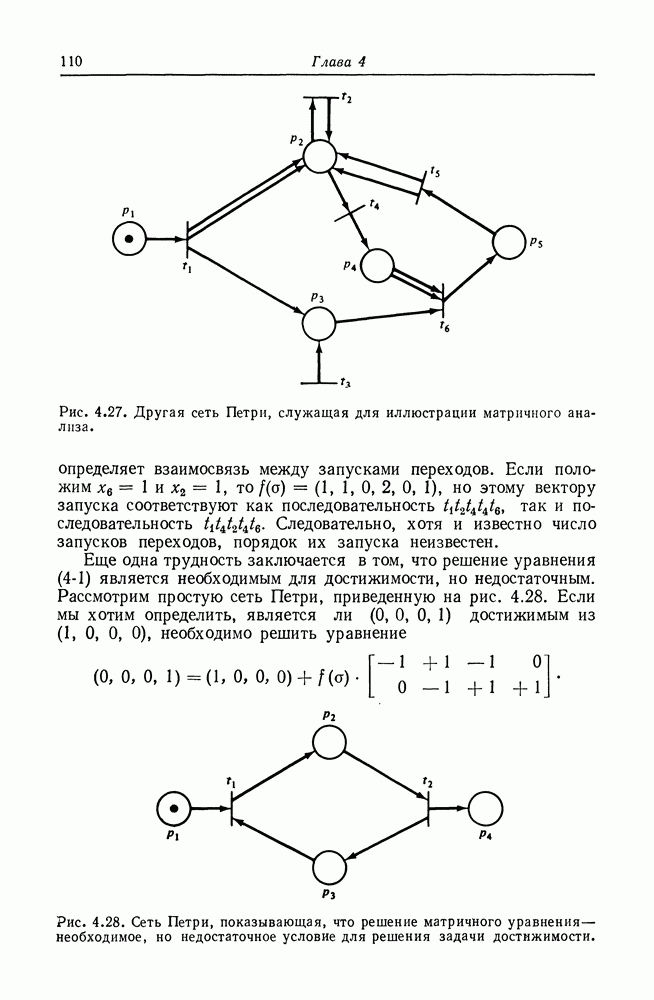
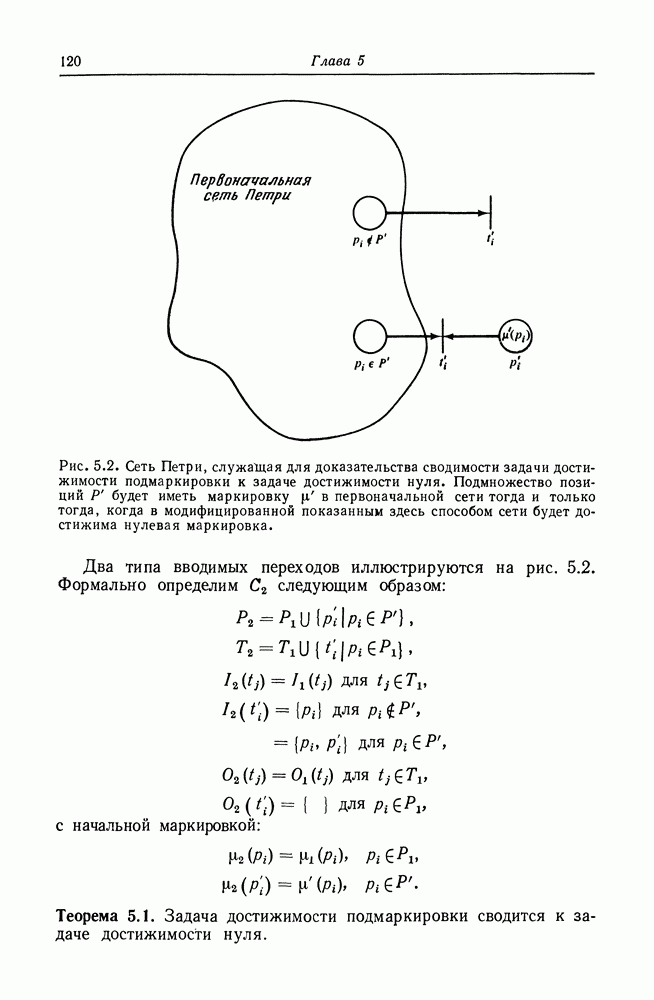
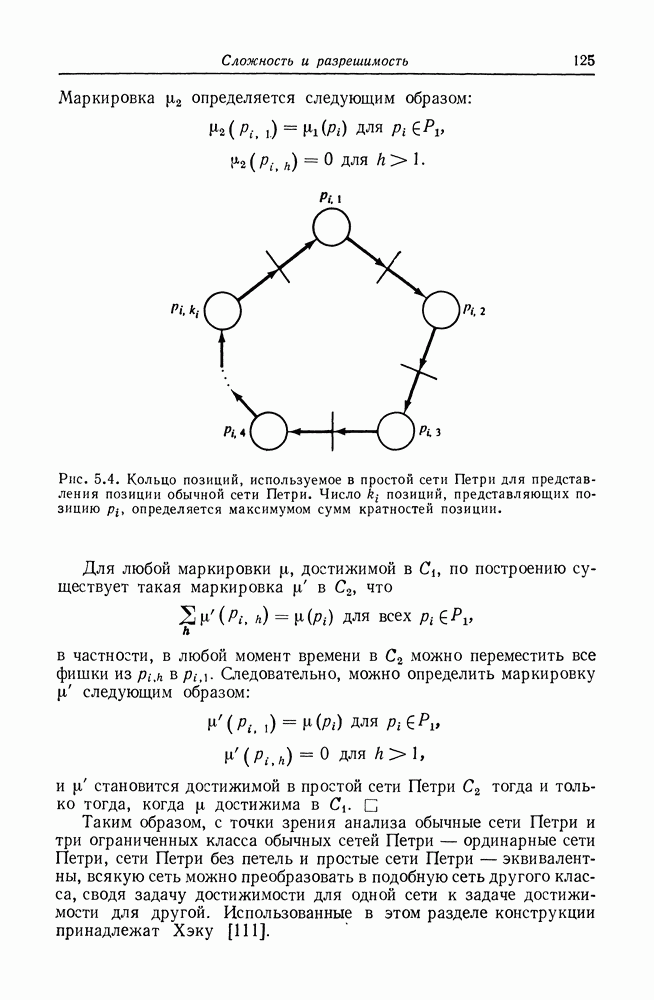
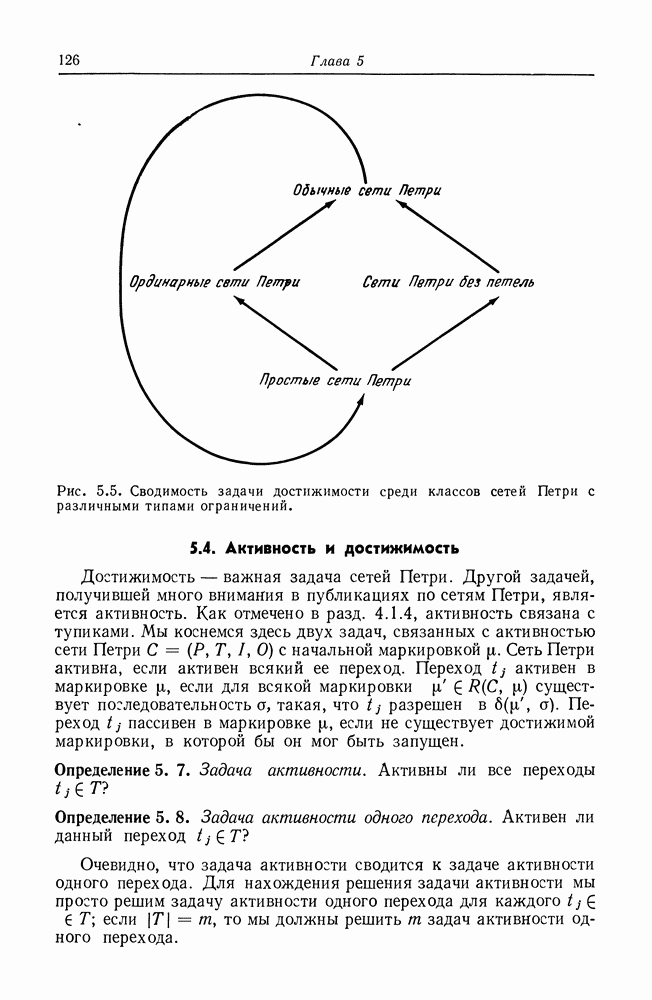
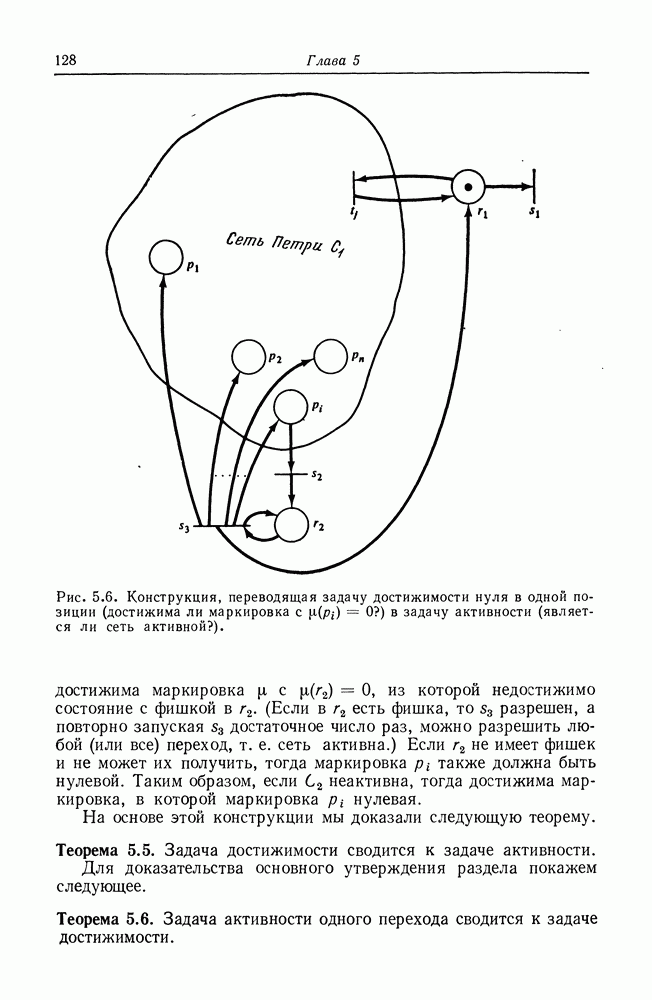
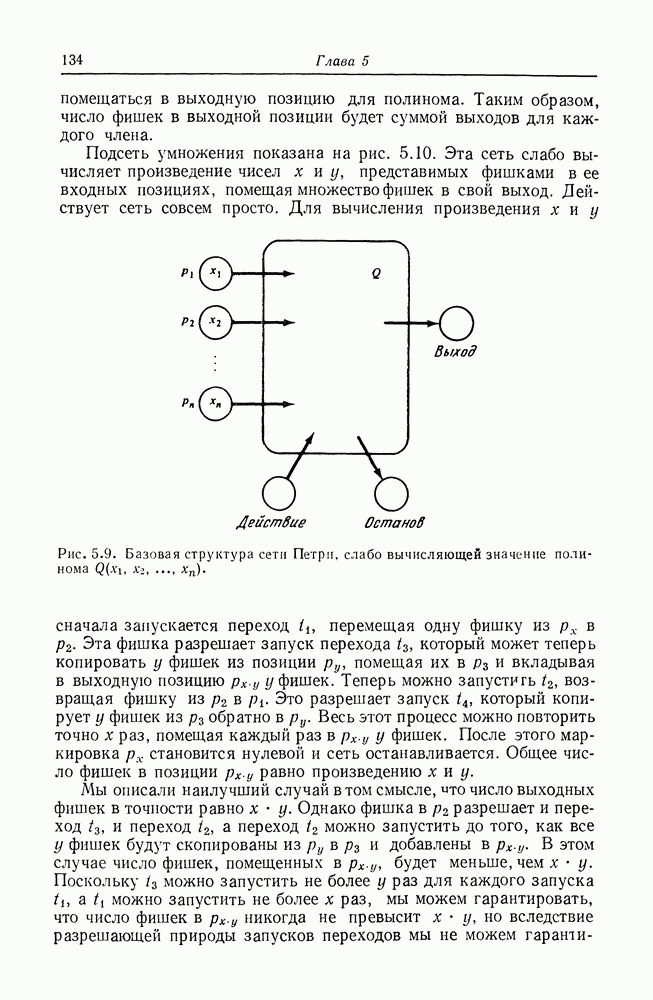
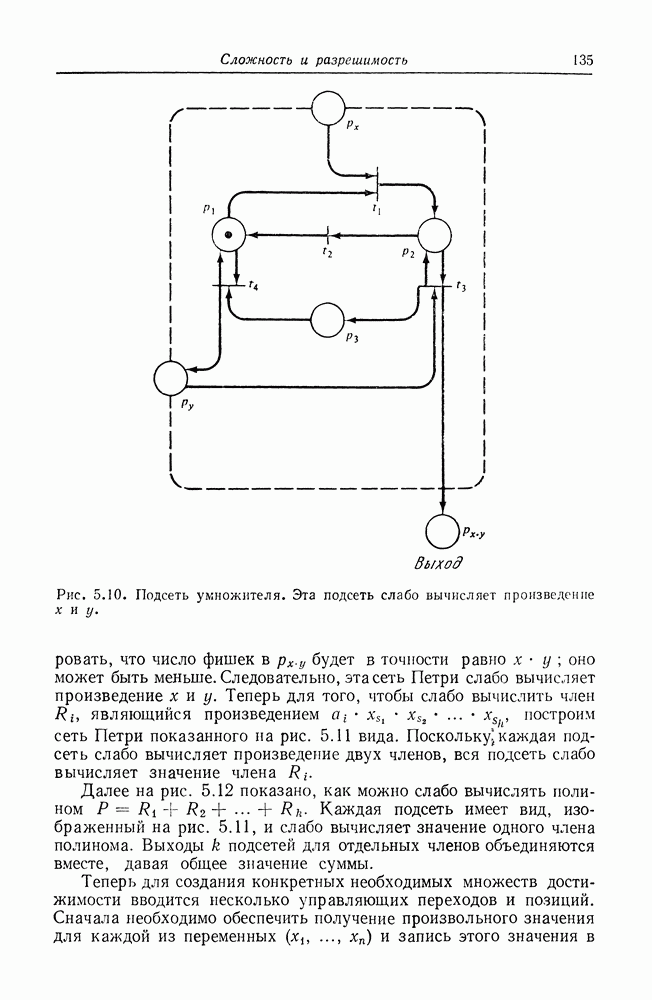
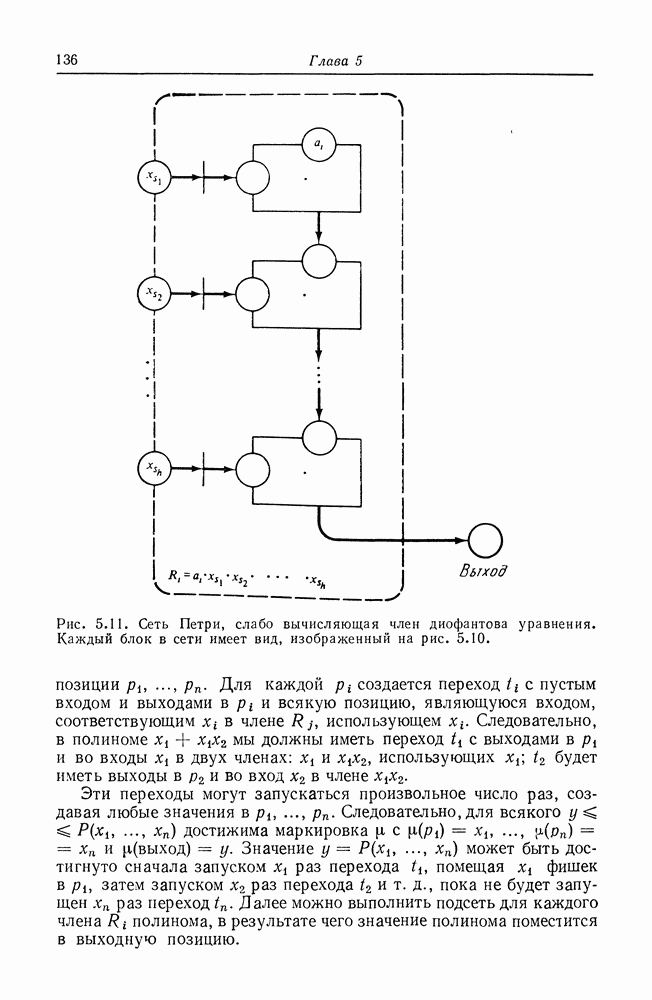
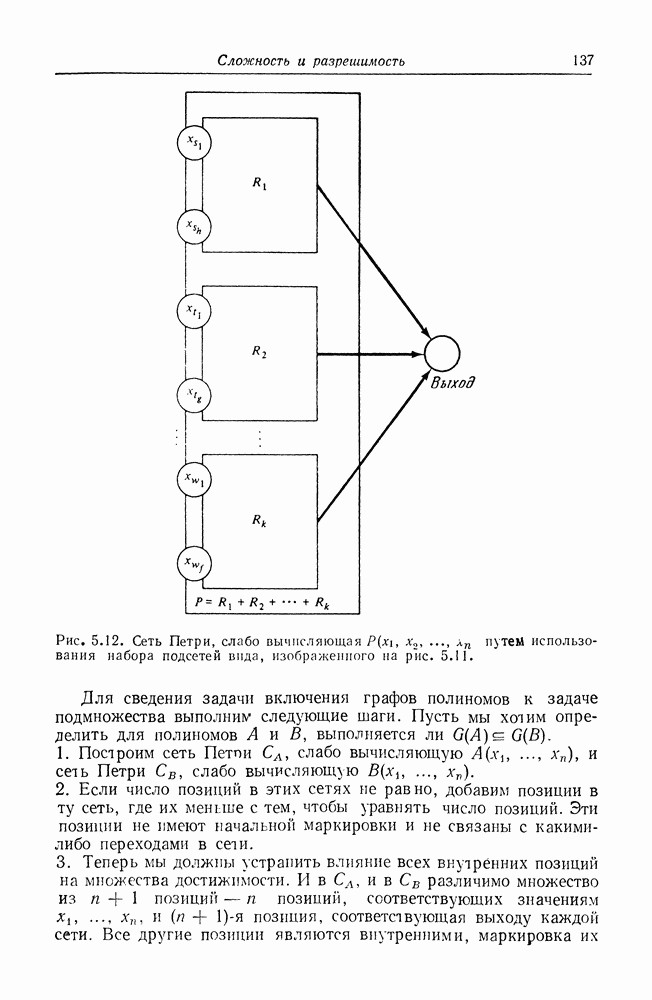
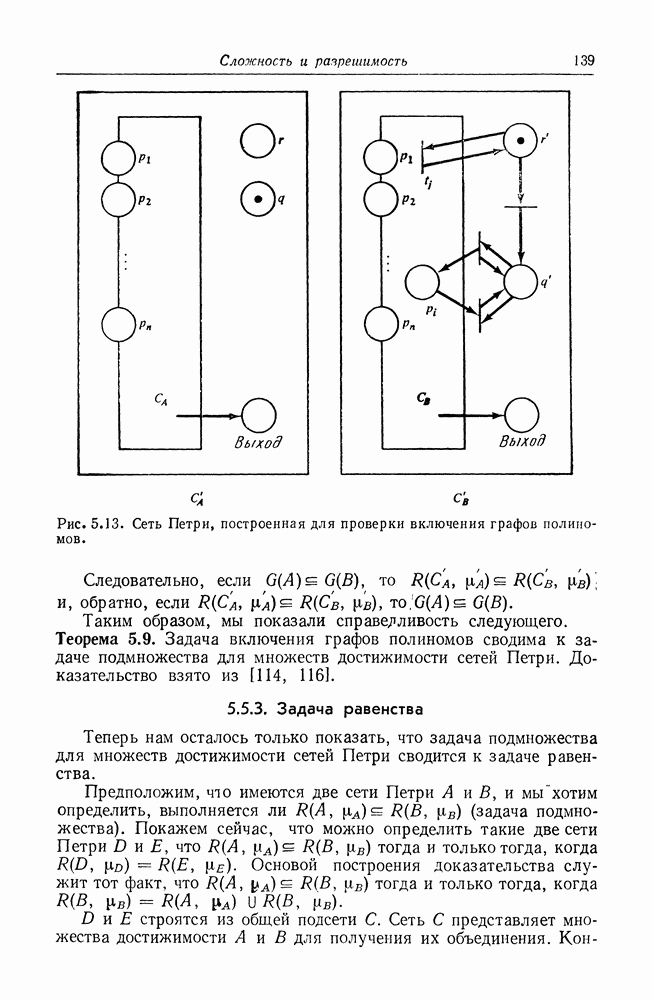
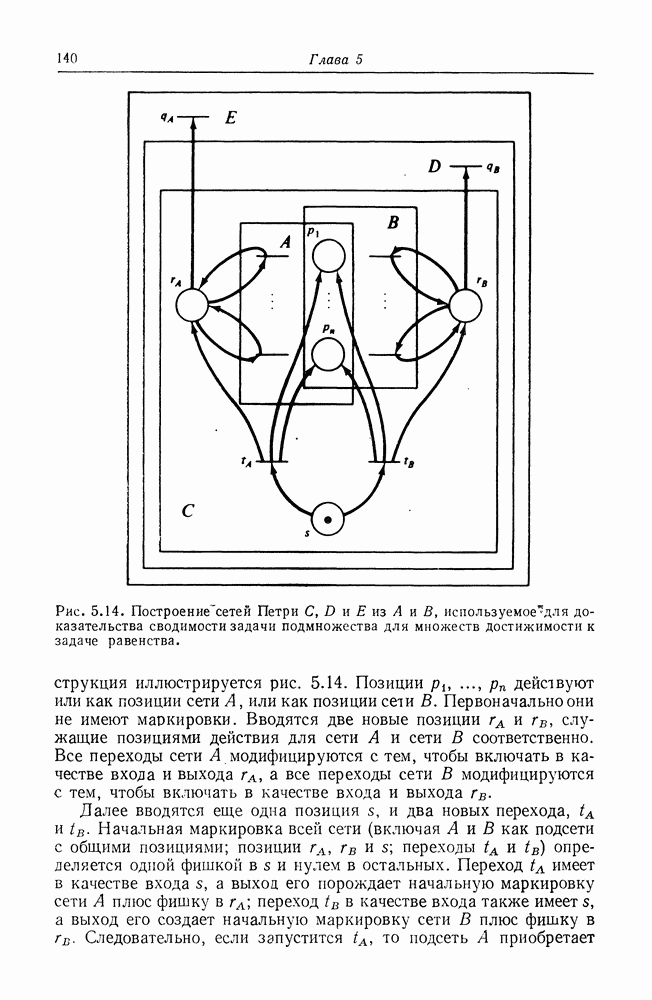
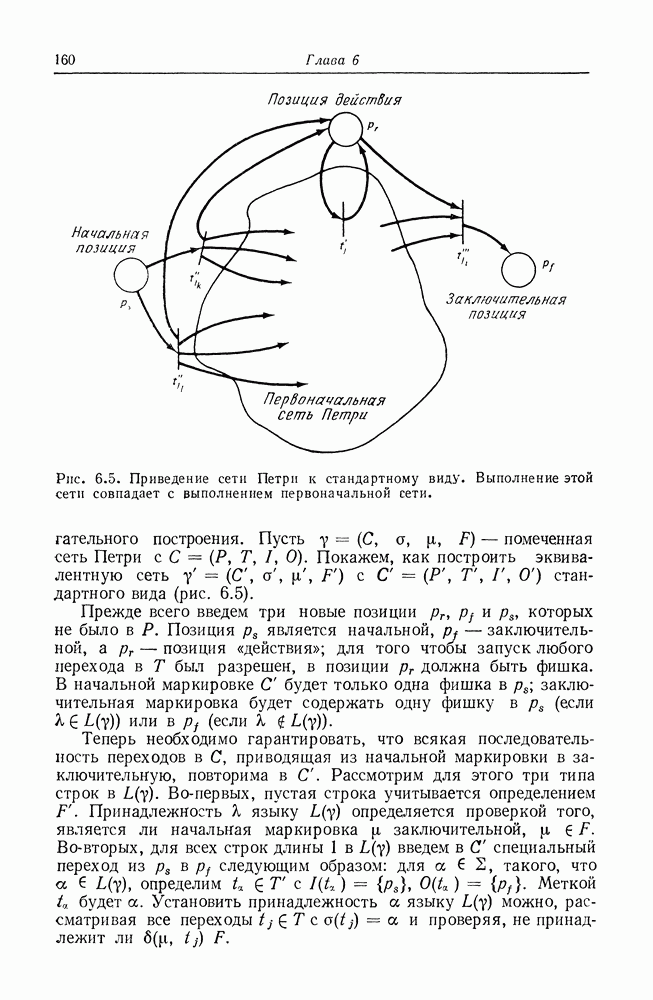
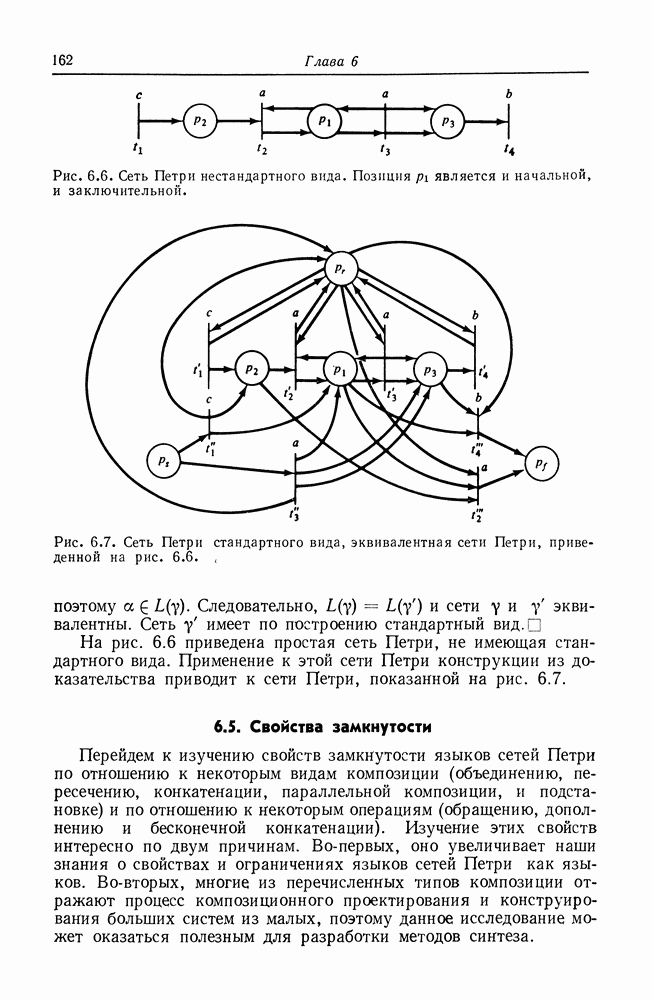
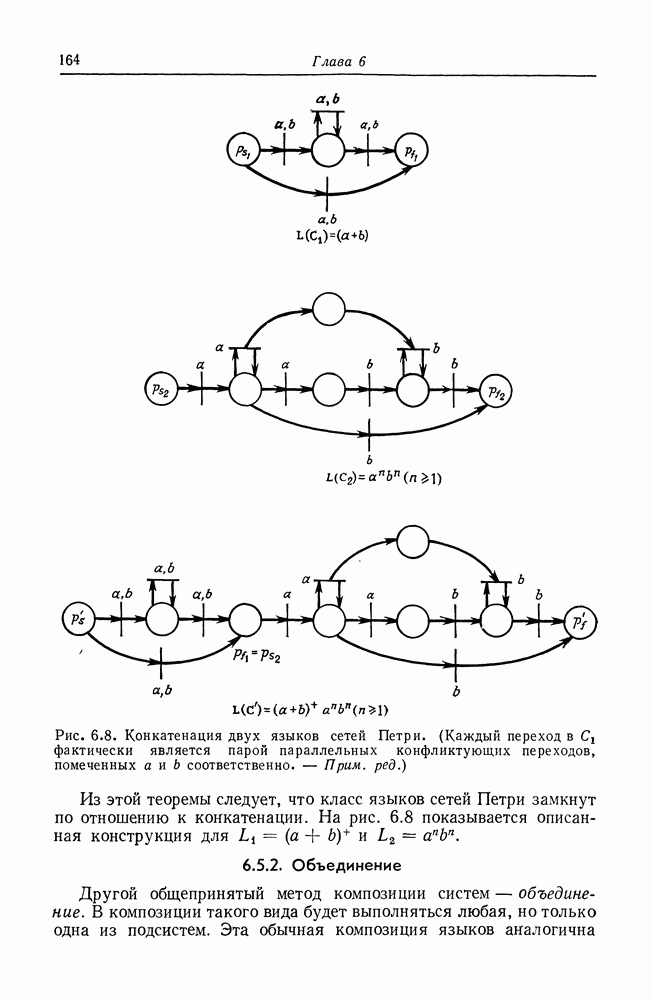
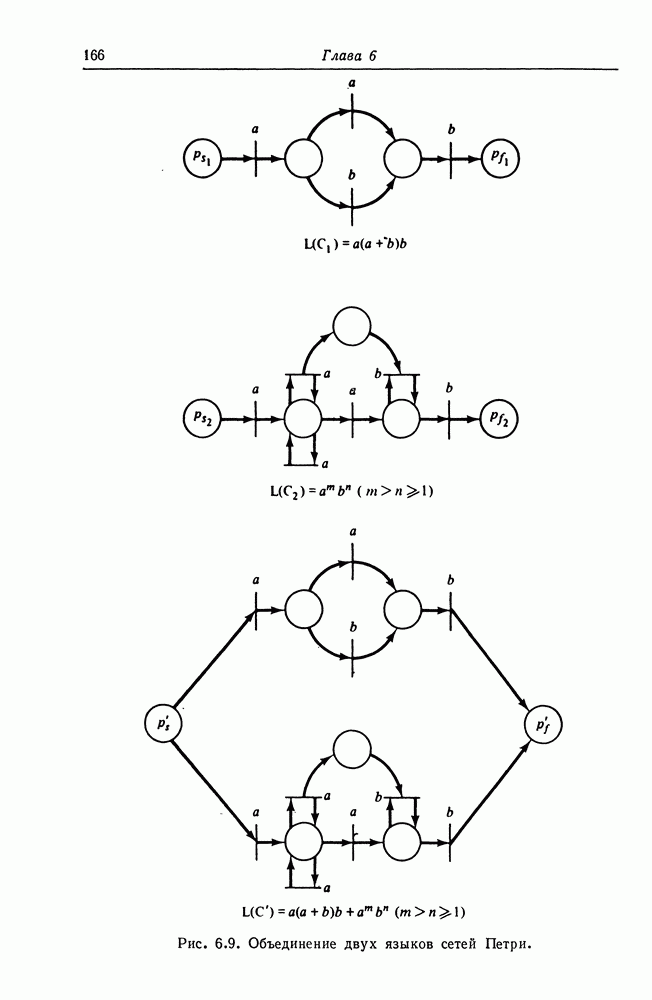
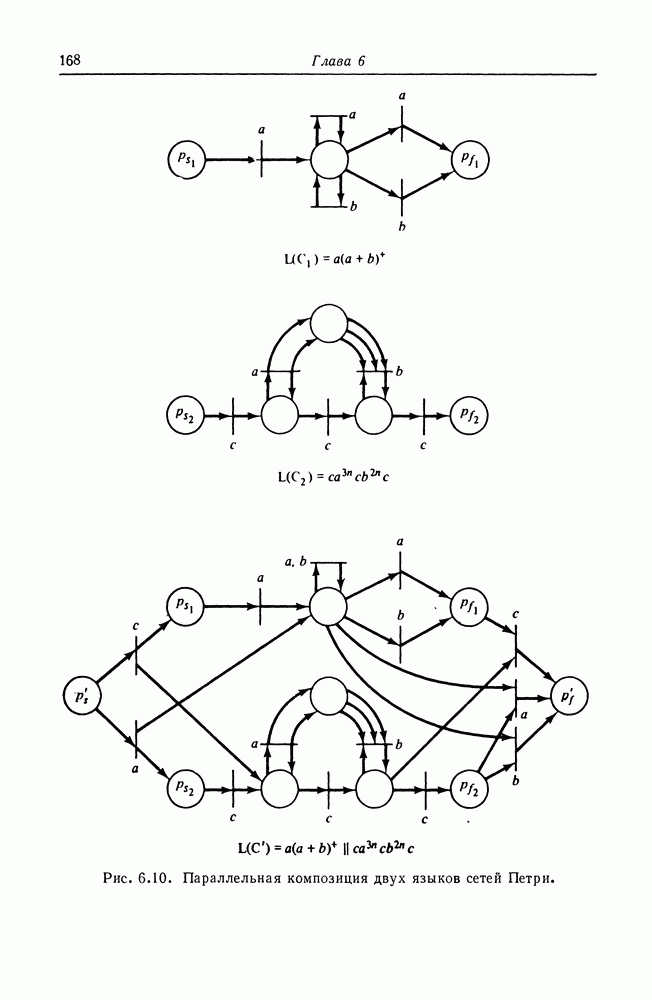
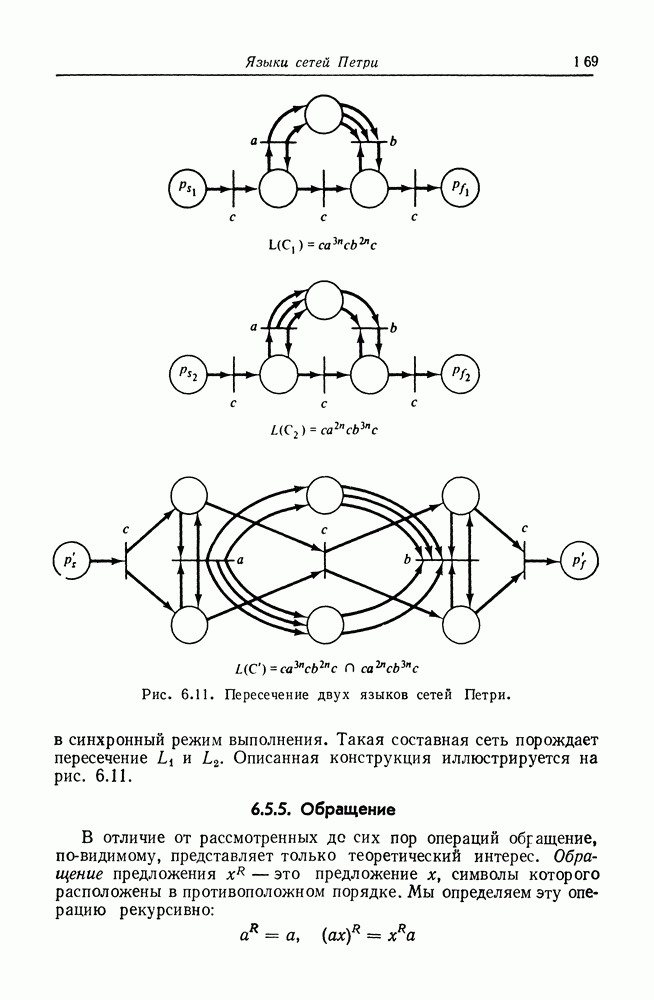
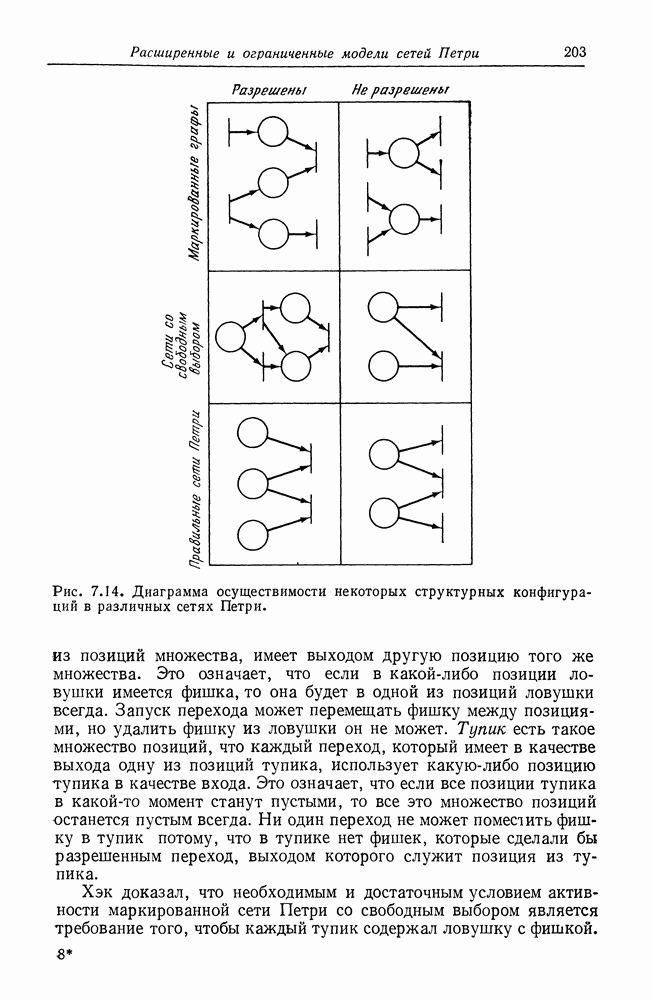
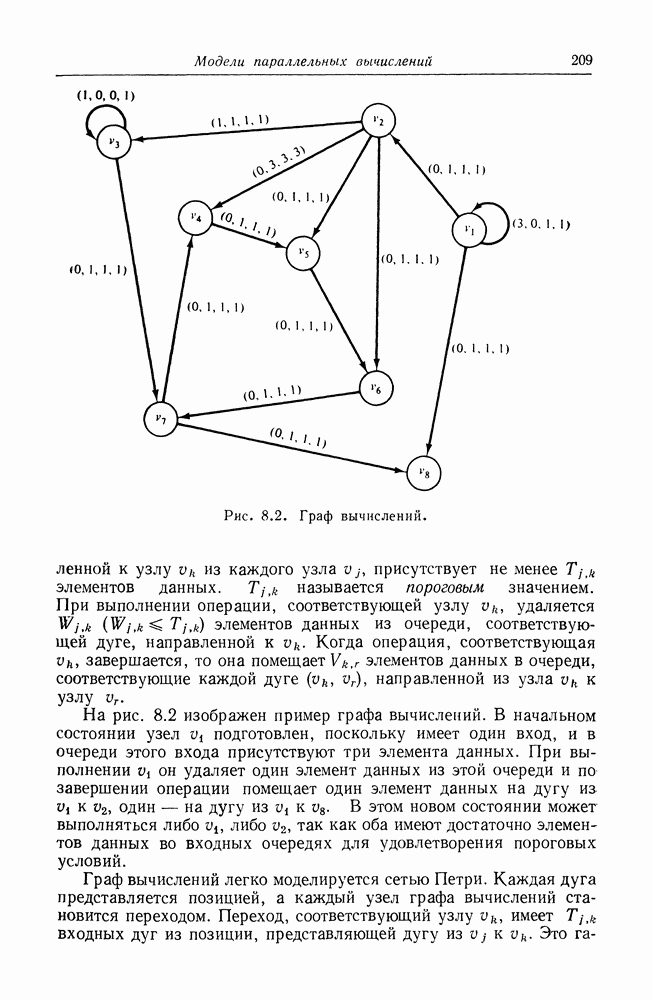
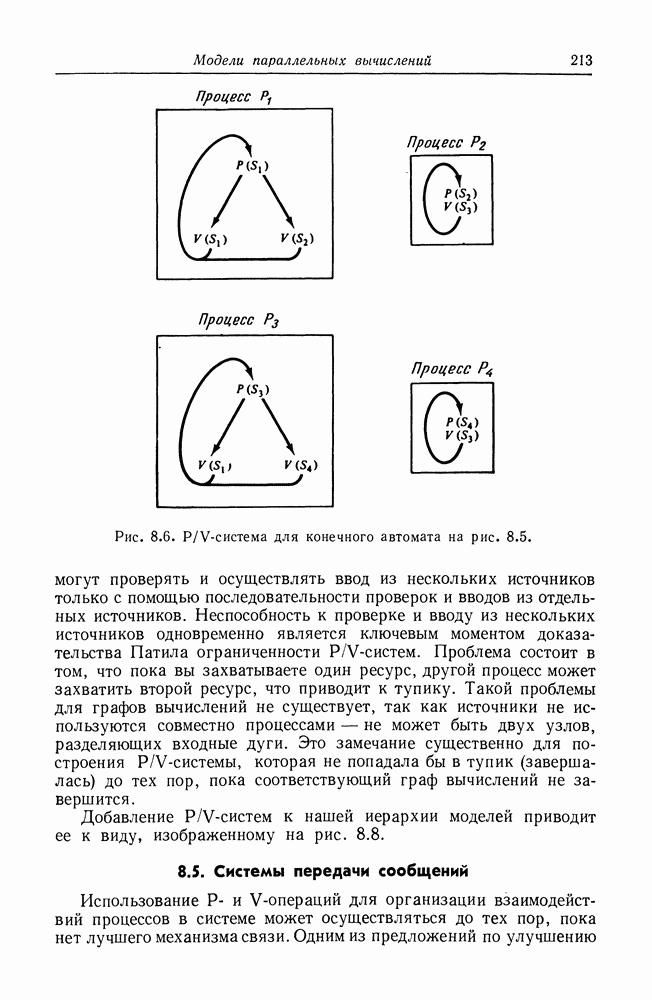
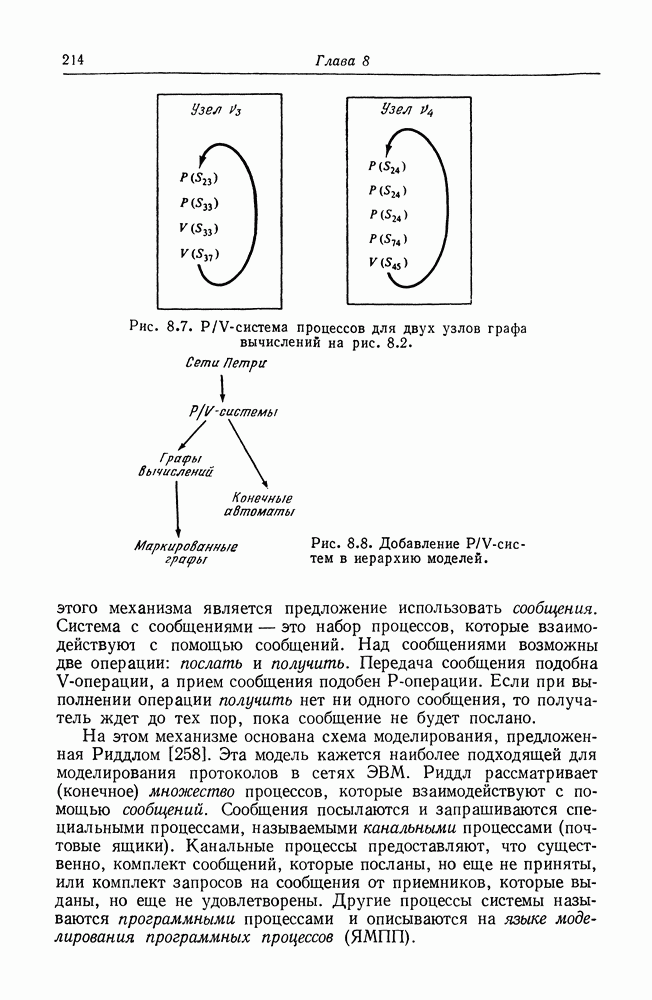
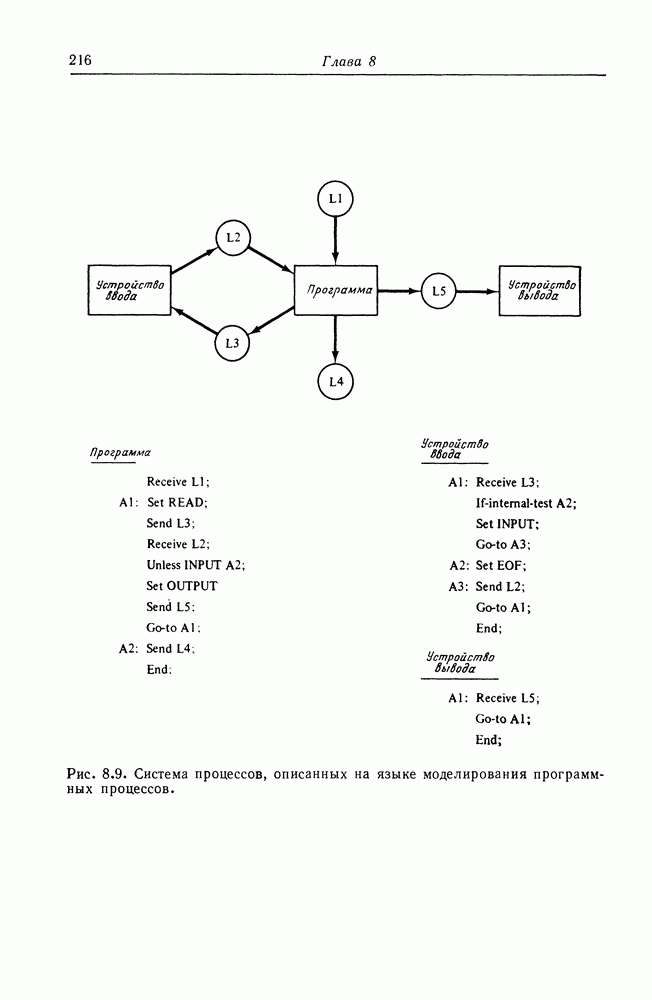
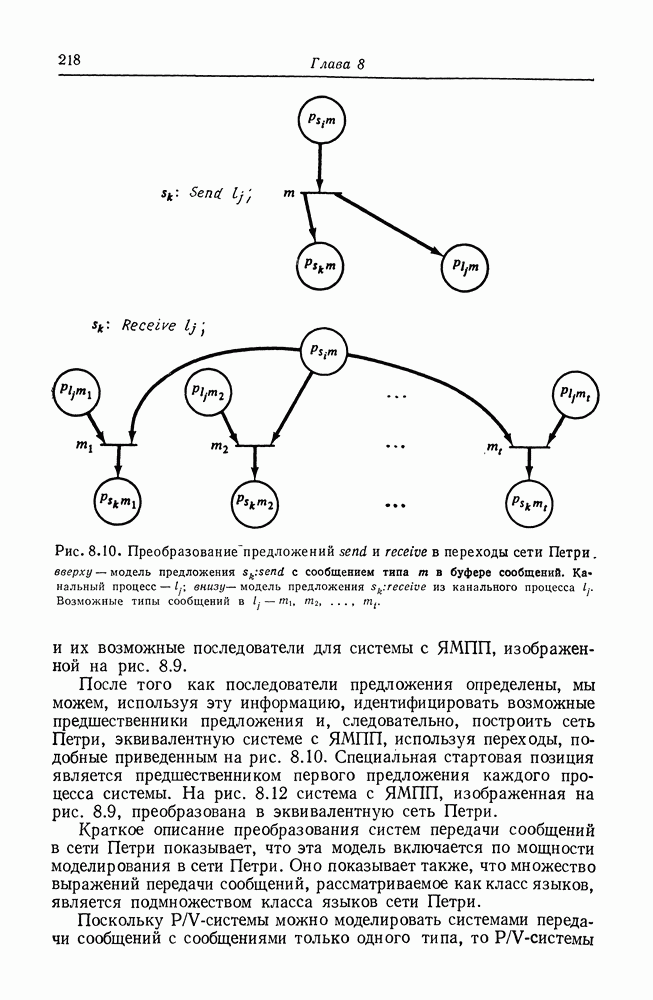
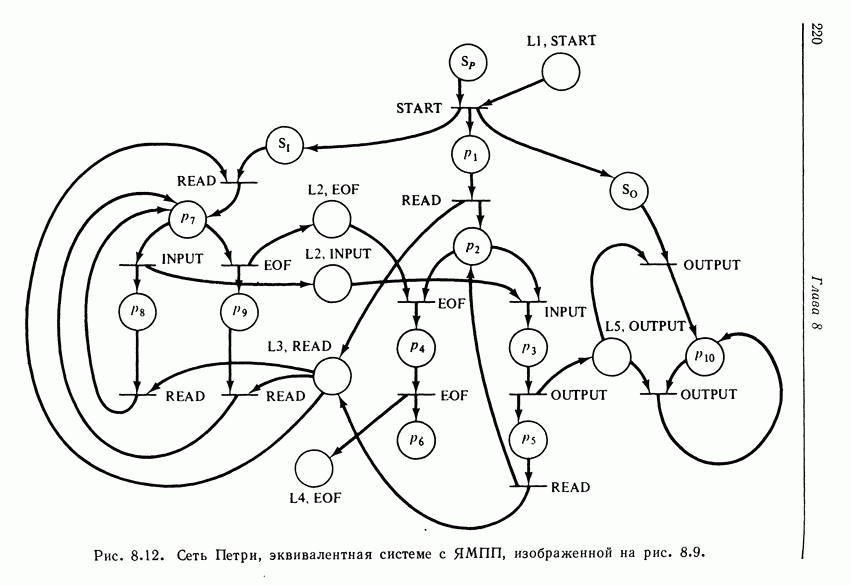
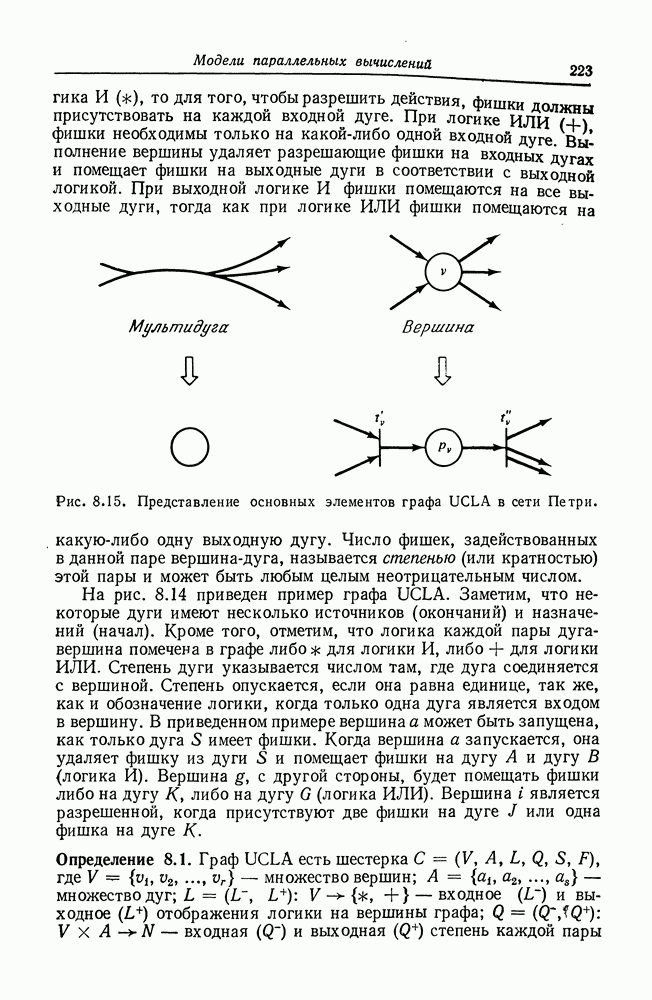
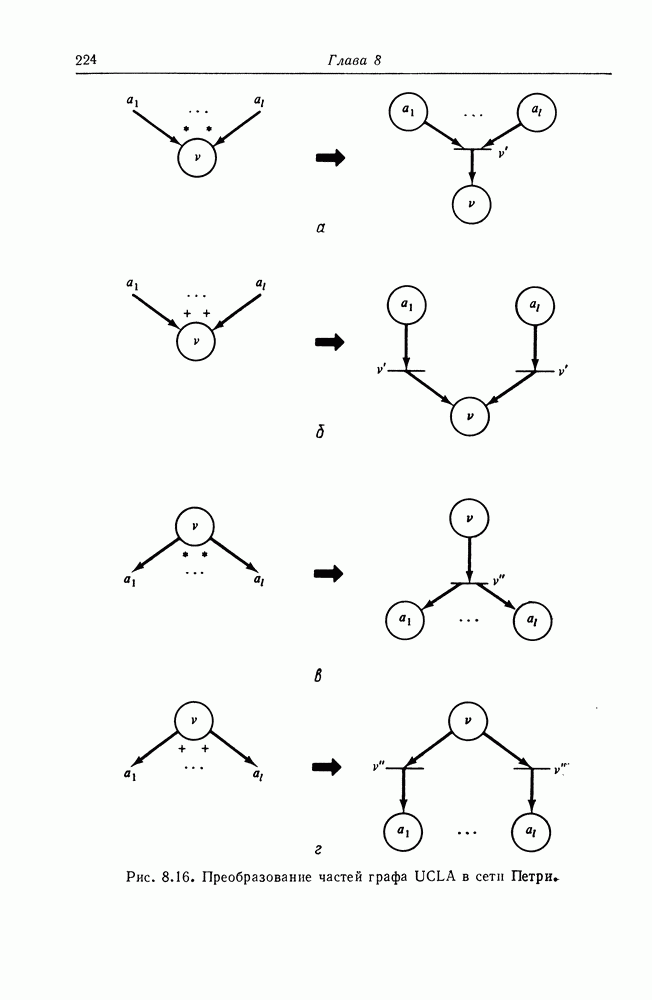
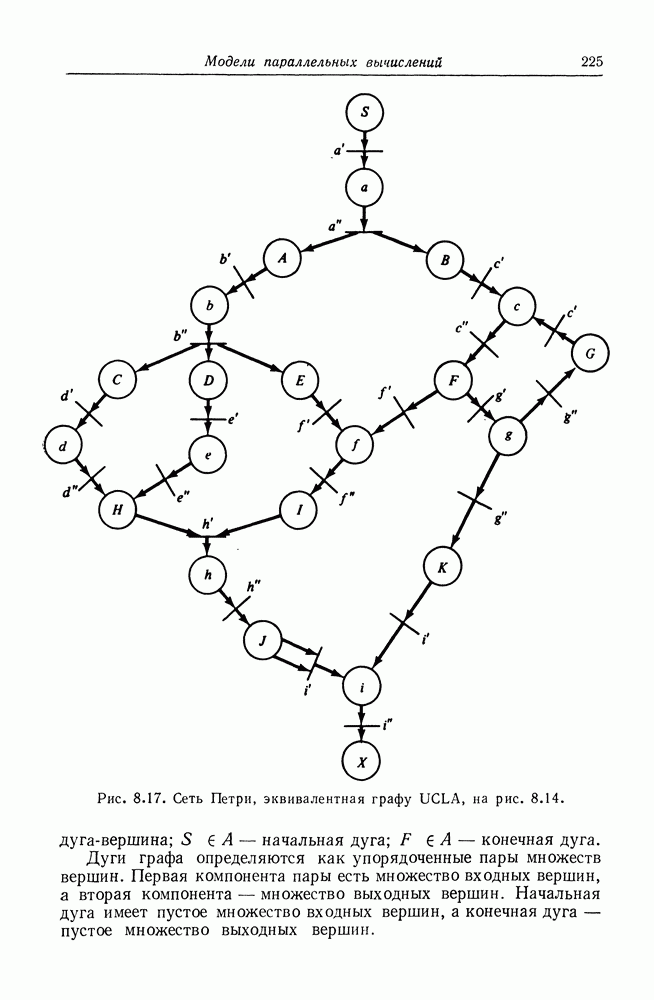
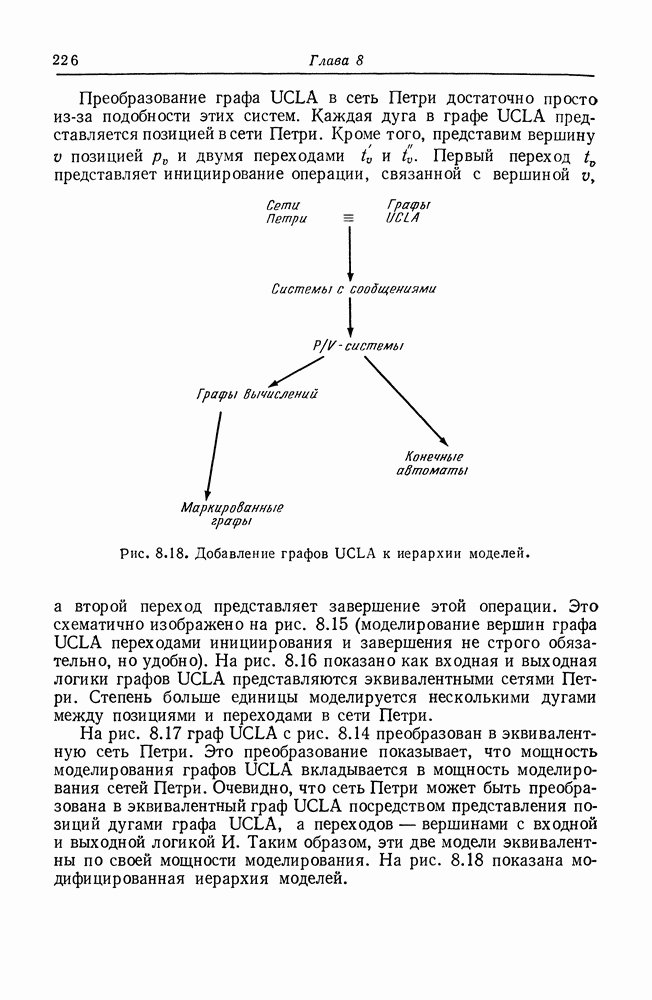
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
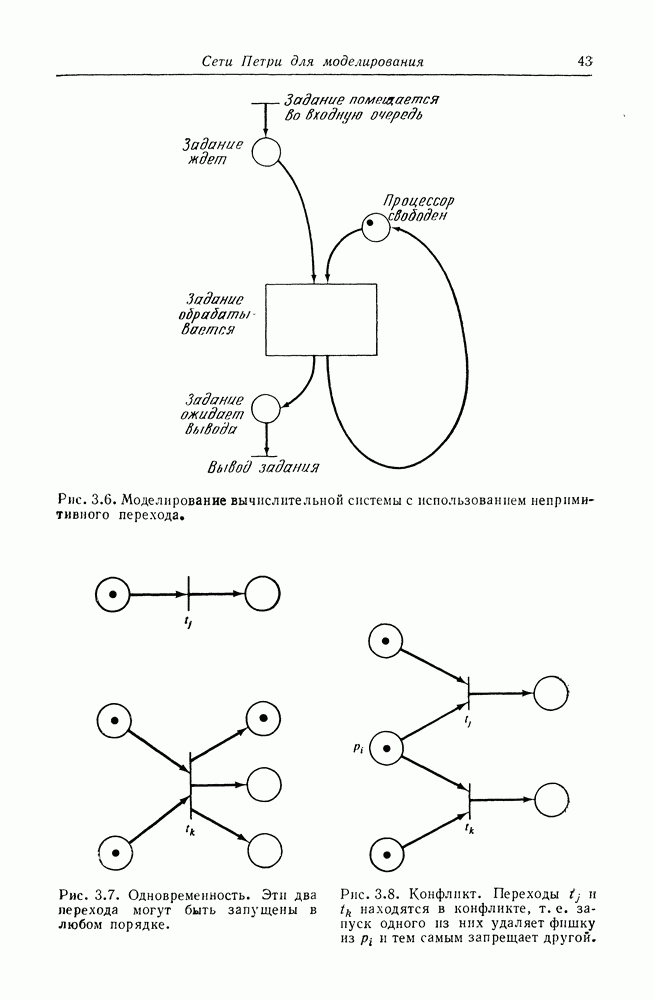
6.6. Языки сетей Петри и другие классы языков
Рассмотрев свойства языков сетей Петри как класса языков, мы обращаемся теперь к исследованию взаимосвязи между языками сетей Петри и другими классами языков. Рассмотрим, в частности,
классы регулярных, контекстно-свободных, контекстно-связанных языков и языков типа 0.
6.6.1. Регулярные языки
Одним из простейших и наиболее изученных классов формальных языков является класс регулярных языков. Эти языки порождаются регулярными грамматиками и конечными автоматами и характеризуются регулярными выражениями. Задачи эквивалентности и включения для двух регулярных языков разрешимы, известны алгоритмы их решения [130].

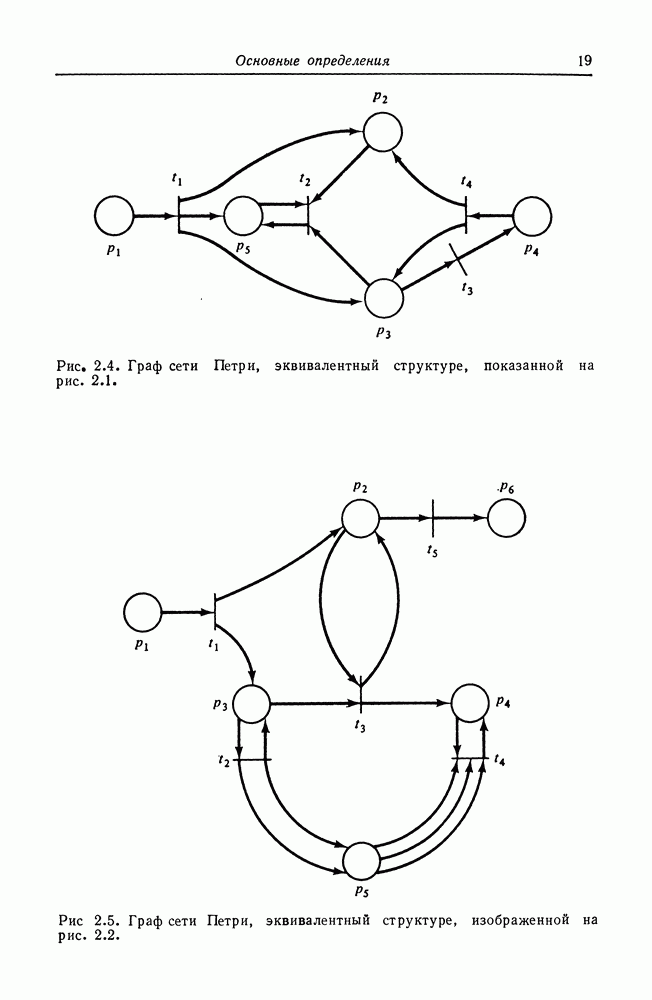
Рис. 6.12. Контекстно-свободный язык сети Петри, не являющийся регулярным.
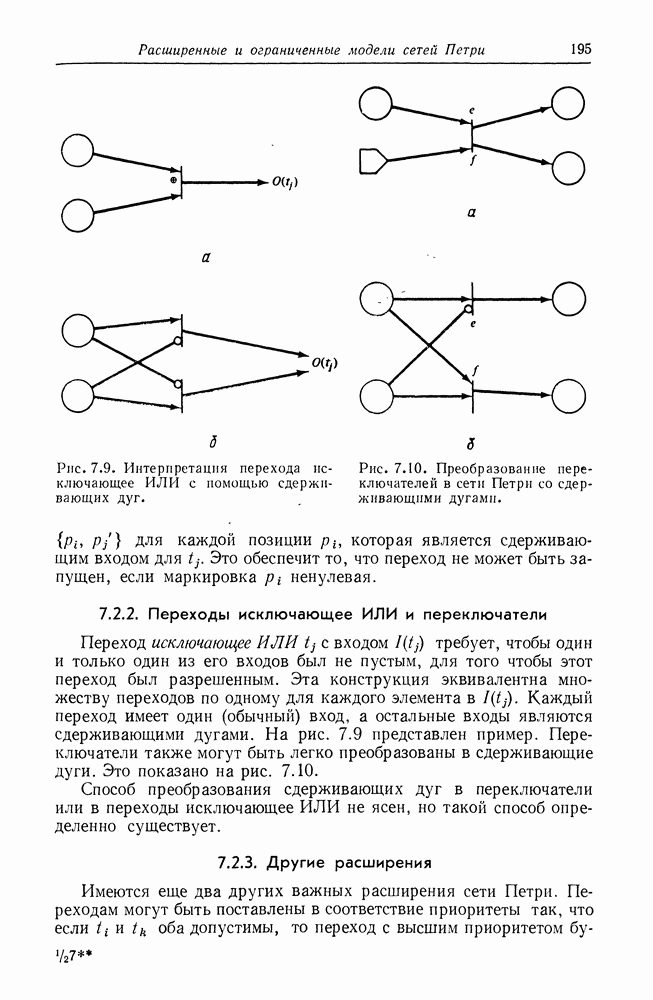
Такой набор желательных свойств языка сделал справедливым следующее утверждение.
Теорема 6.8. Всякий регулярный язык — это язык сети Петри.
Доказательство этой теоремы основано на том, что всякий регулярный язык порождается некоторым конечным автоматом, а мы показали (см. разд. 3.3.1), что всякий конечный автомат можно преобразовать в эквивалентную сеть Петри.
Обратная теорема не верна. На рис. 6.12 изображена сеть Петри, порождающая контекстно-свободный язык  который не является регулярным. Таким образом, не все языки сетей Петри являются регулярными.
который не является регулярным. Таким образом, не все языки сетей Петри являются регулярными.
6.6.2. Контекстно-свободные языки
Сеть на рис. 6.12 свидетельствует о том, что не все сети Петри являются регулярными, поскольку язык показанной сети Петри является контекстно-свободным, но не регулярным. Не все языки сетей Петри являются и контекстно-свободными, о чем
свидетельствует сеть, показанная на рис. 6.13, имеющая контекстно-связанный, но не контекстно-свободный язык. В отличие от случая с регулярными языками существуют также контекстно-свободные языки, не являющиеся языками сетей Петри. Примером такого языка служит контекстно-свободный язык  На основе этого доказывается следующее утверждение.
На основе этого доказывается следующее утверждение.

Рис. 6.13. Контекстно-связанный язык сети Петри, не являющийся контекстно-свободным.
Теорема 6.9. Существуют контекстно-свободные языки, не являющиеся языками сетей Петри.
Доказательство. Допустим, что существует сеть Петри с  позициями и
позициями и  переходами, порождающая язык
переходами, порождающая язык  Пусть
Пусть  число символов в
число символов в  Пусть для входной строки
Пусть для входной строки  равно
равно  т. е. длине строки х. Поскольку возможно
т. е. длине строки х. Поскольку возможно  входных строк х, сеть Петри должна иметь
входных строк х, сеть Петри должна иметь  различных достижимых состояний, получающихся после запуска
различных достижимых состояний, получающихся после запуска  переходов, для того, чтобы запомнить строку х. Если состояний меньше, то для некоторых строк
переходов, для того, чтобы запомнить строку х. Если состояний меньше, то для некоторых строк  Тогда очевидно, что
Тогда очевидно, что  и сеть Петри будет порождать строку
и сеть Петри будет порождать строку  которую не должна порождать.
которую не должна порождать.
В разд. 4.2.2 мы показали, что для каждого перехода существует вектор  такой, что если
такой, что если  определено, то оно принимает значение
определено, то оно принимает значение  Следовательно, после подачи
Следовательно, после подачи  входных символов, т. е. запуска последовательности переходов
входных символов, т. е. запуска последовательности переходов  получим состояние
получим состояние 

Сумму в выражении можно представить другим способом:

где  число запусков перехода
число запусков перехода  в последовательности
в последовательности  вектор запуска). Кроме того, известно, что
вектор запуска). Кроме того, известно, что

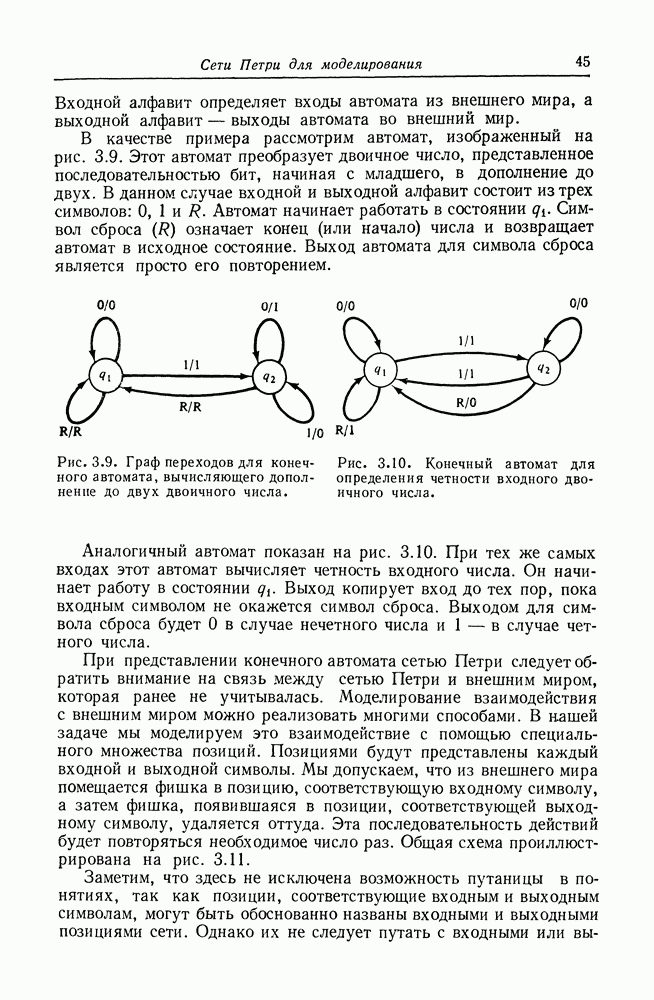
В лучшем случае векторы  будут линейно независимы, и каждый вектор запуска
будут линейно независимы, и каждый вектор запуска  будет представлять единственное состояние
будет представлять единственное состояние  Так как сумма коэффициентов равна
Так как сумма коэффициентов равна  вектор
вектор  образует разбиение целого
образует разбиение целого  на
на  частей. Как показал Кнут [156], число разбиений целого
частей. Как показал Кнут [156], число разбиений целого  на
на  частей равно
частей равно

Теперь, поскольку

то в множестве достижимости после запуска последовательности переходов длины  имеется строго меньше, чем
имеется строго меньше, чем  достижимых состояний. Тогда для достаточно большого
достижимых состояний. Тогда для достаточно большого  имеем
имеем

и, следовательно, невозможно иметь  различных состояний для всякой из
различных состояний для всякой из  возможных входных строк. Таким образом, никакая сеть Петри не может порождать язык
возможных входных строк. Таким образом, никакая сеть Петри не может порождать язык 
Доказательство этого факта проливает некоторый свет на ограниченность сетей Петри как машин, порождающих языки, и, следовательно, на природу языков сетей Петри. В сетях Петри нет возможности запомнить произвольно длинную последовательность произвольных символов. Из доказательства становится очевидно, что в сетях Петри можно запомнить последовательности ограниченной длины (но это возможно и в конечных автоматах). Другой особенностью сетей Петри является способность запоминать число появлений символа, как, например, в языке  в пределах, не доступных для систем, порождающих регулярные и контекстно-свободные языки. Однако сети Петри не обладают «объемом магазинной памяти», необходимым для порождения контекстно-свободных языков. Скорость роста пространства достижимых состояний с ростом длины входной строки для сетей Петри комбинаторна, но не экспоненциальна, т. е. «объема магазинной памяти» недостаточно.
в пределах, не доступных для систем, порождающих регулярные и контекстно-свободные языки. Однако сети Петри не обладают «объемом магазинной памяти», необходимым для порождения контекстно-свободных языков. Скорость роста пространства достижимых состояний с ростом длины входной строки для сетей Петри комбинаторна, но не экспоненциальна, т. е. «объема магазинной памяти» недостаточно.
Причина того, что сети Петри способны порождать языки, которые не могут порождаться автоматами с магазинной памятью, несмотря на меньший размер пространства состояний, заключается в более гибких взаимосвязях между состояниями сети Петри по сравнению с ограниченными путями между состояниями в автомате с магазинной памятью. Это объясняется ограничениями в автомате с магазинной памятью на доступ только к верхнему элементу магазина, тогда как в сетях Петри возможно обращение к любому ее счетчику в любой момент времени.
Теперь, когда мы показали, что не все контекстно-свободные языки являются языками сетей Петри и не все языки сетей Петри являются контекстно-свободными, естественно возникает вопрос: что из себя представляет класс языков, являющихся одновременно контекстно-свободными и языками сетей Петри? В настоящее время мы не в состоянии дать полный ответ на этот вопрос, но известна некоторая информация о языках, входящих в пересечение упомянутых классов. Одним подмножеством класса контекстно-свободных языков сетей Петри является класс регулярных языков. Другим — множество ограниченных контекстно-свободных языков, которые исследовались Гинзбургом [99].
6.6.3. Ограниченные контекстно-свободные языки
Контекстно-свободный язык  называется ограниченным контекстно-свободным, если в
называется ограниченным контекстно-свободным, если в  имеются такие слова (строки)
имеются такие слова (строки)  что
что

Термин «ограниченный» относится к конечному числу слов 
Гинзбург разработал детально описанную процедуру проверки свойств ограниченных контекстно-свободных языков. Он заметил, что в то время не было сведений о неразрешимых задачах, касающихся ограниченных контекстно-свободных языков.
Ограниченные контекстно-свободные языки характеризуются следующей теоремой, предложенной Гинзбургом [99, теорема 5.4].
Теорема 6.10. Семейство ограниченных контекстно-свободных языков является наименьшим семейством множеств, определяемых следующим образом:
1. Если  конечное подмножество 2, то
конечное подмножество 2, то  ограниченный контекстно-свободный язык.
ограниченный контекстно-свободный язык.
2. Если  ограниченные контекстно-свободные языки, то
ограниченные контекстно-свободные языки, то  ограниченные контекстно-свободные языки.
ограниченные контекстно-свободные языки.
3. Если  ограниченный контекстно-свободный язык и
ограниченный контекстно-свободный язык и  то
то  ограниченный контекстно-свободный язык.
ограниченный контекстно-свободный язык.
Мы уже показали (разд. 3.3.1), что всякий конечный автомат, а также всякий регулярный язык и всякое конечное подмножество  являются языками сетей Петри. В разд. 6.5.1 и 6.5.2 показано, что языки сетей Петри замкнуты по отношению к конкатенации и объединению. Следовательно, необходимо показать только, что п. 3 также выполняется для языков сетей Петри. С этой целью построим сеть Петри
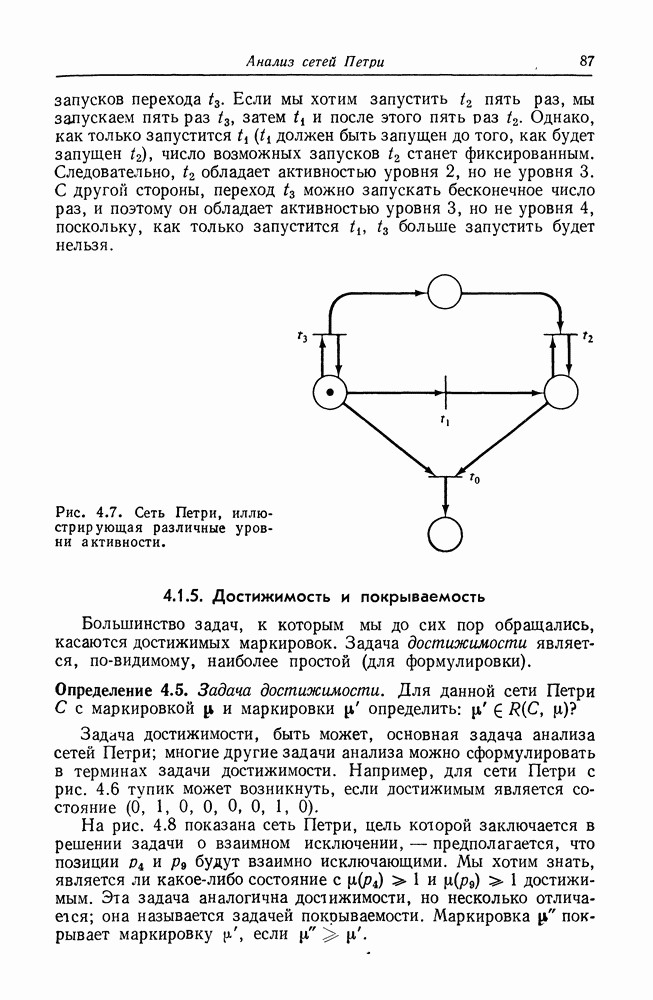
являются языками сетей Петри. В разд. 6.5.1 и 6.5.2 показано, что языки сетей Петри замкнуты по отношению к конкатенации и объединению. Следовательно, необходимо показать только, что п. 3 также выполняется для языков сетей Петри. С этой целью построим сеть Петри  порождающую язык
порождающую язык  по данным сетям Петри стандартного вида
по данным сетям Петри стандартного вида  порождающим
порождающим  соответственно, у объединяет сети Петри
соответственно, у объединяет сети Петри  и новую позицию
и новую позицию  таким образом, что всякий раз после выполнения
таким образом, что всякий раз после выполнения  помещается фишка. Позиция
помещается фишка. Позиция  служит счетчиком числа выполнений сети
служит счетчиком числа выполнений сети  После выполнения необходимого числа раз сети
После выполнения необходимого числа раз сети  выполнится
выполнится  наконец, выполняется повторно
наконец, выполняется повторно  удаляя каждый раз одну фишку из
удаляя каждый раз одну фишку из  Поскольку входная строка порождается корректно, только если сеть Петри пуста (за исключением
Поскольку входная строка порождается корректно, только если сеть Петри пуста (за исключением  определенного, как
определенного, как  мы уверены, что число выполнений
мы уверены, что число выполнений  равно.
равно.
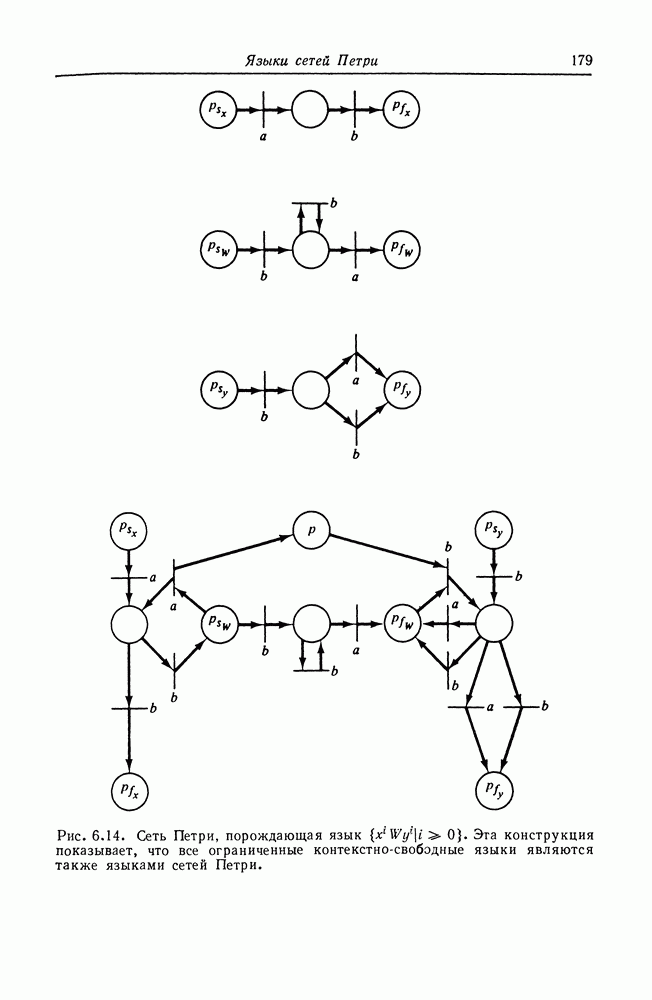
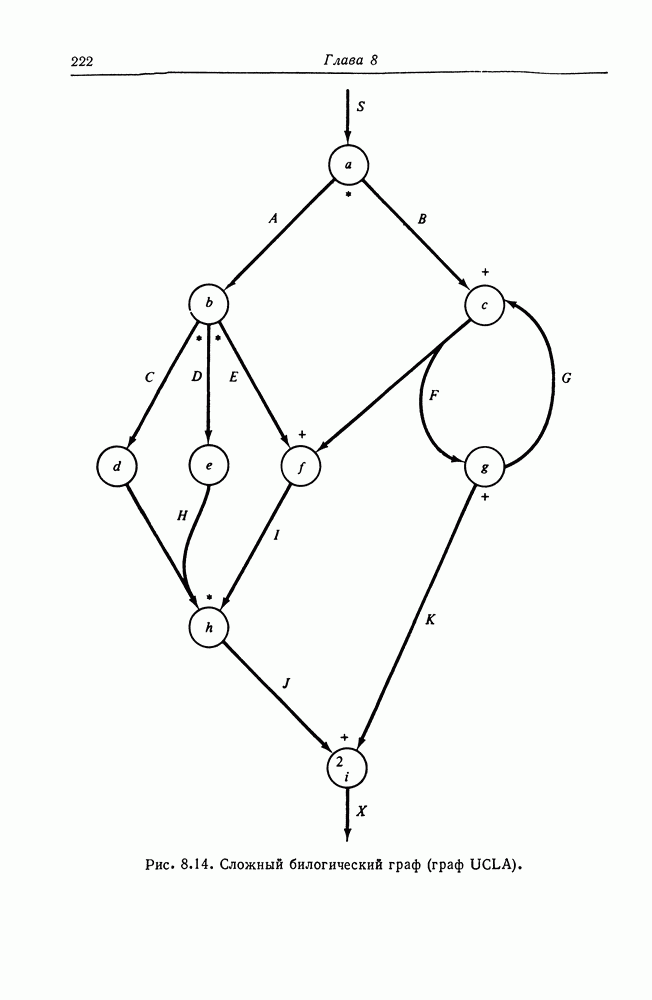
Эта конструкция, иллюстрируемая на рис. 6.14 для  показывает, что
показывает, что  язык сети Петри. Таким образом, любой ограниченный контекстно-свободный язык — это язык сети Петри.
язык сети Петри. Таким образом, любой ограниченный контекстно-свободный язык — это язык сети Петри.
Существуют ли контекстно-свободные языки, являющиеся языками сетей Петри, но не являющиеся ограниченными? К сожалению, ответ положителен. Гинзбург показал, что регулярное выражение  не является ограниченным контекстно-свободным языком. Так как этот язык — контекстно-свободный язык сети Петри, очевидно, что ограниченные контекстно-свободные языки являются лишь собственным подмножеством семейства контекстно-свободных языков сетей Петри. Кроме того, язык
не является ограниченным контекстно-свободным языком. Так как этот язык — контекстно-свободный язык сети Петри, очевидно, что ограниченные контекстно-свободные языки являются лишь собственным подмножеством семейства контекстно-свободных языков сетей Петри. Кроме того, язык  являющийся контекстно-свободным, не ограничен и не регулярен. Для полной характеризации множества контекстно-свободных языков сетей Петри необходимы дальнейшие исследования.
являющийся контекстно-свободным, не ограничен и не регулярен. Для полной характеризации множества контекстно-свободных языков сетей Петри необходимы дальнейшие исследования.
Существование и регулярных множеств, и ограниченных контекстно-свободных языков в качестве подмножеств класса языков сетей Петри оказывается полезным, поскольку оба класса языков имеют желательные свойства и некоторые благоприятные для анализа характеристики.
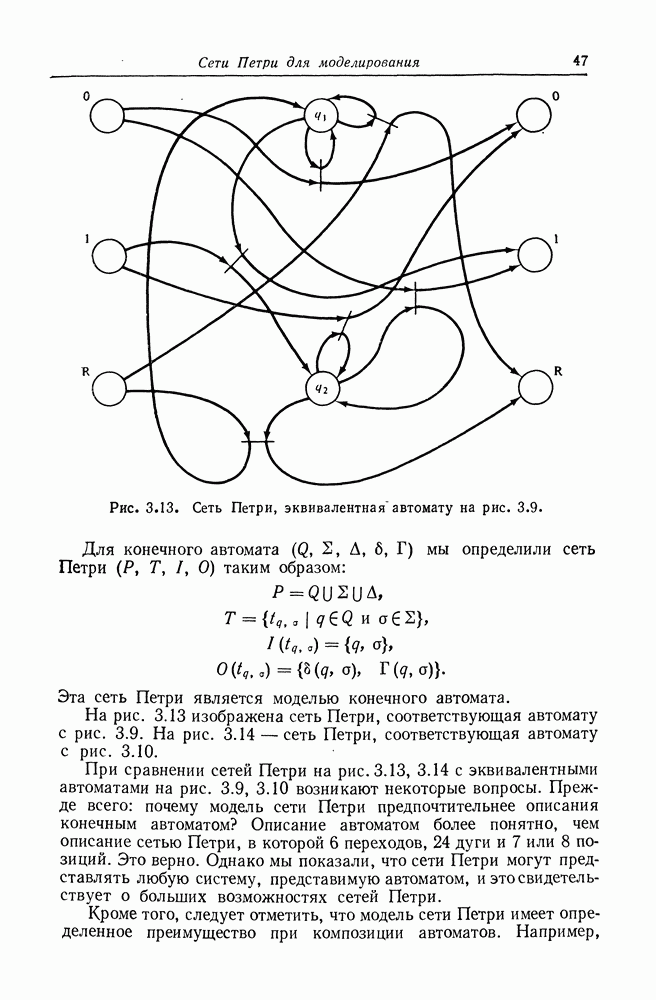
6.6.4. Контекстно-связанные языки
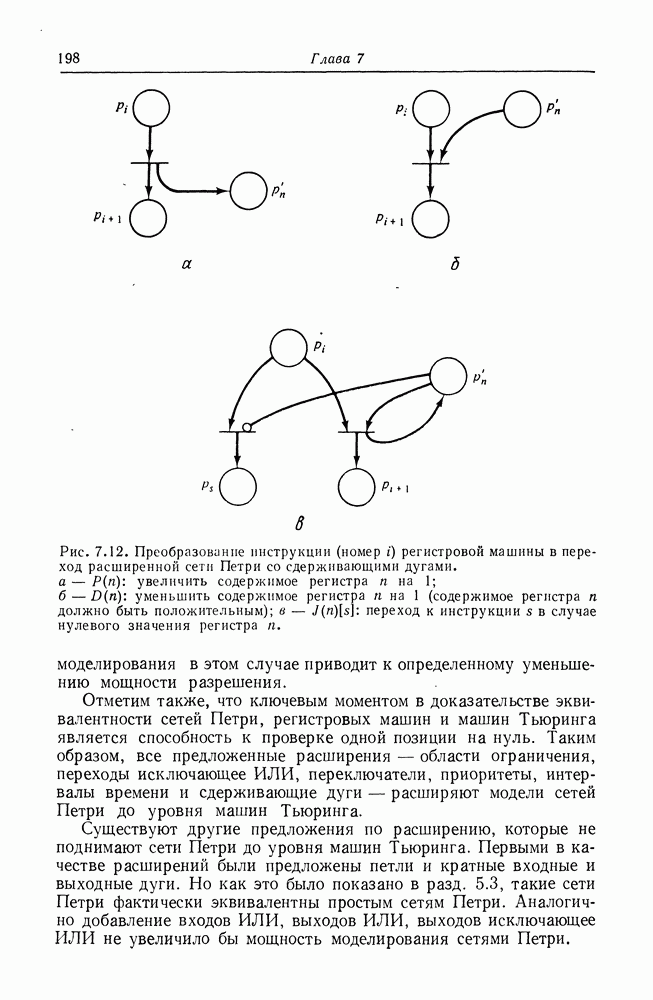
Мы исследовали взаимосвязь языков сетей Петри с регулярными языками и с контекстно-свободными языками. Обратимся теперь к контекстно-связанным языкам. На рис. 6.13 показан язык сети Петри, являющийся контекстно-связанным; мы докажем что все

(кликните для просмотра скана)
языки сетей Петри — контекстно-связанные. Поскольку известно, что все контекстно-свободные языки являются контекстно-связанными и существуют контекстно-свободные языки, не являющиеся языками сетей Петри, приходим к выводу, что существуют контекстно-связанные языки, не являющиеся языками сетей Петри. Следовательно, включение — собственное.
Теорема 6.11. Все языки сетей Петри являются контекстно-связанными.
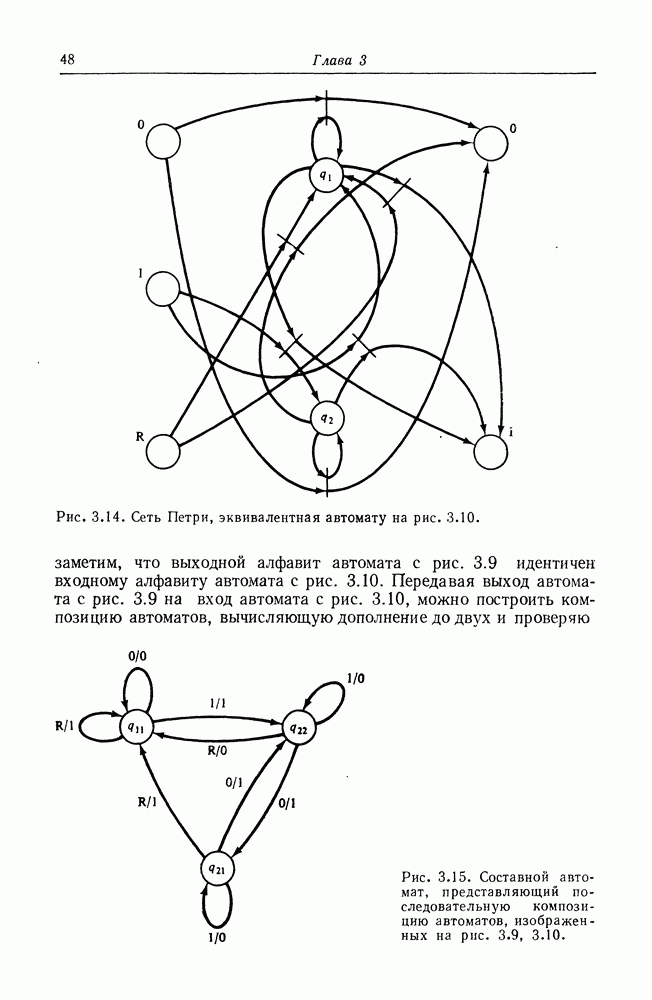
Доказательство того, что все языки сетей Петри являются контекстно-связанными, довольно сложно. Существуют два способа показать, что язык контекстно-связанный: построить контекстносвязанную грамматику, порождающую его, или определить недетерминированный линейно-ограниченный автомат, порождающий этот язык. Питерсон [236] показал, как определяется контекстно-связанная грамматика, порождающая язык сети Петри. Здесь мы показываем как линейно-ограниченный автомат может породить язык сети Петри.
Линейно-ограниченный автомат подобен машине Тьюринга. Он имеет конечное множество состояний, головку чтения/записи и (бесконечную в обе стороны) ленту. Ограничением, отличающим его от машины Тьюринга, служит то, что длина участка ленты, который можно использовать, ограничивается линейной функцией от длины входной строки. В этом смысле он подобен автомату с магазинной памятью, порождающему контекстно-свободный язык (поскольку максимальный размер магазина ограничен линейной функцией от входной строки), за исключением того, что линейноограниченный автомат имеет произвольный доступ к своей памяти, тогда как магазинный автомат имеет доступ к памяти только с одного конца.
Для порождения языка сети Петри ее можно промоделировать, запоминая после каждого входного символа число фишек в каждой позиции. Какова скорость роста числа фишек как функции от длины входной строки? Рассмотрим число фишек, полученное после  запусков переходов. Это число, обозначаемое с, для последовательности переходов
запусков переходов. Это число, обозначаемое с, для последовательности переходов  равно
равно

Так как числа  следовательно,
следовательно,  (мощности входного и выходного комплектов) фиксированы для данной сети Петри, то существует максимальное значение разности I:
(мощности входного и выходного комплектов) фиксированы для данной сети Петри, то существует максимальное значение разности I:

Таким образом, 
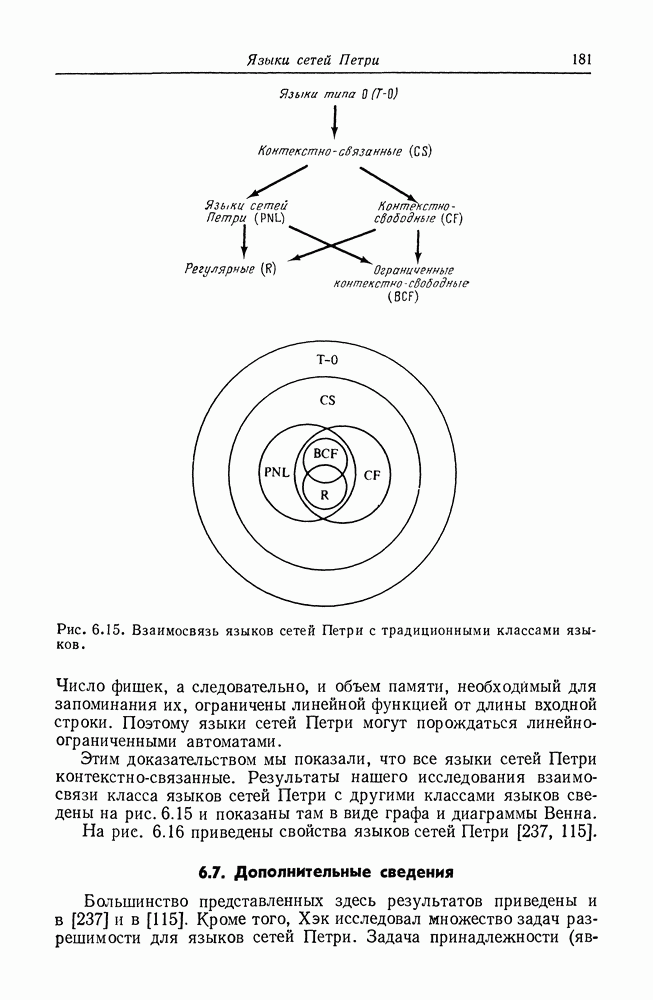
Рис. 6.15. (см. скан) Взаимосвязь языков сетей Петри с традиционными классами языков.
Число фишек, а следовательно, и объем памяти, необходимый для запоминания их, ограничены линейной функцией от длины входной строки. Поэтому языки сетей Петри могут порождаться линейноограниченными автоматами.
Этим доказательством мы показали, что все языки сетей Петри контекстно-связанные. Результаты нашего исследования взаимосвязи класса языков сетей Петри с другими классами языков сведены на рис. 6.15 и показаны там в виде графа и диаграммы Венна.
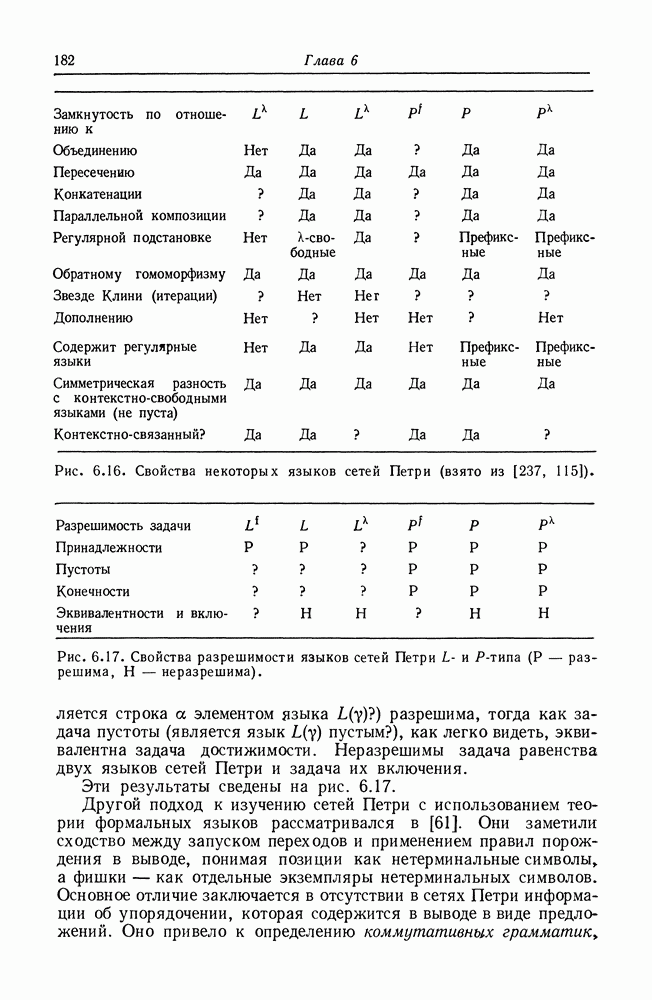
На рис. 6.16 приведены свойства языков сетей Петри [237, 115].
6.7. Дополнительные сведения
Большинство представленных здесь результатов приведены и в [237] и в [115]. Кроме того, Хэк исследовал множество задач разрешимости для языков сетей Петри. Задача принадлежности

Рис. 6.16. Свойства некоторых языков сетей Петри (взято из 

Рис. 6.17. Свойства разрешимости языков сетей Петри  и
и  -типа (
-типа ( разрешима,
разрешима,  неразрешима).
неразрешима).
(является строка а элементом языка  разрешима, тогда как задача пустоты (является язык
разрешима, тогда как задача пустоты (является язык  пустым?), как легко видеть, эквивалентна задача достижимости. Неразрешимы задача равенства двух языков сетей Петри и задача их включения.
пустым?), как легко видеть, эквивалентна задача достижимости. Неразрешимы задача равенства двух языков сетей Петри и задача их включения.
Эти результаты сведены на рис. 6.17.
Другой подход к изучению сетей Петри с использованием теории формальных языков рассматривался в [61]. Они заметили сходство между запуском переходов и применением правил порождения в выводе, понимая позиции как нетерминальные символы, а фишки — как отдельные экземпляры нетерминальных символов. Основное отличие заключается в отсутствии в сетях Петри информации об упорядочении, которая содержится в выводе в виде предложений. Оно привело к определению коммутативных грамматик,
изоморфных сетям Петри. Кроме того, в [61] рассматривалась взаимосвязь сетей Петри с матричными [1], контекстно-рассеянными, нетерминально-ограниченными языками; языками, ограниченными по выводу; равноматричными языками и языками Сциларда. Нетрудно видеть, например, что класс V совпадает с множеством языков Сциларда матричных контекстно-свободных языков [64, 131].
6.8. Замечания к литературе
Имеются три хороших исследования языков сетей Петри: работы [237, 238], вероятно, менее труднодоступные, чем [115] (последнее исследование более строгое и полное); [61] — очень труднодоступная, но прекрасная работа, хорошо продуманная и изложенная.
6.9. Темы для дальнейшего изучения
Хотя в исследовании свойств языков сетей Петри сделано уже немало, многое еще предстоит сделать. Из всех определенных классов языков изучены только два  и
и  -типа, и они только для обычных сетей. Было определено несколько подмножеств множества обычных сетей Петри: маркированные графы, бесконфликтные сети, простые сети, сети со свободным выбором
-типа, и они только для обычных сетей. Было определено несколько подмножеств множества обычных сетей Петри: маркированные графы, бесконфликтные сети, простые сети, сети со свободным выбором  Каждый из этих классов сетей Петри, по-видимому, имеет свой класс языков с присущими им отличительными особенностями. Некоторые исследования этих классов уже проведены. Известно [115], что классы
Каждый из этих классов сетей Петри, по-видимому, имеет свой класс языков с присущими им отличительными особенностями. Некоторые исследования этих классов уже проведены. Известно [115], что классы  для простых сетей Петри (без петель и кратных дуг, все комплекты — множества, и для каждого
для простых сетей Петри (без петель и кратных дуг, все комплекты — множества, и для каждого  идентичны соответствующим классам для обычных сетей Петри. Нетрудно видеть также, что классы
идентичны соответствующим классам для обычных сетей Петри. Нетрудно видеть также, что классы  не изменятся при ограничении сетей до сетей со свободным выбором (см. разд. 7.4.3). Остаются не изученными еще многие интересные случаи. В частности, языки, порождаемые маркированными графами или в общем случае бесконфликтными сетями, как оказалось, имеют структуру, напоминающую структуру детерминированных контекстно-свободных языков, их исследование многообещающе.
не изменятся при ограничении сетей до сетей со свободным выбором (см. разд. 7.4.3). Остаются не изученными еще многие интересные случаи. В частности, языки, порождаемые маркированными графами или в общем случае бесконфликтными сетями, как оказалось, имеют структуру, напоминающую структуру детерминированных контекстно-свободных языков, их исследование многообещающе.
Еще одна важная открытая задача касается отличия между  -свободными языками
-свободными языками  и неограниченными языками
и неограниченными языками  Например, не известно, выполняется ли
Например, не известно, выполняется ли  или нет.
или нет.
1. Выберите класс языков сетей Петри, отличный от языков  -типа, и разработайте его теорию.
-типа, и разработайте его теорию.
2. Определите все множество взаимосвязей между 12 классами языков сетей Петри, в частности для каждой пары классов языков сетей Петри, или покажите, что один класс содержится в другом, или найдите язык, находящийся в одном классе и не присутствующий в другом.
3. Рассмотрите возможность присвоения меток позициям сети Петри, а не переходам. Этот подход использовался в [104]. Определите осуществимость такого подхода и, если он возможен, разработайте новую теорию языков позиций сетей Петри.
4. Разработайте теорию языков сетей Петри, в которой сети Петри рассматриваются не как порождающие язык, а как распознающие его.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ГЛАВА 1. ВВЕДЕНИЕ
- ГЛАВА 2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
- 2.1. Структура сети Петри
- 2.2. Графы сетей Петри
- 2.3. Маркировка сетей Петри
- 2.4. Правила выполнения сетей Петри
- 2.5. Пространство состояний сети Петри
- 2.6. Альтернативные формы определения сетей Петри
- ГЛАВА 3. СЕТИ ПЕТРИ ДЛЯ МОДЕЛИРОВАНИЯ
- 3.2. Одновременность и конфликт
- 3.3. Аппаратное обеспечение ЭВМ
- 3.4. Программное обеспечение ЭВМ
- 3.5. Другие системы
- ГЛАВА 4. АНАЛИЗ СЕТЕЙ ПЕТРИ
- 4.1. Задачи анализа сетей Петри
- 4.2. Методы анализа
- ГЛАВА 5. СЛОЖНОСТЬ И РАЗРЕШИМОСТЬ
- 5.1. Сводимость задач анализа
- 5.2. Задачи достижимости
- 5.3. Сети Петри с ограничениями
- 5.4. Активность и достижимость
- 5.5. Неразрешимые задачи
- 5.6. Сложность задачи достижимости
- ГЛАВА 6. ЯЗЫКИ СЕТЕЙ ПЕТРИ
- 6.2. Некоторые понятия теории формальных языков
- 6.3. Определения языков сетей Петри
- 6.4. Свойства языков сетей Петри
- 6.5. Свойства замкнутости
- 6.6. Языки сетей Петри и другие классы языков
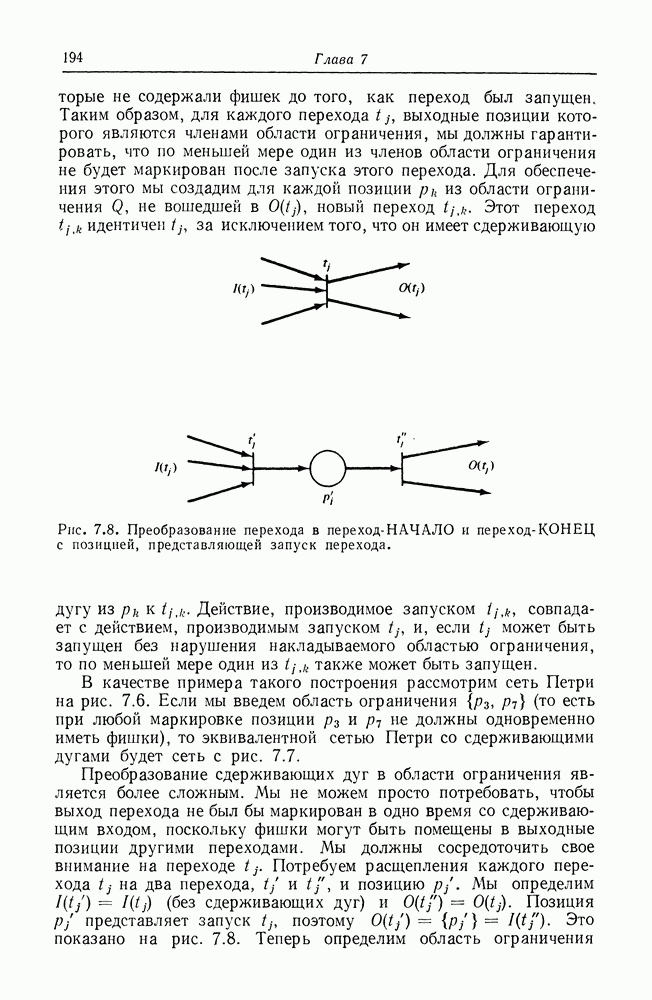
- ГЛАВА 7. РАСШИРЕННЫЕ И ОГРАНИЧЕННЫЕ МОДЕЛИ СЕТЕЙ ПЕТРИ
- 7.1. Границы возможностей моделирования с помощью сетей Петри
- 7.2. Расширения
- 7.3. Расширенные сети Петри и регистровые машины
- 7.4. Подклассы сетей Петри
- ГЛАВА 8. МОДЕЛИ ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ
- 8.2. Маркированные графы
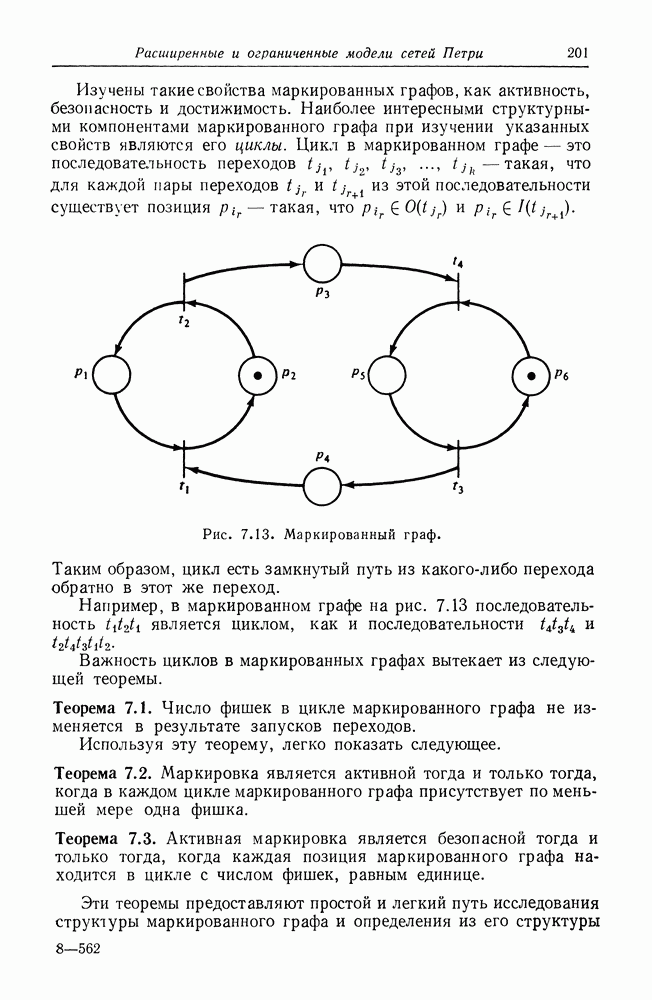
- 8.3. Графы вычислений
- 8.4. P/V-системы
- 8.5. Системы передачи сообщений
- 8.6. Графы UCLA
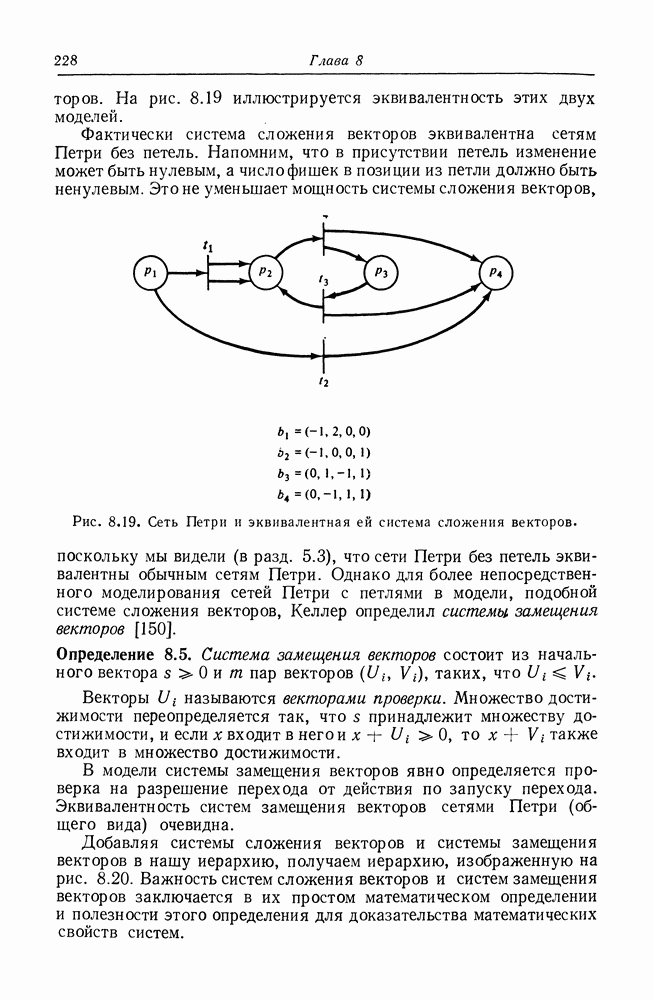
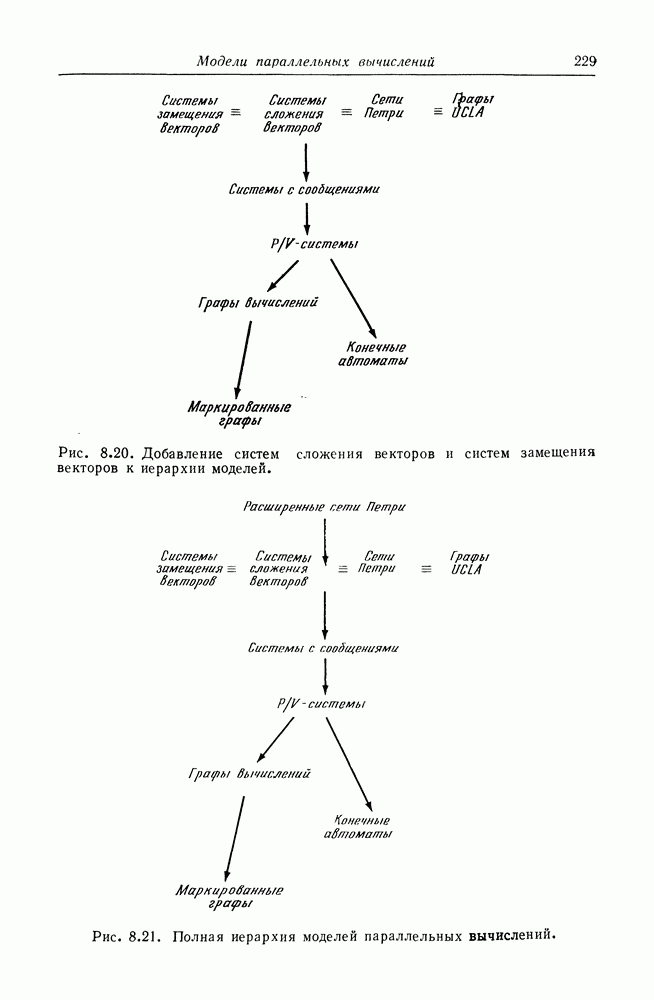
- 8.7. Системы замещения и сложения векторов
- 8.8. Расширенные модели сетей Петри
- ОБЗОР ТЕОРИИ КОМПЛЕКТОВ
- АННОТИРОВАННАЯ БИБЛИОГРАФИЯ