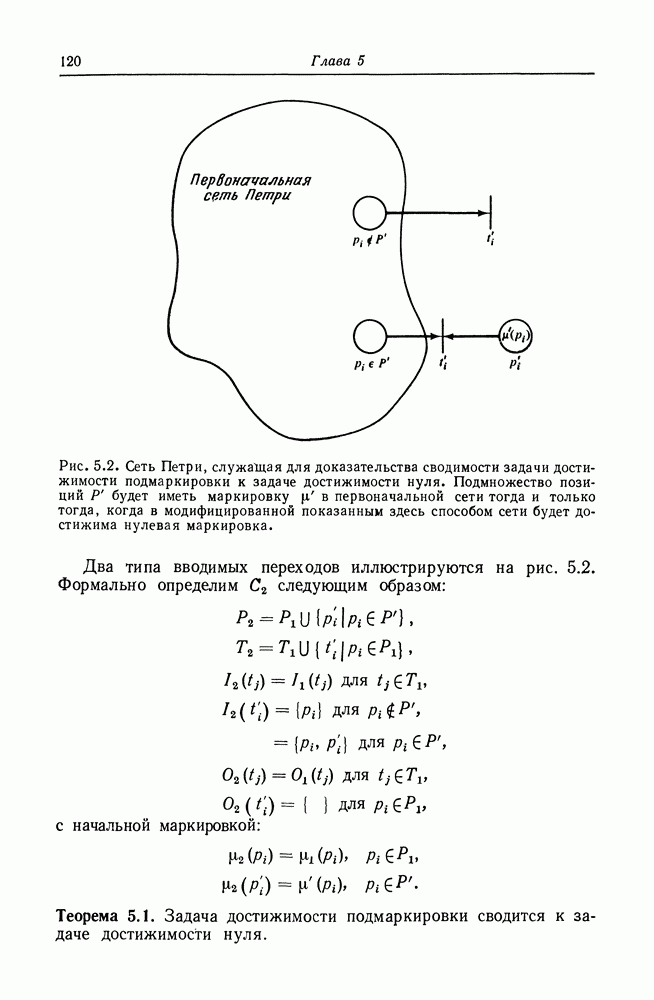
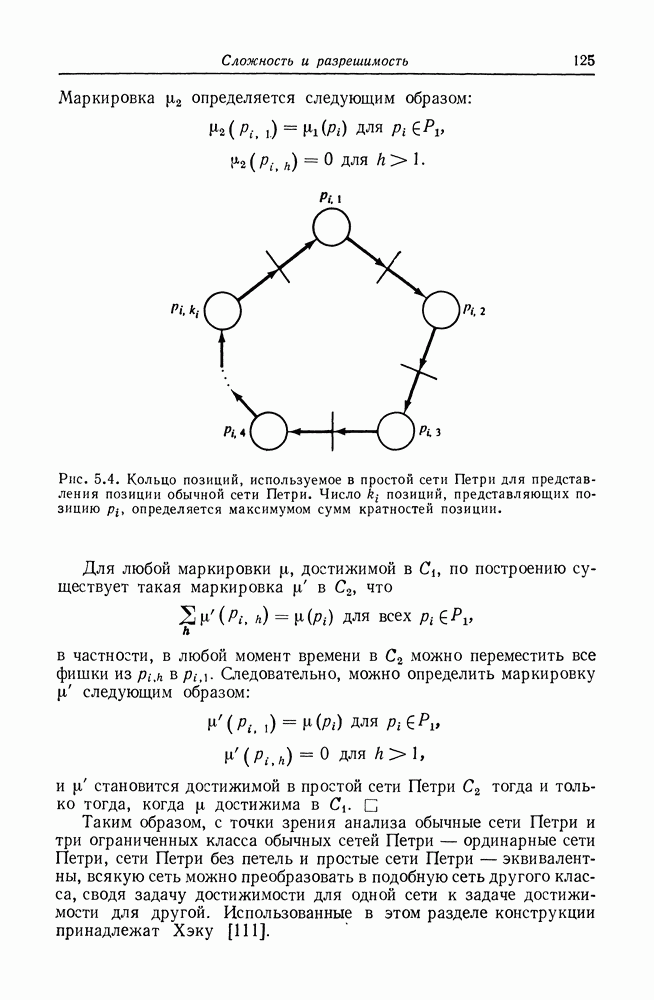
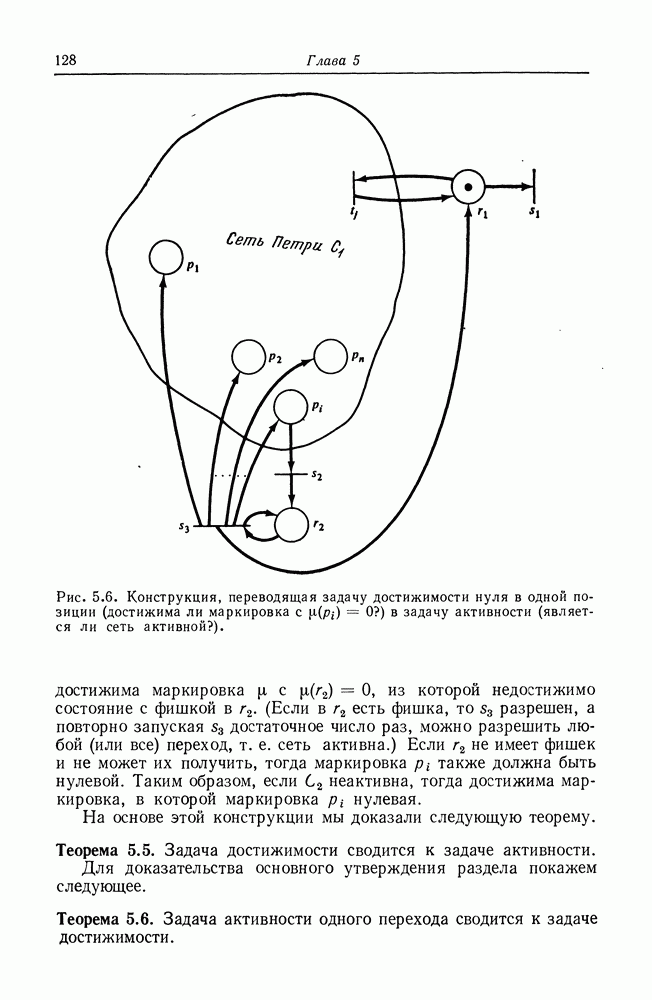
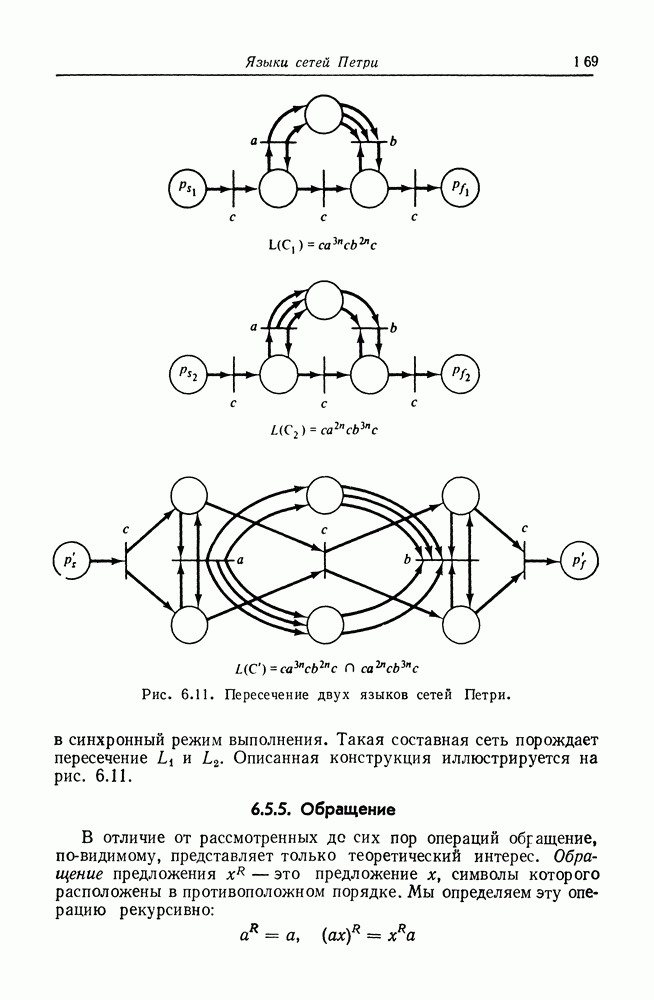
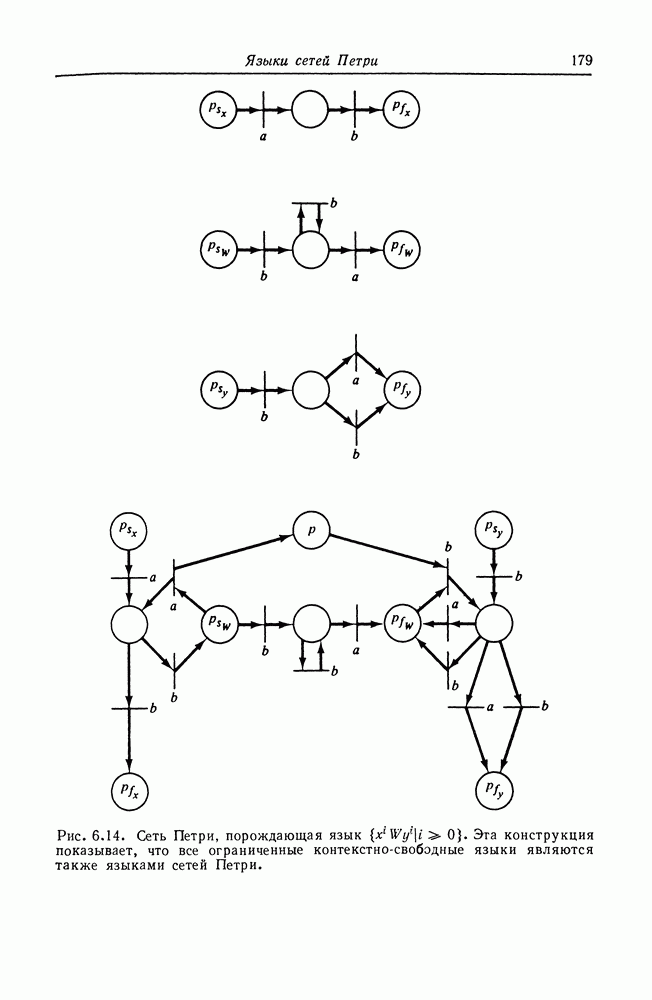
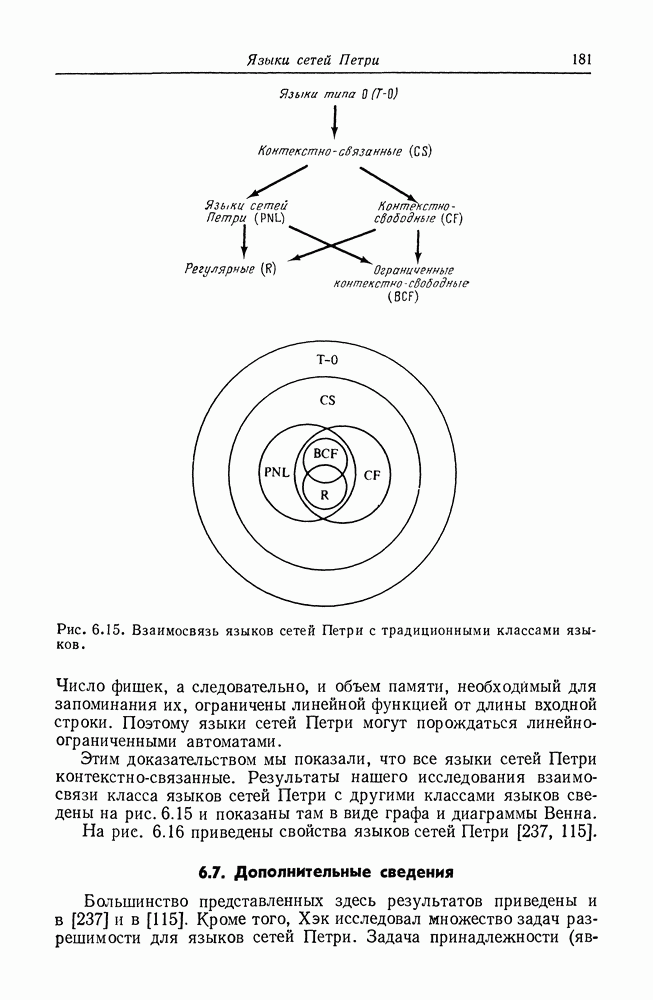
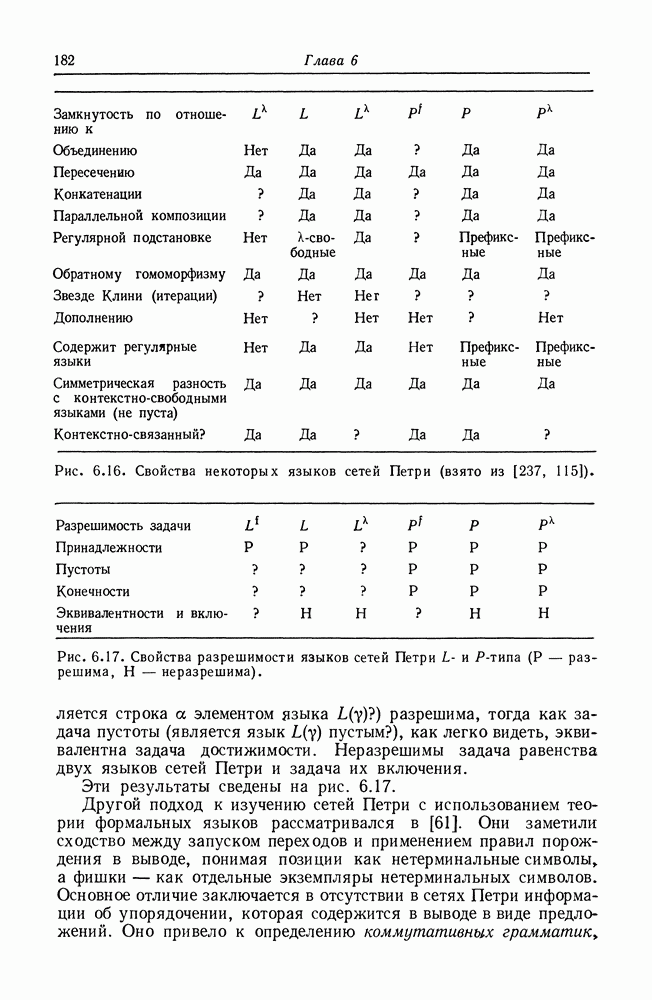
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ОБЗОР ТЕОРИИ КОМПЛЕКТОВ
Теория множеств используется в математике и вычислительной технике длительное время. Теория комплектов является естественным расширением теории множеств. Комплект, подобно множеству, есть набор элементов из некоторой области. Однако в отличие от множества комплекты допускают присутствие нескольких экземпляров одного и того же элемента. В теории множеств элемент есть либо элемент множества, либо не элемент множества. В теории комплектов элемент может входить в комплект нуль раз (не входить в комплект) или один, два, три или любое заданное число раз.
Теория комплектов была разработана в [50, 237].
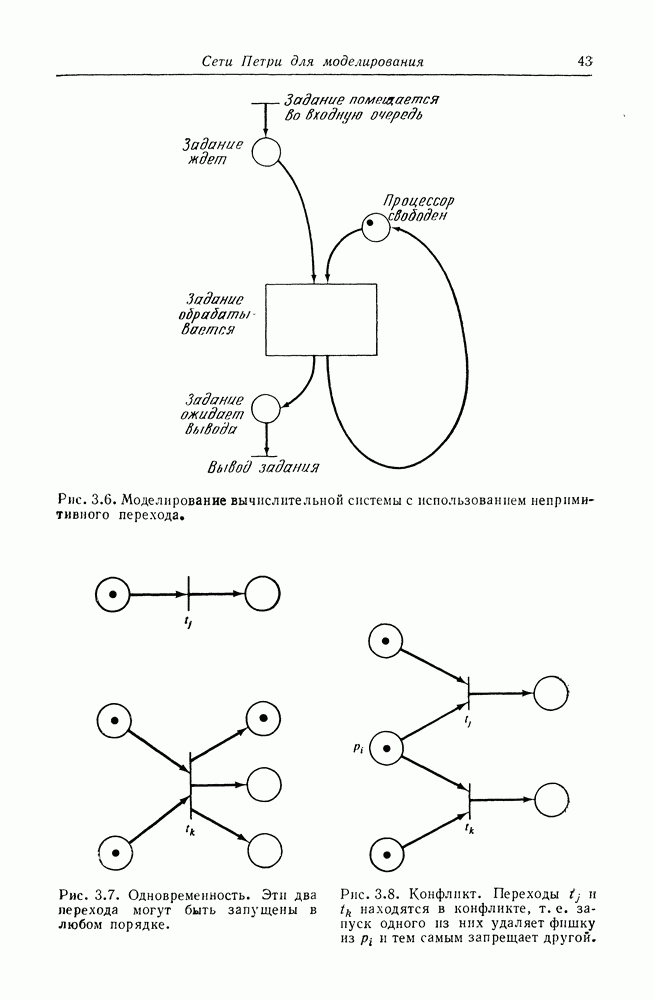
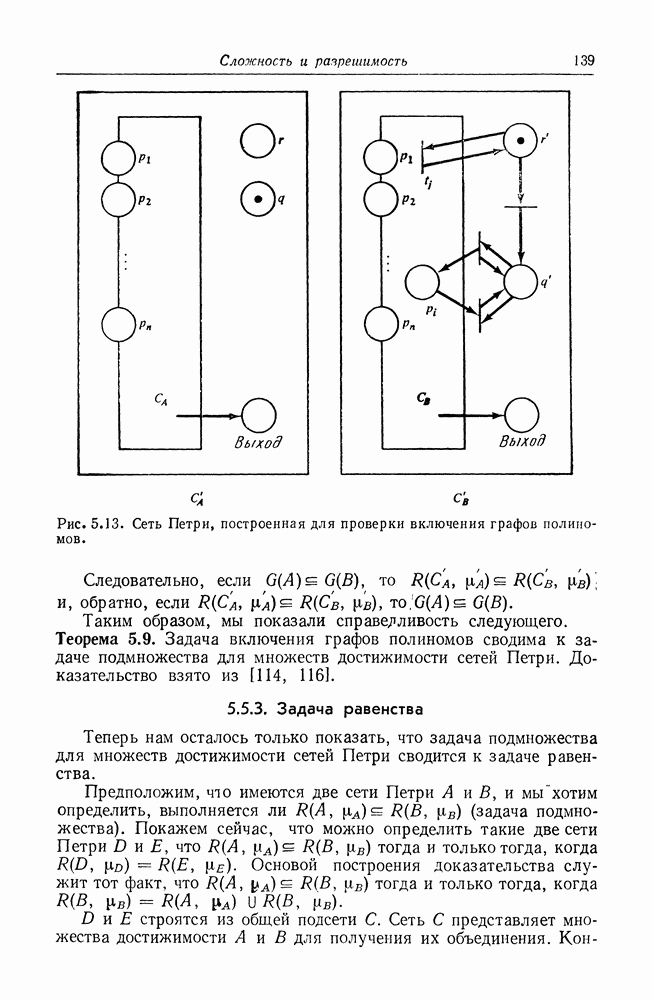
В качестве примера рассмотрим следующие комплекты над областью  Некоторые комплекты являются множествами (например,
Некоторые комплекты являются множествами (например,  Так же как и в множествах, порядок элементов в комплекте не важен. Поэтому
Так же как и в множествах, порядок элементов в комплекте не важен. Поэтому  являются одним и тем же комплектом (упорядоченные комплекты являются последовательн остями).
являются одним и тем же комплектом (упорядоченные комплекты являются последовательн остями).
В теории множеств основным понятием является отношение включения. Это отношение связывает элементы и множества и определяет, какие элементы являются членами каких множеств. Основным понятием теории комплектов является функция числа экземпляров. Эта функция определяет число экземпляров элемента в комплекте. Обозначим число экземпляров элемента х в комплекте В через  (читается «число х в В»).
(читается «число х в В»).
Исходя из этого понятия, можем определить основы теории комплектов. Большинство понятий и обозначений заимствованы из теории множеств. Если мы ограничим число элементов в комплекте так, что  то получим теорию множеств.
то получим теорию множеств.
А.1. Членство
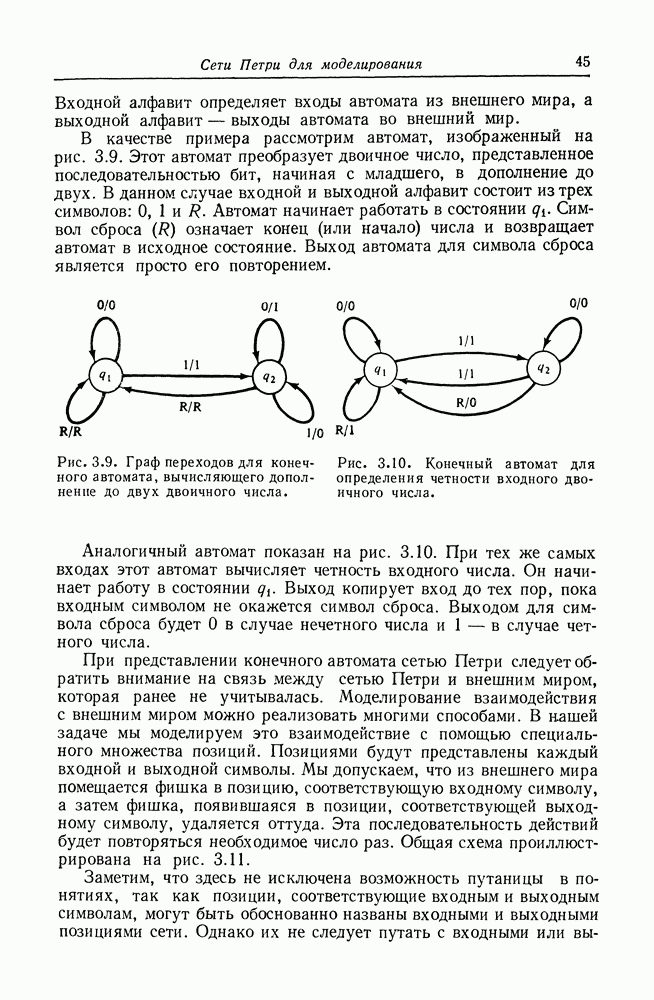
Функция  определяет число экземпляров элемента х в комплекте В. Отсюда следует, что
определяет число экземпляров элемента х в комплекте В. Отсюда следует, что  для всех
для всех  Мы различаем нулевой и ненулевой случаи. Элемент х является членом комплекта В, если
Мы различаем нулевой и ненулевой случаи. Элемент х является членом комплекта В, если  Это мы будем обозначать через
Это мы будем обозначать через  Аналогично, если
Аналогично, если  то
то 
Определим пустой комплект 0, не имеющий членов (для всех 
А.2. Мощность
Мощность  комплекта В есть общее число экземпляров элементов в комплекте
комплекта В есть общее число экземпляров элементов в комплекте

А.3. Включение и равенство комплектов
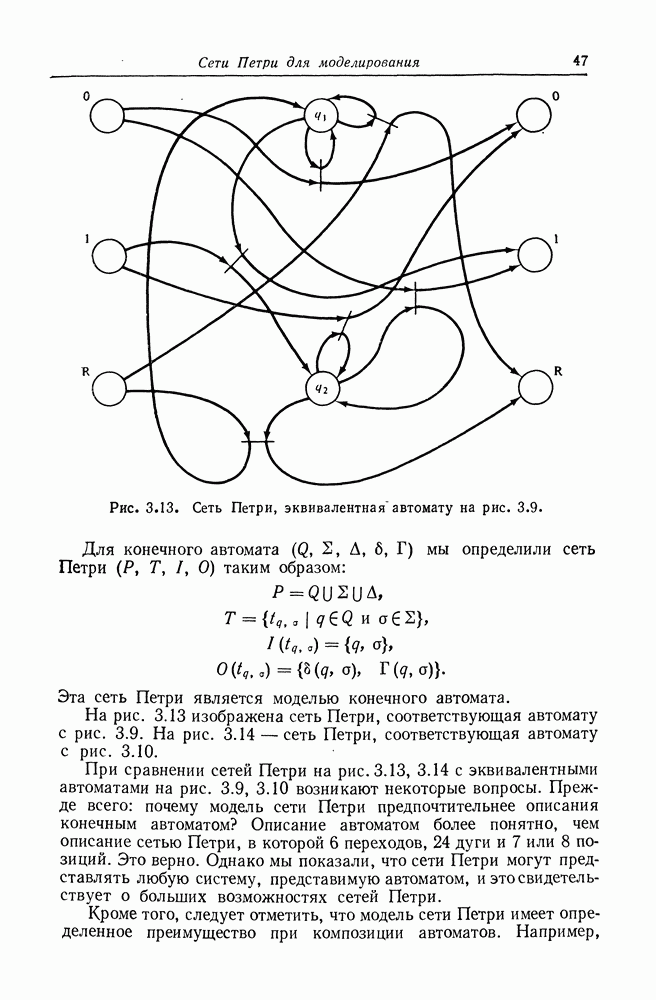
Комплект А есть подкомплект комплекта В (обозначается  если каждый элемент А является элементом В по меньшей мере не большее число раз:
если каждый элемент А является элементом В по меньшей мере не большее число раз:  тогда и только тогда, когда
тогда и только тогда, когда  для всех х. Два комплекта равны
для всех х. Два комплекта равны  если
если  для всех х.
для всех х.
Из этих определений мы можем непосредственно показать, что  тогда и только тогда, когда
тогда и только тогда, когда  для любого комплекта
для любого комплекта  из
из  следует
следует  из
из  следует
следует 
Комплект А строго включен в комплект  если
если  Отметим, что
Отметим, что  не следует из
не следует из  хотя и
хотя и  .
.
А.4. Операции
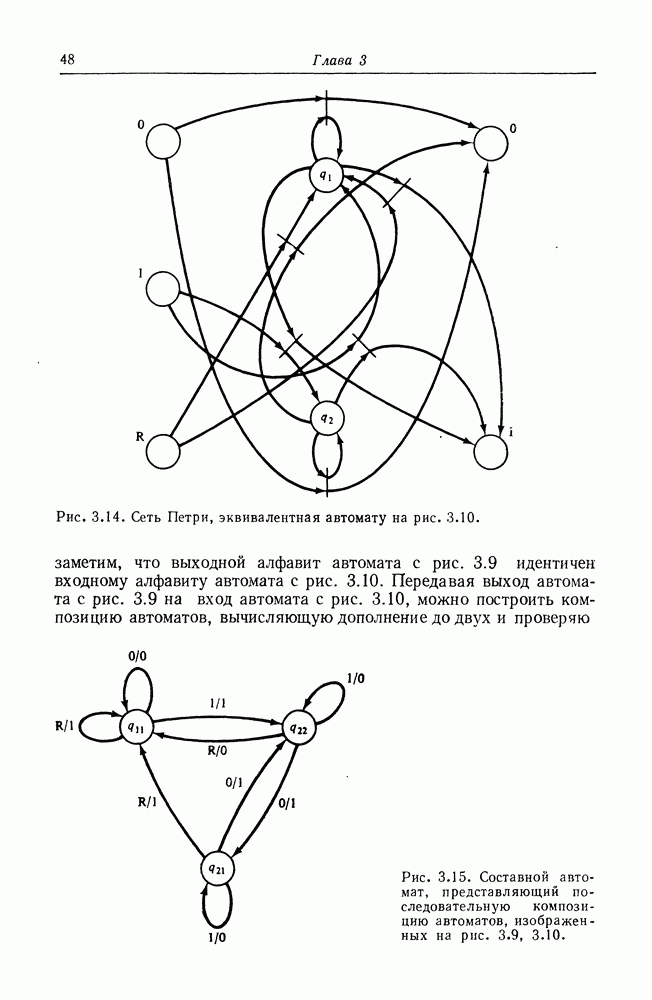
Над комплектами определяются четыре операции. Для двух комплектов  мы определим:
мы определим:
объединение комплектов 
пересечение комплектов 
сумму комплектов  ;
;
разность комплектов 
Эти операции обладают большинством ожидаемых свойств. Объединение, пересечение и сумма коммутативны и ассоциативны, кроме того, справедливы ожидаемые включения:

Различие между объединением и суммой очевидно:

К сожалению, различия между  нельзя так же легко проиллюстрировать, что объясняется невозможностью для операции разности удаления элементов из комплекта, которые не входят в него.
нельзя так же легко проиллюстрировать, что объясняется невозможностью для операции разности удаления элементов из комплекта, которые не входят в него.
А.5. Пространство комплектов
Определим область  как множество элементов, из которых составляются комплекты. Пространство комплектов
как множество элементов, из которых составляются комплекты. Пространство комплектов  есть множество всех таких комплектов, что элементы их принадлежат
есть множество всех таких комплектов, что элементы их принадлежат  и ни один элемент не входит в комплект более
и ни один элемент не входит в комплект более  раз. Иначе говоря, для любого
раз. Иначе говоря, для любого 
1. Из  следует
следует 
2. Для любого 
Множество  есть множество всех комплектов над областью
есть множество всех комплектов над областью  без какого-либо ограничения на число экземпляров элемента в комплекте.
без какого-либо ограничения на число экземпляров элемента в комплекте.
А.6. Отображения Париха
Для конечной области  существует естественное соответствие между каждым комплектом В над
существует естественное соответствие между каждым комплектом В над  и
и  -вектором
-вектором  определяемым соотношением
определяемым соотношением 
Этот вектор известен как отображение Париха [229].
А.7. Примеры
Пусть  область. Тогда для следующих комплектов
область. Тогда для следующих комплектов  имеем:
имеем:

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ГЛАВА 1. ВВЕДЕНИЕ
- ГЛАВА 2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
- 2.1. Структура сети Петри
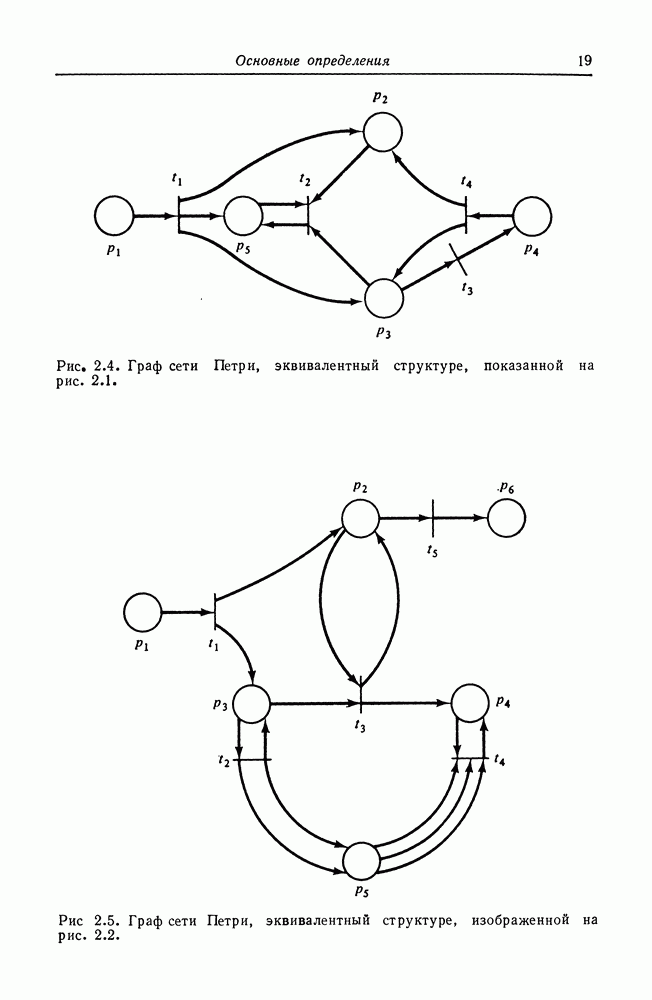
- 2.2. Графы сетей Петри
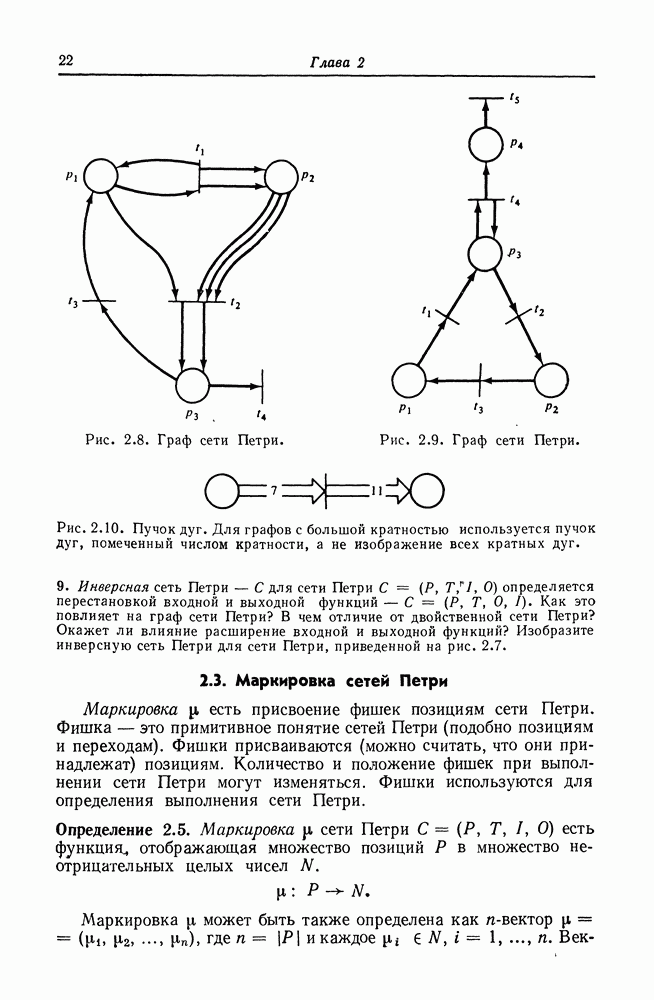
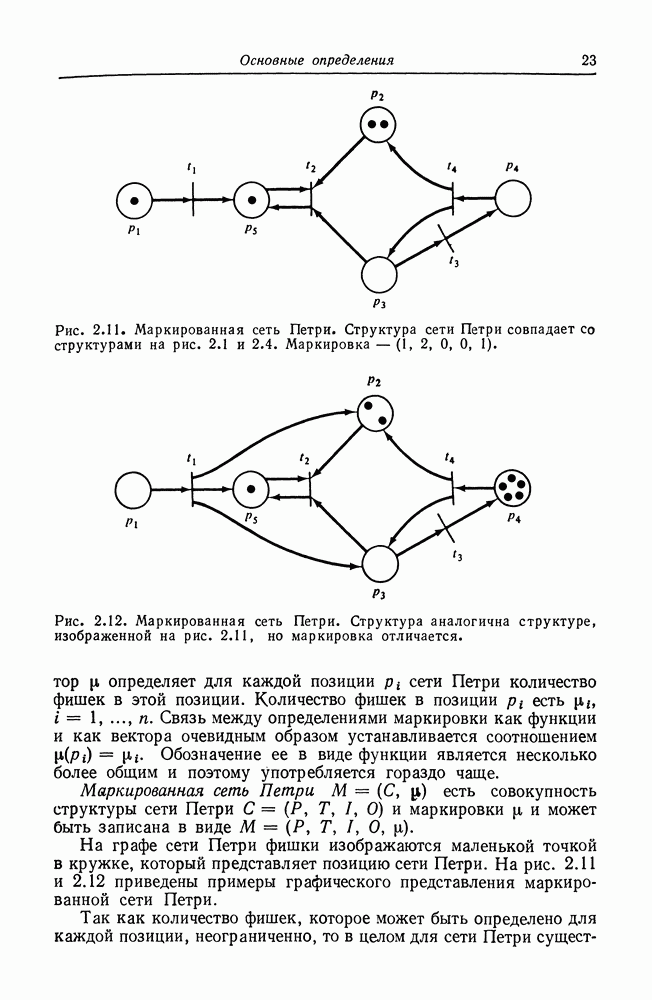
- 2.3. Маркировка сетей Петри
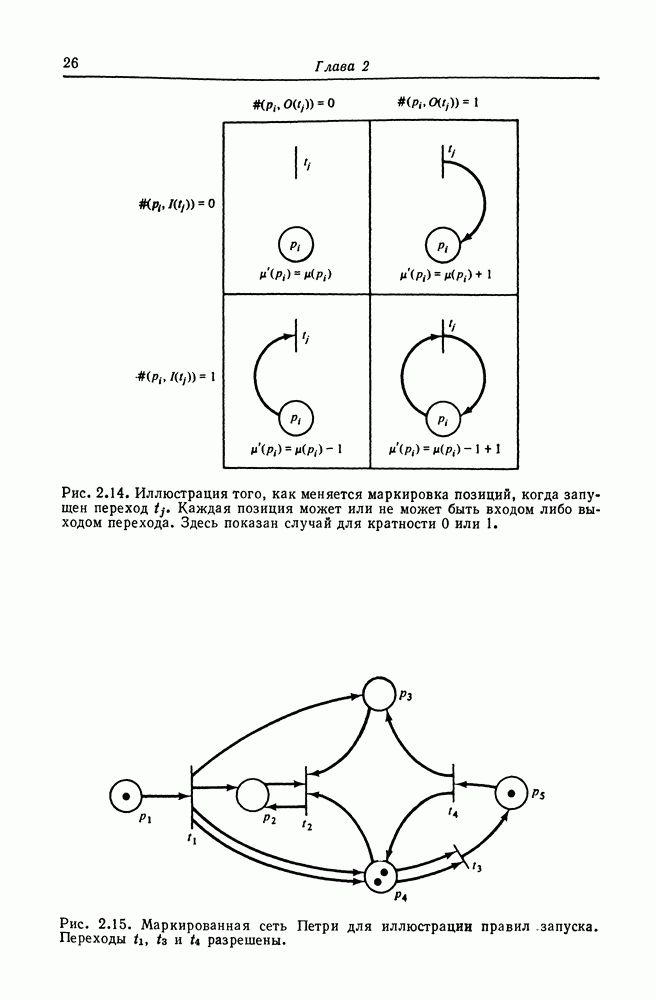
- 2.4. Правила выполнения сетей Петри
- 2.5. Пространство состояний сети Петри
- 2.6. Альтернативные формы определения сетей Петри
- ГЛАВА 3. СЕТИ ПЕТРИ ДЛЯ МОДЕЛИРОВАНИЯ
- 3.2. Одновременность и конфликт
- 3.3. Аппаратное обеспечение ЭВМ
- 3.4. Программное обеспечение ЭВМ
- 3.5. Другие системы
- ГЛАВА 4. АНАЛИЗ СЕТЕЙ ПЕТРИ
- 4.1. Задачи анализа сетей Петри
- 4.2. Методы анализа
- ГЛАВА 5. СЛОЖНОСТЬ И РАЗРЕШИМОСТЬ
- 5.1. Сводимость задач анализа
- 5.2. Задачи достижимости
- 5.3. Сети Петри с ограничениями
- 5.4. Активность и достижимость
- 5.5. Неразрешимые задачи
- 5.6. Сложность задачи достижимости
- ГЛАВА 6. ЯЗЫКИ СЕТЕЙ ПЕТРИ
- 6.2. Некоторые понятия теории формальных языков
- 6.3. Определения языков сетей Петри
- 6.4. Свойства языков сетей Петри
- 6.5. Свойства замкнутости
- 6.6. Языки сетей Петри и другие классы языков
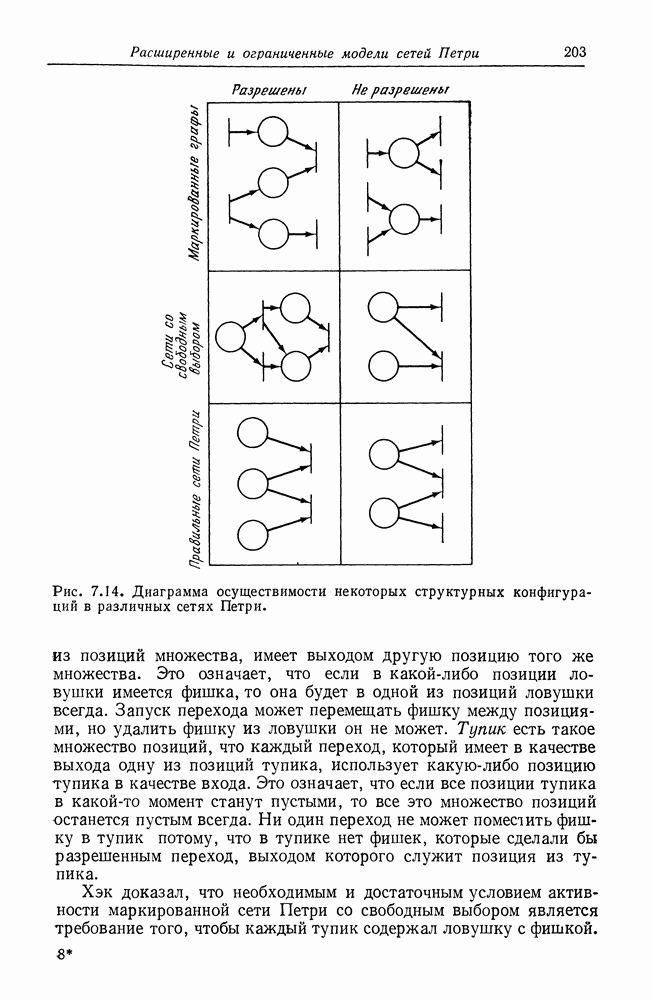
- ГЛАВА 7. РАСШИРЕННЫЕ И ОГРАНИЧЕННЫЕ МОДЕЛИ СЕТЕЙ ПЕТРИ
- 7.1. Границы возможностей моделирования с помощью сетей Петри
- 7.2. Расширения
- 7.3. Расширенные сети Петри и регистровые машины
- 7.4. Подклассы сетей Петри
- ГЛАВА 8. МОДЕЛИ ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ
- 8.2. Маркированные графы
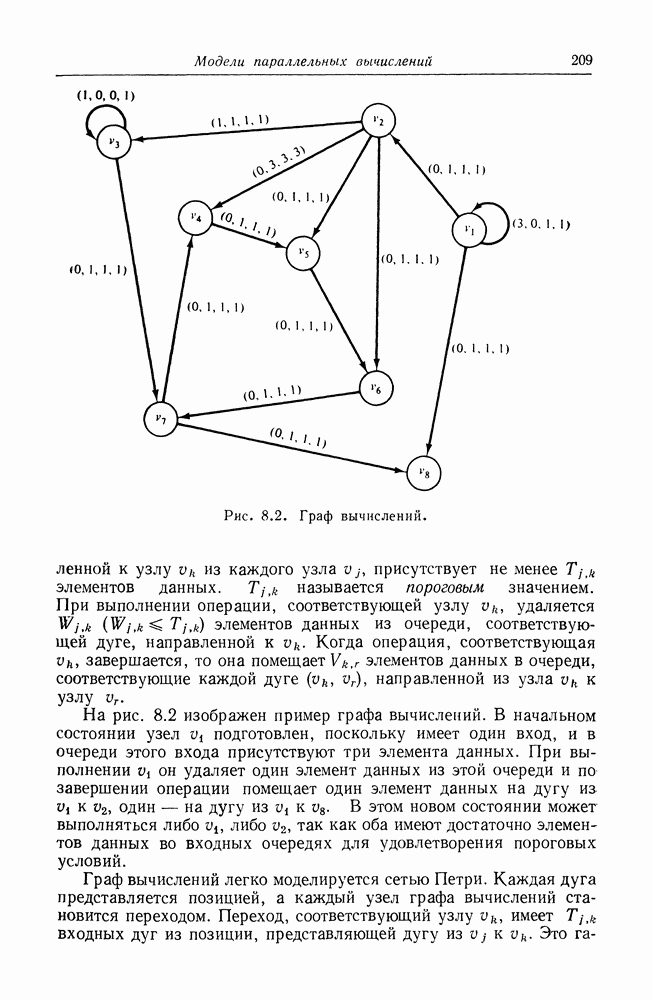
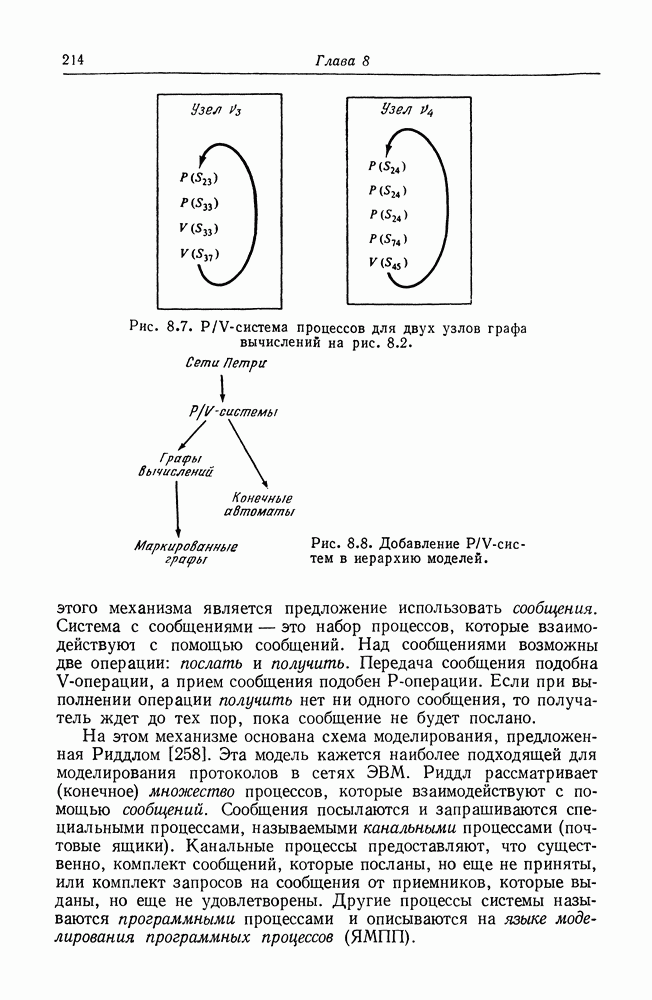
- 8.3. Графы вычислений
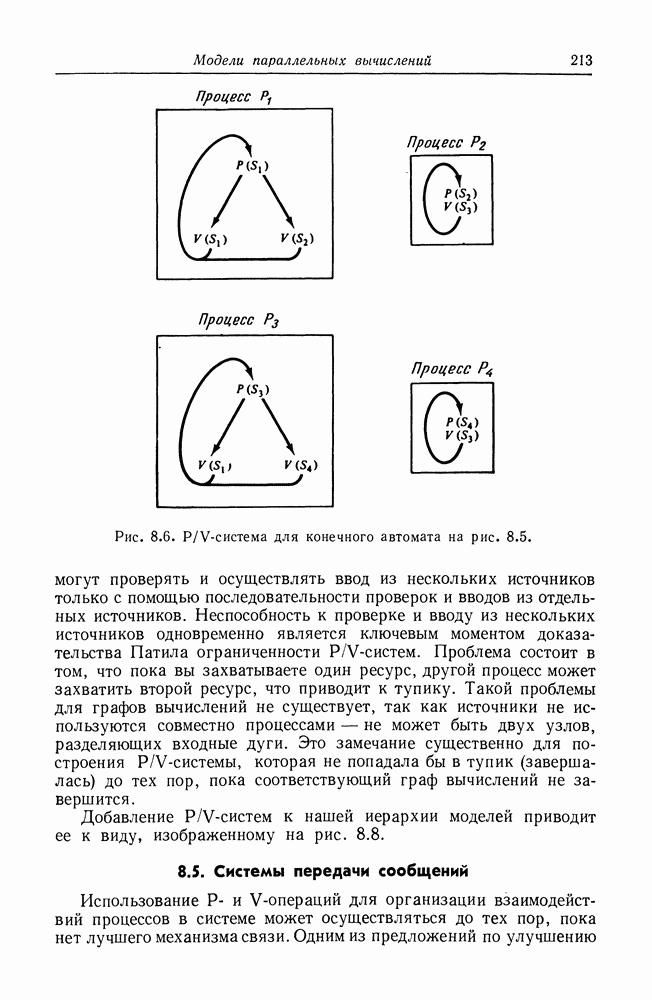
- 8.4. P/V-системы
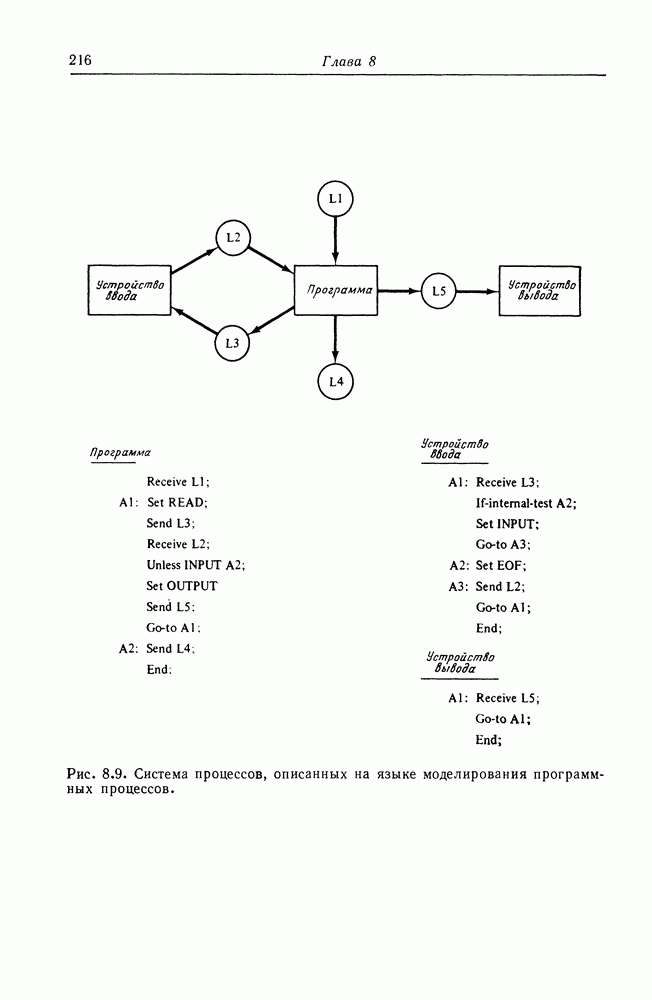
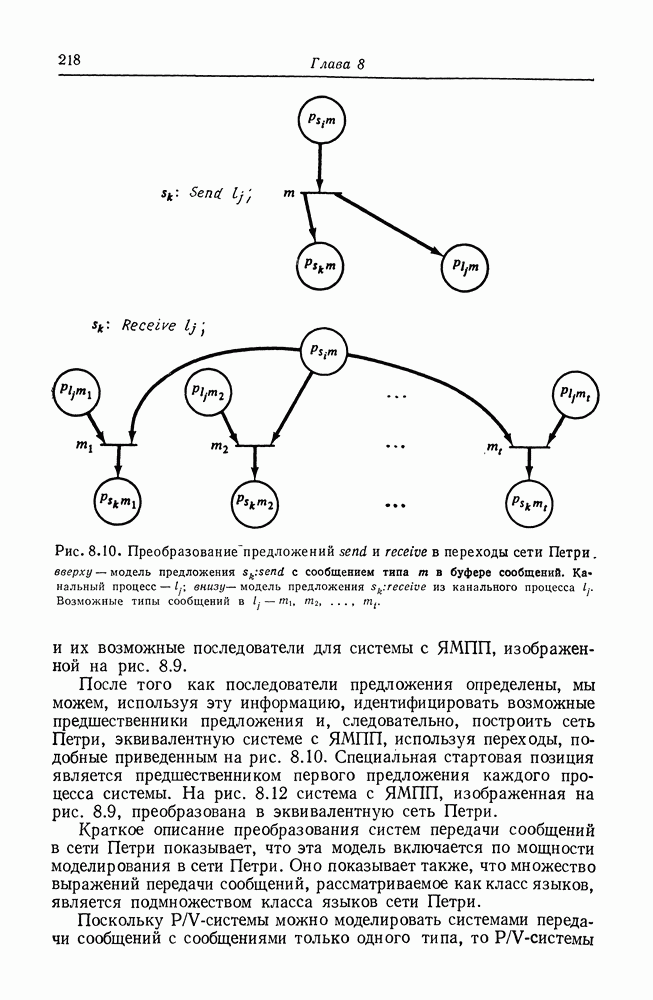
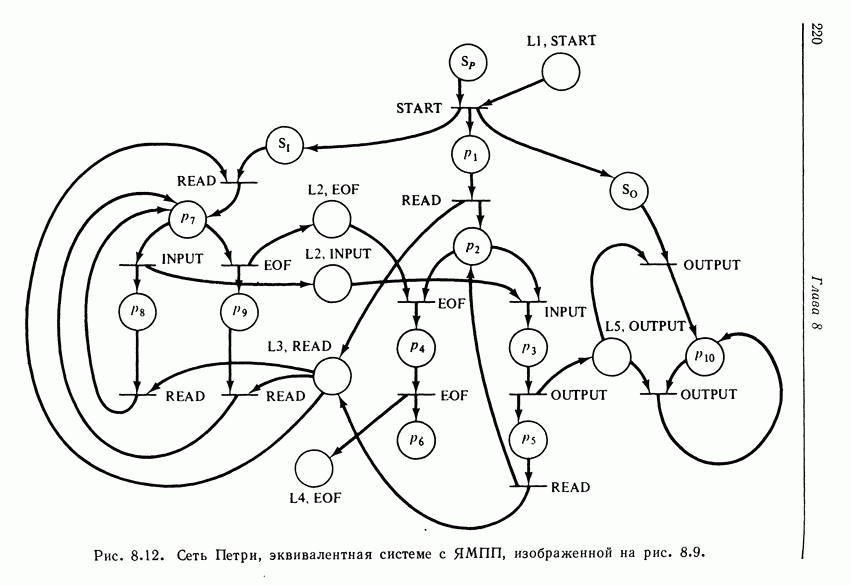
- 8.5. Системы передачи сообщений
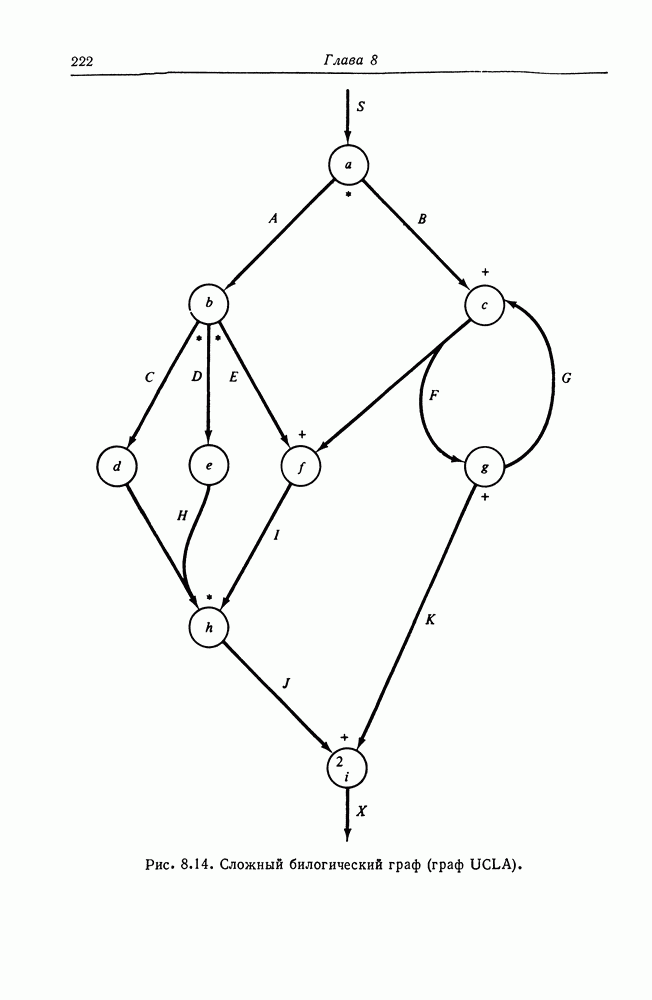
- 8.6. Графы UCLA
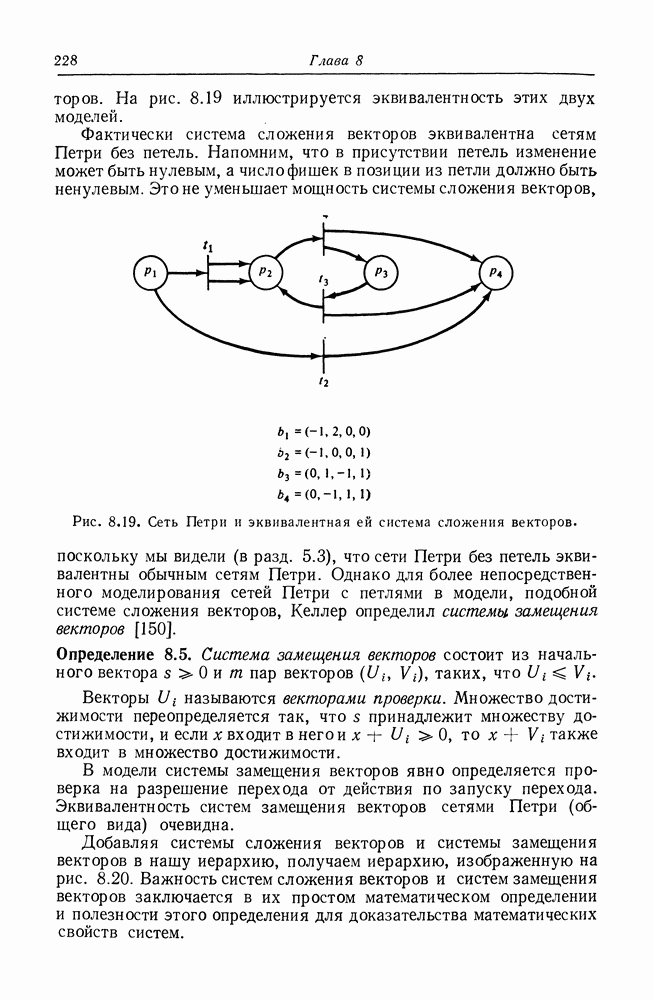
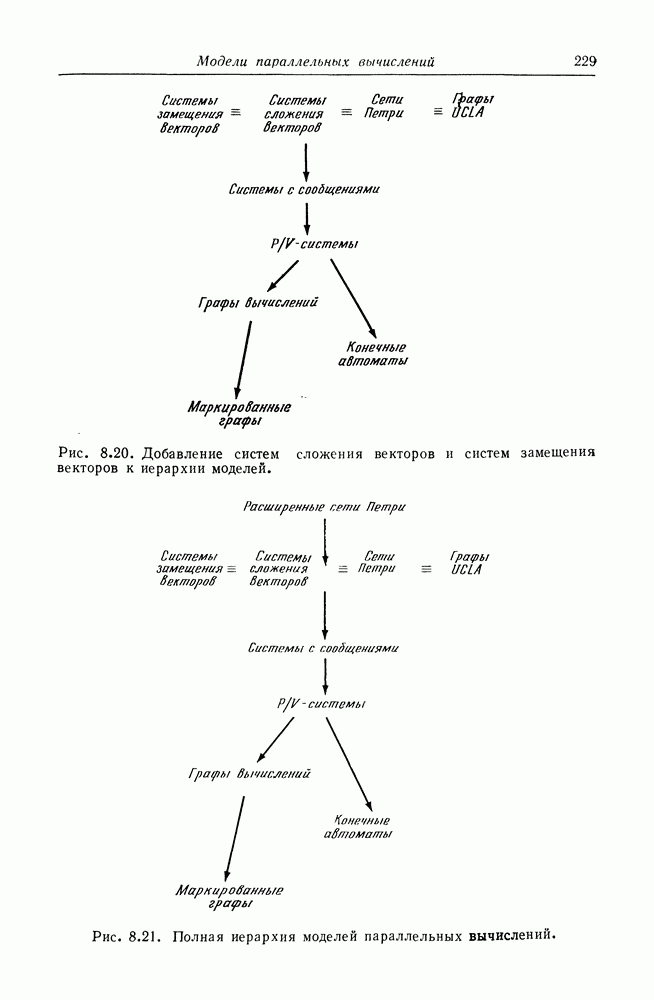
- 8.7. Системы замещения и сложения векторов
- 8.8. Расширенные модели сетей Петри
- ОБЗОР ТЕОРИИ КОМПЛЕКТОВ
- АННОТИРОВАННАЯ БИБЛИОГРАФИЯ