| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
16. РАБОТА В ТЕРМОДИНАМИКЕ
Работа в механике и термодинамике. В механике работа определяется как произведение модулей силы и перемещения, умноженное на косинус угла между ними. Работа совершрется при действии силы на движущееся тело и равна изменению кинетической энергии тела.
В термодинамике движение тела как целого не рассматривается и речь идет о перемещении частей макроскопического тела друг относительно друга. В результате меняется объем

Рис. 39

Рис. 40
тела, а его скорость остается равной нулю. Следовательно, работа в термодинамике, определяемая так же, как и в механике, равна изменению не кинетической энергии тела, а его внутренней энергии.
Изменение внутренней энергии при совершении работы. Почему при сжатии или расширении меняется внутренняя энергия тела? Почему, в частности, нагревается воздух при накачивании велосипедной шины?
Причина изменения температуры в процессе сжатия газа состоит в следующем: при упругих соударениях молекул с движущимся поршнем их кинетическая энергия изменяется. При движении навстречу молекулам поршень передает им во время столкновений часть своей механической энергии, в результате чего газ нагревается. Поршень действует подобно футболисту, встречающему летящий мяч ударом ноги и сообщающему мячу скорость, значительно большую той, которой он обладал до удара.
Если газ, напротив, расширяется, то после столкновения с удаляющимся поршнем скорости молекул уменьшаются, в результате чего газ охлаждается. Так же действует футболист, для того чтобы уменьшить скорость летящего мяча или остановить его; нога футболиста движется от мяча, как бы уступая ему дорогу.
При сжатии или расширении меняется и средняя потенциальная энергия взаимодействия молекул, так как при этом меняется среднее расстояние между молекулами.
Вычисление работы. Вычислим работу в зависимости от изменения объема на примере газа в цилиндре под поршнем (рис. 39). Проще всего вначале вычислить не работу силы  действующей на газ со стороны внешнего тела (поршня), а работу, которую совершает сам газ, действуя на поршень с силой
действующей на газ со стороны внешнего тела (поршня), а работу, которую совершает сам газ, действуя на поршень с силой  Согласно третьему закону Ньютона
Согласно третьему закону Ньютона 
Модуль силы, действующей со стороны газа на поршень, равен:  где
где  — давление газа,
— давление газа,  площадь поршня. Пусть газ расширяется и поршень смещается в направлении
площадь поршня. Пусть газ расширяется и поршень смещается в направлении
силы  малое расстояние
малое расстояние  Если перемещение мало, то давление газа можно считать постоянным.
Если перемещение мало, то давление газа можно считать постоянным.
Работа газа равна:

Эту работу можно выразить через изменение объема газа. Начальный объем  а конечный
а конечный  Поэтому
Поэтому

где  изменение объема газа.
изменение объема газа.
При расширении газ совершает положительную работу, так как направление силы и направление перемещения поршня совпадают. В процессе расширения газ передает энергию окружающим телам.
Если газ сжимается, то формула (4.3) для работы газа остается справедливой. Но теперь  и поэтому
и поэтому  (рис. 40).
(рис. 40).
Работа А, совершаемая внешними телами над газом, отличается от работы газа А только знаком:  так как сила
так как сила  действующая на газ, направлена против снлы
действующая на газ, направлена против снлы  а перемещение остается тем же самым. Поэтому работа внешних сил, действующих на газ, равна:
а перемещение остается тем же самым. Поэтому работа внешних сил, действующих на газ, равна:

Знак минус указывает, что при сжатии газа, когда  работа внешней силы положительна. Понятно, почему в этом случае
работа внешней силы положительна. Понятно, почему в этом случае  при сжатии газа направления силы и перемещения совпадают. Совершая над газом положительную работу, внешние тела передают ему энергию. При расширении газа, наоборот, работа внешних тел отрицательна
при сжатии газа направления силы и перемещения совпадают. Совершая над газом положительную работу, внешние тела передают ему энергию. При расширении газа, наоборот, работа внешних тел отрицательна  так как
так как  Теперь направления силы и перемещения противоположны.
Теперь направления силы и перемещения противоположны.
Выражения (4.3) и (4.4) справедливы не только при сжатии или расширении газа в цилиндре, но и при малом изменении объема любой системы. Если процесс изобарный  то эти формулы можно применять и для больших изменений объема.
то эти формулы можно применять и для больших изменений объема.
Геометрическое истолкование работы. Работе А газа для случая постоянного давления можно дать простое геометрическое истолкование.
Построим график зависимости давления газа от объема (рис. 41). Здесь площадь прямоугольника  ограниченная графиком
ограниченная графиком  осью V и отрезками
осью V и отрезками 

Рис. 41

Рис. 42
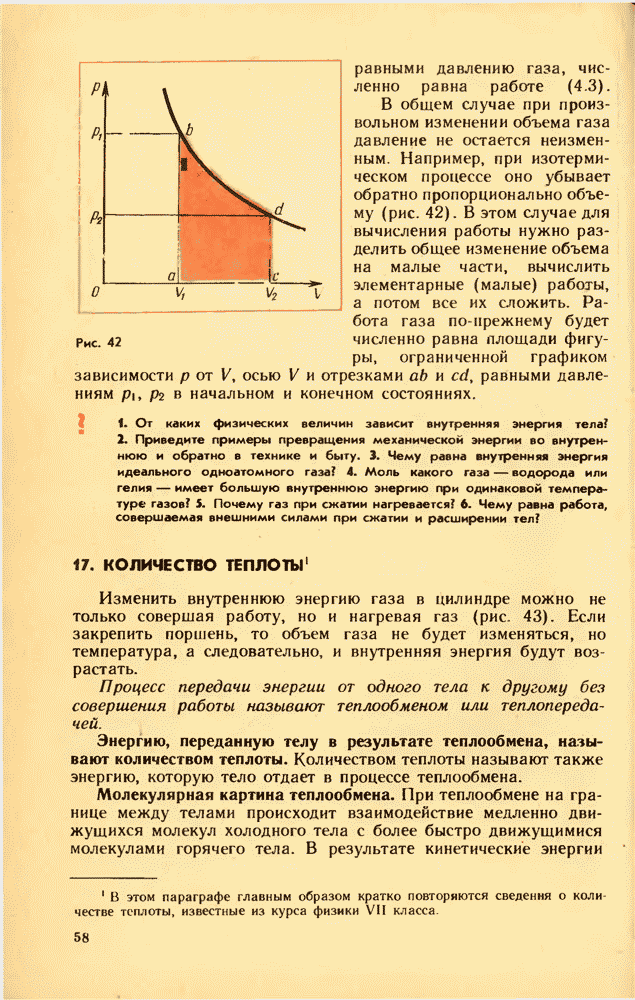
равными давлению газа, численно равна работе (4.3).
В общем случае при произвольном изменении объема газа давление не остается неизменным Например, при изотермическом процессе оно убывает обратно пропорционально объему (рис. 42). В этом случае для вычисления работы нужно разделить общее изменение объема на малые части, вычислить элементарные (малые) работы, а потом все их сложить. Работа газа по-прежнему будет численно равна площади фигуры, ограниченной графиком зависимости  от V, осью V и отрезками
от V, осью V и отрезками  равными давлениям
равными давлениям  в начальном и конечном состояниях.
в начальном и конечном состояниях.
1. От каких физических величин зависит внутренняя энергия тела?
2. Приведите примеры превращения механической энергии во внутреннюю и обратно в технике и быту. 3. Чему равна внутренняя энергия идеального одноатомного газа? 4. Моль какого газа — водорода или гелия — имеет большую внутреннюю энергию при одинаковой температуре газов? 5. Почему газ при сжатии нагревается? 6. Чему равна работа, совершаемая внешними силами при сжатии и расширении тел?
| << Предыдущий параграф | Следующий параграф >> |
- ТЕПЛОВЫЕ ЯВЛЕНИЯ. МОЛЕКУЛЯРНАЯ ФИЗИКА
- Глава I. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ
- 1. ОСНОВНЫЕ ПОЛОЖЕНИЯ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ. РАЗМЕРЫ МОЛЕКУЛ
- 2. МАССА МОЛЕКУЛ. ПОСТОЯННАЯ АВОГАДРО
- 3. БРОУНОВСКОЕ ДВИЖЕНИЕ.
- 4. СИЛЫ ВЗАИМОДЕЙСТВИЯ МОЛЕКУЛ
- 5. СТРОЕНИЕ ГАЗООБРАЗНЫХ, ЖИДКИХ И ТВЕРДЫХ ТЕЛ
- 6. ИДЕАЛЬНЫЙ ГАЗ В МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ
- 7. ОСНОВНОЕ УРАВНЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ I
- Глава II. ТЕМПЕРАТУРА. ЭНЕРГИЯ ТЕПЛОВОГО ДВИЖЕНИЯ МОЛЕКУЛ
- 8. ТЕПЛОВОЕ РАВНОВЕСИЕ. ТЕМПЕРАТУРА
- 9. ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ
- 10. АБСОЛЮТНАЯ ТЕМПЕРАТУРА. ТЕМПЕРАТУРА — МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ
- 11. ИЗМЕРЕНИЕ СКОРОСТЕЙ МОЛЕКУЛ ГАЗА
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ II
- Глава III. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА. ГАЗОВЫЕ ЗАКОНЫ
- 12. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- 13. ПРИМЕНЕНИЕ УРАВНЕНИЯ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА К РАЗЛИЧНЫМ ПРОЦЕССАМ
- 14. ПРИМЕНЕНИЕ ГАЗОВ В ТЕХНИКЕ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ III
- Глава IV. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 16. РАБОТА В ТЕРМОДИНАМИКЕ
- 17. КОЛИЧЕСТВО ТЕПЛОТЫ
- 18. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 19. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА ТЕРМОДИНАМИКИ К РАЗЛИЧНЫМ ПРОЦЕССАМ
- 20. НЕОБРАТИМОСТЬ ПРОЦЕССОВ В ПРИРОДЕ
- 21. ПРИНЦИПЫ ДЕЙСТВИЯ ТЕПЛОВЫХ ДВИГАТЕЛЕЙ
- 22. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ (КПД) ТЕПЛОВОГО ДВИГАТЕЛЯ. ТЕПЛОВЫЕ ДВИГАТЕЛИ И ОХРАНА ПРИРОДЫ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ IV
- Глава V. ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ЖИДКОСТЕЙ И ГАЗОВ
- 23. НАСЫЩЕННЫЙ ПАР
- 24. ЗАВИСИМОСТЬ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА ОТ ТЕМПЕРАТУРЫ. КИПЕНИЕ. КРИТИЧЕСКАЯ ТЕМПЕРАТУРА
- 25. ВЛАЖНОСТЬ ВОЗДУХА
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ V
- Глава VI. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ ЖИДКОСТЕЙ
- 27. СИЛА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ
- 28. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ VI
- Глава VII. ТВЕРДЫЕ ТЕЛА
- 29. КРИСТАЛЛИЧЕСКИЕ ТЕЛА
- 30. АМОРФНЫЕ ТЕЛА
- 31. ДЕФОРМАЦИЯ. ВИДЫ ДЕФОРМАЦИИ ТВЕРДЫХ ТЕЛ
- 32. МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ. ДИАГРАММА РАСТЯЖЕНИЯ
- 33. ПЛАСТИЧНОСТЬ И ХРУПКОСТЬ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ VII
- ОСНОВЫ ЭЛЕКТРОДИНАМИКИ
- 34. ЧТО ТАКОЕ ЭЛЕКТРОДИНАМИКА?
- Глава VIII. ЭЛЕКТРОСТАТИКА
- 35. ЭЛЕКТРИЧЕСКИЙ ЗАРЯД И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 36. ЗАРЯЖЕННЫЕ ТЕЛА. ЭЛЕКТРИЗАЦИЯ ТЕЛ
- 37. ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
- 38. ОСНОВНОЙ ЗАКОН ЭЛЕКТРОСТАТИКИ — ЗАКОН КУЛОНА
- 39. ЕДИНИЦА ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 40. БЛИЗКОДЕЙСТВИЕ И ДЕЙСТВИЕ НА РАССТОЯНИИ
- 41. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 42. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. ПРИНЦИП СУПЕРПОЗИЦИИ ПОЛЕЙ
- 43. СИЛОВЫЕ ЛИНИИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
- 44. ПРОВОДНИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
- 45. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ РАВНОМЕРНО ЗАРЯЖЕННОГО ПРОВОДЯЩЕГО ШАРА И БЕСКОНЕЧНОЙ ПЛОСКОСТИ
- 46. ДИЭЛЕКТРИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ. ДВА ВИДА ДИЭЛЕКТРИКОВ
- 47. ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ. ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ
- 48. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЗАРЯЖЕННОГО ТЕЛА В ОДНОРОДНОМ ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
- 49. ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ И РАЗНОСТЬ ПОТЕНЦИАЛОВ
- 50. ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ТОЧЕЧНОГО ЗАРЯДА
- 51. СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ ЭЛЕКТРИЧЕСКОГО ПОЛЯ И РАЗНОСТЬЮ ПОТЕНЦИАЛОВ. ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ
- 52. ИЗМЕРЕНИЕ РАЗНОСТИ ПОТЕНЦИАЛОВ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 53. ЭЛЕКТРОЕМКОСТЬ. ЕДИНИЦЫ ЭЛЕКТРОЕМКОСТИ
- 54. КОНДЕНСАТОРЫ. ЭЛЕКТРОЕМКОСТЬ ПЛОСКОГО КОНДЕНСАТОРА
- 55. ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА. ПРИМЕНЕНИЯ КОНДЕНСАТОРОВ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ X
- Глава IX. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- 56. ЭЛЕКТРИЧЕСКИЙ ТОК. СИЛА ТОКА
- 57. УСЛОВИЯ, НЕОБХОДИМЫЕ ДЛЯ СУЩЕСТВОВАНИЯ ЭЛЕКТРИЧЕСКОГО ТОКА
- 58. ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ. СОПРОТИВЛЕНИЕ
- 59. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ПРОВОДНИКА ОТ ТЕМПЕРАТУРЫ
- 60. СВЕРХПРОВОДИМОСТЬ
- 61. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ ПРОВОДНИКОВ
- 62. ИЗМЕРЕНИЕ СИЛЫ ТОКА И НАПРЯЖЕНИЯ
- 63. РАБОТА И МОЩНОСТЬ ПОСТОЯННОГО ТОКА
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 64. ЭЛЕКТРОДВИЖУЩАЯ СИЛА
- 65. ЗАКОН ОМА ДЛЯ ЗАМКНУТОЙ ЦЕПИ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ IX
- Глава X. ЭЛЕКТРИЧЕСКИЙ ТОК В РАЗЛИЧНЫХ СРЕДАХ
- 66. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ РАЗЛИЧНЫХ ВЕЩЕСТВ
- 67. ЭЛЕКТРОННАЯ ПРОВОДИМОСТЬ МЕТАЛЛОВ
- 68. ЭЛЕКТРИЧЕСКИЙ ТОК В ЖИДКОСТЯХ
- 69. ЗАКОН ЭЛЕКТРОЛИЗА
- 70. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ
- 71. НЕСАМОСТОЯТЕЛЬНЫЙ И САМОСТОЯТЕЛЬНЫЙ РАЗРЯДЫ
- 72. РАЗЛИЧНЫЕ ТИПЫ САМОСТОЯТЕЛЬНОГО РАЗРЯДА И ИХ ТЕХНИЧЕСКИЕ ПРИМЕНЕНИЯ
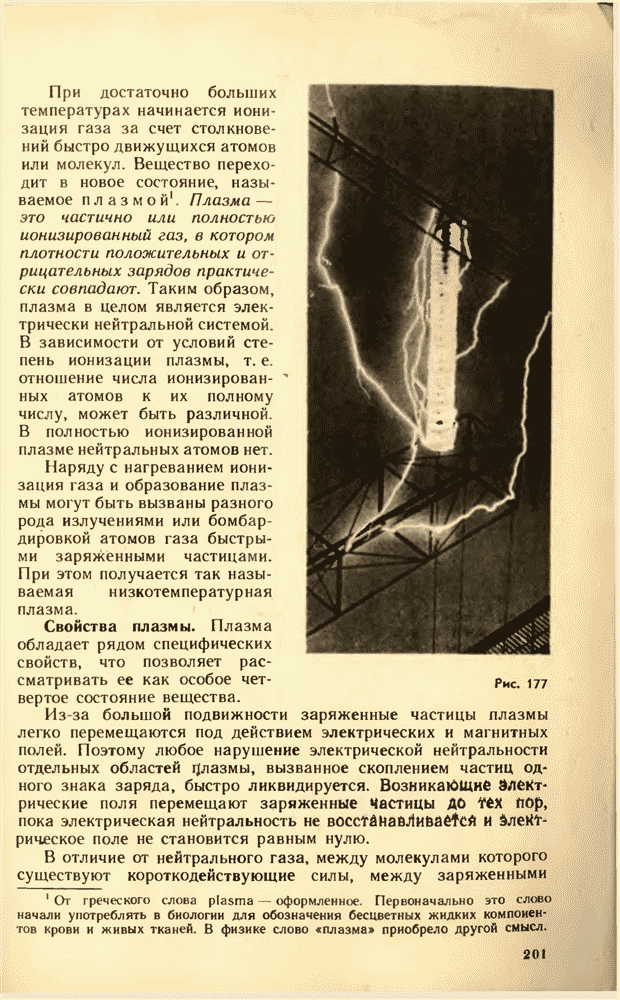
- 73. ПЛАЗМА
- 74. ЭЛЕКТРИЧЕСКИЙ ТОК В ВАКУУМЕ
- 75. ДВУХЭЛЕКТРОДНАЯ ЭЛЕКТРОННАЯ ЛАМПА-ДИОД
- 76. ЭЛЕКТРОННЫЕ ПУЧКИ. ЭЛЕКТРОННОЛУЧЕВАЯ ТРУБКА
- 77. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ
- 78. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ ПОЛУПРОВОДНИКОВ ПРИ НАЛИЧИИ ПРИМЕСЕЙ
- 79. ЭЛЕКТРИЧЕСКИЙ ТОК ЧЕРЕЗ КОНТАКТ ПОЛУПРОВОДНИКОВ p- И n- ТИПОВ
- 80. ПОЛУПРОВОДНИКОВЫЙ ДИОД
- 81. ТРАНЗИСТОР
- 82. ТЕРМИСТОРЫ И ФОТОРЕЗИСТОРЫ
- ПРИМЕР РЕШЕНИЯ ЗАДАЧИ
- КРАТКИЕ ИТОГИ ГЛАВЫ X
- Глава XI. МАГНИТНОЕ ПОЛЕ
- 83. ВЗАИМОДЕЙСТВИЕ ТОКОВ. МАГНИТНОЕ ПОЛЕ
- 84. ВЕКТОР МАГНИТНОЙ ИНДУКЦИИ
- 85. ЛИНИИ МАГНИТНОЙ ИНДУКЦИИ
- 86. ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
- 87. МОДУЛЬ ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ. МАГНИТНЫЙ ПОТОК
- 88. ЗАКОН АМПЕРА
- 89. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЙСЯ ЗАРЯД. СИЛА ЛОРЕНЦА
- 90. МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ XI
- Глава XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
- 91. ОТКРЫТИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
- 92. НАПРАВЛЕНИЕ ИНДУКЦИОННОГО ТОКА. ПРАВИЛО ЛЕНЦА
- 93. ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
- 94. ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 95. ЭДС ИНДУКЦИИ В ДВИЖУЩИХСЯ ПРОВОДНИКАХ
- 96. САМОИНДУКЦИЯ. ИНДУКТИВНОСТЬ
- 97. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА
- 98. ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРОДИНАМИКИ И ИХ ТЕХНИЧЕСКОЕ ПРИМЕНЕНИЕ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ XII
- ЗАКЛЮЧЕНИЕ
- ЛАБОРАТОРНЫЕ РАБОТЫ
- ОТВЕТЫ К УПРАЖНЕНИЯМ