| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
32. МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ. ДИАГРАММА РАСТЯЖЕНИЯ
Чтобы строить надежные дома, мосты, станки, разнообразные машины, необходимо знать механические свойства используемых материалов: бетона, стали, железобетона, пластмасс и т. д. Конструктор должен заранее знать поведение материалов при значительных деформациях, условия, при которых материалы начнут разрушаться. Сведения о механических свойствах различных материалов получают экспериментально.
В этом параграфе мы рассмотрим механические свойства твердого тела на примере исследования деформации растяжения. Но предварительно введем еще одно важное понятие.
Напряжение. В любом сечении деформированного тела действуют силы упругости, препятствующие разрыву тела на части (рис. 88). Состояние деформированного тела характеризуют особой величиной, называемой напряжением или, точнее, механическим напряжением. Напряжение — величина, равная отношению модуля  силы упругости к площади поперечного сечения
силы упругости к площади поперечного сечения  тела:
тела:

В СИ за единицу напряжения принимается  .
.
Диаграмма растяжения. Для исследования деформации растяжения стержень из исследуемого материала при помощи специальных устройств подвергают растяжению и измеряют удлинение образца и возникающее в нем напряжение. По результатам опытов вычерчивают график зависимости напряжения о от относительного удлинения  получивший название диаграммы растяжения (рис. 89).
получивший название диаграммы растяжения (рис. 89).
Закон Гука. Опыт показывает, что при малых деформациях напряжение о прямо пропорционально относительному удлинению  (участок ОА диаграммы). Эта зависимость, называемая законом Гука, записывается так:
(участок ОА диаграммы). Эта зависимость, называемая законом Гука, записывается так:

Относительное удлиненнее в формуле (7.2) взято по модулю, так как закон Гука справедлив как для деформации растяжения, так и для деформации сжатия, когда 

Рис. 88

Рис. 89
Коэффициент пропорциональности Е, входящий в закон Гука, называется модулем упругости или модулем Юнга.
Если относительное удлинение  то
то  Следовательно, модуль Юнга равен напряжению, возникающему в стержне при его относительном удлинении, равном 1. Так как
Следовательно, модуль Юнга равен напряжению, возникающему в стержне при его относительном удлинении, равном 1. Так как  то при
то при  А это значит, что модуль Юнга равен напряжению, возникающему при удвоении длины образца. Практически любое тело при упругой деформации не может удвоить свою длину; значительно раньше любой стержень разорвется. Поэтому модуль Юнга определяют по формуле (7.2), измеряя напряженнее и относительное удлинение
А это значит, что модуль Юнга равен напряжению, возникающему при удвоении длины образца. Практически любое тело при упругой деформации не может удвоить свою длину; значительно раньше любой стержень разорвется. Поэтому модуль Юнга определяют по формуле (7.2), измеряя напряженнее и относительное удлинение  при малых деформациях.
при малых деформациях.
Для большинства широко распространенных материалов модуль Юнга определен экспериментально. Так, для хромоникелевой стали  Па, а для алюминия
Па, а для алюминия  Па. Чем больше Е, тем меньше деформируется стержень при прочих равных условиях (одинаковых
Па. Чем больше Е, тем меньше деформируется стержень при прочих равных условиях (одинаковых  Модуль Юнга характеризует сопротивляемость материала упругой деформации растяжения (сжатия).
Модуль Юнга характеризует сопротивляемость материала упругой деформации растяжения (сжатия).
Закон Гука, записанный в форме (7.2), легко привести к виду, известному из курса физики VIII класса.
Действительно, подставив в  получим:
получим:

Отсюда

Обозначим тогда

Таким образом, жесткость  стержня прямо пропорциональна произведению модуля Юнга на площадь поперечного сечения стержня и обратно пропорциональна его длине.
стержня прямо пропорциональна произведению модуля Юнга на площадь поперечного сечения стержня и обратно пропорциональна его длине.
Пределы пропорциональности и упругости. Мы уже говорили, что закон Гука выполняется при небольших деформациях, а следовательно, при напряжениях, не превосходящих некоторого предела. Максимальное напряжение  при котором еще выполняется закон Гука, называют пределом пропорциональности.
при котором еще выполняется закон Гука, называют пределом пропорциональности.
Если увеличивать нагрузку, то деформация становится нелинейной: напряжение перестает быть прямо пропорциональным относительному удлинению. Тем не менее при небольших нелинейных деформациях после снятия нагрузки форма и размеры тела практически восстанавливаются (участок  диаграммы). Максимальное напряжение, при котором еще не возникают заметные остаточные деформации (относительная остаточная деформация не превышает
диаграммы). Максимальное напряжение, при котором еще не возникают заметные остаточные деформации (относительная остаточная деформация не превышает  называют пределом упругости
называют пределом упругости  Предел
Предел
упругости превышает предел пропорциональности лишь на сотые доли процента.
Предел прочности. Если внешняя нагрузка такова, что напряжение в материале превышает предел упругости, то после снятия нагрузки образец хотя и укорачивается, но не принимает прежних размеров, а остается деформированным.
По мере увеличения нагрузки деформация нарастает все быстрее и быстрее. При некотором значении напряжения, соответствующем на диаграмме точке С, удлинение нарастает практически без увеличения нагрузки. Это явление называют текучестью материала (участок CD). Кривая на диаграмме идет при этом почти горизонтально.
Далее с увеличением деформации  кривая напряжений начинает немного возрастать и достигает максимума в точке Е Затем напряжение быстро спадает и образец разрушается (точка К). Таким образом, разрыв происходит после того, как напряжение достигает максимального значения
кривая напряжений начинает немного возрастать и достигает максимума в точке Е Затем напряжение быстро спадает и образец разрушается (точка К). Таким образом, разрыв происходит после того, как напряжение достигает максимального значения  называемого пределом прочности (образен растягивается без увеличения внешней нагрузки вплоть до разрушения). Эта величина зависит от материала образца и его обработки.
называемого пределом прочности (образен растягивается без увеличения внешней нагрузки вплоть до разрушения). Эта величина зависит от материала образца и его обработки.
| << Предыдущий параграф | Следующий параграф >> |
- ТЕПЛОВЫЕ ЯВЛЕНИЯ. МОЛЕКУЛЯРНАЯ ФИЗИКА
- Глава I. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ
- 1. ОСНОВНЫЕ ПОЛОЖЕНИЯ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ. РАЗМЕРЫ МОЛЕКУЛ
- 2. МАССА МОЛЕКУЛ. ПОСТОЯННАЯ АВОГАДРО
- 3. БРОУНОВСКОЕ ДВИЖЕНИЕ.
- 4. СИЛЫ ВЗАИМОДЕЙСТВИЯ МОЛЕКУЛ
- 5. СТРОЕНИЕ ГАЗООБРАЗНЫХ, ЖИДКИХ И ТВЕРДЫХ ТЕЛ
- 6. ИДЕАЛЬНЫЙ ГАЗ В МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ
- 7. ОСНОВНОЕ УРАВНЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ I
- Глава II. ТЕМПЕРАТУРА. ЭНЕРГИЯ ТЕПЛОВОГО ДВИЖЕНИЯ МОЛЕКУЛ
- 8. ТЕПЛОВОЕ РАВНОВЕСИЕ. ТЕМПЕРАТУРА
- 9. ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ
- 10. АБСОЛЮТНАЯ ТЕМПЕРАТУРА. ТЕМПЕРАТУРА — МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ
- 11. ИЗМЕРЕНИЕ СКОРОСТЕЙ МОЛЕКУЛ ГАЗА
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ II
- Глава III. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА. ГАЗОВЫЕ ЗАКОНЫ
- 12. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- 13. ПРИМЕНЕНИЕ УРАВНЕНИЯ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА К РАЗЛИЧНЫМ ПРОЦЕССАМ
- 14. ПРИМЕНЕНИЕ ГАЗОВ В ТЕХНИКЕ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ III
- Глава IV. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 16. РАБОТА В ТЕРМОДИНАМИКЕ
- 17. КОЛИЧЕСТВО ТЕПЛОТЫ
- 18. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 19. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА ТЕРМОДИНАМИКИ К РАЗЛИЧНЫМ ПРОЦЕССАМ
- 20. НЕОБРАТИМОСТЬ ПРОЦЕССОВ В ПРИРОДЕ
- 21. ПРИНЦИПЫ ДЕЙСТВИЯ ТЕПЛОВЫХ ДВИГАТЕЛЕЙ
- 22. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ (КПД) ТЕПЛОВОГО ДВИГАТЕЛЯ. ТЕПЛОВЫЕ ДВИГАТЕЛИ И ОХРАНА ПРИРОДЫ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ IV
- Глава V. ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ЖИДКОСТЕЙ И ГАЗОВ
- 23. НАСЫЩЕННЫЙ ПАР
- 24. ЗАВИСИМОСТЬ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА ОТ ТЕМПЕРАТУРЫ. КИПЕНИЕ. КРИТИЧЕСКАЯ ТЕМПЕРАТУРА
- 25. ВЛАЖНОСТЬ ВОЗДУХА
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ V
- Глава VI. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ ЖИДКОСТЕЙ
- 27. СИЛА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ
- 28. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ VI
- Глава VII. ТВЕРДЫЕ ТЕЛА
- 29. КРИСТАЛЛИЧЕСКИЕ ТЕЛА
- 30. АМОРФНЫЕ ТЕЛА
- 31. ДЕФОРМАЦИЯ. ВИДЫ ДЕФОРМАЦИИ ТВЕРДЫХ ТЕЛ
- 32. МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ. ДИАГРАММА РАСТЯЖЕНИЯ
- 33. ПЛАСТИЧНОСТЬ И ХРУПКОСТЬ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ VII
- ОСНОВЫ ЭЛЕКТРОДИНАМИКИ
- 34. ЧТО ТАКОЕ ЭЛЕКТРОДИНАМИКА?
- Глава VIII. ЭЛЕКТРОСТАТИКА
- 35. ЭЛЕКТРИЧЕСКИЙ ЗАРЯД И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 36. ЗАРЯЖЕННЫЕ ТЕЛА. ЭЛЕКТРИЗАЦИЯ ТЕЛ
- 37. ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
- 38. ОСНОВНОЙ ЗАКОН ЭЛЕКТРОСТАТИКИ — ЗАКОН КУЛОНА
- 39. ЕДИНИЦА ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 40. БЛИЗКОДЕЙСТВИЕ И ДЕЙСТВИЕ НА РАССТОЯНИИ
- 41. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 42. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. ПРИНЦИП СУПЕРПОЗИЦИИ ПОЛЕЙ
- 43. СИЛОВЫЕ ЛИНИИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
- 44. ПРОВОДНИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
- 45. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ РАВНОМЕРНО ЗАРЯЖЕННОГО ПРОВОДЯЩЕГО ШАРА И БЕСКОНЕЧНОЙ ПЛОСКОСТИ
- 46. ДИЭЛЕКТРИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ. ДВА ВИДА ДИЭЛЕКТРИКОВ
- 47. ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ. ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ
- 48. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЗАРЯЖЕННОГО ТЕЛА В ОДНОРОДНОМ ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
- 49. ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ И РАЗНОСТЬ ПОТЕНЦИАЛОВ
- 50. ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ТОЧЕЧНОГО ЗАРЯДА
- 51. СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ ЭЛЕКТРИЧЕСКОГО ПОЛЯ И РАЗНОСТЬЮ ПОТЕНЦИАЛОВ. ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ
- 52. ИЗМЕРЕНИЕ РАЗНОСТИ ПОТЕНЦИАЛОВ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 53. ЭЛЕКТРОЕМКОСТЬ. ЕДИНИЦЫ ЭЛЕКТРОЕМКОСТИ
- 54. КОНДЕНСАТОРЫ. ЭЛЕКТРОЕМКОСТЬ ПЛОСКОГО КОНДЕНСАТОРА
- 55. ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА. ПРИМЕНЕНИЯ КОНДЕНСАТОРОВ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ X
- Глава IX. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- 56. ЭЛЕКТРИЧЕСКИЙ ТОК. СИЛА ТОКА
- 57. УСЛОВИЯ, НЕОБХОДИМЫЕ ДЛЯ СУЩЕСТВОВАНИЯ ЭЛЕКТРИЧЕСКОГО ТОКА
- 58. ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ. СОПРОТИВЛЕНИЕ
- 59. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ПРОВОДНИКА ОТ ТЕМПЕРАТУРЫ
- 60. СВЕРХПРОВОДИМОСТЬ
- 61. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ ПРОВОДНИКОВ
- 62. ИЗМЕРЕНИЕ СИЛЫ ТОКА И НАПРЯЖЕНИЯ
- 63. РАБОТА И МОЩНОСТЬ ПОСТОЯННОГО ТОКА
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 64. ЭЛЕКТРОДВИЖУЩАЯ СИЛА
- 65. ЗАКОН ОМА ДЛЯ ЗАМКНУТОЙ ЦЕПИ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ IX
- Глава X. ЭЛЕКТРИЧЕСКИЙ ТОК В РАЗЛИЧНЫХ СРЕДАХ
- 66. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ РАЗЛИЧНЫХ ВЕЩЕСТВ
- 67. ЭЛЕКТРОННАЯ ПРОВОДИМОСТЬ МЕТАЛЛОВ
- 68. ЭЛЕКТРИЧЕСКИЙ ТОК В ЖИДКОСТЯХ
- 69. ЗАКОН ЭЛЕКТРОЛИЗА
- 70. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ
- 71. НЕСАМОСТОЯТЕЛЬНЫЙ И САМОСТОЯТЕЛЬНЫЙ РАЗРЯДЫ
- 72. РАЗЛИЧНЫЕ ТИПЫ САМОСТОЯТЕЛЬНОГО РАЗРЯДА И ИХ ТЕХНИЧЕСКИЕ ПРИМЕНЕНИЯ
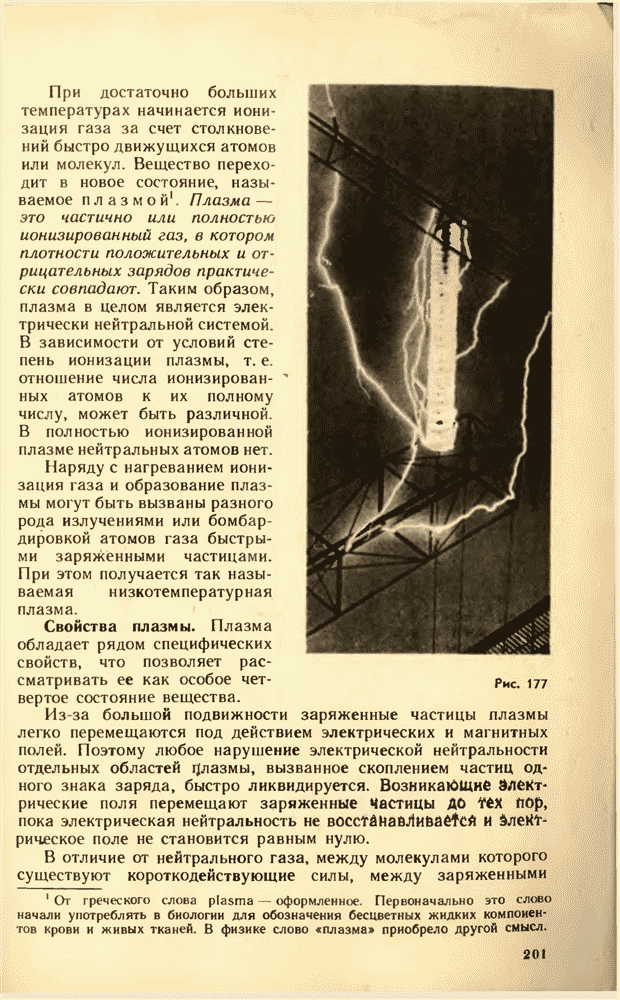
- 73. ПЛАЗМА
- 74. ЭЛЕКТРИЧЕСКИЙ ТОК В ВАКУУМЕ
- 75. ДВУХЭЛЕКТРОДНАЯ ЭЛЕКТРОННАЯ ЛАМПА-ДИОД
- 76. ЭЛЕКТРОННЫЕ ПУЧКИ. ЭЛЕКТРОННОЛУЧЕВАЯ ТРУБКА
- 77. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ
- 78. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ ПОЛУПРОВОДНИКОВ ПРИ НАЛИЧИИ ПРИМЕСЕЙ
- 79. ЭЛЕКТРИЧЕСКИЙ ТОК ЧЕРЕЗ КОНТАКТ ПОЛУПРОВОДНИКОВ p- И n- ТИПОВ
- 80. ПОЛУПРОВОДНИКОВЫЙ ДИОД
- 81. ТРАНЗИСТОР
- 82. ТЕРМИСТОРЫ И ФОТОРЕЗИСТОРЫ
- ПРИМЕР РЕШЕНИЯ ЗАДАЧИ
- КРАТКИЕ ИТОГИ ГЛАВЫ X
- Глава XI. МАГНИТНОЕ ПОЛЕ
- 83. ВЗАИМОДЕЙСТВИЕ ТОКОВ. МАГНИТНОЕ ПОЛЕ
- 84. ВЕКТОР МАГНИТНОЙ ИНДУКЦИИ
- 85. ЛИНИИ МАГНИТНОЙ ИНДУКЦИИ
- 86. ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
- 87. МОДУЛЬ ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ. МАГНИТНЫЙ ПОТОК
- 88. ЗАКОН АМПЕРА
- 89. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЙСЯ ЗАРЯД. СИЛА ЛОРЕНЦА
- 90. МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ XI
- Глава XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
- 91. ОТКРЫТИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
- 92. НАПРАВЛЕНИЕ ИНДУКЦИОННОГО ТОКА. ПРАВИЛО ЛЕНЦА
- 93. ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
- 94. ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 95. ЭДС ИНДУКЦИИ В ДВИЖУЩИХСЯ ПРОВОДНИКАХ
- 96. САМОИНДУКЦИЯ. ИНДУКТИВНОСТЬ
- 97. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА
- 98. ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРОДИНАМИКИ И ИХ ТЕХНИЧЕСКОЕ ПРИМЕНЕНИЕ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ XII
- ЗАКЛЮЧЕНИЕ
- ЛАБОРАТОРНЫЕ РАБОТЫ
- ОТВЕТЫ К УПРАЖНЕНИЯМ