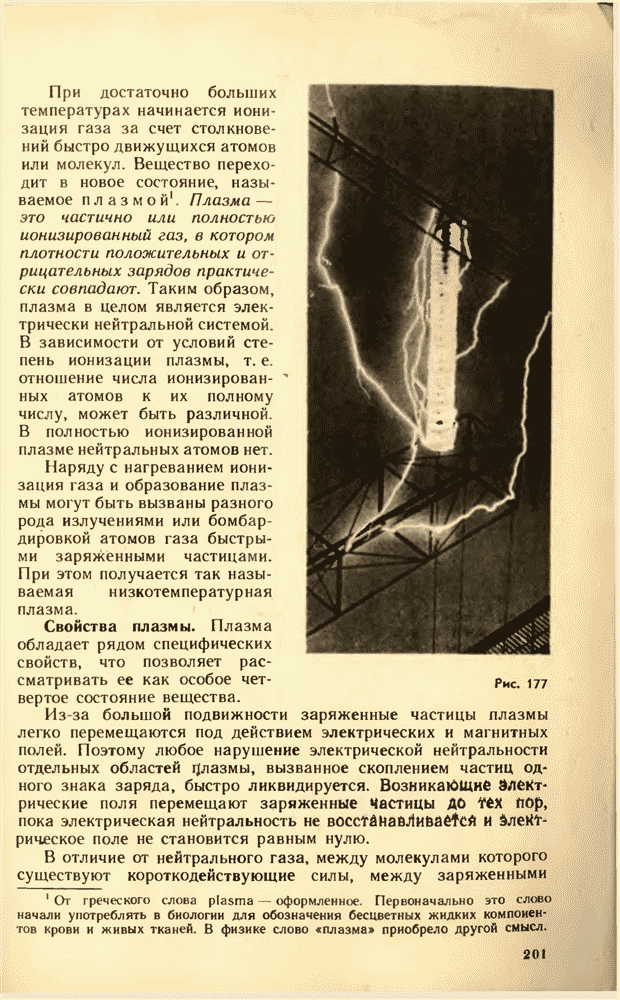
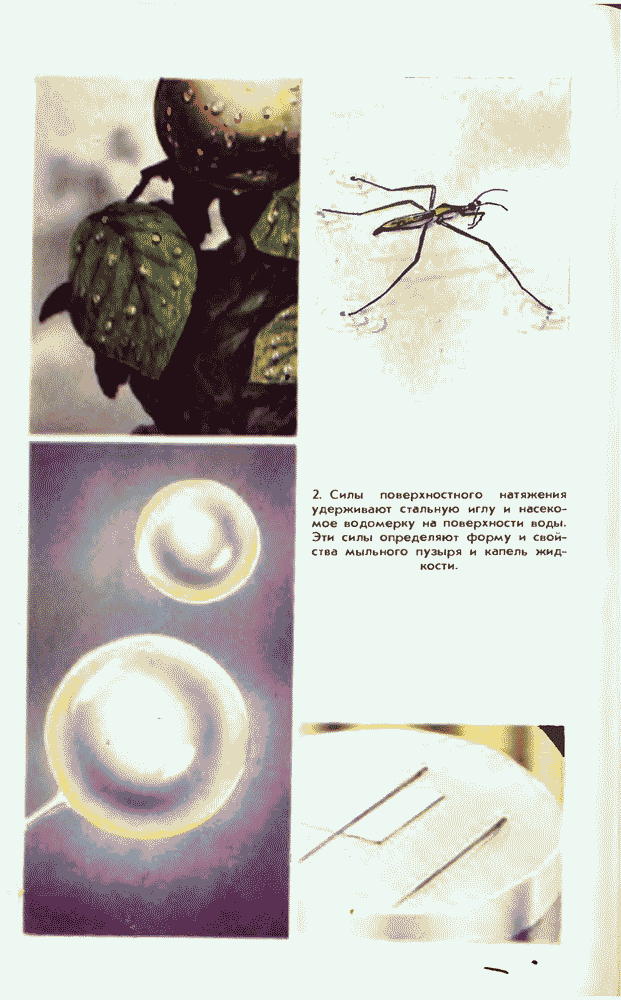
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7. ОСНОВНОЕ УРАВНЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
Вычислим с помощью молекулярно-кинетической теории давление газа. Вывод формулы для давления не очень сложный, но довольно громоздкий. Разобьем его на отдельные этапы.
Пусть газ находится в прямоугольном сосуде  одна из стенок которого представляет собой поршень
одна из стенок которого представляет собой поршень  способный перемещаться без трения (рис. 21). Причем газ и сосуд имеют одинаковые температуры.
способный перемещаться без трения (рис. 21). Причем газ и сосуд имеют одинаковые температуры.
Вычислим давление газа на поршень  имеющий площадь
имеющий площадь  Поверхность поршня расположена перпендикулярно оси
Поверхность поршня расположена перпендикулярно оси  Давление газа возникает в результате столкновений
Давление газа возникает в результате столкновений

Рис. 21

Рис. 22
молекул с поршнем. Чтобы поршень не был вытолкнут из сосуда, к нему извне нужно приложить некоторую силу Т.
Столкновение молекулы с поршнем. Рассмотрим вначале случай, когда скорость  молекулы до соударения с поршнем (рис. 22) перпендикулярна поверхности поршня. Молекулы в нашей модели — это твердые шарики. При столкновениях со стенкой они отскакивают от нее без изменения кинетической энергии. Подобные соударения называют абсолютно упругими. При этом модуль скорости не меняется, а направление движения меняется на противоположное:
молекулы до соударения с поршнем (рис. 22) перпендикулярна поверхности поршня. Молекулы в нашей модели — это твердые шарики. При столкновениях со стенкой они отскакивают от нее без изменения кинетической энергии. Подобные соударения называют абсолютно упругими. При этом модуль скорости не меняется, а направление движения меняется на противоположное:  Изменение импульса молекулы равно:
Изменение импульса молекулы равно:

Если же скорость молекулы направлена под произвольным углом к поршню (рис. 23), то при столкновении молекулы с поршнем проекция  ее скорости на направление, перпендикулярное поверхности поршня, меняет знак
ее скорости на направление, перпендикулярное поверхности поршня, меняет знак  а проекции
а проекции  скоростей на направления, параллельные поверхности поршня, остаются без изменения:
скоростей на направления, параллельные поверхности поршня, остаются без изменения:  То же самое происходит с мячом при столкновении с гладкой стенкой, если считать это столкновение абсолютно упругим
То же самое происходит с мячом при столкновении с гладкой стенкой, если считать это столкновение абсолютно упругим
Изменение проекции импульса молекулы на ось  равно:
равно:

Согласно закону сохранения импульса суммарный импульс молекулы и поршня остается неизменным. Это означает, что модуль изменения импульса поршня равен модулю изменения импульса молекулы. Иначе говоря, при столкновении молекулы с поршнем поршню передается импульс, модуль которого равен 
Согласно второму закону Ньютона изменение импульса тела равно импульсу силы — произведению силы на время ее действия. Поэтому модуль импульса силы, действующей на поршень со стороны молекулы за время удара, равен 
Число соударений молекул с поршнем. Для того чтобы вычислить импульс силы, действующей на поршень со стороны всех молекул, необходимо подсчитать число соударений

Рис. 23

Рис. 24
молекул с поршнем за некоторый интервал времени  много больший времени столкновения с порннем одной молекулы.
много больший времени столкновения с порннем одной молекулы.
За время  поршня могут достичь только молекулы, которые находятся от него на расстоянии, не превышающем
поршня могут достичь только молекулы, которые находятся от него на расстоянии, не превышающем  (рис. 24). Молекулы, находящиеся на больших расстояниях, не успеют долгтеть до поршня. Надо еще учесть, что стенки
(рис. 24). Молекулы, находящиеся на больших расстояниях, не успеют долгтеть до поршня. Надо еще учесть, что стенки  достигают
достигают  это время лишь те молекулы, у которых
это время лишь те молекулы, у которых  т. е. движушиеся слева направо.
т. е. движушиеся слева направо.
Значения проекций скоростей  не влияют на достижение молекулами поршня
не влияют на достижение молекулами поршня  Если молекула упруго столкнется со стенкой
Если молекула упруго столкнется со стенкой  или
или  то проекция скорости
то проекция скорости  при этом не изменится и молекул сместится вдоль оси
при этом не изменится и молекул сместится вдоль оси  все равно на отрезок
все равно на отрезок 
Выделенный объем  равен
равен  Если концентрация молекул составляет
Если концентрация молекул составляет  то число их в выделенном объеме равно
то число их в выделенном объеме равно 
Вследствие хаотичности движения в среднем лишь половина молекул в выделенном объеме имеет проекцию скорости  и движется слева направо.
и движется слева направо.  другой половины молекул
другой половины молекул  и они движутся в противоположном направлении.
и они движутся в противоположном направлении.
Следовательно, число ударов  молекул о поршень за время
молекул о поршень за время  равное половине всех молекул в выделенном объеме, составляет:
равное половине всех молекул в выделенном объеме, составляет:

Импульс средней силы, действующей на поршень со стороны всех молекул. Каждая молекула при соударении меняет импульс поршня на  За время
За время  все
все  молекул изменят его импульс на
молекул изменят его импульс на  Согласно второму закону Ньютона модуль
Согласно второму закону Ньютона модуль  импульса силы, действующей на поршень, равен модулю изменения его импульса:
импульса силы, действующей на поршень, равен модулю изменения его импульса:

Теперь нужно учесть следующее: рассуждения велись так, как будто бы скорости всех молекул одинаковы. На самом деле скорости молекул различны и каждая из них при ударе о поршень вносит свой особый вклад в давление. Для учета этого нужно взять среднее по всем молекулам значение квадрата проекции скорости  вместо
вместо 
Выражение для среднего значения модуля импульса силы определится формулой 
Так как  , то
, то

Давление газа. Разделив левую и правую части уравнения (1.16) на произведение  найдем давление газа:
найдем давление газа:

Это и есть основное уравнение молекулярно-кинетической теории.
Давление идеального газа пропорционально произведению массы молекулы, числа молекул в единице объема и среднего квадрата скорости движения молекул.
Формула (1.17) связывает макроскопическую величину — давление, которое может быть измерено манометром, — с микроскопическими величинами, характеризующими молекулы, и является как бы мостом между двумя мирами - макроскопическим и микроскопическим.
Если через Е обозначить среднюю кинетическую энергию поступательного движения молекулы  то уравнение (1.17) можно записать в форме:
то уравнение (1.17) можно записать в форме:

В следующей главе будет доказано, что средняя кинетическая энергия молекул определяется температурой газа.
1. Что называют идеальным газом в молекулярно-кинетической теории?
2. Каков механизм возникновения давления газа с точки зрения молекулярно-кинетической теории? 3. Чему равно среднее значение проекции скорости молекулы на ось  Дайте определение среднего значения квадрата скорости молекул. 5. Чему равно изменение импульса молекулы при ее соударении со стенкой? 6. От чего зависит число соударений молекул с поршнем площади
Дайте определение среднего значения квадрата скорости молекул. 5. Чему равно изменение импульса молекулы при ее соударении со стенкой? 6. От чего зависит число соударений молекул с поршнем площади  за время
за время  . Запишите основное уравнение молекулярно-кинетической теории.
. Запишите основное уравнение молекулярно-кинетической теории.
| << Предыдущий параграф | Следующий параграф >> |
- ТЕПЛОВЫЕ ЯВЛЕНИЯ. МОЛЕКУЛЯРНАЯ ФИЗИКА
- Глава I. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ
- 1. ОСНОВНЫЕ ПОЛОЖЕНИЯ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ. РАЗМЕРЫ МОЛЕКУЛ
- 2. МАССА МОЛЕКУЛ. ПОСТОЯННАЯ АВОГАДРО
- 3. БРОУНОВСКОЕ ДВИЖЕНИЕ.
- 4. СИЛЫ ВЗАИМОДЕЙСТВИЯ МОЛЕКУЛ
- 5. СТРОЕНИЕ ГАЗООБРАЗНЫХ, ЖИДКИХ И ТВЕРДЫХ ТЕЛ
- 6. ИДЕАЛЬНЫЙ ГАЗ В МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ
- 7. ОСНОВНОЕ УРАВНЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ I
- Глава II. ТЕМПЕРАТУРА. ЭНЕРГИЯ ТЕПЛОВОГО ДВИЖЕНИЯ МОЛЕКУЛ
- 8. ТЕПЛОВОЕ РАВНОВЕСИЕ. ТЕМПЕРАТУРА
- 9. ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ
- 10. АБСОЛЮТНАЯ ТЕМПЕРАТУРА. ТЕМПЕРАТУРА — МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ
- 11. ИЗМЕРЕНИЕ СКОРОСТЕЙ МОЛЕКУЛ ГАЗА
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ II
- Глава III. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА. ГАЗОВЫЕ ЗАКОНЫ
- 12. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- 13. ПРИМЕНЕНИЕ УРАВНЕНИЯ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА К РАЗЛИЧНЫМ ПРОЦЕССАМ
- 14. ПРИМЕНЕНИЕ ГАЗОВ В ТЕХНИКЕ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ III
- Глава IV. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 16. РАБОТА В ТЕРМОДИНАМИКЕ
- 17. КОЛИЧЕСТВО ТЕПЛОТЫ
- 18. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 19. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА ТЕРМОДИНАМИКИ К РАЗЛИЧНЫМ ПРОЦЕССАМ
- 20. НЕОБРАТИМОСТЬ ПРОЦЕССОВ В ПРИРОДЕ
- 21. ПРИНЦИПЫ ДЕЙСТВИЯ ТЕПЛОВЫХ ДВИГАТЕЛЕЙ
- 22. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ (КПД) ТЕПЛОВОГО ДВИГАТЕЛЯ. ТЕПЛОВЫЕ ДВИГАТЕЛИ И ОХРАНА ПРИРОДЫ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ IV
- Глава V. ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ЖИДКОСТЕЙ И ГАЗОВ
- 23. НАСЫЩЕННЫЙ ПАР
- 24. ЗАВИСИМОСТЬ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА ОТ ТЕМПЕРАТУРЫ. КИПЕНИЕ. КРИТИЧЕСКАЯ ТЕМПЕРАТУРА
- 25. ВЛАЖНОСТЬ ВОЗДУХА
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ V
- Глава VI. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ ЖИДКОСТЕЙ
- 27. СИЛА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ
- 28. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ VI
- Глава VII. ТВЕРДЫЕ ТЕЛА
- 29. КРИСТАЛЛИЧЕСКИЕ ТЕЛА
- 30. АМОРФНЫЕ ТЕЛА
- 31. ДЕФОРМАЦИЯ. ВИДЫ ДЕФОРМАЦИИ ТВЕРДЫХ ТЕЛ
- 32. МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ. ДИАГРАММА РАСТЯЖЕНИЯ
- 33. ПЛАСТИЧНОСТЬ И ХРУПКОСТЬ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ VII
- ОСНОВЫ ЭЛЕКТРОДИНАМИКИ
- 34. ЧТО ТАКОЕ ЭЛЕКТРОДИНАМИКА?
- Глава VIII. ЭЛЕКТРОСТАТИКА
- 35. ЭЛЕКТРИЧЕСКИЙ ЗАРЯД И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 36. ЗАРЯЖЕННЫЕ ТЕЛА. ЭЛЕКТРИЗАЦИЯ ТЕЛ
- 37. ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
- 38. ОСНОВНОЙ ЗАКОН ЭЛЕКТРОСТАТИКИ — ЗАКОН КУЛОНА
- 39. ЕДИНИЦА ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 40. БЛИЗКОДЕЙСТВИЕ И ДЕЙСТВИЕ НА РАССТОЯНИИ
- 41. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 42. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. ПРИНЦИП СУПЕРПОЗИЦИИ ПОЛЕЙ
- 43. СИЛОВЫЕ ЛИНИИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
- 44. ПРОВОДНИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
- 45. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ РАВНОМЕРНО ЗАРЯЖЕННОГО ПРОВОДЯЩЕГО ШАРА И БЕСКОНЕЧНОЙ ПЛОСКОСТИ
- 46. ДИЭЛЕКТРИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ. ДВА ВИДА ДИЭЛЕКТРИКОВ
- 47. ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ. ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ
- 48. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЗАРЯЖЕННОГО ТЕЛА В ОДНОРОДНОМ ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
- 49. ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ И РАЗНОСТЬ ПОТЕНЦИАЛОВ
- 50. ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ТОЧЕЧНОГО ЗАРЯДА
- 51. СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ ЭЛЕКТРИЧЕСКОГО ПОЛЯ И РАЗНОСТЬЮ ПОТЕНЦИАЛОВ. ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ
- 52. ИЗМЕРЕНИЕ РАЗНОСТИ ПОТЕНЦИАЛОВ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 53. ЭЛЕКТРОЕМКОСТЬ. ЕДИНИЦЫ ЭЛЕКТРОЕМКОСТИ
- 54. КОНДЕНСАТОРЫ. ЭЛЕКТРОЕМКОСТЬ ПЛОСКОГО КОНДЕНСАТОРА
- 55. ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА. ПРИМЕНЕНИЯ КОНДЕНСАТОРОВ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ X
- Глава IX. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- 56. ЭЛЕКТРИЧЕСКИЙ ТОК. СИЛА ТОКА
- 57. УСЛОВИЯ, НЕОБХОДИМЫЕ ДЛЯ СУЩЕСТВОВАНИЯ ЭЛЕКТРИЧЕСКОГО ТОКА
- 58. ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ. СОПРОТИВЛЕНИЕ
- 59. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ПРОВОДНИКА ОТ ТЕМПЕРАТУРЫ
- 60. СВЕРХПРОВОДИМОСТЬ
- 61. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ ПРОВОДНИКОВ
- 62. ИЗМЕРЕНИЕ СИЛЫ ТОКА И НАПРЯЖЕНИЯ
- 63. РАБОТА И МОЩНОСТЬ ПОСТОЯННОГО ТОКА
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 64. ЭЛЕКТРОДВИЖУЩАЯ СИЛА
- 65. ЗАКОН ОМА ДЛЯ ЗАМКНУТОЙ ЦЕПИ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ IX
- Глава X. ЭЛЕКТРИЧЕСКИЙ ТОК В РАЗЛИЧНЫХ СРЕДАХ
- 66. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ РАЗЛИЧНЫХ ВЕЩЕСТВ
- 67. ЭЛЕКТРОННАЯ ПРОВОДИМОСТЬ МЕТАЛЛОВ
- 68. ЭЛЕКТРИЧЕСКИЙ ТОК В ЖИДКОСТЯХ
- 69. ЗАКОН ЭЛЕКТРОЛИЗА
- 70. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ
- 71. НЕСАМОСТОЯТЕЛЬНЫЙ И САМОСТОЯТЕЛЬНЫЙ РАЗРЯДЫ
- 72. РАЗЛИЧНЫЕ ТИПЫ САМОСТОЯТЕЛЬНОГО РАЗРЯДА И ИХ ТЕХНИЧЕСКИЕ ПРИМЕНЕНИЯ
- 73. ПЛАЗМА
- 74. ЭЛЕКТРИЧЕСКИЙ ТОК В ВАКУУМЕ
- 75. ДВУХЭЛЕКТРОДНАЯ ЭЛЕКТРОННАЯ ЛАМПА-ДИОД
- 76. ЭЛЕКТРОННЫЕ ПУЧКИ. ЭЛЕКТРОННОЛУЧЕВАЯ ТРУБКА
- 77. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ
- 78. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ ПОЛУПРОВОДНИКОВ ПРИ НАЛИЧИИ ПРИМЕСЕЙ
- 79. ЭЛЕКТРИЧЕСКИЙ ТОК ЧЕРЕЗ КОНТАКТ ПОЛУПРОВОДНИКОВ p- И n- ТИПОВ
- 80. ПОЛУПРОВОДНИКОВЫЙ ДИОД
- 81. ТРАНЗИСТОР
- 82. ТЕРМИСТОРЫ И ФОТОРЕЗИСТОРЫ
- ПРИМЕР РЕШЕНИЯ ЗАДАЧИ
- КРАТКИЕ ИТОГИ ГЛАВЫ X
- Глава XI. МАГНИТНОЕ ПОЛЕ
- 83. ВЗАИМОДЕЙСТВИЕ ТОКОВ. МАГНИТНОЕ ПОЛЕ
- 84. ВЕКТОР МАГНИТНОЙ ИНДУКЦИИ
- 85. ЛИНИИ МАГНИТНОЙ ИНДУКЦИИ
- 86. ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
- 87. МОДУЛЬ ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ. МАГНИТНЫЙ ПОТОК
- 88. ЗАКОН АМПЕРА
- 89. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЙСЯ ЗАРЯД. СИЛА ЛОРЕНЦА
- 90. МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ XI
- Глава XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
- 91. ОТКРЫТИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
- 92. НАПРАВЛЕНИЕ ИНДУКЦИОННОГО ТОКА. ПРАВИЛО ЛЕНЦА
- 93. ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
- 94. ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 95. ЭДС ИНДУКЦИИ В ДВИЖУЩИХСЯ ПРОВОДНИКАХ
- 96. САМОИНДУКЦИЯ. ИНДУКТИВНОСТЬ
- 97. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА
- 98. ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРОДИНАМИКИ И ИХ ТЕХНИЧЕСКОЕ ПРИМЕНЕНИЕ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ИТОГИ ГЛАВЫ XII
- ЗАКЛЮЧЕНИЕ
- ЛАБОРАТОРНЫЕ РАБОТЫ
- ОТВЕТЫ К УПРАЖНЕНИЯМ