| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
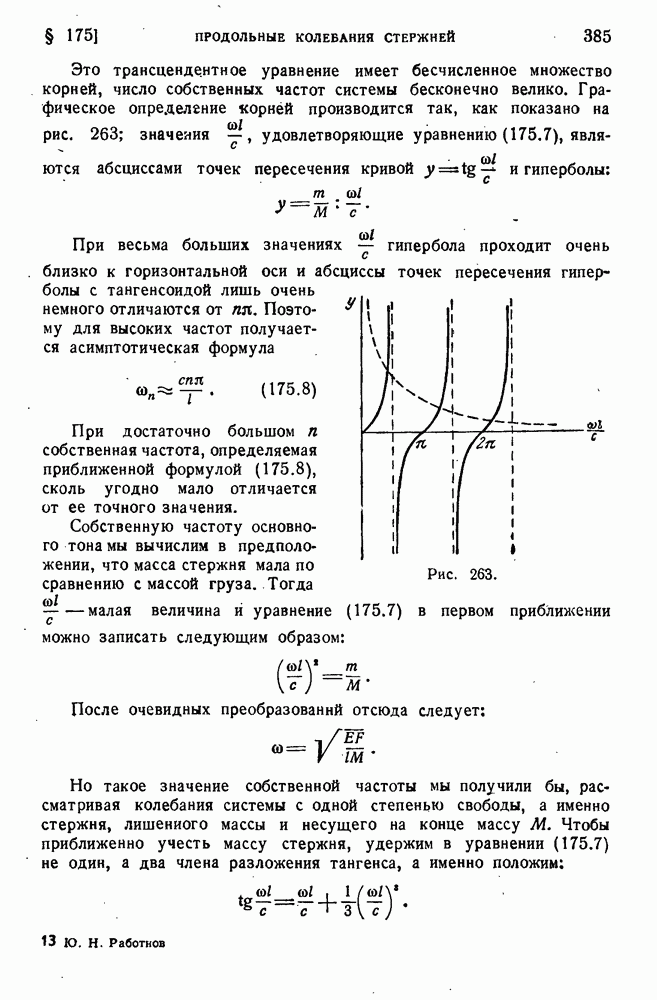
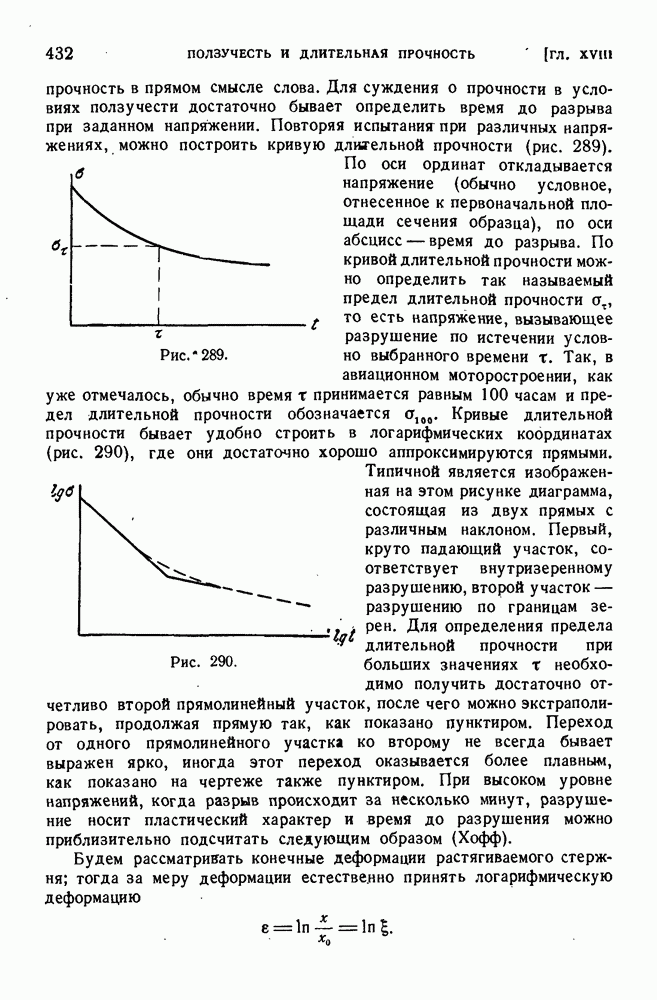
§ 183. Механизм хрупкого разрушения.
Гриффис в 1921 г. предложил следующее объяснение хрупкого разрушения. Представим себе пластинку достаточно больших размеров, толщину которой для удобства примем равной единице. Эта пластинка растянута в одном направлении напряжением о, и края ее неподвижно закреплены, как показано на рис. 268. Потенциальная энергия, приходящаяся на единицу площади пластинки, равна  полная потенциальная энергия получается путем умножения этой величины на площадь.
полная потенциальная энергия получается путем умножения этой величины на площадь.

Рис. 268.
Представим теперь себе, что в пластинке возникла трещина в направлении, перпендикулярном направлению растяжения. Эта трещина не изменит существенно распределения напряжений в большей части пластинки, но в окрестности трещины общий уровень напряженности понизится (вблизи концов, наоборот, возникает концентрация напряжений). Потенциальная энергия пластинки в целом уменьшится на величину U; поскольку единственный линейный размер, характеризующий трещину, есть ее длина I, а величина U должна представлять собой произведение удельной энергии на некоторую площадь, то

Пользуясь решением задачи теории упругости о растяжении полосы с трещиной, Гриффис нашел величину k, она равняется  однако для нас это несущёственно. Поскольку рост трещины сопровождается уменьшением потенциальной энергии пластинки, всякая трещина имеет тенденцию к неограниченному росту, так как всякое тело стремится принять состояние с наименьшей потенциальной энергией. Однако образование свободной поверхности связано с появлением энергии поверхностного натяжения. Обозначим величину поверхностного натяжения через S. Представим себе, что трещина длины
однако для нас это несущёственно. Поскольку рост трещины сопровождается уменьшением потенциальной энергии пластинки, всякая трещина имеет тенденцию к неограниченному росту, так как всякое тело стремится принять состояние с наименьшей потенциальной энергией. Однако образование свободной поверхности связано с появлением энергии поверхностного натяжения. Обозначим величину поверхностного натяжения через S. Представим себе, что трещина длины  увеличилась на
увеличилась на  . Потенциальная энергия при этом уменьшится на величину
. Потенциальная энергия при этом уменьшится на величину  , энергия поверхностного натяжения увеличится на
, энергия поверхностного натяжения увеличится на  Если окажется, что уменьшение потенциальной энергии больше, чем увеличение поверхностной энергии, трещина будет самопроизвольно увеличиваться.
Если окажется, что уменьшение потенциальной энергии больше, чем увеличение поверхностной энергии, трещина будет самопроизвольно увеличиваться.
Приравняв две эти величины, найдем критическую длину трещины.
Из уравнения  следует:
следует:
 (183.1)
(183.1)
С точки зрения этой теории прочность материалов по отношению к хрупкому разрушению определяется наличием микротрещин. Внося в формулу (183.1) вместо  длину микротрещины, мы можем определить напряжение а, при котором эта трещина будет расти и приведет к хрупкому разрушению.
длину микротрещины, мы можем определить напряжение а, при котором эта трещина будет расти и приведет к хрупкому разрушению.
Теория Гриффиса дает объяснение так называемому масштабному эффекту, наблюдаемому при хрупком разрушении. Этот эффект заключается в том, что разрушающее напряжение для образцов малого размера выше, чем для больших образцов, и крупные изделия разрушаются при напряжениях значительно меньших, чем те, которые можно было бы счесть допускаемыми на основании лабораторных опытов над образцами из того же материала. Размеры микротрещин, имеющихся внутри материала, различны, распределение их случайно и подчинено законам статистики. Более крупные трещины встречаются редко, тогда как для начала разрушения по теории Гриффиса достаточно, чтобы было очень немного трещин, длина которых превышает критическую. Вероятность нахождения таких трещин в теле значительного объема больше, чем в теле малых размеров. Эти соображения привели к развитию многочисленных статистических теорий прочности, в которых величина разрушающего напряжения и зависимость ее от размеров оцениваются при помощи теории вероятностей.
Теория Гриффиса подвергалась экспериментальной проверке и дала удовлетворительные результаты применительно к стеклу — твердому аморфному материалу, не обнаруживающему заметных пластических свойств. Для металлов теория в ее первоначальном виде вряд ли применима.
В обычных условиях разрушению металла всегда предшествует некоторая пластическая деформация, поэтому возникает вопрос, может ли пластическая деформация привести к появлению и развитию трещин хрупкого разрушения. Одна из возможных схем такого рода была рассмотрена Стро (1954 г.).
Заметим прежде всего, что около краевой дислокации всегда возникает область растягивающих напряжений, причем растягивающие напряжения будут наибольшими на вертикальной прямой, проходящей через центр дислокации, снизу от нее, если дислокация положительна. Это ясно из схемы образования краевой дислокации, приведенной на рис. 91 (случай г) (§ 67), и иллюстрируется рис. 269.
Как было показано в § 69, группу дислокаций, порожденных источником Франка — Рида и задержанных препятствием, можно представить как группу краевых дислокаций, изображенную на рис. 100 к повторенную на рис. 270. В области, находящейся под препятствием, в которое упирается крайняя дислокация, возникнут растягивающие напряжения. Эти напряжения суммируются от всех дислокаций, следовательно, увеличиваются с увеличением их числа, последнее в свою очередь растет с ростом касательного напряжения  в плоскости скольжения. Наибольшие растягивающие напряжения получаются на
в плоскости скольжения. Наибольшие растягивающие напряжения получаются на

Рис. 269.

Рис. 270.
некоторой прямой  Может случиться, что эти напряжения окажутся достаточно большими для того, чтобы вызвать образование трещины вдоль
Может случиться, что эти напряжения окажутся достаточно большими для того, чтобы вызвать образование трещины вдоль  Тогда дислокации получат свободу перемещаться и каждая из них, дойдя до края трещины, исчезнет, вызвав дополнительное раскрытие трещины за счет сдвига частей кристалла, расположенных выше и ниже плоскости скольжения, на величину вектора Бюргерса
Тогда дислокации получат свободу перемещаться и каждая из них, дойдя до края трещины, исчезнет, вызвав дополнительное раскрытие трещины за счет сдвига частей кристалла, расположенных выше и ниже плоскости скольжения, на величину вектора Бюргерса  . В результате возникает положение, изображенное на рис. 270, б, трещина длины L имеет форму клина с основанием
. В результате возникает положение, изображенное на рис. 270, б, трещина длины L имеет форму клина с основанием  .
.
Переход из состояния а в состояние  возможен только тогда, когда энергии этих состояний одинаковы. В состоянии а речь идет об энергии группы дислокаций в плоскости скольжения, удерживаемых напряжением
возможен только тогда, когда энергии этих состояний одинаковы. В состоянии а речь идет об энергии группы дислокаций в плоскости скольжения, удерживаемых напряжением  ; в случае
; в случае  вокруг трещины возникает некоторое напряженное состояние, следовательно, существует энергия упругой деформации, к которой нужио добавить энергию поверхностного натяження. Энергия трещины, состоящая из упругой анергии и энергии поверхностного натяжения, как оказывается, принимает минимальное значение для некоторой длины трещины L. Приравнивая это минимальное значение энергии трещины энергии группы дислокаций, мы находим условие возникновения трещины. В результате вычислений
вокруг трещины возникает некоторое напряженное состояние, следовательно, существует энергия упругой деформации, к которой нужио добавить энергию поверхностного натяження. Энергия трещины, состоящая из упругой анергии и энергии поверхностного натяжения, как оказывается, принимает минимальное значение для некоторой длины трещины L. Приравнивая это минимальное значение энергии трещины энергии группы дислокаций, мы находим условие возникновения трещины. В результате вычислений  получил следующие оценки.
получил следующие оценки.
Касательное напряжение в плоскости скольжения, при котором появляется трещина:

Как видно, для образования трещины нужно, чтобы число дислокаций было достаточно большим, для меди, например, получается  .
.
Длина трещины при этом
 (183.3)
(183.3)
Следует заметить, что эта трещина, в отличие от той, которая рассматривается в схеме Гриффиса, является равновесной, длина ее сохраняется, так как соответствует минимальному значению потенциальной энергии.
Последующее развитие идеи Гриффиса заключается в следующем. Конец трещины является источником концентрации напряжений, которые достигают в упругом теле весьма большой величины. Поэтому вблизи конца трещины образуется область пластических деформаций, при распространении трещины эта область движется, таким образом все новые объемы материала пластически деформируются, а потом разгружаются, возвращаясь в упругое состояние. При этом совершается необратимая работа. Очевидно, что величина этой работы пропорциональна увеличению длины трещины; если последняя возрастает на  то работа пластического деформирования выразится совершенно так же, как и приращение энергии поверхностного натяжения. Если понимать под S не энергию поверхностного натяжения на единицу площади, а эту энергию, сложенную с половиной работы пластической деформации при продвижении трещины на единицу длины, то формулы (181.1), (181.2) и (181.3) сохранят силу (Оро-ван, 1950 г., Ирвин, 1948 г.). Таким образом, величина S должна рассматриваться как некоторая константа материала, подлежащая опытному определению; анализ пластического напряженного состояния у конца трещины и теоретический подсчет величины работы пластической деформации затруднительны.
то работа пластического деформирования выразится совершенно так же, как и приращение энергии поверхностного натяжения. Если понимать под S не энергию поверхностного натяжения на единицу площади, а эту энергию, сложенную с половиной работы пластической деформации при продвижении трещины на единицу длины, то формулы (181.1), (181.2) и (181.3) сохранят силу (Оро-ван, 1950 г., Ирвин, 1948 г.). Таким образом, величина S должна рассматриваться как некоторая константа материала, подлежащая опытному определению; анализ пластического напряженного состояния у конца трещины и теоретический подсчет величины работы пластической деформации затруднительны.
Модифицированная таким образом теория Гриффиса дает более реальные оценки для условия образования микротрещин в соответствии с дислокационным механизмом и для длины равновесной трещииы по формуле (183.3). С другой стороны, эта теория позволяет объяснить катастрофическое распространение трещин в конструкциях из мягкой стали, которое приводит иногда к очень серьезным авариям. Известны и описаны в литературе случаи, когда огромные резервуары для хранения нефтепродуктов разрывались от верха до низа без заметной пластической деформации. По-видимому, разрушение начиналось в месте концентрации напряжений или какого-либо случайного дефекта, и появившаяся первая трещина оказывалась неустойчивой.
В сороковых годах, во время войны, в американском флоте произошло несколько аварий, когда корабль буквально ломался пополам.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ
- § 1. Задачи и содержание сопротивления материалов.
- § 2. Сопротивление материалов и теоретическая механика.
- § 3. Статически неопределенные задачи.
- § 4. Внешние силы.
- § 5. Принцип отвердения.
- § 6. Недопустимость замены системы сил статически эквивалентной.
- § 7. Однородное тело.
- § 8. Внутренние силы.
- § 9. Напряжение.
- § 10. Простейшие типы напряженного состояния.
- § 11. Простейшие виды деформации.
- § 12. Упругость и пластичность.
- § 13. Закон Гука.
- § 14. Диаграмма пластичности.
- § 15. Тела изотропные и анизотропные.
- ГЛАВА II. РАСТЯЖЕНИЕ СЖАТИЕ
- § 16. Стержни и стержневые системы.
- § 17. Принцип Сен-Венана и гипотеза плоских сечений.
- § 18. Напряжения и деформации при растяжении.
- § 19. Расчеты на прочность при растижении и сжатии.
- § 20. Собственный вес и силы инерции.
- § 21. Стержни переменного сечения.
- § 22. Перемещения узлов стержневых систем.
- § 23. Статически неопределенные задачи на растяжение — сжатие.
- § 24. Температурные и монтажные напряжения.
- § 25. Общие соображения о расчете стержневых систем.
- § 26. Расчет статически неопределимых систем по допускаемым нагрузкам.
- § 27. Остаточные напряжения после пластической деформации.
- § 28. Потенциальная энергия растяжении.
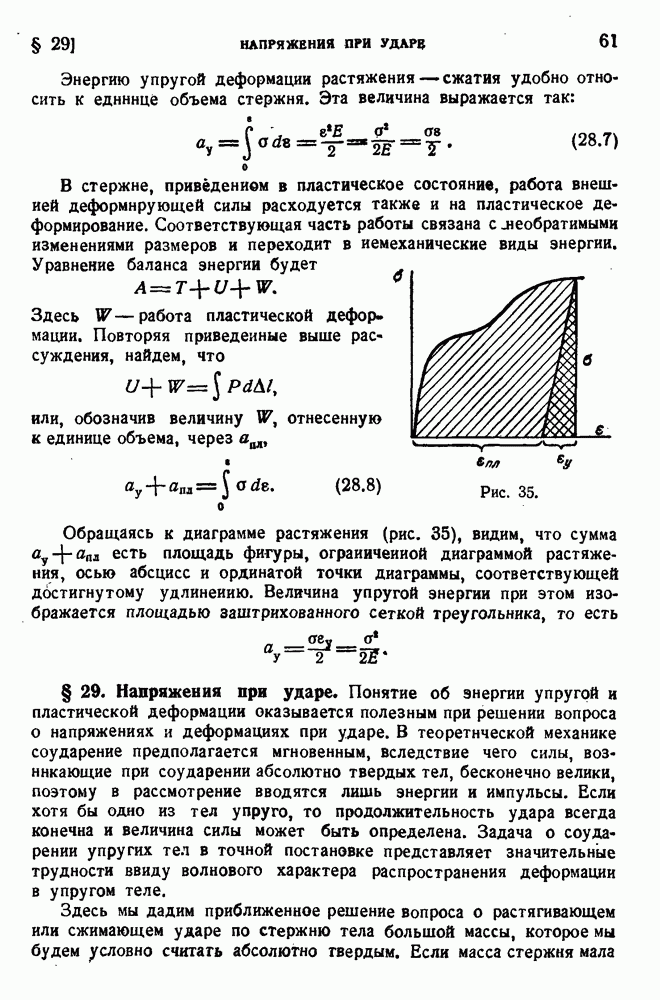
- § 29. Напряжения при ударе.
- § 30. Распространение упругих волн в стержнях.
- § 31. Концентрации напряжений.
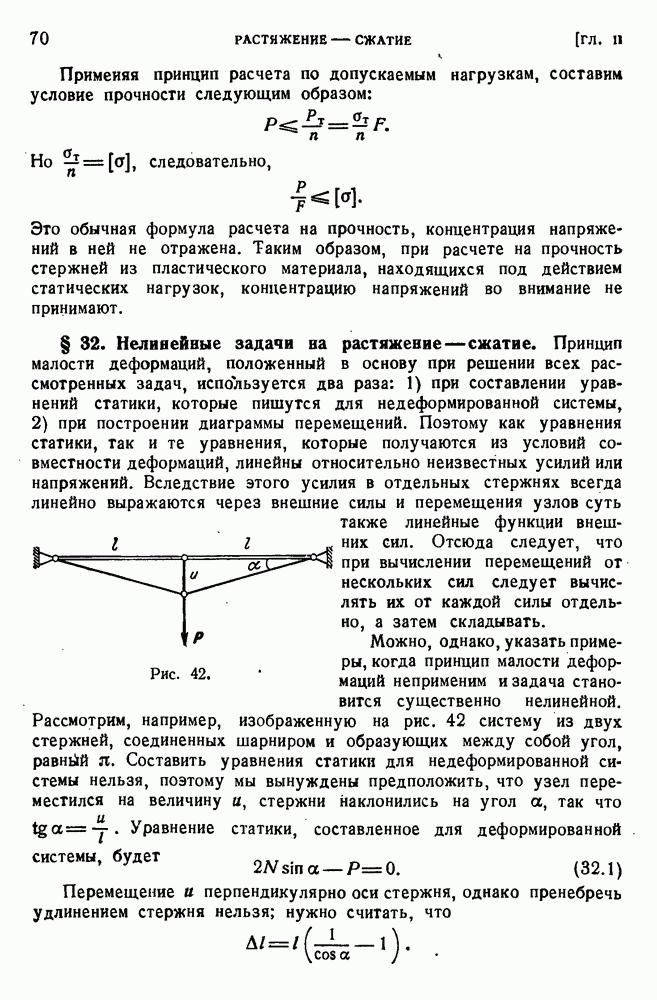
- § 32. Нелинейные задачи на растяжение — сжатие.
- ГЛАВА III. СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
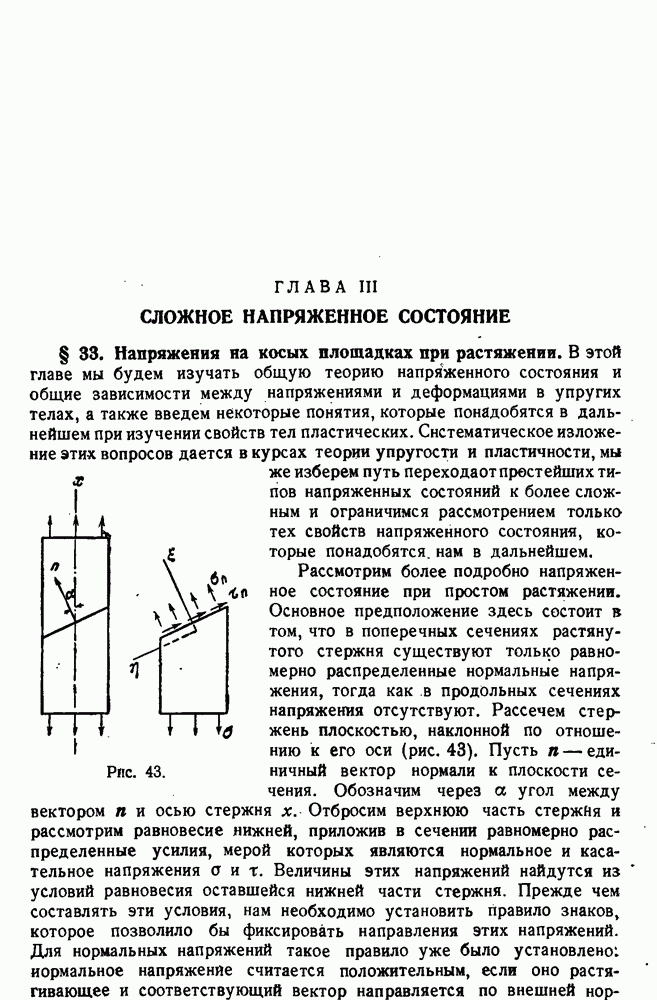
- § 33. Напряжения на косых площадках при растяжении.
- § 34. Напряжения при двухосном растяжении.
- § 35. Круговая диаграмма Мора.
- § 36. Общий случай плоского напряженного состояния.
- § 37. Определение напряжений на произвольной площадке.
- § 38. Пространственное напряженное состояние.
- § 39. Главные напряжения.
- § 40. Главные касательные напряжения.
- § 41. Октаэдрическое напряжение.
- § 42. Закон Гука для главных осей.
- § 43. Изменение объема при упругой деформации.
- § 44. Чистый сдвиг.
- § 45. Деформация элемента объема в общем случае.
- § 46. Условие пластичности Треска — Сен-Венана.
- § 47. Условие пластичности Мизеса.
- § 48. Условия пластичности для плоского напряженного состояния.
- § 49. Потенциальная энергия упругой деформации.
- § 50. Энергия изменения формы.
- ГЛАВА IV. НЕКОТОРЫЕ ПРИМЕРЫ РАСЧЕТА НА ПРОЧНОСТЬ
- § 51. Расчеты на прочность изделий сложной формы.
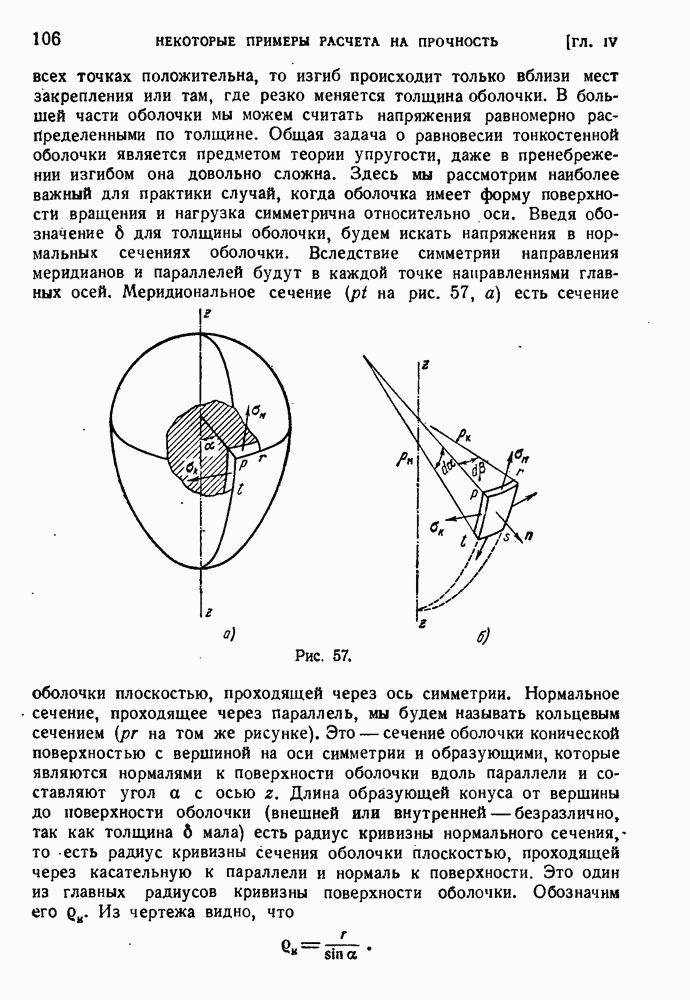
- § 52. Безмоментные оболочки вращении.
- § 53. Местные напряжения в безмоментных оболочках.
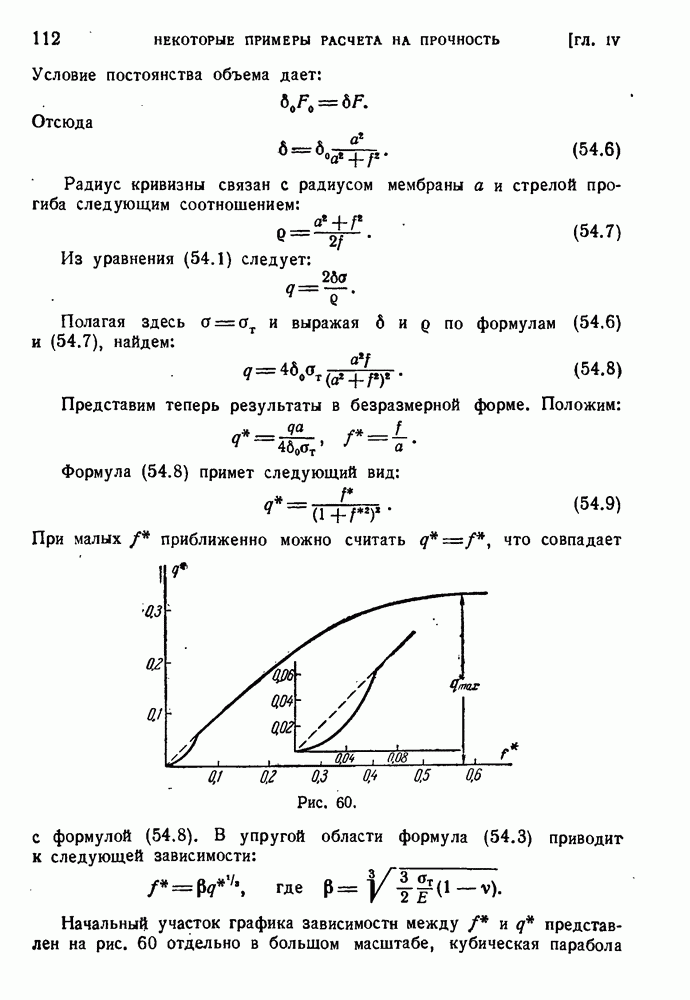
- § 54. Большие прогибы мембраны.
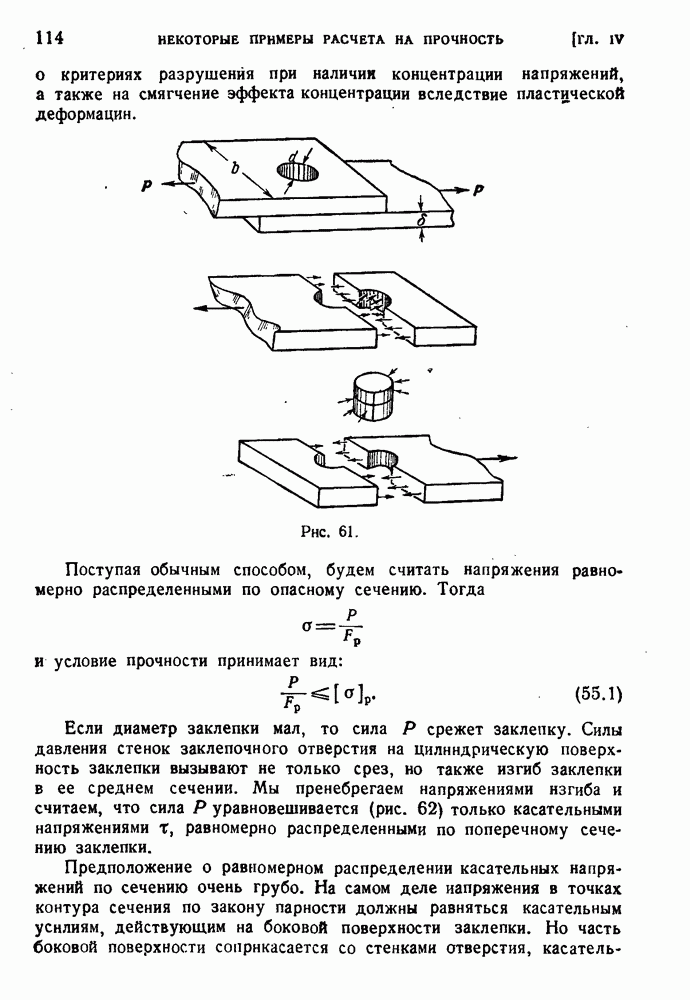
- § 55. Условные расчеты.
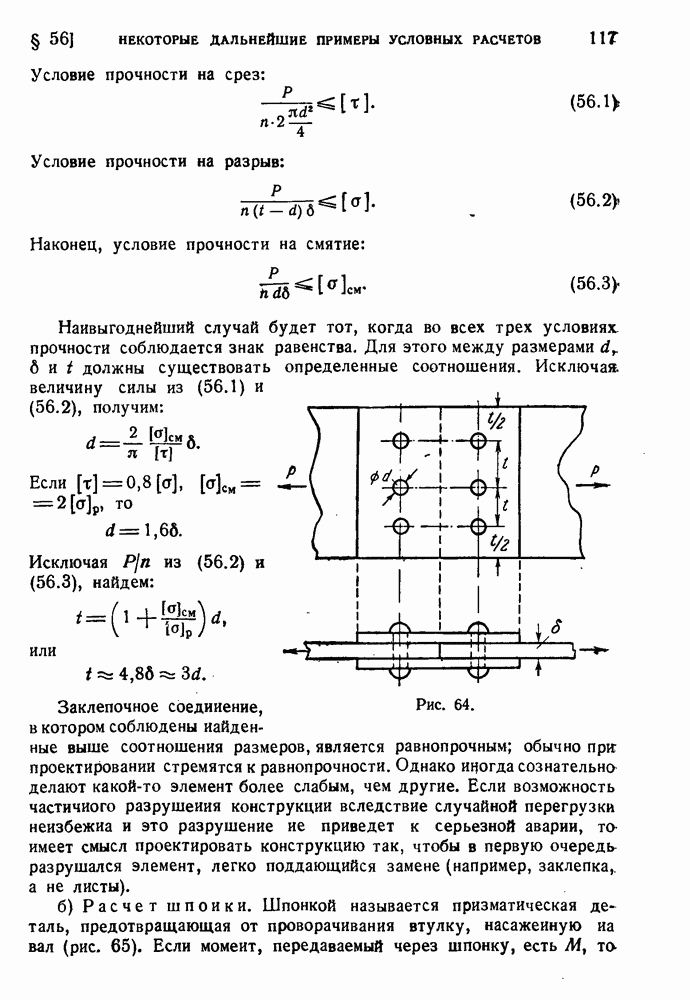
- § 56. Некоторые дальнейшие примеры условных расчетов.
- § 57. Расчет сварных соединений.
- ГЛАВА V. ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ
- § 58. Задачи испытания материалов.
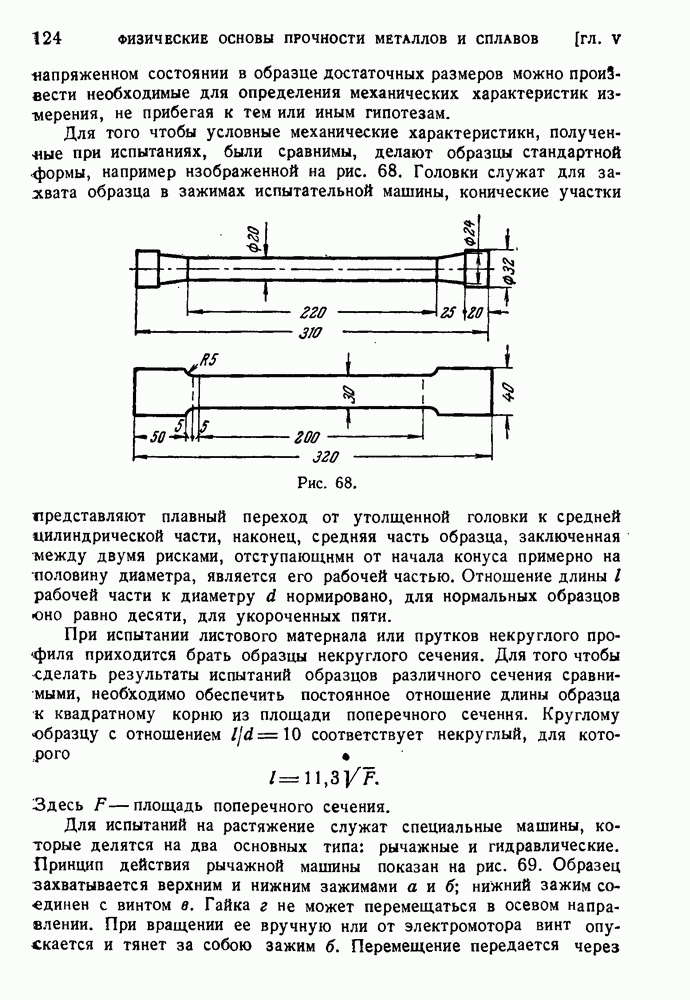
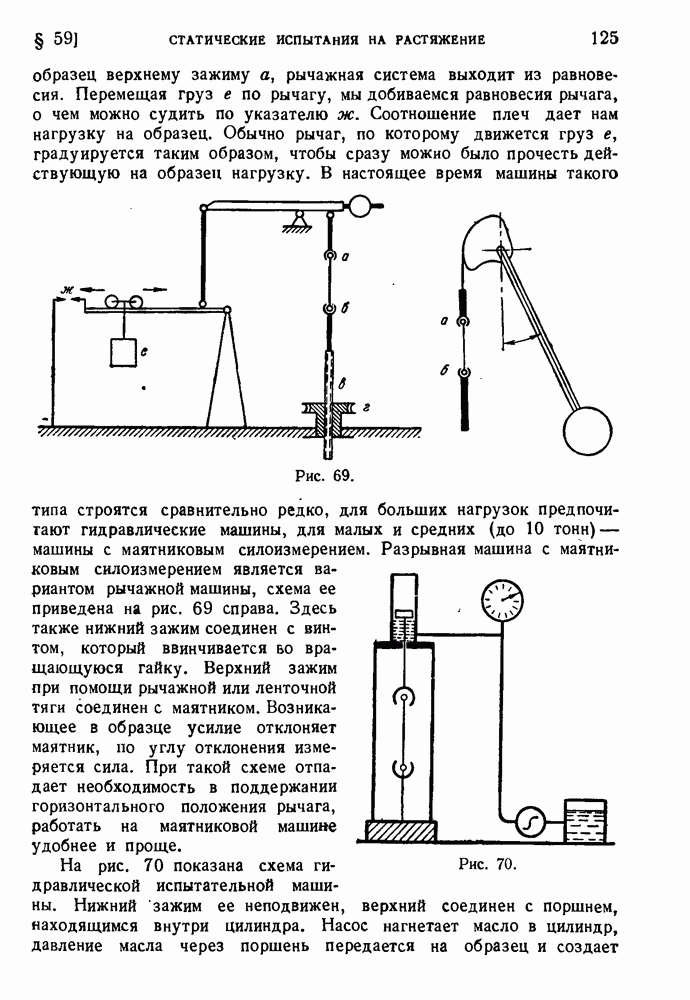
- § 59. Статические испытания на растяжение.
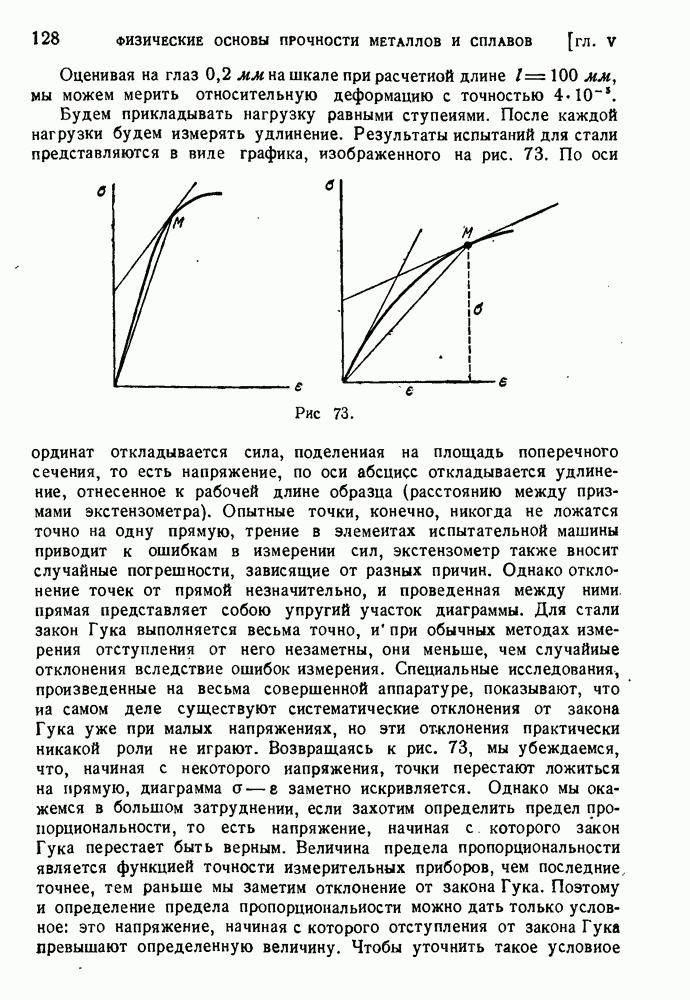
- § 60. Исследование металлов в области малых деформаций.
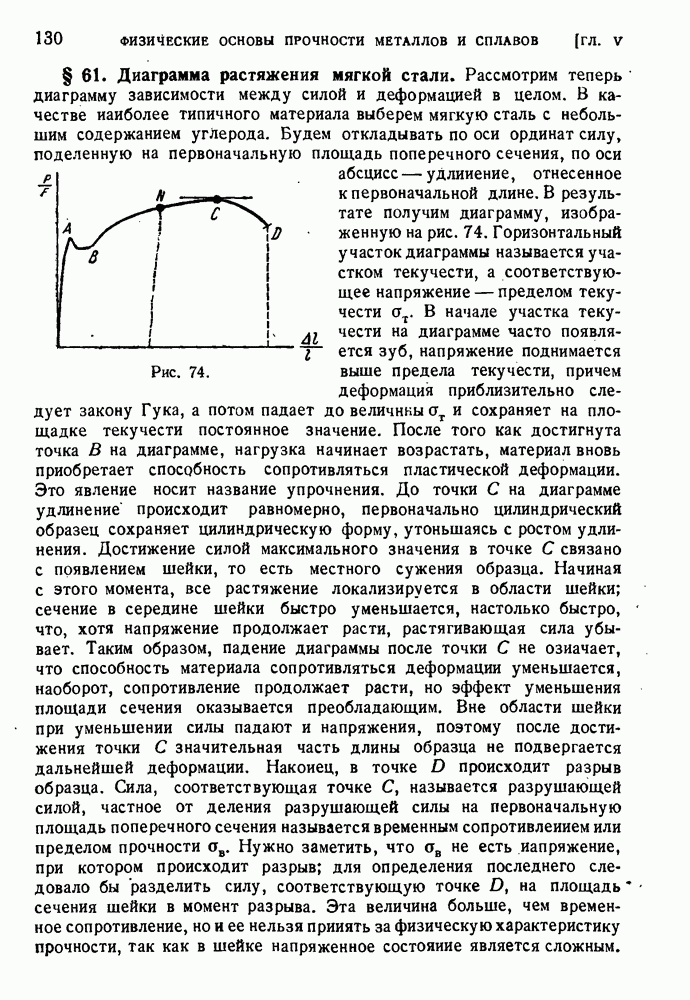
- § 61. Диаграмма растяжения мягкой стали.
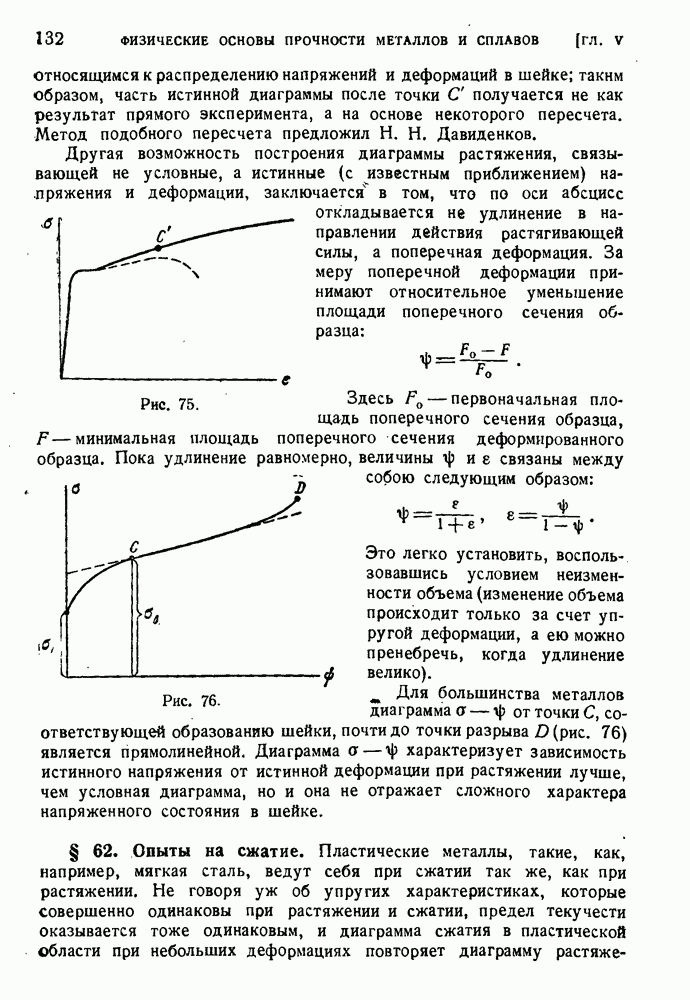
- § 62. Опыты на сжатие.
- § 63. Строение и упругая деформация металлических кристаллов.
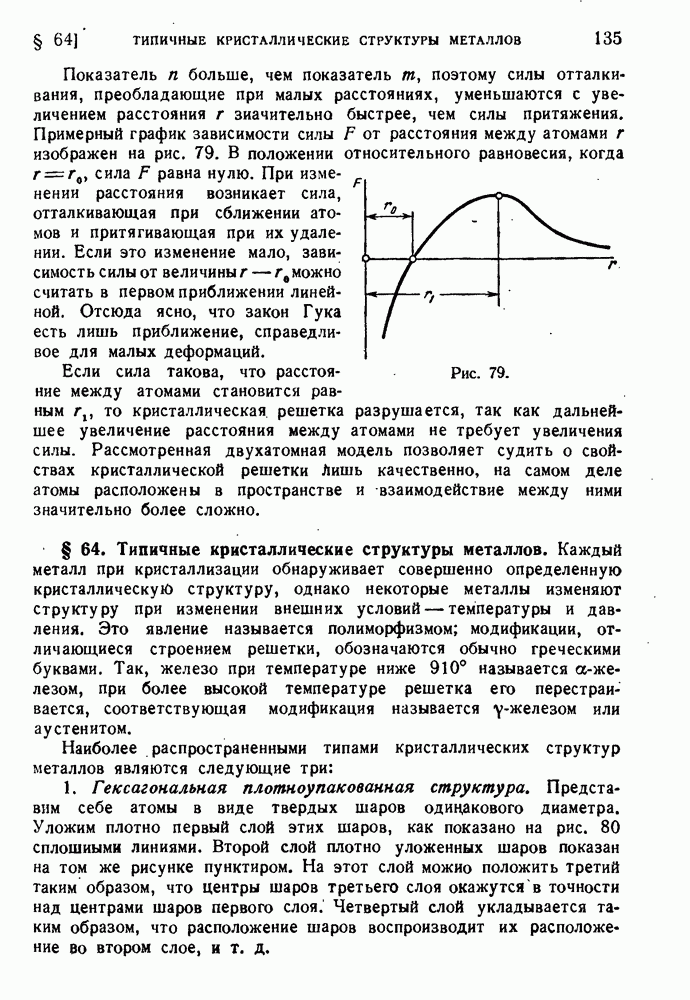
- § 64. Типичные кристаллические структуры металлов.
- § 65. Пластическая деформация монокристаллов.
- § 66. Прочность кристаллов и сопротивление пластическому деформированию.
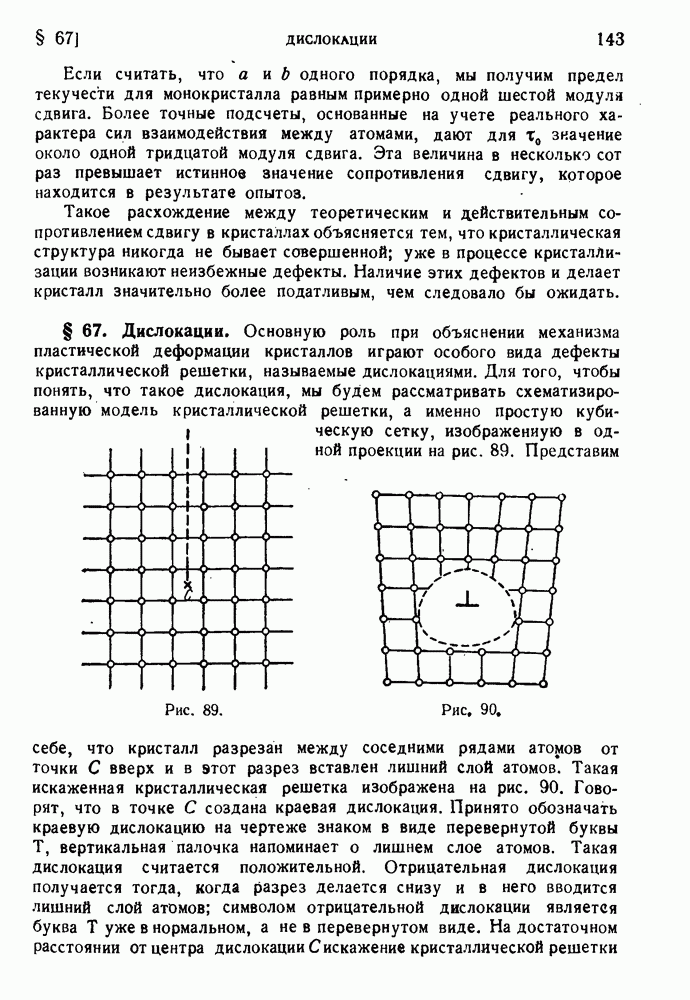
- § 67. Дислокации.
- § 68. Движение и равновесие дислокаций.
- § 69. Источники дислокаций.
- § 70. Границы блоков.
- § 71. Деформация поликристаллических металлов и сплавов.
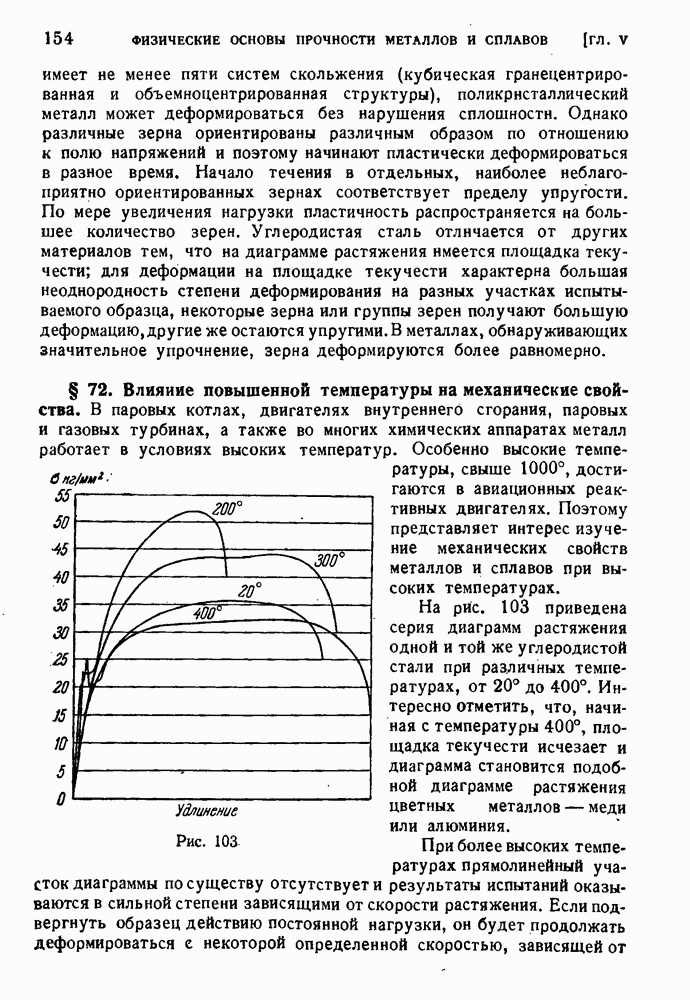
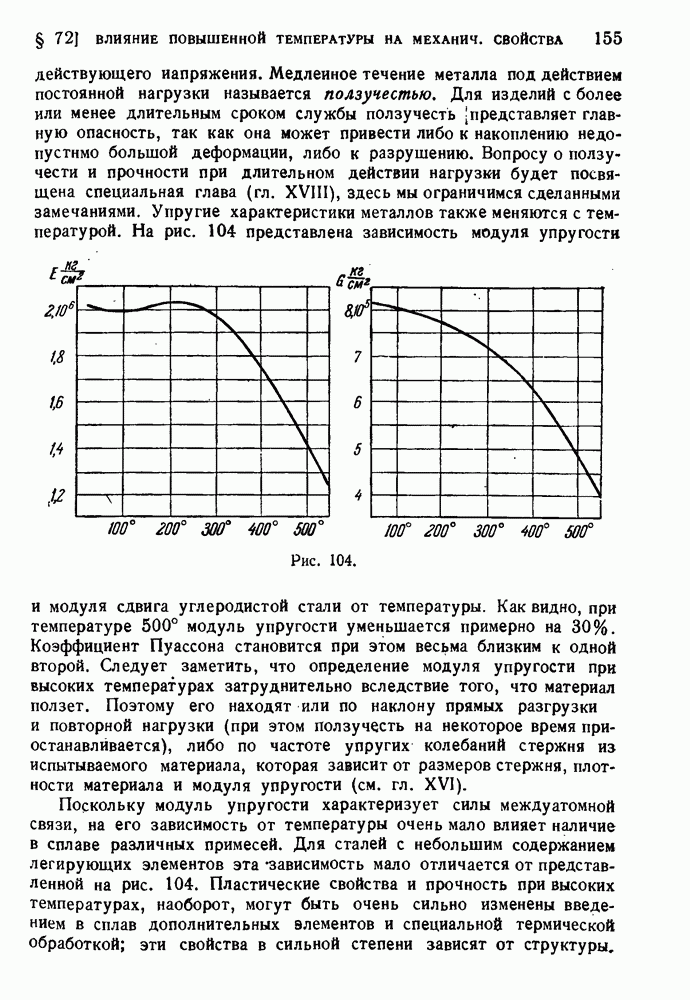
- § 72. Влияние повышенной температуры на механические свойства.
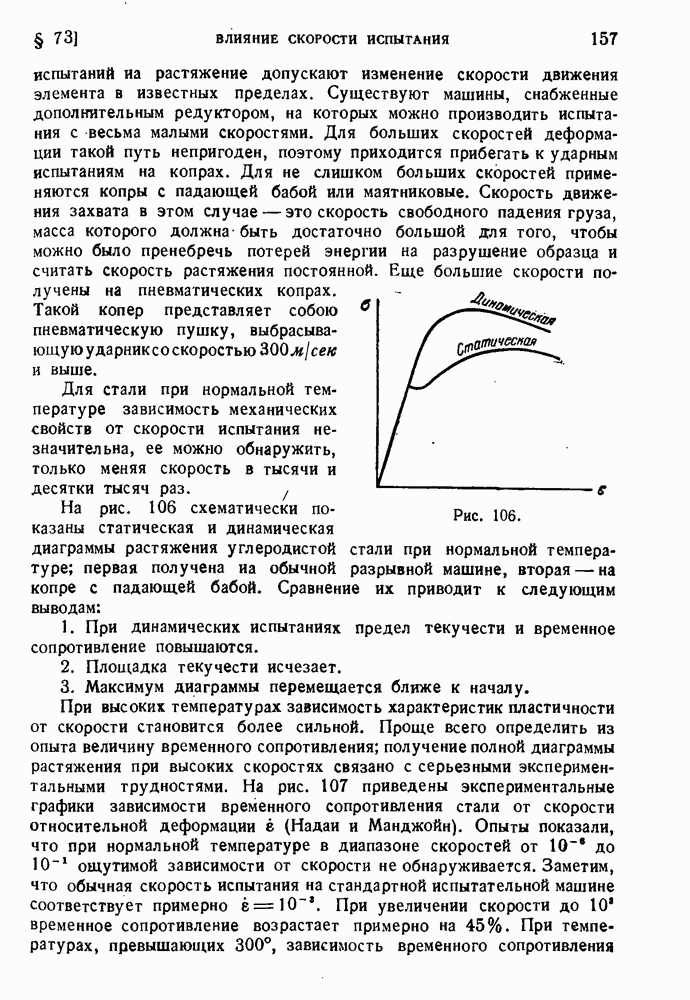
- § 73. Влияние скорости испытания.
- § 74. Испытании на твердость.
- ГЛАВА VI. ТЕОРИИ ПЛАСТИЧНОСТИ, НЕЛИНЕЙНОЙ УПРУГОСТИ И ПОСЛЕДЕЙСТВИЯ
- § 75. Основные принципы построения теории пластичности.
- § 76. Ассоциированный закон течения.
- § 77. Течение при условии пластичности Сен-Венана и Мизеса.
- § 78. Закон упрочнения.
- § 79. Деформационная теория пластичности.
- § 80. Экспериментальная проверка теорий пластичности.
- § 81. Конечная деформация.
- § 82. Нелинейно упругое тело.
- § 83. Высокоэластические деформации.
- § 84. Упругое последействие.
- § 85. Некоторые свойства вязко-упругого тела.
- § 86. Принцип суммирования Больцмана—Вольтерра.
- ГЛАВА VII. КРУЧЕНИЕ
- § 87. Кручение стержней круглого сечеиия.
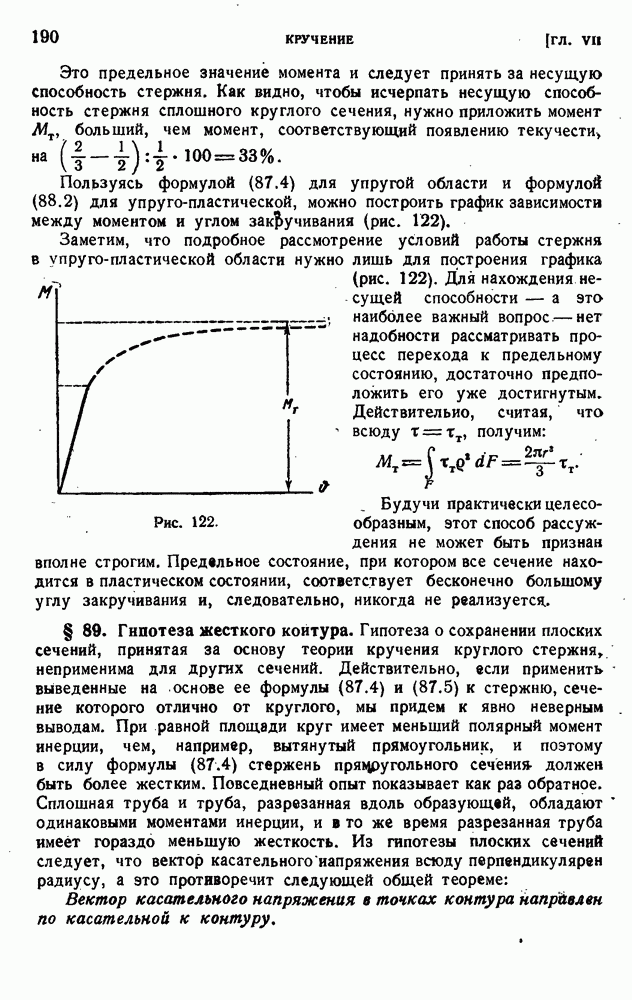
- § 88. Упруго-пластическое кручение стержня круглого сечения.
- § 89. Гипотеза жесткого контура.
- § 90. Кручение тонкостенных стержней замкнутого профиля.
- § 91. Кручение тонкостенных стержней открытого профиля.
- § 92. Кручение упругих стержией сплошного профиля.
- § 93. Опытное исследование кручения.
- § 94. Предельное состояние закрученного стержня из идеально-пластического материала.
- ГЛАВА VIII. ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
- § 96. Общие теоремы о моментах.
- § 97. Преобразование статических моментов и моментов инерции при параллельном переносе осей.
- § 98. Вычисление моментов инерции.
- § 99. Преобразование моментов инерции при повороте осей.
- § 100. Главные оси и главные моменты инерции.
- ГЛАВА IX. НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
- § 101. Действие поперечных сил на балку.
- § 102. Гипотеза плоских сечений и принцип Сен-Венана.
- § 103. Нормальные напряжения при изгибе.
- § 104. Изгибающие моменты и перерезывающие силы.
- § 105. Дифференциальные соотношения между интенсивностью нагрузки, перерезывающей силой и изгибающим моментом. Эпюры.
- § 106. Расчет на прочность при изгибе по допускаемым напряжениям.
- § 107. Упруго-пластический изгиб.
- § 108. Несущая способность стержня при изгибе.
- § 109. Принцип Сен-Венана.
- § 110. Внецентренное растяжение — сжатие.
- § 111. Ядро сечения.
- § 112. Несущая способность внецентренно сжатого стержня.
- § 113. Расчет составных балок.
- § 114. Изгиб кривого бруса.
- § 115. Нахождение нейтральной осн в кривом стержне.
- ГЛАВА X. ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
- § 116. Дифференциальное уравнение изогнутой оси.
- § 117. Пределы применимости приближенной теории.
- § 118. Интегрирование уравнения изгиба.
- § 119. Примеры определения прогибов.
- § 120. Простейшие статически неопределенные задачи.
- § 121. Расчет статически неопределимых балок по способу допускаемых нагрузок.
- § 122. Изгиб стержней переменного сечения.
- § 123. О решении линейных дифференциальных уравнений с постоянными коэффициентами.
- § 124. Продольно-поперечный изгиб.
- § 125. Изгиб балки на упругом основании.
- ГЛАВА XI. ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
- § 126. Нормальные и касательные напряжения при изгибе.
- § 127. Касательные напряжении при изгибе в плоскости симметрии.
- § 128. Центр изгиба.
- § 129. Дополнительные напряжения при кручении.
- § 130. Закон секториальных площадей.
- § 131. Уравнение стесненного кручения.
- § 132. Вычисление секториальных характеристик.
- § 133. Стержень, нагруженный бимоментом.
- § 134. Некоторые примеры стесненного кручения.
- ГЛАВА XII. УСТОЙЧИВОСТЬ УПРУГОГО И ПЛАСТИЧЕСКОГО РАВНОВЕСИЯ
- § 135. Постановка вопроса об устойчивости.
- § 136. Устойчивость сжатого упругого стержня.
- § 137. Эластика Эйлера.
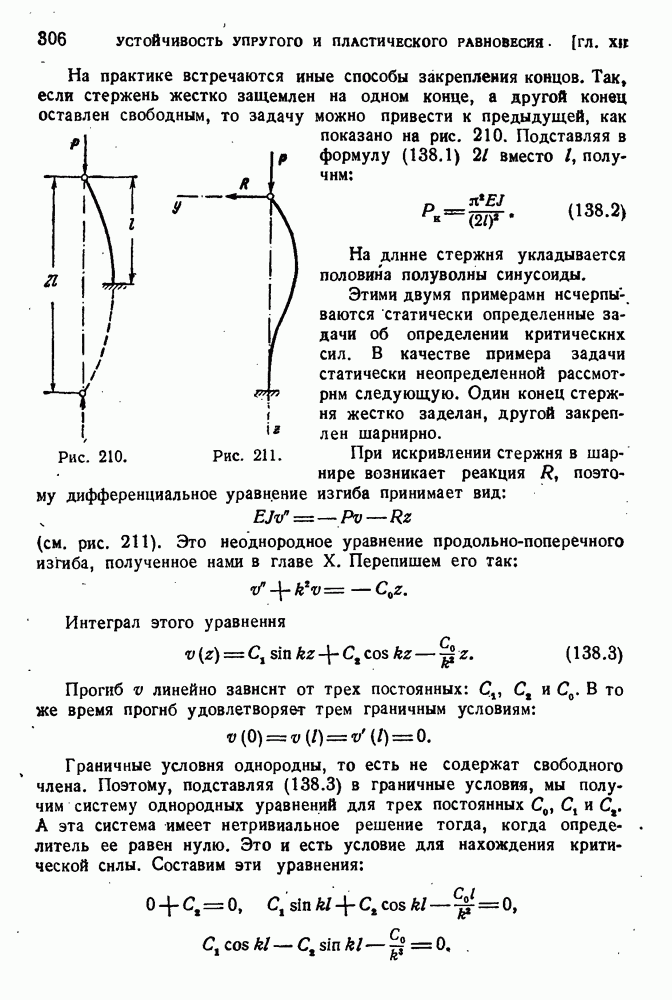
- § 138. Критические силы при иных видах закрепления стержня.
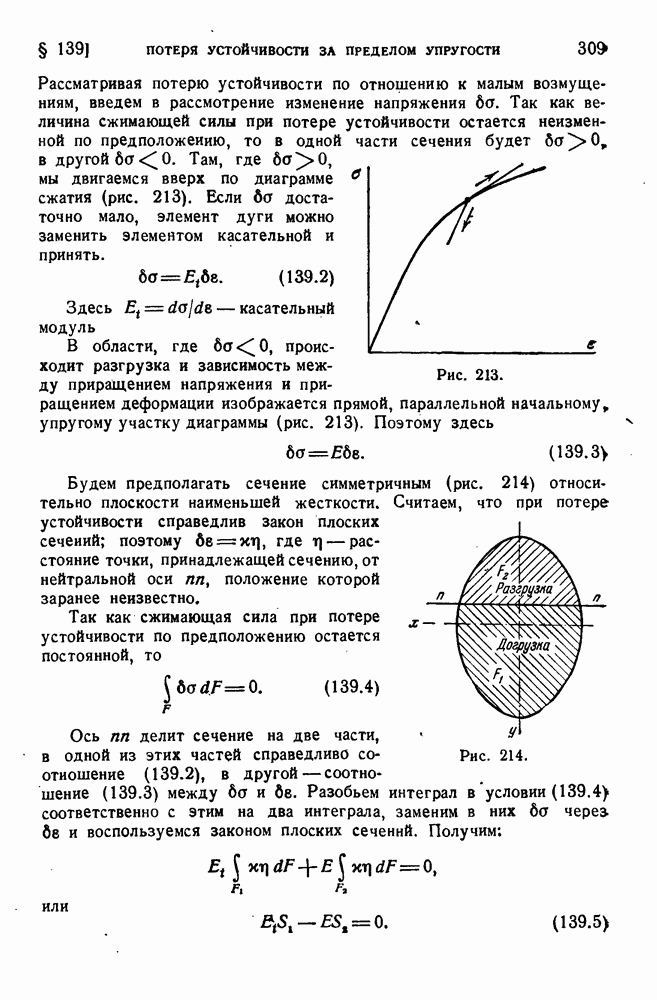
- § 139. Потеря устойчивости за пределом упругости.
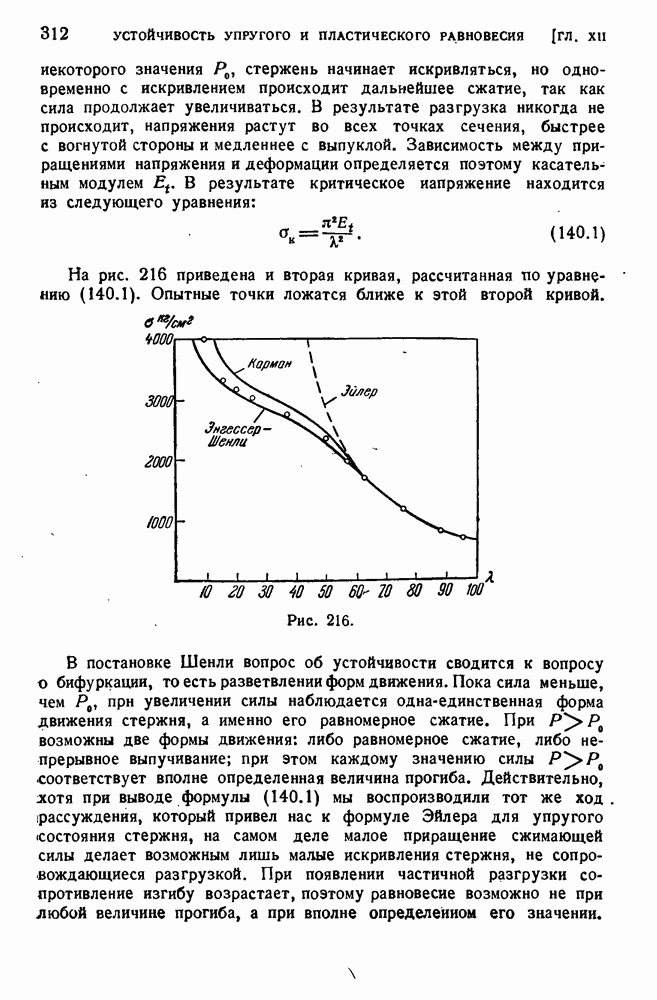
- § 140. Потеря устойчивости за пределом упругости (продолжение).
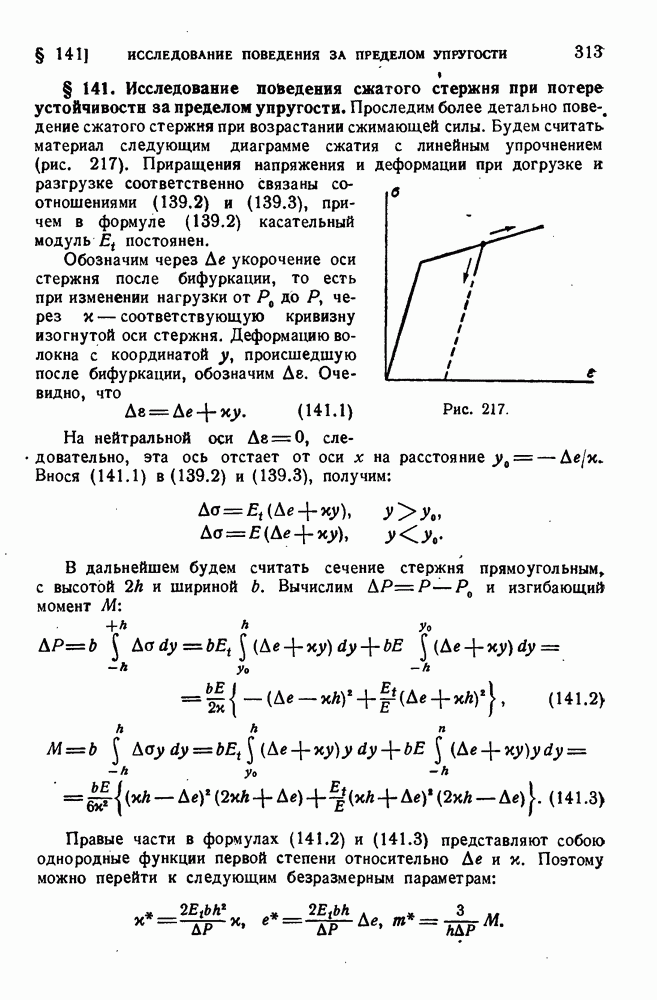
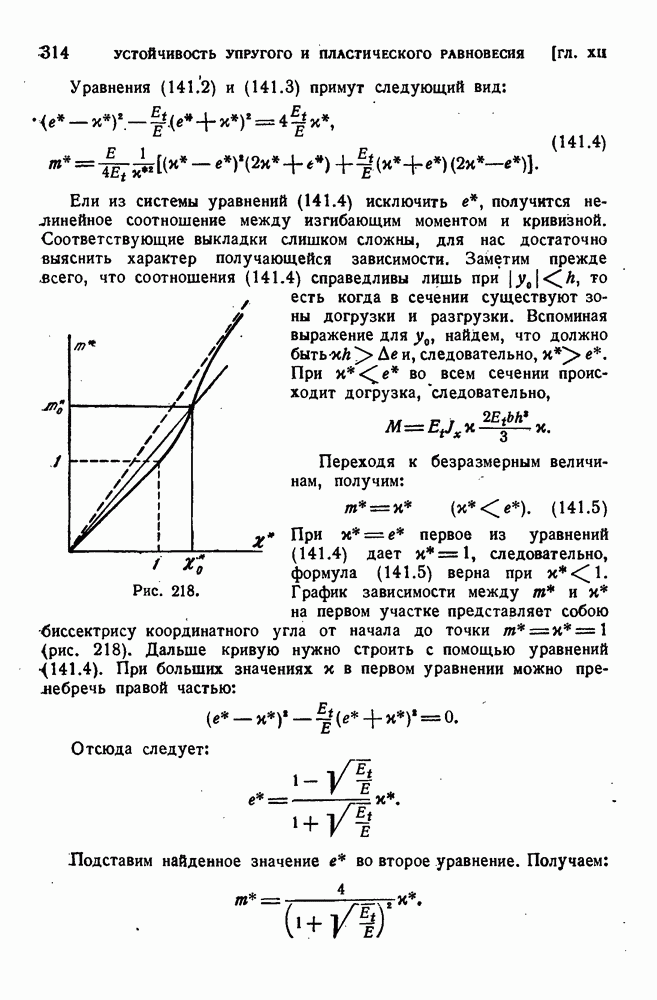
- § 141. Исследование поведения сжатого стержня при потере устойчивости за пределом упругости.
- § 142. Расчет на устойчивость по эмпирическим формулам.
- ГЛАВА XIII. ТРУБЫ И ДИСКИ
- § 143. Толстостенные трубы. Дифференциальные уравнения равновесия и совместности.
- § 144. Упругое состояние трубы. Формулы Ламе.
- § 145. Пластическое состояние трубы.
- § 146. Вращающиеся диски. Упругое состояние.
- § 147. Диск равного сопротивления.
- § 148. Предельное равновесие вращающегося диска.
- ГЛАВА XIV. ОБЩИЕ ТЕОРЕМЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
- § 149. Обобщенные силы и обобщенные перемещения.
- § 150. Начало возможных перемещений для деформируемого тела.
- § 151. Теоремы Лагранжа и Кастильяно.
- § 152. Лииейиые упругие системы.
- § 153. Теорема о взаимности работ.
- § 154. Теорема Кастильяно для линейных упругих систем.
- § 155. Расчет винтовых пружин.
- § 156. Теорема о минимуме энергии.
- § 157. Интеграл перемещений.
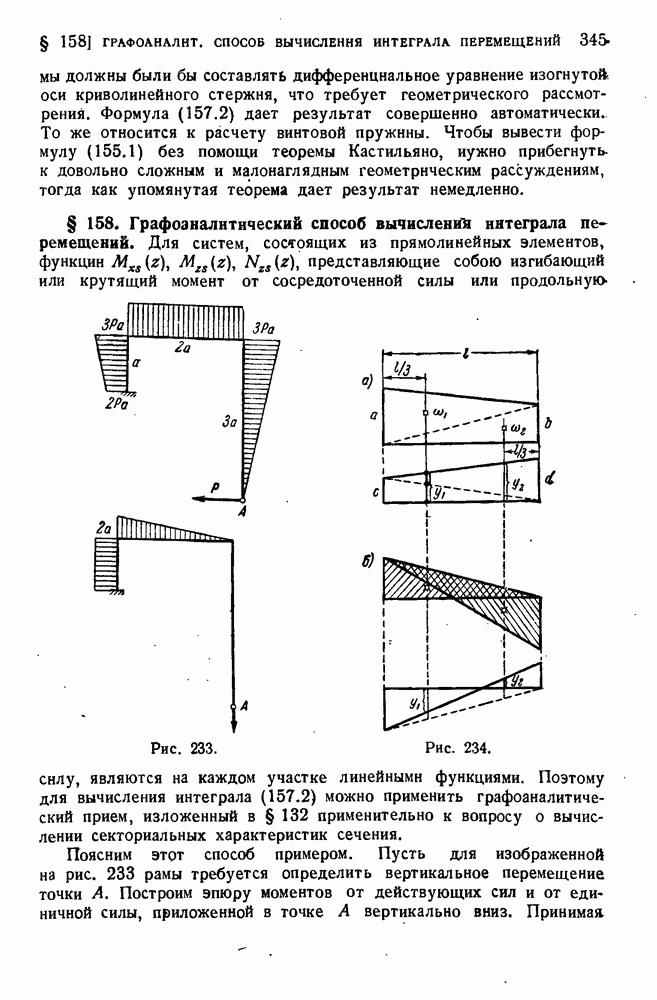
- § 158. Графоаналитический способ вычислений интеграла перемещений.
- § 159. Расчет статически неопределимых систем по методу сил.
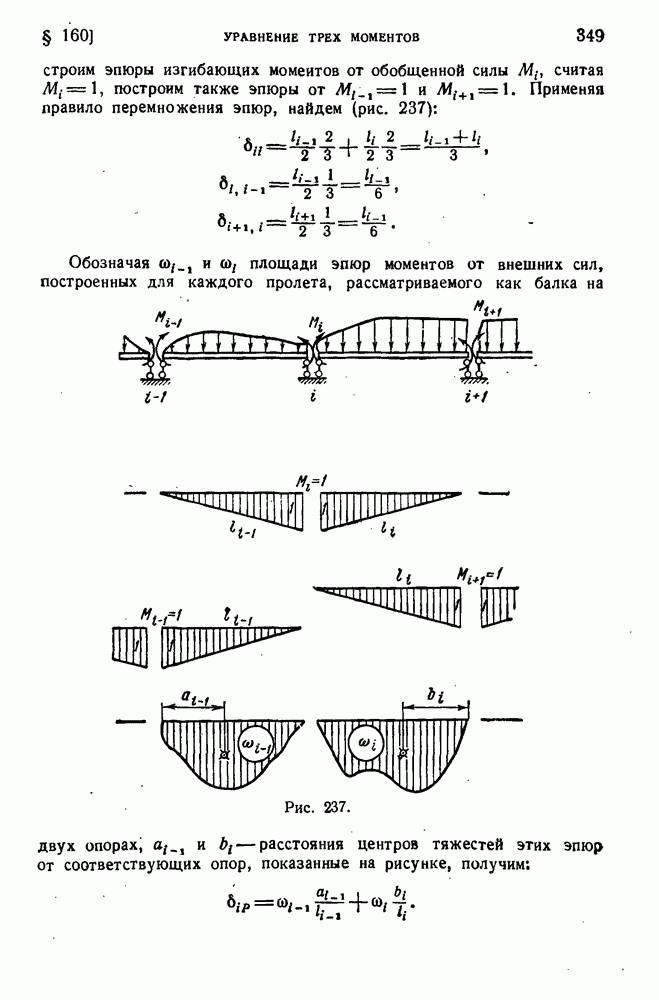
- § 160. Уравнение трех моментов.
- ГЛАВА XV. ТЕОРИЯ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ
- § 161. Жестко-пластическое тело.
- § 162. Поверхности нагружения.
- § 163. Истинное и допустимые состояния элемента.
- § 164. Статический метод определения предельной нагрузки.
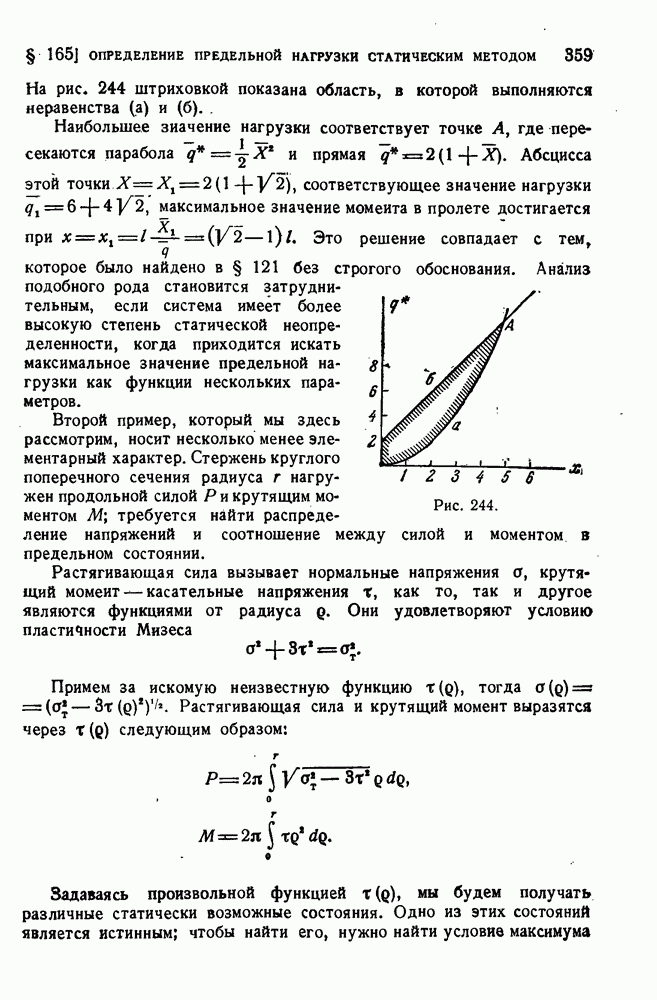
- § 165. Примеры определения предельной нагрузки статическим методом.
- § 166. Кинематически возможные состояния.
- § 167. Кинематический метод определения предельной нагрузки.
- § 168. Примеры определения предельной нагрузки кинематическим методом.
- § 169. Предельное равновесие пластинок.
- ГЛАВА XVI. ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
- § 170. Колебания систем с конечным числом степеней свободы.
- § 171. Собственные частоты и главные формы колебаний.
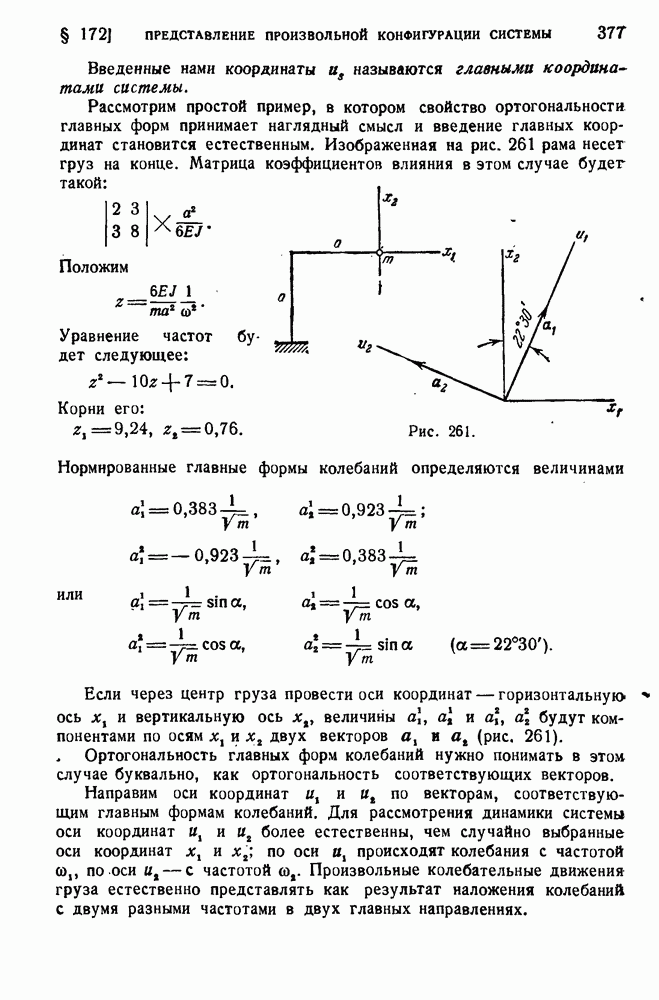
- § 172. Представление произвольной конфигурации системы через главные формы. Главные координаты.
- § 173. Формула и способ Релея.
- § 174. Нижние оценки для частоты основного тона.
- § 175. Продольные колебания стержней.
- § 176. Поперечные колебания стержней.
- § 177. Колебания балок постоянного сечения.
- § 178. Способ Релея — Ритца в применении к поперечным колебаниям стержня.
- § 179. Действие ударных и импульсивных нагрузок на упругие системы.
- ГЛАВА XVII. ТЕОРИИ ПРОЧНОСТИ
- § 180. Постановка вопроса о прочности.
- § 181. Хрупкое и пластическое разрушение.
- § 182. Теория прочности Мора.
- § 183. Механизм хрупкого разрушения.
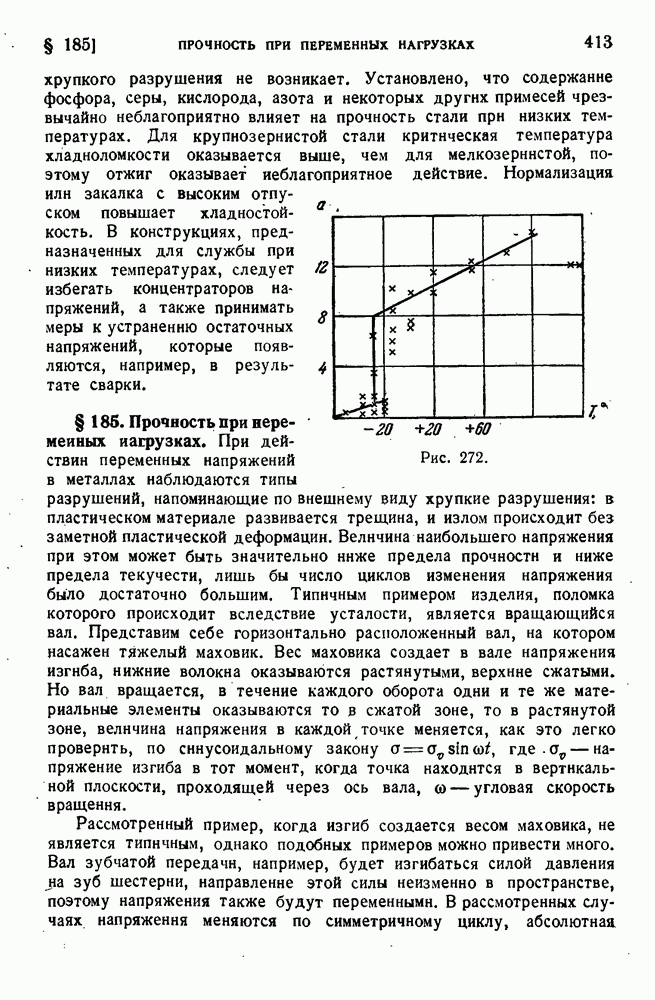
- § 184. Прочность при низких температурах.
- § 185. Прочность при переменных нагрузках.
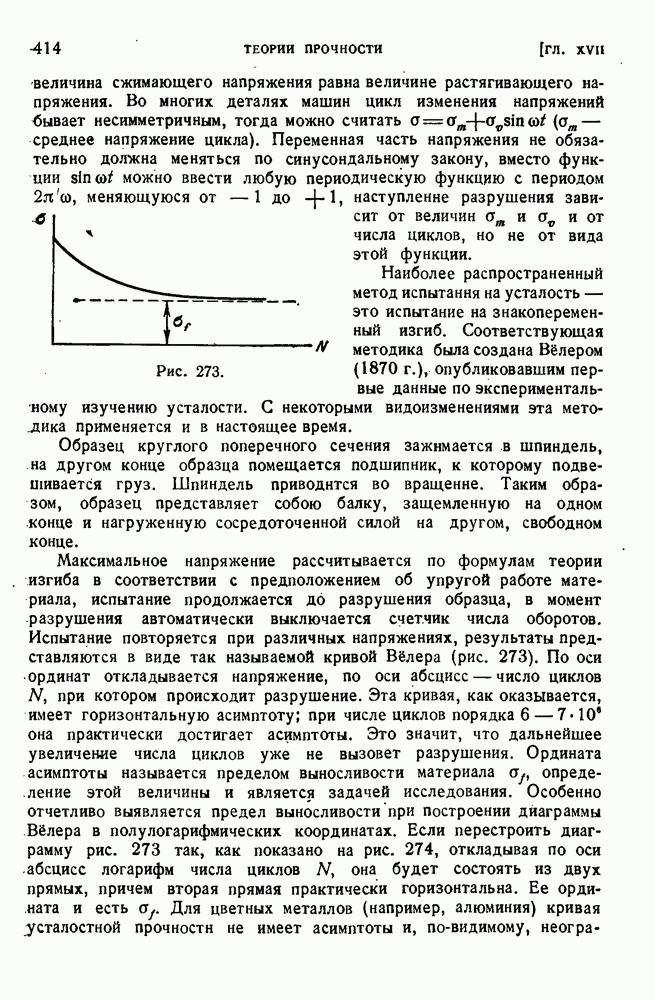
- § 186. Природа усталостного разрушения.
- § 187. Критерии прочности при переменных нагрузках.
- § 188. Влияние концентрации напряжений на усталостную прочность.
- § 189. Усталостная прочность при сложном напряженном состоянии.
- ГЛАВА XVIII. ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ
- § 190. Ползучесть металлов.
- § 191. Процесс ползучести.
- § 192. Длительное разрушение.
- § 193. Температурные зависимости ползучести и длительной прочности.
- § 194. Феноменологические теории одномерной ползучести.
- § 195. Релаксация напряжений.
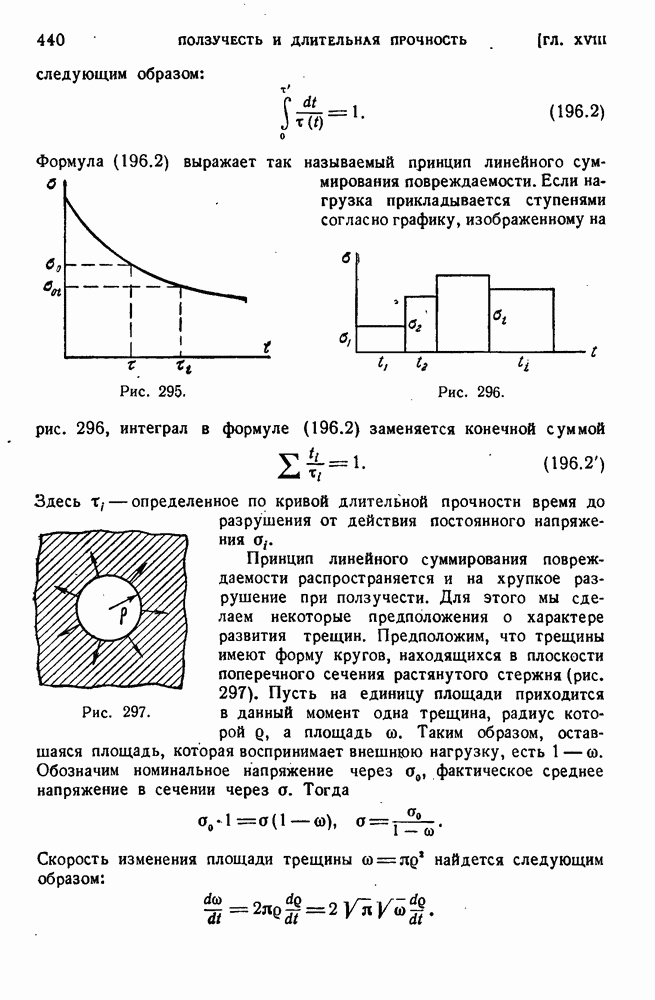
- § 196. Длительная прочность при переменных нагрузках.
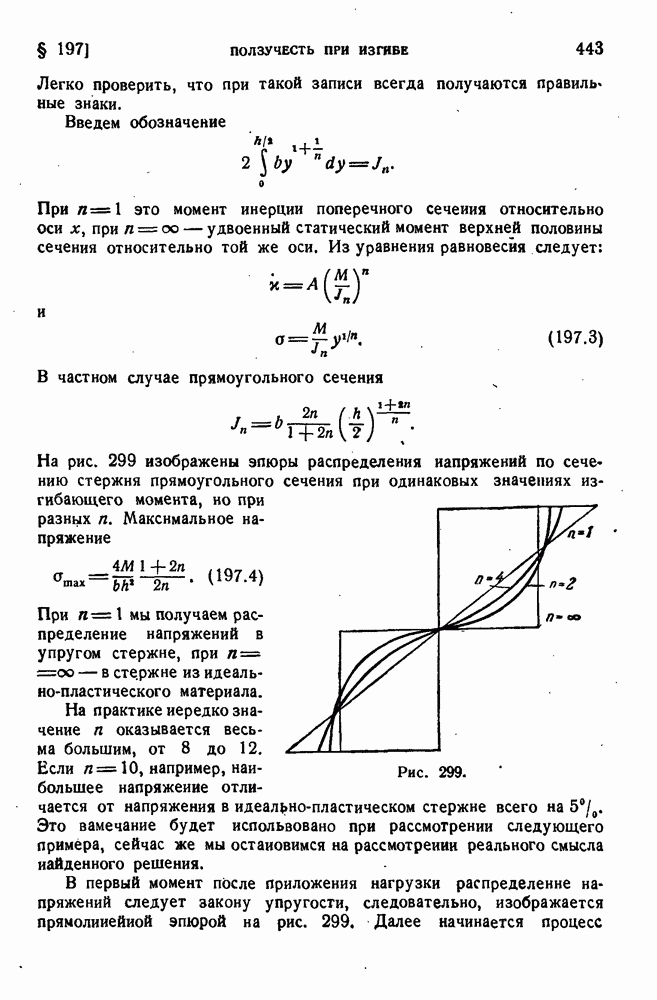
- § 197. Ползучесть при изгибе.
- § 198. Критическое время сжатого стержня.
- § 199. Ползучесть и длительная прочность при сложном напряженном состоянии.
- § 200. Вращающиеся диски в условиях ползучести.
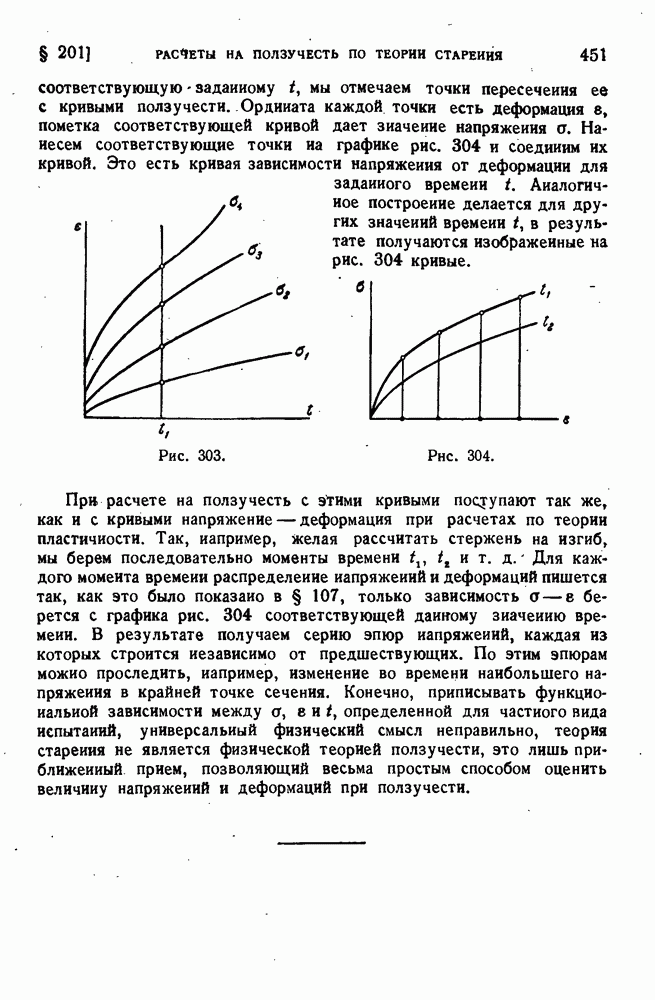
- § 201. Расчеты на ползучесть по теории старении.