| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ
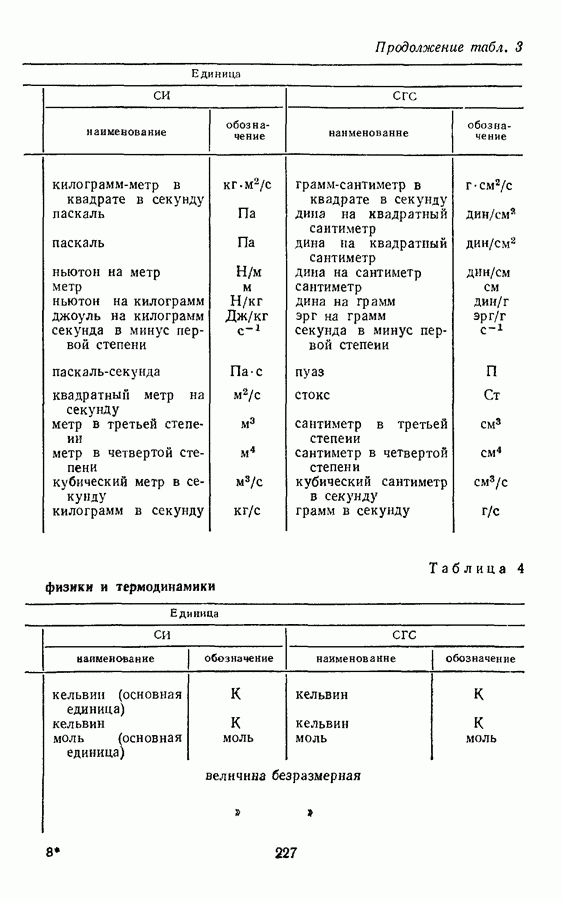
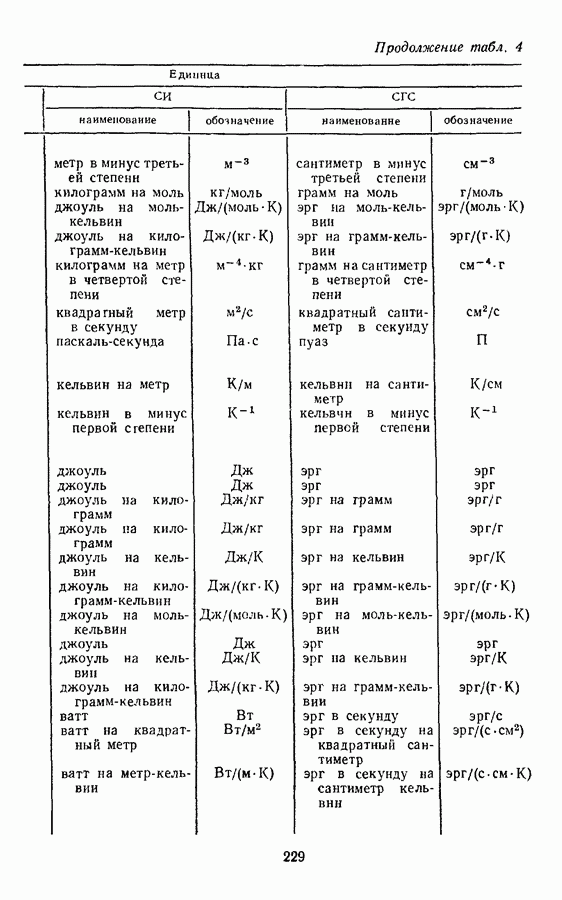
Единицы всех величин молекулярной физики и термодинамики могут быть выражены через пять основных единиц Международной системы — метр, килограмм, секунду, кельвин, моль.
Относительные атомная и молекулярная массы Относительная атомная масса  химического элемента есть отношение массы
химического элемента есть отношение массы  атома данного элемента к 1/12 массы атома изотопа углерода
атома данного элемента к 1/12 массы атома изотопа углерода  т. е.
т. е.

Относительная молекулярная масса  вещества есть отношение массы
вещества есть отношение массы  молекулы данного вещества к 1/12 части массы атома изотопа углерода
молекулы данного вещества к 1/12 части массы атома изотопа углерода  т. е.
т. е.

Из формул (8.1) и (8.2) следует, что относительная атомная масса и относительная молекулярная масса — величины безразмерные и выражаются в безразмерных единицах.
Постоянная Авогадро. Постоянная Авогадро  есть величина, равная отношению числа
есть величина, равная отношению числа  молекул, содержащихся в системе, к количеству вещества
молекул, содержащихся в системе, к количеству вещества  данной системы, т. е.
данной системы, т. е.

Из этой формулы получим единицу постоянной Авогадро:

Размерность постоянной Авогадро:

Концентрация молекул (объемное число молекул). Концентрацией  называют величину, равную отношению
называют величину, равную отношению 
молекул, содержащихся в системе, к ее объему V, т. е.

Положив  найдем единицу концентрации молекул:
найдем единицу концентрации молекул:

Размерность концентрации молекул: 

Молярная масса. Молярная масса  вещества есть величина, равная отношению массы
вещества есть величина, равная отношению массы  системы к количеству вещества
системы к количеству вещества  этой системы, т. е.
этой системы, т. е.

Положив в этой формуле  моль, получим единицу молярной массы:
моль, получим единицу молярной массы:

Килограмм на моль равен молярной массе вещества, имеющего при количестве вещества 1 моль массу 1 кг. Размерность молярной массы:

В некоторых учебных пособиях по курсу общей физики молярная масса как особая величина не вводится, а отождествляется с относительной молекулярной массой. Но относительная молекулярная масса — величина безразмерная и выражается в безразмерных единицах, молярная же масса — величина размерная и выражается в килограммах на моль.
Молярная масса входит в уравнение Клапейрона — Менделеева

где  количество вещества. Если здесь
количество вещества. Если здесь  считать, как это нередко делают, относительной молекулярной массой, то размерности левой и правой частей этого равенства будут разными. В самом деле, размерность левой части
считать, как это нередко делают, относительной молекулярной массой, то размерности левой и правой частей этого равенства будут разными. В самом деле, размерность левой части

Если учесть, что

где  давление и температура при нормальных условиях,
давление и температура при нормальных условиях,  молярный объем, то размерность правой части
молярный объем, то размерность правой части

Ясно, что

Если же в уравнении Клапейрона — Менделеева  считать молярной массой, правая часть этого уравнения имеет такую же размерность, что и левая, т. е.
считать молярной массой, правая часть этого уравнения имеет такую же размерность, что и левая, т. е. 
Молярная (универсальная) газовая постоянная. Молярной газовой постоянной  называют физическую величину, равную отношению работы А, совершаемой идеальным газом при изобарическом его нагревании, к интервалу
называют физическую величину, равную отношению работы А, совершаемой идеальным газом при изобарическом его нагревании, к интервалу  температур и количеству вещества
температур и количеству вещества  нагреваемого газа, т. е.
нагреваемого газа, т. е.

Положив  моль,
моль,  получим единицу молярной газовой постоянной:
получим единицу молярной газовой постоянной:

Подставив размерности величин, входящих в правую часть равенства (8.6), найдем размерность молярной газовой постоянной:

Удельная газовая постоянная. Удельной газовой постоянной В вещества называют величину, равную отношению молярной газовой постоянной  к молярной массе
к молярной массе  данного вещества:
данного вещества:

В отличие от молярной газовой постоянной, удельная газовая постоянная имеет разные значения для различных веществ.
Из формулы (8.7) следует, что единица удельной газовой постоянной

Джоуль на килограмм-кельвин равен удельной газовой постоянной идеального газа массой 1 кг, совершающего при повышении температуры на 1 К и постоянном давлении работу 1 Дж.
Согласно формуле (8.7), размерность удельной газовой постоянной:

Единицу и размерность удельной газовой постоянной можно найти также по формуле

где А — работа, совершаемая газом при изобарическом нагревании на интервал температур  масса газа.
масса газа.
Градиент плотности. Быстроту изменения плотности среды в некотором направлении  характеризуют величиной, называемой градиентом плотности и выражаемой формулой
характеризуют величиной, называемой градиентом плотности и выражаемой формулой

где  единичный вектор оси
единичный вектор оси  . В случае равномерного изменения плотности можно записать
. В случае равномерного изменения плотности можно записать

Подставив сюда  получим единицу градиента плотности:
получим единицу градиента плотности:

Килограмм на метр в четвертой степени равен градиенту плотности среды, плотность которой на участке длиной  в направлении градиента изменяется на
в направлении градиента изменяется на  Размерность градиента плотности:
Размерность градиента плотности:

Коэффициент диффузии. Коэффициент диффузии определяется из формулы

где  масса газа, перенесенного за время
масса газа, перенесенного за время  через площадку
через площадку  градиент плотности. Отсюда получим
градиент плотности. Отсюда получим

Положив  найдем единицу коэффициента диффузии:
найдем единицу коэффициента диффузии:

Квадратный метр в секунду равен коэффициенту диффузии среды, в которой через площадку в  перпендикулярно градиенту плотности, равному
перпендикулярно градиенту плотности, равному  переносится в 1 с вещество массой
переносится в 1 с вещество массой 
Для определения единицы коэффициента диффузии можно воспользоваться формулой

где  средняя скорость хаотического движения молекул,
средняя скорость хаотического движения молекул,  -средняя длина свободного пробега молекул. Чтобы единица коэффициента диффузии оказалась в этом случае когерентной, формулу (8.13) пришлось бы брать с числовым коэффициентом, равным единице:
-средняя длина свободного пробега молекул. Чтобы единица коэффициента диффузии оказалась в этом случае когерентной, формулу (8.13) пришлось бы брать с числовым коэффициентом, равным единице:

Положив здесь  найдем
найдем

Как из формулы (8.12), так и из (8.13) следует, что размерность коэффициента диффузии:

Динамическая вязкость (коэффициент вязкости, коэффициент внутреннего трения). Динамическая вязкость была определена и получена ее единица на основе гидродинамической формулы (7.39). Теперь получим эту единицу с помощью формулы молекулярной физики.
При рассмотрении вязкости, как явления переноса, на основе молекулярно-кинетической теории выведена следующая формула динамической вязкости:

p — плотность газа. Для получения когерентной единицы динамической вязкости образуем по (8.14) формулу

Положив здесь  найдем
найдем 
Как указано на с. 47, эта единица называется паскаль-секунда. Там же дано ее определение.
Из формулы (8.15) найдем размерность динамической вязкости:

что совпадает с размерностью, полученной по формуле (7.39).
Градиент температуры (температурный градиент). Если температура  среды в некотором направлении
среды в некотором направлении  изменяется, то быстроту ее изменения характеризуют величиной, называемой градиентом температуры:
изменяется, то быстроту ее изменения характеризуют величиной, называемой градиентом температуры:

где  единичный вектор оси
единичный вектор оси 
Градиент температуры — величина векторная. Совокупность векторов градиента температуры образует температурное поле.
В случае равномерного изменения температуры в направлении градиента можно записать

Подставив  получим единицу градиента температуры:
получим единицу градиента температуры:

Кельвин на метр равен температурному градиенту поля, в котором на участке длиной  в направлении градиента температура изменяется на 1 К. Размерность градиента температуры:
в направлении градиента температура изменяется на 1 К. Размерность градиента температуры:

Температурный коэффициент давления газа. Температурный коэффициент  давления газа — величина, равная отношению относительного изменения давления газа к изменению его температуры:
давления газа — величина, равная отношению относительного изменения давления газа к изменению его температуры:

Если в некотором интервале  температур температурный
температур температурный
коэффициент  давления газа остается постоянным, то
давления газа остается постоянным, то

где  начальное давление газа,
начальное давление газа,  изменение его давления при изменении температуры на
изменение его давления при изменении температуры на  Подставив в
Подставив в  получим
получим

Эту единицу называют келъвин в минус первой степени. Кельвин в минус первой степени равен температурному коэффициенту относительного изменения физической величины, при котором изменение температуры на 1 К от принятой за начальную вызывает относительное изменение этой величины, равное единице. Размерность температурного коэффициента давления:

Температурный коэффициент линейного расширения. Температурный коэффициент а линейного расширения есть величина, равная отношению относительного удлинения  тела к изменению
тела к изменению  температуры, вызвавшему это удлинение, т. е.
температуры, вызвавшему это удлинение, т. е.

Если коэффициент линейного расширения в интервале  постоянен, то
постоянен, то

Подставив здесь  получим
получим

Размерность коэффициента линейного расширения:

Температурный коэффициент объемного расширения. Температурный коэффициент объемного расширения  есть величина, равная отношению относительного увеличения объема
есть величина, равная отношению относительного увеличения объема  тела к изменению
тела к изменению  температуры, вызвавшему это увеличение объема:
температуры, вызвавшему это увеличение объема:

Если коэффициент объемного расширения в интервале  постоянен, то
постоянен, то

Положив в этой формуле  найдем
найдем

Размерность коэффициента объемного расширения:

Внутренняя энергия. Внутренней энергией  называют энергию, зависящую только от термодинамического состояния системы. Внутренняя энергия состоит из кинетической энергии хаотического движения молекул, атомов, свободных электронов и других микрочастиц, потенциальной энергии взаимодействия этих частиц, внутриатомной и внутриядерной энергии частиц, составляющих систему.
называют энергию, зависящую только от термодинамического состояния системы. Внутренняя энергия состоит из кинетической энергии хаотического движения молекул, атомов, свободных электронов и других микрочастиц, потенциальной энергии взаимодействия этих частиц, внутриатомной и внутриядерной энергии частиц, составляющих систему.
Внутренняя энергия идеального газа состоит только из кинетической энергии его молекул.
Единицу внутренней энергии найдем из первого начала термодинамики для адиабатического процесса, при котором система совершает работу А против внешних сил только за счет убыли своей внутренней энергии 

Из равенства (8.20) следует, что внутренняя энергия выражается в тех же единицах, что и работа, т. е. в джоулях. Размерность внутренней энергии:

Количество теплоты (теплота). Количество теплоты — это внутренняя энергия, которая самопроизвольно (без внешнего воздействия) переходит от тел более нагретых к телам менее нагретым путем теплопроводности или лучеиспускания.
Единица количества теплоты может быть получена из равенства, выражающего первое начало термодинамики для изотермического процесса:

где  количество теплоты, полученное системой, А — работа, совершаемая системой при изменении объема.
количество теплоты, полученное системой, А — работа, совершаемая системой при изменении объема.
Из (8.21) следует, что количество теплоты выражается в тех же единицах, что и работа, т. е. в джоулях. Размерность количества теплоты:

В джоулях выражается также теплота фазового превращения и теплота химической реакции.
Удельное количество теплоты. Удельным количеством теплоты  называют величину, равную отношению количества теплоты
называют величину, равную отношению количества теплоты  полученного (или переданного) системой, к массе
полученного (или переданного) системой, к массе  системы:
системы:

Положив  получим единицу удельного количества теплоты:
получим единицу удельного количества теплоты:

Джоуль на килограмм равен удельному количеству теплоты системы, в которой веществу массой 1 кг сообщается (или отбирается от него) количество теплоты  Размерность удельного количества теплоты:
Размерность удельного количества теплоты:

В джоулях на килограмм выражается также удельная теплота фазового превращения и химической реакции. Приведем формулы, по которым определяются единицы удельной теплоты соответственно парообразования, плавления, сгорания:

где  количество теплоты, необходимое для превращения в пар той же температуры жидкости массой
количество теплоты, необходимое для превращения в пар той же температуры жидкости массой 

где  количество теплоты, необходимое для расплавления кристаллического вещества массой
количество теплоты, необходимое для расплавления кристаллического вещества массой  взятого при температуре плавления;
взятого при температуре плавления;

где  количество теплоты, выделяющееся при полном сгорании топлива массой
количество теплоты, выделяющееся при полном сгорании топлива массой 
Теплоемкость системы. Теплоемкость С тела (системы тел) — величина, равная отношению количества теплоты
 необходимой для нагревания тела (системы тел), к разности
необходимой для нагревания тела (системы тел), к разности  температур тела, т. е.
температур тела, т. е.

Положив в  получим единицу теплоемкости:
получим единицу теплоемкости:

Джоуль на кельвин равен теплоемкости системы, температура которой повышается на 1 К при подведении к системе количества теплоты  Размерность теплоемкости:
Размерность теплоемкости:

Удельная теплоемкость. Удельной теплоемкостью с вещества называют величину, равную отношению теплоемкости однородного тела к его массе, т. е.

или с учетом (8.26)

Положив  получим единицу удельной теплоемкости:
получим единицу удельной теплоемкости:

Джоуль на килограмм-кельвин равен удельной теплоемкости вещества, имеющего при массе 1 кг теплоемкость  Размерность удельной теплоемкости:
Размерность удельной теплоемкости:

Молярная теплоемкость. Молярной теплоемкостью С называют величину, равную произведению удельной теплоемкости с вещества на молярную массу  этого вещества:
этого вещества:

Положив  найдем единицу молярной теплоемкости:
найдем единицу молярной теплоемкости:

Джоуль на моль-кельвин равен молярной теплоемкости вещества, имеющего при количестве вещества 1 моль теплоемкость 
Размерность молярной теплоемкости найдем, подставив в (8.28) размерности удельной теплоемкости и молярной
массы:

Энтальпия. Энтальпией  системы называют термодинамическую функцию, равную сумме внутренней энергии
системы называют термодинамическую функцию, равную сумме внутренней энергии  и произведения давления
и произведения давления  на объем V системы, т. е.
на объем V системы, т. е.

Внутренняя энергия  и произведение
и произведение  выражаются в единицах работы, т. е. в джоулях. Следовательно, и энтальпия выражается в джоулях и имеет размерность:
выражаются в единицах работы, т. е. в джоулях. Следовательно, и энтальпия выражается в джоулях и имеет размерность:

Энтропия. Энтропия  системы есть функция состояния системы, выражаемая соотношением
системы есть функция состояния системы, выражаемая соотношением

где  бесконечно малое количество теплоты, сообщенное системе при температуре
бесконечно малое количество теплоты, сообщенное системе при температуре 
Если система перешла из состояния 1 в состояние 2, то

Для процессов, протекающих при некоторой средней температуре  выражение (8.30) после интегрирования принимает вид
выражение (8.30) после интегрирования принимает вид

Положив в  где
где  положительное число, получим единицу энтропии:
положительное число, получим единицу энтропии:

Джоуль на кельвин равен изменению энтропии системы, в которой при температуре  в изотермическом процессе сообщается количество теплоты
в изотермическом процессе сообщается количество теплоты  Размерность энтропии такая же, как и теплоемкости:
Размерность энтропии такая же, как и теплоемкости:

Удельная энтропия. Удельной энтропией  называют величину, равную отношению энтропии тела к его массе.
называют величину, равную отношению энтропии тела к его массе.
Если в результате некоторого процесса в теле массой  произошло изменение энтропии на
произошло изменение энтропии на  то изменение удельной энтропии выразится формулой
то изменение удельной энтропии выразится формулой

Положив  получим единицу удельной энтропии
получим единицу удельной энтропии

Джоуль на килограмм-кельвин равен изменению удельной энтропии вещества, в котором при массе 1 кг изменение энтропии составляет  Размерность удельной энтропии:
Размерность удельной энтропии:

Тепловой поток (тепловая мощность). Тепловым потоком  через некоторую поверхность называют величину, равную отношению количества теплоты, проходящей через эту поверхность, ко времени, за которое прошло это количество теплоты, т. е.
через некоторую поверхность называют величину, равную отношению количества теплоты, проходящей через эту поверхность, ко времени, за которое прошло это количество теплоты, т. е.

Если поток постоянный, то

где  количество теплоты, прошедшее через поверхность за время
количество теплоты, прошедшее через поверхность за время 
Единицу теплового потока найдем, положив в 

Ранее было установлено (см. с. 40), что эта единица называется ваттом. Ватт равен тепловому потоку, эквивалентному механической мощности  Размерность теплового потока:
Размерность теплового потока:

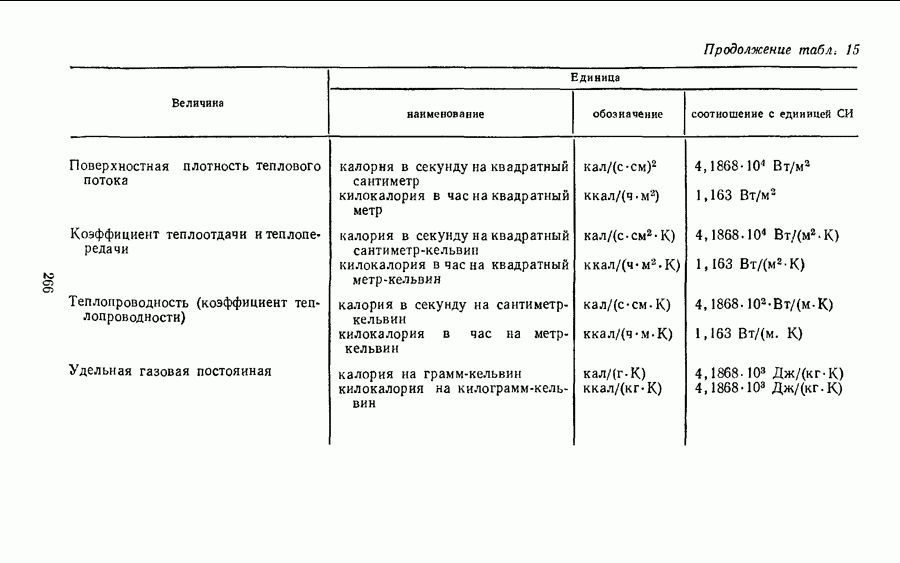
Поверхностная плотность теплового потока (плотность теплового потока, удельный тепловой поток). Поверхностная плотность теплового потока — величина, равная отношению теплового потока  к площади
к площади  поверхности, через которую проходит этот поток, т. е.
поверхности, через которую проходит этот поток, т. е.

В случае равномерного распределения теплового потока
Ф по поверхности площадью 5

Положив  найдем единицу поверхностной плотности теплового потока:
найдем единицу поверхностной плотности теплового потока:

Ватт на квадратный метр равен поверхностной плотности теплового потока  равномерно распределенного по поверхности площадью
равномерно распределенного по поверхности площадью  Размерность поверхностной плотности теплового потока:
Размерность поверхностной плотности теплового потока:

Теплопроводность (коэффициент теплопроводности). Теплопроводность К — величина, равная отношению количества теплоты, перенесенного через единичную плоскую поверхность, нормальную вектору градиента температуры, при градиенте температуры, равном единице, ко времени, в течение которого эта теплота перенесена. Теплопроводность выразим из формулы

где  количество теплоты, перенесенное за время
количество теплоты, перенесенное за время  через поверхность площадью
через поверхность площадью  в направлении нормали
в направлении нормали  к этой поверхности в сторону убывания температуры,
к этой поверхности в сторону убывания температуры,  градиент температуры. Из (8.35) найдем
градиент температуры. Из (8.35) найдем

Положив здесь  получим единицу теплопроводности:
получим единицу теплопроводности:

Ватт на метр-кельвин равен теплопроводности вещества, в котором при стационарном режиме с поверхностной плотностью теплового потока  устанавливается
устанавливается
температурный градиент  Размерность теплопроводности:
Размерность теплопроводности:

Коэффициент теплообмена (теплоотдачи). Если соприкасаются две среды с разностью температур  то через границу этих сред проходит тепловой поток
то через границу этих сред проходит тепловой поток  выражаемый формулой
выражаемый формулой

где  коэффициент пропорциональности, называемый коэффициентом теплообмена. Из (8.37) получим
коэффициент пропорциональности, называемый коэффициентом теплообмена. Из (8.37) получим

Положив  найдем единицу коэффициента теплообмена:
найдем единицу коэффициента теплообмена:

Ватт на квадратный метр-кельвин равен коэффициенту теплообмена, соответствующему поверхностной плотности теплового потока  при разности температур
при разности температур 
Размерность коэффициента теплообмена:

Коэффициент теплопередачи. Теплопередачей называют процесс передачи количества теплоты от одной среды к другой через разделяющую их стенку. Стационарный тепловой поток  через плоскую стенку с площадью
через плоскую стенку с площадью  поверхности определяется по формуле
поверхности определяется по формуле

где  разность температур сред,
разность температур сред,  коэффициент теплопередачи. Из (8.39) получим
коэффициент теплопередачи. Из (8.39) получим

Подставив  найдем единицу коэффициента теплопередачи:
найдем единицу коэффициента теплопередачи:

Следовательно, коэффициент теплопередачи выражается в тех же единицах и имеет ту же размерность, что и коэффициент теплообмена.
Температуропроводность. Температуропроводность а — величина, характеризующая скорость выравнивания температуры в среде при нестационарной теплопроводности и численно равная отношению теплопроводности к объемной теплоемкости:

где  удельная теплоемкость при постоянном давлении,
удельная теплоемкость при постоянном давлении,  плотность вещества,
плотность вещества,  теплоемкость единицы объема.
теплоемкость единицы объема.
Положив в  найдем единицу температуропроводности:
найдем единицу температуропроводности:

Квадратный метр на секунду равен температуропроводности вещества с теплопроводностью  удельной теплоемкостью (при постоянном давлении)
удельной теплоемкостью (при постоянном давлении)  и плотностью
и плотностью  Размерность температуропроводности:
Размерность температуропроводности:

Поверхностное натяжение, удельная поверхностная энергия. Поверхностным натяжением а называют величину, равную отношению силы  действующей на участок контура поверхности жидкости, к длине
действующей на участок контура поверхности жидкости, к длине  этого участка:
этого участка:

Положив в  получим единицу поверхностного натяжения:
получим единицу поверхностного натяжения:

Ньютон на метр равен поверхностному натяжению, создаваемому силой  приложенной к участку контура свободной поверхности длиной
приложенной к участку контура свободной поверхности длиной  и действующей нормально к контуру и по касательной к поверхности.
и действующей нормально к контуру и по касательной к поверхности.
Для увеличения поверхности жидкости необходимо совершить работу против сил поверхностного натяжения. Эта работа может быть выражена по формуле

где а — коэффициент пропорциональности, называемый удельной поверхностной энергией. Отсюда

Единица этой величины

Джоуль на квадратный метр равен удельной поверхностной энергии жидкости, для образования 1м2 поверхности которой затрачивается работа 1 Дж. Заметим, что

Обе величины — поверхностное натяжение и удельная поверхностная энергия имеют одну и ту же размерность:

Эти величины для одной и той же жидкости численно равны. Поэтому их обозначают одной и той же буквой а.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ОБЩИЕ ВОПРОСЫ ВЫБОРА ЕДИНИЦ И ПОСТРОЕНИЯ СИСТЕМ ЕДИНИЦ
- § 1. ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ. СИСТЕМЫ ФИЗИЧЕСКИХ ВЕЛИЧИН
- Системы физических величин. Основные и производные величины
- § 2. РАЗМЕРНОСТИ ПРОИЗВОДНЫХ ФИЗИЧЕСКИХ ВЕЛИЧИН
- § 3. ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН, РАЗМЕР ЕДИНИЦ
- § 4. СИСТЕМЫ ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН
- § 5. НАИМЕНОВАНИЯ И ОБОЗНАЧЕНИЯ ЕДИНИЦ
- Глава II. МЕЖДУНАРОДНАЯ СИСТЕМА ЕДИНИЦ (СИ)
- § 6. ОСНОВНЫЕ, ДОПОЛНИТЕЛЬНЫЕ И ПРОИЗВОДНЫЕ ЕДИНИЦЫ СИСТЕМЫ
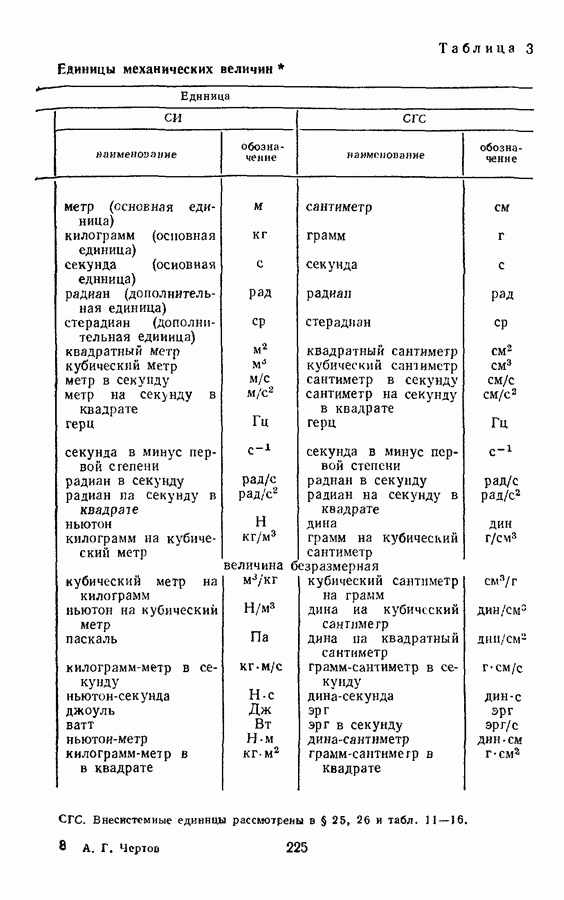
- § 7. ПРОИЗВОДНЫЕ ЕДИНИЦЫ МЕХАНИЧЕСКИХ ВЕЛИЧИН
- § 8. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ
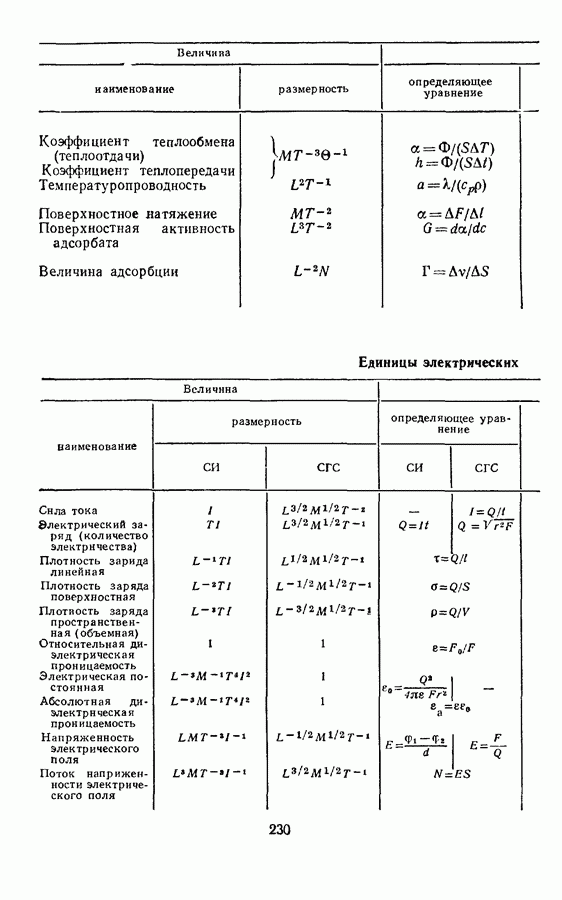
- § 9. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ЭЛЕНТРИЧЕСКИХ И МАГНИТНЫХ ВЕЛИЧИН
- § 10. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН, ХАРАКТЕРИЗУЮЩИХ КОЛЕБАНИЯ И ВОЛНЫ
- § 11. ПРОИЗВОДНЫЕ ЕДИНИЦЫ АКУСТИЧЕСКИХ ВЕЛИЧИН
- § 12. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ОПТИЧЕСКИХ ВЕЛИЧИН
- § 13. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН АТОМНОЙ И ЯДЕРНОЙ ФИЗИКИ
- § 14. ОПРЕДЕЛЕНИЯ И ЭТАЛОНЫ ОСНОВНЫХ И ДОПОЛНИТЕЛЬНЫХ ЕДИНИЦ СИ
- § 15. РАЦИОНАЛИЗАЦИЯ УРАВНЕНИЙ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- Глава III. СИСТЕМА СГС
- § 17. ПРОИЗВОДНЫЕ ЕДИНИЦЫ МЕХАНИЧЕСКИХ ВЕЛИЧИН В СИСТЕМЕ СГС
- § 18. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ В СИСТЕМЕ СГС
- § 19. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ВЕЛИЧИН В СИСТЕМЕ СГС
- § 20. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН, ХАРАКТЕРИЗУЮЩИХ КОЛЕБАНИЯ И ВОЛНЫ В СИСТЕМЕ СГС
- § 21. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ОПТИЧЕСНИХ ВЕЛИЧИН В СИСТЕМЕ СГС
- § 22. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН АТОМНОЙ И ЯДЕРНОЙ ФИЗИКИ В СИСТЕМЕ СГС
- Глава IV. ВНЕСИСТЕМНЫЕ ЕДИНИЦЫ
- § 23. КРАТНЫЕ И ДОЛЬНЫЕ ЕДИНИЦЫ
- § 24. ОТНОСИТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ ЕДИНИЦЫ
- § 25. СПЕЦИАЛЬНЫЕ ЕДИНИЦЫ
- § 26. КРАТКИЕ СВЕДЕНИЯ О НАИБОЛЕЕ ИЗВЕСТНЫХ ВНЕСИСТЕМНЫХ ЕДИНИЦАХ
- § 27. ОПРЕДЕЛЕНИЕ ЧИСЛОВЫХ КОЭФФИЦИЕНТОВ В ФОРМУЛАХ ПРИ ПЕРЕХОДЕ К СИ
- § 28. СООТНОШЕНИЯ ЕДИНИЦ МЕЖДУНАРОДНОЙ СИСТЕМЫ С ЕДИНИЦАМИ СИСТЕМЫ СГС И ВНЕСИСТЕМНЫМИ ЕДИНИЦАМИ