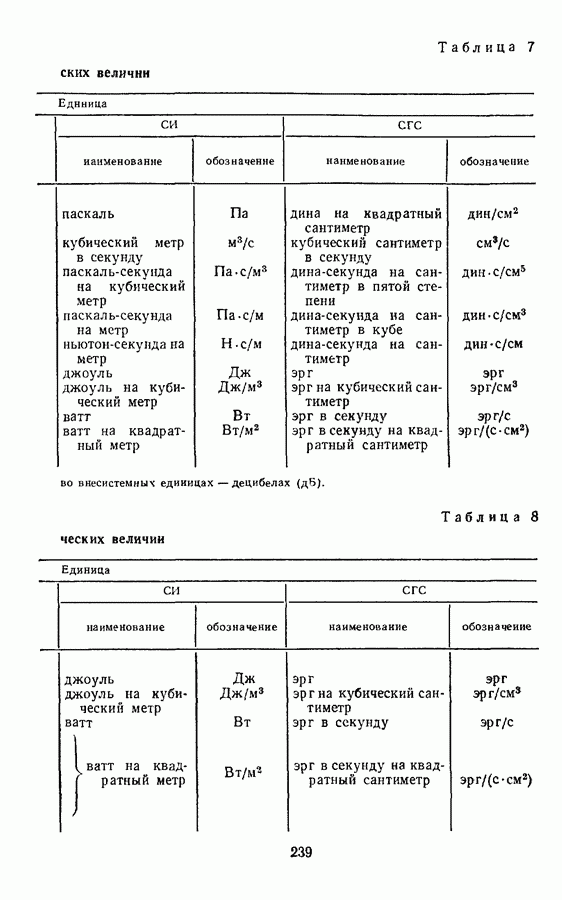
§ 17. ПРОИЗВОДНЫЕ ЕДИНИЦЫ МЕХАНИЧЕСКИХ ВЕЛИЧИН В СИСТЕМЕ СГС

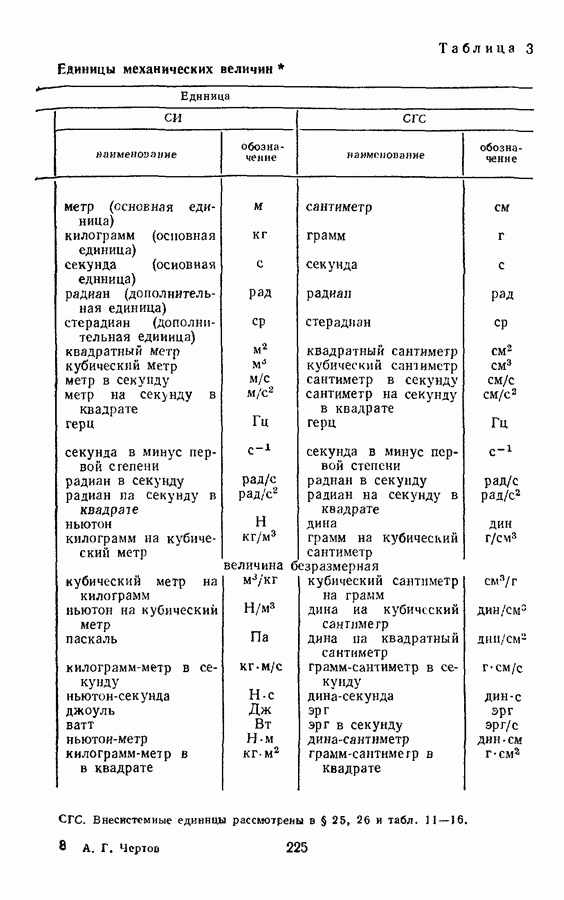
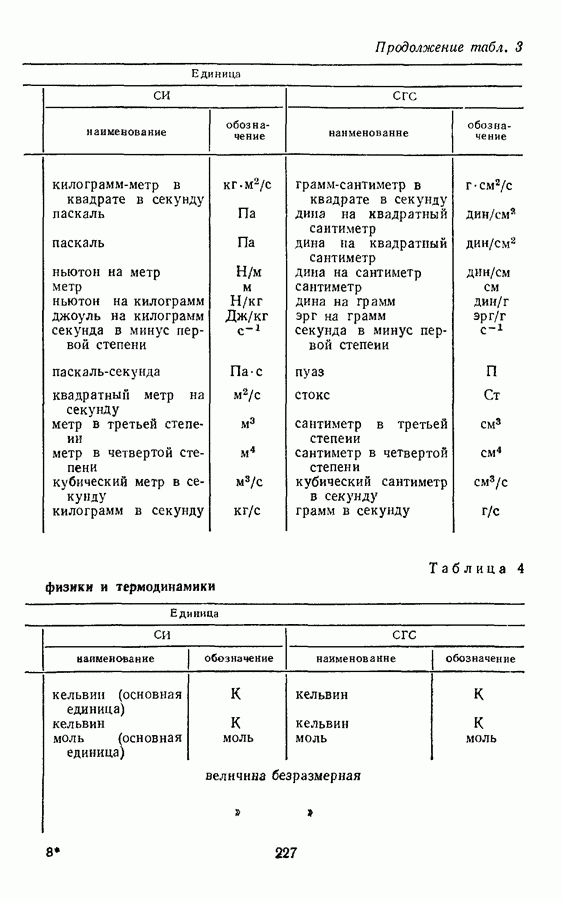
Производные единицы механических величин в системе СГС выражаются через три основные единицы — сантиметр, грамм, секунду и дополнительную единицу — радиан, поэтому размерности этих величин такие же, как в СИ.

Последовательность определяющих уравнений для получения производных механических величин при построении системы СГС такая же, как и при построении СИ (см. § 7 и табл. 3).

Единицы периода, частоты периодического процесса, угловой скорости, углового ускорения, коэффициента трения и некоторых других величин в системе СГС совпадают с единицами СИ (см. § 7) и поэтому в настоящем параграфе не рассматриваются.

Единицы пространства. Единицы величин кинематики

Площадь. Единицу площади найдем по формуле (7.1), подставив в нее см:

Квадратный сантиметр равен площади квадрата со сторонами, длины которых равны 1 см. Найдем соотношение квадратного сантиметра с квадратным метром:

Объем. Для получения единицы объема воспользуемся формулой (7.2), подставив в нее

Кубический сантиметр равен объему куба с ребрами, длины которых равны 1 см. Выразим кубический сантиметр в кубических метрах:

Скорость. Единицу скорости найдем, подставив в формулу см,

Сантиметр в секунду равен скорости прямолинейно и равномерно движущейся точки, при которой эта точка за время 1 с перемещается на расстояние 1 см;

Ускорение. Единицу ускорения найдем по формуле (7.4). Подставив в нее получим

Сантиметр на секунду в квадрате равен ускорению прямолинейно и равноускоренно движущейся точки, при котором за время 1 с скорость точки возрастает на Соотношение с единицей

Единицы величин динамики

Сила. Подставив в формулу , получим единицу силы:

Эта единица называется дина (дин). Дина равна силе, сообщающей телу массой ускорение в направлении действия силы. Найдем соотношение дины с ньютоном:

Плотность. Единицу плотности определим по формуле (7.11). Положив в ней получим

Грамм на кубический сантиметр равен плотности однородного вещества, масса которого при объеме равна 1 г. Выразим единицу плотности системы СГС в единицах плотности СИ:

Давление. Для получения единицы давления воспользуемся формулой (7.15), подставив в нее дин,

Дина на квадратный сантиметр равна давлению, вызываемому силой 1 дин, равномерно распределенной по нормальной к ней поверхности площадью Найдем соотношение этой единицы с паскалем:

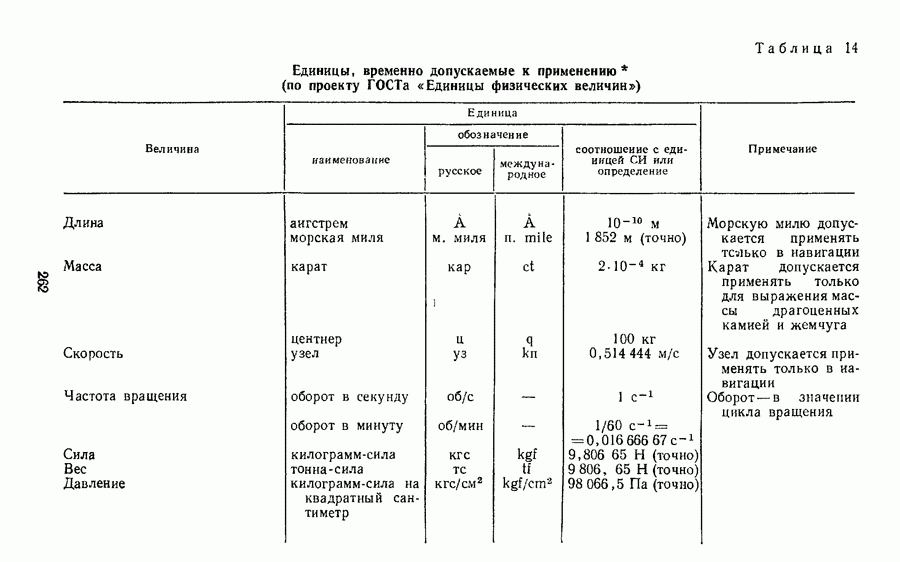
Раньше единицу давления в системе СГС называли бар. Однако в настоящее время это наименование перешло к внесистемной единице давления, равной Па (см. с. 201).

Импульс (количество движения). По формуле (7.16) найдем единицу импульса тела, подставив в нее см/с:

Грамм-сантиметр в секунду равен импульсу (количеству движения) тела массой движущегося поступательно со скоростью 1 см/с. Найдем соотношение это» единицы с соответствующей единицей СИ:

Импульс силы. Единицу импульса силы найдем по формуле (7.17). Подставив в нее дин, получим

Дина-секунда равна импульсу силы, создаваемому силой 1 дин, действующей в течение времени 1 с;

Работа. Энергия. Единицу работы получим по формуле (7.18), подставив в нее дин, см,

Эта единица получила наименование равен работе, совершаемой при перемещении точки приложения силы 1 дин на расстояние 1 см в направлении действия силы. Найдем соотношение эрга с джоулем:

Мощность. Для получения единицы мощности воспользуемся формулой (7.21), подставив в нее

Эрг в секунду равен мощности, при которой за время 1 с совершается работа Соотношение этой единицы с ваттом:

Момент силы. Единицу момента силы получим, подставив в формулу дин, см:

Дина-сантиметр равна моменту силы, создаваемому силой 1 дин относительно точки, расположенной на расстоянии 1 см от линии действия силы;

Момент инерции. Подставив в формулу см, получим единицу момента инерции:

Грамм-сантиметр в квадрате равен моменту инерции материальной точки массой находящейся на расстоянии 1 см от оси инерции;

Момент импульса (момент количества движения). Единицу момента импульса найдем, подставив в формулу

Грамм-сантиметр в квадрате в секунду равен моменту импульса (моменту количества движения) тела с моментом инерции вращающегося с угловой скоростью

Нормальное механическое напряжение. Подставив в формулу дин, найдем единицу напряжения:

Отсюда следует, что напряжение выражается в тех же единицах, что и давление. В динах на квадратный сантиметр выражаются также модули упругости.

Жесткость. Подставив в формулу дин, см, найдем единицу жесткости:

Дина на сантиметр равна жесткости тела, в котором возникает упругая сила 1 дин при абсолютном удлинении его на 1 см;

Коэффициент трения качения. Единицу коэффициента трения качения найдем, положив в формуле

Следовательно, коэффициент трения качения выражается в сантиметрах.

Напряженность гравитационного поля. Единицу напряженности гравитационного поля найдем, положив в формуле дин,

Дина на грамм равна напряженности гравитационного поля, которое на материальную точку массой действует

с силой 1 дин;

Потенциал гравитационного поля. Единицу потенциала гравитационного поля получим, подставив в формулу

Эрг на грамм равен потенциалу гравитационного поля, в котором материальная точка массой обладает потенциальной энергией

Градиент потенциала гравитационного поля. Подставив в формулу см, получим единицу градиента потенциала гравитационного поля:

Градиент скорости. Подставив в формулу , получим единицу градиента скорости:

Эта единица называется секунда в минус первой степени.

Динамическая вязкость. Единицу динамической вязкости получим, положив в формуле

Эта единица получила наименование пуаз Пуаз равен динамической вязкости среды, касательное напряжение в которой при ламинарном течении и при разности скоростей слоев, находящихся на расстоянии 1 см по нормали к направлению скорости, равной 1 см/с, равно 1 дине на квадратный сантиметр. Найдем соотношение пуаза с паскаль-секундой:

Кинематическая вязкость. Положив в формуле получим единицу кинематической вязкости

Эта единица получила наименование стокс Стоке равен кинематической вязкости, при которой динамическая вязкость среды плотностью равна 1 Па.