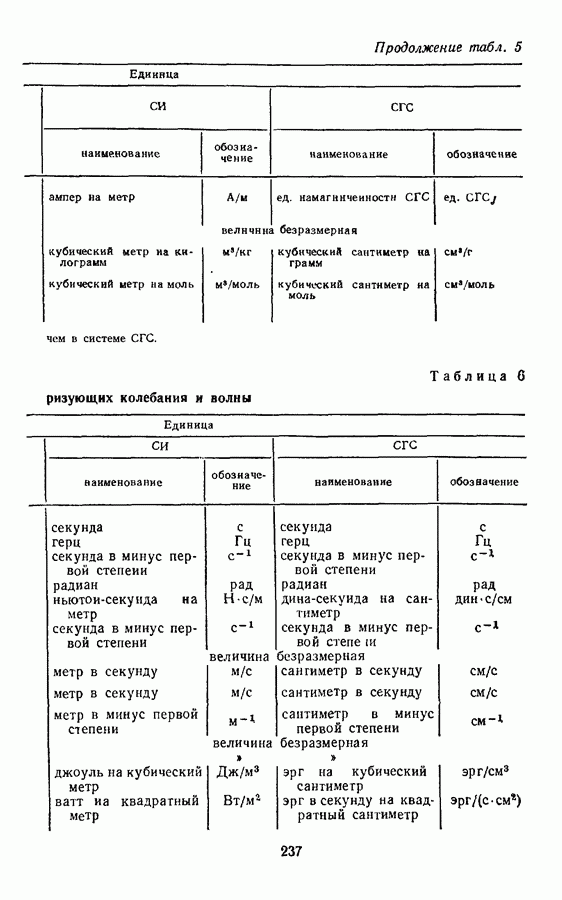
§ 10. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН, ХАРАКТЕРИЗУЮЩИХ КОЛЕБАНИЯ И ВОЛНЫ

Период колебаний. Периодом называют время, в течение которого совершается одно полное колебание. Очевидно, что период выражается в секундах и имеет размерность:

Частота колебаний. Частотой колебаний называют величину, равную числу полных колебаний, совершаемых в единицу времени. Частота колебаний связана с периодом колебаний формулой

Положив в найдем единицу частоты:

Эта единица называется герц (Гц). Герц равен частоте периодического процесса, при которой за время 1 с происходит один цикл периодического процесса. Размерность частоты:

Круговая частота (циклическая частота, угловая частота). Круговой частотой называют величину, равную произведению числа на частоту колебаний

Положив найдем единицу круговой частоты:

Из формулы (10.2) следует также, что круговая частота численно равна числу колебаний, совершаемых за секунд. Размерность круговой частоты:

Фаза колебаний. Фазой колебаний называют аргумент тригонометрической функции, входящей в формулу,

описывающую гармоническое колебание:

где смещение, А — амплитуда колебаний, фаза колебаний, начальная фаза.

Как и любой другой аргумент тригонометрической функции, фаза колебаний выражается в радианах. В этих же единицах выражается и начальная фаза

Приведенная длина физического маятника. Приведенной длиной физического маятника называют величину, равную длине такого математического маятиика, период колебаний которого одинаков с периодом колебаний данного физического маятника. Приведенная длина определяется по формуле

где момент инерции физического маятника, его масса, а — расстояние центра масс маятника от оси качаний.

Положив в получим единицу приведенной длины:

Размерность приведенной длины:

Коэффициент сопротивления. Среда, в которой колеблется тело, оказывает ему сопротивление. При небольших скоростях сила сопротивления пропорциональна скорости тела и выражается формулой

где коэффициент сопротивления. Из формулы (10.5) получим

Положив найдем единицу коэффициента сопротивления:

Ньютон-секунда на метр равен коэффициенту сопротивления среды, в которой на тело, движущееся со скоростью действует сила Размерность коэффициента

ротивления;

Коэффициент затухания (модуль затухания, показатель затухания). Коэффициент затухания величина, характеризующая быстроту убывания амплитуды колебаний во времени вследствие рассеяния энергии. Единицу коэффициента затухания определим из формулы, выражающей смещение затухающих колебаний:

Произведение являясь показателем степени, должно быть безразмерным. Отсюда следует, что единица коэффициента затухания

Эта единица называется секунда в минус первой степени. Размерность коэффициента затухания:

Единицу затухания электрических колебаний можно определить также по формуле

где активное сопротивление колебательного контура, его индуктивность.

Положив в Ом, получим

Заметив, что преобразуем полученную единицу коэффициента затухания:

что совпадает с единицей, полученной по формуле (10.7).

Логарифмический декремент. Логарифмическим декрементом называют величину, равную натуральному логарифму отношения двух последовательных амплитуд колебаний и в моменты времени ( период колебаний), т. е.

Из приведенной формулы следует, что логарифмический декремент есть величина безразмерная и выражается в безразмерных единицах.

В этом можно убедиться также, воспользовавшись формулой:

где коэффициент затухания. Положив в этой формуле получим единицу логарифмического декремента:

Фазовая скорость. Фазовой скоростью волны называют величину, равную скорости, с которой перемещается в пространстве фаза монохроматической волны. Эта скорость определяется по формуле

где длина волны, период колебаний.

Положив найдем единицу фазовой скорости:

т. е. фазовая скорость выражается в метрах в секунду. Размерность фазовой скорости:

Групповая скорость. Скорость распространения реальной волны, представляющей группу синусоидальных волн, в среде, обладающей дисперсией, называется групповой скоростью. Она определяется по формуле

где фазовая скорость волны, X — длина волны, величина, выражающая зависимость фазовой скорости от длины волны.

Из этой формулы следует, что групповая скорость выражается в тех же единицах, что и фазовая скорость, т. е. в метрах в секунду, и имеет размерность

Волновое число. Волновое число величина, равная числу длин волн, укладывающихся на единице длины, т. е.

Положив найдем единицу волнового числа

Метр в минус первой степени равен волновому числу, при котором на отрезке длиной 1 м укладывается одна волна. Размерность волнового числа:

Волновым числом называют также величину, связанную с длиной волны соотношением

Вектор , численно равный волновому числу совпадающий по направлению с лучом бегущей волны, называют волновым вектором.

Волновое число, понимаемое и в этом втором смысле, также выражается в метрах в минус первой степени и имеет размерность

Время релаксации. Время релаксации — величина, равная времени, в течение которого амплитуда колебаний уменьшается в раз. Поэтому время релаксации обратно коэффициенту затухания:

Положив получим

Время релаксации выражается в секундах. Размерность времени релаксации:

Добротность колебательного контура. Добротность колебательного контура — величина, равная отношению амплитуды напряжения на конденсаторе контура при резонансе к амплитуде внешней э. д. с., т. е.

Положив найдем единицу добротности контура:

Следовательно, добротность контура выражается в безразмерных единицах. Размерность добротности

Затухание колебательного контура. Затуханием колебательного контура называют величину, обратную его добротности, т. е.

Затухание контура, как и добротность, выражается в безразмерных единицах.

Энергия волн. Как и любая другая энергия, энергия волн выражается в джоулях.

Объемная плотность энергии волн. Энергия волн распределяется в пространстве неравномерно и, кроме того, меняется во времени. Распределение энергии волн в пространстве в некоторый момент времени характеризуется объемной плотностью энергии

где энергия, заключенная в бесконечно малом объеме , а также средней объемной плотностью энергии

где энергия волн, заключенная в элементе пространства объемом V, линейные размеры которого много больше длины волны К.

Из (10.18) определим единицу объемной плотности энергии волн, положив

Эта единица называется джоуль на кубический метр. Ее определение дано на с. 74. Размерность объемной плотности энергии волн:

Поток энергии волн. Поток энергии есть величина, равная энергии перенесенной волнами через некоторую поверхность, ко времени за которое эта энергия перенесена (предполагается, что где период колебаний)

Подставив в получим единицу потока энергии

Ватт равен потоку энергии волн, эквивалентному механической мощности (см. с. 40). Размерность потока энергии

Плотность потока энергии волн (интенсивность волн). Плотностью потока I энергии волн называют величину, равную отношению потока энергии к площади поверхности, расположенной перпендикулярно направлению распространения волн, т. е.

Положив найдем единицу плотности потока энергии:

Ватт на квадратный метр равен плотности потока энергии волн, при которой через поверхность площадью расположенную перпендикулярно направлению распространения волн, за время 1 с переносится энергия Размерность плотности потока энергии: