| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
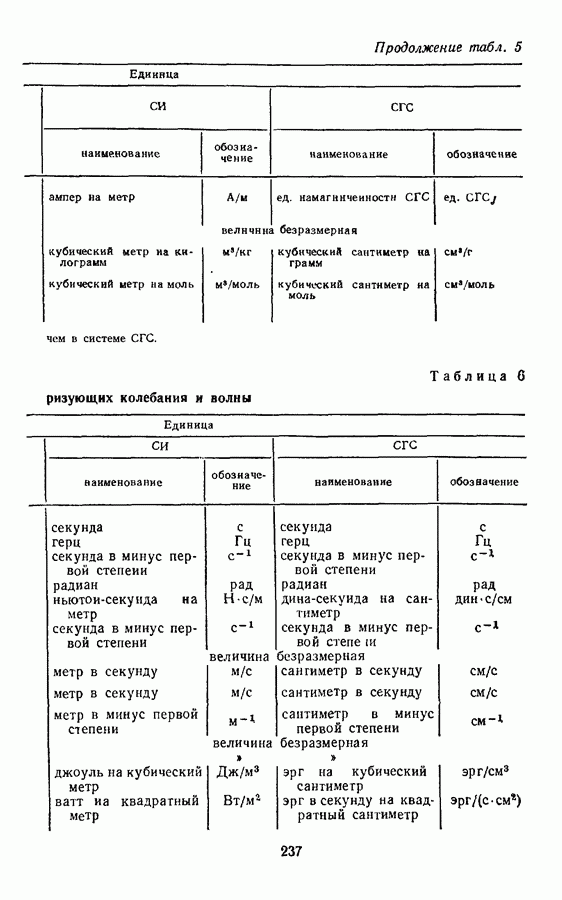
§ 20. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН, ХАРАКТЕРИЗУЮЩИХ КОЛЕБАНИЯ И ВОЛНЫ В СИСТЕМЕ СГС
При получении в системе СГС производных единиц величин, характеризующих колебания и волны (имеются в виду все виды волн, в том числе акустические и
электромагнитные), используются определяющие уравнения и пояснения к ним, помещенные в § 10, 11.
Коэффициент сопротивления. Единицу коэффициента сопротивления получим, положив в формуле 

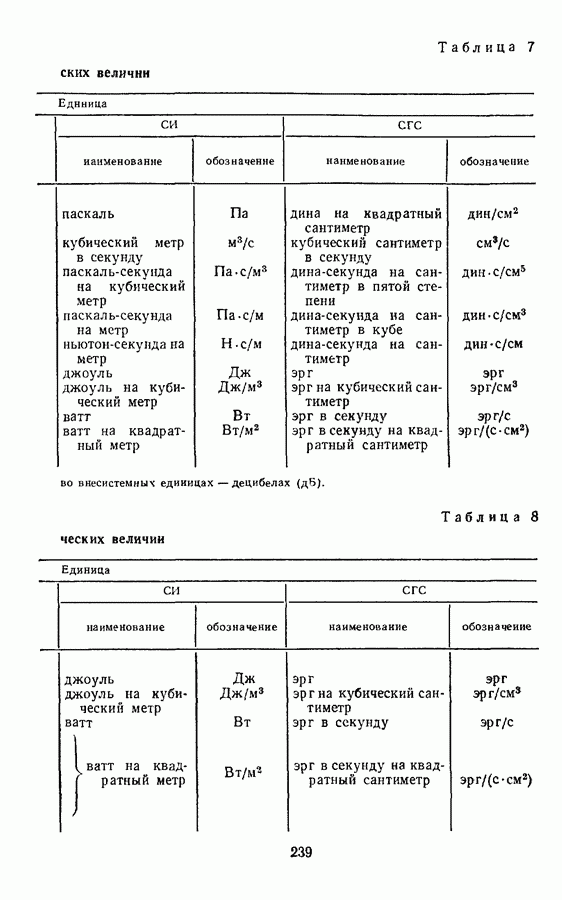
Дина-секунда на сантиметр равна коэффициенту сопротивления среды, в которой на тело, движущееся со скоростью 1 см/с, действует сила 1 дин.
Соотношение между единицами коэффициента сопротивления в единицах СГС и СИ:

Скорость волны (фазовая и групповая). Как и скорость тел, скорость волны (фазовая и групповая) выражается в сантиметрах в секунду. Это следует и из формул (10.10) и (10.11).
Волновое число. Единицу волнового числа найдем по формуле (10.12). Положив в ней  см, получим
см, получим

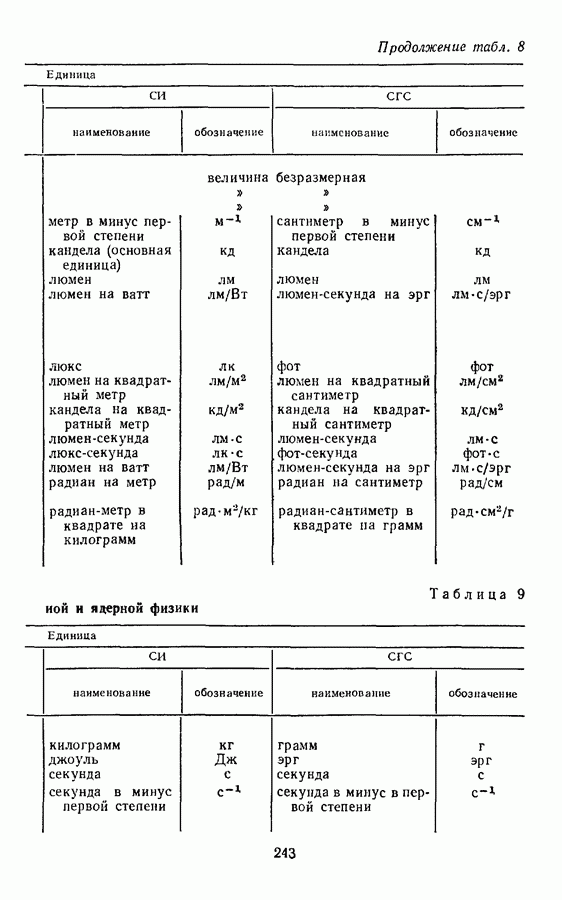
Сантиметр в минус первой степени равен волновому числу, при котором на отрезке длиной 1 см укладывается одна волна.
Энергия волны. Как и любая энергия, энергия волны выражается в эргах.
Объемная плотность энергии волн. Единицу объемной плотности волн найдем, положив в формуле 

Эрг на кубический сантиметр равен объемной плотности энергии волн, при которой в пространстве объемом  содержится энергия 1 эрг;
содержится энергия 1 эрг;

Поток энергии волн. Положив в формуле  получим единицу потока энергии:
получим единицу потока энергии:

Эрг в секунду равен потоку энергии волн, эквивалентному механической мощности  ;
;

Плотность потока энергии. Единицу плотности потока найдем, положив в формуле 

Эрг в секунду на квадратный сантиметр равен плотности потока, при которой поток через поверхность площадью  равен
равен 

Плотность потока энергии звуковых волн называют также интенсивностью звука.
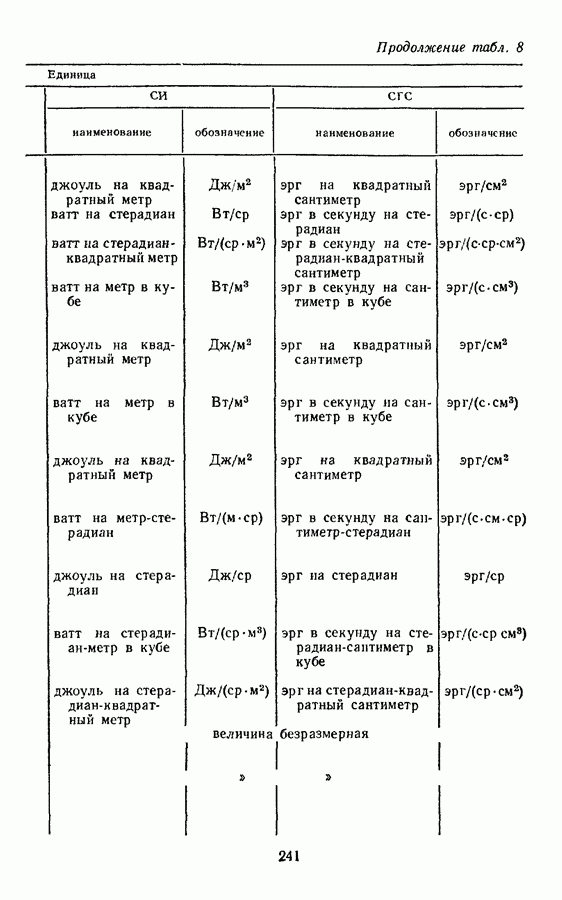
Вектор, численно равный плотности потока энергии волн (интенсивности) и направленный в сторону распространения волн, называется вектором Умова (для акустических волн) и вектором Пойнтинга (для электромагнитных волн). Векторы Умова и Пойнтинга можно выразить формулой

где  объемная плотность энергии,
объемная плотность энергии,  - скорость волн.
- скорость волн.
Векторы Умова и Пойнтинга выражаются в тех же единицах, что и интенсивность, т. е. в эргах в секунду на квадратный сантиметр.
Звуковое давление. Подставив в формулу  получим единицу звукового давления:
получим единицу звукового давления:

Соотношение одной дины на квадратный сантиметр с паскалем:

Объемная скорость звука. Единицу объемной скорости звука найдем по формуле (11.3):

Кубический сантиметр в секунду равен объемной скорости звука при колебательной скорости 1 см/с и площади поперечного сечения канала 

Акустическое сопротивление. Положив в формуле  получим единицу акустического сопротивления:
получим единицу акустического сопротивления:

Дина-секунда на сантиметр в пятой степени равна акустическому сопротивлению области звукового поля, в которой объемная скорость  создается при звуковом давлении
создается при звуковом давлении  :
:

Удельное акустическое сопротивление. Единицу удельного акустического сопротивления найдем по формуле (11.6), положив в ней 

Дина-секунда на кубический сантиметр равна удельному акустическому сопротивлению области звукового поля, которая при площади поперечного сечения  имеет акустическое сопротивление
имеет акустическое сопротивление 

Логарифмический декремент, добротность колебательного контура, затухание контура — величины безразмерные и поэтому выражаются в безразмерных единицах (см. также § 10).
Период колебаний, частота колебаний, круговая частота, фаза, коэффициент затухания, время релаксации в системе СГС выражаются в тех же единицах, что и в СИ (см. § 10).
Единицы остальных величин, характеризующих колебания и волны, рекомендуется получить самому читателю при помощи соответствующих определяющих уравнений, приведенных в § 10, 11.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ОБЩИЕ ВОПРОСЫ ВЫБОРА ЕДИНИЦ И ПОСТРОЕНИЯ СИСТЕМ ЕДИНИЦ
- § 1. ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ. СИСТЕМЫ ФИЗИЧЕСКИХ ВЕЛИЧИН
- Системы физических величин. Основные и производные величины
- § 2. РАЗМЕРНОСТИ ПРОИЗВОДНЫХ ФИЗИЧЕСКИХ ВЕЛИЧИН
- § 3. ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН, РАЗМЕР ЕДИНИЦ
- § 4. СИСТЕМЫ ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН
- § 5. НАИМЕНОВАНИЯ И ОБОЗНАЧЕНИЯ ЕДИНИЦ
- Глава II. МЕЖДУНАРОДНАЯ СИСТЕМА ЕДИНИЦ (СИ)
- § 6. ОСНОВНЫЕ, ДОПОЛНИТЕЛЬНЫЕ И ПРОИЗВОДНЫЕ ЕДИНИЦЫ СИСТЕМЫ
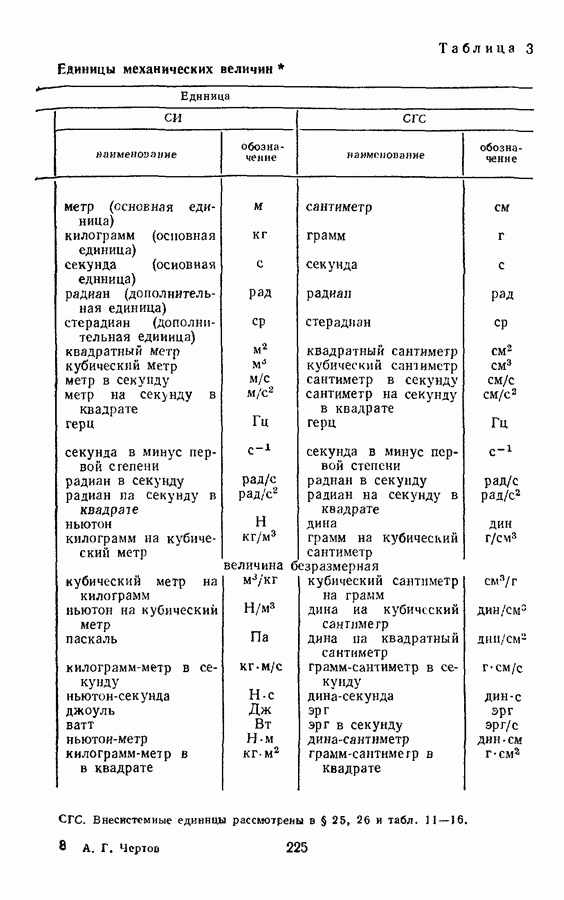
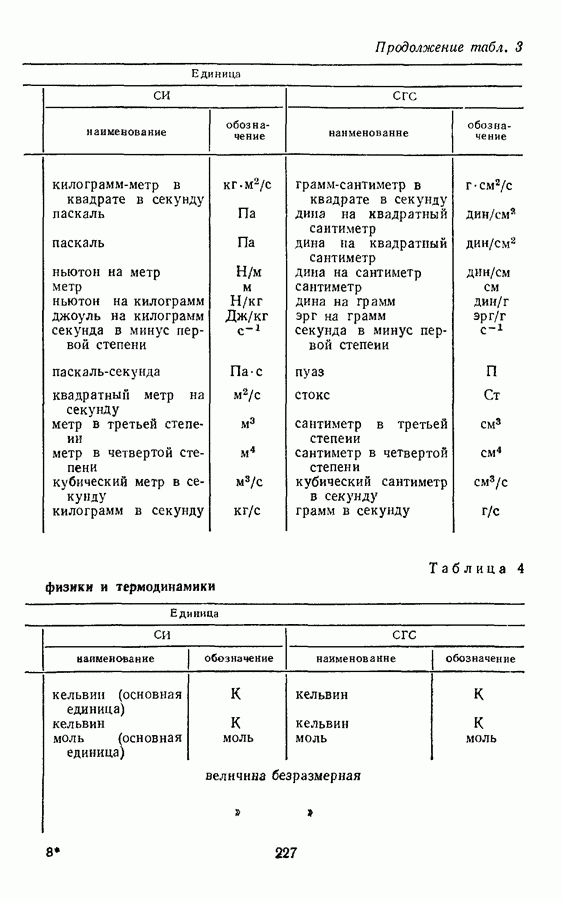
- § 7. ПРОИЗВОДНЫЕ ЕДИНИЦЫ МЕХАНИЧЕСКИХ ВЕЛИЧИН
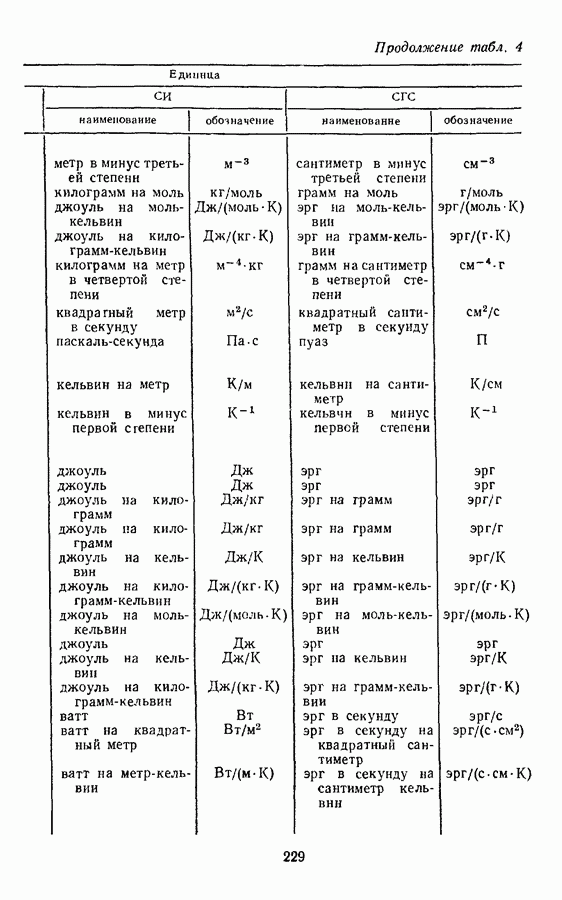
- § 8. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ
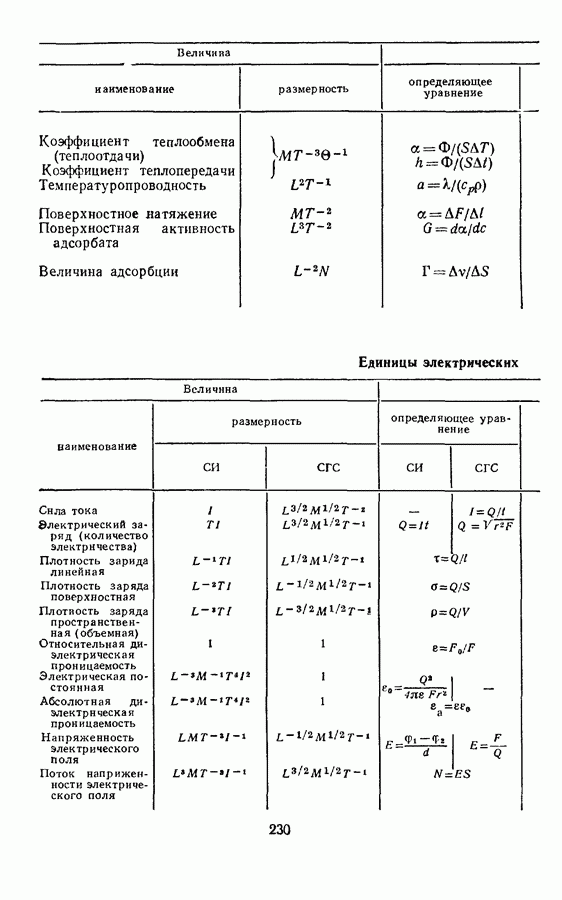
- § 9. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ЭЛЕНТРИЧЕСКИХ И МАГНИТНЫХ ВЕЛИЧИН
- § 10. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН, ХАРАКТЕРИЗУЮЩИХ КОЛЕБАНИЯ И ВОЛНЫ
- § 11. ПРОИЗВОДНЫЕ ЕДИНИЦЫ АКУСТИЧЕСКИХ ВЕЛИЧИН
- § 12. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ОПТИЧЕСКИХ ВЕЛИЧИН
- § 13. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН АТОМНОЙ И ЯДЕРНОЙ ФИЗИКИ
- § 14. ОПРЕДЕЛЕНИЯ И ЭТАЛОНЫ ОСНОВНЫХ И ДОПОЛНИТЕЛЬНЫХ ЕДИНИЦ СИ
- § 15. РАЦИОНАЛИЗАЦИЯ УРАВНЕНИЙ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- Глава III. СИСТЕМА СГС
- § 17. ПРОИЗВОДНЫЕ ЕДИНИЦЫ МЕХАНИЧЕСКИХ ВЕЛИЧИН В СИСТЕМЕ СГС
- § 18. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ В СИСТЕМЕ СГС
- § 19. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ВЕЛИЧИН В СИСТЕМЕ СГС
- § 20. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН, ХАРАКТЕРИЗУЮЩИХ КОЛЕБАНИЯ И ВОЛНЫ В СИСТЕМЕ СГС
- § 21. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ОПТИЧЕСНИХ ВЕЛИЧИН В СИСТЕМЕ СГС
- § 22. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН АТОМНОЙ И ЯДЕРНОЙ ФИЗИКИ В СИСТЕМЕ СГС
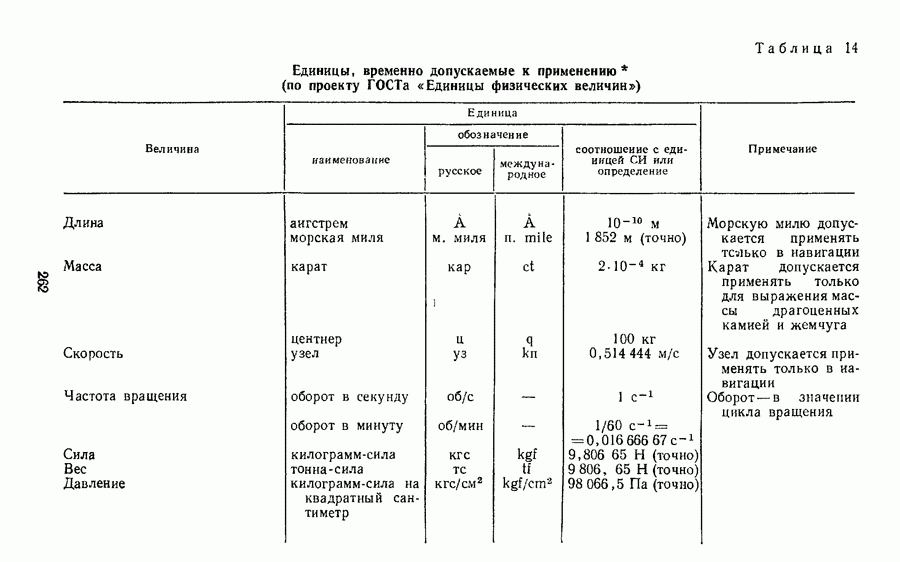
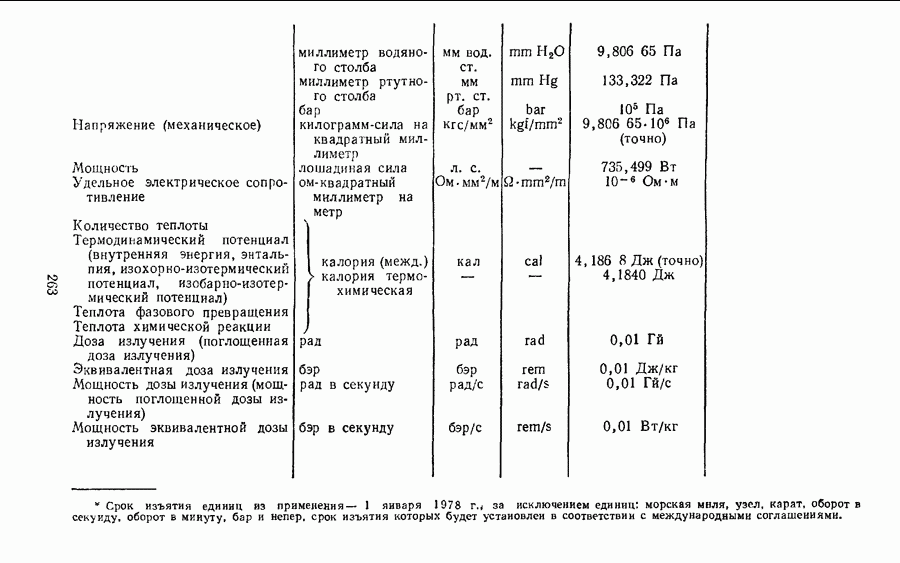
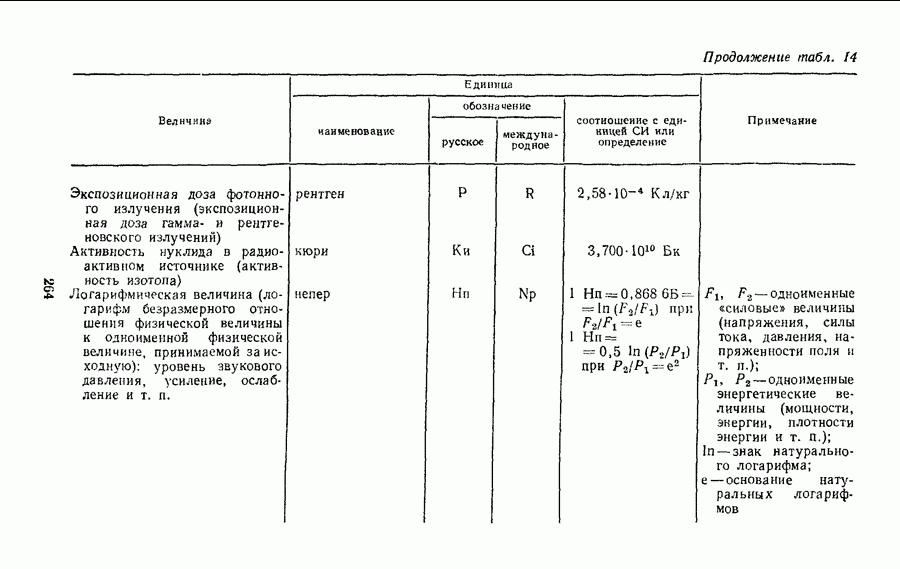
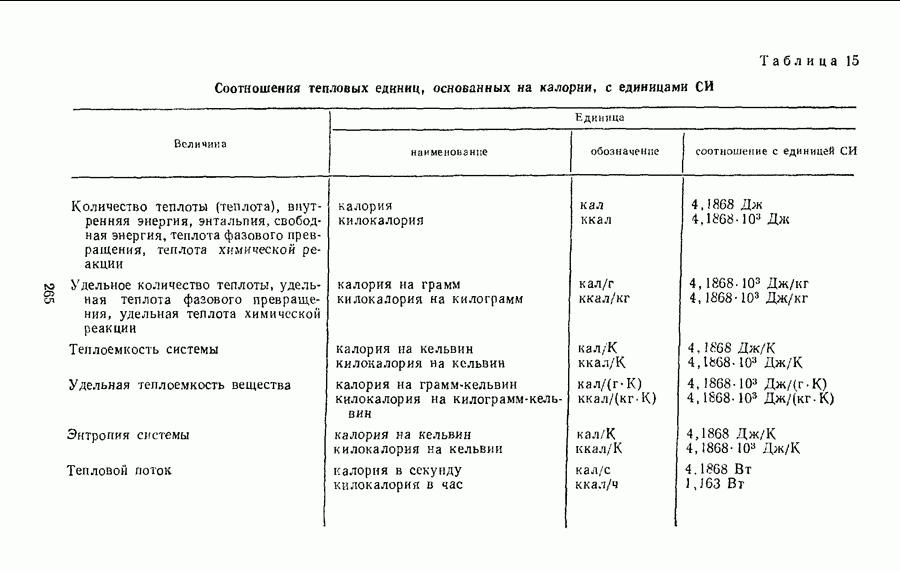
- Глава IV. ВНЕСИСТЕМНЫЕ ЕДИНИЦЫ
- § 23. КРАТНЫЕ И ДОЛЬНЫЕ ЕДИНИЦЫ
- § 24. ОТНОСИТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ ЕДИНИЦЫ
- § 25. СПЕЦИАЛЬНЫЕ ЕДИНИЦЫ
- § 26. КРАТКИЕ СВЕДЕНИЯ О НАИБОЛЕЕ ИЗВЕСТНЫХ ВНЕСИСТЕМНЫХ ЕДИНИЦАХ
- § 27. ОПРЕДЕЛЕНИЕ ЧИСЛОВЫХ КОЭФФИЦИЕНТОВ В ФОРМУЛАХ ПРИ ПЕРЕХОДЕ К СИ
- § 28. СООТНОШЕНИЯ ЕДИНИЦ МЕЖДУНАРОДНОЙ СИСТЕМЫ С ЕДИНИЦАМИ СИСТЕМЫ СГС И ВНЕСИСТЕМНЫМИ ЕДИНИЦАМИ