| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 9. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ЭЛЕНТРИЧЕСКИХ И МАГНИТНЫХ ВЕЛИЧИН
Производные единицы электрических и магнитных величин могут быть выражены через пять основных единиц Международной системы — метр, килограмм, секунду, ампер, кельвин.
Совокупность первых четырех основных единиц и образованных на основе их производных электрических и магнитных единиц ранее составляла систему МКСА, введенную ГОСТ 8033-56. В настоящее время система МКСА вошла в СИ как ее составная часть и как самостоятельная система утратила свое значение.
Производные единицы электрических и магнитных величин в Международной системе единиц устанавливаются для рационализованной формы уравнений электромагнетизма (см. § 15).
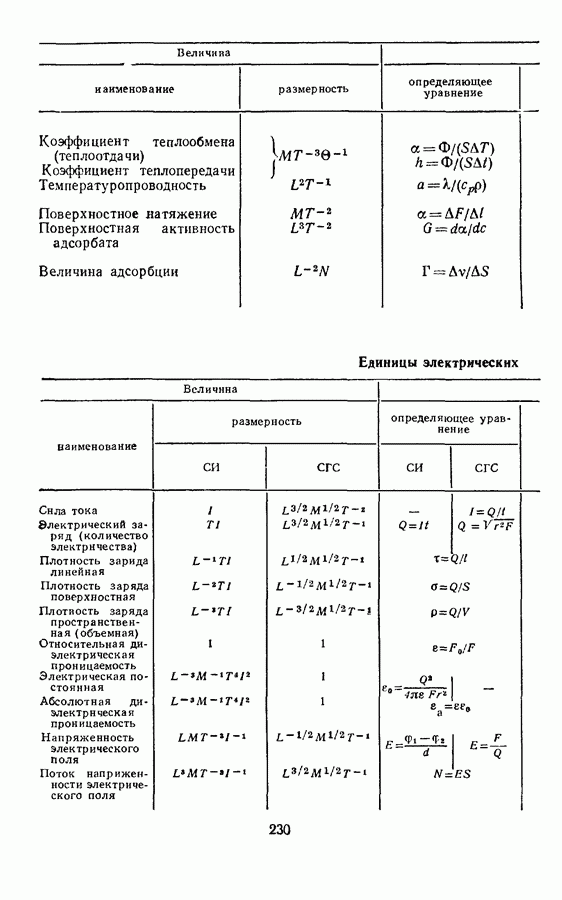
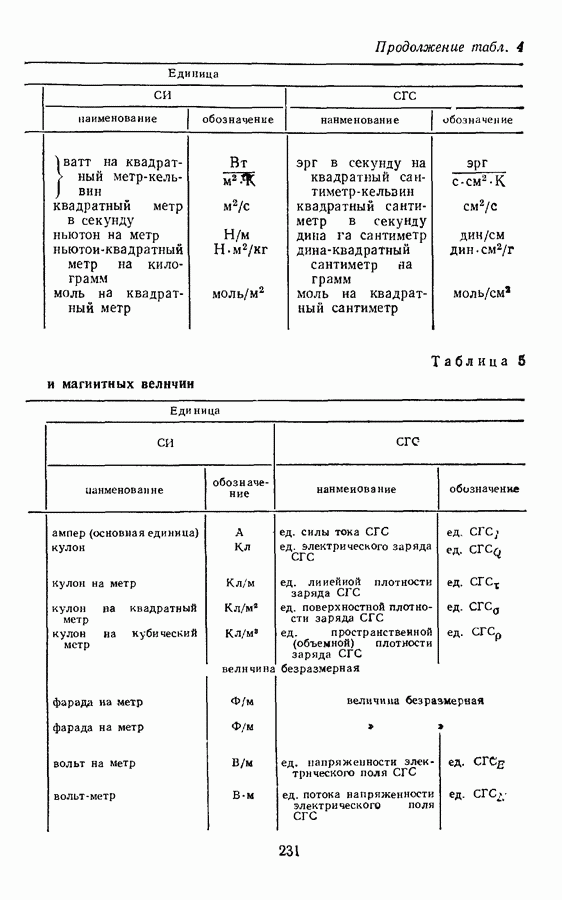
Определим единицы электромагнитных величин, расположив предварительно уравнения электромагнетизма в такой последовательности, которая удовлетворяла бы условиям, указанным на с. II (см. табл. 5).
Единицы электростатических величин
Электрический заряд (количество электричества). Электрический заряд — величина, равная произведению силы тока I на время  в течение которого шел ток, т. е.
в течение которого шел ток, т. е.

Положив  получим
получим

Эта единица получила наименование кулон  Кулон равен электрическому заряду, проходящему через поперечное сечение при токе силой 1 А за время 1 с. Размерность заряда:
Кулон равен электрическому заряду, проходящему через поперечное сечение при токе силой 1 А за время 1 с. Размерность заряда:

Линейная плотность электрического заряда. Линейная плотность электрического заряда  величина, равная отношению заряда
величина, равная отношению заряда  находящегося на элементе линии, к длине
находящегося на элементе линии, к длине  этого элемента, т. е.
этого элемента, т. е.

При равномерном распределении заряда по всей длине нити (цилиндра) линейная плотность

Подставив  найдем единицу линейной плотности заряда:
найдем единицу линейной плотности заряда:

Кулон на метр равен линейной плотности электрического заряда, при которой заряд, равномерно распределенный по линии длиной  равен
равен  Размерность линейной плотности заряда:
Размерность линейной плотности заряда:

Поверхностная плотность электрического заряда. Поверхностной плотностью электрического заряда а называют величину, равную отношению заряда  находящегося на элементе поверхности, к площади
находящегося на элементе поверхности, к площади  этой поверхности, т. е.
этой поверхности, т. е.

Если электрический заряд равномерно распределен по поверхности площадью  то
то

Положив  получим единицу поверхностной плотности электрического заряда:
получим единицу поверхностной плотности электрического заряда:

Кулон на квадратный метр равен поверхностной плотности электрического заряда, при которой заряд, равномерно распределенный по поверхности площадью  равен
равен  Размерность поверхностной плотности заряда:
Размерность поверхностной плотности заряда:

Пространственная плотность электрического заряда (объемная плотность заряда). Пространственная плотность электрического заряда  есть величина, равная отношению заряда
есть величина, равная отношению заряда  находящегося в элементе пространства, к объему
находящегося в элементе пространства, к объему  этого элемента, т. е.
этого элемента, т. е.

При равномерном распределении заряда

Положив  получим единицу пространственной плотности электрического заряда
получим единицу пространственной плотности электрического заряда

Кулон на кубической метр равен пространственной (объемной) плотности электрического заряда, при которой заряд, равномерно распределенный в пространстве объемом  равен
равен  Размерность пространственной плотности заряда:
Размерность пространственной плотности заряда:

Диэлектрическая проницаемость (относительная диэлектрическая проницаемость). Диэлектрическая проницаемость  среды показывает, во сколько раз сила взаимодействия
среды показывает, во сколько раз сила взаимодействия  электрических зарядов в данной среде меньше, чем сила взаимодействия
электрических зарядов в данной среде меньше, чем сила взаимодействия  зарядов в вакууме, т. е.
зарядов в вакууме, т. е.

Из формулы (9.5) следует, что диэлектрическая проницаемость — величина безразмерная и, следовательно, выражается в безразмерных единицах.
Электрическая постоянная. Единицу электрической постоянной  установим, пользуясь законом Кулона:
установим, пользуясь законом Кулона:

где  сила взаимодействия точечных зарядов
сила взаимодействия точечных зарядов  находящихся на расстоянии
находящихся на расстоянии  в среде с диэлектрической проницаемостью
в среде с диэлектрической проницаемостью  коэффициент пропорциональности.
коэффициент пропорциональности.
Этот коэффициент пропорциональности нельзя положить равным безразмерной единице, так как единицы всех величин, входящих в закон Кулона, определены ранее. Единицу и размерность коэффициента  можно было бы определить по формуле (9.6), а числовое его значение — опытным путем.
можно было бы определить по формуле (9.6), а числовое его значение — опытным путем.
Однако поступают иначе. В целях придания формуле закона Кулона более симметричного вида коэффициент  заменяют другим коэффициентом — электрической постоянной
заменяют другим коэффициентом — электрической постоянной  полагая
полагая

После такой замены закон Кулона приобретает вид

Так записывался закон Кулона в классической нерационализованной системе МКСА.
В Международной системе единиц закон Кулона записывается в рационализованной форме, т. е. с множителем  в знаменателе коэффициента пропорциональности:
в знаменателе коэффициента пропорциональности:

где

Для определения единицы электрической постоянной выразим ее из формул (9.8) и (9.8а) соответственно

Отсюда получим

Эта единица называется кулон на вольт-метр.
Однако такое наименование не является широко употребительным. В ГОСТ 8033-56 единице электрической постоянной присвоено наименование фарада на метр (Ф/м). Подробнее об этом см. на с. 74.
Электрическая постоянная относится к числу физических постоянных (фундаментальных физических констант) и имеет значение

или приближенно

Размерность  получим по формулам (9.9) и (9.9а):
получим по формулам (9.9) и (9.9а):

Значение коэффициента пропорциональности  найдем, подставив в формулу (9.7а) значение
найдем, подставив в формулу (9.7а) значение 

Абсолютная диэлектрическая проницаемость. Абсолютная диэлектрическая проницаемость  диэлектрика — величина, равная произведению его диэлектрической проницаемости
диэлектрика — величина, равная произведению его диэлектрической проницаемости  и электрической постоянной
и электрической постоянной  т. е.
т. е.

Один из множителей этой величины — относительная диэлектрическая проницаемость в зависит только от свойств вещества и не зависит от системы единиц, другой множитель  электрическая постоянная
электрическая постоянная  зависит только от выбора системы единиц.
зависит только от выбора системы единиц.
Так как относительная диэлектрическая проницаемость — величина безразмерная, то абсолютная диэлектрическая проницаемость выражается в тех же единицах, что и электрическая постоянная, т. е. в кулонах на вольтметр или фарадах на метр и имеет размерность:

Напряженность электрического поля. Напряженностью  электрического поля в точке называют величину, равную отношению силы
электрического поля в точке называют величину, равную отношению силы  с которой поле действует на
с которой поле действует на
положительный заряд, помещенный в данную точку поля, к этому заряду 

Подставив  получим единицу напряженности электрического поля:
получим единицу напряженности электрического поля:

Ньютон на кулон равен напряженности электрического поля, в котором на точечный заряд  действует сила
действует сила  На практике эта единица напряженности носит название вольт на метр и определяется на основе формулы, устанавливающей связь между напряженностью поля и разностью потенциалов (см. с. 70). Размерность напряженности:
На практике эта единица напряженности носит название вольт на метр и определяется на основе формулы, устанавливающей связь между напряженностью поля и разностью потенциалов (см. с. 70). Размерность напряженности:

Поток напряженности электрического поля (поток вектора напряженности). Потоком  напряженности электрического поля через элемент поверхности называют величину, равную произведению проекции
напряженности электрического поля через элемент поверхности называют величину, равную произведению проекции  напряженности поля на вектор нормали
напряженности поля на вектор нормали  к элементу поверхности на площадь
к элементу поверхности на площадь  этого элемента:
этого элемента:

Поток через всю поверхность

Если в однородном поле перпендикулярно силовым линиям расположена плоская поверхность площадью  то поток напряженности через нее
то поток напряженности через нее

Подставив  получим единицу потока напряженности:
получим единицу потока напряженности:

Вольт-метр равен потоку напряженности через плоскую поверхность площадью  установленную перпендикулярно силовым линиям однородного поля напряженностью
установленную перпендикулярно силовым линиям однородного поля напряженностью  Размерность потока напряженности:
Размерность потока напряженности:

Электрический потенциал (потенциал электрического поля). Электрическим потенциалом  в точке называют
в точке называют
величину, равную отношению потенциальной энергии, которой обладает положительный заряд, помещенный в данную точку поля, к этому заряду. Потенциальная энергия заряда Q в данной точке поля равна работе А, которую совершают силы электрического поля при перемещении заряда из данной точки в бесконечность. Поэтому потенциал может быть определен как величина, численно равная работе, совершаемой полем при удалении единичного положительного заряда из данной точки в бесконечность, т. е.

Подставив  получим
получим

Эта единица называется вольт (В). Вольт равен потенциалу точки поля, в которой заряд в  обладает потенциальной энергией 1 Дж. В вольтах выражаются также напряжение и электродвижущая сила (см. с. 75). Размерность потенциала:
обладает потенциальной энергией 1 Дж. В вольтах выражаются также напряжение и электродвижущая сила (см. с. 75). Размерность потенциала:

Градиент потенциала. Градиент потенциала  вектор, направленный по нормали
вектор, направленный по нормали  к эквипотенциальной поверхности в сторону возрастания потенциала и равный
к эквипотенциальной поверхности в сторону возрастания потенциала и равный  т. е.
т. е.

где  - единичный вектор нормали. В случае однородного поля будет справедливо равенство
- единичный вектор нормали. В случае однородного поля будет справедливо равенство

где  расстояние между эквипотенциальными поверхностями,
расстояние между эквипотенциальными поверхностями,  разность потенциалов этих поверхностей.
разность потенциалов этих поверхностей.
Положив в  найдем
найдем

Между градиентом потенциала и напряженностью электрического поля существует соотношение

т. е. напряженность поля в некоторой точке равна градиенту потенциала в этой же точке, взятому с обратным знаком.
Для однородного поля связь напряженности и потенциала выразится формулой

Из (9.15) и (9.16) следует, что напряженность поля может выражаться в тех же единицах, что и градиент потенциала, т. е. в волыпах на метр (см. также с. 68). Размерность градиента потенциала:

Электрический момент диполя (дипольный момент). Электрический диполь — система двух равных и противоположных по знаку электрических зарядов. Электрический момент  диполя есть вектор, направленный от отрицательного заряда к положительному и равный произведению заряда
диполя есть вектор, направленный от отрицательного заряда к положительному и равный произведению заряда  на плечо 1 диполя, т. е.
на плечо 1 диполя, т. е.

Единицу электрического момента диполя найдем, если в (9.17) положим 

Кулон-метр равен электрическому моменту диполя, заряды которого равные каждый  расположены на расстоянии
расположены на расстоянии  один от другого. Размерность электрического момента диполя:
один от другого. Размерность электрического момента диполя:

Поляризованность (вектор поляризации, интенсивность поляризации). Диэлектрик, помещенный в электрическое поле, поляризуется. При этом любой элемент диэлектрика приобретает электрический момент. Степень поляризации диэлектрика характеризуется поляризованностью. Поляризованность  величина, равная отношению электрического момента
величина, равная отношению электрического момента  элемента диэлектрика к объему
элемента диэлектрика к объему  этого элемента:
этого элемента:

В случае равномерной поляризации

где  электрический момент диэлектрика объемом
электрический момент диэлектрика объемом 
Положив в  получим единицу поляризованности:
получим единицу поляризованности:

Кулон на квадратный метр равен поляризованности диэлектрика, при которой диэлектрик объемом  имеет электрический момент
имеет электрический момент  Размерность поляризованности:
Размерность поляризованности:

Она одинакова с размерностью поверхностной плотности электрического заряда.
Абсолютная диэлектрическая восприимчивость. Поляризованность диэлектрика пропорциональна напряженности  поля внутри этого диэлектрика, т. е.
поля внутри этого диэлектрика, т. е.

где  коэффициент пропорциональности, называемый абсолютной диэлектрической восприимчивостью. Из (9.19) получим
коэффициент пропорциональности, называемый абсолютной диэлектрической восприимчивостью. Из (9.19) получим

Отсюда следует, что абсолютная диэлектрическая восприимчивость численно равна поляризованности диэлектрика при напряженности поля, равной единице.
Единицу абсолютной диэлектрической восприимчивости найдем, положив в 

Эту единицу называют кулон на вольт-метр, или фарада на метр  Фарада на метр равна абсолютной диэлектрической восприимчивости диэлектрика, поляризованность которого
Фарада на метр равна абсолютной диэлектрической восприимчивости диэлектрика, поляризованность которого  при напряженности поля
при напряженности поля 
Абсолютная диэлектрическая восприимчивость выражается в тех же единицах, в которых выражаются электрическая постоянная  и абсолютная диэлектрическая проницаемость
и абсолютная диэлектрическая проницаемость  (см. с. 66 и 67). Размерность абсолютной диэлектрической восприимчивости:
(см. с. 66 и 67). Размерность абсолютной диэлектрической восприимчивости:

Относительная диэлектрическая восприимчивость (диэлектрическая восприимчивость). Относительная диэлектрическая восприимчивость  величина, равная отношению абсолютной диэлектрической восприимчивости к электрической постоянной, т. е.
величина, равная отношению абсолютной диэлектрической восприимчивости к электрической постоянной, т. е.

Так как  выражаются в одних и тех же единицах, то из формулы (9.21) следует, что
выражаются в одних и тех же единицах, то из формулы (9.21) следует, что  величина безразмерная и, следовательно, выражается в безразмерных единицах.
величина безразмерная и, следовательно, выражается в безразмерных единицах.
Электрическое смещение (электрическая индукция). Электрическое смещение  векторная величина, равная геометрической сумме напряженности
векторная величина, равная геометрической сумме напряженности  электрического поля в диэлектрике, умноженной на электрическую постоянную, и его поляризованности
электрического поля в диэлектрике, умноженной на электрическую постоянную, и его поляризованности  т. е.
т. е.

Но  , следовательно,
, следовательно,

или

Подставив в эту формулу  получим единицу электрического смещения:
получим единицу электрического смещения:

Кулон на квадратный метр равен смещению такого электрического поля, напряженность которого в вакууме равна 
В Государственном стандарте «Единицы физических величин» единице электрического смещения дано следующее определение: «Кулон на квадратный метр равен электрическому смещению, при котором поток электрического смещения сквозь поперечное сечение площадью  равен
равен  Такое расхождение в определении единицы электрического смещения объясняется тем, что при изучении курса общей физики сначала вводится электрическое смещение, а затем поток смещения (см. ниже). В стандарте же принята другая последовательность этих величин.
Такое расхождение в определении единицы электрического смещения объясняется тем, что при изучении курса общей физики сначала вводится электрическое смещение, а затем поток смещения (см. ниже). В стандарте же принята другая последовательность этих величин.
Размерность электрического смещения:

Поток электрического смещения (поток электрической индукции). Поток  электрического смещения через элементарный участок
электрического смещения через элементарный участок  поверхности равен произведению электрического смещения
поверхности равен произведению электрического смещения  на площадь
на площадь  проекции этого участка поверхности на плоскость, нормальную
проекции этого участка поверхности на плоскость, нормальную
вектору электрического смещения, т. е.

В однородном электрическом поле поток смещения через плоскую поверхность, нормальную к полю, определяется по формуле

Подставив  получим единицу потока электрического смещения:
получим единицу потока электрического смещения:

Кулон равен потоку электрического смещения через плоскую поверхность площадью  нормальную силовым линиям однородного электрического поля смещением
нормальную силовым линиям однородного электрического поля смещением 
По теореме Остроградского — Гаусса поток  электрического смещения сквозь замкнутую поверхность равен алгебраической сумме зарядов, находящихся внутри этой поверхности:
электрического смещения сквозь замкнутую поверхность равен алгебраической сумме зарядов, находящихся внутри этой поверхности:

Эта теорема показывает, что источником электрического смещения являются электрические заряды и что поток смещения, создаваемый зарядом, численно равен самому заряду. Исходя из этого, кулону дано следующее определение: кулон равен потоку электрического смещения сквозь замкнутую поверхность, образуемому содержащимся во внутреннем пространстве свободным зарядом 
В курсе общей физики теорема Остроградского — Гаусса (9.24) выводится на основе понятия электрического смещения, т. е. поток смещения является величиной вторичной по отношению к электрическому смещению. Поэтому единица потока смещения определяется на основе единицы электрического смещения, а не наоборот, как это сделано в указанном выше государственном стандарте.
Размерность потока электрического смещения одинакова с размерностью заряда:

Электрическая емкость. Электрическая емкость С — величина, равная отношению заряда  внесенного на уединенный проводник, к изменению потенциала
внесенного на уединенный проводник, к изменению потенциала  этого проводника:
этого проводника:

Положив в  найдем единицу электрической емкости проводника:
найдем единицу электрической емкости проводника:

Эта единица называется фарада  Фарада равна электрической емкости уединенного проводника, при которой заряд
Фарада равна электрической емкости уединенного проводника, при которой заряд  повышает потенциал проводника на 1 В.
повышает потенциал проводника на 1 В.
Если в (9.25) под С понимать емкость конденсатора, то единице емкости можно дать следующее определение: фарада равна электрической емкости конденсатора, при которой заряд  создает на конденсаторе разность потенциалов 1 В. Размерность электрической емкости:
создает на конденсаторе разность потенциалов 1 В. Размерность электрической емкости:

На с. 67 была получена единица электрической постоянной  кулон на вольт-метр. Но так как кулон на вольт есть фарада, то единица электрической постоянной, а следовательно, и абсолютной диэлектрической проницаемости:
кулон на вольт-метр. Но так как кулон на вольт есть фарада, то единица электрической постоянной, а следовательно, и абсолютной диэлектрической проницаемости:

В Государственном стандарте «Единицы физических величин» этой единице дано следующее определение: «Фарада на метр равна абсолютной диэлектрической проницаемости, при которой электрическое поле напряженностью  создает электрическое смещение
создает электрическое смещение 
Объемная плотность энергии электрического поля. Объемной плотностью  энергии электрического поля называют величину, равную отношению энергии
энергии электрического поля называют величину, равную отношению энергии  поля, заключенного в элементе объема, к этому объему
поля, заключенного в элементе объема, к этому объему  т. е.
т. е.

В случае однородного поля плотность энергии

Положив  получим единицу объемной плотности энергии:
получим единицу объемной плотности энергии:

Джоуль на кубический метр равен объемной плотности энергии однородного электрического поля, в  которого содержится энергия 1 Дж. Размерность объемной плотности энергии:
которого содержится энергия 1 Дж. Размерность объемной плотности энергии:

Объемная плотность определяется также по формуле

где  напряженность электрического поля. Положив здесь
напряженность электрического поля. Положив здесь  получим
получим

Отсюда следует, что джоуль на кубический метр — это плотность энергии однородного электрического поля, напряженность которого  в вакууме.
в вакууме.
Единицы величин электрического тока
Плотность электрического тока. Плотностью электрического тока  называют векторную величину, численно равную отношению силы тока
называют векторную величину, численно равную отношению силы тока  к элементу
к элементу  площади поперечного сечения проводника:
площади поперечного сечения проводника:

В случае постоянства плотности тока по сечению проводника

Положив  получим единицу плотности электрического тока:
получим единицу плотности электрического тока:

Ампер на квадратный метр равен плотности электрического тока, при которой сила тока, равномерно распределенного по поперечному сечению проводника площадью  равна 1 А. Размерность плотности электрического тока
равна 1 А. Размерность плотности электрического тока

Злектрическое напряжение (падение напряжения), электродвижущая сила. Электрическим напряжением  на концах участка электрической цепи называют величину, определяемую выражением
на концах участка электрической цепи называют величину, определяемую выражением

где  сила тока в цепи,
сила тока в цепи,  сопротивление ее участка.
сопротивление ее участка.
Воспользоваться равенством (9.28) для определения единицы напряжения нельзя, так как в это соотношение входит сопротивление, единица которого пока неизвестна. Поэтому применим формулу мощности постоянного тока  откуда
откуда

Положив  получим единицу электрического напряжения:
получим единицу электрического напряжения:

Эта единица называется вольт  Вольт равен электрическому напряжению на участке электрической цепи, при котором в участке проходит постоянный ток силой 1 А и затрачивается мощность
Вольт равен электрическому напряжению на участке электрической цепи, при котором в участке проходит постоянный ток силой 1 А и затрачивается мощность 
На с. 69 было дано такое определение вольта:  Покажем, что оба эти определения тождественны:
Покажем, что оба эти определения тождественны:

Электродвижущей силой  источника тока называют величину, равную отношению работы А, совершаемой сторонними силами при перемещении положительного заряда вдоль всей электрической цепи, включая источник тока с возвращением в исходную точку цепи, к заряду
источника тока называют величину, равную отношению работы А, совершаемой сторонними силами при перемещении положительного заряда вдоль всей электрической цепи, включая источник тока с возвращением в исходную точку цепи, к заряду 

Положив  получим единицу электродвижущей силы:
получим единицу электродвижущей силы:

Итак, потенциал, напряжение и  выражаются в одних и тех же единицах. Это, в частности, подтверждается и соотношением:
выражаются в одних и тех же единицах. Это, в частности, подтверждается и соотношением:

где  напряжение на участке электрической цепи,
напряжение на участке электрической цепи,  разность потенциалов на его концах,
разность потенциалов на его концах,  электродвижущая сила, имеющаяся на этом участке.
электродвижущая сила, имеющаяся на этом участке.
Размерность напряжения и э. д. с.:

Электрическое сопротивление. По закону Ома сила тока в участке цепи пропорциональна напряжению на его концах,

где  величина, характеризующая участок цепи и называемая электрическим сопротивлением. Из (9.32) получим
величина, характеризующая участок цепи и называемая электрическим сопротивлением. Из (9.32) получим

Отсюда следует, что электрическое сопротивление участка электрической цепи — величина, численно равная отношению напряжения на концах этого участка к силе тока в нем.
Положив в  найдем единицу сопротивления:
найдем единицу сопротивления:

Эту единицу называют ом (Ом). Ом равен электрическому сопротивлению участка электрической цепи, при котором постоянный ток силой 1 А вызывает падение напряжения 1 В. Размерность электрического сопротивления:

Удельное электрическое сопротивление. Удельным электрическим сопротивлением  вещества называют величину, численно равную сопротивлению изготовленного из данного вещества прямолинейного провода с постоянной по длине площадью поперечного сечения, равной единице, и длиной, равной единице.
вещества называют величину, численно равную сопротивлению изготовленного из данного вещества прямолинейного провода с постоянной по длине площадью поперечного сечения, равной единице, и длиной, равной единице.
Единицу удельного электрического сопротивления вещества определим по формуле

где  сопротивление цилиндрического прямолинейного провода длиной I и площадью поперечного сечения 5. Из (9.34) найдем
сопротивление цилиндрического прямолинейного провода длиной I и площадью поперечного сечения 5. Из (9.34) найдем

Положив  Ом,
Ом,  получим единицу удельного сопротивления вещества:
получим единицу удельного сопротивления вещества:  Ом.
Ом. 

Ом-метр равен удельному электрическому сопротивлению вещества, при котором участок выполненной из этого вещества электрической цепи длиной  и площадью
и площадью
поперечного сечения  имеет сопротивление 1 Ом. Размерность удельного электрического сопротивления:
имеет сопротивление 1 Ом. Размерность удельного электрического сопротивления:

Электрическая проводимость. Электрической проводимостью участка электрической цепи называют величину, обратную сопротивлению этого участка, т. е.

Подставив  Ом, получим единицу электрической проводимости:
Ом, получим единицу электрической проводимости:

Эта единица называется сименс (См)  Сименс равен электрической проводимости участка электрической цепи сопротивлением 1 Ом. Размерность электрической проводимости:
Сименс равен электрической проводимости участка электрической цепи сопротивлением 1 Ом. Размерность электрической проводимости:

Удельная электрическая проводимость. Удельной электрической проводимостью  вещества называют величину, численно равную проводимости участка электрической цепи длиной, равной единице, и площадью поперечного сечения, равной единице, и определяют по формуле
вещества называют величину, численно равную проводимости участка электрической цепи длиной, равной единице, и площадью поперечного сечения, равной единице, и определяют по формуле

откуда

Положив  См,
См,  найдем единицу удельной электрической проводимости:
найдем единицу удельной электрической проводимости:

Сименс на метр равен удельной электрической проводимости вещества, при которой участок выполненной из этого вещества электрической цепи длиной  и площадью поперечного сечения
и площадью поперечного сечения  имеет электрическую проводимость 1 См. Размерность удельной электрической проводимости:
имеет электрическую проводимость 1 См. Размерность удельной электрической проводимости:

Единица удельной проводимости может быть найдена также из формулы, полученной на основе электронной теории проводимости металлов:

где  — концентрация свободных электронов,
— концентрация свободных электронов,  соответственно заряд, масса, средние длина свободного пробега и скорость теплового движения электронов. Согласно этой формуле получим ту же единицу удельной проводимости:
соответственно заряд, масса, средние длина свободного пробега и скорость теплового движения электронов. Согласно этой формуле получим ту же единицу удельной проводимости:

Температурный коэффициент сопротивления. Температурным коэффициентом сопротивления а называют величину, равную отношению относительного изменения сопротивления участка электрической цепи к изменению его температуры.
Для металлов и сплавов зависимость удельного сопротивления от температуры в небольшом интервале температур вблизи 0° С выражается формулой

Отсюда получим

Положив в этой формуле  найдем
найдем

Размерность температурного коэффициента сопротивления:

Подвижность носителей тока (ионов, электронов). Подвижность  величина, равная отношению направленной скорости ионов (электронов), вызванной электрическим полем, к напряженности этого поля. Подвижность показывает, на сколько возрастает скорость ионов (электронов) при увеличении напряженности поля на единицу.
величина, равная отношению направленной скорости ионов (электронов), вызванной электрическим полем, к напряженности этого поля. Подвижность показывает, на сколько возрастает скорость ионов (электронов) при увеличении напряженности поля на единицу.
Единицу подвижности  определим по формуле
определим по формуле

где  скорость иона (электрона), приобретенная под действием поля напряженностью
скорость иона (электрона), приобретенная под действием поля напряженностью  Отсюда
Отсюда

Положив  получим единицу подвижности:
получим единицу подвижности:

Квадратный метр на вольт-секунду равен подвижности, при которой ион (электрон) приобретает скорость  при напряженности поля, равной
при напряженности поля, равной  Размерность подвижности:
Размерность подвижности:

Единицу подвижности иона (электрона) можно найти также по формуле, выведенной на основе электронной теории проводимости металлов:

где е - заряд электрона,  средняя длина его свободного пробега,
средняя длина его свободного пробега,  — масса электрона,
— масса электрона,  - средняя скорость теплового движения электронов.
- средняя скорость теплового движения электронов.
Из (9.41) получим

Эмиссионная постоянная. Эмиссионная постоянная В является коэффициентом пропорциональности в формуле Ричардсона — Дешмена, выражающей плотность анодного тока насыщения 

где  абсолютная температура катода, А — работа выхода электрона из металла катода,
абсолютная температура катода, А — работа выхода электрона из металла катода,  постоянная Больцмана. Из этой формулы
постоянная Больцмана. Из этой формулы

Так как — величина безразмерная, то из (9.42) следует, что единица эмиссионной постоянной

Размерность эмиссионной постоянной:

Постоянная термопары. Постоянная термопары а есть величина, равная отношению термоэлектродвижущей силы  возникающей в цепи термопары, к разности температур
возникающей в цепи термопары, к разности температур  между спаями:
между спаями:

Подставив  получим
получим

Вольт на кельвин равен постоянной термопары, термоэлектродвижущая сила которой равна 1 В при разности температур спаев 1 К. Размерность постоянной термопары:

Коэффициент Пельтье. Если по цепи, составленной из двух различных спаянных металлов, пропускать ток, то в одном из спаев выделяется, а в другом поглощается одинаковое количество теплоты  называемое теплотой Пельтье. Она определяется по формуле
называемое теплотой Пельтье. Она определяется по формуле

где  заряд, протекающий через спай,
заряд, протекающий через спай,  коэффициент Пельтье, численно равный количеству теплоты, выделившемуся или поглощенному в спае при прохождении заряда, равного единице. Из этой формулы получим
коэффициент Пельтье, численно равный количеству теплоты, выделившемуся или поглощенному в спае при прохождении заряда, равного единице. Из этой формулы получим

Подставив  найдем единицу коэффициента Пельтье:
найдем единицу коэффициента Пельтье:

Эта единица называется джоуль на кулон. Размерность коэффициента Пельтье:

Коэффициент Томсона. Если по участку электрической цепи, на концах которого поддерживается некоторая разность температур  пропускать ток, то в нем, помимо джоулевой теплоты, будет выделяться некоторое количество теплоты
пропускать ток, то в нем, помимо джоулевой теплоты, будет выделяться некоторое количество теплоты  называемое теплотой Томсона. Она определяется
называемое теплотой Томсона. Она определяется
по формуле

где  заряд, протекщпй через сечение участка цепи, а — коэффициент Томсона, численно равный количеству теплоты, выделившемуся при протекании единичного заряда при разности температур, равной единице. Из этой формулы получим
заряд, протекщпй через сечение участка цепи, а — коэффициент Томсона, численно равный количеству теплоты, выделившемуся при протекании единичного заряда при разности температур, равной единице. Из этой формулы получим

Подставив  найдем единицу коэффициента Томсона:
найдем единицу коэффициента Томсона:

Эта единица называется вольт на кельвин. Размерность коэффициента Томсона:

Степень диссоциации. Явление диссоциации состоит в распаде на ионы молекул растворенного в воде вещества. Число  диссоциировавших молекул пропорционально числу
диссоциировавших молекул пропорционально числу  молекул растворенного вещества, т. е.
молекул растворенного вещества, т. е.

где  коэффициент пропорциональности, называемый степенью диссоциации. Отсюда
коэффициент пропорциональности, называемый степенью диссоциации. Отсюда

т. е. степень диссоциации есть отношение числа молекул, распавшихся на ионы, к общему числу молекул растворенного вещества.
Из (9.46) следует, что степень диссоциации — безразмерная величина и поэтому выражается в безразмерных единицах.
Коэффициент ионизации. Коэффициент ионизации  есть величина, равная отношению числа молекул
есть величина, равная отношению числа молекул  распадающихся на ионы в единице объема, к концентрации
распадающихся на ионы в единице объема, к концентрации  нейтральных молекул и к промежутку времени
нейтральных молекул и к промежутку времени  за которое произошел распад молекул, т. е.
за которое произошел распад молекул, т. е.

Положив  получим единицу коэффициента ионизации:
получим единицу коэффициента ионизации:

Размерность коэффициента ионизации

Коэффициент молизации (коэффициент рекомбинации). Коэффициент молизации у есть величина, равная отношению числа  нейтральных молекул, образовавшихся из ионов в единице объема, к произведению концентраций положительных
нейтральных молекул, образовавшихся из ионов в единице объема, к произведению концентраций положительных  и отрицательных
и отрицательных  ионов и к промежутку времени
ионов и к промежутку времени  за который произошло образование молекул, т. е.
за который произошло образование молекул, т. е.

Положив  получим
получим

Эта единица называется кубический метр-секунда в минус первой степени. Размерность коэффициента молизации:

Эту же размерность коэффициента молизации можно получить и из формулы, связывающей между собой степень диссоциации а, коэффициенты ионизации  и молизации у:
и молизации у:

Отсюда получим

Так как  величина безразмерная, то
величина безразмерная, то

Молярная концентрация (молярность компонента В, концентрация компонента В). Молярной концентрацией компонентов в растворе называют величину, равную отношению количества вещества  этого компонента к объему V раствора:
этого компонента к объему V раствора:

Положив  моль,
моль,  найдем единицу молярной концентрации компонента В:
найдем единицу молярной концентрации компонента В:

Моль на кубический метр равен молярной концентрации вещества в растворе, при которой в объеме раствора  содержится количество растворенного вещества 1 моль. Размерность молярной концентрации:
содержится количество растворенного вещества 1 моль. Размерность молярной концентрации:

Ионный эквивалент концентрации. Ионным эквивалентом концентрации компонента В называют величину, равную отношению молярной концентрации  компонента к степени окисления
компонента к степени окисления  которую он проявляет в соответствующем соединении, т. е.
которую он проявляет в соответствующем соединении, т. е.

Положив  получим единицу ионного эквивалента концентрации:
получим единицу ионного эквивалента концентрации:

Следовательно, ионный эквивалент концентрации выражается в тех же единицах, что и молярная концентрация компонента.
Молярная электрическая проводимость (молярная проводимость). Молярной электрической проводимостью называют величину, равную отношению удельной электрической проводимости  к молярной концентрации
к молярной концентрации  компонента в растворе:
компонента в растворе:

Положив  получим единицу молярной электрической проводимости:
получим единицу молярной электрической проводимости:

Сименс-метр в квадрате на моль равен молярной электрической проводимости растворенного вещества, обладающего удельной проводимостью  при молярной концентрации, равной
при молярной концентрации, равной  Размерность молярной электрической проводимости:
Размерность молярной электрической проводимости:

Эквивалентная электрическая проводимость. Эквивалентной электрической проводимостью называют величину, равную отношению удельной проводимости о к ионному эквиваленту концентрации  т. е.
т. е.

Положив  получим единицу эквивалентной электрической проводимости:
получим единицу эквивалентной электрической проводимости:

Следовательно, эквивалентная электрическая проводимость выражается в тех же единицах, что и молярная электрическая проводимость, однако эти две величины для одного и того же компонента численно не равны. Эквивалентная электрическая проводимость больше в  раз, где
раз, где  степень окисления компонента в соответствующем соединении.
степень окисления компонента в соответствующем соединении.
Электрохимический эквивалент. Электрохимический эквивалент  величина, равная отношению массы вещества
величина, равная отношению массы вещества  отложившегося на электроде при электролизе, к заряду
отложившегося на электроде при электролизе, к заряду  протекшему через электролит:
протекшему через электролит:

Положив  получим единицу электрохимического эквивалента:
получим единицу электрохимического эквивалента:

Килограмм на кулон равен электрохимическому эквиваленту такого вещества, 1 кг которого выделяется на электроде при прохождении через электролит заряда  Размерность электрохимического эквивалента:
Размерность электрохимического эквивалента:

Единицы величин магнетизма
Магнитный момент электрического тока. Магнитным моментом  плоского контура с током называют величину, равную произведению силы тока I в контуре на площадь
плоского контура с током называют величину, равную произведению силы тока I в контуре на площадь  охватываемую этим контуром, т. е.
охватываемую этим контуром, т. е.

Положив в этой формуле  получим единицу магнитного момента:
получим единицу магнитного момента:

Ампер-квадратный метр равен магнитному моменту электрического тока силой 1 А, проходящего по лежащему в плоскости кенгуру площадью  Размерность
Размерность
магнитного момента электрического тока:

Магнитная индукция. Магнитная индукция есть величина, равная отношению максимального вращающего момента  , действующего на контур с током в однородном магнитном поле, к магнитному моменту этого контура:
, действующего на контур с током в однородном магнитном поле, к магнитному моменту этого контура:

Положив в  найдем единицу магнитной индукции:
найдем единицу магнитной индукции:

Эта единица называется тесла  Тесла равен магнитной индукции однородного магнитного поля, в котором на плоский контур с током с магнитным моментом
Тесла равен магнитной индукции однородного магнитного поля, в котором на плоский контур с током с магнитным моментом  действует максимальный вращающий момент, равный
действует максимальный вращающий момент, равный  Размерность магнитной индукции:
Размерность магнитной индукции:

Единицу магнитной индукции можно было бы определить также по закону Ампера, из которого следует

т. е. магнитная индукция — величина, равная отношению силы  действующей в однородном магнитном поле на перпендикулярный полю отрезок проводника с током, к длине этого отрезка и силе тока в нем.
действующей в однородном магнитном поле на перпендикулярный полю отрезок проводника с током, к длине этого отрезка и силе тока в нем.
Положив в  найдем единицу магнитной индукции:
найдем единицу магнитной индукции:

что совпадает с единицей, полученной по формуле (9.54).
На основании закона Ампера единица магнитной индукции определяется так: тесла равен индукции однородного магнитного поля, в котором на отрезок длиной  прямого проводника с током силой 1 А действует максимальная сила
прямого проводника с током силой 1 А действует максимальная сила 
В Государственном стандарте «Единицы физических величин» дано иное определение тесла: «Тесла равен магнитной индукции, при которой магнитный поток сквозь поперечное сечение площадью  равен
равен 
В указанном стандарте из двух величин — магнитной индукции и магнитного потока первичной считается магнитный поток. Поэтому единица магнитной индукции —
тесла определяется через единицу магнитного потока — вебер на основе формулы

где  магнитный поток через поверхность
магнитный поток через поверхность 
В курсе общей физики по методическим соображениям первой величиной вводится магнитная индукция и поэтому ее единица определяется не зависимо от единицы магнитного потока — вебера.
Магнитный поток. Магнитный поток  через элементарную поверхность
через элементарную поверхность  равен произведению проекции
равен произведению проекции  вектора индукции на нормаль
вектора индукции на нормаль  к элементу поверхности на площадь этого элемента, т. е.
к элементу поверхности на площадь этого элемента, т. е.

Поток через всю поверхность 

В случае когда поверхность плоская и расположена в однородном поле перпендикулярно линиям индукции, магнитный поток равен произведению индукции на площадь поверхности 

Подставив  получим единицу магнитного потока:
получим единицу магнитного потока:

Эта единица называется вебер  Вебер — магнитный поток, создаваемый однородным магнитным полем с индукцией
Вебер — магнитный поток, создаваемый однородным магнитным полем с индукцией  через поперечное сечение площадью
через поперечное сечение площадью  Размерность магнитного потока:
Размерность магнитного потока:

В Государственном стандарте «Единицы физических величин» дано иное определение вебера: «Вебер равен магнитному потоку, при убывании которого до нуля в сцепленной с ним электрической цепи сопротивлением 1 Ом через поперечное сечение проводника проходит количество электричества 
Такое определение вебера получено по формуле

где  заряд, протекающий по замкнутой цепи при изменении на
заряд, протекающий по замкнутой цепи при изменении на  магнитного потока через поверхность,
магнитного потока через поверхность,
ограничиваемую цепью,  сопротивление цепи. Отсюда
сопротивление цепи. Отсюда

Положив  , найдем единицу магнитного потока:
, найдем единицу магнитного потока:

Однако при изучении курса общей физики воспользоваться формулой (9.59) для определения вебера и формулой (9.56) для определения тесла нельзя. В этом случае пришлось бы сначала рассмотреть явление электромагнитной индукции, затем магнитный поток и только после этого ввести основную характеристику магнитного поля — магнитную индукцию.
Потокосцепление. По определению, потокосцеплеиие

где  — магнитный поток через
— магнитный поток через  виток,
виток,  число витков.
число витков.
Если все витки одинаковы, как, например, у соленоида или тороида, то

где  магнитный поток через один виток (магнитный поток через поперечное сечение соленоида или тороида),
магнитный поток через один виток (магнитный поток через поперечное сечение соленоида или тороида),  число витков. Из формулы (9.60) следует, что потокосцепление имеет ту же размерность и выражается в тех же единицах, что и магнитный поток, т. е. в веберах.
число витков. Из формулы (9.60) следует, что потокосцепление имеет ту же размерность и выражается в тех же единицах, что и магнитный поток, т. е. в веберах.
Единицу потокосцепления, а следовательно, и магнитного потока можно определить также из формулы, выражающей закон Фарадея — Максвелла:

где  электродвижущая сила индукции, возникающая в замкнутом контуре при изменении потокосцепления на за время А. Из (9.61) найдем
электродвижущая сила индукции, возникающая в замкнутом контуре при изменении потокосцепления на за время А. Из (9.61) найдем

Подставив  получим
получим

Легко показать, что вольт-секунда есть вебер:

Поэтому раньше единица потокосцепления называлась вольт-секунда. Размерность потокосцепления такая же, как и магнитного потока:

Магнитный заряд (магнитная масса, количество магнетизма). Магнитный заряд — фиктивная величина, введенная для удобства магнитостатических расчетов. Из формулы, выражающей работу  по однократному обводу магнитного заряда
по однократному обводу магнитного заряда  вокруг тока:
вокруг тока:  получим
получим

Положив  найдем единицу магнитного заряда:
найдем единицу магнитного заряда:

Джоуль на ампер равен магнитному заряду, при однократном обводе которого вокруг тока силой 1 А совершается работа  Размерность магнитного заряда:
Размерность магнитного заряда:

Индуктивность (статическая индуктивность, коэффициент самоиндукции). Если по замкнутому контуру, например, по соленоиду, течет ток силой  то с этим контуром сцеплен магнитный поток
то с этим контуром сцеплен магнитный поток

где  величина, характеризующая данный контур и называемая индуктивностью. Из формулы (9.64) получим
величина, характеризующая данный контур и называемая индуктивностью. Из формулы (9.64) получим

Отсюда следует, что индуктивность — величина, равная отношению потокосцепления, связанного с контуром, к силе тока, протекающего по нему.
Положив в  найдем единицу индуктивности:
найдем единицу индуктивности:

Эта единица называется генри  Генри равен индуктивности электрической цепи, с которой при силе постоянного тока в ней 1 А сцепляется магнитный поток
Генри равен индуктивности электрической цепи, с которой при силе постоянного тока в ней 1 А сцепляется магнитный поток 
Единицу индуктивности можно определить также по закону Фарадея — Максвелла:

где  - э. д. с. самоиндукции. Из этого уравнения следует
- э. д. с. самоиндукции. Из этого уравнения следует

т. е. индуктивность — величина, равная отношению э. д. с. самоиндукции, возникающей в контуре, к скорости  изменения силы тока в этом контуре.
изменения силы тока в этом контуре.
Положив в  получим
получим

Исходя из закона Фарадея — Максвелла, генри можно дать следующее определение: генри равен индуктивности такого контура, в котором возникает  самоиндукции 1 В при изменении силы тока в этом контуре на 1 А в 1 с.
самоиндукции 1 В при изменении силы тока в этом контуре на 1 А в 1 с.
Размерность индуктивности можно установить при помощи формулы (9.65) или (9.66):

Взаимная индуктивность (статическая взаимная индуктивность, коэффициент взаимной индукции). Магнитный поток, сцепленный с замкнутым контуром, находящимся в магнитном поле тока  другого контура, определяется по формуле
другого контура, определяется по формуле

где  величина, называемая взаимной индуктивностью двух контуров. Она зависит от конфигурации контуров, числа их витков, а также от взаимного их расположения. Из (9.67) получим
величина, называемая взаимной индуктивностью двух контуров. Она зависит от конфигурации контуров, числа их витков, а также от взаимного их расположения. Из (9.67) получим

Положив  найдем единицу взаимной индуктивности:
найдем единицу взаимной индуктивности:

Единицей взаимной индуктивности так же, как и единицей индуктивности, является генри. Исходя из понятия взаимной индуктивности, генри можно определить так: генри — взаимная индуктивность двух контуров, с одним из которых сцеплен магнитный поток 1 Вб, если по другому
течет ток силой 1 А. Размерность взаимной индуктивности:

Напряженность магнитного поля. Единицу напряженности Н магнитного поля определим по формуле, выражающей напряженность этого поля в центре длинного соленоида:

где N - число витков соленоида, I — его длина,  сила тока в нем.
сила тока в нем.
Положив в  где
где  число витков на участке соленоида длиной
число витков на участке соленоида длиной  получим единицу напряженности магнитного поля:
получим единицу напряженности магнитного поля:

Ампер на метр равен напряженности магнитного поля в центре длинного соленоида с равномерно распределенной обмоткой, по которой проходит ток силой  где
где  число витков на участке соленоида длиной
число витков на участке соленоида длиной  Размерность напряженности магнитного поля:
Размерность напряженности магнитного поля:

Абсолютная магнитная проницаемость. Между двумя характеристиками магнитного поля — индукцией В и напряженностью  существует пропорциональная зависимость
существует пропорциональная зависимость

где  — коэффициент пропорциональности, зависящий от среды и системы единиц и называемый абсолютной магнитной проницаемостью. Из (9.70) получим
— коэффициент пропорциональности, зависящий от среды и системы единиц и называемый абсолютной магнитной проницаемостью. Из (9.70) получим

Из этой формулы найдем единицу абсолютной магнитной проницаемости:

Генри на метр равен абсолютной магнитной проницаемости среды, в которой при напряженности магнитного поля  создается магнитная индукция
создается магнитная индукция  Размерность абсолютной магнитной проницаемости:
Размерность абсолютной магнитной проницаемости:

Если при изучении вопросов электромагнетизма ограничиться одной характеристикой — магнитной индукцией, то абсолютную магнитную проницаемость можно ввести иначе. Пользуясь законом Био - Савара - Лапласа, индукцию В магнитного поля, созданного прямым бесконечно длинным током силой  можно выразить следующей формулой:
можно выразить следующей формулой:

где  расстояние от тока до точки, в которой определяется индукция поля,
расстояние от тока до точки, в которой определяется индукция поля,  абсолютная магнитная проницаемость. Из этой формулы получим
абсолютная магнитная проницаемость. Из этой формулы получим

Из формулы (9.73) следует, что абсолютная магнитная проницаемость — величина, равная отношению индукции магнитного поля прямого бесконечно длинного тока в точке, отстоящей от проводника на  к силе тока, протекающего по проводнику. Положив в (9.73)
к силе тока, протекающего по проводнику. Положив в (9.73)  найдем
найдем

Абсолютную магнитную проницаемость можно представить в виде произведения двух множителей:

где  относительная магнитная проницаемость, или просто магнитная проницаемость, зависящая только от среды,
относительная магнитная проницаемость, или просто магнитная проницаемость, зависящая только от среды,  магнитная постоянная — величина, зависящая только от выбора единиц.
магнитная постоянная — величина, зависящая только от выбора единиц.
Относительная магнитная проницаемость (магнитная проницаемость). Магнитная проницаемость  величина, показывающая, во сколько раз магнитная индукция В поля в данной среде больше, чем магнитная индукция
величина, показывающая, во сколько раз магнитная индукция В поля в данной среде больше, чем магнитная индукция  в вакууме, т. е.
в вакууме, т. е.

Из этой формулы следует, что относительная магнитная проницаемость  величина безразмерная и поэтому выражается в безразмерных единицах.
величина безразмерная и поэтому выражается в безразмерных единицах.
Магнитная постоянная. Из формулы (9-74) следует, что

Так как магнитная проницаемость  величина безразмерная, то магнитная постоянная выражается в тех же единицах и имеет ту же размерность, что и абсолютная магнитная
величина безразмерная, то магнитная постоянная выражается в тех же единицах и имеет ту же размерность, что и абсолютная магнитная
проницаемость:

Магнитная постоянная относится к числу физических постоянных (фундаментальных физических констант) и имеет значение

Магнитодвижущая сила. Магнитодвижущая сила  величина, характеризующая намагничивающее действие электрического тока и равная циркуляции напряженности магнитного поля вдоль замкнутого контура, т. е.
величина, характеризующая намагничивающее действие электрического тока и равная циркуляции напряженности магнитного поля вдоль замкнутого контура, т. е.

где  проекция вектора напряженности на направление перемещения
проекция вектора напряженности на направление перемещения  число токов, охватываемых контуром. В случае если замкнутый контур берется вдоль оси тороида, по которому течет постоянный ток силой
число токов, охватываемых контуром. В случае если замкнутый контур берется вдоль оси тороида, по которому течет постоянный ток силой  то магнитодвижущая сила
то магнитодвижущая сила

где  число витков тороида.
число витков тороида.
Положив в последней формуле  получим единицу магнитодвижущей силы:
получим единицу магнитодвижущей силы:

Единицей магнитодвижущей силы является ампер. Ампер равен магнитодвижущей силе вдоль замкнутого контура, сцепленного с цепью постоянного тока силой 1 А. Размерность магнитодвижущей силы:

В амперах выражается также разность магнитных потенциалов.
Единицу магнитодвижущей силы — ампер иногда называют ампер-виток. Однако это название официально не принято.
Магнитное сопротивление. Магнитный поток, создаваемый в магнитной цепи, пропорционален магнитодвижущей силе, т. е.

где  магнитное сопротивление цепи.
магнитное сопротивление цепи.
Из (9.78) получим

Положив  найдем единицу магнитного сопротивления:
найдем единицу магнитного сопротивления:

Ампер на вебер равен магнитному сопротивлению магнитной цепи, в которой магнитный поток  создается при магнитодвижущей силе 1 А. Размерность магнитного сопротивления:
создается при магнитодвижущей силе 1 А. Размерность магнитного сопротивления:

Магнитная проводимость. Магнитная проводимость  магнитной цепи — величина, обратная магнитному сопротивлению, т. е.
магнитной цепи — величина, обратная магнитному сопротивлению, т. е.

Положив  получим единицу магнитной проводимости:
получим единицу магнитной проводимости:

Вебер на ампер равен магнитной проводимости магнитной цепи с магнитным сопротивлением  Размерность магнитной проводимости:
Размерность магнитной проводимости:

Намагниченность (вектор намагничения). Намагниченность  величина, равная отношению магнитного момента тела к его объему. В случае равномерного намагничения вещества
величина, равная отношению магнитного момента тела к его объему. В случае равномерного намагничения вещества

где  магнитный момент, которым обладает тело объемом
магнитный момент, которым обладает тело объемом 
Положив в этой формуле  получим
получим

Ампер на метр равен намагниченности вещества, при которой вещество объемом  имеет магнитный момент
имеет магнитный момент  Размерность намагниченности:
Размерность намагниченности:

Магнитная восприимчивость. Намагниченность вещества пропорциональна напряженности намагничивающего магнитного поля, т. е.

где  величина, характеризующая свойства данного вещества намагничиваться в магнитном поле и называемая магнитной восприимчивостью этого вещества. Из этой формулы имеем
величина, характеризующая свойства данного вещества намагничиваться в магнитном поле и называемая магнитной восприимчивостью этого вещества. Из этой формулы имеем

т. е. магнитная восприимчивость вещества численно равна намагниченности вещества при напряженности поля, равной единице.
Положив в  получим
получим

Отсюда следует, что магнитная восприимчивость — величина безразмерная и выражается в безразмерных единицах.
Удельная магнитная восприимчивость. Удельной магнитной восприимчивостью вещества называют величину, равную отношению магнитной восприимчивости  к плотности
к плотности  вещества:
вещества:

Положив  найдем единицу удельной магнитной восприимчивости:
найдем единицу удельной магнитной восприимчивости:

Эту единицу называют кубический метр на килограмм. Размерность удельной магнитной восприимчивости:

Молярная магнитная восприимчивость. Молярная магнитная восприимчивость — величина, определяемая соотношением

где  молярный объем,
молярный объем,  молярная масса.
молярная масса.
Подставив в  получим единицу молярной магнитной восприимчивости:
получим единицу молярной магнитной восприимчивости:

Эту единицу называют кубический метр на моль. Размерность молярной магнитной восприимчивости:

Точка Кюри. Точкой Кюри называют температуру, при которой полностью исчезает остаточная намагниченность ферромагнетика.
Как и любая температура, точка Кюри выражается в Кельвинах.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ОБЩИЕ ВОПРОСЫ ВЫБОРА ЕДИНИЦ И ПОСТРОЕНИЯ СИСТЕМ ЕДИНИЦ
- § 1. ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ. СИСТЕМЫ ФИЗИЧЕСКИХ ВЕЛИЧИН
- Системы физических величин. Основные и производные величины
- § 2. РАЗМЕРНОСТИ ПРОИЗВОДНЫХ ФИЗИЧЕСКИХ ВЕЛИЧИН
- § 3. ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН, РАЗМЕР ЕДИНИЦ
- § 4. СИСТЕМЫ ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН
- § 5. НАИМЕНОВАНИЯ И ОБОЗНАЧЕНИЯ ЕДИНИЦ
- Глава II. МЕЖДУНАРОДНАЯ СИСТЕМА ЕДИНИЦ (СИ)
- § 6. ОСНОВНЫЕ, ДОПОЛНИТЕЛЬНЫЕ И ПРОИЗВОДНЫЕ ЕДИНИЦЫ СИСТЕМЫ
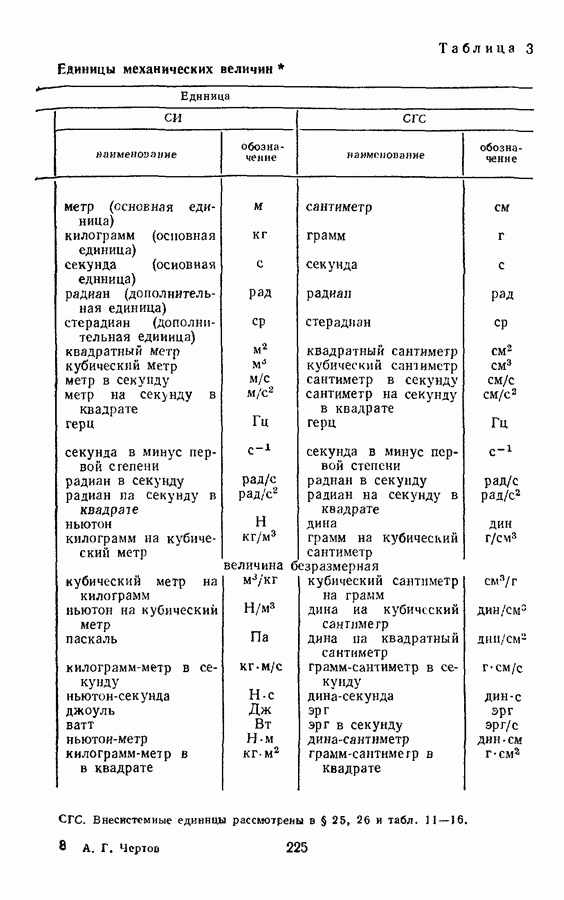
- § 7. ПРОИЗВОДНЫЕ ЕДИНИЦЫ МЕХАНИЧЕСКИХ ВЕЛИЧИН
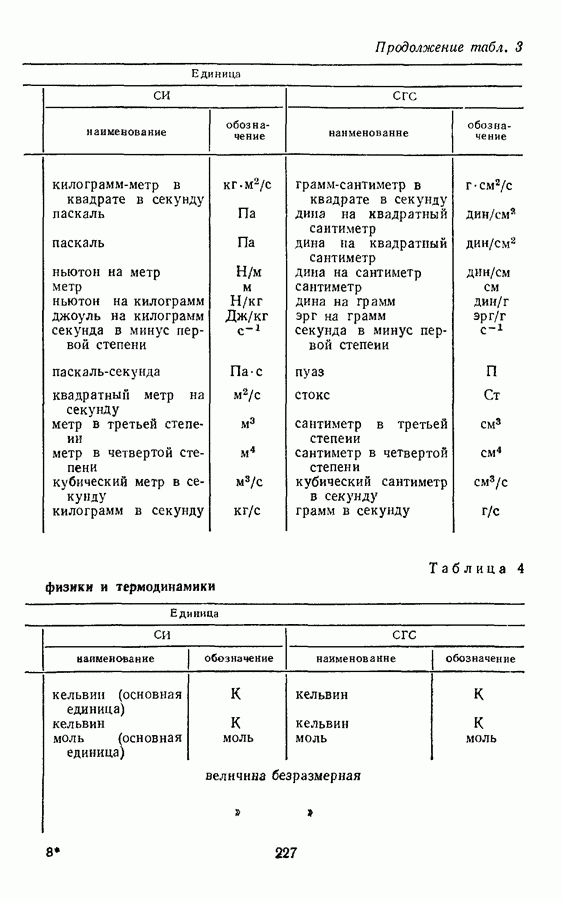
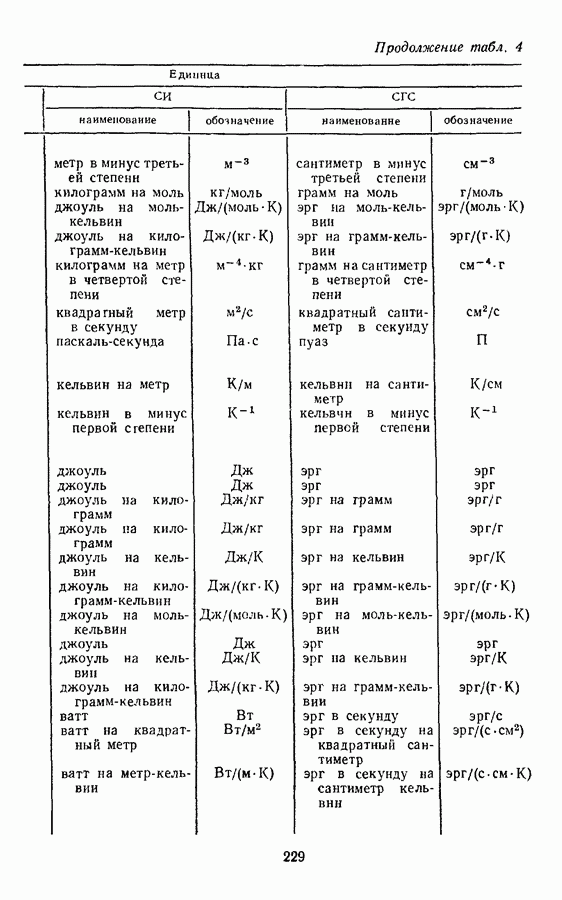
- § 8. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ
- § 9. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ЭЛЕНТРИЧЕСКИХ И МАГНИТНЫХ ВЕЛИЧИН
- § 10. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН, ХАРАКТЕРИЗУЮЩИХ КОЛЕБАНИЯ И ВОЛНЫ
- § 11. ПРОИЗВОДНЫЕ ЕДИНИЦЫ АКУСТИЧЕСКИХ ВЕЛИЧИН
- § 12. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ОПТИЧЕСКИХ ВЕЛИЧИН
- § 13. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН АТОМНОЙ И ЯДЕРНОЙ ФИЗИКИ
- § 14. ОПРЕДЕЛЕНИЯ И ЭТАЛОНЫ ОСНОВНЫХ И ДОПОЛНИТЕЛЬНЫХ ЕДИНИЦ СИ
- § 15. РАЦИОНАЛИЗАЦИЯ УРАВНЕНИЙ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- Глава III. СИСТЕМА СГС
- § 17. ПРОИЗВОДНЫЕ ЕДИНИЦЫ МЕХАНИЧЕСКИХ ВЕЛИЧИН В СИСТЕМЕ СГС
- § 18. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ В СИСТЕМЕ СГС
- § 19. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ВЕЛИЧИН В СИСТЕМЕ СГС
- § 20. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН, ХАРАКТЕРИЗУЮЩИХ КОЛЕБАНИЯ И ВОЛНЫ В СИСТЕМЕ СГС
- § 21. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ОПТИЧЕСНИХ ВЕЛИЧИН В СИСТЕМЕ СГС
- § 22. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН АТОМНОЙ И ЯДЕРНОЙ ФИЗИКИ В СИСТЕМЕ СГС
- Глава IV. ВНЕСИСТЕМНЫЕ ЕДИНИЦЫ
- § 23. КРАТНЫЕ И ДОЛЬНЫЕ ЕДИНИЦЫ
- § 24. ОТНОСИТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ ЕДИНИЦЫ
- § 25. СПЕЦИАЛЬНЫЕ ЕДИНИЦЫ
- § 26. КРАТКИЕ СВЕДЕНИЯ О НАИБОЛЕЕ ИЗВЕСТНЫХ ВНЕСИСТЕМНЫХ ЕДИНИЦАХ
- § 27. ОПРЕДЕЛЕНИЕ ЧИСЛОВЫХ КОЭФФИЦИЕНТОВ В ФОРМУЛАХ ПРИ ПЕРЕХОДЕ К СИ
- § 28. СООТНОШЕНИЯ ЕДИНИЦ МЕЖДУНАРОДНОЙ СИСТЕМЫ С ЕДИНИЦАМИ СИСТЕМЫ СГС И ВНЕСИСТЕМНЫМИ ЕДИНИЦАМИ