| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Системы физических величин. Основные и производные величины
Между физическими величинами существуют связи и зависимости, выражаемые математическими соотношениями и формулами. Эти формулы и соотношения могут представлять собой какой-нибудь закон природы, как, например, второй закон Ньютона:

или определение некоторой физической величины, как, например, напряженности электрического поля:

или, наконец, установленное экспериментально или теоретически соотношение между несколькими физическими величинами.
В приведенных примерах одна величина связана с двумя другими.
В общем же случае физическая величина  при помощи математических действий может быть выражена через другие физические величины
при помощи математических действий может быть выражена через другие физические величины  уравнением вида
уравнением вида

где  коэффициент пропорциональности.
коэффициент пропорциональности.
Формулы вида (1.4), выражающие одни физические величины через другие, называются уравнениями между физическими величинами.
Коэффициент пропорциональности  в уравнениях между физическими величинами, за редким исключением, равен единице. Поэтому подавляющее большинство уравнений между физическими величинами имеет вид
в уравнениях между физическими величинами, за редким исключением, равен единице. Поэтому подавляющее большинство уравнений между физическими величинами имеет вид

В качестве примера уравнения, в котором коэффициент  отличен от единицы, приведем формулу кинетической энергии тела при поступательном движении:
отличен от единицы, приведем формулу кинетической энергии тела при поступательном движении:

где  масса тела,
масса тела,  его скорость.
его скорость.
Значение коэффициента пропорциональности как в формуле (1.6), так и вообще в уравнениях между величинами не зависит от выбора единиц, а определяется исключительно характером связи величин, входящих в данное уравнение. Независимость коэффициента пропорциональности
от выбора единиц является характерной особенностью уравнений между величинами.
Отметим, что под символами a, b, c, ... в уравнении между величинами (1.4) или (1.5) нельзя понимать числовые значения величин, выраженных в заранее выбранных единицах. Каждый из символов a, b, c, ... в этом уравнении представляет собой просто одну из конкретных реализаций соответствующей величины.
Изучение связей между величинами показало, что эти связи не являются случайными и частными, а имеют весьма широкий, можно сказать, общий характер. В частности, было установлено, что если произвольно выбрать несколько физических величин, условно приняв их независимыми друг от друга, а также от других величин, то все остальные величины одного или нескольких разделов физики могут быть выражены через эти произвольно выбранные величины. При этом величины, выбранные произвольно, и величины, выраженные через них, образуют систему большого числа связанных между собой величин.
Совокупность физических величин, связанных между собой зависимостями, называют системой величин.
Физические величины, входящие в систему и условно принятые в качестве независимых от других величин системы, носят название основных величин системы.
Физические величины, входящие в систему и определяемые через основные величины этой системы, называются производными величинами системы.
Число основных величин системы в принципе может быть любым. Однако опыт показал, что для каждой системы число основных величин должно быть вполне определенным, чтобы система была наиболее удобной. Так, систему величии механики целесообразно строить на трех основных величинах, систему тепловых величин — на четырех, систему величин молекулярной физики — на пяти основных величинах и т. д. Система величин, охватывающая все разделы физики, может быть построена на семи основных величинах.
Выбор основных величин системы является произвольным, однако разумно выбрать величины, характеризующие коренные свойства материального мира. В качестве основных величин при построении различных систем были выбраны величины: длина, масса, время, сила, сила электрического тока, термодинамическая температура, количество вещества, сила света.
Каждой основной величине присвоен символ в виде прописной (заглавной) буквы латинского или греческого алфавита, называемый размерностью основной физической величины. Размерности эти следующие:

Символы основных величин данной системы образуют ее обозначение. Так, система величин механики, основными величинами которой являются длина, масса, время, получила обозначение  Система величин механики, в основе которой лежат величины — длина, сила, время, обозначается
Система величин механики, в основе которой лежат величины — длина, сила, время, обозначается  Система величин механики и электричества строится на четырех основных величинах: первые три — длина, масса, время; четвертой является одна из электрических величин — сила тока, электрический заряд, электрическое сопротивление и т. д. Наиболее удобной величиной оказалась сила тока, поэтому система величин механики и электричества обозначается
Система величин механики и электричества строится на четырех основных величинах: первые три — длина, масса, время; четвертой является одна из электрических величин — сила тока, электрический заряд, электрическое сопротивление и т. д. Наиболее удобной величиной оказалась сила тока, поэтому система величин механики и электричества обозначается 
Однако можно построить систему электрических величин и на трех основных величинах механики — длина, масса, время. Но в этом случае одна из электрических или магнитных величин должна быть положена безразмерной (см. с. 18). Так, полагая безразмерной абсолютную диэлектрическую проницаемость, получают электростатическую систему величин LMT, полагая безразмерной абсолютную магнитную проницаемость, получают электромагнитную систему величин 
Система величин механики и тепловых величин строится на четырех основных величинах - длина, масса, время, термодинамическая температура и поэтому обозначается 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ОБЩИЕ ВОПРОСЫ ВЫБОРА ЕДИНИЦ И ПОСТРОЕНИЯ СИСТЕМ ЕДИНИЦ
- § 1. ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ. СИСТЕМЫ ФИЗИЧЕСКИХ ВЕЛИЧИН
- Системы физических величин. Основные и производные величины
- § 2. РАЗМЕРНОСТИ ПРОИЗВОДНЫХ ФИЗИЧЕСКИХ ВЕЛИЧИН
- § 3. ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН, РАЗМЕР ЕДИНИЦ
- § 4. СИСТЕМЫ ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН
- § 5. НАИМЕНОВАНИЯ И ОБОЗНАЧЕНИЯ ЕДИНИЦ
- Глава II. МЕЖДУНАРОДНАЯ СИСТЕМА ЕДИНИЦ (СИ)
- § 6. ОСНОВНЫЕ, ДОПОЛНИТЕЛЬНЫЕ И ПРОИЗВОДНЫЕ ЕДИНИЦЫ СИСТЕМЫ
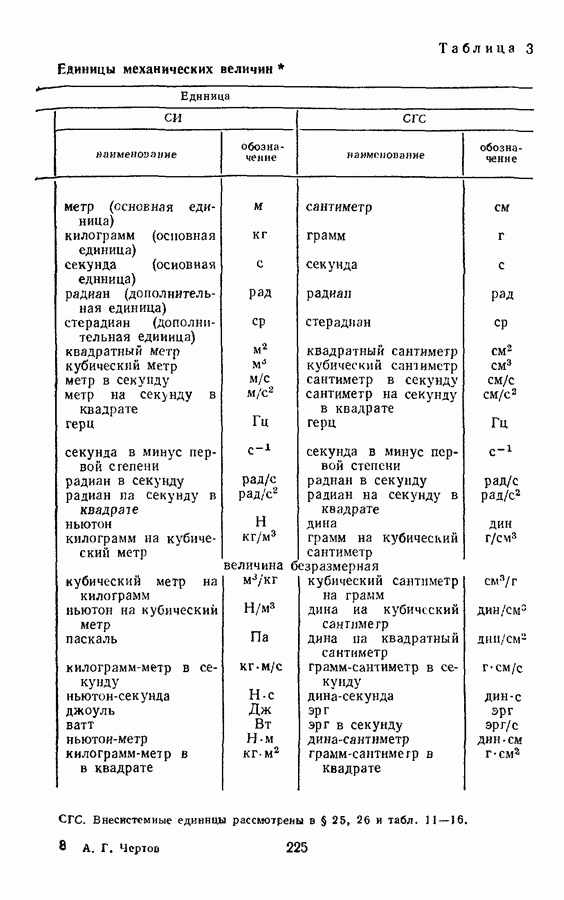
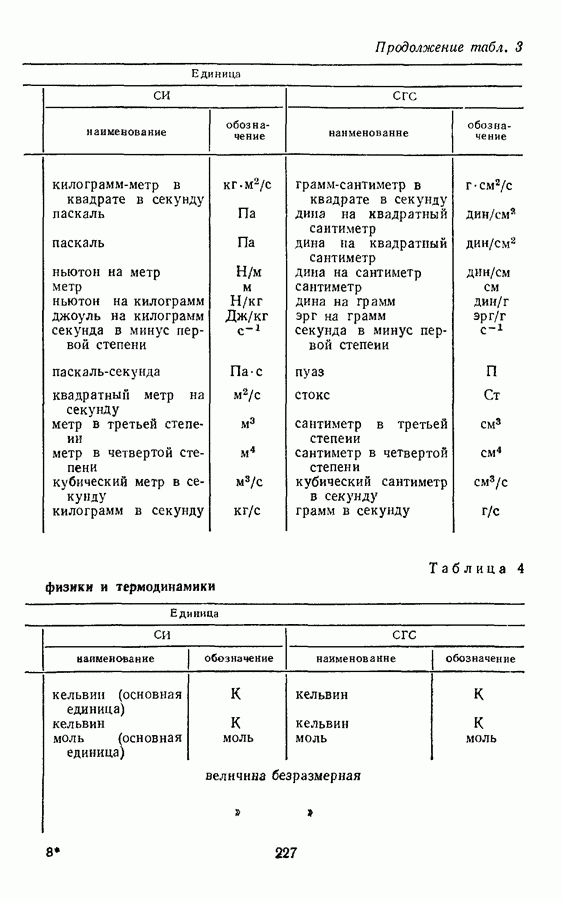
- § 7. ПРОИЗВОДНЫЕ ЕДИНИЦЫ МЕХАНИЧЕСКИХ ВЕЛИЧИН
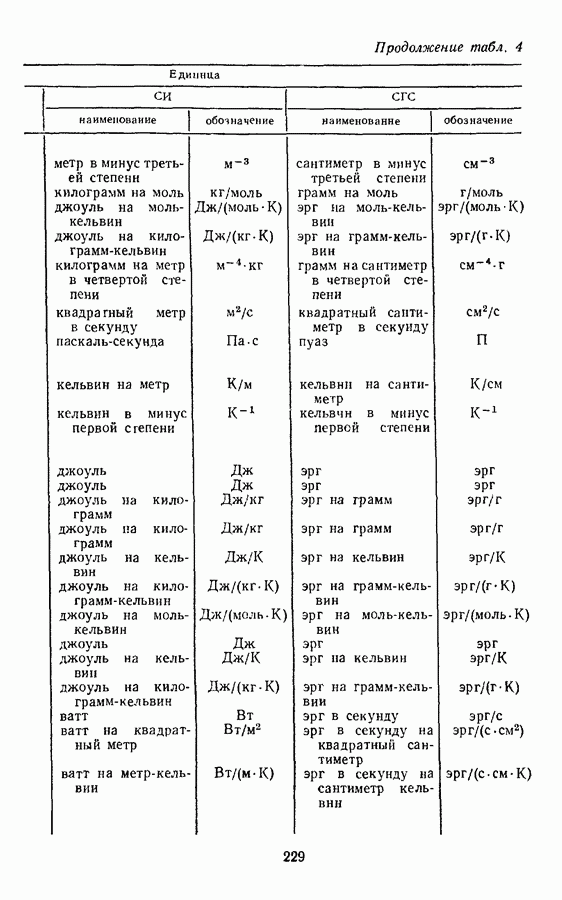
- § 8. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ
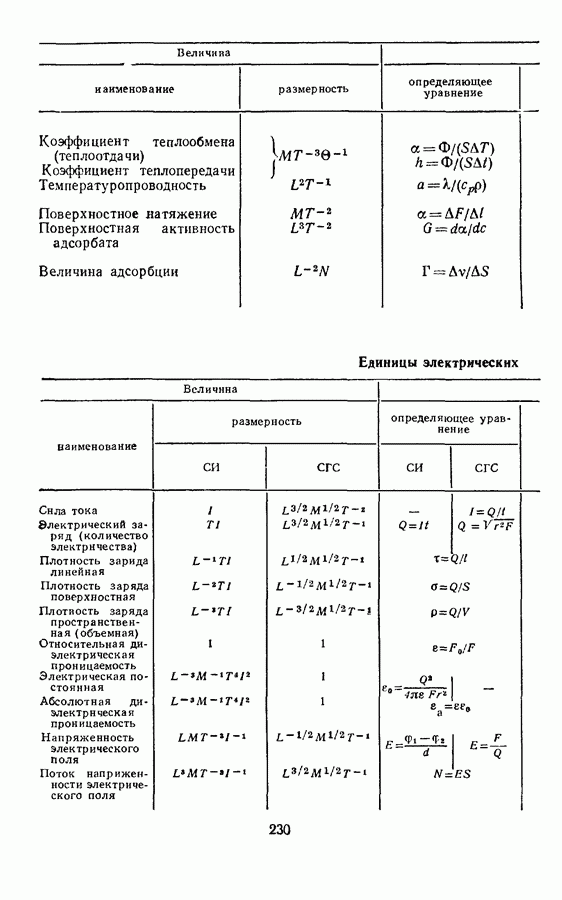
- § 9. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ЭЛЕНТРИЧЕСКИХ И МАГНИТНЫХ ВЕЛИЧИН
- § 10. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН, ХАРАКТЕРИЗУЮЩИХ КОЛЕБАНИЯ И ВОЛНЫ
- § 11. ПРОИЗВОДНЫЕ ЕДИНИЦЫ АКУСТИЧЕСКИХ ВЕЛИЧИН
- § 12. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ОПТИЧЕСКИХ ВЕЛИЧИН
- § 13. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН АТОМНОЙ И ЯДЕРНОЙ ФИЗИКИ
- § 14. ОПРЕДЕЛЕНИЯ И ЭТАЛОНЫ ОСНОВНЫХ И ДОПОЛНИТЕЛЬНЫХ ЕДИНИЦ СИ
- § 15. РАЦИОНАЛИЗАЦИЯ УРАВНЕНИЙ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- Глава III. СИСТЕМА СГС
- § 17. ПРОИЗВОДНЫЕ ЕДИНИЦЫ МЕХАНИЧЕСКИХ ВЕЛИЧИН В СИСТЕМЕ СГС
- § 18. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ В СИСТЕМЕ СГС
- § 19. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ВЕЛИЧИН В СИСТЕМЕ СГС
- § 20. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН, ХАРАКТЕРИЗУЮЩИХ КОЛЕБАНИЯ И ВОЛНЫ В СИСТЕМЕ СГС
- § 21. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ОПТИЧЕСНИХ ВЕЛИЧИН В СИСТЕМЕ СГС
- § 22. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН АТОМНОЙ И ЯДЕРНОЙ ФИЗИКИ В СИСТЕМЕ СГС
- Глава IV. ВНЕСИСТЕМНЫЕ ЕДИНИЦЫ
- § 23. КРАТНЫЕ И ДОЛЬНЫЕ ЕДИНИЦЫ
- § 24. ОТНОСИТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ ЕДИНИЦЫ
- § 25. СПЕЦИАЛЬНЫЕ ЕДИНИЦЫ
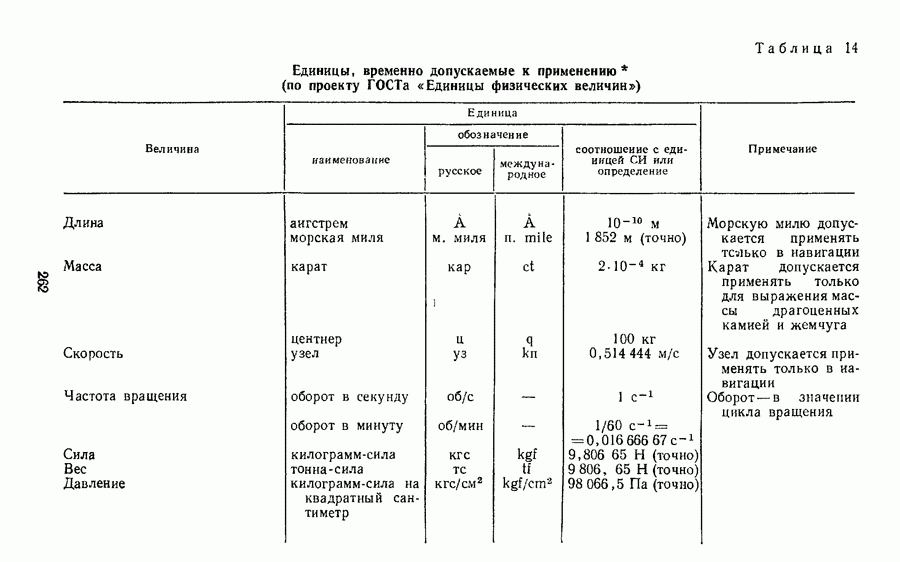
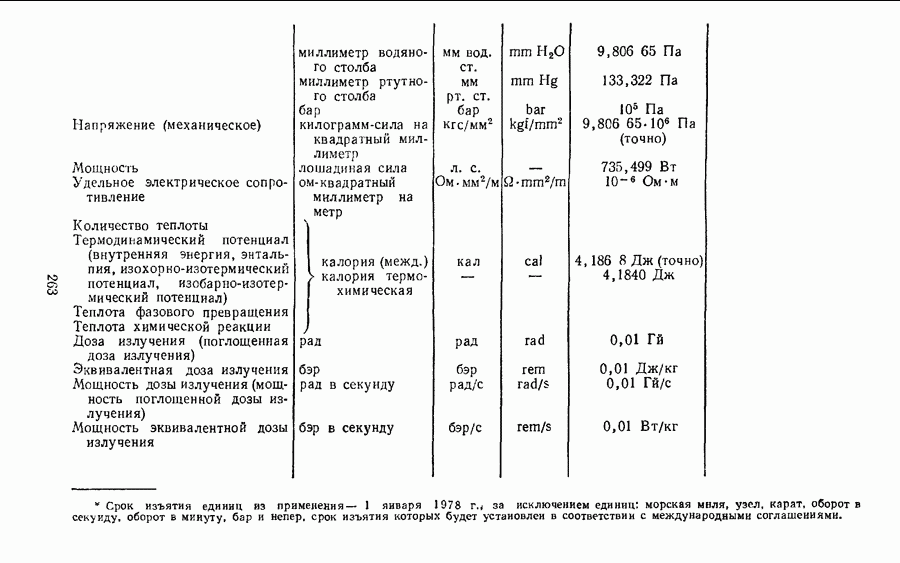
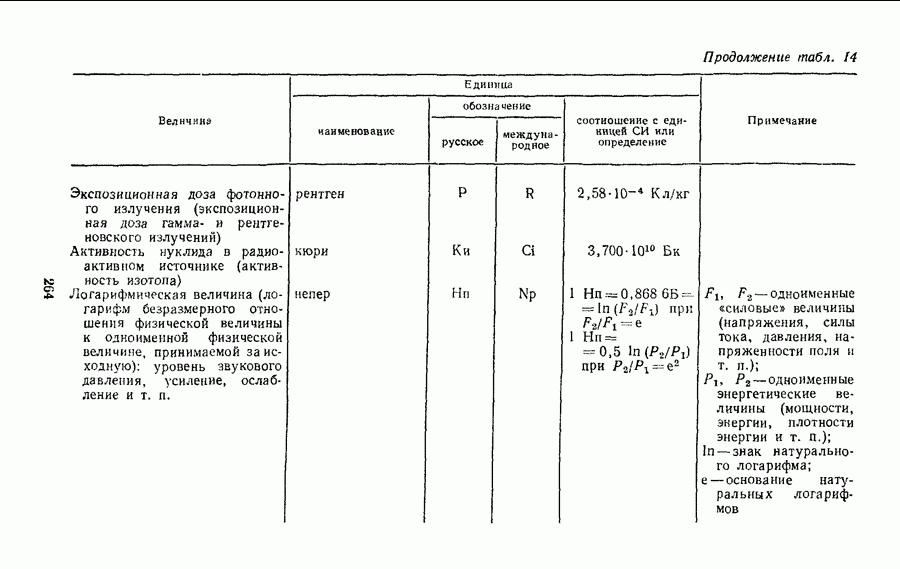
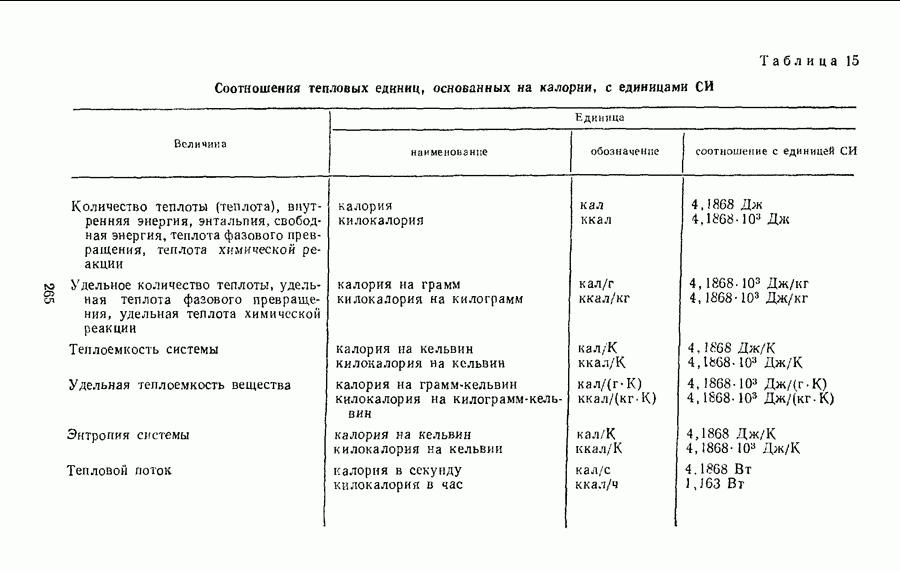
- § 26. КРАТКИЕ СВЕДЕНИЯ О НАИБОЛЕЕ ИЗВЕСТНЫХ ВНЕСИСТЕМНЫХ ЕДИНИЦАХ
- § 27. ОПРЕДЕЛЕНИЕ ЧИСЛОВЫХ КОЭФФИЦИЕНТОВ В ФОРМУЛАХ ПРИ ПЕРЕХОДЕ К СИ
- § 28. СООТНОШЕНИЯ ЕДИНИЦ МЕЖДУНАРОДНОЙ СИСТЕМЫ С ЕДИНИЦАМИ СИСТЕМЫ СГС И ВНЕСИСТЕМНЫМИ ЕДИНИЦАМИ