| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. РАЗМЕРНОСТИ ПРОИЗВОДНЫХ ФИЗИЧЕСКИХ ВЕЛИЧИН
Производные величины, как было указано в § 1, можно выразить через основные. Для этого необходимо ввести два понятия: размерность производной величины и определяющее уравнение.
Размерностью физической величины называют выражение, отражающее связь величины с основными величинами
системы, в котором коэффициент пропорциональности принят равным единице.
Определяющим уравнением производной величины называют формулу, посредством которой физическая величина может быть в явном виде выражена через другие величины системы. При этом коэффициент пропорциональности в данной формуле должен быть равным единице. Например, определяющим уравнением скорости является формула

где  длина пути, пройденного телом при равномерном движении за время
длина пути, пройденного телом при равномерном движении за время  Определяющее уравнение силы
Определяющее уравнение силы  в системе
в системе  второй закон динамики поступательного движения (второй закон Ньютона):
второй закон динамики поступательного движения (второй закон Ньютона):

где а — ускорение, сообщаемое силой  телу массой
телу массой 
Найдем размерности некоторых производных величин механики в системе  Заметим, что начать необходимо с таких величин, которые в явном виде выражаются только через основные величины системы. Такими величинами являются, например, скорость, площадь, объем.
Заметим, что начать необходимо с таких величин, которые в явном виде выражаются только через основные величины системы. Такими величинами являются, например, скорость, площадь, объем.
Чтобы найти размерность скорости, подставим в формулу (2.1) вместо длины пути  и времени
и времени  их размерности
их размерности  и Т:
и Т:

Условимся обозначать размерность величины символом  Тогда размерность скорости запишется в виде
Тогда размерность скорости запишется в виде

Определяющими уравнениями площади и объема являются формулы:

где а — длина стороны квадрата,  длина ребра куба. Подставив вместо
длина ребра куба. Подставив вместо  размерность
размерность  найдем размерности площади и объема:
найдем размерности площади и объема:

Найти же размерность силы  по ее определяющему уравнению (2.2) было бы затруднительно, так как нам неизвестна размерность ускорения а. Прежде чем определять размерность силы, надо найти размерность ускорения,
по ее определяющему уравнению (2.2) было бы затруднительно, так как нам неизвестна размерность ускорения а. Прежде чем определять размерность силы, надо найти размерность ускорения,
используя формулу ускорения равнопеременного движения:

где  изменение скорости тела за время
изменение скорости тела за время 
Подставив сюда уже известные нам размерности скорости и времени, получим

Теперь по формуле (2.2) найдем размерность силы:

Точно так же для получения размерности мощности  по ее определяющему уравнению
по ее определяющему уравнению  где А — работа, совершенная за время
где А — работа, совершенная за время  необходимо предварительно найти размерность работы.
необходимо предварительно найти размерность работы.
Из приведенных примеров следует, что не безразлично, в какой последовательности надо расположить определяющие уравнения при построении данной системы величин, т. е. при установлении размерностей производных величин.
Последовательность расположения производных величин при построении системы должна удовлетворять следующим условиям: 1) первой должна быть величина, которая выражается только через основные величины; 2) каждая последующая должна быть величиной, которая выражается только через основные и такие производные, которые ей предшествуют.
В качестве примера приведем в таблице последовательность величин, которая удовлетворяет таким условиям:
(см. скан)
Последовательность величин, приведенная в таблице, не является единственной, удовлетворяющей указанному выше условию. Отдельные величины в таблице могут быть переставлены. Например, плотность (строка 5) и момент инерции (строка 4) или момент силы (строка 11) и давление (строка 12) можно поменять местами, так как размерности этих величин определяются независимо друг от друга.
Но плотность в этой последовательности нельзя поставить раньше объема (строка 2), так как плотность выражается через объем и для определения ее размерности необходимо знать размерность объема. Момент силы, давление и работа (строка 13) не могут быть поставлены раньше силы, так как для определения их размерности надо знать размерность силы.
Из приведенной таблицы следует, что размерность любой физической величины  в системе
в системе  в общем виде может быть выражена равенством
в общем виде может быть выражена равенством

где  целые числа.
целые числа.
В системе величин механики  размерность величины выразится в общем виде формулой
размерность величины выразится в общем виде формулой

Приведем в общем виде формулы размерности соответственно в системах величин:  в электростатической и электромагнитной LMT, в
в электростатической и электромагнитной LMT, в  и в любой системе с числом основных величин больше трех:
и в любой системе с числом основных величин больше трех:

Из формул (2.5) — (2.10) следует, что размерность величины представляет собой произведение размерностей основных величин, возведенных в соответствующие степени.
Показатель степени  в которую возведена размерность основной величины, входящая в размерность производной величины, называется показателем размерности физической величины. Как правило, показатели размерности являются целыми числами. Исключение составляют показатели в электростатической и
в которую возведена размерность основной величины, входящая в размерность производной величины, называется показателем размерности физической величины. Как правило, показатели размерности являются целыми числами. Исключение составляют показатели в электростатической и
электромагнитной системах LMT, в которых они могут быть и дробными.
Некоторые показатели размерности могут оказаться равными нулю. Так, записав размерности скорости и момента инерции в системе  в виде
в виде

находим, что у скорости равен нулю показатель размерности  момента инерции — показатель размерности у.
момента инерции — показатель размерности у.
Может оказаться, что все показатели размерности некоторой величины равны нулю. Такая величина называется безразмерной. Безразмерными величинами являются, например, относительная деформация, относительная диэлектрическая проницаемость.
Величина называется размерной, если в ее размерности хотя бы одна из основных величин возведена в степень, не равную нулю.
Конечно, размерности одной и той же величины в различных системах могут оказаться разными. В частности, величина безразмерная в одной системе может оказаться размерной в другой системе. Например, абсолютная диэлектрическая проницаемость в электростатической системе  является безразмерной величииой, в электромагнитной системе
является безразмерной величииой, в электромагнитной системе  ее размерность равна
ее размерность равна  а в системе величин
а в системе величин 
Эти примеры показывают, что размерность не есть нечто абсолютное. Понятие размерности есть понятие относительное, поэтому об определенных размерностях физических величин можно говорить, только оставаясь в рамках одной системы величин.
Однако это не мешает использованию размерностей как эффективного средства исследования ряда вопросов метрического характера. Остановимся кратко на некоторых из них.
1. Размерность позволяет определить, как изменяется размер производной величины при изменении размеров основных величин. Если размерность величины  равна
равна  и длина изменяется от
и длина изменяется от  до
до  масса — от
масса — от  до
до  и время — от
и время — от  до
до  то новый размер величины будет больше прежнего в
то новый размер величины будет больше прежнего в  раз, т. е.
раз, т. е.

Пример. Определим, как изменится момент инерции системы с увеличением линейных размеров в 2 раза и массы в 3 раза.
Равномерность момента инерции

Пользуясь формулой (2.11), получим

Следовательно, момент инерции увеличится в 12 раз.
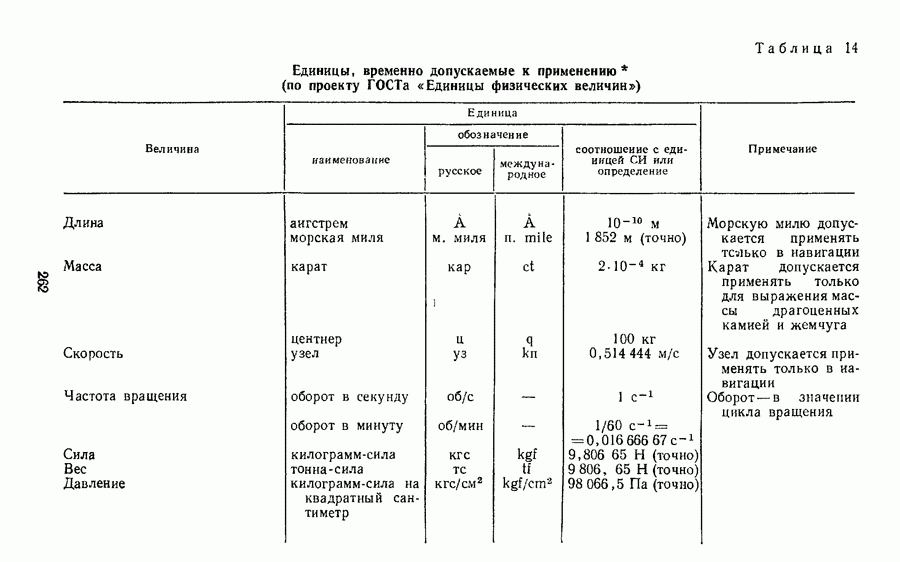
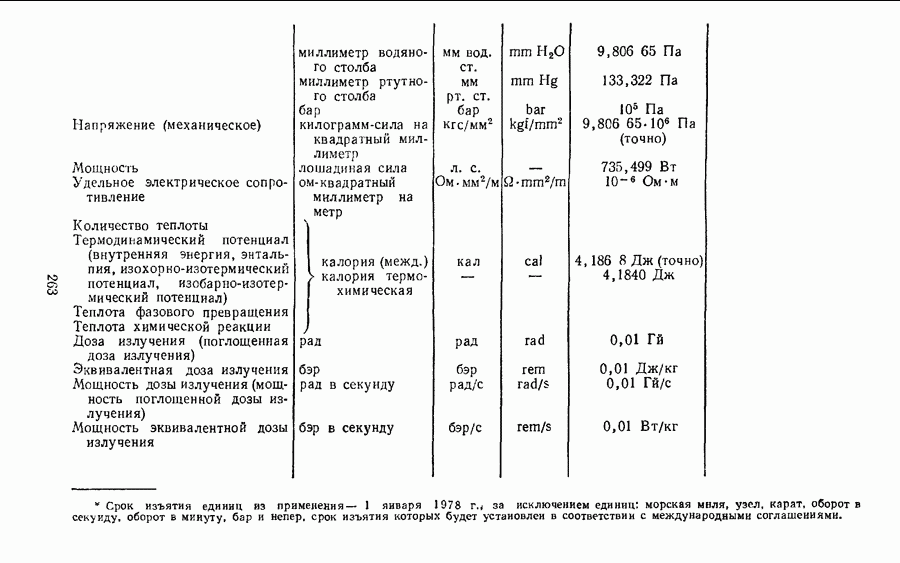
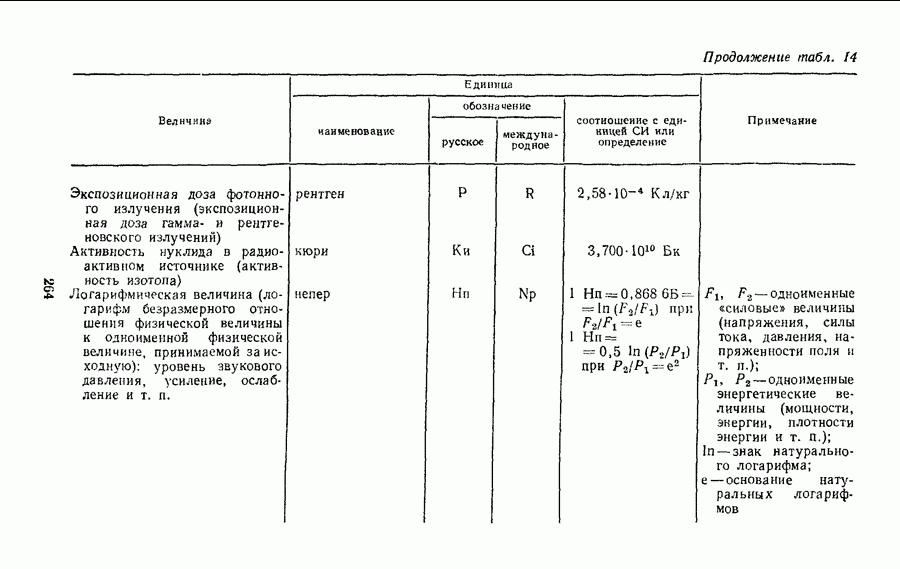
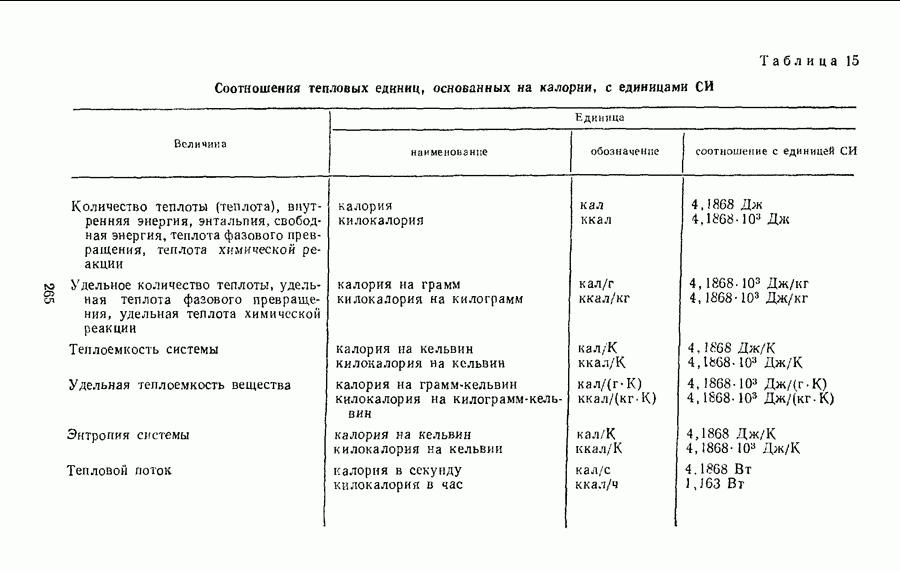
2. Пользуясь размерностями физических величин, можно определить, как изменится размер производной единицы с изменением размеров основных единиц, через которые она выражается, а также установить соотношение единиц в разных системах (см. с. 216).
3. Размерности физических величин позволяют обнаружить ошибки при решении физических задач.
Получив в результате решения расчетную формулу, следует проверить, совпадают ли размерности левой и правой частей формулы. Несовпадение этих размерностей свидетельствует о том, что в ходе решения задачи была допущена ошибка. Конечно, совпадение размерностей еще не означает, что задача решена правильно.
Рассмотрение других практических приложений размерностей выходит за рамки настоящего пособия.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ОБЩИЕ ВОПРОСЫ ВЫБОРА ЕДИНИЦ И ПОСТРОЕНИЯ СИСТЕМ ЕДИНИЦ
- § 1. ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ. СИСТЕМЫ ФИЗИЧЕСКИХ ВЕЛИЧИН
- Системы физических величин. Основные и производные величины
- § 2. РАЗМЕРНОСТИ ПРОИЗВОДНЫХ ФИЗИЧЕСКИХ ВЕЛИЧИН
- § 3. ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН, РАЗМЕР ЕДИНИЦ
- § 4. СИСТЕМЫ ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН
- § 5. НАИМЕНОВАНИЯ И ОБОЗНАЧЕНИЯ ЕДИНИЦ
- Глава II. МЕЖДУНАРОДНАЯ СИСТЕМА ЕДИНИЦ (СИ)
- § 6. ОСНОВНЫЕ, ДОПОЛНИТЕЛЬНЫЕ И ПРОИЗВОДНЫЕ ЕДИНИЦЫ СИСТЕМЫ
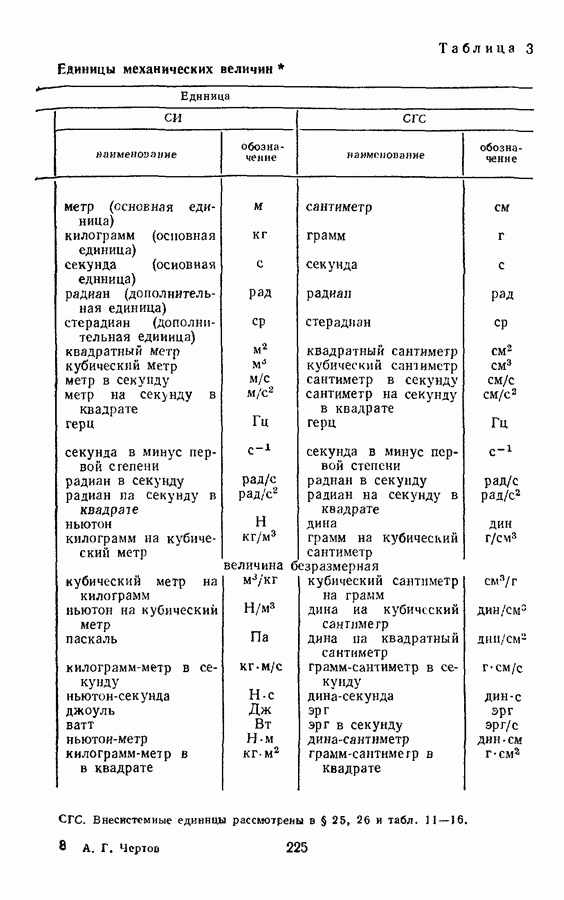
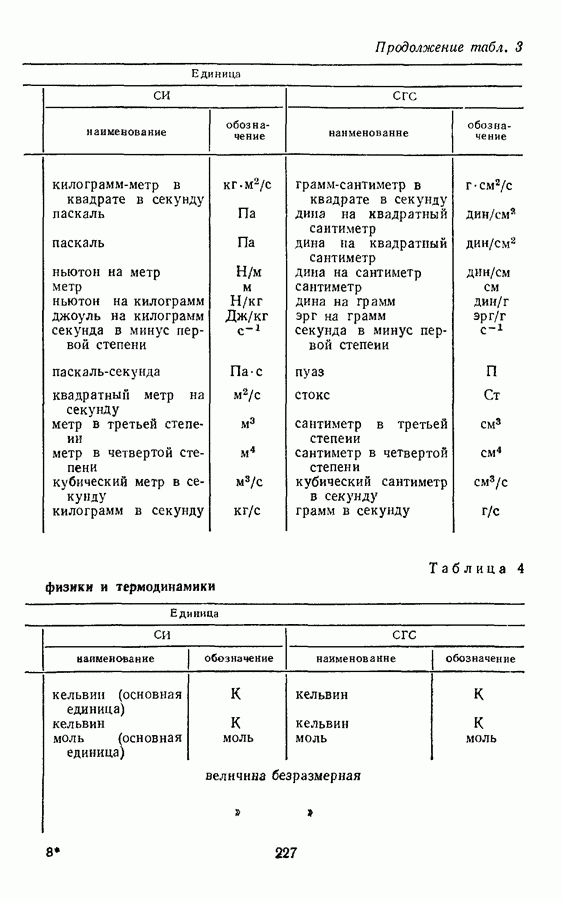
- § 7. ПРОИЗВОДНЫЕ ЕДИНИЦЫ МЕХАНИЧЕСКИХ ВЕЛИЧИН
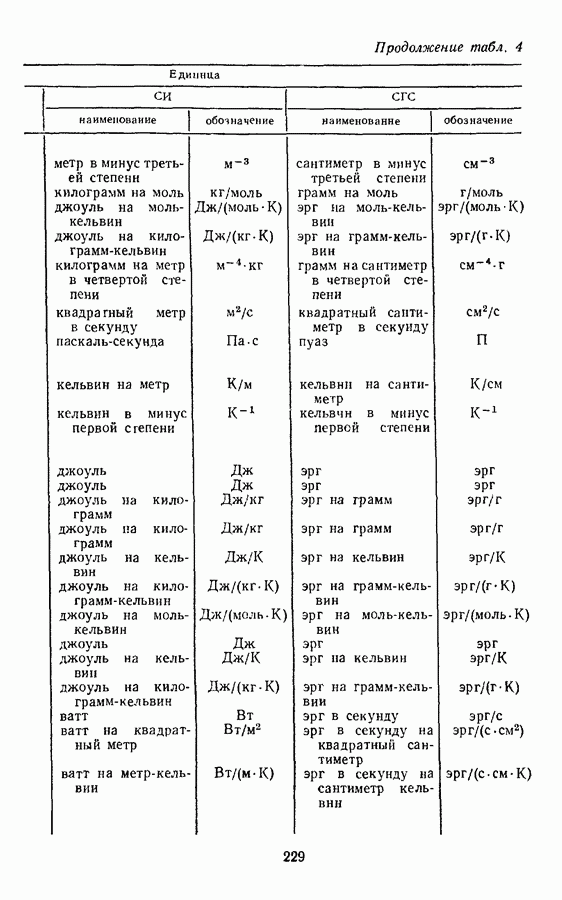
- § 8. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ
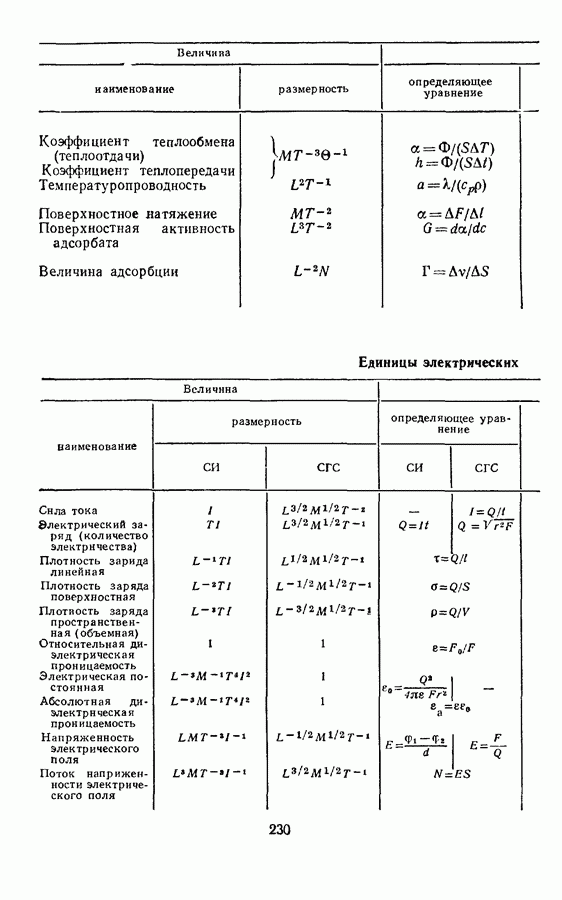
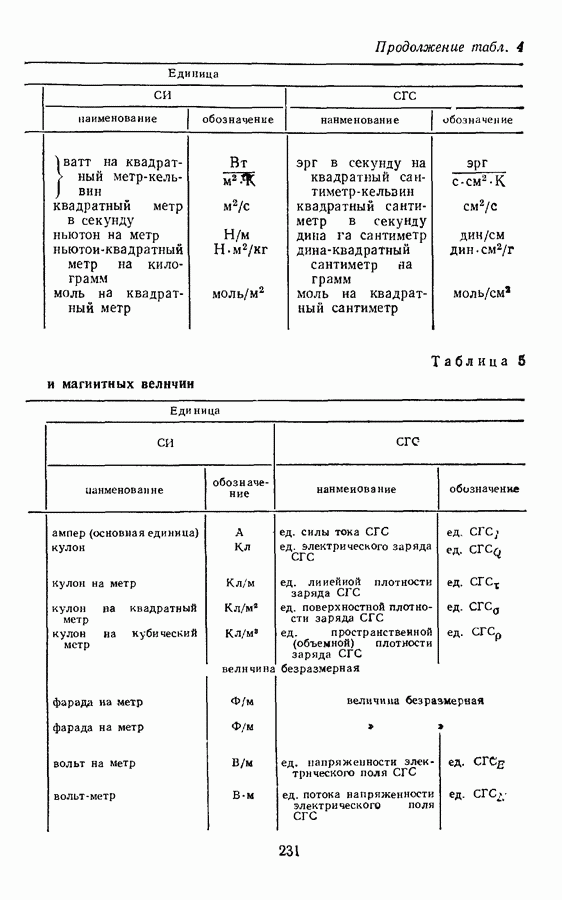
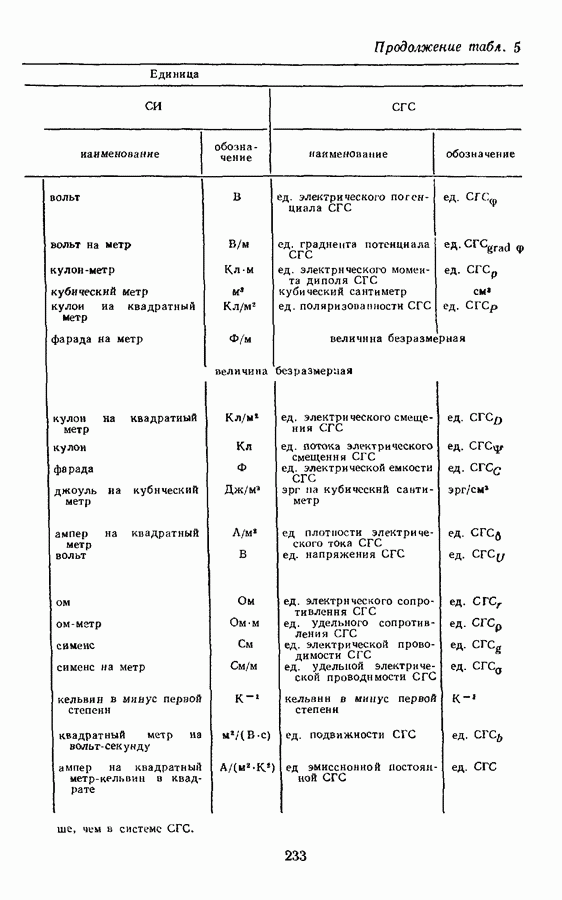
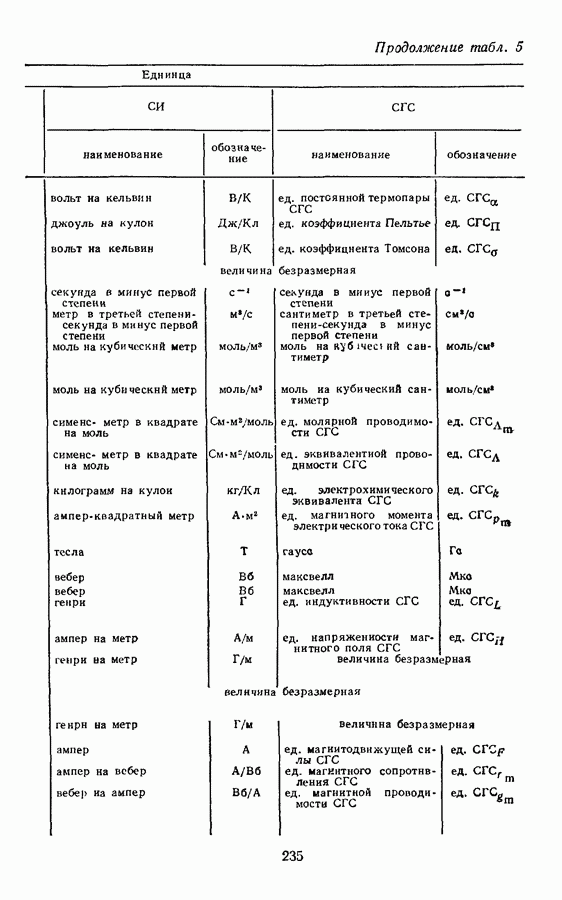
- § 9. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ЭЛЕНТРИЧЕСКИХ И МАГНИТНЫХ ВЕЛИЧИН
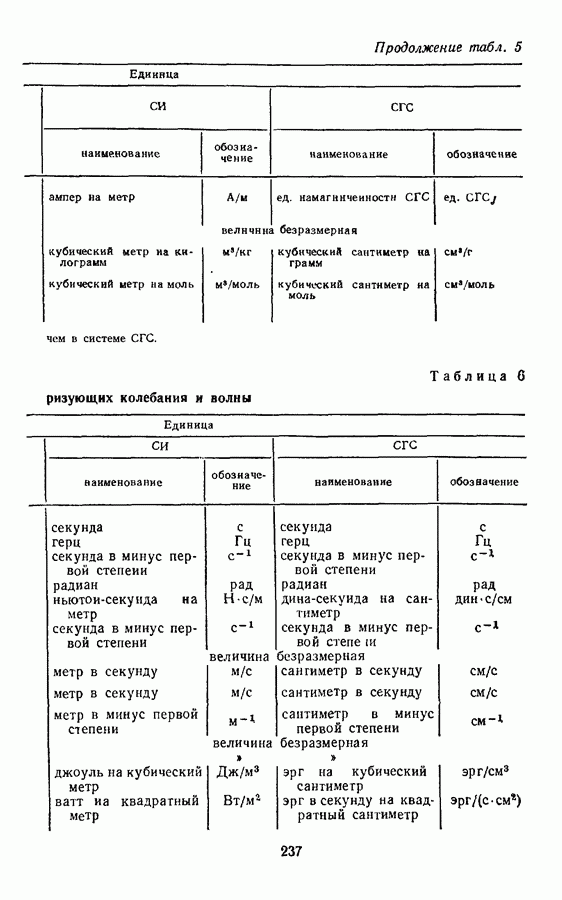
- § 10. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН, ХАРАКТЕРИЗУЮЩИХ КОЛЕБАНИЯ И ВОЛНЫ
- § 11. ПРОИЗВОДНЫЕ ЕДИНИЦЫ АКУСТИЧЕСКИХ ВЕЛИЧИН
- § 12. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ОПТИЧЕСКИХ ВЕЛИЧИН
- § 13. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН АТОМНОЙ И ЯДЕРНОЙ ФИЗИКИ
- § 14. ОПРЕДЕЛЕНИЯ И ЭТАЛОНЫ ОСНОВНЫХ И ДОПОЛНИТЕЛЬНЫХ ЕДИНИЦ СИ
- § 15. РАЦИОНАЛИЗАЦИЯ УРАВНЕНИЙ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- Глава III. СИСТЕМА СГС
- § 17. ПРОИЗВОДНЫЕ ЕДИНИЦЫ МЕХАНИЧЕСКИХ ВЕЛИЧИН В СИСТЕМЕ СГС
- § 18. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ В СИСТЕМЕ СГС
- § 19. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ВЕЛИЧИН В СИСТЕМЕ СГС
- § 20. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН, ХАРАКТЕРИЗУЮЩИХ КОЛЕБАНИЯ И ВОЛНЫ В СИСТЕМЕ СГС
- § 21. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ОПТИЧЕСНИХ ВЕЛИЧИН В СИСТЕМЕ СГС
- § 22. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН АТОМНОЙ И ЯДЕРНОЙ ФИЗИКИ В СИСТЕМЕ СГС
- Глава IV. ВНЕСИСТЕМНЫЕ ЕДИНИЦЫ
- § 23. КРАТНЫЕ И ДОЛЬНЫЕ ЕДИНИЦЫ
- § 24. ОТНОСИТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ ЕДИНИЦЫ
- § 25. СПЕЦИАЛЬНЫЕ ЕДИНИЦЫ
- § 26. КРАТКИЕ СВЕДЕНИЯ О НАИБОЛЕЕ ИЗВЕСТНЫХ ВНЕСИСТЕМНЫХ ЕДИНИЦАХ
- § 27. ОПРЕДЕЛЕНИЕ ЧИСЛОВЫХ КОЭФФИЦИЕНТОВ В ФОРМУЛАХ ПРИ ПЕРЕХОДЕ К СИ
- § 28. СООТНОШЕНИЯ ЕДИНИЦ МЕЖДУНАРОДНОЙ СИСТЕМЫ С ЕДИНИЦАМИ СИСТЕМЫ СГС И ВНЕСИСТЕМНЫМИ ЕДИНИЦАМИ