| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
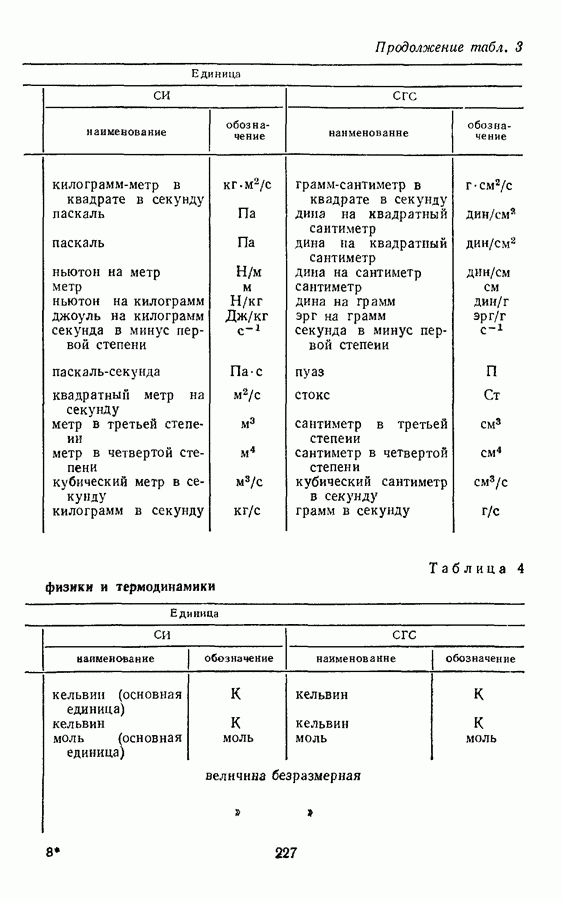
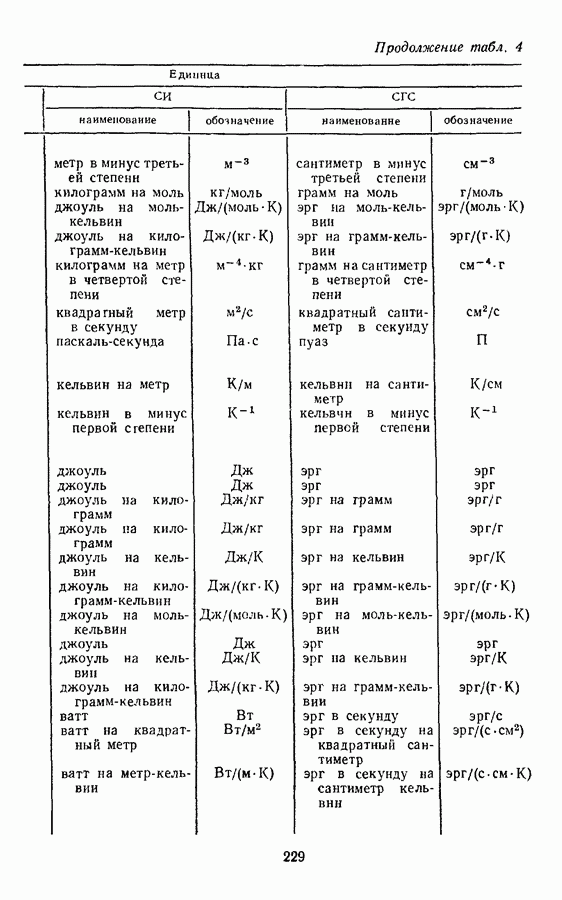
§ 18. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ В СИСТЕМЕ СГС
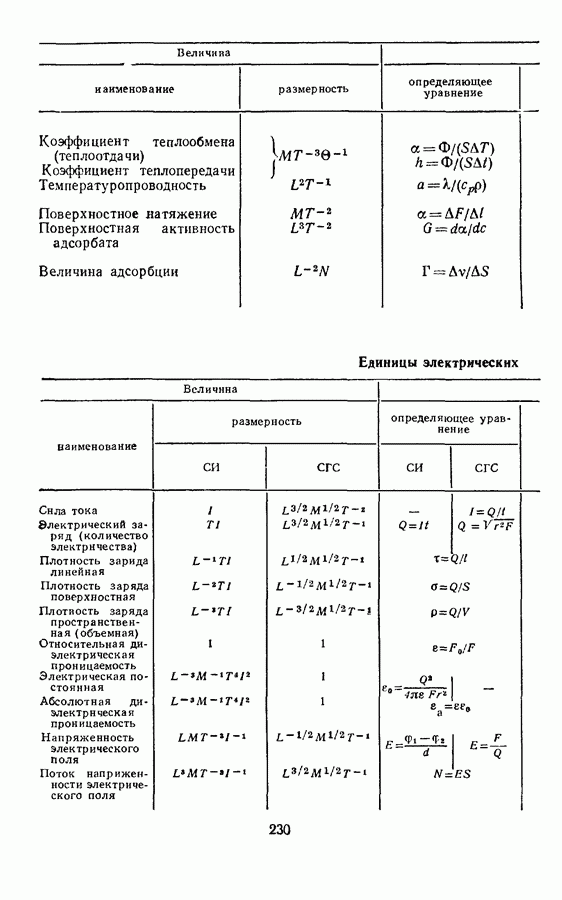
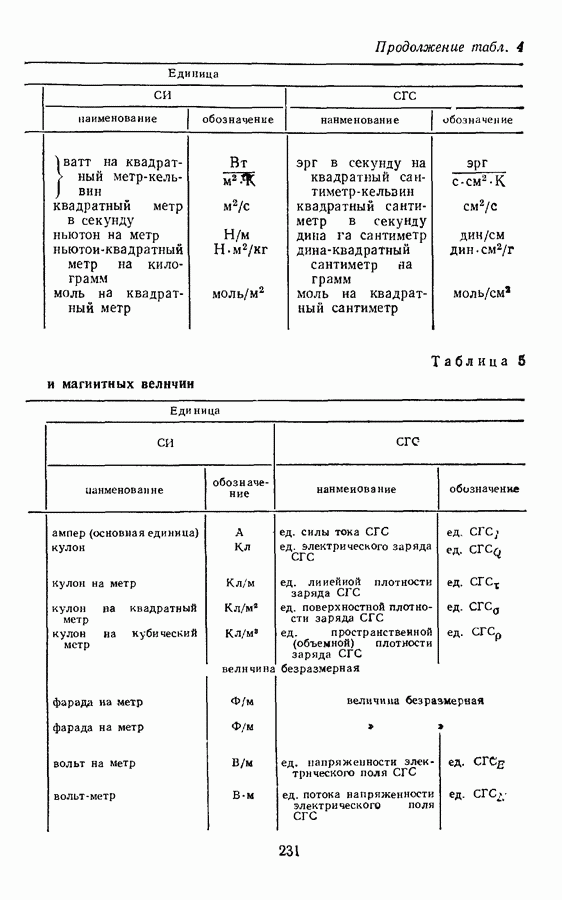
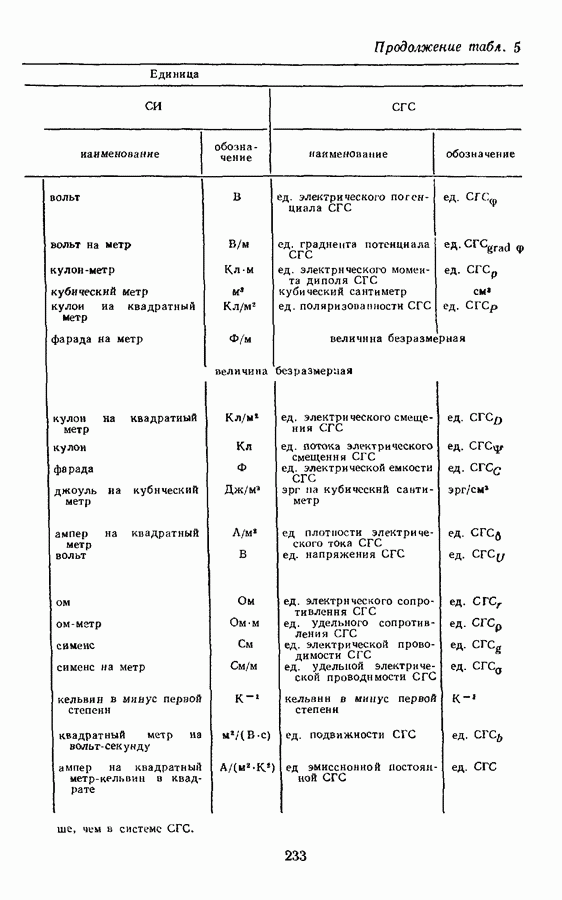
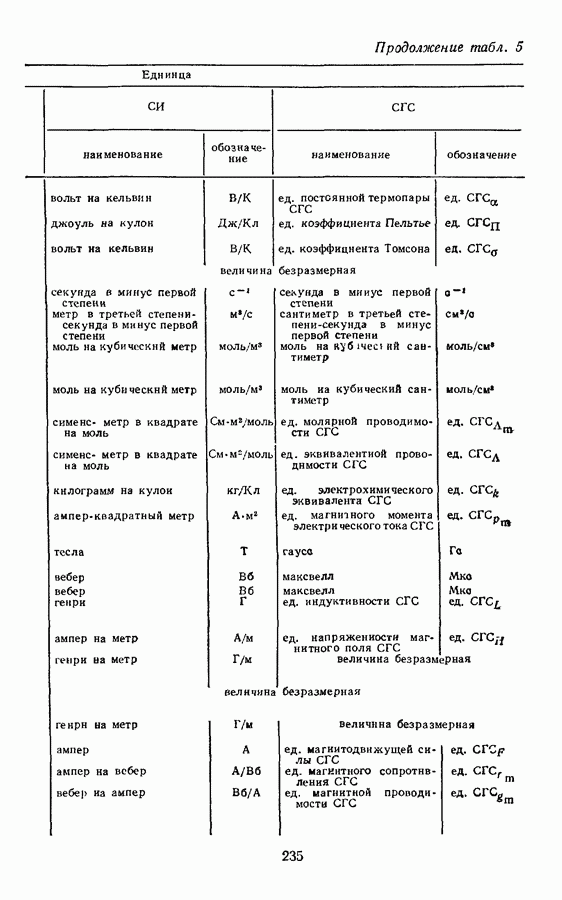
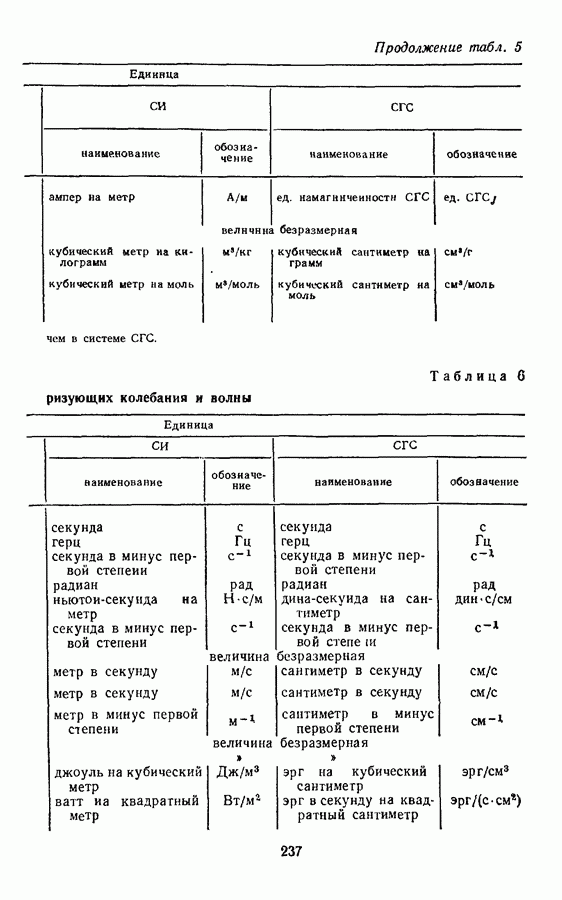
Производные величины молекулярной физики и термодинамики в системе СГС так же, как и в СИ, выражаются через пять основных величин: длину, массу, время, температуру и количество вещества, поэтому размерности этих величин такие же, как в СИ.
При получении производных единиц молекулярной физики будем пользоваться определяющими уравнениями и пояснениями к ним, помещенными в § 8.
Относительная атомная масса, относительная молекулярная масса и другие относительные величины так же, как и в СИ, выражаются в системе СГС в безразмерных единицах, поэтому здесь не рассматриваются. Читателю рекомендуется обратиться к § 8. Не рассматриваются здесь и единицы всех температурных коэффициентов, так как они выражаются в таких же единицах, как и в Международной системе.
Постоянная Аногадро. Единицу постоянной Авогадро получим, положив в формуле  моль:
моль:

Концентрация молекул. Положив в формуле  найдем единицу концентрации молекул:
найдем единицу концентрации молекул:

Установим соотношение этой единицы с соответствующей единицей 

Молярная масса. Подставив в формулу  моль, получим единицу молярной массы:
моль, получим единицу молярной массы:

Грамм на моль равен молярной массе вещества, имеющего при количестве вещества 1 моль массу 

Молярная газовая постоянная. Единицу молярной газовой постоянной найдем по формуле (8.6), положив в ней  моль,
моль, 

Градиент плотности. Единицу градиента плотности получим по формуле (8.10). Положив в этой формуле  см, найдем
см, найдем

Грамм на сантиметр в четвертой степени равен градиенту плотности среды, плотность которой на участке длиной I см в направлении градиента изменяется на 

Коэффициент диффузии. Положив в формуле  найдем единицу коэффициента диффузии
найдем единицу коэффициента диффузии

Квадратный сантиметр в секунду равен коэффициенту диффузии среды, в которой через площадку в  перпендикулярную градиенту плотности, равному
перпендикулярную градиенту плотности, равному  переносится в 1 с вещество массой
переносится в 1 с вещество массой 

Динамическая вязкость. Единицу динамической вязкости получим по формуле (8 15). Положив в ней  найдем
найдем

Эта единица называется пуаз  Определение пуаза и его соотношение с паскаль-секундой дано на с. 159.
Определение пуаза и его соотношение с паскаль-секундой дано на с. 159.
Градиент температуры. Из формулы (8.16) следует, что единицей градиента температуры является кельвин на сантиметр (К/см).
Кельвин на сантиметр равен температурному градиенту поля, в котором на участке длиной 1 см в направлении градиента температура изменяется на 1 К;

Внутренняя энергия. Внутренняя энергия, как и любая другая энергия, выражается в эргах (см. также с. 55):

Количество теплоты (теплота). Единицу количества теплоты найдем по формуле (8.21), положив в ней 

Удельное количество теплоты. Если в формуле (8.22) положим  то найдем
то найдем

Эрг на грамм равен удельному количеству теплоты (удельной теплоте) системы, в которой веществу массой 1 г сообщается (или отбирается от него) количество теплоты 1 эрг;

Теплоемкость системы. Единицу теплоемкости тела (системы тел) найдем, положив в формуле 

Эрг на кельвин равен теплоемкости системы, температура которой повышается на 1 К при подведении к системе количества теплоты 1 эрг;

Удельная теплоемкость. Положив в формуле  найдем единицу удельной теплоемкости:
найдем единицу удельной теплоемкости:

Эрг на грамм-кельвин равен удельной теплоемкости вещества, имеющего при массе  теплоемкость
теплоемкость 

Молярная теплоемкость. Единицу молярной теплоемкости найдем по формуле (8.28), подставив в ней 

Эрг на моль-кельвин равен молярной теплоемкости вещества, имеющего при количестве вещества 1 моль теплоемкость 

Энтропия. Подставив в формуле  где
где  положительное число, получим единицу энтропии:
положительное число, получим единицу энтропии:

Эрг на кельвин равен изменению энтропии системы, в которой при температуре  в изотермическом процессе сообщается количество теплоты
в изотермическом процессе сообщается количество теплоты 

Удельная энтропия. Единицу удельной энтропии найдем по формуле (8.32), положив в ней 

Эрг на грамм-кельвин равен изменению удельной энтропии вещества, в котором при массе  изменение энтропии составляет
изменение энтропии составляет 

Тепловой поток. Подставив в формуле  найдем единицу теплового потока
найдем единицу теплового потока

Эрг в секунду равен тепловому потоку, эквивалентному механической мощности 

Поверхностная плотность теплового потока. Единицу поверхностной плотности теплового потока найдем, положив в формуле 

Эрг в секунду на квадратный сантиметр равен поверхностной плотности теплового потока  равномерно распределенного на поверхности площадью
равномерно распределенного на поверхности площадью 

Теплопроводность. Положив в формуле  К/см,
К/см,  получим единицу теплопроводности:
получим единицу теплопроводности:

Эрг в секунду на сантиметр-кельвин равен теплопроводности вещества, в котором при стационарном режиме с поверхностной плотностью теплового потока  устанавливается температурный градиент 1 К/см;
устанавливается температурный градиент 1 К/см;

Поверхностнее натяжение. Единицу поверхностного натяжения найдем по формуле (8.41), положив в ней  см:
см:

Дина на сантиметр равна поверхностному натяжению, создаваемому силой 1 дин, приложенной к участку контура свободной поверхности длиной 1 см и действующей нормально к контуру и по касательной к поверхности.
Если воспользоваться формулой (8.42), то получим другую единицу, характеризующую явление поверхностного натяжения:

Эрг на квадратный сантиметр равен удельной поверхностной энергии такой жидкости, для образования  поверхности которой затрачивается работа
поверхности которой затрачивается работа  Очевидно, что
Очевидно, что

Соотношение между единицами поверхностного натяжения в системах СГС и СИ:

Единицы остальных величин молекулярной физики рекомендуется получить самому читателю, пользуясь соответствующими определяющими уравнениями, приведенными В § 8.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ОБЩИЕ ВОПРОСЫ ВЫБОРА ЕДИНИЦ И ПОСТРОЕНИЯ СИСТЕМ ЕДИНИЦ
- § 1. ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ. СИСТЕМЫ ФИЗИЧЕСКИХ ВЕЛИЧИН
- Системы физических величин. Основные и производные величины
- § 2. РАЗМЕРНОСТИ ПРОИЗВОДНЫХ ФИЗИЧЕСКИХ ВЕЛИЧИН
- § 3. ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН, РАЗМЕР ЕДИНИЦ
- § 4. СИСТЕМЫ ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН
- § 5. НАИМЕНОВАНИЯ И ОБОЗНАЧЕНИЯ ЕДИНИЦ
- Глава II. МЕЖДУНАРОДНАЯ СИСТЕМА ЕДИНИЦ (СИ)
- § 6. ОСНОВНЫЕ, ДОПОЛНИТЕЛЬНЫЕ И ПРОИЗВОДНЫЕ ЕДИНИЦЫ СИСТЕМЫ
- § 7. ПРОИЗВОДНЫЕ ЕДИНИЦЫ МЕХАНИЧЕСКИХ ВЕЛИЧИН
- § 8. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ
- § 9. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ЭЛЕНТРИЧЕСКИХ И МАГНИТНЫХ ВЕЛИЧИН
- § 10. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН, ХАРАКТЕРИЗУЮЩИХ КОЛЕБАНИЯ И ВОЛНЫ
- § 11. ПРОИЗВОДНЫЕ ЕДИНИЦЫ АКУСТИЧЕСКИХ ВЕЛИЧИН
- § 12. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ОПТИЧЕСКИХ ВЕЛИЧИН
- § 13. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН АТОМНОЙ И ЯДЕРНОЙ ФИЗИКИ
- § 14. ОПРЕДЕЛЕНИЯ И ЭТАЛОНЫ ОСНОВНЫХ И ДОПОЛНИТЕЛЬНЫХ ЕДИНИЦ СИ
- § 15. РАЦИОНАЛИЗАЦИЯ УРАВНЕНИЙ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- Глава III. СИСТЕМА СГС
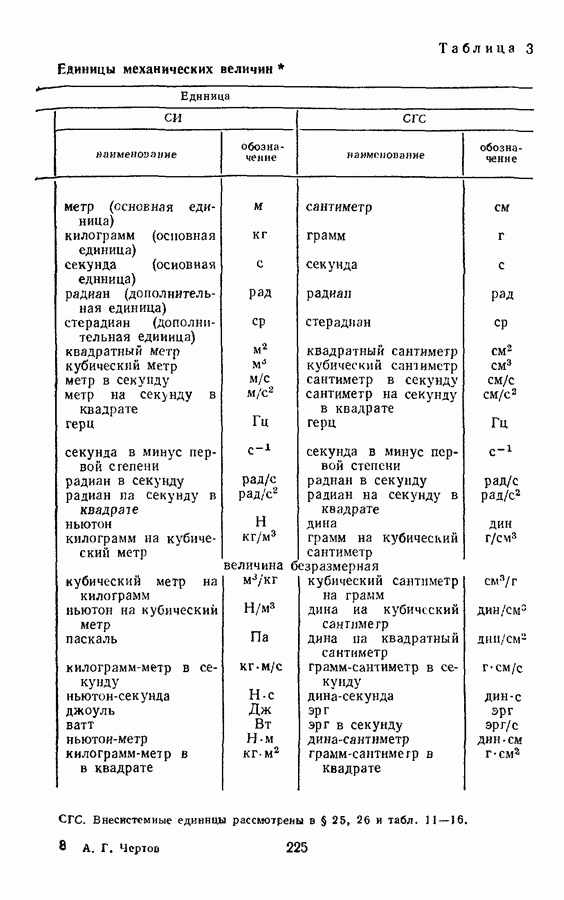
- § 17. ПРОИЗВОДНЫЕ ЕДИНИЦЫ МЕХАНИЧЕСКИХ ВЕЛИЧИН В СИСТЕМЕ СГС
- § 18. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ В СИСТЕМЕ СГС
- § 19. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ВЕЛИЧИН В СИСТЕМЕ СГС
- § 20. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН, ХАРАКТЕРИЗУЮЩИХ КОЛЕБАНИЯ И ВОЛНЫ В СИСТЕМЕ СГС
- § 21. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ОПТИЧЕСНИХ ВЕЛИЧИН В СИСТЕМЕ СГС
- § 22. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН АТОМНОЙ И ЯДЕРНОЙ ФИЗИКИ В СИСТЕМЕ СГС
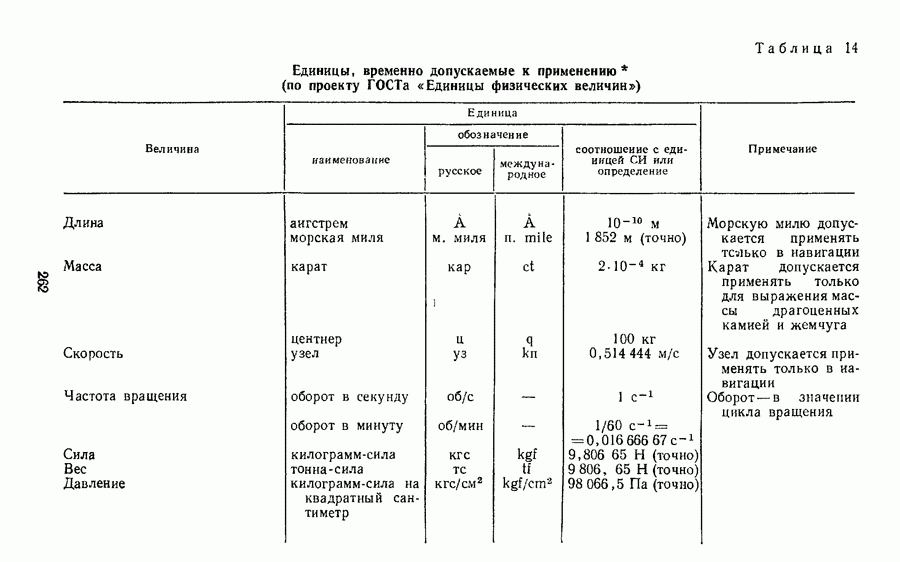
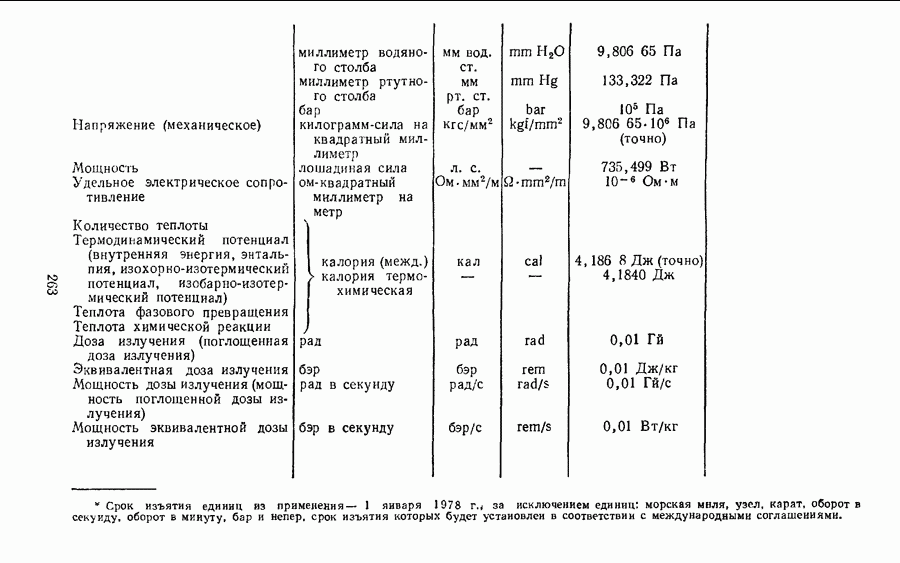
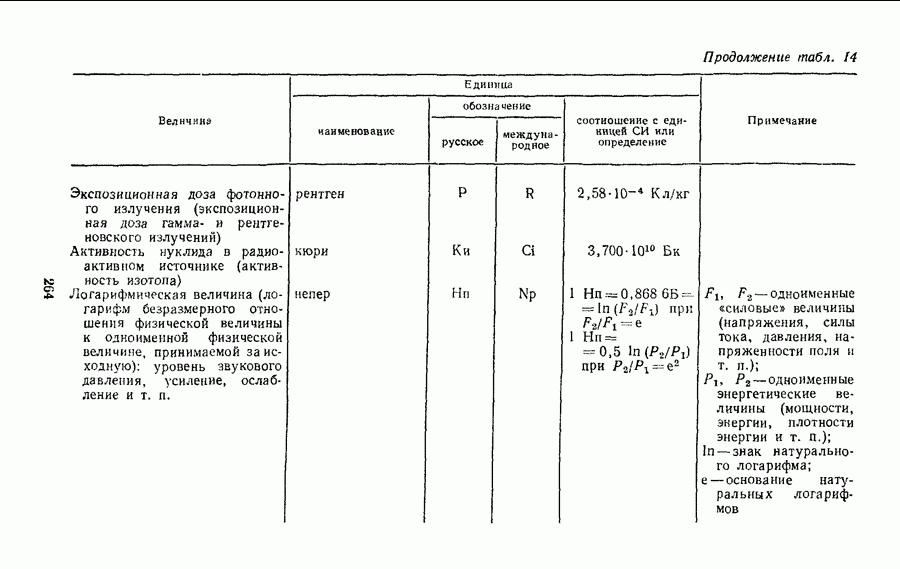
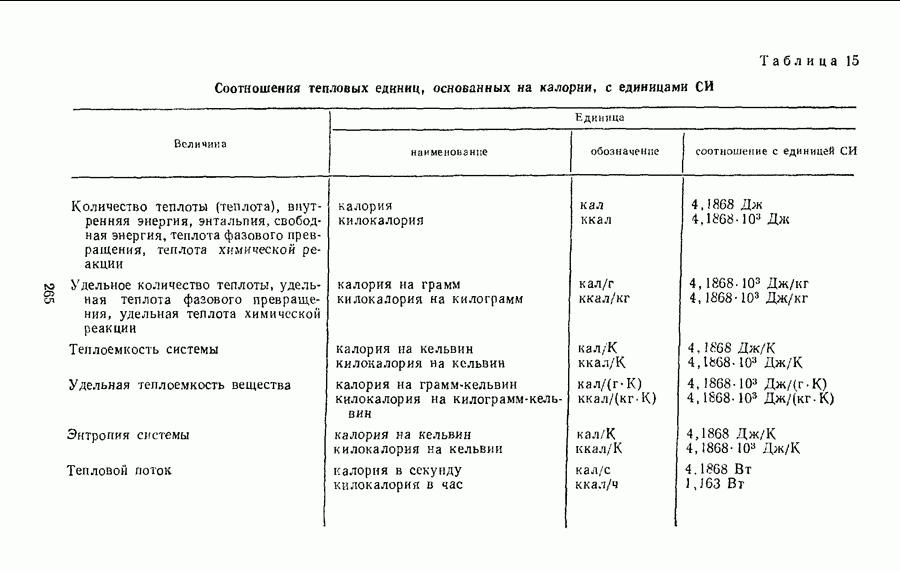
- Глава IV. ВНЕСИСТЕМНЫЕ ЕДИНИЦЫ
- § 23. КРАТНЫЕ И ДОЛЬНЫЕ ЕДИНИЦЫ
- § 24. ОТНОСИТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ ЕДИНИЦЫ
- § 25. СПЕЦИАЛЬНЫЕ ЕДИНИЦЫ
- § 26. КРАТКИЕ СВЕДЕНИЯ О НАИБОЛЕЕ ИЗВЕСТНЫХ ВНЕСИСТЕМНЫХ ЕДИНИЦАХ
- § 27. ОПРЕДЕЛЕНИЕ ЧИСЛОВЫХ КОЭФФИЦИЕНТОВ В ФОРМУЛАХ ПРИ ПЕРЕХОДЕ К СИ
- § 28. СООТНОШЕНИЯ ЕДИНИЦ МЕЖДУНАРОДНОЙ СИСТЕМЫ С ЕДИНИЦАМИ СИСТЕМЫ СГС И ВНЕСИСТЕМНЫМИ ЕДИНИЦАМИ