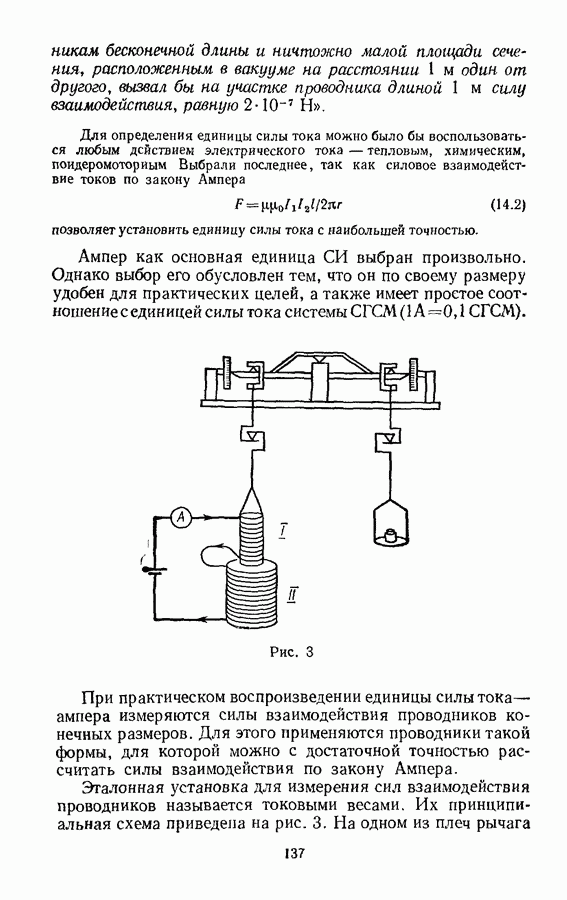
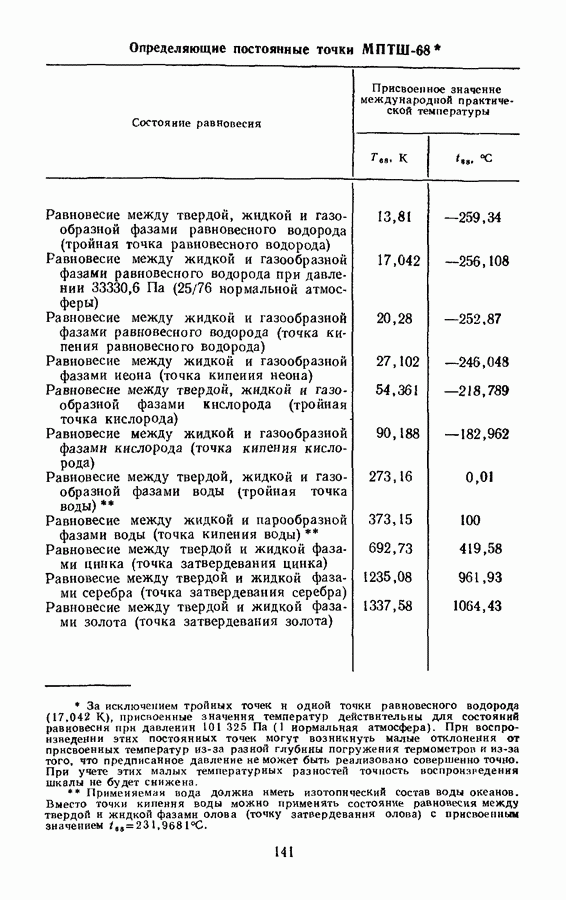
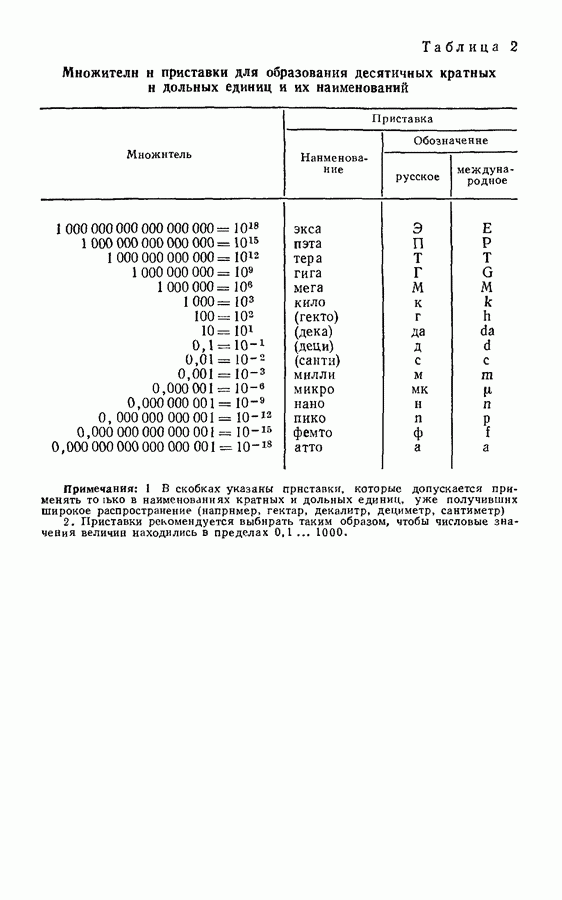
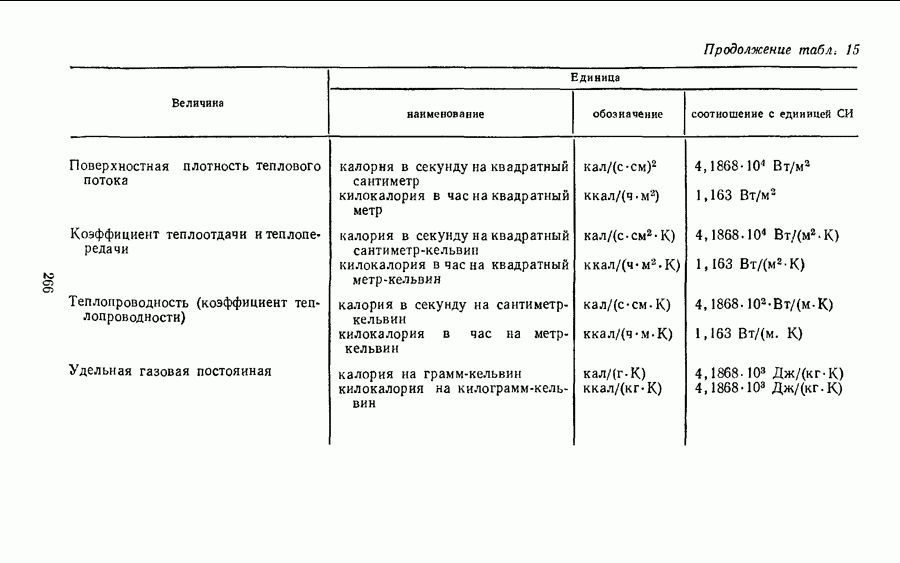
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 27. ОПРЕДЕЛЕНИЕ ЧИСЛОВЫХ КОЭФФИЦИЕНТОВ В ФОРМУЛАХ ПРИ ПЕРЕХОДЕ К СИ
Многие эмпирические формулы, встречающиеся в учебных пособиях и справочниках по техническим дисциплинам, содержат числовые коэффициенты. Такие формулы выражают связь не между физическими величинами, а между их числовыми значениями. Коэффициенты пропорциональности в этих формулах зависят от единиц, в которых выражены величины, входящие в формулы. При замене одних единиц другими коэффициент пропорциональности принимает другое значение.
В связи с переходом к Международной системе единиц возникает необходимость в пересчете коэффициентов. Рассмотрим методику этого пересчета.
Как указывалось в § 1, некоторая физическая величина может быть выражена через другие уравнением вида (1.5):

Если в этом равенстве каждую величину выразить по формуле (1.1) и разделить на соответствующие единицы, то получим

или после сокращения

Такие уравнения называют уравнениями между числовыми значениями.
Если величины  выразить соответственно в единицах
выразить соответственно в единицах  а затем в единицах
а затем в единицах
 то получим два уравнения между числовыми значениями для одних и тех же величин:
то получим два уравнения между числовыми значениями для одних и тех же величин:

Разделим второе из этих равенств на первое:

Если учесть, что числовые значения величины обратно пропорциональны размерам единиц, в которых данная величина выражена (см. с. 15), то последнее равенство можно переписать в виде

Вводя далее обозначения:

получим

Отсюда найдем окончательную формулу для вычисления 

При практическом использовании этой формулы рекомендуется выполнять операции в такой последовательности:
1) величины исходной формулы, в которой требуется пересчитать коэффициент пропорциональности, поставить в соответствие с величинами формулы (27.1);
2) единицы  которых выражены величины в исходной формуле, перевести в соответствующие единицы
которых выражены величины в исходной формуле, перевести в соответствующие единицы  Международной системы или в кратные или дольные единицы от единиц СИ;
Международной системы или в кратные или дольные единицы от единиц СИ;
3) найти отношения:

4) подставить эти отношения в формулу (27.2) и произвести вычисления.
Рассмотрим несколько примеров.
Пример 1. Наибольшее контактное напряжение  в радиальных однородных шарикоподшипниках определяется формулой
в радиальных однородных шарикоподшипниках определяется формулой

где  напряжение
напряжение  радиальная нагрузка на подшипник
радиальная нагрузка на подшипник  радиус кольца (см),
радиус кольца (см),  безразмерный коэффициент. Определить числовой коэффициент в этой формуле, если напряжение выразить в мегапаскалях
безразмерный коэффициент. Определить числовой коэффициент в этой формуле, если напряжение выразить в мегапаскалях  радиальную нагрузку — в ньютонах
радиальную нагрузку — в ньютонах  радиус — в метрах
радиус — в метрах 
Решение. 1. Сравнивая формулы (27.3) и (27.1), устанавливаем следующее соответствие величин:

Формула (27.2) для данного примера принимает вид

2. Переведем единицы, в которых выражены величины в исходной формуле, в единицы Международной системы:

3. Найдем отношения соответствующих единиц:

4. Подставив вычисленные значения отношений в формулу (27.4), определим числовой коэффициент:

Таким образом, если напряжение о выразить в мегапаскалях, радиальную нагрузку  в ньютонах, радиус
в ньютонах, радиус  кольца — в метрах, то формула (27.3) примет вид
кольца — в метрах, то формула (27.3) примет вид

Пример 2. Для определения мощности двигателя применяется формула

где  мощность двигателя
мощность двигателя  — вращающий момент
— вращающий момент  частота вращения (об/мин). Определить числовой коэффициент в этой формуле, если все величины в ней выразить в единицах Международной системы единиц.
частота вращения (об/мин). Определить числовой коэффициент в этой формуле, если все величины в ней выразить в единицах Международной системы единиц.
Решение. 1. Сравнивая формулы (27.5) и (27.1), установим следующее соответствие величин:

Формула (27.2) для данного примера имеет вид

2. Переведем единицы, в которых выражены величины в исходной формуле, в единицы Международной системы:

3. Найдем отношения соответствующих единиц:

4. Подставив вычисленные значения отношений в формулу (27.6), определим числовой коэффициент:

Следовательно, если величины, входящие в формулу (27.5), выразить в единицах Международной системы, то формула запишется в виде

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ОБЩИЕ ВОПРОСЫ ВЫБОРА ЕДИНИЦ И ПОСТРОЕНИЯ СИСТЕМ ЕДИНИЦ
- § 1. ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ. СИСТЕМЫ ФИЗИЧЕСКИХ ВЕЛИЧИН
- Системы физических величин. Основные и производные величины
- § 2. РАЗМЕРНОСТИ ПРОИЗВОДНЫХ ФИЗИЧЕСКИХ ВЕЛИЧИН
- § 3. ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН, РАЗМЕР ЕДИНИЦ
- § 4. СИСТЕМЫ ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН
- § 5. НАИМЕНОВАНИЯ И ОБОЗНАЧЕНИЯ ЕДИНИЦ
- Глава II. МЕЖДУНАРОДНАЯ СИСТЕМА ЕДИНИЦ (СИ)
- § 6. ОСНОВНЫЕ, ДОПОЛНИТЕЛЬНЫЕ И ПРОИЗВОДНЫЕ ЕДИНИЦЫ СИСТЕМЫ
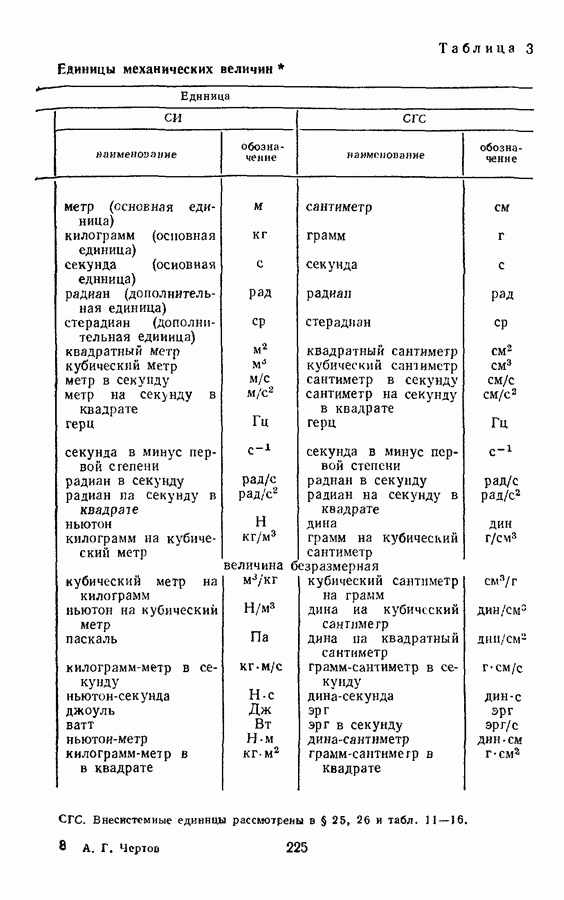
- § 7. ПРОИЗВОДНЫЕ ЕДИНИЦЫ МЕХАНИЧЕСКИХ ВЕЛИЧИН
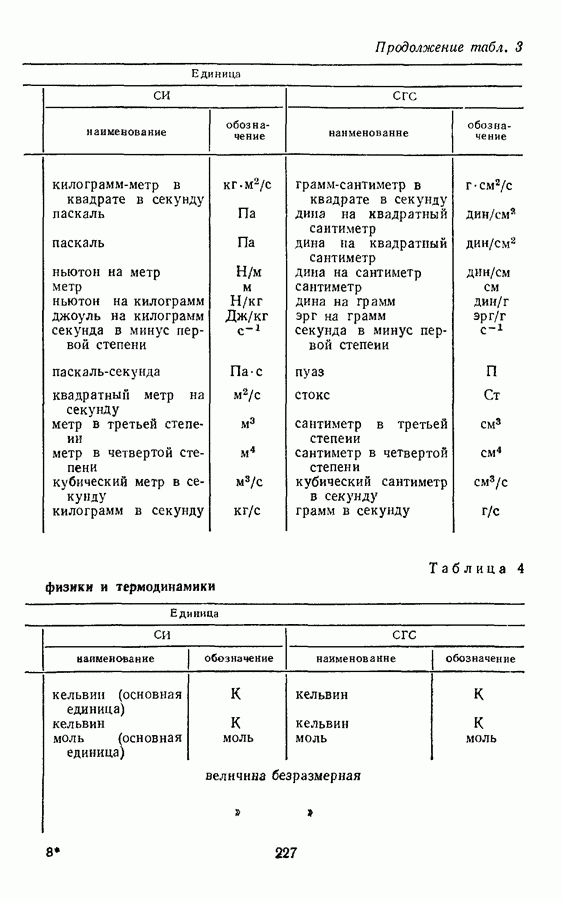
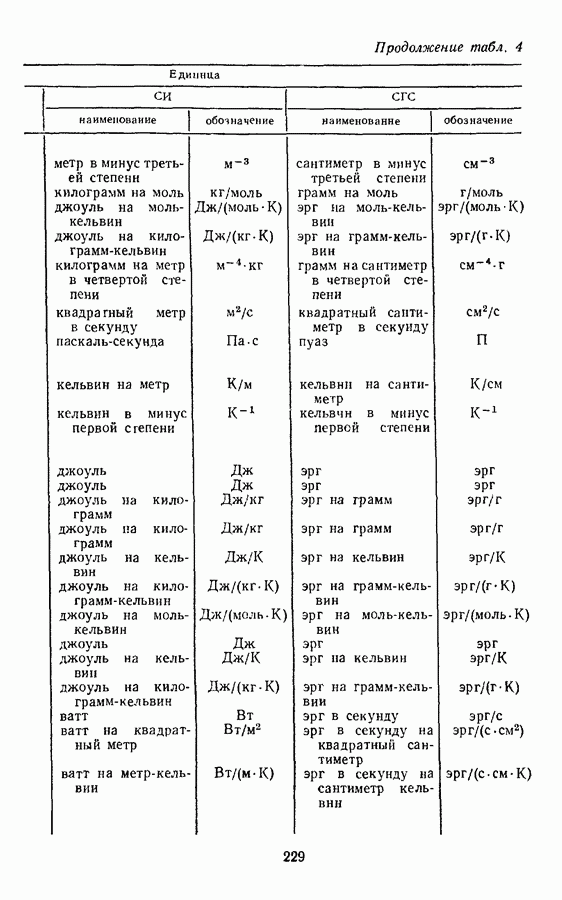
- § 8. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ
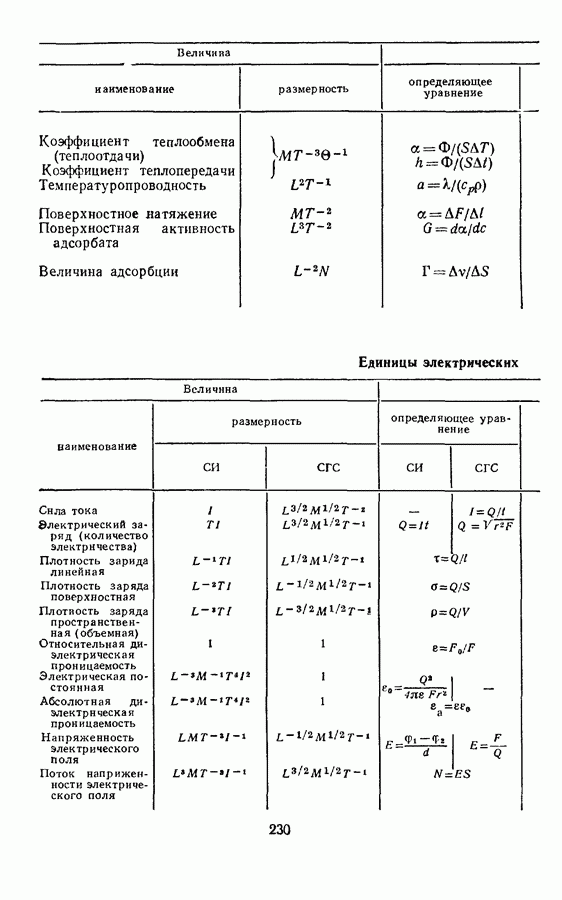
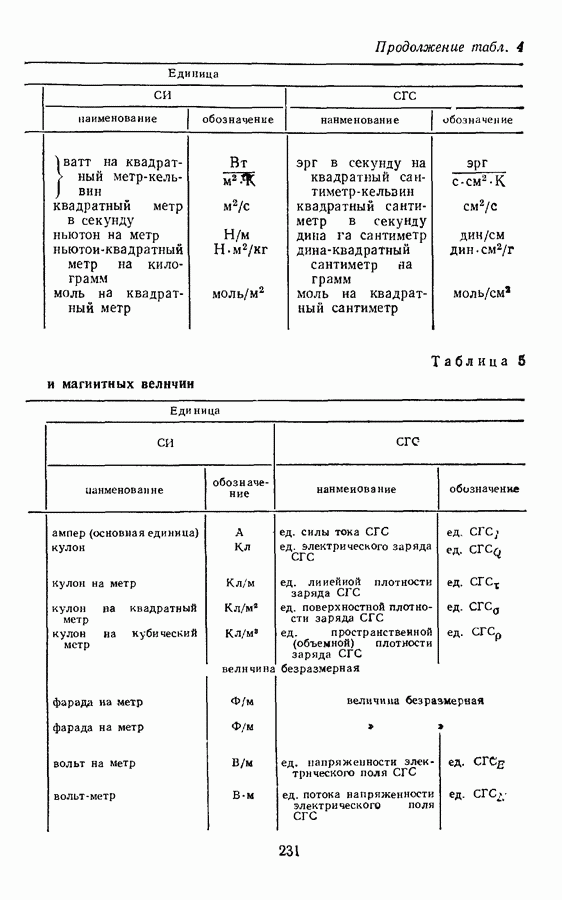
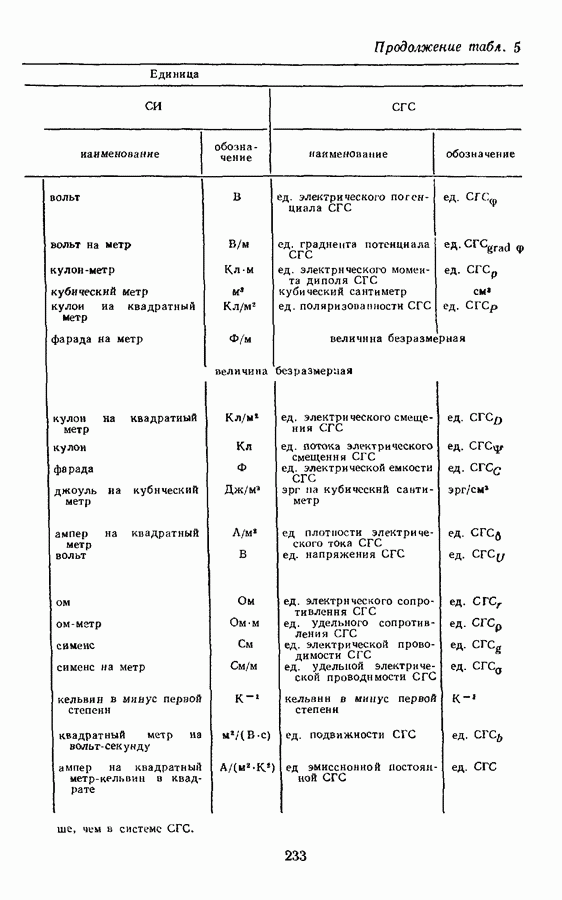
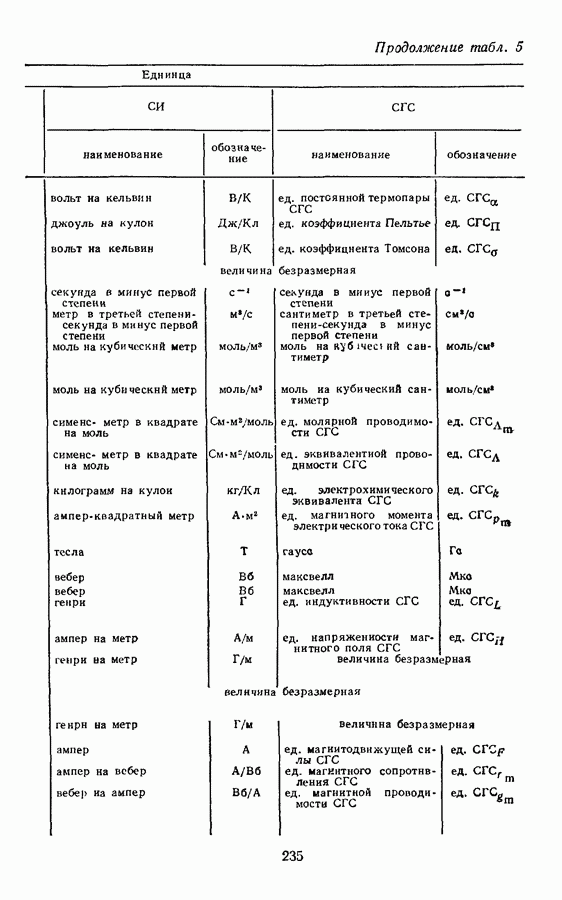
- § 9. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ЭЛЕНТРИЧЕСКИХ И МАГНИТНЫХ ВЕЛИЧИН
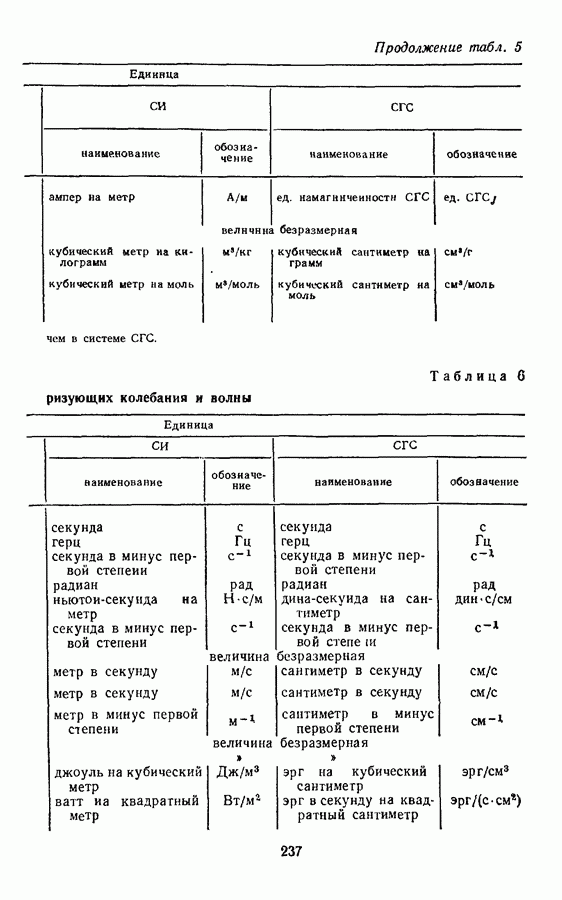
- § 10. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН, ХАРАКТЕРИЗУЮЩИХ КОЛЕБАНИЯ И ВОЛНЫ
- § 11. ПРОИЗВОДНЫЕ ЕДИНИЦЫ АКУСТИЧЕСКИХ ВЕЛИЧИН
- § 12. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ОПТИЧЕСКИХ ВЕЛИЧИН
- § 13. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН АТОМНОЙ И ЯДЕРНОЙ ФИЗИКИ
- § 14. ОПРЕДЕЛЕНИЯ И ЭТАЛОНЫ ОСНОВНЫХ И ДОПОЛНИТЕЛЬНЫХ ЕДИНИЦ СИ
- § 15. РАЦИОНАЛИЗАЦИЯ УРАВНЕНИЙ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- Глава III. СИСТЕМА СГС
- § 17. ПРОИЗВОДНЫЕ ЕДИНИЦЫ МЕХАНИЧЕСКИХ ВЕЛИЧИН В СИСТЕМЕ СГС
- § 18. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ В СИСТЕМЕ СГС
- § 19. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ВЕЛИЧИН В СИСТЕМЕ СГС
- § 20. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН, ХАРАКТЕРИЗУЮЩИХ КОЛЕБАНИЯ И ВОЛНЫ В СИСТЕМЕ СГС
- § 21. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ОПТИЧЕСНИХ ВЕЛИЧИН В СИСТЕМЕ СГС
- § 22. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН АТОМНОЙ И ЯДЕРНОЙ ФИЗИКИ В СИСТЕМЕ СГС
- Глава IV. ВНЕСИСТЕМНЫЕ ЕДИНИЦЫ
- § 23. КРАТНЫЕ И ДОЛЬНЫЕ ЕДИНИЦЫ
- § 24. ОТНОСИТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ ЕДИНИЦЫ
- § 25. СПЕЦИАЛЬНЫЕ ЕДИНИЦЫ
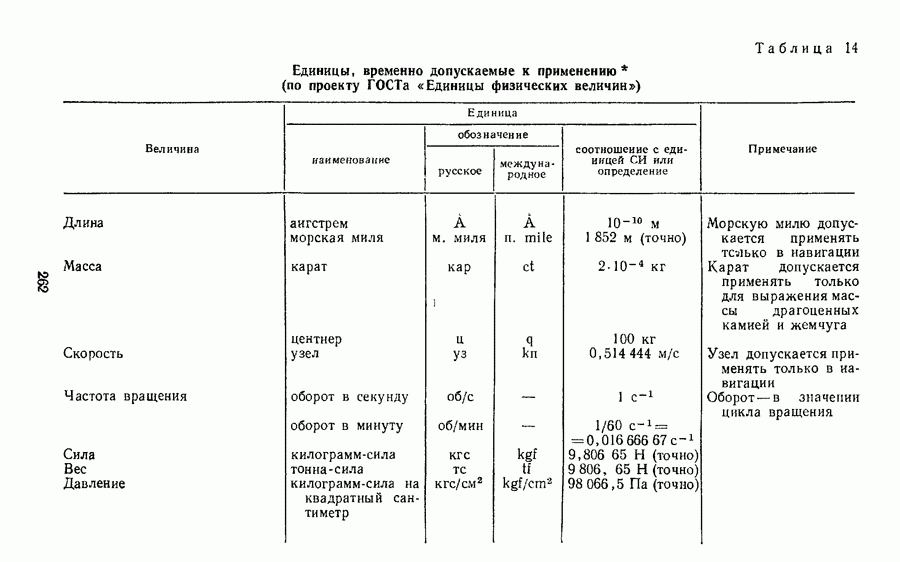
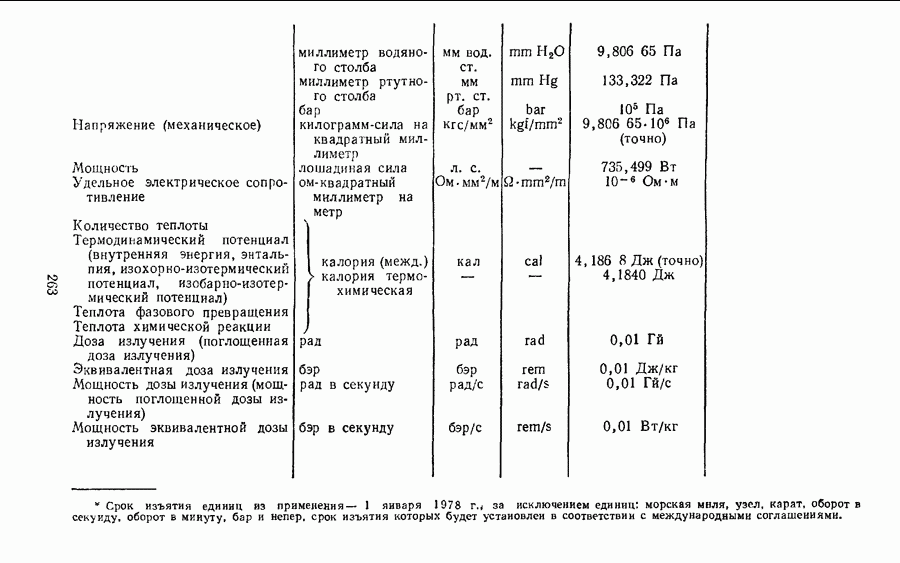
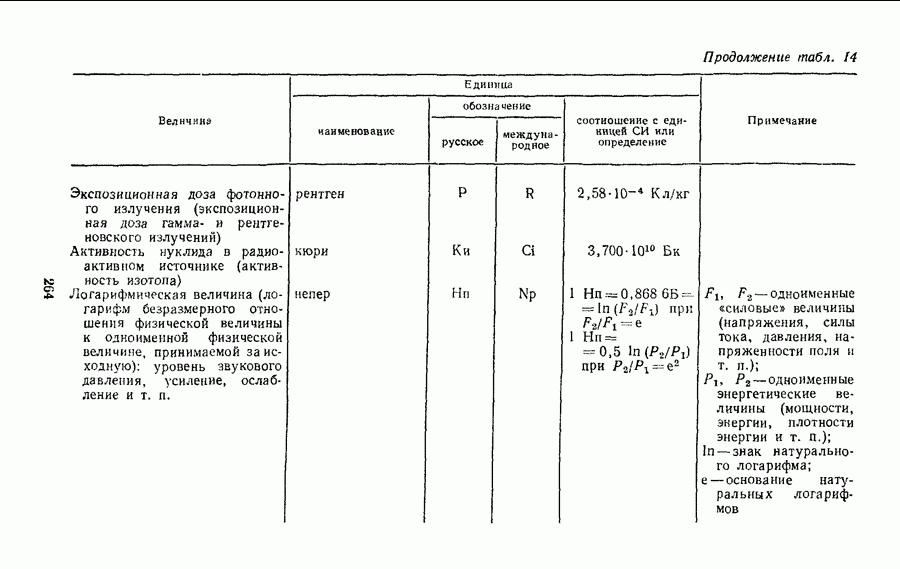
- § 26. КРАТКИЕ СВЕДЕНИЯ О НАИБОЛЕЕ ИЗВЕСТНЫХ ВНЕСИСТЕМНЫХ ЕДИНИЦАХ
- § 27. ОПРЕДЕЛЕНИЕ ЧИСЛОВЫХ КОЭФФИЦИЕНТОВ В ФОРМУЛАХ ПРИ ПЕРЕХОДЕ К СИ
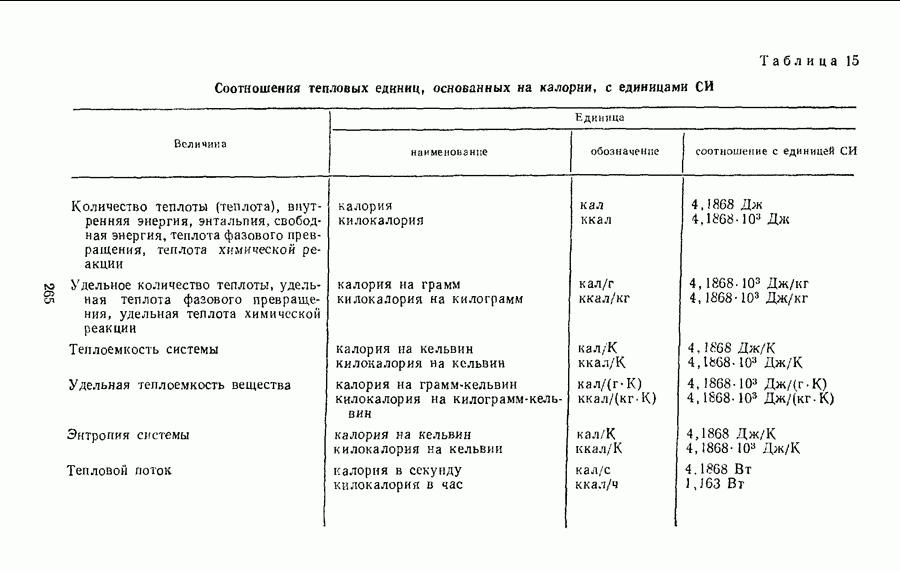
- § 28. СООТНОШЕНИЯ ЕДИНИЦ МЕЖДУНАРОДНОЙ СИСТЕМЫ С ЕДИНИЦАМИ СИСТЕМЫ СГС И ВНЕСИСТЕМНЫМИ ЕДИНИЦАМИ