| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2-5. ПОГРЕШНОСТЬ КОСВЕННЫХ ИЗМЕРЕНИЯ
При косвенных измерениях измеряемая величина А функционально связана с другими величинами  которые подвергаются прямым измерениям:
которые подвергаются прямым измерениям:  Очевидно, что абсолютная погрешность измеряемой величины
Очевидно, что абсолютная погрешность измеряемой величины  является некоторой функцией погрешностей прямых измерений:
является некоторой функцией погрешностей прямых измерений:  В простейшем случае, при одной переменной
В простейшем случае, при одной переменной  в результате измерения получаем
в результате измерения получаем

Разложим правую часть в ряд Тейлора и сохраним члены разложения, содержащие  в первой степени:
в первой степени:

Отсюда абсолютная и относительная погрешности:

В общем случае, когда  абсолютная погрешность результата косвенных измерений находится так же, как сумма случайных погрешностей:
абсолютная погрешность результата косвенных измерений находится так же, как сумма случайных погрешностей:

где слагаемые являются квадратами частных погрешностей прямых измерений.
Аналогично вычисляется и относительная погрешность

Прямые измерения величин  Смогут выполняться статистическим методом, т. е. путем многократных наблюдений и определения их действительных значений
Смогут выполняться статистическим методом, т. е. путем многократных наблюдений и определения их действительных значений  и среднеквадратических отклонений
и среднеквадратических отклонений  Тогда нужно найти оценку среднеквадратического отклонения результата косвенных измерений:
Тогда нужно найти оценку среднеквадратического отклонения результата косвенных измерений:

Приведенные формулы относятся к случайным погрешностям. Однако часто встречаются частные погрешности прямых измерений, содержащие как случайные, так и систематические составляющие:

Погрешность косвенного измерения в этом случае не может быть точно вычислена. Применяют метод, обеспечивающий удовлетворительные результаты, основанный на представлении систематической погрешности эквивалентной случайной величиной, равновероятно находящейся в заданном интервале  т. е. распределенной по равномерному закону. Известно, что дисперсия при равномерном распределении
т. е. распределенной по равномерному закону. Известно, что дисперсия при равномерном распределении  Теперь можно написать, что
Теперь можно написать, что
(см. скан)
дисперсия  Следовательно, среднеквадратическое отклонение общей погрешности косвенного измерения величины А можно записать в следующей форме:
Следовательно, среднеквадратическое отклонение общей погрешности косвенного измерения величины А можно записать в следующей форме:

Формулы для вычислений абсолютных и относительных погрешностей косвенных измерений часто встречающихся функций приведены в табл. 2-1.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА ПЕРВАЯ. ОСНОВНЫЕ СВЕДЕНИЯ О СРЕДСТВАХ ИЗМЕРЕНИЙ
- 1-2. МЕРЫ ЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 1-3. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 1-4. ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
- 1-5. ИЗМЕРИТЕЛЬНЫЕ УСТАНОВКИ И СИСТЕМЫ
- 1-6. ОСНОВНЫЕ СВОЙСТВА СРЕДСТВ ИЗМЕРЕНИЯ
- 1-7. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ
- ГЛАВА ВТОРАЯ. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
- 2-2. СИСТЕМАТИЧЕСКИЕ ПОГРЕШНОСТИ
- 2-3. СЛУЧАЙНЫЕ ПОГРЕШНОСТИ
- 2-4. СУММИРОВАНИЕ ПОГРЕШНОСТЕЙ
- 2-5. ПОГРЕШНОСТЬ КОСВЕННЫХ ИЗМЕРЕНИЯ
- 2-6. НЕКОТОРЫЕ ПРАВИЛА ВЫПОЛНЕНИЯ ИЗМЕРЕНИЯ И ПРЕДСТАВЛЕНИЯ РЕЗУЛЬТАТОВ
- ГЛАВА ТРЕТЬЯ. ИЗМЕРЕНИЕ ТОКА И НАПРЯЖЕНИЯ
- 3-2. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АМПЕРМЕТРЫ И ВОЛЬТМЕТРЫ
- 3-3. ЭЛЕКТРОННЫЕ ВОЛЬТМЕТРЫ
- ГЛАВА ЧЕТВЕРТАЯ. ГЕНЕРАТОРЫ ИЗМЕРИТЕЛЬНЫХ СИГНАЛОВ
- 4-2. ГЕНЕРАТОРЫ СИГНАЛОВ ИНФРАНИЗКИХ И НИЗКИХ ЧАСТОТ
- 4-3. ГЕНЕРАТОРЫ СИГНАЛОВ ВЫСОКИХ И УЛЬТРАВЫСОКИХ ЧАСТОТ
- 4-4. ГЕНЕРАТОРЫ СИГНАЛОВ СВЕРХВЫСОКИХ ЧАСТОТ
- 4-5. ПОНЯТИЕ О СИНТЕЗАТОРАХ ЧАСТОТЫ
- 4-6. ГЕНЕРАТОРЫ ИМПУЛЬСНЫХ СИГНАЛОВ
- 4-7. ГЕНЕРАТОРЫ ШУМОВЫХ СИГНАЛОВ
- ГЛАВА ПЯТАЯ. ЭЛЕКТРОННО-ЛУЧЕВЫЕ ОСЦИЛЛОГРАФЫ
- 5-2. ЭЛЕКТРОННО-ЛУЧЕВЫЕ ТРУБКИ
- 5-3. ОСЦИЛЛОГРАФИЧЕСКИЕ РАЗВЕРТКИ
- 5-4. КАНАЛЫ УПРАВЛЕНИЯ ЛУЧОМ
- 5-5. КАЛИБРАТОРЫ АМПЛИТУДЫ И ДЛИТЕЛЬНОСТИ
- 5-6. СТРОБОСКОПИЧЕСКИЕ ОСЦИЛЛОГРАФЫ
- 5-7. НЕКОТОРЫЕ ОСОБЕННОСТИ ОСЦИЛЛОГРАФИЧЕСКИХ ИЗМЕРЕНИЙ
- ГЛАВА ШЕСТАЯ. ИЗМЕРЕНИЕ СПЕКТРА И ФОРМЫ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ
- 6-2. АНАЛИЗАТОРЫ СПЕКТРА ПОСЛЕДОВАТЕЛЬНОГО ДЕЙСТВИЯ
- 6-3. АНАЛИЗ СПЕКТРА В РЕАЛЬНОМ ВРЕМЕНИ
- 6-4. ИЗМЕРЕНИЕ НЕЛИНЕЙНЫХ ИСКАЖЕНИЙ
- 6-5. ИЗМЕРЕНИЕ ПАРАМЕТРОВ МОДУЛИРОВАННЫХ СИГНАЛОВ
- ГЛАВА СЕДЬМАЯ. ИЗМЕРЕНИЕ ФАЗОВОГО СДВИГА
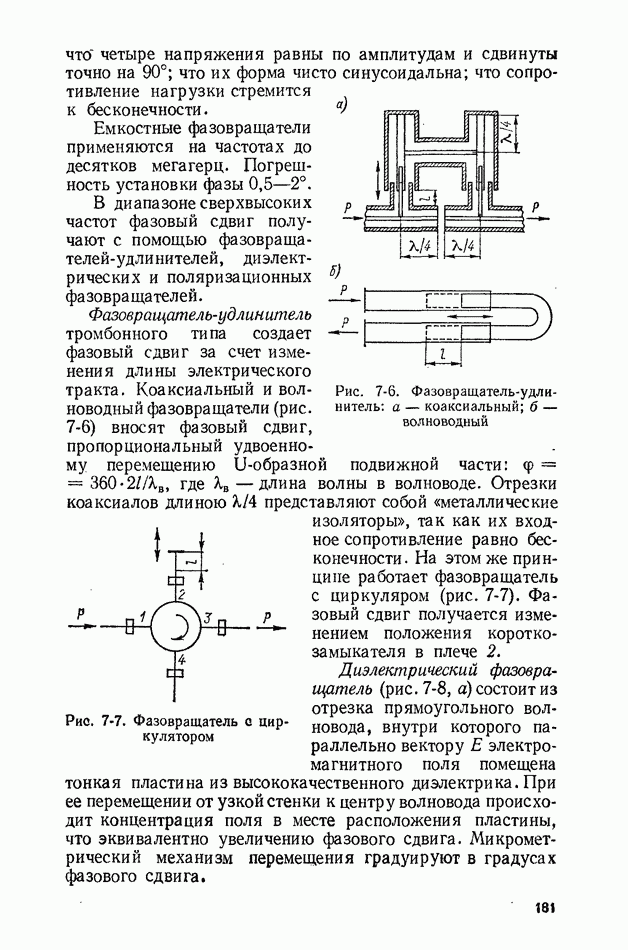
- 7-2. ФАЗОВРАЩАТЕЛИ
- 7-3. ОСЦИЛЛОГРАФИЧЕСКИЙ МЕТОД
- 7-4. КОМПЕНСАЦИОННЫЙ МЕТОД
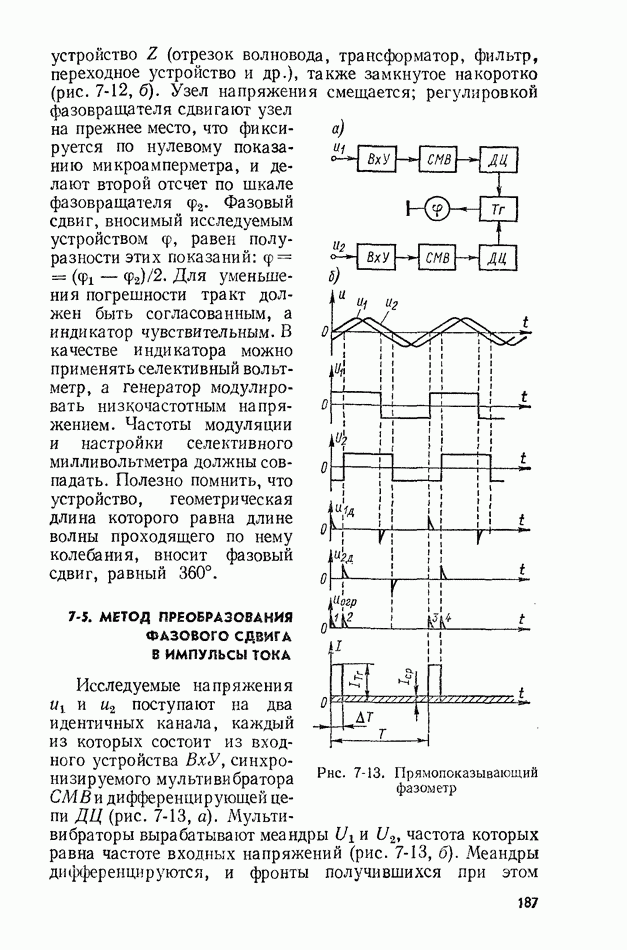
- 7-5. МЕТОД ПРЕОБРАЗОВАНИЯ ФАЗОВОГО СДВИГА В ИМПУЛЬСЫ ТОКА
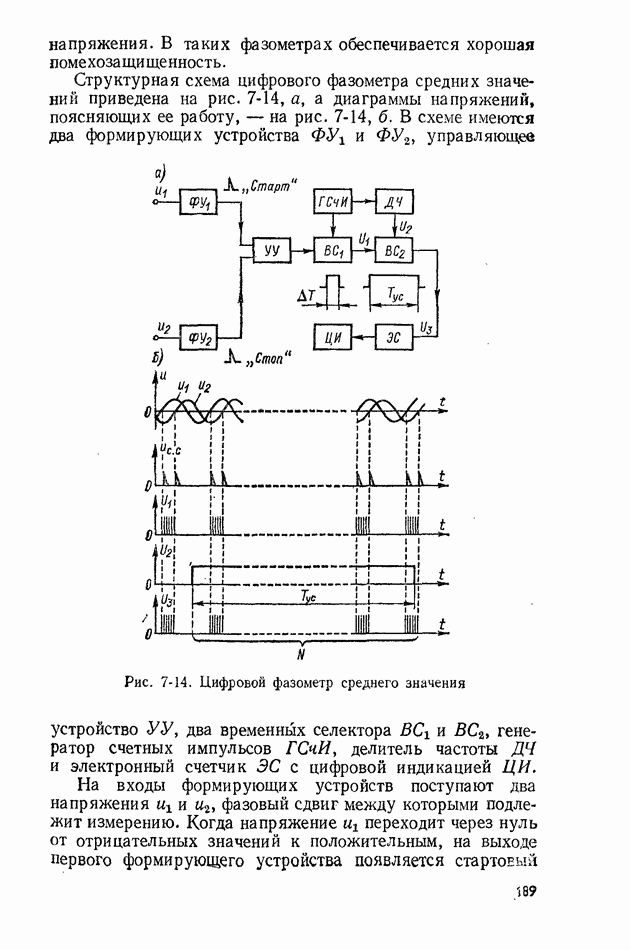
- 7-6. МЕТОД ДИСКРЕТНОГО СЧЕТА
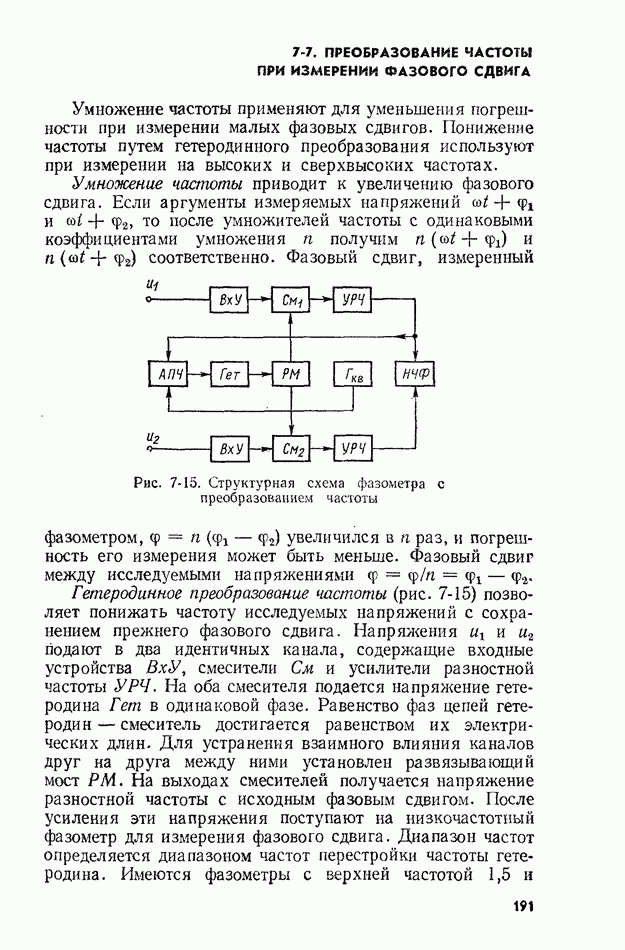
- 7-7. ПРЕОБРАЗОВАНИЕ ЧАСТОТЫ ПРИ ИЗМЕРЕНИИ ФАЗОВОГО СДВИГА
- ГЛАВА ВОСЬМАЯ. ИЗМЕРЕНИЕ ЧАСТОТЫ И ИНТЕРВАЛОВ ВРЕМЕНИ
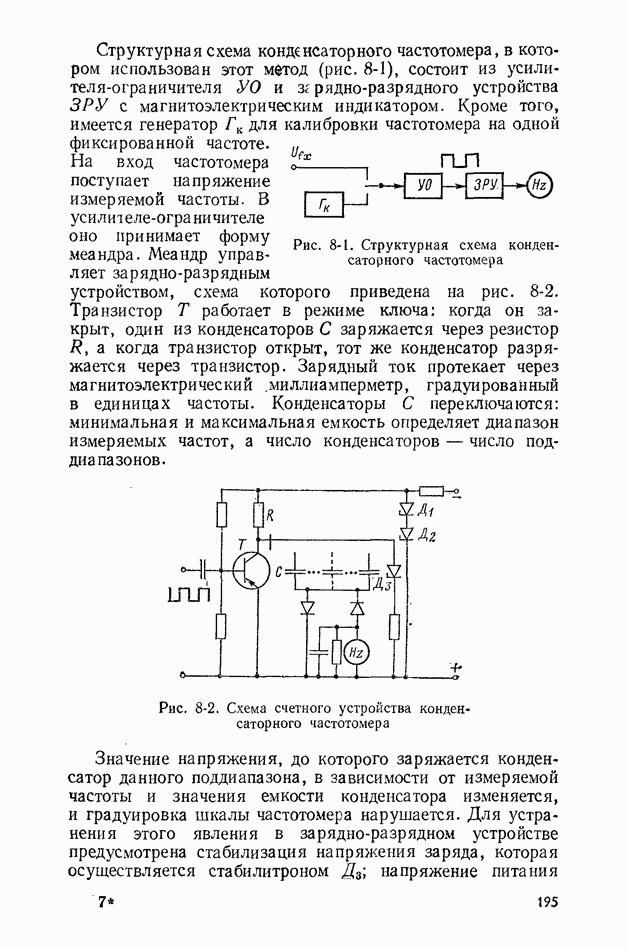
- 8-2. МЕТОД ПЕРЕЗАРЯДА КОНДЕНСАТОРА
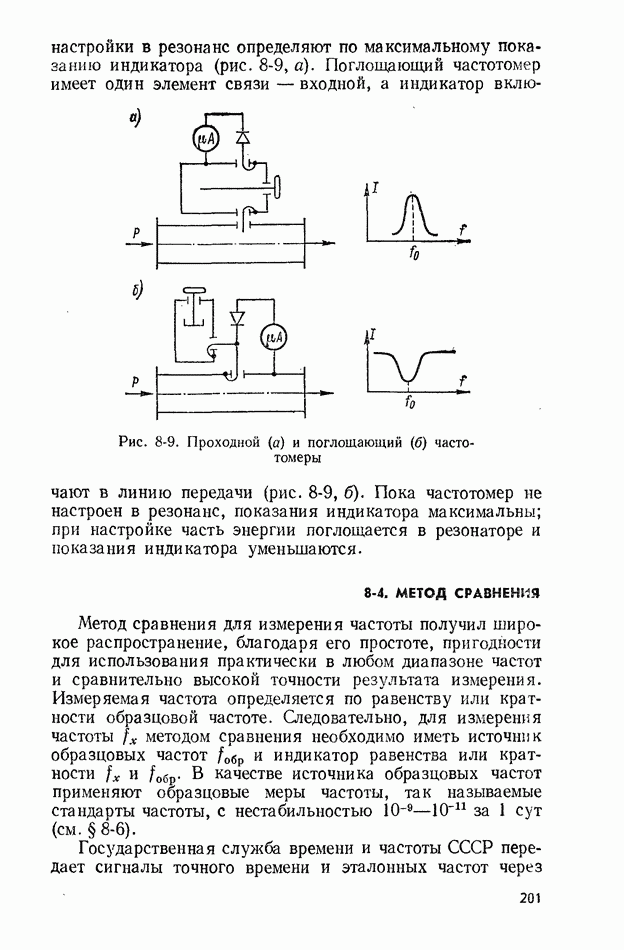
- 8-3. РЕЗОНАНСНЫЙ МЕТОД
- 8-4. МЕТОД СРАВНЕНИЯ
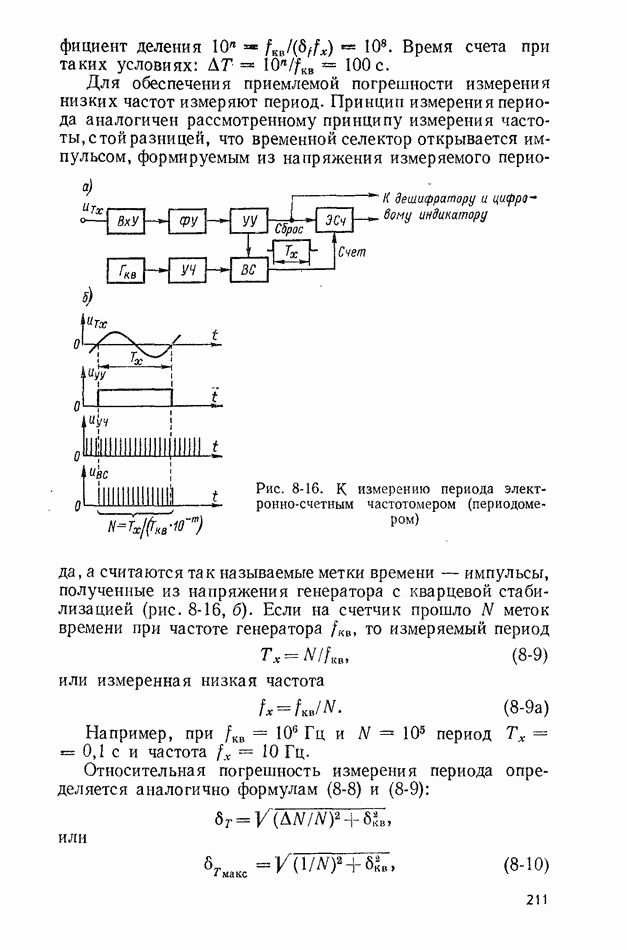
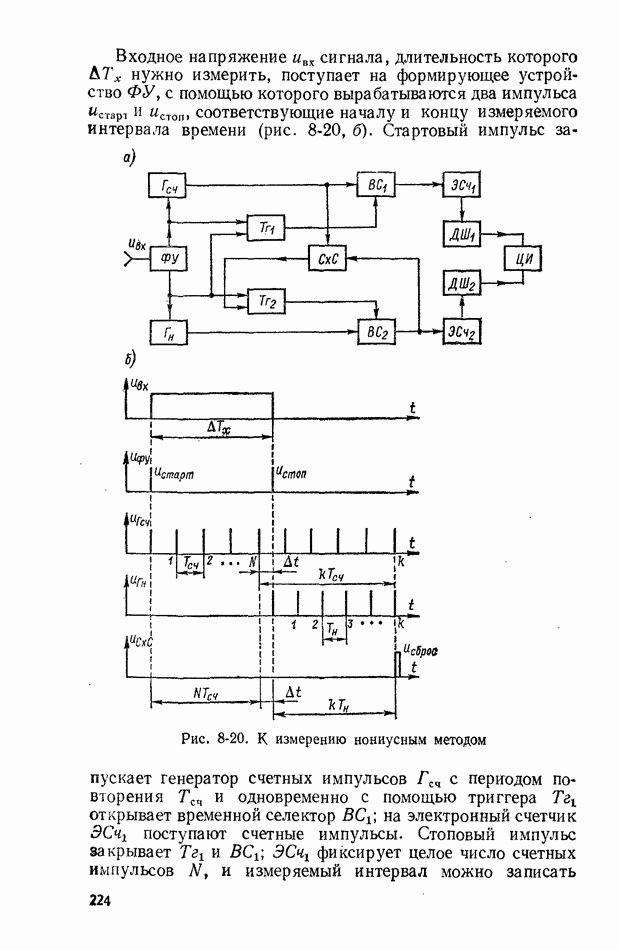
- 8-5. МЕТОД ДИСКРЕТНОГО СЧЕТА
- 8-6. ПОНЯТИЕ О СТАНДАРТАХ ЧАСТОТЫ И ВРЕМЕНИ
- 8-7. ПРЕЦИЗИОННОЕ ИЗМЕРЕНИЕ ЧАСТОТЫ И ВРЕМЕНИ
- ГЛАВА ДЕВЯТАЯ. ИЗМЕРЕНИЕ МОЩНОСТИ
- 9-2. ИЗМЕРЕНИЕ ПОГЛОЩАЕМОЙ МОЩНОСТИ
- 5-3. ИЗМЕРЕНИЕ ПРОХОДЯЩЕЙ МОЩНОСТИ
- 9-4. ИЗМЕРЕНИЕ ВЕСЬМА МАЛОЙ МОЩНОСТИ
- ГЛАВА ДЕСЯТАЯ. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ СИГНАЛОВ
- 10-2. ИЗМЕРЕНИЕ МОМЕНТОВ
- 10-3. ИЗМЕРЕНИЕ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ
- 10-4. ИЗМЕРЕНИЕ ЭНЕРГЕТИЧЕСКОГО СПЕКТРА
- 10-5. ИЗМЕРЕНИЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ И ПЛОТНОСТИ ВЕРОЯТНОСТИ
- ГЛАВА ОДИННАДЦАТАЯ. ИЗМЕРЕНИЕ ПАРАМЕТРОВ ЭЛЕМЕНТОВ ЭЛЕКТРИЧЕСКИХ И РАДИОТЕХНИЧЕСКИХ УСТРОЙСТВ
- 11-2. МЕТОД ВОЛЬТМЕТРА И АМПЕРМЕТРА
- 11-3. МОСТОВОЙ МЕТОД
- 11.4. РЕЗОНАНСНЫЙ МЕТОД
- 11-5. МЕТОД ДИСКРЕТНОГО СЧЕТА
- 11-6. ИЗМЕРЕНИЕ АМПЛИТУДНО-ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 11-7. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК ИНТЕГРАЛЬНЫХ СХЕМ
- ГЛАВА ДВЕНАДЦАТАЯ. ИЗМЕРЕНИЕ ПАРАМЕТРОВ ЦЕПЕЙ СВЕРХВЫСОКИХ ЧАСТОТ
- 12-2. ИЗМЕРИТЕЛЬНЫЕ ЛИНИИ
- 12-3. ИЗМЕРЕНИЕ КОЭФФИЦИЕНТА СТОЯЧЕЙ ВОЛНЫ И КОЭФФИЦИЕНТА ОТРАЖЕНИЯ
- 12-4. ИЗМЕРЕНИЕ ПОЛНОГО СОПРОТИВЛЕНИЯ
- 12-5. ИЗМЕРЕНИЕ НЕОДНОРОДНОСТИ
- ГЛАВА ТРИНАДЦАТАЯ. ИЗМЕРЕНИЕ ОСЛАБЛЕНИЯ
- 13-2. ИЗМЕРЕНИЕ ВНОСИМОГО ОСЛАБЛЕНИЯ
- 13-3. ИЗМЕРЕНИЕ СОБСТВЕННОГО ОСЛАБЛЕНИЯ
- ЗАКЛЮЧЕНИЕ
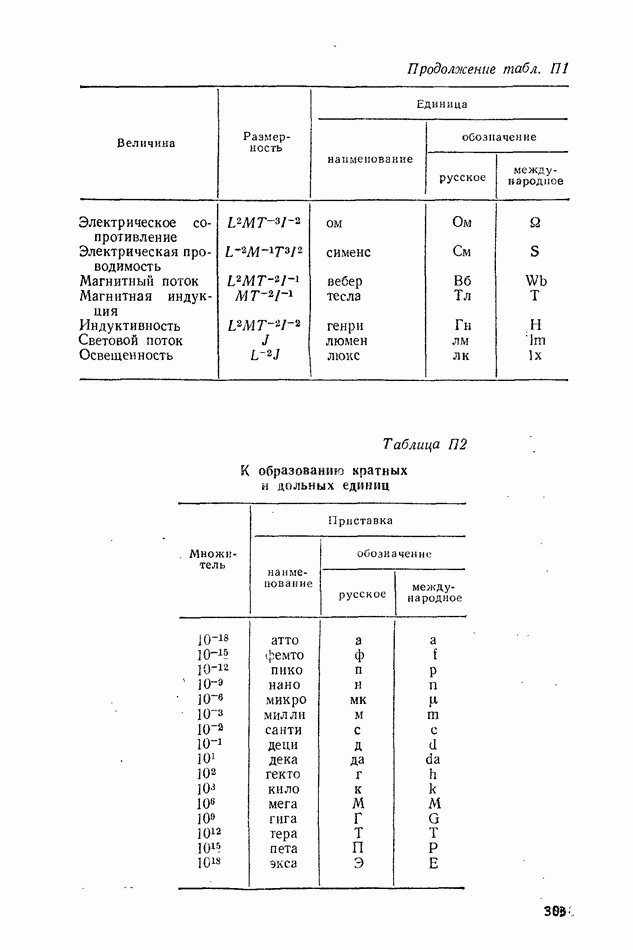
- ПРИЛОЖЕНИЕ П1
- ПРИЛОЖЕНИЕ 2. КЛАССИФИКАЦИЯ РАДИОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ