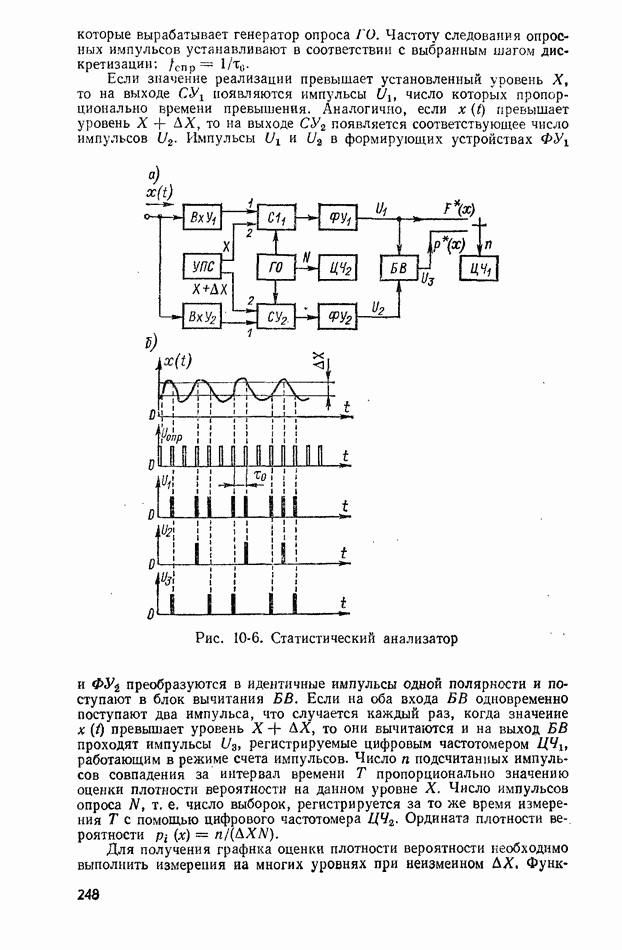
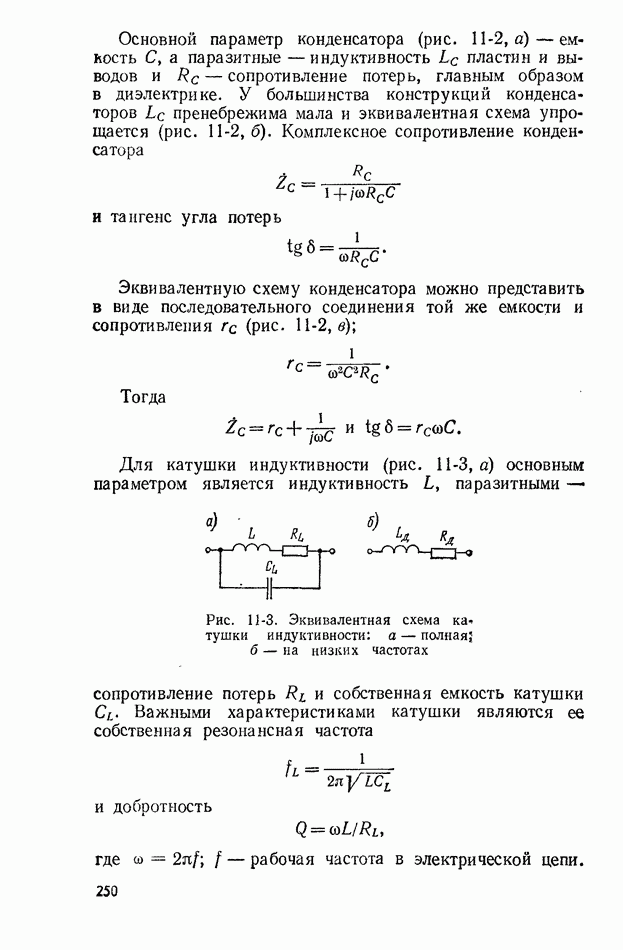
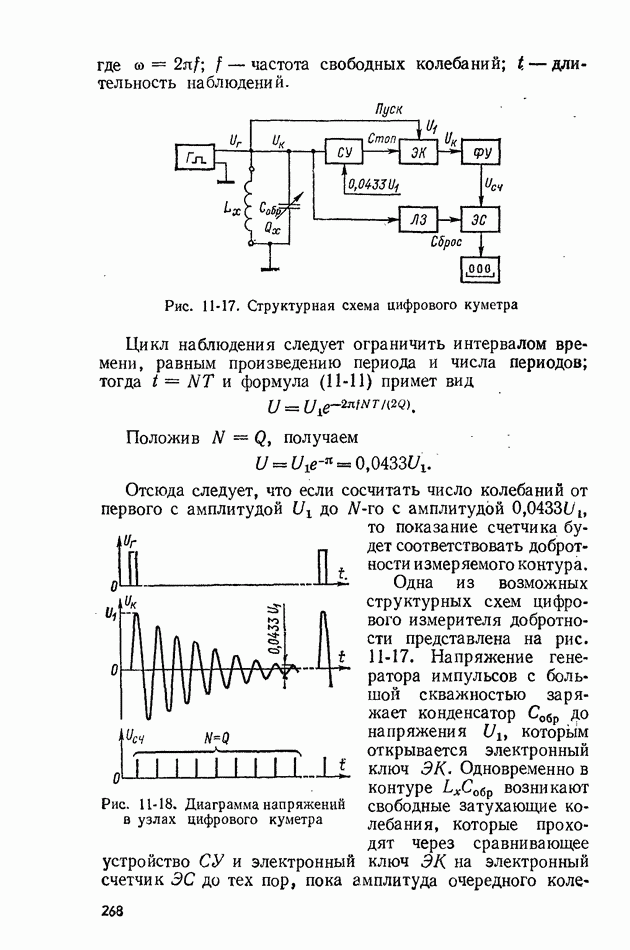
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
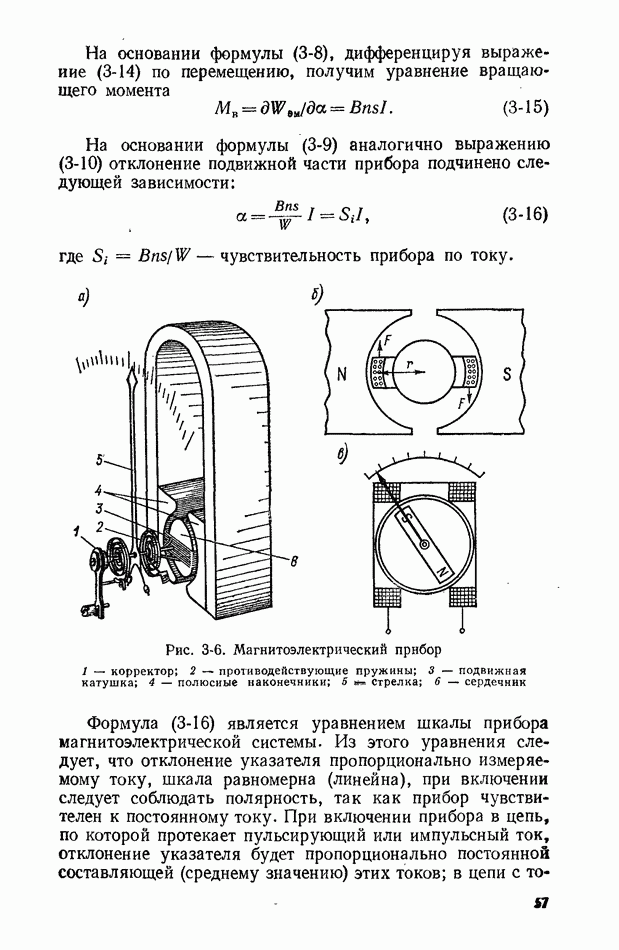
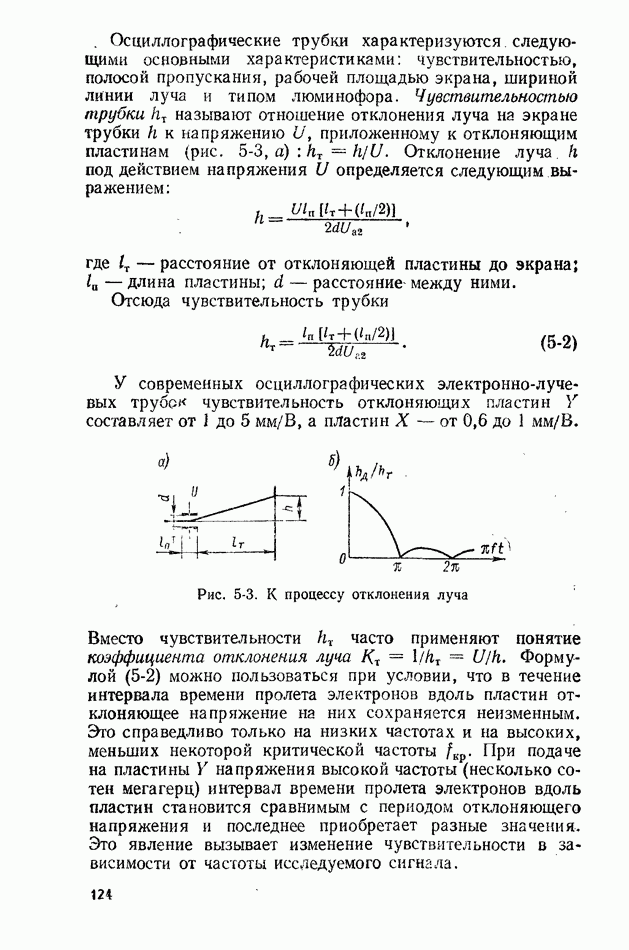
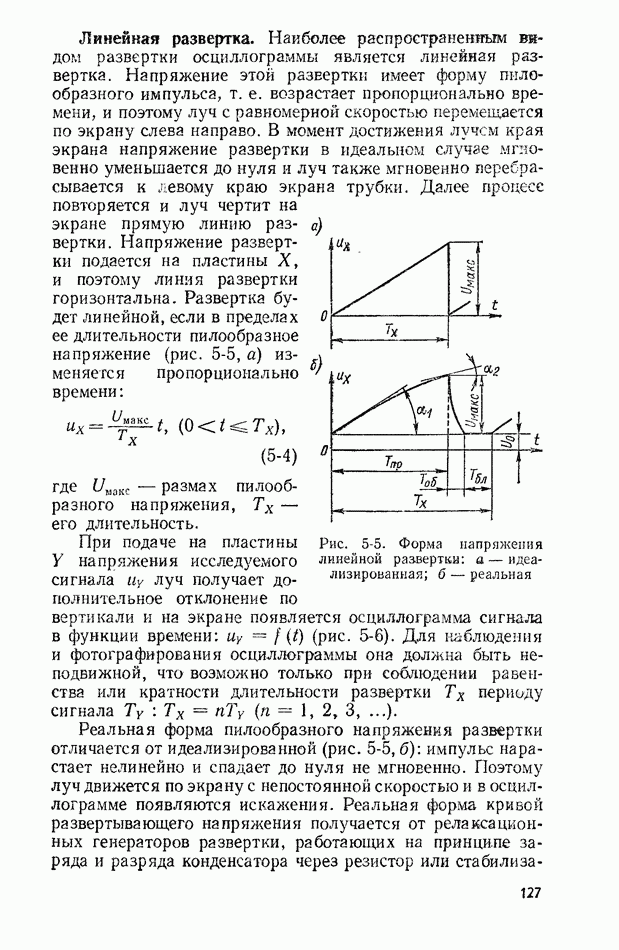
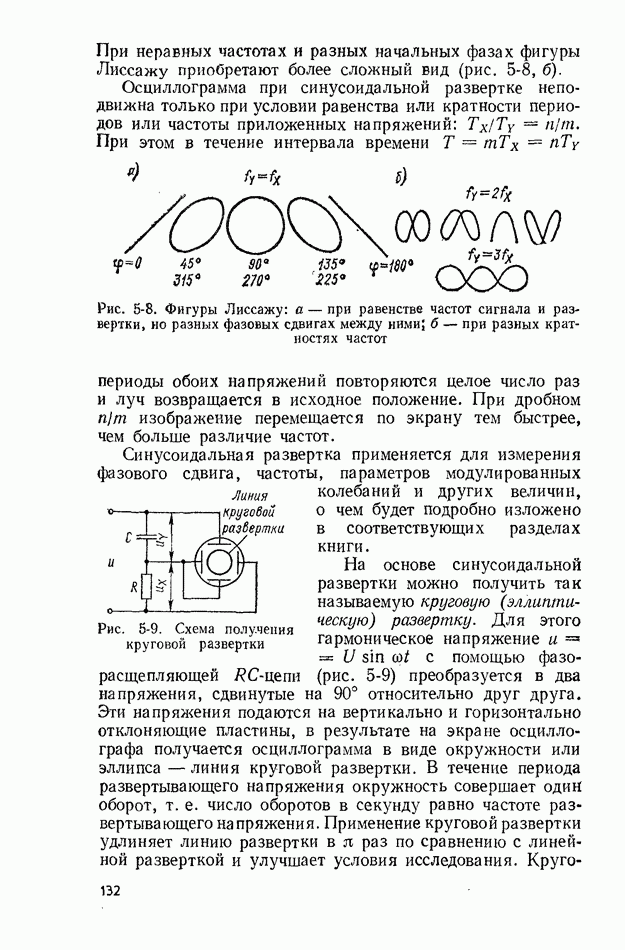
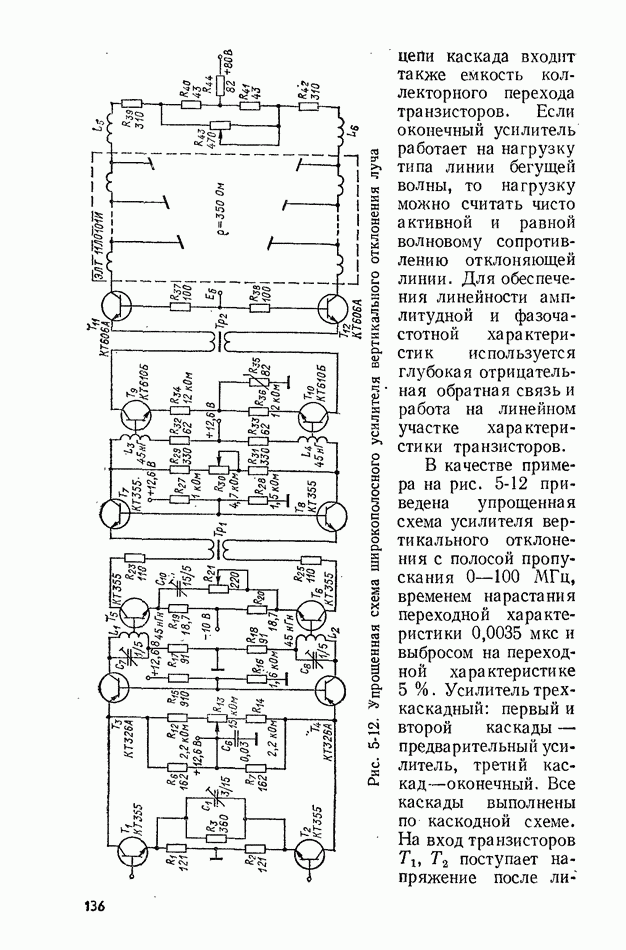
10-2. ИЗМЕРЕНИЕ МОМЕНТОВ
Измерение среднего значения. Этот момент первого порядка определяется по одной реализации длительностью  поэтому вместо значения, определяемого выражением (10-3), получим оценку среднего значения в виде
поэтому вместо значения, определяемого выражением (10-3), получим оценку среднего значения в виде

Измерение оценки среднего значения сводится к интегрированию случайного сигнала, которое можно выполнить с помощью известных
аналоговых интегрирующих устройств: магнитоэлектрических электроизмерительных приборов, интегрирующих RC-цепочек, фильтров нижних частот или интеграторов на базе усилителей постоянного тока. Для уменьшения погрешности измерения необходимо выбирать интервал времени усреднения значительно большим максимального интервала корреляции:  тк макс.
тк макс.
Это же измерение можно выполнить с помощью дискретных устройств, у которых интегрирование заменяется суммированием некоторого числа  дискретных значений реализации
дискретных значений реализации  так называемых выборок, интервал между которыми
так называемых выборок, интервал между которыми  тк макс:
тк макс:

Погрешность измерения тем меньше, чем больше 
Измерение средней мощности и дисперсии. В соответствии с формулой (10-4) оценка средней мощности (момента второго порядка) случайного стационарного эргодического сигнала может быть выражена так:

Измерение сводится к возведению значения сигнала  в квадрат и последующему усреднению. Эти операции выполняются с помощью вольтметров среднеквадратического (действующего) значения о открытым входом (см. § 3-3). Показание такого вольтметра
в квадрат и последующему усреднению. Эти операции выполняются с помощью вольтметров среднеквадратического (действующего) значения о открытым входом (см. § 3-3). Показание такого вольтметра

При возведении показания во вторую степень получим искомое значение оценки:  Применяемый вольтметр должен быть широкополосным с большой протяженностью квадратичного участка характеристики преобразования и значительным временем усреднения (например, микровольтметр
Применяемый вольтметр должен быть широкополосным с большой протяженностью квадратичного участка характеристики преобразования и значительным временем усреднения (например, микровольтметр 
Оценка дисперсии [см. формулу (10-6)] может быть измерена также электронным вольтметром среднеквадратического значения, но с закрытым входом; с помощью разделительного конденсатора исключается постоянная составляющая сигнала и измеряется только переменная. Показание вольтметра соответствует корню квадратному из дисперсии, т. е. среднеквадратическому отклонению о. Динамический диапазон используемого вольтметра должен быть значительным, так как в случайных сигналах возможны большие отношения пикового значения к среднеквадратическому. Дисперсию можно вычислить, как разность между средней мощностью сигнала и мощностью его постоянной составляющей.
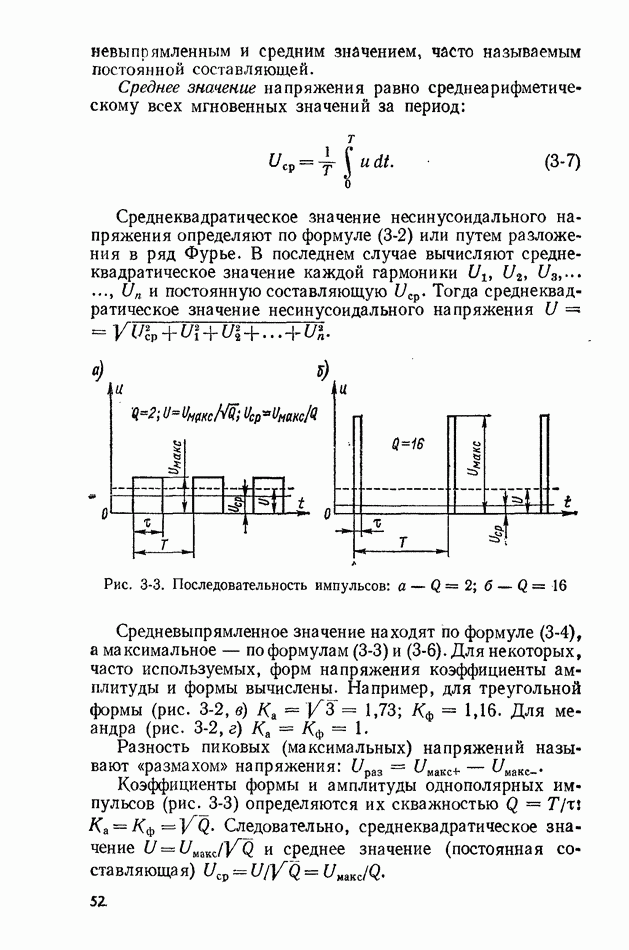
Средневыпрямленное значение случайного сигнала связано с его дисперсией через коэффициент формы  Значение
Значение  известно для различных законов распределения: например, для нормального закона
известно для различных законов распределения: например, для нормального закона  для равномерного 0,865. Следовательно, можно применить вольтметр средневыпрямленного
для равномерного 0,865. Следовательно, можно применить вольтметр средневыпрямленного
значепия, показания которого при измерении напряжения случайного сигкала в  и вычислить среднеквадратическое отклонение
и вычислить среднеквадратическое отклонение 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА ПЕРВАЯ. ОСНОВНЫЕ СВЕДЕНИЯ О СРЕДСТВАХ ИЗМЕРЕНИЙ
- 1-2. МЕРЫ ЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 1-3. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 1-4. ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
- 1-5. ИЗМЕРИТЕЛЬНЫЕ УСТАНОВКИ И СИСТЕМЫ
- 1-6. ОСНОВНЫЕ СВОЙСТВА СРЕДСТВ ИЗМЕРЕНИЯ
- 1-7. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ
- ГЛАВА ВТОРАЯ. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
- 2-2. СИСТЕМАТИЧЕСКИЕ ПОГРЕШНОСТИ
- 2-3. СЛУЧАЙНЫЕ ПОГРЕШНОСТИ
- 2-4. СУММИРОВАНИЕ ПОГРЕШНОСТЕЙ
- 2-5. ПОГРЕШНОСТЬ КОСВЕННЫХ ИЗМЕРЕНИЯ
- 2-6. НЕКОТОРЫЕ ПРАВИЛА ВЫПОЛНЕНИЯ ИЗМЕРЕНИЯ И ПРЕДСТАВЛЕНИЯ РЕЗУЛЬТАТОВ
- ГЛАВА ТРЕТЬЯ. ИЗМЕРЕНИЕ ТОКА И НАПРЯЖЕНИЯ
- 3-2. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АМПЕРМЕТРЫ И ВОЛЬТМЕТРЫ
- 3-3. ЭЛЕКТРОННЫЕ ВОЛЬТМЕТРЫ
- ГЛАВА ЧЕТВЕРТАЯ. ГЕНЕРАТОРЫ ИЗМЕРИТЕЛЬНЫХ СИГНАЛОВ
- 4-2. ГЕНЕРАТОРЫ СИГНАЛОВ ИНФРАНИЗКИХ И НИЗКИХ ЧАСТОТ
- 4-3. ГЕНЕРАТОРЫ СИГНАЛОВ ВЫСОКИХ И УЛЬТРАВЫСОКИХ ЧАСТОТ
- 4-4. ГЕНЕРАТОРЫ СИГНАЛОВ СВЕРХВЫСОКИХ ЧАСТОТ
- 4-5. ПОНЯТИЕ О СИНТЕЗАТОРАХ ЧАСТОТЫ
- 4-6. ГЕНЕРАТОРЫ ИМПУЛЬСНЫХ СИГНАЛОВ
- 4-7. ГЕНЕРАТОРЫ ШУМОВЫХ СИГНАЛОВ
- ГЛАВА ПЯТАЯ. ЭЛЕКТРОННО-ЛУЧЕВЫЕ ОСЦИЛЛОГРАФЫ
- 5-2. ЭЛЕКТРОННО-ЛУЧЕВЫЕ ТРУБКИ
- 5-3. ОСЦИЛЛОГРАФИЧЕСКИЕ РАЗВЕРТКИ
- 5-4. КАНАЛЫ УПРАВЛЕНИЯ ЛУЧОМ
- 5-5. КАЛИБРАТОРЫ АМПЛИТУДЫ И ДЛИТЕЛЬНОСТИ
- 5-6. СТРОБОСКОПИЧЕСКИЕ ОСЦИЛЛОГРАФЫ
- 5-7. НЕКОТОРЫЕ ОСОБЕННОСТИ ОСЦИЛЛОГРАФИЧЕСКИХ ИЗМЕРЕНИЙ
- ГЛАВА ШЕСТАЯ. ИЗМЕРЕНИЕ СПЕКТРА И ФОРМЫ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ
- 6-2. АНАЛИЗАТОРЫ СПЕКТРА ПОСЛЕДОВАТЕЛЬНОГО ДЕЙСТВИЯ
- 6-3. АНАЛИЗ СПЕКТРА В РЕАЛЬНОМ ВРЕМЕНИ
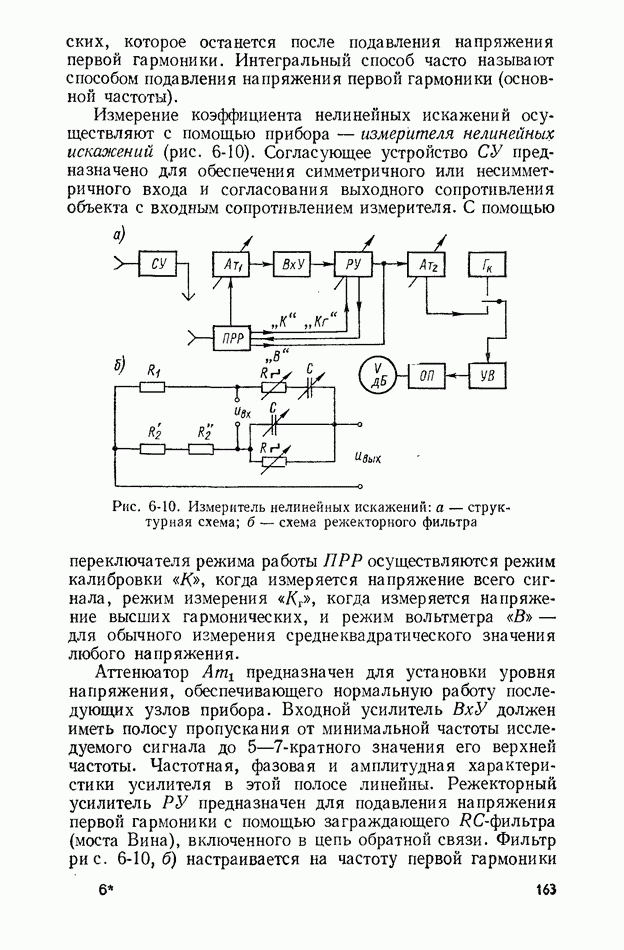
- 6-4. ИЗМЕРЕНИЕ НЕЛИНЕЙНЫХ ИСКАЖЕНИЙ
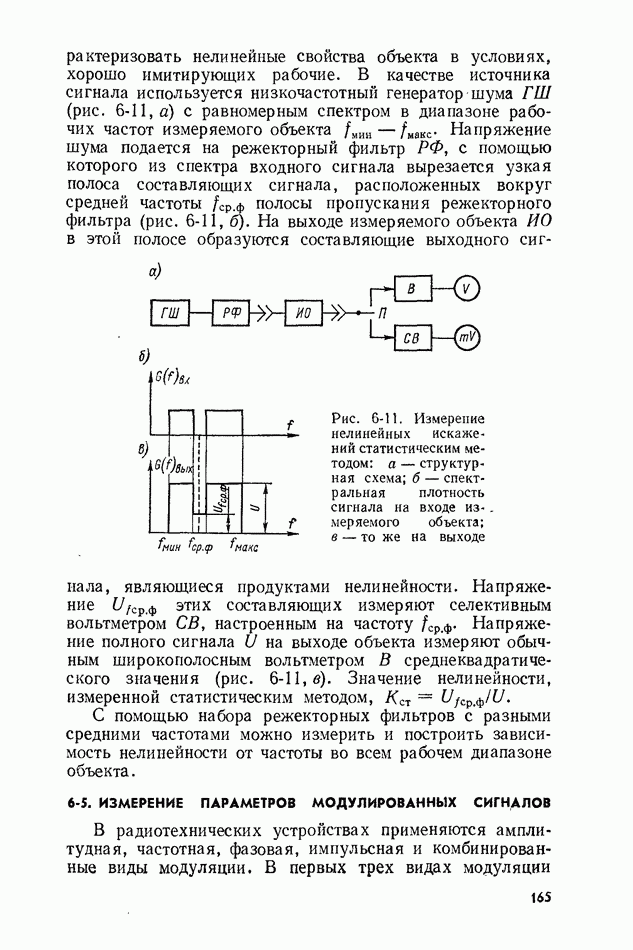
- 6-5. ИЗМЕРЕНИЕ ПАРАМЕТРОВ МОДУЛИРОВАННЫХ СИГНАЛОВ
- ГЛАВА СЕДЬМАЯ. ИЗМЕРЕНИЕ ФАЗОВОГО СДВИГА
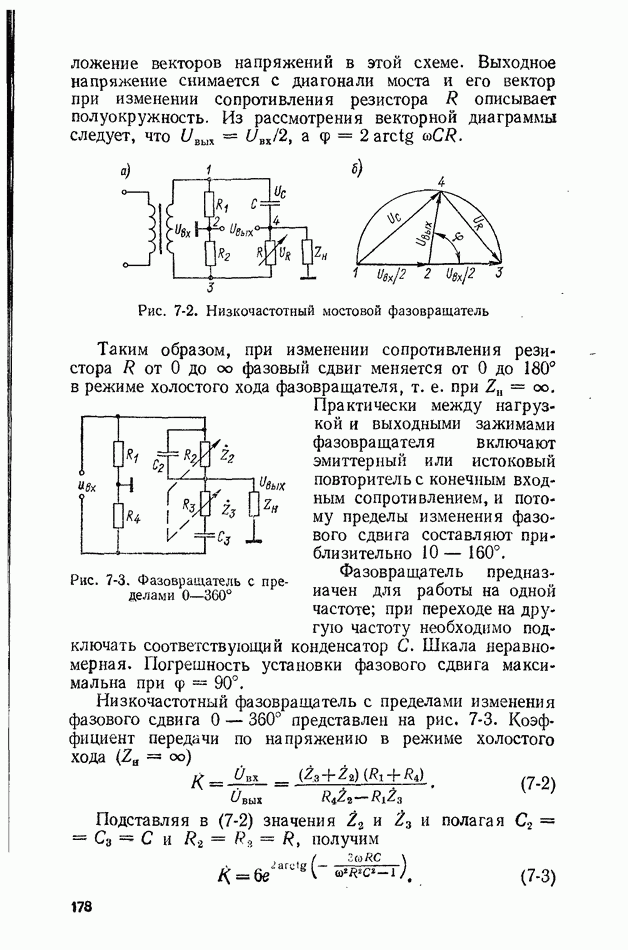
- 7-2. ФАЗОВРАЩАТЕЛИ
- 7-3. ОСЦИЛЛОГРАФИЧЕСКИЙ МЕТОД
- 7-4. КОМПЕНСАЦИОННЫЙ МЕТОД
- 7-5. МЕТОД ПРЕОБРАЗОВАНИЯ ФАЗОВОГО СДВИГА В ИМПУЛЬСЫ ТОКА
- 7-6. МЕТОД ДИСКРЕТНОГО СЧЕТА
- 7-7. ПРЕОБРАЗОВАНИЕ ЧАСТОТЫ ПРИ ИЗМЕРЕНИИ ФАЗОВОГО СДВИГА
- ГЛАВА ВОСЬМАЯ. ИЗМЕРЕНИЕ ЧАСТОТЫ И ИНТЕРВАЛОВ ВРЕМЕНИ
- 8-2. МЕТОД ПЕРЕЗАРЯДА КОНДЕНСАТОРА
- 8-3. РЕЗОНАНСНЫЙ МЕТОД
- 8-4. МЕТОД СРАВНЕНИЯ
- 8-5. МЕТОД ДИСКРЕТНОГО СЧЕТА
- 8-6. ПОНЯТИЕ О СТАНДАРТАХ ЧАСТОТЫ И ВРЕМЕНИ
- 8-7. ПРЕЦИЗИОННОЕ ИЗМЕРЕНИЕ ЧАСТОТЫ И ВРЕМЕНИ
- ГЛАВА ДЕВЯТАЯ. ИЗМЕРЕНИЕ МОЩНОСТИ
- 9-2. ИЗМЕРЕНИЕ ПОГЛОЩАЕМОЙ МОЩНОСТИ
- 5-3. ИЗМЕРЕНИЕ ПРОХОДЯЩЕЙ МОЩНОСТИ
- 9-4. ИЗМЕРЕНИЕ ВЕСЬМА МАЛОЙ МОЩНОСТИ
- ГЛАВА ДЕСЯТАЯ. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ СИГНАЛОВ
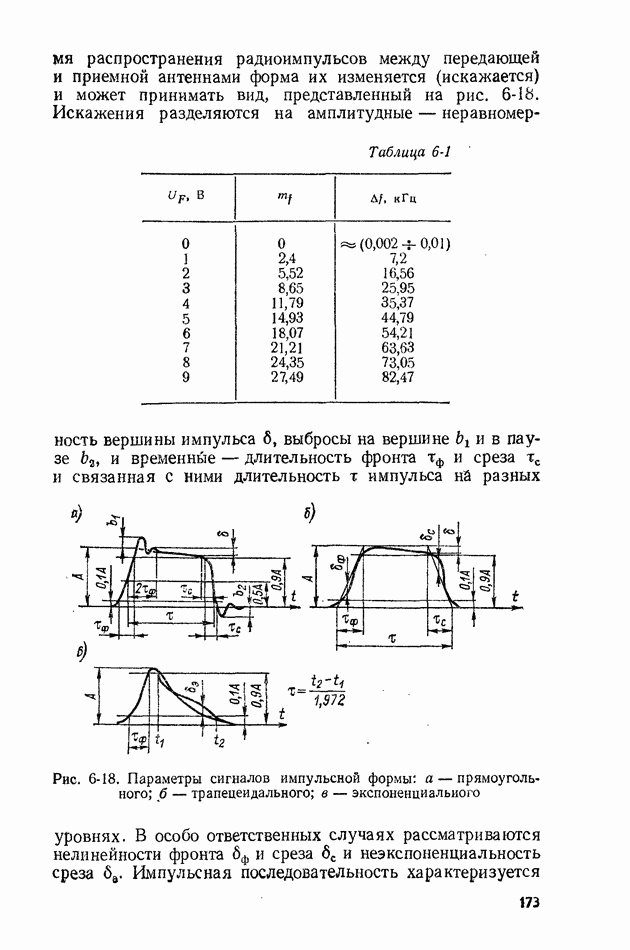
- 10-2. ИЗМЕРЕНИЕ МОМЕНТОВ
- 10-3. ИЗМЕРЕНИЕ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ
- 10-4. ИЗМЕРЕНИЕ ЭНЕРГЕТИЧЕСКОГО СПЕКТРА
- 10-5. ИЗМЕРЕНИЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ И ПЛОТНОСТИ ВЕРОЯТНОСТИ
- ГЛАВА ОДИННАДЦАТАЯ. ИЗМЕРЕНИЕ ПАРАМЕТРОВ ЭЛЕМЕНТОВ ЭЛЕКТРИЧЕСКИХ И РАДИОТЕХНИЧЕСКИХ УСТРОЙСТВ
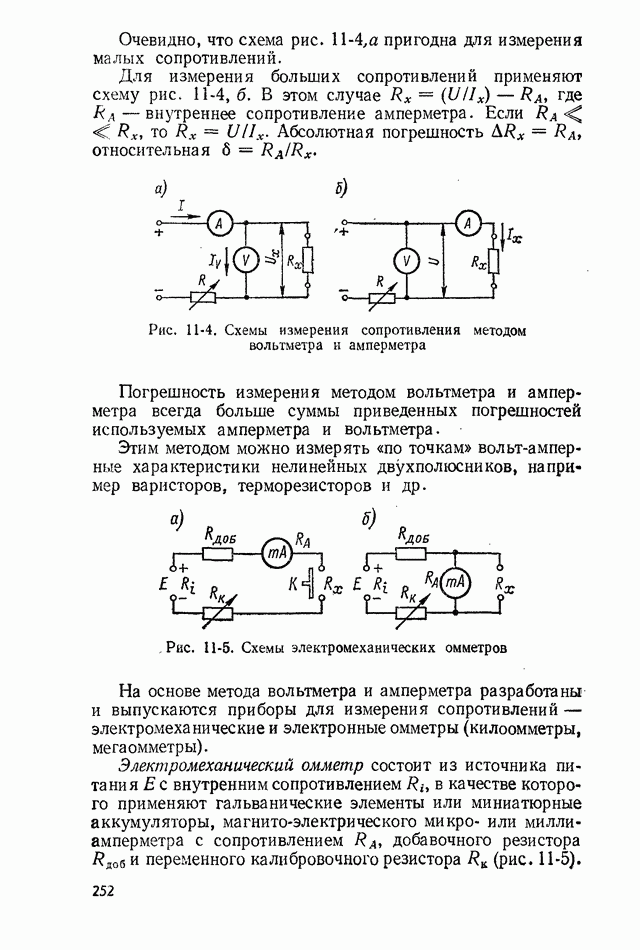
- 11-2. МЕТОД ВОЛЬТМЕТРА И АМПЕРМЕТРА
- 11-3. МОСТОВОЙ МЕТОД
- 11.4. РЕЗОНАНСНЫЙ МЕТОД
- 11-5. МЕТОД ДИСКРЕТНОГО СЧЕТА
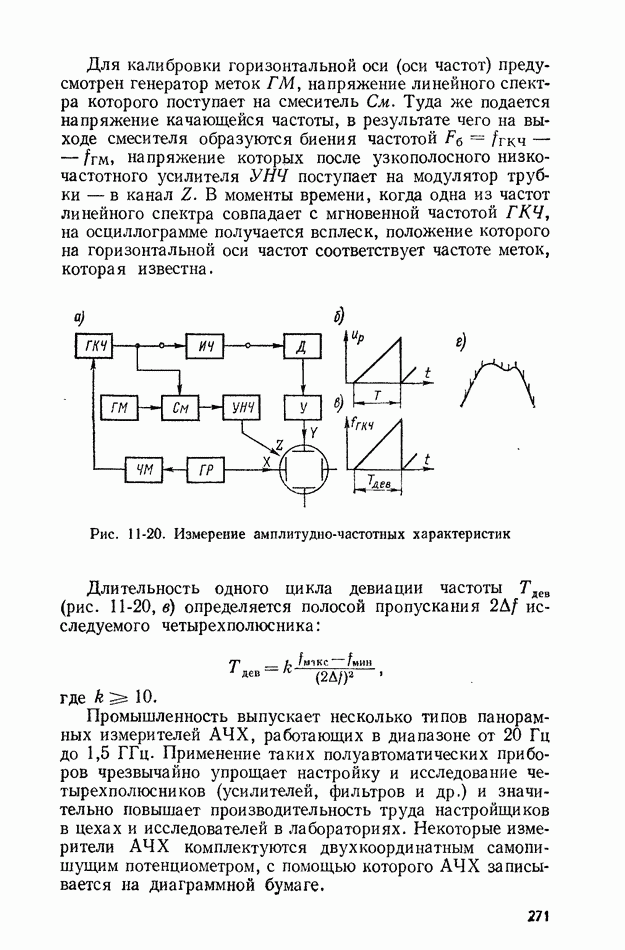
- 11-6. ИЗМЕРЕНИЕ АМПЛИТУДНО-ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 11-7. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК ИНТЕГРАЛЬНЫХ СХЕМ
- ГЛАВА ДВЕНАДЦАТАЯ. ИЗМЕРЕНИЕ ПАРАМЕТРОВ ЦЕПЕЙ СВЕРХВЫСОКИХ ЧАСТОТ
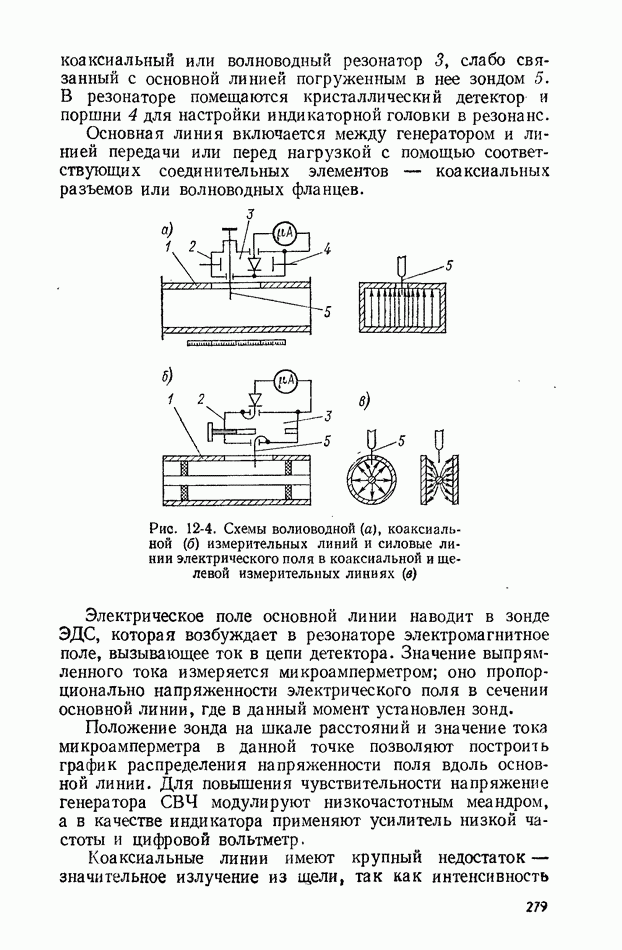
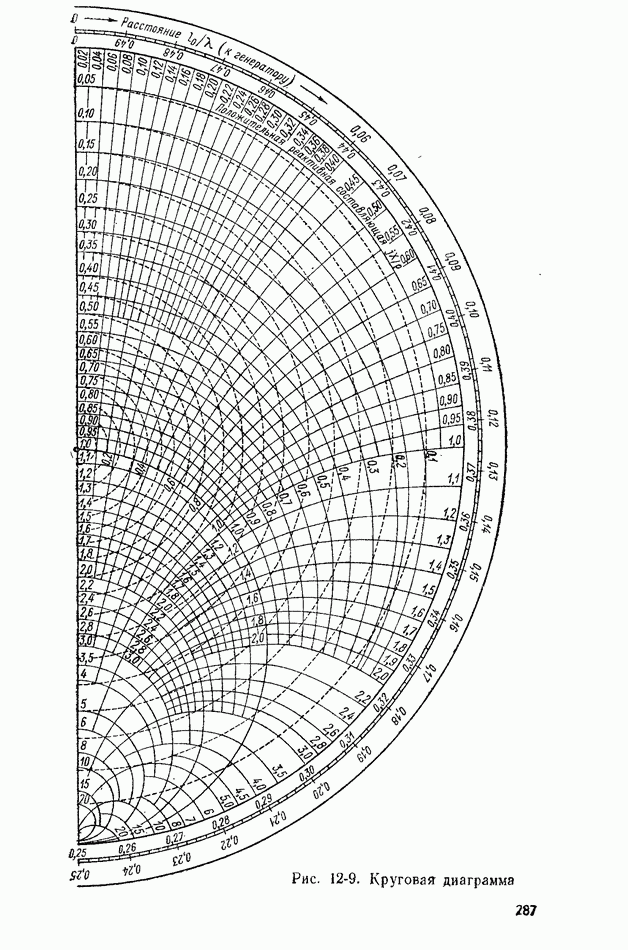
- 12-2. ИЗМЕРИТЕЛЬНЫЕ ЛИНИИ
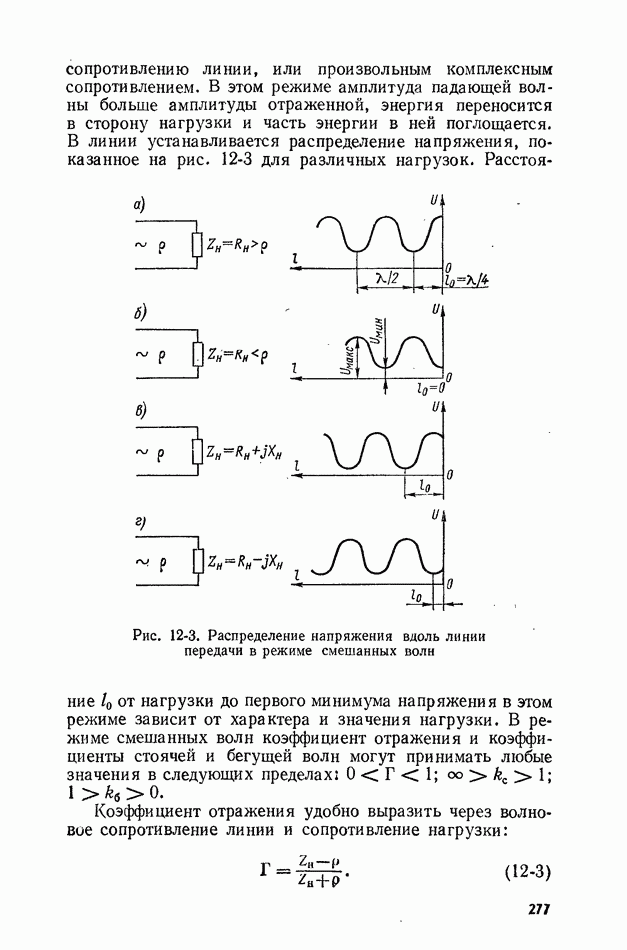
- 12-3. ИЗМЕРЕНИЕ КОЭФФИЦИЕНТА СТОЯЧЕЙ ВОЛНЫ И КОЭФФИЦИЕНТА ОТРАЖЕНИЯ
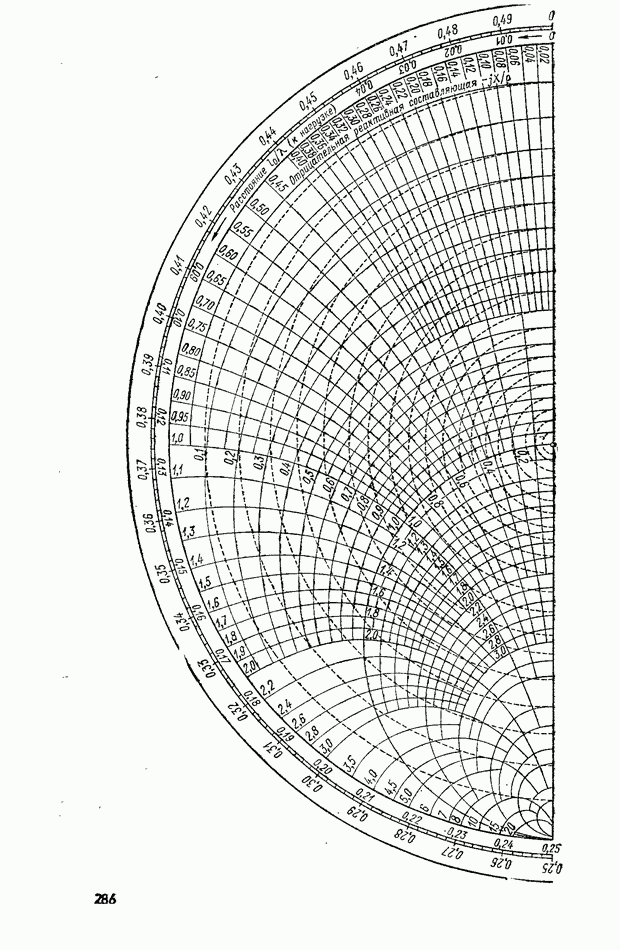
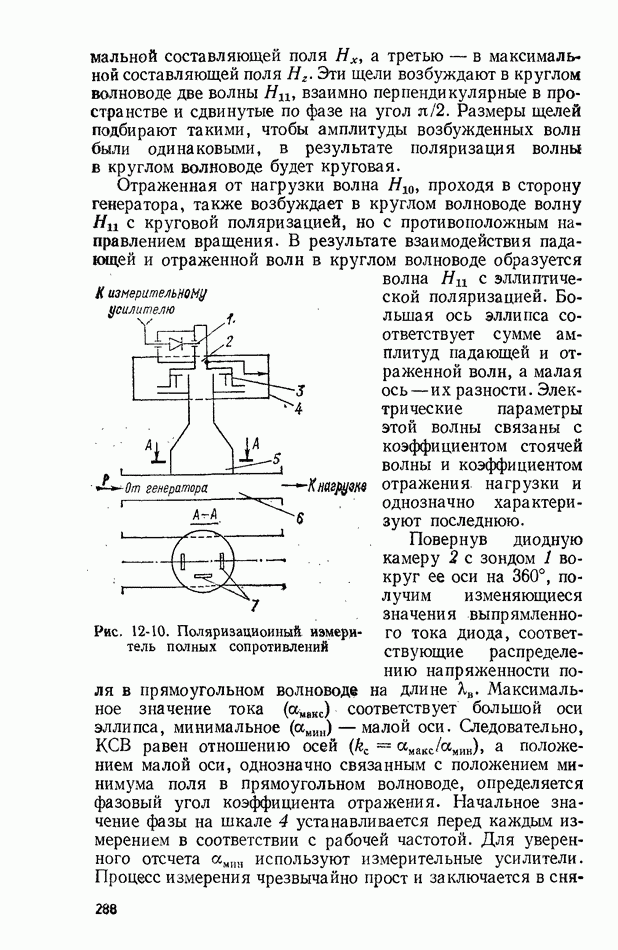
- 12-4. ИЗМЕРЕНИЕ ПОЛНОГО СОПРОТИВЛЕНИЯ
- 12-5. ИЗМЕРЕНИЕ НЕОДНОРОДНОСТИ
- ГЛАВА ТРИНАДЦАТАЯ. ИЗМЕРЕНИЕ ОСЛАБЛЕНИЯ
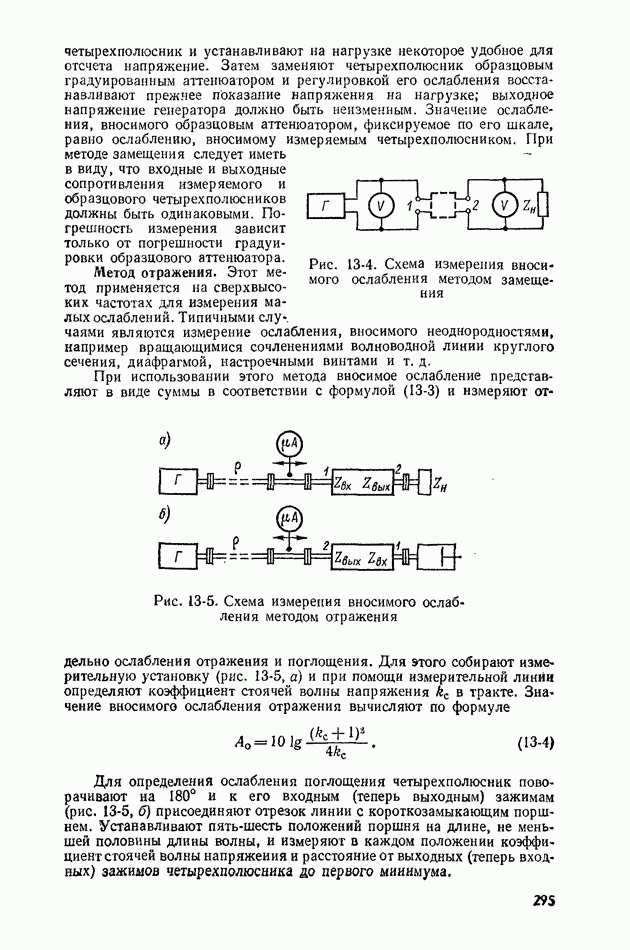
- 13-2. ИЗМЕРЕНИЕ ВНОСИМОГО ОСЛАБЛЕНИЯ
- 13-3. ИЗМЕРЕНИЕ СОБСТВЕННОГО ОСЛАБЛЕНИЯ
- ЗАКЛЮЧЕНИЕ
- ПРИЛОЖЕНИЕ П1
- ПРИЛОЖЕНИЕ 2. КЛАССИФИКАЦИЯ РАДИОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ